1 Introduction

Over twenty years ago, Turcotte and colleagues proposed the use of power-law probability distribution for the estimation of flood frequency (Turcotte 1994a,b; Turcotte and Greene 1993; Malamud and Turcotte 2003; Malamud and Turcotte 2006). Their main argument was that the power-law may offer a better fit to the tail of the distribution of high flows which is more relevant to floods. They demonstrated that the power-law based estimates of low probability of exceedance streamflow (floods) were systematically higher than those based on the standard method, in the United States, of using Log-Pearson Type III (LP3) distribution (IACWD 1982). This is understandable as the application of the standard method to a sample of annual maximum flows is biased low by including many values that, while representing annual maxima, are far from being flood-causing flows. Therefore, referring to the standard method as “flood frequency estimation” is a stretch, as there may be other high-flow events that are not considered. Clearly, there are good reasons for the standard method to be based on annual maxima. These reasons include both methodological aspects of extreme value theory as well as hydrological arguments of avoiding dependency due to the sub-annual hydrologic cycle scale. Many of the above issues have been extensively discussed in the literature and are not the main focus for this brief note.

Herein, we are motivated by two observations. The first one is the socio-economic aspect of the floods in Iowa. Over the past 60 years, there have been well over 1,200 presidential disaster declarations in the state with some counties receiving over twenty of them. This number comes as a surprise as one would expect that such declarations should result from infrequent, i.e. with low probability of occurrence, rather than common events. A quick application of binominal distribution suggests otherwise. This brings into question whether our estimates of flood occurrence probabilities and the resultant decisions regarding engineering design and regional development, including building permits, are biased low.

The second observation has to do with the ubiquitous presence of the power-laws (scaling) in hydrologic processes, in particular with respect to the spatial organization of peak flows in a basin (e.g. Gupta et al. 1994; Gupta et al. 2010; Ayalew et al. 2014a,b; Ayalew et al. 2015; Gupta et al. 2015; Perez et al. 2018a). Should a power-law be a consequence of the interactions of multifractal properties of rainfall and the scaling properties of water transport in self-similar river networks? While a comprehensive addressing of the above question requires concerted effort of a larger research community (e.g. Tessier et al. 1996; Pandey et al. 1998; Dawdy et al. 2012; Ayalew and Krajewski 2017; Perez et al. 2018b; Perez et al. 2019a,b; Merz et al. 2022; Hu et al. 2020; Miniussi et al. 2020), in this note we revisit the proposal of Turcotte and his colleagues (Turcotte and Green 1993; Turcotte 1994a,b; Malamud and Turcotte 2003; Malamud and Turcotte 2006) and study the application of the power-law over watersheds in Iowa. We limit the discussion to the at-site problem, i.e. estimation of the probability distribution of high flows given a record of observed discharge values. We address some methodological issues of distribution fitting and uncertainty estimation, which were neglected in the earlier studies.

Our note is organized as follows. In the next section, we briefly discuss the current method for Flood Frequency Estimation (FFE) in the United States as well as the procedure proposed by Turcotte and colleagues. We follow with a discussion of the power-law fitting approach and estimating the associated uncertainty. Finally, we compare the results of at-station quantiles with those obtained using the standard procedure. We close with conclusions and directions for future research.

2 Flood frequency estimation

In the United States, since the adoption of Bulletin 15 (United States Water Resources Council 1967) the LP3 distribution with the use of annual peak flow data fitted using the method of moments and a regional skew coefficient has been the standard approach to FFE. The LP3 is chosen because “It fits the data about as well as any of the other studied distributions” (Dawdy et al. 2012). This standardization provides a uniform procedure for national flood insurance programs, and allows for evaluation and comparison of flood frequency projects for design flow estimation. To provide a complete guide for analyzing peak flow frequency data at gauging site, the Interagency Advisory Committee on Water Data (IACWD) published Bulletin 17B “Guidelines for Determining the Flood Flow Frequency” (IACWD 1982). The recently revised guidelines have been published in Bulletin 17 C, and subsequently, discussed in later reports (e.g. England et al. 2018). Different federal agencies use it for different purposes. For example, the Federal Emergency Management Agency (FEMA) adopted LP3 for flood zoning activities, while the United States Geological Survey (USGS) uses it to determine regional flood quantiles for engineering design purposes (e.g. Flynn et al. 2006). Many local governments use it for issuing development permits. To date, U.S. federal agencies have continued to follow the standards set by the Advisory Committee on Water Data.

Following the Water Resources Council (WRC) guidelines, annual peak flow data are used for flood frequency analysis. The annual peak flows represent instantaneous discharge data for every water year. They are assumed to be serially independent events (e.g. Lye and Lin 1994; Bray and McCuen 2014; Wall and Englot 1985; Stedinger et al. 1993; Cohn et al. 2013). One problem with using annual peak flow data is that several floods in a given water year may be larger than the annual flood in another water year, and thus, the procedure ignores significant high flow events (e.g. Malamud and Turcotte 2006). To overcome this problem, partial duration series can be exploited which considers more than one flood event in a year (e.g. Rosbjerg 1985; Madsen et al. 1997; Morrison and Smith 2001; Pan et al. 2022). In the parlance of the statistical theory of the extremes, the above two approaches of selecting samples to be analyzed are known as block maxima and peaks-over-threshold (e.g. Coles 2001; Katz 2013). Another major assumption of the guidelines is that of stationarity of the underlying distribution of the stochastic mechanism generating annual peaks (England et al. 2018).

Over the past thirty years, research in geophysics revealed ubiquitous presence of the power-law relations. For example, natural hazards data that display power-law behavior include volcanic eruptions (Pyle 1998), earthquakes (Gutenberg and Richter 1944), forest fires (Malamud 1998), landslides (Guzzetti et al. 2002; Malamud 2004), lightning (Tsonis and Elsner 1987), extreme rainfall (Menabde at al. 1999), and floods (Kidson and Richards 2005; Kidson et al. 2006; Malamud and Turcotte 2006; Ayalew et al. 2014a,b; Ayalew and Krajewski 2017; Gupta et al. 1994). Regarding floods, a mechanistic proof (e.g. Newman 2005; Stumpf and Porter 2012) eludes researchers, despite evidence for the appropriateness of the power-law probability distribution ranging from streamflow data analysis (Tessier et al. 1996; Pandey et al. 1998) to the theory of extremes and the Generalized Extreme Value (GEV) distribution and the imprints of the scaling properties of the river networks (De Michele et al. 2002; Dawdy et al. 2012; Gupta et al. 2015). Search for such a proof is beyond the scope of this study, we just mention recent efforts by Perez et al. (2019a,b) that offer a plausible direction. Instead, we cast the Turcotte’s approach in formal statistical framework and complement it with uncertainty quantification.

2.1 Data source and study area

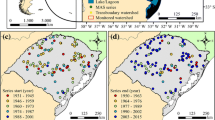
We use the streamflow record from 62 gauging USGS stations located in Iowa (Fig. 1), including both the annual peaks and daily discharge record. The drainage area of the stations.

Fig. 1
figure 1

The 62 USGS streamflow gauges which data were used in this study. The size of the circle indicates the upstream drainage area

Full size image

varies from approximately 65 to 20,000 km2. The criterion for choosing these stations out of some 300 stream gauges that the USGS operates or had operated in Iowa over time, is that they should have at least 50 years of data and are not subject to flow regulation or diversion. We used annual maximum flow data, coined AMS for Annual Maximum Series, for quantile estimation using the LP3 distribution and daily mean data for Turcotte’s partial duration series method (unless instantaneous date were available). Instantaneous discharge data are available from USGS only for recent years thus the use of daily means.

2.2 Revisiting turcotte’s method

According to Turcotte’s approach, for each station’s streamflow record, the maximum daily streamflow, Q1, is selected, and then 30 days are deleted on either side of the time series (Fig. 2).

Fig. 2
figure 2

 A schematic of peak flow selection from Turcotte’s method (T50). The shaded areas indicate the 50-day exclusion windows

Full size image

This value represents the largest flood in a time period. Next, the second largest flood Q2 is determined in the remaining time series, and again 30 days are deleted on either side. This process continues until we have the N peaks selected where N is equal to the number of years in the observed record. This limitation on the sample size is permitting a direct comparison with the annual flood series and the interpretation through the recurrence interval. Thus, the selected flood events are ordered in descending order and ranked. The probability of exceedance is estimated using Weibull plotting position (Weibull 1939). Note, that Turcotte (1994a) used daily mean discharge for the partial duration series selection in flood frequency analysis. We will return to this point in the Discussion.

Following Turcotte and Green (1993) and others, the power-law distribution used for flood frequency takes the form

$$Q\left(T\right)=C{T}^{\theta }$$
(1)

where Q(T) is the maximum discharge associated with a recurrence interval of T years, C is the intercept and θ is the exponent.

Turcotte and colleagues fit these parameters by a simple log-log regression. An implicit assumption in the Turcotte’s approach is that all the data selected come from the tail of the distribution and conform to the power-law. As the power-law is often sought to represent an approximation to the tail of a distribution, it applies for values above a certain threshold (e.g. Clauset et al. 2009). This threshold is either predetermined or estimated from the sample of the random variable. In the studies conducted by Turcotte and others, the threshold is simply the lowest value of the partial duration series.

We prefer to consider Turcotte’s approach in a more generalized and rigorous setting. We combine his procedure for selecting the sample of high flows with a formal framework of the power-law probability distribution fitting. We abstain from using the notion of recurrence interval and simply consider the quantiles of different probability of exceedance. Before we discuss fitting the distribution to a sample of floods, we would like to cast Turcotte’s notation into the standard probability distribution context. After simple manipulations, expression (1) is equivalent to

$$P\left(Q\right)={\left(\frac{Q}{C}\right)}^{-1/\theta }$$
(2)

where P is equal to 1/T and is the probability of exceedance, Q is the random variable (discharge), C and θ are regression coefficients. From here on out, we prefer to use the notation of Clauset et al. (2009)

$$P\left(x\right)={\left(\frac{x}{{x}_{min} }\right)}^{-\alpha +1}$$
(3)

where the power -α + 1 is equal to -1/θ, x is equal to Q, and xmin is equal to C. In general, the minimal flow peak over which the power-law holds (or may hold) is unknown and needs to be estimated or predefined. Also, while Turcotte used simple log-log regression to estimate \(\alpha\) and C, we use the maximum likelihood method (MLM) for parameter estimation. We applied the procedure proposed by Clauset et al. (2009) as it is based on the formal statistical approach and supported by an extensive simulation studies by the authors.

Following Clauset et al. (2009), the lower threshold can be estimated through an iterative procedure as follows. Select consecutive values of \({\widehat{x}}_{min}\) from the ordered sample, beginning with the smallest. Fit the power-law model to the values above \({\widehat{x}}_{min}\) using the MLM given in (Clauset et al. 2009). Calculate

$$D=\underset{x\ge {\widehat{x}}_{{min}}}{\text{max}}\left|S\left(x\right)-P\left(x\right)\right|$$
(4)

where P(x) is cumulative distribution function (CDF) of the power-law model that best fits the data in the region x>\({\widehat{x}}_{min}\), and S(x) is CDF of the data for the observations with value greater than or equal to \({\widehat{x}}_{min}\). D is the familiar Kolmogorov-Smirnov (KS) statistic. It turns out that often a rescaled version D* has better performance (Clauset et al. 2009):

$${D}^{*}=\underset{x\ge {\widehat{x}}_{{min}}}{\text{max}}\frac{\left|S\left(x\right)-P\left(x\right)\right|}{\sqrt{P\left(x\right)(1-P\left(x\right))}}$$
(5)

The final step of the procedure is selecting the value of \({\widehat{x}}_{min}\) for which D* is minimum.

Once xmin is estimated or predetermined, we use the MLM to estimate the exponent. The MLM leads to the following formula for the estimate ofα

$$\widehat{\alpha }=1+n{\left[{\sum }_{i=1}^{n}ln\frac{{x}_{i}}{{\widehat{x}}_{min}}\right]}^{-1}$$
(6)

where n is the size of the sample of values higher than xmin. In Turcotte’s original approach n is equal to N, the number of years of the streamflow record, and \({\widehat{x}}_{min}\) is the smallest value in the sample.

In this note, we coin the sample selected using the Turcotte’s approach, but unrestricted in size to the number of years in the data record, as T30 for the exclusion window of 30 days. Similarly, T50 implies the exclusion window of 50 days. Such selected samples are subject to the above parameter estimation procedure to determine α and xmin.

2.3 Uncertainty estimation

While the ML combined with the KS-based iterative approach works well for parameter estimation of the power-law distribution, assessing uncertainty in the estimates is difficult. A common approach that effectively addresses sampling uncertainty is Monte Carlo simulation. However, note that for our case all samples generated with the power-law with given parameters will have values above xmin. To overcome this problem, we offer a method based on the recently proposed family of generalized power-law distributions (GPL).

Prieto and Sarabia (2017) describe some 14 distributions that have nonlinear exponents and asymptotically converge to power-law tail. We explored several of them but here we present a model we found appropriate for the task. Consider a simple power transformation g(·).

$$g\left(\frac{x}{\sigma }\right)=\alpha {\left(\frac{x}{\sigma }\right)}^{\beta }$$
(7)

leading to a standard power-law for \(\beta =0\) and to

$$P\left(x\right)={\left(\frac{x}{\sigma }\right)}^{-\alpha {\left(\frac{x}{\sigma }\right)}^{\beta }},$$
(8)

for \(\beta >0\), where σ is a scale parameter.

The key idea is to fit this distribution (Eq. 8) to the Turcotte series of peak flows and generate numerous samples of the same size as the data from the fit distribution. Then, fit the power-law to the generated data obtaining a sampling distribution of the parameters α and xmin.

We show the joint-distribution of the two parameters based on 100,000 random samples in Fig. 3. The simulated data allows to establish the 95% confidence interval of α and xmin. Similarly, using the simulated data we estimate the sampling uncertainty for the flood quantiles based on the power-law model.

Fig. 3
figure 3

The 95% bivariate confidence domain based on a Monte Carlo simulation for various series types. The color bar represents the density of the Monte Carlo bivariate distribution. Station example is West Fork Cedar River at Finchford, Iowa

Full size image

2.4 Results of quantile estimation

Using the above methods of sample selection, parameter estimation and quantile uncertainty quantification, we analyzed data from the 62 stations in Iowa. We also used the annual maxima fitted with the standard methods given in Bulletin 17 C. We show examples of the results in Fig. 4.

Fig. 4
figure 4

Flow rate vs. probability of exceedance for two different watersheds of different sizes. The AMS (top) and T30 (bottom) flood frequency curves at two scales: small basin (left) and large basin (right). The tail (power-law aspect) of the data is marked in red, while the red shaded area shows the confidence intervals based on the GPL approach. The LP3 fit and confidence intervals are shown in blue for reference

Full size image

For low probability events, the power-law model estimates similar or larger values compared to current standards. Note, that the uncertainty of the power-law fit is much broader than that of the LP3 model. These conclusions follow what we know of the nature of fractals and thus, do not come as a surprise. These results are consistent with those obtained by Turcotte and colleagues over 25 years ago (Malamud and Turcotte 2006). If power-law distribution is the correct distribution for extreme flood events, there is even greater uncertainty and the potential for larger floods than previously thought.

In Fig. 5, we show the quantile to quantile comparisons for our 62 stations in Iowa. We plot the quantiles and their uncertainty based on our power-law model as well as the corresponding quantities for the current standards (England et al. 2018).

Fig. 5
figure 5

Comparing the flood quantiles with their confidence intervals (95%?) of larger, rarer events obtained from the power-law tail model (y-axis) and the standard LP3 model (x-axis) for the various types of flood frequency series included in this study (AMS: Annual Maximum Series; T50: Turcotte’s method with 50-day window; T30: Turcotte’s method with 30-day window)

Full size image

Comparing the 1% quantile commonly known as 100-year flood with the LP3 distribution, we find that Turcotte’s method (using T50) has resulted in conservative (higher) estimates. The conservative estimates of Turcotte’s method could be easily explained. Even if the sample size in the Turcotte’s method is the same as in the standard method, the included values are higher on average. Additionally, the power-law represents a better fit as it avoids being “pulled” down by values that corresponds to dry years and are far below the flooding regime. In contrast, the LP3 uses annual peak flow record but not all the annual peak flow events are floods.

3 Discussion

This short note neglects several important issues that deserve closer attention and focused investigation. Below we briefly highlight these issues. First, we acknowledge that B17C includes “Potentially-Influential Low Floods” (PILFs) and Perception Thresholds to avoid the problem of including very low values of annual maxima. This is similar, but not necessarily equivalent to estimating xmin in the power law distribution. At the same time the current standard method neglects the contribution of more than one peak flow observations in a given year, which is part of the contribution of this note.

Second, we address the importance of instantaneous daily peak flow. The USGS records include annual peak flow data for all years in the record and thus, the standard analysis of FFE is based on such values. In contrast, using a partial duration series, in the same manner as the Turcotte’s method might seem promising, such an approach faces a difficulty with regard to the data availability. The electronic data available on-line from the USGS for the period prior to 2007 are daily mean values only. Averaging of flow values might render values different (lower) from the actual peak flow during a given day. This effect is scale-dependent with the most pronounced effect occurring in small basins. The difference could be significant. The data shows that the expected relative error for basins larger than 10,000 km2 is 4%, for basins between 1,000 and 10,000 km2 is 20%, and for drainage areas less than 1,000 km2 is as large as 30%. One alternative to overcome this issue, is to estimate daily peaks from daily means (e.g. Chen et al. 2017). In this study, however, we have not adopted that approach, instead we replaced the selected maxima of daily values for the days when annual peak flow values were available.

One could argue against the strategy of replacing the daily means with the annual peaks, when available, on the basis that the instantaneous and averaged quantities have different statistical properties. However, we think that the recorded annual peaks are too valuable to be discarded (see section on paleo-floods and historical floods in Bulletin 17 C). Also, this substitution mainly affects the smallest spatial scales as for the larger scale the two quantities are very similar.

In this note, we did not address the issue of stationarity as we wanted to keep attention on the power-law fit. However, in a quick test, we did combine the Turcotte’s approach with the recommendation outlined in Coles (2001) and Katz (2013) where we modeled the parameters of the power-law as linear functions of time. As expected, for few stations where flood magnitudes seem to have been increasing over the past 50 years (Villarini et al. 2009), linear extrapolation leads to potentially high quantiles. This issue needs to be explored much more thoroughly and thus we do not include the results here.

Our results presented in this note are not meant to replace the current estimates of the at-site quantiles, they merely serve as an illustration of the potential of a revised methodology based on the power-law probability distribution. Our study contributes little to the long-standing question of the choice of an appropriate distribution for flood frequency estimation. Clearly, as discussed by Klemeš (2000a,b) and many others, we are not going to resolve this by simply analyzing small sets of data. A more productive, but also a difficult path, seems to be a mechanistic demonstration that leads to some specific distribution. In this vein, after Turcotte and others, nonlinearities and other features of the complex systems such as river basins suggest power law for the tails of the extreme floods distribution.