Abstract
The lace expansion is a powerful perturbative technique to analyze the critical behavior of random spatial processes such as the self-avoiding walk, percolation and lattice trees and animals. The non-backtracking lace expansion (NoBLE) is a modification that allows us to improve its applicability in the nearest-neighbor setting on the \(\mathbb {Z}^d\)-lattice for percolation, lattice trees and lattice animals. The NoBLE gives rise to a recursive formula that we study in this paper at a general level. We state assumptions that guarantee that the solution of this recursive formula satisfies the infrared bound. In two related papers, we show that these conditions are satisfied for percolation in \(d\ge 11\), for lattice trees in \(d\ge 16\) and for lattice animals in \(d\ge 18\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and results
1.1 Motivation
We use the non-backtracking lace expansion (NoBLE) to prove the infrared bound for several spatial models. The infrared bound implies mean-field behavior for these models. The classical lace expansion is a perturbative technique that can be used to show that the two-point function of a model is a perturbation of the two-point function of simple random walk (SRW). This result was used to prove mean-field behavior for self-avoiding walk (SAW) [26, 28], percolation [24, 29], lattice trees and lattice animals [25], oriented percolation [34], the contact process [33, 41] and the Ising model [42] in high dimensions.
Being a perturbative method in nature, applications of the lace expansion typically necessitate a small parameter. This small parameter is often the inverse of the degree of the underlying graph. There are two possible approaches to obtain a small parameter. The first is to work in a so-called spread-out model, where long-, but finite-range, connections over a distance L are possible, and we take L large. This approach has the advantage that the results hold, for L sufficiently large, all the way down to the critical dimension of the corresponding model. The second approach applies to the simplest and most often studied nearest-neighbor version of the model. For the nearest-neighbor model, the degree of a vertex is 2d, which has to be taken large in order to prove mean-field results.
For the self-avoiding walk (SAW) on the nearest-neighbor lattice, Hara and Slade (1991) [26, 28] proved the seminal result that dimension 5 is small enough for the lace expansion to be applied, thus that mean-field behavior holds in dimension \(d\ge 5\). This result is optimal in the sense that we do not expect mean-field behavior of SAW in dimension 4 and smaller. The dimension 4 thus acts as the upper critical dimension. Results in this direction, proving explicit logarithmic corrections, can be found in a series of papers by Brydges and Slade (some also with Bauerschmidt), see [11] and the references therein.
For percolation, we expect mean-field behavior for dimensions \(d>6\). Hara and Slade also proved this result down to \(d>6\) for the spread-out model with sufficiently large L [24, 29]. For the nearest-neighbor setting, Hara and Slade computed that dimension 19 is large enough. These computations were never published. Through private communication with Takashi Hara, the authors learned that in a recent rework of the analysis and implementation the result was further improved to \(d\ge 15\) for percolation.
To obtain the mean-field result also in smaller dimensions above the upper critical dimensions, we rely on the NoBLE. In the NoBLE, we explicitly take the interaction due to the last edge used into account. Doing this, we reduce the size of the involved perturbation drastically and are able to show the mean-field behavior for dimensions closer to the upper critical dimension.
In this paper, we formalize a number of assumptions on the general model and prove that under these assumptions the two-point function obeys the infrared bound. The derivation of the model-dependent NoBLE and the verification of the assumptions are not part of this article. We use the generalized analysis to obtain mean-field behavior for the following models: lattice trees in \(d\ge 16\) and lattice animals in \(d\ge 18\) [17], and percolation in \(d\ge 11\) [18].
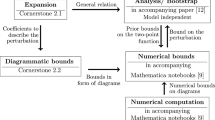
A NoBLE analysis consists of four steps: Firstly, for a given model, we derive the perturbative lace expansion. Secondly, we prove diagrammatic bounds on the perturbation. Thirdly, we analyze the expansion to conclude the infrared bound given certain assumptions on the expansion. In our analysis, we derive diagrammatic bounds on the lace-expansion coefficients in terms of simple random walk integrals, which can be computed explicitly. This allows us to compute numerical bounds on the lace expansion coefficients. The fourth step consists of the numerical computation of these SRW-integrals.
In the accompanying papers [17, 18], we perform the first two steps for percolation, as well as for lattice trees and lattice animals. In this paper and in a model-independent way, we perform the analysis in the third step and explain the numerical computations of the fourth step. The numerical computations and the explicit checks of the sufficient conditions for the NoBLE analysis to be successful are done in Mathematica notebooks that are available on the website of Robert Fitzner [14].
The analysis presented in this paper is an enhancement of the analyses performed by Hara and Slade in [27] (see also [24, 25, 28, 29] for related work by Hara and Slade), and by Heydenreich, the second author and Sakai in [32]. This paper is organized as follows: In Sect. 1.2, we first introduce simple random walk (SRW) and non-backtracking walk (NBW). In Sect. 1.4 we state the two basic NoBLE relations that are perturbed versions of relations describing the NBW. Then, we state the results for percolation, lattice trees and lattice animals proved in [17, 18].
In Sect. 2, we first explain the idea of the proof at a heuristic level. Then, we state all assumptions required to perform the analysis in the generalized setting and state the result we prove in this document, namely the infrared bound. We close in Sect. 2.5 with a discussion of our approach.
In Sect. 3, we prove the technical cornerstone of the analysis, namely, that we can perform the so-called bootstrap argument. For the analysis in Sects. 2–3, we use a simplified NoBLE form of the two-point function that allows us to present the analysis in a clearer way. Thus, we also state the assumptions in Sect. 2.2 in terms of this simplified characterization.
In Sect. 4, we explain how to derive the simplified NoBLE equation starting from the NoBLE equation for the two-point function, and reformulate the assumptions of Sect. 2.2 into assumptions on the NoBLE coefficients that are derived and bounded in the accompanying papers [17, 18].
Section 5 is devoted to the numerical part of the computer-assisted proof. We explain how we compute bounds on the required SRW-integrals. In Sect. 5.3, we explain the ideas to bound the NoBLE coefficients that are used for all models that we consider. We end this paper with a general discussion.
1.2 Random walks
We begin by introducing the random walk models that we perturb around and fix our notation.
1.2.1 Simple random walk
Simple random walk (SRW) is one of the simplest stochastic processes imaginable and has proven to be useful in countless applications. For a review of SRW and related models, we refer the reader to [35, 37, 44].
An n-step nearest-neighbor simple random walk on \(\mathbb {Z}^d\) is an ordered \((n+1)\)-tuple \(\omega =(\omega _0,\omega _1,\omega _2,\dots , \omega _n)\), with \(\omega _i\in \mathbb {Z}^d\) and \(\Vert \omega _i-\omega _{i+1}\Vert _1=1\), where \(\Vert x\Vert _1=\sum _{i=1}^d |x_i|\). Unless stated otherwise, we take \(\omega _0={\vec {0}}=(0,0,\dots ,0)\). The step distribution of SRW is given by
where \(\delta \) is the Kronecker delta. For two functions \(f,g:\mathbb {Z}^d\mapsto \mathbb {R}\) and \(n\in \mathbb {N}\), we define the convolution \(f\star g\) and the n-fold convolution \(f^{\star n}\) by
and
We define \(p_n(x)\) as the number of n-step SRWs with \(\omega _n=x\), so that, for \(n\ge 1\),
We analyze this function using Fourier theory. For an absolutely summable function f, we define the Fourier transform of f by
where \(k\cdot x=\sum ^d_{i=1} k_ix_i\), with inverse
We use the letter k exclusively to denote values in the Fourier dual space \((-\pi ,\pi )^d\). We note that the Fourier transform of \(f^{\star n}(x)\) is given by \(\hat{f}(k)^n\) and conclude that
The SRW two-point function is given by the generating function of \(p_n\), i.e., for \(z\in \mathbb C\),
in x-space and k-space, respectively. We denote the SRW susceptibility by
with critical point \(z_c=1/(2d)\). By the form of \(\hat{C}_z(k)\) in (1.8) and using that \(1-\cos (t)\approx t^2/2\) for small \(t\in \mathbb {R}\), we see that \(\hat{C}_{z_c}(k)=[1-\hat{D}(k)]^{-1}\approx 2d / \Vert k\Vert ^2_2\) for small k, where \(\Vert \cdot \Vert _2\) denotes the Euclidean norm. Since small k correspond to large wave lengths, the above asymptotics is sometimes called the infrared asymptotics. The main aim in this paper is to formulate general conditions under which the infrared bound is valid for general spatial models.
1.2.2 Non-backtracking walk
If an n-step SRW \(\omega \) satisfies \(\omega _i\not =\omega _{i+2}\) for all \(i=0,1,2,\dots ,n-2\), then we call \(\omega \) non-backtracking. In order to analyze non-backtracking walk (NBW), we derive an equation similar to (1.4). The same equation does not hold for NBW as it neglects the condition that the walk does not revisit the origin after the second step. For this reason, we introduce the condition that a walk should not go in a certain direction \(\iota \) in its first step.
We exclusively use the Greek letters \(\iota \) and \(\kappa \) for values in \(\{-d,-d+1,\dots ,-1,1,2,\dots ,d\}\) and denote the unit vector in direction \(\iota \) by \({e}_{\iota }\in \mathbb {Z}^d\), e.g. \(({e}_{\iota })_i=\text {sign}(\iota ) \delta _{|\iota |,i}\).
Let \(b_n(x)\) be the number of n-step NBWs with \(\omega _0=0,\omega _n=x\). Further, let \(b^{\iota }_{n}(x)\) be the number of n-step NBWs \(\omega \) with \(\omega _n=x\) and \(\omega _1 \not ={e}_{\iota }\). Summing over the direction of the first step we obtain, for \(n\ge 1\),
Further, we distinguish between the case that the walk visits \(-{e}_{\iota }\) in the first step or not to obtain, for \(n\ge 1\),
The NBW two-point functions \(B_z\) and \(B^{\iota }_{z}\) are defined as the generating functions of \(b_n\) and \(b_n^{\iota }\), respectively, i.e.,
Using (1.10) and (1.11) for the two-point functions gives
Taking the Fourier transform, we obtain
In this paper, we use \({\mathbb C}^{2d}\)-valued and \({\mathbb C}^{2d}\times {\mathbb C}^{2d}\)-valued functions. For a clear distinction between scalar-, vector- and matrix-valued quantities, we always write \({\mathbb C}^{2d}\)-valued functions with a vector arrow (e.g. \(\vec v\)) and matrix-valued functions with bold capital letters (e.g. \(\mathbf{M}\)). We do not use \(\{1,2,\dots ,2d\}\) as index set for the elements of a vector or a matrix, but use \(\{-d,-d+1,\dots ,-1,1,2,\dots ,d\}\) instead. Further, for a \(k\in (-\pi ,\pi )^d\) and negative index \(\iota \in \{-d,-d+1,\dots ,-1\}\), we write \(k_\iota =-k_{|\iota |}\).
We denote the identity matrix by \(\mathbf{I}\in {\mathbb C}^{2d\times 2d}\) and the all-one vector by \( {\vec {1}} =(1,1,\dots ,1)^T\in {\mathbb C}^{2d}\). Moreover, we define the matrices \(\mathbf{J},{\hat{\mathbf{D}}}(k)\in {\mathbb C}^{2d\times 2d}\) by
We define the vector \(\vec {\hat{B}}_{z}(k)\) with entries \((\vec {\hat{B}}_{z}(k))_\iota =\vec {\hat{B}}^{\iota }_{z}(k)\) and rewrite (1.14) as
We use \(\mathbf{J}\mathbf{J}=\mathbf{I}\) and \({\hat{\mathbf{D}}}(k){\hat{\mathbf{D}}}(-k)=\mathbf{I}\) to modify the second equation as follows:
which implies that
We use \(\mathbf{J}{\vec {1}}={\vec {1}}\) and then combine (1.18) with the first equation in (1.16) to obtain
Then, we use that
and \({\vec {1}}^T{\hat{\mathbf{D}}}(-k){\vec {1}}=2d\hat{D}(k)\) to conclude that
The NBW susceptibility is \(\chi ^\mathrm{ \scriptscriptstyle NBW}(z)=\hat{B}_{z}(0)\) with critical point \(z_c=1/(2d-1)\). The NBW and SRW two-point functions are related by
so that
This link allows us to compute values for the NBW two-point function in x- and k-space. A detailed analysis of the NBW, based on such ideas, can be found in [16].
1.3 General setting
We consider general models defined on the d-dimensional hypercubic lattice \(\mathbb {Z}^d\). For these models, the two-point function \(G_z:\mathbb {Z}^d\mapsto \mathbb {R}\) is the central quantity. The two-point function is defined for parameters \(z\in [0,z_c)\) where \(z_c\) acts as the critical value. As for the SRW and NBW, the susceptibility \(\hat{G}_z(0)\) diverges as z approaches \(z_c\) from below. The behavior of \(G_z\) and \(\hat{G}_z\) as \(z\nearrow z_c\) is of special interest. We use the NoBLE to prove that the two-point function of the general model is a small perturbation of the critical NBW two-point function (1.23) and thereby obeys the infrared bound.
To do this, we define \(G^\iota _z\) as the two-point function of the model where \(e_{\iota }\) is being avoided. The precise definition depends on the model. For NBW, \(e_{\iota }\) is avoided in the first step, for percolation \(G^\iota _z\) is the two-point function of the model defined on the graph \(\mathbb {Z}^d{\setminus }\{{e}_{\iota }\}\). For the NBW, these two-point functions are linked by the relations (1.13). In the NoBLE, we adapt these two relations for the general model with model-dependent perturbations, and bound the arising perturbation coeffcients. For \(d\ge 2\), the NoBLE gives rise to functions \(\Xi _z,\Xi ^{\iota }_z,\Psi ^{\iota }_z\) and \(\Pi ^{\iota ,\kappa }_z\) for \(\iota ,\kappa \in \{\pm 1,\dots ,\pm d\}\), all mapping from \(\mathbb {Z}^d\) to \(\mathbb {R}\), and a function \(\mu _z:\mathbb {R}_+ \rightarrow \mathbb {R}_+\), such that, for all \(x\in \mathbb {Z}^d\) and \(z\in [0,z_c)\),
In our applications, the variable \(\mu _z\) is closely related to the main parameter z, but it is not equal. Therefore, in the analysis we use a second parameter \(\bar{\mu }_z\) that allows us to control the critical value in the models under consideration. For example, for percolation we use
(See Sect. 1.4.1, where the percolation model is formally introduced.)
Our goal is to understand the behavior of \(G_z\), where we consider the functions \(\mu _z, \Xi _z, \Xi ^{\iota }_z,\) \(\Psi ^{\iota }_z,\Pi ^{\iota ,\kappa }_z\) as given. Applying the Fourier transformation on (1.24) and (1.25) gives
We define the vectors \(\vec {\hat{G}}_z(k),\vec {\hat{\Xi }}(k)\) and \(\vec {\hat{\Psi }}(k)\) and the matrix \(\hat{{\varvec{\Pi }}}_z(k)\) by
Then, we can rewrite (1.28) using vectors and matrices as
We obtain from this that
That this matrix inverse is well defined will be shown in Sect. 4.3. Next, we rewrite (1.27) in vector-matrix notation and solve for \(\hat{G}_z(k)\) as
with
When comparing (1.32)–(1.34) to its equivalent for NBW in (1.19), we see that (1.32) reduces to (1.19) when taking \(\mu _z=z, \hat{\Xi }_z(k)=(\vec {\hat{\Psi }}_z(k))_\kappa =(\hat{{\varvec{\Pi }}}_z(k))_{\iota ,\kappa }=(\vec {\hat{\Xi }}_z(k))_\kappa =0\) for all \(z,k,\iota ,\kappa \). Our analysis is based on the intuition that the NoBLE coefficients are small in high dimensions. The majority of our work is to quantify this statement.
Rewrite of the two-point function We use another characterization of the two-point function \(\hat{G}_z(k)\) to perform the analysis. We extract all contributions involving constants and \(\hat{D}(k)\), by defining \(c_{{ \scriptscriptstyle F},z},c_{{ \scriptscriptstyle \Phi },z},\alpha _{{ \scriptscriptstyle \Phi },z},\alpha _{{ \scriptscriptstyle F},z},\hat{R}_{{ \scriptscriptstyle \Phi },z}(k),\hat{R}_{{ \scriptscriptstyle F},z}(k)\) such that
Then,
In Sect. 4, we show how we transform (1.33)–(1.34) into (1.35)–(1.36). Up to that point, we only work with the representation (1.35)–(1.36) as it simplifies and shortens the analysis. The quantity in (1.37) reduces to the NBW-equivalent (1.21), when we set \(\alpha _{{ \scriptscriptstyle \Phi },z}=\hat{R}_{{ \scriptscriptstyle F},z}(k)=\hat{R}_{{ \scriptscriptstyle \Phi },z}(k)=0\) and \(c_{{ \scriptscriptstyle \Phi },z}=1-z^2,\alpha _{{ \scriptscriptstyle F},z}=2d z, \hat{\Phi }_z(0)/\hat{G}_z(0)=1+(2d-1)z^2-2d z\).
1.4 Results for specific models
In this section, we describe the results that our method allows to prove. These results are proved in two accompanying papers [17, 18].
1.4.1 Percolation
Percolation is a central model in statistical physics and is a very active field of research since its rigorous definition by Broadbent and Hammersley in 1957 [10], where this model was proposed to describe the spread of a fluid through a medium. General references for percolation are [6, 20, 36]. A review of recent results can be found in [21, 31] and the references therein. We consider Bernoulli percolation on the hypercubic lattice. We use the definition of [43, Section 9]: To each nearest-neighbor bond \(\{x,y\}\) we associate an independent Bernoulli random variable \(n_{\{x,y\}}\) which takes the value 1 with probability p and the value 0 with probability \(1-p\), where \(p\in [0,1]\). If \(n_{\{x,y\}}=1\), then we say that the bond \(\{x,y\}\) is open, and otherwise we say that it is closed. A configuration is a realization of the random variables of all bonds. The joint probability distribution is denoted by \(\mathbb {P}_p\) with corresponding expectation \(\mathbb {E}_p\).
We say that x and y are connected, denoted by \(x\longleftrightarrow y\), when there exists a path consisting of open bonds connecting x and y, or when \(x=y\). We denote by \({\mathscr {C}}(x)\) the random set of vertices connected to x and denote its cardinality by \(|{\mathscr {C}}(x)|\). The two-point function \(\tau _p(x)\) is the probability that 0 and x are connected, i.e.,
By translation invariance \(\mathbb {P}_p (x \longleftrightarrow y)=\tau _p(x-y)\) for all \(x,y\in \mathbb {Z}^d\). We define the percolation susceptibility, or expected cluster size, by
We say that the system percolates when there exists a cluster \({\mathscr {C}}(x)\) such that \(|{\mathscr {C}}(x)|=\infty \). We define \(\theta (p)\) as the probability that the origin is part of an infinite cluster, i.e.,
For \(d\ge 2\), there exists a critical value \(p_c\in (0,1)\) such that
Menshikov in 1986 [39], as well as Aizenmann and Barsky in 1987 [2], have proven that the critical value can alternatively be characterized as
The percolation probability \(p\mapsto \theta (p)\) is clearly continuous on \([0,p_c)\), and it is also continuous (and even infinitely differentiable) on \((p_c,1]\) by the results of [5] (for infinite differentiability of \(p\mapsto \theta (p)\) for \(p\in (p_c,1]\), see [40]). Thus, the continuity of \(p\mapsto \theta (p)\) on \(\mathbb {Z}^d\) is equivalent to the statement that \(\theta (p_c(d))=0\).
Critical exponents We introduce three critical exponents for percolation. It is widely believed that the following limits exist in all dimensions:
A strong form of (1.43)–(1.45) is that there exist constants \(c_\chi , c_\theta ,c_\delta \in (0,\infty )\) such that
and is expected to hold in all dimensions, expect for the critical dimension \(d=d_c\), where logarithmic corrections are predicted. The constants \(c_\chi , c_\theta \) and \(c_\delta \) depend on the dimension. We say that these exponents exist in the bounded-ratio sense when the asymptotics is replaced with upper and lower bounds with different positive constants. Further, it is believed that there exist \(\eta \) and \(c_1, c_2\) such that
where \(c_1\) and \(c_2\) depend on the dimension only. For percolation, the existence of many more exponents is conjectured and partially also proven. See [20, Section 2.2] for more details. Our main result for percolation is formulated in the following theorem:
Theorem 1.1
(Infrared bound for percolation) The infrared bound \(\hat{\tau }_{p_c}(k)\le A_2(d)/[1-\hat{D}(k)]\) for some constant \(A_2(d)\) holds for nearest-neighbor percolation in dimension d satisfying \(d\ge 11\). As a result, the critical exponents \(\gamma ,\beta ,\delta \) and \(\eta \) exist in the bounded-ratio sense and take their mean-field values \(\gamma =\beta =1\), \(\delta =2\) and \(\eta =0\).
Theorem 1.1 is proved by combining the model-independent results proved in this paper, with the model-dependent results as proved in [18]. There, we also state and prove related results on percolation, such as the existence of the so-called incipient infinite cluster and the existence of one-arm critical exponents. Further, we derive numerical upper bounds on the critical percolation probability \(p_c(d)\).
The critical exponents for percolation have received considerable attention in the literature. For the critical exponents, it is known that \(\beta \le 1\) and \(\gamma \ge 1\) for all \(d\ge 2\), see Chayes and Chayes [13] and Aizenman and Newman [3]. Further, we know that if \(\beta \) and \(\gamma \) exists, then \(\beta \in (0,1]\) and \(\gamma \in [1,\infty )\), see [20, Sections 10.2, 10.4]. In high dimensions, we expect mean-field behavior for percolation. Namely, we expect that for all dimensions \(d>6\), the critical exponents correspond to the exponents of the regular tree given by \(\gamma =\beta =1\), and \(\eta =0\). (For the definition of \(\eta \) for percolation on trees, see Grimmett [20, Section 10.1].) Alternatively, we can interpret \(\gamma =\beta =1\), and \(\eta =0\) as the critical exponents for branching random walk, see the discussion in [31]. An important step to prove mean-field behavior for percolation is the result of Aizenman and Newman [3] that the finiteness of the triangle diagram, defined by
implies that \(\gamma = 1\). This triangle condition also implies that \(\beta =1\), see [4]. In particular, this implies that \(p\mapsto \theta (p)\) is continuous.
Hara and Slade [23] use the lace expansion to prove that \(\eta =0\) in Fourier space as well as the finiteness of triangle diagram for \(d\ge 7\) in the spread-out setting with a sufficiently large parameter L. In the spread-out setting all bonds \(\{x,y\}\) with \(|x-y|\le L\) are independently open or closed. This is an optimal result in the sense that mean-field behavior is not expected in \(d\le 6\), see [46], where Toulouse argues that the upper critical dimensions \(d_c\), above which we can expect mean-field behavior, equals 6. For mathematical arguments why \(d_c=6\), see Chayes and Chayes [13], Tasaki [45] or [31, Section 11.3.3].
For the nearest-neighbor setting, Hara and Slade proved mean-field behavior in sufficiently high dimensions [23]. Later, they numerically verified that \(d= 19\) is sufficiently high by adapting the proof of the seminal result that self-avoiding walk in dimensions \(d\ge 5\) satisfies the infrared bound. In private communication with Takashi Hara, the authors have learned that in a recent improvement of their numerical methods, the mean-field result was established for \(d\ge 15\), and thus this implies Theorem 1.1. The proof for both these results (\(d\ge 15\) and \(d\ge 19\)) were never published.
Let us briefly explain how percolation fits into our general framework. For percolation, in [18], we perform the non-bracktracking lace expansion (NoBLE) for the two-point function \(\tau _p(x)\) and \(\tau _p^\iota (x)=\mathbb {P}_p(0\longleftrightarrow x \text { without using }e_\iota )\). Further, we bound the coefficients arising in this expansion and check that all general assumptions used in the present paper are satisfied. In the NoBLE, we further identify that \(\mu _p=p\mathbb {P}_p(e\in {\mathscr {C}}(0){\mid } \{0,e\}\text { is vacant})\). For our analysis we also require a bound on \(\bar{\mu }_p=p\) (recall (1.26)).
1.4.2 Lattice trees and animals
A nearest-neighbor lattice tree (LT) on \(\mathbb {Z}^d\) is a finite, connected set of nearest-neighbor bonds containing no cycles (closed loops). A nearest-neighbor lattice animal (LA) on \(\mathbb {Z}^d\) is a finite, connected set of nearest-neighbor bonds, which may or may not contain cycles. Although a tree/animal A is defined as a set of bonds, we write \(x\in A\), for \(x\in \mathbb {Z}^d\), to denote that x is an element of a bond of A. The number of bonds in A is denoted by |A|. We define \(t^{ \scriptscriptstyle (a)}_n(x)\) and \(t^{ \scriptscriptstyle (t)}_n(x)\) to be the number of LAs and LTs, respectively, that consist of exactly n bonds and contains the origin and \(x\in \mathbb {Z}^d\). We study LA and LT using the one-point function \(g_z\) and the two-point function \(\bar{G}_z\) defined as
where we sum over lattice animals A and trees T, respectively. For technical reasons, we perform the analysis for the normalised two-point function \(G_z(x)=\bar{G}_z(x)/g_z\). This is not necessary, but simplifies our analysis in the general framework and improves the numerical performance of our method.
We define the LA and LT susceptibilies by
and denote the radii of convergence of these sums by \(z^{ \scriptscriptstyle (a)}_c\) and \(z^{ \scriptscriptstyle (t)}_c\), respectively. As for SRW and NBW, \(1/z_c\) describes the exponential growth of the number of LTs/LAs as the number of bonds n grows. When we drop the superscript (a) or (t), we speak about LTs and LAs simultaneously. The typical length scale of a lattice tree/animal of size n is characterized by the average radius of gyration \(R_n\) given by
Critical exponents The asymptotic behavior of \(t_n\) and \(G_z\) can be described using critical exponents. We define three of these critical exponents for LA and LT. In doing so we drop the superscripts (a) and (t) as the following holds for LA and LT. It is believed that there exist \(\gamma ,\delta ,\nu ,\eta \) and \(A_1,A_2,A_3,A_4>0\) such that
as \(z\nearrow z_c,~n\rightarrow \infty , \Vert x\Vert _2\rightarrow \infty \) and \(k\rightarrow 0\), respectively. The exponents are believed to be universal, in the sense that they do not depend on the detailed lattice structure (as long as the lattice is non-degenerate and symmetric). In particular, it is believed that the values of \(\gamma ,\delta ,\eta \) and \(\nu \) are the same in the nearest-neighbor setting that we consider here, and in the spread-out setting. The constants \(A_i\) do depend on the lattice structure.
For LT/LA, it is believed that the critical exponents take their mean-field values above their upper critical dimension \(d_c\), which are \(\gamma =1/2, \nu =1/4, \eta =0\). These values correspond to the mean-field model of LT/LA, studied in [7]. It is conjectured in [38] that the upper critical dimension of LT and LA is \(d_c=8\). This conjecture is supported by [30], where it is shown that if the “square diagram” is finite at the critical point, as is believed for \(d>8\), then the critical exponent \(\gamma \) satisfies \(\gamma \le 1/2\). In [9], it has been proven that \(\gamma \ge 1/2\) in all dimensions.
For the nearest-neighbor setting that we consider, Hara and Slade give a rigorous proof of mean-field behavior for LT and LA in sufficiently high dimensions, see [25]. What sufficiently high dimensions means was not made precise. The authors learned through private communication with Takashi Hara that it was not investigated in which dimension the classical lace expansion starts to works. In particular, Hara and Slade expected it to only be successful in dimensions much larger than \(d_c=8\). In the spread-out setting with L large enough, Hara and Slade in [25] proved the mean-field behavior for LT and LA in all dimension \(d>8\). Our main result for LTs and LAs is formulated in the following theorem:
Theorem 1.2
(Infrared bound for LTs and LAs) The infrared bound \(\hat{\bar{G}}_{z_c}(k)\le A(d)/[1-\hat{D}(k)]\) holds for some A(d) for nearest-neighbor lattice trees in dimension d satisfying \(d\ge 16\), and for nearest-neighbor lattice animals in dimension d satisfying \(d\ge 18\). As a result, \(\gamma \) takes its mean-field value \(\gamma =1/2\). The critical exponent \(\eta \) exists in the bounded-ratio sense and takes its mean-field value \(\eta =0\).
From our analysis we show directly that \(\eta =0\) in Fourier space, see the right side of (1.56), and can easily deduce that \(\gamma =1/2\). The proof that that \(\eta =0\) in x-space is non-trivial and is explained in [17] using the results by Hara [22].
For LTs and LAs, in [17], we perform the non-bracktracking lace expansion (NoBLE) on the two-point function \(\bar{G}_z(x)\) and \(\bar{G}_z^\iota (x),\) which is the two-point function in which the LT and LA partially avoid \({e}_{\iota }\). In the expansion, we identify \(\mu _z=zg^\iota _z\) and \(\bar{\mu }_z=zg_z\), where \(g_z=\bar{G}_z(0)\) and \(g^\iota _z=\bar{G}^\iota _z(0)\) are the one-point functions.
The expansion proves two relations for \(\bar{G}_z(x)\) and \(\bar{G}_z^\iota (x)\) that are perturbations of (1.14). The NoBLE can further be used to obtain bounds on the NoBLE coefficients and to verifies that the assumptions formulated in this paper indeed hold in the dimensions in Theorem 1.2.
2 Main results
The main result of this paper is the infrared bound in a general setting. In this section, we first explain the idea of the proof. Then, we state the assumptions on the general model and prove the infrared bound under these assumptions. We close this section with a discussion of our results.
2.1 Overview
The NoBLE writes \(\hat{G}_z(k)\) as a perturbation of the NBW two-point function, see (1.32), where the perturbation is described by certain NoBLE-coefficients that we denote by \(\Xi _z,\Xi _z^\iota , \Psi ^\kappa _z\) and \(\Pi ^{\iota ,\kappa }_z\). In the accompanying papers, we derive the NoBLE and its coefficients and prove that they can be bounded by a combination of simple diagrams. When we can bound these simple diagrams, then we are able to bound the perturbation, and thereby also to derive asymptotics for the two-point function.
Thus, we would like to bound simple diagrams for all \(z\le z_c\). It turn out there exists a \(z_I\in (0,z_c)\) such that we can bound the simple diagrams in terms of NBW diagrams for all \(z\le z_I\). For example, for percolation, \(z_I=1/(2d-1)\). To obtain bounds also for \(z\in (z_I,z_c)\), we use a bootstrap argument, which is a common tool in lace-expansion proofs, see e.g. [12, 24, 25]. We next explain how such a bootstrap argument works.
We use the following minor modification of the classical bootstrap argument:
Lemma 2.1
(Bootstrap argument) For \(i=1,2,3\), let \(z\mapsto f_i(z)\) be continuous functions on the interval \([z_I,z_c)\). Further, let \(\gamma _i,\Gamma _i\in \mathbb {R}\) be such that \(1\le \gamma _i<\Gamma _i\) and \(f_i(z_I)\le \gamma _i\). If for \(z\in (z_I,z_c)\) the condition \(f_i(z)\le \Gamma _i\) for all \(i\in \{1,2,3\}\) implies that \(f_i(z)\le \gamma _i\) for all \(i\in \{1,2,3\}\), then in fact \(f_i(z)\le \gamma _i\) for all \(z\in [z_I,z_c)\) and \(i\in \{1,2,3\}\).
Proof
We consider the continuous function \(z\mapsto \max _{i=1,2,3} f_i(z)/\Gamma _i\) and see that the lemma follows directly from the intermediate value theorem for continuous functions. \(\square \)
To apply the bootstrap argument, we use three different functions that we need in order to bound the lace-expansion coefficients:
-
(a)
\(f_1\) to bound the critical values of \(\bar{\mu }_z\), \(\mu _z\) and \(z\in (z_I,z_c)\);
-
(b)
\(f_2\) to bound the two-point function \(G_z(x)\) in Fourier space;
-
(c)
\(f_3\) to bound so-called weighted diagrams, such as weighted bubbles or triangles.
We define and explain these functions at the end of this section. We first continue our explanation at a more heuristic level.
For \(z=z_I\), we bound the simple diagrams using the NBW diagrams and use these bounds to prove that \(f_i(z_I)\le \gamma _i\). This ‘initializes’ the bootstrap argument. For \(z\in (z_I,z_c)\), we use the idea depicted in Fig. 1. First, we assume that \(f_i(z)\le \Gamma _i\) and use this assumption to conclude bounds on various diagrams consisting of combinations of two-point functions. Then, we use these bounds to bound the lace-expansion coefficients. This, in turn, enables us to conclude bounds on the bootstrap functions \(f_i(z)\). If these bounds turn out to be such that \(f_i(z)\le \gamma _i<\Gamma _i\), then we can use Lemma 2.1 to conclude that \(f_i(z)\le \gamma _i\) for all \(z<z_c\). These bounds then imply the infrared bound. We extend the result to \(z_c\) using a left-continuity property of the two-point function and the NoBLE coefficients, which we prove in the accompanying papers as these arguments are model-dependent.
The structure of the proof, shown in Fig. 1, is the reason that we are not able to prove the infrared bound for all dimensions above the upper critical dimensions \(d_c\). The perturbation, identified by the NoBLE, is for dimensions close to \(d_c\) quite large and reduces as we increase the dimension. Thus, for high dimensions such as \(d\ge 100\), it is relatively simple to show that the statement that \(f_i(z)\le \Gamma _i\) implies that \(f_i(z)\le \gamma _i<\Gamma _i\). However, it is very difficult to prove such a statement for dimension closer to the upper critical dimension \(d_c\). The dimensions stated in Theorem 1.1 and 1.2 do not show anything specific about the model, but only the limitation of our technique. In fact, for example for percolation, \(d>d_c=6\) is the proper condition.
Using exhaustive bounds on the model-dependent NoBLE coefficients and a more tedious computer-assisted proof might allow to prove the infrared bound in dimensions above, yet closer to, \(d_c\). Thereby, it is not clear whether it can be used to obtain the infrared bound for all dimension above \(d_c\) for percolation, LT and LA.
We next explain the idea of our proof in more detail, so as to further highlight the ideas in this paper. We continue by defining and discussing the bootstrap functions.
Bootstrap functions For the bootstrap, we use the following functions:
where \(c_\mu >1\) and \(c_{n,l,S}>0\) are some well-chosen constants and \(\mathcal {S}\) is some finite set of indices. Let us now start to discuss the choice of these functions.
The functions \(f_1\) and \(f_3\) can been seen as the combinations of multiple functions. We group these functions together as they play a similar role and are analyzed in the same way. We do not expect that the values of the bounds on the individual functions constituting \(f_1\) and \(f_3\) are comparable. This is the reason that we introduce the constants \(c_\mu \) and \(c_{n,l,S}\).
The value of n is model-dependent. For SAW, we would use only \(n=0\). For percolation we use \(n=0,1\) and \(n=0,1,2\) for LT and LA. This can intuitively be understood as follows. By the x-space asymptotics in (1.49) and (1.56), and the fact that \((f\star f)(x)\sim \Vert x\Vert _2^{4-d}\) when \(d>4\) and \(f(x)\sim \Vert x\Vert _2^{2-d}\), we have that \(\Vert y\Vert _2^2G_z(y)\sim (G_z\star G_z)(y)\). As a result, this suggests that
so that finiteness of \(\sum _{y}\Vert y\Vert _2^2G_z(y)(G_z^{\star n}\star D^{\star l})(x-y)\) is related to finiteness of the bubble when \(n=0\), of the triangle when \(n=1\) and of the square when \(n=2\).
The choices of point-sets \(S\in \mathcal {S}\) improve the numerical accuracy of the method. For example, we obtain much better estimates in the case when \(x=0\), since this leads to closed diagrams, than for \(x\ne 0\). For x being a neighbor of the origin, we can use symmetry to improve our bounds significantly. To obtain the infrared bound for percolation in \(d\ge 11\) we use
with \(\mathcal {X}=\{x\in \mathbb {Z}^d:\Vert x\Vert _2>1\}\). This turns out to be sufficient for our main results.
2.2 Assumptions
In this section, we state the assumptions that we need to perform the general NoBLE analysis. The assumptions are in terms of the simplified form of the NoBLE in (1.37). In Sect. 4, we derive this simplified NoBLE form of the NoBLE and translate the following assumption in terms of the NoBLE-coefficients. We begin with two assumptions on the two-point function that are completely independent of the expansion:
Assumption 2.2
(Bound for the initial value) There exists a \(z_I\in [0,z_c)\) such that
for all \(x\in \mathbb {Z}^d\) and \(z\in [0,z_I]\).
To control the growth of the two-point function as we approach the critical value \(z_c\), we use the following two assumptions:
Assumption 2.3
(Growth of the two-point function) For every \(x\in \mathbb {Z}^d\), the two-point functions \(z\mapsto G_z(x)\) and \(z\mapsto G^\iota _z(x)\) are non-decreasing and differentiable in \(z\in (0,z_c)\). For all \(\varepsilon >0\) there exists a constant \(c_{\varepsilon }\ge 0\) such that for all \(z\in (0,z_c-\varepsilon )\) and \(x\in \mathbb {Z}^d{\setminus }\{0\}\),
For all \(z\in (0,z_c)\), there exists a constant \(K(z)<\infty \) such that \(\sum _{x\in \mathbb {Z}^d} \Vert x\Vert _2^2 G_{z}(x)<K(z)\).
Assumption 2.4
(Continuity) For \(z\in [0,z_c)\), \(z\mapsto \bar{\mu }_z\) and \(z\mapsto \mu _z\) are continuous.
We only consider models where the two-point function has the following set of symmetries:
Definition 2.5
(Total rotational symmetry) We denote by \(\mathcal {P}_d\) the set of all permutations of \(\{1,2,\dots , d\}\). For \(\nu \in \mathcal {P}_d\), \(\delta \in \{-1,1\}^d\) and \(x\in \mathbb {Z}^d\), we define \(p(x;\nu ,\delta )\in \mathbb {Z}^d\) to be the vector with entries \((p(x;\nu ,\delta ))_j=\delta _j x_{\nu _j}\). We say that a function \(f:\mathbb {Z}^d\mapsto \mathbb {R}\) is totally rotationally symmetric when \(f(x)=f(p(x;\nu ,\delta ))\) for all \(\nu \in \mathcal {P}_d\) and \(\delta \in \{-1,1\}^d\).
Assumption 2.6
(Symmetry) We assume that \(x\mapsto G_z(x),x\mapsto R_{{ \scriptscriptstyle F},z}(x)\) and \(x\mapsto R_{{ \scriptscriptstyle \Phi },z}(x)\) are totally rotationally symmetric. Further, we assume that the lace-expansion coefficients satisfy
for all \(\iota ,\kappa \in \{\pm 1,\pm 2,\dots ,\pm d\}\) and \(z\le z_c\).
The following is the central assumption to perform the bootstrap. We assume that if \(f_1(z),\) \(f_2(z),\) \(f_3(z)\) are bounded for a given \(z\in [0,z_c)\), then the functions \(\alpha _{{ \scriptscriptstyle F},z},\alpha _{{ \scriptscriptstyle \Phi },z},R_{{ \scriptscriptstyle F},z},R_{{ \scriptscriptstyle \Phi },z}\) obey certain diagrammatic bounds. The form of these bounds is delicate and depends sensitively on the precise model under consideration.
Assumption 2.7
(Diagrammatic bounds) Let \(\Gamma _1,\Gamma _2,\Gamma _3\ge 0\). Assume that \(z\in (z_I,z_c)\) is such that \(f_i(z)\le \Gamma _i\) holds for all \(i\in \{1,2,3\}\). Then, \(\hat{G}_z(k)\ge 0\) for all \(k\in (-\pi ,\pi )^d\), and the following bounds hold with \(\beta _{\bullet }\) depending only on \(\Gamma _1,\Gamma _2,\Gamma _3,d\) and the model:
-
(a)
There exist \(\beta _{ \scriptscriptstyle \mu }>1, \underline{\beta }_{ \scriptscriptstyle \alpha ,F},\overline{\beta }_{ \scriptscriptstyle \alpha ,F},\beta _{ \scriptscriptstyle |\alpha ,\Phi |},\underline{\beta }_{ \scriptscriptstyle c,\Phi },\overline{\beta }_{ \scriptscriptstyle c,\Phi }>0 \), such that
$$\begin{aligned}&\displaystyle \frac{\bar{\mu }_z}{\mu _z}\le \beta _{ \scriptscriptstyle \mu },\quad \underline{\beta }_{ \scriptscriptstyle c,\Phi }\le c_{{ \scriptscriptstyle \Phi },z}\le \overline{\beta }_{ \scriptscriptstyle c,\Phi }, \end{aligned}$$(2.8)$$\begin{aligned}&\displaystyle \underline{\beta }_{ \scriptscriptstyle \alpha ,F}\le \alpha _{{ \scriptscriptstyle F},z}\le \overline{\beta }_{ \scriptscriptstyle \alpha ,F}, \quad |\alpha _{{ \scriptscriptstyle \Phi },z}| \le \beta _{ \scriptscriptstyle |\alpha ,\Phi |}. \end{aligned}$$(2.9) -
(b)
There exist \(\overline{\beta }_{ \scriptscriptstyle \Pi ^{\iota }}, \underline{\beta }_{ \scriptscriptstyle \Psi ^{\kappa }}>0\), such that
$$\begin{aligned} \sum _{x,\kappa }\Pi ^{\iota ,\kappa }_z(x)\le \overline{\beta }_{ \scriptscriptstyle \Pi ^{\iota }},\quad \sum _{x}\Psi ^{\kappa }_z(x)\ge -\underline{\beta }_{ \scriptscriptstyle \Psi ^{\kappa }}. \end{aligned}$$(2.10) -
(c)
There exist \(\beta _{{ \scriptscriptstyle R,F}},\beta _{{ \scriptscriptstyle R,\Phi }}, \beta _{ \scriptscriptstyle \Delta R,\Phi }, \beta _{ \scriptscriptstyle \Delta R,F}, \underline{\beta }_{ \scriptscriptstyle \Delta R,F}>0\) such that
$$\begin{aligned} \sum _{x} |R_{{ \scriptscriptstyle F},z}(x)|&\le \beta _{{ \scriptscriptstyle R,F}}, \quad \sum _{x}|R_{{ \scriptscriptstyle \Phi },z}(x)|\le \beta _{{ \scriptscriptstyle R,\Phi }}, \end{aligned}$$(2.11)$$\begin{aligned} \sum _{x}\Vert x\Vert _2^2 |R_{{ \scriptscriptstyle \Phi },z}(x)|&\le \beta _{ \scriptscriptstyle \Delta R,\Phi },\quad \sum _{x}\Vert x\Vert _2^2 |R_{{ \scriptscriptstyle F},z}(x)|\le \beta _{ \scriptscriptstyle \Delta R,F}, \end{aligned}$$(2.12)$$\begin{aligned} \hat{R}_{{ \scriptscriptstyle F},z}(0)-\hat{R}_{{ \scriptscriptstyle F},z}(k)&\ge - \underline{\beta }_{ \scriptscriptstyle \Delta R,F}[1-\hat{D}(k)], \end{aligned}$$(2.13)
for all \(k\in (-\pi ,\pi )^d\). Further, we assume that \(\underline{\beta }_{ \scriptscriptstyle \alpha ,F}- \underline{\beta }_{ \scriptscriptstyle \Delta R,F}>0\) and \(\underline{\beta }_{ \scriptscriptstyle c,\Phi }-\beta _{ \scriptscriptstyle |\alpha ,\Phi |}-\beta _{{ \scriptscriptstyle R,\Phi }}>0\). If Assumption 2.2 holds, then the bounds stated above also hold for \(z=z_I\), where in this case the constants \(\beta _{\bullet }\) only depend on the dimension d and the model.
To extend the infrared bound to \(z=z_c\), we use the following assumption:
Assumption 2.8
(Growth at the critical point) We assume that, if the bounds stated in Assumption 2.7 hold uniformly for \(z\in [z_I,z_c)\), then \(z\mapsto \hat{G}_z(k)\) is left-continuous at \(z=z_c\) for any \(k\ne 0\), and that the bounds stated in Assumption 2.7 also hold for \(z=z_c\).
Assumptions 2.6–2.8 depend on the NoBLE and are stated in terms of its simplified form (1.37). In Sect. 4, we replace these assumptions by assumptions on the NoBLE-coefficients. We have chosen to use the form (1.37) for the analysis, as it simplifies the presentation of the analysis considerably.
2.3 Main result: infrared bound
To successfully apply the bootstrap argument, we require that we can improve the bound on the bootstrap functions. This is the content of the following condition:
Definition 2.9
(Sufficient condition for the improvement of bounds) For \(\gamma ,\Gamma \in \mathbb {R}^3\) and \(z\in [z_I,z_c)\), we say that \(P(\gamma ,\Gamma ,z)\) holds when \(f_i(z)\le \Gamma _i\) for \(i\in \{1,2,3\}\) and the following conditions hold:
and \(\gamma _3\) is larger than the maximum of the right-hand sides of (3.31) and (3.87).
The last condition states that the initial condition \(f_3(z_I)\le \gamma _3\) holds and that the improvement of bounds succeeds for \(f_3\). We do not give a formal statement at this point, as it is involved and would require notation that has not yet been introduced. If the bootstrap succeeds, then we are able to prove our main result:
Theorem 2.10
(Infrared bound) Let \(k\in [-\pi ,\pi ]^d,z_I\in [0,z_c)\) and \(\gamma ,\Gamma \in \mathbb {R}^3\). If Assumptions 2.2–2.8 and \(P(\gamma ,\Gamma ,z)\) hold for all \(z\in [z_I,z_c)\), then, for all \(z\in [z_I, z_c]\),
with
We postpone the discussion of Theorem 2.10 to Sect. 2.5. We continue to discuss the strategy of proof.
2.4 Proof subject to a successful bootstrap
The central statement, that we prove in Sect. 3, is that we can apply the bootstrap argument when \(P(\gamma ,\Gamma ,z)\) holds. We now formalize this statement in Proposition 2.11:
Proposition 2.11
(A successful bootstrap) Let \(\gamma ,\Gamma \in \mathbb {R}^3\). If Assumptions 2.2–2.8 and \(P(\gamma ,\Gamma ,z)\) hold for all \(z\in [z_I,z_c)\), then the functions \(f_1,f_2,f_3\) defined in (2.1)–(2.3) are continuous, \(f_i(z_I)<\gamma _i\) for \(i\in \{1,2,3\}\) hold, and \(f_i(z)\le \Gamma _i\) for all \(i\in \{1,2,3\}\) implies that \(f_i(z)\le \gamma _i\) for all \(i\in \{1,2,3\}\).
We prove Proposition 2.11 in Sect. 3 one function \(f_i\) at a time. Now we prove our main result, Theorem 2.10, assuming that Proposition 2.11 holds:
Proof of Theorem 2.10 subject to Proposition 2.11 By Lemma 2.1,
By Assumption 2.8, \(z\mapsto \hat{G}_{z}(k)\) is left-continuous at \(z=z_c\) for \(k\ne 0\). From this, we conclude that (2.20) also holds for \(z=z_c\) and \(k\ne 0\), which proves (2.17). To prove (2.18), we use the bounds of Assumption 2.7 on \(\hat{G}_z(k)\) as given in (1.37)
which implies (2.18) and derives the expression for A(d) in (2.19). \(\square \)
2.5 Discussion
In general, a proof using the NoBLE consists of four parts, see also Fig. 2: (a) the derivation of the non-backtracking lace expansion or NoBLE; (b) diagrammatic bounds on the NoBLE coefficients; (c) the analysis of the NoBLE equation; and (d) a numerical verification of the conditions in \(P(\gamma ,\Gamma ,z)\), using a computer-assisted proof.
Parts (a) and (b) are performed in the model-dependent papers [17, 18]. Part (c) is performed here in a generalized setting. Part (d) is explained in Sect. 5, and is numerically performed in three Mathematica notebooks. In the first notebook, we compute SRW-integrals for a given dimension, see Sects. 5.1–5.2. In the second notebook, we implement bounds on the simplified rewrite (1.37) and the bound necessary for the improvement of \(f_3\), see Appendix D and Sect. 3.3.5, respectively. These two parts are completely model independent. In the third notebook, we use the values of the SRW-integrals and the bootstrap assumptions to compute numerical bounds on the diagrammatic bounds on the NoBLE coefficients. These bounds are then used to verify the conditions \(P(\gamma ,\Gamma ,z)\), which, when successful, imply that the analysis here yields the infrared bounds in the specific dimension under consideration. Since the bounds are monotone in the dimension, the bounds then also follow for all dimensions larger than that specific dimension.
In the thesis of the first author [15], the analysis was performed in two ways. The first was based on the x-space approach, as originally worked out by Hara and Slade in [27]. This approach was used by Hara and Slade in [27, 28] to obtain that mean-field behavior holds for self-avoiding walk (SAW) in all dimensions \(d\ge 5\). This is optimal in the sense that mean-field behavior for SAW in \(d\le 4\) should not be true. See [11] and references therein for results in this direction. Further, Hara and Slade adapted their method to percolation [24], which led to the famous result that mean-field behavior for percolation holds for \(d\ge 19\).
The second analysis was based on the trigonometric approach, first used for finite tori in [8] and worked out for \(\mathbb {Z}^d\) in [32, 43]. However, it was never verified above which dimension this technique can be applied. Thus, it was initially not obvious to us which method would be numerically optimal. It was only by implementing both methods that we discovered that the x-space approach, combined with the NoBLE analysis, is numerically superior. This is the reason that we only describe this method here. In conclusion, our method is, after the derivation of the NoBLE, heavily inspired by that of Hara and Slade [27]. We have benefitted tremendously from their work, as well as from the many discussion that we have had with Takashi Hara and Gordon Slade over the past years. From private communication, we have learned that Takashi Hara also managed to prove that percolation in dimension \(d\ge 15\) obeys the infrared bound, although this result has not appeared in print. We hope that our method, as well as the accompanying Mathematica notebooks that are publicly available [14] to anyone who is interested, increase the transparency of the proof of the infrared bound for all the models involved.
The main difference between our work and the work by Hara and Slade [27] is that in our method, the loops creating the perturbative terms are made to consist of at least 4 bonds, while in the classical lace expansion they could consist of immediate reversals (2 bonds). This makes the perturbation considerably smaller, and allows for an analysis that is to a much larger extent model-independent as the analysis in [27] and its adaptation to percolation. It also explains why our method gives reasonable results for lattice trees and lattice animals, models that previously had not been attempted by Hara and Slade. In discussions with Takashi Hara, we have found that our bounds on e.g. the triangle diagram are slightly better in dimension 15, whereas he has a much more sophisticated and model-dependent analysis of the lace-expansion coefficients.
For the SAW, we also derived a NoBLE and implemented the bootstrap. In this way, we can show that mean-field behavior holds for SAW in \(d\ge 7\), see [15] and [14]. While the proof for \(d\ge 7\) is relatively simple, we expect that an extension of the technique to \(d=5,6\) will not produce a substantially simpler proof than that of Hara and Slade, that is already optimal in the sense that it proves the result in all dimension above the SAW-upper critical dimension 4. Thus, we have not attempted to improve upon our result.
Let us dwell a bit on the distinction between the x-space approach and the k-space or trigonometric approach. We require bounds on weighted diagrams, alike
We can either bound the underlying diagram directly in Fourier space or use the following lemma to translate it into the x-space approach:
Lemma 2.12
(Fourier transforms and step distributions) For a summable, non-negative function g that is totally rotationally symmetric, as defined in Definition 2.5, the following bound holds:
To distribute the weight \(\Vert x\Vert _2^2\) over a large diagram into the weights of parts of the diagram, we use the relation that, for \(x_i\in \mathbb {Z}^d\):
The diagrammatic bounds for the k-space approach are very similar, due the following analogous result, which is of independent interest:
Lemma 2.13
(Split of cosines) Let \(t\in \mathbb {R}\) and \(t_i\in \mathbb {R}\) for \(i=1,\dots ,J\) such that \(t=\sum _{i=1}^Jt_i\). Then,
The inequality (2.26) with a factor \(2J+1\) is commonly used in the lace-expansion literature. While reviewing the proof, the authors found that a minor adaptation improves the leading factor to be J. The proof of Lemmas 2.12 and 2.13 can be found in Appendix B.
Let us close this section by proposing some extensions of our work. We do not manage to prove the infrared bound all the way down to the upper critical dimension for percolation. For this, we need even better arguments. One might hope that this can be done by a more careful analysis that compares the interacting models with memory-m walk for large values of m. Here, a SRW is called a memory-m walk when it has no loops of length at most m. Thus, NBW is memory-2. We can easily derive such a memory-m expansion for SAW, for percolation, LT and LA this is already more involved. However, the analysis required for this expansion is much more involved, and we have not tried this more general approach. One particular problem is that we do not know what the memory-m Green’s function is, so that it is harder to explicitly expand around this. We think that also for this approach a numerical (and thus computer-assisted) proof is necessary.
3 Verification of the bootstrap conditions
In this section, we prove Proposition 2.11 one function \(f_i\) at a time.
3.1 Conditions for \(f_1\)
In this section, we prove that the properties of \(f_1\) in Proposition 2.11 hold.
By Assumption 2.4, \(z\mapsto \bar{\mu }_z\) and \(z\mapsto \mu _z\) are continuous, so that \(z\mapsto f_1(z)\) is also continuous. From (2.15), we conclude that \(f_1(z_I)\le \gamma _1\). To show that for all \(z\in (z_I,z_c)\), \(f_i(z)\le \Gamma _i\) for all \(i\in \{1,2,3\}\) implies that \(f_1(z)\le \gamma _1\), we prove a relation between \(\hat{B}_{\mu }(0)\) and \(\hat{G}_z(0)\). We use the abbreviations \(\psi _z= \hat{\Psi }^{\iota }(0)\) and \(\pi ^\iota _z=\sum _\kappa \hat{\Pi }^{\iota ,\kappa }(0)\), where the choice of \(\iota \in \{\pm 1,\dots , \pm d\}\) is by Assumption 2.6 not relevant.
Lemma 3.1
(Link between NBW and general susceptibility) Let Assumption 2.6 hold and define
Then, \(\hat{B}_{\lambda _z}(0)\hat{\Phi }_z(0)=\hat{G}_{z}(0)\) for all \(z<z_c\).
Proof
Since \({\hat{\mathbf{D}}}(0)=\mathbf{I}\) and \(\vec {\hat{\Psi }}(0)=\psi _z{\vec {1}}\), the two-point function \(\hat{G}_{z}(k)\) in the form of (1.32) simplifies for \(k=0\) to
Due to the simple form of \(\mathbf{I}\) and \(\mathbf{J}\) and the symmetry of \(\Pi ^{\iota ,\kappa }_z\) stated in Assumption 2.6, the sum of each column and the sum of each row of \(\mathbf{I}+\mu _z\mathbf{J}+ \hat{{\varvec{\Pi }}}_z(0)\) equals \(1+\mu _z+\pi ^\iota \). Thus, the one vector \({\vec {1}}\) is an eigenvector of \(\mathbf{I}+\mu _z\mathbf{J}+ \hat{{\varvec{\Pi }}}_z(0)\) corresponding to the eigenvalue \(1+\mu _z+\pi ^\iota \) and we can compute that
Solving \(\hat{B}_{\lambda _z}(0)\hat{\Phi }_z(0)=\hat{G}_{z}(0)\) for \(\lambda _z\) for the first equality, and for \(\mu _z\) for the second, gives the desired result. \(\square \)
The above identification allows us to improve the bound on \(f_1\) as required in the bootstrap analysis:
Lemma 3.2
(Improvement of \(f_1\)) Let \(z\in (z_I,z_c)\) and \(\gamma ,\Gamma \in \mathbb {R}^3\). If Assumptions 2.6–2.7 and condition \(P(\gamma ,\Gamma ,z)\) hold, then \(f_1(z)\le \gamma _1\).
Proof
Recall that \(f_1(z)=\max \left\{ (2d-1)\bar{\mu }_z,c_\mu (2d-1)\mu _z\right\} \). We select \(\lambda _z\) as in Lemma 3.1 and note that \(\lambda _z<(2d-1)^{-1}\) if \(z<z_c\) as \(\hat{G}_{z}(0)=\hat{B}_{\lambda _z}(0)\hat{\Phi }_z(0)<\infty \). Hence, we can compute that
Using \(\frac{\bar{\mu }_z}{\mu _z}\le \beta _{ \scriptscriptstyle \mu }\) from Assumption 2.7, we obtain
Thus,
which is by (2.15) smaller than \(\gamma _1\) when condition \(P(\gamma ,\Gamma ,z)\) holds. \(\square \)
3.2 Conditions for \(f_2\)
In this section, we prove that the properties of \(f_2\) in Proposition 2.11 hold. We start with the required continuity.
Lemma 3.3
(Continuity of \(f_2\)) The function \(z\mapsto f_2(z)\) defined in (2.2) is continuous for z in \([0,z_c)\).
Proof
We follow the proof of [32, Lemma 5.3]. To show that \(f_2\) is continuous on \([0,z_c)\), we prove that it is continuous on the closed interval \([0,z_c-\varepsilon ]\) for any \(\varepsilon >0\). Using Assumption 2.3, we know that for any k and \(z\in [0,z_c-\varepsilon ]\),
where we can interchange differentiation and summation as the sum is bounded in absolute value, as just shown. From this, we conclude that the derivative of \(f_2(z)\) is uniformly bounded on \([0,z_c-\varepsilon ]\), which implies the continuity of \(f_2\) on \([0,z_c-\varepsilon ]\).
\(\square \)
We continue to prove the bootstrap for \(f_2\):
Lemma 3.4
(Improvement of \(f_2\)) Let \(z\in [z_I,z_c)\) be such that Assumptions 2.6–2.7 and \(P(\gamma ,\Gamma ,z)\) hold. Then \(f_2(z)\le \gamma _2\).
Proof
Recall that \(f_2(z)=\frac{2d-1}{2d-2}\sup _{k\in (-\pi ,\pi )^d} [1-\hat{D}(k)]\hat{G}_{z}(k).\) As already used in the proof of Theorem 2.10, we know that Assumption 2.7 implies that
and
where we use in the last step that \(1-\hat{F}_z(0)=(\hat{\Phi }_z(0)\hat{G}^{-1}_{z}(0))=\hat{B}^{-1}_{\lambda _z}(0)\ge 0\) by Lemma 3.1. We conclude from this that
If condition \(P(\gamma ,\Gamma ,z)\) holds, then this is smaller than \(\gamma _2\), see (2.16), which completes the proof. \(\square \)
3.3 Conditions for \(f_3\)
In this section, we show that the function \(f_{3}\), defined in (2.3), satisfies the conditions of the Bootstrap Lemma (Lemma 2.1). Namely, we prove that \(z\mapsto f_{3}(z)\) is continuous, that \(f_3(z_I)\le \gamma _3\), and that for all \(z\in (z_I,z_c)\), \(f_i(z)\le \Gamma _i\) for all \(i\in \{1,2,3\}\) implies that \(f_3(z)\le \gamma _3\). As this is more elaborate for \(f_3\) than for \(f_1\) and \(f_2\), we divide the proof into multiple steps.
The techniques of this section are an adaptation of those used by Hara and Slade to prove the mean-field behavior for SAW in \(d\ge 5\), see [28]. The central idea needed for the adaptation was developed in discussions with Takashi Hara.
3.3.1 Rewrite of \(f_3\)
We analyze the function
and conclude the desired results on \(f_3\) using that, by definition (2.3),
We bound \(\mathcal {H}^{n,l}_z\) using the continuous Laplace operator \(\bigtriangleup \). For a differentiable function g and \(s\in \{1,2,\dots ,d\}\), let \(\partial _s g(k)=\frac{\partial }{\partial k_s} g(k)\) and \(\bigtriangleup g(k)=\sum _{s=1}^d\partial _s^2 g(k)\). Then,
Thus, we can bound \(\mathcal {H}^{n,l}_z(x)\) using the Fourier representation
If we replace \(G_z\) in (3.14) by \(C_{1/2d}\) (recall (1.8)), then we can compute the value directly, see Sect. 3.3.3. To obtain a bound for \(z\in (z_I,z_c)\), in Sects. 3.3.4, 3.3.5, we extract a dominant SRW-like contribution from \(G_z\), which we compute directly and then we bound the remainder terms separately. The bounds are expressed using several SRW-integrals that can also be computed numerically as we explain in Sect. 5.
3.3.2 Continuity of \(f_3\)
Lemma 3.5
(Continuity) The function \(z\mapsto f_3(z)\) as defined in (3.10) is continuous in \(z\in [z_I,z_c)\).
Proof
We fix an \(\varepsilon >0\) and prove that \((\mathcal {H}^{n,l}_z(x))_{x\in \mathbb {Z}^d}\) is an equicontinuous family of functions and is uniformly bounded for all x, n, l for all \(z\in [0,z_c-\varepsilon )\). This allows us to obtain the continuity of \(z\mapsto \sup _{x\in S} \mathcal {H}^{n,l}_z(x)\) for all sets S directly from the Arzela-Ascoli Theorem. This implies the continuity of \(z\mapsto f_3(z)\) as the index set \(\mathcal {S}\) over which we take the maximum in (2.3) is finite. By Assumption 2.3, there exists a constant \(K(z_c-\varepsilon )<\infty \) such that
Further, \(\hat{G}_{z_c-\varepsilon }(0)=\chi (z_c-\varepsilon )<\infty \), so that, uniformly for \(z\in [z_I,z_c-\varepsilon ]\),
By Assumption 2.3,
We use that \(\Vert w+x+y\Vert ^2_2\le 3 (\Vert w\Vert ^2_2+\Vert x\Vert ^2_2+\Vert y\Vert ^2_2)\) for all \(w,x,y\in \mathbb {Z}^d\) to obtain
We conclude that
By the uniformity of this bound in x, we conclude that \((\mathcal {H}^{n,l}_z(x))_{x\in \mathbb {Z}^d}\) is equicontinuous. \(\square \)
3.3.3 Bound for the initial point \(f_3(z_I)\)
In this section, we prove that \(f_3(z_I)\le \gamma _3\). By Assumption 2.2, we can bound \(G_{z_I}(x)\le \frac{2d-2}{2d-1} C_{1/(2d)}(x)\). Thus, we can bound \(f_{3}(z_I)\) using only SRW-quantities. We start by computing the derivatives of \(\hat{C}_{1/2d}(k)=\hat{C}(k)=[1-\hat{D}(k)]^{-1}\) and \(\hat{D}(k)\), where \(\partial _s\) denotes the derivative w.r.t. \(k_s\):
and
We use
to compute that
We define \(\hat{M}(k)=\hat{D}(k)-2 \hat{D}^{\sin }(k)\hat{C}(k)\) and conclude from the computations above that
We use this representation to compute the SRW analogue of \(\mathcal {H}^{n,l}_z(x)\) as
As we explain in more detail in Sect. 5.1, we can numerically compute the SRW-integral
We use this integral to compute (3.28) numerically as
Thus, \(f_3(z_I)\) is bounded by
By the assumption in \(P(\gamma ,\Gamma ,z)\), this is smaller than \(\gamma _3\).
Remark 3.6
(Close to the upper critical dimension) The bound (3.30) can only be used in dimension \(d\ge 2(n+3)+1\) as it uses \(I_{n+3,l+1}(x)\), which is only finite in these dimensions. This restricts the analysis shown here to dimensions \(d\ge d_c+3\), e.g. for percolation we can only use this bound for \(d\ge 9\) as we require a bound on \(\mathcal {H}^{1,0}_z(x)\) to successfully apply the bootstrap argument. This problem can be avoided using a different bound for the integral. For example, using the bound
in (3.27), we obtain that
where we introduce the SRW-integral \(K_{n+2,l}(x)\) in (3.36) below. This and other bounds applicable in \(d=d_c+1,d_c+2\), perform numerically worse than the bound in (3.31). As we are not able to prove mean-field behavior in dimension \(d_c+1,d_c+2\) anyway, we use the numerically better bound (3.31) instead.
3.3.4 Preparations for the improvement of bounds for \(f_3\)
We wish to prove for all \(z\in (z_I,z_c)\) that \(f_i(z)\le \Gamma _i\) for all \(i\in \{1,2,3\}\) implies \(f_3(z)\le \gamma _3\). This is the most technical part of our proof. We do this by deriving a bound on
For this bound, we extract the SRW-like contributions from \((-\bigtriangleup \hat{G}_z(k))\) by decomposing it into five terms \(H_1,\dots ,H_5\). We compute the SRW-like contributions \(H_1\) as in the preceding section and bound the remainder terms using Assumption 2.7 and certain SRW-integrals that we define next.
SRW-integrals Here we introduce several SRW integrals that we use to bound \(\mathcal {H}^{n,l}_z(x)\). Using the terminology introduced in Definition 2.5, we define
Performing the sum over \(\delta \) gives cosines, so that \(\hat{D}^{(x)}(k)\) is real. The following SRW-integrals are adaptations of the integrals used in [27, Section 1.6]: For \(x\in \mathbb {Z}^d\) and \(n,l\in \mathbb {N}\), we let
where \(\hat{C}(k)=\hat{C}_{1/2d}(k)\) is the critical SRW two-point function and \(\hat{M}(k)\) is defined above (3.26). For any function f such that \(f(x)=f(p(x;\nu ,\delta ))\) for all \(\nu ,\delta \) (see Definition 2.5), we see that
The functions \(G_z\) and D have these symmetries, so that we can replace \({\mathrm e}^{{\mathrm i}k\cdot x}\) in (3.14) by \(\hat{D}^{(x)}(k)\). In Sect. 5.1, we show how to compute \(I_{n,l}(x)\), and in Sect. 5.2, we bound the other integrals in terms of \(I_{n,l}(x)\).
Decomposition of the two-point function We decompose \(\hat{G}_z(k)\) and \(\bigtriangleup \hat{G}_z(k)\) into several pieces, which we then bound in the next section. We start with some preparations for this decomposition. For the SRW-contributions, we define
As \(\hat{F}_z(0)\le 1\) and \(\alpha _{{ \scriptscriptstyle F},z}>\underline{\beta }_{ \scriptscriptstyle \alpha ,F}\), we know that \(\hat{C}^*(k)<\frac{1}{\alpha _{{ \scriptscriptstyle F},z}} \hat{C}(k)<\underline{\beta }_{ \scriptscriptstyle \alpha ,F}^{-1} \hat{C}(k)\). Further, we conclude from
with
and the monotonicity of \(C_\lambda (x)\) in the parameter of the generating function \(\lambda \) that
Thus, \(C^*\) can be bounded by \(\alpha _{{ \scriptscriptstyle F},z}^{-1}C\) in x-space as well as in k-space. We abbreviate
Bounds on key quantities To bound the remainder terms, we define
Further, we assume that \(f_2(z)\le \Gamma _2\), i.e., that
and from now on abbreviate \(\Gamma _2'=\frac{2d-2}{2d-1}\Gamma _2\). We use the bound (2.12) in Assumption 2.7 to obtain
Arguing as in (3.12), (3.13) we can show that
We conclude the same bounds for \(\hat{R}_{{ \scriptscriptstyle \Phi },z}(0;k)\), where \( \beta _{ \scriptscriptstyle \Delta R,F}\) is replaced by \( \beta _{ \scriptscriptstyle \Delta R,\Phi }\).
Combining these bounds with \(\hat{C}(k)=1/[1-\hat{D}(k)]\) we obtain
and
Decomposition of \(\bigtriangleup \hat{G}_z(k)\) We decompose \(\bigtriangleup \hat{G}_z(k)\) into five contributions \(\hat{H}_i(k)\). The dominant contribution is \(\hat{H}_1(k)\), which is defined to be
The remainder terms \(\hat{H}_2(k), \hat{H}_3(k), \hat{H}_4(k)\) and \(\hat{H}_5(k)\) are defined as
In Appendix C, we explicitly show that
This computation is quite long and tedious. However, since it is crucial to our analysis, we give the derivation in detail in Appendix C. Let us now give some insight into the origin of the different contributions. The first term \(\hat{H}_1(k)\) is a SRW-like contribution that can be bounded similarly as in Sect. 3.3.3. The second term \(\hat{H}_2(k)\) corresponds to everything that has the factor \(\hat{M}^{*}(k)\) and a remainder term. In \(\hat{H}_3(k)\), we collect the remaining \(\hat{D}^{\sin }(k)\) contributions. In \(\hat{H}_4(k)\), we put the contributions of \(\bigtriangleup \hat{R}_{{ \scriptscriptstyle \Phi },z}(k)\) and \(\bigtriangleup \hat{R}_{{ \scriptscriptstyle F},z}(k)\), and in \(\hat{H}_5(k)\), we collect all products of single derivatives.
3.3.5 Improvement of bounds for \(f_3\)
In this section we bound \(\mathcal {H}^{n,l}_{z}(x)\) by deriving bounds on
for \(i=1,\dots ,5\). We do this for \(i=1,2,\ldots , 5\) one by one, starting with \(\mathcal {H}^{n,l}_{1,z}(x)\). This is the most technical part of the analysis. We bound each term of \(\mathcal {H}^{n,l}_{i,z}(x)\) using the bounds of Assumption 2.7 and the SRW-integrals (3.35)–(3.38).
Step 1: Bound on \(\mathcal {H}^{n,l}_{1,z}(x)\) We first recall the rearrangement of (3.28)–(3.30) to see that, for \(m\ge 0\),
We perform the bounds for \(n=0\), \(n=1\) and \(n=2\) separately.
Bound on a weighted line (\(n=0\)) Substituting the definition of \(\mathcal {H}^{0,l}_{1,z}(x)\), we see that (3.52) leads to three terms. We bound the first and second term using (3.59). For the third term we can not use an x-space representation like in (3.59). To bound this term we repeat (3.27)–(3.30) to see that
In this way, we obtain
Bound on a weighted bubble (\(n=1\)) To bound \(\mathcal {H}^{1,l}_{1,z}(x)\), we expand \(\hat{G}_z(k)\) as follows:
so that
We bound the first line using (3.59) and the second line using (3.51) to obtain
with \(T_{n,l}\) as defined in (3.37).
Bound on a weighted triangle (\(n=2\)). We decompose \(\hat{G}_z^2(k)\) into two terms as
We compute the contribution (3.65) to be
We expand the brackets and then use (3.59) to bound this contribution by
where we use that \(\mathcal {J}_{n,l}(x)\ge 0\) for every \(x\in \mathbb {Z}^d, n,l\ge 0\) by (3.28)–(3.30).
Using (3.51) we bound the absolute value of the minor contributions given in (3.66) by
Thus, we bound the contributions due to (3.66) by
Conclusion of Step 1 We have bounded the contribution due to \(\hat{H}_1(k)\) and have obtained that
By the sum of two equation numbers we mean the sum of the terms given in the right-hand sides of the corresponding equations. As for \(z=z_I\), this bound uses \(I_{n+2,l}(x)\) and can therefore not be used in \(d=d_c+1,d_c+2\). We have chosen to use these bounds, even if other bounds would be available, as they give numerically better bounds.
Step 2: Bound on \(\mathcal {H}^{n,l}_{2,z}(x)\) For this bound we use
which is an adaptation of \(T_{n,l}\) defined in (3.37). In Sect. 5.2 we will bound \(T^*_{n,l}\) in the same way as \(T_{n,l}\). We bound the absolute value of \(\hat{H}_2(k)\), defined in (3.53), by
We use that \(|\hat{G}_z(k)|\le \Gamma _2'\hat{C}(k)\) and the integrals \(T^*_{n,l}\) to bound \(\mathcal {H}^{n,l}_{2,z}(x)\) by
Step 3: Bound on \(\mathcal {H}^{n,l}_{3,z}(x)\) In (3.54), we have defined \(\hat{H}_3(k)\) to be
We bound \(|\hat{H}_3(k)|\) as
and use this bound and the integral \(U_{n,l}\), defined in (3.38), to bound \(|\mathcal {H}^{n,l}_{3,z}(x)|\) as follows:
Step 4: Bound on \(\mathcal {H}^{n,l}_{4,z}(x)\) We first bound \(\hat{H}_4(k)\) in Fourier space as
Then, we use the definition of \(K_{n,l}\) in (3.36) to bound
Step 5: Bound on \(\mathcal {H}^{n,l}_{5,z}(x)\) We recall that
To bound the single derivatives we note that for a totally rotationally symmetric function f, see Definition 2.5, the following holds:
for \(s\in \{1, \ldots , d\}\), so that
Since \(|\sin (n t)|\le n|\sin (t)|\) for integer n, we obtain that
The total rotational symmetry of f also implies that
for all \(s,t\in \{1,\ldots ,d\}\). From this we conclude for two totally rotationally symmetric functions f, g that
where we recall (3.23). Using this relation we can bound \(\hat{H}_5(k)\) by
and obtain the following bound on \(\mathcal {H}^{n,l}_{5,z}(x)\):
Final bound on \(f_3\) In this section, we have bounded \(f_3\) by
We recall that by the sum of several equation numbers we mean the sum of the terms given in the right-hand sides of the corresponding equations.
In summary and recalling Definition 2.9, when \(P(\gamma ,\Gamma ,z)\) holds, this bound on \(f_3(z)\) is smaller than \(\gamma _3\). Thus, the improvement of all bounds is successful and we have thus successfully performed the bootstrap. The computation of a numerical value for the bound in (3.87) requires the computation of the SRW-integrals \(I_{n,l},K_{n,l},T_{n,l},U_{n,l}\). In Sect. 5.2, we show how to bound SRW-integrals and explain for which x the supremum over S is obtained.
The bootstrap function \(f_3\) provides various bounds on weighed diagrams. The real size of these diagram depends heavily on the values of n, l and the set S involved. For example, we can expect that \(\mathcal {H}^{2,0}_{z}(x)\) is of order O(1) while \(\mathcal {H}^{2,4}_{z}(x)\) is of order \(O(d^{-2})\). Since the form of the bounds on \(\mathcal {H}^{n,l}_{z}(x)\) is the same for all n, l, we have introduced the constants \(c_{n,l,S}\) to merge them into one bootstrap function. Alternatively, we could consider \(f_3\) to consist of multiple bootstrap functions that are individually bounded by \(\Gamma _3c_{n,l,S}\) within the bootstrap argument.
4 Rewrite of the NoBLE equation
In the preceding part of this paper, we have performed the analysis using the form (1.37) for the two-point function. This form is related to the classical lace expansion. We have decided to use this as it considerably simplifies the presentation of the analysis in the preceding section.
In this section, we first derive this characterization from the NoBLE equation, meaning that we identify \(\alpha _{{ \scriptscriptstyle \Phi },z},\alpha _{{ \scriptscriptstyle F},z},R_{{ \scriptscriptstyle F},z}\) and \(R_{{ \scriptscriptstyle \Phi },z}\). Then, we translate the assumptions made on the rewrite (1.37) into assumptions on the NoBLE-coefficients \(\Xi _z,\Xi ^{\iota }_z,\Psi ^{\iota }_z,\Pi ^{\iota ,\kappa }_z\).
The aim of the rewrite is to extract the dominant SRW-like contributions from \(\hat{\Phi }_z\) and \(\hat{F}_z\), see (1.33), (1.34). These SRW-like contributions will give rise to \(\alpha _{{ \scriptscriptstyle \Phi },z},\alpha _{{ \scriptscriptstyle F},z},c_{{ \scriptscriptstyle \Phi },z},c_{{ \scriptscriptstyle F},z}\). The remainder is put into \(R_{{ \scriptscriptstyle F},z}\) and \(R_{{ \scriptscriptstyle \Phi },z}\).
Here we show how we extract SRW contributions from \(\hat{\Phi }_z\) and \(\hat{F}_z\) and use them in our analysis. More terms could be extracted from \(\hat{\Phi }_z\) and \(\hat{F}_z\), thereby reducing the value of \(R_{{ \scriptscriptstyle F},z}\) and \(R_{{ \scriptscriptstyle \Phi },z}\) and thus increasing the performance of the perturbative technique. This might allow to prove the infrared bound in even smaller dimensions above the upper critical dimension. We however found the possible gain not in relation with the necessary efforts.
4.1 Derivation of the rewrite
In this section, we rewrite the functions \(\hat{\Phi }_z(k)\) and \(\hat{F}_z(k)\), as defined in (1.33), (1.34), and identify \(\alpha _{{ \scriptscriptstyle \Phi },z},\alpha _{{ \scriptscriptstyle F},z},R_{{ \scriptscriptstyle F},z}\) and \(R_{{ \scriptscriptstyle \Phi },z}\). The NoBLE-coefficients are defined as alternating series of non-negative real-valued functions \(\Xi ^{{ \scriptscriptstyle ( \mathrm{N})}}_z, \Xi ^{{{ \scriptscriptstyle ( \mathrm{N})}},\iota }_z, \Psi ^{{{ \scriptscriptstyle ( \mathrm{N})}},\iota }_z, \Pi ^{{{ \scriptscriptstyle ( \mathrm{N})}},\iota ,\kappa }_z\):
4.1.1 The model-dependent split of the coefficients
When rewriting the two-point function, we extract a major SRW-like contribution. We are guided by the intuition that coefficients are of order \(O((2d)^{-1})\) and that the main contributions to the NoBLE coefficients are
Due to the limitation of our bounds it is not beneficial to extract all these contributions. Thus, we create a model-dependent split of the coefficients to improve the performance of the technique. We define non-negative functions
Here these functions satisfy that, for \(N=0,1\) and all \(x\in \mathbb {Z}^d\),
and, for \(x\in \mathbb {Z}^d\) with \(\Vert x\Vert _2>1\),
and
for \(x\not \in \{ {e}_{\iota },{e}_{\iota }+{e}_{\kappa }\}\). Further, these functions have the same symmetries as the original coefficients. The idea behind these two different splits (giving rise to the terms with subscripts I and II, respectively) is that we split off specific contributions that can be explicitly incorporated in the constant and \(\hat{D}(k)\) terms in our expansion. Contributions with subscript I correspond to x for which \(\Vert x-{e}_{\iota }\Vert \le 1\), while contributions with subscript II correspond to x for which \(\Vert x\Vert \le 1\). In Fourier space, this corresponds to contributions with a factor \({\mathrm e}^{{\mathrm i}k(x-{e}_{\iota })}\) and \({\mathrm e}^{{\mathrm i}k x},\) respectively. See (4.14) below for how such contributions will arise.
4.1.2 The Fourier inverse of \(\hat{F}\) and \(\hat{\Phi }\)
Throughout this section, we omit z from our notation and write, e.g., \(\mu _z=\mu \) and \(\hat{F}_z(k)=\hat{F}(k)\). As a first step, we use the Neumann-series to rewrite \(\hat{F}\) and \(\hat{\Phi }\) into a form without matrices. We use that \(({\hat{\mathbf{D}}}(k) + \mu \mathbf{J})^{-1}=({\hat{\mathbf{D}}}(-k)-\mu \mathbf{J})/(1-\mu ^2)\) to rearrange \(\hat{F}(k)\) as
We define \(\hat{F}_{n}\) as the nth contribution in the sum in (4.5) and analyze these terms separately. The Fourier inverse of \(\hat{F}_{n}=\hat{F}_{n,z}\) is given by
In a similar way, we define \(\Phi _n\) such that
These function are given by
The Fourier inverses of these functions are
4.1.3 Definition of the rewrite
In the rewrite, we extract explicit terms that are independent of k and terms that involve \(\hat{D}(k)\) for \(\hat{F}\) and \(\hat{\Phi }\). Everything else is put into the remainder terms \(\hat{R}_{{ \scriptscriptstyle F},z}\) and \(\hat{R}_{{ \scriptscriptstyle \Phi },z}\). The major contributions that we can extract are part of \(\hat{F}_0\) and \(\hat{\Phi }_0\). Also \(\hat{F}_1\) gives some contributions. We begin with \(\hat{F}_0\) and rewrite it as
Recall that the lace-expansion coefficients are defined via an alternating series of non-negative functions, see (4.1), (4.2). For \(N=0,1\), we split the sum into
where we see how the splits involving the subscripts I and II are used to extract random-walk contributions. From
we extract the contribution of \(1 \times {\mathrm e}^{-{\mathrm i}k_{\iota _{0}}} \Pi ^{{ \scriptscriptstyle ( \mathrm{0})},\iota _0,\iota _1} \times {\mathrm e}^{-{\mathrm i}k_{\iota _{1}}} \) and split it as
We have now collected all the terms of the split in the lines (4.13)–(4.16). The constant terms contribute to \(c_{{ \scriptscriptstyle F},z}\). Terms involving \(\hat{D}(k)\) give rise to \(\alpha _{{ \scriptscriptstyle F},z}\). All other terms contribute to \(\hat{R}_{{ \scriptscriptstyle F},z}(k)\). Thus, we conclude that
and
which is the sum of the final contributions to the right hand side of (4.13), (4.14), (4.16) and the remainder of (4.15). We rewrite \(\hat{\Phi }(k)\) in the same way. We begin by noting that
For \(N=0,1\), we split \(\hat{\Xi }^{{ \scriptscriptstyle ( \mathrm{N})}}(k)\) as
Further, we extract the contribution of the factor 1 and \(\Xi ^{{ \scriptscriptstyle ( \mathrm{0})}, \iota }\) in the second line of (4.20) as
We define
This completes the derivation of the rewrite (1.35) and (1.36) and identifies \(\alpha _{{ \scriptscriptstyle F},z},\alpha _{{ \scriptscriptstyle \Phi },z},c_{{ \scriptscriptstyle F},z}, c_{{ \scriptscriptstyle \Phi },z}, \hat{R}_{{ \scriptscriptstyle F},z}\) and \(\hat{R}_{{ \scriptscriptstyle \Phi },z}\).
At this point, it is worth mentioning that this is not the only possible split. Indeed, we could try to put more terms into \(\alpha _{{ \scriptscriptstyle F},z},\alpha _{{ \scriptscriptstyle \Phi },z}\), thus reducing \(\hat{R}_{{ \scriptscriptstyle F},z},\hat{R}_{{ \scriptscriptstyle \Phi },z}\), and thereby improving the efficiency of the analysis. However, numerically we found that the possible gain would not be in relation to the necessary efforts, so we refrain from this.
4.2 Assumption on the NoBLE coefficients
In this section, we reformulate Assumptions 2.6–2.8 on \(\alpha _{{ \scriptscriptstyle F},z},\alpha _{{ \scriptscriptstyle \Phi },z},\hat{R}_{{ \scriptscriptstyle F},z}\) and \(\hat{R}_{{ \scriptscriptstyle \Phi },z}\) in terms of the NoBLE coefficients. We assume that the NoBLE coefficients have the following properties:
Assumption 4.1
(Symmetry of the models) Let \(\iota ,\kappa \in \{\pm 1,\pm 2,\dots ,\pm d\}\). The following symmetries hold for all \(x\in \mathbb {Z}^d\), \(z\le z_c\), \(N\in \mathbb {N}\) and \(\iota ,\kappa \):
For all \(N\in \mathbb {N}\), the coefficients
as well as the remainder terms of the split
are totally rotationally symmetric functions of \(x\in \mathbb {Z}^d\). Further, the dimensions are exchangeable, i.e., for all \(\iota ,\kappa \),
The next assumption states a bound on \(\Psi ^{{ \scriptscriptstyle ( \mathrm{N})},\kappa }_z\) and \(\Pi ^{{ \scriptscriptstyle ( \mathrm{N})},\iota ,\kappa }_z\) in terms of \(\Xi ^{{ \scriptscriptstyle ( \mathrm{N})},\iota }_z\):
Assumption 4.2
(Relation between coefficients) For all \(x\in \mathbb {Z}^d\), \(p\le p_c\), \(N\in \mathbb {N}\) and \(\iota ,\kappa \in \{\pm 1,\pm 2,\dots ,\pm d\}\), the following bounds hold:
As explained in Sect. 2.1, to successfully apply the bootstrap argument, we assume that the coefficients obey certain bounds when the bootstrap assumption \(f_i(z)\le \Gamma _i\) holds for all \(i\in \{1,2,3\}\) for a given \(z\in [0,z_c)\). These bounds do not depend on the value of z. However, their form is delicate and depends sensitively on the precise model under consideration. We assume that the same bounds hold for \(z_I\) regardless of the values \(f_1(z_I),f_2(z_I),f_3(z_I)\). Assumption 4.3 is the most technical assumption of this paper, and is phrased so as to allow maximal flexibility in the application of the NoBLE:
Assumption 4.3
(Diagrammatic bounds) Let \(\Gamma _1,\Gamma _2,\Gamma _3\ge 0\). Assume that \(z\in (z_I,z_c)\) is such that \(f_i(z)\le \Gamma _i\) for \(i\in \{1,2,3\}\) holds. Then \(\hat{G}_z(k)\ge 0\) for all \(k\in (-\pi ,\pi )^d\). There exists \(\beta _{ \scriptscriptstyle \mu }\ge 1,\underline{\beta }_{ \scriptscriptstyle \mu }>0\) such that
Further, there exist \(\beta _{ \scriptscriptstyle \Xi }^{ \scriptscriptstyle ( \mathrm{N})},\beta _{ \scriptscriptstyle \Xi ^\iota }^{ \scriptscriptstyle ( \mathrm{N})},\beta _{{ \scriptscriptstyle \Delta \Xi }}^{ \scriptscriptstyle ( \mathrm{N})},\beta _{{ \scriptscriptstyle \Delta \Xi ^{\iota }},0}^{ \scriptscriptstyle ( \mathrm{N})},\beta _{{ \scriptscriptstyle \Delta \Xi ^{\iota }},\iota }^{ \scriptscriptstyle ( \mathrm{N})} \ge 0\), such that
for all \(N\ge 0\) and \(k\in (-\pi ,\pi )^d\). Moreover, we assume that \(\sum _{N=0}^\infty \beta _{\bullet }^{ \scriptscriptstyle ( \mathrm{N})} <\infty \) for \(\bullet \in \{ \Xi , \Xi ^{\iota }, \Delta \Xi , \{\Delta \Xi ^\iota ,0\},\{\Delta \Xi ^\iota ,\iota \}\}\) and that
Further, there exist \(\underline{\beta }_{ \scriptscriptstyle \Psi }^{ \scriptscriptstyle ( \mathrm{0})}\), \(\underline{\beta }_{ \scriptscriptstyle \sum \Pi }^{ \scriptscriptstyle ( \mathrm{1})}\) such that
Additionally, there exist \(\beta _{{ \scriptscriptstyle \Xi _\alpha (0)}}^{ \scriptscriptstyle ( \mathrm{1-0})},\beta _{{ \scriptscriptstyle \Xi _\alpha (0)}}^{ \scriptscriptstyle ( \mathrm{0-1})}, \beta _{{ \scriptscriptstyle \Xi _\alpha ({e}_{1})}}^{ \scriptscriptstyle ( \mathrm{1-0})},\beta _{{ \scriptscriptstyle \Xi _\alpha ({e}_{1})}}^{ \scriptscriptstyle ( \mathrm{0-1})}\) with
and \(\beta _{{ \scriptscriptstyle \Xi ^{\iota }_\alpha ,I}}^{ \scriptscriptstyle ( \mathrm{0})},\beta _{{ \scriptscriptstyle \sum }{ \scriptscriptstyle \Xi ^{\iota }_\alpha ,I}}^{ \scriptscriptstyle ( \mathrm{0})},\beta _{{ \scriptscriptstyle \Xi ^{\iota }_\alpha ,II}}^{ \scriptscriptstyle ( \mathrm{0})}, \beta _{ { \scriptscriptstyle \sum \Xi ^{\iota }_\alpha ,II}}^{ \scriptscriptstyle ( \mathrm{0})}, \ge 0\) such that
Also, there exist \(\beta _{{ \scriptscriptstyle \sum \Psi ^{\iota }_\alpha ,I}}^{ \scriptscriptstyle ( \mathrm{0-1})},\beta _{{ \scriptscriptstyle \sum \Psi ^{\iota }_\alpha ,II}}^{ \scriptscriptstyle ( \mathrm{0-1})}, \beta _{{ \scriptscriptstyle \sum \Psi ^{\iota }_\alpha ,I}}^{ \scriptscriptstyle ( \mathrm{1-0})}, \beta _{{ \scriptscriptstyle \sum \Psi ^{\iota }_\alpha ,II}}^{ \scriptscriptstyle ( \mathrm{1-0})}, \underline{\beta }_{ \scriptscriptstyle \sum \Pi _\alpha }^{ \scriptscriptstyle ( \mathrm{0})}, \beta _{ \scriptscriptstyle \sum \Pi _\alpha }^{ \scriptscriptstyle ( \mathrm{0})}\), such that
For \(N=0,1\), there exist \(\beta _{ \scriptscriptstyle \Xi ,R}^{ \scriptscriptstyle ( \mathrm{N})}, \beta _{\Delta \scriptscriptstyle \Xi ,R}^{ \scriptscriptstyle ( \mathrm{N})}, \beta _{ \scriptscriptstyle \Psi ,R,I}^{ \scriptscriptstyle ( \mathrm{N})}, \beta _{\Delta \scriptscriptstyle \Psi ,R,I}^{ \scriptscriptstyle ( \mathrm{N})}, \beta _{ \scriptscriptstyle \Psi ,R,II}^{ \scriptscriptstyle ( \mathrm{N})}\), \(\beta _{\Delta \scriptscriptstyle \Psi ,R,II}^{ \scriptscriptstyle ( \mathrm{N})}\ge 0\), such that
Further, there exist \(\beta _{ \scriptscriptstyle \Xi ^\iota ,R,I}^{ \scriptscriptstyle ( \mathrm{0})}\), \(\beta _{\Delta \scriptscriptstyle \Xi ^\iota ,R,I}^{ \scriptscriptstyle ( \mathrm{0})}\), \(\beta _{ \scriptscriptstyle \Xi ^\iota ,R,II}^{ \scriptscriptstyle ( \mathrm{0})}\), \(\beta _{\Delta \scriptscriptstyle \Xi ^\iota ,R,II}^{ \scriptscriptstyle ( \mathrm{0})}\), \(\beta _{ \scriptscriptstyle \Pi ,R}^{ \scriptscriptstyle ( \mathrm{0})}\), \(\beta _{\Delta \scriptscriptstyle \Pi ,R}^{ \scriptscriptstyle ( \mathrm{0})}\ge 0\), such that
For all \(\bullet \in \{ \Xi , \Xi ^{\iota }, \Delta \Xi , \{\Delta \Xi ^\iota ,0\},\{\Delta \Xi ^\iota ,\iota \}\}\) and \(N\in \mathbb {N}\), \(\beta _{\bullet }^{{ \scriptscriptstyle ( \mathrm{N})}}\) depends only on \(\Gamma _1,\Gamma _2,\Gamma _3,d\) and on the model. If Assumption 2.2 holds, then the bounds stated above also holds for \(z=z_I\) with the constants \(\beta _{\bullet }\) only depending on the dimension d and the model.
Only the bounds (4.30)–(4.33) are essential to perform the analysis for the NoBLE. The bounds stated in (4.36)–(4.48) are used to obtain good bounds on \(c_{{ \scriptscriptstyle \Phi },z},\alpha _{{ \scriptscriptstyle \Phi },z},\alpha _{{ \scriptscriptstyle F},z},\hat{R}_{{ \scriptscriptstyle F},z}\) and \(\hat{R}_{{ \scriptscriptstyle \Phi },z}\) that allow us to increase the performance of the analysis and to show mean-field result in lower dimensions than otherwise possible.
We denote by \(\beta _{\bullet }^{ \scriptscriptstyle \text {abs}}\), \(\beta _{\bullet }^{ \scriptscriptstyle \text {odd}}\) and \(\beta _{\bullet }^{ \scriptscriptstyle \text {even}}\) the sum over all (resp. odd/even) N of \(\beta _{\bullet }^{ \scriptscriptstyle ( \mathrm{N})}\), i.e.,
for \(\bullet \in \{ \Xi , \Xi ^{\iota }, \Delta \Xi , \{\Delta \Xi ^\iota ,0\},\{\Delta \Xi ^\iota ,\iota \}\}\). By (4.1), the values \(\beta _{{ \scriptscriptstyle \Xi }}^{{ \scriptscriptstyle \mathrm{even}}}, \beta _{{ \scriptscriptstyle \Xi }^{\iota }}^{{ \scriptscriptstyle \mathrm{even}}}\) and \((-\beta _{{ \scriptscriptstyle \Xi }}^{{ \scriptscriptstyle \mathrm{odd}}}),(-\beta _{{ \scriptscriptstyle \Xi }^{\iota }}^{{ \scriptscriptstyle \mathrm{odd}}})\) are explicit upper and lower bounds on \(\hat{\Xi }_z(0)\) and \(\hat{\Xi }^\iota _z(0)\), respectively. By Assumption 4.2 they also imply bounds on \(\hat{\Psi }^{\iota }_z(0)\) and \(\hat{\Pi }^{\iota ,\kappa }_z(0)\).
We next discuss the left-continuity of the coefficients at \(z=z_c\):
Assumption 4.4
(Growth at the critical point) The functions \(z\mapsto \hat{\Xi }_z(k),z\mapsto \hat{\Xi }^{\iota }_z(k),z\mapsto \hat{\Psi }^{\kappa }_z(k),z\mapsto \hat{\Pi }^{\iota ,\kappa }_z(k)\) are continuous for \(z\in (0,z_c)\). Further, let \(\Gamma _1,\Gamma _2,\Gamma _3\ge 0\) be such that \(f_i(z)\le \Gamma _i\) and that Assumption 4.3 holds. Then, the functions stated above are left-continuous in \(z_c\) with a finite limit \(z\nearrow z_c\) for all \(x\in \mathbb {Z}^d\). Further, for technical reasons, we assume that \(z_c<1/2\).
In the remainder of this section we show that Assumptions 4.1–4.4 imply Assumptions 2.6–2.8, as formulated in the following proposition:
Proposition 4.5
(Translation of the assumptions) The assumptions stated in Sect. 2.2 are implied by the assumptions stated in Sect. 4.2. More precisely,
- (i)
- (ii)
- (iii)
The proof of parts (i),(iii) are relatively straightforward and are performed in Sect. 4.3. Part (ii) is proven using a tedious, but also straightforward, application of the bounds stated in Assumption 4.3. We add the details of this in Appendix D.
4.3 Properties of the rewrite
In this section, we prove Proposition 4.5(i) and (iii).
Proof of Proposition 4.5(i)
In Assumption 4.1, we assume that the dimensions are interchangeable (recall (4.28)), so that (2.7) clearly holds. Further, we also assume in Assumption 4.1 that the two-point function \(x\mapsto G_z\) is totally rotationally symmetric.
To see that \(R_{{ \scriptscriptstyle F},z}\) and \(R_{{ \scriptscriptstyle \Phi },z}\) are totally rotationally symmetric, we note that convolutions maintain symmetry and that the NoBLE-coefficients, in the way they are combined in the definition of \(R_{{ \scriptscriptstyle F},z}\) and \(R_{{ \scriptscriptstyle \Phi },z}\), are thus also totally rotationally symmetric. This completes the proof of Proposition 4.5(i). \(\square \)
Proof of Proposition 4.5(iii)
We prove the statement in three steps:
-
(a)
We prove that \([{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}+\hat{{\varvec{\Pi }}}_z(k)]^{-1}\) is well defined for all k and \(z\le z_c\);
-
(b)
We conclude that \(z\mapsto \hat{\Phi }_z(k)\), \(z\mapsto \hat{F}_z(k)\) are continuous at z and well defined at \(z_c\), which implies that the bounds stated in Assumption 2.7 also hold for \(z=z_c\);
-
(c)
We show that \(\hat{G}_z(k)\) can be continuously extended to \(z=z_c\) for \(k\ne 0\).
This implies the desired statement that \(z\mapsto \hat{G}_z(k)\) is left-continuous at \(z=z_c\) for any \(k\ne 0\) and that the bounds stated in Assumption 2.7 also hold for \(z=z_c\).
-
(a)
We begin by showing that
$$\begin{aligned} \Big \Vert \big [{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}\big ]^{-1}\hat{{\varvec{\Pi }}}_z(k)\Big \Vert _\infty =\sup _{\vec v:\Vert v\Vert _\infty =1} \max _{\iota } \Big |\Big ( \big [{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}\big ]^{-1}\hat{{\varvec{\Pi }}}_z(k) \vec v\Big )_\iota \Big |<1. \end{aligned}$$(4.50)We start by noting that \([{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}]^{-1}=\frac{1}{1-\mu _z^2} ({\hat{\mathbf{D}}}(-k)-\mu _z\mathbf{J}),\) so that
$$\begin{aligned} \Big ( \big [{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}\big ]^{-1}\hat{{\varvec{\Pi }}}_z(k)\vec v\Big )_\iota&=\frac{1}{1-\mu _z^2}\sum _{\kappa } (\hat{\Pi }^{\iota ,\kappa }_z(k){\mathrm e}^{{\mathrm i}k_\iota } -\mu _z\hat{\Pi }^{-\iota ,\kappa }_z(k)) v_\kappa . \end{aligned}$$(4.51)Thus, for \(\vec v\) with \(\Vert v\Vert _\infty =1\),
$$\begin{aligned} \Big \Vert \big [{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}\big ]^{-1}\hat{{\varvec{\Pi }}}_z(k)\vec v\Big \Vert _\infty&\le \frac{1+\mu _z}{1-\mu _z^2} \Vert v\Vert _\infty \sum _{N,\kappa ,x}\Pi ^{{ \scriptscriptstyle ( \mathrm{N})}\iota ,\kappa }(x) \nonumber \\&\mathop {\le }\limits ^{(4.29),(4.31)}\frac{2d \mu _z}{1-\mu _z} \beta _{ \scriptscriptstyle \Xi ^\iota }^{ \scriptscriptstyle \text {abs}} \mathop {<}\limits ^{(4.34)}1, \end{aligned}$$(4.52)which proves (4.50). From (4.50), it follows that the matrix \(\mathbf{I}+\left[ {\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}\right] ^{-1}\hat{{\varvec{\Pi }}}_z(k)\) is invertible. Then, we use standard linear algebra to compute
$$\begin{aligned}&\left[ \mathbf{I}+\big [{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}\big ]^{-1}\hat{{\varvec{\Pi }}}_z(k)\right] ^{-1} \big [{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}\big ]^{-1} \big [{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}+\hat{{\varvec{\Pi }}}_z(k)\big ] \nonumber \\&\quad =\left[ \mathbf{I}+\big [{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}\big ]^{-1}\hat{{\varvec{\Pi }}}_z(k)\right] ^{-1} \left[ \mathbf{I}+\big [{\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}\big ]^{-1}\hat{{\varvec{\Pi }}}_z(k)\right] =\mathbf{I}, \end{aligned}$$(4.53)which implies that the matrix \({\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}+\hat{{\varvec{\Pi }}}_z(k)\) is invertible.
-
(b)
By Assumption 4.4, we know that the NoBLE coefficients are continuous in z. This also implies that \({\hat{\mathbf{D}}}(k)+\mu _z\mathbf{J}+\hat{{\varvec{\Pi }}}_z(k)\) is continuous in z and, as it is well defined by (a), its inverse is also continuous. Further, we note that the bounds on the coefficients \(\beta _{\bullet }\) are independent of the value of \(z\in (z_{I},z_c)\) and the coefficients are left-continuous in \(z=z_c\). Reviewing the definition of \(\hat{\Phi }_z(k)\) and \(\hat{F}_z(k)\) in (1.33)–(1.34), we conclude that these functions are continuous in \(z\in (z_I,z_c)\) and left-continuous at \(z=z_c\).
-
(c)
The dominated convergence theorem implies that
$$\begin{aligned} G_{z_c}(x)&= \lim _{z\nearrow z_c}G_z (x) = \lim _{z\nearrow z_c} \int _{(-\pi ,\pi )^d}\frac{\hat{\Phi }_z(k)}{1-\hat{F}_z(k)} {\mathrm e}^{{\mathrm i}k\cdot x}\frac{d^dk}{(2\pi )^d}\nonumber \\&=\int _{(-\pi ,\pi )^d}\frac{\hat{\Phi }_{z_c}(k)}{1-\hat{F}_{z_c}(k)}{\mathrm e}^{{\mathrm i}k\cdot x}\frac{d^dk}{(2\pi )^d}, \end{aligned}$$(4.54)where we use the left-continuity of \(z\mapsto \hat{\Phi }_z(k)\) and \(z\mapsto \hat{F}_z(k)\) at \(z=z_c\) proved above, and we further note that \(\underline{\beta }_{ \scriptscriptstyle \alpha ,F}- \underline{\beta }_{ \scriptscriptstyle \Delta R,F}>0\) and \(\underline{\beta }_{ \scriptscriptstyle c,\Phi }-\beta _{ \scriptscriptstyle |\alpha ,\Phi |}-\beta _{{ \scriptscriptstyle R,\Phi }}>0\) together with (1.37) imply the infrared bound holds uniformly in \([z_I,z_c)\) for \(\hat{\Phi }_z(k)/[1-\hat{F}_z(k)]\), so that the integral in (4.54) is well defined. Thus, we still have the Fourier representation (1.32), with the understanding that \(\hat{G}_{z_c}(k)\) for \(k\ne 0\) is defined by \(\hat{G}_{z_c}(k)=\hat{\Phi }_{z_c}(k)/(1-\hat{F}_{z_c}(k))\). Since \(\hat{F}_{z_c}(0)=1\), this characterization can not be used for \(k=0\). This completes the proof of Proposition 4.5(iii).
\(\square \)
5 Numerical bounds
In this section we discuss the ideas underlying the numerical computation of our bounds on the NoBLE coefficients. These ideas are model independent, while the implementation itself is not. We first explain how we compute the numerical bounds on the SRW-integrals that we have used for the improvement of bounds in Sect. 3 and to obtain numerical bounds on the coefficients. Then, we explain how the bootstrap functions are used to bound simple diagrams. At the end of this section, we explain how we compute the \(\beta ^{\text {abs}}_{\bullet }\) as sums over \(\beta ^{{ \scriptscriptstyle ( \mathrm{N})}}_{\bullet }\), which is not straightforward as the bounds on the NoBLE coefficients are stated in the form of matrix-products.
5.1 Simple random walk integrals
We bound the SRW-integrals \(I_{n,l}, K_{n,l}, T_{n,l}, U_{n,l}\) defined in (3.35)–(3.38). We first compute \(I_{n,m}(x)\) and then show that the other integrals can be bounded in terms of it. We compute \(I_{n,m}(x)\) using
which is obtained by writing \(\hat{D}(k)=1-[1-\hat{D}(k)]\) in (3.29). Using (5.1), the problem of computing \(I_{n,m}\) for general \(n,m\in \mathbb {N}\) simplifies to the computation of \(I_{n,0}\) and \(I_{0,m}\) for all \(n,m\in \mathbb {N}\).
5.1.1 Computation of the Green’s function
We compute \(I_{n,0}\) in the same way as Hara and Slade in [27, Appendix B], as we explain now. Let b(n, s) be the modified Bessel function of the first kind and F(t, d, n) the modified Bessel function, i.e.,
see e.g. [19, (8.401) and (8.406)] or [1, Section 9.6]. Using
we compute
see [27, Appendix B]. Most mathematical software packages, such as Mathematica, Matlab, and R, come with a method to compute the modified Bessel Integral. We have used Mathematica which allows to control the precision of the computation. With the built-in function we compute \(I_{4,0}(x)\) in \(d\ge 15\) and \(I_{5,0}(x)\) in \(d\ge 18\) up to a precision of \(10^{-20}\). To be able to compute these basic SRW-integrals in lower dimensions, we implement the algorithm given in [27, Appendix B], where also a rigorous bound on the error is proven. This algorithm is based on a Taylor approximation of the Bessel function.
5.1.2 Computation of the random walk transition probability
The computation of \(I_{0,m}(x)\) is a purely combinatorial problem as \((2d)^m I_{0,m}(x)=p_m(x)\), where \(p_m(x)\) is the number of m-step SRWs with \(\omega _0=0,\omega _m=x\). The value of \(p_n(x)\) can be obtained by simple combinatorial means. As an example, we explain the computation of \(p_6(0)\).
When \(\omega _0=\omega _6=0,\) the walk uses at most three different dimensions as it needs to undo all its steps. In the following, we distinguish between the number of dimensions used by the walker:
-
\(\rhd \) When the walk only uses one dimension, it steps three times to the positive direction (right) and three times to the negative direction (left). As any combination of left and right steps is allowed there are 6! / (3!3!) different possibilities for that. As there are d choices for the dimension used, there are \(d\frac{6!}{3!3!}\) such walks.
-
\(\rhd \) When the walk uses two dimensions, it makes 4 steps in one dimension and 2 in the other. As any combination of moves is allowed, there are 6! / (2!2!1!1!) different possibilities for that. Further, there are d choices for the dimension in which to take 4 steps, and likewise \(d-1\) choices for the dimension where 2 steps are made. Thus, there are \(d(d-1) \frac{6!}{2!2!}\) SRW 6-step loops using steps in exactly two dimensions.
-
\(\rhd \) When the walk uses three dimensions, then there are 2 steps in each dimension. There are 6! different orders for these 6 steps (including the back and forth steps in each of the three dimensions). Further, we have to choose 3 out of the d dimensions (without repetition). This gives a factor \(\frac{d(d-1)(d-2)}{3!}6!\).
This means that
where the multinomial coefficient is defined as
For our analysis, we use the values of \(p_n(x)\) for \(n\in \{0,\dots , 20\}\) for about 24 different values of x. We have implemented a program for this, and the algorithm can be found in the accompanying Mathematica notebooks (see also Sect. 6, where the Mathematica notebooks are described in more detail).
5.2 Bounds on related SRW-integrals
In this section, we show how to bound the integrals defined in (3.36)–(3.38). This section is an adaption of [27, Appendix B.1] by Hara and Slade, who computed numerical bounds on these integrals to prove mean-field behaviour for nearest-neighbour SAW in \(d\ge 5\).
Bound in terms of \(I_{n,l}, L_{n}, V_{n}\) We first show how we bound the integrals defining \(K_{n,l}(x),\) \(U_{n,l}(x)\) and \(T_{n,l}\) in terms of \(I_{n,l}\), as well as the related integrals \(L_n(x)\) and \(V_{n,l}\) defined by
and
We use the Cauchy–Schwarz inequality to bound \(K_{n,l}(x)\) and \(U_{n,l}(x)\) defined in (3.36) and (3.38) by
To bound \(T_{n,l}\) defined in (3.37), we use (3.32) and \(|\hat{D}^{\sin }(k)|\le 1/d\), respectively, to compute
This leads to
Next, we discuss improvements for the bounds on \(K_{n,l}(x)\) and \(U_{n,l}\). As \(|\hat{D}^{\sin }(k)|\le 1/d\) (recall (3.32)), we know that
For \(x=0\) and even l, we use \(\hat{D}^{ \scriptscriptstyle (0)}(k)=1, \hat{D}^{\sin }(k)\ge 0\) and (3.25) to compute
For \(x=0\) we can use a better bound for \(K_{n,l}\) in the form
Moreover, we use a different bound for \(l=0\). We note that, for \(n\ge 1\),
which implies that \(K_{n,l}(x)\le K_{n-1,l}(x)+K_{n-1,l+1}(x)+K_{n,l+2}(x)\), and thus
Computation of \(L_{n}\). By the definition of \(\hat{D}^{(x)}(k)\) in (3.34), it is not difficult to see that
The set \(\mathcal {P}_d\) and the operator \(p(x;\nu ,\delta )\) are defined in Definition 2.5. As we can compute \(I_{n,0}(x)\), we can also compute the sum in (5.17) directly.
The value of \(I_{n,0}(x)\) only depends on the number of entries that have a given absolute value, so that we can reduce the domain over which we sum. We explain this in two examples:
Example 1: Computation of \(L_n({e}_{1})\) As the first example, we show that
By symmetry, \(I_{n,0}({e}_{1}+ p({e}_{1};\nu ,\delta ))=I_{n,0}({e}_{1}+{e}_{2})\) for all \(\delta \in \{-1,1\}^d\) and \(\nu \in \mathcal {P}_d\) with \(\nu _1\ne 1\). This explains the third summand of (5.18), where we note that there are \((d-1)!(d-1)\) permutations \(\nu \) with \(\nu _1\ne 1\). That leaves \((d-1)!\) permutations \(\nu \) with \(\nu _1=1\). As all entries of \(p({e}_{1};\nu ,\delta )\) except the first one are zero, the values \(\delta _{2},\dots ,\delta _{d}\) do not affect the summand. If \(\delta _1=1\), then \({e}_{1}+ p({e}_{1};\nu ,\delta )=2{e}_{1}\) and if \(\delta _1=-1\), then \({e}_{1}+ p({e}_{1};\nu ,\delta )=0\). The two cases correspond to the first and second term in (5.18) and complete the proof of (5.18).
Example 2: Computation of \(L_n({e}_{1}+{e}_{2})\) As the second example, we derive that
There are \(2(d-2)!\) permutations \(\nu \) with \(\{\nu _1,\nu _2\}=\{1,2\}\). Further, there are \(2(d-2)!(2d-2)\) permutation \(\nu \) that map 1 to \(\{3,\dots , d\}\) and 2 to \(\{1,2\}\). That leaves
permutations \(\nu \) that do not map 1 and 2 to the first coordinates, i.e., \(\nu \) for which \(\{\nu _1,\nu _2\}\cap \{1,2\}=\varnothing \). For these \(\nu \),
which yields the first summand of (5.19). The second corresponds to the case that either \({e}_{1}\) or \({e}_{2}\) is mapped to one of the first two coordinates. For example, let us assume \(\nu _1=1\) and \(\nu _2=3\), then
depending on the sign of \(\delta _1\). This gives the second summand of (5.19). If we map \({e}_{1}+{e}_{2}\) to both of the first two coordinates, then
which only depends on \(\delta _1\) and \(\delta _2\). This gives the third summand of (5.19) and completes the proof of (5.19).
Computation of \(V_{n,l}\) The equality (3.25) implies that
From this, we conclude that
Bounds on the suprema of \(I_{n,l}(x), K_{n,l}(x), T_{n,l}(x), U_{n,l}(x)\) In Sect. 3.3, we have bounded \(\mathcal {H}^{n,l}_z(x)\) in terms of SRW-integrals. To compute the bound on \(f_3\), we need to rely on
for different sets of vertices S. For finite sets, we simply take the maximum of the elements. To obtain bounds for infinite S, we use monotonicity of the SRW-integrals as formulated in the following lemma:
Lemma 5.1
(Monotonicity of \(I_{n,l}(x)\) and \(L_{n,l}(x)\) in x) Let n be a positive integer and consider \(x,y\in \mathbb {Z}^d\) with \(x_1\ge x_2\ge \dots \ge x_d\ge 0\) and \(y_1\ge y_2\ge \dots \ge y_d\ge 0\). Then,
This lemma is a combination of [27, Lemmas B.3, B.4]. In the previous section, we have obtained bounds on \(K_{n,l}(x), T_{n,l}(x), U_{n,l}(x)\) for a given x in terms of \(I_{n,l}(x), L_{n}(x)\) and \(V_{n,l}\). Thus, the supremum in (5.26) is obtained for an x with the lowest order in the sense of Lemma 5.1. Therefore, when we use the following infinite set \(Q=\{ x \in \mathbb {Z}^d:\sum _i |x_i|>2\}\), we bound the corresponding SRW-integrals by
5.3 Bounds implied by the bootstrap functions and SRW integrals
For the analysis presented in the previous sections, we use that bounds on the bootstrap functions \(f_1, f_2\) and \(f_3\) imply bounds on the NoBLE coefficients, see e.g., Assumptions 2.7 and 4.3. In the model-dependent papers, we prove that the coefficients can be bounded by combinations of simple diagrams. Simple diagrams are diagrams arising from combinations of two-point functions, like the triangle diagram that we have already seen for percolation:
The simple diagrams can then be bounded using the bootstrap function \(f_2\), e.g.,
which can be computed numerically. In this section, we present the bounds that we use in our implementation of the analysis. These bounds are optimized so as to obtain the best numerical bounds on \(\beta \) possible for Assumption 4.3.
5.3.1 Simple and repulsive diagrams
In this section, we explain how to bound simple diagrams and repulsive diagrams, that we define below.
The bounds on the simple diagrams are model dependent. However, for all models that we consider, the bounds are using the same idea that we present below. We require some notions that have not been introduced yet, namely, the minimal length of an interaction, the modified two-point function and repulsive diagrams. As an example, we give the definitions for percolation. The definitions for LT and LA are straightforward generalizations.
For percolation, we define \(\{x \mathop {\longleftrightarrow }\limits ^{m} y\}\) to be the event that there exists a path consisting of at least m open bonds connecting x and y. Similarly, we define \(\{x \mathop {\longleftrightarrow }\limits ^{\underline{m}} y\}\) as the event that there exists a path consisting of exactly m open bonds connecting x and y. [This is not the same as the event that the graph distance in the percolation cluster equals m, but it implies that it is at most m.] To characterize these interactions, we define the adapted two-point function, which are given for percolation by
For all models under consideration the following holds, for all \(n \in \mathbb {N}\),
where \(c_m(x)\) is the number of m-step self-avoiding walks starting at the origin and ending at x. A diagram is repulsive if the paths involved do not intersect. For percolation, for example, the repulsive bubble and triangle are given by
where the symbol \(\circ \) denotes the disjoint occurrence, which is a standard notion in percolation theory, see e.g., [20]. For the examples above, it means that the occupied paths that are required to exist make use of disjoint sets of bonds.
Below, we use the symbol \((f\otimes g)(x)\) to describe that the paths involved for f are disjoint from the path involved in g. For example, \((G_{n,z}\otimes G_{m,z})(x)\) represents the diagram where the path used in \(G_{n,z}\) is disjoint from that used in \(G_{m,z}\). We define \(a_n(x)\) to be the number of n-step simple random walk from 0 to x that never use a bond twice, and note that \((a_{n}\otimes a_{m})(x)\le a_{n+m}(x)\). Further, \((a_n\otimes G_{m,z})(x)\) represents the combination of an n-step SRW path counted in \(a_n\) and a percolation path of length at most m, where, given the n-step SRW path, \(G_{m,z}(x)\) is the probability that an occupied percolation path exists that uses different bonds than the n-step SRW. The bounds that we explain below rely on the following bounds on the two-point function that hold for all models that we consider:
for \(s,n,m\in \mathbb {N}\) with \(s>m\).
5.3.2 Bounds on simple diagrams
Here we derive efficient numerical bounds on simple diagrams. Throughout this section, we fix \(n\in \mathbb {N}\) and \(m_i\in \mathbb {N}\) for \(i=1,\dots , n\). Further, we use the notation \(m_{i,j}=\sum _{s=i}^j m_s\).
Assuming bounds on the bootstrap functions, we obtain the following bound for non-repulsive diagrams from (5.33):
When \(m_{1,n}\ge 10\), we also use this bound also for the repulsive diagrams. For \(m_{1,n}<10\), we instead use the repulsiveness to reduce the numerical bounds in most cases by around \(50\%\). We obtain these improved bound by extracting short, explicit contributions. In high dimensions, short connections typically give the leading contribution to diagrams, so treating them more precisely often pays off. This requires the computation of \(a_n(x)\), for all \(x\in \mathbb {Z}^d\) and \(n\in \mathbb {N}\). For \(n<10\), we compute these values using a simple Java program that can be downloaded from the website of the first author [14].
We start by explaining the bound on the repulsive bound for the example of a bubble. We fix an \(M\in \mathbb {N}\) with \(M \ge m_1+m_2\) and use (5.38) to obtain
We extend this idea to obtain a bound on the triangle of the form
In the same way, we bound the square by
5.3.3 Bounds on weighted diagrams
Weighted diagrams, such as \(\mathcal {H}^{n,l}_z(x)\) in (3.10), are bounded using the bootstrap function \(f_3\), defined in (2.3). It is especially beneficial to extract explicit contributions from the weighted diagrams, as the bound produced by \(f_3\) is not very sharp and \(\mathcal {H}^{1,l}_z(x)\) decreases quite fast when we increase l. We conclude from (5.37) that, for \(l\le M\),
For x that are close to the origin we can bound \(\mathcal {H}^{0,i}_z(x)\) quite efficiently. We abbreviate \(H_{z}(x)=\Vert x\Vert _2^2G_z(x)\) and compute that
Most of the weighted diagram that arise in our bounds on the NoBLE coefficient are repulsive. Using this repulsiveness, we can make another substantial improvement. As an example, let us consider \((a_1\otimes H_{z})(0)\). All connections counted in \(H_z\) need to make at least three steps as the direct step is used by \(a_1\), so that
which is numerically a factor 1 / 2d better than the bound in (5.45). If we consider two explicit steps of \({e}_{\iota }+{e}_{\kappa }\), then we obtain the bound
In our computations we have extracted all paths up to a length of six and manually computed the number of percolation paths that do not use any bond of the first path. This leads to excellent bounds on closed weighted repulsive diagrams. For bubbles and triangles, we extend the idea used in (5.40), (5.41) for \(m_1,m_2\in \mathbb {N}\) with \(m_1+m_2<6\), to compute that
The terms involving \(a_{i}\otimes H_{z}\) are computed explicitly. All contributions involving a \(G_z\) factor also contain a factor \(a_6\), numerically making them of order \(d^{-3}\). Since \(H_z(y)=\Vert y\Vert ^2G_z(y)\), we can bound these minor contributions using \(f_3\) by removing the added restrictions that the \(\otimes \) convolution imposes and replacing it by a normal convolution. In this bound, we even bound \(a_6(y)\le (2d)^6 D^{\star 6}(y)\). Following this strategy, we reduce the effect of the bad bound \(f_3\) and enhance our numerical bounds.
5.4 Analysis of matrix-valued diagrammatic bounds
In Sect. 4, we use the bounds in Assumption 4.3 to bound the terms appearing in the rewrite of the NoBLE equation. These bounds are stated in terms of the functions \(\Xi ^{{ \scriptscriptstyle ( \mathrm{N})}}\) and \(\Xi ^{{ \scriptscriptstyle ( \mathrm{N})},\iota }\). Bounds on these quantities are proved in the model-dependent articles, where they are stated in terms of matrix products, such as
where \(\vec h,\vec v,\vec w\in \mathbb {R}_+^n\) and \(\mathbf{B},\mathbf{C}\in \mathbb {R}_+^{n\times n}\) for some \(n\ge 2\) and \(N\ge 0\). We need to sum these bounds over various sets of N to create \(\beta _{\bullet }^{ \scriptscriptstyle \text {abs}},\beta _{\bullet }^{ \scriptscriptstyle \text {odd}}\) and \(\beta _{\bullet }^{ \scriptscriptstyle \text {even}}\).
In this section, we explain how we compute the sum of these estimates. As a first step, we compute the eigensystem/spectrum of \(\mathbf{B}\), so the left eigenvectors \(\vec \eta _i\) and right eigenvectors \(\vec \zeta _i\) to the eigenvalue \(\lambda _i\). In our applications, there always exists a set of n independent left and right eigenvectors. As these vectors are linearly independent, there exists \(r_1,\dots , r_n\) and \(b_1,\dots ,b_n\) such that
We compute \(r_1,\ldots ,r_n\) using relations of the form
where \(\vec {r}^T=(r_1,\ldots , r_n)\), while the ith row of the matrix \({\varvec{\eta }}\) equals \(\vec \eta _i^T\). As the rows of the matrix \({\mathbf \eta }\) are independent vectors, \({\varvec{\eta }}\) is invertible, so that
which allows us to compute the \(a_i\). The \(b_i\)’s are computed in the same way. We define
and note that these are also eigenvectors of \(\mathbf{B}\) to the eigenvalue \(\lambda _i\). Thus, for \(N\ge 0\),
Using a geometric sum, we obtain
To create a closed form expression for the bound on the weighted diagrams appearing in (5.52) and use that \(\vec v_i\) and \(\vec w_j\) are eigenvectors of \(\mathbf{B}\) to obtain
For the second line, we rewrite the sums over N, M for fixed i, j as
We use the geometric sum identity
to bound (5.52) as
This highlight how we bound \(\Xi ^{{ \scriptscriptstyle ( \mathrm{N})}}\). The bounds on \(\Xi ^{{ \scriptscriptstyle ( \mathrm{N})},\iota }\) are obtained in a similar way.
Remark 5.2
(The numerics of the matrix powers and the eigensystem) In the classical lace expansion, similar exponential bounds appear for the Nth lace-expansion coefficient as a function of N, in which the base of the exponential is roughly bounded by the sum of the matrix elements \(\sum _{i,j} \mathbf{B}_{i,j}\) (in fact, it is worse, since there loops do not have length at least 4). We use the matrix-valued bound to optimally use the fact that the number of steps in shared lines in loops appearing in our lace-expansion bounds provide information about the number of steps in other lines that are part of the same loop. Such bounds are most easily expressed in terms of matrix products. In these matrix bounds, the largest eigenvalue of \(\mathbf{B}\) decides the magnitude of the bounds (see (5.58) and (5.62)). For example, for percolation and \(d=11\), the matrix \(\mathbf{B}\) equals
For this matrix, the largest eigenvalue equals \(\lambda _1\approx 0.073\), which is quite small, certainly when compared to \(\sum _{i,j} \mathbf{B}_{i,j}\approx 0.2\).
6 Completion of the bootstrap argument and conclusions
In this section, we complete the bootstrap argument, and explain how the conditions are verified in Mathematica notebooks. We start by summarizing where we stand.
Verification of the bootstrap conditions In Sect. 3, we have verified the bootstrap conditions. Part of this verification was the improvement of the bootstrap bounds on the functions \(f_1\), \(f_2\) and \(f_3\) defined in (2.1)–(2.3), the latter being technically the most demanding. A sufficient condition on the bounds on the NoBLE coefficients that allows us to improve the bounds on \(f_1,f_2\) and \(f_3\) is formulated in Definition 2.9 in terms of bounds on a simplified rewrite of the NoBLE formulated in (1.37), that is formulated in Assumption 2.7. These bounds on the rewrite are reformulated in terms of the original NoBLE coefficients \(\Xi _z,\Xi _z^\iota ,\Psi ^\kappa _z\) and \(\Pi ^{\iota ,\kappa }_z\) in Appendix D. The assumptions that we need to verify in the model-dependent papers [17] and [18] are Assumptions 2.2–2.4 and Assumptions 4.1–4.3. The initial Assumptions 2.6–2.8 are replaced using Proposition 4.5 in Sect. 4.
Implications of the completed bootstrap and proof main result The bound on \(f_1\) implies a bound on \(z_c\), while that on \(f_2\) implies that the infrared bound holds with an explicit estimate on the constant given by \(\Gamma _2\). Thus, \(f_1\) and \(f_2\) imply our main results for the model-dependent analysis for percolation in [18] and for LT and LA in [17]. The bound on \(f_3\) implies bounds on simple weighted diagrams, such as weighted lines, bubbles and triangles. These bounds are crucial in improving the bound on \(f_2\), which implies our main result.
We now discuss the improvement of \(f_3\) in more detail, splitting between the model-independent and the model-dependent parts, and their relations to SRW integrals, the bounds on the NoBLE coefficients and the Mathematica notebooks that finally complete the analysis and thus complete our proofs. We begin by discussing the model-independent improvement of \(f_3\) and SRW integrals.
Model-independent improvement of \(f_3\) and SRW integrals In Sect. 3.3, we have proven that the bootstrap conditions on \(f_3\) hold. Both for the verification of the conditions on the initial point in Sect. 3.3.3, as well as for the improvement of the bounds on \(f_3\) in Sects. 3.3.4, 3.3.5, we have formulated our conditions in terms of x-space SRW integrals such as \(I_{n,l}(x), K_{n,l}(x), T_{n,l}(x), U_{n,l}(x), L_{n}(x), V_{n}(x)\) and \(\mathcal {J}_{n,l}(x)\). The numerical values of these functions are crucial to allow us to verify that the required bounds on the initial point hold, and to improve the bound on \(f_3\). Thus, in order to perform a successful bootstrap analysis, we need to obtain rigorous numerical bounds on such SRW integrals. These numerical bounds are explained in detail in Sect. 5, using the ideas by Hara and Slade in [27]. These values are formulated in terms of integrals of Bessel-functions and are computed analytically, up to a specified precision in the Mathematica notebook available at [14]. This notebook needs to be compiled before the model-dependent parts can be performed, as the model-dependent analyses use them. We will explain the Mathematica notebooks in the next paragraphs. We first explain how the bounds on \(f_1,f_2\) and \(f_3\) can be used to obtain sharp numerical bounds on the NoBLE coefficients.
Model-dependent improvement of \(f_3\) and bounds on NoBLE coefficients Having accurate numerical bounds on all the SRW-integrals involved at hand, we can obtain all bounds on \(f_3\) formulated in Sect. 3.3, see in particular (3.87). The remaining main ingredient of the bounds on \(f_3\) is formed by the bounds on the NoBLE coefficients. The initial bounds on \(f_1,f_2,f_3\) imply bounds on \(z_c\), \(\hat{G}_z(k)\), as well as on several simple weighted diagrams implied by \(f_3\), in terms of \(\Gamma _1,\Gamma _2\) and \(\Gamma _3\). These, in turn, allow us to prove bounds on the NoBLE coefficients and to identify \(\beta _{\bullet }^{ \scriptscriptstyle ( \mathrm{N})}\) for every \(N\ge 0\) and \(\bullet \in \{ \Xi , \Xi ^{\iota }, \Delta \Xi , \{\Delta \Xi ^\iota ,0\},\{\Delta \Xi ^\iota ,1\}\}\), as formulated in Assumption 4.3. This is, next to the derivation of the NoBLE, the second main result in the model-dependent papers [17, 18], where [18] treats percolation, and [17] LT and LA. As a result, we then have all necessary bounds needed to verify the improvement of the bootstrap bounds. The numerical verification is performed in several Mathematica notebooks as we explain next.
Model-dependent and computer-assisted verifications using mathematica In order to complete the model-dependent and computer-assisted proof, we need to run the model-dependent Mathematica notebooks that can be found at the first author’s web page [14]. We first need to choose the dimension in SRW_basic.nb and run the file. This creates the numerical input needed for the model-dependent NoBLE computations, which is done in the files Percolation.nb, LT.nb, and LA.nb.Footnote 1 When compiled, these model-dependent files compute whether \(P(\gamma ,\Gamma ,\cdot )\) holds for the given input, \(\Gamma _1,\Gamma _2,\Gamma _3\) and \(c_\mu ,c_{n,l,S}\), by going through the loop described in Fig. 1: We first compute bounds on simple diagrams for the initial point \(z_I\), for which we do not need to rely on the bootstrap bounds in terms of \(\Gamma _1,\Gamma _2,\Gamma _3\), but we can rely directly on the link to SRW as formulated in Assumption 2.2. For \(z\in (z_I,z_c)\), we do rely on the bootstrap bounds to conclude bounds on the bootstrap functions. When both the bounds for \(z_I\) and for \(z\in (z_I,z_c)\), are bounded by the chosen \(\Gamma _i\) for \(i=1,2,3\), we conclude the existence of appropriate \(\gamma _i\), e.g. \(\gamma _i=(\Gamma _i+\text {(computed bound)})/2\), we have proven that \(P(\gamma ,\Gamma ,\cdot )\) holds. This numerical verification completes the argument for the given model in the given dimension. In [17, 18], it is also explained how we can then use monotonicity in the dimension d to obtain the result for all dimensions larger than the specified dimension. Further, the model-dependent notebooks contains an algorithm that helps to choose the optimal value for the constants \(\Gamma _1,\Gamma _2,\Gamma _3\) and \(c_\mu ,c_{n,l,S}\). This is explained in the implementation. See e.g., [18] for a more extensive discussion for percolation.
Complete version of the mathematica SRW files Next to the basic version of the SRW notebooks, we also provide a complete version, which should be used when dealing with the models in relatively low dimensions. The notebook SRW.nb serves two purposes. First, it allows us to compute SRW integrals with the desired precision in dimensions close to the upper critical dimension. The file SRW_basic.nb uses built-in Mathematica functions, and can only be used for percolation in \(d\ge 15\), as otherwise the desired numerical precision cannot be guaranteed. In the file SRW.nb, we use a Taylor approximation of the Bessel function, as explained in detail in [27, Appendix B], instead, that gives reliable results for \(d\ge 9\). These computations make compiling SRW.nb take around an hour, while SRW_basic.nb is compiled in less than a minute. Second, SRW.nb allows the use of arbitrary index sets \(\mathcal {S}\) for \(f_3\), see (2.3). Using the basic version only the vertex sets \(S=0\) and \(S=\mathbb {Z}^d{\setminus }\{0\}\) can be considered. These extensions are crucial to reduce the dimension above which our results apply.
Notes
At the time of publication the LT and LA Mathematica files are not made publicly available, as the corresponding article is not finalised.
References
Abramowitz, M., Stegun, I.A. (eds.): Handbook of mathematical functions with formulas, graphs, and mathematical tables. Dover Publications Inc., New York, (1992) (Reprint of the 1972 edn.)
Aizenman, M., Barsky, D.J.: Sharpness of the phase transition in percolation models. Commun. Math. Phys. 108, 489–526 (1987)
Aizenman, M., Newman, C.M.: Tree graph inequalities and critical behavior in percolation models. J. Stat. Phys. 36, 107–143 (1984)
Barsky, D.J., Aizenman, M.: Percolation critical exponents under the triangle condition. Ann. Probab. 19, 1520–1536 (1991)
van den Berg, J., Keane, M.: On the continuity of the percolation probability function. In: Conference in modern analysis and probability (New Haven, Conn., 1982), vol. 26 of Contemp. Math., pp. 61–65. American Mathematical Society, Providence, RI (1984)
Bollobás, B., Riordan, O.: Percolation. Cambridge University Press, New York (2006)
Borgs, C., Chayes, J., van der Hofstad, R., Slade, G.: Mean-field lattice trees. Ann. Comb. 3(2–4), 205–221 (1999) (On combinatorics and statistical mechanics)
Borgs, C., Chayes, J., van der Hofstad, R., Slade, G., Spencer, J.: Random subgraphs of finite graphs. II. The lace expansion and the triangle condition. Ann. Probab. 33(5), 1886–1944 (2005)
Bovier, A., Fröhlich, J., Glaus, U.: Branched polymers and dimensional reduction. Phénomènes critiques. systèmes aléatoires, théories de jauge, Part I, II (Les Houches, 1984), pp. 725–893. North-Holland, Amsterdam (1986)
Broadbent, S.R., Hammersley, J.M.: Percolation processes. I. Crystals and mazes. Proc. Camb. Philos. Soc. 53, 629–641 (1957)
Brydges, D.C., Slade, G.: A renormalisation group method. I. Gaussian integration and normed algebras. J. Stat. Phys. 159(3), 421–460 (2015)
Brydges, D.C., Spencer, T.: Self-avoiding walk in 5 or more dimensions. Commun. Math. Phys. 97, 125–148 (1985)
Chayes, J.T., Chayes, L.: On the upper critical dimension of Bernoulli percolation. Commun. Math. Phys. 113(1), 27–48 (1987)
Fitzner, R.: http://www.fitzner.nl/noble/
Fitzner, R.: Non-backtracking lace expansion. Ph.D. thesis, TU Eindhoven (2013)
Fitzner, R., van der Hofstad, R.: Non-backtracking random walk. J. Stat. Phys. 150(2), 264–284 (2013)
Fitzner, R., van der Hofstad, R.: Mean-field behaviour for lattice animals for \(d\ge 18\) and lattice trees for \(d\ge 16\) (2015) (in preparation)
Fitzner, R., van der Hofstad, R.: Mean-field behavior for nearest-neighbor percolation in \(d > 10\) (2015) (preprint)
Gradshteyn, I.S., Ryzhik, I.M.: Table of Integrals, Series, and Products. Cambridge Studies in Advanced Mathematics, 5th edn. Academic press, USA (1994)
Grimmett, G.: Percolation, 2nd edn. Springer, Berlin (1999)
Grimmett, G., Kesten, H.: Percolation since Saint-Flour (2012) (preprint)
Hara, T.: Decay of correlations in nearest-neighbor self-avoiding walk, percolation, lattice trees and animals. Ann. Probab. 36(2), 530–593 (2008)
Hara, T., Slade, G.: The mean-field critical behaviour of percolation in high dimensions. In: Simon, B., Truman, A., Davies, I.M. (eds.) Proceedings of the IXth International Congress on Mathematical Physics, pp. 450–453. Bristol and New York (1989)
Hara, T., Slade, G.: Mean-field critical behaviour for percolation in high dimensions. Commun. Math. Phys. 128, 333–391 (1990)
Hara, T., Slade, G.: On the upper critical dimension of lattice trees and lattice animals. J. Stat. Phys. 59, 1469–1510 (1990)
Hara, T., Slade, G.: Critical behaviour of self-avoiding walk in five or more dimensions. Bull. Am. Math. Soc. 25, 417–423 (1991)
Hara, T., Slade, G.: The lace expansion for self-avoiding walk in five or more dimensions. Rev. Math. Phys. 4, 235–327 (1992)
Hara, T., Slade, G.: Self-avoiding walk in five or more dimensions. I. The critical behaviour. Commun. Math. Phys. 147, 101–136 (1992)
Hara, T., Slade, G.: Mean-field behaviour and the lace expansion. In: Grimmett, G. (ed.) Probability and Phase Transition. Kluwer, Dordrecht (1994)
Hara, T., Tasaki, H.: Critical behavior in a system of branched polymers. Prog. Theor. Phys. Suppl. 92, 14–25 (1987)
Heydenreich, M., van der Hofstad, R.: Progress in high-dimensional percolation and random graphs. Lecture notes for the CRM-PIMS Summer School in Probability (2016) (preprint)
Heydenreich, M., van der Hofstad, R., Sakai, A.: Mean-field behavior for long- and finite range Ising model, percolation and self-avoiding walk. J. Stat. Phys. 132(5), 1001–1049 (2008)
van der Hofstad, R., Sakai, A.: Gaussian scaling for the critical spread-out contact process above the upper critical dimension. Electron. J. Probab. 9, 710–769 (2004) (electronic)
van der Hofstad, R., Slade, G.: A generalised inductive approach to the lace expansion. Probab. Theory Relat. Fields 122(3), 389–430 (2002)
Hughes, B.D.: Random walks and random environments, vol. 1. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York (1995)
Hughes, B.D.: Random walks and random environments, vol. 2. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York (1996)
Lawler, G.F., Limic, V.: Random Walk: A Modern Introduction. Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (2010)
Lubensky, T.C., Isaacson, J.: Statistics of lattice animals and dilute branched polymers. Phys. Rev. A 20(5), 2130–2146 (1979)
Menshikov, M.V.: Coincidence of critical points in percolation problems. Soviet Math. Dokl. 33, 856–859 (1986)
Russo, L.: A note on percolation. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 43(1), 39–48 (1978)
Sakai, A.: Mean-field critical behavior for the contact process. J. Stat. Phys. 104(1–2), 111–143 (2001)
Sakai, A.: Lace expansion for the Ising model. Commun. Math. Phys. 272(2), 283–344 (2007)
Slade, G.: The lace expansion and its applications. Lecture Notes in Mathematics, vol. 1879. Springer, Berlin (2006)
Spitzer, F.: Principles of Random Walk, 2nd edn. Springer, New York (1976)
Tasaki, H.: Hyperscaling inequalities for percolation. Commun. Math. Phys. 113(1), 49–65 (1987)
Toulouse, G.: Perspectives from the theory of phase transitions. Il Nuovo Cim. 24, 234–240 (1974)
Acknowledgements
This work was supported in part by the Netherlands Organisation for Scientific Research (NWO) through VICI grant 639.033.806 and the Gravitation Networks grant 024.002.003. We thank David Brydges, Takashi Hara and Gordon Slade for their constant encouragement, as well as for several stimulating discussions. This work builds upon the work by Takashi Hara and Gordon Slade. We particularly thank Takashi Hara for sharing his handwritten notes on the proof of mean-field behavior for \(d\ge 19\), and explaining how this can be extended to \(d\ge 15\). We have thoroughly enjoyed our animated discussions with Takashi in July 2013, which allowed us to compare notes and estimates on triangles, two-point functions, etc. Without these discussions, it would have been much harder to compare our results to those of Hara and Slade. The work of RF was performed in part at Stockholm University in the period September 2013 until September 2015. The authors gratefully acknowledge the advice of the referee, who found many typos and gave many suggestions that significantly improved the presentation of this paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Notation
See Table 1 in Appendix.
Appendix B: Proof of lemmas 2.12, 2.13
Proof of Lemma 2.12
Using a telescoping sum identity, we write
We reorder the sum over x using the symmetry of \(x\mapsto g(x)\), to obtain
We use \(1-\cos (nt)\le n^2 [1-\cos (t)]\), see e.g. Lemma 2.13 below, and the symmetry of g to see that
\(\square \)
Proof of Lemma 2.13
We obtain (2.25) by taking the real part of the telescoping sum identity
In the following, we use that \(|\sin (x+y)|\le |\sin (x)|+|\sin (y)|\), \(|ab|\le (a^2+b^2)/2\) and \(1-\cos ^2(a)\le 2[1-\cos (a)]\) to conclude from (2.25) that
\(\square \)
Appendix C: Decomposition of \(\bigtriangleup \hat{G}_z(k)\) for the bootstrap function \(f_3\)
We improve the bound on the bootstrap function \(f_3\) in Sect. 3.3.5 using the decomposition of \(\bigtriangleup \hat{G}_z(k)\) into the five pieces \(\hat{H}_1(k)-\hat{H}_5(k)\) defined in (3.52)–(3.56), as stated in (3.57). We create this decomposition by expanding \(\bigtriangleup \hat{G}_z(k)\) in the form of the simplified rewrite, defined in (1.35)–(1.37), and group the terms with common factors. This decomposition is a key step in our analysis. The decomposition is long and tedious and, due to the many terms, prone to errors. For this reason, we explicitly perform it here in the appendix.
Expanding the terms. Our strategy is to first expand
and then group them in terms of their common factors. To not loose track of terms, we label them using the line number in the formula in which they appear, e.g., (C.6.a) and (C.8.d).
Before stating this, we remark how we extract SRW-contributions \(\hat{C}^*(k)\) from inverse powers of \((1-\hat{F}_z(k))\) using the notation introduced in (3.40)–(3.44):
Further, we recall the form of \(\hat{\Phi }_z(k)\) and \(\hat{F}_z(k)\), see (1.35)–(1.36), and note that
Then, we proceed by expanding the terms in (C.1).
First term of (C.1) Using (C.2) we compute
Second term of (C.1) We first note that
We use (C.3), (C.5) and \(\hat{\Phi }_z(k)=c_{{ \scriptscriptstyle \Phi },z}+\alpha _{{ \scriptscriptstyle \Phi },z}\hat{D}(k)+\hat{R}_{{ \scriptscriptstyle \Phi },z}(k)\) for the term containing \(\bigtriangleup \hat{F}_z(k)\) and obtain
For the term including the mixed derivatives we compute that
Third term of (C.1). The expand the last term of (C.1) as follows
Regrouping the terms In this section we group the terms (C.6.a)-(C.9.e) to derive \(\hat{H}_1(k)-\hat{H}_5(k)\).
Let us start by recalling that \(\hat{M}^*(k)=\hat{D}(k)-2 \hat{D}^{\sin }(k)\hat{C}^*(k)\) and see that
Reviewing the definition of \(\hat{H}_1(k)\) we see that
Then, we proceed with the term \(\hat{H}_2(k)\):
\(\hat{H}_3(k)\) captures the following terms:
In \(\hat{H}_4(k)\), we collect the double derivatives of the remainder terms.
The two remaining terms consist of mixed derivatives and are put into \(\hat{H}_5(k)\):
This completes the derivation of the split into \(\hat{H}_1(k)-\hat{H}_5(k)\).
Appendix D: Bound on the rewrite
Here we prove Proposition 4.5(ii). Namely, we prove that the bounds stated in Assumption 2.7 are implied by Assumptions 4.1–4.3, by computing expressions for the bounds required in Assumption 2.7 one after the other.
For better readability, we divide this into five steps: Step 1 contains the six relatively simple bounds stated in (2.8 2.9)–(2.10), while Steps 2-5 show the more elaborate bounds stated in (2.11)–(2.13). The bounds involved are not difficult, but rather somewhat tedious. Throughout this section, we omit the subscripts z and write, e.g., \(\mu =\mu _z\) and \(\bar{\mu }=\bar{\mu }_z\).
Step 1: bounds stated in (2.8 2.9)–(2.10)
-
(a)
The bound \(\beta _{ \scriptscriptstyle \mu }\) in (2.8 2.9) is also assumed in (4.30) of Assumption 4.3.
-
(b)
We recall the definition of \(c_{{ \scriptscriptstyle \Phi },z}\) in (4.23), use the bounds of Assumption 4.3 and the fact that the coefficients \(\Xi _z^{ \scriptscriptstyle ( \mathrm{N})},\Xi _z^{{ \scriptscriptstyle ( \mathrm{N})},\iota }\) are non-negative to conclude
$$\begin{aligned} 1-\beta _{{ \scriptscriptstyle \Xi _\alpha (0)}}^{ \scriptscriptstyle ( \mathrm{1-0})}- \frac{2d \mu }{1-\mu ^2}\beta _{{ \scriptscriptstyle \Xi ^{\iota }_\alpha ,I}}^{ \scriptscriptstyle ( \mathrm{0})}\le c_{{ \scriptscriptstyle \Phi },z}\le 1+\beta _{{ \scriptscriptstyle \Xi _\alpha (0)}}^{ \scriptscriptstyle ( \mathrm{0-1})} +\frac{2d \mu ^2}{1-\mu ^2}\beta _{{ \scriptscriptstyle \Xi ^{\iota }_\alpha ,II}}^{ \scriptscriptstyle ( \mathrm{0})}. \end{aligned}$$(D.1)In this and the following lines we bound \(\mu \) by \(\tfrac{\Gamma _1c_\mu }{2d-1}\).
-
(c)
For \(\alpha _{{ \scriptscriptstyle F},z}\), defined in (4.18), we use the bounds of Assumption 4.3 to obtain
$$\begin{aligned}&\frac{2d \mu }{1-\mu ^2} \left[ 1-\beta _{{ \scriptscriptstyle \sum \Psi ^{\iota }_\alpha ,I}}^{ \scriptscriptstyle ( \mathrm{1-0})} -\mu \beta _{{ \scriptscriptstyle \sum \Psi ^{\iota }_\alpha ,II}}^{ \scriptscriptstyle ( \mathrm{0-1})} -\frac{1}{1-\mu ^2} \bar{\beta }_{\sum \scriptscriptstyle \Pi _{\alpha }}^{ \scriptscriptstyle ( \mathrm{0})}\right] \nonumber \\&\quad \le \alpha _{{ \scriptscriptstyle F},z}\le \frac{2d \mu _z}{1-\mu _z^2} \left[ 1+\beta _{{ \scriptscriptstyle \sum \Psi ^{\iota }_\alpha ,I}}^{ \scriptscriptstyle ( \mathrm{0-1})} +\mu \beta _{{ \scriptscriptstyle \sum \Psi ^{\iota }_\alpha ,II}}^{ \scriptscriptstyle ( \mathrm{1-0})} -\frac{1}{1-\mu ^2} \underline{\beta }_{ \scriptscriptstyle \sum \Pi _{\alpha }}^{ \scriptscriptstyle ( \mathrm{0})}\right] . \end{aligned}$$(D.2)We bound \(\mu \) on the left-hand side of the inequality from below by \(\underline{\beta }_{ \scriptscriptstyle \mu }\).
-
(d)
The absolute value of \(\alpha _{{ \scriptscriptstyle \Phi },z}\) defined in (4.24) is bounded by
$$\begin{aligned} |\alpha _{{ \scriptscriptstyle \Phi },z}|=\max \left\{ 2d\beta _{{ \scriptscriptstyle \Xi _\alpha ({e}_{1})}}^{ \scriptscriptstyle ( \mathrm{1-0})} + \frac{2d \mu }{1-\mu ^2} \beta _{{ \scriptscriptstyle \sum \Xi ^{\iota }_\alpha ,I}}^{ \scriptscriptstyle ( \mathrm{0})}, 2d\beta _{{ \scriptscriptstyle \Xi _\alpha ({e}_{1})}}^{ \scriptscriptstyle ( \mathrm{0-1})}+ \frac{2d \mu ^2}{1-\mu ^2} \beta _{{ \scriptscriptstyle \sum \Xi ^{\iota }_\alpha ,II}}^{ \scriptscriptstyle ( \mathrm{0})}\right\} . \end{aligned}$$(D.3) -
(e)
To bound \(\sum _{x,\kappa }\Pi _z^{\kappa ,\iota }(x)\) we use that the coefficients are defined by an alternating series, as well as Assumptions 4.2, 4.3, to obtain
$$\begin{aligned} \sum _{x,\kappa }\Pi _z^{\kappa ,\iota }(x)&\le \sum _{N=0}^\infty \sum _{x,\kappa } \Pi _z^{{ \scriptscriptstyle ( \mathrm{2N})},\kappa ,\iota }(x) -\Pi _z^{{ \scriptscriptstyle ( \mathrm{1})},\kappa ,\iota }(x)\nonumber \\&\le \bar{\mu }\sum _{x,N,\kappa }\Xi _z^{{ \scriptscriptstyle ( \mathrm{2N})},\iota }(x) -\sum _{\kappa }\hat{\Pi }_z^{{ \scriptscriptstyle ( \mathrm{1})},\kappa ,\iota }(0) \nonumber \\&\le 2d \bar{\mu }\left( \sum _{N=0}^\infty \beta ^{ \scriptscriptstyle ( \mathrm{2N})}_{ \scriptscriptstyle \Xi ^\iota }\right) -\underline{\beta }_{ \scriptscriptstyle \sum \Pi }^{ \scriptscriptstyle ( \mathrm{1})}. \end{aligned}$$(D.4) -
(f)
In the same way, we obtain that
$$\begin{aligned} \sum _{x}\Psi _z^{\kappa }(x)\ge -\beta _{ \scriptscriptstyle \mu }\left( \sum _{N=0}^\infty \beta ^{ \scriptscriptstyle ( \mathrm{2N+1})}_{ \scriptscriptstyle \Xi }\right) +\underline{\beta }_{ \scriptscriptstyle \Psi }^{ \scriptscriptstyle ( \mathrm{0})}. \end{aligned}$$(D.5)
Step 2: bounds stated in (2.11) In the steps 2-5 we create bounds for the remainder terms, as defined in Sect. 4.1.3. For the bounding it is useful to note the explicit formulae for the remainder \(\hat{R}_{{ \scriptscriptstyle F},z}(k)\) and \(\hat{R}_{{ \scriptscriptstyle \Phi },z}(k)\):
and
Now, we start by bounding \(\hat{F}_n\) and \(\hat{\Phi }_n\), for \(n\ge 1\). Starting from (4.7), we take the absolute value into the sums and use Assumption 4.2 for all \(\Psi _z^\iota \) and \(\Pi ^{\iota ,\kappa }_z\) to obtain
As we sum over all x, the sums factorize and we obtain
In the same way, we obtain
Using the geometric sum, we compute that
Using these bounds, we obtain that \(R_{{ \scriptscriptstyle F},z}\) (defined in (D.6)) is bounded by
and \(R_{{ \scriptscriptstyle \Phi },z}\) (given in (D.7)) by
This proves the bounds stated in (2.11).
Step 3: The first bound in (2.12) We call a sum as appearing on the left hand side of (2.12) a weighted sum, where the factor \(\Vert x\Vert _2^2\) is called the weight (see also Sect. 2.5). To obtain a bound on weighted sums, we split the weight using (2.24). We explain this now in detail for the following contribution to \(\sum _x\Vert x\Vert _2^2|R_{{ \scriptscriptstyle \Phi },z}(x)|\):
We use Assumption 4.2 to bound \(\Psi ^{\iota }_z\) by \(\Xi _z\), and obtain
Then, we rewrite \(\Vert x\Vert _2^2\) using the equality in (2.24) as
Since \(\Xi \) is totally rotationally symmetric, we know that \(\sum _{x}x_i|\Xi (x)|=0\). Thus, the last term cancels. We apply the bounds of Assumption 4.3 to obtain
Now we extend this idea. First we use Assumption 4.2 to obtain
Then, we split the weight using the equality in (2.24). We note that \(x\mapsto \sum _{\iota } \Xi ^{\iota }(x)\) is totally rotationally symmetric so that any contribution due to the second sum in the equality in (2.24) cancels. After the split of the weight, the sums factor and we obtain
Other contributions to \(R_{{ \scriptscriptstyle \Phi },z}\) (recall (D.7)) are bounded in a similar straightforward manner, leading to the final bound
This proves (2.12) with \(\beta _{ \scriptscriptstyle \Delta R,\Phi }\) equal to the right-hand side of (D.21).
Step 4: The second bound in (2.12) We bound the weighted sum of \(R_{{ \scriptscriptstyle F},z}\) in the same way as for \(R_{{ \scriptscriptstyle \Phi },z}\). We require the following three additional bounds:
Next we explain how to derive these bounds for the example of (D.22).
First, we use (4.29) and then (2.24) to obtain
Then, we note that all terms containing a single \(x_\kappa \) cancel by the total rotational symmetry of \(\Xi \) and \(\sum _{\iota }\Xi ^\iota \), i.e.,
Applying the bounds of Assumption 4.3, we obtain (D.22).
For \(n\ge 2\), we bound \(F_n\) as we have bounded \(\Phi _n\) in Step 3. Indeed, first, we use that
We split the weight using the equality in (2.24), use that the sums factor and then use the bounds stated above to obtain
The additional contribution \(R_{{ \scriptscriptstyle F},z}\) (recall (D.6)) are bounded in a straightforward manner and we obtain the bound
We complete Step 4 by defining \( \beta _{ \scriptscriptstyle \Delta R,F}\) as the right-hand of (D.29).
Step 5: The bounds in (2.13) Now we compute a lower bound on \(\hat{R}_{{ \scriptscriptstyle F},z}(0)-\hat{R}_{{ \scriptscriptstyle F},z}(k)\):
which could also be negative. We could apply Lemma 2.12 and bound (D.30) from below by \(- \beta _{ \scriptscriptstyle \Delta R,F}[1-\hat{D}(k)]\). Since this bound plays a central role, we prefer to use a better bounds. For this, we note that \([1-\cos (k\cdot x)]\ge 0\) for all k and x. So we can create a lower bound by only consider the negative part of the function \(R_{{ \scriptscriptstyle F},z}\).
We are not able to identify the points x at which \(R_{{ \scriptscriptstyle F},z}(x)\) is negative. However, we can decompose all summands defining \(\hat{R}_{{ \scriptscriptstyle F},z}\) in (D.6) into a negative and a positive part as the coefficients were defined via alternating sequences. In this ways, we create the lower bound as follows:
where we applied Lemma 2.12 and (D.24) only in the very last step. We use this idea to bound all terms in (D.6), except the minor term \(\sum _{n=2}^\infty \hat{F}_n(k)\) and in this way obtain
We modified the desired inequality (2.13) here slightly for better readability. This proves the lower bound in (2.13) with \(- \underline{\beta }_{ \scriptscriptstyle \Delta R,F}\) equal to the right-hand side of (D.32).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fitzner, R., van der Hofstad, R. Generalized approach to the non-backtracking lace expansion. Probab. Theory Relat. Fields 169, 1041–1119 (2017). https://doi.org/10.1007/s00440-016-0747-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-016-0747-8