Sensitivity analysis of nonlinear frequency response of defected structures

Abstract

The computation of the steady-stateresponse of large finite element discretized systems subject to periodic excitations is unfeasible because of excessive run time and memory requirements. One could in principle resort to reduced order models stemming from the high fidelity counterparts, which typically require a solution time orders of magnitude smaller. However, when many simulations are required, as in the case of parametric studies, the overall effort could be still significant and the analysis process could be severely hindered. In this work, we propose a sensitivity approach to assess the influence of model parameters on the nonlinear dynamic response. As opposed to the costly evaluation of reduced order solutions over a range of excitation frequencies and model parameters, the sensitivities of a nominal response allow one to approximate the dynamic response by a simple evaluation of an expansion in the directions spanning the parameter space. Special care must be taken on the closure equation that needs to be appended to the system of equations stemming from the harmonic balance method. We discuss the limitations of the current constant frequency approach and propose an improvement. We demonstrate the merits of the proposed approach on a micro-electro-mechanical system affected by parameterized manufacturing defects. Leveraging from a previous contribution, the nonlinear response and the sensitivities are obtained from a reduced order model which is analytical in the defect parameters. Our procedure is able to deliver accurate probability density functions of quantities of interest (e.g. nonlinear resonance peaks, triple solution bandwidth, etc) against statistical distributions of manufacturing defects at negligible computational cost.

1 Introduction

Numerical methods for steady-state solutions of harmonically forced nonlinear systems are well established in the literature. A popular method is the Harmonic Balance (HB) [1], a frequency-based approach that relies on the expansion of the system steady-state response in truncated Fourier series. This results in a set of nonlinear algebraic equations for the unknown Fourier coefficients, which can be solved to obtain the steady-state response. Continuation algorithms are employed together with HB to compute the Frequency Response Curve (FRC), that is the set of steady-state solutions for varying excitation frequency. For many years, HB has been successfully applied to study deterministic systems.

In the last decade the field of nonlinear dynamics has made some efforts towards the investigation of parameter uncertainties on the FRCs. In order to model random processes and/or to take into account the lack of knowledge on the real system (epistemic uncertainty), mathematical models may feature uncertain input parameters. Common sources of uncertainties in mechanical systems are: variable geometry introduced by manufacturing tolerances, non uniform material properties, non-uniform contact surface parameters, non-ideal boundary conditions, or in case of epistemic uncertainties, inaccurate measured system properties. Uncertainties in the parameters result in non-deterministic frequency responses that can be investigated with Uncertainty Quantification (UQ) techniques.

In this article we focus the attention on uncertainties introduced by small shape imperfections in geometrically nonlinear structures. Defects in the geometry, stemming for example from manufacturing process, may result in non-negligible modifications of the nonlinear frequency response, as in the case of MEMS devices [2, 3].

The Monte Carlo Method (MC) [4] is one of the first tools developed in the literature for UQ and is still nowadays considered the benchmark for solution accuracy. This classical approach is based on repeated simulations of the nonlinear system for a set of deterministic parameters, randomly sampled from the stochastic parameter distribution. When the quantity of interest is the stochastic FRC, this translates in a repeated application of HB. For large systems, however, solving the nonlinear algebraic HB equations could be computationally unfeasible even for one simulation. It is for instance the case of MEMS, for which the equations of motions (EoM) are derived from a FE discretization that requires detailed meshing for a thorough description of complex geometry.

A possible option to overcome this issue is to apply HB to Reduced Order Models (ROM) of the original model, namely the Full Order Model (FOM). Projection-based ROMs can be constructed by selecting a suitable and reasonably small collection of vectors (reduced order basis) to approximate the full solution [5]. In this way, the number of degrees of freedom (dof) of the original system is significantly reduced, making HB computationally feasible.

Unfortunately, rate of converge of MC algorithm is slow, thus the number of responses required to obtain relevant statistical quantities is usually large. For this reason, even if computationally feasible, performing a MC analysis based on ROM to propagate uncertainties for nonlinear structures with stochastic imperfections, results in high computational cost. In fact, this approach sees the construction of a new ROM for each of the randomly sampled geometries. The cost associated to a single run for this operation is usually significant and scales with the size of the FOM, strongly impacting on overall time for MC. A possible solution to this problem is presented in [6, 7] and relies on the construction of a Parametric Reduced Order Model in the uncertain structural defects (DpROM). This operation is done only once upstream of MC and represents a fixed cost, independent of the number of parameter samples. With this latter approach, the computational cost associated to a single simulation run is considerably cut down, so that the overall computational burden for MC is also greatly reduced. Still, as it was described in [6, 7], DpROM requires additional generalized coordinates to properly describe the contribution of imperfections. For this reason, if on the one hand the explicit parametrization eliminates the cost associated to the ROM construction for every new parameter realization, on the other hand the increased size of the ROM impacts on the simulation times.

All in all, it seems more sensible and efficient to perform MC studies relying on methods which do not involve repeated simulations. Polynomial Chaos Expansion (PCE), Taylor series expansions and interval arithmetic are some methods falling into this category. PCE-based methods consist in expanding the HB Fourier coefficients of the response in a truncated series of orthogonal polynomials of the uncertain parameters. Coefficients of chaos polynomials can be determined following two different approaches: intrusive approaches based on a recast of HB equations to account for stochastic parameters or non-intrusive approaches that rely on nullification of the error at selected collocation points. Once coefficients of expansion are known, any large set of responses corresponding to different uncertain parameters could be obtained at almost null computational cost by multiple polynomial evaluations. In [8, 9], an intrusive PCE in combination with Multi Harmonic Balance was successfully applied to quantify the effects of uncertainties on the FRF of a linear rotor system. By the same authors, the PCE-based method was modified in order to propagate uncertainties in systems with geometric nonlinearities [10, 11]. In that context, the excitation frequency was considered non-deterministic but parameter dependent and thus was expanded in the polynomial chaos basis. This modification of the method was necessary to assure precise approximations, even in correspondence of returning points of the FRC, where multiple solutions for same excitation frequency may exist. In the computation of chaos polynomial coefficients, the author compared points on different FRCs satisfying a prescribed phase condition. In [12], a non-intrusive PCE-based method is used with the Asymptotic Numerical Method - Harmonic Balance (ANM-HB) [13]. In this case, spurious oscillations in the set of responses provided by PCE were successfully avoided by comparing points on different FRCs with the same “arc-length ratio”, a measure defined by the author. In [14,15,16] instead, stochastic amplitudes and excitation frequency were referred to the phase of first harmonic, in the non-intrusive computation of PCE coefficients. This approach is restricted to the case in which the phase is a monotonic function of the frequency for all the uncertain parameter values. In [17], the authors applied PCE to investigate the effect of uncertainties on the steady-state response of a Jeffcott rotor subjected to rub-impact and parameter uncertainties.

In [18], a surrogate model of the system is created exploiting an expansion of the response in Chebyshev Polynomials to which follows an interval problem to find the bounds of the FRC corresponding to prescribed parameter intervals. Coefficients of polynomial approximations are found by comparing points on different FRCs at the same polar angle in the frequency-amplitude plane, in the “Polar Angle Interpolation” approach as defined by the author. In [19], Chebyshev Polynomials have been exploited to model uncertainties in the steady state response of a system with backlash nonlinearity, in the framework of Interval Harmonic Balance Method (IHBM).

Taylor series-based UQ methods are far less popular than PCE methods in the field on stochastic nonlinear FRCs, probably for limited applicability to small parameter uncertainties. In [20], the author expanded the HB Fourier coefficients of nonlinear FRCs in a second-order Taylor series of the uncertain parameters. Coefficients of the Taylor series, namely Parameter Sensitivities, allowed easy prediction of frequency response bounds corresponding to small parameter intervals. Instead in [21], parameter sensitivities were used to asses statistical distributions of nonlinear FRCs of a bladed disk, for stochastic distribution of friction parameters, showing good agreement with MC results.

Both in [21] and [20], sensitivity-based approximations proved to accurately describe FRCs for small parameter variations from the nominal. However, even if in a nonlinear setting, in the test cases considered by the author, FRCs did not exhibit multiple solutions for the same excitation frequency. Moreover, sensitivity were performed at constant frequency. As it will be demonstrated in the present work, this approach to sensitivities leads to poor results in case of multiple solutions for same frequency. To deal with this problem, a new approach to sensitivity-based approximations of FRCs is here presented, in which frequency is allowed to vary. Once sensitivities are available, any FRC corresponding to any small perturbation in the uncertain parameters can be obtained by updating the nominal solution with Taylor series approximations. This “update” operation is practically inexpensive and can be exploited in a sensitivity-based MC approach to compute the FRCs.

In this paper we present a Sensitivity-Based MC (SB-MC) method for UQ of structures with geometrical imperfections, leveraging the availability of the parametric ROM (DpROM) presented in [7] and the small variance of flaws in real engineering applications.

The work is organized as follows: Section 2 recovers the fundamentals of HB and introduces the notation used throughout the paper; Section 3 reviews the sensitivity approach for nonlinear FRCs at constant frequency and presents our new approach, showcasing the main results and differences on a simple 1-dof problem. Section 4 sketches the main features of the DpROM which is then used in Section 5 to study a MEMS resonator. Finally, in Section 6 conclusions are drawn.

2 Harmonic balance for mechanical systems

We here briefly describe the HB method and introduce notation; the interested reader is referred to [1] for a complete dissertation. Let us consider the EoM of a n-dof nonlinear mechanical system, stemming from the FE discretization of the continuous problem:

$$\begin{aligned} {\varvec{M}}\ddot{{\varvec{q}}}+ {\varvec{D}}\dot{{\varvec{q}}}+ {\varvec{K}}{\varvec{q}}+ {\varvec{f}}({\varvec{q}},\dot{{\varvec{q}}}) = {\varvec{f}}_{\omega }(t), \end{aligned}$$

(1)

where ${\varvec{q}}\in \mathbb {R}^n$ is the vector of generalized coordinates, ${\varvec{M}}$, ${\varvec{D}}$, ${\varvec{K}}\in \mathbb {R}^{n\times n}$ are respectively the mass, damping and stiffness matrices, ${\varvec{f}}$ is the vector of nonlinear forces and ${\varvec{f}}_{\omega }$ is an external periodic forcing with angular frequency $\omega$, defined as

$$\begin{aligned} {\varvec{f}}_{\omega }(t) = {\varvec{f}}_{\omega ,c} \cos (\omega t) + {\varvec{f}}_{\omega ,s} \sin (\omega t). \end{aligned}$$

(2)

At steady state the response is assumed to be periodic, with the same period of excitation $T = \frac{2\pi }{\omega }$ and is expanded in a truncated Fourier series with H harmonic components as

$$\begin{aligned}{} & {} {\varvec{q}}(t) \approx ({\varvec{\psi }}\otimes {\varvec{I}}_n) {\varvec{Q}}, \end{aligned}$$

(3a)

$$\begin{aligned}{} & {} {\varvec{\psi }}(t) \triangleq \left[ 1,\, \cos (\omega t),\, \sin (\omega t),\, \dots ,\, \cos (H \omega t),\, \sin (H \omega t) \right] ,\nonumber \\ \end{aligned}$$

(3b)

$$\begin{aligned}{} & {} {\varvec{Q}}\triangleq \left[ {\varvec{Q}}_0^T,\,{\varvec{Q}}_{c,1}^T,\,{\varvec{Q}}_{s,1}^T,\,\dots ,\,{\varvec{Q}}_{c,H}^T,\,{\varvec{Q}}_{s,H}^T \right] ^T, \end{aligned}$$

(3c)

where ${\varvec{\psi }}\in \mathbb {R}^{1\times (2H+1)}$ is the basis of the Fourier expansion, ${\varvec{I}}_n$ is the identity matrix of dimension n, ${\varvec{Q}}\in \mathbb {R}^{n(2H+1)\times 1}$ is the unknown vector of harmonic amplitudes (with ${\varvec{Q}}_0,\,{\varvec{Q}}_{c,k},\,{\varvec{Q}}_{s,k},\,\in \mathbb {R}^{n\times 1}$, for $k=1,\dots ,H$) and $\otimes$ denotes the Kronecker product.

By taking time derivatives of the ansatz, expressions for velocities and accelerations write

$$\begin{aligned} \dot{{\varvec{q}}}(t)= & {} ( \dot{{\varvec{\psi }}} \otimes {\varvec{I}}_n) {\varvec{Q}}= \omega ( {\varvec{\psi }}\nabla \otimes {\varvec{I}}_n) {\varvec{Q}}, \end{aligned}$$

(4a)

$$\begin{aligned} \ddot{{\varvec{q}}}(t)= & {} (\ddot{{\varvec{\psi }}} \otimes {\varvec{I}}_n) {\varvec{Q}}= \omega ^2 ({\varvec{\psi }}\nabla ^2 \otimes {\varvec{I}}_n) {\varvec{Q}}, \end{aligned}$$

(4b)

where the derivative operator $\nabla$ is defined as

$$\begin{aligned} \nabla \triangleq \text {diag}\, (0, \nabla _1, \nabla _2, \dots , \nabla _H ),\quad \text {with} \quad \nabla _k \triangleq \begin{bmatrix} 0 &{} k \\ -k &{} 0 \end{bmatrix}. \end{aligned}$$

From Eq. (1), the residual in time domain is defined as

$$\begin{aligned} {\varvec{r}}(t) \triangleq {\varvec{M}}\ddot{{\varvec{q}}}+ {\varvec{D}}\dot{{\varvec{q}}}+ {\varvec{K}}{\varvec{q}}+ {\varvec{f}}({\varvec{q}},\dot{{\varvec{q}}}) - {\varvec{f}}_{\omega }(t). \end{aligned}$$

(5)

Time dependence is eliminated by applying a weighted residual approach in which the weight functions are the components of the Fourier basis ${\varvec{\psi }}$. In this way we define the HB residual as

$$\begin{aligned}{} & {} {\varvec{R}}({\varvec{Q}},\omega ) \triangleq \frac{1}{T} \int _0^{T}\begin{bmatrix} {\varvec{r}}(t,{\varvec{Q}})\\ 2 {\varvec{r}}(t,{\varvec{Q}}) \cos (\omega t)\\ 2 {\varvec{r}}(t,{\varvec{Q}}) \sin (\omega t)\\ \vdots \\ 2 {\varvec{r}}(t,{\varvec{Q}}) \cos (H \omega t)\\ 2 {\varvec{r}}(t,{\varvec{Q}}) \sin (H \omega t) \end{bmatrix}\text {dt}\nonumber \\{} & {} = \frac{1}{T} \int _0^{T}\left( {\varvec{C}}{\varvec{\psi }}^T \otimes \, {\varvec{I}}_n\right) \, {\varvec{r}}(t,{\varvec{Q}}) \text { dt}, \end{aligned}$$

(6)

where ${\varvec{R}}({\varvec{Q}},\omega ) \in \mathbb {R}^{n(2H+1)}$ and

$$\begin{aligned} {\varvec{C}}= \text {diag}(1,\,2,\,\dots ,\,2), \quad {\varvec{C}}\in \mathbb {R}^{(2H+1)\, \times \, (2H+1)}. \end{aligned}$$

Notice that the so defined HB residual is nothing but the collection of the first H+1 Fourier coefficients (using the sine-cosine representation) of the time domain residual ${\varvec{r}}(t)$.

By plugging Eqs. (3a), (4) and (5) into Eq. (6) we obtain

$$\begin{aligned} \begin{aligned}&{\varvec{R}}({\varvec{Q}},\omega ) =\, \frac{1}{T} \int _0^{T}({\varvec{C}}\, {\varvec{\psi }}^T \otimes \, {\varvec{I}}_n)\,( {\varvec{M}}\ddot{{\varvec{q}}}+ {\varvec{D}}\dot{{\varvec{q}}}+ {\varvec{K}}{\varvec{q}}\\&\qquad + {\varvec{f}}({\varvec{q}},\dot{{\varvec{q}}}) - {\varvec{f}}_{\omega }(t))\text { dt}\\&\quad = \, \underbrace{ \left( \omega ^2 \nabla ^2 \otimes {\varvec{M}}+ \omega \nabla \otimes {\varvec{D}}+ {\varvec{I}}_{2H+1} \otimes {\varvec{K}}\right) {\varvec{Q}}- {\varvec{F_{\omega }}}}_{{\varvec{R}}^{\,lin}}\\ {}&\qquad + \underbrace{ \frac{1}{T} \int _0^{T}({\varvec{C}}\, {\varvec{\psi }}^T \otimes \, {\varvec{I}}_n)\, {\varvec{f}}({\varvec{q}},\dot{{\varvec{q}}}) \text { dt}}_{{\varvec{R}}^{\,nl}}, \end{aligned}\nonumber \\ \end{aligned}$$

(7)

in which the expression of the linear residual ${\varvec{R}}^{\,lin}$ was derived by applying the mixed-product property¹ of the Kronecker product. Considering for example the residual of mass related terms we have that

$$\begin{aligned} \begin{aligned}&\frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n) {\varvec{M}}\ddot{{\varvec{q}}}\ \text {dt} \\&\quad =\, \frac{1}{T} \int _0^{T}\omega ^2 ({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{M}}) ({\varvec{\psi }}\nabla ^2 \otimes {\varvec{I}}_n)\,{\varvec{Q}}\text { dt}\\&\quad =\, \frac{1}{T} \int _0^{T}\omega ^2\,( ({\varvec{C}}{\varvec{\psi }}^T {\varvec{\psi }}\nabla ^2) \otimes {\varvec{M}}){\varvec{Q}}\text { dt}\\&\quad = \left( \frac{1}{T}\int _0^{T}{\varvec{C}}{\varvec{\psi }}^T {\varvec{\psi }}\text { dt }\right) \omega ^2 (\nabla ^2 \otimes {\varvec{M}}) {\varvec{Q}}\\&\quad = \, \omega ^2 (\nabla ^2 \otimes {\varvec{M}}) {\varvec{Q}}, \end{aligned} \end{aligned}$$

(8)

where we also have exploited orthogonality properties of Fourier basis functions. Moreover, the residual vector of forcing ${\varvec{F_{\omega }}}$ in Eq. (7) can be developed as

$$\begin{aligned}{} & {} {\varvec{F_{\omega }}}= ({\varvec{e}}_c \otimes {\varvec{I}}_n) {\varvec{f}}_{\omega ,c}+ ({\varvec{e}}_s \otimes {\varvec{I}}_n) {\varvec{f}}_{\omega ,s}\,, \end{aligned}$$

(9a)

$$\begin{aligned}{} & {} {{\textbf {e}}}_c \triangleq [0\ 1\ 0\ \dots \ 0]^T, \nonumber \\{} & {} {{\textbf {e}}}_s \triangleq [0\ 0\ 1\ 0\ \dots \ 0]^T, \quad {{\textbf {e}}}_c, {{\textbf {e}}}_s \in \mathbb {R}^{2H+1}. \end{aligned}$$

(9b)

Nullifying ${\varvec{R}}$ in Eq. (7) leads to the HB residual equation, that is a set of nonlinear algebraic equations in the unknown vector ${\varvec{Q}}$:

$$\begin{aligned} {\varvec{R}}({\varvec{Q}},\omega ) \, = \, {\varvec{0}}. \end{aligned}$$

(10)

2.1 Numerical solution

Usually the analyst’s interest is not in a single frequency response, but in the FRC, that is a branch of solutions of the HB equations in a frequency span. For this reason, $\omega$ is taken not as a constant parameter, but as an additional unknown, so that the FRC can be obtained using a Newton–Raphson method along with a pseudo arc-length continuation algorithm. According to this scheme, discrete points ${\textbf {X}}^{i} = [{\varvec{Q}}^{i\,T},\omega ^i]^T$ on the FRC are obtained, at the $i^{th}$ step of the continuation algorithm, by solving:

$$\begin{aligned} \tilde{{\varvec{R}}}\,({\textbf {X}}^i,{\textbf {X}}^{i-1},ds) = {\varvec{0}}\,, \quad \tilde{{\varvec{R}}} \triangleq {\left\{ \begin{array}{ll} {\varvec{R}}\,({\textbf {X}}^i) \\ p\,({\textbf {X}}^i,{\textbf {X}}^{i-1},ds)\, \end{array}\right. } \end{aligned}$$

(11)

where $p\,({\textbf {X}}^i,{\textbf {X}}^{i-1},ds) \in \mathbb {R}$ is the additional closure equation depending on the adopted continuation algorithm, ${\textbf {X}}^{i-1}$ is the solution of the previous continuation step and ds is the user provided value of the pseudo arc length.

At each continuation step the iterative Newton–Raphson method is employed to compute the solutions of the nonlinear algebraic system of equations:

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} \delta {\textbf {X}}_{(k)}^i = - {\varvec{J}}^{-1}\tilde{{\varvec{R}}}_{(k)}\\ {\textbf {X}}^i_{(k+1)} = {\textbf {X}}^i_{(k)} + \delta {\textbf {X}}^i_{(k)}, \end{array}\right. }\nonumber \\{} & {} \quad {\varvec{J}} = \frac{\partial \tilde{{\varvec{R}}}}{\partial {\textbf {X}}^i} \bigg |_{{\textbf {X}}^i_{(k)}}, \quad \tilde{{\varvec{R}}}_{(k)} = \tilde{{\varvec{R}}}\,({\textbf {X}}^i_{(k)},{\textbf {X}}^{i-1}), \end{aligned}$$

(12)

where the subscript k denotes the iteration number and ${\textbf {J}}$ is the Jacobian matrix.

While the linear part of the residual and of the Jacobian can be trivially evaluated, usually their nonlinear counterpart must be computed numerically, although in some special cases analytic solutions are available (e.g. for polynomials). Nonlinear residual is numerically computed by means of the Alternating Frequency-Time (AFT) algorithm, while we refer the reader to Appendix C for details on Jacobian evaluation. According to the AFT scheme, displacement vector ${\varvec{q}}(t)$ and velocity vector $\dot{{\varvec{q}}}(t)$ are evaluated at equidistant time snapshots in the period from the value of the Ansatz Coefficients ${\varvec{Q}}$. Upon substitution of these quantities into the nonlinear force relation ${\varvec{f}}({\varvec{q}},\dot{{\varvec{q}}})$, time snapshots of the nonlinear force vector are retrieved. Eventually the integral in Eq. (7) is numerically approximated by applying the Discrete Fourier Transform (DFT) to the snapshots of nonlinear forces, efficiently implemented with the Fast Fourier Transform (FFT) algorithm. It is important to remark that the number of time samples N in the AFT algorithm impacts on accuracy of the numerically computed residual. If N is not sufficiently large, aliasing phenomena may occur leading to inexact residual evaluation. For the derivatives, because of nonlinearities, the number of required time samples is usually larger. For more details on the choice of N the reader is again referred to [1].

3 Sensitivity analysis

The nonlinear mechanical system in Eq. (1) can depend on a set of parameters, here collected in vector ${\varvec{p}}\in \mathbb {R}^m$. In this case the EoM read:

$$\begin{aligned}{} & {} {\varvec{M}}({\varvec{p}}) \ddot{{\varvec{q}}}+ {\varvec{D}}({\varvec{p}}) \dot{{\varvec{q}}}+ {\varvec{K}}({\varvec{p}}) {\varvec{q}}+ {\varvec{f}}({\varvec{q}},\dot{{\varvec{q}}},{\varvec{p}})\nonumber \\{} & {} \quad = {\varvec{f}}_{\omega ,c}({\varvec{p}}) \cos (\omega t) + {\varvec{f}}_{\omega ,s}({\varvec{p}}) \sin (\omega t)\, , \end{aligned}$$

(13)

in which the mass, damping and stiffness matrices along with the nonlinear force vector and forcing are assumed to be dependent on ${\varvec{p}}$.

By applying the HB method, we obtain a system of nonlinear algebraic equations parametrized by ${\varvec{p}}$:

$$\begin{aligned} {\varvec{R}}\,({\varvec{Q}},\omega ,{\varvec{p}}) = {\varvec{0}}. \end{aligned}$$

(14)

In many structural applications ${\varvec{p}}$ can be used to model a source of uncertainty acting on the system. The response can be computed for a nominal value of parameter ${\varvec{p}}^*$ and variations in the response can be investigated by considering its sensitivity to ${\varvec{p}}$. In this context we define a nominal solution point of the parametric HB equations as a point $\{{\varvec{Q}}^*,\omega ^*,{\varvec{p}}^*\}$ satisfying:

$$\begin{aligned} {\varvec{R}}\, ({\varvec{Q}}^*,\omega ^*,{\varvec{p}}^*) = {\varvec{0}}. \end{aligned}$$

(15)

In the following, $\bullet ^*$ denotes a quantity referred to the nominal conditions, although often the superscript will be omitted to ease notation.

3.1 Sensitivity at constant frequency

An approach commonly followed in the literature [20,21,22,23] is to compute the sensitivity of the response at constant excitation frequency $\omega$. For each nominal solution point, first-order sensitivities are obtained by total differentiation of the parametric HB equations in Eq. (14) with respect to the parameter vector ${\varvec{p}}$, at fixed nominal angular frequency $\omega ^*$:

$$\begin{aligned} \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}} \frac{d {\varvec{Q}}}{d {\varvec{p}}} + \frac{\partial {\varvec{R}}}{\partial {\varvec{p}}} = {\varvec{0}}\,, \quad \quad \frac{d {\varvec{Q}}}{d {\varvec{p}}} = -\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\frac{\partial {\varvec{R}}}{\partial {\varvec{p}}}\,. \end{aligned}$$

(16)

where all partial derivatives are implicitly assumed to be evaluated at the considered nominal solution point $\{{\varvec{Q}}^*,\omega ^*,{\varvec{p}}^*\}$ and under the hypothesis of non-singular Jacobian. Through further differentiation we get

$$\begin{aligned}{} & {} \left( \frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{Q}} ^2}\,\cdot \,\frac{d {\varvec{Q}}}{d {\varvec{p}}} + \frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{p}} \partial {\varvec{Q}}} \right) \, \cdot _{21}\, \frac{d {\varvec{Q}}}{d {\varvec{p}}} + \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}\,\cdot \, \frac{d^2 {\varvec{Q}}}{d {\varvec{p}}^2}\nonumber \\{} & {} + \frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{Q}} \partial {\varvec{p}}}\,\cdot \,\frac{d {\varvec{Q}}}{d {\varvec{p}}}+\frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{p}} ^2} = {\varvec{0}}\,, \end{aligned}$$

(17)

where we denoted with “$\cdot$” the contraction operation between last dimension of the first (multidimensional) matrix and the first dimension of the second matrix, while similarly “$\cdot _{ij}$” denotes the contraction between the i-th dimension of the first matrix and the j-th dimension of the second one². Moreover, the order of elements in derivatives corresponds to the order of derivation (see Appendix C). Again, all quantities are assumed to be evaluated at the considered nominal solution point, while the first-order sensitivity matrix is obtained from Eq. (16).

From Eq. (17), second-order sensitivities can be retrieved by solving $m^2$ systems of linear equations in $n(2H+1)$ unknowns:

$$\begin{aligned}{} & {} \frac{d^2 {\varvec{Q}}}{d {\varvec{p}}^2}_{:IJ} = -\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1} \left( \frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{Q}} \partial {\varvec{p}}}\,\cdot \,\frac{d {\varvec{Q}}}{d {\varvec{p}}} + \frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{p}} ^2} \right. \nonumber \\{} & {} \qquad \quad \qquad \left. +\left( \frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{Q}} ^2}\cdot \frac{d {\varvec{Q}}}{d {\varvec{p}}}{+} \frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{p}} \partial {\varvec{Q}}} \right) \,\cdot _{21}\,\frac{d {\varvec{Q}}}{d {\varvec{p}}} \right) _{:I J}\,, \nonumber \\ \end{aligned}$$

(18)

where $I,J \in \{1,\dots ,m\}$ and the sign “:” indicates all elements in the corresponding matrix dimension. The computational burden can be reduced exploiting Schwartz theorem

$$\begin{aligned} \frac{d^2 {\varvec{Q}}}{d {\varvec{p}}^2}_{IJK} = \frac{d^2 {\varvec{Q}}}{d {\varvec{p}}^2}_{IKJ}, \end{aligned}$$

(19)

so that the number of systems of equations to be solved for is reduced to $\frac{m^2}{2}+\frac{m}{2}$. Notice also that the solution of Eqs. (16) and (18) involves the inversion of the same Jacobian, thus enabling a faster solution process. The expressions for the partial derivatives of the residual ${\varvec{R}}$ with respect to ${\varvec{Q}}$ and ${\varvec{p}}$ appearing in the definition of the sensitivities are given in full in Appendix C.

Finally, it is possible to obtain Taylor series approximations of the FRCs corresponding to small perturbations of the parameter vector from the nominal as

$$\begin{aligned} {\varvec{Q}}({\varvec{p}}^* + \delta {\varvec{p}}) \approx {\varvec{Q}}^* + \frac{d {\varvec{Q}}}{d {\varvec{p}}} \delta {\varvec{p}}+ \frac{1}{2} \left( \frac{d^2 {\varvec{Q}}}{d {\varvec{p}}^2} \cdot \delta {\varvec{p}}\right) \delta {\varvec{p}}, \nonumber \\ \end{aligned}$$

(20)

where ${\varvec{Q}}^*$ is the nominal coefficient vector and $\delta {\varvec{p}}\in \mathbb {R}^m$ is the perturbation of the parameter vector from its nominal value ${\varvec{p}}^*$.

3.1.1 A practical case study

In order to asses quality of sensitivity-based approximations, let us consider the practical case study of a Duffing oscillator subjected to Coulomb friction. The equation of motion for the harmonically excited system is

Fig. 1

Nonlinear oscillator with friction scheme (top) and friction law plot (bottom)

$$\begin{aligned} m\, \ddot{q} + c\, \dot{q} + k\, q + k_3 \, q^3 + f_{\mu }(\dot{q}) = F \cos (\omega t), \end{aligned}$$

(21)

where

$$\begin{aligned} f_{\mu } = f_{lim} \tanh \left( \frac{\dot{q}}{\epsilon } \right) \end{aligned}$$

(22)

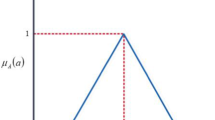
is the friction force regularized with the hyperbolic tangent smoothening function, $f_{lim}$ is the limit friction force and $\epsilon$ is the velocity tolerance [24]. A sketch of this system and of the regularized friction law is provided in figure 1. Sensitivities of the system’s response are computed at constant frequency with respect to the parameter vector ${\varvec{p}}= [k,\,k_3,\,f_{lim},\,F]^T$, taking as nominal parameters $k = 1$, $k_3 = 1$, $f_{lim} = 0.05$ and $F = 0.08$, with $m = 1$, $c = 0.06$ and $\epsilon = 0.02$.

In figure 2, we show the sensitivity-based approximations for a $-5\%$ reduction of $f_{lim}$ (Fig. 2a), for a $+5\%$ increase of the forcing F (Fig. 2b), for a $-4\%$ reduction in both the linear and cubic stiffness coefficients k and $k_3$ (Fig. 2c) and for all these variations at the same time (Fig. 2d), that is for $\delta {\varvec{p}}_\%=[-4,\,-4,\,-5,\,+5]^T$. This latter parameter perturbation results in a significant increase in the resonance peak amplitude, since external forcing increases while the stiffness and the limit friction force decrease, hence it is a good test case for evaluating sensitivity-based approximations.

Fig. 2

FRCs (for $F=0.08$) of the nonlinear oscillator for nominal parameters ${\varvec{p}}^*$ (), for a variation ${\varvec{p}}^*+\delta {\varvec{p}}$ () and corresponding approximations using first () and second-order () sensitivities computed at constant frequency. In each plot a different variation is considered and the modulus of first harmonic of the response is shown

Fig. 3

FRCs (for $F=0.12$ and $\delta {\varvec{p}}_\%=[-4,\,-4,\,-5,\,+5]^T$) of the nonlinear oscillator for nominal parameters ${\varvec{p}}^*$ (), for a variation ${\varvec{p}}^*+\delta {\varvec{p}}$ () and corresponding approximations using first () and second-order () sensitivities computed at constant frequency. (a) Modulus of the first harmonic, (b) cosine coefficient $A=Q_{c,1}$ and (c) sine coefficient $B=Q_{s,1}$

Both first- and second-order sensitivity-basedapproximations well capture the variation in the response resulting from the perturbations of the parameters. As expected, second-order sensitivity-based approximations are more accurate, especially close to the resonance peak. However, if the nominal forcing is increased from $F =0.08$ to $F=0.12$, considering once again the percentage parameter variation $\delta {\varvec{p}}_\%=[-4,\,-4,\,-5,\,+5]^T$, some points on the perturbed FRC are not anymore approximated correctly by the sensitivities, as shown in Fig. 3. This is due to the fact that sensitivities at constant frequency do not allow the points on the nominal FRC to move to neighboring points on the perturbed FRC, as they are at different frequency.

3.2 Sensitivity with the normal–direction approach

To overcome the limits of approximations based on sensitivities computed at constant excitation frequency, we introduce a new approach in which the frequency $\omega$ is allowed to vary with the parameter vector ${\varvec{p}}$. First, let us collect the harmonic amplitude vector ${\varvec{Q}}$ and excitation frequency $\omega$ in a unique column vector as

$$\begin{aligned} {\textbf {X}}= \begin{bmatrix} {\varvec{Q}}\\ \omega \end{bmatrix}, \quad {\textbf {X}}\in \mathbb {R}^{n(2H+1)+1}. \end{aligned}$$

(23)

We now seek a unique mapping from each nominal solution point to a point on the FRC corresponding to a slightly perturbed parameter vector ${\varvec{p}}= {\varvec{p}}^* + \delta {\varvec{p}}$. More precisely, we implicitly define ${\textbf {X}}$ as a function of ${\varvec{p}}$ only as

$$\begin{aligned}&{\textbf {X}}({\varvec{p}}) :U \subset \mathbb {R}^m \mapsto V \subset \mathbb {R}^{n(2H+1)+1} \nonumber \\&\quad \text {such that:} \quad \hat{{\varvec{R}}}\triangleq \begin{bmatrix} {\varvec{R}}\,({\textbf {X}}({\varvec{p}}),{\varvec{p}}) \\ g\,({\textbf {X}}({\varvec{p}}),{\varvec{p}}) \end{bmatrix} = {\varvec{0}} \end{aligned}$$

(24)

where U and V are open sets in the neighbourhood of ${\varvec{p}}^*$ and ${\textbf {X}}^*$, respectively, and $g({\textbf {X}}({\varvec{p}}),{\varvec{p}})\in \mathbb {R}$ is an additional closure equation. Notice that all the points belonging to a branch of the FRC in V, corresponding to any parameter value ${\varvec{p}}\in U$, satisfy the first condition ${\varvec{R}}={\varvec{0}}$ in Eq. (24), therefore the additional closure equation is essential to identify a unique point on the FRC, as qualitatively depicted in Fig. 4a. In other words, this scalar equation ensures that the number of equations equals the number of unknowns, that is $\dim ( \hat{{\varvec{R}}}) = \dim ({\textbf {X}}) = n(2H+1)+1$. If $\hat{{\varvec{R}}}\,({\textbf {X}}^*,{\varvec{p}}^*) = {\varvec{0}}$ and if $\det \left( \frac{\partial \hat{{\varvec{R}}}}{\partial {\textbf {X}}}\big |_{*}\right) \ne 0$, the Implicit Function Theorem ensures the existence of ${\textbf {X}}({\varvec{p}})$, U and V as defined in Eq. (24).

Fig. 4

(a) Qualitative sketch of implicit function definition. Without any closure equation $g({\textbf {X}},{\varvec{p}}) = 0$ in addition to HB equations, starting from a nominal solution point ${\textbf {X}}^*$ we could end up in any of the blue points on the FRC corresponding to the perturbed parameter value ${\varvec{p}}= {\varvec{p}}^* + \delta {\varvec{p}}$. The closure equation allows to uniquely define one point on this curve (in red). (b) Constant frequency approach ($g=\omega ({\varvec{p}})-\omega ^*=0$)

Differentiating the implicit function defined in Eq. (24) it is then possible to compute the total derivatives of ${\textbf {X}}$ with respect to ${\varvec{p}}$, and thus first- and second-order sensitivities as

$$\begin{aligned} \frac{d {\textbf {X}}}{d {\varvec{p}}} = -\frac{\partial \hat{{\varvec{R}}}}{\partial {\textbf {X}}}^{-1}\frac{\partial \hat{{\varvec{R}}}}{\partial {\varvec{p}}}\,, \end{aligned}$$

(25)

and

$$\begin{aligned}{} & {} \frac{d^2 {\textbf {X}}}{d {\varvec{p}}^2}_{:IJ} = -\frac{\partial \hat{{\varvec{R}}}}{\partial {\textbf {X}}}^{-1} \left( \frac{\partial ^2 \hat{{\varvec{R}}}}{\partial {\textbf {X}} \partial {\varvec{p}}}\,\cdot \,\frac{d {\textbf {X}}}{d {\varvec{p}}}+ \frac{\partial ^2 {\textbf {X}}}{\partial {\varvec{p}} ^2}\nonumber \right. \\{} & {} \qquad \qquad \left. +\left( \frac{\partial ^2 \hat{{\varvec{R}}}}{\partial {\textbf {X}} ^2}\,\cdot \,\frac{d {\textbf {X}}}{d {\varvec{p}}}\right. \right. \left. \left. + \frac{\partial ^2 \hat{{\varvec{R}}}}{\partial {\varvec{p}} \partial {\textbf {X}}} \right) \,\cdot _{21}\,\frac{d {\textbf {X}}}{d {\varvec{p}}} \right) _{:I J}\,, \end{aligned}$$

(26)

for $I,J \in \{1,\dots ,m\}$. Again, refer to Appendix C for the expressions of all partial derivatives of ${\varvec{R}}$ with respect to ${\textbf {X}}$ and ${\varvec{p}}$.

Eventually, sensitivity-based approximations are obtained as

$$\begin{aligned} {\textbf {X}}({\varvec{p}}^* + \delta {\varvec{p}}) \approx {\textbf {X}}^* + \frac{d {\textbf {X}}}{d {\varvec{p}}} \delta {\varvec{p}}+ \frac{1}{2} \left( \frac{d^2 {\textbf {X}}}{d {\varvec{p}}^2} \cdot \delta {\varvec{p}}\right) \delta {\varvec{p}}. \nonumber \\ \end{aligned}$$

(27)

Notice that in the constant frequency approach, discussed in Section 3.1, the implicit function definition with $g = \omega ({\varvec{p}}) - \omega ^*$ is tacitly assumed before taking the total derivatives with respect to ${\varvec{p}}$. A qualitative sketch of this parametrization is provided in Fig. 4b.

The choice of the closure equation g has a strong impact on the accuracy of sensitivity-based approximations. As already mentioned, while many points satisfy the HB residual equation (blue dots in Fig. 4a), not all of them are at the same distance from the starting nominal point (black dot). As the sensitivity-based solution uses a Taylor expansion, the more the mapping from ${\textbf {X}}^*$ to ${\textbf {X}}({\varvec{p}}^*+\delta {\varvec{p}})$ is close to linear in the expansion direction, the greater the accuracy we can expect.

To this purpose, let us consider a nominal solution point and a first-order expansion of the HB residual in (14):

$$\begin{aligned}{} & {} {\varvec{R}}\,({\textbf {X}},{\varvec{p}}) \approx \underbrace{{\varvec{R}}({\textbf {X}}^*,{\varvec{p}}^*)}_{= \,{\varvec{0}}} + \underbrace{\frac{\partial {\varvec{R}}}{\partial {\textbf {X}}} \bigg |_{*}\delta {\textbf {X}}+ \frac{\partial {\varvec{R}}}{\partial {\varvec{p}}} \bigg |_{*}\delta {\varvec{p}}}_{\delta {\varvec{R}}}, \end{aligned}$$

(28)

where $\delta {\textbf {X}}= {\textbf {X}}- {\textbf {X}}^*$ and $\delta {\varvec{p}}= {\varvec{p}}- {\varvec{p}}^*$. For a perturbation $\delta {\varvec{p}}$ of the parameter vector, we obtain an approximated FRC by nullifying the first variation of the HB residual $\delta {\varvec{R}}$ and solving for $\delta {\textbf {X}}$ the resulting one time underdetermined system:

$$\begin{aligned}{} & {} \frac{\partial {\varvec{R}}}{\partial {\textbf {X}}} \bigg |_{*}\delta {\textbf {X}}+ \frac{\partial {\varvec{R}}}{\partial {\varvec{p}}} \bigg |_{*}\delta {\varvec{p}}= {\varvec{0}}, \nonumber \\{} & {} \text {with} \quad \frac{\partial {\varvec{R}}}{\partial {\textbf {X}}}\bigg |_{*} \in \mathbb {R}^{n(2H+1)\times n(2H+1)+1}. \end{aligned}$$

(29)

The associated homogeneous system writes

$$\begin{aligned} \frac{\partial {\varvec{R}}}{\partial {\textbf {X}}}\bigg |_{*}{\varvec{\tau }}^* = {\varvec{0}}, \quad \quad {\varvec{\tau }}^* \in \mathbb {R}^{n(2H+1)+1}, \end{aligned}$$

(30)

where ${\varvec{\tau }}^*$ is one of the $\infty ^1$ solution vectors and is tangent to the nominal FRC at the nominal solution point. Thus, the linear system in Eq. (29) admits solutions of the form

$$\begin{aligned} \delta {\textbf {X}}= \delta {\textbf {X}}^p + c {\varvec{\tau }}^*, \end{aligned}$$

(31)

in which $\delta {\textbf {X}}^p$ is a particular solution of Eq. (29), $c \in \mathbb {R}$ an arbitrary constant and ${\varvec{\tau }}^*$ a particular non-null solution of Eq. (30).

Fig. 5

(a) Linear approximations of FRCs in a neighborhood of ${\textbf {X}}^*$; (b) mapping between FRCs based on the normal–direction approach; (c) mapping between FRCs based on the normal–direction approach neglecting the frequency dimension

Therefore, in a neighbourhood V of $\{{\textbf {X}}^*,{\varvec{p}}^*\}$, the linear approximation of the FRC corresponding to ${\varvec{p}}= {\varvec{p}}^* + \delta {\varvec{p}}$ is given by the set of points $\{{\textbf {X}}:{\textbf {X}}= {\textbf {X}}^* + \delta {\textbf {X}}^p + c {\varvec{\tau }}^*,\, c \in \mathbb {R}\}$, while the linear approximation of the nominal FRC, corresponding to ${\varvec{p}}= {\varvec{p}}^*$, is given by the set of points $\{{\textbf {X}}: {\textbf {X}}= {\textbf {X}}^* + c{\varvec{\tau }}^*, \, c \in \mathbb {R}\}$. Thus, in the space of harmonic coefficients ${\varvec{Q}}$ and frequency $\omega$, the linear approximations of the two FRCs are two parallel lines, as sketched in figure 5a.

Since the Taylor series approximations in Eq. (28) worsen as variations in $\delta {\textbf {X}}$ increase, a first reasonable option would be to map the nominal solution point to the closest point on the perturbed FRC. According to the geometric construction here presented, the closest perturbed point lies on the hyperplane orthogonal to the nominal curve, passing from the nominal solution point, as sketched in figure 5b. This condition can be embedded in the closure equation as

$$\begin{aligned} g = {\varvec{\tau }}^{*T}({\textbf {X}}({\varvec{p}}) - {\textbf {X}}^*) = 0\,, \end{aligned}$$

(32)

where ${\varvec{\tau }}^*$ is a non-null solution of Eq. (30).

In order to find a solution for Eq. (30), let us partition the tangent vector as ${\varvec{\tau }}^* = [{\varvec{\tau _Q}}^{*T},\tau _{\omega }^*]^T$ and solve the linear system of equations with arbitrary non-null $\tau _{\omega }^*$ as

$$\begin{aligned}{} & {} \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}\bigg |_{*}{\varvec{\tau _Q}}^* + \frac{\partial {\varvec{R}}}{\partial \omega } \bigg |_{*} \tau _{\omega }^* = {\varvec{0}},\nonumber \\{} & {} \quad \longrightarrow \quad {\varvec{\tau _Q}}^* = - \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}\bigg |_{*}^{-1} \frac{\partial {\varvec{R}}}{\partial \omega } \bigg |_{*}\tau _{\omega }^*. \end{aligned}$$

(33)

With the closure equation g, $\hat{{\varvec{R}}}({\textbf {X}}^*) = {\varvec{0}}$ and, if $\det (\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}} |_{*}) \ne 0$, then $\det (\frac{\partial \hat{{\varvec{R}}}}{\partial {\textbf {X}}} |_{*}) \ne 0$, as proved in Appendix A. The Implicit Function Theorem hypothesis are then satisfied and Eq. (24) implicitly defines ${\textbf {X}}({\varvec{p}})$ in the neighbourhood of each nominal solution point.

3.2.1 Limitations of the closure equation

Fig. 6

Comparison of different mappings between FRCs of a friction free nonlinear oscillator with varying stiffness. Each nominal solution point is mapped to the closest point on each perturbed FRC in the ${\varvec{Q}}-\omega$ (a, b, c) or, neglecting the frequency dimension, in the coefficients space only (d, e, f). In (a, d), for the two mappings, modulus of the response is computed for the nominal solution ($k^*$, ), and, for $\delta k \% = +10 \%$, with second-order sensitivities () and by re-running HB (). In (b-e), the two mappings (X(k), ) in the modulus-frequency plane. In (c,f), the two mappings in the Nyquist plot

Let us now consider the nonlinear oscillator presented in Section 3.1.1, this time with $m = 1,\, k = k_3 = 10,\, c = 0.05,\, F = 0.1$ and $f_{lim} = 0$. The forced steady-state response for this system can be accurately captured with a single harmonic resulting in a FRC in a three dimensional space ($Q_{s,1},\,Q_{c,1},\,\omega$), allowing for an effective graphical representation of the mapping introduced by the constraint equation g.

In Fig. 6a we plot the sensitivity-based approximation for a $+10\%$ increase of the linear stiffness k. As it can be observed, in some frequency ranges the accuracy of the sensitivity-based approximation is low.

In Fig. 6b and 6c, we plot the mapping introduced by closure equation (32) for equidistant interval increase in stiffness k, in the modulus-frequency and coefficients space (Nyquist plot), respectively. The mapping (red lines) has been obtained by exactly solving Eq. (24) for different values of the parameter ${\varvec{p}}= k$, starting from different nominal solution points. It can be observed that increasing k the FRC shifts to higher frequencies and the resonance peak gradually decreases, as expected. However, it can also be observed that since we are mapping each nominal solution point to the closest point on the perturbed FRC considering also the distance in the frequency space, we end up associating different “operating points”. This is clearly visible around frequency $\omega \approx 3.4$, where two red lines cross. The reason why this happens is that the proposed approach minimizes the distance between solutions in the ${\varvec{Q}}-\omega$ space. Ultimately, this attempt to minimize also $\delta \omega$ makes the mapping highly nonlinear and harder to capture with a Taylor expansion, effectively reducing the parameter validity range of the approximation.

3.2.2 A modified closure equation

Following these considerations, we modify the closure equation in such a way that the distance in the frequency space is no longer weighted in the mapping. The modified closure equation we choose is

$$\begin{aligned} g = {\varvec{\tau _Q}}^{*T}({\varvec{Q}}({\varvec{p}})-{\varvec{Q}}^*) = 0, \end{aligned}$$

(34)

where ${\varvec{\tau _Q}}^*$ is defined in Eq. (33). In other words, we map the nominal solution point to the point on the perturbed FRC such that the variation in the HB coefficient vector $\delta {\varvec{Q}}= {\varvec{Q}}({\varvec{p}}) - {\varvec{Q}}^*$ is orthogonal to the tangent restricted to the HB coefficients space. A qualitative geometric sketch of this parametrization is provided in Fig. 5c.

As proved in Appendix A, with this closure equation we have that under the (generally met) two conditions $\det (\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}) \ne 0$ and $\frac{\partial {\varvec{R}}}{\partial \omega } \ne {\varvec{0}}$, the Implicit Function Theorem hypothesis are satisfied. Moreover, in Appendix B, we also prove that this modified approach minimizes $||\delta {\varvec{Q}}||$ in a linear approximation of FRCs.

Going back to the example of the nonlinear oscillator already presented in the previous section, with the same increase in stiffness of $10\%$, we now see that second-order approximations of the mapping based on closure equation (34) (Fig. 6d) are more accurate than those based on closure equation (32) (Fig. 6a). Moreover, notice that in this second approach the mapping is orthogonal to the FRC in the space of HB coefficients (space of $A_1=Q_{c,1}$ and $B_1=Q_{s,1}$, in this example) as shown in Fig. 6f. This translates into a map where the modulus is approximately constant, as depicted in Fig. 6e, since now the frequency $\omega$ is free to move and the minimization is restricted to the norm of the HB coefficients variations.

Fig. 7

Comparison of approximations based on different closure equations for the friction free nonlinear oscillator subjected to increase in stiffness ($\delta k = +10 \%$). In (a) cosine coefficient $A = Q_{c,1}$, in (b) sine coefficient $B = Q_{s,1}$, in (c) modulus of the first harmonic for the nominal solution () and for the perturbed solution (). From each nominal solution point () a linear approximation of the perturbed FRC can be derived (). With first-order sensitivities, nominal points are mapped to the points on these approximations that are identified by () and (), for closure equations (32) and (34) respectively

A notable case is the one of pure translation in frequency of the FRC. Approximations based on closure equation (32), indeed, may lead to inaccurate results when the FRC is mainly subjected to a translation along the frequency axis for a given variation of the parameter vector. This is the case of the nonlinear oscillator introduced in section 3.1.1 with nominal parameters $m = 1$, $k = k_3 = 10^3$, $c = 0.2$, $F = 3$ and $f_{lim} = 0$ for an increase in linear stiffness $\delta k = 10 \%$. For this example we provide in Fig. 7 the HB coefficients $Q_{s,1}$,$Q_{c,1}$ and the modulus $||Q_{s,1} + i\, Q_{c,1}||$ (i is the imaginary unit) for the nominal and the perturbed FRCs, computed by running HB with a single harmonic. With reference to the current section, we recall that starting from each nominal solution point it is possible to obtain a linear approximation of the FRC corresponding to a perturbation in the parameters, through the linearization of the HB residual provided in Eq. (28). This approximation is given by the set of points $\{{\textbf {X}}: {\textbf {X}}= {\textbf {X}}^* +\delta {\textbf {X}}^p + c{\varvec{\tau }}^*\}$ and is plotted in Fig. 7 with dashed line, for different nominal expansion points ${\textbf {X}}^*$ identified with markers “$*$”. Notice that each approximation describes well small different sections of the curves. In a sensitivity-based expansion (Eq. (27)) limited to first-order terms, with the choice of closure equation g, we uniquely identify only one of these points, that will become part of the final approximation of the perturbed FRC. With reference to Fig. 7 this is equivalent to select the points on the linear approximations (dashed lines) marked with “${\varvec{\times }}$”, if closure equation g weighs variations in frequency (Eq. (32)), or marked with “${\varvec{+}}$”, if frequency dimension is neglected (Eq. (34)). As it can be observed, in the first case, since distance in frequency is weighted, the closure equation “forces” the points on the perturbed FRC to be at a similar frequency of the corresponding nominal solution points. In this way, the method displays the same issues presented by the constant frequency approach, resulting in poor approximations. Conversely, in the second case, since closure equation does not weigh variations in frequency, approximation points can freely move in the frequency dimension, allowing for greater accuracy.

3.2.3 A practical case study: monte carlo analysis

Let us consider the example of the nonlinear oscillator with friction presented in Section 3.1.1 and with nominal parameter vector ${\varvec{p}}^* = [1,\,1,\,0.2,\,0.12]^T$. The perturbed FRC for percentage parameter variation $\delta {\varvec{p}}_\% = [-20,-20,+5,+5]^T$, obtained with the sensitivities in the normal–direction approach formulation, is given in Fig. 8. Notice that the so computed approximation is smooth and solves the problems related to the constant frequency approach. Moreover, greater accuracy is achieved with respect to the case presented in Fig. 3 that featured the same nominal parameters, even if percentage parameters perturbations are increased.

Fig. 8

Approximations of the perturbed FRCs for the nonlinear oscillator with friction, based on first () and second-order () sensitivities in the normal–direction approach formulation. For comparison, the exact perturbed FRCs () and the nominal FRCs () are also plotted. Percentage parameter variation is $\delta {\varvec{p}}_\% = [-20,\,-20,\,-5,\,+5]^T$. In (a) we show the modulus of the first harmonic, in (b) the cosine coefficient $A=Q_{c,1}$ and in (c) the sine coefficient $B=Q_{s,1}$

Sensitivity-based approximations can be efficiently used to propagate uncertainty in the system’s parameters to the response, following a Monte Carlo (MC) approach. From the knowledge of the stochastic distribution of the parameters, the stochastic distribution of the response is retrieved by computing a set of responses for a sufficiently large number of randomly sampled parameter perturbations.

In contrast to conventional Monte Carlo, instead of running the numerical solution of the nonlinear HB equations, the solution is cheaply obtained with the sensitivities by applying the update Eq. (27), for each parameter variation. This comes at the expense of an additional fixed cost to compute sensitivities, which is easily amortized as the number of MC samples is increased. Finally, stochastic distributions of selected Quantities of Interest (QoI) can be obtained by post-processing the set of responses.

As a demonstration of accuracy and efficiency of the sensitivity-based MC, we apply the method to the nonlinear oscillator with friction, assuming different stochastic distributions of the parameters. The quantities of interest we consider are the resonance frequency and resonance amplitude. In Fig. 9 we show the Probability Density Function (PDF) for each of these quantities, computed for a Gaussian distribution of the linear and cubic stiffness k and $k_3$ (Fig. 9a), for a Gaussian distribution of friction limit force $f_{lim}$ (Fig. 9b), for a Gaussian distribution of external forcing F (Fig. 9c) and for the combination of all these distributions (Fig. 9d).

Each of the stochastic distributions is obtained both with conventional MC (i.e. solving the HB equations for the perturbed system) and with the sensitivity-based MC, randomly sampling the parameter distribution 1000 times (same seed). As it can be seen, the distributions computed with the two different approaches are in good agreement. For this 1-dof example, we obtained a speedup factor of 15.

Fig. 9

Probability Density Function of resonance frequency (red) and resonance amplitude (blue), numerically computed with classic MC (exact) and sensitivity-based MC (sensitivity). Parameter uncertainties considered are: (a) Gaussian distribution of linear and cubic stiffness ($3\sigma _p\% = [20,\,20,\,0,\,0]$); (b) Gaussian distribution of friction limit force $f_{lim}$ ($3\sigma _p \% =[0,\,0,\,20,\,0]$); (c) Gaussian distribution of forcing amplitude ($3\sigma _p \% =[0,\,0,\,0,\,20]$); (d) all the uncertainties presented before combined ($3\sigma _p \% =[20,\,20,\,20,\,20]$)

3.2.4 Hardening, softening and stability considerations

Before concluding this section, we report the frequency responses for an oscillator with no friction ($f_{lim}=0$) and with cubic stiffness $k_3=0$ (Fig. 10a) and $k_3=0.015$ (Fig. 10b). The remaining parameters $m=1$, $k=1$, $c=0.06$, $F=0.25$ are fixed. In the present case, changing the cubic spring value has the effect of changing the type of nonlinearity from hardening to softening, and vice versa. However, as it can be observed, the accuracy of the approximation is not affected by the type of nonlinearity, but rather by the magnitude of the variation, as expected from Taylor expansion theory. In some cases, the maximum allowed variation can be analytically derived [13], but this usually requires the knowledge and computation of derivatives one order higher than the desired order of the approximation.

Fig. 10

FRCs (with $H=5$) for a Duffing oscillator with nominal $k_3=0$ (a) and $k_3=0.015$ (b). For both cases, a variation $\varDelta k_3=\{-0.02,\,-0.01,\,+0.01,\,+0.02\}$ has been considered to produce a softening/hardening behavior. The frequency responses are shown for the nominal (), reference () models and for the second-order approximation (); for the former two, the unstable branches are dotted

Lastly, in Fig. 10 we also show with dotted lines the unstable branches of the solutions, obtained computing the eigenvalues of the monodromy matrix [1, 25], obtained with the shooting method implemented in NLvib. Although stability information is usually desired, this is not readily available neither for the HB-computed solutions nor for the sensitivity-based approximation. This means that for each point of the solution one has to set a proper analysis to determine stability and, for the monodromy matrix method we used, a forward time integration has to be performed for each solution point. This has been done for the nominal and reference curves. However, using the shooting method, the underlying hypothesis is that the solution point (used to set the initial conditions of the time integration) is actually on a periodic orbit, which is in general not true for the sensitivity-based solution (or even for HB-solutions with an insufficient number of harmonics). For this reason, such a stability analysis proves unreliable for the approximated solutions and is not shown here. As a final remark, we also point out that the computational burden associated to the stability analysis of the FRC would have probably defeated the benefits of the proposed method.

4 Defect-parametric reduced order model

Until now we presented the sensitivity analysis method for a generic case, showing some examples with lumped parameter models. In this section, we want to apply the method to FE structures with the aim to study the effect of manufacturing variations on the shape of the structures themselves. This task poses at least two issues. First, even a single solution with the Harmonic Balance method can be too expensive (or even unfeasible) for a FE model with a moderate number of dofs; secondly, shape parametrization techniques often involve a high number of parameters, meaning that a high number of sensitivities would need to be computed. As anticipated in Section 1, we propose to solve these problems applying the sensitivity approach to a Defect-parametric Reduced Order Model (DpROM). The latter, introduced in [6] and extended in [7], is here described in brief, leaving the details on its implementation to the aforementioned works.

4.1 DpROM description

The DpROM is a projection-based ROM which can parametrically describe a shape imperfection in a regime of geometric nonlinearity. Shape imperfections, or defects, are simply given by displacement fields which move the nodes of the nominal (i.e. without imperfections) structure into the defected configuration. These displacement fields may come from a previous study, measurements, or they can be artificially constructed. Each displacement field $\varvec{U}_j$ can be independently defined, and the final defected configuration will be given by the linear superposition of all the defects, that is:

$$\begin{aligned} {\textbf {x}}_d = {\textbf {x}}_0 + \varvec{U}\varvec{\xi }, \end{aligned}$$

(35)

where ${\textbf {x}}_d$ and ${\textbf {x}}_0$ are the defected and nominal configuration coordinates, respectively, ${\textbf {U}}=[{\textbf {U}}_1,\, \dots , \, {\textbf {U}}_m]$ is the matrix collecting m defect shapes, and where $\varvec{\xi }=[\xi _1,\,\dots ,\,\xi _m]^T$ is a column vector collecting each defect shape’s amplitude. In this context, $\varvec{\xi }$ takes the role of the parameter vector which governs the final defected shape of the structure under study.

The projection basis ${\textbf {V}}\in \mathbb {R}^{n \times r}$, being r the number of reduced coordinates $\varvec{\eta }\in \mathbb {R}^r$, is built using a set Vibration Modes (VM), their associated (Static) Modal Derivatives (MD) and Defect Sensitivities (DS), collected in the matrices $\varvec{\varPhi }$, $\varvec{\varTheta }$ and $\varvec{\varXi }$, respectively, so that the displacement vector ${\textbf {u}}$ can be approximated as

$$\begin{aligned} {\textbf {u}}\approx {\textbf {V}}\varvec{\eta }= \left[ \varvec{\varPhi },\, \varvec{\varTheta },\, \varvec{\varXi }\right] \varvec{\eta }. \end{aligned}$$

(36)

This choice, loosely speaking, is an extension of classic modal analysis, where the truncated set of eigenvectors of the system is augmented with MD to take into account nonlinearities and DS to take into account shape parametrization. Retaining a number $n_{vm}$ of VM, we have $n_{vm}(n_{vm}+1)/2$ MD and $n_{vm} m$ DS, for a total $r=n_{vm}(n_{vm}+2m+3)/2$. For more details on this projection method, again, see [7] and references therein.

Operating a Galerkin projection, we can write the governing equations for the DpROM as

(37)

where $\tilde{{\varvec{M}}}={\textbf {V}}^T{\varvec{M}}{\textbf {V}}$, and the nonlinear elastic forces take on a polynomial shape in the displacements³, the stiffness tensors also depending in a polynomial way on $\varvec{\xi }$ as

(38a)

(38b)

(38c)

In Eqs. (38), the left-subscripts denote with a number the order of the tensor, with a “n” a tensor computed for the nominal geometry and with a “d” (“dd”) a tensor whose last (two) dimensions are of size m (which are otherwise equal to r). For instance, . The full expressions for these tensors can be found in [7]. Furthermore, each of the above tensors and the reduced mass matrix write

$$\begin{aligned} \tilde{{\varvec{P}}}= \tilde{{\varvec{P}}}^\prime + \sum _{i=1}^{m} \xi _i \tilde{{\varvec{P}}}^{\prime \prime ,i}, \end{aligned}$$

(39)

where $\tilde{{\varvec{P}}}$ is a generic reduced matrix/tensor, $\tilde{{\varvec{P}}}^\prime$ is evaluated on the nominal volume and $\tilde{{\varvec{P}}}^{\prime \prime ,i}$ is a corrective term required to approximate the volume change introduced by the i-th defect⁴. For this reason, the mass matrix is also parameter-dependent. In the present work, Rayleigh damping is assumed as $\tilde{{\varvec{D}}}=\alpha _M\tilde{{\varvec{M}}}+\beta _K\tilde{{\varvec{K}}}$ and can be introduced in Eq. (37). We will also assume that the external forcing ${\varvec{f}}$ is approximately constant and does not depend on $\varvec{\xi }$. Finally, sensitivities can be computed for the DpROM using the derivatives of the stiffness and mass tensors given in Appendix D.

All in all, DpROM features a small set of reduced coordinates and an easy way to parametrize shape imperfections which results into polynomials, that can be efficiently used to compute sensitivities. Finally, notice once more that although greatly reducing the computational burden with respect to its corresponding FOM and its non-parametric ROM counterparts, DpROM may still take quite some time if several thousands of runs are required, as in the MC method. In the numerical example, we will show how beneficial the sensitivity analysis is in this sense.

5 Numerical test: MEMS oscillator

To demonstrate the potentialities of the proposed method, we now present the case of a single-axis MEMS gyroscope [26]. The structure is fixed in correspondence of the anchor points and is harmonically driven by comb-finger electrodes along the y-direction (see Fig. 11a). Due to this motion, when an external angular rate is present, the sense mass will experience a Coriolis force which will make the mass move in a direction orthogonal to the drive-axis (i.e. x or z-axes); this movement is then sensed by specifically designed electrodes to infer the angular rate [2]. Since the Coriolis-induced motion amplitude is typically 1-2 orders of magnitude smaller than the one along the drive-axis, manufacturing imperfections may have a great impact over the performances of these transducers and must be taken into account in the design phase.

Fig. 11

(a) Single-axis MEMS gyroscope model. The structure is fixed to the ground by the anchor points. (b) Mesh is swept along the z-axis and counts 23,307 hexahedral elements (Lagrangian, quadratic shape functions) and 451,089 dofs

5.1 Model and chosen defects

We constructed a FE model of the device using three-dimensional continuum elements (Lagrangian hexahedra with quadratic shape functions), counting 451,089 dofs. We used the material properties of Silicon (Young’s modulus $E=148\,GPa$, Poisson’s ration $\nu =0.23$, density $\rho =0.93\times 2330\,kg/m^3$, where 0.93 is the filling fraction to take into account the holes required by the production process), a Rayleigh damping with $\alpha _M=71.4$ and $\beta _K=0$ (corresponding to a quality factor of 2200 on the first vibration mode), and an equivalent concentrated forcing $F=0.5\, \mu N$ located in the middle of the drive combs. The DpROM⁵ is constructed using 2 VM, 2 shape defects, and their associated MD (3) and DS (4), for a total of 9 dofs.

Fig. 12

Shape defects (top view). (a) Overetch (values normalized over $oe=1\,\mu m$). (b) Detail with nominal mesh (black line, gray fill), defect deformation field (blue arrows) and defected mesh (red line). Underetch case is plotted for better readability. (c) Wall-angle defect, with $\theta =30^{\circ }$ for visibility and values normalized over the maximum displacement

The first shape defect is the so-called overetch, which corresponds to the erosion of the Silicon wafer happening during the MEMS fabrication process [27]. The latter may indeed result in excessive/deficient erosion of the material (over/underetching) with respect to the nominal overetch value, meaning that the final geometry will appear slightly thicker/thinner than the nominal one. In our FE model, this defect is obtained from a static linear analysis, performed in Comsol Multiphysics 6.0, where an inward/outward normal unitary displacement is imposed to all the vertical walls, while the top and bottom faces are fixed along the z-direction by rollers. This way, the $\xi _1$ parameter will correspond to the effective overetch (for $\xi _1>0$) or underetch (for $\xi _1<0$) variation. The results of the static analysis are shown in Fig. 12(a,b). The second defect shape is the so-called wall-angle, consisting in the fact that the vertical walls will have an angle with respect to the z-axis. The field we consider for our model, shown in Fig. 12c, is given by

$$\begin{aligned}{} & {} u(z)=\xi _2 \tan (\theta )(z-z_0), \nonumber \\ {}{} & {} v(z)=\xi _2 \tan (\theta )(z-z_0), w=0, \end{aligned}$$

(40)

being $u,\,v,\,w$ the displacement fields along x, y, z-axes, respectively, $z_0$ the elevation of the bottom surface, $\theta$ a typical (3$\sigma$-)value for the wall angle and $\xi _2 \in \left[ -1,\,1\right]$ the amplitude parameter. Notice that with this choice we consider simultaneously an angle with respect to the xz and yz-planes.

5.2 Monte Carlo analysis

For each shape defect amplitude, we consider a Gaussian distribution with null mean value and $3\sigma$-value equal to $\hat{\xi }_1=1$⁶ and $\hat{\xi }_2=1$. We first preliminary check that the approximated solutions provided by the DpROM and the sensitivity approach are sufficiently accurate with respect to a solution obtained with the non-parametric corresponding ROM⁷. To this purpose, in Fig. 13(a, d) the FRCs measured at forcing location for $\varvec{\xi }=[\pm \hat{\xi }_1,\,\hat{\xi }_2]$ are shown, corresponding to the $3\sigma$-corners of the parameter domain (notice that the sign of $\xi _2$ does not affect the solution). The FRCs show a significant hardening behavior, induced by the geometric nonlinearities of the clamp-clamp suspension beams connected to the drive frame. Under the assumption that the approximation improves for lower defect amplitudes, we deem these results accurate enough, even though a small deviation from the reference (ROM) is present. Notice that this error is to impute to the DpROM approximation, whereas the sensitivity approach reproduces the DpROM solutions accurately. Upon these considerations and for time constraints, the ROM solutions will not be computed anymore, and the comparison will be only between the DpROM solutions and their respective sensitivity-based approximations.

Fig. 13

(a,  d): First harmonic modulus and phase of the drive motion at forcing location, for DpROM$^*$ at $\varvec{\xi }={\varvec{0}}$ (), ROM (), 2$^{nd}$ order sensitivities (), DpROM () for $\varvec{\xi }=[\pm \hat{\xi }_1,\,\hat{\xi }_2]$. (b, c, e, f) Probability Density Functions for DpROM (blue, filled) and sensitivity-based approach (black solid line) for: (b) $\hat{f}$, frequency corresponding to the drive’s maximum amplitude (“resonance”); (c) $\varDelta f$, interval of frequencies where a triple solution exists (“bandwidth”); (e) drive maximum amplitude; (f) sense maximum amplitude

All the computations were carried out in YetAnotherFEcode v1.3.0 [28], with the addition of dedicated routines for the DpROM and sensitivity computation. For computational efficiency, some parts of the DpROM are built using Julia subroutines for tensor operations [29], as it will be indicated later in the computational times (see Table 1). The FRC are computed in NLvib [1], which is also included in YetAnotherFEcode v1.3.0, using MATLAB 2021b on a local machine equipped with an Intel(R) Xeon(R) Silver 4214 CPU @2.20 GHz and 256 GB RAM @2666 MHz. For the HB method, we used $H=5$ harmonics, a number $N_t=3H+1$ of time samples for the AFT of the nonlinear terms [30] and twice this number of samples for the AFT of the sensitivities.

For the Monte Carlo analysis, we generated 5000 random $\varvec{\xi }$ parameters vectors extracted from the aforementioned Gaussian distributions, then we ran as many simulations with the DpROM and computed as many solutions with the sensitivity approach. However, since the same solver parameters had to remain fixed while changing $\varvec{\xi }$, some solutions failed, so that the effective number of samples that we considered is $N_{mc}=4612$. Notice that this is a problem only for the DpROM, where a simulation must be performed, but not for the sensitivity approach, where the solution is simply an update of the nominal solution. However, for the sake of comparison, we discarded the failed cases for both the approaches.

Figure 13b, c, e, f show the Probability Density Functions for some QoI, namely the frequency at maximum amplitude (b), the span of frequencies where three solutions exist (c), the maximum displacement along y (e) and along z (f), measured at the forcing location. The latter is usually referred to as quadrature error (in that it is a spurious motion which superimposes to the Coriolis reading), and it is nicely captured by the sensitivity method in spite of its small magnitude. As it can be observed, DpROM and sensitivity-based results are in almost perfect agreement.

Table 1 Computational times for each step in the construction of the reduced models and simulations. For each model, we denoted with an F/V a fixed/variable cost (if present).

Finally, in Table 1 computational times are reported, where we distinguish between fixed costs, computed once and for all independently from the total number of analyses, and variable costs that must be sustained for each new analysis. Considering only the variable costs, we find that the sensitivity approach is almost 300 times faster than the DpROM, and more than 3000 times faster than the repeated construction and evaluation of a non-parametric ROM, with a modest increment of the fixed costs. The latter, however, can be largely amortized when a sufficient number of samples is used for the MC analysis.

6 Conclusions

In this contribution we proposed a sensitivity-based method to alleviate the computation of the frequency responses of nonlinear systems, when the latter have to be repeated for a large number of parameter realizations and for small parameter deviations from the nominal values. The typical case scenario in this sense is the Monte Carlo analysis. After recalling the governing equations for the Harmonic Balance method, we discussed how to compute sensitivities and how appending an appropriate closure equation to the HB residual equations is essential to achieve accurate results. We then introduced a closure equation ensuring that the sought approximated solution lies along a direction which is normal in the HB coefficient space. With the aid of the example of a nonlinear oscillator, accuracy and limitations of the discussed approaches were thoroughly illustrated. Finally, the method is applied to a large FE model of a MEMS gyroscope. As the direct evaluation of the response of such a system through HB is not feasible, we resorted to a parametric Reduced Order Model which we studied in a previous work (DpROM), and where the parameters represent the amplitudes of some imposed shape defect. Using the HB and DpROM, a Monte Carlo analysis was run for 4612 sampled parameter vectors, computing the Frequency Response Curves for both the DpROM (reference solution) and the sensitivity-based approximation. The probability density functions of some quantities of interest for the two batches of results showed excellent agreement. The computational times, however, were greatly reduced, going from the 2.6 days of the re-simulated DpROM to the 45.2 minutes of the sensitivity-based approach, with an effective speedup factor of approximately 300 (if neglecting fixed costs). All in all, the proposed method represents an accurate and cheap solution to evaluate the frequency responses of systems subject to parameter uncertainties and featuring a marked nonlinear behavior, finding potential applications in the MEMS industry as well as in other fields, as for the study of friction related phenomena [31].

Appendices

A Non-singularity of Jacobian matrix

In this subsection we demonstrate that, with the implicit function definition in Eq. (24), conditions for the Implicit function theorem are satisfied if:

• (i) $\det (\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}) \ne 0$, for closure Eq. (32);

• (ii) $\det (\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}) \ne 0$ and $\frac{\partial {\varvec{R}}}{\partial \omega } \ne {\varvec{0}}$, for closure Eq. (34).

The Jacobian of the extended residual is

$$\begin{aligned} \frac{\partial \hat{{\varvec{R}}}}{\partial {\textbf {X}}} = \begin{bmatrix} \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}} &{} \frac{\partial {\varvec{R}}}{\partial \omega }\\ {} &{} \\ {\varvec{\tau _Q}}^{*T} &{} \alpha \, \tau _{\omega }^*\end{bmatrix}, \end{aligned}$$

(41)

with $\alpha = 1$ for closure equation (32), or $\alpha = 0$ for closure equation (34). Since $\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}$ is invertible for hypothesis, the determinant of the extended Jacobian can be developed using Eq. (33) as

$$\begin{aligned} \begin{aligned} \text {det}\left( \frac{\partial \hat{{\varvec{R}}}}{\partial {\textbf {X}}}\right) =&\, \text {det}\left( \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}\right) \left( \alpha \, \tau _{\omega }^*- {\varvec{\tau _Q}}^{*T} \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1} \frac{\partial {\varvec{R}}}{\partial \omega } \right) ,\\ =&\, \text {det}\left( \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}\right) \left( \alpha \, \tau _{\omega }^*+ \frac{1}{\tau _{\omega }^*} {\varvec{\tau _Q}}^{*T} {\varvec{\tau _Q}}^* \right) , \end{aligned}\nonumber \\ \end{aligned}$$

(42)

which is different from zero if and only if

$$\begin{aligned} \alpha \, \tau _{\omega }^*+ \frac{1}{\tau _{\omega }^*} {\tau _Q^{*}}^{T} {\tau _Q^{*}} \ne 0 \Leftrightarrow \; \alpha \, \tau _{\omega }^*+ || {\tau _Q^{*}} ||^2 \ne 0. \end{aligned}$$

(43)

If $\alpha = 1$, then condition (43) is always satisfied, since the norm of a tangent vector is positive definite. However, for $\alpha = 0$, condition (43) is satisfied if and only if ${\varvec{\tau _Q}}^* \ne {\varvec{0}}$. As it can be seen from the definition of ${\varvec{\tau }}_{{\varvec{Q}}}$ in Eq. (33), since $\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}$ has full rank for hypothesis, ${\varvec{\tau _Q}}^*$ is null if and only if $\frac{\partial {\varvec{R}}}{\partial \omega } = {\varvec{0}}$. Hence, in this second case, for $\frac{\partial \hat{{\varvec{R}}}}{\partial {\textbf {X}}}$ to be invertible, the additional condition $\frac{\partial {\varvec{R}}}{\partial \omega } \ne {\varvec{0}}$ is required (and is generally satisfied, as in the case of periodic forcing).

B Euclidean distance minimization in the coefficients space

In Section 3.2 we introduced a mapping between FRCs that made possible accurate sensitivity-based approximations for small parameter perturbations from the nominal. The choice we made was to map each nominal solution point to the closest point on each perturbed FRC, relying on the fact that Taylor series-based approximations worsen as variations increase. In this way, after some geometric considerations we identified the closure equations in (32) and (34). With the first constraint we minimize the euclidean distance in the ${\varvec{Q}}-\omega$ space, while with the second we minimize the distance restricted to the space of HB coefficients ${\varvec{Q}}$ only. In this section we show that the latter choice corresponds to the minimization of the distance between the solution coefficients (in a linear approximation).

Let us consider the linear system of Eq. (25), both with closure equation (32) and (34). We can rewrite the system in terms of ${\varvec{Q}}$ and $\omega$ as

with $\alpha = 1$ if we consider closure equation in (32), or $\alpha = 0$ if we consider closure equation in (34).

From equation (44a) we get

$$\begin{aligned} \frac{d {\varvec{Q}}}{d {\varvec{p}}} = - \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\left( \frac{\partial {\varvec{R}}}{\partial \omega }\frac{d \omega }{d {\varvec{p}}} + \frac{\partial {\varvec{R}}}{\partial {\varvec{p}}}\right) , \end{aligned}$$

(45)

that upon substitution in (44b) yields

$$\begin{aligned} \frac{d \omega }{d {\varvec{p}}} = \frac{\displaystyle {\varvec{\tau _Q}}^{*T}\, \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\, \frac{\partial {\varvec{R}}}{\partial {\varvec{p}}}}{\displaystyle -{\varvec{\tau _Q}}^{*T} \, \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\, \frac{\partial {\varvec{R}}}{\partial \omega }\, + \, \alpha \, \tau _{\omega }^*}, \end{aligned}$$

(46)

and eventually

$$\begin{aligned} \frac{d {\varvec{Q}}}{d {\varvec{p}}} = \frac{\displaystyle -\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\, \frac{\partial {\varvec{R}}}{\partial \omega }\, {\varvec{\tau _Q}}^{*T}\, \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\, \frac{\partial {\varvec{R}}}{\partial {\varvec{p}}}}{\displaystyle -{\varvec{\tau _Q}}^{*T} \, \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\, \frac{\partial {\varvec{R}}}{\partial \omega }\, + \, \alpha \, \tau _{\omega }^*} - \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\, \frac{\partial {\varvec{R}}}{\partial {\varvec{p}}}.\nonumber \\ \end{aligned}$$

(47)

The corresponding first-order variations in HB coefficients and frequency obtained with the sensitivities are thus

$$\begin{aligned} \delta \tilde{{\varvec{Q}}}&= \frac{d {\varvec{Q}}}{d {\varvec{p}}} \delta {\varvec{p}}, \end{aligned}$$

(48a)

$$\begin{aligned} \delta \tilde{\omega }&= \frac{d \omega }{d {\varvec{p}}} \delta {\varvec{p}}. \end{aligned}$$

(48b)

Let us now consider the following constrained minimization problem

in $\delta {\varvec{Q}}$ and $\delta \omega$, for a fixed $\delta {\varvec{p}}$. The one time underdetermined system (49b) is obtained from a first-order expansion of the HB residual in the neighbourhood of a nominal solution point, as in Eq. (28). For fixed $\delta {\varvec{p}}$, this system of equations defines a linear approximation of the perturbed FRC. The functional J returns the euclidean distance of the expansion nominal solution point from any point on the linearized perturbed FRC, in ${\varvec{Q}}-\omega$ space when $\alpha = 1$, or in ${\varvec{Q}}$ space when $\alpha = 0$.

We now prove that the sensitivity-based solution in Eq. (48) is a solution of the minimization problem, for $\alpha = 0$ and for $\alpha = 1$. In order to do so we solve (49b) with respect to $\delta {\varvec{Q}}$ and substitute the so obtained expression in the functional definition (49a) obtaining

$$\begin{aligned} \begin{aligned} J(\delta \omega )&= \left( \frac{\partial {\varvec{R}}}{\partial \omega }^T\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-T}\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\frac{\partial {\varvec{R}}}{\partial \omega }+ \alpha \right) \delta \omega ^2 \\&\quad + 2 \left( \frac{\partial {\varvec{R}}}{\partial \omega }^T\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-T}\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\frac{\partial {\varvec{R}}}{\partial {\varvec{p}}}\delta {\varvec{p}}\right) \delta \omega \\ {}&\quad + \delta {\varvec{p}}^T \frac{\partial {\varvec{R}}}{\partial {\varvec{p}}}^T \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-T}\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\frac{\partial {\varvec{R}}}{\partial {\varvec{p}}}\delta {\varvec{p}}. \end{aligned} \end{aligned}$$

(50)

Notice that in this expression, the functional J is a scalar quadratic function in the scalar variable $\delta \omega$. Moreover, if $\alpha \ge 0$, the term multiplying $\delta \omega$ in Eq. (50) is always positive, hence the stationary point is a minimum.

The optimality condition, $\frac{d \,J}{d \,\delta \omega } = 0$, writes

$$\begin{aligned}{} & {} \left( \frac{\partial {\varvec{R}}}{\partial \omega }^T\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-T}\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\frac{\partial {\varvec{R}}}{\partial \omega }+ \alpha \right) \delta \omega \nonumber \\{} & {} \quad + \frac{\partial {\varvec{R}}}{\partial \omega }^T\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-T}\frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}}^{-1}\frac{\partial {\varvec{R}}}{\partial {\varvec{p}}}\delta {\varvec{p}}= 0. \end{aligned}$$

(51)

By substituting the sensitivity-based solution provided in (48b) in Eq. (50), recalling the definition of the nominal tangent vector ${\varvec{\tau _Q}}^*$ given in (33), it is easy to verify that the optimality condition is satisfied for both $\alpha = 0$ and $\alpha = 1$. Hence the sensitivity-based solution is also a solution of the minimization problem, proving the thesis.

C Computation of residual derivatives

In this section we provide a possible method for the numerical evaluation of the partial derivatives of the HB residual ${\varvec{R}}$ with respect to harmonic amplitude vector ${\varvec{Q}}$, parameter vector ${\varvec{p}}$ and excitation frequency $\omega$. In the differentiation process, we assume a dependence of the EoM on the parameter vector ${\varvec{p}}$, as stated in Eq. (13). The HB residual vector ${\varvec{R}}$ can be split into a linear contribution in the harmonic amplitude vector ${\varvec{R}}^{\,lin}$ and a nonlinear one ${\varvec{R}}^{\,nl}$, as shown in Eq. (7). Also, we assume that the order of the elements in derivatives corresponds to the order of derivation, for instance

$$\begin{aligned} \left( \frac{\partial ^2 R}{\partial Q \partial p}\right) _{ijk} = \frac{\partial ^2 R_i}{\partial Q_k \partial p_j}. \end{aligned}$$

1.1 C.1 Partial derivatives of linear residual

Partial derivatives of the linear part are trivial, and are hereafter reported:

$$\begin{aligned} \frac{\partial {\varvec{R}}}{\partial {\varvec{Q}}} =&\, \omega ^2 \nabla ^2 \otimes {\varvec{M}}+ \omega \nabla \otimes {\varvec{D}}+ {\varvec{I}}_{2H+1} \otimes {\varvec{K}}, \end{aligned}$$

(52a)

$$\begin{aligned} \frac{\partial {\varvec{R}}}{\partial p_j} =&\, \left( \omega ^2 \nabla ^2 \otimes \frac{\partial {\varvec{M}}}{\partial p_j} + \omega \nabla \otimes \frac{\partial {\varvec{D}}}{\partial p_j} + {\varvec{I}}_{2H+1} \otimes \frac{\partial {\varvec{K}}}{\partial p_j}\right) {\varvec{Q}}\nonumber \\&- \left( {\varvec{e}}_{c} \otimes {\varvec{I}}_n\right) \frac{\partial {\varvec{f}}_{\omega ,c}}{\partial p_j} - \left( {\varvec{e}}_{s} \otimes {\varvec{I}}_n\right) \frac{\partial {\varvec{f}}_{\omega ,s}}{\partial p_j}, \end{aligned}$$

(52b)

$$\begin{aligned} \frac{\partial {\varvec{R}}}{\partial \omega }\, =&\, \left( 2 \omega \nabla ^2 \otimes {\varvec{M}}+ \nabla \otimes {\varvec{D}}\right) {\varvec{Q}}, \end{aligned}$$

(52c)

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}}{\partial p_k \partial p_j} \, =&\, \left( \omega ^2 \nabla ^2 \otimes \frac{\partial ^2 {\varvec{M}}}{\partial p_k \partial p_j} + \omega \nabla \otimes \frac{\partial ^2 {\varvec{D}}}{\partial p_k \partial p_j} \right. \nonumber \\&+ \left. {\varvec{I}}_{2H+1} \otimes \frac{\partial ^2 {\varvec{K}}}{\partial p_k \partial p_j}\right) {\varvec{Q}}- \left( {\varvec{e}}_{c} \otimes {\varvec{I}}_n\right) \frac{\partial ^2 {\varvec{f}}_{\omega ,c}}{\partial p_k \partial p_j} \nonumber \\&- \left( {\varvec{e}}_{s} \otimes {\varvec{I}}_n\right) \frac{\partial ^2 {\varvec{f}}_{\omega ,s}}{\partial p_k \partial p_j}, \end{aligned}$$

(52d)

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}}{\partial \omega ^2} \,=&\, \left( 2 \nabla ^2 \otimes {\varvec{M}}\right) {\varvec{Q}}, \end{aligned}$$

(52e)

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{Q}} \partial p_j} \, =&\, \omega ^2 \nabla ^2 \otimes \frac{\partial {\varvec{M}}}{\partial p_j} + \omega \nabla \otimes \frac{\partial {\varvec{D}}}{\partial p_j} + {\varvec{I}}_{2H+1} \otimes \frac{\partial {\varvec{K}}}{\partial p_j}, \end{aligned}$$

(52f)

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}}{\partial {\varvec{Q}} \partial \omega } \, =&\, 2 \omega \nabla ^2 \otimes {\varvec{M}}+ \nabla \otimes {\varvec{D}}, \end{aligned}$$

(52g)

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}}{\partial \omega \partial p_j}\, =&\, \left( 2 \omega \nabla ^2 \otimes \frac{\partial {\varvec{M}}}{\partial p_j} + \nabla \otimes \frac{\partial {\varvec{D}}}{\partial p_j} \right) {\varvec{Q}}, \end{aligned}$$

(52h)

with $i,j,k \in \{1,\dots ,m\}$.

1.2 C.2 Partial derivatives of nonlinear residual

Partial derivatives of ${\varvec{R}}^{nl}$ are instead computed with the Alternating Frequency Time scheme (AFT) that was presented in section 2.1. Before going into the details, let us recall the structure of ${\varvec{R}}^{nl}$:

$$\begin{aligned} {\varvec{R}}^{nl}\triangleq \frac{1}{T} \int _0^{T}({\varvec{C}}\,{\varvec{\psi }}^T \otimes {\varvec{I}}_n) f({\varvec{q}},\dot{{\varvec{q}}},{\varvec{p}}) \text { dt}, \end{aligned}$$

(53)

1.2.1 First-order derivatives

First-order partial derivatives of ${\varvec{R}}^{nl}$ with respect to the parameter vector ${\varvec{p}}$ can be developed in Einstein notation as

$$\begin{aligned} \begin{aligned} \frac{\partial R^{nl}_I}{\partial p_J} =&\ \frac{\partial }{\partial p_J} \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n)_{Ii}\, f_i({\varvec{p}}) \text { dt}\\ =&\frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n)_{Ii}\, \frac{\partial f_i}{\partial p_J} \text { dt},\\ \end{aligned} \end{aligned}$$

(54)

and in matrix notation read

$$\begin{aligned} \frac{\partial {\varvec{R}}^{nl}}{\partial {\varvec{p}}} =\ \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n)\, \frac{\partial {\varvec{f}}}{\partial {\varvec{p}}} \text { dt}. \end{aligned}$$

(55)

Partial derivatives of ${\varvec{R}}^{nl}$ with respect to HB coefficients ${\varvec{Q}}$ are developed exploiting chain differentiation rule, the ansatz definition in Eq. (3a) and the velocities relation in Eq. (4a), as follows

$$\begin{aligned} \begin{aligned} \frac{\partial R^{nl}_I}{\partial Q_J} =&\ \frac{\partial }{\partial Q_J} \frac{1}{T} \int _0^{T}({\varvec{C}}\,{\varvec{\psi }}^T \otimes {\varvec{I}}_n)_{Ii}\,f_i({\varvec{q}},\dot{{\varvec{q}}}) \text { dt}\\ =&\ \frac{1}{T} \int _0^{T}({\varvec{C}}\,{\varvec{\psi }}^T \otimes {\varvec{I}}_n)_{Ii} \left( \frac{\partial f_i}{\partial q_j}\, \frac{\partial q_j}{\partial Q_J} \right. \\ {}&+ \left. \frac{\partial f_i}{\partial \dot{q}_j}\, \frac{\partial \dot{q}_j}{\partial Q_J} \right) \text { dt}\\ =&\ \frac{1}{T} \int _0^{T}({\varvec{C}}\,{\varvec{\psi }}^T \otimes {\varvec{I}}_n)_{Ii} \left( \frac{\partial f_i}{\partial q_j}\, ({\varvec{\psi }}\otimes {\varvec{I}}_n)_{jJ} \right. \\ {}&+ \left. \omega \frac{\partial f_i}{\partial \dot{q}_j} ({\varvec{\psi }}\nabla \otimes {\varvec{I}}_n)_{jJ}\right) \text { dt}, \end{aligned} \end{aligned}$$

(56)

and in matrix notation read

$$\begin{aligned} \frac{\partial {\varvec{R}}^{nl}}{\partial {\varvec{Q}}}= & {} \ \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n)\, \left( \frac{\partial {\varvec{f}}}{\partial {\varvec{q}}}\, ({\varvec{\psi }}\otimes {\varvec{I}}_n)\right. \,\nonumber \\ {}{} & {} \left. + \omega \frac{\partial {\varvec{f}}}{\partial \dot{{\varvec{q}}}}\, ({\varvec{\psi }}\nabla \otimes {\varvec{I}}_n) \right) \text { dt}.\nonumber \\ \end{aligned}$$

(57)

When it comes to the computation of the partial derivatives of ${\varvec{R}}^{nl}$ with respect to $\omega$, it is useful to perform the linear change of variables $t = T\tau = \frac{2\pi }{\omega }\tau$, from physical time t to adimensional time $\tau$. With this transformation, the nonlinear residual ${\varvec{R}}^{nl}$ defined in (7) rewrites

$$\begin{aligned} {\varvec{R}}^{nl}= \int _0^1 ({\varvec{C}}\,{\varvec{\psi }}^T \otimes {\varvec{I}}_n) {\varvec{f}}({\varvec{q}},\dot{{\varvec{q}}},{\varvec{p}})\, \text {d}\tau . \end{aligned}$$

(58)

Notice that, with this transformation, integration bounds as well as ${\varvec{\psi }}$ become independent from $\omega$. As a result of this, exploiting Eqs. (3a), (4a)

$$\begin{aligned} \frac{\partial {\varvec{q}}}{\partial \omega } =&\ {\varvec{0}}, \end{aligned}$$

(59a)

$$\begin{aligned} \frac{\partial \dot{{\varvec{q}}}}{\partial \omega } =&\ {\varvec{\psi }}\nabla \otimes {\varvec{I}}_n= \frac{\dot{{\varvec{q}}}}{\omega }, \end{aligned}$$

(59b)

and

$$\begin{aligned} \frac{\partial {\varvec{R}}^{nl}}{\partial \omega }= & {} \ \int _0^1 ({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n)\, \frac{\partial {\varvec{f}}}{\partial \dot{{\varvec{q}}}} \frac{\dot{{\varvec{q}}}}{\omega }\, d\tau \nonumber \\= & {} \ \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n) \frac{\partial {\varvec{f}}}{\partial \dot{{\varvec{q}}}} \frac{\dot{{\varvec{q}}}}{\omega }\, \text { dt}, \end{aligned}$$

(60)

in which we exploited the chain derivation rule. Moreover, notice that, if the nonlinear force vector ${\varvec{f}}$ is independent from the velocities, $\frac{\partial {\varvec{R}}^{nl}}{\partial \omega } = {\varvec{0}}$.

1.2.2 Second-order derivatives

Through further differentiation of the first-order derivatives given in the previous section, we get second-order derivatives of ${\varvec{R}}^{nl}$ and mixed derivatives with respect to parameter vector ${\varvec{p}}$, HB coefficients ${\varvec{Q}}$ and frequency $\omega$. In this way, second-order derivatives are

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}^{nl}}{\partial {\varvec{p}} ^2}&= \ \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n) \cdot \frac{\partial ^2 {\varvec{f}}}{\partial {\varvec{p}} ^2} \text { dt}, \end{aligned}$$

(61a)

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}^{nl}}{\partial {\varvec{Q}} ^2}&= \ \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n) \cdot \left[ \left( \frac{\partial ^2 {\varvec{f}}}{\partial {\varvec{q}} ^2}\, \cdot \left( {\varvec{\psi }}\otimes {\varvec{I}}_n\right) \right. \right. \nonumber \\ {}&\left. \left. + \frac{\partial ^2 {\varvec{f}}}{\partial \dot{{\varvec{q}}} \partial {\varvec{q}}}\, \cdot (\omega \,{\varvec{\psi }}\nabla \otimes {\varvec{I}}_n) \right) \, \cdot _{21} \, \left( {\varvec{\psi }}\otimes {\varvec{I}}_n\right) \right. \nonumber \\&+ \left( \frac{\partial ^2 {\varvec{f}}}{\partial \dot{{\varvec{q}}} ^2}\,\cdot (\omega \,{\varvec{\psi }}\nabla \otimes {\varvec{I}}_n) + \frac{\partial ^2 {\varvec{f}}}{\partial {\varvec{q}} \partial \dot{{\varvec{q}}}} \, \cdot ({\varvec{\psi }}\nabla \otimes {\varvec{I}}_n) \right) \nonumber \\&\cdot _{21} \left( \omega \, {\varvec{\psi }}\nabla \otimes {\varvec{I}}_n\right) \bigg ] \text { dt}, \end{aligned}$$

(61b)

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}^{nl}}{\partial \omega ^2}&=\ \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n) \left( \frac{\partial ^2 {\varvec{f}}}{\partial \dot{{\varvec{q}}} ^2} \cdot \frac{\dot{{\varvec{q}}}}{\omega }\,\frac{\dot{{\varvec{q}}}}{\omega }\right) \text { dt}, \end{aligned}$$

(61c)

and eventually mixed derivatives are

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}^{nl}}{\partial {\varvec{p}} \partial {\varvec{Q}}}&=\ \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n) \cdot \nonumber \\ {}&\quad \left( \frac{\partial ^2 {\varvec{f}}}{\partial {\varvec{p}} \partial {\varvec{q}}}\, \cdot _{21} ({\varvec{\psi }}\otimes {\varvec{I}}_n) \, + \frac{\partial ^2 {\varvec{f}}}{\partial {\varvec{p}} \partial \dot{{\varvec{q}}}}\,\nonumber \right. \\&\quad \left. \cdot _{21} (\omega \,{\varvec{\psi }}\nabla \otimes {\varvec{I}}_n) \right) \text { dt}, \end{aligned}$$

(62a)

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}^{nl}}{\partial \omega \partial {\varvec{Q}}}&=\ \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n) \left( \frac{\partial ^2 {\varvec{f}}}{\partial \dot{{\varvec{q}}} \partial {\varvec{q}}}\,\cdot \nonumber \right. \\&\quad \left. \frac{\dot{{\varvec{q}}}}{\omega } ({\varvec{\psi }}\otimes {\varvec{I}}_n) + \frac{\partial ^2 {\varvec{f}}}{\partial \dot{{\varvec{q}}} ^2}\, \cdot \dot{{\varvec{q}}}\left( {\varvec{\psi }}\nabla \otimes {\varvec{I}}_n\right) \right) \text { dt}, \end{aligned}$$

(62b)

$$\begin{aligned} \frac{\partial ^2 {\varvec{R}}^{nl}}{\partial \omega \partial {\varvec{p}}}&=\ \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n) \left( \frac{\partial ^2 {\varvec{f}}}{\partial \dot{{\varvec{q}}} \partial {\varvec{p}}} \cdot \frac{\dot{{\varvec{q}}}}{\omega }\right) \text { dt}. \end{aligned}$$

(62c)

Once again notice that if the vector of nonlinear forces ${\varvec{f}}$ is independent from velocities, then derivatives with respect to $\omega$ are null.

1.2.3 Numerical evaluation of partial derivatives

Notice that all partial derivatives of ${\varvec{R}}^{nl}$ in the previous sections all present the same form, that is

$$\begin{aligned} \frac{1}{T} \int _0^{T}({\varvec{C}}{\varvec{\psi }}^T \otimes {\varvec{I}}_n) \cdot {\varvec{A}}({\varvec{q}}(t))\, \text { dt}, \end{aligned}$$

(63)

where ${\varvec{A}}({\varvec{q}}(t))$ is a multidimensional matrix depending on time through the displacement vector ${\varvec{q}}(t)$. According to Eq. (6), this latter integral implements the truncated Fourier series with H harmonics of matrix ${\varvec{A}}({\varvec{q}}(t))$ (with Fourier coefficients collected in the fashion of Eq. (6)).

Upon this consideration, we can apply the AFT algorithm for the computation of these quantities. At first, through the Ansatz definition in (3a), snapshots of displacements ${\varvec{q}}(t)$ at equidistant time instants in the period T are evaluated and, with them, time snapshots of ${\varvec{A}}({\varvec{q}}(t))$ are retrieved. Eventually the FFT is applied to the time snapshots of ${\varvec{A}}({\varvec{q}}(t))$ and the so obtained Fourier coefficients are rearranged according to the order defined in Eq. (6).

D Derivatives for the DpROM

With reference to EoM of the DpROM (Eq. (37)), the vector of internal reduced forces writes

(64)

Recalling the definitions for stiffness tensors given in Eq. (38) and volume integration formula in Eq. (39), internal forces and mass tensor derivatives, required to compute the sensitivities for the DpROM write in Einstein notation:

(65a)

(65b)

(65c)

(65d)

(65e)

(65f)

where we highlighted dimensions over which summation is performed with indices in lowercase. All derivatives are evaluated at the nominal parameter value $\varvec{\xi }= {\varvec{0}}$.