A Novel Equation of Motion to Predict Elastoplastic Deformation of 1-D Stochastic Bars

Abstract

Based on stochasticity in local and nonlocal deformation-gamuts, a stochastic nonlocal equation of motion to model elastoplastic deformation of 1-D bars made of stochastic materials is proposed in this study. Stochasticity in the energy-densities as well as energy-states across the spatial domain of given material and stochasticity in the deformation-gamuts parameters are considered, and their physical interpretations are discussed. Numerical simulations of the specimens of two distinct materials, subjected to monotonic as well as cyclic loadings, are carried out. Specimens are discretized using stochastic as well as uniform grids. Thirty realizations of each stochastic process are considered. The mean values of the results from all realizations are found to be in good agreement with deterministic values, theoretical estimations and experimental results published in open literature.

1 Introduction

Continuum field theories based on variational principle using partial spatial derivatives are ill-suited to model natural development of discontinuities in pristine materials. To overcome this limitation, based on the relative states of the material points on the deforming body, Eringen et al. proposed the mathematical framework of nonlocal continuum field theory [1,2,3,4,5,6] that used integral functionals instead of spatial derivatives. Silling [7] extended this mathematical framework as “peridynamics” by taking into account the relative change in the states of the material points as well. While “peridynamics” was defined using Greek roots for near and force, there was no clear definition of “nearness” provided.

In last two decades, substantial research has been carried out in the area of linear and stochastic peridynamics. Motivated by Langevin dynamics [8,9,10], in the early works on stochastic peridynamics, Gunzburger and Stoyanov [11] proposed to upscale the stochastic thermostat for molecular dynamics to the peridynamics model. They proposed to add stochastic perturbation to the peridynamics kernel and the stochastic thermostat to create a realistic behavior for cracks formation and growth. Further, Chen and Gunzburger [12] and Chen [13] presented a stochastic peridynamics model by considering the forcing terms as a finite-dimensional distributions of a stochastic process. Evangelatos [14] presented a stochastic peridynamics theory by considering the micromodulus function as a random process. Demmie and Ostoja-Starzewski [15, 16] formulated stochastic peridynamics model by considering randomness in the material properties like mass density, bulk modulus, and yield strength and in the critical stretch of the bonds. Decklever [17] used non-uniform grid for bond-based peridynamics to effectively predict material properties of, and quasi-static crack propagation in, single-walled carbon nanotube via Monte Carlo simulation. R$\ddot{\text {a}}$del et al. [18] explored the dependencies of the peridynamic solutions on the discretization schemes by incorporating stochastic distribution of elastic material properties into Peridigm, an open-source peridynamics code developed at Sandia National Laboratories.

In conventional peridynamics, nonlocality is parsed in terms of some finite Euclidean distance between two material points. The domain of influence of a material point on its neighborhood is called its horizon. In order to address non-uniform horizon sizes across the material domain, the concept of dual-horizon peridynamics was proposed by Ren et al. [19]. It was also demonstrated that this concept is able to address the “ghost force” issue and thus eliminates the need of surface correction. Li and Guo [20] applied dual-horizon peridynamics to simulate debonding failure in FRP-to-concrete bonded joints. They used non-uniform grid for discretization to model the stochastic nature of the cracking process. Their predicted results were found to be in good agreement with the experimental results.

A great amount of research in stochastic peridynamics area available in open literature is undertaken to model corrosion and concrete. Based on couplings between diffusion bonds and mechanical bonds, a peridynamic formulation of stochastic nature was proposed by Chen and Bobaru [21, 22], called as concentration-dependent damage model, to model pitting corrosion damage. The stochastic nature of their model lay in the “bond-breaking chance” of the intact mechanical bonds as a measure of a random number from a given uniform distribution. Further, Jafarzadeh et al. [23] incorporated mechanisms for repassivation in this damage model, allowing autonomous formation of perforated covers in pitting corrosion and development of secondary pits. Zhao et al. [24] adopted the stochastic “intermediately homogenized” peridynamic formulation, originally proposed for functionally graded materials [25, 26], to model fracture due to rebar corrosion in reinforced concrete. Additionally, Wu et al. [27] applied intermediately homogenized peridynamic model to predict quasi-static crack propagation in concrete. Niazi [28] used this intermediate-homogenization approach to model porosity in elastic materials. Porosity in the model was introduced by stochastically pre-breaking peridynamic bonds.

All the models proposed thus far for stochastic peridynamics are based on the conventional peridynamics proposed by Silling [7].

Considering the subjective nature of the definition of “nearness”, localization and nonlocalization in the material domain were explicitly quantified as a measure of direct and indirect interactions respectively between the material points regardless of the Euclidean distance between them [29]. The concept of direct and indirect interactions is based on the degrees of separation between two material points. Any two material points with one degree of separation, directly interacting with each other, are classified as locally interacting. Any two indirectly interacting material points are considered nonlocal to each other. This concept of direct and indirect interactions was inspired by the phenomenon of modification in the direct interaction between two material points due to the presence of some third material point. Based on these definitions, a novel multiscale notion of local and nonlocal deformation-gamuts was introduced and a new equation of motion to model elastoplastic deformation of the pristine materials in the most natural way was proposed. This study extends the application of this novel notion to stochastic materials.

This paper is structured as follows. The equation of motion based on local and nonlocal deformation-gamuts is briefly discussed in Section 2. The stochastic equation of motion is proposed in Section 3 by considering stochasticity in the energy-densities as well as energy-states across the material’s spatial domain, and stochasticity in the deformation-gamuts parameters. Physical interpretations of these stochasticities are discussed in Section 3.1. Numerical simulations of the specimens of two distinct materials are carried out in Section 4. Specimens are discretized using stochastic as well as uniform grids. One of the reasons behind considering stochasticity in the energy-densities, energy-states, material properties and deformation-gamuts parameters on uniform and stochastic grids is to demonstrate that the proposed equation of motion is independent of the grid-type and the horizon size. Thirty realizations of each stochastic process are considered, and the mean as well as the deterministic results for monotonic as well as cyclic loadings are compared against the published results. Concluding remarks are provided in Section 5.

2 Equation of Motion Based on Local and Nonlocal Deformation-Gamuts

The local and nonlocal deformation-gamuts based equation of motion, proposed by Desai [29], to model elastoplastic deformation of materials in 1-D, is,

$$\begin{aligned} & \rho _{L@x} \ddot{u}(x,t) + \int \limits _{V_{L}(x)}(1-\mathcal {R}_{x, x'})\nabla _{{{x}}}\mathbb {U}_{L}(x, x', t)dV_{L}(x')\\&\;\;\; + \int \limits _{V_{NL}(x)}\; \int \limits _{V_{NL}(x)}w_{x, x'}\nabla _{x}\mathbb {U}_{NL}( x, x',t)dV_{NL}( x')dV_{NL}( x') = {F}_{d}({x},t). \end{aligned}$$

(1)

In Eq. (1), $\rho _{L@ x}$ is the material’s mass density associated with the local volume around material point x, L@x is read as “localized at x”, $\ddot{u}$ is the acceleration of the material point x in the reference configuration, ${F}_{d}(x,t)$ is the external force-density that the local volume around material point x is subjected to, $V_{L}(x)$ as well as $V_{NL}(x)$ are local and nonlocal volumes respectively around material point x, and $\mathbb {U}_{L}(x, x', t)$ and $\mathbb {U}_{NL}(x, x', t)$ are local and nonlocal potentials associated with material point x. Additionally, $x'$ in $V_{L}(x)$ directly interacts with x, and $x'$ in $V_{NL}(x)$ indirectly interacts with x. The direct interaction between x and $x'$ is identified as local via a local bond, and the indirect interaction is identified as nonlocal via a nonlocal bond. Thus the local and nonlocal bonds comprise the local and nonlocal volumes respectively in the material’s spatial domain. The subscripts L and NL distinguish between local and nonlocal interactions. The gradient $\nabla _{x}$ operates on the position of the material point x resulting in the required local and nonlocal force-fields. The parameter $\mathcal {R}_{x, x'}$ quantifies the modulus of softness of the local bond between x and $x'$. It assumes a value between 0 and 1. The calibrated weight fractions $w_{x, x'}$ quantify the correct gain in the inability of the nonlocal bond between x and $x'$ to absorb elastic energy as it deforms. In other words, the weight fraction inherently quantifies the critical deformation of the corresponding nonlocal bond. These weight fractions are subjected to the condition, $\int \limits _{V_{NL}(x)}w_{x, x'}dV_{NL}(x') = 1$.

The local and nonlocal volumes in Eq. (1) quantify the variation in energy-density across material’s spatial domain, and thus the energy-states of the material points they encompass. Nonlocality is manifested as a measure of the shared energy-states in the material’s spatial domain. The shared energy-state of a material point x quantifies its local and nonlocal deformation-gamuts as,

$$\begin{aligned} DG_{_{_L}}(x, t) = \int \limits _{V_{_L}(x)}\mathcal {R}_{x, x'}\mathbb {U}_{_L}(x, x', t)dV_{_L}(x') \end{aligned}$$

(2)

and

$$\begin{aligned} DG_{_{_{NL}}}(x, t) = \int \limits _{V_{_{NL}}(x)}\mathbb {U}_{_{NL}}(x, x', t)dV_{_{NL}}(x'). \end{aligned}$$

(3)

Local and nonlocal interactions in a 1-D specimen of some materials system are depicted in Fig. 1. The continuous domain of the specimen is discretized using some optimal number of material points n, each indexed by p and q, as shown. If we allow material points q to locally and nonlocally interact with material points p, then by definition [29], local (or direct) interactions are those for which $|p-q| = 1$ and nonlocal interactions are those for which $|p-q| \ne 1$. It can also be noticed that if local interactions are considered as indirect, then nonlocal interactions are direct. Thus, there is a duality between local and nonlocal interactions (or deformation-gamuts).

Fig. 1

Local and nonlocal interactions constituting local and nonlocal deformation-gamuts in a 1-D bar

In Eqs. (2) and (3), $DG_{_{_L}}$ (local deformation-gamut) quantifies localized energy that is nonlocalized and shared with the nonlocal deformation-gamut. This is the energy that causes the deformation of the corresponding nonlocal deformation-gamut. The nonlocal deformation is measured via $DG_{_{_{NL}}}$ (nonlocal deformation-gamut). In order to ensure that the total energy remains conserved at any instant t, it is required that,

$$\begin{aligned} DG_{_{_L}}(x, t) = DG_{_{_{NL}}}(x, t). \end{aligned}$$

(4)

For a material undergoing periodic elastic deformation, considering the duality between local and nonlocal deformation-gamuts, $DG_{_{_L}}(x, t) \rightleftharpoons DG_{_{_{NL}}}(x, t)$.

3 The Stochastic Model

Equation (1) is based on the variation in energy-density and energy-states across the material’s spatial domain. Since these variations could be stochastic, the proposed equation of motion can be applied to the materials with stochastically varying material properties as well.

Stochasticities in local and nonlocal potentials $\mathbb {U}_{_L}(x, x', t)$ and $\mathbb {U}_{_{NL}}(x, x', t)$, in the parameter $\mathcal {R}_{x, x'}$, and in the weight fractions $w_{x, x'}$ are considered in this study. Additionally, stochasticity in the material’s mass density $\rho _{_{V_{_{L@x}}}}$ is also taken into account. Stochasticity in these elements is quantified using Karhunen-Loève (KL) Expansion. The details about KL Expansion and the parameters used in it are provided in Appendix A.

The proposed governing equation of motion for deformation dynamics of stochastic materials is given in Eq. (5),

$$\begin{aligned} \begin{aligned} \rho _{L@x}(x, \omega ^{(\mathfrak {d})}) \ddot{u}(x,t)&+ \int \limits _{V_{_L}(x)}(1-\mathcal {R}_{x, x'}(x, x',\omega ^{(\mathfrak {r}_{{{x, x'}}})}))\nabla _{_{{x}}}\mathbb {U}_{_L}(x, x', t, \omega ^{(\mathfrak {u}_{{{l}}})})dV_{_L}(x') \\&+ \int \limits _{V_{_{NL}}(x)}\int \limits _{V_{_{NL}}(x)}w_{x, x'}(x, x',\omega ^{(\mathfrak {w}_{{{x, x'}}})})\nabla _{_{{x}}}\mathbb {U}_{_{NL}}(x, x', t, \omega ^{(\mathfrak {u}_{{{nl}}})})dV_{_{NL}}(x')dV_{_{NL}}(x') = {F}_{d}({x},t). \end{aligned} \end{aligned}$$

(5)

The local and nonlocal deformation-gamuts of the material point x, at the instant t, for the stochastic model are expressed as,

$$\begin{aligned} DG_{_{_L}}(x, t, \omega ^{(\mathfrak {dg}_{{{L}}})}) = \int \limits _{V_{_L}(x)} \mathcal {R}_{x, x'}(x, x',\omega ^{(\mathfrak {r}_{{{x, x'}}})}) \mathbb {U}_{_L}(x, x', t, \omega ^{(\mathfrak {u}_{{{l}}})})dV_{_L}(x') \end{aligned}$$

(6)

and

$$\begin{aligned} DG_{_{_{NL}}}(x, t, \omega ^{(\mathfrak {dg}_{{{NL}}})}) = \int \limits _{V_{_{NL}}({\textbf {x}})}\mathbb {U}_{_{NL}}(x, x', t, \omega ^{(\mathfrak {u}_{{{nl}}})})dV_{_{NL}}(x'). \end{aligned}$$

(7)

In order that the total energy is conserved,

$$\begin{aligned} DG_{_{_L}}(x, t, \omega ^{(\mathfrak {dg}_{{{L}}})}) = DG_{_{_{NL}}}(x, t, \omega ^{(\mathfrak {dg}_{{{NL}}})}). \end{aligned}$$

(8)

At any instant t, the stochasticity in $\mathbb {U}_{_L}$, $\mathbb {U}_{_{NL}}$, $\mathcal {R}_{x, x'}$, $w_{x, x'}$, and $\rho _{_{V_{_{L}}(x)}}$ are expressed using Karhunen-Loève (KL) Expansion as shown in Eqs. (9)–(14) respectively.

The stochasticity in $\mathbb {U}_{_L}$ as a result of the stochasticity in the direct (local) interactions between x and $x'$, is expressed as,

$$\begin{aligned} \begin{aligned} \mathbb {U}_{_L}(x, x', t, \omega ^{(\mathfrak {u}_{{{L}}})})&= \bar{\mathbb {U}}_{_L}(x, x', t) + {\mathfrak {u}_{{{L}}}}(x, x', t,\omega ^{(\mathfrak {u}_{{{L}}})})\\&= \bar{\mathbb {U}}_{_L}(x, x', t) + \sum _{j=1}^{\infty } \sqrt{\lambda ^{{(\mathfrak {u}_{{{L}}})}}_{_j}}\phi ^{{(\mathfrak {u}_{{{L}}})}}_{_j}(x, x', t) \{\mathscr {H}^{{\;\,(\mathfrak {u}_{{{L}}})}}_{_j}(\omega ^{{(\mathfrak {u}_{{{L}}})}})\}. \end{aligned} \end{aligned}$$

(9)

Similarly, the stochasticity in $\mathbb {U}_{_{NL}}$ as a result of the stochasticity in the indirect (nonlocal) interactions between x and $x'$, is expressed as,

$$\begin{aligned} \begin{aligned} \mathbb {U}_{_{NL}}(x, x', t, \omega ^{(\mathfrak {u}_{{{NL}}})})&= \bar{\mathbb {U}}_{_{NL}}(x, x', t) + {\mathfrak {u}_{{{NL}}}}(x, x', t,\omega ^{(\mathfrak {u}_{{{NL}}})})\\&= \bar{\mathbb {U}}_{_{NL}}(x, x', t) + \sum _{j=1}^{\infty } \sqrt{\lambda ^{{(\mathfrak {u}_{{{NL}}})}}_{_j}}\phi ^{{(\mathfrak {u}_{{{NL}}})}}_{_j}(x, x', t) \{\mathscr {H}^{{\;\,(\mathfrak {u}_{{{NL}}})}}_{_j}(\omega ^{{(\mathfrak {u}_{{{NL}}})}})\}. \end{aligned} \end{aligned}$$

(10)

Stochasticity in $\mathcal {R}_{x, x'}$ for direct interactions between x and $x'$ is expressed as,

$$\begin{aligned} \begin{aligned} \mathcal {R}_{x, x'}(x, x',\omega ^{(\mathfrak {r}_{{{x, x'}}})})&= \bar{\mathcal {R}}_{x, x'}(x, x') + \mathfrak {r}_{{{x, x'}}}(x, x',\omega ^{(\mathfrak {r}_{{{x, x'}}})}) \\&= \bar{\mathcal {R}}_{x, x'}(x, x') + \sum _{j=1}^{\infty } \sqrt{\lambda ^{{(\mathfrak {r}_{{{x, x'}}})}}_{_j}}\phi ^{{(\mathfrak {r}_{{{x, x'}}})}}_{_j}(x, x') \{\mathscr {H}^{{\;\,(\mathfrak {r}_{{{x, x'}}})}}_{_j}(\omega ^{{(\mathfrak {r}_{{{x, x'}}})}})\}. \end{aligned} \end{aligned}$$

(11)

Similarly, the stochasticity in $w_{x, x'}$ for the indirect interactions between x and $x'$ is expressed as,

$$\begin{aligned} \begin{aligned} w_{x, x'}(x, x',\omega ^{(\mathfrak {w}_{{{x, x'}}})})&= \bar{w}_{x, x'}(x, x') + \mathfrak {w}_{{{x, x'}}}(x, x',\omega ^{(\mathfrak {w}_{{{x, x'}}})}) \\&= \bar{w}_{x, x'}(x, x') + \sum _{j=1}^{\infty } \sqrt{\lambda ^{{(\mathfrak {w}_{{{x, x'}}})}}_{_j}}\phi ^{{(\mathfrak {w}_{{{x, x'}}})}}_{_j}(x, x') \{\mathscr {H}^{{\;\,(\mathfrak {w}_{{{x, x'}}})}}_{_j}(\omega ^{{(\mathfrak {w}_{{{x, x'}}})}})\}. \end{aligned} \end{aligned}$$

(12)

For any realization, the weight fractions are subjected to the condition,

$$\begin{aligned} \int \limits _{V_{_{NL}}(x)}w_{x, x'}(x, x',\omega ^{(\mathfrak {w}_{{{x, x'}}})})dV_{_{NL}}(x') = 1. \end{aligned}$$

(13)

Stochasticity in the mass density, $\rho _{_{V_{_{L@x}}}}$, is expressed as,

$$\begin{aligned} \begin{aligned} \rho _{_{{{L@x}}}}(x, \omega ^{(\mathfrak {d})})&= \bar{\rho }{_{_{{{L@x}}}}}(x) + \mathfrak {d}(x,\omega ^{(\mathfrak {d})})\\&= \bar{\rho }{_{_{{{L@x}}}}}(x) + \sum _{j=1}^{\infty } \sqrt{\lambda ^{(\mathfrak {d})}_{_j}}\phi ^{(\mathfrak {d})}_{_j}(x) \{\mathscr {H}^{\;\,(\mathfrak {d})}_{_j}(\omega ^{(\mathfrak {d})})\}. \end{aligned} \end{aligned}$$

(14)

3.1 Physical Interpretation(s) of Stochasticity

Physical interpretation(s) of stochasticity are discussed in the following subsections.

3.1.1 Local Potentials

Stochasticity in localized potentials bears a direct relationship with the stochasticity in material properties. If both are quantified over the same probability space, it can be inferred from Eq. (9) that, for any particular type of deformation,

$$\begin{aligned} \begin{aligned} \mathbb {U}_{_L}(x, x', t, \omega ^{(\mathfrak {u}_{{{L}}})})&= \frac{1}{2}\left( \bar{\mathbb {C}}_{_L}(x, x') + {\mathfrak {c}_{{{L}}}}(x, x',\omega ^{(\mathfrak {c}_{{{L}}})})\right) \epsilon _{{x, x'}}^2(t)\\&= \frac{1}{2}\left( \bar{\mathbb {C}}_{_L}(x, x') + \sum _{j=1}^{\infty } \sqrt{\lambda ^{{(\mathfrak {c}_{{{L}}})}}_{_j}}\phi ^{{(\mathfrak {c}_{{{L}}})}}_{_j}(x, x') \{\mathscr {H}^{{\;\,(\mathfrak {c}_{{{L}}})}}_{_j}(\omega ^{{(\mathfrak {c}_{{{L}}})}})\}\right) \epsilon _{{x, x'}}^2 (t)\\&= \frac{1}{2} \mathbb {C}_{_L}(x, x', \omega ^{(\mathfrak {c}_{{{L}}})}) \epsilon _{{x, x'}}^2(t). \end{aligned} \end{aligned}$$

(15)

In Eq. (15), $\epsilon _{{x, x'}}(t)$ is the strain between x and $x'$ at t due to the type of deformation considered, and $\mathbb {C}_{_L}$ is the local bond-constant between x and $x'$ causing it. $\omega ^{(\mathfrak {c}_{{{L}}})}$ and $\omega ^{(\mathfrak {u}_{{{L}}})}$ are quantified over the same probability space. This implies that any deviation in $\mathbb {U}_{_L}$ is solely due to the same amount of deviation in $\mathbb {C}_{_L}$.

3.1.2 Nonlocal Potentials

Nonlocal potentials in general quantify the amount of shared material properties in the domain. Stochasticity in nonlocal potentials, thus, quantify stochasticity in shared material properties like bulk modulus or Young’s modulus of elasticity. Using a similar argument as used in Eq. (15), we can re-express $\mathbb {U}_{_{NL}}(x, x', t, \omega ^{(\mathfrak {u}_{{{NL}}})})$ as,

$$\begin{aligned} \begin{aligned} \mathbb {U}_{_{NL}}(x, x', t, \omega ^{(\mathfrak {u}_{{{NL}}})})&= \frac{1}{2}\left( \bar{\mathbb {C}}_{_{NL}}(x, x') + {\mathfrak {c}_{{{NL}}}}(x, x',\omega ^{(\mathfrak {c}_{{{NL}}})})\right) \epsilon _{{x, x'}}^2(t)\\&= \frac{1}{2}\left( \bar{\mathbb {C}}_{_{NL}}(x, x') + \sum _{j=1}^{\infty } \sqrt{\lambda ^{{(\mathfrak {c}_{{{NL}}})}}_{_j}}\phi ^{{(\mathfrak {c}_{{{NL}}})}}_{_j}(x, x') \{\mathscr {H}^{{\;\,(\mathfrak {c}_{{{NL}}})}}_{_j}(\omega ^{{(\mathfrak {c}_{{{NL}}})}})\}\right) \epsilon _{{x, x'}}^2 (t)\\&= \frac{1}{2} \mathbb {C}_{_{NL}}(x, x', \omega ^{(\mathfrak {c}_{{{NL}}})}) \epsilon _{{x, x'}}^2(t). \end{aligned} \end{aligned}$$

(16)

In Eq. (16), $\mathbb {C}_{_{NL}}$ is the nonlocal bond-constant between x and $x'$ causing the deformation of the type under consideration, and $\epsilon _{{x, x'}}(t)$ is the strain between x and $x'$ at t due to this deformation. Besides, $\omega ^{(\mathfrak {c}_{{{NL}}})}$ and $\omega ^{(\mathfrak {u}_{{{NL}}})}$ are quantified over the same probability space.

3.1.3 The Notion $\mathcal {R}_{x, x'}$

As identified by Desai [29], each material point in the material domain undergoes deformation identical to the stress-strain behavior of its corresponding material. Thus in stochastic materials, any material point x will undergo deformation due to the homogenized material properties localized at x, and its deformation locus would be identical to that of isotropic material having these homogenized material properties.

Figure 2 depicts the uncertainty in the modulus of softness, $U_S$, of the material or any local bond. $U_S$ is defined as the inability of the material or a bond to absorb elastic energy. The other parameters in Fig. 2 are, the modulus of toughness $U_T$, yield-stress $\sigma _y$, failure-stress $\sigma _f$, failure-strain $\epsilon _f$, and the Young’s modulus of elasticity E. The stress-strain curve shown with black line demonstrates the behavior of material or the bond due to the homogenized effect of material properties.

Fig. 2

Stress-strain curves depicting uncertainty in $U_S$

The notion of $\mathcal {R}$, in general, is expressed as,

$$\begin{aligned} \begin{aligned} \mathcal {R}(E, \sigma _y, \epsilon _y, \sigma _f, \epsilon _f, K_{ro}, n_{ro})&= \frac{U_S}{U_S + U_T} \\&= \frac{\frac{1}{2}E\epsilon _f^2 - \sigma _f\epsilon _f + \frac{\sigma _f^2}{2E} + \frac{K_{ro}\sigma _y}{n_{ro} + 1}\left( \frac{\sigma _f}{\sigma _y}\right) ^{n_{ro} + 1}}{\frac{1}{2}E\epsilon _f^2}. \end{aligned} \end{aligned}$$

(17)

In Eq. (17), $n_{ro}$ and $K_{ro}$ are the Ramberg-Osgood parameters. They are material constants characterizing the hardening behavior. $n_{ro}$ is usually $\ge 5$ and the yield-offset $K_{ro} = 0.002$. $\mathcal {R}$ becomes effective when the material or the bond starts yielding, that is, as the material or the bond starts gaining the inability to absorb elastic energy. Stress-strain curves in other colors represent uncertainties in the modulus of softness of the material. Each color corresponds to a particular quantified uncertainty. In Fig. 2, $U_S$ for any colored curve is the area between the corresponding stress-strain curve and the black dashed-dotted line. From Fig. 2 it can be interpreted that this uncertainty manifests a combined effect of the uncertainties in the yield-stress $\sigma _y$, yield-strain $\epsilon _y$ and failure-stress $\sigma _f$ of the material.

The homogenized form of the notion $\mathcal {R}_{x, x'}$, expressed as $\mathcal {R}_{x}$, quantifies the modulus of softness localized at x [29]. It is expressed in Eq. (18) as,

$$\begin{aligned} \mathcal {R}_{x} = \frac{\frac{1}{2}E_{@\text {{x}}}\epsilon _{f@\text {{x}}} ^2 - \sigma _{f@\text {{x}}}\epsilon _{f@\text {{x}}} + \frac{\sigma _{f@\text {{x}}}^2}{2E_{@\text {{x}}}} + \frac{K_{ro}\sigma _{y@\text {{x}}}}{n_{ro@\text {{x}}} + 1}\left( \frac{\sigma _{f@\text {{x}}}}{\sigma _{y@\text {{x}}}}\right) ^{n_{ro@\text {{x}}} + 1}}{\frac{1}{2}E_{@\text {{x}}}\epsilon _{f@\text {{x}}} ^2}. \end{aligned}$$

(18)

All the quantities in Eq. (18) collectively imitate some equivalent-isotropic material having the localized material properties as described in this paragraph. $E_{@\text {{x}}}$ is the Young’s modulus of elasticity localized at x, $\sigma _{y@\text {{x}}}$ is the yield-stress localized at x, $\sigma _{f@\text {{x}}}$ is the failure-stress localized at x, $\epsilon _{f@\text {{x}}}$ is the failure-strain localized at x, and $E_{@\text {{x}}}\epsilon _{f@\text {{x}}}$ is the failure-stress localized at x had the corresponding equivalent-isotropic material been brittle. $K_{ro}$ and $n_{ro@\text {{x}}}$ are the material constants describing the hardening behavior of the material localized at x. Conclusively, for the stochastic model,

$$\begin{aligned} \bar{\mathcal {R}}_{x, x'} = \mathcal {R}_{x}, \end{aligned}$$

(19)

unless any local interaction is already assigned a different value of $\bar{\mathcal {R}}_{x, x'}$ to ensure the conservation of localized potential energy.

$\mathcal {R}_{x}$ is positive if material points x are influencing material points $x'$, and negative if material points $x'$ are influencing material points x [29]. It is usually decomposed into $\mathcal {R}_{x, x'}$ as needed. $\mathcal {R}_{x}$ quantifies the homogenized modulus of softness between x and all of its local (direct) interactions with $x'$, and $\mathcal {R}_{x, x'}$ quantifies the modulus of softness of a particular local interaction, that is, between x and a particular $x'$. Stochasticity in $\mathcal {R}_{x, x'}$, as expressed in Eq. (11), is thus manifested as uncertainties in $\sigma _{y@\text {{x}}}$, $\epsilon _{y@\text {{x}}}$, $\sigma _{f@\text {{x}}}$, $\epsilon _{f@\text {{x}}}$, $E_{@\text {{x}}}$, and $n_{ro@\text {{x}}}$, and at a subtle outlook, uncertainties in these quantities for the bond between x and the particular $x'$.

3.1.4 Weight Fractions $w_{x, x'}$

Calibrated weight fractions $w_{x, x'}$ are a measure of the optimal decomposition of $U_S$ over the material’s nonlocal domain. These calibrated weights quantify the correct gain in the inability of the corresponding family of nonlocal bonds to absorb elastic energy [29]. This gain in the inability is expressed as a measure of the rate with which the nonlocal potential approaches zero, as shown in Eq. (35),

$$\begin{aligned} \frac{d\mathbb {U}_{{{_{NL}}}}(x, x', t)}{dt} \rightarrow 0. \end{aligned}$$

(20)

Material starts yielding as Eq. (20) begins to manifest itself during the deformation, and a discontinuity, either as material degradation or crack, between x and $x'$ naturally occurs when the bond between them is no longer capable of absorbing more energy. The decomposition of $U_S$ is carried out using pair-potentials. These pair-potentials provide a measure of the modulus of softness of the bond between x and $x'$ as a function of the distance between them. Conclusively, the stochasticity in $w_{x, x'}$, as expressed in Eq. (12), manifests itself as uncertainties in the localized yield-stress $\sigma _{y@\text {{x}}}$ and localized yield-strain $\epsilon _{y@\text {{x}}}$, and as stochasticity in the critical deformation of the bonds.

As demonstrated in [29], calibration of the weight fractions is carried out using Eqs. (21) and (22),

$$\begin{aligned} w_{x, x'} = w(x, x') = \frac{y(x, x')}{\int \limits _{V_{_{NL}}(x)}{y(x, x')d x'}}, \end{aligned}$$

(21)

where

$$\begin{aligned} y(x, x') =\frac{e^{-\frac{l^2(x, x')}{2\sigma ^2{_{{\text {stdev@{x}}}}}}}}{\sqrt{2\pi \sigma ^2{_{{\text {stdev@{x}}}}}}}. \end{aligned}$$

(22)

In Eqs. (21) and (22), l is the Euclidean distance between the material points x and $x'$. It is a function of their positions in the reference configuration. $\sigma {_{{\text {stdev@{x}}}}}$ is the standard deviation of the distribution of weight fractions over the nonlocal domain of x. $\sigma {_{{\text {stdev@{x}}}}}$ is calibrated ensuring the conservation of $U_S$. $\sigma {_{{\text {stdev@{x}}}}}$ physically quantifies length of effective interaction between x and $x'$ [29].

For an optimally calibrated¹ deterministic distribution of weights (shown with black line), several stochastic distributions of weight fractions due to stochasticity in $w_{x, x'}$ are shown in Fig. 3 with other colors. The red dotted-dashed curve depicts uncalibrated weights. It is noticeable that the distribution of weight fractions, due to stochasticity in $w_{x, x'}$, is likely to assume any other shape as well as long as $U_S$ remains conserved. Stochasticity in $w_{x, x'}$, thus, manifests itself as an uncertainty in $\sigma {_{{\text {stdev@{x}}}}}$ giving rise to an uncertainty in the size of the nonlocal volume surrounding the material point x.

Fig. 3

Distributions of weight fractions

$\sigma {_{{\text {stdev@{x}}}}}$ is expressed as,

$$\begin{aligned} \sigma {_{{\text {stdev@{x}}}}} = \sqrt{\frac{l^2(x, x'_{_{NL:j}})-l^2(x, x'_{_{NL:i}})}{2\ln \left( \frac{\mathbb {U}_{_{NL}}(x, x'_{_{NL:i}})}{\mathbb {U}_{_{NL}}(x, x'_{_{NL:j}})}\right) }}. \end{aligned}$$

(23)

In Eq. (23), the subscripts NL : i and NL : j indicate the $i^{th}$ and $j^{th}$ nonlocal material points ${\textbf {x}}'$ in the nonlocal domain of ${\textbf {x}}$. The two nonlocal potentials typically chosen are the maximum and the minimum potentials from the ensemble of the uncalibrated nonlocal potentials [29].

Once the weight fractions are determined, $\mathbb {U}_{_{NL}}(x, x')$ is calibrated as,

$$\begin{aligned} \mathbb {U}_{_{NL}}(x, x') = w_{x, x'} \mathcal {R}_{x, x'} \mathbb {U}_{_L}(x, x'). \end{aligned}$$

(24)

In Eq. (24), ${\textbf {x}}'$ in $\mathcal {R}_{x, x'}$ and $\mathbb {U}_{_L}(x, x')$ belongs to the local domain of x, and $x'$ in $w_{x, x'}$ and $\mathbb {U}_{_{NL}}(x, x')$ belongs to the nonlocal domain of x.

3.1.5 Mass Density

Stochasticity in mass density, as expressed in Eq. (14), is manifested as stochasticity in the mass distribution across the material’s spatial domain and/or as an uncertainty in the size of the local volume surrounding the material point x.

4 Numerical Implementation

For a material domain discretized using some optimal number of material points that are locally and nonlocally interacting with each other, the computational form of the stochastic model expressed in Eq. (5) is,

$$\begin{aligned} {\textbf {M}} \ddot{{\textbf {U}}} + {\textbf {K}}_{_{NL}} {\textbf {U}} = {\textbf {F}}. \end{aligned}$$

(25)

The derivation of Eq. (25) is provided in Appendix B. In Eq. (25), ${\textbf {M}}$ is the diagonal mass matrix. Each element of ${\textbf {M}}$ is computed by multiplying the local volume around the material point with the mass density associated with it. $\ddot{{\textbf {U}}}$ is the second time-derivative of the vector valued displacement of masses, ${\textbf {U}}$ is the displacement vector of masses, and ${\textbf {F}}$ is the external force vector. ${\textbf {K}}_{_{NL}}$ is the nonlocal elasticity matrix. It is computed from the material’s local elasticity matrix ${\textbf {K}}_{_{L}}$ by effectively and strategically distributing the material properties associated with the local elements of the local elasticity matrix over the local and nonlocal elements of the nonlocal elasticity matrix. This is done using a pairwise functional capable of modeling the pair-potential. These functionals are similar to the ones used in molecular dynamics. The elements of ${\textbf {K}}_{_{L}}$ are computed from the localized potentials or the strain energies of a deforming material using the notions from classical mechanics. The local and nonlocal elements of any matrix are identified by means of the degrees of separation (“social distance”) between two masses or by means of the direct as well as indirect interaction between them. The degree of separation between any two masses in the local elasticity matrix is 1 [29].

Equation (25) is simulated to demonstrate elastoplastic deformation in the stochastic materials.

Consider a deterministic discretized one-dimensional prismatic² specimen as shown in Fig. 4. It represents the discretization of a specimen with uniform material properties on a uniform grid. Its corresponding stochastic model, Eq. (5), is illustrated in Fig. 5. In the deterministic specimen, any material property, $\mathcal {M}$, for the interaction between any p and q is deterministic throughout the material domain and is expressed as $\bar{\mathcal {M}}$ or $\bar{\mathcal {M}}_{p,q}$. The same applies to any of its characterizations as well. The local and nonlocal interactions are depicted as springs in both the figures. Uniform geometries of the springs between the material points with same degrees of separation indicate that these interactions are characterized by deterministic material properties. It also indicates that the nonlocalization (or distribution) of material properties over the nonlocal interactions with the same degrees of separation is uniform. The decreasing widths of the springs with the increasing degrees of separation, and/or the distance between two nonlocally interacting material points, indicate that the magnitude of nonlocalization of the material properties decreases as the degree of separation, and/or the distance between two nonlocally interacting material points, increases.

Fig. 4

The deterministic model

Fig. 5

Stochastically varying material properties on a uniform grid

Figure 5 illustrates the specimen with stochastically varying material properties on a uniform grid. Non-uniform geometries of the springs indicate that these interactions are characterized by non-uniform material properties. Let any material property $\mathcal {M}$ between material points p and q be identified as $\mathcal {M}_{p,q}$, and subsequently, any of its characterizations by adding the suffix p, q to the corresponding notation.

Let both the specimens have length $= L$ and cross-sectional area $= A$, and are subjected to an external tensile force F on their both ends. Let the total number of material points used for discretization are n, each indexed by p and q. All of the material points q are allowed to interact material points p locally and nonlocally. Let any local material point be identified as $q_{_L}$ and a nonlocal material point as $q_{_{NL}}$. The corresponding local and nonlocal elasticity matrices are determined based on the methodology provided by Desai [29]. The finer modeling details for both are provided in the following subsections.

4.1 Modeling Methodology

Although the proposed stochastic models build on the deterministic models considered by Desai [29], a new computer program in MATLAB was written from scratch to incorporate stochasticity. Stochasticity in any material property $\mathcal {M}$, and in any of its characterizations, was generated using “wblrnd()” function for Weibull Distribution in MATLAB as,

$$\begin{aligned} \begin{aligned} \mathcal {M}_{x, x'}(x, x',\omega ^{(\mathfrak {m}_{{{x, x'}}})})&= \bar{\mathcal {M}}_{x, x'}(x, x') + \mathfrak {m}_{{{x, x'}}}(x, x',\omega ^{(\mathfrak {m}_{{{x, x'}}})}) \\&= \bar{\mathcal {M}}_{x, x'}(x, x') + \text {sign(randn())} \times \text {wblrnd(scale,shape)}\frac{\bar{\mathcal {M}}_{x, x'}(x, x')}{10}. \end{aligned} \end{aligned}$$

(26)

In Eq. (26), “sign(randn())” randomly returns “+1” or “-1” in MATLAB. The scale and shape parameters for Weibull distribution were chosen as 1 and 2 respectively. The stochastic process was optimally truncated using Karhunen-Loève Expansion (Appendix A) as,

$$\begin{aligned} \mathcal {M}_{x, x'}(x, x',\omega ^{(\mathfrak {m}_{{{x, x'}}})}) = \bar{\mathcal {M}}_{x, x'}(x, x') + \sum _{j=1}^{n} \sqrt{\lambda ^{{(\mathfrak {m}_{{{x, x'}}})}}_{_j}}\phi ^{{(\mathfrak {m}_{{{x, x'}}})}}_{_j}(x, x') \{\mathscr {H}^{{(\mathfrak {m}_{{{x, x'}}})}}_{_j}(\omega ^{{(\mathfrak {m}_{{{x, x'}}})}})\}. \end{aligned}$$

(27)

• (a) To begin with, the deterministic Young’s modulus of elasticity at each material point, $\bar{E}_{@p}$, was randomized using Eq. (27), and each local bond, $p, p+1$, was assigned the random Young’s modulus, $E_{@p}$.³ Local elasticity matrix for each specimen was computed. The elements were obtained using the notions from classical mechanics as,

  $$\begin{aligned} \mathbb {C}_{_{p,q_{_L}}} = \frac{A_{_{p,q_{_L}}} E_{_{p,q_{_L}}}}{l_{_{p,q_{_L}}}}. \end{aligned}$$

  (28)

  Based on the procedure given in [29], static displacement field was determined using local elasticity matrix. The localized potential between material points p and q is given as,

  $$\begin{aligned} \mathbb {U}_{_{p,q_{_L}}} = \frac{1}{2} \mathbb {C}_{_{p,q_{_L}}} \epsilon ^2_{_{p,q_{_L}}}. \end{aligned}$$

  (29)

  Here, $p,q_{_L}$ is the local bond, $A_{_{p,q_{_L}}}$ is the cross-sectional area of the local element, $l_{_{p,q_{_L}}}$ is the distance between materials points p and $q_{_L}$, $\mathbb {C}_{_{p,q_{_L}}}$ is the local bond-constant as defined in Eq. (15), and $\epsilon _{_{p,q_{_L}}}$ is the strain that the local bond experiences.

• (b) Using the static displacement field computed via the local elasticity matrix obtained in step (a), the stress, $\bar{\sigma }_{f@\text {{p}}}$, and the strain, $\bar{\epsilon }_{f@\text {{p}}}$, at p, when the material fails, were estimated using the methodology provided in section 4.1 of [29]. $\bar{\mathcal {R}}_{p}$ was estimated for each material point using Eq. (30) as,

  $$\begin{aligned} \bar{\mathcal {R}}_{{p}} = \frac{\frac{1}{2}\bar{E}_{@p}\bar{\epsilon }_{f@\text {{p}}} ^2 - \bar{\sigma }_{f@\text {{p}}}\bar{\epsilon }_{f@\text {{p}}} + \frac{\bar{\sigma }_{f@\text {{p}}}^2}{2\bar{E}_{@p}} + \frac{K_{ro}\bar{\sigma }_y}{\bar{n}_{ro} + 1}\left( \frac{\bar{\sigma }_{f@\text {{p}}}}{\bar{\sigma }_y}\right) ^{\bar{n}_{ro} + 1}}{\frac{1}{2}\bar{E}_{@p}\bar{\epsilon }_{f@\text {{p}}} ^2}. \end{aligned}$$

  (30)

  To ensure the stochasticity in all other quantities, other than $\bar{E}_{@p}$ and $K_{ro}$, in Eq. (30), $\bar{\mathcal {R}}_{{p}}$ was randomized using Eqs. (26) and (27), and each local bond, $p, p+1$, was assigned this random value. For the cases considered in this study, stochasticity in $\bar{R}_{p}$ ensures stochasticity in $\bar{R}_{p,q_L}$ as defined in Eq. (11).

• (c) Nonlocal Elasticity Matrix was developed for the computed values of $\mathcal {R}_{p}$ based on the procedure given in [29].

• (d) Using Eqs. (31) and (32) respectively, $\bar{\sigma }{_{{\text {stdev@{p}}}}}$ for each material point and the corresponding calibrated weights, $\bar{w}_{p,q_{_{NL}}}$, were estimated from ensemble of uncalibrated nonlocal potentials and weights obtained from the nonlocal elasticity matrix computed in step (c),

  $$\begin{aligned} \bar{\sigma }{_{{\text {stdev@{p}}}}} = \sqrt{\frac{l^2_{{p,q_{_{NL:farthest}}}}-l^2_{{p,q_{_{NL:nearest}}}}}{2\ln \left( \frac{\text {max}\left( \mathbb {U}_{{p,q_{_{NL}}}}\right) }{\text {min}\left( \mathbb {U}_{{p,q_{_{NL}}}}\right) }\right) }}, \end{aligned}$$

  (31)

  and

  $$\begin{aligned} \bar{w}_{p,q_{_{NL}}} = 2\frac{e^{-\frac{l^2_{p,q_{_{NL}}}}{2\bar{\sigma }^2_{\text {stdev@p}}}}}{\sqrt{2\pi \bar{\sigma }^2_{\text {stdev@p}}}}. \end{aligned}$$

  (32)

  In Eq. (31), $q_{_{NL:farthest}}$ and $q_{_{NL:nearest}}$ are respectively the farthest and nearest nonlocal material points from p. The calibrated weights, $\bar{w}_{p,q_{_{NL}}}$ were randomized using Eqs. (12), (26) and (27).

• (e) To obtain the stochastic nonlocal elastic matrix, nonlocal potentials were determined as,

  $$\begin{aligned} \mathbb {U}_{{p,q_{_{NL}}}} = w_{p,q_{_{NL}}} \mathcal {R}_{p,q_{_{L}}}\mathbb {U}_{p,q_{_{L}}} = \frac{1}{2} w_{p,q_{_{NL}}} \left( \mathcal {R}_{p,q_{_{L}}}\Vert {\textbf{f}}_{{\textit{ff}}_{p,q_{_{L}}}}\Vert \right) l_{p,q_{_{NL}}}\epsilon _{p,q_{_{NL}}}. \end{aligned}$$

  (33)

  In Eq. (33), $\Vert {\textbf{f}}_{{\textit{ff}}_{p,q_{_{L}}}}\Vert$ is the magnitude of the localized internal force between material points p and $q_{_L}$.

The discretized equation of motion was simulated using implicit Modal Analysis used in LS-DYNA [30]. The critical time step, $\Delta t_{cri}$, was determined using Eq. (34) as,

$$\begin{aligned} \Delta t_{cri} = 4\pi \sqrt{\frac{\bar{\rho }L^2}{\bar{E}}}. \end{aligned}$$

(34)

For the simulations, $\Delta t$ was taken as $\Delta t_{cri}$. Equation (35) served as a general criterion to break bonds. All the bonds associated with the weights $w_{p,q_{_{NL}}}$ were broken as the specimen experienced their corresponding strain $\epsilon _{p,q_{_{NL}}}$, as shown in Eq. (33).

$$\begin{aligned} \frac{d\mathbb {U}_{{p,q_{_{NL}}}}}{dt} \rightarrow 0. \end{aligned}$$

(35)

The simulation was carried out for monotonic as well as cyclic loadings. For monotonic loading, an initial external tensile force of 0.01 N was applied on both ends of the prismatic bar, and it was increased by $1\%$ after every static displacement until the specimens started experiencing strains larger than their respective failure strains $\bar{\epsilon }_f$. For cyclic loading, the tensile force was unloaded in the similar fashion as the external stress on the specimens became larger than the corresponding yield stress.

The simulation results are presented in the following subsections.

4.2 Deterministic Model

Material 1: For the deterministic model, Fig. 4, let Young’s Modulus $\bar{E} = 71.6$ GPa, $\bar{\sigma }_f = 665.8$ MPa, $\bar{\epsilon }_f = 0.115$, $\bar{\sigma }_y = 538.6$ MPa, $\bar{\epsilon }_y = 0.009522$, $\bar{n}_{ro} = 17.8702$, and $K_{ro} = 0.002$, Mass Density $\bar{\rho } = 2810$ $kg/m^3$, Poisson’s Ratio $\bar{\nu } = 0.33$.

Material 2: For the deterministic model, Fig. 4, let Young’s Modulus $\bar{E} = 115.7$ GPa, $\bar{\sigma _f} = 933$ MPa, $\bar{\epsilon _f} = 0.516$, $\bar{\sigma _y} = 867$ MPa, $\bar{\epsilon _y} = 0.009494$, $\bar{n}_{ro} = 47.61$, and $K_{ro} = 0.002$, Mass Density $\bar{\rho } = 4430$ $kg/m^3$, Poisson’s Ratio $\bar{\nu } = 0.31$.

For the specimens of both materials, let length $L = 0.1$ m and cross-sectional area $A = 0.01 \times 0.01$ $m^2$.

4.3 Stochastic and Uniform Grids

In addition to the uniform grids, stochastic grids were also considered. Material properties were thus allowed to vary stochastically on uniform grids as well as stochastic grids. Specimens for both materials were discretized with 500 local bonds for both the grid types. The spacings between the material points for stochastic grids were determined using “rand()” function in MATLAB as,

$$\begin{aligned} \text{random}\_\text{spacing} = \text{average}\_\text{spacing} + 0.65 \times \text{sign}(\text{randn}()) \times \text{rand}()\times \text{average}\_\text{spacing}. \end{aligned}$$

(36)

In Eq. (36), average_spacing corresponds to the spacing between two material points on a uniform grid, 0.65 is an arbitrary number to ensure that the maximum spacing between any two material points on the stochastic grid is not more than $165\%$ of the average_spacing.

A new realization of stochastic grid was generated for each set of realizations of the stochastic parameters illustrated in Section 4.4. To prevent mathematical or computational singularity, those cases in which any two material points overlapped (or nearly overlapped) were ignored, and a new realization was considered instead.

The spacing between the material points on the uniform grid was considered as $\frac{L}{500}$.

Typical stochastic and uniform grids considered for the specimens are depicted in Fig. 6.

Fig. 6

Typical stochastic and uniform grids

4.4 Stochastic Model

Thirty realizations of each stochastic parameter were considered, and the $30^{th}$ realization of the corresponding stochastic parameter is illustrated in Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15, and 16.

Fig. 7

Stochasticity in the Young’s modulus of elasticity for Material 1

Fig. 8

Stochasticity in the Young’s modulus of elasticity for Material 2

Fig. 9

Randomness in $\mathcal {R}$ mechanism for Material 1

Fig. 10

Randomness in $\mathcal {R}$ mechanism for Material 2

Fig. 11

Stochastic $\mathcal {R}$ mechanism for Material 1

Fig. 12

Stochastic $\mathcal {R}$ mechanism for Material 2

Fig. 13

Randomness in calibrated weights for material points @ $L = 0$ and $L = \frac{L}{8}$ for Material 1

Fig. 14

Randomness in calibrated weights for material points @ $L = 0$ and $L = \frac{L}{8}$ for Material 2

Fig. 15

Typical stochastic calibrated weights for material points @ $L = 0$ and $L = \frac{L}{8}$ on Material 1 specimen

Fig. 16

Typical stochastic calibrated weights for material points @ $L = 0$ and $L = \frac{L}{8}$ on Material 2 specimen

Stochasticities in the local and nonlocal potentials are manifested as a result of the stochasticity in the material properties. For the two materials considered in this study, the stochasticity in the Young’s Modulus of Elasticity is illustrated in Figs. 7 and 8. This stochasticity may appear in a deterministic specimen due to many factors like manufacturing defects, natural phenomenon — like corrosion, or some unknown reason.

4.4.1 Deformation-Gamuts Parameters

$\mathcal {R}$ mechanisms for the deterministic cases and the randomness in them are illustrated in Figs. 9 and 10. The mechanisms for stochastic $\mathcal {R}$ are illustrated in Figs. 11 and 12.

Typical deterministic calibrated weights for material points located at the lengths $L = 0$ and $L = \frac{L}{8}$ of both specimens and the randomness in these weights are shown in Figs. 13 and 14. The stochastic calibrated weights are shown in Figs. 15 and 16. The gap between the two curves at $L = \frac{L}{8}$ in these figures is the local domain of that material point [29].

The deterministic effective length of interaction of each material point for both materials, as well as the randomness in it due to the stochastic calibrated weights, is given in Figs. 17 and 18. The stochastic effective lengths of interaction for all material points of both materials are shown in Figs. 19 and 20. It is noticeable that even though the stochasticity in $\sigma_{\text{stdev}@{\textbf{x}}}$ is not explicitly quantified in this study, the summation of the deterministic and random values in Figs. 17 and 18 is equal to the stochastic values in Figs. 19 and 20 respectively.

Fig. 17

Randomness in $\sigma_{\text{stdev}@{\textbf{x}}}$ for Material 1

Fig. 18

Randomness in $\sigma_{\text{stdev}@{\textbf{x}}}$ for Material 2

Fig. 19

Stochastic $\sigma_{\text{stdev}@{\textbf{x}}}$ for Material 1

Fig. 20

Stochastic $\sigma_{\text{stdev}@{\textbf{x}}}$ for Material 2

4.4.2 Monotonic Loading

The stress-strain curves for 30 realizations of both materials and of their deterministic models are illustrated in Figs. 21 and 22. In Figs. 23 and 24, the mean stress-strain curves of these 30 realizations of both materials are compared with the deterministic curves and the stress-strain curves obtained using Ramberg-Osgood equations. The mean curves are found to be in good agreement with both these curves.

Fig. 21

Engineering stress vs. strain curves for 30 realizations of Material 1

Fig. 22

Engineering stress vs. strain curves for 30 realizations of Material 2

Fig. 23

Mean, deterministic and theoretical engineering stress vs. strain curves of Material 1

Fig. 24

Mean, deterministic and theoretical engineering stress vs. strain curves of Material 2

4.4.3 Cyclic Loading

Stable hysteresis loops for several cycles for the $30^{th}$ realization of both materials are shown in Figs. 25 and 26. The log-log plots of the stress amplitudes vs. plastic-strain amplitudes are given in Figs. 27 and 28. The slopes (cyclic strain hardening exponents) and the y-intercepts (stress-strain coefficients) of the linear fits were obtained using the “poly1” fit function available in MATLAB. The cyclic strain hardening exponents and the stress-strain coefficients for all the realizations are given in Figs. 29, 30, 31, and 32.

Fig. 25

Several cycles of steady-state cyclic stress-strain behavior for realization 30 of Material 1

Fig. 26

Several cycles of steady-state cyclic stress-strain behavior for realization 30 of Material 2

Fig. 27

Log-log fit for stress vs. plastic-strain amplitudes of realization 30 of Material 1

Fig. 28

Log-log fit for stress vs. plastic-strain amplitudes of realization 30 of Material 2

Fig. 29

Cyclic strain hardening exponents ($n'$) of Material 1

Fig. 30

Cyclic strain hardening exponents ($n'$) of Material 2

Fig. 31

Cyclic stress-strain coefficients ($K'$) of Material 1

Fig. 32

Cyclic stress-strain coefficients ($K'$) of Material 2

The simulated mean values of the cyclic strain hardening exponents and cyclic strength coefficients for the stochastic material properties over stochastic and uniform grids, and their comparison with the deterministic values [29] and experimental results [31, 32], are provided in Table 1.

Table 1 Mean values of cyclic strain hardening exponent $n'$ and cyclic strength coefficient $K'$

5 Concluding Remarks

Based on stochastic local and nonlocal deformation-gamuts, in this study, a novel multiscale nonlocal stochastic equation of motion to model elastoplastic deformation of 1-D bars made of stochastic materials is introduced. To quantify stochasticity in material properties, stochasticity in the energy-densities and energy-states across the material’s spatial domain as well as stochasticity in the deformation-gamuts parameters is considered. Specimens of two distinct materials subjected to monotonic as well as cyclic loadings are simulated. Simulations for stochastic material properties on uniform grids, and stochastic material properties on stochastic grids are carried out. Thirty realizations for each stochastic process are considered. It is demonstrated that the mean values of the results from all the realizations of material properties on uniform grid are in good agreement with the results for the deterministic case as well as the theoretical estimations and experimental results published in open literature for the corresponding equivalent-isotropic material. The results for the stochastic material properties on stochastic grids are fairly acceptable. It is important to note that the accuracy of the results largely depends on the quantification of the stochasticity. For example, if the denominator in the term $\frac{\bar{\mathcal {M}}_{x, x'}(x, x')}{10}$ of Eq. (26) is increased, the material properties still remain stochastic. However, accuracy of the results will improve. For the cases considered in this paper, this denominator is the same for all $\bar{\mathcal {M}}$, for any of its characterizations, and all the stochastic DG parameters. However, to capture a more realistic case, depending on their mutual correlations, the denominator may be allowed to assume different values for $\bar{\mathcal {M}}$, different characterizations of $\bar{\mathcal {M}}$, and different DG parameters. Additionally, the scale and shape parameters for Weibull distribution also have an effect on the final results. Further, if the arbitrary number in Eq. (36) is reduced, convergence of the mean values of the results for stochastic material properties on the stochastic grid will be better.

Unlike conventional peridynamics, at any modeling scale the proposed stochastic equation of motion is independent of the horizon size, uniformity in bond-lengths, grid-size, and the grid-type. The effective distance of interaction of the material point x is $3 \times \sigma {_{{\text {stdev@{x}}}}}$ in the proposed equation of motion. From Figs. 17, 18, 19, and 20 it can be noticed that $\sigma {_{{\text {stdev@{x}}}}}$ is determined by the “material” itself, either deterministic or stochastic, for the scale it is modeled at. No explicit change in the “horizon” is needed while transitioning from the deterministic medium to stochastic medium, an issue identified in [16]. Additionally, from the discussion in Section 3.1.4 it can be noticed that the “critical stretch” need not be explicitly adjusted to the grid-type, an issue identified in [18].

In this study, all random fields are generated from Weibull distribution at the scale of analysis. This ensures spatial correlation between material properties at the scale under consideration. It can also be noticed from the discussion in Section 3.1 that all stochastic parameters in Eq. (5) are correlated via other stochastic parameters as well, for instance $\mathcal {R}_{x, x'}(x, x',\omega ^{(\mathfrak {r}_{{{x, x'}}})})$ and $w_{x, x'}(x, x',\omega ^{(\mathfrak {w}_{{{x, x'}}})})$ are correlated via localized yield-stress $\sigma _{y@\text {{x}}}$ and localized yield-strain $\epsilon _{y@\text {{x}}}$. Considering the duality between local and nonlocal deformation-gamuts and the conservation of total potential energy at any scale of analysis, the understanding of multiscale correlation of stochastic DG parameters to recognize the manifestation of stochasticity during the process of upscaling from atomistic-scale to macro-scale is identified as an active challenge.

Appendices

Appendix A. Karhunen-Loève (KL) Expansion

The Karhunen-Loève Expansion [33, 34] is a bi-orthogonal stochastic process expansion. It is the representation of a stochastic process as an infinite linear combination of orthogonal functions, analogous to a Fourier series representation of a function on a bounded domain. It is helpful in the numerical modeling of abstract measure spaces with no or little physical intuitive support.

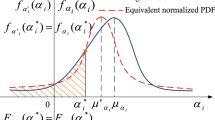
Consider some stochastic process, $\mathcal {G}(\chi ,\omega ^{(\mathfrak {p})})$, as depicted in Fig. 33, is defined on a common probability space $(\Omega , \mathcal {F}, P)$, where $\Omega$ is the sample space, $\mathcal {F}$ represents $\sigma \text {-algebra}$, and P is the probability measure. Let $\chi \in \text {some bounded domain } \mathcal {D}$ and the process is characterized by a finite variance $\sigma _{\text {var}-\mathfrak {p}}$. If the deterministic (mean) values are given by $\bar{\mathcal {G}}(\chi )$ and the deviation from the mean for any realization is denoted by $\mathfrak {p}(\chi , \omega ^{(\mathfrak {p})})$. Then,

$$\begin{aligned} \mathcal {G}(\chi ,\omega ^{(\mathfrak {p})}) = \bar{\mathcal {G}}(\chi ) + \mathfrak {p}(\chi , \omega ^{(\mathfrak {p})}). \end{aligned}$$

(A.1)

Fig. 33

Stochastic process

The Karhunen-Loève decomposition of the zero-mean stochastic process $\mathfrak {p}(\chi , \omega ^{(\mathfrak {p})})$, depicted by any realization in Fig. 33, is expressed as its projection on the Hilbert basis $\{\mathscr {H}^{(\mathfrak {p})}_{_j}(\omega ^{(\mathfrak {p})})\}$, as shown in Eq. (A.2),

$$\begin{aligned} \mathfrak {p}(\chi , \omega ^{(\mathfrak {p})}) = \sum _{j=1}^{\infty } \sqrt{\lambda ^{(\mathfrak {p})}_{_j}}\phi ^{(\mathfrak {p})}_{_j}(\chi ) \{\mathscr {H}^{(\mathfrak {p})}_{_j}(\omega ^{(\mathfrak {p})})\}. \end{aligned}$$

(A.2)

The bracketed superscripts indicate the realization which the superscripted quantity is associated with. The Hilbert basis, in Eq. (A.2), serves as the set of uncorrelated random variables. This set is expressed as,

$$\begin{aligned} \mathscr {H}^{\mathfrak {(p})}_j(\omega ^{(\mathfrak {p})}) = \frac{1}{\sqrt{\lambda ^{(\mathfrak {p})}_{_j}}}\int \limits _{\mathcal {D}}\mathfrak {p}(\chi ,\omega ^{(\mathfrak {p})})\phi ^{(\mathfrak {p})}_{_j}(\chi )d\chi . \end{aligned}$$

(A.3)

$\lambda ^{(\mathfrak {p})}_{_j}$ and $\phi ^{(\mathfrak {p})}_{_j}$ are the eigen values and eigen functions of the bounded, symmetric and positive-definite co-variance function $\mathcal {C}^{(\mathfrak {p})}(\chi _{_1},\chi _{_2})$ for the stochastic process under consideration. They are the solution of the homogeneous Fredholm integral equation of the second kind, as expressed in Eq. (A.4),

$$\begin{aligned} \int \limits _{\mathcal {D}} \mathcal {C}^{(\mathfrak {p})}(\chi _{_1},\chi _{_2}) \phi ^{(\mathfrak {p})}_{_j}(\chi _{_1})d\chi _{_1} = \lambda ^{{(\mathfrak {p})}}_{_j} \phi ^{{(\mathfrak {p})}}_{_j}(\chi _{_2}). \end{aligned}$$

(A.4)

where,

$$\begin{aligned} \int \limits _{\mathcal {D}} \phi ^{(\mathfrak {p})}_{_i}(\chi ) \phi ^{(\mathfrak {p})}_{_j}(\chi )d\chi = \delta _{_{ij}}. \end{aligned}$$

(A.5)

Here, $\delta _{_{ij}}$ is the Kronecker-delta function. According to Mercer’s Theorem [37], $\mathcal {C}^{(\mathfrak {p})}(\chi _{_1},\chi _{_2})$ is expressed as,

$$\begin{aligned} \mathcal {C}^{(\mathfrak {p})}(\chi _{_1},\chi _{_2}) = \sum _{j=1}^{\infty }\lambda ^{_{(\mathfrak {p})}}_{_j} \phi ^{_{(\mathfrak {p})}}_{_j}(\chi _{_1})\phi ^{_{(\mathfrak {p})}}_{_j}(\chi _{_2}). \end{aligned}$$

(A.6)

$\mathcal {C}^{(\mathfrak {p})}(\chi _{_1},\chi _{_2})$ can be optimally truncated using first M terms [35, 36] as,

$$\begin{aligned} \mathcal {C}^{(\mathfrak {p})}(\chi _{_1},\chi _{_2}) = \sum _{j=1}^{M}\lambda ^{_{(\mathfrak {p})}}_{_j} \phi ^{_{(\mathfrak {p})}}_{_j}(\chi _{_1})\phi ^{_{(\mathfrak {p})}}_{_j}(\chi _{_2}). \end{aligned}$$

(A.7)

In order to demonstrate the convergence of Karhunen-Loève (KL) Expansion, an approximation of realization 6 in Fig. 33 is shown below in Fig. 34.

Fig. 34

Karhunen-Loève expansion of realization 6

Appendix B. Computational form of the stochastic model

The proposed governing equation of motion for deformation dynamics of stochastic materials in 1-D is,

$$\begin{aligned} \begin{aligned} \rho _{_{{{L@x}}}}(x, \omega ^{(\mathfrak {d})}) \ddot{u}(x,t)&+ \int \limits _{V_{_L}(x)}(1-\mathcal {R}_{x, x'}(x, x',\omega ^{(\mathfrak {r}_{{{x, x'}}})}))\nabla _{_{{x}}}\mathbb {U}_{_L}(x, x', t, \omega ^{(\mathfrak {u}_{{{l}}})})dV_{_L}(x') \\ {}&+ \int \limits _{V_{_{NL}}(x)}\int \limits _{V_{_{NL}}(x)}w_{x, x'}(x, x',\omega ^{(\mathfrak {w}_{{{x, x'}}})})\nabla _{_{{x}}}\mathbb {U}_{_{NL}}(x, x', t, \omega ^{(\mathfrak {u}_{{{nl}}})})dV_{_{NL}}(x')dV_{_{NL}}(x') = {F}_{d}({x},t). \end{aligned} \end{aligned}$$

(B.1)

Its discretized version for the bar in Fig. 1 takes the form,

$$\begin{aligned} \begin{aligned} \rho _{_{{{L@p}}}}(p, \omega ^{(\mathfrak {d})}) \ddot{u}_p&+ \sum _{\begin{array}{c} q \\ |p-q| = 1 \end{array}} (1-\mathcal {R}_{p, q}(p, q,\omega ^{(\mathfrak {r}_{{{p, q}}})}))\nabla _{_{{p}}}\mathbb {U}_{_L}(p, q, t, \omega ^{(\mathfrak {u}_{{{l}}})}) \\ {}&+ \sum _{\begin{array}{c} q \\ |p-q| \ne 1 \end{array}}\sum _{\begin{array}{c} q \\ |p-q| \ne 1 \end{array}}w_{p, q}(p, q,\omega ^{(\mathfrak {w}_{{{p, q}}})})\nabla _{_{{p}}}\mathbb {U}_{_{NL}}(p, q, t, \omega ^{(\mathfrak {u}_{{{nl}}})}) = {F}_{d}(p, t). \end{aligned} \end{aligned}$$

(B.2)

In terms of localized and nonlocalized material points q, we have,

$$\begin{aligned} \begin{aligned} \rho _{_{{{L@p}}}}(p, \omega ^{(\mathfrak {d})}) \ddot{u}_p&+ \sum _{\begin{array}{c} q_{_L} \end{array}} (1-\mathcal {R}_{p, q_{_L}}(p, q_{_L},\omega ^{(\mathfrak {r}_{{{p, q_{_L}}}})}))\nabla _{_{{p}}}\mathbb {U}_{_L}(p, q_{_L}, t, \omega ^{(\mathfrak {u}_{{{l}}})}) \\ {}&+ \sum _{\begin{array}{c} q_{_{NL}} \end{array}}\sum _{\begin{array}{c} q_{_{NL}} \end{array}}w_{p, q_{_{NL}}}(p, q_{_{NL}},\omega ^{(\mathfrak {w}_{{{p, q_{_{NL}}}}})})\nabla _{_{{p}}}\mathbb {U}_{_{NL}}(p, q_{_{NL}}, t, \omega ^{(\mathfrak {u}_{{{nl}}})}) = {F}_{d}(p, t). \end{aligned} \end{aligned}$$

(B.3)

This gives,

$$\begin{aligned} \begin{aligned} \rho _{_{{{L@p}}}}(p, \omega ^{(\mathfrak {d})}) \ddot{u}_p&+ \sum _{\begin{array}{c} q_{_L} \end{array}} (1-\mathcal {R}_{p, q_{_L}}(p, q_{_L},\omega ^{(\mathfrak {r}_{{{p, q_{_L}}}})}))\nabla _{_{{p}}}\mathbb {U}_{_L}(p, q_{_L}, t, \omega ^{(\mathfrak {u}_{{{l}}})}) \\ {}&+ \sum _{\begin{array}{c} q_{_{NL}} \end{array}}w_{p, q_{_{NL}}}(p, q_{_{NL}},\omega ^{(\mathfrak {w}_{{{p, q_{_{NL}}}}})})\sum _{\begin{array}{c} q_{_{NL}} \end{array}}\nabla _{_{{p}}}\mathbb {U}_{_{NL}}(p, q_{_{NL}}, t, \omega ^{(\mathfrak {u}_{{{nl}}})}) = {F}_{d}(p, t). \end{aligned} \end{aligned}$$

(B.4)

In Eq. (B.4), $\sum _{\begin{array}{c} q_{_L} \end{array}} (1-\mathcal {R}_{p, q_{_L}}(p, q_{_L},\omega ^{(\mathfrak {r}_{{{p, q_{_L}}}})}))\nabla _{_{{p}}}\mathbb {U}_{_L}(p, q_{_L}, t, \omega ^{(\mathfrak {u}_{{{l}}})})$ is the fraction of localized internal force that remains localized, and $\sum _{\begin{array}{c} q_{_{NL}} \end{array}}\nabla _{_{{p}}}\mathbb {U}_{_{NL}}(p, q_{_{NL}}, t, \omega ^{(\mathfrak {u}_{{{nl}}})})$ is the remaining fraction of the localized internal force that is nonlocalized (or distributed) over the interactions of p with nonlocal material points $q_{_{NL}}$. Thus,

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} q_{_{NL}} \end{array}}\nabla _{_{{p}}}\mathbb {U}_{_{NL}}(p, q_{_{NL}}, t, \omega ^{(\mathfrak {u}_{{{nl}}})}) = \mathcal {R}_{p, q_{_L}}(p, q_{_L},\omega ^{(\mathfrak {r}_{{{p, q_{_L}}}})})\nabla _{_{{p}}}\mathbb {U}_{_L}(p, q_{_L}, t, \omega ^{(\mathfrak {u}_{{{l}}})}). \end{aligned} \end{aligned}$$

(B.5)

Thus, from Eqs. (B.4) and (B.5), we get,

$$\begin{aligned} \begin{aligned} \rho _{_{{{L@p}}}}(p, \omega ^{(\mathfrak {d})}) \ddot{u}_p&+ \sum _{\begin{array}{c} q_{_L} \end{array}} (1-\mathcal {R}_{p, q_{_L}}(p, q_{_L},\omega ^{(\mathfrak {r}_{{{p, q_{_L}}}})}))\nabla _{_{{p}}}\mathbb {U}_{_L}(p, q_{_L}, t, \omega ^{(\mathfrak {u}_{{{l}}})}) \\ {}&+ \sum _{\begin{array}{c} q_{_{NL}} \end{array}}w_{p, q_{_{NL}}}(p, q_{_{NL}},\omega ^{(\mathfrak {w}_{{{p, q_{_{NL}}}}})}) \mathcal {R}_{p, q_{_L}}(p, q_{_L},\omega ^{(\mathfrak {r}_{{{p, q_{_L}}}})})\nabla _{_{{p}}}\mathbb {U}_{_L}(p, q_{_L}, t, \omega ^{(\mathfrak {u}_{{{l}}})}) = {F}_{d}(p, t). \end{aligned} \end{aligned}$$

(B.6)

Using the aforementioned arguments and Eq. (33), Eq. (B.6) can be rewritten as,

$$\begin{aligned} m_{_{{{L@p}}}} \ddot{u}_p + \sum _{\begin{array}{c} q_{_L} \end{array}} \mathbb {C}_{_{p, q_{_L}}} u_{_{p, q_{_L}}} + \sum _{\begin{array}{c} q_{_{NL}} \end{array}}\mathbb {C}_{p,q_{_{NL}}} u_{_{p, q_{_{NL}}}} = \mathscr {F}_{L@p}(t). \end{aligned}$$

(B.7)

In Eq. (B.7), $m_{_{{{L@p}}}}$ is the mass of the material point p localized at p, $\ddot{u}_p$ is the acceleration of the material point p, $\mathbb {C}_{_{p, q_{_L}}}$ is the local bond-constant defined in Eq. (15), $u_{_{p, q_{_L}}}$ is the relative displacement between material points p and $q_{_{L}}$, $\mathbb {C}_{p,q_{_{NL}}}$ is the nonlocal bond-constant defined in Eq. (16), $u_{_{p, q_{_{NL}}}}$ is the relative displacement between material points p and $q_{_{NL}}$, and $\mathscr {F}_{L@p}(t)$ is the time dependent external force localized at p.

For the entire bar, Eq. (B.7) can be written in the matrix form as,

$$\begin{aligned} {\textbf {M}} \ddot{{\textbf {U}}} + {\textbf {K}}_{_{NL}} {\textbf {U}} = {\textbf {F}}. \end{aligned}$$

(B.8)

Equation (B.8) is the required Eq. (25).