Skip to main content
SpringerLink
Log in

Hopf bifurcation and Turing instability in a predator–prey model with Michaelis–Menten functional response

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

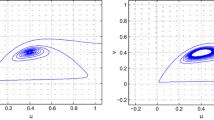
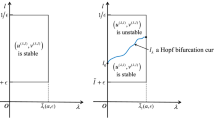
In this paper, the predator–prey model with Michaelis–Menten functional response subject to the Neumann boundary conditions is considered. The stability of the positive equilibrium and the direction of the Hopf bifurcations for the corresponding ordinary differential equation and partial differential equation are studied, respectively. To this end, the normal form method and the center manifold theorem are applied to determine the direction of the Hopf bifurcation and the stability of the bifurcated limit cycle when the diffusion terms are present. It is shown that the corresponding system can undergo either the supercritical or subcritical Hopf bifurcation at the equilibrium point within certain parameter range. Meanwhile, the Turing instability conditions for the equilibrium and the limit cycle bifurcated from the Hopf bifurcation are derived. As a result, some patterns occur in the model. Numerical simulations are carried out to verify the theoretical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Turing, A.M.: The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci 237, 37–72 (1952)

    Article  MathSciNet  Google Scholar 

  2. Epstein, I.R., Pojman, J.A.: An Introduction to Nonlinear Chemical Dynamics. Oxford University Press, Oxford (1998)

    Google Scholar 

  3. Lengyel, I., Epstein, I.R.: Modeling of Turing structure in the chlorite-iodide-malonic acid-starch reaction system. Science 251, 650–652 (1991)

    Article  Google Scholar 

  4. Li, X., Jiang, W.H., Shi, J.P.: Hopf bifurcation and Turing instability in the reaction–diffusion Holling–Tanner predator–prey model. IMA J. Appl. Math. 78, 287–306 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  5. Peng, R., Wang, M.X.: On pattern formation in the Gray-Scott model. J. Sci. China Ser. A Math. 50, 377–386 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Ruan, S.G.: Diffusion-driven instability in the Gierer–Meinhardt model of morphogenesis. Nat. Resour. Modell. 11, 131–142 (1998)

    Article  MathSciNet  Google Scholar 

  7. Faria, T.: Stability and bifurcation for a delayed predator–prey model and the effect of diffusion. J. Math. Anal. Appl. 254, 433–463 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chen, F.D.: On a nonlinear nonautonomous predator–prey model with diffusion and distributed delay. J. Comput. Appl. Math. 180, 33–49 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ko, W., Ryu, K.: Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a prey refuge. J. Differ. Equ. 231, 534–550 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Xiao, Y.N., Chen, L.S.: A ratio-dependent predator–prey model with disease in the prey. Appl. Math. Comput. 131, 397–414 (2002)

    MathSciNet  MATH  Google Scholar 

  11. Jiang, G.R., Lu, Q.S.: Impulsive state feedback control of a predator–prey model. J. Comput. Appl. Math. 200, 193–207 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  12. Du, Y.H., Hsu, S.B.: A diffusive predator–prey model in heterogeneous environment. J. Differ. Equ. 203, 331–364 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Xiao, D.M., Li, W.X., Han, M.A.: Dynamics in a ratio-dependent predator–prey model with predator harvesting. J. Math. Anal. Appl. 324, 14–29 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  14. Kar, T.K., Ghorai, A.: Dynamic behaviour of a delayed predator–prey model with harvesting. Appl. Math. Comput. 217, 9085–9104 (2011)

    MathSciNet  MATH  Google Scholar 

  15. Hu, D.P., Cao, H.J.: Stability and bifurcation analysis in a predator–prey system with Michaelis–Menten type predator harvesting. Nonlinear Anal. RWA 33, 58–82 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  16. Wang, K.: Periodic solutions to a delayed predator-prey model with Hassell–Varley type functional response. Nonlinear Anal. RWA 12, 137–145 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  17. Chen, W.Y., Wang, M.X.: Qualitative analysis of predator–prey models with Beddington–De Angelis functional response and diffusion. Math. Comput. Modell. 42, 31–44 (2005)

    Article  MATH  Google Scholar 

  18. Chen, J.P., Zhang, H.D.: The qualitative analysis of two species predator–prey model with Holling’s type III functional response. J. Biomath. 7, 77–86 (1986)

    MathSciNet  MATH  Google Scholar 

  19. Wang, Q., Dai, B.X., Chen, Y.M.: Multiple periodic solutions of an impulsive predator–prey model with Holling-type IV functional response. Math. Comput. Modell. 49, 1829–1836 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. Liu, X.Q., Zhong, S.M., Tian, B.D., Zheng, F.X.: Asymptotic properties of a stochastic predator–prey model with Crowley–Martin functional response. J. Appl. Math. Comput. 43, 479–490 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  21. Seo, G., Kot, M.: A comparison of two predator–prey models with Holling type I functional response. Math. Biosci. 212, 161–179 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  22. May, R.M., Beddington, J.R., et al.: Management of multispecies fisheries. Science 205, 267–277 (1979)

    Article  Google Scholar 

  23. Hsu, S.B., Huang, T.W.: Global stability for a class of predator–prey system. SIAM J. Appl. Math. 55, 763–783 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  24. Beddington, J.R., May, R.M.: Maximum sustainable yields in systems subject to harvesting at more than one trophic level. Math. Biosci. 51, 261–281 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  25. Beddington, J.R., Cooke, J.G.: Harvesting from a prey–predator complex. Ecol. Modell. 14, 155–177 (1982)

    Article  Google Scholar 

  26. Zhu, C.R., Lan, K.Q.: Phase portraits, Hopf bifurcation and limit cycles of Leslie–Gower predator-prey systems with harvesting rates. Discr. Cont. Dynam. Syst. Ser. B. 14, 289–306 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  27. Gong, Y.J., Huang, J.C.: Bogdanov–Takens bifurcation in a Leslie–Gower predator–prey model with prey harvesting. Acta Math. Appl. Sin. Eng. Ser. 30, 239–244 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  28. Kar, T.K., Chaudhuri, K.S.: Regulation of a prey–predator fishery by taxation: a dynamic reaction model. J. Biol. Syst. 11, 173–187 (2003)

    Article  MATH  Google Scholar 

  29. Bairagi, N., Chakraborty, S., Pal, S.: Heteroclinic bifurcation and multistability in a ratio-dependent predator–prey system with Michaelis–Menten type harvesting rate. Proc. World Congr. Eng. 1, 4–6 (2012)

    Google Scholar 

  30. Clark, C.W.: Aggregation and fishery dynamics: a theoretical study of schooling and the purse seine tuna fisheries. Fish. Bull. 77, 317–337 (1979)

    Google Scholar 

  31. Yi, F.Q., Wei, J.J., Shi, J.P.: Diffusion-driven instability and bifurcation in the Lengyel–Epstein system. Nonlinear Anal. RWA 9, 1038–1051 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  32. Sambath, M., Gnanavel, S., Balachandran, K.: Stability and Hopf bifurcation of a diffusive predator–prey model with predator saturation and competition. Appl. Anal. 92, 2439–2456 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  33. Wang, L., Zhao, H.Y.: Hopf bifurcation and Turing instability of 2-D Lengyel–Epstein system with reaction–diffusion terms. Appl. Math. Comput. 219, 9229–9244 (2013)

    MathSciNet  MATH  Google Scholar 

  34. Peng, Y.H., Zhang, T.H.: Turing instability and pattern induced by cross-diffusion in a predator–prey system with Allee effect. Appl. Math. Comput. 275, 1–12 (2016)

    MathSciNet  Google Scholar 

  35. Chen, J.X., Zhang, H., et al.: Interaction of excitable waves emitted from two defects by pulsed electric fields. Commun. Nonlinear Sci. Numer. Simul. 54, 202–209 (2018)

    Article  MathSciNet  Google Scholar 

  36. Chen, J.X., Guo, M.M., Ma, J.: Termination of pinned spirals by local stimuli. EPL 113, 38004 (2016)

    Article  Google Scholar 

  37. Chen, J.X., Peng, L., Zhao, Y.H., You, S.P., Wu, N.J., Ying, H.P.: Dynamics of spiral waves driven by a rotating electric field. Commun. Nonlinear Sci. Numer. Simul. 19, 60–66 (2014)

    Article  Google Scholar 

  38. Ma, J., Xu, Y., Ren, G.D., Wang, C.N.: Prediction for breakup of spiral wave in a regular neuronal network. Nonlinear Dyn. 84, 497–509 (2016)

    Article  MathSciNet  Google Scholar 

  39. Wiggins, S.: Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd edn. Springer, New York (1990)

    Book  MATH  Google Scholar 

  40. Yi, F.Q., Wei, J.J., Shi, J.P.: Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator–prey system. J. Differ. Equ. 246, 1944–1977 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  41. Hassard, B.D., Kazarinoff, N.D., Wan, Y.H.: Theory and Application of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)

    MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Science Foundation of China (No.11571016, 61403115).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Anhui University, Hefei, 230601, China

    Ranchao Wu, Mengxin Chen & Biao Liu

  2. School of Electrical Engineering and Automation, Hefei University of Technology, Hefei, 230009, China

    Liping Chen

Authors
  1. Ranchao Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mengxin Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Biao Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Liping Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ranchao Wu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, R., Chen, M., Liu, B. et al. Hopf bifurcation and Turing instability in a predator–prey model with Michaelis–Menten functional response. Nonlinear Dyn 91, 2033–2047 (2018). https://doi.org/10.1007/s11071-017-4001-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-4001-4

Keywords

Search

Navigation