Influence of isolation degree of spatial patterns on persistence of populations

Abstract

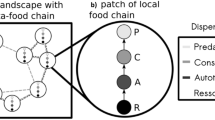
Spatial patterns are ubiquitous in nature, which have been identified as important factors in dynamics of ecosystems. However, how pattern structures have influence on persistence of populations is far from well being understood. Particularly, whether some characters of spatial pattern can be indicators for ecosystems collapse is not well studied. As a result, we presented a predator–prey system with spatial motion and found that isolation degree (average distance between patterns with high density) of spatial patterns plays an important role in the persistence of populations: If isolation degree is much smaller, then the population will persist; if isolation degree is much larger, then the population density will decrease with increasing space size and run a high risk of extinction as space size is large enough. Our results highlight the relationship between pattern structures and ecosystems collapse.

Appendices

Appendix 1: Derivation of Laplacian operator

We want to demonstrate that if an individual moves randomly in the space, then Laplacian operator can describe such motion. We firstly show the derivation of Laplacian operator in one-dimensional space. Random walk assumes that an individual takes steps of length $\triangle x$ to its left or right side along a line, and after each $\triangle t$ time unit, the individual will take one step. Initially, the individual locates at $x_0$ at initial time $t_0$, then after one step, the individual will locate at either $x_0-\triangle x$ or $x_0+\triangle x$ at time $t_0+\triangle t$ with the same probability 1 / 2 (see Fig. 6). Denote P(t, x) as the number (or density) of individuals at time t and location x. Then, we have

$$\begin{aligned} P(t+\triangle t, x)=\frac{1}{2}P(t, x-\triangle x)+\frac{1}{2}P(t, x+\triangle x).\nonumber \\ \end{aligned}$$

(5.1)

Fig. 6

An individual moves randomly in the one-dimensional space. Space step is $\triangle x$ and time step is $\triangle t$

Taylor expansion gives rise to:

$$\begin{aligned} P(t+\triangle t, x)= & {} P(t,x)+\frac{\partial P}{\partial t}(t,x)\triangle t\nonumber \\&+\,\frac{1}{2}\frac{\partial ^{2} P}{\partial t^{2}}(t,x)(\triangle t)^2+\cdots , \end{aligned}$$

(5.2a)

$$\begin{aligned} P(t, x-\triangle x)= & {} P(t,x)+\frac{\partial P}{\partial x}(t,x)(-\triangle x)\nonumber \\&+\,\frac{1}{2}\frac{\partial ^{2} P}{\partial x^{2}}(t,x)(-\triangle x)^2+\cdots , \nonumber \\\end{aligned}$$

(5.2b)

$$\begin{aligned} P(t, x+\triangle x)= & {} P(t,x)+\frac{\partial P}{\partial x}(t,x)(\triangle x)\nonumber \\&+\,\frac{1}{2}\frac{\partial ^{2} P}{\partial x^{2}}(t,x)(\triangle x)^2+\cdots , \end{aligned}$$

(5.2c)

which induces that:

$$\begin{aligned} \frac{\partial P}{\partial t}(t,x)\triangle t+\cdots =\frac{1}{2}\frac{\partial ^{2} P}{\partial x^{2}}(t,x)(\triangle x)^2+\cdots .\nonumber \\ \end{aligned}$$

(5.3)

Since $\triangle t$ and $\triangle x$ are small enough, the higher-order terms are very close to zero. As a result, one can have:

$$\begin{aligned} \frac{\partial P}{\partial t}(t,x)\triangle t=\frac{1}{2}\frac{\partial ^{2} P}{\partial x^{2}}(t,x)(\triangle x)^2. \end{aligned}$$

(5.4)

With the assumption that:

$$\begin{aligned} \triangle t\rightarrow 0,\quad \triangle x\rightarrow 0, \quad \frac{(\triangle x)^{2}}{2 \triangle t}\rightarrow D, \end{aligned}$$

(5.5)

we obtain that:

$$\begin{aligned} \frac{\partial P}{\partial t}(t,x)=D\frac{\partial ^{2} P}{\partial x^{2}}(t,x). \end{aligned}$$

(5.6)

The derivation in two-dimensional space is the same with that in one-dimensional space.

Appendix 2: Conditions of Turing pattern in system (2.3)

The Jacobian matrix corresponding to the equilibrium point $E^*$ is that

$$\begin{aligned} M=\left( \begin{array}{cc} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \\ \end{array} \right) . \end{aligned}$$

We address the temporal stability of the uniform states which is associated with non-uniform perturbations

$$\begin{aligned} \left( {\begin{array}{c}u\\ v\end{array}}\right) =\left( {\begin{array}{c}u^{*}\\ v^{*}\end{array}}\right) +\theta \left( {\begin{array}{c}u_\kappa \\ v_\kappa \end{array}}\right) e^{\lambda t +\mathrm{i} \kappa x}+\mathrm{c.c.}+{\mathcal {O}}(\theta ^2),\nonumber \\ \end{aligned}$$

(5.7)

where $\lambda$ is the perturbation growth rate, $\kappa$ is the wavenumber, and c.c. stands for complex conjugate. The linear instability $(\theta \ll 1)$ of each one of the uniform states, is deduced from the dispersion relations. Substituting expression (5.7) into system (2.3) and neglecting all nonlinear terms in u and v, one finds the characteristic equation for the growth rate $\lambda$ as $\mathrm{det}(J)$, where

$$\begin{aligned} J=\left( \begin{array}{cc} \lambda -a_{11}+d_{1}\kappa ^2 &{} -a_{12}\\ -a_{21} &{} \lambda -a_{22}+d_{2}\kappa ^2\\ \end{array} \right) . \end{aligned}$$

(5.8)

As a result, the corresponding eigenvalues are

$$\begin{aligned} \lambda _{\kappa }=\frac{-\alpha _{\kappa }\pm \sqrt{\alpha _{\kappa }^{2}-4\beta _{\kappa }}}{2}, \end{aligned}$$

(5.9)

where

$$\begin{aligned} \alpha _{\kappa }= & {} (d_{1}+d_{2})\kappa ^{2}-(a_{11}+a_{22}),\\ \beta _{\kappa }= & {} d_{1}d_{2}\kappa ^{4}-(d_{2}a_{11}+d_{1}a_{22})\kappa ^{2} +a_{11}a_{22}-a_{12}a_{21}. \end{aligned}$$

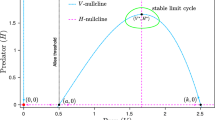
Consequently, the conditions of Turing pattern in system (2.3) are $\mathrm Re(\lambda _{\kappa =0})<0$ and $\mathrm Re(\lambda _{\kappa >0})>0$ for some $\kappa >0$.