Effect of magnetic field on the slow motion of a porous spheroid: Brinkman’s model

Abstract

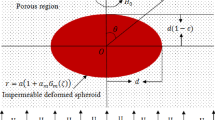
The major goal of this work is to analyze the magnetic effect on the creeping viscous flow past a porous spheroidal particle, a particle of slightly deformed spherical shape. Brinkman’s model is proposed to govern the flow in the porous media. Boundary value problem considers the conditions of continuity of velocity components, continuity of normal stresses, and stress jump boundary condition for tangential stress. A transverse magnetic field of uniform nature is applied to the flow. An expression for the drag force acting on the spheroidal particle is derived analytically. The effects of the physical parameters involved in the flow like permeability, deformation, Hartmann number’s, viscosity ratio, and stress jump coefficient parameters are visualized through graphs and tables. The applied magnetic field seems to suppress the flow of fluid that leads to the increase in the drag experienced on the porous spheroid. It is also observed that the increase in the deformation, stress jump, and permeability decreases the drag coefficient. Our results without magnetic effect match with the results reported earlier in the literature.

Appendices

Appendix A

On applying Eqs. (25) to (28) up to first order of $\alpha _{m}$, we obtain the following equations

$$\begin{aligned}&\left[ -1-a_2-S_{2}\ b_2+c_2+T_{2}\ d_2\right] P_{1}(\zeta ) +\alpha _{m}\omega _{1}\left[ \vartheta _{m}{(\zeta )}P_{1}(\zeta )+\vartheta _{2}(\zeta )P_{m-1}(\zeta )\right] \nonumber \\&\quad +\,\sum _{n=3}^{\infty }\left[ -A_n-S_{7}\ B_n+C_n+T_{7}\ D_n\right] P_{n-1}(\zeta )=0 \end{aligned}$$

(A.1)

$$\begin{aligned}&\left[ 2-a_2-S_{3}\ b_2-2\ c_2+T_{3}\ d_2\right] \vartheta _{2}(\zeta )+\alpha _{m}\omega _2\vartheta _{m}{(\zeta )}\vartheta _{2}(\zeta ) \nonumber \\&\quad +\,\sum _{n=3}^{\infty }\left[ (1-n)A_n-S_{8}\ B_n-n\ C_n+T_{8}\ D_n\right] \vartheta _{n}(\zeta )=0 \end{aligned}$$

(A.2)

$$\begin{aligned}&\left[ -\alpha ^{2}+(6+\alpha ^{2}/2)\ a_2+2\ S_{4}\ b_2+\gamma ^{2}\beta ^{2}\ c_2-2\gamma ^{2}\ T_{4}\ d_2\right] P_{1}(\zeta )\nonumber \\&\quad +\,\alpha _{m}\omega _3\vartheta _{m}(\zeta )P_{1}(\zeta ) +\alpha _{m}\omega _4\left[ P_{1}(\zeta )\vartheta _{m}(\zeta )+\vartheta _{2}(\zeta )P_{m-1}(\zeta )\right] \nonumber \\&\quad +\,\sum _{n=3}^{\infty }\left[ \left( 2(n+1)+{\alpha ^{2}}/n\right) \ A_n+2\ S_{9}\ B_n+\left( 2\gamma ^{2}(n-2)+\frac{\gamma ^{2}\beta ^{2}}{(n-1)}\right) \ C_n -2\gamma ^{2}\ T_{9}\ D_n\right] P_{n-1}(\zeta )=0 \end{aligned}$$

(A.3)

$$\begin{aligned}&[-6a_2-S_{5}\ b_2-2\sigma \xi _{1}\gamma \ c_2+\left( \gamma ^{2}\ T_{5}+\sigma \xi _{1}\gamma \ T_{3}\right) \ d_2]\vartheta _{2}(\zeta )\nonumber \\&\quad +\,\alpha _{m}\omega _5\vartheta _2(\zeta )\vartheta _m(\zeta ) +2\alpha _m\omega _6\ P_{1}(\zeta )\vartheta _2(\zeta )P_{m-1}(\zeta )\nonumber \\&\quad +\,\sum _{n=3}^{\infty }[2(1-n^{2})A_n-S_{10}\ B_n+\left( n\gamma (2\gamma (n-2)-\sigma \xi _{1})\right) C_n+ \left( \gamma ^{2}\ T_{10}+\sigma \xi _{1}\gamma \ T_{8}\right) D_n]\vartheta _{n}(\zeta )=0\nonumber \\ \end{aligned}$$

(A.4)

where

$$\begin{aligned} S_{1}= & {} K_{1/2}(\alpha ),\qquad T_{1}=I_{1/2}(\beta ),\\ S_{2}= & {} K_{3/2}(\alpha ),\qquad T_{2}=I_{3/2}(\beta ),\\ S_{3}= & {} S_{2}+\alpha \ S_{1}, \qquad T_{3}=T_{2}-\beta \ T_{1},\\ S_{4}= & {} 3\ S_{2}+\alpha \ S_{1},\qquad T_{4}=3\ T_{2}-\beta \ T_{1},\\ S_{5}= & {} (6+\alpha ^{2})\ S_{2}+2\ \alpha \ S_{1},\qquad T_{5}=(6+\beta ^{2})\ T_{2}-2\ \beta \ T_{1},\\ S_{6}= & {} K_{n-3/2}(\alpha ), \qquad T_{6}=I_{n-3/2}(\beta ),\\ S_{7}= & {} K_{n-1/2}(\alpha ), \qquad T_{7}=I_{n-1/2}(\beta ),\\ S_{8}= & {} (n-1)\ S_{7}+\alpha \ S_{6}, \qquad T_{8}=(n-1)\ T_{7}-\beta \ T_{6},\\ S_{9}= & {} (n+1)\ S_{7}+\alpha \ S_{6}, \qquad T_{9}=(n+1)\ T_{7}-\beta \ T_{6},\\ S_{10}= & {} (2(n^{2}-1)+\alpha ^{2})\ S_{7}+2\ \alpha \ S_{6}, \qquad T_{10}=(2(n^{2}-1)+\beta ^{2})\ T_{10}-2\ \beta \ T_{9},\\ \omega _{1}= & {} -2+a_2+S_{3}\ b_2+2\ c_2-T_{3}\ d_2, \\ \omega _{2}= & {} 2+2\ a_2+\left( 2+\alpha ^{2}\right) \ S_{2}\ b_2-2c_2-\left( 2+\beta ^{2}\right) T_{2}\ d_2, \\ \omega _{3}= & {} -\alpha ^{2}-(\alpha ^{2}+12)\ a_2-4\ S_{4}\ b_2+\gamma ^{2}\beta ^{2}\ c_2+4\gamma ^{2}\ T_{4}\ d_2, \\ \omega _{4}= & {} -12\ a_2-2\ S_{5}\ b_2+2\gamma ^{2}\ T_{5}\ d_2, \\ \omega _{5}= & {} 18a_2+(6+\alpha ^{2})\ S_{4}\ b_2-2\sigma \xi _{1}\gamma \ c_2-\left( \gamma ^{2}(6+\beta ^{2})\ T_{4}+\sigma \xi _{1}\gamma (2+\beta ^{2})\ T_{2}\right) \ d_2,\\ \omega _{6}= & {} -9a_2- 3\ S_{4}\ b_2+\sigma \xi _{1}\gamma c_2+\left( 3\gamma ^{2}\ T_{4}\ +\sigma \xi _{1}\gamma \ T_{2}\right) \ d_2, \end{aligned}$$

The leading terms of Eqs. (A.1)–(A.4) are equated to zero, and we get

$$\begin{aligned}&-1-a_2-S_{2}\ b_2+c_2+T_{2}\ d_2=0 \end{aligned}$$

(A.5)

$$\begin{aligned}&2-a_2-S_{3}\ b_2-2\ c_2+T_{3}\ d_2=0 \end{aligned}$$

(A.6)

$$\begin{aligned}&-\alpha ^{2}+(6+\alpha ^{2}/2)\ a_2+2\ S_{4}\ b_2+\gamma ^{2}\beta ^{2}\ c_2-2\gamma ^{2}\ T_{4}\ d_2=0 \end{aligned}$$

(A.7)

$$\begin{aligned}&-6a_2-S_{5}\ b_2-2\sigma \xi _{1}\gamma \ c_2+\left( \gamma ^{2}\ T_{5}+\sigma \xi _{1}\gamma \ T_{3}\right) \ d_2=0 \end{aligned}$$

(A.8)

Solving this system of Eqs. (A.5)–(A.8), the values of $a_2$, $b_2$, $c_2$, and $d_2$ are obtained. Now, Eqs. (A.1)–(A.4) are

$$\begin{aligned}&\sum _{n=3}^{\infty }\left[ -A_n-S_{7}\ B_n+C_n+T_{7}\ D_n\right] P_{n-1}(\zeta )+\alpha _{m}\omega _{1}\left[ \vartheta _{m}{(\zeta )}P_{1}(\zeta )+\vartheta _{2}(\zeta )P_{m-1}(\zeta )\right] =0 \end{aligned}$$

(A.9)

$$\begin{aligned}&\sum _{n=3}^{\infty }\left[ (1-n)A_n-S_{8}\ B_n-n\ C_n+T_{8}\ D_n\right] \vartheta _{n}(\zeta )+\alpha _{m}\omega _2\vartheta _{m}{(\zeta )}\vartheta _{2}(\zeta )=0 \end{aligned}$$

(A.10)

$$\begin{aligned}&\sum _{n=3}^{\infty }\left[ \left( 2(n+1)+{\alpha ^{2}}/n\right) \ A_n+2\ S_{9}\ B_n+\left( 2\gamma ^{2}(n-2)+\frac{\gamma ^{2}\beta ^{2}}{(n-1)}\right) \ C_n -2\gamma ^{2}\ T_{9}\ D_n\right] P_{n-1}(\zeta )\nonumber \\&\quad +\,\alpha _{m}\omega _3\vartheta _{m}(\zeta )P_{1}(\zeta ) +\alpha _{m}\omega _4\left[ P_{1}(\zeta )\vartheta _{m}(\zeta )+\vartheta _{2}(\zeta )P_{m-1}(\zeta )\right] =0 \end{aligned}$$

(A.11)

$$\begin{aligned}&\sum _{n=3}^{\infty }[2(1-n^{2})A_n-S_{10}\ B_n+\left( n\gamma (2\gamma (n-2)-\sigma \xi _{1})\right) C_n+ \left( \gamma ^{2}\ T_{10}+\sigma \xi _{1}\gamma \ T_{8}\right) D_n]\vartheta _{n}(\zeta )\nonumber \\&\quad +\,\alpha _{m}\omega _5\vartheta _2(\zeta )\vartheta _m(\zeta ) +2\alpha _m\omega _6\ P_{1}(\zeta )\vartheta _2(\zeta )P_{m-1}(\zeta )=0 \end{aligned}$$

(A.12)

To find the arbitrary constants $A_n$, $B_n$, $C_n$, and $D_n$, we use the following identities

$$\begin{aligned}&\vartheta _{m}{(\zeta )}\vartheta _{2}{(\zeta )}=-\,\frac{(m-2)(m-3)}{2(2m-1)(2m-3)}\vartheta _{m-2}{(\zeta )}+\frac{m(m-1)}{(2m+1)(2m-3)}\vartheta _{m}{(\zeta )} -\frac{(m+1)(m+2)}{2(2m-1)(2m+1)}\vartheta _{m+2}{(\zeta )} \end{aligned}$$

(A.13)

$$\begin{aligned}&\vartheta _{m}{(\zeta )}P_{1}{(\zeta )}+P_{m-1}{(\zeta )}\vartheta _{2}{(\zeta )}=-\frac{(m-2)(m-3)}{2(2m-1)(2m-3)}P_{m-3}{(\zeta )}\nonumber \\&\quad +\,\frac{m(m-1)}{(2m+1)(2m-3)}P_{m-1}{(\zeta )}-\frac{(m+1)(m+2)}{2(2m-1)(2m+1)}P_{m+1}{(\zeta )} \end{aligned}$$

(A.14)

$$\begin{aligned}&P_{1}{(\zeta )}\vartheta _{2}{(\zeta )}P_{m-1}{(\zeta )}=-\frac{(m-1)(m-2)(m-3)}{2(2m-1)(2m-3)}\vartheta _{m-2}{(\zeta )}+\frac{m(m-1)}{2(2m+1)(2m-3)}\vartheta _{m}{(\zeta )}+\frac{m(m+1)(m+2)}{2(2m-1)(2m+1)}\vartheta _{m+2}{(\zeta )} \end{aligned}$$

(A.15)

$$\begin{aligned}&\vartheta _{m}{(\zeta )}P_{1}{(\zeta )}=\frac{(m-2)}{(2m-1)(2m-3)}P_{m-3}{(\zeta )}+\frac{1}{(2m+1)(2m-3)}P_{m-1}{(\zeta )}-\frac{(m+1)}{(2m-1)(2m+1)}P_{m+1}{(\zeta )} \end{aligned}$$

(A.16)

In solving Eqs. (A.9)–(A.12), it is observed that

$$\begin{aligned} A_n=B_n=C_n=D_n=0 \quad \text{ for } \quad n\ne m-2,m,m+2 \end{aligned}$$

(A.17)

For $n=m-2,m,m+2$, we have the following system of equations

$$\begin{aligned}&-\,A_n-S_{7}\ B_n+C_n+T_{7}\ D_n+\omega _{1} \overline{a}_n=0 \end{aligned}$$

(A.18)

$$\begin{aligned}&(1-n)A_n-S_{8}\ B_n-n\ C_n+T_{8}\ D_n+\omega _2 \overline{a}_n=0 \end{aligned}$$

(A.19)

$$\begin{aligned}&\left( 2(n+1)+{\alpha ^{2}}/n\right) \ A_n+2\ S_{9}\ B_n+\left( 2\gamma ^{2}(n-2)+\frac{\gamma ^{2}\beta ^{2}}{(n-1)}\right) \ C_n -2\gamma ^{2}\ T_{9}\ D_n\nonumber \\&\quad +\,\omega _3 \overline{c}_n+\omega _4 \overline{a}_n=0 \end{aligned}$$

(A.20)

$$\begin{aligned}&2(1-n^{2})A_n-S_{10}\ B_n+\left( n\gamma (2\gamma (n-2)-\sigma \xi _{1})\right) C_n+ \left( \gamma ^{2}\ T_{10}+\sigma \xi _{1}\gamma \ T_{8}\right) D_n\nonumber \\&\quad +\,\omega _5 \overline{a}_n+2\omega _6 \overline{b}_n=0 \end{aligned}$$

(A.21)

where

$$\begin{aligned} \overline{a}_{n}= & {} \frac{n(n-1)\alpha _{n}}{(2n+1)(2n-3)}, \end{aligned}$$

(A.22)

$$\begin{aligned} \overline{b}_{n}= & {} \frac{n(n-1)\alpha _{n}}{2(2n+1)(2n-3)}, \end{aligned}$$

(A.23)

$$\begin{aligned} \overline{c}_{n}= & {} \frac{\alpha _{n}}{(2n+1)(2n-3)}. \end{aligned}$$

(A.24)

Solving Eqs. (A.18)–(A.21) gives the expressions for $A_n$, $B_n$, $C_n$, and $D_n$ when $n=m-2,m,m+2$.

Appendix B

The symbols present in Eqs. (41)–(47) are defined by

$$\begin{aligned} \delta _{1}= & {} \alpha _{1}^{2}+3\alpha _{1}+3, \\ \delta _2= & {} {\alpha _{1}}^{2}+3\alpha _{1}-9, \\ \delta _3= & {} \alpha _{1}^{2}+9\alpha _{1}+9, \\ \delta _4= & {} \alpha _{1}^{2}+\alpha _{1}+9, \\ \delta _5= & {} {\alpha _{1}}^{2}+7 \alpha _{1}+3, \\ \delta _6= & {} {\alpha _{1}}^{3}+3 \alpha _{1}^{2}+6{\alpha _{1}}+6, \\ \delta _7= & {} {\alpha _{1}}^{3}+3 \alpha _{1}^{2}+18{\alpha _{1}}+18, \\ \delta _8= & {} \beta _{1}^4-3\beta _{1}^{2}-12, \\ \delta _9= & {} \beta _{1}^{2}+3, \\ \delta _{10}= & {} \beta _{1}^{2}+2, \\ \Delta _{1}= & {} 4 \left( \sinh \beta _{1} \ \delta _9-3 {\beta _{1}}\ \cosh \beta _{1}\right) +\gamma ^{2} \left( \sinh \beta _{1} \ \delta _8-{\beta _{1}}\ \left( \beta _{1}^{2}-12\right) \ \cosh \beta _{1}\right) , \\ \Delta _2= & {} \gamma ^{4} \left( 3 \sinh \beta _{1}\delta _{10}-\beta _{1}\ \left( \beta _{1}^{2}+6\right) \ \cosh {\beta _{1}}\right) , \\ \Delta _3= & {} \sinh \beta _{1}\delta _9-3 \beta _{1} \cos \beta _{1} \\ \Delta _4= & {} \gamma ^{3}\left( \sinh \beta _{1}\delta _8-{\beta _{1}}\left( \beta _{1}^{2}-12 \right) \cosh {\beta 1}\right) , \\ \Delta _5= & {} \sinh {\beta _{1}}\ \left( 3 {\beta 1}^{2}{\delta _5}+6{\delta _3}-2 \left( {\alpha _{1}}+3\right) \ {\beta _{1}}^{4}\right) -\cosh {\beta _{1}}\ \left( 6{\delta _3}+{\beta _{1}}^{2}{\delta _2}\right) {\beta _{1}}, \\ \nu _{1}= & {} \left( \chi _{1}^4-3 {\chi _{1}}^{2}-12\right) \sinh \chi _{1} -{\chi _{1}}\ \left( \chi _{1}^{2}-12\right) \ \cosh \chi _{1}, \\ \nu _2= & {} \left( \chi _{1}^{2}+3\right) \sinh \chi _{1} -3{\chi _{1}} \cosh \chi _{1}, \\ \nu _3= & {} 3\left( \chi _{1}^{2}+2\right) \ \sinh \chi _{1} -{\chi _{1}}\ \left( \chi _{1}^{2}+6\right) \ \cosh \chi _{1}, \\ \nu _4= & {} \left( 2 \chi _{1}^4-3 {\chi _{1}}^{2}-18\right) \ \sinh \chi _{1} -3{\chi _{1}}\ \left( \chi _{1}^{2}-6\right) \ \cosh \chi _{1}. \end{aligned}$$