Steady Viscous Flow Around a Permeable Spheroidal Particle

Abstract

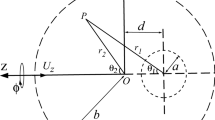
Stokes incompressible viscous fluid flow through a permeable spheroidal particle which is a bit deformed from the shape of a sphere is studied and solved analytically. It consists of two regions, porous region which obeys Darcy’s law and liquid region in which Stokes approximation is used. Boundary conditions used at the interface are mass conservation, balance of normal stress, and Beavers–Joseph–Saffman–Jones condition. Expression for drag which acts on the spheroid is obtained and well known results are deduced in the limiting cases. Variation of drag coefficient with various parameters like deformation, slip, permeability, no slip are shown by graphs.

Appendix

On applying the Eqs. (21) to (23) upto first order of $\alpha _{m}$, we obtain the following equations

$$\begin{aligned}&\left( 1+a_2+b_2-c_2\right) P_1{(\zeta )}+\alpha _{m}(2-a_2+b_2-2c_2)[\vartheta _{m}{(\zeta )}P_1{(\zeta )}+\vartheta _{2}{(\zeta )}P_{m-1}{(\zeta )}] \nonumber \\&\quad +\sum _{n=3}^{\infty }(A_n+B_n-C_n)P_{n-1}{(\zeta )}=0 \end{aligned}$$

(48)

$$\begin{aligned}&\left( (6\lambda +\alpha )a_2-\alpha b_2-2\alpha \right) \vartheta _{2}{(\zeta )}+\alpha _{m}\vartheta _2{(\zeta )}\left[ -((18\lambda + 2\alpha )a_2+2\alpha )\vartheta _{m}{(\zeta )}\right. \nonumber \\&\quad +\left. \left( (18\lambda +2\alpha )a_2+(6\lambda +2\alpha )2b_2+2\alpha \right) P_{1}{(\zeta )}P_{m-1}{(\zeta )}\right] \nonumber \\&\quad -\sum _{n=3}^{\infty }[\left( 2(1-n^2)\lambda +\alpha (1-n)\right) A_n+\left( 2n(2-n)\lambda +\alpha (3-n)\right) B_n]\vartheta _{n}{(\zeta )}=0\qquad \end{aligned}$$

(49)

$$\begin{aligned}&(6a_2+3b_2+\alpha ^2c_2)P_1{(\zeta )}+\alpha _{m}[-12a_2-6b_2+\alpha ^2c_2]\vartheta _{m}{(\zeta )}P_1{(\zeta )}\nonumber \\&\quad -12a_2\alpha _{m}[\vartheta _{2}{(\zeta )}P_{m-1}{(\zeta )}+\vartheta _{m}{(\zeta )}P_{1}{(\zeta )}] \nonumber \\&\quad +\sum _{n=3}^{\infty }\left[ 2(n+1)A_n+\frac{2(n^2+n-3)}{n}B_n+\frac{\alpha ^2}{n-1}C_n\right] P_{n-1}{(\zeta )}=0 \end{aligned}$$

(50)

Solving the leading terms of Eqs. (48) to (50), we get the values of $a_2$,  $b_2$, and $c_2$ as

$$\begin{aligned} a_2= & {} \frac{\alpha ({{\alpha }^{2}}+6) }{6\left( {{\alpha }^{2}}+3\right) \lambda +\alpha (2 {{\alpha }^{2}}+9) } \end{aligned}$$

(51)

$$\begin{aligned} b_2= & {} -\frac{3\alpha (2 {{\alpha }} \lambda +{{\alpha }^{2}}+4) }{6\left( {{\alpha }^{2}}+3\right) \lambda +\alpha (2 {{\alpha }^{2}}+9) } \end{aligned}$$

(52)

$$\begin{aligned} c_2= & {} \frac{3(6 \lambda +\alpha ) }{6\left( {{\alpha }^{2}}+3\right) \lambda +\alpha (2 {{\alpha }^{2}}+9) } \end{aligned}$$

(53)

In order to calculate other arbitrary constants $A_n$, $B_n$,  and $C_n$,we require the following identities

$$\begin{aligned} \vartheta _{m}{(\zeta )}\vartheta _{2}{(\zeta )}= & {} -\frac{(m-2)(m-3)}{2(2m-1)(2m-3)}\vartheta _{m-2}{(\zeta )}\nonumber \\&+\frac{m(m-1)}{(2m+1)(2m-3)}\vartheta _{m}{(\zeta )} \nonumber \\&-\frac{(m+1)(m+2)}{2(2m-1)(2m+1)}\vartheta _{m+2}{(\zeta )} \end{aligned}$$

(54)

$$\begin{aligned} \vartheta _{m}{(\zeta )}P_1{(\zeta )}+P_{m-1}{(\zeta )}\vartheta _{2}{(\zeta )}= & {} -\frac{(m-2)(m-3)}{2(2m-1)(2m-3)}P_{m-3}{(\zeta )}\nonumber \\&+\frac{m(m-1)}{(2m+1)(2m-3)}P_{m-1}{(\zeta )}\nonumber \\&-\frac{(m+1)(m+2)}{2(2m-1)(2m+1)}P_{m+1}{(\zeta )} \end{aligned}$$

(55)

$$\begin{aligned} P_{1}{(\zeta )}\vartheta _{2}{(\zeta )}P_{m-1}{(\zeta )}= & {} -\frac{(m-1)(m-2)(m-3)}{2(2m-1)(2m-3)}\vartheta _{m-2}{(\zeta )}\nonumber \\&+\frac{m(m-1)}{2(2m+1)(2m-3)}\vartheta _{m}{(\zeta )}\nonumber \\&+\frac{m(m+1)(m+2)}{2(2m-1)(2m+1)}\vartheta _{m+2}{(\zeta )} \end{aligned}$$

(56)

$$\begin{aligned} \vartheta _{m}{(\zeta )}P_1{(\zeta )}= & {} \frac{(m-2)}{(2m-1)(2m-3)}P_{m-3}{(\zeta )}\nonumber \\&+\frac{1}{(2m+1)(2m-3)}P_{m-1}{(\zeta )}\nonumber \\&-\frac{(m+1)}{(2m-1)(2m+1)}P_{m+1}{(\zeta )} \end{aligned}$$

(57)

By taking the use of these identities in Eqs (43) to (45) we see that the values of $A_n$, $B_n$ and $C_n$ $=0$ for $n\ne m-2,m,m+2$ and for $n=m-2,m,m+2$ we have the following expressions

$$\begin{aligned}&A_n+B_n-C_n+\xi _1 {{\overline{a}}}_n=0 \end{aligned}$$

(58)

$$\begin{aligned}&\left( 2(1-n^2)\lambda +\alpha (1-n)\right) A_n+\left( 2n(2-n)\lambda +\alpha (3-n)\right) B_n+\xi _2 {{\overline{a}}}_n+\xi _3 {{\overline{b}}}_n=0\qquad \end{aligned}$$

(59)

$$\begin{aligned}&2(n+1)A_n+\frac{2(n^2+n-3)}{n}B_n+\frac{\alpha ^2}{n-1}C_n+\xi _4 {{\overline{c}}}_n+\xi _5 {{\overline{a}}}_n=0 \end{aligned}$$

(60)

where

$$\begin{aligned}&\xi _1=2-a_2+b_2-2c_2 \\&\xi _2=-(18\lambda + 2\alpha )a_2-2\alpha \\&\xi _3=(18\lambda +2\alpha )a_2+(6\lambda +2\alpha )2b_2+2\alpha \\&\xi _4=-12a_2-6b_2+\alpha ^2 c_2 \\&\xi _5=-12a_2 \end{aligned}$$

and

$$\begin{aligned} {{\overline{a}}}_n= & {} \frac{n(n-1)\alpha _{n}}{(2n+1)(2n-3)} \end{aligned}$$

(61)

$$\begin{aligned} {{\overline{b}}}_n= & {} \frac{n(n-1)\alpha _{n}}{2(2n+1)(2n-3)} \end{aligned}$$

(62)

$$\begin{aligned} {{\overline{c}}}_n= & {} \frac{\alpha _{n}}{(2n+1)(2n-3)} \end{aligned}$$

(63)

The expression for $B_2$ is

$$\begin{aligned} B_2=-\frac{6\alpha \varepsilon \, \left( 36 \alpha \, \left( {{\alpha }^{2}}+5\right) \, {{\lambda }^{2}}+12 \left( 2 {{\alpha }^{4}}+13 {{\alpha }^{2}}+12\right) \lambda +\alpha \, \left( 4 {{\alpha }^{4}}+33 {{\alpha }^{2}}+60\right) \right) }{5{{\left( 6 {{\alpha }^{2}} \lambda +18 \lambda +2 {{\alpha }^{3}}+9 \alpha \right) }^{2}}} \end{aligned}$$

(64)