MHD Viscous Flow Past a Weakly Permeable Cylinder Using Happel and Kuwabara Cell Models

Abstract

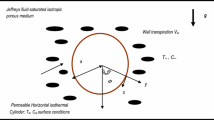
The present work deals with studying magneto-viscous fluid flow around a weakly permeable cylinder bounded by a cylindrical container under the effect of an applied magnetic field. Based on Happel and Kuwabara cell model technique, an analytical solution of the problem is evaluated. Considered flow is separated into the outer viscous fluid region and inner permeable region governed by modified Stoke’s equations and modified Darcy’s law, respectively. Applicable boundary conditions at the fluid porous interface are continuity of normal component of velocity, Saffman’s slip condition together with the continuity of pressure. The expressions for the drag, hydrodynamic permeability, and Kozeny constant for the permeable cylinder are achieved in this analysis. Numerical values of Kozeny constant against porosity are presented, and new results are also acquired. Analytical and numerical results that correspond to the earlier published works are obtained as reduction cases.

Appendix

$$\begin{aligned}&w_1=S_1U_4+S_4U_1, \quad w_2=S_2U_4-S_4U_2, \quad w_3=S_1U_2+S_2U_1,\\&w_4=S_1U_3-S_3U_1, \quad w_5=S_2U_3+S_3U_2, \quad w_6=S_3U_4+S_4U_3,\\&w_7=w_1\alpha +w_2, \quad w_8=w_1\alpha +2w_2, \quad w_9=w_4\alpha +2w_5, \\&w_{10}=w_4\alpha +w_5, \quad w_{11}=((w_9-2w_3)\beta ^2-\alpha ^2w_{10}),\\&w_{12}=((w_8\alpha -4(w_1-w_6))\beta ^2-w_7\alpha (\alpha ^2+4)),\\&w_{13}=(w_{10}\alpha +w_4\beta ^2),\quad w_{14}=\alpha ^2(w_1\beta ^2+w_7\alpha ),\\&w_{15}=w_2{\alpha }^{2}+w_1 \alpha +2w_2,\quad w_{16}=w_2{\alpha }+w_1,\\&w_{17}=w_5{\alpha }+w_4,\\&w_{18}=\left( {w_5}{{\alpha }^{2}}+{w_9}-2{w_3}\right) {{\beta }^{2}}-{w_5}{{\alpha }^{4}}-{w_4}{{\alpha }^{3}}-2{w_5}\, {{\alpha }^{2}},\\&w_{19}=\left( -w_{16}\, {{\alpha }^{2}}+2{w_2} \alpha -4{w_6}+4 {w_1}\right) \, {{\beta }^{2}}+{w_2}\, {{\alpha }^{5}}+{w_1}\, {{\alpha }^{4}}\\&\quad+\,6 {w_2}{{\alpha }^{3}}+4 \left( {w_6}+{w_1}\right) \, {{\alpha }^{2}}+8{w_2}\alpha ,\\&w_{20}= w_{17}\, {{\beta }^{2}}+w_{17}{{\alpha }^{2}}+2 w_{5} \alpha , \quad w_{21}= \left( w_9-2w_3\right) {{\beta }^{2}}-w_{10}{{\alpha }^{2}}, \\&w_{22} = \left( -{w_8} \alpha -4{w_6}+4{w_1}\right) {{\beta }^{2}}+{w_7}\, {{\alpha }^{3}}+4{w_7}\alpha ,\\&\Delta _1 = 2 {w_3}\, {{\alpha }^{3}}{{\lambda }^{3}}+4 ({w_2}\, {{\alpha }^{2}}-w_{15}\, {{\beta }^{2}}) {{\lambda }^{2}}+2 \alpha ( \left( {w_5} {{\alpha }^{2}}+{w9}\right) \, {{\beta }^{2}} \\ &\quad -\,{w_5}\, {{\alpha }^{2}}) \lambda -{{\alpha }^{2}}\, \left( w_{16} \alpha +2{w_2}\right) \, {{\beta }^{2}}+{w_2} {{\alpha }^{4}},\\&\Delta _2 = 2 {w_3}{{\alpha }^{3}}{{\lambda }^{3}}-4{w_8}\,{{\beta }^{2}}\, {{\lambda }^{2}}+2 {w_9} \alpha \, {{\beta }^{2}} \lambda -{w_8}{{\alpha }^{2}}\, {{\beta }^{2}}, \\&\Delta _3 = 2 w_{18}{{\lambda }^{3}}+w_{19} {{\lambda }^{2}}-2 w_{20} \alpha \lambda +w_{16}\, {{\alpha }^{2}}\, {{\beta }^{2}}+w_{16} {{\alpha }^{4}}+2{w_2} {{\alpha }^{3}}, \\&\Delta _4 = 2w_{21}\, {{\lambda }^{3}}+w_{22}\, {{\lambda }^{2}}-2 \alpha \, \left( {w_4}\, {{\beta }^{2}}+w_{10} \alpha \right) \lambda +w_{1}\, {{\alpha }^{2}}\, {{\beta }^{2}}+w_{7}\, {{\alpha }^{3}}, \\&\Delta _5 = w_{15}\, \left( {{\beta }^{2}}-{{\alpha }^{2}}\right) \, {{\lambda }^{2}}-w_{16} \alpha \, \left( {{\beta }^{2}}+{{\alpha }^{2}}\right) -2 w_{2}\, {{\alpha }^{2}}, \\&\Delta _6 = \left( {w_8}\,{{\beta }^{2}}-{w_7}\, {{\alpha }^{2}}\right) {{\lambda }^{2}}-{w_{14}}{\alpha }^{-1}, \quad \Delta _7=w_{15}{{\beta }^{2}}-{w_2}\, {{\alpha }^{2}}, \\&\Delta _8 = 2( w_9-2w_3)\lambda ^3-( w_8\alpha -4(w_1-w_6)) \lambda ^2-2w_4\alpha \lambda +w_1 \alpha ^2,\\&\Delta _9 = (2w_{11}\lambda ^3-w_{12}\lambda ^2-2\alpha w_{13}\lambda +w_{14}),\\&S_1=K_{0}(\alpha ),\, S_2 = K_{1}(\alpha ),\,S_3=K_{0}(\alpha /\lambda ),\,S_4= K_{1}(\alpha /\lambda ),\\&U_1=I_{0}(\alpha ),\, U_2 = I_{1}(\alpha ), \,U_3=I_{0}(\alpha /\lambda ),\, U_4= I_{1}(\alpha /\lambda ). \end{aligned}$$