Abstract
Solar prominences are one of the most common features of the solar atmosphere. They are found in the corona but they are one hundred times cooler and denser than the coronal material, indicating that they are thermally and pressure isolated from the surrounding environment. Because of these properties they appear at the limb as bright features when observed in the optical or the EUV cool lines. On the disk they appear darker than their background, indicating the presence of a plasma absorption process (in this case they are called filaments). Prominence plasma is embedded in a magnetic environment that lies above magnetic inversion lines, denoted a filament channel.
This paper aims at providing the reader with the main elements that characterize these peculiar structures, the prominences and their environment, as deduced from observations. The aim is also to point out and discuss open questions on prominence existence, stability and disappearance.
The review starts with a general introduction of these features and the instruments used for their observation. Section 2 presents the large scale properties, including filament morphology, thermodynamical parameters, magnetic fields, and the properties of the surrounding coronal cavity, all in stable conditions. Section 3 is dedicated to small-scale observational properties, from both the morphological and dynamical points of view. Section 4 introduces observational aspects during prominence formation, while Section 5 reviews the sources of instability leading to prominence disappearance or eruption. Conclusions and perspectives are given in Section 6.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Solar prominences are intriguing structures of the solar atmosphere. As shown in Figures 1 and 4, they appear as bright arcade-like structures (or long and thin clouds) on or above the solar limb when observed at chromospheric temperatures (7 × 103 ≤ T ≤ 2 × 104 K). They are not seen, or are seen in absorption, at coronal temperatures (Figure 1). These observations suggest that these features are made of dense cool chromospheric material immersed into the 1 MK corona. The interface between the two environments is called the Prominence-Corona-Transition Region (PCTR). As a consequence of the low temperature, the prominence core is made of partially-ionized plasma and, because of its high density, it is optically thick to certain wavelengths (e.g., most of the hydrogen and helium resonance lines and continua). For this reason, when prominences are observed on the disk, for example in Hα 6562.8 Å or in He II 304 Å (which are among the brightest lines produced by the chromosphere) they appear darker than the surrounding quiet Sun (see Figures 1 and 2, these observations are discussed in Section 1.3). In this case they were historically called filaments. For simplicity, in the present work we will use both terms interchangeably to indicate these features.
A prominence at the limb and its filament part on the disk as seen by SDO/AIA. The off-limb prominence appears bright in the 304 Å; passband (left panel, chromospheric emission) while the on-disk part, the filament, appears darker than the surrounding quiet Sun suggesting absorption effects. The filament is still dark in the 171 Å; band on the disk image (right panel, coronal emission) and off-limb it is almost invisible, suggesting the lack of emission at these temperatures. Courtesy of NASA/SDO and the AIA science team.
Left: image of the Sun as seen in the He II 304 Å; channel on SOHO/EIT, on 23 February 2004, revealing three dark filaments (arrows). One of them extends over almost a solar diameter. Right: image of the Sun in Hα on the same day revealing different details of these three structures. Credits: ESA/NASA/EIT; Catania Astrophysical Observatory.
Prominence properties may vary over wide ranges. Based on these differences, various classifications of prominences have been made based on their activity, morphology, location and on the properties of the magnetic field in the photosphere below them. A review of their classification can be found in Tandberg-Hanssen (1995). Updates, when necessary, will be given in the present text.
Prominence properties depend upon the environment where they form, and in particular upon the magnetic field below them: filaments are always found above the neutral lines separating opposite polarities of the photospheric magnetic field (Polarity Inversion Line, PIL). The filament width, length and shape follow and adapt to the extension of the neutral line (even though it does not always cover its full length). The extension of the PIL depends upon the strength and distribution of the local magnetic field, so that filaments and the local magnetic field are closely interrelated. Since PILs can be found almost everywhere on the Sun, so can prominences, particularly during the maximum of the solar cycle. For all these reasons their appearance may vary a lot as shown, for example, in Figure 2.
However, filaments are primarily found all around the border of polar coronal holes (this location is called the polar crown), between active regions or surrounding them (intermediate filaments) and inside active regions (active filaments). In the first and second cases the filaments are generally longer (depending also on the extension of the nearby active region), wider, extend more in height, and have longer lifetimes (particularly the first class) than in the last case. This is probably due to the more stable nature of the environment where they live. These are called quiescent filaments. The longest filaments can cover almost the solar diameter (transequatorial filament), as shown in Figures 1 and 2 marked by the yellow arrows. This suggests a connection between filaments and the large scale magnetic structure of the Sun.
The regular observations of the full disk made historically on the ground by Hα telescopes and later on from space in the He II 304 Å; channel (e.g., by SOHO/EIT, STEREO/EUVI or SDO/AIA) are sources of data for statistical studies aimed at determining general prominence and filament properties. In order to help the statistical analysis, several automated detection procedures have been developed or are under development (e.g., Bernasconi et al., 2005; Romeuf et al., 2007; Aboudarham et al., 2008; Wang et al., 2010; Labrosse et al., 2010a; Joshi et al., 2010; Buchlin et al., 2010). For example, Bernasconi et al. (2005) analyzed almost five years of BBSO Hα filtergrams (19 211 filaments between 2000 and 2005), which revealed that the average filament length varies from about 3 × 104 to about 1.1 × 105 km. Active filaments are the shortest and last from minutes to hours.
The recent EUV prominence statistical study by Wang et al. (2010) confirms these values. These results are obtained from the analysis of 9477 limb prominences in the period 2007–2009 (minimum of solar activity during the end of cycle 23 and the beginning of cycle 24) observed with the STEREO/EUVIs 304 Å; imager. Their results also show that the long prominences were located mostly between 30° and 60°; 82% of them had a height of about 2.6 × 104 km above the solar surface. However, quiescent prominences can reach much higher altitudes. Their brightness is almost constant, or slightly diminishing with height.
No detailed statistical information is found in the literature on the filament width; however the reported values vary between 103 and 104 km (e.g., Malherbe et al., 1983; Pouget et al., 2006; Labrosse et al., 2010b).
1.1 Motivations for prominence study
Decades of study have shown that it is very difficult to characterize filament properties. Filaments show differences in morphology, lifetime, position on the solar disk, complexity of their magnetic field environments, etc. They are not uniform in shape and show a fine, dynamic structure at the limit of the instrumental resolution. This high variability makes their classification difficult and also results in a wide range of physical conditions deduced from observations that poorly constrain the models of prominence formation and disappearance (Vial, 1998). At the same time, understanding the origin of such variety and attaining better knowledge of these structures and their environment during the different phases of their life can provide valuable information on the physics of the solar atmosphere. In fact, prominences are commonly found in the solar atmosphere, which indicates that it is easy to find favorable conditions for their formation and stability. This tells us that prominences are manifestations of a common physical process found in the solar atmosphere. An overview of the large scale properties of prominences, including the morphological aspects, will be given in Section 2.
The following still-unsettled issues motivate prominence studies:
-
Support and stability. In the quiescent state, prominences are interesting for their puzzling equilibrium condition that allows their mass to be supported in the tenuous corona. Clearly the magnetic field plays a major role, but still we do not have sufficient observational information to identify the different mechanisms and/or magnetic configurations responsible for their stability.
Figure 3 shows the magnetic topology of the first static prominence model proposed by Kippenhahn and Schlüter (1957). The prominence is represented by a thin sheet of current, perpendicular to the magnetic field. In this configuration the gravity force of the prominence is balanced by the Lorentz force. Since then prominence models have evolved and, as reviewed by Mackay et al. (2010), they may be divided into two main groups: those in which the prominence mass has a major role in the stability of the magnetic configuration, and those in which its role is not important. Figure 3 also shows the two main magnetic configurations thought to host filament plasma: the sheared arcade (middle panel) connecting opposite magnetic polarities at the side of the neutral line (thick-light lines) overlain by an unsheared arcade (solid-dark lines), and the flux rope (right panel) where the magnetic field has a helical configuration. In all cases the stationary prominence material is found in or nearby the dipped regions (concave-up fields, as in Figure 3). Section 2.4 reviews the information on the magnetic field in prominences and their surroundings that led to the development of these models.
-
Mass motions. Mass flows inside a prominence can also have a role in the equilibrium, mass support, and mass refurnishing. As we will see in Section 3, observations reveal a variety of mass motions inside prominences, even though the spatial resolution of instruments may limit their diagnostic capability. However, only a few prominence models include such observed dynamics.
-
Radiative losses. Partially-ionized prominence plasma is an interesting laboratory for testing our knowledge of the radiation-transfer mechanisms in an optically-thick medium. In addition, non-local thermodynamic conditions (NLTE) generally exist in these plasmas. Even if the prominence density is quite high (and so the mean free path of electrons is small), collisions are unable to compete with radiation in populating the energy levels of the atoms, so that the Local Thermodynamic Equilibrium Condition (LTEC) does not hold. The incoming radiation due to the environmental solar emission is, in fact, another element affecting the prominence physical conditions. Proper treatment of radiative transfer in prominences is also important for quantifying the amount of radiative losses: this mechanism acts as a cooling mechanism in the energy equilibrium equation. In quiescent conditions, the prominence radiation is steady, requiring a source of still unknown heating to maintain energy balance in the structure.
The plasma properties derived from observational measurements are given in Section 2.2. A distinction between the properties of the cool prominence core (Section 2.2.1) and its interface with the corona (Section 2.2.2) is also discussed.
-
Magnetic field. The lack of extensive magnetic-field measurements in prominences limits our knowledge of the physics of the coronal magnetic field and its interaction with the plasma. We often assume that the observed prominence-plasma-emission morphology traces the magnetic field lines. One of the paradoxes in prominence studies is that prominences at the limb can show a vertical fine bright structure, while disk observations and the few magnetic field measurements suggest that the field is almost horizontal. Several ideas have been proposed as solutions, and we review them in Section 3. Solving this conundrum will help to understand the coronal magnetic environment and to identify the dominant physical process in the solar atmosphere.
-
Formation and disappearance. Prominences as a whole can be very stable for a few months, or can be part of large-scale dynamic and energetic events such as flares and coronal mass ejections (see for example van Driel-Gesztelyi and Culhane, 2009, for a review). These enormous eruptions (about 3 × 1015 g on average, Hudson et al., 2006) perturb the interplanetary medium, and their effects can be seen on Earth. For example, they are the origin of geomagnetic storms, which can affect everyday life through electric blackouts. As modern life is very technology dependent, such solar activity is a concern. It is well known that the technology of satellites for telecommunication and human space activity are very sensitive to solar eruptions. For all these reasons the past decade has seen the development of Space Weather as a new branch of science aimed at forecasting solar activity and its consequences on Earth. For accurate predictions it is essential to ascertain whether some phenomena are systematic precursors of solar eruptions, for example, instabilities in the filament-channel magnetic field. The instability conditions and the following disappearance of prominences are reviewed in Section 5. For further discussions on coronal eruptions and space weather see the reviews by Schwenn (2006), Benz (2008), and Chen (2011) in this journal, and Kunow et al. (2006).
1.2 Historical background
Being visible during eclipses, prominences have been known for a long time. However, only during the eclipse of 1860, when photography was introduced for the first time, were prominences finally recognized as solar features and not an effect of the Earth’s atmosphere (Foukal, 2004). In the following years spectroscopy started to develop; during the eclipse of 1868 the yellow D3 line at 5877 Å was observed for the first time in prominences, later identified as coming from solar He emission (Janssen, 1869; Secchi, 1870). Further advances in prominence knowledge and spectroscopic methods came with the discovery that prominence emission could be observed outside the limb even during daylight (Lockyer, 1868) with coronagraphs. In the 1890s the observations of filaments on the disk with spectroheliographs began, and the first systematic photometric measurements in prominences were made by Schwarzschild in 1906. Lyot developed the coronagraph in 1936, ushering in a new era in which systematic prominence limb observations can be made outside of eclipses (Lyot, 1939). The first studies relating prominences to the solar cycle were published by Bocchino (1933) and Barocas (1939). Further information on historical prominence observations can be found in Tandberg-Hanssen (1974, 1998) and references therein.
Daily images of the Sun from the ground and from space are available today.Footnote 1 They allow us to fully record solar activity in all structures, including prominences. These observations are presented in the next Section 1.3.
1.3 Prominence observations today
Similar to the rest of the Sun, prominence material is made almost completely of hydrogen and helium. Because of their low temperature, prominences abound in neutral or low ionization charge states. Observations of their emission/absorption aim at inferring their cooler core properties. For these reasons, prominences are best observed in the intense hydrogen and helium Lyman and Balmer lines series. Most often, observations are taken in the strong red visible Balmer Hα line, be it from the groundFootnote 2 or from space (Hinode/SOT, Tsuneta et al., 2008). This long wavelength allows spatial resolutions of fractions of an arcsecond to be achieved.
When observing on the disk, the Hα line is optically thick most of the time. For this reason, by scanning the line at different wavelengths it is possible to image different plasma layers: the filament is seen at line center, while at about 0.5 Å away from this position we see the chromospheric fibrils below it (see Section 2.1 for details on these structures).
Being dynamic objects, prominences require short exposure times. These could be achieved using bright lines such as the UV H Lyα (1215.67 Å) and Balmer Hα. However, in the UV passband the great difference between the intensity of the H Lyα and the other lines produces a technical challenge when trying to observe all of them with the same instrument. For this reason often the easiest choice is made by sacrificing one or the other wavelength window, unfortunately introducing a restriction in the scientific return from the instrument. For example, this is the case for the spectrometer SOHO/SUMER, which uses an attenuator to partially obscure this line, but accesses the other lines of the H Ly series (at about 1″ spatial resolution). This is a limitation for the diagnostics of prominences. Improvements were obtained later in the SOHO mission with increased interest in this line. New solutions for the operation modes were found, allowing access to the full line profile (e.g., Wilhelm et al., 1995, 2004, 2007; Ebadi et al., 2009; Curdt and Tian, 2010).
In conjunction with its high radiance, the Lyα line is optically thick most of the time, which, similar to Hα, makes its interpretation very difficult. The complexity of this emission has been recently illustrated by Vourlidas et al. (2010) using data from the VAULT rocketborne telescope.Footnote 3 VAULT (Korendyke et al., 2001) imaged the chromosphere and the bottom of the transition region in Lyα at the best spatial resolution to date (about 0.15″). An example of a prominence in emission at the limb and a dark filament on the disk are given in Figure 4, where the very fine scale structure of these objects can be observed. The VAULT data study by Vourlidas et al. (2010) revealed that the Lyα flux in filaments is highly anisotropic and that it may be optically thin in certain parts. Unfortunately, the line profile was not accessible.
VAULT Lyα images of a prominence at the limb (left) and a filament on the disk (right) observed on June 14, 2002 (see Vourlidas et al., 2010).
These difficulties explain why the Lyα prominence observations have not been very popular thus far, and only a few instruments have been dedicated to it (for example, see the TRACEFootnote 4 mission Handy et al., 1999).
The near infrared absorption triplet at 10830 Å and the D3 multiplet 5876 Å of He I are also often used for prominence observations and magnetic field measurements (see Section 2.4). The prominence-corona-transition-region (PCTR) is easily accessible through space observations of the EUV He II 304 Å resonance line. As mentioned already, several missions provide images of the full Sun at this wavelength (for example, SOHO/EITFootnote 5, STEREO/EUVIFootnote 6 and SDO/AIAFootnote 7). Spectroscopic measurements of several of the most intense EUV He I and II lines are made by the SOHO/CDS and Hinode/EIS spectrometers (Harrison et al., 1995; Culhane et al., 2007). Alternatively, the Ca II H-line 3968.5 Å is another chromospheric line used to observe prominences from space with ground based instruments.
Because of the strong absorption of the H and He continua, filaments on disk appear as dark features when observed in the EUV-FUV below 912 Å, that is in the H Lyman continuum head (504 Å for He I and 228 Å for He II). This property is used to investigate the opacity of the medium and derive information on the prominence mass and degree of ionization. Furthermore, the dark aspect of filaments at high temperature emission observed in this waveband may come from what is called volume blocking, which means the lack of emission at such high temperatures (Heinzel and Anzer, 2001; Schwartz et al., 2006, and reference therein). At wavelengths longer than 912 Å filaments are often not visible on the Sun at chromospheric temperatures, meaning that their plasma is transparent to such wavelengths and that their emission is probably too faint to be measured against the disk emission. Instead, at the limb, at chromospheric temperatures the optically thin emission of a prominence has been estimated to be about one third that of the solar disk. Emissions from different layers of prominences, together with the thermal structuring of the PCTR, are useful for evaluating the radiation losses and energy balance. Despite being addressed by several studies (see for example Del Zanna et al., 2004; Parenti and Vial, 2007, and reference therein), these prominence aspects are still poorly understood.
Prominences can also be observed at longer wavelengths. In particular, they are bright at the limb against the ambient corona when observed in the microwave range. On the contrary, they appear in absorption, similar to Hα images, when observed on the disk. Due to the density dependence of the radio wave propagation and the optical thickness of the medium, only the shorter radio waves (λ ≤ 1 cm) can emerge from the deepest (and densest) prominence layers. Longer wavelengths can be used to sample the PCTR (Chiuderi Drago, 1990). It should also be taken into account that, due to the non-uniform geometry of prominences and the density-dependent radio-wave propagation, radio observations at the limb provide information on a different layer of the prominence than sampled in disk observations.
To conclude, we mention the newly launched Interface Region Imaging Spectrograph (IRIS) NASA mission. Its high resolution instruments (about 0.4″) can provide prominence data, such as the Mg II k&h lines profile. These are among the brightest lines of the solar chromosphere. To date the literature does not yet include results on prominence studies with IRIS, but throughout this review the diagnostics capability of this instrument will be discussed.
2 Large-Scale Properties
This section is dedicated to the general properties of prominences and their environment. With this term we indicate the photosphere and the chromosphere under the prominence, and the corona above it. For a complete understanding of this environment, ideally all these layers should be observed at the same time. However, because of the spatial extent and vastly differing temperatures of the regions involved, multi-wavelength and multi-resolution observations are needed. Unfortunately, they are not always available. Hence, the global structure and equilibrium of the prominence environment remain open questions.
2.1 Morphology
The right panel of Figures 2 and 4 show examples of filaments lying in different parts of the Sun. These locations have a common property: a filament is invariably found to overlay the neutral line (PIL) separating concentrations of photospheric magnetic fields having opposite vertical polarities.
At the same location, surrounding the PIL, is the filament channel, which extends up to the corona. The filament channel is thought to be the magnetic structure within which lies the filament plasma. It can be recognized through the properties of the chromospheric fibrils, which are almost aligned with the underlying neutral line as shown in Figure 7. This does not happen elsewhere outside the channel, where it is possible to find fibrils crossing the PIL.
In most of the filaments observed in Hα and He II away from the disk center, it is possible to identify a narrow upper dark spine running horizontally along the axis of the structure. Depending upon the direction of the line of sight, it is possible to see barbs, or lateral plasma extensions (see Figures 5 and 6). The information coming from the high-spatial-resolution images of SDO/AIA and the Doppler motion measurements (EUV and Hα) inside barbs suggest that their magnetic field is inclined with respect to the local vertical to the Sun’s surface. Some barbs seem to reach down into the chromosphere and possibly into the photosphere, as in the case of, e.g., Schmieder et al. (2013) (and probably even deeper into its magnetic field), even though observationally this aspect is still controversial (e.g., Li and Zhang, 2013). For their role in the formation and stability of filaments, barbs and filament ends are important components that need to be characterized in great detail.
Close views of filaments show a fine dark structure made of long thin loops or threads also almost aligned along the prominence spine (the angle is about 20°–35°), as shown in Figures 4 and 5. Both chromospheric fibrils and filament threads are considered to trace the magnetic field, so that they suggest a highly-sheared magnetic field (Martin, 1998b) almost aligned with the neutral line in the photosphere. This is true both for the main body and barbs in filaments. The highly-sheared magnetic configuration appears to have a role in prominence eruptions (see Section 5).
Not all filament channels are filled with filament plasma, even though the observation of empty filament channels is quite rare. In certain cases only segments of a filament are seen along the same PIL. This may be the case for a partially-filled filament and/or for different transparency of the medium. To understand where and why filaments form are among the key goals of the study of prominences. What we can tell is that an empty filament channel is part of the filament formation process (see details in Section 4). Time sequences in Hα obtained during the filament formation show that fibril orientations change in time; only when they become almost aligned with the PIL does the filament channel start to be filled up with material (Martin, 1998b). An example of an apparently-empty filament channel and its aligned fibrils is given in Figure 7.
Detail of a complex active region in Hα showing an empty filament channel (between the white arrows) with aligned fibrils along the PIL. Image reproduced by permission from Martin (1998b), copyright by Springer.
Filaments seen at the limb show different properties. They may look like structures made of fine vertical threads, like that shown in Figure 22, or of horizontal threads as in Figure 8. They may also appear to have more complex morphologies, including arcades, like that shown in Figure 9. Some of these differences may be attributed to different viewing angles at the times the images were recorded. For example, in some cases it is possible that we see just the final end of the structure (the barb), which is compatible with seeing mainly vertical substructures. In contrast an observation of a prominence perpendicular to its spine often reveals almost horizontal substructuring. However, it is not always easy to make this distinction and, if this fine structure traces the fine-scale magnetic morphology, the vertical structuring is not apparently compatible with the horizontal magnetic field deduced from on-disk observations. Possible solutions to this paradox come from measurements of the magnetic field, as discussed in Section 2.4. However, clear differences in the fine-scale morphology exist for which we still do not have a complete explanation.
High-resolution image on the solar limb obtained with Hinode/SOT Ca II H-line 3968 Å. Image reproduced by permission from Okamoto et al. (2007); copyright by AAAS.
If the morphology of a filament marks its magnetic skeleton, interesting information may be deduced during the liftoff of an erupting prominence. In this case, prominences are stretched and isolated from their environment, giving a better view of their structure. Some observations of erupting prominences reveal the presence of a helical structure (see Figures 10 and 33), even though it is not clear yet whether this is a consequence of the eruption or whether it was already present during the quiescent period. In fact, there is also evidence for on-disk filaments with a similar structure, which supports the flux rope models. Further details on prominence eruptions are given in Section 5.4.
mpg-Movie (12200.71875 kB) Still from a movie showing One of the first prominence eruptions observed by SDO/AIA. Movie taken from http://sdo.gsfc.nasa.gov/gallery/main.php?v=item&id=1. Courtesy of SDO (NASA) and the AIA consortium. (For video see appendix)
2.2 Plasma parameters
One of the main steps in the comprehension of a prominence is determining its plasma parameters, such as electron density, ionization degree, and temperature. These are obtained through plasma diagnostics of the emitted and/or absorbed radiation, possibly in combination with modeling.
Hydrogen and helium spectral lines and continua emissions are the main tools used for the diagnostics of the cooler prominence core. The outer prominence’s envelope, the PCTR, is hotter so it is instead mainly investigated by the observation of transition-region spectral lines: that is, the emission from heavier elements, but still in low ionization states.
It is important to point out the difficulties in the interpretation of the prominence spectrum, which is produced by both optically-thin and thick plasma. Optically-thick lines such as H Lyα return information on the plasma at different depths along the line of sight as we move from their center toward the wings. Conversely, for optically-thin lines, we deduce information from the integrated emission along the full depth of the emitting plasma (even though the intensity scales as the square of the electron density, for collisionally-excited transitions).
It is extremely important to study both core and PCTR environments, in quiet and dynamic conditions, in order to understand the occurrence of prominences, their stability, and destabilization. However, there is a difficulty when trying to combine the results from these two regions, which are obtained using data with different spatial and temporal resolutions. We recall that the EUV instruments used to observe the PCTR have a spatial resolution about a factor 10 lower than those used to observe the cool core at longer wavelengths. Therefore, the PCTR is observationally much less detailed, and so are the plasma parameters derived in this region.
A recent review (Labrosse et al., 2010b) describes all the different diagnostic methodologies, together with a set of results, for both prominence layers. Here we present a summary of observational results with some updates.
2.2.1 Prominence core
The prominence core is dense, cool and mostly made of optically-thick plasma. The radiation process is very complex here because the plasma completely or partially absorbs the incoming and auto-produced radiation, and should be diagnosed through solving a non-LTE (non-Local Thermodynamic Equilibrium) radiative transfer problem. Forward methods compare the observed spectrum to a synthetic one obtained from a parameterized prominence model, and solve the associated set of equations for the transfer of radiation through the medium (Labrosse et al., 2010b). Indirect measurements of plasma parameters can also be obtained using, for example, prominence seismology.
The simplest model used to solve the radiative transfer problem is the 1D slab, whose capabilities in deriving important general properties of prominences have been quite-well analyzed. A clear example of the use of this model is found in Gouttebroze et al. (1993). These authors analyzed 140 models characterized by different prominence conditions to derive the behavior of the hydrogen emission, and provide its spectral signatures together with the tools for their interpretation.
Starting from the 1D models, 2D slab and multi-thread prominence models have been developed. Unless a multi-thread model is applied, the prominence is considered as a monolithic body, often static, in contrast to what observations show. Besides this approximation, the results revealed the models to be quite good in reproducing the general properties of the structure. Interested readers may refer to Labrosse et al. (2010b) and references therein for further details on the subject.
The prominence core plasma can also be optically thin to some radiations, such as those produced by less abundant elements. In this case the plasma parameters can be derived without solving the radiative transfer analysis. However, the emitted spectral lines should fall at wavelengths far from the continuum emissions of the most abundant elements H or He (λ > 912 Å), these being the most significant absorbers. Next we review the physical parameters of the prominence core inferred via different techniques.
-
Electron Density. Various methods are used to derive the electron density, for example: broadening of lines due to Stark effect, depolarization by the Hanle effect, or comparing lines with continuum emission. Most of these methods yield a density value between ∼ 109 and 1011 cm−3. From recent observation, Lites et al. (2010) inferred a few times 1015 cm−3 in an active region filament using a magnetic filling factor deduced from observations in the filament channel and a density deduced in the photosphere. If the hypotheses used in this work are correct, this is one of the highest values reported in the literature. This will have important bearings on the study of the equilibrium conditions of these structures, implying that the stability conditions must be valid over a large range of density values. This should be an element for constraining models.
-
Temperature. The temperature in the prominence core can be derived from H-Ly continuum observations (Parenti et al., 2005) [the color temperature of which is representative of the electron temperature (Gouttebroze et al., 1993)], or by measuring the kinetic temperature from the width of spectral lines (e.g., Stellmacher et al., 2003). Figure 11 shows an example of the application of the first method over about 100 Å of a SOHO/SUMER spectrum of a prominence observed on 8 October 1999 (Parenti et al., 2004). By fitting these data it was possible to derive, under given approximations, an electron temperature of about 8200 K. The values reported in the literature, as derived applying different methods, give a range of values between 7500 and 9000 K.
-
Gas pressure. The pressure in prominences is in the range 0.02–1 dyne cm−2. This was already reported in the Hvar reference atmosphere (Engvold et al., 1990b), and has been confirmed by the latest results (Labrosse et al., 2010b).
-
Mass. Determining the prominence mass is also required to properly model the prominence equilibrium. For this purpose, it is necessary to know the geometrical thickness (and the whole volume) of the structure as well as the ionization degree. There are not many studies aimed at determining the ionization degree. The range of values listed by the Hvar reference atmosphere for hydrogen is still valid (0.2 < N(H+)/N(H0) < 0.9, Ruždjak and Tandberg-Hanssen, 1990), while for helium the range is 0.1 < N(He0)//N(H0) < 0.2 (Del Zanna et al., 2004, see also Labrosse et al., 2010b for more details on these results). The typical value for the solar corona is N(He0)/./N(H0) ≈ 0.9 (Feldman, 1992), while the hydrogen is completely ionized above ≈ 3 × 104 K (Mazzotta et al., 1998).
Radiance of the H I Ly continuum as a function of wavelength in a prominence observed in 1999. The crosses indicate data corrected for temporal variations. The solid curve represents the fit to the corrected data. Image reproduced by permission from Parenti et al. (2005); copyright by ESO.
Currently it is acknowledged that the same filament appears wider in the EUV and radio wavelengths than in Hα (e.g., Heinzel et al., 2001, 2003; Schmieder et al., 2003, 2004; Marqué, 2004; Schwartz et al., 2004, 2006; Vial et al., 2012). This extra width is called the EUV filament extension. To illustrate, Figure 12 shows the intensity of four different lines (Hα, H Lyα, He II 304 Å and Fe IX 171 Å) along a cut perpendicular to the filament axis shown in Figure 4 (right panel) and observed on 14 June 2002.
This different appearance of the filament width may be due to the different absorption properties of the H Lyman and Helium continua with respect to the Hα line, to the different amounts of density or filling factor in the two regions, and/or to the lack of high transition region and coronal emission of the prominence. As a consequence, in order to estimate the whole mass of the filament we need to investigate both wavelength regions. In this respect, by comparing the amount of absorption in the EUV lines on top of the H continuum and estimating the Hα absorption, it was established that the optical thickness at the Lyman continuum head (τ912) can be one order of magnitude greater than that of the Hα line center for the same column density. This is also confirmed by non-LTE radiative transfer modeling of filaments by Anzer and Heinzel (2005). In particular, there may be semi-transparent material that is thin to the Hα wavelength and thick to the H Lyman continuum (meaning that the filament is still visible in the continuum emission but not in the Hα images). This is also one reason why the same filament seen in the H Lyman continuum appears bigger than in Hα images. Taking into account this property, the prominence mass established through H and He measurements has been given values in the range of 1014 − 2 × 1015 g (Labrosse et al., 2010b). Lower values, down to 5 × 1012 g, can be obtained for the neutral hydrogen mass using simple geometrical considerations. A recent multi-wavelength study by Heinzel et al. (2008) established the hydrogen column density of 1 − 5 × 1019 cm−2.
2.2.2 Prominence corona transition region
The PCTR emission falls mainly in the UV-EUV and is produced mostly by optically thin plasma. Some of the techniques mentioned before can also be applied in this case. In addition, when multiple spectral lines are available, density, temperature, and Differential Emission Measure (DEM) can be derived.
Differential Emission Measure. Even if the PCTR accounts for only a small fraction of the mass of the whole cool prominence body, the PCTR demands particular attention because of its interface role. To address this need, there were a few early attempts to build spectral atlases of these structures with the aim of providing as many identified emission lines as possible (e.g., Mariska et al., 1979; Moe et al., 1979; Engvold et al., 1990a). These provide the fingerprints of the structure and the physical parameters obtained through the inversion of this large quantity of lines have low uncertainties. To our knowledge, the most complete spectral atlas available includes more than 400 line profiles in the range 800–1250 Å observed with the SOHO/SUMER spectrometer (Parenti et al., 2004, 2005). In addition, the authors built a similar atlas for the quiet Sun observed on the same day, providing additional material for comparison with quiet solar conditions. In terms of prominence plasma parameters, at a given time ideally we would like to determine the plasma distribution in space and temperature. At present, the best that can be done is to try to invert a large set of emission lines to derive the Differential Emission Measure (DEM). This gives the distribution of plasma in temperature, along the line of sight, under the assumption of a constant density. The importance of a large set of lines comes from the need to sample the plasma well enough in temperature to localize the minimum of the DEM, generally found around log T(K) = 5–5.3, and the DEM gradient. These quantities, among others, are elements used to test the energy balance in prominences. The DEMs for two different prominences are plotted in the top half of Figure 13. These are obtained from the SUMER spectral atlas of Parenti and Vial (2007), and from a similar observing program run on a prominence in June 2004 (Gunár et al., 2011). The 1999 prominence is estimated to be denser than the 2004 prominence, but what is mostly different is the gradient of the DEM at low transition region temperatures, with the 2004’s DEM being flatter (the coronal DEM is discussed below). It would be interesting to further investigate whether this difference is systematic in prominences or not. At present very few DEMs are available in the literature. When compared to the quiet sun (QS) DEM on the lower panel of Figure 13, we notice the following differences: lower DEM values at transition region temperatures and a minimum located at lower temperatures. Beside the large amount of lines used to build the curves in Figure 13, we note that the interval log T(K) = 5–5.5 is less well sampled for the QS and prominences alike. This is a general problem with solar observations of the transition region. Different results have been obtained in this context for other prominences (Kucera and Landi, 2006, 2008) and the issue is not yet solved. The precision of the DEM distribution in this region could be improved by data in other wavebands obtained with multi-instrument and co-temporal observations. In addition, we point out that often a given instrument can provide co-temporal data only in a limited range of wavelengths, such as in the case of SUMER. A full spectrum can be covered in up to 1–2 hours, depending on the exposure times. This means that the DEMs are built assuming the absence of structural changes in prominences. Therefore, we cannot rule out the possibility that the dynamic nature of these structures has a role in the different results obtained for the DEMs.
Differential Emission Measure for two prominences (top) and the QS (bottom). The prominence DEMs were inferred with 20% uncertainty using 1999 (solid line, Parenti and Vial, 2007) and 2004 (dashed-line, Gunár et al., 2011) SOHO/SUMER data. The dashed-line on the QS plot is the QS DEM available in the CHIANTI database. Bottom image reproduced by permission from Parenti and Vial (2007), copyright by ESO.
It is generally believed that a prominence does not emit at coronal temperatures, and the coronal part of the DEMs of Figure 13 is the result of the foreground and background emission of the off-limb corona. At the same time, the maximum temperature of emission of prominences is still unknown. This is another open issue in prominence physics, whose solution requires a detailed investigation of the emission of the environment around these structures. The difficulties of this task are discussed in Kucera and Landi (2006). Interestingly, the high S/N imagers of SDO/AIA are revealing a faint emission in prominences in the 171 Å channel, for example. The sensitivity of this channel peaks in the Fe IX line, which has its maximum emissivity at 0.8 MK. This would suggest that the PCTR contains more material at hot temperatures than previously thought. Preliminary results on this issue indicate that the prominence emission above 3 × 104 K, which is measured by this channel, is indeed dominated by the Fe IX, confirming that more mass is present at this temperature than expected (Parenti et al., 2012).
Electron density and pressure. A summary of the most-recent electron-density values derived from EUV observations of prominences can be found in Table 4 of Labrosse et al. (2010b). Most of these results are in the range from ∼ 109 to a few 1010 cm−3 with a few cases over 1011 cm−3. Similar to measurements in the core, in the PCTR we obtain quite a large range of densities and, as expected, they tend to be lower than in the core. This range of values not only includes the variation of density from one prominence to another (although there is no special difference between active and quiescent prominences), but also variations inside the same prominence. This is not surprising considering that these measurements have always been made with limited spatial resolution at or above the known prominence fine scale. As will be discussed in Section 3, in fact, prominences are composed of dynamic fine-scale components, smaller than the resolution of the EUV instruments used to observe the PCTR.
2.3 The coronal cavity
Observations at the limb in the optical, EUV and soft X-ray bands generally reveal variation of the flux with height, which traces a well-defined magnetic-field structure extending above prominences. A darker area, the coronal cavity, extends above and around the prominence up to about 0.6 R⊙ from the solar surface, and it is overlaid by a faint but visible loop system, the arcade (Figure 14). At present we recognize that the coronal cavity is how the coronal portion of the filament channel appears at the limb. Over larger scales the arcade is generally part of a streamer structure. A historical review of the existing literature on cavity studies can be found in Gibson et al. (2006, 2010), while in the following we mention a few more recent results.
Small cavity (left) and a large cavity (right) imaged in white-light polarization brightness from the MLSO Mk4 coronameter (top), and by the EIT telescope onboard the SOHO satellite, at 304 Å (middle) and 195 Å (bottom). In the 304 Å images, the prominences lying within the cavities are clearly visible. The small cavity is visible at 195 Å while the large cavity does not show up at this wavelength. Image reproduced by permission from Fuller and Gibson (2009); copyright by AAS.
Morphologically cavities may have different appearances, due both to different properties in different cavities and/or to line-of-sight effects. An example of the different appearance of cavities is illustrated in Figure 14, which shows the SW quadrant of the Sun where two prominences have been observed at three different wavebands. The prominences are seen in emission at chromospheric temperatures (middle panels) in the EUV. The top panels show the corresponding dark cavity observed in white light (WL). While the two prominences have a similar apparent dimension in the plane of the sky, the two cavities differ in size. The bottom panel shows the same area in EUV at coronal temperatures. While the small cavity is seen in absorption in the left panel, a large cavity is not visible on the right. In addition, their shape often suggests an elliptical cross section (Fuller and Gibson, 2009). More systematic observations of these structures reveal that a coronal cavity’s properties change as a function of the solar cycle, being larger and less dark during the maximum of the cycle.
WL images generally show a decrease of intensity of about 25 to 50% (e.g., Fuller et al., 2008) in the coronal cavity, with respect to the surrounding arcade and streamer. This has been interpreted as a reduced density and has also been confirmed by radio measurements (e.g., Marqué, 2004). The density variation with height, however, results to be flatter in the cavity than in the arcade.
Contrary to the traditional dark aspect of coronal cavities, the recent results from eclipse data by Habbal et al. (2010) have documented a coronal cavity that is not darkened in WL images. This is illustrated in Figure 15, which also shows a bright cavity at coronal temperature suggesting the high temperature of this region. Analyzing cases of different prominence projections with respect to the plane of the sky, these authors suggest that the darkening appears mostly when the prominence axis is along the east-west direction. This may be caused by the longer line-of-sight (LOS) integration path in a reduced-density environment with respect to a prominence (and then a cavity) located along the north-south direction. This aspect has been further investigated by Gibson et al. (2010) using a forward model of a coronal cavity.
Top: detail of the 2008 eclipse studied by Habbal et al. (2010). Second and third rows: close-up views of the prominence regions in Fe x, Fe XI, Fe XIII, and Fe XIV, 7878.6 Å continuum (the limb is oriented horizontally, at the bottom of the image). Bottom row: spectral line intensities normalized to their corresponding maximum values (y-axis) vs. P.A. (x-axis), at 1.05, 1.15, and 1.3R⊙, with green = Fe X, dashed-green = Fe XI, red = Fe XIII, dashed-red = Fe XIV, and black = 7878.6 Å continuum. The horizontal dashed lines correspond to the radial distances, where the normalized emission-line intensities are plotted. Image reproduced by permission from Habbal et al. (2010), copyright by AAS.
In terms of thermodynamic parameters, as for prominences, the coronal environment of the cavity is still only partially understood. The faint emission of the cavities makes their study difficult and probably accounts for the variability of the measured parameters. Because of the lack of signal in EUV and X-ray, the data inversion for cavities is mostly limited to WL data, from which we may obtain the electron density. The electron temperature and magnetic structures are generally deduced assuming a hydrostatic model, even though recent efforts have been able to abandon this assumption (Kucera et al., 2012).
Similar to Habbal et al. (2010), several recent studies converge in finding the cavity as hot as, or hotter than, the surrounding streamer. The EUV measurements by Vásquez et al. (2009) obtained using tomography and STEREO/EUVI data, support this result together with a broad temperature distribution. Habbal et al. (2010) assigned a value of at least 2 × 106 K to one of the EUV cavities, bright in the hottest available filter (Fe XIV). Slightly lower values were found by Hudson et al. (1999) and Hudson and Schwenn (2000) using soft X-ray Yohkoh SXT data in the core of the cavity and by Kucera et al. (2012) using Hinode/EIS data. In some cases measurements imply a temperature substructure that might be due to the presence of fine structure in the magnetic field that cannot be observed directly (Kucera et al., 2012).
Even though cavities have been observed for decades, only recently has it been possible to observe their fine scale dynamics. For example, Schmit et al. (2009) investigated prominences using the EUV and infrared spectroscopic information of Hinode/EIS (Fe XII 195 Å) and CoMP (Coronal Multichannel Polarimeter).Footnote 8 For the first time, they detected coherent Doppler velocity structures (several tens of Mm) of 5–10 km s−1 in the cavity, along the prominence axis in both directions and lasting for about 1 h (see Figure 16), whose origin is still unknown. Wang and Stenborg (2010) have instead detected spinning motions in cavities from observations in the Fe XII 195 Å line with STEREO/EUVI. This transverse motion is about 5–10 km s−1 in the plane of the sky and can last for 2–3 days. Interestingly it is of similar amplitude as the axial motion measured inside prominences (see Section 3.1.2). These authors noticed that the spinning direction is associated with the asymmetry of the magnetic-polarity concentration at one side of the PIL, and is directed from the strongest concentration to the weakest. They interpret it in terms of siphon flow, which has already been postulated in the presence of asymmetric heating (due in this case to the asymmetric magnetic flux) at loop footpoints. In this picture, the flow highlights the magnetic helical flux rope of the cavity. Indeed, several authors interpret the coronal cavity (and the filament channel) as the location of a twisted magnetic structure (the flux rope) embedding the prominence (e.g., Tandberg-Hanssen, 1995; Lites, 2005; Ciaravella et al., 2000; Gibson et al., 2010; Habbal et al., 2010, and references therein).
(a) Image of a cavity and its prominence observed with Hinode/EIS Fe XII 195 Å. The green contour marks the edge of the prominence as seen from SOHO/EIT 304 Å. The blue and red contours show ± 7 km s−1 LOS velocity. (b) LOS velocity in Fe XII 195 Å. Image reproduced by permission from Schmit et al. (2009); copyright by AAS.
Another question is the origin of hot plasma in the cavity. We need to better characterize it and understand whether it can really be hotter than the surrounding streamer. Some continuous heating mechanism should be at work if the plasma is heated locally. Does it originate at the solar surface or within the cavity?
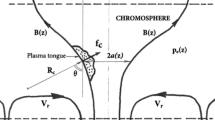
A few explanations have been proposed. For example, Hudson et al. (1999) suggested the presence of hot filamentary plasma along the magnetic structure, which supports and envelops the cool prominence material. This is consistent with the Parenti et al. (2012) interpretion of AIA/SDO prominence images (see also Section 2.2.2). The origin of this hot plasma was suggested to be chromospheric evaporation due to asymmetric heating localized at the footpoints, as discussed in Antiochos and Klimchuk (1991). Further explorations of this scenario have reproduced the dynamic filamentary mixture of hot and cool plasmas in prominences and surrounding cavities. For example, Luna et al. (2012b) recently investigated prominence and cavity formation in a 3D model of a sheared magnetic arcade, heated asymmetrically at the footpoints. Their simulations imply that transition region and coronal temperature plasmas surround every prominence thread, both parallel and transverse to the field.
One of the first prominence investigations with the SDO/AIA imagers (Berger et al., 2011), in combination with earlier high-resolution studies with Hinode/SOT (Berger et al., 2008, 2010), has motivated an alternative concept: a cycle driven by a magneto-thermal convective instability, in which hot plasma escaping from the solar surface passes through prominences, altering their structure and supplying the corona cavity with hot plasma. This promising idea is still under investigation (Berger et al., 2012; Liu et al., 2012; Low et al., 2012b, a), although it is not clear yet how the hot material is produced at the base of the corona. In addition, this model is based on observations of polar-crown prominences, which generally have significant vertical motions and structures (see also Section 3). It is still to be seen whether this instability could work in prominences characterized by different structural properties, and whether this instability could provide enough energy to initiate eruptions.
Both sheared arcade and flux rope models can produce the cavity (for example, see Figure 3). The presence of a detached flux rope can explain the observed flatter density gradient with height (Fuller et al., 2008), the sharp boundary between cavity and streamer, and the spinning motion, but it is unclear at present whether these results are unique to this model. Fan and Gibson (2006) simulations of the evolution of a quasi-static emergence of a flux rope showed the formation of the cavity, where current sheets form at the interfaces of separatrix layers. These regions can potentially be seen as the location for energy dissipation and plasma heating. This configuration and the others mentioned above are all good candidates that need to be further investigated; in particular, the plasma distribution and evolution in these flux-rope filament-channel models have not been modeled with full thermodynamics, as in the Luna et al. (2012b) and earlier simulations of sheared-arcade filament channels. Clearly, better knowledge of the magnetic configuration is the key to resolving these issues.
2.4 Magnetic field
It is widely believed that, analogous to other solar coronal environments, the magnetic field in prominences plays a dominant role over the plasma (low β environment). However, a recent investigation using a semi-empirical model of massive, well-developed prominences by Anzer and Heinzel (2007) indicates that the plasma β locally can take values in the range of 0.2 < β < 1.5, from a magnetic-field-dominated plasma to a matter-dominated plasma. Therefore the discussion of the role of the magnetic field in massive prominences can still be debated.
Information on the magnetic field of prominences and their surroundings is sometimes deduced using the morphology and apparent dynamics of the plasma, including the apparent bulk flow thought to highlight the magnetic field lines of the fine structure. However, the reduced emission of prominences at the limb limits the identification of magnetic fine structures, generally well highlighted in other solar structures (e.g., coronal loops). The magnetic field strength and direction can also be inferred from measurements but with large uncertainties, both because of the faint emission of the prominence plasma and the low magnetic-field amplitude. These aspects make the determination of the global magnetic structure in prominences more difficult.
2.4.1 Properties deduced from morphology
The ubiquitous presence of filaments and prominences on the Sun allows the accumulation of a good sample of data, which helps to identify certain morphological characteristics and to classify objects according to common properties. One of these is the magnetic chirality. Optical and EUV-X ray observations have revealed that the magnetic field of the filament environment (filament, filament channel and coronal arcade) follows a handedness rule called chirality, which is described in detail by Martin (1998b) and illustrated in Figures 17 and 18. Opposite chilarity appears to be dominant in each hemisphere: negative in the north hemisphere and positive in the south. However, there is no clear observational evidence yet for a change with the cyclic polarity reversal of the polar field (e.g., Pevtsov et al., 2003), as has been predicted by some models (van Ballegooijen et al., 1998).
One-to-one chirality relationships for (1) fibril patterns, (2) filament spines and barbs, and (3) overlying arcades of coronal loops, are shown in each column. The patterns in the left column are dominant in the northern hemisphere and those in the right column are dominant in the southern hemisphere. Image reproduced by permission from Martin (1998a), copyright by ASP.
High-resolution Hα image of a chromospheric filament observed on October 30, 2002 at 14:46 UT. Upper right and lower left corners: Dextral and sinistral patterns. The small filament in the lower right corner exhibits both sinistral and dextral barbs. USAF, ISOON image courtesy D. Neidig; from work of A.A. Pevtsov; http://solarmuri.ssl.berkeley.edu/~welsch/brian/solar/glossary/glossary.html.
Once the magnetic polarity of the filament channel is known from photospheric measurements, and we look at the filament from the positive side, the chirality is dextral if the filament axis is directed rightward, and sinistral if directed in the opposite way. When there is no direct access to the magnetic field, the key aspects to identify the “dextral” or “sinistral” chirality in a filament are the extensions of the barbs from the spine: from left-to-right or right-to-left (Figures 17 and 18).
This chirality rule is also valid for the chromospheric fibrils inside the filament channel. We have already mentioned that they are almost aligned with the PIL and are rooted in small magnetic concentrations having the same polarity as the underlying photospheric network magnetic field. The loop arcade overlying a filament and its barbs also has a chirality pattern, but it is inverse to the filament: the arcade forms an angle which is generally almost perpendicular to the PIL, but the arcade skew is in the opposite sense to the filament chirality (Figure 17).
Further information on the magnetic structure may be inferred from the sign of the magnetic helicity,Footnote 9 which is a measure of how many twists and turns there are in the magnetic field. By definition the helicity is positive for a right-handed twist, and negative if in the opposite direction. In general, the solar magnetic field has negative helicity in the northern hemisphere and positive helicity in the southern hemisphere. Understanding whether this rule also applies to filaments will shed further light on the link they might have with the surrounding magnetic environment, for example, in terms of their formation. Filaments are also associated with coronal eruptions (see Section 5.4), so they may be used to trace the helicity transport in the corona and in the interplanetary medium. Several theoretical models and simulations suggest that magnetic twist arises from the differential rotation, meridional flow, and diffusion, as well as direct transport during flux emergence (e.g., van Ballegooijen et al., 2000; Martens and Zwaan, 2001; Yeates et al., 2008). However, some of these surface effects imply a dependence of the filament chirality on the PIL orientation, which is not supported by the observations (Lim and Chae, 2009).
Figure 19 shows an example of how the magnetic helicity in the different temperature regimes can be investigated. In this case the author (Chae, 2000) analyzed the position of the filament threads observed in Hα in comparison with the 171 Å TRACE images and photospheric magnetograms from NSO/KP. In agreement with previous work, he showed that there were threads with positive helicity in sinistral filament channels, and negative helicity for dextral filament channels. The result supports the idea that filaments have the same helicity as their surroundings (including the nearby active region), implying the same origin for these magnetic features. More recently Lim and Chae (2009) arrived at a similar conclusion by finding a strong correlation between filament chirality (deduced from the barbs’ orientation in Hα images of intermediate filaments) and the active region helicity (deduced from SXT images).
Observed thread crossings in an inverse S-shaped filament. Note that the filament is dextral. (a) High-resolution Hα data and line-of-sight magnetogram taken at BBSO. The positive flux density levels are represented by white contours, and the negative ones by black contours. (b–d) TRACE images at different times. Image reproduced by permission from Chae (2000); copyright by AAS.
2.4.2 Magnetic field inferred from measurements
Spectro-polarimetry is the main method used to infer magnetic field amplitude and direction. The line emission processes in prominences are dominated by the scattering of photospheric radiation, which produces mainly linear polarization due to the anisotropy of the solar incident radiation (e.g., Landi Degl’Innocenti et al., 1987; Bommier et al., 1994). This polarization is modified if a magnetic field is present. Indeed, the data reveal the presence of fine structure splitting due to the Zeeman effect, and/or depolarization through the Hanle effect (Leroy et al., 1983; Kim, 1990).
The first polarimetric measurements were carried out by J. L. Leroy using the Pic du MidiFootnote 10 facility, starting from the 1970s. For a review on the methodology and these first results see Tandberg-Hanssen (1995) and Paletou et al. (2001). In recent years the spectro-polarimetry method has evolved significantly. This is due to the development of more sophisticated analysis techniques combined with the availability of higher quality data, provided, for example, by the optical telescopes THEMIS, the near infrared Vacuum Tower Telescope of the Teide ObservatoryFootnote 11 (see Figure 20) and the Dunn Solar TowerFootnote 12 (DST, NSO/SP, USA). These telescopes measure the flux of the most used lines for polarimetry: the He I D3 multiplet at 5876 Å and 10830 Å, and/or the H I Hα or Hβ (Paletou et al., 2001). In order to infer the magnetic-field amplitude and direction, an inversion method of line flux needs to be used. Because these lines are often optically thick in prominences (e.g., Stellmacher et al., 2003; Wiehr and Bianda, 2003; Labrosse and Gouttebroze, 2004; Léger and Paletou, 2009) the radiative transfer effects have to be taken into account in their modeling. The difficulties in the inversion of the 10830 Å triplet are discussed by López Ariste and Casini (2002). In general, we need to remember that the inversion method relies on some assumption about the observed atmosphere; hence, we cannot say that we obtain a direct measurement of the magnetic field.
Stokes parameters from a multi-line inversion of simultaneous and cospatial spectro-polarimetric observations of He I 10830 (left) and D3 (right) in a quiescent prominence, taken with THEMIS on 29 June 2007. Image reproduced by permission from Casini et al. (2009); copyright by AAS.
A recent detailed study of the He I 5876 and 10830 Å lines by Casini et al. (2009) has shown that the first multiplet is more suitable for diagnosing stronger fields (∼ 10 G and higher), while the He I 10830 Å is most suitable for weaker fields (0.1–10 G), due to the different sensitivity of these lines to the Hanle effect.
Modern instruments used to infer magnetic field values have a typical polarimetry sensitivity of about 103 or better, spatial resolution equal to or greater than half an arcsecond, and exposure times of 1–2 mins for prominence observations (or coarser spatial resolution for faster exposures, e.g., Stellmacher et al., 2003). Unfortunately, these are still low resolutions compared to the fine spatial and dynamical scales of filaments.
Measurements of the direction of the magnetic field perpendicular to the line of sight (that is, in the plane of the PIL or filament axis) deduced from polarimetry have an uncertainty called the 180° ambiguity, because linear polarization is independent of the transverse magnetic field direction. In this case the inversion methods for the Stokes parameters cannot distinguish between the two opposite transverse solutions. Several methods have been developed to resolve this ambiguity, and we refer to Metcalf et al. (2006) and López Ariste et al. (2006) and references therein for details. However, in filaments and filament channels the uncertainty in the measurements of the weak field, the assumptions about the observed atmosphere, and other factors make this issue harder to resolve than in other regions. Observation of prominence chirality may help solve this problem (Martin et al., 2008).
Previous reviews of magnetic field measurements in prominences are found in Démoulin (1998), Anzer and Heinzel (2007), Paletou (2008), and Mackay et al. (2010). The most relevant results about the magnetic field include: the strength of the field from polarimetric measurements is between 8 and 10 G on average for quiescent filaments; magnetic field strengths deduced from filament thread oscillations are within this range, even though some strong assumptions (e.g., electron density) weaken the results (Lin et al., 2009, filament oscillations will be discussed in Section 3.1.3); most recent polarimetric measurements suggest higher values of a few tens of Gauss in localized patches (e.g., Casini et al., 2003, 2005), while higher values are associated with active region filaments (up to 600–700 G from Kuckein et al., 2009). These differences appear to be associated with the recent inclusion of circular polarization into the inversion method. In addition, the instrument spatial resolution has improved substantially from about 5″ in the 1980s and 1990s to less than 1″ today. The low spatial resolution data provide only a lower limit on the magnetic field strength.
The magnetic field strength can also be deduced from radio emission, by using the relation between temperature brightness, circular polarization, and optical depth (Apushkinskij et al., 1990, 1996). The published results are generally in agreement with those from spectro-polarimetry. One recent measurement at the centimeter-wave radio emission (using the Russian RATAN-600 telescope) from a quiescent prominence gives a strength of 100–550 G (Golubchina et al., 2008), a value much higher than those inferred from the polarimetric measurements in these regions. This discrepancy highlights once more that much more effort should be made to derive reliable magnetic-field measurements in the corona.
Leroy et al. (1983) found a slight increase of the magnetic field strength with height in prominences. This is apparently in contrast with Casini et al. (2003), where the authors give the distribution of magnetic field amplitude in patches. This discrepancy as well could be attributed to the much lower spatial resolution data used by Leroy et al. (1983), but further investigation of this issue is needed.
Polarimetric measurements also provide information on the magnetic field direction. In the main filament body the field is directed almost horizontally and lies in a plane that forms an angle of about 35° with the filament axis (e.g., Trujillo Bueno et al., 2002), confirming results from the morphology of fine fibrils and threads observed in the filament channel and in barbs (e.g., Lin et al., 2008). However, these results are apparently in contradiction with the observation of the fine structure of some quiescent prominences (as those belonging to the polar crown) where vertical threads dominate. We will come back to discuss this point in Section 3.
At the photospheric level, it is often possible to observe small areas of opposite polarity with respect to the dominant one, on either side of the PIL. These minor polarities (also called spurious or parasite) are candidates for the location where filament barbs are rooted, as discussed in Section 2.4.3 below.
2.4.3 Interpretation of the global magnetic configuration
Joining the measurements and observations of morphology and/or dynamics at photospheric and chromospheric levels, it is possible to infer the global configuration of the magnetic structure embedding the filament at different levels.
To this purpose, the 3D reconstruction of prominence morphology is certainly an important constraining element. When we try to infer the 3D morphology of prominences from their emission we are aware that the angle of view, amount of opacity (prominence mass), and temperature of the structure with respect to the temperature sensitivity of the observing instruments all matter. The observed differences among prominences may be partially due to these elements. For example, does a characteristic length, height, and width of prominences exist? We know that these parameters depend on how magnetically active the environment is where the prominences form. While efforts were made in the past to classify these different parameters, the most recent observations reveal a wide spectrum of dimensions with less definite limits between active, intermediate, and quiescent filaments. This may suggest a continuity in spatial scales of the strength and topological complexity of the magnetic field. Clearly, if the 3D morphology of prominences were observable we could better infer the enveloping magnetic field structure (for example, helical vs. sheared arcade) and the forces governing prominence support and stability. Unfortunately, due to the difficulty of isolating the emission of the lower portion of the structure (or the full structure if it does not extend much in height) from the surrounding bright environment, this reconstruction is, as of today, not easily accessible. In addition, we know that magnetic field measurements, which scan the structure in height, are also difficult. On the contrary, interesting results have been achieved in the case of erupting prominences (where the contrast in brightness with the corona is stronger), as discussed in Section 5.5.
Concerning magnetic field measurements, in addition to the simple configuration where the magnetic field crossing the prominence has the same direction as the underlying photospheric field (as in a simple arcade, called normal polarity), polarimetric measurements have revealed the presence of the inverse polarity of the prominence magnetic field in most cases. The inverse term refers to two directions: the magnetic field perpendicular to the filament axis has a direction opposite to that of the overlying prominence arcade; the field direction along the prominence axis is opposite to what is expected from photospheric magnetic-field extrapolations of the underlying bipolar field (that is, directed from the negative photospheric polarity to the positive one, see Figure 21).
Detail of the vector photospheric magnetic field in regions around a filament channel observed on 11 December 2007. Arrows of equal length show the orientation of the horizontal component of the magnetic field vector. The field is directed mainly along the filament channel running from lower left to upper right, but over most of its length the field has inverse configuration: the arrows have a component directed from negative polarity (lower right) toward positive polarity (upper left). This is especially true in the naked bald patch region above and to the right of the center of the image where the filament channel is not flanked by strong plage. A naked bald patch region is characterized by an inverse configuration of the transverse field, while the longitudinal component is almost absent. The gray scale ranges from 0 (white) to 2000 Gauss (black). Low-polarization pixels where no inversion technique has been applied appear as white areas. Image reproduced by permission from Lites (2009), copyright by Springer.
Several 2D and 3D models have been proposed that result in these possibly stable configurations, including the above-mentioned sheared arcade (which produces mixed polarity), the flux rope (with normal or inverse polarity), quadrupolar regions (inverse polarity), etc. We suggest consulting Tandberg-Hanssen (1995) and Mackay et al. (2010) for details. Some of these configurations are illustrated in a schematic view in Figure 3. Statistical observational studies reveal that most of the prominences have inverse polarity (between 75% and 90%, Démoulin, 1998), while normal polarity prominences have a stronger field and are located closer to active regions (e.g., Bommier et al., 1994).
We point out that the identification of inverse or normal polarity in quiescent filaments is very difficult because of the weak magnetic field; for correct measurement, high spatial resolution and instrument sensitivities are required (Lites, 2005), as well as systematic measurements at different heights, particularly above the photosphere.
Affirming the presence of a flux rope in the data is also quite difficult; only in the last decade have a few cases been found, but only near active regions. Erupting filaments (see Section 5.4) often appear to be twisted, as expected if their magnetic envelope were a flux rope (see Schmieder et al., 1985; Vršnak et al., 1988; Wang et al., 1996, for a few early examples and Figures 31 and 10). However, this does not imply that such a configuration was already present before eruption, as further discussed in Section 4. In conclusion, it is possible that the results on the distribution of inverse and normal polarities just mentioned might be affected by uncertainties in inferring the magnetic field from observations.
The question arises on how the prominence plasma is supported inside these different magnetic configurations. Most stationary models require the presence of magnetic dips (Figure 3), which create a vertical Lorentz force that can balance the plasma gravitational force. Dips can be formed by the weight of the filament plasma through deformation of the potential magnetic field, or can be formed independently, before the channel is filled by prominence plasma. However, the latter possibility is better supported by the observations: the time observed to fill a filament channel (days) is generally much longer than the time estimated to deform the field lines under plasma weight (hours, Démoulin, 1998). Observationally a dip is consistent with a slight increase in the magnetic field amplitude with height. Their presence is also suggested by observations as highlighted by dynamical studies at small scales, as discussed in Section 3.1.2. For example, their presence can explain the observed periodic longitudinal oscillations of prominence threads, as shown by Luna et al. (2012a) and Luna and Karpen (2012).
Models built to explain signatures of the presence of dips have shown that dips can exist, for example, in sheared arcades, in a flux rope, or in a quadrupolar configuration. The question is, can we find observational signatures to distinguish among these different models? High resolution studies of plasma flows (which could resolve the motion of the plasma filling the dips) could allow to distinguish between flux rope and sheared arcade magnetic configurations by detecting different observational signatures: helical or almost horizontal flows. From the model side, they can indeed reproduce several of the observed properties of dips, but they are not completely mutually exclusive (e.g., Karpen et al., 2003). Indeed, observations suggest that at the present reachable spatial resolution, filaments with different magnetic configurations exist.
As mentioned, additional information on the magnetic field can be obtained from the investigations of barbs and their endpoints. For example, signatures of dips have also been found in barbs, and their endpoints were found to be located in small bipoles of parasitic photospheric polarities (e.g., Zong et al., 2003; López Ariste et al., 2006; Martin, 1998b). These again are signatures of inverse polarity of the magnetic topology (see also Xu et al., 2012). Lin et al. (2005) inferred the photosphere as the anchorage location of prominences. They found barbs to root in faint magnetic-field regions located in the intergranular part of the photosphere, even if they do not give any indication about the polarity of those regions.
3 Small-Scale Properties
In this section, we review the main properties of prominences at small scales, which provide additional information on the global properties of these structures.
Recent observations of prominence cores show thin dark threads, thanks to the high spatial resolution that long wavelength instruments can reach (e.g., a few tenths of an arcsec in Hα). However, the highest spatial resolution ground-based instruments, such as the Dutch Open Telescope (DOT)Footnote 13 or the Swedish Solar Telescope (SST),Footnote 14 have limitations for high cadence dynamical studies due to the atmospheric seeing. Space observatories such as the Hinode/SOT instrumentFootnote 15 do not have this problem. The situation is different for studies aimed at observing the hotter PCTR and the coronal environment through UV and soft X-ray instruments, for which only 1″–2″ resolution could be reached until now (e.g., SOHO/SUMER, Hinode/EIS-XRT, STEREO/EUVI and now SDO/AIA. The lack of suitable resolution for resolving the filament threads at shorter wavelengths makes it difficult to better picture the PCTR and the cool filament as a whole, even when multi-wavelength data are available. However, it is likely that the IRIS mission will obtain new results at higher resolution.
3.1 Prominence core
Recent reviews of prominence fine-scale observations can be found in Labrosse et al. (2010b) and Mackay et al. (2010). Here we mention a few past results and an update of these recent reviews.
3.1.1 Morphology
Recent statistical work on threads of quiescent and active region filaments made using Hα filtergrams of the SST instrument by Lin et al. (2005, 2008) confirms previous results with better precision. The width of filament threads has a narrow distribution centered on 0.3″ (for comparison, this is the chromospheric fibrils’ average width), even though these authors did not exclude the existence of sub-resolution structures. Their findings imply thread widths from about 150 to 450 km, where the lower limit is given by the instrumental resolution.
The length of the threads is on the order of a few thousand kilometers, which is generally less than the full filament length, particularly for intermediate and polar-crown filaments (e.g., Engvold, 1989), even though exceptions are observed.
We have mentioned that prominences observed at the limb in the Hα or Ca II bands show fine-scale threads dominantly horizontal or vertical, even though mixed orientations are also present. In general, vertical fine scales dominate quiescent prominences, horizontal threads dominate active region prominences, and intermediate prominences may show both substructures.
3.1.2 Dynamics in the core
Filaments can be stable for a long time or can show different types of global dynamics such as oscillations, lifting off, and eruptions (these will be discussed in Section 5). However, even if a filament is stable its threads are dynamic, showing mass flows along their axes and/or transverse displacement on timescales of a few minutes. Internal flows are inferred from the time variability of the darkening of threads, which allow their identification against the disk. Such variations may last from a few minutes up to 20 min (Engvold, 1976, 1981; Lin et al., 2005). This could have several origins, one of which could be density variations due to the mass motions. Observing and characterizing the fine scale dynamics can yield important information on the magnetic field topology, estimate its amplitude, and measure velocity variations in time. In addition, the mass motions are an ingredient of the prominence plasma energy balance and mark the loading or draining of mass into and from the structure.
In images of the cool filament core, the plane of the sky velocities can be deduced from the tracking of proper motions. Transverse motion is instead deduced from Doppler shifts. If the full line profile is not available, this may be deduced by using a minimum of three intensity measurements: at the line center and at both sides in the line wings. However, sampling multiple points in both wings is a better solution for studying possible distortions of the line profile (multi-velocity components). This method is often used for the Hα line through tunable filters. The combination of the two measurements can give better estimates of the vector velocity, unless the full geometry of the structure is available.
However, these measurements are affected by the possible presence of sub-resolution dynamics and/or the presence of multiple threads along the line of sight, as well as the instrument spatial resolution and the optical thickness of the medium. In addition, the data inversion method and hypothesis adopted may affect the results. All these aspects are thoroughly discussed in Chae (2007).
Filaments on the disk. Fine-scale quiescent filaments on the disk show both single and grouped thread dynamics. The work by Lin et al. (2005) using Hα data from the SST revealed the presence of a relative single-thread motion of 2–3 km s−1. The typical size of coherent motions (1500 × 15 000 km) of grouped threads has been measured, for example, by Schmieder et al. (1991).
The most striking aspect of filament bulk motion is counter-streaming: a mass flow along the full filament length and barbs, which is nearly horizontal along the spine and of the same amplitude in both directions in adjacent threads (Zirker et al., 1998; Schmieder et al., 1991; Lin et al., 2003). The magnitude of this motion has been estimated to vary from about a few to 30 km s−1. These values were obtained by using different spatial resolutions and diagnostic techniques on data from different types of prominences. In the 1990s literature (e.g., Tandberg-Hanssen, 1995) it is reported that quiescent prominences do not show this plasma flow or that it is of only a few km s−1, where the highest values are found in active prominences. However, the most recent studies made with the highest-spatial-resolution data seem to indicate higher values also in quiescent prominences. This is the case in the studies by Lin et al. (2003) (8 km s−1) and Lin et al. (2005) (∼ 15 km s−1), for example, where the same time-slice technique and Doppler-shift measurements were applied to different spatial resolution Hα data. Lin et al. (2008) found flows up to 25 km s−1 in active region filaments.
Chae et al. (2005) and Chae (2007) made use of the tunable Hα filter at BBSOFootnote 16 to scan the line. They interpreted the observations using the profiles of single and multi-velocity component cloud models,Footnote 17 to derive information on the plasma flow along the line of sight in the filament barbs and spine. In both regions they found that some threads are almost stationary while others exhibit a high-speed component of about 15 km s−1 along the line of sight, from which they deduced a total amplitude of the vector velocity of 30 km s−1 (under the assumption of horizontal motion). Using their models, these authors inferred that the stationary component could well be the result of the superposition of opposite velocity components of threads along the line of sight (they estimated five-six threads), as it would occur in the presence of counter-streaming motions. This result could be consistent with, for example, the Lin et al. (2003, 2005) results when the effects of different spatial resolutions are taken into account.
Doppler shifts both red and blue (but predominantly blue), from a few to 15 km s−1, are observed in threads within barbs and at the filament ends. This line-of-sight velocity decreases approaching the center of the filament (Schmieder and Mein, 1989; Schmieder et al., 1991). Under the hypothesis that barbs root down in the chromosphere or photosphere, these motions have been interpreted as a signature of an inclined magnetic field with respect to the vertical to the solar surface. These flows could be the source of the material for the prominence, even though the imbalance between blue and red-shift should be confirmed and better explained. Similar results on plasma flows are obtained through the study of filament destabilization and eruption, as will be discussed in Section 5. Line-of-sight velocity measurements also reveal oscillatory motions of threads that will be discussed in Section 3.1.3.
The bulk motions inside threads have velocities on average lower than the sound speed for prominence plasma (20–40 km s−1). This suggests that waves may not be the origin of these motions. The mechanisms at the origin of such motions are still under debate, and are part of the problem of mass supply in prominences. This is discussed further in Section 4.
Investigations of the motions around the filament and inside the channel reveal that fibrils have similar flow patterns as threads, and that both are of lower amplitude than for chromospheric fibrils outside the filament channel (Schmieder et al., 1991; Lin et al., 2008). This may be a further indication that a common global magnetic structure of the whole filament-filament channel system exists.
Prominences at the limb. Limb observations also show that prominences are highly dynamic on timescales of a few minutes, but they exhibit more variety of motions than when viewed on the disk. This is probably due to the optical thickness of the environment in conjunction with the line-of-sight effect. The high resolution and cadence of Hinode/SOT confirmed and discovered substructures that demonstrate the complexity of this environment. The prominences observed by Berger et al. (2008) in the Ca II 3968 Å H line (Fi gure 22) had mainly vertical substructures. They showed downflows in bright streams (∼ 10 km s−1 with a lifetime of about 10 min, 200–700 km wide, labeled D in the figure) sometimes transforming into vortices, turbulence, and oscillatory motions with finer details than previously reported. These downflows were already detected in the past in the prominence footpoints, with less detail and lower resolution (e.g., see Schmieder and Mein, 1989; Schmieder et al., 1991). Despite the difficulty of matching velocity features between data taken at different spatial resolutions, all these studies agree that the velocities are lower than the value expected for a free fall (around 20 km s−1 at the surface for a 15 Mm height prominence), implying the presence of an external unknown upward force.
Chae et al. (2008) came to a similar conclusion by following the descent of a blob into a prominence observed in Hα, using an optical flow technique to follow the flows. They could identify a vertical upflow path from the prominence base, which transformed first in an almost horizontal path and then in a downflow through the formation of blobs. This path persisted longer than the lifetime of the single emission patch used to trace it.
Other characteristics were found in the work of Chae (2010), who studied in detail these vertical bright threads and knots in a Ca II hedgerow prominence observed by SOT. He reported a very small variation of the thread intensity with height and the quasi-absence of flows. He estimated a pressure-scale height greater than the hydrostatic scale height, therefore supporting the idea of the presence of non-hydrostatic support for the prominence plasma. In this work, the downward vertical motion identified by Berger et al. (2008) was more associated with the bright knots than with the thread itself. It also confirmed that the bright vertical threads are not straight and homogeneous, and suggested either a spatial resolution problem or a different nature of the fine structure than simple straight flux tubes. The implication of these results will be discussed at the end of this chapter.
In Figure 22 it is also possible to recognize dark inclusions (labeled U) called plumes which are the location of turbulent upflows (≈ 20 km s−1, 180–740 km in width). These dark plumes, originating from dark cavities at the base of the prominences, are seen intermittently. The discovery of the plumes opens the question of whether they correspond to the Doppler upflows measured in earlier lower resolution observations of filaments. In more recent works Berger et al. (2010, 2011) investigated these outflows in more detail in different quiescent prominences. The characteristics of these turbulent flows (listed in Table 3 of Berger et al., 2010) not only confirms the Berger et al. (2008) values, but also extends the earlier results to a larger set of studied prominences. Studying the evolution of the dark cavity regions at the base of prominences that may be the origin of plumes, they found a growth of the cavity at a velocity consistent with buoyancy. The observed stability of certain cavities with respect to others is seen as the result of the relative strengths of the buoyancy force and magnetic tension of the overlying prominence. Certain cavities can evolve in turbulent plumes through classical Rayleigh-Taylor instability in a magnetized environment. An important aspect highlighted by the authors is the possibility that this mechanism could supply mass to the prominence and the overlying coronal cavity. This would balance the continuous draining of mass in prominences and allow the structure to be seen as quasi stable (over larger scales) for weeks. The authors also supported the idea that the dark appearance is produced by a higher temperature of the plasma outside the sensitivity range of the Ca II filter (between 2.5 and 12 × 105 K), which feeds the coronal cavity, as has been discussed in Section 2.3. This new interpretation of the small-scale turbulent motions has become a hot topic in the past few years. The effectiveness of the Rayleigh-Taylor instability in the prominence environment has been simulated by Hillier et al. (e.g., 2012a, and references therein) and Hillier et al. (2012b) assuming a 3D Kippenhahn-Schlüter model. These first efforts could reproduce several properties resembling those derived from observations (such as up and downflows), but quantitative comparisons of results with observations should be further demonstrated, particularly considering the properties of the magnetic field whose strength and direction are difficult to measure.
Prominence at the limb as seen by Hinode/SOT in the Ca II H-line 3968 Å spectral line on 2006 November 30. “D” indicates examples of bright downflow streams. “U” shows several dark inclusions in the sheet that are regions of turbulent upflow. “V” indicates dark “voids” that are not upflows. Image reproduced by permission from Berger et al. (2008), copyright by AAS.
3.1.3 Prominence oscillations
Oscillating motions of filaments or part of filaments are regularly observed. These periodic motions are generally associated with the presence of magnetohydrodynamic (MHD) waves and their study is called prominence seismology. Oscillations are detected via local flux variations in high spatial and temporal resolution images, and through varying Doppler shifts along the line of sight. The study of prominence oscillations allows the derivation of several important parameters such as plasma density or Alfvén speed, from which the magnetic field strength can be deduced (e.g., Régnier et al., 2001; Lin et al., 2009).
For an overview of the different modes of oscillations, see Vršnak (1993) and Nakariakov and Verwichte (2005). Oliver and Ballester (2002) and Oliver (2009) reviewed small-scale-prominence-oscillation observations and modeling, and recommended several important aspects that should be taken into account for a correct and complete analysis of oscillations. Tripathi et al. (2009b) reviewed large-amplitude oscillations, while a general review of oscillations is given in Banerjee et al. (2007), Mackay et al. (2010) and Arregui et al. (2012), where open questions are discussed. Here are a few general properties and examples.
Oscillating motions are observed both in prominence at the limb and on the disk, indicating that the plane of oscillation may have different directions with respect to the structure. In certain cases the oscillations are observed only in the vertical (e.g., Okamoto et al., 2007) or transverse directions (e.g., Berger et al., 2008). On-disk oscillations were observed in both directions (e.g., Lin et al., 2009).
The parameters of oscillations, like amplitude of the velocity, period and spatial distribution, may vary, implying the influence of several physical mechanisms. In terms of amplitude of the velocity of threads, oscillations are classified as large (a few tens of km s−1) and small (a few km s−1 or less) amplitudes. The measured periods may be divided in three groups: short (< 5 min), intermediate (6–20 min) and long (> 20 min).
The triggers of oscillating motions can be internal or external. External agents can be, for example, p mode excitation or EIT or Moreton waves (Ramsey and Smith, 1966) or other CME/flareinitiated disturbances (Jing et al., 2003, 2006; Vršnak et al., 2007; Luna and Karpen, 2012). Internal agents can be flux emergence or disappearance (Feynman and Martin, 1995). These perturbations, if large enough, can also lead to the destabilization of the structure, as discussed in Section 5.
For small amplitude oscillations, a range of periods from a few minutes to more than one hour is observed. A large variety in the spatial distribution is also reported. The disturbance rarely involves the whole structure, but most frequently only a few threads, or part of the threads. Different threads of the same structure may be subject to different stimulations: for example, Ning et al. (2009) detected the oscillatory motion of a group of threads associated with their drifting.
The oscillations generally last for a few periods, then decay and disappear from the data, indicating a damping process. Theoretical studies have then to address the different mechanisms that either stimulate or suppress the waves in prominences (see, e.g., Oliver, 2009). A recent example is given by the self-consistent model by Luna et al. (2012a) and Luna and Karpen (2012), where their results highlight interesting properties of large-amplitude oscillations. Earlier studies of prominence plasma formation through thermal nonequilibrium showed that thin flux tubes heated asymmetrically at the footpoints develop longitudinal oscillations, while condensation of material fills the threads’ magnetic dips (Antiochos and Klimchuk, 1991; Luna et al., 2012b). Luna and Karpen (2012) found that gravity is the restoring force for these oscillations, and continuous mass accretion onto the prominence threads is responsible for the damping. This investigation also demonstrated that the same forces govern observed prominence oscillations initiated by external disturbances, and that the very existence of these large-amplitude oscillations provide strong evidence for the presence of dips in filament-channel magnetic fields. A new diagnostic tool was revealed: by measuring the frequency of oscillations, the radius of curvature of dips and magnetic field amplitude can be derived from observations.
At the same time, restrictions in the prominence oscillation observations due to technical constraints of the instruments, and the uncertainty regarding the real thread structure, limit the possibility of testing the various proposed scenarios for wave formation and damping. As discussed by Oliver (2009), much work still needs to be done to reconcile the observational aspects with the theoretical predictions, even though recent efforts on both sides are improving the situation.
3.2 Dynamics and small scale structure of the PCTR
Due to the lower spatial and temporal resolutions available for the UV-EUV data with respect to the optical domain, studies addressing the dynamic behavior of prominences access mainly bulk and (spatially and temporally) averaged velocities, including sub-feature (blob) motions. Table 6 of Labrosse et al. (2010b) summarizes the latest studies, in which motions from a few to several tens km s−1 were measured. The different values listed in this Table are found for different features, using different lines of sight and spectral lines with different formation temperatures. These results all indicate the dynamic nature of prominences throughout their layers, highlighting the necessity for increased efforts to access the finest temporal and spatial scales in order to obtain a clear unified picture of these motions.
Line widths of the PCTR emission exhibit signatures of non-thermal motions, even for quiescent structures. Figure 23 reports the results for non-thermal velocities as a function of temperature by Parenti and Vial (2007) for a quiescent prominence (bottom panel) to be compared to the QS values (top panel). As shown in this figure, this velocity component increases generally with temperature, reaching about 30 km s−1 at log T(K) = 5.5 (e.g., Parenti and Vial, 2007, and references therein), then decreases for higher temperatures. Some measurements reported a less continuous distribution (Stellmacher et al., 2003). The existence of unresolved fine structure along the line of sight may cause the different results listed in the literature. Non-thermal motions derived from line widths have been interpreted as a signature of waves and used to show that the energy they transport is not enough to balance the radiative losses of the prominence. Another interpretation is microturbulence, although not much attention has been given yet to this aspect. There is also the possibility that this extra line width is the result of the superimposition of the internal motions of the unresolved fine structure. At present, we are not able to disentangle these various possibilities; only when EUV data at higher spatial resolution are available, will we be able to infer further fine scale properties.
QS (top) and quiescent prominence NTV (bottom) as functions of temperature derived using SOHO/SUMER observations on 8 October 1999. The different symbols are for lines emitted by different elements. Image reproduced by permission from (Parenti and Vial, 2007), copyright by ESO.
In the presence of unresolved structures, it is generally useful to introduce the filling factor, which provides an estimate of the amount of space occupied by the unresolved fine structure in the observed data. This can be defined in various ways, and may depend on the temperature of the emitted radiation, the emitting volume along the line of sight, and the instrument resolution (Labrosse et al., 2010b). The different estimates found in the literature point at a volumetric filling factor in the range 0.001–0.2, which indeed suggests that the PCTR emission comes from a small fraction of the observed volume.
Starting from this information, the next step is to establish how the PCTR is structured. In the various pictures proposed, cool threads can be surrounded by their own PCTR, a bundle of threads can have a common PCTR.
The investigation of the bright H Lyα line is a powerful tool to link the properties of the cooler filament core, formed by threads of sub-arcsec diameter, with its PCTR. This line is indeed formed between the chromosphere and the bottom of the PCTR, so that it images warmer plasma than Hα. Using H Lyα data from the rocket-borne VAULT instrument, Vial et al. (2012) have found that the typical size of threads on the disk is between 1″ and 2″, with a minimum of 0.4″. This is comparable with the picture of cool threads sharing a common PCTR.
Another interesting recent observation brings unique information on the small scale structure of the PCTR and the corona. This was made by the High-resolution Coronal Imager (Hi-C) on board a sounding rocket (Cirtain et al., 2013) which observed, on 11 July 2012, an active region with a filament in the 195 Å waveband. For the first time a spatial resolution of 0.3″ in this waveband was reached. Alexander et al. (2013) concentrated their analysis of these data on bright threads of the filament and measured their width using the FWHM of the intensity profile across a coherent fine structure. The result gives substructures of about 0.8″ ± 0.1″, which is larger than the spatial resolution of the instrument and the 0.3″ typical width of Hα threads. Even if this instrument is imaging hotter plasma than VAULT, the values found from the data of the two sounding rockets are compatible. The Alexander et al. (2013) thread width could suggest a single thread surrounded by its own PCTR, but this needs to be confirmed by co-spatial and co-temporal high-resolution analysis using both cool threads and PCTR data.
Various methods are used to estimate the number of threads along the line of sight when observing at higher temperatures (which means lower resolution) than H Lyα: inferred from the Doppler and non-thermal velocities, or from the density and differential emission measures (with some assumptions). For example, when the structure of a thread with its own PCTR is assumed, results from EUV observations suggest that the number of threads along the line of sight is from a few to 30 (see Labrosse et al., 2010b for details, Gunár et al., 2011), and their diameters are between a few km and more than 200 km (Wiik et al., 1999; Patsourakos and Vial, 2002). These values have to be compared with values of about 200 km inferred from observing the cooler plasma in Hα presented in Section 3.1.1. For example, we have seen that Chae (2007) inferred five to six threads along the line of sight using the Hα line profile at less than 0.5″ spatial resolution. These values are consistent with the EUV estimates, even though the latter vary over a larger range. One reason could be the large uncertainties in the EUV data inversion, which has too many free parameters and hence may have multiple solutions.
Cool threads have been estimated to have widths of a fraction of 1″ (see Section 3). This is also consistent with a few tens of threads estimated within the 1″ pixel of the EUV common data, assuming that the threads are all the same and each is enveloped by its own PCTR. However, these comparisons are certainly not exhaustive and different diagnostics have to be investigated. Recent work by Soler et al. (2011), for example, shows that the damping of kink waves in prominence threads depends on the transverse inhomogeneity scale length. This property offers a promising way to test the different models for the PCTR, but actual application to the data has still to come.
3.2.1 Discussion
Various interpretations have been raised to explain the different plasma motions mentioned above, with the attempt, where possible, of reconciling limb and on-disk observations of vertical and horizontal fine structures. These motions need to be interpreted in the context of the different global magnetic-field configurations proposed by the different models mentioned in Section 2.4.
Lin et al. (2005), as other authors, found their observations compatible with the model of filaments made of thin, horizontal, sheared magnetic flux tubes partially filled with condensed coronal plasma: the threads, suggested by Karpen and Antiochos (2008) (and references therein, see also the middle panel of Figure 3). However, this model cannot easily explain the vertical appearance of threads at the limb.
A different interpretation of threads is given by a group of models (e.g., Low, 1982; Poland and Mariska, 1986; Heinzel and Anzer, 2001; Heinzel et al., 2005; Heinzel and Anzer, 2006) which aim at explaining both the vertical aspect of Hα threads at the limb and the horizontal aspect on the disk. They introduce vertical magnetic dips in a horizontal magnetic field as the location where the thread plasma is concentrated (see also Section 2.4.3). The vertical superposition of these dips gives the observed appearance of vertical threads at the limb and as dark horizontal fine threads when observed from above. This picture can explain, for example, the observations by Chae et al. (2008), Schmieder et al. (2010) and Chae (2010). The threads form magnetic dips filled with cool material (the bright knots of Chae, 2010) that deforms by gravity the magnetic structure, to give the impression of vertical threads. In support of this idea Ahn et al. (2010) also identified returning flows that could be a signature of the counter-streaming flows observed in filaments from above. However, in this proposed picture the full filament length flow is not real but the result of a superposition effect. Chae (2010) extended this idea of magnetic dips by proposing the presence of reconnection and interchange of material between knots and their surrounding to justify the long descending paths (up to 15 000 km) and the local impulsive accelerations detected in knots (up to 0.1 km s−2 in absolute value). These new ideas on the presence of multiple dips offer significant promise to solve the paradox of the orientation of the cool threads. Higher-spatial-resolution magnetic-field measurements and PCTR velocity studies will certainly help by better testing these ideas. In addition, setting up more realistic modeling will improve the comparison with the observations. Encouraging first attempts in such a direction include the Hillier et al. (2012b) simulation of plume dynamics. Certainly, the counter-streaming motion along the full filament is an established observational property (within the accessible spatial resolutions) and needs to be accounted for in all models, including those proposing magnetic dips.
The models for the fine magnetic structure should also be tested in terms of compatibility with other observational properties. One example is given by the small-scale turbulent dynamics inside prominences recently observed with Hinode/SOT, and which have been interpreted in terms of plasma buoyancy. Indeed a preliminary numerical MHD simulation on a Kippenhahn-Schluüter prominence model (Hillier et al., 2011) found that such a mechanism may be compatible with the presence of the horizontal magnetic field without being completely inhibited. Further investigations should reveal if and how this process affects the stability of the whole structure.
On the issue of the cool-PCTR fine structure of filaments, we understand that the observational results are generally obtained under certain assumptions, which may vary from one study to the next, and that these results span a large range and may not be in agreement. In particular, in determining the number of threads along the line of sight, values derived from velocity measurements disagree with those derived from the density (Cirigliano et al., 2004). Even if the high resolution Hα data are bringing us closer to resolving a single thread element, much work should be done to improve the data inversion by limiting the free parameters of the used models. A better constraint will arise combining IRIS UV and optical data, allowing systematic studies with similar resolutions in order to establish the coherence in the fine scale structure. This could confirm, for example, the results obtained using the few minutes observations by VAULT H-Lyα and Hi-C 193 Å. To better analyze the plasma conditions inside threads, it is important to compare the fast changes (a few minutes) in a typical thread’s darkness observed by Lin et al. (2005) with the characteristic time scale for the stationary radiative state. We have mentioned that such variations may be the result of a density change due to mass motion, which affects the amount of absorbed underlying chromospheric emission, or to local temperature changes due to some cooling/heating events. Engvold (1980) has tested this and found that the relaxation time of a hydrogen plasma is on the order of 1–2.5 mins, which is of the same order as the observed intensity change. This lack of thermal equilibrium should be better tested and taken into account in the diagnostics and modeling of prominence fine structure.
4 Prominence Formation
Filament formation is generally quite a slow process that may take a few days, especially when the structure is located far from an active region. Two elements are needed for this process: the formation of the particular magnetic structure, which supports the dense filament plasma and the surrounding coronal cavity, and a mechanism to partially fill this magnetic structure with filament plasma. To understand how the filament channel is filled with plasma, it is important to establish whether the filament plasma and its magnetic structure have photospheric, chromospheric, or coronal origin. Some models invoke the direct injection of chromospheric plasma into a pre-existing filament-channel field; others postulate levitation of chromospheric mass accompanying flux rope emergence or lifted into the corona by photospheric or chromospheric reconnection; in a third class of models, chromospheric material is evaporated into the corona and condenses to form the cool filament (Mackay et al., 2010). Therefore, as will become apparent throughout this section, it is not always straightforward to separate the magnetic-structure formation problem from the plasma-formation problem.
The frequent presence of filaments on the disk, particularly during the high activity phase of the solar cycle, suggests that they are a common product of the solar atmosphere. Observations reveal that, after a filament eruption, the feature may reform in the same place (e.g., Bone et al., 2009). This suggests that the conditions for filament formation may not be destroyed by the eruption or that they can be easily reproduced. An overview of our knowledge of the filament formation processes is presented below; more details can be found in Mackay et al. (2010).
Filaments can be found above the PIL separating a simple bipolar region or more complex magnetic structures, including multiple bipolar regions. A classification in these terms was done in the past (Tandberg-Hanssen, 1995), with the result that filaments favor the second (more complex) magnetic configuration (e.g., Tang, 1987). A recent update of classification was done by Mackay et al. (2008), who concentrated on long stable structures. They introduced new magnetic categories for the classification, as illustrated in Figure 24, and we direct the reader to their work for further information. They showed that indeed 92% of filaments are found between multiple dipoles. As pointed out by these authors, the existence of a preferred magnetic configuration where filaments are located is indicative of the physical conditions suitable for their formation.
Classification scheme for solar filaments based on those of Tang (1987) and Tandberg-Hanssen (1995) where two new categories (c and d) are introduced by Mackay et al. (2008). (a) Filaments that form above the internal PIL of a single bipole are classified as IBR. (b) Those forming on the external PIL between bipoles or between bipoles and unipolar flux regions are classified as EBR. (c) Filaments that lie both above the internal PIL within a bipole and the external PIL outside the bipoles are classified as I/EBR. (d) Finally, those filaments that form in diffuse bipolar distributions (formed through multiple flux emergence) are classified as DBR. This category is expected to lie only at high latitudes. Image reproduced by permission from Mackay et al. (2008), copyright by Springer.
We have mentioned the different magnetic topologies that have been proposed for the filament support: sheared arcade (Antiochos et al., 1994; DeVore and Antiochos, 2000) and/or flux rope (e.g., Amari et al., 2000, 2010). There are two possibilities for their formation: either they emerge from the photosphere, or they are the result of the modification of an existing magnetic structure due to photospheric flux cancellation and/or coronal reconnection. In the latter case we expect to find the properties of the magnetic envelope of the filament to be similar to those of the pre-existing magnetic region.
To interpret the observed filament formation in terms of these different proposed pictures we need to infer the magnetic field configuration of the filament and that of the pre-existing field. Considering the difficulty of their measurement, the information should be complemented or supplied by identifying all other possible observational signatures associated with filament formation. These various identified factors that influence or are associated with the filament formation and its magnetic structure are, in summary, the following: photospheric flow motion toward the PIL, photospheric magnetic topology and intensity, large scale plasma flows in the photosphere due to meridional circulation and differential rotation, magnetic flux emergence and cancellation, chromospheric small-scale flows, flows along the PIL.
In the literature, cases are found where one or more of these phenomena were recognized during filament formation (e.g., Mackay, 2003; Mackay and van Ballegooijen, 2006). The presence of one process, or the combination of several of them, may lead to one or the other of the above mentioned filament magnetic-field topologies. Furthermore, the dominance of one or another of these mechanisms appears to be linked to the different activity levels on the Sun. For example, large-scale flux emergence is typical of AR areas and not of polar-crown regions (Mackay et al., 1998), so flux emergence will be more likely to be associated with active filament formation.
The first phase of filament formation, which lasts a few hours, is characterized by the Hα fibrils aligning along the PIL to form the filament channel, as shown in Figure 25. Then the filament channel typically can be filled with plasma in a few days. The fibril alignment on both sides of the PIL can be parallel or anti-parallel. One proposed cause of such alignment is in the relative motion of the photospheric fibril footpoints in the two different polarities (e.g., Wang and Muglach, 2007). Photospheric flux convergence is often caused by supergranular divergence motions at the sides and across the PIL (e.g., Rondi et al., 2007). Both cases studied by Wang and Muglach (2007) exhibited convergence toward the neutral line, but in the first case there was also parallel motion, while it was anti-parallel in the second case. However, Gaizauskas et al. (1997) noted that the change of the fibrils’ direction was too fast to originate in local reconnection in the photosphere driven by converging motions. They also associated the filament channel formation with the emergence of an activity complex. Hence, the question of the origin of the fibril realignment probably remains open.
Evolution of the decaying NOAA region 10003 during June 2002, showing the fibril structures changing their orientation from nearly perpendicular to nearly parallel to the PIL, as the opposite-polarity sectors diffuse toward each other. Left panels: Hα filtergrams; middle panels: corresponding MDI magnetograms saturated at Blos = ± 50 G; right panels: magnetograms saturated at Blos = ± 7 G. Image reproduced by permission from Wang and Muglach (2007), copyright by AAS.
The filling of the channel with plasma is not a homogeneous process. It can proceed by involving pack of threads or thread segments, each of them happening at different times. Thread segments may evolve into a unique longer filament. In addition, we recall that the channel of a well-formed prominence does not necessary overlap the full PIL length. It is not yet clear what governs this filling and the eventual filament channel evolution. The process is days and even weeks long, which means, to be properly monitored it needs to be observed continuously. This would also require observations in the far side of the Sun, which is yet to be accomplished by the available instrumentation.
Once a filament is formed, the dynamics around and beneath the filament continue, changing the filament shape and, in certain cases, possibly destabilizing it. One of the signatures of these dynamics is the continuous local convergence of magnetic flows toward the PIL. The presence of sporadic minor polarity concentrations around the PIL has also been considered important for filament formation. Rondi et al. (2007) claim that the converging motions may transport these small scale polarities across the PIL, thus forming the parasitic polarities in which filament barbs are thought to be rooted. They identified this process as causing the formation of the filament barbs, as supported by other observations (e.g., Schmieder et al., 2006) and modeling (e.g., Aulanier and Schmieder, 2002).
As mentioned, a pre-eruption flux rope structure in a filament channel has been identified only in a few cases. Okamoto et al. (2008, 2009), using SOHO/MDI and HINODE/SOT Hα, Ca II H and G bands images, claimed to have recorded the emergence of a flux rope inside an active region. Observationally this was associated with the temporal change of the horizontal magnetic-field region along the PIL, including its broadening and narrowing in time, and the change from normal-polarity to inverse-polarity, suggesting the lifting off of the structure. Okamoto et al. (2009) also measured diverging motions in granular cells (3000–5000 km wide and 60 km deep). In a similar way, Lites et al. (2010) interpreted their data as the result of the emergence of a preexisting flux rope from below the photosphere. In both cases, the local granular motions dominate over the photospheric flows, and there is absence of magnetic flux converging toward the PIL. However, the interpretation of these observational elements are not straightforward: the magnetic field measurements are from photospheric data, which have the uncertainties we already discussed, and the lack of chromospheric and coronal field measurements prevents this study from clearly establishing whether the rope reaches coronal heights or not.
The region of emergence of the flux rope observed by Okamoto et al. (2009) was partially located in a region previously occupied by another filament. The authors could not definitively determine whether the mechanism of mass loading played any role; however, the presence of small reconnection sites suggested an interaction between the pre-existing and newly-emerged magnetic fields, causing an exchange of material. This is a case where the observations give no exhaustive answers to prominence formation.
The picture proposed by Lites et al. (2010) is different. Their data were interpreted as evidence for the emergence of a flux rope in an active region, with the filament plasma coming from the upper convection zone. The data suggested that the magnetic structure did not rise high in the corona. At the same time, several areas along the filament channel showed an absence of a strong vertical field, suggesting the absence of a coronal arcade that could prevent the rise of the filament structure. From this information they concluded that the filament was massive enough to keep the structure stable (see also Section 2.2.1).
As illustrated by the previous examples, the interpretation of the data is not straightforward and some conclusions remain controversial. At present there is no clear evidence that flux ropes can emerge fully and reach the coronal heights where filaments are found. Unfortunately, this is a limitation for properly testing and constraining filament formation models based on magnetic and plasma levitation.
The few examples presented here illustrate how the problems of filament magnetic-field and plasma formation are still far from being solved. One difficulty is the existence of only a few well-documented cases. For proper collection of useful information it is necessary to follow the target area for days, or even full disk passages, with multiple instruments. Today this may be possible with the SDO instruments, supported by ground-based instruments, but cannot be accomplished with the existing ground-based instrumentation alone.
5 Instabilities and Prominence Disappearance
Prominences end their lives either through a slow process of decaying emission, or through a more sudden disappearance (disparitions brusques) triggered by a thermal or dynamical instability. The decay of emission can also be transient: the disappearance of a filament in a monochromatic image sampling the cool plasma (Hα for example) can be the result of the change of its temperature as a consequence of a transient heating injection. Thus, the filament will become visible in the hotter EUV lines, but eventually will go back to its original thermal condition. A more violent phenomenon is the prominence eruption, which implies an explosive rearrangement of the magnetic structure and its ejection into the extended corona (see Section 5.4). Nevertheless, intermediate dynamic phenomena are also observed, such as partial or failed eruptions. Prominence eruptions are associated with flares (impulsive release of energy, Benz, 2008) and coronal mass ejections (see Figures 31, 32 and Schwenn, 2006), indicating that a common magnetic structure (the filament channel) links these energetic phenomena.
5.1 The sources of instabilities
Prominence destabilization has been observed in connection with several phenomena, including magnetic flux emergence, local and large scale photospheric motions with their transport of magnetic flux, and a remote flare that initiates wave disturbances (e.g., Wang et al., 2001).
The photospheric motions can be responsible for the shearing of magnetic field and flux cancellation through collisions of opposite polarities. Both photospheric motions and flux emergence perturb the existing magnetic field whose changes are considered to be the energy source for the eruptions. Magnetic reconnection is one of the primary ways this energy is released.
Flux emergence, small-scale surface flows, and reconnection associated with filament eruption can easily be identified in the data. Various cases will be presented in Section 5.4 in the context of CMEs. The relation between filaments and large-scale photospheric motion, on the other hand, is well studied by modeling and numerical simulations (Mackay et al., 2010), but is rarely found in observations.
However, a nice observational example of this scenario is shown in Figure 26 from Roudier et al. (2008). These authors followed the time changes of the topology of the flow around and under a filament before and after its eruption. They found important changes in the horizontal component (which is associated with the differential rotation) in the region where the filament eruption started. Such a change was also associated with the presence of north-south streams and to a change of the orientation (toward the streams’ direction) of this part of the filament. From these observations the authors concluded that the flow dragged the filament footpoints, stretching the coronal magnetic field and enabling the subsequent instability. Further investigation is needed to confirm this picture for more observed events, and to include similar processes in existing CME models (e.g., Aulanier et al., 2010).
Map of the amplitude of the change of the velocity vector direction. The closer this quantity is to 1, the better the alignment between two vector fields. Black areas indicate the location where a lot of changes between horizontal velocities take place. The filament observed before the eruption is superimposed. The hexagon indicates the location where the filament eruption started. Image reproduced by permission from Roudier et al. (2008), copyright by ESO.
5.2 Observed precursors of eruptions
The disappearance or eruption of a prominence is generally preceded by an activation phase. This shows up as an increase of mass or turbulent motion inside and at the structure footpoints (for example, as shown in Figure 27), fragmentary brightening and fading due to sporadic heating events (e.g., Ofman et al., 1998; Schmieder et al., 2000; Kucera and Landi, 2008), EUV brightenings due to reconnections, deformation and helical rotation of the filament (Sterling et al., 2011), and the start of lifting off (e.g., Gilbert et al., 2000; Engvold et al., 2001; Sterling and Moore, 2004; Bemporad, 2009; Liewer et al., 2009). Figure 28 shows a further example of these pre-erupting signatures: the Hα intensity variation in a segment of a filament, which will start disappearing at around 12:30 UT.
Hα intensity and velocity images observed using MSDP instrument at Meudon Solar Tower on 21 May 2008, at 09:00 UT. The left panel shows the line center intensity while the right panel shows, in grey scale, the dopplergram overlaid by contours of the filament. The white arrows mark the maximum (white) and minimum (black) velocities, respectively, +800 m/s and −200 m/s. The white circle indicates upward and downward flows at the end of one foot of the filament. Elongated areas of blue and red-shifts (marked by the arrows) suggest some twist along the filament body. Image reproduced by permission from Gosain et al. (2009), copyright by Springer.
Light curve and stackplots in X and Y directions showing the variation in the Hα filament intensity on 19 May 2007 prior to the filament eruption at around 12:50 UT. The top panel shows the total emission, the middle is the variation in Y intensity and the bottom is the variation in X intensity. Image reproduced by permission from Bone et al. (2009), copyright by Springer.
Prominence oscillations are also observed in the pre-erupting phase of a filament (e.g., Isobe and Tripathi, 2006; Pintér et al., 2008). An example is given in the movie of Figure 29 obtained from the STEREO/EUVI data. Contrary to the quiescent case, where only a few periods of oscillations are observed, the number of periods in an activated filament may be numerous, as observed by Chen et al. (2008) using SOHO/SUMER data. These long-lasting oscillations were interpreted as the signature of the repetitive action of the exciting force. The authors also noted an association between the oscillation and the presence of surges and siphon flow in the Hα images. Such events were interpreted as signatures of reconnection of emerging flux with the existing coronal field (Figure 30), as we will discuss later in this section.
Left panel: evolution of the C I 1118.45 Å intensity along the SUMER slit; Middle panel: same for S III/Si III 1113 Å; Right panel: evolution of the Dopplergram along the SUMER slit observed at S III/Si III 1113 Å. Image reproduced by permission from Chen et al. (2008), copyright by ESO.
Martin (1980), Gopalswamy et al. (2006), and Schrijver et al. (2008) review in further detail the pre-erupting conditions and ejection phase.
5.3 Eruption phase
In most cases (particularly for quiet region structures) the initial rise phase of the filament is quite slow (1–15 km s−1) and can last a few hours, while this phase can be much shorter (10 min) for active region structures (Sterling and Moore, 2004; Williams et al., 2005). This is followed by an acceleration phase in which the filament may reach about 100–1000 km s−1, together with the rest of the expelled coronal material to form the CMEs (e.g., Schrijver et al., 2008; Gosain et al., 2009). In a final stage the structure expands at a nearly constant speed or may decelerate. Depending on the magnetic environment, the prominence eruption can be either almost symmetric or asymmetric with respect to its endpoints (Liu et al., 2009a).
Partial or failed eruptions of prominences have an initial phase similar to that of a full prominence eruption up to the acceleration phase, which lasts for a shorter time. The prominence is then observed to decelerate, reaching a maximum height, while prominence material simultaneouly drains back to the solar surface. Failed eruptions sometimes are associated with CMEs. In this case the remaining filament reforms soon, to finally be completely ejected in the CME (Zhou et al., 2006). Other times there is no sign of a CME or opening of the coronal magnetic field. Often these events are associated with compact flares. Similar to full prominence eruption, failed eruptions show properties that can be reproduced by models that use different destabilizing mechanisms, as we will see in Section 5.4.
In the off-limb images showing the eruption phase, the prominence generally can be better isolated against the darker coronal background than on the disk. Often in this case the prominence structure turns out to be composed of bright (emitting) and dark (absorbing) parts highlighting a twisting topology, suggesting the presence of a magnetic flux rope (see Figure 31 and, e.g., Patsourakos and Vial, 2002). As discussed earlier, it is not yet clear whether this topology results from the instability and following eruption or existed beforehand.
5.4 Eruption of prominences associated to flares and CMEs
Since the SkyLab era, several statistical studies have addressed the relation between filament eruptions, flares, and the ejection of CMEs (e.g., Munro et al., 1979; Webb and Hundhausen, 1987; Gilbert et al., 2000; Zhang et al., 2001); the results range from a 10% (Hori and Culhane, 2002) to a 90% (Gopalswamy et al., 2003) association. More recently, Al-Omari et al. (2010) used the NGDC filament catalogueFootnote 18 and the SOHO/LASCO CME catalogue to feed the SVM learning algorithms and study the association between CMEs and filament eruptions in the period 1996–2001. They found that about 4% of the observed CMEs were associated with filaments. Aschwanden et al. (2009) made a recent survey of flares using the first two years of STEREO/EUVI data (November 2006–November 2008) and claim that only 3% of them were associated with filament eruptions. Taliashvili et al. (2009) investigated 42 sudden disappearances of quiescent prominences during solar minima and classified them as thermal or dynamic. Their main results show that 50% of the thermal and 60% of the dynamic disappearances were associated with coronal hole proximity and/or CME occurrence.
These diverse results obtained before the launch of SDO indicate difficulties in defining the strength of the association among filament eruptions, CMEs, and flares. Different results may originate from different selection criteria adopted for the events, differences in the solar height of the FOV of the observations, differences in the chosen temperature coverage, and the presence or absence of simultaneous observations of CMEs, flares and filaments. More systematic selection criteria need to be assured in the future, together with full temporal and temperature coverage of the events (even though SDO data are now improving much on these latest two aspects).
When a filament eruption is associated with a CME, the filament is identified as the brightest part of the CME in white light images (for example, see Figure 31). Observationally, a CME structure is often very similar to the large scale structure in which we find the filament: a bright leading edge, a dark cavity, and a bright core (the erupted filament) (Hundhausen, 1999). This suggests that in many cases a large fraction of the whole filament-channel magnetic structure is destabilized and erupts (see Figure 32).
Left panel: a Solar Maximum Mission archive image showing the principal features of a CME Image reproduced by permission from van Driel-Gesztelyi and Culhane (2009), copyright by Springer. Right panel: schematic view of the CME features. Image reproduced by permission from (Forbes, 2000), copyright by AGU.
To assess how much of the coronal environment is involved in the prominence eruption, how the destabilization is triggered, and how it evolves, we need good time sampling of the event at multiple wavebands. As a result of recent advances, some common observational signatures of the pre and post-eruption have now been identified, as sketched in Figure 32 and described below. In addition, other signatures may be present and may change from case to case (these will also be mentioned later). The diagnostics and timing during the eruption of all these properties have been used to constrain and develop different models, which are summarized next.
5.4.1 Models for eruptions
Different eruption models predict that different triggering mechanisms are responsible for the energy release through the eruption of the CME, after sufficient magnetic energy has been accumulated up to a critical point. The energy release can be the result of instabilities invoking ideal or resistive processes. Models associated with the first group, for example, invoke helical kink or torus instabilities of a flux rope (e.g., Démoulin and Priest, 1989; Amari et al., 2003a; Fan and Gibson, 2003; Török and Kliem, 2005; Williams et al., 2005). Kink instability occurs when the twist reaches a critical value, while for torus instability the background magnetic field gradient plays a key role. In both cases, the flux rope then deforms and rises up to its ejection.
Those models that evoke instabilities by flux cancellation and reconnection belong to the second group (e.g., van Ballegooijen and Martens, 1989). In “tether-cutting” models (Moore and Roumeliotis, 1992; Moore et al., 2001), the instability and reconnection can originate first below the filament in a bipolar sheared system. Here the filament and the formed flux rope are pulled outwards by the release of magnetic tension associated with the underlying reconnection, simultaneously powering a flare below the reconnection site. In the “breakout” model (Antiochos, 1998; Lynch et al., 2008; Karpen et al., 2012), which requires a multipolar magnetic flux system (e.g., a delta spot) and a sheared filament channel, two reconnections are involved: “breakout reconnection”, which removes the overlying field restraining the ejection, and “flare reconnection” beneath the filament, which forms the CME flux rope as in the tether-cutting paradigm.
Within these models, explanations also have been developed for the partial or failed eruptions of filaments (e.g., Gilbert et al., 2000; Gibson and Fan, 2006; DeVore and Antiochos, 2008, and references therein).
Most observed events can be interpreted with one or more of these models. For a more extensive overview of CMEs and prominence eruption modeling see, e.g., Forbes (2000), Forbes et al. (2006) and Chen (2011).
5.4.2 General observational properties
The general observational aspects that can be seen during an eruption, which should be reproduced by models, are sketched in Figure 32 and reviewed by Webb and Howard (2012). Before and during an eruption, EUV and HXR local brightenings as well as radio burst emission, are present and are considered signatures of magnetic reconnection.
The eruption models agree that a formed flux rope erupts once it exceeds the instability threshold, which forces the overlying magnetic field to open. However, they differ in the location where the different events happens, as well as their temporal sequence (the formation of a current sheet, for instance). Magnetic equilibrium is eventually recovered as a consequence of reconnection in the current sheet. Below the erupting large-scale structure, the core flaring region is filled with a post-eruption arcade whose loops are observed in the EUV and SXR images. The footpoints of these loops are identified in two bright ribbons seen in Hα and UV-EUV images and in HXR sources. The ribbons separate in time and their inner edges mark a transient coronal hole. This separation is interpreted as a consequence of the rising of the magnetic reconnection point at the current sheet formed below a CME. HXR sources observed between the top of the loop arcade and the bottom of the erupting flux rope (see Figures 32 and 33) have been identified as either the reconnection site or the termination shock of the downward reconnection jet. While the location of the reconnection-site HXR source is expected to move up as the separation of the ribbons from the PIL increases (implying a rising reconnection point), in some cases it is observed to move along it (Grigis and Benz, 2005; Tripathi et al., 2006). This aspect has been interpreted as the consequence of an asymmetric eruption of a filament, i.e., when one end of the filament erupts before the other. However, the signature of these HXR sources is still debated. Radio emission as bursts, particularly type II, III and IV are also detected during CMEs. Type II bursts are tracing shock waves, type III are due to fast electrons escaping the corona along the magnetic field, and type IV are due to non-thermal emission, typical of the regions where magnetic reconnection is at work. Type III bursts are sometimes detected a few hours before onset of the eruption (see Webb and Howard (2012) for details).
Prominence eruption interpreted as the result of a kink instability. TRACE 195 images overlaid onto RHESSI X-ray contours at 10%, 20%, 50%, and 80% of the peak intensity at 1220 keV (gray), and 2040 keV (black). Coronal sources are marked by white arrows. The integration time for each RHESSI image is 12 s around the time of the corresponding TRACE image. Image reproduced by permission from Liu and Alexander (2009), copyright by AAS.
In addition to the timing of the coronal brightenings described here (examples relevant to model predictions are given below), another element that can provide insight into the eruption initial phase is studying and comparing the kinematics of different components of the global eruption, in particular the height and acceleration of the moving filament and the CME leading edge. For the models that predict a whole flux-rope instability, the eruption of the rope (the magnetic support embedding the prominence plasma) is almost uniform, leading to synchronized motion of both prominence and CME leading edge (the upper part of the flux rope). This is the case, for example of Török and Kliem (2005).
For those models that invoke resistive instabilities, such as the breakout and tether-cutting models, we expect less synchronization in the initial phase of the whole CME eruption. In a detailed study of a simulated breakout CME, Karpen et al. (2012) found that the prominence-carrying portion of the structure undergoes a short stage of Alfvénic speeds during the classic impulsive phase of the CME/eruptive flare, but then travels more slowly than the CME front.
Results of observational studies focusing on relative kinematics have shown that there is not a unique picture. Most of the 18 cases studied by Maričić et al. (2009), for example, revealed that the motions of the leading edge of the CME and the erupting prominence were very similar and almost co-temporal. However, they also found exceptions where the prominence acceleration started earlier (> 40 mins) than that of the CME leading edge, and others where the opposite happened (with a similar delay) prior to eruption.
A distinction between these two latter cases is difficult, however, so that this kind of analysis should be accompanied by a more reliable study on the whole erupting environment. Among other factors, the relative delay of the two fronts can depend on the location within the magnetic configuration where the instability starts (e.g., the position of the reconnection site). To clarify this situation, the full-time history of the reconnection sites should be identified and recorded. In addition, the possible natural expansion of the erupting flux rope, which affects the synchronization of the two fronts, should be taken into account and, in some way, disentangled from a lack of synchronization due to the initial conditions of the eruption.
Furthermore, we must consider the difficulty of these kinematic studies arising from the fact that the CME emission is quite faint compared to the background corona. Multi-instrument observations (such as those from the STEREO mission) can follow the initial phase of the events using the overlapping field of views of the disk imagers (showing the solar disk and only a small fraction of the off-limb corona in the EUV) and coronagraphs (showing only the off-limb corona in the optical band). However, up to now this overlapping region is quite small and the emissions recorded by these instruments are due to different physical processes. Such difference should be taken into account in the data interpretation. However, additional information is obtained through the technology of the new generation of ground-based coronagraphs (e.g., COSMO K-cor at NHOFootnote 19) and space instruments (e.g., the SOLAR Orbiter/METIS coronagraph and EUI imager), where the overlapping field of view is increased.
Finally, in terms of localization of the initial instability, the additional data provided by the latest solar mission, SDO, with AIA’s high temporal (10 s) cadence and multi-temperatures images, together with the magnetogram data provided by HMI, are now helping to solve this problem.
At present, we have collected enough examples of prominence eruptions and CMEs to realize that it is very difficult to associate all of them with well-established (tested) models. The corona is highly structured and dynamic over large spatial scales, so that unusual events may always occur, or external factors may have a role in the dynamic evolution of the eruption. For example, a series of observations has shown that there may be an offset between the direction of the filament eruption and the CME expansion, an indication that a complex magnetic configuration was present before the instability (Gopalswamy et al., 2000) and/or the pre-existing large-scale coronal structure influenced the CME expansion. Recent results indeed indicate that the pre-existing coronal streamer above the filament may constrain the filament and CME expansions after their eruption (Bemporad et al., 2005; Jiang et al., 2009). An interesting point has recently been raised by Liu (2008) and Liu et al. (2009c) on the role of the strength and asymmetric background magnetic coronal field in constraining the filament eruption. Using simple potential field modeling and observational cases, they showed that an asymmetric field can produce a stronger confinement in the trajectory of a filament eruption than in an symmetric case, also causing failed eruptions. These observed events suggest that models predicting the CME expansion need to evolve to include a more realistic coronal environment.
Magnetic field reconnection. We summarize some recent research that identifies the EUV and X-ray brightenings with the signatures of reconnection associated with eruptions. These cases are meant to illustrate the different interpretations that may be given to various observed events, showing that it is not always clear whether reconnections are at the origin of the eruption or its consequence (for example, see Forbes and Lin, 2000).
One of the key approaches to answering this question depends on our ability to identify the location and timing of the EUV and X-ray brightenings. Their position within the magnetic structure, inferred from the photospheric magnetic field and its extrapolation (when available), can help distinguish among the various magnetic models for the eruption. For example, the presence of a photospheric multipolar region and pre-eruption reconnection far above the filament channel are consistent with the breakout model, while a simple photospheric dipolar region is consistent with a tether-cutting configuration. Both models predict signatures of reconnection below the filament during the impulsive phase and eruption, with the presence of sigmoids (an ‘S’ shaped SXR structure).
An example showing the difficulty in data interpretation for the brightenings is given by Sterling et al. (2001b). They observed the gradual lift off of a quiescent filament, followed by a more rapid phase ending with its eruption in correlation with a flare. The absence of SXR emission below the filament prior to its eruption suggested to the authors a gradual initial phase consistent with breakout reconnection. However, the lack of high cadence data that could catch the brightenings/dimmings associated with early reconnection implied that they could not rule out the tether-cutting scenario (see also Sterling and Moore, 2004). This is a clear case showing the importance of full coverage and high cadence data in order to fully capture the ongoing dynamics. Similar cases to those observed by Sterling et al. (2001b) were also found in other observations by the same authors (Sterling and Moore, 2001; Sterling et al., 2001a); generally they support the presence of a mechanism that induces filament destabilization prior to the explosive phase.
EUV and X-ray brightenings have also been interpreted as signatures of reconnections due to, for instance, filament kink instability. This is the case of Liu and Alexander (2009) who detected the formation of multiple hard X-ray sources visible at the interacting filament legs in the first phase of prominence activation, and beneath the filament arch during its rising phase (Figure 33). Liu et al. (2009b) instead, found their data consistent with both tether-cutting and kink instability as the triggering mechanism for the observed flare and filament eruption. They observed thermal hard X-ray emission close to one filament leg and the subsequent formation or increase of filament twisting.
Other observations detect reconnection sites both above and below the filament during different phases of the eruption. This was, for example, the case of the failed active-region filament eruption followed by Alexander et al. (2006) with TRACE and RHESSI, that was associated with an M2 flare but not with a CME. The initial rising phase of the event was interpreted as a flux rope eruption due to a kink instability (Török and Kliem, 2005). By studying the changing positions of the HXR sources with respect to the evolution of the lifting filament, the authors inferred that a weakening, through reconnection, of the coronal magnetic field occurred above the filament, while interaction/reconnection of the two footpoints was going on at the coronal base.
In the case of Nagashima et al. (2007), on the other hand, a sequence of small flares close to the filament footpoints was identified at the time the filament was slowly lifting off (40 h before the eruption). This was followed by the filament eruption and a CME. This sequence of events was interpreted in terms of reconnections in the photosphere that produced changes in the magnetic configuration above the filament of the overlying loop arcade, leading to the filament eruption.
As we have seen, the location of the brightenings can be different for different erupting events. A systematic study to interpret this aspect was done by Tripathi et al. (2006) using data from seventeen events, relating the separation of the two-ribbon flare with the propagation along the neutral line of the SOHO/EIT 195 channel brightenings associated with filament lift off. They could distinguish symmetric from asymmetric eruptions. In the first case the brightening started from the center of the filament and propagated toward its end, while in the latter the brightening moves from one end to the other of the erupting filament. A sketch of their 3D picture of the two eruptions is shown in Figure 34.
Schematic diagrams showing asymmetric (left panel) and symmetric (right panel) eruption of a filament. The arrows indicate the direction of propagation along and separation away from the polarity inversion line of the SOHO/EIT 195 channel brightenings. Image reproduced by permission from Tripathi et al. (2006), copyright by ESO.
In conclusion we can say that a large amount of data has been published in which EUV and X-ray brightenings are associated with reconnection and eruptions. They are interpreted as the signature of conversion of magnetic energy into kinetic energy and/or heat. They are also generally observed during coronal magnetic-field reconfigurations, such as twisting of the filament structure and changes of the large-scale magnetic field. The interpretation of such brightenings in the frame of models for energy ejection is not unique. The different existing configurations of the magnetic field, the long-term energy buildup by photospheric motions and by the emergence of a new magnetic field, and other factors mentioned above all contribute to the wide variation in observable signatures.
Magnetic flux emergence and cancellation. As mentioned, simulations have shown that differential rotation coupled with surface flows contribute to the transport of photospheric magnetic-field flux and may cause field-line shearing, reconnection and/or magnetic flux rope formation (for the theory of flux rope and helicity see, for example, Berger, 1984; House and Berger, 1987; Rust, 2003). We give here a few examples that show that the reconnection events can result from flux emergence or cancellation associated with diffusion through the photospheric surface (Feynman and Martin, 1995; Muglach et al., 2009). A recent statistical work by Yan et al. (2011) shows that flux emergence and cancellation have about the same effect on active-region filament destabilization.
Chen and Shibata (2000) proposed a model where destabilization and reconnection within the filament channel or at the outer edge of the channel were initiated by nearby flux emergence. Data analyzed by Sterling and Moore (2005) were consistent with predictions of this model during both the initial gradual liftoff of the filament and the eruption.
Even though several models can predict partial-filament eruptions, the event studied by Tripathi et al. (2009a) had several elements consistent with the partially-expelled flux rope (PEFR) model by Gibson and Fan (2006), in which a flux rope emerges and becomes unstable, reconnecting with the surrounding existing field. They observed the change of the magnetic structure from a sigmoid into a new sigmoid surrounded by a cup shaped arcade, and the formation of a dimming area outside the eruption source region.
Mackay and van Ballegooijen (2006) show that flux cancellation at the PIL between bipoles may result in the formation of a flux rope, its elevation and consequent reconnection below it, and subsequent ejection. Amari et al. (2010), for example, also showed that such cancellation may transform a sheared arcade into a stable or unstable flux rope. These ideas have been supported by data on several eruptive events (e.g., Green and Kliem, 2009; Green et al., 2011; Sterling et al., 2010) and are beginning to be confirmed by the SDO/AIA data. In addition, Sterling et al. (2011) observed a case of flux cancellation below the filament with successive building up of the flux rope. The eruption was preceded by UV brightenings (attributed to reconnection) consistent with those described by the tether-cutting model.
Some of these models rely on the efficiency of photospheric diffusive motions to drive reconnection, but observational evidence for this process is sparse (for example, see the case shown in Section 5.1) and therefore still inconclusive. The event studied by Schmieder et al. (2008), for instance, show no evidence of reconnection or flux emergence (even though the authors cannot rule out their presence), while a decrease of the magnetic field strength in the network surrounding the structure was inferred during the rise of the filament. The authors suggested an interpretation in line with the presence of the photospheric diffusion process.
Several studies also suggest that the transportation of minor polarities (where the filaments barbs root) toward the PIL can lead to their cancellation and to magnetic destabilization (Lin et al., 2005; Gosain et al., 2009).
5.4.3 Magnetic helicity
Similar to other coronal structures, the magnetic envelope of filaments (e.g., the flux rope or sheared arcade) may present a helicity that evolves in time (see also Section 2.4.1). In particular, flux emergence and photospheric flows can change the magnetic helicity in a filament channel, trigger its instabilities, and set off the ensuing filament eruption.
An increase in helicity due to flux emergence was identified by Williams et al. (2005), who suggested that this phenomenon triggered a kink instability and the following filament eruption. Similarly, Romano et al. (2009) associated the increase of helicity in an observed filament with flux emergence. In particular they identified the filament footpoints as the location of helicity injection into the corona, which led the structure to take on a sigmoid shape and then to erupt.
The role of photospheric flow in the transport of helicity from the photosphere to the corona was investigated by Romano et al. (2005). This motion was associated with an M6.3 flare and filament eruption on 15 June 2001 in the active region NOAA 9502. They showed that, during the ‘S’ shaped filament activation phase, a horizontal counterclockwise motion at both filament footpoints was associated with an increase of magnetic helicity change rate (negative, in their case as shown in Figure 35), without any significant magnetic flux variation (contrary to their later work mentioned in the previous paragraph). In addition, an impulsive variation of the helicity change rate was observed at the beginning of the filament eruption. This was interpreted as a signature of flux cancellation or expansion in the corona caused by the flare. In this work the important role of the horizontal motion in the helicity transport is obvious.
Accumulated change of the magnetic helicity as a function of time in AR 9502 on June 2001, prior to a flare and filament eruption. t = 0 corresponds to 13:00 UT on June 14. The error bar represents the standard deviation of the signal. The vertical lines indicate the start and end of the flare. Image reproduced by permission from Romano et al. (2005), copyright by ESO.
Big Bear Solar Observatory Hα images of active region 9077 on 19 July 2000 showing the counterclockwise rotation of the filament. The TRACE 1600 Å image shows the formation of flare ribbons which form a reverse-S shape and indicate negative helicity. Image reproduced by permission from Green et al. (2007), copyright by Springer.
Flux emergence and photospheric motions are other factors that possibly trigger instabilities, as they may lead to a change of sign of the pre-existing helicity.
Evidence for these processes was presented by Su et al. (2005), who studied a ‘U’ shaped Hα filament several hours prior to its eruption. During this period they noticed an inversion in the chirality of one barb, which could have been associated with a local change of the helicity of the filament. They suggest this change could be the origin of the filament destabilization, but they could not identify the origin of the chirality change.
Another phenomenon often visible during the lift off of a filament is its rotation in a direction that appears to be correlated with the chirality of the magnetic environment. In particular, Green et al. (2007) and Rust and LaBonte (2005) found several cases that were consistent with the picture of a filament contained in a magnetic flux rope that twists as it erupts. The twist was in the same direction as the internal twist of the flux rope, indicating the conservation of the helicity.
5.5 3D reconstruction of erupting filaments
To conclude this review, it is worth mentioning the new insights on prominence eruptions and CMEs arising from the use of the 3D reconstruction of STEREO/SECCHI images (Howard et al., 2008). The STEREO mission is composed of two identical satellites. The payload includes SECCHI, a suite composed of the Extreme UltraViolet Imager (EUVI), inner (COR1) and outer (COR2) coronagraphs, and inner (HI1) and outer (HI2) heliospheric imagers. Since 2006 the two satellites have been orbiting the Sun, one ahead and one behind the Earth, allowing a stereoscopic vision of the Sun (see the cartoon in Figure 37). Here a few examples are given to show that new constraints can be obtained on the propagation direction, timing between the filament acceleration vs. CME acceleration, 3D morphology etc. Stereoscopic and tomographic methods are reviewed by Aschwanden (2011), Bemporad (2011) reviews in detail 3D prominence reconstruction techniques and presents several results, while Mierla et al. (2010) reviews 3D CME reconstruction. This new approach to the study of filaments and CME eruption will certainly provide more insights in the future.
Cartoon showing the geometry of simultaneous observation from STEREO A and B of a prominence eruption. Given the two different projected altitudes (RA and RB) and latitudes (ϕA and ϕB) of the same point P, knowing the angular distance γ between the two spacecrafts, it is possible to derive via triangulation the 3D coordinates of this point. Image reproduced by permission from Bemporad (2009), copyright by AAS.
Among the first studies on this subject, Liewer et al. (2009) and Gissot et al. (2008) independently reconstructed the 3D configuration of the asymmetric eruption analyzed by Li et al. (2008). The two studies used different stereoscopic techniques (stereoscopic tiepointing and triangulation for the former, and the Optical-Flow Algorithm for the latter), and their results were in good agreement. From these reconstructions they could estimate the direction and speed (≈ 100 km s−1) of the prominence, and establish that it was below that derived for the associated CME.
Using a 3D reconstruction, Bemporad (2009) estimated the expansion factor in three dimensions of an erupting prominence, establishing that it was non-isotropic. In addition, he pointed out that the observed structure was more similar to a 2D ribbon-like feature, without the twisted morphology and untwisting motion usually expected for an erupting flux rope. The measurement of the magnetic field of this evolving structure could confirm and complete these inferred properties.
Gosain et al. (2009) used the STEREO data to follow the evolution of an erupting filament, and establish its high inclination with respect to the solar vertical (about 43°) and its altitude (about 100 Mm) before its ejection. They also observed untwisting motion as the filament rose in the corona.
Among the new techniques developed for stereoscopic purposes we mention the recent effort by Artzner et al. (2010). Their “difference method” applied to the 304 Å EUVI filtergrams data uses differences between the images taken by the two satellites. In this way the background emission is canceled out, while the filament image is enhanced (Figure 38).
The different steps needed to obtain the difference image by Artzner et al. (2010) and isolate the prominence from the rest of the data. The top panel shows the STEREO-A (right) and STEREO-B (left) images in epipolar orientation after the raw images have been centered and re-scaled. The middle panel shows the STEREO-B image projected onto the STEREO-A view (left) and the STEREO-A view (right). The bottom panel shows the difference of the two images in the middle panel. Image reproduced by permission from Artzner et al. (2010), copyright by Springer.
The 3D reconstruction of prominence eruptions is also useful for understanding the evolving helicity of the prominence environment. The reconstruction performed by Bemporad et al. (2011) allowed the authors to clearly follow the rotational and twisting dynamics of the filament during the eruption, and to compare it with the overlying coronal arcade before and after the eruption. As found by other authors (see the previous paragraph and, e.g., Green et al., 2007), they suggested that the magnetic energy for the eruption was stored in the nonpotentiality of the magnetic environment surrounding the filament and not in the filament itself, and that during the eruption the filament followed the global dynamics of the system. This confirms most of the models in which the energy for eruption builds up throughout the whole filament channel.
6 Conclusions
This paper reviews the main properties of prominences and filaments as derived from observations. We have seen that they are inhomogeneous structures over large and small spatial and temporal scales. They have long stable periods or a short unstable life. Because the physical mechanisms that allow all these different conditions are still partially unknown, throughout this review we have pointed out several open questions. They are summarized and discussed below in view of the challenges that future investigations have to face.
6.1 3D structure
Improvements in our understanding of their 3D plasma structure could be made by processing all relevant data provided by continuous observations from ground and space. We have now several automatic detection algorithms and long-term catalogs that use these data and can provide material for complementing the limited existing statistical studies. This is a challenge, because such algorithms should be first normalized in terms of selection criteria to identify a filament among the other solar structures. However, automated detection has the advantage of being less biased than manual selection, so this approach should be able to determine whether different categories exist or the filament population is made by a gradual continuum change of morphologies.
Progress in inferring the 3D morphology has been obtained from reconstruction using the STEREO data. However only a few data sets have been processed, and most of them relate to erupting prominences. The few results are probably due to the limitations imposed by the continuous changes of the relative position of the two satellites, because reconstruction with the STEREO data is only feasible for certain configurations. The experience learned from the STEREO mission should be further used in designing future missions to obtain observations from multiple points of view.
6.2 Thermodynamic properties
-
Density. We have seen that the electron density measurements extend over a wide range of values and their uncertainties are still large. We must determine whether this result reflects the real range of variability of the parameter or depends on the data inversion methods. The uncertainties are due to the limited spatial resolution of the instruments and to the unknown emitting volume, among other causes. The uncertainties in the density values is relevant, for example, to the prominence’s plasma and magnetic pressures used in estimating the equilibrium conditions. Access to the whole prominence volume and that of its fine structure (filling factor) is a compelling goal, because it would enable an important step forward in prominence diagnostics.
-
DEM. We mentioned that the investigation of the structure of the PCTR will greatly benefit from improvements in spatial resolution of UV-EUV instruments. The inferred DEM does not yield direct spatial information on the thermal structure of the PCTR, but establishing the DEM variation (and hence the radiative losses), if any, over less than 1″ spatial scale (that is, the actual resolution of the cool threads) will give us important hints. With this better constraint to fine scale modeling, we could establish whether the PCTR surrounds each individual single thread or is a common envelope to the whole structure.
At the same time it is urgent to obtain a more complete estimate of the radiative losses over the full core-to-PCTR temperature range. The hardest part is to estimate the core component via NLTE inversion, which has not been completely achieved. Once this temperature coverage is achieved and the small spatial scales are accessible, we could investigate the physical processes at that scale: for example, spatial variations of the radiative losses over fine scales suggest local (small scale) energy dissipation.
The recently launched NASA mission, IRISFootnote 20 will contribute to filling those gaps. With its 0.3″ resolution in the UV (in contrast to 0.1″ of optical instruments) it decreases the difference between the optical (for the prominence core) and UV data (for the PCTR). Similar or better improvements are also proposed for future instruments. Nevertheless, in the near future we also must improve data diagnostics and simulations that provide observable parameters of unresolved fine structures.
-
Hot plasma in the cavity. Among the various properties of coronal cavities, the latest studies converge in suggesting that they contain hotter plasma than the prominence itself. One of the most appealing ideas is that this plasma originates under the prominences and escapes from them through magneto-thermal convection in the form of bubbles and plumes. The whole process needs to be better understood, but if confirmed, it will open completely new doors on physical processes that may influence prominence formation, dynamics, or stability. More generally, the origin of this hot plasma is not yet identified, although flux emergence and local reconnection have been suggested. If confirmed, these ideas also may contribute to our understanding of coronal heating.
-
Internal dynamics. Another open question we have encountered is about the properties of the various measured forms of plasma flows and their role in the prominence support, mass loading, and energy balance. This is particularly important in the prominence core, where most of the prominence mass is concentrated. In addition, by reducing the difference in spatial resolution between optical and EUV data (as done for only few minutes by VAULT and Hi-C), we could possibly link counter-streaming flows and EUV motions to infer the fine structure properties and the filling factor also in the PCTR. This is important in order to understand how much the PCTR flows contribute to in the whole kinetic energy budget of the prominence.
We also need to better interpret the observational inconsistency between the different flow patterns observed on disk and at the limb. In addition to what was previously mentioned on the importance of the stereoscopic observations, progress in the interpretation of the flow patterns (including resolving the full velocity vector) should be possible by co-temporal and multi-angular (on disk and at the limb) observations, to overcome line of sight and opacity effects. This could be possibly be achieved by the ground-based and SDO measurements together with the future observations of Solar Orbiter.
Finally, we need to better understand the origin of the unresolved motions measured from the non-thermal widths of EUV spectral lines: are they waves, turbulence, or superimposition of blue and red-shift motions along the line of sight? All these measurements and their interpretation should shed light on how important the plasma dynamics is to the prominence support.
In this review we have only briefly mentioned the modeling aspect of prominence investigation. However, we have pointed out the role of non-LTE modeling in inferring prominence core density, ionization state, optical depth, and element abundance, all of which are important for establishing the mass and producing synthetic spectra. As the latter are intended to be directly comparable to observations, we stress the importance of developing more sophisticated and realistic non-LTE modeling. Similarly, some models assume that the filament sits statically on a large scale magnetic structure, completely ignoring the flows which may play a role in the prominence evolution. Such important differences between modeling and observations should be overcome.
6.3 Magnetic field
-
Spatial distribution. Only direct vector magnetic-field measurements, coupled with plasma diagnostics applied to the 3D inferred morphology, will allow us to recover the full information on the spatial distribution of prominences. For example, these observations could confirm the presence of multiple dips needed by some models to solve the paradox of vertical and horizontal flow patterns. However, the magnetic field measurements and data inversion methods available at present are not able yet to give a clear picture. Limitations include the low spatial resolution of the data used for spectro-polarimetric inversion with respect to those for plasma parameter determination. In addition, the few published inferred measurements are obtained using emissions at the temperature of the cool core.
To date there are no magnetic field measurements in the PCTR. However, understanding the efficiency of the thermal conduction (which among other parameters depends on the magnetic field), is interesting as it controls the thickness of the PCTR by transporting the heating energy into the structure. In particular, the cross-field thermal conduction in typical prominence conditions is much less efficient than the field aligned component, which works along the thread, between the hot part and the cooler one. For this reason we expect a very thin PCTR in the cross-field direction.
However, few modeling works suggest that, under thermally usable conditions, cross-field thermal conduction in filaments may have a role in structuring its small scales and affecting its lifetime (e.g., van der Linden, 1993; Soler et al., 2011). More attention to this aspect would allow to better quantify its importance in the the prominence sub-structuring.
Finally, modeling studies have to make a stronger effort to address the small as well as the large scale structure at the same time, to reproduce the overall observed properties of prominence environment. Although this is a challenging goal, a model able to reproduce the richness of these details will fill significant gaps in our lack of knowledge on prominence support and stability.
-
Temporal evolution. Knowing the temporal evolution of the magnetic field will help explain filament formation, stability, and destabilization. Not only flux emergence but also the interaction with pre-existing fields are important aspects that need to be better characterized by observations. The emergence of a flux rope has been suggested in a few observations of active region areas, while the concentration of helicity in pre-existing coronal magnetic field at PILs is the best candidate process for the formation of quiescent and intermediate filament magnetic structures. A definitive affirmation of these scenarios cannot yet be given. Optimal data able to confirm these results would require continuous magnetic field measurement over several or more hours at high resolution, from the photosphere to the corona, together with multi-temperature data to access plasma flows (which provide information on the photospheric magnetic flux transport or mass injection into the filament channel) and density variations at all layers.
6.4 Connectivity between atmospheric layers
The stability of a prominence and its magnetic envelope can vary due to nearby changes of physical conditions, either in the corona or in the underlying chromosphere and photosphere. Observations reveal multiple signatures of instability, but their timings with respect to the initial rearrangement of the magnetic configuration and prominence lift off are not clear. One reason is that we lack complete mapping of the connections between the prominence, the photosphere (if any), and the corona. Barb properties derived from observations are incomplete. For example, an open debate is on the distribution of the barb’s plasma along the field, and whether or not the barb reaches the photosphere. We have inferred that the magnetic field should be weak in barbs; this makes it more difficult to measure and localize the barbs rooting points and their relation to the minor polarities identified in the photosphere. Some argue that barbs play a key role in the loss of stability. However, more comprehensive and more detailed observations of barbs should allow a more rigorous evaluation of their role in the formation, stability, and eruption of prominences.
We have seen that prominence eruptions are large scale events which are often associated with flares and CMEs. The SDO mission, in conjunction with STEREO, is suitable for their study. The AIA multi-temperature images, together with the HMI data (photospheric magnetic field and velocity maps), are probably frequent enough (about 12 s cadence) to distinguish the signatures of the filament instabilities and those of the surrounding magnetic structure. This is helping, for example, to better map the relative timing between the EUV brightenings, the lifting-off of the prominence, and the CME acceleration and would, in turn, help discriminate among the proposed CME models.
6.5 Perspectives
Some of the issues that we have discussed here will be solved only when data with specific properties are available.
One new solar space mission now in preparation is the ESA Solar Orbiter,Footnote 21 to be launched in 2017. This will be an encounter mission which will resolve about 150 km on the Sun with the UV-EUV imager. The EUV imager and EUV spectrometer will observe several hydrogen and helium lines, as well other chromospheric and coronal lines suitable for density and temperature diagnostics. As anticipated from the new IRIS mission, these cutting-edge EUV data, together with the improved temporal resolution, will reduce the discrepancies between the UV and optical spectroscopic data, and better access the prominence fine-scale morphology and thermodynamic properties. This high resolution will also be reached in the photosphere and help to clarify the dynamics of the plasma flows and their role in the magnetic flux transport as ingredients for prominence formation and instability. The localization and characterization of the minor polarities and flux emergence, as well as polarimetric measurements, will be possible with the high sensitivity instruments being developed for this mission. However, because of the limited pointing capabilities imposed by the mission profile, targeting prominences will be a challenge. The next few years will be dedicated to optimizing the scientific return of the mission.
New ground-based data will be available from the US Advanced Technology Solar Telescope (ATST)Footnote 22 and the European Solar Telescope (EST).Footnote 23 They will be optimized for the study of the photosphere-chromosphere connection with an angular resolution of ≤ 0.03″.
More diagnostic capabilities for prominences should also be obtained by the proposed Japanese Solar-C mission, for which sub-arcsec spectroscopic and imaging UV-EUV instruments are under consideration.
Notes
H = ∫ A · B dV, where A is the vector potential and B the magnetic field.
The cloud model (Tziotziou, 2007, and references therein) is based on the estimate of the contrast between the incoming and outgoing radiation inside the filament.
References
Aboudarham, J., Scholl, I., Fuller, N., Fouesneau, M., Galametz, M., Gonon, F., Maire, A. and Leroy, Y., 2008, “Automatic detection and tracking of filaments for a solar feature database”, Ann. Geophys., 26, 243–248. [DOI], [ADS]. (Cited on page 5.)
Ahn, K., Chae, J., Cao, W. and Goode, P.R., 2010, “Patterns of Flows in an Intermediate Prominence Observed by Hinode”, Astrophys. J., 721, 74–79. [DOI], [ADS]. (Cited on page 44.)
Al-Omari, M., Qahwaji, R., Colak, T. and Ipson, S., 2010, “Machine Leaning-Based Investigation of the Associations between CMEs and Filaments”, Solar Phys., 262, 511–539. [DOI], [ADS]. (Cited on page 54.)
Alexander, C.E., Walsh, R.W., Régnier, S. et al., 2013, “Anti-parallel EUV Flows Observed along Active Region Filament Threads with Hi-C”, Astrophys. J. Lett., 775, L32. [DOI], [ADS], [arXiv:1306.5194 [astro-ph.SR]]. (Cited on pages 42 and 44.)
Alexander, D., Liu, R. and Gilbert, H.R., 2006, “Hard X-Ray Production in a Failed Filament Eruption”, Astrophys. J., 653, 719–724. [DOI], [ADS]. (Cited on page 59.)
Amari, T., Luciani, J.F., Mikić, Z. and Linker, J., 2000, “A Twisted Flux Rope Model for Coronal Mass Ejections and Two-Ribbon Flares”, Astrophys. J. Lett., 529, L49–L52. [DOI], [ADS]. (Cited on page 46.)
Amari, T., Luciani, J.F., Aly, J.J., Mikić, Z. and Linker, J., 2003a, “Coronal Mass Ejection: Initiation, Magnetic Helicity, and Flux Ropes. I. Boundary Motion-driven Evolution”, Astrophys. J., 585, 1073–1086. [DOI], [ADS]. (Cited on page 55.)
Amari, T., Luciani, J.F., Aly, J.J., Mikić, Z. and Linker, J., 2003b, “Coronal Mass Ejection: Initiation, Magnetic Helicity, and Flux Ropes. II. Turbulent Diffusion-driven Evolution”, Astrophys. J., 595, 1231–1250. [DOI], [ADS]. (Cited on page 9.)
Amari, T., Aly, J.-J., Mikić, Z. and Linker, J., 2010, “Coronal Mass Ejection Initiation: On the Nature of the Flux Cancellation Model”, Astrophys. J. Lett., 717, L26–L30. [DOI], [ADS], [arXiv:1005.4669 [astro-ph.SR]]. (Cited on pages 46 and 61.)
Antiochos, S.K., 1998, “The Magnetic Topology of Solar Eruptions”, Astrophys. J. Lett., 502, L181–L184. [DOI], [ADS], [arXiv:astro-ph/9806030]. (Cited on page 56.)
Antiochos, S.K. and Klimchuk, J.A., 1991, “A model for the formation of solar prominences”, Astrophys. J., 378, 372–377. [DOI], [ADS]. (Cited on pages 27 and 41.)
Antiochos, S.K., Dahlburg, R.B. and Klimchuk, J.A., 1994, “The magnetic field of solar prominences”, Astrophys. J. Lett., 420, L41–L44. [DOI], [ADS]. (Cited on page 46.)
Anzer, U. and Heinzel, P., 2005, “On the Nature of Dark Extreme Ultraviolet Structures Seen by SOHO/EIT and TRACE”, Astrophys. J., 622, 714–721. [DOI], [ADS]. (Cited on page 19.)
Anzer, U. and Heinzel, P., 2007, “Is the magnetic field in quiescent prominences force-free?”, Astron. Astrophys., 467, 1285–1288. [DOI], [ADS]. (Cited on pages 28 and 33.)
Apushkinskij, G.P., Nesterov, N.S., Topchilo, N.A. and Tsyganov, A.N., 1990, “Polarization of a Prominence Observed with the RT-22 Radio Telescope”, Sov. Astron., 34, 530. [ADS]. (Cited on page 33.)
Apushkinskij, G.P., Topchilo, N.A., Tsyganov, A.N. and Nesterov, N.S., 1996, “Magnetic field of solar prominences: the procedure of radio observations”, Astron. Nachr., 317, 417. [ADS]. (Cited on page 33.)
Arregui, I., Oliver, R. and Ballester, J.L., 2012, “Prominence Oscillations”, Living Rev. Solar Phys., 9, lrsp-2012-2. [DOI], [ADS]. URL (accessed 30 January 2013): http://www.livingreviews.org/lrsp-2012-2. (Cited on page 41.)
Artzner, G., Gosain, S. and Schmieder, B., 2010, “A Technique for Removing Background Features in SECCHI-EUVI He II 304 Å Filtergrams: Application to the Filament Eruption of 22 May 2008”, Solar Phys., 262, 437–447. [DOI], [ADS], [arXiv:1001.4884 [astro-ph.SR]]. (Cited on pages 64 and 65.)
Aschwanden, M.J., 2011, “Solar Stereoscopy and Tomography”, Living Rev. Solar Phys., 8, lrsp-2011-5. [DOI], [ADS]. (Cited on page 62.)
Aschwanden, M.J., Wülser, J.P., Nitta, N.V. and Lemen, J.R., 2009, “Solar Flare and CME Observations with STEREO/EUVI”, Solar Phys., 256, 3–40. [DOI], [ADS]. (Cited on page 54.)
Aulanier, G. and Schmieder, B., 2002, “The magnetic nature of wide EUV filament channels and their role in the mass loading of CMEs”, Astron. Astrophys., 386, 1106–1122. [DOI], [ADS]. (Cited on page 48.)
Aulanier, G., Török, T., Démoulin, P. and DeLuca, E.E., 2010, “Formation of Torus-Unstable Flux Ropes and Electric Currents in Erupting Sigmoids”, Astrophys. J., 708, 314–333. [DOI], [ADS]. (Cited on page 50.)
Banerjee, D., Erdélyi, R., Oliver, R. and O’Shea, E., 2007, “Present and Future Observing Trends in Atmospheric Magnetoseismology”, Solar Phys., 246, 3–29. [DOI], [ADS]. (Cited on page 41.)
Barocas, V., 1939, “Prominences and the Sunspot Cycle”, Astrophys. J., 89, 486. [DOI], [ADS]. (Cited on page 9.)
Bemporad, A., 2009, “Stereoscopic Reconstruction from STEREO/EUV Imagers Data of the Three-dimensional Shape and Expansion of an Erupting Prominence”, Astrophys. J., 701, 298–305. [DOI], [ADS]. (Cited on pages 50 and 64.)
Bemporad, A., 2011, “Prominence 3D reconstruction in the STEREO era: A review”, J. Atmos. Sol.-Terr. Phys., 73, 1117–1128. [DOI], [ADS]. (Cited on page 62.)
Bemporad, A., Sterling, A.C., Moore, R.L. and Poletto, G., 2005, “A New Variety of Coronal Mass Ejection: Streamer Puffs from Compact Ejective Flares”, Astrophys. J. Lett., 635, L189–L192. [DOI], [ADS]. (Cited on page 58.)
Bemporad, A., Mierla, M. and Tripathi, D., 2011, “Rotation of an erupting filament observed by the STEREO EUVI and COR1 instruments”, Astron. Astrophys., 531, A147. [DOI], [ADS]. (Cited on page 64.)
Benz, A.O., 2008, “Flare Observations”, Living Rev. Solar Phys., 5, lrsp-2008-1. [DOI], [ADS]. URL (accessed 30 January 2013): http://www.livingreviews.org/lrsp-2008-1. (Cited on pages 9 and 50.)
Berger, M.A., 1984, “Rigorous new limits on magnetic helicity dissipation in the solar corona”, Geophys. Astrophys. Fluid Dyn., 30, 79–104. [DOI], [ADS]. (Cited on page 60.)
Berger, T.E., Shine, R.A., Slater, G.L. et al., 2008, “Hinode SOT Observations of Solar Quiescent Prominence Dynamics”, Astrophys. J. Lett., 676, L89–L92. [DOI], [ADS]. (Cited on pages 27, 39, 40, and 41.)
Berger, T.E., Slater, G., Hurlburt, N. et al., 2010, “Quiescent Prominence Dynamics Observed with the Hinode Solar Optical Telescope. I. Turbulent Upflow Plumes”, Astrophys. J., 716, 1288–1307. [DOI], [ADS]. (Cited on pages 27 and 40.)
Berger, T.E., Testa, P., Hillier, A. et al., 2011, “Magneto-thermal convection in solar prominences”, Nature, 472, 197–200. [DOI], [ADS]. (Cited on pages 27 and 40.)
Berger, T.E., Liu, W. and Low, B.C., 2012, “SDO/AIA Detection of Solar Prominence Formation within a Coronal Cavity”, Astrophys. J. Lett., 758, L37. [DOI], [ADS], [arXiv:1208.3431 [astro-ph.SR]]. (Cited on page 28.)
Bernasconi, P.N., Rust, D.M. and Hakim, D., 2005, “Advanced Automated Solar Filament Detection and Characterization Code: Description, Performance, and Results”, Solar Phys., 228, 97–117. [DOI], [ADS]. (Cited on page 5.)
Bocchino, G., 1933, “Migrazione delle protuberanze durante il ciclo undecennale dell’ attività solare”, Osserv. Mem. Oss. Astrofis. Arcetri, 51, 5–47. [ADS]. (Cited on page 9.)
Bommier, V., Landi Degl’Innocenti, E., Leroy, J.-L. and Sahal-Bréchot, S., 1994, “Complete determination of the magnetic field vector and of the electron density in 14 prominences from linear polarization measurements in the HeI D3 and Hα lines”, Solar Phys., 154, 231–260. [DOI], [ADS]. (Cited on pages 31 and 34.)
Bone, L.A., van Driel-Gesztelyi, L., Culhane, J.L., Aulanier, G. and Liewer, P., 2009, “Formation, Interaction and Merger of an Active Region and a Quiescent Filament Prior to Their Eruption on 19 May 2007”, Solar Phys., 259, 31–47. [DOI], [ADS]. (Cited on pages 46 and 52.)
Buchlin, É., Mercier, C., Engin, S., Parenti, S. and Vial, J.-C., 2010, “Automated detection of filaments in SDO data”, in SF2A-2010, Proceedings of the annual meeting of the French Society of Astronomy and Astrophysics, 21–24 June 2010, Marseille, (Eds.) Boissier, S., Heydari-Malayeri, M., Samadi, R., Valls-Gabaud, D., pp. 297–298, SF2A, France. [ADS]. (Cited on page 5.)
Casini, R., López Ariste, A., Tomczyk, S. and Lites, B.W., 2003, “Magnetic Maps of Prominences from Full Stokes Analysis of the He I D3 Line”, Astrophys. J. Lett., 598, L67–L70. [DOI], [ADS]. (Cited on page 33.)
Casini, R., Bevilacqua, R. and López Ariste, A., 2005, “Principal Component Analysis of the He I D3 Polarization Profiles from Solar Prominences”, Astrophys. J., 622, 1265–1274. [DOI], [ADS]. (Cited on page 33.)
Casini, R., López Ariste, A., Paletou, F. and Léger, L., 2009, “Multi-Line Stokes Inversion for Prominence Magnetic-Field Diagnostics”, Astrophys. J., 703, 114–120. [DOI], [ADS], [arXiv:0906.2144]. (Cited on page 32.)
Chae, J., 2000, “The Magnetic Helicity Sign of Filament Chirality”, Astrophys. J. Lett., 540, L115–L118. [DOI], [ADS]. (Cited on pages 30 and 31.)
Chae, J., 2007, “Measurements of magnetic helicity injected through the solar photosphere”, Adv. Space Res., 39, 1700–1705. [DOI], [ADS]. (Cited on pages 38 and 44.)
Chae, J., 2010, “Dynamics of Vertical Threads and Descending Knots in a Hedgerow Prominence”, Astrophys. J., 714, 618–629. [DOI], [ADS]. (Cited on pages 39, 44, and 45.)
Chae, J., Moon, Y.-J. and Park, Y.-D., 2005, “The Magnetic Structure of Filament Barbs”, Astrophys. J., 626, 574–578. [DOI], [ADS]. (Cited on page 38.)
Chae, J., Ahn, K., Lim, E.-K., Choe, G.S. and Sakurai, T., 2008, “Persistent Horizontal Flows and Magnetic Support of Vertical Threads in a Quiescent Prominence”, Astrophys. J. Lett., 689, L73–L76. [DOI], [ADS]. (Cited on pages 39 and 44.)
Chen, P.F., 2011, “Coronal Mass Ejections: Models and Their Observational Basis”, Living Rev. Solar Phys., 8, lrsp-2011-1. [DOI], [ADS]. URL (accessed 30 January 2013): http://www.livingreviews.org/lrsp-2011-1. (Cited on pages 9 and 56.)
Chen, P.F. and Shibata, K., 2000, “An Emerging Flux Trigger Mechanism for Coronal Mass Ejections”, Astrophys. J., 545, 524–531. [DOI], [ADS]. (Cited on page 60.)
Chen, P.F., Innes, D.E. and Solanki, S.K., 2008, “SOHO/SUMER observations of prominence oscillation before eruption”, Astron. Astrophys., 484, 487–493. [DOI], [ADS], [arXiv:0802.1961]. (Cited on pages 52 and 53.)
Chiuderi Drago, F., 1990, “Radio observations of prominences”, in Dynamics of Quiescent Prominences, Proceedings of IAU Colloquium 117, held in Hvar, SR Croatia, Yugoslavia 1989, (Eds.) Ruždjak, V., Tandberg-Hanssen, E., Lecture Notes in Physics, 363, pp. 70–83, Springer, Berlin. [ADS]. (Cited on page 11.)
Ciaravella, A., Raymond, J.C., Thompson, B.J. et al., 2000, “Solar and Heliospheric Observatory Observations of a Helical Coronal Mass Ejection”, Astrophys. J., 529, 575–591. [DOI], [ADS]. (Cited on page 27.)
Cirigliano, D., Vial, J.-C. and Rovira, M., 2004, “Prominence-corona transition region plasma diagnostics from SOHO observations”, Solar Phys., 223, 95–118. [DOI], [ADS]. (Cited on page 45.)
Cirtain, J.W., Golub, L., Winebarger, A.R. et al., 2013, “Energy release in the solar corona from spatially resolved magnetic braids”, Nature, 493, 501–503. [DOI], [ADS]. (Cited on page 42.)
Culhane, J.L., Harra, L.K., James, A.M. et al., 2007, “The EUV Imaging Spectrometer for Hinode”, Solar Phys., 243, 19–61. [DOI]. (Cited on page 11.)
Curdt, W. and Tian, H., 2010, “Hydrogen Lyman Emission through the Solar Cycle”, in SOHO-23: Understanding a Peculiar Solar Minimum, Northeast Harbor, Maine, USA, 21–25 September 2009, (Eds.) Cranmer, S.R., Hoeksema, J.T., Kohl, J.L., ASP Conference Series, 428, p. 81, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:1002.3551]. (Cited on page 10.)
Del Zanna, G., Chiuderi Drago, F. and Parenti, S., 2004, “SOHO CDS and SUMER observations of quiescent filaments and their interpretation”, Astron. Astrophys., 420, 307–317. [DOI], [ADS]. (Cited on pages 11 and 18.)
Démoulin, P., 1998, “Magnetic Fields in Filaments”, in New Perspectives on Solar Prominences, Proceedings of IAU Colloquium 167, held in Aussois, France, 28 April–4 May 1997, (Eds.) Webb, D.F., Schmieder, B., Rust, D.M., ASP Conference Series, 150, pp. 78–85, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on pages 33, 34, and 35.)
Démoulin, P. and Priest, E.R., 1989, “How to Form a Dip in a Magnetic Field Before the Formation of a Solar Prominence”, Hvar Obs. Bull., 13, 261. [ADS]. (Cited on page 55.)
DeVore, C.R. and Antiochos, S.K., 2000, “Dynamical Formation and Stability of Helical Prominence Magnetic Fields”, Astrophys. J., 539, 954–963. [DOI], [ADS]. (Cited on pages 9 and 46.)
DeVore, C.R. and Antiochos, S.K., 2008, “Homologous Confined Filament Eruptions via Magnetic Breakout”, Astrophys. J., 680, 740–756. [DOI], [ADS]. (Cited on page 56.)
Ebadi, H., Vial, J.-C. and Ajabshirizadeh, A., 2009, “The He II Lines in the Lyman Series Profiles of Solar Prominences”, Solar Phys., 257, 91–98. [DOI], [ADS]. (Cited on page 10.)
Engvold, O., 1976, “The fine structure of prominences. I: Observations — Hα filtergrams”, Solar Phys., 49, 283–295. [DOI], [ADS]. (Cited on page 37.)
Engvold, O., 1980, “Thermodynamic models and fine structure of prominences”, Solar Phys., 67, 351–355. [DOI], [ADS]. (Cited on page 45.)
Engvold, O., 1981, “The small scale velocity field of a quiescent prominence”, Solar Phys., 70, 315–324. [DOI], [ADS]. (Cited on page 37.)
Engvold, O., 1989, “Prominence environment”, in Dynamics and Structure of Quiescent Solar Prominences, Proceedings of the Workshop, Palma de Mallorca, Spain, November 1987, (Ed.) Priest, E.R., Astrophysics and Space Science Library, 150, pp. 47–76, Kluwer Academic, Dordrecht. [ADS], [Google Books]. (Cited on page 37.)
Engvold, O., Hansteen, V., Kjeldseth-Moe, O. and Brueckner, G.E., 1990a, “A UV spectral atlas of a prominence”, Astrophys. Space Sci., 170, 179–183. [DOI], [ADS]. (Cited on page 21.)
Engvold, O., Hirayama, T., Leroy, J.L., Priest, E.R. and Tandberg-Hanssen, E., 1990b, “Hvar Reference Atmosphere of Quiescent Prominences”, in Dynamics of Quiescent Prominences, Proceedings of IAU Colloquium 117, held in Hvar, SR Croatia, Yugoslavia 1989, (Eds.) Ruždjak, V., Tandberg-Hanssen, E., Lecture Notes in Physics, 363, p. 294, Springer, Berlin; New York. [DOI], [ADS]. (Cited on page 18.)
Engvold, O., Jakobsson, H., Tandberg-Hanssen, E., Gurman, J.B. and Moses, D., 2001, “On the Nature of Prominence Absorption and Emission in Highly Ionized Iron and in Neutral Hydrogen”, Solar Phys., 202, 293–308. [DOI], [ADS]. (Cited on page 50.)
Fan, Y. and Gibson, S.E., 2003, “The Emergence of a Twisted Magnetic Flux Tube into a Preexisting Coronal Arcade”, Astrophys. J. Lett., 589, L105–L108. [DOI], [ADS]. (Cited on page 55.)
Fan, Y. and Gibson, S.E., 2006, “On the Nature of the X-Ray Bright Core in a Stable Filament Channel”, Astrophys. J. Lett., 641, L149–L152. [DOI], [ADS]. (Cited on page 28.)
Feldman, U., 1992, “Elemental abundances in the upper solar atmosphere”, Phys. Scripta, 46, 202–220. [DOI], [ADS]. (Cited on page 18.)
Feynman, J. and Martin, S.F., 1995, “The initiation of coronal mass ejections by newly emerging magnetic flux”, J. Geophys. Res., 100, 3355–3367. [DOI], [ADS]. (Cited on pages 41 and 60.)
Forbes, T.G., 2000, “A review on the genesis of coronal mass ejections”, J. Geophys. Res., 105, 23, 153–23, 166. [DOI], [ADS]. (Cited on page 56.)
Forbes, T.G. and Lin, J., 2000, “What can we learn about reconnection from coronal mass ejections?”, J. Atmos. Sol.-Terr. Phys., 62, 1499–1507. [DOI], [ADS]. (Cited on page 58.)
Forbes, T.G., Linker, J.A., Chen, J. et al., 2006, “CME Theory and Models”, Space Sci. Rev., 123, 251–302. [DOI], [ADS]. (Cited on page 56.)
Foukal, P.V., 2004, Solar Astrophysics, Wiley-VCH, Weinheim, 2nd rev. edn. [ADS], [Google Books]. (Cited on page 9.)
Fuller, J. and Gibson, S.E., 2009, “A Survey of Coronal Cavity Density Profiles”, Astrophys. J., 700, 1205–1215. [DOI], [ADS]. (Cited on pages 24 and 25.)
Fuller, J., Gibson, S.E., de Toma, G. and Fan, Y., 2008, “Observing the Unobservable? Modeling Coronal Cavity Densities”, Astrophys. J., 678, 515–530. [DOI], [ADS]. (Cited on pages 25 and 28.)
Gaizauskas, V., Zirker, J.B., Sweetland, C. and Kovacs, A., 1997, “Formation of a Solar Filament Channel”, Astrophys. J., 479, 448–457. [DOI], [ADS]. (Cited on page 47.)
Gibson, S.E. and Fan, Y., 2006, “The Partial Expulsion of a Magnetic Flux Rope”, Astrophys. J. Lett., 637, L65–L68. [DOI], [ADS]. (Cited on pages 56 and 61.)
Gibson, S.E., Foster, D., Burkepile, J., de Toma, G. and Stanger, A., 2006, “The Calm before the Storm: The Link between Quiescent Cavities and Coronal Mass Ejections”, Astrophys. J., 641, 590–605. [DOI], [ADS]. (Cited on page 24.)
Gibson, S.E., Kucera, T.A., Rastawicki, D. et al., 2010, “Three-dimensional Morphology of a Coronal Prominence Cavity”, Astrophys. J., 724, 1133–1146. [DOI], [ADS]. (Cited on pages 24, 25, and 27.)
Gilbert, H.R., Holzer, T.E., Burkepile, J.T. and Hundhausen, A.J., 2000, “Active and Eruptive Prominences and Their Relationship to Coronal Mass Ejections”, Astrophys. J., 537, 503–515. [DOI], [ADS]. (Cited on pages 50, 54, and 56.)
Gilbert, H.R., Holzer, T.E. and Burkepile, J.T., 2001, “Observational Interpretation of an Active Prominence on 1999 May 1”, Astrophys. J., 549, 1221–1230. [DOI], [ADS]. (Cited on page 9.)
Gissot, S.F., Hochedez, J.-F., Chainais, P. and Antoine, J.-P., 2008, “3D Reconstruction from SECCHI-EUVI Images Using an Optical-Flow Algorithm: Method Description and Observation of an Erupting Filament”, Solar Phys., 252, 397–408. [DOI], [ADS]. (Cited on page 62.)
Golubchina, O.A., Bogod, V.M., Korzhavin, A.N., Bursov, N.N. and Tokhchukova, S.K., 2008, “Centimeter-wave radio emission of a high-latitude prominence”, Astrophys. Bull., 63, 34–42. [DOI], [ADS]. (Cited on page 33.)
Gopalswamy, N., Hanaoka, Y. and Hudson, H.S., 2000, “Structure and Dynamics of the Corona Surrounding an Eruptive Prominence”, Adv. Space Res., 25, 1851–1854. [DOI], [ADS]. (Cited on page 58.)
Gopalswamy, N., Shimojo, M., Lu, W., Yashiro, S., Shibasaki, K. and Howard, R.A., 2003, “Prominence Eruptions and Coronal Mass Ejection: A Statistical Study Using Microwave Observations”, Astrophys. J., 586, 562–578. [DOI], [ADS]. (Cited on page 54.)
Gopalswamy, N., Mikić, Z., Maia, D., Alexander, D., Cremades, H., Kaufmann, P., Tripathi, D. and Wang, Y.-M., 2006, “The Pre-CME Sun”, Space Sci. Rev., 123, 303–339. [DOI], [ADS]. (Cited on page 52.)
Gosain, S., Schmieder, B., Venkatakrishnan, P., Chandra, R. and Artzner, G., 2009, “3D Evolution of a Filament Disappearance Event Observed by STEREO”, Solar Phys., 259, 13–30. [DOI], [ADS], [arXiv:0910.0786]. (Cited on pages 51, 54, 61, and 64.)
Gouttebroze, P., Heinzel, P. and Vial, J.-C., 1993, “The hydrogen spectrum of model prominences”, Astron. Astrophys. Suppl., 99, 513–543. [ADS]. (Cited on pages 17 and 18.)
Green, L.M. and Kliem, B., 2009, “Flux Rope Formation Preceding Coronal Mass Ejection Onset”, Astrophys. J. Lett., 700, L83–L87. [DOI], [ADS], [arXiv:0906.4794 [astro-ph.SR]]. (Cited on page 61.)
Green, L.M., Kliem, B., Töoröok, T., van Driel-Gesztelyi, L. and Attrill, G.D.R., 2007, “Transient Coronal Sigmoids and Rotating Erupting Flux Ropes”, Solar Phys., 246, 365–391. [DOI], [ADS]. (Cited on pages 62, 63, and 64.)
Green, L.M., Kliem, B. and Wallace, A.J., 2011, “Photospheric flux cancellation and associated flux rope formation and eruption”, Astron. Astrophys., 526, A2. [DOI], [ADS], [arXiv:1011.1227 [astro-ph.SR]]. (Cited on page 61.)
Grigis, P.C. and Benz, A.O., 2005, “The Evolution of Reconnection along an Arcade of Magnetic Loops”, Astrophys. J. Lett., 625, L143–L146. [DOI], [ADS], [arXiv:astro-ph/0504436]. (Cited on page 57.)
Gunár, S., Parenti, S., Anzer, U., Heinzel, P. and Vial, J.-C., 2011, “Synthetic differential emission measure curves of prominence fine structures: II. The SoHO/SUMER prominence of 8 June 2004”, Astron. Astrophys., 535, A122. [DOI], [ADS]. (Cited on pages 21, 23, and 44.)
Habbal, S.R., Druckmüller, M., Morgan, H., Scholl, I., Rušin, V., Daw, A., Johnson, J. and Arndt, M., 2010, “Total Solar Eclipse Observations of Hot Prominence Shrouds”, Astrophys. J., 719, 1362–1369. [DOI], [ADS]. (Cited on pages 25, 26, and 27.)
Handy, B.N., Acton, L.W., Kankelborg, C.C. et al., 1999, “The transition region and coronal explorer”, Solar Phys., 187, 229–260. [DOI], [ADS]. (Cited on page 10.)
Harrison, R.A., Sawyer, E.C., Carter, M.K. et al., 1995, “The Coronal Diagnostic Spectrometer for the Solar and Heliospheric Observatory”, Solar Phys., 162, 233–290. [DOI], [ADS]. (Cited on page 11.)
Heinzel, P. and Anzer, U., 2001, “Prominence fine structures in a magnetic equilibrium: Two-dimensional models with multilevel radiative transfer”, Astron. Astrophys., 375, 1082–1090. [DOI], [ADS]. (Cited on pages 11 and 44.)
Heinzel, P. and Anzer, U., 2006, “On the Fine Structure of Solar Filaments”, Astrophys. J. Lett., 643, L65–L68. [DOI], [ADS]. (Cited on page 44.)
Heinzel, P., Schmieder, B. and Tziotziou, K., 2001, “Why Are Solar Filaments More Extended in Extreme-Ultraviolet Lines than in Hα?”, Astrophys. J. Lett., 561, L223–L227. [DOI], [ADS]. (Cited on page 18.)
Heinzel, P., Anzer, U., Schmieder, B. and Schwartz, P., 2003, “EUV-filaments and their mass loading”, in Solar Variability as an Input to the Earth’s Environment, Proceedings of ISCS 2003, 23–28 June 2003, Tatranská Lomnica, Slovak Republic, (Ed.) Wilson, A., ESA Special Publication, SP-535, pp. 447–457, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 18.)
Heinzel, P., Anzer, U. and Gunár, S., 2005, “Prominence fine structures in a magnetic equilibrium. II. A grid of two-dimensional models”, Astron. Astrophys., 442, 331–343. [DOI], [ADS]. (Cited on page 44.)
Heinzel, P., Schmieder, B., Fárník, F. et al., 2008, “Hinode, TRACE, SOHO, and Ground-based Observations of a Quiescent Prominence”, Astrophys. J., 686, 1383–1396. [DOI], [ADS]. (Cited on page 19.)
Hillier, A., Isobe, H., Shibata, K. and Berger, T., 2011, “Numerical Simulations of the Magnetic Rayleigh-Taylor Instability in the Kippenhahn-Schlüter Prominence Model”, Astrophys. J. Lett., 736, L1. [DOI], [ADS], [arXiv:1107.4882 [astro-ph.HE]]. (Cited on page 45.)
Hillier, A., Berger, T., Isobe, H. and Shibata, K., 2012a, “Numerical Simulations of the Magnetic Rayleigh-Taylor Instability in the Kippenhahn-Schlüter Prominence Model. I. Formation of Upflows”, Astrophys. J., 746, 120. [DOI], [ADS]. (Cited on page 40.)
Hillier, A., Isobe, H., Shibata, K. and Berger, T., 2012b, “Numerical Simulations of the Magnetic Rayleigh-Taylor Instability in the Kippenhahn-Schlüter Prominence Model. II. Reconnection-triggered Down-flows”, Astrophys. J., 756, 110. [DOI], [ADS], [arXiv:1106.2613 [astro-ph.SR]]. (Cited on pages 40 and 45.)
Hori, K. and Culhane, J.L., 2002, “Trajectories of microwave prominence eruptions”, Astron. Astrophys., 382, 666–677. [DOI], [ADS]. (Cited on page 54.)
House, L.L. and Berger, M.A., 1987, “The ejection of helical field structures through the outer corona”, Astrophys. J., 323, 406–413. [DOI], [ADS]. (Cited on page 60.)
Howard, R.A., Moses, J.D., Vourlidas, A. et al., 2008, “Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI)”, Space Sci. Rev., 136, 67–115. [DOI], [ADS]. (Cited on page 62.)
Hudson, H. and Schwenn, R., 2000, “Hot Cores in Coronal Filament Cavities”, Adv. Space Res., 25, 1859–1861. [DOI], [ADS]. (Cited on page 25.)
Hudson, H.S., Acton, L.W., Harvey, K.L. and McKenzie, D.E., 1999, “A Stable Filament Cavity with a Hot Core”, Astrophys. J. Lett., 513, L83–L86. [DOI], [ADS]. (Cited on pages 25 and 27.)
Hudson, H.S., Bougeret, J.-L. and Burkepile, J., 2006, “Coronal Mass Ejections: Overview of Observations”, Space Sci. Rev., 123, 13–30. [DOI], [ADS]. (Cited on page 8.)
Hundhausen, A.J., 1999, “Coronal Mass Ejections”, in The Many Faces of the Sun: A Summary of the Results from NASA’s Solar Maximum Mission, (Eds.) Strong, K.T., Saba, J.L.R., Haisch, B.M., Schmelz, J.T., p. 143, Springer, New York. [ADS]. (Cited on page 55.)
Isobe, H. and Tripathi, D., 2006, “Large amplitude oscillation of a polar crown filament in the pre-eruption phase”, Astron. Astrophys., 449, L17–L20. [DOI], [ADS], [arXiv:astro-ph/0602432]. (Cited on page 52.)
Janssen, M., 1869, “The Total Solar Eclipse of August 1868. Part II.”, Astron. Reg., 7, 131–133. [ADS]. (Cited on page 9.)
Jiang, Y., Yang, J., Zheng, R., Bi, Y. and Yang, X., 2009, “A Narrow Streamer-Puff Coronal Mass Ejection from the Nonradial Eruption of an Active-Region Filament”, Astrophys. J., 693, 1851–1858. [DOI], [ADS]. (Cited on page 58.)
Jing, J., Lee, J., Spirock, T.J., Xu, Y., Wang, H. and Choe, G.S., 2003, “Periodic Motion along a Solar Filament Initiated by a Subflare”, Astrophys. J. Lett., 584, L103–L106. [DOI], [ADS]. (Cited on page 41.)
Jing, J., Lee, J., Spirock, T.J. and Wang, H., 2006, “Periodic Motion Along Solar Filaments”, Solar Phys., 236, 97–109. [DOI], [ADS]. (Cited on page 41.)
Joshi, A.D., Srivastava, N. and Mathew, S.K., 2010, “Automated Detection of Filaments and Their Disappearance Using Full-Disc Hα Images”, Solar Phys., 262, 425–436. [DOI], [ADS], [arXiv:0905.3055 [astro-ph.SR]]. (Cited on page 5.)
Karpen, J.T. and Antiochos, S.K., 2008, “Condensation Formation by Impulsive Heating in Prominences”, Astrophys. J., 676, 658–671. [DOI], [ADS]. (Cited on page 44.)
Karpen, J.T., Antiochos, S.K., Klimchuk, J.A. and MacNeice, P.J., 2003, “Constraints on the Magnetic Field Geometry in Prominences”, Astrophys. J., 593, 1187–1194. [DOI], [ADS]. (Cited on page 36.)
Karpen, J.T., Antiochos, S.K. and DeVore, C.R., 2012, “The Mechanisms for the Onset and Explosive Eruption of Coronal Mass Ejections and Eruptive Flares”, Astrophys. J., 760, 81. [DOI], [ADS]. (Cited on pages 56 and 57.)
Kim, I.S., 1990, “Prominence magnetic field observations”, in Dynamics of Quiescent Prominences, Proceedings of IAU Colloquium 117, held in Hvar, SR Croatia, Yugoslavia 1989, (Eds.) Ruždjak, V., Tandberg-Hanssen, E., Lecture Notes in Physics, 363, pp. 49–69, Springer, Berlin; New York. [DOI], [ADS]. (Cited on page 31.)
Kippenhahn, R. and Schlüter, A., 1957, “Eine Theorie der solaren Filamente”, Z. Astrophys., 43, 36–62. [ADS]. (Cited on page 7.)
Korendyke, C.M., Vourlidas, A., Cook, J.W. et al., 2001, “High-resolution Imaging of the Upper Solar Chromosphere: First Light Performance of the Very-high-Resolution Advanced ULtraviolet Telescope”, Solar Phys., 200, 63–73. [DOI], [ADS]. (Cited on page 10.)
Kucera, T.A. and Landi, E., 2006, “Ultraviolet Observations of Prominence Activation and Cool Loop Dynamics”, Astrophys. J., 645, 1525–1536. [DOI]. (Cited on pages 21 and 22.)
Kucera, T.A. and Landi, E., 2008, “An Observation of Low-Level Heating in an Erupting Prominence”, Astrophys. J., 673, 611–620. [DOI], [ADS]. (Cited on pages 21 and 50.)
Kucera, T.A., Gibson, S.E., Schmit, D.J., Landi, E. and Tripathi, D., 2012, “Temperature and Extreme-ultraviolet Intensity in a Coronal Prominence Cavity and Streamer”, Astrophys. J., 757, 73. [DOI], [ADS]. (Cited on page 25.)
Kuckein, C., Centeno, R., Martínez Pillet, V., Casini, R., Manso Sainz, R. and Shimizu, T., 2009, “Magnetic field strength of active region filaments”, Astron. Astrophys., 501, 1113–1121. [DOI], [ADS], [arXiv:0904.4876]. (Cited on page 33.)
Kunow, H., Crooker, N.U., Linker, J.A., R., Schwenn and von Steiger, R. (Eds.), 2006, Coronal Mass Ejections, Space Sci. Rev. (Special Issue), 123, Springer, Dordrecht. [DOI], [ADS]. (Cited on page 9.)
Labrosse, N. and Gouttebroze, P., 2004, “Non-LTE Radiative Transfer in Model Prominences. I. Integrated Intensities of He I Triplet Lines”, Astrophys. J., 617, 614–622. [DOI], [ADS]. (Cited on page 32.)
Labrosse, N., Dalla, S. and Marshall, S., 2010a, “Automatic Detection of Limb Prominences in 304 Å EUV Images”, Solar Phys., 262, 449–460. [DOI], [ADS], [arXiv:0912.1099 [astro-ph.SR]]. (Cited on page 5.)
Labrosse, N., Heinzel, P., Vial, J.-C., Kucera, T., Parenti, S., Gunár, S., Schmieder, B. and Kilper, G., 2010b, “Physics of Solar Prominences: I — Spectral Diagnostics and Non-LTE Modelling”, Space Sci. Rev., 151, 243–332. [DOI], [ADS], [arXiv:1001.1620]. (Cited on pages 6, 17, 18, 19, 22, 37, 42, and 44.)
Landi Degl’Innocenti, E., Bommier, V. and Sahal-Brechot, S., 1987, “Linear polarization of hydrogen Balmer lines in optically thick quiescent prominences”, Astron. Astrophys., 186, 335–353. [ADS]. (Cited on page 31.)
Léger, L. and Paletou, F., 2009, “2D non-LTE radiative modelling of He I spectral lines formed in solar prominences”, Astron. Astrophys., 498, 869–875. [DOI], [ADS], [arXiv:0811.4753]. (Cited on page 32.)
Leroy, J.L., Bommier, V. and Sahal-Brechot, S., 1983, “The magnetic field in the prominences of the polar crown”, Solar Phys., 83, 135–142. [DOI], [ADS]. (Cited on pages 31 and 33.)
Li, L. and Zhang, J., 2013, “The Evolution of Barbs of a Polar Crown Filament Observed by SDO”, Solar Phys., 282, 147–174. [DOI], [ADS]. (Cited on page 13.)
Li, Y., Lynch, B.J., Stenborg, G., Luhmann, J.G., Huttunen, K.E.J., Welsch, B.T., Liewer, P.C. and Vourlidas, A., 2008, “The Solar Magnetic Field and Coronal Dynamics of the Eruption on 2007 May 19”, Astrophys. J. Lett., 681, L37–L40. [DOI], [ADS]. (Cited on page 62.)
Liewer, P.C., de Jong, E.M., Hall, J.R., Howard, R.A., Thompson, W.T., Culhane, J.L., Bone, L. and van Driel-Gesztelyi, L., 2009, “Stereoscopic Analysis of the 19 May 2007 Erupting Filament”, Solar Phys., 256, 57–72. [DOI], [ADS], [arXiv:0904.1055]. (Cited on pages 50 and 62.)
Lim, E.-K. and Chae, J., 2009, “Chirality of Intermediate Filaments and Magnetic Helicity of Active Regions”, Astrophys. J., 692, 104–108. [DOI], [ADS], [arXiv:0901.0360]. (Cited on page 30.)
Lin, Y., Engvold, O.R. and Wiik, J.E., 2003, “Counterstreaming in a Large Polar Crown Filament”, Solar Phys., 216, 109–120. [DOI], [ADS]. (Cited on page 38.)
Lin, Y., Engvold, O., Rouppe van der Voort, L., Wiik, J.E. and Berger, T.E., 2005, “Thin Threads of Solar Filaments”, Solar Phys., 226, 239–254. [DOI], [ADS]. (Cited on pages 36, 37, 38, 44, 45, and 61.)
Lin, Y., Martin, S.F. and Engvold, O., 2008, “Filament Substructures and their Interrelation”, in Subsurface and Atmospheric Influences on Solar Activity, Proceedings of a workshop held at the NSO/Sac, Sunspot, New Mexico, USA, 16–20 April 2007, (Eds.) Howe, R., Komm, R.W., Balasubramaniam, K.S., Petrie, G.J.D., ASP Conference Series, 383, pp. 235–242, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on pages 33, 37, 38, and 39.)
Lin, Y., Soler, R., Engvold, O., Ballester, J.L., Langangen, Ø., Oliver, R. and Rouppe van der Voort, L.H.M., 2009, “Swaying Threads of a Solar Filament”, Astrophys. J., 704, 870–876. [DOI], [ADS], [arXiv:0909.2792]. (Cited on pages 33 and 41.)
Lites, B.W., 2005, “Magnetic Flux Ropes in the Solar Photosphere: The Vector Magnetic Field under Active Region Filaments”, Astrophys. J., 622, 1275–1291. [DOI], [ADS]. (Cited on pages 27 and 34.)
Lites, B.W., 2009, “The Topology and Behavior of Magnetic Fields Emerging at the Solar Photosphere”, Space Sci. Rev., 144, 197–212. [DOI], [ADS]. (Cited on page 35.)
Lites, B.W., Kubo, M., Berger, T.E. et al., 2010, “Emergence of Helical Flux and the Formation of an Active Region Filament Channel”, Astrophys. J., 718, 474–487. [DOI], [ADS]. (Cited on pages 18 and 49.)
Liu, R. and Alexander, D., 2009, “Hard X-ray Emission in Kinking Filaments”, Astrophys. J., 697, 999–1009. [DOI], [ADS]. (Cited on pages 58 and 59.)
Liu, R., Alexander, D. and Gilbert, H.R., 2009a, “Asymmetric Eruptive Filaments”, Astrophys. J., 691, 1079–1091. [DOI], [ADS]. (Cited on page 54.)
Liu, W., Wang, T.-J., Dennis, B.R. and Holman, G.D., 2009b, “Episodic X-Ray Emission Accompanying the Activation of an Eruptive Prominence: Evidence of Episodic Magnetic Reconnection”, Astrophys. J., 698, 632–640. [DOI], [ADS], [arXiv:0902.1805]. (Cited on page 59.)
Liu, W., Berger, T.E. and Low, B.C., 2012, “First SDO/AIA Observation of Solar Prominence Formation Following an Eruption: Magnetic Dips and Sustained Condensation and Drainage”, Astrophys. J. Lett., 745, L21. [DOI], [ADS], [arXiv:1201.0811 [astro-ph.SR]]. (Cited on page 28.)
Liu, Y., 2008, “Magnetic Field Overlying Solar Eruption Regions and Kink and Torus Instabilities”, Astrophys. J. Lett., 679, L151–L154. [DOI], [ADS]. (Cited on page 58.)
Liu, Y., Su, J., Xu, Z., Lin, H., Shibata, K. and Kurokawa, H., 2009c, “New Observation of Failed Filament Eruptions: The Influence of Asymmetric Coronal Background Fields on Solar Eruptions”, Astrophys. J. Lett., 696, L70–L73. [DOI], [ADS]. (Cited on page 58.)
Lockyer, J.N., 1868, “Notice of an Observation of the Spectrum of a Solar Prominence, by J. N. Lockyer, Esq”, Proc. R. Soc. London, 17, 91–92. [DOI], [ADS]. (Cited on page 9.)
López Ariste, A. and Casini, R., 2002, “Magnetic Fields in Prominences: Inversion Techniques for Spectropolarimetric Data of the He I D3 Line”, Astrophys. J., 575, 529–541. [DOI], [ADS]. (Cited on page 32.)
López Ariste, A., Aulanier, G., Schmieder, B. and Sainz Dalda, A., 2006, “First observation of bald patches in a filament channel and at a barb endpoint”, Astron. Astrophys., 456, 725–735. [DOI], [ADS]. (Cited on pages 33 and 36.)
Low, B.C., 1982, “The vertical filamentary structures of quiescent prominences”, Solar Phys., 75, 119–131. [DOI], [ADS]. (Cited on page 44.)
Low, B.C., Berger, T., Casini, R. and Liu, W., 2012a, “The Hydromagnetic Interior of a Solar Quiescent Prominence. I. Coupling between Force Balance and Steady Energy Transport”, Astrophys. J., 755, 34. [DOI], [ADS], [arXiv:1203.1056 [astro-ph.SR]]. (Cited on page 28.)
Low, B.C., Liu, W., Berger, T. and Casini, R., 2012b, “The Hydromagnetic Interior of a Solar Quiescent Prominence. II. Magnetic Discontinuities and Cross-field Mass Transport”, Astrophys. J., 757, 21. [DOI], [ADS]. (Cited on page 28.)
Luna, M. and Karpen, J., 2012, “Large-amplitude Longitudinal Oscillations in a Solar Filament”, Astrophys. J. Lett., 750, L1. [DOI], [ADS]. (Cited on pages 36 and 41.)
Luna, M., Díaz, A.J. and Karpen, J., 2012a, “The Effects of Magnetic-field Geometry on Longitudinal Oscillations of Solar Prominences”, Astrophys. J., 757, 98. [DOI], [ADS]. (Cited on pages 36 and 41.)
Luna, M., Karpen, J.T. and DeVore, C.R., 2012b, “Formation and Evolution of a Multi-threaded Solar Prominence”, Astrophys. J., 746, 30. [DOI], [ADS]. (Cited on pages 27, 28, and 41.)
Lynch, B.J., Antiochos, S.K., DeVore, C.R., Luhmann, J.G. and Zurbuchen, T.H., 2008, “Topological Evolution of a Fast Magnetic Breakout CME in Three Dimensions”, Astrophys. J., 683, 1192–1206. [DOI], [ADS]. (Cited on page 56.)
Lyot, B., 1939, “The study of the solar corona and prominences without eclipses (George Darwin Lecture, 1939)”, Mon. Not. R. Astron. Soc., 99, 538. [ADS]. (Cited on page 9.)
Mackay, D.H., 2003, “Magnetic Flux Transport Simulations of Solar Surface Magnetic Distributions During a Grand Minimum”, Solar Phys., 213, 173–193. [ADS]. (Cited on page 46.)
Mackay, D.H. and van Ballegooijen, A.A., 2006, “Models of the Large-Scale Corona. I. Formation, Evolution, and Liftoff of Magnetic Flux Ropes”, Astrophys. J., 641, 577–589. [DOI], [ADS]. (Cited on pages 46 and 61.)
Mackay, D.H., Priest, E.R., Gaizauskas, V. and van Ballegooijen, A.A., 1998, “Role of Helicity in the Formation of Intermediate Filaments”, Solar Phys., 180, 299–312. [DOI], [ADS]. (Cited on page 47.)
Mackay, D.H., Gaizauskas, V. and Yeates, A.R., 2008, “Where Do Solar Filaments Form?: Consequences for Theoretical Models”, Solar Phys., 248, 51–65. [DOI], [ADS]. (Cited on pages 46 and 47.)
Mackay, D.H., Karpen, J.T., Ballester, J.L., Schmieder, B. and Aulanier, G., 2010, “Physics of Solar Prominences: II — Magnetic Structure and Dynamics”, Space Sci. Rev., 151, 333–399. [DOI], [ADS], [arXiv:1001.1635]. (Cited on pages 7, 33, 34, 37, 41, 46, and 50.)
Malherbe, J.M., Schmieder, B., Ribes, E. and Mein, P., 1983, “Dynamics of solar filaments. II. Mass motions in an active region filament from Hα center to limb observations”, Astron. Astrophys., 119, 197–206. [ADS]. (Cited on page 6.)
Maričić, D., Vršnak, B. and Roša, D., 2009, “Relative Kinematics of the Leading Edge and the Prominence in Coronal Mass Ejections”, Solar Phys., 260, 177–189. [DOI], [ADS]. (Cited on page 57.)
Mariska, J.T., Doschek, G.A. and Feldman, U., 1979, “Extreme-ultraviolet limb spectra of a prominence observed from Skylab”, Astrophys. J., 232, 929–939. [DOI], [ADS]. (Cited on page 21.)
Marqué, C., 2004, “Radio Metric Observations of Quiescent Filament Cavities”, Astrophys. J., 602, 1037–1050. [DOI], [ADS]. (Cited on pages 18 and 25.)
Martens, P.C. and Zwaan, C., 2001, “Origin and Evolution of Filament-Prominence Systems”, Astrophys. J., 558, 872–887. [DOI], [ADS]. (Cited on page 30.)
Martin, S.F., 1980, “Preflare conditions, changes and events”, Solar Phys., 68, 217–236. [DOI], [ADS]. (Cited on page 52.)
Martin, S.F., 1998a, “Filament Chirality: A Link Between Fine-Scale and Global Patterns”, in New Perspectives on Solar Prominences, IAU Colloq. 167, Aussois, France, April 28–May 4, 1997, (Eds.) Webb, D.F., Schmieder, B., Rust, D.M., ASP Conference Series, 150, pp. 419–429, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 29.)
Martin, S.F., 1998b, “Conditions for the Formation and Maintenance of Filaments (Invited Review)”, Solar Phys., 182, 107–137. [DOI], [ADS]. (Cited on pages 13, 14, 15, 28, and 36.)
Martin, S.F., Lin, Y. and Engvold, O., 2008, “A Method of Resolving the 180-Degree Ambiguity by Employing the Chirality of Solar Features”, Solar Phys., 250, 31–51. [DOI], [ADS]. (Cited on page 33.)
Mazzotta, P., Mazzitelli, G., Colafrancesco, S. and Vittorio, N., 1998, “Ionization balance for optically thin plasmas: Rate coefficients for all atoms and ions of the elements H to NI”, Astron. Astrophys. Suppl., 133, 403–409. [DOI], [ADS]. (Cited on page 18.)
Metcalf, T.R., Leka, K.D., Barnes, G. et al., 2006, “An Overview of Existing Algorithms for Resolving the 180° Ambiguity in Vector Magnetic Fields: Quantitative Tests with Synthetic Data”, Solar Phys., 237, 267–296. [DOI], [ADS]. (Cited on page 33.)
Mierla, M., Inhester, B., Antunes, A. et al., 2010, “On the 3-D reconstruction of Coronal Mass Ejections using coronagraph data”, Ann. Geophys., 28, 203–215. [DOI], [ADS]. (Cited on page 62.)
Moe, O.K., Cook, J.W. and Mango, S.A., 1979, “EUV observations of quiescent prominences from Skylab”, Solar Phys., 61, 319–334. [DOI], [ADS]. (Cited on page 21.)
Moore, R.L. and Roumeliotis, G., 1992, “Triggering of eruptive flares: Destabilization of the preflare magnetic field configuration”, in Eruptive Solar Flares, Proceedings of IAU Colloquium 133, held at Iguazú, Argentina, 2–6 August 1991, (Eds.) Švestka, Z., Jackson, B.V., Machado, M.E., Lecture Notes in Physics, 399, pp. 69–78, Springer, Berlin; New York. [DOI], [ADS]. (Cited on page 55.)
Moore, R.L., Sterling, A.C., Hudson, H.S. and Lemen, J.R., 2001, “Onset of the Magnetic Explosion in Solar Flares and Coronal Mass Ejections”, Astrophys. J., 552, 833–848. [DOI], [ADS]. (Cited on page 55.)
Muglach, K., Wang, Y.-M. and Kliem, B., 2009, “Evidence for Mixed Helicity in Erupting Filaments”, Astrophys. J., 703, 976–981. [DOI], [ADS], [arXiv:0907.4446]. (Cited on page 60.)
Munro, R.H., Gosling, J.T., Hildner, E., MacQueen, R.M., Poland, A.I. and Ross, C.L., 1979, “The association of coronal mass ejection transients with other forms of solar activity”, Solar Phys., 61, 201–215. [DOI], [ADS]. (Cited on page 54.)
Nagashima, K., Isobe, H., Yokoyama, T., Ishii, T.T., Okamoto, T.J. and Shibata, K., 2007, “Triggering Mechanism for the Filament Eruption on 2005 September 13 in NOAA Active Region 10808”, Astrophys. J., 668, 533–545. [DOI], [ADS], [arXiv:0706.3519]. (Cited on page 59.)
Nakariakov, V.M. and Verwichte, E., 2005, “Coronal Waves and Oscillations”, Living Rev. Solar Phys., 2, lrsp-2005-3. [DOI], [ADS]. URL (accessed 30 January 2013): http://www.livingreviews.org/lrsp-2005-3. (Cited on page 41.)
Ning, Z., Cao, W., Okamoto, T.J., Ichimoto, K. and Qu, Z.Q., 2009, “Small-scale oscillations in a quiescent prominence observed by HINODE/SOT. Prominence oscillations”, Astron. Astrophys., 499, 595–600. [DOI], [ADS]. (Cited on page 41.)
Ofman, L., Kucera, T.A., Mouradian, Z. and Poland, A.I., 1998, “SUMER Observations of the Evolution and the Disappearance of a Solar Prominence”, Solar Phys., 183, 97–106. [DOI], [ADS]. (Cited on page 50.)
Okamoto, T.J., Tsuneta, S., Berger, T.E. et al., 2007, “Coronal Transverse Magnetohydrodynamic Waves in a Solar Prominence”, Science, 318, 1577–1580. [DOI], [ADS], [arXiv:0801.1958]. (Cited on pages 15 and 41.)
Okamoto, T.J., Tsuneta, S., Lites, B.W. et al., 2008, “Emergence of a Helical Flux Rope under an Active Region Prominence”, Astrophys. J. Lett., 673, L215–L218. [DOI], [ADS], [arXiv:0801.1956]. (Cited on page 48.)
Okamoto, T.J., Tsuneta, S., Lites, B.W. et al., 2009, “Prominence Formation Associated with an Emerging Helical Flux Rope”, Astrophys. J., 697, 913–922. [DOI], [ADS], [arXiv:0904.0007]. (Cited on pages 48 and 49.)
Oliver, R., 2009, “Prominence Seismology Using Small Amplitude Oscillations”, Space Sci. Rev., 149, 175–197. [DOI], [ADS], [arXiv:0902.4136]. (Cited on pages 41 and 42.)
Oliver, R. and Ballester, J.L., 2002, “Oscillations in Quiescent Solar Prominences Observations and Theory (Invited Review)”, Solar Phys., 206, 45–67. [DOI], [ADS]. (Cited on page 41.)
Paletou, F., 2008, “The magnetic field of solar prominences”, in SF2A 2008, Paris, June 30–July 4, 2008, (Eds.) Charbonnel, C., Combes, F., Samadi, R., pp. 559–563, SF2A, Paris. [ADS], [arXiv:0810.2662]. (Cited on page 33.)
Paletou, F., López Ariste, A., Bommier, V. and Semel, M., 2001, “Full-Stokes spectropolarimetry of solar prominences”, Astron. Astrophys., 375, L39–L42. [DOI], [ADS]. (Cited on page 31.)
Parenti, S. and Vial, J.-C., 2007, “Prominence and quiet-Sun plasma parameters derived from FUV spectral emission”, Astron. Astrophys., 469, 1109–1115. [DOI], [ADS]. (Cited on pages 11, 21, 23, 42, and 43.)
Parenti, S., Vial, J.-C. and Lemaire, P., 2004, “Prominence atlas in the SUMER range 800–1250 Å: I. Observations, data reduction and preliminary results”, Solar Phys., 220, 61–80. [DOI], [ADS]. (Cited on pages 18 and 21.)
Parenti, S., Lemaire, P. and Vial, J.-C., 2005, “Solar hydrogen-Lyman continuum observations with SOHO/SUMER”, Astron. Astrophys., 443, 685–689. [DOI], [ADS]. (Cited on pages 18, 19, and 21.)
Parenti, S., Heinzel, P. and Schmieder, B., 2012, “On the Nature of Prominence Emission Observed by SDO/AIA”, Astron. Astrophys., 754, 66. [DOI], [ADS]. (Cited on pages 22 and 27.)
Patsourakos, S. and Vial, J.-C., 2002, “SOHO Contribution to Prominence Science”, Solar Phys., 208, 253–281. [DOI], [ADS]. (Cited on pages 44 and 54.)
Pevtsov, A.A., Fisher, G.H., Acton, L.W., Longcope, D.W., Johns-Krull, C.M., Kankelborg, C.C. and Metcalf, T.R., 2003, “The Relationship Between X-Ray Radiance and Magnetic Flux”, Astrophys. J., 598, 1387–1391. [DOI], [ADS]. (Cited on page 28.)
Pintér, B., Jain, R., Tripathi, D. and Isobe, H., 2008, “Prominence Seismology: Wavelet Analysis of Filament Oscillations”, Astrophys. J., 680, 1560–1568. [DOI], [ADS]. (Cited on page 52.)
Poland, A.I. and Mariska, J.T., 1986, “A siphon mechanism for supplying prominence mass”, Solar Phys., 104, 303–312. [DOI], [ADS]. (Cited on page 44.)
Pouget, G., Bocchialini, K. and Solomon, J., 2006, “Oscillations in a solar filament: first observation of long periods in the HeI 584.33 Å line, modelling and diagnostic”, Astron. Astrophys., 450, 1189–1198. [DOI], [ADS]. (Cited on page 6.)
Ramsey, H.E. and Smith, S.F., 1966, “Flare-initiated filament oscillations”, Astrophys. J., 71, 197–199. [DOI], [ADS]. (Cited on page 41.)
Régnier, S., Solomon, J. and Vial, J.-C., 2001, “Oscillations in an active region filament: Observations and comparison with MHD waves”, Astron. Astrophys., 376, 292–301. [DOI], [ADS]. (Cited on page 41.)
Romano, P., Contarino, L. and Zuccarello, F., 2005, “Observational evidence of the primary role played by photospheric motions in magnetic helicity transport before a filament eruption”, Astron. Astrophys., 433, 683–690. [DOI], [ADS]. (Cited on pages 61 and 62.)
Romano, P., Zuccarello, F., Poedts, S., Soenen, A. and Zuccarello, F.P., 2009, “Magnetic helicity and active filament configuration”, Astron. Astrophys., 506, 895–900. [DOI], [ADS]. (Cited on page 61.)
Romeuf, D., Meunier, N., Noens, J.-C., Koutchmy, S., Jimenez, R., Wurmser, O. and Rochain, S. [‘Observateurs Associés’ Team], 2007, “Analysis of broad-band Hα coronagraphic observations”, Astron. Astrophys., 462, 731–741. [DOI], [ADS]. (Cited on page 5.)
Rondi, S., Roudier, T., Molodij, G. et al., 2007, “Photospheric flows around a quiescent filament”, Astron. Astrophys., 467, 1289–1298. [DOI], [ADS]. (Cited on pages 47 and 48.)
Roudier, T., Švanda, M., Meunier, N. et al., 2008, “Large-scale horizontal flows in the solar photosphere. III. Effects on filament destabilization”, Astron. Astrophys., 480, 255–263. [DOI], [ADS], [arXiv:0711.3112]. (Cited on pages 50 and 51.)
Rust, D.M., 2003, “The helicial flux rope structure of solar filaments”, Adv. Space Res., 32, 1895–1903. [DOI], [ADS]. (Cited on page 60.)
Rust, D.M. and LaBonte, B.J., 2005, “Observational Evidence of the Kink Instability in Solar Filament Eruptions and Sigmoids”, Astrophys. J. Lett., 622, L69–L72. [DOI], [ADS]. (Cited on page 62.)
Ruždjak, V. and Tandberg-Hanssen, E. (Eds.), 1990, Dynamics of Quiescent Prominences, Proceedings of IAU Colloquium 117, held in Hvar, SR Croatia, Yugoslavia 1989, Lecture Notes in Physics, 363, Springer, Berlin; New York. [DOI], [ADS]. (Cited on page 18.)
Schmieder, B. and Mein, P., 1989, “Evolution of Fine Structures in a Filament”, Hvar Obs. Bull., 13, 31. [ADS]. (Cited on page 39.)
Schmieder, B., Malherbe, J.M. and Raadu, M.A., 1985, “Twisting motions in a disturbed solar filament”, Astron. Astrophys., 142, 249–255. [ADS]. (Cited on page 35.)
Schmieder, B., Raadu, M.A. and Wiik, J.E., 1991, “Fine structure of solar filaments. II. Dynamics of threads and footpoints”, Astron. Astrophys., 252, 353–365. [ADS]. (Cited on pages 38 and 39.)
Schmieder, B., Delannée, C., Yong, D.Y., Vial, J.-C. and Madjarska, M., 2000, “Multi-wavelength study of the slow ‘disparition brusque’ of a filament observed with SOHO”, Astron. Astrophys., 358, 728–740. [ADS]. (Cited on page 50.)
Schmieder, B., Tziotziou, K. and Heinzel, P., 2003, “Spectroscopic diagnostics of an Hα and EUV filament observed with THEMIS and SOHO”, Astron. Astrophys., 401, 361–375. [DOI], [ADS]. (Cited on page 18.)
Schmieder, B., Lin, Y., Heinzel, P. and Schwartz, P., 2004, “Multi-wavelength study of a high-latitude EUV filament”, Solar Phys., 221, 297–323. [DOI], [ADS]. (Cited on page 18.)
Schmieder, B., Aulanier, G., Mein, P. and López Ariste, A., 2006, “Evolving Photospheric Flux Concentrations and Filament Dynamic Changes”, Solar Phys., 238, 245–259. [DOI], [ADS]. (Cited on page 48.)
Schmieder, B., Bommier, V., Kitai, R., Matsumoto, T., Ishii, T.T., Hagino, M., Li, H. and Golub, L., 2008, “Magnetic Causes of the Eruption of a Quiescent Filament”, Solar Phys., 247, 321–333. [DOI], [ADS]. (Cited on page 61.)
Schmieder, B., Chandra, R., Berlicki, A. and Mein, P., 2010, “Velocity vectors of a quiescent prominence observed by Hinode/SOT and the MSDP (Meudon)”, Astron. Astrophys., 514, A68. [DOI], [ADS], [arXiv:0911.5091]. (Cited on page 44.)
Schmieder, B., Kucera, T.A., Knizhnik, K., Luna, M., Loopez-Ariste, A. and Toot, D., 2013, “Propagating Waves Transverse to the Magnetic Field in a Solar Prominence”, Astrophys. J., 777, 108. [DOI], [ADS], [arXiv:1309.1568 [astro-ph.SR]]. (Cited on page 13.)
Schmit, D.J., Gibson, S.E., Tomczyk, S., Reeves, K.K., Sterling, A.C., Brooks, D.H., Williams, D.R. and Tripathi, D., 2009, “Large-Scale Flows in Prominence Cavities”, Astrophys. J. Lett., 700, L96–L98. [DOI], [ADS]. (Cited on pages 25 and 27.)
Schrijver, C.J., Elmore, C., Kliem, B., Töoroök, T. and Title, A.M., 2008, “Observations and Modeling of the Early Acceleration Phase of Erupting Filaments Involved in Coronal Mass Ejections”, Astrophys. J., 674, 586–595. [DOI], [ADS], [arXiv:0710.1609]. (Cited on pages 52 and 54.)
Schwartz, P., Heinzel, P., Anzer, U. and Schmieder, B., 2004, “Determination of the 3D structure of an EUV-filament observed by SoHO/CDS, SoHO/SUMER and VTT/MSDP”, Astron. Astrophys., 421, 323–338. [DOI], [ADS]. (Cited on page 18.)
Schwartz, P., Heinzel, P., Schmieder, B. and Anzer, U., 2006, “Study of an extended EUV filament using SoHO/SUMER observations of the hydrogen Lyman lines”, Astron. Astrophys., 459, 651–661. [DOI], [ADS]. (Cited on pages 11 and 18.)
Schwenn, R., 2006, “Space Weather: The Solar Perspective”, Living Rev. Solar Phys., 3, lrsp-2006-2. [DOI], [ADS]. URL (accessed 30 January 2013): http://www.livingreviews.org/lrsp-2006-2. (Cited on pages 9 and 50.)
Secchi, A., 1870, Le Soleil, Gauthier-Villars, Paris. [ADS]. (Cited on page 9.)
Soler, R., Oliver, R. and Ballester, J.L., 2011, “Spatial Damping of Propagating Kink Waves in Prominence Threads”, Astrophys. J., 726, 102. [DOI], [ADS], [arXiv:1009.4871 [astro-ph.SR]]. (Cited on pages 44 and 68.)
Stellmacher, G., Wiehr, E. and Dammasch, I.E., 2003, “Spectroscopy of Solar Prominences Simultaneously From Space and Ground”, Solar Phys., 217, 133–155. [DOI], [ADS], [arXiv:1303.1126]. (Cited on pages 18, 32, 33, and 42.)
Sterling, A.C. and Moore, R.L., 2001, “Internal and external reconnection in a series of homologous solar flares”, J. Geophys. Res., 106, 25, 227–25, 238. [DOI], [ADS]. (Cited on page 58.)
Sterling, A.C. and Moore, R.L., 2004, “Evidence for Gradual External Reconnection before Explosive Eruption of a Solar Filament”, Astrophys. J., 602, 1024–1036. [DOI], [ADS]. (Cited on pages 50, 54, and 58.)
Sterling, A.C. and Moore, R.L., 2005, “Slow-Rise and Fast-Rise Phases of an Erupting Solar Filament, and Flare Emission Onset”, Astrophys. J., 630, 1148–1159. [DOI], [ADS]. (Cited on page 60.)
Sterling, A.C., Moore, R.L., Qiu, J. and Wang, H., 2001a, “Hα Proxies for EIT Crinkles: Further Evidence for Preflare ‘Breakout’-Type Activity in an Ejective Solar Eruption”, Astrophys. J., 561, 1116–1126. [DOI], [ADS]. (Cited on page 58.)
Sterling, A.C., Moore, R.L. and Thompson, B.J., 2001b, “EIT and SXT Observations of a Quiet-Region Filament Ejection: First Eruption, Then Reconnection”, Astrophys. J. Lett., 561, L219–L222. [DOI], [ADS]. (Cited on page 58.)
Sterling, A.C., Chifor, C., Mason, H.E., Moore, R.L. and Young, P.R., 2010, “Evidence for magnetic flux cancelation leading to an ejective solar eruption observed by Hinode, TRACE, STEREO, and SoHO/MDI”, Astron. Astrophys., 521, A49. [DOI], [ADS]. (Cited on page 61.)
Sterling, A.C., Moore, R.L. and Freeland, S.L., 2011, “Insights into Filament Eruption Onset from Solar Dynamics Observatory Observations”, Astrophys. J. Lett., 731, L3. [DOI], [ADS]. (Cited on pages 50 and 61.)
Su, J.T., Liu, Y., Zhang, H.Q. et al., 2005, “Evolution of Barb Angle and Filament Eruption”, Astrophys. J. Lett., 630, L101–L104. [DOI], [ADS]. (Cited on page 61.)
Taliashvili, L., Mouradian, Z. and Páez, J., 2009, “Dynamic and Thermal Disappearance of Prominences and Their Geoeffectiveness”, Solar Phys., 258, 277–295. [DOI], [ADS]. (Cited on page 54.)
Tandberg-Hanssen, E., 1974, Solar Prominences, Geophysics and Astrophysics Monographs, 12, D. Reidel, Dordrecht. [ADS]. (Cited on page 9.)
Tandberg-Hanssen, E., 1995, The Nature of Solar Prominences, Astrophysics and Space Science Library, 199, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on pages 5, 27, 31, 34, 38, 46, and 47.)
Tandberg-Hanssen, E., 1998, “The History of Solar Prominence Research (Review)”, in New Perspectives on Solar Prominences, Proceedings of IAU Colloquium 167, held in Aussois, France, 28 April–4 May 1997, (Eds.) Webb, D.F., Schmieder, B., Rust, D.M., ASP Conference Series, 150, p. 11, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 9.)
Tang, F., 1987, “Quiescent prominences — Where are they formed?”, Solar Phys., 107, 233–237. [DOI], [ADS]. (Cited on pages 46 and 47.)
Török, T. and Kliem, B., 2005, “Confined and Ejective Eruptions of Kink-unstable Flux Ropes”, Astrophys. J. Lett., 630, L97–L100. [DOI], [ADS], [arXiv:astro-ph/0507662]. (Cited on pages 55, 57, and 59.)
Tripathi, D., Isobe, H. and Mason, H.E., 2006, “On the propagation of brightening after filament/prominence eruptions, as seen by SoHO-EIT”, Astron. Astrophys., 453, 1111–1116. [DOI], [ADS]. (Cited on pages 57 and 60.)
Tripathi, D., Gibson, S.E., Qiu, J., Fletcher, L., Liu, R., Gilbert, H. and Mason, H.E., 2009a, “Partiallyerupting prominences: a comparison between observations and model-predicted observables”, Astron. Astrophys., 498, 295–305. [DOI], [ADS], [arXiv:0902.1228]. (Cited on page 61.)
Tripathi, D., Isobe, H. and Jain, R., 2009b, “Large Amplitude Oscillations in Prominences”, Space Sci. Rev., 149, 283–298. [DOI], [ADS], [arXiv:0910.4059]. (Cited on page 41.)
Trujillo Bueno, J., Landi Degl’Innocenti, E., Collados, M., Merenda, L. and Manso Sainz, R., 2002, “Selective absorption processes as the origin of puzzling spectral line polarization from the Sun”, Nature, 415, 403–406. [DOI], [ADS], [arXiv:astro-ph/0201409]. (Cited on page 33.)
Tsuneta, S., Ichimoto, K., Katsukawa, Y. et al., 2008, “The Solar Optical Telescope for the Hinode Mission: An Overview”, Solar Phys., 249, 167–196. [DOI], [ADS], [arXiv:0711.1715]. (Cited on page 10.)
Tziotziou, K., 2007, “Chromospheric Cloud-Model Inversion Techniques”, in The Physics of Chromospheric Plasmas, Proceedings of the conference held at the University of Coimbra in Coimbra, Portugal, 9–13 October, 2006, (Eds.) Heinzel, P., Dorotovič, I., Rutten, R.J., ASP Conference Series, 368, pp. 217–237, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:0704.1558]. (Cited on page 38.)
van Ballegooijen, A.A. and Martens, P.C.H., 1989, “Formation and eruption of solar prominences”, Astrophys. J., 343, 971–984. [DOI], [ADS]. (Cited on page 55.)
van Ballegooijen, A.A., Cartledge, N.P. and Priest, E.R., 1998, “Magnetic Flux Transport and the Formation of Filament Channels on the Sun”, Astrophys. J., 501, 866–881. [DOI], [ADS]. (Cited on page 28.)
van Ballegooijen, A.A., Priest, E.R. and Mackay, D.H., 2000, “Mean Field Model for the Formation of Filament Channels on the Sun”, Astrophys. J., 539, 983–994. [DOI], [ADS]. (Cited on page 30.)
van der Linden, R.A.M., 1993, “Can fine-structure in prominences be due to perpendicular thermal conduction”, Geophys. Astrophys. Fluid Dyn., 69, 183–199. [DOI], [ADS]. (Cited on page 68.)
van Driel-Gesztelyi, L. and Culhane, J.L., 2009, “Magnetic Flux Emergence, Activity, Eruptions and Magnetic Clouds: Following Magnetic Field from the Sun to the Heliosphere”, Space Sci. Rev., 144, 351–381. [DOI], [ADS]. (Cited on pages 8 and 56.)
Vásquez, A.M., Frazin, R.A. and Kamalabadi, F., 2009, “3D Temperatures and Densities of the Solar Corona via Multi-Spacecraft EUV Tomography: Analysis of Prominence Cavities”, Solar Phys., 256, 73–85. [DOI], [ADS]. (Cited on page 25.)
Vial, J.-C., 1998, “Solar Prominence Diagnostics (Review)”, in New Perspectives on Solar Prominences, Proceedings of IAU Colloquium 167, held in Aussois, France, 28 April–4 May 1997, (Eds.) Webb, D.F., Schmieder, B., Rust, D.M., ASP Conference Series, 150, p. 175, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 7.)
Vial, J.-C., Olivier, K., Philippon, A.A., Vourlidas, A. and Yurchyshyn, V., 2012, “High spatial resolution VAULT H-Lyα observations and multiwavelength analysis of an active region filament”, Astron. Astrophys., 541, A108. [DOI], [ADS]. (Cited on pages 18, 20, and 42.)
Vourlidas, A., Sanchez Andrade-Nuño, B., Landi, E., Patsourakos, S., Teriaca, L., Schühle, U., Korendyke, C.M. and Nestoras, I., 2010, “The Structure and Dynamics of the Upper Chromosphere and Lower Transition Region as Revealed by the Subarcsecond VAULT Observations”, Solar Phys., 261, 53–75. [DOI], [ADS], [arXiv:0912.2272]. (Cited on pages 10 and 11.)
Vršnak, B., 1993, “Classification of Prominence Oscillations”, Hvar Obs. Bull., 17, 23. [ADS]. (Cited on page 41.)
Vršnak, B., Ruždjak, V., Brajša, R. and Džubur, A., 1988, “Structure and stability of prominences with helical structure”, Solar Phys., 116, 45–60. [DOI], [ADS]. (Cited on page 35.)
Vršnak, B., Veronig, A.M., Thalmann, J.K. and Žic, T., 2007, “Large amplitude oscillatory motion along a solar filament”, Astron. Astrophys., 471, 295–299. [DOI], [ADS], [arXiv:0707.1752]. (Cited on page 41.)
Wang, H., Chae, J., Yurchyshyn, V., Yang, G., Steinegger, M. and Goode, P., 2001, “Inter-Active Region Connection of Sympathetic Flaring on 2000 February 17”, Astrophys. J., 559, 1171–1179. [DOI], [ADS]. (Cited on page 50.)
Wang, J., Shi, Z. and Martin, S.F., 1996, “Filament disturbance and associated magnetic changes in the filament environment”, Astron. Astrophys., 316, 201–214. [ADS]. (Cited on page 35.)
Wang, Y., Cao, H., Chen, J. et al., 2010, “Solar Limb Prominence Catcher and Tracker (SLIPCAT): An Automated System and its Preliminary Statistical Results”, Astrophys. J., 717, 973–986. [DOI], [ADS], [arXiv:1004.4553 [astro-ph.SR]]. (Cited on page 5.)
Wang, Y.-M. and Muglach, K., 2007, “On the Formation of Filament Channels”, Astrophys. J., 666, 1284–1295. [DOI], [ADS]. (Cited on pages 47 and 48.)
Wang, Y.-M. and Stenborg, G., 2010, “Spinning Motions in Coronal Cavities”, Astrophys. J. Lett., 719, L181–L184. [DOI], [ADS]. (Cited on page 25.)
Webb, D.F. and Howard, T.A., 2012, “Coronal Mass Ejections: Observations”, Living Rev. Solar Phys., 9, lrsp-2012-3. [DOI], [ADS]. URL (accessed 22 November 2013): http://www.livingreviews.org/lrsp-2012-3. (Cited on pages 56 and 57.)
Webb, D.F. and Hundhausen, A.J., 1987, “Activity associated with the solar origin of coronal mass ejections”, Solar Phys., 108, 383–401. [DOI], [ADS]. (Cited on page 54.)
Wiehr, E. and Bianda, M., 2003, “Solar prominence polarimetry”, Astron. Astrophys., 404, L25–L28. [DOI], [ADS]. (Cited on page 32.)
Wiik, J.E., Dammasch, I.E., Schmieder, B. and Wilhelm, K., 1999, “Multiple-Thread Model of a Prominence Observed by SUMER and EIT on SOHO”, Solar Phys., 187, 405–426. [DOI], [ADS]. (Cited on page 44.)
Wilhelm, K., Curdt, W., Marsch, E. et al., 1995, “SUMER — Solar Ultraviolet Measurements of Emitted Radiation”, Solar Phys., 162, 189–231. [DOI], [ADS]. (Cited on page 10.)
Wilhelm, K., Dwivedi, B.N., Marsch, E. and Feldman, U., 2004, “Observations of the Sun at Vacuum-Ultraviolet Wavelengths from Space. Part I: Concepts and Instrumentation”, Space Sci. Rev., 111, 415–480. [DOI], [ADS]. (Cited on page 10.)
Wilhelm, K., Marsch, E., Dwivedi, B.N. and Feldman, U., 2007, “Observations of the Sun at Vacuum-Ultraviolet Wavelengths from Space. Part II: Results and Interpretations”, Space Sci. Rev., 133, 103–179. [DOI], [ADS]. (Cited on page 10.)
Williams, D.R., Török, T., Démoulin, P., van Driel-Gesztelyi, L. and Kliem, B., 2005, “Eruption of a Kink-unstable Filament in NOAA Active Region 10696”, Astrophys. J. Lett., 628, L163–L166. [DOI], [ADS], [arXiv:astro-ph/0507661]. (Cited on pages 54, 55, and 61.)
Xu, Z., Lagg, A., Solanki, S.K. and Liu, Y., 2012, “Magnetic Fields of an Active Region Filament from Full Stokes Analysis of Si I 1082.7 nm and He I 1083.0 nm”, Astrophys. J., 749, 138. [DOI], [ADS], [arXiv:1202.4562 [astro-ph.SR]]. (Cited on page 36.)
Yan, X.-L., Qu, Z.-Q. and Kong, D.-F., 2011, “Relationship between eruptions of active-region filaments and associated flares and coronal mass ejections”, Mon. Not. R. Astron. Soc., 414, 2803–2811. [DOI], [ADS], [arXiv:1101.3625 [astro-ph.SR]]. (Cited on page 60.)
Yeates, A.R., Mackay, D.H. and van Ballegooijen, A.A., 2008, “Modelling the Global Solar Corona II: Coronal Evolution and Filament Chirality Comparison”, Solar Phys., 247, 103–121. [DOI], [ADS], [arXiv:0711.2887]. (Cited on page 30.)
Zhang, J., Dere, K.P., Howard, R.A., Kundu, M.R. and White, S.M., 2001, “On the Temporal Relationship between Coronal Mass Ejections and Flares”, Astrophys. J., 559, 452–462. [DOI], [ADS]. (Cited on page 54.)
Zhou, G.P., Wang, J.X., Zhang, J., Chen, P.F., Ji, H.S. and Dere, K.P., 2006, “Two Successive Coronal Mass Ejections Driven by the Kink and Drainage Instabilities of an Eruptive Prominence”, Astrophys. J., 651, 1238–1244. [DOI], [ADS]. (Cited on page 54.)
Zirker, J.B., Engvold, O. and Martin, S.F., 1998, “Counter-streaming gas flows in solar prominences as evidence for vertical magnetic fields”, Nature, 396, 440–441. [DOI], [ADS]. (Cited on page 38.)
Zong, W.G., Tang, Y.H., Fang, C., Mein, P., Mein, N. and Xu, A.A., 2003, “Spectro-polarimetric observation of the fine structure of a quiescent filament”, Astron. Astrophys., 412, 267–270. [DOI], [ADS]. (Cited on page 36.)
Acknowledgements
Many thanks to Living Review in Solar Physics for the invitation to write this review and the support all along the manuscript preparation. The author thanks Jean-Claude Vial and Nicolas Labrosse for their comments on the first draft of the manuscript, and Giannina Poletto for the time she dedicated to improve a later version of it. The author is also grateful to Andrei Zhukov for the discussion. Sincere thanks go to Judy Karpen and the second anonymous referee for their extremely valuable comments and suggestions. Acknowledgments go the ISSI team “Solar prominence formation and equilibrium: new data, new models” for the stimulating discussions, and the Institut d’Astrophysique Spatiale (IAS, France) for the support. The author acknowledges the financial support from the Belgian Federal Science Policy Office through the international cooperation programs and the ESA-PRODEX program.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
41116_2015_9169_MOESM1_ESM.mov
mpg-Movie (12200.71875 kB) Still from a movie showing One of the first prominence eruptions observed by SDO/AIA. Movie taken from http://sdo.gsfc.nasa.gov/gallery/main.php?v=item&id=1. Courtesy of SDO (NASA) and the AIA consortium.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Parenti, S. Solar Prominences: Observations. Living Rev. Sol. Phys. 11, 1 (2014). https://doi.org/10.12942/lrsp-2014-1
Published:
DOI: https://doi.org/10.12942/lrsp-2014-1