Evaluation of Methods for Estimating Time to Steady State with Examples from Phase 1 Studies

Abstract

An overview is provided of the methodologies used in determining the time to steady state for Phase 1 multiple dose studies. These methods include NOSTASOT (no-statistical-significance-of-trend), Helmert contrasts, spline (quadratic) regression, effective half life for accumulation, nonlinear mixed effects modeling, and Bayesian approach using Markov Chain Monte Carlo (MCMC) methods. For each methodology we describe its advantages and disadvantages. The first two methods do not require any distributional assumptions for the pharmacokinetic (PK) parameters and are limited to average assessment of steady state. Also spline regression which provides both average and individual assessment of time to steady state does not require any distributional assumptions for the PK parameters. On the other hand, nonlinear mixed effects modeling and Bayesian hierarchical modeling which allow for the estimation of both population and subject-specific estimates of time to steady state do require distributional assumptions on PK parameters. The current investigation presents eight case studies for which the time to steady state was assessed using the above mentioned methodologies. The time to steady state estimates obtained from nonlinear mixed effects modeling, Bayesian hierarchal approach, effective half life, and spline regression were generally similar.

INTRODUCTION

If the drug is intended for chronic use, an estimate of the time it takes for a drug plasma concentration to reach steady state is required for regulatory labeling. Further, regulatory guidance for studies conducted in special populations or for assessing drug interaction may specify that the measurements of interest be obtained when drug concentrations have reached steady state.

Although regulatory guidances discuss the need to conduct certain types of studies while drug concentrations are at steady state, there is limited information on exactly how to determine that steady state has in fact been reached.

During any dosing interval at steady state, the amount of the drug lost from the body for a dosage form equals the amount of the drug introduced into the body from the dosage form. Quantification of such a situation is practically impossible, because it will take an infinite number of half-lives to reach steady state. Therefore, as Hauck et al. (1) characterized it, “From a clinical perspective, ninety percent (90%) of the theoretic steady-state value is often used as a practical definition, as the difference in response to a 10% difference in concentration can rarely be assessed”. Throughout this paper, we will define steady state as being at 90% of the theoretical steady state value in accordance with Hauck et al.

Chiou (2) and Perrier et al. (3) deduced steady state estimates from single dose studies based on certain PK assumptions. It is quite possible that drugs may or may not meet these assumptions. As a confirmatory approach, steady state parameters are routinely estimated from Phase 1 multiple dose studies which provide some real time assurance that the PK thus obtained represents steady state conditions.

In the present paper, limiting ourselves to the estimation of time to steady state from Phase 1 multiple dose trial data, we attempt first to describe the ideas and methods currently available for estimating the steady state parameters for drugs. Next, we contrast these methods by examining their parameter estimates using eight data sets from Phase 1 multiple-dose studies in healthy volunteers.

In general methods for determining time to steady state fall into two broad categories based on the pharmacokinetic parameter used in the calculations, (1) area under the plasma concentration-time curve (AUC) or (2) trough concentrations. Within each of these broad categories one may calculate aggregate and individual times to steady state. In the current paper, the methods for assessing the time to steady state are classified based on the parameter used i.e., AUC or trough concentrations.

AUC to Estimate the Time to Steady State

This section considers aggregate and individual methods for estimating time to steady state based on AUC. In our Phase 1 multiple dose studies, AUC over each dosing interval is typically determined on first day and last day of dosing.

Aggregate Assessment using AUC

Equivalence of AUC at two Time Points

When a drug has reached steady state, the AUC over each dosing interval should be approximately the same. The AUCs measured over two (not necessarily consecutive) dosing intervals after the time at which steady state is thought to have been reached, are tested for equality using bioequivalence bounds (0.80, 1.25). If the confidence interval lay completely within these bounds, one could then conclude that steady state was reached by the dosing interval on which the first AUC was measured.

Individual Assessment using AUC

Effective Half-Life for Drug Accumulation

The effective half-life of drug accumulation, calculated for each subject from AUC determined over two dosing intervals, can be used to estimate the time to steady state for each subject assuming the drug displays linear pharmacokinetics. That is, multiple dose pharmacokinetics must be predictable from single dose pharmacokinetics (4).

During multiple dose administration of a drug at a constant dose over intervals of time τ, under the assumption of linear pharmacokinetics, the ratio of AUCs measured over any two dosing intervals a and b (b > a) for subject, i, can be approximated by

$$\frac{{{\text{AUC}}_{b_i \left( {0 - \tau } \right)} }}{{{\text{AUC}}_{a_i \left( {0 - \tau } \right)} }} = \frac{{\left( {1 - e^{ - \eta _i b_i \tau } } \right)}}{{\left( {1 - e^{ - \eta _i a_i \tau } } \right)}}$$

(1)

where η _i is the effective rate of drug accumulation such that half-life equals ln(2)/η _i and τ is the length of the dosing interval.

In our multiple dose studies, AUC_0−τ for each subject, i, is typically calculated for first dose (a = 1) and for the last dose (b = last). In this setting, the left side of Eq. 1 becomes the AUC accumulation ratio. The corresponding value of η _i can then be solved for iteratively, by substituting values of η _i into the right side of the equation, until the result equals the accumulation ratio.

The value of η _i in turn, can be used to estimate the subject’s fraction of steady state, $f_{{\text{ss}}_i }$, attained as follows:

$$f_{{\text{ss}}_i } = \left( {1 - \exp ^{ - N\eta _i \tau } } \right)$$

(2)

for N = 1, 2,…, b. The number of dosing intervals needed to reach 90% of steady state, $t_{0.9_i }$, may be calculated as

$$t_{0.9_i } = \frac{{2.3}}{{\eta _i }}$$

(3)

The proportion of subjects who have reached 90% of theoretical steady state by a particular dosing interval may then be summarized for each dose.

For application of this methodology the following inequality should hold true.

$$1 < \left( {{{{\text{AUC}}_b } \mathord{\left/ {\vphantom {{{\text{AUC}}_b } {{\text{AUC}}_a }}} \right. \kern-\nulldelimiterspace} {{\text{AUC}}_a }}} \right) < \left( {{b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a}} \right)$$

(4)

Trough Concentrations to Estimate Time to Steady State

This section describes the methodologies used to assess the time to steady state using trough plasma concentrations obtained from Phase 1 multiple dose studies. The trough concentration is measured at the end of the dosing interval, immediately prior to the next dose.

Aggregate Assessment using Trough Concentrations

The two aggregate methods described in this section all use a hypothesis testing approach to conclude that steady state has been reached by a particular day.

Stepwise Tests of Linear Trend

Since, at steady state, trough concentrations are expected to be approximately the same over any dosing interval, this approach involves an examination of the concentration curve over time to determine whether there is a range of time points over which the curve has “flattened out” after first increasing. The method for testing whether the curve is flat involves stepwise testing for linear trend, similar to the NOSTASOT (No-Statistical-Significance-of-Trend) method of Tukey et al. (5). The NOSTASOT method was developed in the context of testing for progressiveness of response to a drug with increasing dose; for example, in animal toxicity studies.

One difference between the scenarios described by Tukey et al. (5) and our Phase 1 multiple dose studies is related to the independence of observations. The studies described in their paper employ separate groups of subjects at each dose (the “treatment” of interest). In typical multiple dose studies, trough concentrations are measured at multiple time points in the same group of subjects. Rather than being independent, these multiple observations within each subject are correlated. The correlation can be modeled using the linear mixed-effect model approach and having a random effect for subject in the model.

Another difference is that this testing procedure assumes that the plasma concentration curve is monotonically nondecreasing. Misleading results can be obtained if the procedure is applied to drugs with a nonmonotonic profile (e.g., drug for which autoinduction occurs).

The application of the NOSTASOT methodology to trough concentrations involves straight line approximations to the aggregate plasma concentration curve over specified time intervals; therefore, the null hypothesis is that there is no linear trend, i.e., the slope of the regression line equals zero. The alternative is that there is a linear trend (slope not equal to zero). The first linear contrast uses the entire range of time points included in the model. If the contrast is significantly different from zero at alpha = 0.05, a new linear contrast is tested, this time excluding the earliest time point. This testing continues, based on contrasts successively excluding the next earliest time point from the start of the study, until the contrast is no longer significantly different from zero or until only three time points remain in the contrast. If the final contrast is not statistically significant, then the first time point included in that contrast is considered to be the time point at which steady state is attained. If the final contrast includes three time points and is still statistically significant, then steady state is considered not to have been attained by the end of the study.

In addition to testing whether each contrast (i.e., slope) equals zero, a 90% confidence interval for the true slope may be constructed using the repeated measures ANOVA model. It should be noted that the above stepwise procedure is a closed test in the sense of Marcus et al. (6), due to the assumption of monotonically nondecreasing mean trough concentrations. Therefore, no adjustment for the significance level is needed at each test step; the overall Type 1 error rate is controlled at 0.05.

Helmert Transform

In Helmert transformation, as discussed by Chow and Liu (7), the first contrast tested compares the mean concentration at the first time point to the pooled mean over all remaining time points. The second contrast compares the mean at the second time point to the pooled mean over all remaining time points. Testing continues until the contrast is not statistically significant. The first time point included in this last contrast is concluded to be the dosing interval on which steady state is attained. For example, if there were five time points included in the ANOVA, then the four contrasts would have coefficients as shown in Table I.

Table I Coefficients for Four Sequential Linear Contrasts in Helmert Approach

Individual Assessment using Trough Concentrations

The following sections discuss three methods for modeling each subject’s trough concentration–time curve individually.

Spline (Quadratic Plateau) Regression

Quadratic plateau regression offers another means of estimating an individual’s time to steady state based on trough plasma concentrations. This approach uses a segmented model, in which a quadratic equation $\left( {Y = A + Bx + Cx^2 } \right)$is assumed to fit the trough concentrations, up to a certain point x ₀, after which the data are assumed to follow a horizontal line. The point x ₀ is the time at which the maximum of the quadratic curve occurs $\left( {x_0 = {{ - 0.5B} \mathord{\left/ {\vphantom {{ - 0.5B} C}} \right. \kern-\nulldelimiterspace} C}} \right)$and this “cut-point” x ₀ is declared to be the time to steady state.

This method assumes that the curve to be totally flat from a certain point onward.

Nonlinear Mixed Effects Modeling

The application of nonlinear mixed effects modeling to estimate steady state is gaining considerable attention as it estimates both population and subject-specific parameters. Hoffman et al. (8) presented a comprehensive review on the usage of nonlinear mixed effects modeling in assessing the time to steady state. The authors cover the theoretical background of the methodology and compared the performance of the nonlinear mixed effects modeling approach to ANOVA based approaches by means of simulation. Nonlinear mixed effects modeling allows for subject-specific as well as population-specific estimates of the time to steady state for both data-rich and data-sparse situations.

Assuming a monoexponential mean model for the time course of the drug plasma trough concentrations, we have the following expression (9):

$$f\left( {t_{ij} ,\theta _i } \right) = C_{{\text{ss}}\left( i \right)} \left( {1 - e^{{{ - 2.3t_{ij} } \mathord{\left/ {\vphantom {{ - 2.3t_{ij} } {t_{0.9i} }}} \right. \kern-\nulldelimiterspace} {t_{0.9i} }}} } \right)$$

(5)

f is a scalar function of t _ij, jth dosing interval for ith subject. θ _i is a vector of unknown effects parameters to be estimated.

The intra-individual variation in the plasma trough concentrations C _ij , is modeled as,

$$C_{ij} = f\left( {t_{ij} ,\theta _i } \right)e^{\varepsilon _{ij} } $$

(6)

where, ɛ _ij  ~ N(0, σ ²) is the intra-individual random error.

The inter-individual variation in the parameters is modeled as

$$\theta _i = \theta e^{\gamma {}_i} $$

(7)

where θ is the vector of population mean steady state parameters [C_ss and t _0.9 (the time at which 90% of the asymptotic steady state concentration C_ss, is reached)], γ_i ~ N([0 0]′, ω) is a vector of inter-individual random effects, and ω is a covariance matrix of γ _i. Both intra-individual errors (ɛ _ij ) and inter-individual effects (γ _i ) are assumed to be log-normally distributed.

This methodology assumes one compartment system with continuous infusion or oral administration with rapid absorption rate.

Bayesian Approach using MCMC methods

Jordan et al. (10) proposed Bayesian hierarchical model using MCMC and Gibbs sampling for estimating both population and subject specific times to steady state based on the simple pharmacokinetic model used in Hoffman et al. (8). The authors used the following model:

$$C_t^{\left( i \right)} = C_{{\text{ss}}}^{\left( i \right)} \left( {1 - \exp \left( {\frac{{1n\left( {0.1} \right)t}}{{t_{0.9}^i }}} \right)} \right)e^{\varepsilon _i^{\left( i \right)} } $$

(8)

$$t_{0.9}^{\left( i \right)} = \frac{{1n\left( {0.1} \right)}}{{ - K^{\left( i \right)} }}$$

(9)

Where, $C_t^{\left( i \right)}$is measured individual concentrations, $t_{0.9}^{\left( i \right)}$is the time to steady state for an individual i with log-normal distribution, K is the elimination rate obtained from one compartment model, and assumed to be constant over time, and $C_{{\text{ss}}}^{\left( i \right)}$is asymptotic steady-state concentration for each individual with log normal distribution. The within-subject error is denoted by $\varepsilon _t^{\left( i \right)} \sim N\left( {0,\tau _\varepsilon ^{\left( i \right)} } \right)$, where $\tau _\varepsilon ^{\left( i \right)}$ is the individual error precision defined as $\tau = {1 \mathord{\left/ {\vphantom {1 {\sigma ^2 }}} \right. \kern-\nulldelimiterspace} {\sigma ^2 }}$. The joint distribution of ln($C_{{\text{ss}}}^{\left( {\text{i}} \right)}$) and ln($t_{0.9}^{\left( i \right)}$) is given by the following equation (10)

$$\left( {\matrix {\ln \left( {C_{{\text{ss}}}^{\left( i \right)} } \right)} \\ {\ln \left( {t_{0.9}^{\left( i \right)} } \right)} \ } \right) \sim N\left( {\left( {\matrix {C_{{\text{ss}}}^{{\text{pop}}} } \\ {t_{0.9}^{{\text{pop}}} } \ } \right),T} \right)$$

(10)

T is the precision matrix ($\Omega ^{ - 1}$, where Ω is the covariance matrix of (ln($C_{{\text{ss}}}^{\left( {\text{i}} \right)}$), ln($t_{0.9}^{\left( i \right)}$))', $C_{{\text{ss}}}^{{\text{pop}}}$, $t_{0.9}^{{\text{pop}}}$, T, and Ω are population parameters.

$$q80 = \exp \left( {\ln \left( {t_{0.9}^{{\text{pop}}} } \right) + z80 \cdot \sigma _{t_{0.9} } } \right)$$

(11)

where, q80 is the 80th percentile of the posterior distribution of $t_{0.9}^{\left( i \right)}$, z80 is the 80th percentile of the standard normal distribution and $\sigma _{t_{0.9} }$ is the population standard deviation. For discussion on how the priors for the population parameters and the individual error precision were set, and for further details on the model, inference and probabilistic considerations refer to Jordan et al. (10). Using the above model, the authors computed posterior distribution of the individual times to steady state and extracted an estimate of time where, with 90% certainty, at least 80% of the individuals in the population have attained steady state.

METHODS

In this paper we have applied all of the above discussed methodologies for estimating steady state (with the exception of aggregate AUC approach) to eight case studies. The compounds examined in the current investigation are limited to those that follow one compartmental pharmacokinetics with rapid absorption. The study designs and sample sizes are representative of some of the typical Phase 1 multiple dose studies in which time to steady state is estimated. Due to confidentiality reasons the data and conditions of the trials have not been disclosed.

Each of the studies employed a parallel group design (if more than one treatment regimen was administered), and doses were administered once daily. All the doses in the case studies examined were administered orally. Trough concentrations represent the drug concentrations in the blood samples collected prior to next dosing. AUC_(0–24h) was obtained over first and final dosing intervals. A brief description of the studies is provided below.

• Study 1. Twelve subjects received 25-mg once daily doses of the study drug. Trough concentrations were obtained for dosing intervals 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.

• Study 2. Sixteen subjects received 12.5-mg once daily doses of the study drug. Trough concentrations were obtained for dosing intervals 1, 4, 5, 6, and 7.

• Study 3. Eight subjects received 100-mg once daily doses of the study drug for 10 days. Trough concentrations were obtained for dosing intervals 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11.

• Study 4. Thirty subjects received once daily doses of the study drug. Five different doses, 25-, 50-, 100-, 200-, and 400-mg were administered to five groups, each group consisting of six subjects. Both trough concentrations and AUC_(0–24h) values exhibited dose-proportionality, therefore, all the data were dose-adjusted to 200-mg and analyzed together. Trough concentrations were obtained for dosing intervals 2, 3, 5, 7, 9, 11, 13, 14, and 15.

• Study 5. Six subjects received 25-mg once daily doses of the study drug. Trough concentrations were obtained for dosing intervals 2, 4, 6, 8, 9, and 11.

• Study 6. Twenty four subjects received 125-mg once daily doses of study drug. Trough concentrations were obtained for dosing intervals 1, 2, 3, 4, 5, 6, 7, 8, and 9.

• Study 7. Twenty five subjects received 100-mg once daily doses of study drug. Trough concentrations were obtained for dosing intervals 1, 2, 3, 4, 6, 9, 13, 16, 18, 19, 20, and 21.

• Study 8. Twenty four subjects received once daily doses of the study drug. Four different doses 0.3-, 1.0-, 3.0- and 7.0-mg doses were administered to 4 groups. Each group consisted of 6 subjects. Both trough concentrations and AUC_(0–24h) values exhibited dose-proportionality, therefore, all the data were dose-adjusted to 1.0-mg and analyzed together. Trough concentrations were obtained for dosing intervals 1, 2, 3, 4, 5, 6, 8, 10, 12, 13, and 14.

SAS (11) PROC MIXED was used for the NOSTASOT and Helmert methods, and SAS (11) PROC NLIN was used for the quadratic modeling. SAS (11) PROC NLMIXED was used for the non linear mixed effects modeling. In the current investigation the Gaussian quadrature for approximating the integral of the likelihood over random effects was utilized. As discussed previously, the Bayesian analysis was run using WinBUGS® (12) to estimate steady state parameters. WinBUGS® (12), a free downloadable software from the Web, provides extensive statistical summary with mean, standard deviation (equivalent to standard error in other methods), and quantile values. It is commonly used for performing hierarchical problem-solving using various types of distributions. The algorithm to solve for effective rate of drug accumulation was written in SAS (11).

RESULTS

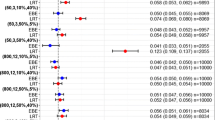
Estimates of time to steady state for these clinical trials are presented in Table II. In all cases, methods including Bayesian, nonlinear mixed effects modeling, and spline regression provided generally similar time to steady state estimates. Bayesian analysis was effective in providing both population and individual estimates for all the studies, while nonlinear mixed effect modeling failed to provide meaningful individual time to steady state estimates in two studies where the numbers of subjects were ≤8 (Study 3 and Study 5). In these studies, the estimate for inter-individual variation in the parameter t_0.9 had extremely poor precision.

Table II Steady State Estimates for Case Studies

Except for Study 2, the time to steady state estimates determined using the effective half life for accumulation were also generally similar to those obtained from the above methods. In Study 2, because of the design of the study, trough concentrations were collected for dosing intervals 1 and 4–7. No data were available for dosing intervals 2 and 3, therefore, all other methodologies estimated steady state to have been reached by ~ sixth dose. Also, NOSTASOT could not estimate the time to steady state because the final contrast which included the last three time points (dosing intervals 5, 6, and 7) was still statistically significant.

The mean steady state estimates calculated from quadratic modeling were slightly higher for some studies as compared to the estimates obtained from Bayesian or nonlinear mixed effect modeling. This may be attributed to the fact that the mean is influenced by the extreme values.

From the case studies, it appears that methods that provide individual estimates of steady state are preferable, as they allow estimation of both the mean and variance of the population distribution. In addition, some methods allow estimation of how long it takes to reach any specified percent of steady state. Subjects reach steady state at different times, therefore, aggregate assessment approaches such as NOSTASOT and Helmert contrasts have limited value. Individual methods evaluated in this paper included: (1) nonlinear mixed effect modeling, (2) Bayesian hierarchical modeling, (3) spline regression (quadratic modeling) and (4) calculating individual effective half-life of drug accumulation using AUC and determining time to steady state from that. These methods will also enable one to calculate confidence intervals for steady state estimates, fraction of steady state achieved and the percentage of subjects at 90% of steady state for each study day. In our limited experience we found in some studies with smaller number of subjects nonlinear mixed effects modeling resulted in extremely poor precision for the estimate of the parameter of interest in terms of inter-individual variability.

If the linearity assumption in AUC is valid, calculating effective half life of drug accumulation using AUC and determining time to steady state from that may be used as primary method of assessing the time to steady state in our Phase 1 multiple dose trials. As a confirmatory approach, trough concentrations values may be analyzed, with a nonlinear mixed effects model or Bayesian hierarchical modeling. If there is reason to believe that the kinetics of the compound are not linear, time to steady state can be assessed using a method that does not require any assumptions about the underlying compartmental model (e.g., stepwise tests of linear trend in trough concentrations or spline regression if applicable).

DISCUSSION

Time to steady state can be estimated by using either an aggregate or individual approach. Aggregate methods yield one result like, “steady state was achieved by day x”. Individual methods yield this result for each individual in the clinical trial, allowing for characterization of the distribution of time to steady state for the entire population. Because of the additional information obtained about the range and variability in individual response, individual methods are generally preferred.

Based on our experience with Phase 1 multiple dose studies, we listed advantages and disadvantages of various methodologies evaluated in this paper in estimating the time to steady state

Using Area under the Curve (AUC) to Estimate the Time to Steady State

Aggregate assessment using AUC

• Advantages

  • 1. Most are familiar with this methodology, as it is a commonly accepted (bioequivalence) approach for showing that two AUCs are “the same”

• Disadvantages

  • 1. It is formally hypothesized that steady state is reached by a particular day. If the hypothesis is not met, there is no further data from which to deduce when steady state is really achieved.

  • 2. For drugs with a long half-life, the AUCs on two consecutive dosing intervals might meet the bioequivalence criterion, but steady state may not have been attained, therefore, other confirmatory approaches should be applied.

  • 3. Not all subjects reach steady state at the same time, and this method fails to provide inter-individual variability

  • 4. The method does not utilize the definition of steady state as the day at which 90% of the asymptotic concentration is reached.

Individual Assessment using AUC

• Advantages

  • 1. An estimate of the time to steady state and fraction of steady state can be calculated for each subject.

• Disadvantages

  • 1. This approach is applicable to drugs that exhibit linear pharmacokinetics, i.e., multiple dose PK is predictable from single dose PK.

  • 2. Effective half-life can only be calculated if the inequality 1 < (AUC _b /AUC _a ) < (b/a) holds true.

  • 3. Computationally more difficult to implement

Using Trough Concentrations to Estimate the Time to Steady State

Application of the trough concentrations for estimating steady state can be more economical, timely, and practical as it is more costly to acquire AUC data (requiring full PK profiles on two days).

Aggregate Assessment using Trough Concentrations

Stepwise Tests of Linear Trend

• Advantages

  • 1. The approach makes no assumptions about the underlying PK model.

  • 2. The dosing interval at which steady state is expected to be attained does not have to be pre-specified.

• Disadvantages

  • 1. Most obvious problem with the procedure is lack of adequate power. The size of the detectable slope decreases with increasing sample size, and with increasing dosing intervals in the contrast. Thus, during the later part of the study, when the true slope is getting smaller, the ability to detect that slope is also reduced and one might conclude that steady state was attained on a particular day, because there was inadequate power to detect the slope at that time point. A study with smaller number of subjects might conclude that steady state was attained on an earlier day than a larger study because the large study would have the power to detect smaller slopes. It should be further noted that, because of the decreasing number of time points included in the contrast, the power to detect a particular slope decreases as the stepwise testing progresses. At the same time, the true slope being estimated is decreasing.

  • 2. The application of bounds on slope which corresponds to the Bioequivalence bounds may not be appropriate as the slope being estimated is dependent on the study design, such as number of time points sampled and length of the study. As well, the underlying curvature between any two time points, which the slope approximates, varies with the elimination rate constant of the drug. In summation, drugs with a longer half-life have a more gradual approach to steady state. Therefore, the slope over a particular time interval will be smaller for a drug with a longer half-life.

  • 3. Since the procedure is limited only to the dosing intervals included in the contrasts, it may over or underestimate time to steady state if trough concentrations were not measured in each dosing interval.

  • 4. No measure of between-subject variability is obtained.

  • 5. This procedure does not guarantee that the concentration measured on the estimated day on which steady state is attained is within 90% of the theoretical steady state concentration

Helmert Transformation

• Advantages

  • 1. An advantage over the stepwise tests of linear trend is that it may be easier to set clinically meaningful bounds for this approach than for the slope test. The usual bioequivalence bounds of 0.80 to 1.25 might be considered in testing based on the 90% confidence interval for the contrasts.

• Disadvantages

  • 1. In order for the testing procedure to be closed, testing has to stop when the first nonsignificant contrast is reached. It is possible, however, that one or more contrasts further on in the study may be statistically significant.

  • 2. As discussed in the stepwise test of linear trends, the power associated with the contrasts decreases as fewer (later) days are included in the contrast.

  • 3. Since the procedure is limited only to the dosing intervals included in the contrasts, it may over or underestimate time to steady state if trough concentrations were not measured in each dosing interval.

  • 4. No measure of between-subject variability is obtained.

  • 5. This procedure does not guarantee that the concentration measured on the estimated day on which steady state is attained is within 90% of the theoretical steady state concentration.

Individual Assessment using Trough Concentrations

Spline (Quadratic Plateau) Regression

• Advantages

  • 1. This method may be useful in approximating the form of a curve that is not adequately modeled by a monoexponential equation.

  • 2. It does not require any distributional assumptions on PK parameters.

• Disadvantages

  • 1. The curve is assumed to be totally flat from a certain point onward whereas the true concentrations follow some curve.

  • 2. A subject is declared to be “at steady state” on a particular day without providing information on the true fraction of steady state attained on that day.

Nonlinear Mixed Effects Modeling

• Advantages

  • 1. This approach could estimate both average and individual steady state estimates.

  • 2. This approach yields parameter estimates for both data-rich and data-sparse cases.

  • 3. Model could be extended to subpopulations or covariates

• Disadvantages

  • 1. The model specified here is limited to one compartment model with continuous infusion, IV bolus administration or oral administration with fast absorption.

  • 2. Limited number of samples and highly variable drugs among individuals may likely cause convergence problems.

Bayesian Approach using MCMC methods

• Advantages

  • 1. This methodology provides both population and subject specific steady state estimates.

  • 2. Jorden et al. (10) claim that this approach is applicable to possibly more complex pharmacokinetic relationships.

  • 3. Bayesian framework allows drawing of additional conclusions by providing certainty about the steady state estimates.

• Disadvantages

  • 1. Requires familiarity with Bayesian methodology.