Abstract
The axisymmetric problem in two-dimensional transversely isotropic magneto-thermoelastic (TIMT) solid due to inclined load with Green–Naghdi (GN)-III theory and two temperature (2T) has been studied. The Laplace and Hankel transform has been used to get the expressions of temperature distribution, displacement, and stress components with the horizontal distance in the physical domain. The effect of Green–Naghdi theories of type I, II, and III theories of thermoelasticity has been studied graphically on the resulting quantities. A special case for the magneto-thermoelastic isotropic medium has also been studied.
Similar content being viewed by others
Introduction
The study of deformation in a thermoelastic medium is one of the wide and dynamic domains of continuum dynamics. It is well known that all the rotating large bodies have angular velocity, as well as magnetism; therefore, the thermoelastic interactions in a rotating medium under magnetic field are of importance. The study of thermoelasticity is beneficial to analyze the deformation field such as geothermal engineering, advanced aircraft structure design, thermal power plants, composite engineering, geology, high-energy particle accelerators, and many developing technologies.
Eubanks and Sternberg (1954) discussed the axisymmetric issue of elasticity concept for a transversely isotropy medium. Vendhan and Archer (1978) electrostatically analyzed transversely isotropic (TI) finite stress-free cylinders with lateral surfaces using displacement potential. Green and Naghdi (1992, 1993) dealt with the linear and the nonlinear theories of the thermoelastic body with and without energy dissipation. Three new thermoelastic theories were proposed by them, based on entropy equality. Their theories are known as GN-I, GN-II, and GN-III theories of thermoelasticity. On linearization, type I becomes the classical heat equation, whereas on linearization, type II as well as type III theories predicts the finite speed of thermal wave. Savruk (1994) discussed the axisymmetric deformation of a TI body containing cracks.
Tarn et al. (2009) analyzed the axisymmetric and stress dispersal in a TI roundabout barrel-shaped body utilizing Hamiltonian variational definition through Legendre’s change. Liang and Wu (2012) discussed the axisymmetric deformation of one TI cylinder with the Lure method. Mahmoud (2012) considered the impact of relaxation times, the rotation, and the initial stress on Rayleigh waves. Shi et al. (2016) presented the thermomagnetoelectroelastic field in a heterogeneous annular multi-ferric composite plate with thermal loadings which is uniformly distributed on the boundaries. Kumar et al. (2016a, 2016b) studied the conflicts of thermomechanical sources in a TI homogeneous thermoelastic rotating medium with magnetic effect as well as two temperature applied to the thermoelasticity GN-III theories. Li et al. (2016) presented a set of axisymmetric solutions of the thermoelastic field in a heterogeneous circular plate which could either simply reinforced or fastened persuaded by the external thermal load.
Including these, various researchers dealt with various theory of thermoelasticity such as Marin (Marin 1997a, 1997b; Marin 1998; Marin 1999), Marin (Marin 2008; Marin 1997a, 1997b), Ezzat et al. (2012), Atwa (2014), Marin et al. (2013), Marin (2016), Marin and Baleanu (2016), Bijarnia and Singh (2016), Sharma et al. (Sharma et al. 2015a, 2015b; 2016; 2017), Ezzat et al. (2017), Lata (2018), Lata et al. (2016), Marin and Öchsner (2017), Othman and Marin (2017), Ezzat et al. (2017), Chauthale and Khobragade (2017), Kumar et al. (2017), Lata and Kaur (2018), Shahani and Torki (2018), Lata and Kaur (2019a, 2019b, 2019c, 2019d), Kaur and Lata (2019a, 2019b), Bhatti and Lu (2019a, 2019b), and Marin et al. (2019).
Despite these, very less work has been done in thermomechanical interactions in TIMT rotating solid with GN-III theory, with two temperature in the axisymmetric medium. Remembering these contemplations, analytic expressions for the displacement components, stress components, and temperature distribution in two-dimensional homogeneous, TIMT rotating solids with GN-III theories, with two temperature have been derived.
Basic equations
The field equations with and without energy dissipation, without body forces and heat sources for an anisotropic thermoelastic medium following Lata and Kaur (2019d), are:
and the equation of motion for a medium rotating uniformly and Lorentz force is
where
Ω = Ωn, n is a unit vector signifying the direction of the rotating axis.
Method and formulation of the problem
Consider a TIMT homogeneous medium with an initial temperature T0. We consider a cylindrical polar coordinate system (r, θ, z) with symmetry about the z-axis. For a plane axisymmetric problem, v = 0, and u, w, and φ are independent of θ. Additionally, we take
and
The density components J1and J3 are given as
Using the appropriate transformation following Slaughter (2002) on Eqs. (1)–(3) to determine the conditions for TI thermoelastic solid with 2T and with and without energy dissipation, we get
Constitutive relations are
where
We consider that a primary medium is at rest. Therefore, the preliminary and symmetry conditions are assumed as
To simplify the solution, the following dimensionless quantities are introduced
Applying the dimensionless quantities introduced in (13) on Eqs. (9)–(11) and subsequently suppressing the primes and using the following Laplace and Hankel transforms
on the resulting quantities, we obtain
where
The non-trivial solution of (16)–(18) by eliminating\( \overset{\sim }{\ u} \), \( \overset{\sim }{w} \), and \( \overset{\sim }{\varphi } \) yields
where
The solutions of Eq. (19) can be written as
where Aj being arbitrary constants, ±λj represents the roots of Eq. (19) and dj and lj are given by
where
Boundary conditions
The boundary conditions when normal force and tangential load are applied to the half-space (z = 0) are
where ψ1(r) and ψ2(r) are the vertical and the tangential load applied on along the r-axis and
Solving Eqs. (27)–(29) with the aid of (20)–(25), we obtain
where
Special cases
Concentrated normal force (CNF)
The CNF applied on the half-space is taken as
Applying Hankel transform, we get
The solution of Eqs. (30)–(35) with CNF is obtained using (37).
Uniformly distributed force (UDF)
Let a uniform force F1/constant temperature F2 be applied over a uniform circular region of radius a. We obtained the solution with UDF applied on the half-space by taking
where H(a − r) is a Heaviside function. The Hankel transforms of ψ1(r) and ψ2(r)are given by
The solution of Eqs. (30)–(35) with UDF is obtained using (39).
Applications
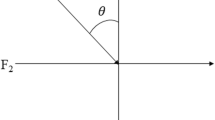
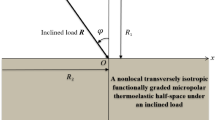
We considered an inclined load (F0/unit length) applied on a uniform circular region and its inclination with the z-axis is θ (see Fig. 1), we have
Using Eq. (40) in Eqs. (30)–(35) and with the aid of Eqs. (37) and (39), we obtain displacement components, stress components, and conductive temperature with uniformly distributed force and concentrated force on the surface of TIMT body with and without energy dissipation.
Particular cases
-
a)
If we take\( {K}_{ij}^{\ast}\ne 0 \), Eq. (2) is GN-III theory, and thus we obtain the solution of (30)–(35) for TIMT solid with rotation and GN-III theory.
-
b)
Equation (2) becomes GN-II theory if we take \( {K}_{ij}^{\ast }=0 \), and we obtain the solution of (30)–(35) for TIMT solid with rotation and GN-II theory.
-
c)
If we take Kij = 0, the equation of GN-III theory reduces to the GN-I theory, which is identical with the classical theory of thermoelasticity, and thus we obtain the solution of (30)–(35) for TIMT solid with rotation and GN-I theory.
-
d)
If \( {C}_{11}={C}_{33}=\lambda +2\mu, {C}_{12}={C}_{13}=\lambda, {C}_{44}=\mu, \kern0.5em {\alpha}_1={\alpha}_3={\alpha}^{\prime },\kern0.5em {a}_1={a}_3=a,\kern0.5em {b}_1={b}_3=b,{K}_1={K}_3=K,{K}_1^{\ast }={K}_3^{\ast }={K}^{\ast } \), we obtain the solution of (30)–(35) for TIMT materials with rotation and with GN-III theory.
Inversion of the transformation
To obtain the solution to the problem in the physical domain following Sharma et al. (2015a, 2015b), invert the transforms in Eqs. (30)–(35) by inverting the Hankel transform using
The integral in Eq. (41) is calculated using Romberg’s integration through adaptive step size as defined in Press et al. (1986).
Numerical results and discussion
For determining the theoretical results and influence of GN-I, GN-II, and GN-III theories of thermoelasticity, the physical data for cobalt material has been considered from Dhaliwal and Singh (1980) as
Using these values, the graphical illustrations of displacement components (u and w), conductive temperature φ, normal force stress tzz, tangential stress tzr, and radial stress trr,for a TIMT solid with GN-III theory and with 2T due to inclined load, have been illustrated. The numerical calculations have been obtained by developing a FORTRAN program using the above values for cobalt material.
- i.
The black line with a square symbol relates to \( {K}_{ij}^{\ast}\ne 0 \) for TIMT solid with rotation and GN-III theory.
- ii.
The red line with a circle symbol relates to \( {K}_{ij}^{\ast }=0 \) for TIMT solid with rotation and GN-II theory.
- iii.
The blue line with a triangle symbol relates to Kij = 0 the GN theory of type I.
Case 1: Concentrated normal force
Figures 2, 3, 4, 5, 6, and 7 illustrate the deviations of u and w, conductive temperature φ, and trr, trz, and tzz for a TIMT medium with concentrated normal force, with rotation, and due to inclined load. From the graph, we find that that the displacement component (u) and conductive temperature φ decreases while stress components ( trr, trz, and tzz) and displacement component (w) show a sharp increase and then an oscillatory pattern with an amplitude difference.
Case II: Uniformly distributed force (UDF)
Figures 8, 9, 10, 11, 12, and 13 illustrate the deviations of u and w, conductive temperature φ, and trr, trz, and tzz for a TIMT medium with UDF and with rotation, and due to inclined load. The displacement components (u), stress components ( trr, trz, and tzz), and temperature φ decrease sharply and then show the small oscillatory pattern, while the displacement component (w) first increases during the initial range of distance near the loading surface and follows the small oscillatory pattern for the rest of the values of distance.
Conclusions
In the above research, we conclude:
The components of displacement, stress, and temperature distribution for TIMT solid with GN-III theory, with 2T with inclined load, are calculated numerically.
The study motivates to consider magneto-thermoelastic materials as an inventive field of thermoelastic solids. The shape of curves demonstrates the effect of various GN theories and rotation on the body and fulfills the purpose of the study.
The outcomes of this research are extremely helpful in the 2-D problem with dynamic response of inclined load in TIMT medium with rotation which is beneficial to detect the deformation field such as geothermal engineering, advanced aircraft structure design, thermal power plants, composite engineering, geology, high-energy particle accelerators, geophysics, auditory range, and geomagnetism. The proposed model is significant to different problems in thermoelasticity and thermodynamics.
Nomenclature
Symbol | Name of Symbol | SI Unit | Symbol | Name of Symbol | SI Unit |
|---|---|---|---|---|---|
δ ij | Kronecker delta, | ω | Frequency | Hz | |
C ijkl | Elastic parameters, | Nm −2 | β ij | Thermal elastic coupling tensor, | Nm −2 K −1 |
τ 0 | Relaxation Time | s | Ω | Angular Velocity of the Solid | s −1 |
Fi | Components of Lorentz force | N | T | Absolute temperature, | K |
\( {\overrightarrow{H}}_0 \) | Magnetic field intensity vector | Jm−1nb−1 | e ij | Strain tensors, | Nm −2 |
φ | conductive temperature, | Wm −1 K −1 | \( \overrightarrow{j} \) | Current Density Vector | Am −2 |
t ij | Stress tensors, | Nm −2 | \( \overrightarrow{u} \) | Displacement Vector | m |
μ 0 | Magnetic permeability | Hm−1 | T 0 | Reference temperature, | K |
u i | Components of displacement, | m | ε 0 | Electric permeability | Fm−1 |
ρ | Medium density, | Kgm −3 | δ(t) | Dirac’s delta function | |
C E | Specific heat, | JKg −1 K −1 | K ij | Materialistic constant, | Wm −1 K −1 |
α ij | Linear thermal expansion coefficient, | K −1 | \( {K}_{ij}^{\ast } \) | Thermal conductivity, | Ns −2 K −1 |
H(t) | Heaviside unit step function | F1, F2 | magnitude of applied forces | N |
Availability of data and materials
For the numerical outcomes, the physical data of cobalt material has been considered from Dhaliwal and Singh (1980).
References
Atwa, S. Y. (2014). Generalized magneto-thermoelasticity with two temperature and initial stress under Green-Naghdi theory. Applied Mathematical Modelling, 38, 21–22.
Bhatti, M. M., & Lu, D. Q. (2019a). An application of Nwogu's Boussinesq model to analyze the head-on collision process between hydroelastic solitary waves. Open Physics, 233(17), 6135.
Bhatti, M. M., & Lu, D. Q. (2019b). Analytical study of the head-on collision process between hydroelastic solitary waves in the presence of a uniform current. Symmetry, 11(3), 333.
Bijarnia, R., & Singh, B. (2016). Propagation of plane waves in a rotating transversely isotropic two temperature generalized thermoelastic solid half-space with voids. International Journal of Applied Mechanics and Engineering, 21(1), 285–301.
Chauthale, S., & Khobragade, N. W. (2017). Thermoelastic Response of a Thick Circular Plate due to Heat Generation and its Thermal Stresses. Global Journal of Pure and Applied Mathematics., 7505-7527.
Dhaliwal, R., & Singh, A. (1980). Dynamic coupled thermoelasticity. New Delhi,India: Hindustan Publication Corporation.
Eubanks, R. A., & Sternberg, E. (1954). On the Axisymmetric Problem of Elasticity Theory for a Medium with Transverse Isotropy. Journal of Rational Mechanics and Analysis, 3, 89–101.
Ezzat, M. A., El-Karamany, A. S., & El-Bary, A. A. (2017). Two-temperature theory in Green–Naghdi thermoelasticity with fractional phase-lag heat transfer. Microsystem Technologies- Springer Nature, 24(2), 951–961.
Ezzat, M. A., El-Karamany, A. S., & Ezzat, S. M. (2012). Two-temperature theory in magneto-thermoelasticity with fractional order dual-phase-lag heat transfer. Nuclear Engineering and Design (Elsevier), 252, 267–277.
Green, A., & Naghdi, A. P. (1992). On undamped heat waves in an elastic solid. Journal of Thermal Stresses, 15(2), 253–264.
Green, A., & Naghdi, P. (1993). Thermoelasticity without energy dissipation. Journal of Elasticity, 31(3), 189–208.
Kaur, I., & Lata, P. (2019a). Effect of hall current on propagation of plane wave in transversely isotropic thermoelastic medium with two temperature and fractional order heat transfer. SN Applied Sciences, 1, 900.
Kaur, I., & Lata, P. (2019b). Transversely isotropic thermoelastic thin circular plate with constant and periodically varying load and heat source. International Journal of Mechanical and Materials Engineering, 14(10), 1–13.
Kumar, R., Sharma, N., & Lata, P. (2016a). Thermomechanical Interactions Due to Hall Current in Transversely Isotropic Thermoelastic with and Without Energy Dissipation with Two Temperatures and Rotation. journal of solid mechanics, 840-858.
Kumar, R., Sharma, N., & Lata, P. (2016b). Thermomechanical interactions in transversely isotropic magnetothermoelastic medium with vacuum and with and without energy dissipation with combined effects of rotation, vacuum and two temperatures. Applied Mathematical Modelling, 40, 6560–6575.
Kumar, R., Sharma, N., & Lata, P. (2017). Effects of Hall current and two temperatures in transversely isotropic magnetothermoelastic with and without energy dissipation due to ramp-type heat. Mechanics of Advanced Materials and Structures, 625-635.
Lata, P. (2018). Effect of energy dissipation on plane waves in sandwiched layered thermoelastic medium. Steel and Composite Structures, An Int'l Journal , 27(4).
Lata, P., & Kaur, I. (2018). Effect of hall current in Transversely Isotropic magnetothermoelastic rotating medium with fractional order heat transfer due to normal force. Advances in Materials Research, 7(3), 203–220.
Lata, P., & Kaur, I. (2019a). Transversely isotropic thick plate with two temperature and GN type-III in frequency domain. Coupled Systems Mechanics-Techno Press, 8(1), 55–70.
Lata, P., & Kaur, I. (2019b). Thermomechanical Interactions in Transversely Isotropic Thick Circular Plate with Axisymmetric Heat Supply. Structural Engineering and Mechanics, 69(6), 607–614.
Lata, P., & Kaur, I. (2019c). Transversely isotropic magneto thermoelastic solid with two temperature and without energy dissipation in generalized thermoelasticity due to inclined load. SN Applied Sciences, 1, 426.
Lata, P., & Kaur, I. (2019d). Effect of rotation and inclined load on transversely isotropic magneto thermoelastic solid. Structural Engineering and Mechanics, 70(2), 245–255.
Lata, P., Kumar, R., & Sharma, N. (2016). Plane waves in an anisotropic thermoelastic. Steel & Composite Structures, 22(3), 567–587.
Li, X.-Y., Li, P.-D., Kang, G.-Z., & Pan, D.-Z. (2016). Axisymmetric thermo-elasticity field in a functionally graded circular plate of transversely isotropic material. Mathematics and Mechanics of Solids, 18(5), 464–475.
Liang, J., & Wu, P. (2012). The Refined Analysis of Axisymmetric Transversely Isotropic Cylinder under Radial Direction Surface Loading. Applied Mechanics and Materials, 198-199, 212–215.
Mahmoud, S. (2012). Influence of rotation and generalized magneto-thermoelastic on Rayleigh waves in a granular medium under effect of initial stress and gravity field. Meccanica, Springer, 47, 1561–1579.
Marin, M. (1997a). Cesaro means in thermoelasticity of dipolar bodies. Acta Mechanica, 122(1-4), 155–168.
Marin, M. (1997b). On weak solutions in elasticity of dipolar bodies with voids. Journal of Computational and Applied Mathematics, 82(1-2), 291–297.
Marin, M. (1998). Contributions on uniqueness in thermoelastodynamics on bodies with voids. Revista Ciencias Matemáticas, 16(2), 101–109.
Marin, M. (1999). An evolutionary equation in thermoelasticity of dipolar bodies. Journal of Mathematical Physics, 40(3), 1391–1399.
Marin, M. (2008). Weak solutions in elasticity of dipolar porous materials. Mathematical Problems in Engineering, 1–8.
Marin, M. (2016). An approach of a heat flux dependent theory for micropolar porous media. Meccan., 51(5), 1127–1133.
Marin, M., Agarwal, R. P., & Mahmoud, S. R. (2013). Modeling a Microstretch Thermoelastic Body with Two Temperatures. Abstract and Applied Analysis, 2013, 1–7.
Marin, M., & Baleanu, D. (2016). On vibrations in thermoelasticity without energy dissipation for micropolar bodies. Boundary Value Problems, Springer, 111.
Marin, M., & Öchsner, A. (2017). The effect of a dipolar structure on the Hölder stability in Green–Naghdi thermoelasticity. Continuum Mechanics and Thermodynamics, 29, 1365–1374.
Marin, M., Vlase, S., & Bhatti, M. (2019). On the Partition of Energies for the Backward in Time Problem of Thermoelastic Materials with a Dipolar Structure. Symmetry, 11(7), 863.
Othman, M., & Marin, M. (2017). Effect of thermal loading due to laser pulse on thermoelastic porous medium under G-N theory. Results in Physics, 7, 3863–3872.
Press, W., Teukolshy, S. A., Vellerling, W. T., & Flannery, B. (1986). Numerical recipes in Fortran. Cambridge: Cambridge University Press.
Savruk, M. (1994). Axisymmetric deformation of a transversely isotropic body containing cracks. Materials Science, 29(4), 420–430.
Shahani, A. R., & Torki, H. S. (2018). Determination of the thermal stress wave propagation in orthotropic hollow cylinder based on classical theory of thermoelasticity. Continuum Mechanics and Thermodynamics, Springer, 30(3), 509–527.
Sharma, N., Kumar, R., & Lata, P. (2015a). Effect of two temperature and anisotropy in an axisymmetric problem in transversely isotropic thermoelastic solid without energy dissipation and with two temperature. American Journal of Engineering Research, 4(7), 176–187.
Sharma, N., Kumar, R., & Lata, P. (2015b). Effect Of Two Temperature On The Time Harmonic Behaviour Of An Axisymmetric Problem In Transversely Isotropic Thermoelastic Solid With Green-Naghdi Theory Of Type-II. Afro Asian J SciTech, 199–214.
Shi, T. F., Wang, C. J., Liu, C., Liu, Y., Dong, Y. H., & Li, A. X. (2016). Axisymmetric thermo-elastic field in an annular plate of functionally graded multiferroic composites subjected to uniform thermal loadings. Smart Materials and Structures, 25(3), 1–19.
Slaughter, W. S. (2002). The Linearized Theory of Elasticity. Birkhäuser.
Tarn, J.-Q., Chang, H.-H., & Tseng, W.-D. (2009). Axisymmetric Deformation of a Transversely Isotropic Cylindrical Body: A Hamiltonian State-Space Approach. Journal of Elasticity, 97(2), 131–154.
Vendhan, C. P., & Archer, R. R. (1978). Axisymmetric stresses in transversely isotropic finite cylinders. International Journal of Solids and Structures, 14(4), 305–318.
Acknowledgements
NA
Funding
No fund/scholarship/grant has been taken for this research work.
Author information
Authors and Affiliations
Contributions
The research work is done by IK under the supervision of PL. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kaur, I., Lata, P. Axisymmetric deformation in transversely isotropic magneto-thermoelastic solid with Green–Naghdi III due to inclined load. Int J Mech Mater Eng 15, 3 (2020). https://doi.org/10.1186/s40712-019-0111-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40712-019-0111-8