Transversely isotropic magneto thermoelastic solid with two temperature and without energy dissipation in generalized thermoelasticity due to inclined load

Abstract

The mathematical model has been formulated using Lord-Shulman theory for transversely isotropic magneto thermoelastic solid with two temperature and without energy dissipation due to inclined load. The entire thermo-elastic medium is rotating with a uniform angular velocity. The Laplace and Fourier transform techniques have been used to find the solution to the problem. The displacement components, stress components and conductive temperature distribution with the horizontal distance are computed in the transformed domain and further calculated in the physical domain using numerical inversion techniques. The effect of two temperature and angle of inclination of inclined load is depicted graphically on the resulting quantities.

1 Introduction

During the past few years, wide spread attention has been given to thermoelasticity theories that defines the deformation and heat flow in continuum. The classical theory of elasticity deals with the systematic study of the stress and strain distribution that develops in an elastic body due to the application of forces or change in temperature. The study of dynamical system whose interaction with surroundings is restricted to external forces, mechanical work and thermal fields is one of the most extensive and productive areas of continuum dynamics. The proposed model is helpful for finding the type of interaction between mechanical and thermal forces, as most of the structural elements of heavy industries are frequently related to mechanical and thermal stresses at a higher temperature.

Chen et al. [1,2,3] formulated a two temperature thermoelasticity of deformable bodies for the conduction of heat depending on two types of temperatures. Ailawalia and Narah [4] had studied the deformation of a rotating generalized thermoelastic solid beneath the impact of gravity with a superimposing infinite thermoelastic fluid due to different forces acting along the interface. Ailawalia et al. [5] had studied a rotating generalized thermoelastic medium with two temperatures beneath hydrostatic stress and gravity with different types of sources using integral transforms. Marin [6] had proved the Cesaro means of the kinetic and strain energies of dipolar bodies with finite energy. Sharma and Kaur [7] presented the propagation of Rayleigh waves in a generalized thermoelastic half-space with voids. The surface chosen is stress-free and thermally insulated. They detected the elliptical paths during the Rayleigh wave motion without rotation. Abd-Alla et al. [8] investigated the Rayleigh waves propagation in a homogeneous orthotropic elastic medium with impact of rotation, initial stress and gravity field by Lame’s potentials and governing equations.

Singh and Yadav [9] solved the equations of transversely isotropic rotating magnetothermoelastic medium by cubic velocity equation of three plane waves without anisotropy, rotation, and thermal and magnetic effects. Banik and Kanoria [10] studied the thermoelastic interaction in an isotropic infinite elastic body with a spherical cavity for the three-phase-lag heat equation with two-temperature generalized thermoelasticity theory and has shown dissimilarities between two models: the two-temperature Green-Naghdi theory with energy dissipation and two-temperature three-phase-lag model and has shown the effects of ramping parameters and two-temperature. Mahmoud [11] had considered the influence of rotation, magnetic field, relaxation times, initial stress and gravity field on attenuation coefficient and Rayleigh waves in an elastic half-space of granular medium and obtained the analytical solution of Rayleigh waves velocity by using Lame’s potential techniques.

Abd-alla and Alshaikh [12] had discussed the effect of rotation and magnetic field on plane waves in transversely isotropic thermoelastic medium under the Green-Lindsay theory with two relaxation times of generalized thermoelasticity to show the presence of three quasi plane waves in the medium. Marin et al. [13] had modelled a micro stretch thermoelastic body with two temperatures and eliminated divergences among the classical elasticity and research. Mahmoudet al. [14] studied the impact of the initial stress and rotation on harmonic waves propagation in a human long dry bone (transversely isotropic material). They solved the equations of elastodynamic in terms of displacements. Sharma et al. [15] investigated the two dimensional deception in a homogeneous, transversely isotropic thermoelastic solids with two temperatures in Green-Naghdi -II theory with an inclined load (linear combination of normal load and tangential load). Shaw and Mukhopadhyay [16] exemplified the generalized theory of thermoelasticity including the thermal relaxation time, electric displacement current, and the coupling of heat transfer and microrotation of the material to study the propagation of plane harmonic waves in an infinitely long, isotropic, micropolar plate with a uniform magnetic field. Two potential functions were used to determine the effect of the presence of thermal and magnetic fields on the phase velocity.

Kumar et al. [17] investigated the effects of Hall current in a transversely isotropic magnetothermoelastic with and without energy dissipation due to normal force. Bijarnia and Singh [18] studied the propagation of plane waves using Lord and Shulman theory of generalized thermoelasticity in a transversely isotropic thermoelastic solid half-space with voids and rotation and solved to illustrate the existence of four plane waves and its reflection from thermally insulated stress free surface. Kumar et al. [19] illustrated the effect of Hall current and magnetic field due to thermomechanical sources on GN-II and GN-III theories in a rotating transversely isotropic homogeneous thermoelastic medium with two temperatures. Lata et al. [20] studied two temperature and rotation aspect for GN-II and GN-III theory of thermoelasticity in a homogeneous transversely isotropic magnetothermoelastic medium for the case of the plane wave propagation and reflection. Mona and SE [21] compared the theory of thermoelasticity with two relaxation times and without energy dissipation. Kumar et al. [22] considered a thick circular plate with axisymmetric heat supply with traction free lower and upper surfaces of the plate. Ezzat et al. [23] proposed a mathematical model of electro-thermoelasticity for heat conduction with memory-dependent derivative. Kumar et al. [24]. analyzed the Rayleigh waves in a homogeneous transversely isotropic magnetothermoelastic medium with two temperature, with Hall current and rotation.

Marin et al. [25] studied the GN-thermoelastic theory for a dipolar body using mixed initial BVP and proved a result of Hölder’s -type stability. Lata [26] studied the effect of energy dissipation on plane waves in sandwiched layered thermoelastic medium of uniform thickness, with combined effects of two temperature, rotation and Hall current in the context of GN Type-II and Type-III theory of thermoelasticity. Ezzat and El-Bary [27] gave mathematical model of phase-lag G-N magneto-thermoelasticty theories for perfectly conducting media based on fractional derivative heat transfer in the presence of a constant magnetic field. Abo-Dahab [28] analyzed the wave propagation in a microstretch elastic medium with GN theory with impact of gravity. Ezzat and El-Bary [29] had applied the magneto-thermoelasticity model to a one-dimensional thermal shock problem of functionally graded half-space based on memory-dependent derivative. Hassan et al. [30] investigated water base nanofluid flow over wavy surface in a porous medium (copper oxides particles) of spherical packing beds. Othman et al. [31] discussed the deformation in rotating infinite microstretch generalized thermoelastic medium. Despite of this several researchers worked on different theory of thermoelasticity as Marin [32,33,34], Marin and Baleanu [33], Ezzat et al. [35,36,37], Marin and Stan [38], Ezzat and El-Bary [39, 40], Ezzat et al. [41], Chauthale et al. [42], Marin [43,44,45], Kumar et al. [46] and Lata and Kaur [47,48,49].

Inspite of these, not much work has been carried out in magneto-thermoelastic transversely isotropic solid with the combined effects of rotation and two temperatures in generalized thermoelasticity without energy dissipation. Keeping these considerations in mind, analytic expressions for the displacements, stresses and temperature distribution in two-dimensional homogeneous, transversely isotropic magneto-thermoelastic solids with two temperatures and rotation due to inclined load have been obtained.

2 Basic equations

For a general anisotropic thermoelastic medium, the constitutive relations in absence of heat source and body forces following Green and Naghdi [50] are given by

$$t_{ij} = C_{ijkl} e_{kl} - \beta_{ij} T.$$

(1)

Equation of motion as described by Schoenberg and Censor [51] for a transversely isotropic thermoelastic medium rotating uniformly with an angular velocity ${\varvec{\Omega}} = \varOmega {\varvec {n}}$, where n is a unit vector representing the direction of axis of rotation and taking into account Lorentz force

$$t_{ij,j} + F_{i} = \rho \left\{ {\ddot{u}_{i} + \left( {\varOmega \times (\varOmega \times u} \right)) }_{i} + (2\varOmega \times \dot{u})_{i }\right\} ,$$

(2)

where $F_{i} = \mu_{0} \left( {\vec{j} \times \vec{H}_{0} } \right)$ are the components of Lorentz force, $\vec{H}_{0}$ is the external applied magnetic field intensity vector, $\vec{j}$ is the current density vector, $\vec{u}$ is the displacement vector, $\mu_{0}$ and $\varepsilon_{0}$ are the magnetic and electric permeabilities respectively. The terms $\varOmega \times \left( {\varOmega \times u} \right)$ and $2\varOmega \times \dot{u}$ are the additional centripetal acceleration due to the time-varying motion and Coriolis acceleration respectively.

The heat conduction equation without energy dissipation using Lord-Shulman [52] model is

$$K_{ij} \varphi_{,ij} + \rho \left( {Q + \tau_{0} \dot{Q}} \right) = \beta_{ij} T_{0} \left( { \dot{e}_{ij} + \tau_{0} \ddot{e}_{ij} } \right) + \rho C_{E} \left( {\dot{T} + \tau_{0} \ddot{T}} \right),$$

(3)

where

$$\beta_{ij} = C_{ijkl} \alpha_{ij} ,$$

(4)

$$\begin{aligned} e_{ij} & = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right),\quad i,j = 1,2,3. \\ T & = \varphi - a_{ij} \varphi_{,ij} \\ \beta_{ij} & = \beta_{i} \delta_{ij} , \quad K_{ij} = K_{i} \delta_{ij} , \quad {\text{i}}\;{\text{is}}\;{\text{not}}\;{\text{summed}}. \\ \end{aligned}$$

(5)

Here $C_{ijkl}$ are elastic parameters and having symmetry $(C_{ijkl} = C_{klij} = C_{jikl} = C_{ijlk} ).$ The basis of these symmetries of $C_{ijkl}$ is due to

• 1. The stress tensor is symmetric, which is only possible if $\left( {C_{ijkl} = C_{jikl} } \right)$

• 2. If a strain energy density exists for the material, the elastic stiffness tensor must satisfy $C_{ijkl} = C_{klij}$

• 3. From stress tensor and elastic stiffness tensor symmetries infer $\left( {C_{ijkl} = C_{ijlk} } \right)$ and $C_{ijkl} = C_{klij} = C_{jikl} = C_{ijlk}$.

$\beta_{ij}$ is the thermal elastic coupling tensor, $T$ is the absolute temperature, $T_{0}$ is the reference temperature, $\varphi$ is the conductive temperature, $t_{ij}$ are the components of stress tensor, $e_{ij}$ are the components of strain tensor, $u_{i}$ are the displacement components, $\rho$ is the density, $C_{E}$ is the specific heat, $K_{ij}$ is the materialistic constant, $a_{ij}$ are the two temperature parameters, $\alpha_{ij}$ is the coefficient of linear thermal expansion, $\tau_{0}$ is the relaxation time, which is the time required to maintain steady state heat conduction in an element of volume of an elastic body when sudden temperature gradient is imposed on that volume element, $\delta_{ij}$ is the Kronecker delta and $\varOmega$ is the angular velocity of the solid.

3 Formulation and solution of the problem

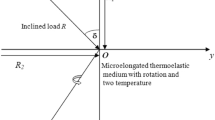
We consider a homogeneous transversely isotropic magneto-thermoelastic medium, permeated by an initial magnetic field $\vec{H}_{0} = \left( {0, H_{0} , 0} \right)$ acting along $y$-axis. The rectangular Cartesian co-ordinate system $\left( {x, y, z} \right)$ having origin on the surface $\left( {z = 0} \right)$ with $z$-axis pointing vertically into the medium is introduced. The surface of the half-space is subjected to an inclined load acting at $z = 0$.

We also assume that

$${\varvec{\Omega}} = \left( {0,\varOmega , 0} \right).$$

In From the generalized Ohm’s law

$$J_{2} = 0 .$$

The current density components $J_{1}$ and $J_{3}$ are given as

$$J_{1} = - \varepsilon_{0} \mu_{0} H_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }},$$

(6)

$$J_{3} = \varepsilon_{0} \mu_{0} H_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }}.$$

(7)

The components of displacement vector $\left( {\vec{u}, \vec{v}, \vec{w} } \right)$ and conductive temperature $\varphi$ for the two dimensional problem have the form

$$\vec{u} = u\left( {x, z,t} \right),\quad \vec{v} = 0, \quad \vec{w} = w\left( {x, z,t} \right)\;{\text{and}}\; \varphi = \varphi \left( {x,z,t} \right).$$

(8)

Following Slaughter [53], using appropriate transformations, on the set of Eqs. (1)–(3) and using (8), we derive the basic equations for perfectly homogeneous transversely isotropic magneto-thermoelastic solid as,

$$C_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + C_{13} \frac{{\partial^{2} w}}{\partial x\partial z} + C_{44 } \left( {\frac{{\partial^{2} u}}{{\partial z^{2} }} + \frac{{\partial^{2} w}}{\partial x\partial z}} \right) - \beta_{1 } \frac{\partial }{\partial x}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} - \mu_{0} J_{3} H_{0} = \rho \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }} - \varOmega^{2} u + 2\varOmega \frac{\partial w}{\partial t}} \right),$$

(9)

$$\left( {C_{13} + C_{44 } } \right)\frac{{\partial^{2} u}}{\partial x\partial z} + C_{44} \frac{{\partial^{2} w}}{{\partial x^{2} }} + C_{33 } \frac{{\partial^{2} w}}{{\partial z^{2} }} - \beta_{3 } \frac{\partial }{\partial z}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} + \mu_{0} J_{1} H_{0} = \rho \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - \varOmega^{2} w - 2\varOmega \frac{\partial u}{\partial t}} \right),$$

(10)

$$K_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + K_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }} + \rho \left( {Q + \tau_{0} \dot{Q}} \right) = \rho C_{E} \left( {\dot{T} + \tau_{0} \ddot{T}} \right) + T_{0} \frac{\partial }{\partial t}\left\{ {\beta_{1 } \left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\frac{\partial u}{\partial x} + \beta_{3 } \left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\frac{\partial w}{\partial z}} \right\},$$

(11)

and

$$t_{11} = C_{11} e_{11} + C_{13} e_{13} - \beta_{1 } T,$$

(12)

$$t_{33} = C_{13} e_{11} + C_{33} e_{33} - \beta_{3 } T,$$

(13)

$$t_{13} = 2C_{44} e_{13} ,$$

(14)

where

$$T = \varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right),$$

$$\beta_{1 } = \left( {C_{11} + C_{12} } \right)\alpha_{1} + C_{13} \alpha_{3} ,$$

$$\beta_{3 } = 2C_{13} \alpha_{1} + C_{33} .$$

We assume that medium is initially at rest. The undisturbed state is maintained at reference temperature. Then we have the initial and regularity conditions as given by

$$u\left( {x,z,0} \right) = 0 = \dot{u}\left( {x, z,0} \right),$$

$$w\left( {x, z,0} \right) = 0 = \dot{w}\left( {x, z,0} \right), \varphi \left( {x,z,0} \right) = 0 = \dot{\varphi }\left( {x,z,0} \right) \ for \ z \ge 0, - \infty < x < \infty ,$$

$$u\left( {x,z,t} \right) = w\left( {x,z,t} \right) = \varphi \left( {x,z,t} \right) = 0 \ for \ t > 0\ when\ z \to \infty .$$

To facilitate the solution, following dimensionless quantities are introduced:

$$\begin{aligned} x^{\prime } & = \frac{x}{L}, \quad z^{\prime } = \frac{z}{L}, \quad t^{'} = \frac{{c_{1} }}{L}t, \quad u^{'} = \frac{{\rho c_{1}^{2} }}{{L\beta_{1} T_{0} }}u, \quad w^{'} = \frac{{\rho c_{1}^{2} }}{{L\beta_{1} T_{0} }}w, \quad T^{\prime } = \frac{T}{{T_{0} }}, \quad t_{11}^{'} = \frac{{t_{11} }}{{\beta_{1} T_{0} }}, \\ t_{33}^{'} & = \frac{{t_{33} }}{{\beta_{1} T_{0} }}, \quad t_{31}^{'} = \frac{{t_{31} }}{{\beta_{1} T_{0} }}, \quad \varphi^{\prime } = \frac{\varphi }{{T_{0} }}, \quad a_{1}^{'} = \frac{{a_{1} }}{{L^{2} }}, \quad a_{3}^{'} = \frac{{a_{3} }}{{L^{2} }}, \quad h^{\prime } = \frac{h}{{H_{0} }}, \quad \varOmega^{\prime } = \frac{L}{{C_{1} }}\varOmega . \\ \end{aligned}$$

(15)

Making use of (15) in Eqs. (9)–(11), after suppressing the primes, yield

$$\frac{{\partial^{2} u}}{{\partial x^{2} }} + \delta_{4} \frac{{\partial^{2} w}}{\partial x\partial z} + \delta_{2} \left( {\frac{{\partial^{2} u}}{{\partial z^{2} }} + \frac{{\partial^{2} w}}{\partial x\partial z}} \right) - \frac{\partial }{\partial x}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \left( {\frac{{\varepsilon_{0} \mu_{0}^{2} H_{0}^{2} }}{\rho } + 1} \right)\frac{{\partial^{2} u}}{{\partial t^{2} }} - \varOmega^{2} u + 2\varOmega \frac{\partial w}{\partial t},$$

(16)

$$\delta_{1} \frac{{\partial^{2} u}}{\partial x\partial z} + \delta_{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \delta_{3} \frac{{\partial^{2} w}}{{\partial z^{2} }} - \frac{{\beta_{3} }}{{\beta_{1} }}\frac{\partial }{\partial z}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \left( {\frac{{\varepsilon_{0} \mu_{0}^{2} H_{0}^{2} }}{\rho } + 1} \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} - \varOmega^{2} w + 2\varOmega \frac{\partial u}{\partial t},$$

(17)

$$\frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + \frac{{K_{3} }}{{K_{1} }}\frac{{\partial^{2} \varphi }}{{\partial z^{2} }} + \rho \left( {1 + \tau_{0} \frac{{c_{1} }}{L}\frac{\partial }{\partial t}} \right)Q = \delta_{5} \frac{\partial }{\partial t}\left( {1 + \tau_{0} \frac{{c_{1} }}{L}\frac{\partial }{\partial t}} \right)\left[ {\varphi - a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} - a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right] + \delta_{6} \frac{\partial }{\partial t}\left( {1 + \tau_{0} \frac{{c_{1} }}{L}\frac{\partial }{\partial t}} \right)\left[ {\beta_{1} \frac{\partial u}{\partial x} + \beta_{3} \frac{\partial w}{\partial z}} \right],$$

(18)

where

$$\delta_{1} = \frac{{c_{13} + c_{44} }}{{c_{11} }},\quad \delta_{2} = \frac{{c_{44} }}{{c_{11} }},\quad \delta_{3} = \frac{{c_{33} }}{{c_{11} }},\quad \delta_{4} = \frac{{c_{13} }}{{c_{11} }},\quad \delta_{5} = \frac{{\rho C_{E} C_{1} L}}{{K_{1} }},\quad \rho C_{1 = }^{2} C_{11} ,\quad \delta_{6} = \frac{{T_{0} \beta_{1} L}}{{\rho C_{1} K_{1} }}.$$

Apply Laplace and Fourier transforms defined by

$$\tilde{f}\left( {x,z,s} \right) = \mathop \int \limits_{0}^{\infty } f\left( {x,z,t} \right)e^{ - st} dt,$$

(19)

$$\hat{f}\left( {\xi ,z,s} \right) = \mathop \int \limits_{ - \infty }^{\infty } \tilde{f}\left( {x,z,s} \right)e^{i\xi x} dx.$$

(20)

On Eqs. (16)–(18), we obtain a system of equations

$$\left[ { - \xi^{2} + \delta_{2} D^{2} - \delta_{7} s^{2} + \varOmega^{2} } \right]\hat{u}\left( {\xi ,z,s} \right) + \left[ {\delta_{4} Di\xi + \delta_{2} Di\xi - 2\varOmega s} \right]\hat{w}\left( {\xi ,z,s} \right) + \left( { - i\xi } \right)\left[ {1 + a_{1} \xi^{2} - a_{3} D^{2} } \right]\hat{\varphi }\left( {\xi ,z,s} \right) = 0,$$

(21)

$$\left[ {\delta_{1} Di\xi + 2\varOmega s} \right]\hat{u}\left( {\xi ,z,s} \right) + \left[ { - \delta_{2} \xi^{2} + \delta_{3} D^{2} - \delta_{7} s^{2} + \varOmega^{2} } \right]\hat{w}\left( {\xi ,z,s} \right) - \frac{{\beta_{3} }}{{\beta_{1} }}D\left[ {1 + a_{1} \xi^{2} - a_{3} D^{2} } \right]\hat{\varphi }\left( {\xi ,z,s} \right) = 0,$$

(22)

$$\left[ {\delta_{6} s\delta_{8} \beta_{1} i\xi } \right]\hat{u}\left( {\xi ,z,s} \right) + \left[ {\delta_{6} s\delta_{8} \beta_{3} D} \right]\hat{w}\left( {\xi ,z,s} \right) + \left[ {\xi^{2} - \frac{{K_{3} }}{{K_{1} }}D^{2} + \delta_{5} \delta_{8} s\left( {1 + a_{1} \xi^{2} - a_{3} D^{2} } \right)} \right]\hat{\varphi }\left( {\xi ,z,s} \right) = \rho \delta_{8} \hat{Q}\left( {\xi ,z,s} \right),$$

(23)

where $\delta_{7} = \frac{{\varepsilon_{0} \mu_{0}^{2} H_{0}^{2} }}{\rho } + 1$, $\delta_{8} = 1 + \tau_{0} \frac{{C_{1} }}{L}s$.

Without considering internal heat source and setting $\hat{Q}\left( {\xi ,z,s} \right) = 0$ we yield a set of homogeneous equations which will have a non trivial solution if determinant of coefficient $\left( {\hat{u}, \hat{w},\hat{\varphi }} \right)$ vanishes and we obtain the following characteristic equation

$$AD^{6} + BD^{4} + CD^{2} + E = 0 ,$$

(24)

where

$$\begin{aligned} D & = \frac{d}{dz}, \\ A & = \delta_{2} \delta_{3} \zeta_{7} - \zeta_{5} \delta_{2} \frac{{\beta_{3} }}{{\beta_{1} }}a_{3} , \\ B & = \delta_{3} \zeta_{1} \zeta_{7} - a_{3} \zeta_{1} \zeta_{5} \frac{{\beta_{3} }}{{\beta_{1} }} + \delta_{2} \delta_{3} \zeta_{6} + \delta_{2} \zeta_{7} \zeta_{3} - \zeta_{5} \zeta_{9} \delta_{2} - \zeta_{8} \delta_{1} i\xi \zeta_{7} + \zeta_{8} \zeta_{4} \frac{{\beta_{3} }}{{\beta_{1} }}a_{3} - a_{3} \xi^{2} \zeta_{5} \delta_{1} - a_{3} \delta_{3} \zeta_{4} i\xi \\ C& = \delta _{3} \zeta _{1} \zeta _{6} + \zeta _{1} \zeta _{3} \zeta _{7} - \zeta _{1} \zeta _{5} \zeta _{9} + \delta _{2} \zeta _{6} \zeta _{3} + \zeta _{4} \zeta _{8} \zeta _{9} - \zeta _{8} \delta _{1} i\xi \zeta _{6} + 4\Omega ^{2} s^{2} \zeta _{7} + \zeta _{2} \delta _{1} i\xi \zeta _{5} - \zeta _{2} \zeta _{4} \delta _{3} - a_{3} \zeta _{4} i\xi \zeta _{3} \\E & = \zeta_{3} \zeta_{1} \zeta_{6} + 4\varOmega^{2} s^{2} \zeta_{6} - \zeta_{2} \zeta_{4} \zeta_{3} \\ \zeta_{1} & = \xi^{2} - \delta_{7} s^{2} + \varOmega^{2} ,\quad \zeta_{2} = - i\xi \left( {1 + a_{1} \xi^{2} } \right),\quad \zeta_{3} = - \delta_{2} \xi^{2} - \delta_{7} s^{2} + \varOmega^{2} ,\quad \zeta_{4} = \delta_{6} \delta_{8} s\beta_{1} i\xi , \\ \zeta_{5} & = \delta_{6} \delta_{8} s\beta_{3} ,\quad \zeta_{6} = \xi^{2} + \delta_{5} \delta_{8} s\left( {1 + a_{1} \xi^{2} } \right),\quad \zeta_{7} = - \frac{{K_{3} }}{{K_{1} }} - a_{3} \delta_{5} \delta_{8} s,\quad \zeta_{8} = \delta_{1} i\xi ,\quad \zeta_{9} = - \left( {1 + a_{1} \xi^{2} } \right)\frac{{\beta_{3} }}{{\beta_{1} }}. \\ \end{aligned}$$

The roots of the Eq. (24) are ± λ_i, (i = 1, 2, 3), the solution of the Eq. (24) satisfying the radiation condition that ${\tilde{u}},{\tilde{w}}, {\tilde{\varphi }} \to 0 \;{\text{as}}\; z \to \infty ,$ yields

$$\bar{u}\left( {\xi ,z,s} \right) = \mathop \sum \limits_{i = 1}^{3} A_{i} e^{{ - \lambda_{i} z}} ,$$

(25)

$$\bar{w}\left( {\xi ,z,s} \right) = \mathop \sum \limits_{i = 1}^{3} d_{i} A_{i} e^{{ - \lambda_{i} z}} ,$$

(26)

$$\bar{\varphi }\left( {\xi ,z,s} \right) = \mathop \sum \limits_{i = 1}^{3} l_{i} A_{i} e^{{ - \lambda_{i} z}} ,$$

(27)

where $A_{i,} i = 1, 2, 3$ being undetermined constants and $d_{i}$ and $l_{i}$ are given by

$$d_{i} = \frac{{\delta_{2} \zeta_{7} \lambda_{i}^{4} + \left( {\zeta_{7} \zeta_{1} - a_{3} \zeta_{4} i\xi + \delta_{2} \zeta_{6} } \right)\lambda_{i}^{2} + \zeta_{1} \zeta_{6} - \zeta_{4} \zeta_{2} }}{{\left( {\delta_{3} \zeta_{7} - \frac{{\beta_{3} }}{{\beta_{1} }}a_{3} \zeta_{5} } \right)\lambda_{i}^{4} + \left( {\delta_{3} \zeta_{6} + \zeta_{3} \zeta_{7} - \zeta_{5} \zeta_{9} } \right)\lambda_{i}^{2} + \zeta_{3} \zeta_{6} }},$$

$$l_{i} = \frac{{\delta_{2} \delta_{3} \lambda_{i}^{4} + \left( {\delta_{2} \zeta_{3} + \zeta_{1} \delta_{3} - \delta_{1} \zeta_{8} i\xi } \right)\lambda_{i}^{2} + 4\varOmega^{2} s^{2} + \zeta_{3} \zeta_{1} }}{{\left( {\delta_{3} \zeta_{7} - \frac{{\beta_{3} }}{{\beta_{1} }}a_{3} \zeta_{5} } \right)\lambda_{i}^{4} + \left( {\delta_{3} \zeta_{6} + \zeta_{3} \zeta_{7} - \zeta_{5} \zeta_{9} } \right)\lambda_{i}^{2} + \zeta_{3} \zeta_{6} }}.$$

4 Boundary conditions

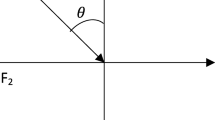
We consider a normal line load F₁ per unit length acting in the positive z-axis on the plane boundary z = 0 along the y-axis and a tangential load F₂ per unit length, acting at the origin in the positive x-axis. The appropriate boundary conditions are

• 1.
  $$t_{33} \left( {x,z,t} \right) = - F_{1} \psi_{1} \left( x \right)H\left( t \right),$$

  (28)
• 2.
  $$t_{31} \left( {x,z,t} \right) = - F_{2} \psi_{2} \left( x \right)H\left( t \right),$$

  (29)
• 3.
  $$\varphi \left( {x,z,t} \right) = 0,$$

  (30)

where F₁ and F₂ are the magnitude of the forces applied, $\psi_{1} \left( x \right)\, {\text{and}} \, \psi_{2} \left( x \right)$ specify the vertical and horizontal load distribution function along x-axis, and $H\left( t \right)$ is the Heaviside unit step function and is given by $H\left( t \right) = \left\{ {\begin{array}{*{20}c} {1,} & { t \ge 0} \\ {0,} & { t < 0} \\ \end{array} } \right.$.

Applying the Laplace and Fourier transform defined by (19) and (20) on the boundary conditions (28)–(30), (13)-(14) and with the help of Eqs. (25)–(27), we obtain the components of displacement, conductive temperature normal stress and tangential stress as,

$$\hat{u} = \frac{{F_{1} \hat{\psi }_{1} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} \varLambda_{1i} e^{{ - \lambda_{i} z}} } \right] + \frac{{F_{2} \hat{\psi }_{2} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} \varLambda_{2i} e^{{ - \lambda_{i} z}} } \right],$$

(31)

$$\hat{w} = \frac{{F_{1} \hat{\psi }_{1} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} d_{i} \varLambda_{1i} e^{{ - \lambda_{i} z}} } \right] + \frac{{F_{2} \hat{\psi }_{2} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} d_{i} \varLambda_{2i} e^{{ - \lambda_{i} z}} } \right],$$

(32)

$$\hat{\varphi } = \frac{{F_{1} \hat{\psi }_{1} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} l_{i} \varLambda_{1i} e^{{ - \lambda_{i} z}} } \right] + \frac{{F_{2} \hat{\psi }_{2} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} l_{i} \varLambda_{2i} e^{{ - \lambda_{i} z}} } \right],$$

(33)

$$\widehat{{t_{11} }} = \frac{{F_{1} \hat{\psi }_{1} \left( \xi \right))}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} S_{i} \varLambda_{1i} e^{{ - \lambda_{i} z}} } \right] + \frac{{F_{2} \hat{\psi }_{2} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} S_{i} \varLambda_{2i} e^{{ - \lambda_{i} z}} } \right],$$

(34)

$$\widehat{{t_{13} }} = \frac{{F_{1} \hat{\psi }_{1} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} N_{i} \varLambda_{1i} e^{{ - \lambda_{i} z}} } \right] + \frac{{F_{2} \hat{\psi }_{2} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} N_{i} \varLambda_{2i} e^{{ - \lambda_{i} z}} } \right]$$

(35)

$$\widehat{{t_{33} }} = \frac{{F_{1} \hat{\psi }_{1} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} M_{i} \varLambda_{1i} e^{{ - \lambda_{i} z}} } \right] + \frac{{F_{2} \hat{\psi }_{2} \left( \xi \right)}}{s\varLambda }\left[ {\mathop \sum \limits_{i = 1}^{3} M_{i} \varLambda_{2i} e^{{ - \lambda_{i} z}} } \right],$$

(36)

where

$$\begin{aligned} \varLambda_{11} & = - N_{2} l_{3 } + l_{2} N_{3} , \\ \varLambda_{12} & = N_{1} l_{3 } - l_{1} N_{3} , \\ \varLambda_{13} & = - N_{1} l_{2 } + l_{1} N_{2} , \\ \varLambda_{21} & = M_{2} l_{3 } - l_{2} M_{3} , \\ \varLambda_{22} & = - M_{1} l_{3 } + l_{1} M_{3} , \\ \varLambda_{23} & = M_{1} l_{2 } - l_{1} M_{2} , \\ \varLambda & = - M_{1} \varLambda_{11} - M_{2} \varLambda_{12} - M_{3} \varLambda_{13} , \\ N_{j} & = - \delta_{2} \lambda_{j} + i\xi d_{j} , \\ M_{j} & = i\xi - \delta_{3} d_{j} \lambda_{j} - \frac{{\beta_{3} }}{{\beta_{1} }}l_{j} \left[ {\left( {1 + a_{1} \xi^{2} } \right) - a_{3} \lambda_{j}^{2} } \right], \\ S_{j} & = - i\xi - \delta_{4} d_{j} \lambda_{j} - l_{j} \left[ {\left( {1 + a_{1} \xi^{2} } \right) - a_{3} \lambda_{j}^{2} } \right]. \\ \end{aligned}$$

5 Special cases

5.1 Concentrated force

The solution due to concentrated normal force on the half space is obtained by setting

$$\psi_{1} \left( x \right) = \delta \left( x \right), \psi_{2} \left( x \right) = \delta \left( x \right),$$

(37)

where $\delta \left( x \right)$ is dirac delta function.

Applying Fourier transform defined by (20) on (37), we obtain

$$\hat{\psi }_{1} \left( \xi \right) = 1, \quad \hat{\psi }_{2} \left( \xi \right) = 1 .$$

(38)

Using (38) in (31)-(36), the components of displacement, stress and conductive temperature are obtained.

5.2 Uniformly distributed force

The solution due to uniformly distributed force applied on the half space is obtained by setting

$$\psi_{1} \left( x \right), \psi_{2} \left( x \right) = \left\{ {\begin{array}{*{20}c} 1 & { if \left| x \right| \le m} \\ 0 & { if \left| x \right| > m} \\ \end{array} } \right. .$$

(39)

The Fourier transforms of $\psi_{1} \left( x \right)$ and $\psi_{2} \left( x \right)$ with respect to the pair (x, ξ) for the case of a uniform strip load of non-dimensional width 2 m applied at origin of co-ordinate system x = z = 0 in the dimensionless form after suppressing the primes becomes

$$\hat{\psi }_{1} \left( \xi \right) = \hat{\psi }_{2} \left( \xi \right) = \left\{ {\frac{{2 { \sin }\left( {\xi m} \right)}}{\xi }} \right\}, \quad \xi \ne 0.$$

(40)

Using (40) in (31)–(36), the components of displacement, conductive temperature and stress are obtained.

5.3 Linearly distributed force

The solution due to linearly distributed force applied on the half space is obtained by setting

$$\left\{ {\psi_{1} \left( x \right), \psi_{2} \left( x \right)} \right\} = \left\{ {\begin{array}{*{20}c} {1 - \frac{\left| x \right|}{m} } & {if \left| x \right| \le m} \\ 0 & { if \left| x \right| > m} \\ \end{array} } \right. .$$

(41)

Here 2 m is the width of the strip load, using (15) and applying the transform defined by (20) on (41), we get

$$\hat{\psi }_{1} \left( \xi \right) = \hat{\psi }_{2} \left( \xi \right) = \left\{ {\frac{{2\{ 1 - cos\left( {\xi m} \right))}}{{\xi^{2} m}}} \right\},\quad \xi \ne 0.$$

(42)

Using (42) in (31)-(36), the components of displacement, stress and conductive temperature are obtained.

6 Applications

Inclined line load Suppose an inclined load, F₀ per unit length is acting on the y-axis and its inclination with z-axis is $\theta$, we have (Fig. 1)

$$F_{1} = F_{0} \cos \theta \; {\text{and}}\; F_{2} = F_{0} \sin \theta .$$

(43)

Fig. 1

Inclined load over a transversely isotropic magneto-thermoelastic solid

Using Eq. (43) in Eqs. (31)–(36) and with aid of Eqs. (37)–(42) we obtain the expressions for displacements, conductive temperature and stresses for concentrated force, uniformly distributed force and linearly distributed force on the surface of transversely isotropic magneto-thermoelastic body without energy dissipation.

7 Inversion of the transformation

To find the solution of the problem in physical domain, we must invert the transforms in Eqs. (31)–(36),. Here the displacement components, normal and tangential stresses and conductive temperature are functions of z, the parameters of Laplace and Fourier transforms s and ξ respectively and hence are of the form ${\hat{\text{f}}}\left( {\upxi, {\text{z}}, {\text{s}}} \right)$. To find the function ${\tilde{\text{f}}}\left( {{\text{x}}, {\text{z}}, {\text{t}}} \right)$ in the physical domain, we first invert the Fourier transform using

$$\tilde{f}\left( {x,z,s} \right) = \frac{1}{2\pi }\mathop \int \limits_{ - \infty }^{\infty } e^{ - i\xi x} \hat{f}\left( {\xi ,z,s} \right)d\xi = \frac{1}{2\pi }\mathop \int \limits_{ - \infty }^{\infty } \left| {cos\left( {\xi x} \right)f_{e} - isin\left( {\xi x} \right)f_{o} } \right|d\xi$$

where f_e and f_o are respectively the odd and even parts of $\hat{f}\left( {\xi ,z,s} \right).$ Following Honig and Hirdes [54], the Laplace transform function $\tilde{f}\left( {x,z,s} \right)$ can be inverted to f(x, z, t) by

$$f\left( {x,z,t} \right) = \frac{1}{2\pi i}\mathop \int \limits_{{e^{ - i\infty } }}^{{e^{ + i\infty } }} \tilde{f}\left( {x,z,s} \right)e^{ - st} ds.$$

(44)

The last step is to calculate the integral in Eq. (44). The method for evaluating this integral is described in Press et al. [55]. It involves the use of Romberg’s integration with adaptive step size. This also uses the results from successive refinements of the extended trapezoidal rule followed by extrapolation of the results to the limit when the step size tends to zero.

8 Numerical results and Discussion

In order to illustrate our theoretical results in the proceeding section and to show the effect of two temperature and rotation, we now present some numerical results. Following Dhaliwal and Singh [56], cobalt material has been taken for transversely isotropic thermoelastic material as

$$\begin{aligned} c_{11} & = 3.07 \times 10^{11} \,{\text{Nm}}^{ - 2} ,\quad c_{33} = 3.581 \times 10^{11} \,{\text{Nm}}^{ - 2} , \quad c_{13} = 1.027 \times 10^{10} \,{\text{Nm}}^{ - 2} , \\ c_{44} & = 1.510 \times 10^{11} \,{\text{Nm}}^{ - 2} ,\quad \beta_{1} = 7.04 \times 10^{6} \,{\text{Nm}}^{ - 2} { \deg }^{ - 1} , \quad \beta_{3} = 6.90 \times 10^{6} \,{\text{Nm}}^{ - 2} { \deg }^{ - 1} , \\ \rho & = 8.836 \times 10^{3} \,{\text{Kgm}}^{ - 3} ,\quad C_{E} = 4.27 \times 10^{2} \,{\text{jKg}}^{ - 1} \,{ \deg }^{ - 1} , \quad K_{1} = 0.690 \times 10^{2} {\text{Wm}}^{ - 1} \,{\text{K}}\,{ \deg }^{ - 1} , \\ K_{3} & = 0.690 \times 10^{2} \,{\text{Wm}}^{ - 1} {\text{K}}^{ - 1} ,\quad {\text{T}}_{0} = 298\,{\text{K}},\quad {\text{H}}_{0} = 1\,{\text{Jm}}^{ - 1} {\text{nb}}^{ - 1} ,\quad\upvarepsilon _{0} = 8.838 \times 10^{ - 12} \,{\text{Fm}}^{ - 1} , {\text{L}} = 1. \\ \end{aligned}$$

Using the above values, the graphical representations of displacement component u, normal displacement w, conductive temperature $\varphi$, stress components $t_{11}$, $t_{13}$ and $t_{33}$ for transversely isotropic thermoelastic medium have been investigated and the effect of inclination with two temperature has been depicted.

• 1. The black solid line with square symbols corresponds to transversely isotropic magneto-thermoelastic medium with $\varOmega = 0.5,\theta = 0^\circ$ and a₁ = 0.0, a₃ = 0.0 i.e. without two temperature.

• 2. The red solid line with circle symbols corresponds to transversely isotropic magneto-thermoelastic medium with $\varOmega = 0.5$,$\theta = 45^\circ$ and a₁ = 0.0, a₃ = 0.0 i.e. without two temperature.

• 3. The green solid line with circle symbols corresponds to transversely isotropic magneto-thermoelastic medium with $\varOmega = 0.5$,$\theta = 0^\circ$ and a₁ = 0.02, a₃ = 0.040 i.e. with two temperature.

• 4. The blue solid line with diamond symbols corresponds to transversely isotropic magneto-thermoelastic medium with $\varOmega = 0.5$,$\theta = 45^\circ$ and a₁ = 0.02, a₃ = 0.040 i.e. with two temperature.

8.1 Event 1: Concentrated force due to inclined load and with and without two temperature and with rotation

Figures 2 and 3 shows the variations of the displacement component u and w for transversely isotropic magneto-thermoelastic medium with and without two temperature and rotation respectively. The values of displacement component u and w decreases for without two temperure and increases for with two temperature for the initial values of distance and follow oscillatory pattern for rest of the range of distance. Figure 4 represents the variations of the conductive temperature $\varphi$ for transversely isotropic magneto-thermoelastic medium with and without two temperature and with rotation. The values of conductive temperature $\varphi$, first increases for the range $0 \le x \le 2$ and then follow small oscillatory pattern for rest of the range of distance for both with and without two temperature. Figure 5 represents the values of stress component $t_{11}$., the values of $t_{11}$ f or $\theta = 0^\circ$ follow oscillatory pattern with smaller amplitude whereas for $\theta = 45^\circ$ it follows oscillatory pattern with larger amplitude. Figure 6 describes the variations of stress component $t_{13}$. Near the loing surface, the values of $t_{13 }$ decrease sharply and then somehow oscillates. Figure 7 interprets the variations of stress component $t_{33}$. The values decrease sharply near the loading surface with $\theta = 0^\circ$ and increase sharply near the loading surface with $\theta = 45^\circ$ and then follow small oscillatory pattern for rest of the range for both with and without two temperature.

Fig. 2

Variations of displacement component u with distance x

Fig. 3

Variations of displacement component w with distance x

Fig. 4

Variations of conductive temperature φ with distance x

Fig. 5

Variations of stress component t₁₁ with distance x

Fig. 6

Variations of stress component t₁₃ with distance x

Fig. 7

Variations of stress component t₃₃ with distance x

8.2 Event 2: Uniformly distributed force due to inclined load and with and without two temperature and with rotation

Figure 8 shows the variations of the displacement component u for uniformly distributed force for transversely isotropic magneto-thermoelastic medium with and without two temperature and with fixed rotation. The values of displacement component u, first increases for the range $0 \le x \le 2$ and for $\theta = 0^\circ ,$ a₁ = 0.0, a₃ = 0.0 while for this range it first decreases for $\theta = 45^\circ$, a₁ = 0.0, a₃ = 0.0 and $\theta = 0^\circ$, a₁ = 0.02, a₃ = 0.04; $\theta = 45^\circ ,$ a₁ = 0.02, a₃ = 0.04 for the initial values of distance and then for all four cases follows oscillatory pattern, for rest of the range of distance. Figure 9 depicts variations of the displacement component w for transversely isotropic magneto-thermoelastic medium with and without two temperature and with rotation. For the range $0 \le x \le 3$, the values of displacement component w, increases for $\theta = 0^\circ$ and for both with and without two temperature and then oscillates; while it decreases for $\theta = 45^\circ$ and for both with and without two temperature for the initial values of distance and then follow small oscillatory pattern for rest of the range of distance for both with and without two temperature. Figure 10 represents the variations of the conductive temperature $\varphi$ for transversely isotropic magneto-thermoelastic medium with and without two temperature and with rotation. The values of conductive temperature $\varphi$, first decreases for $\theta = 0^\circ$, a₁ = 0.0, a₃ = 0.0 then follow small oscillatory pattern for rest of the range of distance and for rest of three cases it first increases and then follows small oscillatory pattern. Figure 11 represents the values of stress component $t_{11}$. Near the loading surface, the values of $t_{11}$ decrease and then follows oscillatory pattern. Figure 12 describes the variations of stress component $t_{13}$. Near the loading surface, and for $\theta = 0^\circ$, a₁ = 0.0, a₃ = 0.0 the values of $t_{13 }$ sharply decreases and for rest cases it increases for the range $0 \le x \le 2$ and then somehow oscillates for all the cases. Figure 13 interprets the variations of stress component $t_{33}$. Near the loading surface, the values of $t_{33}$ decrease and then follows oscillatory pattern for all the four cases considered above.

Fig. 8

Variations of displacement component u with distance x

Fig. 9

Variations of displacement component w with distance x

Fig. 10

Variations of conductive temperature φ with distance x

Fig. 11

Variations of stress component t₁₁ with distance x

Fig. 12

Variations of stress component t₁₃ with distance x

Fig. 13

Variations of stress component t₃₃ with distance x

8.3 Event 3: Linearly distributed force due to inclined load and with and without two temperature and with rotation

Figure 14 shows the variations of the displacement component u for transversely isotropic magneto-thermoelastic medium with linearly distributed force and with and without two temperature and with rotation. The values of displacement component u, increases somehow for $\theta = 0^\circ$, a₁ = 0.0, a₃ = 0.0 and it decreases for rest all the cases in the initial values of distance and then follow an oscillatory pattern. Figure 15 shows the variations of the displacement component w for transversely isotropic magneto-thermoelastic medium with linearly distributed force and with and without two temperature and with rotation. The values of displacement component w, sharply increases for $\theta = 0^\circ$ in the initial values of distance and decreases for $\theta = 45^\circ$ and follow small oscillatory pattern for rest of the range of distance. Figure 16 represents the variations of the conductive temperature $\varphi$ for transversely isotropic magneto-thermoelastic medium with linearly distributed force and with and without two temperature and rotation. The values of conductive temperature $\varphi$, decreases for $\theta = 0^\circ ,$ a₁ = 0.0, a₃ = 0.0 sharply increases for rest of the three cases in the initial values of distance and follow small revere oscillatory pattern for $\theta = 0^\circ and \theta = 45^\circ$ in rest of the range of distance. Figure 17 represents the values of stress component $t_{11}$. From the initial range if distance, $t_{11}$ show the large oscillation. Figure 18 describes the variations of stress component $t_{13}$. Near the loading surface, the values of $t_{13 }$ decrease sharply and then somehow oscillates. Figure 19 interprets the variations of stress component $t_{33}$.The values increase sharply near the loading surface when $\theta = 45^\circ$ and decrease for $\theta = 0^\circ$ with all the values of two temperatures then small oscillatory pattern for rest of the range.

Fig. 14

Variations of displacement component u with distance x

Fig. 15

Variations of displacement component w with distance x

Fig. 16

Variations of conductive temperature φ with distance x

Fig. 17

Variations of stress component t₁₁ with distance x

Fig. 18

Variations of stress component t₁₃ with distance x

Fig. 19

Variations of stress component t₃₃ with distance x

9 Conclusions

From above investigation, it is observed that the magnetic effect of two temperature, rotation as well as the angle of inclination of the applied load plays a major role in the distribution of all the physical quantities. The amplitude of all the physical quantities differ (either increase or decrease) with and without two temperature as well as the angle of inclined load. Two temperature plays a major role for the oscillation of physical quantities near the point of application of source as well as away from the source. In presence and absence of two temperature and inclined load, the displacement components and stress components show an oscillatory nature with respect to x. The inclined load plays a significant role in the distribution of all the physical quantities. The concentrated and uniformly distributed force show more effect on stress component. The result gives an inspiration to study magneto-thermoelastic materials as an innovative domain of applicable thermoelastic solids. The results of this paper become useful for those researchers who works in material science, inventers of new materials, in addition to those working on the magneto-thermoelasticity and in real life as in geophysics, acoustics, geomagnetic etc. The proposed methods in this research is relevant to a wide range of problems in thermodynamics and thermoelasticity.