1 Background

Natural convection in fluids has been a topic of interest for researchers like Nield and Bejan [1], Pop and Ingham [2], Ingham and Pop [3], Vafai [4,5], Vadasz [6], due to its appearance in industry and machineries where heat transfer is encountered. In the present scenario where the focus has shifted from ordinary fluids to nanofluids to be used as heat transfer mediums, the phenomena needs to be critically studied for them [7]. Accordingly, natural convection has been studied in nanofluids by Buongiorno [8], Tzou [9,10], Kim et al. [11-13], and based on these results in the current decade by Nield and Kuznetsov [14], Kuznetsov and Nield [15] for the Horton-Rogers-Lapwood Problem of onset of thermal instability in a porous medium saturated by a nanofluid, using Darcy and Brinkman models, respectively, and incorporating the effects of Brownian motion and thermophoresis of Nanoparticles. They found that the critical thermal Rayleigh number can be reduced or increased by a substantial amount, depending on whether the basic nanoparticle distribution is top-heavy or bottom-heavy, by the presence of the nanoparticles. Based on these conservation equations, some recent studies have been performed by Agarwal et al. [16,17], Bhadauria and Agarwal [18,19], Agarwal and Bhadauria [20], Rana and Agarwal [21], Agarwal [22]. For the case of a simple nanofluid layer, studies have been performed by Yadav et al. [23] for fluid layer, Bhadauria and Agarwal [24], Agarwal and Bhadauria [25-27], for a rotating nanofluid layer.

In the above studies, investigations have been done assuming local thermal equilibrium(LTE) between the fluid and particle phases as well as fluid and solid-matrix phases, i.e., the temperature gradient at any location between the two phases is assumed to be negligible. But, as thermal lagging between the particle and fluid phases has been proposed by Vadasz as an explanation for the observed increase in the thermal conductivity of nanofluids, we need to study local thermal non equilibrium(LTNE) model. The LTNE model of convective heat transfer in porous medium has been dealt by Kuznetsov and Nield [15], Agarwal and Bhadauria [20], Bhadauria and Agarwal [18,19] to claim that the effect of LTNE can be significant for some circumstances but remains insignificant for typical dilute nanofluids.

Apart from the above few studies on thermal instability in nanofluids, no other study is available on this problem, therefore we intend to investigate this problem further. Assuming that the nanoparticles being suspended in the nanofluid using either surfactant or surface charge technology Nield and Kuznetsov [14], preventing the agglomeration and deposition of these on the porous matrix, in the present article, we study the linear and non-linear thermal instability in a nanofluid layer, using Rayleigh Bénard problem, considering LTNE between the fluid/particle interphase.

2 Methods

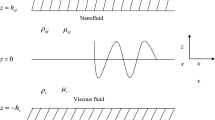
We consider a horizontal layer of nanofluid, confined between two horizontal boundaries at z =0 and z =d, heated from below and cooled from above. The boundaries are impermeable and perfectly thermally conducting. The fluid layer is extended infinitely in x and y-directions, and z-axis is taken vertically upward with the origin at the lower boundary. The local thermal non-equilibrium between the fluid and particle phase has been considered, thus heat flow has been described using two temperature model. T h and T c are the temperatures at the lower and upper walls respectively, the former being greater. The conservation equations for the total mass, momentum, thermal energy in the fluid phase,thermal energy in the particle phase, and nanoparticles, come out to be as below. A detailed derivation of the conservation equations has been dealt by Buongiorno, Tzou, and Nield and Kuznetsov:

$$\begin{array}{@{}rcl@{}} \nabla\cdot \mathbf{v} =0 \end{array} $$
((1))
$$ \begin{aligned} \rho_{f}\!\left(\frac{\partial \mathbf{v}}{\partial t} \,+\, \mathbf{v}\cdot\!\nabla\mathbf{v}\right)&=\ -\nabla p +\mu\nabla^{2}\mathbf{v} \\ &\quad+ \left[\phi \rho_{p}\,+\, (1\,-\,\phi)\!\left\{\rho_{f}(1\,-\,\beta(T_{f}\,-\,T_{c}))\right\}\right]g \end{aligned} $$
((2))
$$ \begin{aligned} (\rho c)_{f} \left[\frac{\partial T_{f}}{\partial t} + \mathbf{v}\cdot \nabla T_{f}\right]&= k_{f}\nabla^{2} T_{f} +\, (\rho c)_{p}\\ &\quad\times\!\left[\!D_{B} \nabla \phi \!\cdot\! \nabla T_{f} \,+\, D_{T} \frac{\nabla T_{f}\cdot \nabla T_{f}}{T_{f}}\!\right]\\ &\quad+ \frac{h_{fp}}{1-\phi_{0}}\left(T_{p} - T_{f}\right) \end{aligned} $$
((3))
$$ \begin{aligned} \phi_{0}(\rho c)_{p}\left[\frac{\partial T_{p}}{\partial t} + \mathbf{v}_{D} \cdot \nabla T_{p}\right]&=\phi_{0}k_{p}\nabla^{2} T_{p}\\ &\quad+ h_{fp}\left(T_{f} - T_{p}\right) \end{aligned} $$
((4))
$$\begin{array}{@{}rcl@{}} \frac{\partial \phi}{\partial t} + \mathbf{v} \cdot \nabla \phi = D_{B}\nabla^{2} \phi + \frac{D_{T}}{T_{c}} \nabla^{2} T_{f} \end{array} $$
((5))

where v=(u,v,w) is the fluid velocity. In these equations, ρ is the fluid density, (ρ c) f , (ρ c) p , the effective heat capacities of the fluid and particle phases respectively, and k f the effective thermal conductivity of fluid phase. D B and D T denote the Brownian diffusion coefficient and thermophoretic diffusion respectively. In the above equations, both Brownian transport and thermophoresis coefficients are taken to be time independent, in tune with the recent studies that neglect the effect of thermal transport attributed to the small size of the nanoparticles (as per recent arguments by Keblinski and Cahill [28]). Further, Thermophoresis and Brownian transport coefficients are assumed to be temperature - independent due to the fact that the temperature ranges under consideration are not far away from the critical value, and the volume averages over a representative elementary volume.

Assuming the temperature and volumetric fraction of the nanoparticles to be constant at the stress-free boundaries, we may assume the boundary conditions on T and ϕ to be:

$$ \textbf{v}=0,\ \ T=T_{h}, \ \phi=\phi_{1}\ at \ z=0, $$
((6))
$$ \textbf{v}=0,\ \ T=T_{c},\ \phi=\phi_{0}\ at\ z=d, $$
((7))

where ϕ 1 is greater than ϕ 0. To non-dimensionalize the variables we take

$$\begin{array}{@{}rcl@{}} &&\left(x^{*},y^{*},z^{*}\right)=(x,y,z)/d,\ t^{*}=t \alpha_{f} / d^{2}, \alpha_{f} = \frac{k_{f}}{\left(\rho c\right)_{f}}\\ &&\left(u^{*},v^{*},w^{*}\right)=(u,v,w)d/\alpha_{f},\ p^{*}=p d^{2}/\mu \alpha_{f}, \\ &&\phi^{*} = \frac{\phi - \phi_{0}}{\phi_{1} - \phi_{0}},\ \ T^{*}=\frac{T - T_{c}}{T_{h} - T_{c}},\\ \end{array} $$

Equations (1)–(7), then take the form (after dropping the asterisk):

$$ \nabla \cdot \textbf{v} =0, $$
((8))
$$ \begin{aligned} \frac{1}{Pr}\left(\frac{\partial \textbf{v}}{\partial t} + \mathbf{v}\cdot\nabla\mathbf{v}\right)&= -\nabla p +\nabla^{2}\textbf{v} - Rm \hat{e_{z}}\\ &\quad+ Ra T \hat{e_{z}} - Rn \phi \hat{e_{z}}, \end{aligned} $$
((9))
$$ \begin{aligned} \frac{\partial T_{f}}{\partial t} + \textbf{v} \cdot \nabla T_{f} &= \nabla^{2} T_{f} + \frac{N_{B}}{Le} \nabla\phi\cdot\nabla T_{f}\\ &\quad+ \frac{N_{A} N_{B}}{Le}\nabla T_{f} \cdot \nabla T_{f} + N_{H}\left(T_{p} - T_{f}\right), \end{aligned} $$
((10))
$$\begin{array}{@{}rcl@{}} \frac{\partial T_{p}}{\partial t} +\textbf{v}\cdot \nabla T_{p} = \varepsilon\nabla^{2} T_{p} + \gamma N_{H}\left(T_{f} - T_{p}\right) \end{array} $$
((11))
$$\begin{array}{@{}rcl@{}} \frac{\partial\phi}{\partial t} + \textbf{v}\cdot\nabla\phi = \displaystyle\frac{1}{Le} \nabla^{2} \phi + \displaystyle\frac{N_{A}}{Le} \nabla^{2} T_{f}, \end{array} $$
((12))
$$\begin{array}{@{}rcl@{}} \textbf{v}=0,\ \ T=1, \ \phi=1 \ at\ z=0 \end{array} $$
((13))
$$\begin{array}{@{}rcl@{}} \textbf{v}=0,\ \ T=0, \ \phi =0 \ at \ z=1 \end{array} $$
((14))

Here

$$\begin{array}{@{}rcl@{}} &Pr& = \frac{\mu}{\rho \alpha_{f}}, \rm{is\ the\ Prandtl\ number,}\\ &Le&=\frac{\alpha_{f}}{D_{B}}, \rm{is\ the\ Lewis\ number,}\\ &Ra&=\frac{\rho g\beta d^{3}\left(T_{h} - T_{c}\right)}{\mu \alpha_{f}}, \rm{is\ the\ Rayleigh}\\ &&\quad-\rm{Darcy\ number},\\ &Rm&=\frac{\left[\rho_{p} \phi_{0} +\rho\left(1- \phi_{0}\right)\right]g d^{3}}{\mu \alpha_{f}}, \rm{is\ the\ basic\ density}\\ &&\rm{Rayleigh\ number,}\\ &Rn&=\frac{\left(\rho_{p} - \rho\right)\left(\phi_{1} - \phi_{0}\right)g d^{3}}{\mu \alpha_{f}}, \rm{is\ the\ concentration}\\ &&\rm{Rayleigh\ number,}\\ &N_{B}&= \frac{\left(\rho c\right)_{p} \left(\phi_{1} - \phi_{0}\right)}{\left(\rho c\right)_{f}}, \rm{is\ the\ modified\ particle}\\ &&\rm{density\ increment,} \end{array} $$

and

$$\begin{array}{@{}rcl@{}} &N_{A}&= \frac{D_{T}(T_{h} - T_{c})}{D_{B} T_{c} (\phi_{1} - \phi_{0})}, \;\text{is the modified diffusivity}\\ &&\text{ratio which is similar to the Soret parameter that}\\[-2pt] &&\text{arises in cross diffusion in thermal instability,} \end{array} $$
$$\begin{array}{@{}rcl@{}} &N_{H}& = \frac{h_{fp} d^{2}}{\left(1-\phi_{0}\right)k_{f}},\;\text{is the interphase heat transfer}\\ &&\text{parameter or the Nield number},\\ &\gamma & =\frac{\left(1-\phi_{0}\right)\left(\rho c\right)_{f}}{\phi_{0} (\rho c)_{p}},\; \text{is the modified thermal capacity}\\ &&\text{ratio},\\ &\varepsilon & = \frac{k_{p}/(\rho c)_{p}}{k_{f} (\rho c)_{f}},\; \text{is the thermal diffusivity ratio}. \end{array} $$

3 Basic solution

The basic state of the nanofluid layer is assumed to be at rest, therefore we have

$$\begin{array}{@{}rcl@{}} \textbf{v}\,=\,0,\ p\,=\,p_{b}(z), \ T_{f}\,=\,T_{fb}(z),\ T_{p}\,=\,T_{pb}(z), \ \phi \,=\, \phi_{b}(z)\quad\;\; \end{array} $$
((15))

Substituting eq. (15) in Eqs. (10)–(12), we get

$$\begin{array}{@{}rcl@{}} \frac{d^{2} T_{fb}}{d z^{2}} &+& \frac{N_{B}}{Le}\frac{d \phi_{b}}{d z}\frac{d T_{fb}}{d z} + \frac{N_{A} N_{B}}{Le} \left(\frac{d T_{fb}}{d z}\right)^{2} \qquad \\ &+&N_{H}(T_{p}-T_{f})=0 \end{array} $$
((16))

The second and third terms in equation (16) are small [Nield and Kuznetsov [29]], so we have:

$$\begin{array}{@{}rcl@{}} \frac{d^{2} T_{pb}}{d z^{2}}=0,\ \frac{d^{2} T_{fb}}{d z^{2}}=0,\ \frac{d^{2} \phi_{b}}{d z^{2}}=0,\ \end{array} $$
((17))

The boundary conditions for solving the above equation are found as

$$\begin{array}{@{}rcl@{}} T_{fb}=T_{pb}=1,\ \phi_{b}=1,\ \ \rm{at}\ z=0, \end{array} $$
((18))
$$\begin{array}{@{}rcl@{}} T_{fb}=T_{pb}=0,\ \phi_{b}=0,\ \ \rm{at}\ z=1. \end{array} $$
((19))

On solving eq. (17), subject to conditions (18) and (19), we obtain the basic temperature and concentration fields as

$$ T_{fb}\ =\ T_{pb}\ =\ 1-z $$
((20))
$$ \phi_{b} =1-z. $$
((21))

4 Stability analysis

To superimpose the perturbations on the basic state we write

$$\begin{array}{@{}rcl@{}} \textbf{v}=\textbf{v}^{\prime},\ p=p_{b} +p', \ T_{f}=T_{fb} + T_{f}', \qquad \\ T_{p}=T_{pb} + T_{p}',\ \phi = \phi_{b} + \phi'. \end{array} $$
((22))

We substitute the expression (22) in Eqs. (9)–(12), and use the expressions (20) and (21). For simplicity, we consider the case of two dimensional rolls, assuming all physical quantities to be independent of y. The reduced dimensionless governing equations after eliminating the pressure term are

$$ \frac{1}{Pr}\frac{\partial}{\partial t}\left({\nabla_{1}^{2}} \psi\right)= {\nabla_{1}^{4}} \psi - Ra \frac{\partial T_{f}}{\partial x} + Rn\frac{\partial\phi}{\partial x} + \frac{1}{Pr}\displaystyle\frac{\partial\left(\psi,{\nabla_{1}^{2}} \psi\right)}{\partial(x,z)} $$
((23))
$$ \frac{\partial T_{f}}{\partial t} + \frac{\partial \psi}{\partial x} = {\nabla_{1}^{2}} T_{f} + \frac{\partial\left(\psi,T_{f}\right)}{\partial(x,z)} + N_{H} \left(T_{p} -T_{f}\right) $$
((24))
$$ \frac{\partial T_{p}}{\partial t} + \frac{\partial \psi}{\partial x} = {\varepsilon\nabla_{1}^{2}} T_{p} + \frac{\partial\left(\psi,T_{p}\right)}{\partial(x,z)} + \gamma N_{H} \left(T_{f} -T_{p}\right) $$
((25))
$$ \frac{\partial\phi}{\partial t} + \frac{\partial \psi}{\partial x} = \frac{1}{Le} {\nabla_{1}^{2}} \phi+ \frac{N_{A}}{Le} {\nabla_{1}^{2}} T_{f} + \frac{\partial\left(\psi,\phi\right)}{\partial(x,z)} $$
((26))

The equations (23)–(26) are solved subject to stress-free, isothermal, iso-nanoconcentration boundary conditions:

$$\begin{array}{@{}rcl@{}} \psi\ =\ \frac{\partial^{2}\psi}{\partial z^{2}}\ =\ T_{f}\ =\ T_{p}\ =\ \phi\ =\ 0\ \rm{at}\ \ z=0,1 \end{array} $$
((27))

For linear stability analysis we use the normal mode technique and then critical Rayleigh numbers for stationary and oscillatory onset of convection and the frequency of oscillations, ω, are given by

$$ \begin{aligned} Ra^{st}=& \frac{\delta^{6}}{{\alpha_{c}^{2}}}\left(1 + \frac{N_{H}(\varepsilon -1) }{\varepsilon \delta^{2} + (1+\gamma)N_{H}}\right)\\ &- Rn \left\{N_{A} - Le - \frac{N_{H} Le(\varepsilon -1) }{\varepsilon \delta^{2} + (1+\gamma)N_{H}} \right\} \end{aligned} $$
((28))
$$ {\small\begin{aligned} Ra^{osc}=& \frac{\delta^{2}}{\alpha^{2}}\left[\!\delta^{4}\!\left(\!1 \,+\, \frac{N_{H}\left(\varepsilon -1\right)P_{1}}{{P_{1}^{2}} + \omega^{2}}\!\right)\! - \!\frac{\omega^{2}}{Pr}\!\left(\!1 \,-\, \displaystyle\frac{N_{H}(\varepsilon -1)\delta^{2} }{{P_{1}^{2}} + \omega^{2}}\!\right)\!\right] \\ &- \frac{Rn}{\left(\delta^{2} /Le\right)^{2} + \omega^{2}}\left[\frac{\delta^{2}}{Le}\left(P_{2} - \frac{N_{H} \left(\varepsilon - 1\right)\delta^{2} P_{1}}{{P_{1}^{2}} + \omega^{2}}\right) \right.\\&\left.- \,\omega^{2} \left(1 - \displaystyle\frac{N_{H}(\varepsilon -1)\delta^{2} }{{P_{1}^{2}} + \omega^{2}}\right)\right] \end{aligned}} $$
((29))
$$\begin{array}{@{}rcl@{}} {\omega^{2}_{c}}\ = \frac{-X_{2} + \sqrt{{X_{2}^{2}} - 4X_{1}X_{3}}}{2X_{1}} \end{array} $$
((30))

where

$$\begin{array}{@{}rcl@{}} \delta^{2} = \pi^{2} + {\alpha^{2}_{c}} \ \rm{and}\ \alpha_{c}=\displaystyle\frac{\pi}{\sqrt{2}}. \end{array} $$

Also

$$\begin{array}{@{}rcl@{}} X_{1} = P_{3} + \frac{\delta^{4}}{\alpha^{2}} \end{array} $$
$$ \begin{aligned} X_{2} = \frac{P_{3} \delta^{4}}{Le^{2}} &+ P_{3} {P_{1}^{2}} + P_{3} N_{H} P_{1} (\varepsilon -1) + \frac{\delta^{8}}{\alpha^{2} Le^{2}} + \frac{\delta^{4} {P_{1}^{2}}}{\alpha^{2}} \\ &- \frac{N_{H} (\varepsilon -1)\delta^{6}}{\alpha^{2}} + {RnP}_{2} + \frac{Rn\delta^{2}}{Le} \end{aligned} $$
$${\begin{aligned} X_{3} =& \,P_{3} {P_{1}^{2}} \frac{\delta^{4}}{Le^{2}} + P_{3}P_{1}N_{H}(\varepsilon -1)\frac{\delta^{4}}{Le^{2}} + \frac{\delta^{8} {P_{1}^{2}}}{\alpha^{2} Le^{2}} \\ &- \frac{\delta^{10} N_{H} (\varepsilon-1)}{\alpha^{2} Le^{2}} + {RnP}_{2} {P_{1}^{2}} - {RnP}_{1} N_{H} \delta^{2} (\varepsilon -1) \\ &+ \frac{Rn {P_{1}^{2}}\delta^{2}}{Le} - \frac{Rn N_{H} \delta^{4}(\varepsilon -1)}{Le}\\ \end{aligned}} $$

These expressions were obtained from Nield and Kuznetsov by dropping the terms pertaining to porous media.

For local nonlinear stability analysis we take the following Fourier expressions:

$$ \psi =\sum\limits_{n=1}^{\infty}\sum\limits_{m=1}^{\infty} {A_{m n}sin\left(m \alpha x\right)sin\left(n \pi z\right)} $$
((31))
$$ T_{f}=\sum\limits_{n=1}^{\infty}\sum\limits_{m=1}^{\infty} {B_{mn}(t)cos(m \alpha x)sin(n \pi z)} \quad $$
((32))
$$ T_{p}=\sum\limits_{n=1}^{\infty}\sum\limits_{m=1}^{\infty} {C_{mn}(t)cos(m \alpha x)sin(n \pi z)} \quad $$
((33))
$$ \phi=\sum\limits_{n=1}^{\infty}\sum\limits_{m=1}^{\infty} {D_{mn}(t)cos(m\alpha x)sin(n\pi z)} $$
((34))

In what follows we take the modes (1,1) for stream function, and (0,2) and (1,1) for temperature and nanoparticle concentration

$$ \psi =A_{11}(t)sin(\alpha x)sin(\pi z) $$
((35))
$$ T_{f}=B_{11}(t)cos(\alpha x)sin(\pi z)+B_{02}(t)sin(2\pi z) \quad $$
((36))
$$ T_{p}=C_{11}(t)cos(\alpha x)sin(\pi z)+C_{02}(t)sin(2\pi z) \quad $$
((37))
$$ \phi=D_{11}(t)cos(\alpha x)sin(\pi z)+D_{02}(t)sin(2\pi z) \quad $$
((38))

where the amplitudes A 11(t),B 11(t),B 02(t),C 11(t),C 02(t), D 11(t) and D 02(t) are functions of time and are to be determined. Substituting equations (35)–(38) in equations (23)–(26) taking the orthogonality condition with the eigenfunctions associated with the considered minimal model, we get

$$ \frac{d A_{11}(t)}{dt}\ =\ \displaystyle\frac{Pr}{\delta^{2}}\left\{ \alpha \left[Rn D_{11}(t) - Ra B_{11}(t)\right] - \ \delta^{4} A_{11}(t)\right\} $$
((39))
$$ \begin{aligned} \frac{d B_{11}(t)}{dt} =&\, N_{H} \left[C_{11}(t) - B_{11}(t)\right]-\left[{\vphantom{\delta^{2}}}\alpha A_{11}(t) \right.\\ &\left.+ \,\delta^{2} B_{11}(t) + \pi \alpha A_{11}(t) B_{02}(t)\right] \end{aligned} $$
((40))
$$ \begin{aligned} \frac{d B_{02}(t)}{dt} =&\, \frac{1}{2}\left\{\pi \alpha A_{11}(t) B_{11}(t) - 8 \pi^{2} B_{02}(t) \right.\\ &\left.+ \,2 N_{H}\left[C_{02} - B_{02}\right]\right\} \end{aligned} $$
((41))
$$ \begin{aligned} \frac{d C_{11}(t)}{dt}\! = &\!- \!\left\{\alpha A_{11}(t)\! +\! \varepsilon\delta^{2} C_{11}(t)\! -\! \gamma N_{H} [B_{11}(t) - C_{11}(t)]\right.\\ &+\left.\pi\alpha A_{11}(t) C_{02}(t){\vphantom{8\pi^{2}\varepsilon C_{02}}}\right\} \end{aligned} $$
((42))
$$ \begin{aligned} \frac{d C_{02}(t)}{dt} =& \frac{1}{2} \left\{ \pi\alpha A_{11}(t) C_{11}(t) - 8\pi^{2}\varepsilon C_{02}(t)\right.\\ &\left.+ \,2\gamma N_{H}\left[B_{02}(t) - C_{02}(t)\right] \!{\vphantom{8\pi^{2}\varepsilon C_{02}}}\right\} \end{aligned} $$
((43))
$$ \begin{aligned} \frac{d D_{11}(t)}{dt} =& -\alpha A_{11}(t) - \frac{\delta^{2}}{Le}D_{11}(t) - \frac{N_{A} \delta^{2}}{Le}B_{11}(t)\\ &- \pi\alpha A_{11}(t) D_{02}(t) \end{aligned} $$
((44))
$$ \begin{aligned} \frac{d D_{02}(t)}{dt}\ =&\, - \frac{4\pi^{2}}{Le}\left[D_{02}(t) + N_{A} B_{02}(t)\right] \\&+\pi \alpha A_{11}(t)D_{11}(t) \end{aligned} $$
((45))

The above system of simultaneous autonomous ordinary differential equations be subsequently solved numerically using Runge-Kutta-Gill method.

5 Heat and nanoparticle concentration transport

The thermal Nusselt number for fluid phase, N u f (t) is defined as

$$ \begin{aligned} {Nu}_{f}(t) &= \frac{\rm{Heat\ transport\ by}\ (\rm{conduction} + \rm{convection})}{\rm{Heat\ transport\ by\ conduction}}\\ &= 1 + \left[\frac{\int\limits_{0}^{2\pi/\alpha_{c}}{\left(\frac{\partial T_{f}}{\partial z}\right)dx}}{\int\limits_{0}^{2\pi/\alpha_{c}}{\left(\frac{\partial T_{b}}{\partial z}\right)dx}}\right]_{z=0} \end{aligned} $$
((46))

substituting equations (20) and (36) in eq. (46), we get

$$\begin{array}{@{}rcl@{}} {Nu}_{f}(t)= 1 - 2\pi B_{02}(t) \end{array} $$
((47))

The thermal Nusselt number for particle phase, N u p (t), and the nanoparticle concentration Nusselt number, N u ϕ (t), are defined similar to the thermal Nusselt number. Following the procedure adopted for arriving at N u f (t), one can obtain the expression for N u p (t) and N u ϕ (t) in the form:

$$\begin{array}{@{}rcl@{}} {Nu}_{p}(t)= 1 - 2\pi C_{02}(t) \end{array} $$
((48))
$$\begin{array}{@{}rcl@{}} {Nu}_{\phi}(t)= \left(1- 2\pi D_{02}(t)\right) + N_{A}\left(1-2\pi B_{02}(t)\right) \end{array} $$
((49))

6 Results and discussion

The expressions for the Rayleigh number for both stationary and oscillatory convection have been presented analytically in equations (28) and (29) respectively. Considering the expression for stationary convection in eq. (28), we have

$$ \begin{aligned} Ra^{st}=&\, \frac{\delta^{6}}{{\alpha_{c}^{2}}}\left(1 + \frac{N_{H}(\varepsilon -1) }{\varepsilon \delta^{2} + \left(1+\gamma\right)N_{H}}\right)\\ &- Rn \left\{N_{A} - Le - \frac{N_{H}(\varepsilon -1)\delta^{2}}{\varepsilon \delta^{2} + (1+\gamma)N_{H}} \right\} \end{aligned} $$
((50))

For thermal equilibrium condition N H =0, so we get

$$\begin{array}{@{}rcl@{}} Ra^{st}= \frac{\delta^{6}}{{\alpha_{c}^{2}}} - Rn \left(N_{A} - Le\right) \end{array} $$
((51))

This result agrees with the result obtained by Nield and Kuznetsov under LTNE.

In Figure 1, we present linear stability curves showing the stationary and oscillatory modes of convection. In the figure we see that the region of over stability under-lies the region of damped oscillations, i.e. at the start of instability, oscillatory or periodic pattern of motion prevails. Therefore we can say that the Principle of Exchange of stabilities is invalid [30,31]. This can be explained as since oscillatory motion is prevalent at the onset of convection, the restoring forces provoked are strong enough to prevent the system from tending away from equilibrium.

Figure 1
figure 1

Linear stability curve showing stationary and oscillatory modes of convection.

Full size image

In Figure 2(a-f) we present neutral stability curves for R a st versus the wavenumber α for the fixed values of R n,L e,N A ,ε,γ and N H , respectively, with variation in one of these parameters. In all these plots, it is interesting to note that the value of Ra starts from a higher note, falls rapidly with increasing α, and then increases steadily. The Figure 2(a), (b), (d) and (e) correspond to the variation of Ra with respect to α at different values of concentration Rayleigh number Rn, Lewis number Le, thermal diffusivity ratio ε, and modified thermal capacity ratio γ. These plots reveal that on increasing the value of these parameters, the value of R a cr increases, i.e. the system tends to stabilize. However, in the Figure 2(c) and (f), it is to be noted that the effect of the parameters N A and N H is to destabilize the system. As we increase their value, the value of R a cr decreases, indicating that the convection starts earlier.

Figure 2
figure 2

Neutral stability curves for different values of (a) R n , (b) L e , (c) N A , (d) ε , (e) γ , (f) N H .

Full size image

In the Figure 3, we draw the neutral stability curve for LTNE and LTE. We see that the value of Rayleigh number Ra is less in case of LTNE than LTE. This implies that convections starts earlier in the case of LTNE than LTE. The observed phenomenon may be attributed to the fact that because of temperature difference between the fluid and particle phases, there occurs transfer of energy between them. This leads to a chaotic state and enhances the onset of convection in case of LTNE.

Figure 3
figure 3

Comparison of the value of Rayleigh number R a for LTNE and LTE.

Full size image

In the Figure 4, we compare the Rayleigh number Ra for nanofluids with ordinary fluids under thermal nonequilibrium conditions. It is to be noted that the value of Rayleigh number is less in the case of ordinary fluid than nanofluid, or to say convection sets in earlier in ordinary fluids than nanofluids. This implies that the thermal conductivity of nanofluids is higher than ordinary fluids.

Figure 4
figure 4

Comparison of the value of Rayleigh number Ra for Nanofluid with Ordinary fluid.

Full size image

The nature of critical values of Rayleigh number Ra and the critical values of wave number α as functions of inter phase heat transfer parameter or Nield number for fluid/nanoparticle inter phase, N H , for R n=4,L e=900,N A =1,ε=0.04,γ=5, with a variation in the value of one of these parameters, are shown in Figures 5 and 6 respectively. For very small and large values of N H , we observe that the stability criterion is independent of its value, and that the value of N H play a significant role in the stability criterion only in the intermediate range. The reason behind this state being, that at N H →0, there occurs almost zero heat transfer between fluid/nanoparticle inter phase, and the properties of nanoparticle do not interfere in the onset of convection. While, when N H →∞, the two have attained almost the equal temperatures and behave as a single phase. Between these two extremes, a LTNE effect is observed being attributed to N H .

Figure 5
figure 5

Variation of critical Rayleigh number R a cr with N H for different values of (a) R n , (b) L e , (c) N A , (d) γ and (e) ε .

Full size image
Figure 6
figure 6

Variation of critical wave number α c with N H for different values of (a) R n , (b) L e , (c) N A , (d) γ and (e) ε .

Full size image

In the Figure 5, we present the variation of critical Rayleigh number R a cr with Nield number for the fluid/particle inter phase N H for different parameters. The figure indicates that the value of R a cr decreases from high values for very small N HP to small LTNE value for large N HP . The system tends to destabilize for the intermediate values of N HP . The effect of the parameters concentration Rayleigh number Rn, Lewis number Le, thermal diffusivity ratio ε, and modified thermal capacity ratio γ, on the system is to inhibit the decrease in the value of the critical Rayleigh number R a cr , thus preventing the system from destabilization. While for the other parameter, modified diffusivity ratio N A , on increasing its values, the value of R a cr falls further trending the system towards destabilization.

In the Figure 6, we have exhibited the critical wavenumber α c as a function of N H for both stationary and oscillatory convection. We observe that value of critical wavenumber α c decreases with increasing N H from high values when N H is small, to its minimum LTNE value for intermediate N H , and finally bounces back to higher values for large N H . This implies that the the value of critical wavenumber α c approaches to its LTE value when N H →0 and N H →∞. This is quite obvious as the corresponding physical situation are anonymous. At N H →0, the particle phase does not interfere with the thermal field of the fluid, which is free to act independently, while as N H →∞, the particle/fluid phase have attained the identical temperatures, and behave as single phase only. We conclude that as time passes, and heat intensifies, the nanofluids behave more like a single phase fluid rather than like a conventional solid-liquid mixture. For the parameters, R n,L e,N A , and ε, we see that an increase in their values has effect on the critical value of wave number α c only when N H →0 and N H →∞. For intermediate values of N, i.e. when α c falls to its minimum LTNE value, the value of α c remains independent of these parameters. But for γ, as we increase its value, minimum value of α c decreases. Also, we notice that the minimum value of α c is less for oscillatory convection as compared to stationary convection.

The variation of critical frequency \({\omega _{c}^{2}}\) for the oscillatory mode of convection with Nield number N H for different parameter values is shown in Figure 7(a)–(f). It is clear from these figures that the critical frequency decreases from a constant value, when N H is very small to its minimum value, and then with further increase in N H , it bounces back to another constant value for large values of N H . Figure 7(a) displays the effect of concentration Rayleigh number Rn on the value of critical frequency \({\omega _{c}^{2}}\). We can observe that an increase in the value of Rn inhibits the decrease in the value of critical frequency \({\omega _{c}^{2}}\). A similar effect on critical frequency \({\omega _{c}^{2}}\) has been observed in Figure 7(d), 7(e) and 7(f) with modified thermal capacity ratio γ, thermal diffusivity ratio ε, and Prandtl number Pr. The parameters, Lewis number Le, and modified diffusivity ratio N A do not have a very pronounced effect on the value of critical frequency \({\omega _{c}^{2}}\). In general, the value of critical frequency \({\omega _{c}^{2}}\) decreases from its LTE value to its LTNE value, and then increases back to attain another constant value in the intermediate range.

Figure 7
figure 7

Variation of critical frequency \({{\omega _{c}^{2}}}\) with N H for different values of (a) R n , (b) L e , (c) N A , (d) γ , (e) ε and P r .

Full size image

6.1 Non-linear unsteady stability analysis

The linear solutions exhibit a considerable variety of behavior of the system and the transition from linear to non-linear convection can be quite complicated, but interesting to deal with. We need to study the time dependent results to analyze the same. This transition can be well understood by the analysis of the seven coupled ordinary differential eqs. (39)–(45) whose solutions give a detailed description of the two-dimensional problem. We solve the eqs. (39)–(45) numerically, using Runge −Kutta−Gill Method, and calculate Nusselt numbers as function of time t. Also the seven-mode Differential eqs. (39)–(45) have an interesting property in phase-space:

$$ \begin{aligned} \frac{\partial \dot{{A}_{11}}}{\partial A_{11}} + \frac{\partial \dot{{B}_{11}}}{\partial B_{11}}+ \frac{\partial \dot{{B}_{02}}}{\partial B_{02}}+ \frac{\partial \dot{{C}_{11}}}{\partial C_{11}}+ \frac{\partial \dot{{C}_{02}}}{\partial C_{02}} + \frac{\partial \dot{{D}_{11}}}{\partial D_{11}}+ \frac{\partial \dot{{D}_{02}}}{\partial D_{02}}\\ = - \left[\vphantom{\frac{\delta^{2}}{Le}}\delta^{2} Pr + N_{H} + \delta^{2} +4\pi^{2} + N_{H} + \gamma_{p} N_{H}\right.\\ +\left. \varepsilon \delta^{2} + 4\pi^{2} \varepsilon + \gamma N_{H} + \frac{\delta^{2}}{Le} + \frac{4\pi^{2}}{Le} \right] <0 \end{aligned} $$
((52))

which indicates that the system is dissipative and bounded. This implies that the trajectories of the eqs. (39)–(45) will be attracted to a set of measure zero in the phase space, in other words they will approach to a fixed point, a limit cycle or to a unknown attractor.

The nature of Nusselt numbers, N u ϕ,N u(fluid), and Nu(particle), as a function of time t, for R n=4,L e=10,N A =5,R a=5000,P r=0.75,ε=0.04,N H =20, and γ=0.5 with a variation in the value of one of these parameters, is shown in Figures 8 and 9 respectively. These figures indicate that initially, when time is small, there occurs large scale oscillations in the values of N u ϕ,N u(fluid), and Nu(particle), indicating an unsteady rate of mass and heat transfer in the fluid and particle phases. As time passes by, these approach to steady values, corresponding to a near conduction instead of convection stage.

Figure 8
figure 8

Variation of Concentration Nusselt Number N u ϕ with time t for different values of (a) R n , (b) L e , (c) N A , (d) R a , (e) ε , (f) P r , (g) γ , and (h) N H .

Full size image
Figure 9
figure 9

Variation of Nusselt Number N u ( f l u i d ) with time t for different values of (a) R n , (b) L e , (c) N A , (d) R a , (e) ε , (f) P r , (g) γ , and (h) N H .

Full size image

In the Figure 8, the transient nature of concentration Nusselt number or Sherwood number (as some researchers name it), is visible. We can observe that the effect of increasing the value of modified diffusivity ratio or Soret parameter N A , thermal Rayleigh number Ra, Prandtl number Pr, modified thermal capacity ratio γ, and the Nield number N H , on the amplitude of oscillations is to increase it, i.e., an increase in the value of these parameters brings about an increase in the rate of mass transfer across the nanofluid layer.

Figure 9 depicts the transient nature of Nusselt number for the fluid phase. There occurs large amount of heat transfer in the fluid phase initially, and with large time the amount of heat transfer approaches a near constant value. We can observe that the effect of increasing the value of thermal Rayleigh number Ra, Prandtl number Pr, modified thermal capacity ratio γ, and the Nield number N H , on the amplitude of oscillations is to increase it, i.e., an increase in the value of these parameters brings about an increase in the rate of heat transfer across the fluid phase.

The transient nature of Nusselt number for particle phase has been shown in Figure 10. We see that the amplitude of heat transfer in particle phase is small initially, but increases rapidly with time t to approach a steady value for large values of time t. The effect of the parameters R a,P r,γ, and N H on the amplitude of oscillations is to increase them.

Figure 10
figure 10

Variation of Nusselt Number N u ( p a r t i c l e ) with time t for different values of (a) R n , (b) L e , (c) N A , (d) R a , (e) ε , (f) P r , (g) γ , and (h) N H .

Full size image

7 Conclusions

We considered linear stability analysis in a horizontal nanofluid layer, heated from below and cooled from above, incorporating the effect of Brownian motion along with thermophoresis, under non-equilibrium conditions. Further bottom heavy suspension of nanoparticles has been considered. Linear analysis has been made using normal mode technique, while for weakly nonlinear analysis, we have used a minimal representation of truncated Fourier Series involving only two terms. Then the effect of various parameters on the onset of thermal instability has been found.The results have been presented graphically. We draw the following conclusions:

  1. 1.

    The effect of the concentration Rayleigh number Rn, Lewis number Le, modified thermal capacity ratio γ, and thermal diffusivity ratio ε is to stabilize the system.

  2. 2.

    Convection sets in earlier for LTNE as compared to LTE.

  3. 3.

    The value of critical wave number α c is lower for oscillatory convection then for stationary convection.

  4. 4.

    The effect of time on Nusselt numbers is found to be oscillatory, when t is small. However when time t becomes very large Nusselt number approaches the steady value.

  5. 5.

    On increasing the value of thermal Rayleigh number Ra, the rate of mass and heat transfer is increased.

8 Nomenclature

8.1 Latin Symbols

D B Brownian Diffusion coefficient. D T thermophoretic diffusion coefficient.Pr Pradtl number.d dimensional layer depth.Le Lewis number. N A modified diffusivity ratio. N B modified particle-density increment. N H Nield Number.p pressure.g Gravitational acceleration.Ra thermal Rayleigh-Darcy number, Rm basic density Rayleigh number,Rn concentration Rayleigh number, t time.T nanofluid temperature. T c temperature at the upper wall. T h temperature at the lower wall. v nanofluid velocity. (x,y,z) Cartesian coordinates.

8.2 Greek symbols

α f thermal diffusivity of the fluid. β proportionality factor. γ modified thermal capacity ratio. ε thermal diffusivity ratio. ψ stream function. μ viscosity of the fluid. ρ f fluid density. ρ p nanoparticle mass density (ρ c) f Heat capacity of the fluid. (ρ c) p Heat capacity of the nanoparticle material. ϕ nanoparticle volume fraction. α wave number. ω frequency of oscillations.

Subscriptsb basic solution.f Fluid phase.p Particle phase.c critical.

Superscripts ∗ dimensional variable’ perturbation variable

Operators ∇2 \(\displaystyle \frac {\partial ^{2}}{\partial x^{2}} + \displaystyle \frac {\partial ^{2}}{\partial y^{2}} + \displaystyle \frac {\partial ^{2}}{\partial z^{2}}\).\({\nabla _{1}^{2}}\) \(\displaystyle \frac {\partial ^{2}}{\partial x^{2}} + \displaystyle \frac {\partial ^{2}}{\partial z^{2}}\).