Flow patterns in linear state of Rayleigh–Bénard convection in a rotating nanofluid layer

Abstract

In this paper, we study the flow patterns of a rotating, horizontal layer of a Newtonian nanofluid. The nanofluid layer incorporates the effect of Brownian motion along with thermophoresis. In order to find the expressions for streamlines, isotherms, and iso-nanohalines, a minimal representation of the truncated Fourier series of two terms, has been used. The results obtained imply that the magnitude of the streamlines, and the contours of the isotherms and the iso-nanohalines, turn flatter and concentrated near the boundaries for large value of Ra _cr , indicating a delay in the onset of convection.

Introduction

The word “Nanofluids” was first used by Choi (1995), at the A.N.L.,USA., while he was working on improved heat transfer mediums to be used in industries like power manufacturing, transportation, electronics, HVAC etc. Nanofluids are engineered colloidal suspensions of nanometer sized (1–100 nm) particles in ordinary heat transfer fluids such as water, ethylene glycol, engine oils to name a few. Since then, researchers have gained interest in studying these fluids. The nanoparticles used in these base fluids include metallic or metallic oxide particles (Cu, Cuo, Al₂O₃), carbon nanotubes, etc. In the past one and a half decades, researchers like Choi (1999), Masuda et al. (1993), Eastman et al. (2001), Das et al. (2003), Xie et al. (2001, 2002), Wang et al. (1999), Patel et al. (2003), have found an increase in the thermal conductivity of ordinary fluids by 10 to 40 %, using nanoparticle concentrations ranging in between 0.11 vol.% and 4.3 vol.%. They used nanoparticles of copper, silver, gold, copper-oxide, alumina, SiC, in base fluids such as water, ethylene-glycol, toulene, etc.

Buongiorno, conducted an extensive study of nanofluids in an attempt to account for the unusual positive behavior of nanofluids over ordinary fluids, and came out with a model incorporating the effects of Brownian diffusion and the thermophoresis. With the help of these equations, studies were conducted by Tzou (2008a, b), Kim et al. (2004, 2007) and more recently by Nield and Kuznetsov (2009, 2010), Agarwal et al. (2012), Bhadauria and Agarwal et al. (2011a, b, 2012), Agarwal and Bhadauria (2011, 2013).

In this study, the flow patterns of a rotating nanofluid layer, for the classical Rayleigh B$\acute{\hbox {e}}$nard problem, have been investigated, It has been assumed that the nanoparticles are suspended in the nanofluid using either surfactant or surface charge technology, preventing the agglomeration and deposition of these.

Governing equations

We consider a nanofluid layer, confined between two free-free horizontal boundaries atz = 0 andz = d, heated from below and cooled from above. The boundaries are perfect conductors of heat and nanoparticle concentration. The nanofluid layer is extended infinitely in x and y-directions, and z-axis is taken vertically upward with the origin at the lower boundary. The fluid layer is rotating uniformly about z-axis with uniform angular velocity $\mathbf{\Upomega}.$ The Coriolis effect has been taken into account by including the Coriolis force term in the momentum equation, whereas, the centrifugal force term has been considered to be absorbed into the pressure term. In addition, the local thermal equilibrium between the fluid and solid has been considered, thus the heat flow has been described using one equation model. T _h and T _c are the temperatures at the lower and upper walls respectively such that T _h  > T _c . Employing the Oberbeck–Boussinesq approximation, the governing equations to study the thermal instability in a nanofluid layer are (Buongiorno 2006; Tzou 2008a, b; Nield and Kuznetsov 2009, 2010):

$$ \nabla\cdot {\mathbf{v}} =0 $$

(1)

$$ \begin{aligned} \rho_{\rm f}\left(\frac{\partial {\mathbf{v}}}{\partial t} + {\mathbf{v}} \cdot\nabla{\mathbf{v}}\right)&=\,-\nabla p +\mu\nabla^2{\mathbf{v}} + [\phi \rho_{\rm p} + (1-\phi)\{\rho_{\rm f}(1-\beta(T_f-T_c))\}]{\mathbf{g}}\\ &\quad+ \frac{2}{\delta}({\mathbf{v}}\times {\mathbf{\Upomega}}) \end{aligned} $$

(2)

$$ (\rho c)_f \left[\frac{\partial T_f}{\partial t} + {\mathbf{v}}\cdot \nabla T_f\right]= k_f\nabla^2 T_f + (\rho c)_p \left[D_B \nabla \phi \cdot \nabla T_f + D_T \frac{\nabla T_f\cdot \nabla T_f}{T_f}\right] $$

(3)

$$ \frac{\partial \phi}{\partial t} + {\mathbf{v}} \cdot \nabla \phi = D_B\nabla^{2} \phi + \frac{D_T}{T_c} \nabla^{2} T_f $$

(4)

where $\mathbf{v} = (u,v,w)$ is the fluid velocity. In these equations,ρ is the fluid density, (ρc)_f, (ρc)_p, the effective heat capacities of the fluid and particle phases respectively, and k _f the effective thermal conductivity of fluid phase. D_B and D_T denote the Brownian diffusion coefficient and thermophoretic diffusion respectively.

Assuming the temperature and volumetric fraction of the nanoparticles to be constant at the stress-free boundaries, we may assume the boundary conditions on T andϕ to be:

$$ {\mathbf{v}}=0, \, T=T_h, \, \phi=\phi_1\,\, at \, z=0, $$

(5)

$$ {\mathbf{v}}=0, \, T=T_c,\, \phi=\phi_0\,\, at \, z=d, $$

(6)

whereϕ₁ is greater thanϕ₀. To non-dimensionalize the variables we take

$$ \begin{aligned} &(x^*,y^*,z^*)=(x,y,z)/d,\,(u^*,v^*,w^*)=(u,v,w)d/\alpha_f,\,t^*=t \alpha_f / d^2, \\ &\alpha_f = \frac{k_f}{(\rho c)_f},\,\,p^*=p d^2/\mu \alpha_f,\,\,\phi^* = \frac{\phi - \phi_0}{\phi_1 - \phi_0},\,\,T^*= \frac{T - T_c}{T_h - T_c}. \end{aligned} $$

Equations (1)–(6), then take the form (after dropping the asterisk):

$$ \nabla \cdot {\mathbf{v}} =0, $$

(7)

$$ \frac{1}{Pr}\left(\frac{\partial {\mathbf{v}}}{\partial t} + {\mathbf{v}}\cdot\nabla{\mathbf{v}}\right)= -\nabla p +\nabla^2{\mathbf{v}} - Rm \hat{ e_z} + Ra T \hat{e_z} - Rn \phi \hat{e_z}+\sqrt{Ta}({\mathbf{v}}\times\hat{k}), $$

(8)

$$ \frac{\partial T_f}{\partial t} + {\mathbf{v}} \cdot \nabla T_f = \nabla^2 T_f + \frac{N_B}{Le} \nabla\phi\cdot\nabla T_f + \frac{N_A N_B}{Le}\nabla T_f \cdot \nabla T_f, $$

(9)

$$ \frac{\partial\phi}{\partial t} + {\mathbf{v}}\cdot\nabla\phi = \frac{1}{Le} \nabla^2 \phi + \frac{N_A}{Le} \nabla^2 T_f, $$

(10)

$$ {\mathbf{v}}=0,\, \, T=1, \, \phi=1 \, at\,\, z=0, $$

(11)

$$ {\mathbf{v}}=0,\, \, T=0, \, \phi =0 \,\, at \, z=1. $$

(12)

Here

Ta :

$\left(\frac{2 \mathbf{\Upomega} K}{\nu \delta}\right)^2,$ is the Taylor's number,

Pr :

$\frac{\mu}{\rho_f\,k_T},$ is the Prandtl number,

Le :

$\frac{\alpha_f}{D_B},$ is the Lewis number,

Ra :

$\frac{\rho g\beta d^3(T_h - T_c)}{\mu \alpha_f},$ is the Thermal Rayleigh number,

Rm :

$\frac{[\rho_p \phi_0 +\rho(1- \phi_0)]g d^3}{\mu \alpha_f},$ is the basic density Rayleigh number,

Rn :

$\frac{(\rho_p - \rho)(\phi_1 - \phi_0)g d^3}{\mu \alpha_f},$ is the concentration Rayleigh number,

N _B :

$\frac{(\rho c)_p (\phi_1 - \phi_0)}{(\rho c)_f},$ is the modified particle density increment,

and

N _A :

$\frac{D_T(T_h - T_c)}{D_B T_c (\phi_1 - \phi_0)},$ is the modified diffusivity ratio which is similar to the Soret parameter that arises in cross diffusion in thermal instability.

Basic solution

At the basic state the nanofluid is assumed to be at rest, therefore the quantities at the basic state will vary only in z-direction, and are given by

$$ {\mathbf{v}}=0,\,T=T_{\rm b}(z),\,\phi = \phi_{\rm b}(z)\,p=p_{\rm b}(z). $$

(13)

Substituting Eq. (13) in Eqs. (9) and (10), we get

$$ \frac{d^2 T_{\rm b}}{d z^2} + \frac{N_B}{Le}\frac{d \phi_{\rm b}}{d z}\frac{d T_b}{d z} + \frac{N_A N_B}{Le} \left(\frac{d T_{\rm b}}{d z}\right)^2=0, $$

(14)

$$ \frac{d^2 \phi_{\rm b}}{d z^2}+N_A\frac{d^2 T_{\rm b}}{d z^2} =0. $$

(15)

Employing an order of magnitude analysis (Kuznetsov and Nield 2010), we have:

$$ \frac{d^2 T_{\rm b}}{d z^2}=0,\,\,\,\frac{d^2 \phi_{\rm b}}{d z^2}=0 $$

(16)

The boundary conditions for solving (16) can be obtained from Eqs. (11) and (12) as:

$$ T_{\rm b}=1,\,\phi_{\rm b}=1,\,\mathrm{{at}\,z=0,} $$

(17)

$$ T_b=0,\,\phi_b=0,\,\mathrm{{at}\,z=1.} $$

(18)

The remaining solution p_b(z) at the basic state can easily be obtained by substituting T_b in Eq. (16), and then integrating Eq. (8) for p_b.

Solving Eq. (16), subject to conditions (17) and (18), we obtain:

$$ T_{\rm b}=1-z, $$

(19)

$$ \phi_{\rm b} =1-z. $$

(20)

Stability analysis

Superimposing perturbations on the basic state as listed below:

$$ {\mathbf{v}}={\mathbf{v}}^\prime,\,p=p_{\rm b} +p^{\prime }, \,T=T_{\rm b} + T^{\prime }, \,\phi = \phi_{\rm b} + \phi^{\prime }. $$

(21)

We consider the situation corresponding to two dimensional rolls for the ease of calculations, and take all physical quantities to be independent of y. The reduced dimensionless governing equations after eliminating the pressure term and introduction of the stream function come out as

$$ \frac{1}{Pr}\frac{\partial}{\partial t}(\nabla_1^2 \psi)= \nabla_1^4 \psi - Ra \frac{\partial T_f}{\partial x} + Rn \frac{\partial\phi}{\partial x} + \frac{ \partial(\psi,\nabla_1^2 \psi)}{\partial(x,z)} +Ta\frac{ \partial^2}{\partial z^2}\frac{\partial\psi}{\partial x} $$

(22)

$$ \frac{\partial T_f}{\partial t} + \frac{\partial \psi}{\partial x} = \nabla_1^2 T_f + \frac{\partial(\psi,T_f)}{ \partial(x,z)} $$

(23)

$$ \frac{\partial\phi}{\partial t} + \frac{\partial \psi}{\partial x} = \frac{1}{Le} \nabla_1^2 \phi+ \frac{N_A}{Le} \nabla_1^2 T_f + \frac{\partial(\psi,\phi)}{ \partial(x,z)} $$

(24)

The Eqs. (22)–(24) are solved subject to idealized stress-free, isothermal, iso-nanoconcentration boundary conditions so that temperature and nanoconcentration perturbations vanish at the boundaries, that is

$$ \psi\,=\,\frac{\partial^2\psi}{\partial z^2}\,=\,T\,=\,\phi\,=\, 0\,\,{{\rm at}\,\,z=0,1} $$

(25)

The choice of these boundary conditions, though not very liable physically, eases the difficulty of mathematical calculations not ignoring the physical effects totally.

The linear stability analysis is well studied and reported by Kuznetsov and Nield (2010). The critical Rayleigh numbers for stationary and oscillatory onset of convection and the frequency of oscillations are obtained as

$$ Ra^{st}= \frac{1}{\alpha_c ^2}(\delta^6+Ta\pi^2) + Rn (Le-N_A) $$

(26)

$$ Ra^{osc}= Ra^{st} + \omega^2\left[\frac{Rn N_A Le^2}{\delta^4 + \omega_c^2 Le^2} + \frac{Ta \pi^2(1-1/Pr)}{\alpha^2_c Pr (\delta^4 + \omega_c ^2/Pr^2)}\right], $$

(27)

$$ \omega^2 =\,\frac{-X_2 + \sqrt{X_2^2 - 4 X_1 X_3}}{2 X_1} $$

(28)

where δ² = π² + α ² _c and $\alpha_c= \frac{\pi}{\sqrt{2}}$

$$ \begin{aligned} &X_1=\frac{T_2Le^2}{Pr^2}, \qquad X_2 = \frac{T_1 }{Pr^2}+T_2\delta^4\left(Le^2 + \frac{1}{Pr^2}\right)+T_3Le^2, \qquad X_3=(T_1+T_2\delta^4+T_3)\delta^4. \\ &T_1=Rn Le\delta^2(1-Le+N_A), \qquad T_2=\frac{\delta^4}{ \alpha_c^2}\left(1+\frac{1}{Pr}\right), \qquad T_3=\frac{Ta \pi^2\delta^2}{\alpha_c^2}\left(1-\frac{1}{Pr}\right). \end{aligned} $$

The minimal expression of a severely truncated representation of Fourier series for stream function, temperature and nanoparticle concentration, is of the form

$$ \psi =A_{11}(t){\rm sin}(\alpha x){\rm sin}(\pi z) $$

(29)

$$ T=B_{11}(t){\rm cos}( \alpha x){\rm sin}(\pi z)+B_{02}(t){\rm sin}(2\pi z) $$

(30)

$$ \phi=C_{11}(t){\rm cos}(\alpha x){\rm sin}(\pi z)+C_{02}(t){\rm sin}(2\pi z) $$

(31)

where the amplitudes A₁₁(t), B₁₁(t), B₀₂(t), C₁₁(t) and C₀₂(t) are functions of time and are to be determined. It has been shown recently by Siddheshwar et al. (2010, 2013) that the minimal system mimics many properties of the full system. In particular, it has been shown that a higher-mode model predicts essentially the same results as the minimal system. This points to convergence of the double Fourier series.

Results and discussion

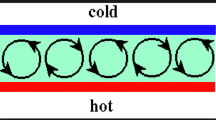
Analytical expressions have been obtained for the Rayleigh numbers pertaining to linear mode of convection. These are used to study the flow patterns by drawing the Figs. 1, 2, 3 respectively for streamlines, isotherms and the iso-nanohalines for Ra _cr and Ra _cr  × 10 at Rn = 4, Le = 10, N _A  = 5, Ta = 50. The range of the numerical values of these physical quantities, though not fixed, have been considered in accordance as specified by Buongiorno, and Tzou in their articles. Streamlines depict fluid flow, isotherms indicate the temperature distribution, while the iso-nanohaline depict the movement of the nanoparticles with in the system. Their study with respect to the critical Rayleigh number will help us in understanding the onset of convective rolls with in the system. This type of conditions are encountered in some places like in the case of geothermal regions, or in the atmosphere, where the fluid layer could be a nanofluid. The expression for stationary Rayleigh number is

$$ Ra^{st}= \frac{1}{\alpha_c ^2}(\delta^6+Ta\pi^2) + Rn (Le-N_A) $$

(32)

For ordinary fluids, Le = 0 = N _A and non-rotating case Ta = 0, we obtain

$$ Ra^{st}= \frac{1}{\alpha_c ^2}(\delta^6) $$

(33)

which is a classical result for all fluids. Thus it is interesting to observe in this case, that to the value of Rayleigh number for ordinary fluids, we have added a positive term in the form of Rn(Le − N _A ). We can say that this is a positive term as the experimentally determined values of Rn are in the range 1 − 10, for N _A are 1 − 10, while of Le are large enough, of the order 10 − 10⁶. Thus the value of Ra _cr will be higher in the case of nanofluids than ordinary fluids implying a delay in the onset of convection in this case. Thus to say, more heat is required by nanofluids for convection to start in. This behavior may be attributed to the property of high thermal conductivity of nanofluids which delays the occurrence of density differences across the fluid layer brought about by heating, thus delaying the onset of convection. This implies that the heat transferred by nanofluids will be more than ordinary fluids, making them ideal heat transfer mediums.

Fig. 1

Streamlines for Rn = 4,  Le = 10,  N _A  = 5,  Ta = 50 aRa _cr ,   bRa = Ra _cr  × 10 and cRa = Ra _cr  × 100

First we consider Fig. 1a–c for streamlines. From the figures we observe that the magnitude of the stream function increases with an increase in the value of Ra. In these figures,the sense of motion in the subsequent cells is alternately identical with and opposite to that of the adjoining cell. From the Fig. 2a–c, which show the isotherms, we find that isotherms are flat near the walls, while they are in the form of contour in the middle of the fluid layer. Further the contours become more flat and concentrated near the boundaries as we increase the critical Rayleigh number. This depicts a delay in the onset of instability with an increase in the value of the critical Rayleigh number.

Fig. 2

Isotherms for Rn = 4,  Le = 10,  N _A  = 5,  Ta = 50 aRa _cr ,   bRa = Ra _cr  × 10 and cRa = Ra _cr  × 100

In Fig. 3a–c, we depict the iso-nanohalines. These iso-nanohalines show more homogeneous structure. Here also the contours turn concentrated towards the boundaries with an increase in the value of the critical Rayleigh number. This pattern is also in denotes a delay in the onset of instability with an increase in the value of the critical Rayleigh number.

Fig. 3

Iso-nanoconcentrations for Rn = 4,  Le = 10,  N _A  = 5,  Ta = 50  aRa _cr ,  bRa = Ra _cr  × 10 and cRa = Ra _cr  × 100

Conclusions

Dealing with a bottom heavy suspension of nanoparticles, heated from below and cooled from above, we obtained the Rayleigh numbers for the linear onset of convection. These were used to draw streamlines, isotherms and iso-nanohalines, and the it was concluded that

• 1. The magnitude of stream functions increases on increasing the value of Ra.

• 2. The isotherms are flat near the boundaries, while they are in the form of contours in the center of the porous medium.