Abstract
The extraordinary enhancement in heat transfer efficiency of nanofluids at extremely low volume fractions has attracted a lot of attention in identifying the governing mechanisms. The nanoscale effects, Brownian motion (random motion of particles inside the base fluid) and thermophoresis (diffusion of particles due to temperature gradient) are found to be important slip mechanisms in nanofluids. Based on these findings, a set of partial differential equations for conservation laws for nanofluids was formed. Since then, a large number of mathematical studies on convective heat transfer in nanofluids became feasible. The present paper summarizes the studies pertaining to instability of a horizontal nanofluid layer under the impact of various parameters such as rotation, magnetic field, Hall currents and LTNE effects in both porous and non-porous medium. Initially, investigations were made using the model considering fixed initial and boundary conditions on the layer, gradually the model was revised in the light of more practical boundary conditions and recently it has been modified to get new and more interesting results. The exhaustive analysis of instability problems is presented in the paper and prospects for future research are also identified.
Similar content being viewed by others
Introduction
With the advancement in industrial sector, effective cooling techniques have become the significant requirement for many industrial processes. Efficient transfer of energy in the form of heat from one body to another is commonly needed in most industries. There are many examples related to successful production and safety that hinge upon effective transfer of heat namely, thermal and nuclear power plant, refrigeration and air conditioning system, chemical and processing plants, electronic devices, space shuttles and rocket-launching vehicles. Often a fluid is chosen as a medium for transferring heat and consequently the mode of heat transfer is convection. The amount of heat transposition in convection is explained by a clear easy seeming connection, that is known as Newton’s law of cooling; q = h A ∆T, where q is the heat transfer rate, h is the convective heat transfer coefficient, A is the surface area and ∆T is the temperature that varies across which the transfer of thermal energy occurs. It has been always the pursuit of the thermal engineers to maximize q for given ∆T or A which can be done by increasing h. Heat transfer coefficient is a complex function of the fluid property, velocity and surface geometry. From various fluid properties, thermal conductivity influences the heat transfer coefficient in the most direct way as this is the property that regulates the thermal transport at the micro-scale level. Heat transfer by conduction through solid is much larger than as compared to the conductive or convective heat transfer through a fluid. For example, when copper is kept at room temperature, its conductivity is approximately 700 times more than that of water and almost 3000-folds greater in comparison to engine oil. Regular fluids like water, ethylene glycol and oil were used initially for such procedures but due to their restricted heat transfer properties, they were not able to serve the purpose completely. On the contrary, metal’s thermal conductivity is very high in comparison to the regular fluids. These facts elicited and caught the eye of research workers to club both to generate a heat transfer mode which has attributes of fluid as well as metal. Keeping this perspective in consideration theoretical as well as practical work has been done considerably to enhance the thermal properties of fluids by suspending solid particles. Almost a century ago, Maxwell [1] initiated the theoretical work on thermal conductivity enhancement by addition of micrometer and millimetre sized particles and gradually nanoparticles were suspended in the fluids termed as the nanofluids [2].
Afterwards, nanofluids have emerged as an exciting area for advance research and development. The thermal conductivity enhancement in nanofluids was explored by Masuda et al. [3], Eastman et al. [4], Das et al. [5] and others. They alleged an increment varying 10–30% in thermal conductivity with the use of nanofluids at very low concentration. Buongiorno [6] formulated a mathematical model to study nanofluid instability phenomenon for the first time. He made an observation that the velocity of nanoparticles can be perceived as a sum of base fluid and relative (slip) velocities. To prosecute his research, he considered seven slip mechanisms; inactivity, magnus effect, Brownian motion, diffusiophoresis, thermophoresis, gravitational settling and fluid drainage. Throughout his investigation, he agreed that out of all the seven techniques, Brownian diffusion and thermophoresis have a significant role in the absence of turbulent effects. Choi et al. [7] established that the highest thermal conductivity enhancement in fluids is with the addition of carbon nanotubes. A lot of analytical and experimental work has been done on thermal conductivity of nanofluids in the past [8,9,10,11]. Das and Choi [12], Ding et al. [13] and Das et al. [14] studied convective heat transfer in nanofluids extensively. Chen [15] derived heat conduction equations from Boltzmann equation. The presence of nanoparticles enhances the conductivity of base fluids [4, 7, 16] and rate of heat transfer [17,18,19]. A small amount of nanoparticle volume fractions (< 0.1%) leads to conductivity enhancement up to 40% [8] and it rises with rise in temperature [5] and nanoparticles [16]. The results of Choi et al. [7] established the unexpected non-linear character of measured thermal conductivity with nanotube loadings at low concentration while all theoretical studies concluded a linear relationship. Also, it was discovered that thermal conductivity strongly depends on temperature [5] and particle size [20]. Pak and Cho [21] considered aluminium and titanium nanoparticles in circular tubes to study turbulent flow of nanofluids and found 30% increase in the value of Nusselt number in comparison to base fluid. Kleinstreuer et al. [22] and Buongiorno and Hu [23] found the applications of nanofluids in drug delivery systems and advanced nuclear systems, respectively. Novel projected applications of nanofluids include sensor and diagnostics that instantly detect chemical warfare agents in water or water-or food borne contamination; biomedical applications such as cooling medical devices, detect unhealthy substance in the blood, cancer treatment, or drug delivery; and development of advanced technologies such as advanced vapour compression refrigeration systems. The present paper largely summarizes the mathematical findings related to convective heat transfer in nanofluids under effects of rotation, magnetic field, hall currents and local thermal non-equilibrium in porous and non-porous medium. The partial differential equations for nanofluids based on conservation laws are studied by various researchers to establish significant and interesting results which are presented and analysed in the subsequent sections.
Instability of nanofluids
Thermal instability
A horizontal fluid layer is heated underside with maintained temperature difference across its boundaries leads to convection currents in the fluid. At the onset of instability, the temperature difference exceeds a certain value was observed first time by Bénard [24] in 1900. He found that the fluid at the bottom becomes lighter and rises up while the fluid density higher on the top makes the system top heavy. Further, Bénard [25] carried out an experiment using metallic plate and a thin non-volatile liquid layer which is maintained under constant temperature. He found that fluid layer was decomposed into number of cells at the onset of instability called Bénard cells.
Lord Rayleigh [26] explored the phenomenon analytically in detail. The work carried out by Rayleigh and Bénard to study thermal instability of fluids is known as Rayleigh Bénard convection. The schematic representation of Rayleigh–Bénard convection is shown in Fig. 1. They found that at the onset of convection, Rayleigh number, given by \(Ra = g\beta \,d^{3} \Delta T/\nu \,\alpha_{f} ;\) exceeds a certain critical value; where \(\beta\) is the volumetric coefficient of thermal expansion, g is the acceleration due to gravity, \(\Delta T\) is the temperature difference between boundaries of the layer, \(\alpha_{f}\) is the thermal diffusivity of fluid, d is depth of the layer, and \(\nu\) is the kinematic viscosity. For the stabilizing viscous force, \(Ra\) parameter gives the force of destabilizing buoyancy. Chandra [27] explained that the instability of the fluid layer depends on its depth by conducting an experiment on the layer in air. Spiegel and Veronis [28] simplified the partial differential equations for the fluid flow by taking depth of the layer to be very small as compared to the height and equations for porous medium were derived by Joseph [29] using Boussinesq approximation. The thermal convection of a fluid layer using different assumptions of rotation and magnetic field has been considered in detail by Chandrasekhar [30]. Kim et al. [31] showed that heat capacity and density of nanoparticles influence the convective motions directly while conductivity has adverse impact. Hwang et al. [32] found that the presence of alumina nanoparticles enhances the stability of the base fluid which rises with the volume fraction of nanoparticles while decreases with the size of nanoparticles. Buongiorno [6] initiated the analytical treatment on nanofluid convection by deriving the conservation equations of nanofluids based on nano effects (Brownian and thermophoretic diffusion) as follows:
where \({\varvec{v}} = (u,v,w)\) is the nanofluid velocity, \(\phi\) is the nanoparticles volume fraction, \(\rho_{p}\) is the nanoparticle mass density, \(D_{B}\) is the Brownian diffusion coefficient, \(D_{T}\) is the thermophoretic diffusion coefficient, \(\mu\) is the viscosity of the fluid, \(t\) is the time, \(\left( {\rho c} \right)_{f}\) is the heat capacity of fluid, \(\left( {\rho c} \right)_{p}\) is the heat capacity of nanoparticle, \(k\) is the thermal conductivity of the medium, \(T\) is the temperature and the nanofluid’s density \(\rho\) is given by:
where \(\rho_{f}\) is the base-fluid’s density, \(T_{0}\) is the reference temperature and \(\rho_{f0}\) is the fluid density at reference temperature. The partial differential Eqs. (1–5) along with momentum equation for different instability problems are considered to study the convective motions in the fluid. The momentum equation based on conservation of mass is redefined by researchers in each case to investigate the different hydrodynamic and hydromagnetic problems. The conservation equations were non-dimensionalized to get new parameters and further the expression for thermal Rayleigh number was found to study the various instability problems. Tzou [33, 34] analytically solved the conservation equations of nanofluids for convective situations and established that the presence of nanoparticles hastens the onset of instability of the fluid layer significantly. Nield and Kuznetsov [35] considered the nanofluid layer heated from below as shown in Fig. 2 and same geometry was further used by many researchers to study problems. They solved the conservation Eqs. (1–5) by using Galerkin method and normal mode technique for free-free, rigid-free and rigid-rigid boundaries.
For free-free boundaries, the expression of thermal Rayleigh number for stationary motions was obtained by Nield and Kuznetsov [35] as:
where Rn, Le, Na represent the concentration Rayleigh number, the Lewis number and the modified diffusivity ratio, respectively which are non-dimensional parameters. This result is complementary to the result of Tzou [21, 22] as the reduction of critical Rayleigh number for bottom-heavy case was established [21, 22] whereas Nield and Kuznetsov [35] claimed the increase in the value of the critical Rayleigh number for non-oscillatory instability. Also, Nield and Kuznetsov [35] presented the impact of nanofluid parameters and concluded that Rn, Le, Na destabilize the system for bottom heavy case. Yadav et al. [36] also performed the analytically investigation on thermal instability of nanofluids by carrying the conservation Eqs. (1–5). In addition to the nanofluid parameters they also examined the impact of temperature gradient and found that temperature gradient postpones the convective motions and nano-effects destabilize the layer significantly. Further, the nanofluid convection problem was revisited by Sharma and Gupta [37] to explore the problem in detail without combining the terms at any stage and the expression of thermal Rayleigh number was found in terms of physical properties of nanofluids. Recently, both experimental and analytical studies were carried out by Kumar et al. [38] to investigate Rayleigh–Bénard instability in nanofluids. Silver and selenium nanoparticles were synthesized using plant extract and base fluid was taken to be water to study the onset of convection. It was observed that the presence of nanoparticles delay the onset of instability in the fluid. A few additional complexities crop up due to the interactions between fluid and porous material. In the past investigation of thermal instability of fluids in porous medium became prominent due to its large applications. The impact of strong magnetic field of earth on the stability of this flow is a key area of interest in geophysics. It becomes more prominent while studying earth’s core where earth’s mantle conducts like a porous medium comprising of conducting fluids. A great amount of work on the convection problem for Newtonian/non-Newtonian fluids in a porous medium has been accounted by Lapwood [39], Wooding [40], MacDonald et al. [41], Ingham and Pop [42], Vafai and Hadim [43], and Nield and Bejan [44]. Owing to the applications of convection in porous media and keeping in mind the thermal properties of nanofluids, convection problem for nanofluids in porous medium has also been given due attention in the research work. The investigations in porous medium were started with Darcy model and further it has been extended to develop as Darcy–Brinkman model. By taking Darcy resistance term into consideration, Lapwood [39] and Wooding [40] examined the stability of a flow of the fluid saturating porous medium. Following Rayleigh’s procedure, they have shown that the value of critical Rayleigh number for the convective flow in porous medium is \(4\pi^{2}\). A detailed and thorough review of the work related to convection of fluids in porous medium has been published in a book by Nield and Bejan [44]. Lapwood problem for nanofluids was solved by Nield and Kuznetsov [45] using Darcy model and Kuznetsov and Nield [46] further extended the problem in porous medium using Brinkman model. In Darcy model, porous medium is assumed to have porosity ε and permeability K. The Darcy velocity is denoted by \({\varvec{v}}_{{\varvec{D}}} = \varepsilon {\varvec{v}}\). Then the conservation Eqs. (1–5) for Darcy model were modified as [45]:
On solving Eqs. (7–10), Nield and Kuznetsov [45] obtained an expression of thermal Rayleigh number in porous medium as:
and concluded that Rn, Le, Na destabilize the system of nanofluid layer for bottom heavy distribution of nanoparticles whereas porosity stabilizes it. It was found that the critical thermal Rayleigh number has a substantial change in its value depending on whether the basic nanoparticle distribution is top-heavy or bottom-heavy, by the presence of the nanoparticles. They claimed that oscillatory instability is possible only for bottom-heavy nanoparticle distribution. Kuznetsov and Nield [46] further extended their work in porous medium by incorporating Brinkman model. For Brinkman model conservation equation of momentum changes to:
where \(\tilde{\mu }\,\) is the effective viscosity. Thus, the set of Eqs. (7, 8, 10 and 12) constitutes the governing equations of the system for Brinkman model. Kuznetov and Nield [46] processed this system for analysis by using normal mode technique and obtained the expression of thermal Rayleigh number as:
where Da is Darcy number which got introduced in Brinkman model. They established that for a typical nanofluid (having larger Lewis number) buoyancy forces along with the conservation of nanoparticles has a primarily effect on the system while the concentration of nanoparticles has a second-order effect. They found the critical value of thermal Rayleigh number with Darcy number effect and concluded that for large values of Darcy number critical Rayleigh number is 3% greater than the classical result of Chandrasekhar while in the absence of Darcy number it is 11% greater than the classical result. Chand and Rana [47] also examined the oscillating convection of nanofluids in porous medium and questioned the validity of principle of exchange of stability for the problem and also derived the condition of non-existence of oscillatory motions.
Thermosolutal instability
Melvin Stern [48] was first to consider the case of linear opposing gradients of two properties between horizontal boundaries at fixed concentrations. He revealed that the interesting effect in binary convection is due to sharp difference between diffusivities of heat and solute. Since then many more researchers, including Veronis [49] and Nield [50] have developed the idea. The problem of thermosolutal convection in a layer of fluid under a stable solute gradient which is heated from below has been studied by Veronis [49]. Linear calculations for the problem have been made for a variety of boundary conditions by Nield [50]. It has shown by Turner [51, 52] that the convective motions depend on the component having higher or lower diffusivity leading to driving forces. When lighter fluid layer is placed over denser of different diffusivities, two types of convective motions crop up; diffusive and finger configurations. The excellent review works on double diffusive system were given by Huppert and Turner [53] and Turner [54]. The interference of multi-components transport processes produce the cross-diffusion (Soret and Dufour) effects. The mass flux due to temperature gradient is defined as Soret effect and the Dufour effect refers to heat flux due to solute gradient. Insignificant role of the Soret and Dufour effects allows ignoring their presence in simple models of coupled heat and mass transfer [44]. Mc Dougall [55] has made an in-depth study of double diffusive convection considering both the solutal effects (Soret and Dufour). The existence of these ideas has observed in the field of oceanography and the role of theoreticians, laboratory experiments and sea-going oceanographers became vital to explore this process. The field has also broadened considerably, with new applications becoming apparent in addition to those outlined by Turner [52]. The double-diffusive concepts are mainly applied in large-scale engineering applications and can be observed in solar ponds, shallow artificial lakes etc. A direct analogue of thermosolutal convection has been used to describe the properties of large stars with a helium-rich core which is heated from below. Spiegel [56] has shown that the helium/hydrogen ratio has significant impact on density gradient and can limits the helium transport by double diffusive convection. Another example of double diffusive convection process is solidification of metals.
Kuznetsov and Nield [57] initiated the mathematical work on double diffusive instability in a nanofluid layer saturating porous medium under Darcy model. They classified the investigated problem as triple diffusion-type process due to involvement of the heat, the nanoparticles and the solute. The complex equations were simplified by analytical expressions for non-oscillatory and oscillatory cases. The results predicted that the non-oscillatory mode is expected for top heavy distribution of nanoparticles, a situation which corresponds to the fact that the existence of oscillations requires two of the buoyancy forces acting in opposite directions. Further, Kuznetsov and Nield [58] studied the companion paper in non-porous medium. The momentum, thermal energy and solute conservation equations were redefined for a horizontal binary nanofluid layer which is heated and soluted from below as:
where \(\rho = \phi \rho_{p} + \left( {1 - \phi } \right)\rho_{f} \cong \phi \rho_{p} + \left( {1 - \phi } \right)\left\{ {\rho_{f0} \left( {1 - \beta \left( {T - T_{0} } \right) - \beta^{\prime}\left( {C - C_{0} } \right)} \right)} \right\},\)
where \(\beta^{\prime}\) is the solutal volumetric coefficient, \(D_{S}\) is the diffusivity of solute, \(D_{TC}\) is the Dufour type diffusivity, \(D_{CT}\) is the Soret type diffusivity and \(C\) is the solute concentration. The one term Galerkin approximation method was used to analyze the stability and the expression for the Rayleigh number was found as
The expression contains four additional nano-dimensional solute numbers; \(N_{CT}\) Soret parameter, \(N_{TC}\) Dufour parameter, \(L_{S}\) Solute Lewis number and \(Rs\) solute Rayleigh number. The stability boundaries were approximated using single term Galerkin approximation which produced the critical Rayleigh number about 5% higher than the true value. The analytical results for oscillatory instability were established by simplifying complex expressions with the assumptions of large Prandtl number and large nanoparticle Lewis number. Same problem of binary nanofluid convection was revisited by Gupta et al. [59] to show the existence of oscillatory motions. They analyzed the impact of different parameters on onset of thermosolutal convection in a nanofluid layer in detail using the software Mathematica. Further, Yadav et al. [60] investigated the problem of binary nanofluid layer using a Darcy–Brinkman model. The numerical results on the onset of convection were derived using alumina-water nanofluid. Thermosolutal natural instability boundary layer nanofluid flow past a vertical plate was investigated by Kuznetsov and Nield [61]. In this paper, numerical calculations were performed in order to obtain the terms. Agarwal et al. [62] studied non-linear convection in binary nanofluid layer saturating porous medium in terms of Nusselt number and found that initially the effect of time on Nusselt number is oscillatory while it becomes steady as the time increases. Yadav et al. [63] explored the thermal conductivity and viscosity variations effects on binary nanofluid convection in porous medium. Further, Umavathi [64] conducted the studies to analyze the impact of variable viscosity and conductivity on linear and nonlinear stability analysis of binary convection in a porous medium layer saturated in a Maxwell nanofluid.
In all the above studies it was assumed that nanoparticle flux can be controlled across the boundary as the temperature thereat. Further, it turned out that these boundary conditions are hard to achieve physically so need was felt for more realistic boundary conditions. Nield and Kuznetsov [65, 66] came out with new conditions on boundaries of the layer and assumed that nanoparticle flux across the boundaries is zero written as (which is more realistic than top heavy/bottom heavy configuration of nanoparticles).
The expression of Rayleigh number for revised boundary conditions was found to be:
The concentration Rayleigh number was involved with a new scaling and a major difference was that the sign of concentration Rayleigh number cannot be negative and hence oscillatory convection was ruled out, in contrast to the conclusion in Nield and Kuznetsov [35] and Nield and Kuznetsov [45]. Realizing the fact that original and revised models mentioned so far were not sensitive to the conductivity of nanoparticles; Sharma et al. [67] modified the model by assuming initial constant nanoparticle volume fraction in the fluid layer and derived the expression for Rayleigh number (in the absence of solute parameters) as:
which was obtained to be independent of Lewis number and hence established the sensitivity of \(Ra\) for both density and conductivity of nanoparticles. It was found that density of nanoparticles hastens the onset of convection in the fluid whereas increase in conductivity delays the same. The stability pattern followed by non-metals is: alumina–water > silica–water > > copper oxide–water > titanium oxide–water and metals is: aluminium–water > copper–water > silver–water > > iron–water are shown in Figs 3 and 4 [67].
Effect of non-metals on Rayleigh number [67]
Effect of metals on Rayleigh number [67]
Effects of different parameters on instability of nanofluids
Effect of rotation
When a fluid spreads under gravity in a rotating system, motions normal to the rotation vector induce Coriolis forces that tend to oppose the spreading. In the absence of boundaries intersecting isopotential surfaces and of instability or viscous dissipation, the flow approaches a state of geotropic equilibrium in which buoyancy and Coriolis forces are in balance. The rotation has an important impact on the onset of convective motions in the fluid. Such problem has an application in oceanography, limnology and engineering processes where thermal instability of rotating fluid is needed to examine. It defines some new parameters in fluid dynamics, and its outcomes are surprising, like the function of viscosity is reversed [30]. Impact of rotation on the system of a nanofluid layer has been analyzed by Yadav et al. [68] and Chand [69]. For non-porous medium conservation equation of momentum in the presence of vertical rotation was defined as [68, 69].
where \({{\varvec{\Omega}}} = (0,0,\Omega )\) is the angular velocity and the term \({\varvec{2}}\rho \left( {{\varvec{v}} \times {{\varvec{\Omega}}}} \right)\) represents the Coriolis force term which was introduced due to the presence of rotation while for porous medium momentum equation due to rotation was modified as [70,71,72].
Chand [69] considered the top-heavy configuration of nanoparticles in non-porous medium and performed the numerical calculations by using Normal mode technique. The obtained expression of thermal Rayleigh number for stationary mode of convection was obtained as:
where Ta is Taylor number representing the effect of rotation. He claimed that rotating nanofluid is more stable than non-rotating layer. Also, in the stationary convection it is found that Taylor number Ta (rotation), Lewis number Le, have stabilizing effect on the system while concentration Rayleigh number Rn and modified diffusivity ratio Na have destabilizing effect on the system. Bhadauria and Agarwal [70] considered Brinkman model to investigate the instability of nanofluid layer in porous medium and obtained the expression for bottom heavy configuration of nanoparticles as:
where \(J^{2} = \pi^{2} + \alpha^{2} ,\) and Da is Darcy number which got introduced due to Brinkman model and was found to have stabilizing effect for the stationary mode of convection along with other nanofluid parameters effect except Na which has a destabilizing effect on the system. They also found the expression of Rayleigh number for oscillatory motions (bottom heavy distribution of nanoparticles). Bhadauria and Agarwal [70] also dealt with nonlinear study of instability of rotating nanofluid layer in porous medium. With a Brinkman model in porous medium, they used minimal representation of the truncated Fourier series analysis for non-linear. In their analysis, Nusselt number got introduced that represent the rate of heat transfer and found that with the rise of Rayleigh number, the Nusselt number also rises, thus the rate of heat transfer increases. But for large values of Rayleigh number, the Nusselt number tends to a fixed value and becomes constant thus the rate of heat transfer becomes constant. They also showed that rate of mass transfer of nanoparticles increases with the increase of Darcy number and modified diffusivity ratio. Further, Chand and Rana [71] also employed the Brinkman model but for top heavy configuration of nanoparticles and obtained Ra as:
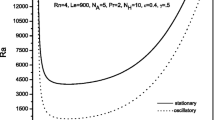
They found that porosity and concentration Rayleigh number decrease the stability of the system while Darcy number was found to have dual character both stabilizing/destabilizing effect for the stationary mode of convection depending on the value of Taylor number. In the absence of rotation, the Darcy number has stabilizing effect on the system. Agarwal et al. [72] used Darcy model to investigate the effect of rotation on a nanofluid layer in anistropic porous medium. Their outcomes were that bottom-heavy and top-heavy arrangement favour oscillatory and stationary convections, respectively. Rotation aids either of the two in this trend. For both the arrangements, rotation parameter (Taylor number) gives an enhancement in the stability of the system. Yadav et al. [73] solved the thermal instability problem of rotating nanofluid layer numerically. Six-term Galerkin method has been adopted to solve the Eigen-value equation for rigid-free and rigid-rigid boundary conditions. The results for two different types of boundary conditions were compared and found that system with both rigid boundaries is more stable than rigid-free boundaries at small Taylor number domain however stress-free boundaries offer more stability than rigid boundaries when its values are higher. Rana et al. [74] and Rana and Agarwal [75] investigated the effect of rotation on double diffusive nanofluid convection saturating a porous medium. The stabilizing impact of rotation parameter was established in their work. Agarwal [76], Rana and Chand [77] and Yadav et al. [78] re-explored the problem of convective motions in a nanofluid layer subjected to rotation with new boundary conditions (nanoparticle flux is zero across the boundaries) for porous and non-porous medium. Yadav et al. [78] solved the eigenvalue problem numerically using 6-term Galerkin method for water based nanofluid with alumina and copper nanoparticles. Stability of alumina–water nanofluid was compared with that copper water nanofluid and observed that with these new boundary conditions alumina–water nanofluid shows more destabilizing effect under the constant nanoparticle boundary conditions, while reverse trend was observed for copper–water nanofluid. This is because the modified diffusivity ratio has a significant effect for zero nanoparticles flux on boundaries and its value is higher for alumina–water nanofluid than copper–water nanofluid. The stabilizing impact of rotation on binary nanofluid convection was analyzed by Sharma et al. [79]. Oscillatory motions come into existence for bottom heavy arrangement of nanoparticles in the fluid layer saturating porous medium. The stabilizing effect of Taylor number for stationary as well as oscillatory mode of convection is shown in Fig. 5 and mode of convection is found to be oscillatory [80].
Effect of rotation parameter on Rayleigh number [80]
Further, the onset of thermosolutal convection in a rotating porous nanofluid layer was investigated in many works [81, 82] using Darcy and Darcy Brinkman model.
Effect of magnetic field
When an electrically conducting fluid comes under the influence of a uniform magnetic field, two kind of electromagnetic effects are observed within the fluid. Firstly, the currents are induced in the fluid due to its motion across the magnetic field which tends to modify the existing fields. Secondly, electric current transverse to the magnetic lines of forces within the fluid exert forces that adds up to the existing fields. This twofold interaction among the fluid motions and magnetic fields causing unexpected patterns of behaviour are depicted and well contained in Maxwell’s equations. Hydrodynamic equations are modified in more suitable way by considering Maxwell’s equations [30]. Thomson [83] modified the theory of slow thermal convection proposed by Rayleigh [26] and Jeffrey [84] by adding the Lorentz force which is induced by the interaction of magnetic field and conducting fluid. The result of such interaction has also been concluded by Fermi [85] and Alfvén [86]. Riley [87] carried out further investigation on Rayleigh–Bénard convection under the influence of vertical magnetic field called magneto-convection. Ghasemi et al. [88] and Hamada et al. [89] considered water based nanofluids with copper, alumina and silver nanoparticles, to investigate thermal instability for numerical computations. Ghasemi et al. [88] investigated the impact of both magnetic field and nanofluids on natural convection in square cavity while Mahmoudi et al. [90] investigated the same impact for rectangular cavity. They argued that the magnetic field resulted in the decrease of convective circulating flows within the enclosures which resulted in the reduction of heat transfer rate. The work (magneto-convection) has contributed in the field of engineering in the form of various applications such as crystal growth in liquids, cooling of rods in nuclear reactor, cooling of microchips in electronics and microelectronic devices, solar technology etc. By conceptualizing the utility aspect of applying magnetic field, Heris et al. [91] studied the impact of both magnetic field and nanofluid on two phases closed thermosyphon and found that with the increase in magnetic field strength as well as nanoparticle concentration; thermal efficiency of thermosyphon has significantly increased. Nemati et al. [92] in their theoretical study investigated the impact of magnetic field on nanofluid convection in a rectangular cavity by considering the Lattice Boltzman model. They concluded that increase in magnetic field reduces the convective heat transfer rate while conductive heat transfer rate becomes dominant. Gupta et al. [93] and Yadav et al. [94] considered the magneto-convection of a nanofluid layer for bottom heavy and top-heavy distributions of nanoparticles, respectively. By applying magnetic field on a nanofluid layer, Lorentz force is induced which combines with the element of thermal buoyancy. Thus, the system of conservation equations in the presence of magnetic field includes Eqs. (1–3) along with,
and Maxwell’s equations
where \({\varvec{h}} = (0,0,h)\) is the magnetic field that is applied in vertical direction and \(\frac{{\mu_{e} }}{4\pi }\left( {\nabla \times {\varvec{h}}} \right) \times {\varvec{H}}\) represents the Lorentz force term which was introduced due to applied magnetic field. System of Eqs. (1–3 and 27–29) were analyzed to examine the effect of magnetic field for bottom heavy distribution of nanoparticles and the expression for stationary convection [93, 94] was obtained as:
Expression for oscillatory convection was also found. Due to the presence of magnetic field Chandrasekhar number \(Q\) came into existence. The authors found that Chandrasekhar number delays the onset of convection and the oscillatory mode of heat transfer was established for bottom heavy distribution whereas it was found to be through stationary convection for top heavy arrangement of nanoparticles. Shaw and Sibanda [95] used Brinkman model to investigate the hydromagnetic instability of a nanofluid layer in Darcy porous medium using convective boundary condition. It has been shown that for the case of stationary convection the critical Rayleigh number increases with the increase of Darcy number and the magnetic field parameter. Gupta et al. [96] and Ahuja et al. [97, 98] carried out their research of hydromagnetic stability by comparing thermal instabilities of Al2O3–water and CuO–water nanofluids in non-porous medium and in porous medium. They interpreted that magnetic field parameter stabilizes the system for all types of nanofluids. Further, nanofluid with alumina nanoparticles is found to exhibit more stability than the nanofluid containing copper-oxide nanoparticles. In porous medium, analysis is done for three different boundaries free-free, rigid-free and rigid-rigid using Brinkman model. For free-free boundaries, the expression of Rayleigh number was obtained as [98]:
In the presence of magnetic field stability of Cu–water nanofluid and Ag–water nanofluid was compared and it was found that Cu–water nanofluid is more stable than Ag–water nanofluid for top heavy configuration of nanoparticles. The system with both-rigid boundaries is found to have more stability as compared to rigid-free boundaries which in turn are more stable than free-free boundaries. In porous medium they also examined the effect of volume fraction of nanoparticles and temperature difference across the boundaries on stability of the system and found that temperature difference stabilizes the nanofluid layer appreciably, whereas the volume fraction of nanoparticles and porosity destabilize the layer. Chand and Rana [99] found the solution of the nanofluid layer for more realistic boundary conditions in the presence of uniform vertical magnetic field in a porous medium. They derived the stability criterion for stationary and oscillatory convection in the presence of magnetic field and depicted that oscillatory motions do not occur. Sharma et al. [100] and Gupta et al. [101] established the stabilizing impact of vertical magnetic field on binary nanofluid convection in a horizontal fluid layer in porous and non-porous medium, respectively. The stabilizing influence of magnetic field parameter is shown in Fig. 6 for both stationary and oscillatory convection [101].
Effect of magnetic field parameter on Rayleigh number [101]
Effect of Hall currents
When an applied electric and magnetic field are both perpendicular to each other, the current does not flow in the direction of electric field. So, when an electric current pass through a conducting fluid in the presence of magnetic field, transverse force is exerted by the magnetic field which produces a measurable voltage across the two sides of a conducting fluid. The presence of this measurable transverse voltage under the effect of magnetic field due to which electric current tends to flow across an electric field is called Hall effect. Thus, Lorentz forces acting on the charges in the current induced the Hall effect. Gupta [102] studied the effect of Hall currents and described that these currents hasten the onset of thermal convection under the presence of uniform magnetic field. A considerable work has been done by many researchers in the past [103,104,105] on the effects of magnetic field/Hall currents on Newtonian/non-Newtonian (viscoelastic) fluids, and associated problems. It was shown that a vertical component of vorticity induced by Hall currents is one of the possible reasons for destabilizing effect of Hall currents. Gupta and Sharma [106] further studied the impact of Hall currents and rotation on the double-diffusive convection of Rivlin–Erickson elastic–viscous fluid. Gupta et al. [107, 108] considered the Hall effect on thermal stability of a nanofluid layer in porous and non-porous medium. Due to the presence of Hall currents, conservation equations in non-porous medium were modified as:
along with Maxwell equation
Thus Eqs. (1, 2, 4) along with (33–35) form the system of conservation equations in the presence of Hall currents. For bottom heavy distribution of nanoparticles, Gupta et al. [107, 108] got the expression
where additional Hall current parameter \(M\) was found to exist. Effect of Hall currents is to hasten the convection (Fig. 7) while magnetic field delays it. It was also established that stability of alumina is more than copper nanoparticles in water in the presence of Hall currents (Fig. 8). The mode of heat transfer is found to be through stationary convection for top heavy configuration of nanoparticles. Further, for porous medium velocity is replaced by Darcy velocity in the Eqs. (1, 2, 4) alongwith (33–35) to get the conservation equations of nanofluid in the presence of Hall currents for porous medium. Yadav and Lee [109] and Yadav et al. [110] modified the convective boundary conditions and presented a more realistic feasible system of nanofluid layer in the presence of Hall currents for non-porous and porous medium, respectively. They examined the stability of a nanofluid layer with large magnetic fields and obtained the expression of Rayleigh number [110] in porous medium as:
Effect of Hall current parameter on Rayleigh number [107]
Effect of alumina and copper nanoparticles on Rayleigh number in the presence of Hall effects [108]
According to their result, for small values of the Hall current parameter, it has a destabilizing effect on the system while for its large values no significant effect is observed on the system. On the same way, magnetic field parameter is found to delay the onset of convection appreciably, for small values of the Hall current parameter while for large values of Hall current parameter it has no effect on the system. They also observed that the size of convection cells depends on the magnetic field parameter and the Hall current parameter for small values of the Hall current parameter while for large values of the Hall current parameter roll of magnetic field and Hall current become insignificant. The conditions for the instability through stationary convection is also found and showed that the oscillatory convection cannot occur with the new boundary conditions. In porous medium, Hall current parameter and nanoparticles parameters are found to accelerate the onset of convection, while the Darcy number, magnetic Darcy number and porosity parameter delay the onset of instability in the fluid layer.
Effect of LTNE
All the above-mentioned studies are based on local thermal equilibrium (LTE) where temperature gradient is assumed to be negligible between the fluid and particle phases but Vadasz [111, 112] clarified that there is always a thermal lagging among the fluid and particle phases if the thermal conductivity is increased. Kuznetsov and Nield [113, 114] and Nield and Kuznetsov [115] explored the impact of this thermal lagging named as local thermal non-equilibrium model (LTNE) for the thermal instability of a nanofluid layer for both porous and non-porous medium. In non-porous medium to account the influence of thermally non-equilibrium phases two temperature model has been used which was described by Nield and Kuznetsov [115] as follows:
Due to LTNE effects additional variables \(k_{f} ,k_{p} ,T_{f} ,T_{p} ,h_{fp}\) got introduced in which \(k_{f} ,k_{p}\) denote respectively the effective thermal conductivity of the fluid and particle phase, \(T_{f} ,T_{p}\) denote the temperature of fluid and particle phase and \(h_{fp}\) is the interphase heat transfer coefficient between the fluid/particle phases. While for porous medium a three-temperature model suited well to analyse the thermal lagging among fluid phase, particle phase and solid matrix phase [113] was given as:
Thus, for non-porous medium Eqs. (38, 39) along with Eqs. (1–3) form a system of conservation equations for LTNE model while for porous medium set of Eqs. (7–9) along with (40–42) constitute the system of equations. Expression of Rayleigh number [115] for non porous medium was:
where additional parameters Nield number, NH, modified thermal capacity ratio γ and modified thermal diffusivity \(\delta\) ratio came into existence in the process of non dimensionalization due to LTNE model while for porous medium these parameters came into existence for particle phase and solid phase separately and effect of all these parameters is also analysed. Here, modified thermal capacity ratio γ, and modified thermal diffusivity \(\delta\) increases the stability of the system while Nield number NH tends to reduce it. They found that impact of LTNE is significant in case of non-oscillatory stability but insignificant for typical dilute nanofluids. Further, the thermal instability in porous medium for both linear and non-linear conditions using LTNE model is investigated by Bhadauria and Agarwal [116]. Convection in LTNE is found to set earlier as compared to LTE. For linear conditions Bhadauria and Agarwal [116] obtained the expression as:
where \(J^{2} = \pi^{2} + \alpha_{c}^{2} \,\,and\,\,\alpha_{c} = {\pi \mathord{\left/ {\vphantom {\pi {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }},\) NHP, NHS are interface heat transfer parameters and \(\gamma_{p} ,\,\gamma_{s}\) are modified thermal capacity ratios and \(\varepsilon_{p} ,\,\varepsilon_{s}\) are modified thermal capacity ratios. With the increase in concentration Rayleigh number, Nield number and modified diffusivity ratio, the decrease in Nusselt number is observed thus diminishing the heat transfer rate. While it increases on increasing the values of modified thermal capacity ratio, thus the rate of heat transfer is increased. On the other hand, for solid-matrix phase an unsteady rate of heat transfer is observed initially and with the passage of time it approaches to a constant value. Agarwal and Bhadauria [117] studied the thermal instability of a rotating nanofluid layer in non-equilibrium conditions. In addition to the above results, they noted a slight variation in critical Rayleigh number for small values of nanoparticle concentration Rayleigh number, Lewis number and Taylor’s number and then rises steadily with an increase in the value of these parameters whereas for modified diffusivity ratio, an opposite trend was observed. Ahuja and Gupta [118] examined the MHD effects of rotating nanofluid layer using LTNE model. One term Galerkin approximation has been used to analyse the stability. For top heavy distribution of nanoparticles they got the expression as:
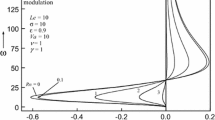
They found that Taylor number, Chandrasekhar number, modified thermal diffusivity ratio and modified thermal capacity ratio enhance the stability of the system while concentration Rayleigh number, Nield number, modified diffusivity ratio and Lewis number hasten the onset of thermal convection for top heavy distribution of nanoparticles in LTNE. Further, Yadav et al. [119] used zero nanoparticle flux boundary condition to study the effect of local thermal non-equilibrium on the onset of nanofluid convection in a porous layer subjected to rotation. For porous medium, Brinkman model was employed. The influence of double-diffusion and LTNE on the onset of convection in porous medium was considered by Nield and Kuznetsov [120]. They found that the system with LTNE exhibits lesser stability than LTE model as shown in Fig. 9.
Comparison of LTNE and LTE model [120]
It is worthwhile to mention that all the studies assume that the nanoparticles volume fractions are constant along the boundaries of the layer which is very difficult to achieve practically. As a result, this model is revised by considering zero nanoparticle volume fractions at the boundaries. Most of the problems were revisited by making use of revised model. In both the models (Original and Revised), nanoparticle volume fractions are assumed to vary in horizontal direction only and the model is recently modified by taking constant value of nanoparticles at the basic state which established more effectively the contribution of metallic and non-metallic nanoparticles on the convection in the layer. By considering these facts, it is concluded that different alternations can be made on the applied models to study convective motions which altogether could make a significant difference.
Concluding remarks and scope for future work
The paper presents an overview of various instability problems for nanofluids under the effects of different hydrodynamic and hydromagnetic parameters. The significant heat transfer enhancement of convective fluids at very low nanoparticles concentration has been established by many researchers and related literature has been reviewed in detail. As a consequence, mathematical investigations to explore the related mechanisms were initiated and the effects produced due to the presence of nanoparticles lead to new set of equations based on conservation laws which further encouraged theorists to formulate the instability problems for nanofluids. The paper considers detailed review of work pertaining to analytical and numerical studies on nanofluid convection along with impact of various parameters like rotation, magnetic field, Hall effects and LTNE effects in porous and non-porous medium. Presence of nanoparticles hastens the instability of nanofluids and porous medium add onto this characteristic of nanofluids. Rotation and magnetic field delays the convection while Hall currents and local thermal non-equilibrium effects are found to hasten the onset of convection in the fluid layer. Initially, it was assumed that nanoparticle flux can be controlled across the boundary as the temperature thereat. But in due course, original model was revised with the assumption of zero nanoparticle flux across the boundaries which are more realistic than top heavy/bottom heavy configuration of nanoparticles. The revised model was further modified to study the instability problem which assumes the initial condition for nanoparticle volume fraction as constant and the expression for Rayleigh number is significant to both the physical properties (density and conductivity) which decide the stability of the system. It was found that oscillations are not possible and hence conductive heat transfer is through non-oscillatory mode only. Further, surveyed literature is analyzed for possibility of future work and some observations are made like (i) the investigations need to be explored in more detail using advanced analytical methods and mathematical software for calculations to make the study more efficient. (ii) The experiments must be performed in order to validate the results and hence the need for interdisciplinary research is found which would lead to motivation and practical significance of presented work.
Availability of data and materials
Not applicable.
References
Maxwell JC (1873) Electricity and magnetism. Clarendon Press, Oxford
Choi S (1995) Enhancing thermal conductivity of fluids with nanoparticles. In: Siginer DA, Wang HP (eds) Development and applications of non-Newtonian flows. ASME FED-231/MD, vol 66, pp 99–105
Masuda H, Ebata A, Teramae K, Hishinuma N (1993) Alteration of thermal conductivity and viscosity of liquid by dispersing ultra fine particles. Netsu Bussei 7:227–233
Eastman JA, Choi SUS, Li S, Yu W, Thompson LJ (2001) Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl Phys Lett 78:718–720
Das SK, Putra N, Thiesen P, Roetzel W (2003) Temperature dependence of thermal conductivity enhancement for nanofluids. ASME J Heat Transf 125:567–574
Buongiorno J (2006) Convective transport in nanofluids. ASME J Heat Transf 128(3):240–250
Choi SUS, Zhang ZG, Yu W, Lockwood FE, Grulke EA (2001) Anomalous thermal conductivity enhancement in nanotube suspensions. Appl Phys Lett 79:2252–2254
Wang X, Xu X, Choi SUS (1999) Thermal conductivity of nanoparticle fluid mixture. J Thermophys Heat Transf 13(4):474–480
Murshed SMS, Leong KC, Yang C (2005) Enhanced thermal conductivity of TiO2–water based nanofluids. Int J Therm Sci 44:367–373
Choi SUS (2009) Nanofluids: from vision to reality through research. J Heat Transf 131(3):033106
Wen D, Lin G, Vafaei S, Zhang K (2009) Review of nanofluids for heat transfer applications. Particuology 7:141–150
Das SK, Choi SUS (2009) A review of heat transfer in nanofluids. Adv Heat Transf 41:81–197
Ding Y, Alias H, Wen D, Williams RA (2006) Heat transfer of aqueous suspension of carbon nanotubes (CNT nanofluids). Int J Heat Mass Transf 49:240–250
Das SK, Choi SUS, Yu W, Pradeep T (2008) Nanofluids: science and technology. Wiley, Hoboken
Chen G (2001) Ballistic-diffusive heat conduction equations. Phys Rev Lett 86:2297–2300
Syam Sundar L, Sharma KV (2008) Thermal conductivity enhancement of nanoparticles in distilled water. Int J Nanopart 1(1):66–77
Xuan Y, Li Q (2003) Investigation on convective heat transfer and flow features of nanofluids. J Heat Transf 125:151–155
Yu W, Choi SUS (2003) The role of interfacial layers in the enhanced thermal of nanofluids: a renovated Maxwell model. J Nanopart Res 5(1–2):167–171
Vassallo P, Kumar R, Amico SD (2004) Pool boiling heat transfer experiments in silica–water nano-fluids. Int J Heat Mass Transf 47:407–411
Chon CH, Kihm KD (2005) Thermal conductivity enhancement of nanofluids by Brownian motion. ASME J Heat Transf 127:810
Pak BC, Cho Y (1998) Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. J Exp Heat Transf 11(2):151–170
Kleinstreuer C, Li J, Koo J (2008) Microfluidics of nano-drug delivery. Int J Heat Mass Transf 51:5590–5597
Buongiorno J, Hu W (2005) Nanofluid coolants for advanced nuclear power plants. In: Proceedings of ICAPP’05 Seoul. p 5705
Bénard H (1900) Les Tourbillons cellulaires dans une nappe liquid. Revue générale des Sciences pures et appliquées 11:1261–1271 and 1309–1328
Bénard H (1901) Les tourbillions cellularies dans une nappe liquide transportant de la chaleur par convection en regime permanent. Ann Che Phys 23:62–144
Rayleigh L (1916) On convective currents in a horizontal layer of fluid when the higher temperature is on the underside. Phil Mag 32:529–546
Chandra K (1938) Instability of fluids heated from below. Proc R Soc Lond A164:231–242
Spiegal EA, Veronis G (1960) On the Bousinessq approximation for a compressible fluid. Astrophys J 131:442
Joseph DD (1976) Stability of fluid motions, vol 1 & 2. Springer, Berlin
Chandrasekhar S (1981) Hydrodynamic and hydromagnetic stability. Dover Publication, New York
Kim J, Kang YT, Choi CK (2004) Analysis of convective instability and heat transfer characteristics of nanofluids. Phys Fluids 16:2395–2401
Hwang KS, Lee JH, Jang SP (2007) Buoyancy driven heat transfer of water based Al2O3 nanofluids in a rectangular cavity. Int J Heat Mass Transf 50:4003–4010
Tzou DY (2008a) Instability of nanofluids in natural convection. ASME J of Heat Transf 130:372–401
Tzou DY (2008b) Thermal instability of nanofluids in natural convection. Int J Heat Mass Transf 51:2967–2979
Nield DA, Kuznetsov AV (2010a) The onset of convection in a horizontal nanofluid layer of finite depth. Eur J Mech B/Fluids 29:217–223
Yadav D, Agrawal GS, Bhargava R (2011a) Rayleigh Bénard convection in nanofluid. Int J Appl Math Mech 7(2):61–76
Sharma J, Gupta U (2020) Convection currents in nanofluids under small temperature gradient. In: Applications of Nanobiotechnology ISBN: 978-1-78985-978-2, Print ISBN: 978-1-78985-977-5, eBook (PDF) ISBN: 978-1-83880-997-3. https://doi.org/10.5772/intechopen.88887
Kumar R, Sharma J, Sood J (2020) Rayleigh–Bénard cell formation of green synthesized nano-particles of silver and selenium. Mater Today 28(3):1781–1787. https://doi.org/10.1016/j.matpr.2020.05.191
Lapwood ER (1948) Convection of a fluid in a porous medium. Proc Camb Philos Soc 44:508–521
Wooding RA (1960) Rayleigh instability of a thermal boundary layer in flow through a porous medium. J Fluid Mech 9:183–192
MacDonald IF, El-Sayed MS, Mow K, Dullien FAL (1979) Flow through porous media: the Ergun equation revisited. Ind Chem Fundam 18:199–208
Ingham DB, Pop I (1998) Transport phenomenon in porous media. Pergamon, Oxford
Vafai KA, Hadim HA (2000) Handbook of porous media. M. Decker, New York
Nield DA, Bejan A (2006) Convection in porous medium. Springer, New York
Nield DA, Kuznetsov AV (2009) Thermal instability in a porous medium layer saturated by a nanofluid. Int J Heat Mass Transf 52:5796–5801
Kuznetsov AV, Nield DA (2010a) Thermal instability in a porous medium layer saturated by a nanofluid: Brinkman model. Trans Porous Med 81:409–422
Chand R, Rana GC (2012a) Oscillating convection of nanofluid in porous medium. Transp Porous Med 95:269–284
Stern ME (1960) The salt fountain and thermohaline convection. Tellus 12:172–175
Veronis G (1965) On finite amplitude instability in thermohaline convection. J Mar Res 23:1–17
Nield DA (1967) The thermohaline Rayleigh–Jeffreys problem. J Fluid Mech 29:545
Turner JS (1973) Buoyancy effects in fluids. Cambridge University Press, London
Turner JS (1974) Double-diffusive phenomena. Ann Rev Fluid Mech 6:37–56
Huppert HE, Turner JS (1981) Double-diffusive convection. J Fluid Mech 106:299–329
Turner JS (1985) Multi component convection. Ann Rev Fluid Mech 17:11–44
McDougall J (1983) Double-diffusive convection caused by coupled molecular diffusion. J Fluid Mech 126:379–397
Spiegel EA (1972) Convection in stars II: special effects. Ann Rev Astron Astrophy 10:261–304
Kuznetsov AV, Nield DA (2010b) The onset of double diffusive nanofluid convection in a layer of a saturated porous medium. Trans Porous Med 85:941–951
Kuznetsov AV, Nield DA (2011a) The onset of double-diffusive convection in a nanofluid layer. Int J Heat Fluid Flow 32:771–776
Gupta U, Sharma J, Wanchoo, RK (2014) Thermosolutal convection in a horizontal nanofluid layer: introduction of oscillatory motions. In: Proceedings of recent advances in engineering and computation sciences. IEEE, Chandigarh, India
Yadav D, Agrawal GS, Bhargava R (2012) The onset of convection in a binary nanofluid saturated porous layer. Int J Theor Appl Multiscale Mech 2(3):198–224
Kuznetsov AV, Nield DA (2011b) Double-diffusive natural convective boundary-layer flow of a nanofluid past a vertical plate. Int J Therm Sci 50:712–717
Agarwal S, Sachati N, Chandran P, Bhadauria BS, Singh AK (2012) Non-linear convective transport in a binary nanofluid saturated porous layer. Trans Porous Med 93:29–49
Yadav D, Agrawal GS, Bhargava R (2013) The onset of double diffusive nanofluid convection in a layer of a saturated porous medium with thermal conductivity and viscosity variation. J Porous Media 16:105–121
Umavathi JC, Yadav D, Mohite MB (2015) Linear and nonlinear stability analyses of double-diffusive convection in a porous medium layer saturated in a Maxwell nanofluid with variable viscosity and conductivity. Elixir Mech Eng 79:30407–30426
Nield DA, Kuznetsov AV (2014a) The onset of convection in a horizontal nanofluid layer of finite depth: a revised model. Int J Heat Mass Transf 77:915–918
Nield DA, Kuznetsov AV (2014b) Thermal instability in a porous medium layer saturated by a nanofluid: a revised model. Int J Heat Mass Transf 68:211–214
Sharma J, Gupta U, Sharma V (2017) Modified model for binary nanofluid convection with constant nanoparticle volume fraction. J Appl Fluid Mech 10(5):1387–1395
Yadav D, Agrawal GS, Bhargava R (2011b) Thermal instability of rotating nanofluid layer. Int J Eng Sci 49:1171–1184
Chand R (2013) Thermal instability of rotating nanofluid. Int J Appl Math Mech 9(3):70–90
Bhadauria BS, Agarwal S (2011a) Natural convection in a nanofluid saturated rotating porous layer: a nonlinear study. Transp Porous Media 87(2):585–602
Chand R, Rana GC (2012b) On the onset of thermal convection in rotating nanofluid layer saturating a Darcy–Brinkman porous medium. Int J Heat Mass Transf 55:5417–5424
Agarwal S, Bhadauria BS, Siddheshwar PG (2011) Thermal instability of a nanofluid saturating a rotating anistropic porous medium. Spec Top Rev Porous Media Int J 2(1):53–64
Yadav D, Bhargava R, Agrawal GS (2013a) Numerical solution of a thermal instability problem in a rotating nanofluid layer. Int J Heat Mass Transf 63:313–322
Rana GC, Thakur RC, Kango SK (2014a) On the onset of double diffusive convection in a layer of nanofluid under rotation saturating a porous medium. J Porous Media 17:657–667
Rana P, Agarwal S (2015) Convection in a binary nanofluid saturated rotating porous layer. J Nanofluids 4:59–65
Agarwal S (2014) Natural convection in a nanofluid saturated rotating porous layer: a more realistic approach. Trans Porous Med 104(3):581–592
Rana GC, Chand R (2015) On the thermal convection in a rotating nanofluid layer saturating a Darcy–Brinkman porous medium: a more realistic model. J Porous Media 18(6):629–635
Yadav D, Agrawal GS, Jinho L (2016) Thermal instability in a rotating nanofluid layer: a revised model. Ain Shams Eng J 7:431–440
Sharma J, Gupta U (2015) Instability of a rotating binary nanofluid layer: Darcy model. In: Proceedings of recent advances in engineering and computation sciences. IEEE, Chandigarh, India
Sharma J, Gupta U, Wanchoo RK (2016a) Numerical study on binary nanofluid convection in a rotating porous layer. Differ Equ Dyn Syst. https://doi.org/10.1007/s12591-015-0268-4
Rana GC, Thakur RC, Kango SK (2014b) On the onset of double-diffusive convection in a layer of nanofluid under rotation saturating a porous medium. J Porous Media 17:657–667
Sharma J, Gupta U (2015) Double-diffusive nanofluid convection in porous medium with rotation: Darcy–Brinkman model. Procedia Eng 127C:783–790
Thomson WB (1951) Thermal convection in a magnetic field. Philos Mag 42(7):1417–1432
Jeffrey H (1928) Some cases of instability in fluid motion. Proc R Soc A 118:195
Fermi E (1949) On the origin of cosmic radiation. Phys Rev 75:1169
Alfvén H (1950) Cosmical electrodynamics. International Series of Monographs on Physics. Oxford University, Oxford
Riley RD (1964) Magnetohydrodynamic free convection. J Fluid Mech 18:577
Ghasemi B, Aminossadati SM, Raisi A (2011) Magnetic field effect on natural convection in a nanofluid-filled square enclosure. Int J Therm Sci 50:1748–1756
Hamada MAA, Pop I, Md Ismail AI (2011) Magnetic field effects on free convection flow of a nanofluid past a vertical semi-infinite flat plate. Nonlinear Anal R World Appl 12:1338–1346
Mahmoudi AH, Pop I, Shahi M (2012) Effect of magnetic field on natural convection in a triangular enclosure filled with nanofluid. Int J Therm Sci 59:126–140
Heris SZ, Salehi H, Noie SH (2012) The effect of magnetic field and nanofluid on thermal performance of two phase closed thermosyphon. Int J Phys Sci 7(4):534–543
Nemati H, Farhadi M, Sedighi K, Ashory Nejad HR, Fattahi E (2012) Magnetic field effects on natural convection flow of nanofluid in a rectangular using the lattice Boltzmann model. Sci Iran 19(2):303–310
Gupta U, Ahuja J, Wanchoo RK (2013) Magneto convection in a nanofluid layer. Int J Heat Mass Transf 64:1163–1171
Yadav D, Bhargava R, Agrawal GS (2013b) Thermal instability in a nanofluid layer with a vertical magnetic field. J Eng Math 80(1):147–164
Shaw S, Sibanda P (2013) Thermal instability in a non-darcy porous medium saturated with a nanofluid and with a convective boundary condition. Bound Value Probl 186:1–13
Gupta U, Ahuja J, Wanchoo RK (2015) Rayleigh–Bénard convection of nanofluids with magnetic field and permeability effects. Procedia Eng 127C:325–332
Ahuja J, Gupta U, Wanchoo RK (2016) Hydromagnetic stability of a metallic nanofluids (Cu–water and Ag–water) using Darcy–Brinkman model. Int J Geophys 2016:1–9. https://doi.org/10.1155/2016/5864203
Ahuja J, Sharma J, Gupta U, Wanchoo RK (2016) Hydromagnetic stability of a nanofluid layer using Darcy–Brinkman model. J Nanofluids 5(3):436–443
Chand R, Rana GC (2015) Magneto convection in a layer of nanofluid in porous medium—a more realistic approach. J Nanofluids 4:196–202
Sharma J, Gupta U, Wanchoo RK (2016b) Magneto binary nanofluid convection in porous medium. Int J Chem Eng 2016:1–8. https://doi.org/10.1155/2016/9424036
Gupta U, Sharma J, Sharma V (2015) Instability of binary nanofluid with magnetic field. Appl Math Mech 36(6):693–706
Gupta AS (1967) Hall effects on thermal instability. Rev Roum Math Pures Appl 12:665
Bhatia PK, Steiner JM (1972) Convective instability in a rotating viscoelastic fluid layer. Z Angew Math Mech 52(6):321–327
Siddheshwar PG, Pranesh S (1998) Magneto-convection in a micropolar fluid. Int J Eng Sci 36(10):1173–1181
Sharma RC, Thakur KD (2000) Hall effect on thermal instability of Rivlin–Ericksen fluid in porous medium. Appl Mech Eng 5(2):355–366
Gupta U, Sharma G (2008) Thermosolutal instability of a compressible Rivlin–Ericksen fluid in the presence of rotation and hall currents saturating a porous medium. Appl Math Comput 196(1):158–173
Gupta U, Ahuja J (2014) Hall effect on thermal convection of a nanofluid layer saturating a porous medium. Int J Technol 4(1):214–219
Gupta U, Ahuja J, Kumar R (2016) On the hydromagnetic stability of a horizontal nanofluid layer with Hall currents. Mater Phys Mech 27:9–21
Yadav D, Lee J (2015a) The onset of MHD nanofluid convection with hall current effect. Eur Phys J Plus 130:162–184
Yadav D, Mohamed RA, Cho H, Hee Lee J (2016) Effect of hall current on the onset of MHD convection in a porous medium layer saturated by a nanofluid. J Appl Fluid Mech 9(5):2379–2389
Vadasz P (2006) Heat conduction in nanofluid suspensions. ASME J Heat Transf 128:465–477
Vadasz P (2008) Emerging topics in heat and mass transfer in porous media. Springer, New York
Kuznetsov AV, Nield DA (2010c) Effect of local thermal non-equilibrium on the onset of convection in a porous medium layer saturated by a nanofluid. Transp Porous Media 83:425–436
Kuznetsov AV, Nield DA (2011c) The effect of local thermal non-equilibrium on the onset of convection in a porous medium layer saturated by a nanofluid: Brinkman model. J Porous Media 14(4):285–293
Nield DA, Kuznetsov AV (2010b) The effect of local thermal non-equilibrium on the onset of convection in a nanofluid. J Heat Transf 132(5):052405
Bhadauria BS, Agarwal S (2011b) Convective transport in a nanofluid saturated porous layer with thermal non equilibrium model. Transp Porous Media 88:107–131
Agarwal S, Bhadauria BS (2011) Natural convection in a nanofluid saturated rotating porous layer with thermal non-equilibrium model. Trans Porous Med 90(2):627–654
Ahuja J, Gupta U (2016) MHD effects for a rotating nanofluid layer for LTNE model. Int J Technol 6(2):209–214
Yadav D, Lee J (2015b) The effect of local thermal non-equilibrium on the onset of Brinkman convection in a nanofluid saturated rotating porous layer. J Nanofluids 4(3):335–342
Nield DA, Kuznetsov AV (2015) The effect of double-diffusion and local thermal non-equilibrium on the onset of convection in a layered porous medium: non oscillatory motion. Transp Porous Media 107:261–279
Acknowledgements
The authors would like to thank Prof. (Dr.) Urvashi Gupta for her valuable suggestions. The authors also express their gratefulness to the reviewers for their valuable comments which have gone a long way in improving the paper.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
JA surveyed the literature on thermal instability of nanofluids. JS surveyed the literature on thermosolutal instability of nanofluids. Both authors wrote the final manuscript. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ahuja, J., Sharma, J. Rayleigh–Bénard instability in nanofluids: a comprehensive review. Micro and Nano Syst Lett 8, 21 (2020). https://doi.org/10.1186/s40486-020-00123-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40486-020-00123-y