Variance-constrained filtering for nonlinear systems with randomly occurring quantized measurements: recursive scheme and boundedness analysis

Abstract

In this paper, the robust optimal filtering problem is discussed for time-varying networked systems with randomly occurring quantized measurements via the variance-constrained method. The stochastic nonlinearity is considered by statistical form. The randomly occurring quantized measurements are expressed by a set of Bernoulli distributed random variables, where the quantized measurements are described by the logarithmic quantizer. The objective of this paper is to design a recursive optimal filter such that, for all randomly occurring uncertainties, randomly occurring quantized measurements and stochastic nonlinearity, an optimized upper bound of the estimation error covariance is given and the desired filter gain is proposed. In addition, the boundedness analysis problem is studied, where a sufficient condition is given to ensure the exponential boundedness of the filtering error in the mean-square sense. Finally, simulations with comparisons are proposed to demonstrate the validity of the presented robust variance-constrained filtering strategy.

1 Introduction

Over the past few years, the state estimation or filtering problems have been widely discussed owing to its practical applications in various fields, such as in navigation system, dynamic positioning, tracking of objects in computer vision, and so on [1,2,3,4,5,6,7]. In particular, based on a series of observed measurements over time, the Kalman filtering known as a linear optimal estimation algorithm can provide the globally optimal estimation for linear stochastic systems [8]. Regarding the complex dynamics systems with higher performance requirements, the traditional Kalman filtering method might not achieve satisfactory accuracy especially when the systems are contaminated with the nonlinear disturbances. Thus, a large number of filtering approaches under different performance constraints have been given, such as Kalman filtering [9], extended Kalman filtering [10,11,12], variance-constrained filtering [13,14,15], unscented Kalman filtering [16], $H_{\infty}$ filtering [17, 18], and security-guaranteed filtering [4, 5]. More specifically, some security-guaranteed filtering methods have been presented in [4, 5] for complex systems under different performance indices. In [17], a robust $H_{\infty}$ filtering algorithm has been designed to cope with the effects of the randomly occurring nonlinearities, parameter uncertainties and signal quantization. In [10, 11], the robust extended Kalman filtering methods have been proposed for time-varying nonlinear systems, and the related performance analyses concerning the boundedness of the filtering errors have been provided. In recent years, the variance-constrained method has been presented in [13, 14] to handle the filtering problems for time-varying nonlinear networked systems with missing measurements under deterministic/uncertain occurrence probabilities, where the authors have obtained the optimized upper bounds of estimation error covariance and proposed the expression forms of the time-varying filter gains via the stochastic analysis technique. Subsequently, the variance-constrained state estimation problem has been discussed in [15] for time-varying complex networks and a new time-varying estimation algorithm has been given based on the results in [13, 14].

As it is well known, the existence of the uncertainties would deteriorate the whole performance of addressed systems [19,20,21,22]. Accordingly, it is necessary to propose appropriate means to reduce the influence from uncertainties onto the filtering algorithm performance [23, 24]. Up to now, a variety of results have been reported concerning the filtering problems for uncertain time-varying systems [25,26,27]. To mention a few, a robust recursive filter has been designed in [25] for uncertain systems with missing measurements, where a sufficient criterion has been given such that the exponential mean-square stability of filtering error has been ensured. In the networked environment, the uncertainties might emerge in a random way with certain probability [28]. For example, the state estimation scheme has been proposed in [28] for discrete time-invariant networked systems subject to distributed sensor delays and randomly occurring uncertainties, under which the sufficient criterion has been given such that the stability of the resulted estimation error dynamics has been guaranteed. It is worthwhile to point out that it is necessary to compensate the negative effects caused by randomly occurring uncertainties for time-varying systems and propose more efficient filtering scheme with improved algorithm accuracy.

In a networked setting, the signals before transmission might be quantized due to the limited data-processing capacity of the transmission channels [29], hence the quantization errors should be properly addressed in order to reduce the resulted effects on the filtering algorithm performance [13]. Generally, the logarithmic quantization and uniform quantization are commonly discussed [29, 30]. So far, a large amount of efforts have been made to discuss the filtering/control problems subject to signal quantization; see e.g. [13, 17, 29, 31, 32]. Accordingly, a great deal of attention has been given with respect to the quantization errors. For instance, the sector-bound approach has been employed in [33] to convert the quantization errors into the sector-bound uncertainties, and such a method has been widely utilized when handling the control and filtering problems for networked systems with quantization effects. For example, a robust ${H_{\infty}}$ filtering algorithm under variance constraint has been proposed in [31] for nonlinear time-varying systems with randomly varying gain perturbations as well as quantized measurements, where the pre-defined estimation error variance constraint and ${H_{\infty}}$ performance have been discussed by proposing the sufficient condition. In [34], an ${H_{\infty}}$ filtering problem has been addressed for time-varying systems and a new algorithm has been given to handle the effects of signal measurements and non-Gaussian noises, moreover, the applicability of the proposed filtering scheme has been illustrated by means of a mobile robot localization scenario. So far, most of available filtering methods can be applied to tackle the deterministic quantization effects only. However, there is a need to take the randomly occurring quantization effects into account in order to further reflect the unreliable networked environments with communication constraints. Hence, new filtering approach is desirable for addressing the filtering problem of time-varying systems in the simultaneous presence of randomly occurring uncertainties and quantized measurements under variance constraint. Accordingly, it is very necessary to provide efficient analysis criterion to evaluate the proposed filtering algorithm. As such, the objective of this paper is to shorten the gap by proposing a robust variance-constrained filtering method under certain optimization criterion and conducting the desired algorithm performance analysis issue.

In this paper, we aim to design the robust variance-constrained optimal filtering algorithm for time-varying networked systems with randomly occurring uncertainties and quantized measurements. Both the randomly occurring uncertainties and the quantized measurements are modeled by Bernoulli distributed random variables. Owing to the existence of the randomly occurring uncertainties, signal quantization and stochastic nonlinearity, it is difficult to obtain the accurate value of the estimation error covariance. Therefore, we aim to propose a new robust variance-constrained filtering method under certain optimization criterion. In particular, we need to find a locally optimal upper bound of estimation error covariance and design proper filter gain at each sampling step. The main contributions of this paper lie in: (1) a new variance-constrained filtering algorithm is given for addressed networked systems with stochastic nonlinearity, randomly occurring uncertainties and signal quantization; (2) the obtained upper bound of resulting filtering error covariance can be minimized by properly designing the filtering gain, under which the stochastic analysis techniques are used; and (3) the detailed boundedness analysis of filtering error is discussed and a sufficient condition is given. Finally, we utilize the simulations to illustrate the validity of main results.

Notations

The notations in this paper are standard. $\mathbb {R}^{n}$ and $\mathbb{R}^{n\times m}$, denote the n-dimensional Euclidean space and the set of $n\times m$ matrices, respectively. $\mathbb{E}\{x\}$ represents the expectation of the random variable x. $P^{T}$ and $P^{-1}$ stand for the transpose and inverse of matrix P. We use $P\geq0$ ($P>0$) to depict that P is symmetric positive semi-definite (symmetric positive definite). The $\operatorname{diag}\{Y_{1}, Y_{2}, \ldots, Y_{m}\}$ represents a block-diagonal matrix with $Y_{1}, Y_{2}, \ldots, Y_{m}$ in the diagonal. I represents an identity matrix with appropriate dimension. ∘ is the Hadamard product.

2 Problem formulation and preliminaries

In this paper, we consider the following class of discrete time-varying systems with randomly occurring uncertainties and stochastic nonlinearity:

$$\begin{aligned}& x_{k+1} = (A_{k}+\alpha_{k}\Delta A_{k})x_{k}+f(x_{k},\xi _{k})+B_{k} \omega_{k}, \end{aligned}$$

(1)

$$\begin{aligned}& y_{k} = C_{k}x_{k}+\nu_{k}, \end{aligned}$$

(2)

where $x_{k}\in{\mathbb{R}}^{n}$ is the system state vector to be estimated and its initial value $x_{0}$ has mean $\bar{x}_{0}$ and covariance $P_{0|0}>0$, $y_{k}\in{\mathbb{R}^{m}}$ denotes the measurement output, $\xi_{k}\in{\mathbb{R}}$ is a zero-mean Gaussian white noise, $\omega_{k}\in{\mathbb{R}^{l}}$ and $\nu_{k}\in{\mathbb {R}^{m}}$ are the zero-mean noises with covariance $Q_{k}>0$ and $R_{k}>0$, respectively. $A_{k}$, $B_{k}$ and $C_{k}$ are known and bounded matrices.

The uncertain matrix $\Delta A_{k}$ has the following form:

$$ \Delta A_{k} = H_{k}F_{k}M_{k}, $$

(3)

where $H_{k}$ and $M_{k}$ are known matrices, and uncertain matrix $F_{k}$ satisfies $F^{T}_{k}F_{k}\leq I$.

The Bernoulli distributed random variable $\alpha_{k}\in{\mathbb{R}}$, which is used to model the phenomenon of the randomly occurring uncertainties, takes the values of 0 or 1 with

$$ \operatorname{Prob}\{\alpha_{k}=1\}={\mathbb{E}}\{ \alpha_{k}\}=\bar{\alpha }_{k}, \qquad \operatorname{Prob}\{ \alpha_{k}=0\}=1-\bar{\alpha}_{k}, $$

(4)

where $\bar{\alpha}_{k}\in[0,1]$ is a known scalar. The function $f(x,\xi_{k})$ represents the stochastic nonlinearity with $f(0,\xi _{k})=0$ and has the following statistical properties for all $x_{k}$:

$$\begin{aligned}& \mathbb{E}\bigl\{ f(x_{k},\xi_{k})|x_{k}\bigr\} =0, \end{aligned}$$

(5)

$$\begin{aligned}& \mathbb{E}\bigl\{ f(x_{k},\xi_{k})f^{T}(x_{j}, \xi_{j})|x_{k}\bigr\} =0, k \neq j, \end{aligned}$$

(6)

$$\begin{aligned}& \mathbb{E}\bigl\{ f(x_{k},\xi_{k})f^{T}(x_{k}, \xi_{k})|x_{k}\bigr\} =\sum^{s}_{i=1} \varPi_{i}x^{T}_{k}\varGamma_{i}x_{k}, \end{aligned}$$

(7)

where $s>0$ is a known integer, $\varPi_{i}$ and $\varGamma_{i}$ ($i=1,2,\ldots,s$) are known matrices with suitable dimensions.

Remark 1

In fact, it is not always possible to obtain the accurate system model during the system modeling, hence there is a need to address the modeling errors and discuss their effects on the desired performance. On the other hand, it could be the case that the modeling errors undergo the random changes, thus the randomly occurring uncertainties are characterized by introducing the random variable $\alpha_{k}$ with known occurrence probability as in (4), which is used to cater the practical feature especially in the networked environment.

Remark 2

The stochastic nonlinearity $f(\cdot)$ satisfying the statistical features (5)–(7) could cover many known nonlinearities addressed in the literature. For example, it could describe the functions in some linear systems with the state-multiplicative noises $x_{k}\xi_{k}$, where $\xi_{k}$ is a zero-mean noise with bounded second moment; and the nonlinearities in some nonlinear systems with random disturbances (e.g. $\operatorname{sgn}(\psi (x_{k}))x_{k}\xi_{k}$ with sgn representing the signum function). In this paper, the effects induced by the stochastic nonlinearity will be examined later and the available information (e.g. $\varPi_{i}$ and $\varGamma_{i}$) will be reflected in the main results.

Owing to the limited bandwidth and the unreliable link of the network communication, the signal quantizations maybe occur in a random way. Firstly, the map of the quantization process is expressed by

$$q(y_k)={\left[\begin{array}{cccc}{q}_1(y_k^1)& q_2(y_k^2)& \cdots & q_m(y_k^m)\end{array}\right]}^T.$$

For each $q_{j}(\cdot)$ ($j=1,2,\ldots,m$), the following set of quantization levels are considered:

$$\begin{aligned} {\mathscr{U}}_{j} =& \bigl\{ \pm u^{(j)}_{i}, u^{(j)}_{i}= \bigl(\chi ^{(j)} \bigr)^{i}u^{(j)}_{0}, i=0,\pm1,\pm2,\ldots \bigr\} \\ &{}\cup \{0 \}, \quad 0< \chi^{(j)}< 1, u^{(j)}_{0}>0, \end{aligned}$$

where $\chi^{(j)}$ ($j=1,2,\ldots,m$) characterizes the quantization density. According to [33, 35], we use the following logarithmic quantizer:

$$ q_{j}\bigl(y^{j}_{k}\bigr)= \textstyle\begin{cases} u^{(j)}_{i}, & \frac{1}{1+\delta _{j}}u^{(j)}_{i}< y^{j}_{k}\leq\frac{1}{1-\delta_{j}}u^{(j)}_{i}, \\ 0, & y^{j}_{k}=0, \\ -q_{j}(-y^{j}_{k}), & y^{j}_{k}< 0, \end{cases} $$

where $\delta_{j}=\frac{1-\chi^{(j)}}{1+\chi^{(j)}}$. It is not difficult to verify that $q_{j}(y^{j}_{k})= (1+\Delta ^{(j)}_{k} )y^{j}_{k}$ with $|\Delta^{(j)}_{k}|\leq\delta_{j}$. Letting $\mathcal{F}_{k}=\Delta_{k}\varUpsilon^{-1}$, $\varUpsilon=\operatorname{diag}\{\delta_{1}, \delta_{2},\ldots,\delta_{m}\}$ and $\Delta _{k}=\operatorname{diag}\{\Delta^{(1)}_{k},\Delta^{(2)}_{k},\ldots,\Delta ^{(m)}_{k}\}$, we can know that $\mathcal{F}_{k}$ is an unknown real-valued matrix satisfying $\mathcal{F}_{k}\mathcal {F}^{T}_{k}=\mathcal{F}^{T}_{k}\mathcal{F}_{k}\leq I$.

The following model is introduced to describe the real measurement signals received by the remoter filter side:

$$ \tilde{y}_{k}=\varLambda_{k}y_{k}+(I- \varLambda_{k})q(y_{k}), $$

(8)

where $\varLambda_{k}:=\operatorname{diag}\{\lambda_{k,1},\lambda_{k,2},\ldots ,\lambda_{k,m}\}$, and $\lambda_{k,i}$ ($i=1,2,\ldots,m$) are random variables satisfying

$$ \operatorname{Prob} \{\lambda_{k,i}=1 \}={\mathbb{E}} \{ \lambda _{k,i} \}=\bar{\lambda}_{k,i}, \qquad \operatorname{Prob} \{\lambda _{k,i}=0 \}=1-\bar{\lambda}_{k,i}, $$

(9)

with $\bar{\lambda}_{k,i}$ being known scalars. Meanwhile, suppose that $\xi_{k}$, $\alpha_{k}$, $\omega_{k}$, $\lambda_{k,i}$, $\nu_{k}$ as well as $x_{0}$ are all mutually independent.

In this paper, the following time-varying filter is designed:

$$\begin{aligned}& \hat{x}_{k+1|k} = A_{k}\hat{x}_{k|k}, \end{aligned}$$

(10)

$$\begin{aligned}& \hat{x}_{k+1|k+1} = \hat{x}_{k+1|k}+K_{k+1}( \tilde{y}_{k+1}-\bar{\varLambda }_{k+1}C_{k+1} \hat{x}_{k+1|k}), \end{aligned}$$

(11)

where $\hat{x}_{k|k}$ is the state estimate of $x_{k}$ at time k, $\hat{x}_{k+1|k}$ is the one-step prediction at time k, $\bar{\varLambda }_{k+1}={\mathbb{E}}\{\varLambda_{k+1}\}$, and $K_{k+1}$ is the filter gain to be determined.

The purpose of this paper mainly has three aspects. Firstly, we seek the upper bound of the filtering error covariance by using inequality technique. Secondly, we design the filter gain $K_{k+1}$ so as to minimize the upper bound. In addition, we will propose a sufficient condition to guarantee the exponential boundedness of the filtering error in the mean-square sense.

For later derivations, the following lemmas are introduced.

Lemma 1

For p, q $\in\mathbb{R}^{n}$ and scalar $\varepsilon>0$, the inequality

$$ pq^{T}+qp^{T} \leq\varepsilon pp^{T}+ \varepsilon^{-1}qq^{T} $$

(12)

holds.

Lemma 2

([36])

For matrices A, B, C, D ($CC^{T}\leq I$), if the matrix $X>0$ and scalar $\mu>0$ satisfy

$$ \mu^{-1}I-DXD^{T}>0, $$

one has

$$ (A+BCD)X(A+BCD)^{T}\leq A\bigl(X^{-1}-\mu D^{T}D\bigr)^{-1}A^{T}+\mu^{-1}BB^{T}. $$

(13)

Lemma 3

([37])

For a real-valued matrix $A=[a_{ij}]_{n\times n}$ and a stochastic matrix $B=\operatorname{diag}\{b_{1},b_{2},\ldots,b_{n}\}$, we have

$$\mathbb{E}\left\{BA{B}^T\right\}=\left[\begin{array}{cccc}\mathbb{E}\{b_1^2\}& \mathbb{E}\{b_1{b}_2\}& \cdots & \mathbb{E}\{b_1{b}_n\}\\ \mathbb{E}\{b_2{b}_1\}& \mathbb{E}\{b_2^2\}& \cdots & \mathbb{E}\{b_2{b}_n\}\\ ⋮& ⋮& \ddots & ⋮\\ \mathbb{E}\{b_n{b}_1\}& \mathbb{E}\{b_n{b}_2\}& \cdots & \mathbb{E}\{b_n^2\}\end{array}\right]\circ A,$$

with ∘ being the Hadamard product.

3 Design of optimal filtering algorithm

In this section, an optimized upper bound of the filtering error covariance is obtained based on the matrix theory and stochastic analysis technique. Moreover, we derive the desired filter gain based on the solutions to recursive matrix equations.

Firstly, let us calculate the one-step prediction error and filtering error. Define $\tilde{x}_{k+1|k}=x_{k+1}-\hat{x}_{k+1|k}$ and $\tilde {x}_{k+1|k+1}=x_{k+1}-\hat{x}_{k+1|k+1}$, respectively. Subtracting (10) from (1) yields

$$ \tilde{x}_{k+1|k}=A_{k}\tilde{x}_{k|k}+ \bar{\alpha}_{k}\Delta A_{k}x_{k}+\tilde{ \alpha}_{k}\Delta A_{k}x_{k}+f(x_{k}, \xi _{k})+B_{k}\omega_{k}, $$

(14)

where $\tilde{\alpha}_{k}=\alpha_{k}-\bar{\alpha}_{k}$. Similarly, we have

$$\begin{aligned} \tilde{x}_{k+1|k+1} =&(I-K_{k+1}\bar{\varLambda}_{k+1}C_{k+1}) \tilde {x}_{k+1|k}-K_{k+1}\tilde{\varLambda}_{k+1}C_{k+1}x_{k+1}-K_{k+1} \boldsymbol {\varLambda}_{k+1} \\ &{}\times(I+\Delta_{k+1})C_{k+1}x_{k+1}+K_{k+1} \tilde{\varLambda }_{k+1}(I+\Delta_{k+1})C_{k+1}x_{k+1} \\ &{}-K_{k+1}\boldsymbol {\varLambda}_{k+1}\Delta_{k+1} \nu_{k+1}+K_{k+1}\tilde{\varLambda }_{k+1} \Delta_{k+1}\nu_{k+1}-K_{k+1}\nu_{k+1}, \end{aligned}$$

(15)

where $\tilde{\varLambda}_{k+1}=\varLambda_{k+1}-\bar{\varLambda}_{k+1}$ and $\boldsymbol {\varLambda}_{k+1}=I-\bar{\varLambda}_{k+1}$.

Now, the following theorems provide the desired recursions of the one-step prediction error covariance and filtering error covariance via the above definitions.

Theorem 1

The covariance $P_{k+1|k}$ of the one-step prediction error satisfies

$$\begin{aligned} P_{k+1|k} =& A_{k}P_{k|k}A^{T}_{k}+ \bar{\alpha}_{k}\Delta A_{k}\mathbb {E}\bigl\{ x_{k}x^{T}_{k}\bigr\} \Delta A_{k}^{T}+B_{k}Q_{k}B^{T}_{k}+ \bar{\alpha }_{k}A_{k}\mathbb{E}\bigl\{ \tilde{x}_{k|k}x^{T}_{k} \bigr\} \\ &{}\times\Delta A^{T}_{k}+\bar{\alpha}_{k} \Delta A_{k}\mathbb{E}\bigl\{ x_{k}\tilde{x}^{T}_{x|k} \bigr\} A^{T}_{k}+\sum_{i=1}^{s} \varPi_{i} \operatorname{tr}\bigl(\mathbb{E}\bigl\{ x_{k}x^{T}_{k} \bigr\} \varGamma_{i}\bigr). \end{aligned}$$

(16)

Proof

According to (14) and the independent properties of random variables, we can get (16) easily. □

Theorem 2

The recursion of the filtering error covariance $P_{k+1|k+1}$ can be given by

$$\begin{aligned} P_{k+1|k+1} =&(I-K_{k+1}\bar{\varLambda }_{k+1}C_{k+1})P_{k+1|k}(I-K_{k+1} \bar{\varLambda }_{k+1}C_{k+1})^{T}+K_{k+1}R_{k+1} \\ &{}\times K^{T}_{k+1}+\mathcal{M}_{1}+ \mathcal{M}^{T}_{1}+K_{k+1}\boldsymbol { \varLambda}_{k+1}(I+\Delta_{k+1})C_{k+1}\mathbb{E}\bigl\{ x_{k+1}x^{T}_{k+1}\bigr\} \\ &{}\times C^{T}_{k+1}(I+\Delta_{k+1})^{T} \boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}+\mathcal{M}_{2}+ \mathcal{M}^{T}_{2}+K_{k+1}\boldsymbol { \varLambda}_{k+1}\Delta_{k+1} \\ &{}\times R_{k+1}\Delta^{T}_{k+1}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}+K_{k+1} \bigl\{ \check{ \varXi}_{k+1}\circ\bigl[C_{k+1}\mathbb {E}\bigl\{ x_{k+1}x^{T}_{k+1}\bigr\} C^{T}_{k+1} \\ &{}+(I+\Delta_{k+1})C_{k+1}\mathbb{E}\bigl\{ x_{k+1}x^{T}_{k+1}\bigr\} C^{T}_{k+1}(I+ \Delta_{k+1})^{T}+\Delta_{k+1}R_{k+1} \\ &{}\times\Delta^{T}_{k+1}+\mathcal{M}_{3}+ \mathcal{M}^{T}_{3}\bigr] \bigr\} K^{T}_{k+1}, \end{aligned}$$

(17)

where

$$\begin{aligned}& \mathcal{M}_{1} = K_{k+1}R_{k+1} \Delta^{T}_{k+1}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}, \\& \mathcal{M}_{3} = -C_{k+1}\mathbb{E}\bigl\{ x_{k+1}x^{T}_{k+1}\bigr\} C^{T}_{k+1}(I+ \Delta_{k+1})^{T}, \\& \mathcal{M}_{2} = -(I-K_{k+1}\bar{\varLambda}_{k+1}C_{k+1}) \mathbb{E}\bigl\{ \tilde{x}_{k+1|k}x^{T}_{k+1}\bigr\} C^{T}_{k+1}(I+\Delta_{k+1})^{T}\boldsymbol { \varLambda}_{k+1}K^{T}_{k+1}, \\& \check{\varXi}_{k+1} = \operatorname{diag}\bigl\{ \bar{ \lambda}_{k+1,1}(1-\bar{\lambda }_{k+1,1}),\bar{ \lambda}_{k+1,2}(1-\bar{\lambda}_{k+1,2}),\ldots,\bar { \lambda}_{k+1,m}(1-\bar{\lambda}_{k+1,m})\bigr\} . \end{aligned}$$

Proof

In terms of (15) and Lemma 3, it is easy to see that

$$\begin{aligned} P_{k+1|k+1} =&(I-K_{k+1}\bar{\varLambda }_{k+1}C_{k+1})P_{k+1|k}(I-K_{k+1} \bar{\varLambda }_{k+1}C_{k+1})^{T}+K_{k+1}R_{k+1} \\ &{}\times K^{T}_{k+1}+\mathcal{M}_{1}+ \mathcal{M}^{T}_{1} +K_{k+1}\boldsymbol { \varLambda}_{k+1}(I+\Delta_{k+1})C_{k+1}\mathbb{E}\bigl\{ x_{k+1}x^{T}_{k+1}\bigr\} \\ &{}\times C^{T}_{k+1}(I+\Delta_{k+1})^{T} \boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}+\mathcal{M}_{2}+ \mathcal{M}^{T}_{2}+K_{k+1}\boldsymbol { \varLambda}_{k+1}\Delta_{k+1} \\ &{}\times R_{k+1}\Delta^{T}_{k+1}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}+K_{k+1} \bigl\{ \check{ \varXi}_{k+1}\circ\bigl[C_{k+1}\mathbb {E}\bigl\{ x_{k+1}x^{T}_{k+1}\bigr\} C^{T}_{k+1} \\ &{}+(I+\Delta_{k+1})C_{k+1}\mathbb{E}\bigl\{ x_{k+1}x^{T}_{k+1}\bigr\} C^{T}_{k+1}(I+ \Delta_{k+1})^{T}+\Delta_{k+1}R_{k+1} \\ &{}\times\Delta^{T}_{k+1}+\mathcal{M}_{3}+ \mathcal{M}^{T}_{3}\bigr] \bigr\} K^{T}_{k+1} +\sum^{18}_{l=1}\bigl(\mathcal{N}_{l}+ \mathcal{N}^{T}_{l}\bigr), \end{aligned}$$

where

$$\begin{aligned}& \mathcal{N}_{1} = -\mathbb{E}\bigl\{ (I-K_{k+1}\bar{\varLambda }_{k+1}C_{k+1})\tilde{x}_{k+1|k}x^{T}_{k+1}C^{T}_{k+1} \tilde{\varLambda }_{k+1}K^{T}_{k+1}\bigr\} , \\& \mathcal{N}_{2} = \mathbb{E}\bigl\{ (I-K_{k+1}\bar{\varLambda }_{k+1}C_{k+1})\tilde{x}_{k+1|k}x^{T}_{k+1}C^{T}_{k+1}(I+ \Delta _{k+1})^{T}\tilde{\varLambda}_{k+1}K^{T}_{k+1} \bigr\} , \\& \mathcal{N}_{3} = -\mathbb{E}\bigl\{ (I-K_{k+1}\bar{\varLambda }_{k+1}C_{k+1})\tilde{x}_{k+1|k}\nu^{T}_{k+1} \Delta_{k+1}^{T}\boldsymbol {\varLambda}_{k+1}K^{T}_{k+1} \bigr\} , \\& \mathcal{N}_{4} = \mathbb{E}\bigl\{ (I-K_{k+1}\bar{\varLambda }_{k+1}C_{k+1})\tilde{x}_{k+1|k}\nu^{T}_{k+1} \Delta_{k+1}^{T}\tilde {\varLambda}_{k+1}K^{T}_{k+1} \bigr\} , \\& \mathcal{N}_{5} = -\mathbb{E}\bigl\{ (I-K_{k+1}\bar{\varLambda }_{k+1}C_{k+1})\tilde{x}_{k+1|k}\nu^{T}_{k+1}K^{T}_{k+1} \bigr\} , \\& \mathcal{N}_{6} = \mathbb{E}\bigl\{ K_{k+1}\tilde{\varLambda }_{k+1}C_{k+1}x_{k+1}x^{T}_{k+1}C^{T}_{k+1}(I+ \Delta_{k+1})^{T}\boldsymbol {\varLambda}_{k+1}K^{T}_{k+1} \bigr\} , \\& \mathcal{N}_{7} = \mathbb{E}\bigl\{ K_{k+1}\tilde{\varLambda }_{k+1}C_{k+1}x_{k+1}\nu_{k+1}^{T} \Delta^{T}_{k+1}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1} \bigr\} , \\& \mathcal{N}_{8} = -\mathbb{E}\bigl\{ K_{k+1}\tilde{\varLambda }_{k+1}C_{k+1}x_{k+1}\nu_{k+1}^{T} \Delta^{T}_{k+1}\tilde{\varLambda }_{k+1}K^{T}_{k+1} \bigr\} , \\& \mathcal{N}_{9} = \mathbb{E}\bigl\{ K_{k+1}\tilde{\varLambda }_{k+1}C_{k+1}x_{k+1}\nu_{k+1}^{T}K^{T}_{k+1} \bigr\} , \\& \mathcal{N}_{10} = -\mathbb{E}\bigl\{ K_{k+1}\boldsymbol { \varLambda}_{k+1}(I+\Delta _{k+1})C_{k+1}x_{k+1}x^{T}_{k+1}C^{T}_{k+1}(I+ \Delta_{k+1})^{T}\tilde {\varLambda}_{k+1}K^{T}_{k+1} \bigr\} , \\& \mathcal{N}_{11} = \mathbb{E}\bigl\{ K_{k+1}\boldsymbol { \varLambda}_{k+1}(I+\Delta _{k+1})C_{k+1}x_{k+1} \nu^{T}_{k+1}\Delta^{T}_{k+1}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}\bigr\} , \\& \mathcal{N}_{12} = -\mathbb{E}\bigl\{ K_{k+1}\boldsymbol { \varLambda}_{k+1}(I+\Delta _{k+1})C_{k+1}x_{k+1} \nu^{T}_{k+1}\Delta^{T}_{k+1}\tilde{\varLambda }_{k+1}K^{T}_{k+1}\bigr\} , \\& \mathcal{N}_{13} = \mathbb{E}\bigl\{ K_{k+1}\boldsymbol { \varLambda}_{k+1}(I+\Delta _{k+1})C_{k+1}x_{k+1} \nu^{T}_{k+1}K^{T}_{k+1}\bigr\} , \\& \mathcal{N}_{14} = -\mathbb{E}\bigl\{ K_{k+1}\tilde{ \varLambda}_{k+1}(I+\Delta _{k+1})C_{k+1}x_{k+1} \nu^{T}_{k+1}\Delta^{T}_{k+1}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}\bigr\} , \\& \mathcal{N}_{15} = \mathbb{E}\bigl\{ K_{k+1}\tilde{ \varLambda}_{k+1}(I+\Delta _{k+1})C_{k+1}x_{k+1} \nu^{T}_{k+1}\Delta^{T}_{k+1}\tilde{\varLambda }_{k+1}K^{T}_{k+1}\bigr\} , \\& \mathcal{N}_{16} = -\mathbb{E}\bigl\{ K_{k+1}\tilde{ \varLambda}_{k+1}(I+\Delta _{k+1})C_{k+1}x_{k+1} \nu^{T}_{k+1}K^{T}_{k+1}\bigr\} , \\& \mathcal{N}_{17} = -\mathbb{E}\bigl\{ K_{k+1}\boldsymbol { \varLambda}_{k+1}\Delta _{k+1}\nu_{k+1} \nu^{T}_{k+1}\Delta^{T}_{k+1}\tilde{\varLambda }_{k+1}K^{T}_{k+1}\bigr\} , \\& \mathcal{N}_{18} = -\mathbb{E}\bigl\{ K_{k+1}\tilde{ \varLambda}_{k+1}\Delta _{k+1}\nu_{k+1} \nu^{T}_{k+1}K^{T}_{k+1}\bigr\} . \end{aligned}$$

Notice that $\nu_{k+1}$ and $\varLambda_{k+1}$ are mutually independent and the expectation of $\tilde{\varLambda}_{k+1}$ is a zero matrix, then we know that $\mathcal{N}_{i}$ ($i=1,2,\ldots,18$) are zero terms. Consequently, the result in (17) can be obtained easily. □

Remark 3

Generally, it could be better if a global optimal filtering method can be given. Unfortunately, it is impossible to attain this objective due to the existence of the parameter uncertainties, nonlinearity and randomly occurring quantized measurements. In view of these obstacles, we decide to derive an upper bound of filtering error covariance and minimize this upper bound by designing proper filtering gain matrix at each time step, which is acceptable with certain admissible estimation accuracy.

So far, we have provided the recursions of the one-step prediction error covariance and the filtering error covariance. Next, we are ready to obtain the desired upper bound of filtering error covariance and choose the filter gain properly.

Theorem 3

Let $\gamma_{k+1,1}$ and $\varepsilon_{i}$ $(i=1,2,\ldots,6)$ be positive scalars. If the following two recursive matrix equations:

$$\begin{aligned} \varSigma_{k+1|k} =&(1+\bar{\alpha}_{k}\varepsilon_{1})A_{k} \varSigma _{k|k}A^{T}_{k}+\varOmega_{k}+B_{k}Q_{k}B^{T}_{k} \\ &{}+\bigl(1+\varepsilon^{-1}_{1}\bigr)\bar{ \alpha}_{k}\operatorname{tr}\bigl(M_{k}\bar{\mathcal {L}}_{k}M^{T}_{k}\bigr)H_{k}H^{T}_{k} \end{aligned}$$

(18)

and

$$\begin{aligned} \varSigma_{k+1|k+1} =&(1+\varepsilon_{5}) (I-K_{k+1}\bar{ \varLambda }_{k+1}C_{k+1})\varSigma_{k+1|k}(I-K_{k+1} \bar{\varLambda }_{k+1}C_{k+1})^{T} \\ &{}+(1+\varepsilon_{4})K_{k+1}R_{k+1}K^{T}_{k+1}+ \bigl(1+\varepsilon ^{-1}_{5}\bigr)\operatorname{tr} \bigl(C_{k+1}\bar{\varPi}_{k+1} C^{T}_{k+1} \bigr) \\ &{}\times K_{k+1}\boldsymbol {\varLambda}_{k+1}\bigl[(I- \gamma_{k+1,1}\varUpsilon\varUpsilon)^{-1} +\gamma^{-1}_{k+1,1}I \bigr]\boldsymbol {\varLambda}_{k+1}K^{T}_{k+1}+K_{k+1} \\ &{}\times\varPsi_{k+1}K^{T}_{k+1}+\bigl(1+ \varepsilon^{-1}_{4}\bigr)\operatorname{tr}(\varUpsilon R_{k+1}\varUpsilon)K_{k+1}\boldsymbol {\varLambda}_{k+1}^{2} K^{T}_{k+1}, \end{aligned}$$

(19)

under the constraint $\gamma^{-1}_{k+1,1}I-\varUpsilon\varUpsilon>0$ and initial condition $\varSigma_{0|0}=P_{0|0}>0$, have solutions $\varSigma _{k+1|k}>0$ and $\varSigma_{k+1|k+1}>0$, then $P_{k+1|k+1}\leq\varSigma_{k+1|k+1}$. Moreover, if we choose the following form of the filter gain matrix $K_{k+1}$:

$$\begin{aligned} K_{k+1} =&(1+\varepsilon_{5})\varSigma_{k+1|k}C^{T}_{k+1} \bar{\varLambda }_{k+1} \bigl\{ (1+\varepsilon_{4})R_{k+1}+ \bigl(1+\varepsilon^{-1}_{5}\bigr)\operatorname{tr} \bigl(C_{k+1}\bar{\varPi}_{k+1} \\ &{}\times C^{T}_{k+1}\bigr)\boldsymbol {\varLambda}_{k+1} \bigl[(I-\gamma_{k+1,1}\varUpsilon \varUpsilon)^{-1}+ \gamma^{-1}_{k+1,1}I\bigr]\boldsymbol {\varLambda}_{k+1}+(1+ \varepsilon _{5})\bar{\varLambda}_{k+1}C_{k+1} \\ &{}\times\varSigma_{k+1|k}C^{T}_{k+1}\bar{{ \varLambda}}_{k+1}+\bigl(1+\varepsilon ^{-1}_{4}\bigr) \operatorname{tr}(\varUpsilon R_{k+1}\varUpsilon)\boldsymbol {\varLambda}_{k+1}^{2}+ \varPsi _{k+1} \bigr\} ^{-1}, \end{aligned}$$

(20)

it is shown that $\operatorname{tr} (\varSigma_{k+1|k+1})$ can be minimized, where

$$\begin{aligned}& \varOmega_{k} = \sum_{i=1}^{s} \varPi_{i}\operatorname{tr}(\bar{\mathcal{L}}_{k}\varGamma _{i}), \\& \bar{\varPi}_{k+1} = (1+\varepsilon_{3})\varSigma_{k+1|k}+ \bigl(1+\varepsilon ^{-1}_{3}\bigr)\hat{x}_{k+1|k} \hat{x}^{T}_{k+1|k}, \\& \varPsi_{k+1}= \check{\varXi}_{k+1}\circ \bigl\{ \bigl(1+ \varepsilon^{-1}_{6}\bigr)\operatorname{tr} \bigl(C_{k+1}\bar{\varPi}_{k+1}C^{T}_{k+1}\bigr) \bigl[(I-\gamma_{k+1,1}\varUpsilon\varUpsilon )^{-1}+ \gamma^{-1}_{k+1,1}I\bigr] \\& \hphantom{\varPsi_{k+1}={}}{}+\operatorname{tr}(\varUpsilon R_{k+1}\varUpsilon)+(1+ \varepsilon_{6})C_{k+1}\bar{\varPi }_{k+1}C^{T}_{k+1} \bigr\} , \\& \bar{\mathcal{L}}_{k} = (1+\varepsilon_{2}) \varSigma_{k|k}+\bigl(1+\varepsilon ^{-1}_{2}\bigr) \hat{x}_{k|k}\hat{x}^{T}_{k|k}. \end{aligned}$$

(21)

Proof

To prove this theorem, we resort to the mathematical induction method. By considering (16) and Lemma 1, we can deduce that

$$\begin{aligned}& \bar{\alpha}_{k}A_{k}\mathbb{E}\bigl\{ \tilde{x}_{k|k}x^{T}_{k}\bigr\} \Delta A_{k}^{T}+\bar{\alpha}_{k}\Delta A_{k} \mathbb{E}\bigl\{ x_{k}\tilde {x}^{T}_{x|k}\bigr\} A^{T}_{k} \\& \quad \leq\bar{\alpha}_{k}\varepsilon_{1}A_{k}P_{k|k}A^{T}_{k}+ \bar{\alpha }_{k}\varepsilon_{1}^{-1}\Delta A_{k}\mathbb{E}\bigl\{ x_{k}x^{T}_{k} \bigr\} \Delta A_{k}^{T}, \end{aligned}$$

(22)

where $\varepsilon_{1}$ is a positive scalar. So, we can get

$$\begin{aligned} P_{k+1|k} \leq&(1+\bar{\alpha}_{k}\varepsilon_{1})A_{k}P_{k|k}A^{T}_{k} +\sum_{i=1}^{s}\varPi_{i} \operatorname{tr}\bigl(\mathbb{E}\bigl\{ x_{k}x^{T}_{k} \bigr\} \varGamma _{i}\bigr)+\bigl(1+\varepsilon^{-1}_{1} \bigr)\bar{\alpha}_{k}\Delta A_{k} \\ &{}\times\mathbb{E}\bigl\{ x_{k}x^{T}_{k}\bigr\} \Delta{A_{k}}^{T}+B_{k}Q_{k}B^{T}_{k}. \end{aligned}$$

(23)

Next, we get

$$\begin{aligned} \mathbb{E}\bigl\{ x_{k}x^{T}_{k}\bigr\} \leq& \mathbb{E} \bigl\{ (1+\varepsilon _{2})\tilde{x}_{k|k} \tilde{x}^{T}_{k|k} +\bigl(1+\varepsilon^{-1}_{2} \bigr)\hat{x}_{k|k}\hat{x}^{T}_{k|k} \bigr\} \\ =&(1+\varepsilon_{2})P_{k|k}+\bigl(1+\varepsilon^{-1}_{2} \bigr)\hat{x}_{k|k}\hat {x}^{T}_{k|k}:= \mathcal{L}_{k}, \end{aligned}$$

(24)

where $\varepsilon_{2}$ is a positive scalar. Noticing the norm-bounded parameter uncertainties defined in (3), the following term can be tackled:

$$ \Delta A_{k}\mathbb{E}\bigl\{ x_{k}x^{T}_{k} \bigr\} \Delta A_{k}^{T}\leq\operatorname{tr} \bigl(M_{k}\mathcal{L}_{k}M^{T}_{k} \bigr)H_{k}H^{T}_{k}. $$

(25)

Finally, it follows from (23)–(25) that

$$\begin{aligned} P_{k+1|k} \leq&(1+\bar{\alpha}_{k}\varepsilon _{1})A_{k}P_{k|k}A^{T}_{k}+ \sum_{i=1}^{s}\varPi_{i} \operatorname{tr}({\mathcal {L}}_{k}\varGamma_{i})+\bigl(1+ \varepsilon^{-1}_{1}\bigr)\bar{\alpha}_{k} \operatorname{tr}\bigl(M_{k}\mathcal{L}_{k}M^{T}_{k} \bigr) \\ &{}\times H_{k}H^{T}_{k}+B_{k}Q_{k}B^{T}_{k}. \end{aligned}$$

(26)

Secondly, it is easy to see that

$$ \mathbb{E}\bigl\{ x_{k+1}x^{T}_{k+1} \bigr\} \leq (1+\varepsilon _{3})P_{k+1|k}+\bigl(1+ \varepsilon^{-1}_{3}\bigr)\hat{x}_{k+1|k}\hat {x}^{T}_{k+1|k}:=\varPi_{k+1}, $$

(27)

where $\varepsilon_{3}>0$ is a scalar. Next, we tackle the uncertain terms in (17). According to Lemma 1 and (27), we can arrive at

$$\begin{aligned}& \mathcal{M}_{1}+\mathcal{M}^{T}_{1} \leq \varepsilon _{4}K_{k+1}R_{k+1}K^{T}_{k+1}+ \varepsilon^{-1}_{4}K_{k+1}\boldsymbol {\varLambda }_{k+1}\Delta_{k+1}R_{k+1}\Delta^{T}_{k+1} \boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}, \\& \mathcal{M}_{2}+\mathcal{M}^{T}_{2} \leq \varepsilon_{5}(I-K_{k+1}\bar {\varLambda}_{k+1}C_{k+1})P_{k+1|k}(I-K_{k+1} \bar{\varLambda }_{k+1}C_{k+1})^{T}+\varepsilon^{-1}_{5} \\& \hphantom{\mathcal{M}_{2}+\mathcal{M}^{T}_{2} \leq{}}{} \times K_{k+1}\boldsymbol {\varLambda}_{k+1}(I+ \Delta_{k+1})C_{k+1}\varPi _{k+1}C^{T}_{k+1}(I+ \Delta_{k+1})^{T}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}, \\& \mathcal{M}_{3}+\mathcal{M}^{T}_{3} \leq \varepsilon_{6}C_{k+1}\varPi _{k+1}C^{T}_{k+1}+ \varepsilon^{-1}_{6}(I+\Delta_{k+1})C_{k+1} \varPi _{k+1}C^{T}_{k+1} \\& \hphantom{\mathcal{M}_{3}+\mathcal{M}^{T}_{3} \leq{}}{} \times(I+\Delta_{k+1})^{T}, \end{aligned}$$

(28)

where $\varepsilon_{i}>0$ ($i=4,5,6$) are scalars. Based on (28), one has

$$\begin{aligned} P_{k+1|k+1} \leq& (1+\varepsilon_{5}) (I-K_{k+1}\bar{ \varLambda }_{k+1}C_{k+1})P_{k+1|k}(I-K_{k+1}\bar{ \varLambda }_{k+1}C_{k+1})^{T} \\ &{}+(1+\varepsilon_{4})K_{k+1}R_{k+1}K^{T}_{k+1}+ \bigl(1+\varepsilon ^{-1}_{5}\bigr)K_{k+1}\boldsymbol { \varLambda}_{k+1}(I+\Delta_{k+1})C_{k+1} \\ &{}\times\varPi_{k+1}C^{T}_{k+1}(I+ \Delta_{k+1})^{T}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}+ \bigl(1+\varepsilon^{-1}_{4}\bigr)K_{k+1}\boldsymbol {\varLambda }_{k+1}\Delta_{k+1} \\ &{}\times R_{k+1}\Delta^{T}_{k+1}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}+K_{k+1} \bigl\{ \check{ \varXi}_{k+1}\circ\bigl[(1+\varepsilon _{6})C_{k+1} \varPi_{k+1}C^{T}_{k+1} \\ &{}+\bigl(1+\varepsilon^{-1}_{6}\bigr) (I+ \Delta_{k+1})C_{k+1}\varPi _{k+1}C^{T}_{k+1}(I+ \Delta_{k+1})^{T} \\ &{}+\Delta_{k+1}R_{k+1}\Delta^{T}_{k+1} \bigr] \bigr\} K^{T}_{k+1}. \end{aligned}$$

(29)

Noting $\Delta_{k+1}=\mathcal{F}_{k+1}\varUpsilon$ ($\mathcal {F}_{k+1}\mathcal{F}^{T}_{k+1}\leq I$), together with Lemma 2 and the property of trace, we have

$$\begin{aligned}& (I+\Delta_{k+1})C_{k+1}\varPi_{k+1}C^{T}_{k+1}(I+ \Delta _{k+1})^{T} \\& \quad \leq \operatorname{tr}\bigl(C_{k+1}\varPi_{k+1}C^{T}_{k+1} \bigr)\bigl[(I-\gamma _{k+1,1}\varUpsilon\varUpsilon)^{-1} + \gamma ^{-1}_{k+1,1}I\bigr], \end{aligned}$$

(30)

$$\begin{aligned}& \Delta_{k+1}R_{k+1}\Delta^{T}_{k+1}\leq \operatorname{tr}(\varUpsilon R_{k+1} \varUpsilon)I, \end{aligned}$$

(31)

where $\gamma_{k+1,1}$ is a positive scalar. Taking (30)–(31) into account, we arrive at

$$\begin{aligned} P_{k+1|k+1} \leq&(1+\varepsilon_{5}) (I-K_{k+1}\bar{ \varLambda }_{k+1}C_{k+1})P_{k+1|k}(I-K_{k+1}\bar{ \varLambda }_{k+1}C_{k+1})^{T} \\ &{}+(1+\varepsilon_{4})K_{k+1}R_{k+1}K^{T}_{k+1}+ \bigl(1+\varepsilon ^{-1}_{5}\bigr)\operatorname{tr} \bigl(C_{k+1}\varPi_{k+1}C^{T}_{k+1} \bigr)K_{k+1} \\ &{}\times \boldsymbol {\varLambda}_{k+1}\bigl[(I-\gamma_{k+1,1}\varUpsilon \varUpsilon )^{-1}+\gamma^{-1}_{k+1,1}I\bigr]\boldsymbol { \varLambda}_{k+1}K^{T}_{k+1}+K_{k+1} \bigl\{ \check{\varXi}_{k+1} \\ &{}\circ \bigl\{ \bigl(1+\varepsilon^{-1}_{6}\bigr) \operatorname{tr}\bigl(C_{k+1}\varPi _{k+1}C^{T}_{k+1} \bigr)\bigl[(I-\gamma_{k+1,1}\varUpsilon\varUpsilon)^{-1}+\gamma ^{-1}_{k+1,1}I\bigr] \\ &{}+\operatorname{tr}(\varUpsilon R_{k+1}\varUpsilon)I+(1+ \varepsilon_{6})C_{k+1}\varPi _{k+1}C^{T}_{k+1} \bigr\} \bigr\} K^{T}_{k+1}+\bigl(1+\varepsilon ^{-1}_{4}\bigr) \\ &{}\times\operatorname{tr}(\varUpsilon R_{k+1}\varUpsilon)K_{k+1} \boldsymbol {\varLambda }_{k+1}^{2} K^{T}_{k+1}. \end{aligned}$$

(32)

Then it follows from (18), (19), (26) and (32) that $P_{k+1|k+1} \leq\varSigma_{k+1|k+1}$.

Finally, we aim to minimize the trace of the upper bound $\varSigma _{k+1|k+1}$ and determine the corresponding filter gain. Firstly, calculating the partial derivative of the trace of (19) with respect to $K_{k+1}$ leads to

$$\begin{aligned}& \frac{\partial\operatorname{tr}(\varSigma_{k+1|k+1})}{\partial K_{k+1}} \\& \quad = -2(1+\varepsilon_{5}) (I-K_{k+1}\bar{ \varLambda}_{k+1}C_{k+1})\varSigma_{k+1|k} C^{T}_{k+1} \bar{\varLambda}_{k+1}+2(1+\varepsilon _{4})K_{k+1}R_{k+1} \\& \qquad {} +2\bigl(1+\varepsilon^{-1}_{5}\bigr) \operatorname{tr}\bigl(C_{k+1}\bar{\varPi }_{k+1}C^{T}_{k+1} \bigr)K_{k+1}\boldsymbol {\varLambda}_{k+1}\bigl[(I-\gamma_{k+1,1} \varUpsilon \varUpsilon)^{-1}+\gamma^{-1}_{k+1,1}I\bigr] \\& \qquad {} \times \boldsymbol {\varLambda}_{k+1}+2\bigl(1+\varepsilon^{-1}_{4} \bigr)\operatorname{tr}(\varUpsilon R_{k+1}\varUpsilon)K_{k+1}\boldsymbol { \varLambda}_{k+1}^{2}+2K_{k+1}\varPsi_{k+1}, \end{aligned}$$

(33)

where $\bar{\varPi}_{k+1}$ and $\varPsi_{k+1}$ are defined in (21). Let the derivative in (33) be zero, we can obtain the following optimal filter gain $K_{k+1}$:

$$\begin{aligned} K_{k+1} =&(1+\varepsilon_{5})\varSigma_{k+1|k}C^{T}_{k+1} \bar{\varLambda }_{k+1} \bigl\{ (1+\varepsilon_{4})R_{k+1}+ \bigl(1+\varepsilon^{-1}_{5}\bigr)\operatorname{tr} \bigl(C_{k+1}\bar{\varPi}_{k+1} \\ &{}\times C^{T}_{k+1}\bigr)\boldsymbol {\varLambda}_{k+1} \bigl[(I-\gamma_{k+1,1}\varUpsilon \varUpsilon)^{-1}+ \gamma^{-1}_{k+1,1}I\bigr]\boldsymbol {\varLambda}_{k+1}+(1+ \varepsilon _{5})\bar{\varLambda}_{k+1}C_{k+1} \\ &{}\times\varSigma_{k+1|k}C^{T}_{k+1}\bar{{ \varLambda}}_{k+1}+\bigl(1+\varepsilon ^{-1}_{4}\bigr) \operatorname{tr}(\varUpsilon R_{k+1}\varUpsilon)\boldsymbol {\varLambda}_{k+1}^{2}+ \varPsi _{k+1} \bigr\} ^{-1}, \end{aligned}$$

(34)

which is the same as in (20). Therefore, the proof is complete. □

Remark 4

As shown in Theorem 3, the obtained upper bound of filtering error covariance can be minimized by the filter gain $K_{k+1}$ in (34) at each sampling instant. It is worth pointing out that the value of $\gamma_{k+1,1}$ can be chosen firstly according to the constraint condition $\gamma ^{-1}_{k+1,1}I-\varUpsilon\varUpsilon>0$. Then we can adjust the value of $\gamma_{k+1,1}$ to improve the solvability of the new filtering scheme under certain estimation accuracy requirement. Besides, the randomly occurring uncertainties, quantized measurements as well as the stochastic nonlinearity are all examined, and the corresponding information is reflected in main results. In particular, the scalar $\bar{\alpha}_{k}$ and the matrices $H_{k}$, $M_{k}$ correspond to the randomly occurring uncertainties, the matrices $\varPi_{i}$ and $\varGamma _{i}$ reflect the variance information of the stochastic nonlinearity $f(x_{k},\xi_{k})$ in (1), and the scalar $\bar{\lambda }_{k,i}$ as well as matrix ϒ refer to the randomly occurring quantized measurements addressed in the paper. Moreover, it is worthwhile to note that the newly proposed robust variance-constrained filtering scheme has the recursive feature, which is suitable for online applications particularly in the networked environments.

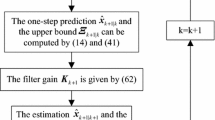
Summarizing the result in Theorem 3, the robust variance-constrained filtering (RVCF) algorithm can be provided as follows:

Algorithm RVCF

Step 1::

Set $k = 0$ and select the initial values.

Step 2::

Compute the one-step prediction $\hat{x}_{k+1|k}$ based on (10).

Step 3::

Calculate the value of $\varSigma_{k+1|k}$ by (18).

Step 4::

Solve the estimator gain matrix $K_{k+1}$ by (20).

Step 5::

Compute the filtering update equation $\hat{x}_{k+1|k+1}$ by (11).

Step 6::

Obtain $\varSigma_{k+1|k+1}$ by (19).

Step 7::

Set $k = k + 1$, and go to Step 2.

4 Boundedness analysis

In this section, the desired boundedness analysis concerning the filtering error is conducted. Before proceeding, the concept of exponential boundedness of stochastic process is firstly given.

Definition 1

([38])

If there exist real numbers $\rho>0$, $\nu>0$, and $0 <\vartheta<1$ such that

$$ \mathbb{E}\bigl\{ \Vert\zeta_{k} \Vert^{2} \bigr\} \leq \rho\Vert\zeta_{0} \Vert ^{2} \vartheta^{k}+\nu, $$

(35)

holds for every $k\geq0$, then the stochastic process $\zeta_{k}$ is said to be exponentially mean-square bounded.

In order to conduct the boundedness analysis about the filtering error, we need the following assumption.

Assumption 1

For every $1\leq i \leq m$ and $k\geq0$, there exist positive numbers a̅, $\underline{c}$, c̅, h̅, m̅, $\overline{l}_{1}$, $\overline{l}_{2}$ f̅, $\underline{b}_{1}$, $\overline{b}_{1}$, $\underline{\omega}$, ω̅, ν̅, $\underline{\lambda}$, λ̅ such that

$$\begin{aligned}& \Vert A_{k} \Vert\leq\overline{a}, \qquad \Vert H_{k} \Vert\leq \overline{h}, \qquad \Vert M_{k} \Vert\leq\overline{m}, \qquad \underline{c} \leq\Vert C_{k} \Vert\leq\overline{c}, \qquad \underline{\lambda}\leq \bar{\lambda}_{k,i} \leq\overline{\lambda}, \\& \operatorname{tr}(\bar{\mathcal{L}}_{k}) \leq\overline{l}_{1}, \qquad \operatorname{tr}(\varOmega_{k})\leq\overline{f}, \qquad \operatorname{tr}(\bar{\varPi}_{k+1}) \leq \overline{l}_{2}, \qquad \underline{b}_{1}I \leq B_{k}B^{T}_{k} \leq \overline{b}_{1}I, \\& \underline{\omega}I\leq Q_{k}\leq\overline{\omega} I, \qquad R_{k} \leq \overline{\nu}I. \end{aligned}$$

Furthermore, the inequality

$$ \overline{a} \biggl(1+\frac{\overline{c}^{2}}{\underline{c}^{2}} \biggr)< 1 $$

(36)

holds.

Theorem 4

Consider the time-varying systems (1)–(2) and the filter (10)–(11). Under the Assumption 1, the filtering error $\tilde{x}_{k|k}$ is exponentially mean-square bounded.

Proof

Substituting (14) into (15) leads to

$$ \tilde{x}_{k+1|k+1}=\check{A}_{k+1} \tilde{x}_{k|k}+r_{k+1}+z_{k+1}, $$

(37)

where

$$\begin{aligned}& \check{A}_{k+1} = \varXi_{k+1}A_{k}, \\& \varXi_{k+1} = I-K_{k+1}\bar{\varLambda}_{k+1}C_{k+1}, \\& r_{k+1} = \bar{\alpha}_{k} \varXi_{k+1} \Delta A_{k}x_{k}-K_{k+1}\boldsymbol {\varLambda}_{k+1}(I+ \Delta_{k+1})C_{k+1}x_{k+1}, \\& \begin{aligned} z_{k+1} &={} \tilde{\alpha}_{k} \varXi_{k+1}\Delta A_{k}x_{k}+\varXi _{k+1}f(x_{k}, \xi_{k})+\varXi_{k+1}B_{k}\omega_{k}-K_{k+1} \tilde{\varLambda }_{k+1}C_{k+1}x_{k+1} \\ &\quad {} -K_{k+1}\nu_{k+1}+K_{k+1}\tilde{ \varLambda}_{k+1}(I+\Delta _{k+1})C_{k+1}x_{k+1}-K_{k+1} \boldsymbol {\varLambda}_{k+1}\Delta_{k+1} \\ &\quad {} \times\nu_{k+1}+K_{k+1}\tilde{\varLambda}_{k+1} \Delta_{k+1}\nu_{k+1}. \end{aligned} \end{aligned}$$

Based on (20) and Assumption 1, it is not difficult to obtain

$$\begin{aligned} \Vert K_{k+1} \Vert < & \bigl\Vert (1+\varepsilon_{5}) \varSigma _{k+1|k}C^{T}_{k+1}\bar{\varLambda}_{k+1} \bigl[(1+\varepsilon_{5})\bar{\varLambda }_{k+1}C_{k+1} \varSigma_{k+1|k}C^{T}_{k+1}\bar{\varLambda}_{k+1} \bigr]^{-1} \bigr\Vert \\ \leq& \frac{\overline{c}}{\underline{c}^{2}\underline{\lambda }}:=\overline{k} \end{aligned}$$

and

$$\begin{aligned} \Vert\varXi_{k+1} \Vert < & \bigl\Vert I-(1+\varepsilon_{5}) \varSigma _{k+1|k}C^{T}_{k+1}\bar{\varLambda}_{k+1} \bigl[(1+\varepsilon_{5})\bar{\varLambda }_{k+1}C_{k+1} \varSigma_{k+1|k}C^{T}_{k+1} \\ &{}\times\bar{\varLambda}_{k+1}\bigr]^{-1}\bar{ \varLambda}_{k+1}C_{k+1} \bigr\Vert \leq 1+\frac{\overline{c}^{2}}{\underline{c}^{2}}:= \overline{\varsigma}_{1}. \end{aligned}$$

Then we have

$$ \Vert\check{A}_{k+1} \Vert= \Vert\varXi_{k+1}A_{k} \Vert\leq\Vert\varXi _{k+1} \Vert\Vert A_{k} \Vert\leq\overline{ \varsigma}_{1}\overline{a} :=\overline{a}_{1}. $$

According to Lemma 1 and Assumption 1, the following inequality holds:

$$\begin{aligned} \mathbb{E}\bigl\{ r^{T}_{k+1}r_{k+1}\bigr\} \leq& \mathbb{E}\bigl\{ (1+\sigma_{1})\bar {\alpha}^{2}_{k}x^{T}_{k} \Delta A_{k}^{T}\varXi^{T}_{k+1} \varXi_{k+1}\Delta A_{k}x_{k}+\bigl(1+ \sigma^{-1}_{1}\bigr)x^{T}_{k+1}C^{T}_{k+1} \\ &{}\times(I+\Delta_{k+1})^{T}\boldsymbol {\varLambda}_{k+1} K^{T}_{k+1}K_{k+1}\boldsymbol {\varLambda}_{k+1}(I+ \Delta_{k+1})C_{k+1}x_{k+1}\bigr\} \\ \leq& (1+\sigma_{1})\bar{\alpha}^{2}_{k} \overline{\varsigma}_{1}^{2}\overline{h}^{2} \overline{m}^{2}\overline{l_{1}} +\bigl(1+ \sigma^{-1}_{1}\bigr) (1-\underline{\lambda})^{2}(1+ \delta)^{2}\overline {c}^{2}\overline{k}^{2} \overline{l_{2}} \\ :=&\overline{r}^{2}, \end{aligned}$$

where $\sigma_{1}$ is a positive scalar and $\delta=\max\{\delta _{1},\delta_{2},\ldots,\delta_{m}\}$. Similarly, we can show

$$\begin{aligned} \mathbb{E}\bigl\{ z^{T}_{k+1}z_{k+1}\bigr\} \leq& \mathbb{E}\bigl\{ \tilde{\alpha }^{2}_{k}x^{T}_{k} \Delta A^{T}_{k}\varXi^{T}_{k+1} \varXi_{k+1}\Delta A_{k}x_{k}+f^{T}(x_{k}, \xi_{k})\varXi^{T}_{k+1}\varXi_{k+1} \\ &{}\times f(x_{k},\xi_{k})+\omega^{T}_{k}B^{T}_{k} \varXi^{T}_{k+1}\varXi _{k+1}B_{k} \omega_{k}+(1+\sigma_{2})x^{T}_{k+1}C^{T}_{k+1} \tilde{\varLambda }_{k+1} \\ &{}\times K^{T}_{k+1}K_{k+1}\tilde{ \varLambda}_{k+1}C_{k+1}x_{k+1}+(1+\sigma _{3}) \nu^{T}_{k+1}K^{T}_{k+1} K_{k+1} \nu_{k+1} \\ &{}+\bigl(1+\sigma^{-1}_{3}\bigr)\nu^{T}_{k+1} \Delta^{T}_{k+1}\boldsymbol {\varLambda }_{k+1}K^{T}_{k+1}K_{k+1} \boldsymbol {\varLambda}_{k+1}\Delta_{k+1}\nu_{k+1} \\ &{}+\bigl(1+\sigma^{-1}_{2}\bigr)x^{T}_{k+1}C^{T}_{k+1}(I+ \Delta_{k+1})^{T}\tilde {\varLambda}_{k+1} K^{T}_{k+1}K_{k+1}\tilde{\varLambda}_{k+1} \\ &{}\times(I+\Delta_{k+1})C_{k+1}x_{k+1}+ \nu^{T}_{k+1}\Delta ^{T}_{k+1}\tilde{ \varLambda}_{k+1}K^{T}_{k+1}K_{k+1}\tilde{ \varLambda}_{k+1} \\ &{}\times\Delta_{k+1}\nu_{k+1}\bigr\} \\ \leq&\bigl(\bar{\alpha}_{k}-\bar{\alpha}^{2}_{k} \bigr)\overline{h}^{2}\overline {\varsigma}_{1}^{2} \overline{m}^{2}\overline{l}_{1}+\overline{\varsigma }_{1}^{2}\overline{f} +\overline{\varsigma}_{1}^{2}l \overline{b}_{1}\overline{\omega }+(1+\sigma_{2}) \overline{k}^{2}\hat{\lambda}^{2}\overline {c}^{2}\overline{l}_{2} \\ &{}+(1+\sigma_{3})\overline{k}^{2}m\overline{\nu}+ \bigl(1+\sigma ^{-1}_{3}\bigr)\overline{k}^{2}(1- \underline{\lambda})^{2}\delta ^{2}m\overline{\nu}+\bigl(1+ \sigma^{-1}_{2}\bigr) \\ &{}\times(1+\delta)^{2}\overline{k}^{2}\hat{ \lambda}^{2}\overline {c}^{2}\overline{l}_{2}+m \overline{k}^{2}\hat{\lambda}^{2}\delta ^{2} \overline{\nu} \\ :=&\overline{z}^{2}, \end{aligned}$$

where $\sigma_{2}$ as well as $\sigma_{3}$ are positive scalars and $\hat{\lambda}=\max\{1-\underline{\lambda},\overline{\lambda}\}$.

Next, we consider the following iterative matrix equation with respect to $\varTheta_{k}$:

$$ \varTheta_{k+1}=\check{A}_{k+1} \varTheta_{k}\check{A}^{T}_{k+1}+B_{k}Q_{k}B^{T}_{k}, $$

(38)

with the initial condition $\varTheta_{0}=B_{0}Q_{0}B^{T}_{0}$. It is not difficult to find that

$$ \Vert\varTheta_{k+1} \Vert\leq\Vert\varTheta_{k}\Vert\Vert\check {A}_{k+1} \Vert^{2}+ \bigl\Vert B_{k}Q_{k}B^{T}_{k} \bigr\Vert \leq\overline {a}^{2}_{1}\Vert \varTheta_{k}\Vert+\overline{\omega} \overline{b}_{1}. $$

By iteration, we obtain

$$ \Vert\varTheta_{k}\Vert\leq\overline{a}^{2k}_{1} \Vert\varTheta_{0}\Vert +\overline{\omega} \overline{b}_{1}\sum _{i=0}^{k-1}\overline{a}^{2i}_{1}. $$

From (36), we have $0 < \overline{a}_{1} < 1$ and then we arrive at

$$ \Vert\varTheta_{k}\Vert\leq\Vert\varTheta_{0} \Vert+\overline{\omega} \overline{b}_{1}\sum _{i=0}^{\infty}\overline{a}^{2i}_{1} = \Vert\varTheta_{0}\Vert+\frac{\overline{b}_{1}\overline{\omega} }{1-\overline{a}^{2}_{1}}. $$

(39)

Due to the positive definite property of $\varTheta_{k}$, it is obvious that

$$ \varTheta_{k+1}\geq B_{k}Q_{k}B^{T}_{k} \geq\underline{b}_{1}\underline {\omega} I. $$

(40)

In view of (39) and (40), it follows that there exist $\underline{\theta}>0$ and $\overline{\theta}>0$ satisfying $\underline {\theta}I \leq\varTheta_{k}\leq\overline{\theta}I$ for every $k\geq0$.

According to (38) and the matrix inversion lemma, we have

$$\begin{aligned}& \check{A}^{T}_{k+1}\varTheta^{-1}_{k+1} \check{A}_{k+1}-\varTheta^{-1}_{k} \\& \quad = \check{A}^{T}_{k+1}\bigl(\check{A}_{k+1} \varTheta_{k}\check {A}^{T}_{k+1}+B_{k}Q_{k}B^{T}_{k} \bigr)^{-1}\check{A}_{k+1}-\varTheta^{-1}_{k} \\& \quad = \bigl(\varTheta_{k}+\check{A}^{-1}_{k+1}B_{k}Q_{k}B^{T}_{k} \check {A}^{-T}_{k+1}\bigr)^{-1}-\varTheta^{-1}_{k} \\& \quad = -\varTheta^{-1}_{k}\check{A}^{-1}_{k+1} \bigl[\bigl(B_{k}Q_{k}B^{T}_{k} \bigr)^{-1}+\check{A}^{-T}_{k+1}\varTheta^{-1}_{k} \check {A}^{-1}_{k+1} \bigr]^{-1}\check{A}^{-T}_{k+1} \varTheta^{-1}_{k} \\& \quad = - \bigl[\check{A}^{T}_{k+1}\bigl(B_{k}Q_{k}B^{T}_{k} \bigr)^{-1}\check {A}_{k+1}\varTheta_{k}+I \bigr]^{-1}\varTheta^{-1}_{k} \\& \quad \leq - \biggl[\frac{ \overline{a}^{2}_{1}\overline{\theta} }{ \underline{b}_{1}\underline{\omega} }+1 \biggr]^{-1} \varTheta^{-1}_{k}. \end{aligned}$$

Let $\eta_{0}= [\frac{ \overline{a}^{2}_{1}\overline{\theta} }{ \underline{b}_{1}\underline{\omega} }+1 ]^{-1}$ and $V_{k}(\tilde {x}_{k|k})=\tilde{x}^{T}_{k|k}\varTheta^{-1}_{k}\tilde{x}_{k|k}$. Then it is not difficult to see that $\eta_{0} \in(0,1)$, and there exists $\beta>0$ satisfying $\eta=(1-\eta_{0})(1+\beta)<1$. Thus, it follows from (12) and (37) that

$$\begin{aligned}& \mathbb{E}\bigl\{ V_{k+1}(\tilde{x}_{k+1|k+1})|x_{k|k} \bigr\} -(1+\beta )V_{k}(\tilde{x}_{k|k}) \\& \quad = \mathbb{E}\bigl\{ \tilde{x}^{T}_{k+1|k+1} \varTheta^{-1}_{k+1}\tilde {x}_{k+1|k+1}|\tilde{x}_{k|k} \bigr\} -(1+\beta)V_{k}(\tilde{x}_{k|k}) \\& \quad = \mathbb{E}\bigl\{ (\check{A}_{k+1}\tilde {x}_{k|k}+r_{k+1}+z_{k+1})^{T} \varTheta^{-1}_{k+1}(\check {A}_{k+1}x_{k|k}+r_{k+1}+z_{k+1})| \tilde{x}_{k|k}\bigr\} \\& \qquad {} -(1+\beta)V_{k}(\tilde{x}_{k|k}) \\& \quad \leq \mathbb{E}\bigl\{ (1+\beta)\tilde{x}^{T}_{k|k} \check{A}^{T}_{k+1}\varTheta ^{-1}_{k+1} \check{A}_{k+1}\tilde{x}_{k|k}-(1+\beta)\tilde {x}^{T}_{k|k}\varTheta^{-1}_{k} \tilde{x}_{k|k}|\tilde{x}_{k|k}\bigr\} \\& \qquad {} +\bigl(1+\beta^{-1}\bigr)\mathbb{E}\bigl\{ r^{T}_{k+1} \varTheta^{-1}_{k+1}r_{k+1}|\tilde {x}_{k|k}\bigr\} +\mathbb{E}\bigl\{ z^{T}_{k+1}\varTheta^{-1}_{k+1}z_{k+1}| \tilde {x}_{k|k}\bigr\} \\& \quad = (1+\beta)\mathbb{\mathbb{E}}\bigl\{ \tilde{x}^{T}_{k|k} \bigl[\check {A}^{T}_{k+1}\varTheta^{-1}_{k+1} \check{A}_{k+1}-\varTheta^{-1}_{k}\bigr]\tilde {x}_{k|k}|\tilde{x}_{k|k}\bigr\} +\mathbb{E}\bigl\{ z^{T}_{k+1}\varTheta ^{-1}_{k+1}z_{k+1}| \tilde{x}_{k|k}\bigr\} \\& \qquad {} +\bigl(1+\beta^{-1}\bigr)\mathbb{E}\bigl\{ r^{T}_{k+1} \varTheta^{-1}_{k+1}r_{k+1}|\tilde {x}_{k|k}\bigr\} \\& \quad \leq -\eta_{0}(1+\beta)V_{k}(\tilde{x}_{k|k})+ \tau, \end{aligned}$$

where $\tau=\frac{(1+\beta^{-1})\overline{r}^{2}+\overline {z}^{2}}{\underline{\theta}}$. Accordingly, we know that

$$ \mathbb{ E}\bigl\{ V_{k+1}(\tilde{x}_{k+1|k+1})| \tilde{x}_{k|k}\bigr\} \leq\eta V_{k}(\tilde{x}_{k|k})+ \tau. $$

By iteration and $\frac{ 1 }{ \overline{\theta} }I \leq\varTheta ^{-1}_{k} \leq\frac{ 1 }{ \underline{\theta} }I$, the following inequality holds:

$$ \mathbb{E}\bigl\{ \Vert\tilde{x}_{k|k} \Vert^{2} \bigr\} \leq \frac{ \overline {\theta} }{ \underline{\theta} } \Vert\tilde{x}_{0|0} \Vert^{2}\eta ^{k}+\tau\overline{\theta}\sum_{i=0}^{\infty} \eta^{i}= \frac{ \overline{\theta} }{ \underline{\theta} } \Vert\tilde{x}_{0|0} \Vert ^{2}\eta^{k}+\frac{\tau\overline{\theta}}{1-\eta}, $$

under $0<\eta<1$. Then it follows from Definition 1 that the stochastic process $\tilde{x}_{k|k}$ is exponentially mean-square bounded. □

Remark 5

By utilizing the stochastic analysis technique, a new sufficient condition under certain assumption has been given in Theorem 4 to testify the exponentially mean-square boundedness of the filtering error, which provides a helpful method to evaluate the performance of the proposed optimal variance-constrained filtering scheme.

Remark 6

Note that some effective filtering methods have been presented in [39, 40] for networked systems with energy bounded noises, where the envelope-constrained $H_{\infty}$ filtering and distributed event-triggered set-membership filtering schemes have been given. Compared with the results in [39, 40], we have developed a new RVCF algorithm with performance evaluation under variance-constrained index for addressed uncertain time-varying nonlinear systems subject to randomly occurring quantized measurements and stochastic noises with known statistical properties. In particular, it should be noted that the advantages of the proposed filtering lie in its local optimality in the minimum variance sense and the online implementations. Moreover, it could be possible to extend the proposed method to handle the mean-square consensus problem for time-varying multi-agent systems as in [41], which could be expected in a near future.

5 An illustrative example

In this section, we use numerical simulations to demonstrate the usefulness of the proposed variance-constrained filtering algorithm.

The system parameters in (1)–(2) are given by

$$\begin{array}{c}{A}_k=\left[\begin{array}{cc}0.6-0.6cos(k)& -0.35\\ 0.5-sin(k)cos(k)& 0.65+0.4cos(k)\end{array}\right],B_k=\left[\begin{array}{c}0.1\\ 0.1-1.5sin(k)\end{array}\right],\hfill \\ F=sin(5k),H_k={\left[\begin{array}{cc}0.01& 0.02\end{array}\right]}^T,\hfill \\ M_k=\left[\begin{array}{cc}0.03& 0.01\end{array}\right],C_k=\left[\begin{array}{cc}0.9& 0.85\end{array}\right].\hfill \end{array}$$

The state vector is $x_{k}=[x_{1,k}\ x_{2,k}]^{T}$. The noises $\omega_{k}$ and $\nu_{k}$ are zero-mean noises with covariances 0.05 and 0.075, respectively.

The stochastic nonlinearity $f(x_{k},\xi_{k})$ is given as follows:

$$f(x_k,{\xi }_k)=\left[\begin{array}{c}0.3\\ 0.2\end{array}\right][0.2sign(x_{1,k})x_{1,k}{\xi }_{1,k}+0.3sign(x_{2,k})x_{2,k}{\xi }_{2,k}],$$

where $\xi_{i,k}$ ($i=1,2$) are zero-mean noises with unity covariances. It is easy to check that $f(x_{k},\xi_{k})$ satisfies (5)–(7) with

$${\Pi }_1=\left[\begin{array}{cc}0.09& 0.06\\ 0.06& 0.04\end{array}\right],{\Gamma }_1=\left[\begin{array}{cc}0.04& 0\\ 0& 0.09\end{array}\right].$$

The parameters of the logarithmic quantizer are chosen $u^{1}_{0}=0.5$ and $\chi^{(1)}=0.01$. Other parameters are given by $\varepsilon _{1}=0.01$, $\varepsilon_{2}=1$, $\varepsilon_{3}=0.1$, $\varepsilon _{4}=0.01$, $\varepsilon_{5}=0.01$, $\varepsilon_{6}=1$, $\gamma _{k+1,1}=0.68$, $\bar{\alpha}_{k}=0.59$ and $\bar{\varLambda}_{k}=0.35$. From (18)–(19), we can obtain the filter gain at each sampling step and plot the relevant simulation results in Figs. 1–5 with the initial conditions $x_{0}=\hat {x}_{0|0}=[ 1.8 \ 2.5]^{T}$ and $\varSigma_{0|0}=2.5I_{2}$, where MSEi ($i=1,2$) denote the mean-square errors for the estimations of the states $x_{i,k}$ ($i=1,2$).

Figure 1

$y_{k}$ without and with randomly occurring signal quantization

In the simulations, Fig. 1 plots the measurement outputs with and without randomly occurring signal quantization. In order to propose the comparison with existing method, the states are plotted and the state estimations are also provided in Figs. 2–3 based on the developed recursive variance-constrained filtering method and Kalman filter (KF) strategy. The obtained upper bound and $\log(\mathrm{MSE}i)$ ($i=1,2$) are described in Figs. 4–5, which confirm that the upper bound is indeed above the mean-square errors. The $\log(\mathrm{MSE}i)$ ($i=1,2$) caused by the robust variance-constrained filtering algorithm in this paper and the KF strategy are shown in Figs. 6–7, in which we can see that the filtering algorithm presented in this paper possesses smaller error than the conventional KF method.

Figure 2

State $x_{1,k}$ and its estimation $\hat{x}_{1,k|k}$

Figure 3

State $x_{2,k}$ and its estimation $\hat{x}_{2,k|k}$

Figure 4

$\log(\mbox{MSE}1)$ and its upper bound

Figure 5

$\log(\mbox{MSE}2)$ and its upper bound

Figure 6

$\log(\mbox{MSE}1)$ in different methods

Figure 7

$\log(\mbox{MSE}2)$ in different methods

In addition, for the purpose of illustration of the effects from the randomly occurring quantization effects, the traces of the upper bounds are depicted in Fig. 8 under different occurrence probabilities $\bar{\varLambda}_{k}=0.35$, $\bar{\varLambda}_{k}=0.85$, $\bar {\varLambda}_{k}=0.95$ and $\bar{\varLambda}_{k}=1$. From the simulations, we can see that the filtering algorithm performance can be improved if less quantized measurements are used in the filter side, i.e., more original measurements are transmitted to the remote filter and the filtering algorithm accuracy is better.

Figure 8

$\log(\operatorname{trace}(\varSigma_{k|k}))$ under different occurrence probabilities

6 Conclusions

In this paper, we have investigated the robust variance-constrained filtering problem for networked time-varying systems subject to stochastic nonlinearity, randomly occurring uncertainties and quantized measurements. The phenomena of the randomly occurring uncertainties and signal quantization have been modeled by a set of mutually independent Bernoulli random variables. A recursive variance-constrained filtering algorithm has been proposed, where the filter gain has been designed to minimize the obtained upper bound of the filtering error covariance. Moreover, we have given a sufficient condition to ensure the exponential mean-square boundedness of the filtering error. Finally, we have provided the simulations to demonstrate the validity and feasibility of the obtained filtering algorithm. It should be noted that the effects induced by the stochastic nonlinearity has been examined in the conducted topic. When the other types of nonlinearities (e.g. continuous differentiable nonlinearities or Lipschitz nonlinearities) exist in the system model, the proposed filtering method can also be applicable as long as the Taylor expansion or matrix inequality technique are utilized. Accordingly, the desirable filtering algorithm can be given along the same lines as provided in this paper.