1 Introduction

During the past decades, a neural networks model has been studied intensively. Broad applications have been explored in various areas ranging from signal processing, parallel computation and engineering optimization to pattern recognition, which rely heavily on the dynamical behaviors of this kind of model. As a result, many researchers have been attracted to study it and lots of achievements on various dynamical behaviors have arisen [1–3]. A weighting delay and space partitioning method was proposed in [1, 2], and the stability criterion was established by establishing the relation among the connection parameters, delay parameters and dynamic variables of systems, which are less conservative than previous results. Moreover, as everyone knows, when studying the dynamical behaviors of this model, obtaining the state information for the networks is usually very important. Unfortunately, in practice, it is difficult to obtain the exact and complete information of neural states in the network outputs because of many reasons. Thus, in order to fully exploit the neural networks, it becomes significant and essential to use a reasonable measurement to estimate the neuron state. Accordingly, many fruitful achievements on state estimation problems for neural networks have been reported [4–17].

In the early 1970s, Chua [18] presented theoretically the existence of a new basic electrical circuit element, named the memristor, which describes the relationship between electric charge and flux linkage. A practical memristor device has been realized practically by the research team of HP Lab in 2008. As a new two-terminal passive device which follows resistor, inductor and capacitor, the memristor shares many properties of resistor and the same unit of measurement. Moreover, it is also shown to be similar to the synapses in the human brain. Based on these features, the memristive neural networks model established by replacing a resistor with a memristor has attracted more and more attention, and various dynamical behaviors of this model have been investigated, see [19–27] and the references therein. However, when it comes to the state estimation problem, only [28, 29] studied the related content. For instance, the \(H_{\infty}\) state estimation problem of discrete-time memristive neural networks is studied in [29]. Here, the discrete-time memristive neural networks are recast into a tractable model by defining a series of state-dependent switched signals and the calculation cost is reduced effectively when dealing with the connection weights by a robust analysis method.

On the other hand, the dynamical behavior analysis of the complex-valued neural networks model has undergone a research upsurge, due to the more extensive applications, including radar imaging, electromagnetic waves, remote sensing, quantum devices, and so on [30]. As an extension of the real-valued neural networks, the complex-valued system with complex-valued states, activation functions and connection weights possesses more complicated and abundant properties than real-valued one. Moreover, they can be used to solve many complicated real-life problems that the real-valued model cannot do, such as the speed and direction in wind profile model [31]. So far, effective achievements on the dynamical behaviors of complex-valued neural networks have emerged in large numbers [32–39]. Moreover, for memristor-based complex-valued neural networks, abundant relevant results have also been achieved [40–46]. However, there are only a few results focusing on the state estimation problem for complex-valued networks [47–49]. Moreover, there is still no information published about the state estimation problem for memristor-based complex-valued neural networks. This situation prompts our current research.

Considering the inevitability of time delay in many practical projects [50–57] and motivated by the above discussions, the state estimation problem for complex-valued memristive neural networks with time-varying delays is investigated in this paper. The contribution of this paper is mainly embodied in the following respects: (1) The state estimation of complex-valued memristive neural networks with time-varying delays is studied for the first time. (2) Based on the Lyapunov stability theory, differential inclusion theory and some matrix inequality techniques, and by constructing a novel Lyapunov functional, a sufficient delay-dependent condition is proposed, under which the error system is globally asymptotically stable. On the other hand, the LMI-based results consider the sign difference of the memristive weights. (3) By solving certain matrix inequalities, the state estimator gain matrix can be determined easily by solving certain matrix inequalities.

2 Preliminaries and problem description

Consider the memristor-based complex-valued neural networks and the network measurements equation described as follows:

$$ \left \{ \textstyle\begin{array}{l} \dot{z}_{p}(t)=-d_{p}z_{p}(t)+ {\sum_{k=1}^{n}}a_{pk}(z_{k}(t))f_{k}(z_{k}(t))+\sum_{k=1}^{n}b_{pk}(z_{k}(t))f_{k}(z_{k}(t-\tau(t))),\\ l_{q}(t)= {\sum_{k=1}^{n}}c_{qk}z_{k}(t)+g_{q}(t,z(t)), \end{array}\displaystyle \right . $$
(1)

or equivalently

$$ \left \{ \textstyle\begin{array}{l} \dot{z}(t)=-Dz(t)+A(z(t))f(z(t))+B(z(t))f(z(t-\tau(t))),\\ l(t)=Cz(t)+g(t,z(t)), \end{array}\displaystyle \right . $$
(2)

where \(D=\operatorname{diag}\{d_{1},d_{2},\ldots,d_{n}\}\in\mathbf{R}^{n\times n}\) with \(d_{p}>0\) (\(p=1,2,\ldots,n\)) is the self-feedback connection weight matrix, \(z(t)=(z_{1}(t), z_{2}(t),\ldots,z_{n}(t))^{T}\in\mathbf{C}^{n}\) is the neuron state vector, \(l(t)=(l_{1}(t), l_{2}(t),\ldots,l_{m}(t))^{T}\in\mathbf{C}^{m}\) is the measurement output of the networks, \(C=(c_{qk})_{m\times n}\in\mathbf{C}^{m\times n}\) is for the output weights, \(f(z(t))=(f_{1}(z_{1}(t)),f_{2}(z_{2}(t)), \ldots,f_{n}(z_{n}(t)))^{T}\in\mathbf {C}^{n}\) and \(f(z(t-\tau(t)))=(f_{1}(z_{1}(t-\tau(t))),f_{2}(z_{2}(t-\tau (t))),\ldots,f_{n}(z_{n}(t-\tau(t))))^{T}\in\mathbf{C}^{n}\) are the vector-valued activation functions without and with time delays, \(g(t,z(t)): \mathbf{R^{+}}\times\mathbf{C}^{n}\rightarrow\mathbf {C}^{m}\) denotes the neuron-dependent nonlinear disturbances on the network outputs. \(\tau(t)\) is the time-varying delay and satisfies \(\tau _{1}\leq\tau(t)\leq\tau_{2}\) and \(\dot{\tau}(t)\leq\rho\), where \(\tau _{1}\), \(\tau_{2}\), ρ are scalar constants, \(A(z(t))=(a_{pk}(z_{k}(t)))_{n\times n}\in\mathbf{C}^{n\times n}\) and \(B(z(t))=(b_{pk}(z_{k}(t)))_{n\times n}\in\mathbf{C}^{n\times n}\) are the connection memristive weight matrices, and they are defined as follows:

$$ \begin{aligned}[b] a_{pk} \bigl(z_{k}(t) \bigr)=\left \{ \textstyle\begin{array}{l@{\quad}l} a_{pk}^{\prime}, &|z_{k}(t)|< \delta_{k}, \\ a_{pk}^{\prime\prime},& |z_{k}(t)|>\delta_{k}, \end{array}\displaystyle \right .\qquad b_{pk} \bigl(z_{k}(t) \bigr)=\left \{ \textstyle\begin{array}{l@{\quad}l} b_{pk}^{\prime},& |z_{k}(t)|< \delta_{k}, \\ b_{pk}^{\prime\prime},& |z_{k}(t)|>\delta_{k}, \end{array}\displaystyle \right . \\ a_{pk}^{R} \bigl(z_{k}(t) \bigr)=\left \{ \textstyle\begin{array}{l@{\quad}l} a_{pk}^{R^{\prime}}, &|x_{k}(t)|< \delta_{k}, \\ a_{pk}^{R^{\prime\prime}},& |x_{k}(t)|>\delta_{k}, \end{array}\displaystyle \right .\qquad a_{pk}^{I} \bigl(z_{k}(t) \bigr)=\left \{ \textstyle\begin{array}{l@{\quad}l} a_{pk}^{I^{\prime}},& |y_{k}(t)|< \delta_{k}, \\ a_{pk}^{I^{\prime\prime}}, &|y_{k}(t)|>\delta_{k}, \end{array}\displaystyle \right . \\ b_{pk}^{R} \bigl(z_{k}(t) \bigr)=\left \{ \textstyle\begin{array}{l@{\quad}l} b_{pk}^{R^{\prime}},& |x_{k}(t)|< \delta_{k}, \\ b_{pk}^{R^{\prime\prime}}, &|x_{k}(t)|>\delta_{k}, \end{array}\displaystyle \right .\qquad b_{pk}^{I} \bigl(z_{k}(t) \bigr)=\left \{ \textstyle\begin{array}{l@{\quad}l} b_{pk}^{I^{\prime}},& |y_{k}(t)|< \delta_{k}, \\ b_{pk}^{I^{\prime\prime}},& |y_{k}(t)|>\delta_{k}, \end{array}\displaystyle \right . \end{aligned} $$
(3)

where \(a_{pk}^{R}(z_{k}(t))=\operatorname{Re}(a_{pk}(z_{k}(t)))\), \(a_{pk}^{I}(z_{k}(t))=\operatorname{Im}(a_{pk}(z_{k}(t)))\), \(b_{pk}^{R}(z_{k}(t))=\operatorname{Re}(b_{pk}(z_{k}(t)))\), \(b_{pk}^{I}(z_{k}(t))=\operatorname{Im}(b_{pk}(z_{k}(t)))\), the switching jumps \(\delta_{k}>0\), and \(a_{pk}^{\prime}\), \(a_{pk}^{\prime\prime}\), \(b_{pk}^{\prime}\), \(b_{pk}^{\prime\prime}\), \(a_{pk}^{R^{\prime}}\), \(a_{pk}^{R^{\prime\prime}}\), \(b_{pk}^{R^{\prime }}\), \(b_{pk}^{R^{\prime\prime}}\), \(a_{pk}^{I^{\prime}}\), \(a_{pk}^{I^{\prime\prime}}\), \(b_{pk}^{I^{\prime}}\), \(b_{pk}^{I^{\prime \prime}}\) are constants.

By applying the differential inclusion feature and the theory of set-valued maps, the memristor-based complex-valued system (1) can be rewritten as

$$ \dot{z}_{p}(t)\in-d_{p}z_{p}(t)+ { \sum_{k=1}^{m}}\operatorname{co} \bigl\{ a_{pk}^{\prime},a_{pk}^{\prime\prime} \bigr\} f_{k} \bigl(z_{k}(t) \bigr) + {\sum _{k=1}^{m}}\operatorname{co} \bigl\{ b_{pk}^{\prime},b_{pk}^{\prime \prime} \bigr\} f_{k} \bigl(z_{k} \bigl(t-\tau(t) \bigr) \bigr), $$
(4)

or in the compact form given by

$$ \dot{z}(t)\in-Dz(t)+\operatorname{co} \bigl\{ A^{\prime},A^{\prime\prime} \bigr\} f \bigl(z(t) \bigr) +\operatorname{co} \bigl\{ B^{\prime},B^{\prime\prime} \bigr\} f \bigl(z \bigl(t-\tau(t) \bigr) \bigr), $$
(5)

where \(A^{\prime}=(a_{pk}^{\prime})_{n\times n}\), \(A^{\prime\prime }=(a_{pk}^{\prime\prime})_{n\times n}\), \(B^{\prime}=(b_{pk}^{\prime})_{n\times n}\), \(B^{\prime\prime}=(b_{pk}^{\prime\prime})_{n\times n}\); or equivalently, there exist measurable function matrices \(\bar{A}(t)\in \operatorname{co}\{A^{\prime},A^{\prime\prime}\}\) and \(\bar{B}(t)\in \operatorname{co}\{B^{\prime},B^{\prime\prime}\}\), such that

$$ \dot{z}(t)=-Dz+\bar{A}(t)f \bigl(z(t) \bigr)+\bar{B}(t)f \bigl(z \bigl(t-\tau(t) \bigr) \bigr). $$
(6)

For system (2), we construct the full-order state estimator as follows:

$$ \left \{ \textstyle\begin{array}{l} \dot{\hat{z}}(t)=-D\hat{z}(t)+\bar{A}f(\hat{z}(t))+\bar{B}f(\hat {z}(t-\tau(t))) +K(l(t)-\hat{l}(t)),\\ \hat{l}(t)=C\hat{z}(t)+g(t,\hat{z}(t)), \end{array}\displaystyle \right . $$
(7)

where \(\hat{z}=(\hat{z}_{1}, \hat{z}_{2},\ldots,\hat{z}_{n})^{T}\in\mathbf {C}^{n}\) is the estimation of the neuron state, and \(K\in\mathbf {C}^{n\times m}\) is the estimator gain matrix to be designed.

Let \(e(t)=z(t)-\hat{z}(t)\), \(f(e(t))=f(z(t))-f(\hat{z}(t))\), \(f(e(t-\tau (t)))=f(z(t-\tau(t)))-f(\hat{z}(t-\tau(t)))\), \(g(e(t))=g(t,z(t))-g(t,\hat{z}(t))\), then the error-state system is given by

$$ \dot{e}(t)=-(D+KC)e(t)+\bar{A}f \bigl(e(t) \bigr)+\bar{B}f \bigl(e \bigl(t- \tau(t) \bigr) \bigr)-Kg \bigl(e(t) \bigr). $$
(8)

In the following, some assumptions and basic lemmas are given, which will be used in establishing the main results.

Assumption 1

For any \(z_{1}, z_{2}\in\mathbf{C}\), the neuron activation functions \(f_{k}(\cdot)\) satisfy the following Lipschitz conditions:

$$ \big|f_{k}(z_{1})-f_{k}(z_{2})\big| \leq l_{k}|z_{1}-z_{2}|, $$
(9)

where \(l_{k}>0\) (\(k=1,2,\ldots,n\)) are constants, let \(L=\operatorname {diag}\{l_{1},l_{2},\ldots,l_{n}\}\).

Assumption 2

For any \(z, z^{\prime}\in\mathbf{C}^{n}\), there exists a real matrix M such that the neuron-dependent nonlinear disturbances satisfy the following inequality:

$$ \big\| g(t,z)-g \bigl(t,z^{\prime} \bigr) \big\| \leq \big\| M \bigl(z-z^{\prime} \bigr) \big\| . $$
(10)

Lemma 1

([47])

For any constant Hermitian matrix \(M \in\mathbf{C}^{n\times n}\) and \(M>0\), a vector function \(\Phi (s):[p,q]\rightarrow\mathbf{C}^{n}\) with scalars \(p< q\) such that the integrations concerned are well defined, then

$$ \biggl( \int_{p}^{q}\Phi(s)\,ds \biggr)^{\ast}M \biggl( \int_{p}^{q}\Phi(s)\,ds \biggr) \leq(q-p) \int_{p}^{q}\Phi^{\ast}(s)M\Phi(s)\,ds. $$

Lemma 2

Given a Hermitian matrix Ω, let \(\Omega^{R}=\operatorname {Re}(\Omega)\), \(\Omega^{I}=\operatorname{Im}(\Omega)\), then \(\Omega< 0\) if and only if

$$ \left [ \textstyle\begin{array}{c@{\quad}c} \Omega^{R} & -\Omega^{I}\\ \Omega^{I} &\Omega^{R} \end{array}\displaystyle \right ]< 0. $$

3 Main results

In this section, an effective state estimator for system (1) or (2) will be designed, and a sufficient condition will be developed to guarantee the global asymptotical stability of the error-state system. First, for convenience, we denote \(z(t)\), \(\hat{z}(t)\), \(z(t-\tau(t))\), \(\hat{z}(t-\tau(t))\), \(e(t-\tau(t))\), \(e(t-\tau_{1})\) and \(e(t-\tau _{2})\) as z, ẑ, \(z^{\tau}\), \(\hat{z}^{\tau}\), \(e^{\tau}\), \(e^{\tau_{1}}\) and \(e^{\tau_{2}}\), respectively.

Theorem 1

Suppose that Assumption 1 holds; the error-state system (8) is globally asymptotically stable, if there exist positive definite Hermitian matrices P, \(W_{1}\), \(W_{2}\), \(Q_{1}\), \(Q_{2}\), \(R_{1}\), \(R_{2}\), any complex matrix R, and positive scalars \(\epsilon_{\kappa}\) (\(\kappa =1,2,\ldots,5\)) such that the following matrix inequalities hold:

$$ \Theta^{j}=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \Omega^{j} & \tau_{1}S_{j}^{\ast}R_{1} & \tau_{12}S_{j}^{\ast}R_{2}\\ \ast& -R_{1} & 0\\ \ast& \ast& -R_{2} \end{array}\displaystyle \right ]< 0, \quad j=1,2,3,4, $$
(11)

where

$$ \begin{gathered} \Omega^{j}= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad }c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \Omega_{11} & R_{1} & 0 & 0 & (RC)^{\ast}&0&\Omega^{j}_{17}& \Omega ^{j}_{18}& -R&\Omega^{j}_{1,10}&\Omega^{j}_{1,11}\\ \ast& \Omega_{22} & R_{2} & 0& 0& 0& 0& 0& 0& 0& 0\\ \ast& \ast& \Omega_{33} & 0 & 0& 0& 0& 0& 0& 0& 0\\ \ast& \ast& \ast& \Omega_{44} & 0 & 0& 0& 0& 0& 0& 0\\ \ast& \ast& \ast&\ast& \Omega_{55} & 0 & 0& 0 & R& \Omega ^{j}_{5,10} & \Omega^{j}_{5,11}\\ \ast& \ast& \ast&\ast&\ast&\Omega_{66} & 0 & 0 & 0& 0 & 0\\ \ast& \ast& \ast&\ast&\ast& \ast& -\epsilon_{1}I & 0 & 0& 0 & 0\\ \ast& \ast& \ast&\ast&\ast& \ast&\ast&-\epsilon_{2}I & 0& 0 & 0\\ \ast& \ast& \ast&\ast&\ast& \ast&\ast& \ast& -\epsilon_{3}I& 0 & 0\\ \ast& \ast& \ast&\ast&\ast& \ast& \ast&\ast& \ast& -\epsilon _{4}I& 0 \\ \ast& \ast& \ast&\ast&\ast& \ast& \ast&\ast& \ast& \ast& -\epsilon_{5}I \end{array}\displaystyle \right ], \\ \Omega_{11}=-DP-(RC)^{\ast}-PD-RC+W_{1}+Q_{1}+Q_{2}-R_{1}+ \epsilon _{1}\bar{L}+\epsilon_{3}\bar{M}, \\ \Omega_{15}=(RC)^{\ast},\qquad \Omega^{1}_{17}= \Omega^{3}_{17}=PA^{\prime},\qquad \Omega^{2}_{17}=\Omega^{4}_{17}=PA^{\prime\prime}, \qquad \Omega^{1}_{18}=\Omega^{3}_{18}=PB^{\prime}, \\ \Omega^{2}_{18}=\Omega^{4}_{18}=PB^{\prime\prime}, \qquad \Omega^{1}_{1,10}=\Omega^{2}_{1,10}=0, \qquad \Omega^{3}_{1,10}=P \bigl(A^{\prime}-A^{\prime\prime} \bigr), \\ \Omega^{4}_{1,10}=P \bigl(A^{\prime\prime}-A^{\prime} \bigr),\qquad \Omega_{22}=-(Q_{1}+R_{1}+R_{2}), \qquad \Omega^{1}_{1,11}=\Omega^{2}_{1,11}=0, \\ \Omega^{3}_{1,11}=P \bigl(B^{\prime}-B^{\prime\prime} \bigr),\qquad \Omega^{4}_{1,11}=P \bigl(B^{\prime\prime}-B^{\prime} \bigr),\qquad \Omega_{33}=-(Q_{2}+R_{2}), \\ \Omega_{44}=-(1-\rho)W_{1}+\epsilon_{2}\bar{L}, \qquad \Omega_{55}=-DP-PD+W_{2}+\epsilon_{4}L, \qquad \Omega^{1}_{5,10}=\Omega^{4}_{5,10}=PA^{\prime}, \\ \Omega^{2}_{5,10}=\Omega^{3}_{5,10}=PA^{\prime\prime}, \qquad \Omega^{1}_{5,11}=\Omega^{4}_{5,11}=PB^{\prime}, \qquad \Omega^{2}_{5,11}=\Omega^{3}_{5,11}=PB^{\prime\prime}, \\ \Omega_{66}=-(1-\rho)W_{2}+\epsilon_{5}L, \\ A^{\prime}= \bigl(a_{pk}^{\prime} \bigr)_{n\times n}, \qquad A^{\prime\prime }= \bigl(a_{pk}^{\prime\prime} \bigr)_{n\times n},\qquad B^{\prime}= \bigl(b_{pk}^{\prime} \bigr)_{n\times n}, \\ S_{1}= \bigl[-(D+KC), 0, 0, 0, 0,0,A^{\prime}, B^{\prime}, -K,0,0 \bigr],\qquad B^{\prime\prime}= \bigl(b_{pk}^{\prime\prime} \bigr)_{n\times n}, \\ S_{2}= \bigl[-(D+KC), 0, 0, 0, 0,0,A^{\prime\prime}, B^{\prime\prime}, -K,0,0 \bigr], \\ S_{3}= \bigl[-(D+KC), 0, 0, 0, 0,0,A^{\prime}, B^{\prime}, -K,A^{\prime }-A^{\prime\prime},B^{\prime}-B^{\prime\prime} \bigr], \\ S_{4}= \bigl[-(D+KC), 0, 0, 0, 0,0,A^{\prime\prime}, B^{\prime\prime}, -K,A^{\prime\prime}-A^{\prime},B^{\prime\prime}-B^{\prime} \bigr], \\ \xi(t)= \bigl[e^{\ast}, e^{\ast\tau_{1}}, e^{\ast\tau_{2}}, e^{\ast\tau}, z^{\ast}, z^{\ast\tau}, f^{\ast}(e), f^{\ast}\bigl(e^{\tau}\bigr), g^{\ast}(e), f^{\ast}(z), f^{\ast}\bigl(z^{\tau}\bigr) \bigr]^{\ast}.\end{gathered} $$

Moreover, the estimator gain matrix is given by \(K=P^{-1}R\).

Proof

Consider the candidate Lyapunov functional

$$ \begin{aligned}[b] V(t)={}&e^{\ast}(t)Pe(t)+ \int_{t-\tau(t)}^{t}e^{\ast}(s)W_{1}e(s) \,ds+\hat {z}^{\ast}(t)P\hat{z}(t) \\ & + \int_{t-\tau(t)}^{t}\hat{z}^{\ast}(s)W_{2} \hat{z}(s)\,ds+ \int_{t-\tau _{1}}^{t}e^{\ast}(s)Q_{1}e(s) \,ds+ \int_{t-\tau_{2}}^{t}e^{\ast }(s)Q_{2}e(s) \,ds \\ & +\tau_{1} \int_{-\tau_{1}}^{0} \int_{t+\theta}^{t}\dot{e}^{\ast }(s)R_{1} \dot{e}(s)\,ds\,d\theta +\tau_{12} \int_{-\tau_{2}}^{-\tau_{1}} \int_{t+\theta}^{t}\dot{e}^{\ast }(s)R_{2} \dot{e}(s)\,ds\,d\theta. \end{aligned} $$
(12)

By the feature of memristors described in (3), the following four cases may exist.

Case 1: When \(|z_{k}(t)|<\delta_{k}\), \(|\hat{z}_{k}(t)|<\delta_{k}\), at time t, systems (6) and (7) can turn into the following systems, respectively:

$$ \dot{z}=-Dz+A^{\prime}f(z)+B^{\prime}f \bigl(z^{\tau} \bigr) $$
(13)

and

$$ \dot{\hat{z}}=-D\hat{z}+A^{\prime}f(\hat{z})+B^{\prime}f \bigl( \hat{z}^{\tau } \bigr)+K \bigl(l-C\hat{z}-g(t,\hat{z}) \bigr). $$
(14)

Then the error-state system can be obtained:

$$ \dot{e}=-(D+KC)e+A^{\prime}f(e)+B^{\prime}f \bigl(e^{\tau} \bigr)-Kg(t,e). $$
(15)

Based on Lemma 1 and along the trajectories of systems (14) and (15), the derivative of \(V(t)\) can be estimated as

$$ \begin{aligned}[b] \dot{V}(t)={}& 2\hat{z}^{\ast}P\dot{\hat{z}}+ \hat{z}^{\ast}W_{2} \hat{z} +2e^{\ast}P \dot{e}+e^{\ast}(W_{1}+Q_{1}+Q_{2})e -(1- \eta)\hat{z}^{\ast\tau}W_{2}\hat{z}^{\tau} \\ & -(1-\eta)e^{\ast\tau}W_{1}e^{\tau} -e^{\ast\tau_{1}}Q_{1}e^{\tau_{1}}-e^{\ast\tau_{2}}Q_{2}e^{\tau _{2}}+ \tau_{1}^{2}\dot{e}^{\ast}R_{1}\dot{e} \\ & -\tau_{1} \int_{t-\tau_{1}}^{t}\dot{e}^{\ast}(s)R_{1} \dot{e}(s)\,ds +\tau_{12}^{2}\dot{e}^{\ast}R_{2} \dot{e}-\tau_{12} \int_{t-\tau _{2}}^{t-\tau_{1}}\dot{e}^{\ast}(s)R_{2} \dot{e}(s)\,ds \\ \leq{}& 2\hat{z}^{\ast}P \bigl(-D\hat{z}+A^{\prime}f( \hat{z})+B^{\prime}f \bigl(\hat {z}^{\tau} \bigr)+KCe+Kg(e) \bigr)+ \hat{z}^{\ast}W_{2}\hat{z} \\ & +2e^{\ast}P \bigl(-(D+KC)e+A^{\prime}f(e)+B^{\prime}f \bigl(e^{\tau} \bigr)-Kg(e) \bigr)-(1-\eta )\hat{z}^{\ast\tau}W_{2} \hat{z}^{\tau} \\ & +e^{\ast}(W_{1}+Q_{1}+Q_{2})e-(1- \eta)e^{\ast\tau}W_{1}e^{\tau} -e^{\ast\tau_{1}}Q_{1}e^{\tau_{1}}-e^{\ast\tau_{2}}Q_{2}e^{\tau_{2}} \\ & +\tau_{1}^{2} \bigl(-(D+KC)e+A^{\prime}f(e)+B^{\prime}f \bigl(e^{\tau} \bigr)-Kg(e) \bigr)^{\ast} \\ & \times R_{1} \bigl(-(D+KC)e+A^{\prime}f(e)+B^{\prime}f \bigl(e^{\tau} \bigr)-Kg(e) \bigr) - \bigl(e^{\ast}-e^{\ast\tau_{1}} \bigr)R_{1} \bigl(e-e^{\tau_{1}} \bigr) \\ & +\tau_{12}^{2} \bigl(-(D+KC)e+A^{\prime}f(e)+B^{\prime}f \bigl(e^{\tau} \bigr)-Kg(e) \bigr)^{\ast} \\ &\times R_{2} \bigl(-(D+KC)e+A^{\prime}f(e)+B^{\prime}f \bigl(e^{\tau} \bigr)-Kg(e) \bigr) - \bigl(e^{\ast\tau_{1}}-e^{\ast\tau_{2}} \bigr)R_{2} \bigl(e^{\tau_{1}}-e^{\tau_{2}} \bigr). \end{aligned} $$
(16)

Moreover, from (10), it is clear that

$$ \begin{aligned}[b] &\epsilon_{1} \bigl(e^{\ast}\bar{L}e-f^{\ast}(e)f(e) \bigr)\geq0, \\ &\epsilon_{2} \bigl(e^{\tau\ast}\bar{L}e^{\tau}-f^{\ast}\bigl(e^{\tau} \bigr)f \bigl(e^{\tau } \bigr) \bigr)\geq0, \\ &\epsilon_{3} \bigl(e^{\ast}\bar{M}e-g^{\ast}(e)g(e) \bigr)\geq0, \\ &\epsilon_{4} \bigl(\hat{z}^{\ast}\bar{L} \hat{z}-f^{\ast}(\hat{z})f(\hat {z}) \bigr)\geq0, \\ &\epsilon_{5} \bigl(\hat{z}^{\tau\ast}\bar{L} \hat{z}^{\tau}-f^{\ast}\bigl(\hat {z}^{\tau} \bigr)f \bigl( \hat{z}^{\tau} \bigr) \bigr)\geq0\end{aligned} $$
(17)

for \(\epsilon_{\varrho}>0\), \(\varrho=1,2,\ldots,5\), where \(\bar {L}=L^{T}L\), \(\bar{M}=M^{T}M\). Then, combining (16) with (17), we have

$$\begin{aligned} \dot{V}(t)\leq{}& e^{\ast} \bigl(-DP-(RC)^{\ast}-PD-RC+W_{1}+Q_{1}+Q_{2}-R_{1}+ \epsilon_{1}\bar {L}+\epsilon_{3}\bar{M} \bigr)e \\ & +2e^{\ast}R_{1}e^{\tau_{1}}-e^{\ast\tau_{1}}(Q_{1}+R_{1}+R_{2})e^{\tau_{1}} +2e^{\ast\tau_{1}}R_{2}e^{\tau_{2}}-e^{\ast\tau_{2}}(Q_{2}+R_{2})e^{\tau _{2}} \\ & +2e^{\ast}PA^{\prime}f(e)+2e^{\ast}PB^{\prime}f \bigl(e^{\tau} \bigr)-2e^{\ast}Rg(e) -e^{\ast\tau} \bigl((1- \eta)W_{1}-\epsilon_{2}L \bigr)e^{\tau} \\ & -\epsilon_{1}f^{\ast}(e)f(e)-\epsilon_{2}f^{\ast}\bigl(e^{\tau} \bigr)f \bigl(e^{\tau } \bigr)- \epsilon_{3}g^{\ast}(e)g(e) -\epsilon_{4}f^{\ast}( \hat{z})f(\hat{z}) \\ & -\epsilon_{5}f^{\ast}\bigl(\hat{z}^{\tau} \bigr)f \bigl(\hat{z}^{\tau} \bigr) +\hat{z}^{\ast}(-DP-PD+W_{2}+ \epsilon_{4}\bar{L})\hat{z} +2\hat{z}^{\ast}RCe \\ & -\hat{z}^{\ast\tau} \bigl((1-\eta)W_{2}-\epsilon_{5} \bar{L} \bigr)\hat{z}^{\tau} +2\hat{z}^{\ast}PA^{\prime}f( \hat{z})+2\hat{z}^{\ast}PB^{\prime}f \bigl(\hat {z}^{\tau} \bigr) +2\hat{z}^{\ast}Rg(e) \\ & +\xi^{\ast}(t) \bigl(\tau_{1}^{2}S_{1}^{\ast}R_{1}S_{1} \bigr)\xi(t) +\xi^{\ast}(t) \bigl(\tau_{12}^{2}S_{1}^{\ast}R_{2}S_{1} \bigr)\xi(t) \\ ={}&\xi^{\ast}(t) \bigl[\Omega^{1}+\tau_{1}^{2}S_{1}^{\ast}R_{1}S_{1}+ \tau _{12}^{2}S_{1}^{\ast}R_{2}S_{1} \bigr]\xi(t). \end{aligned}$$
(18)

Case 2: When \(|z_{k}(t)|>\delta_{k}\), \(|\hat{z}_{k}(t)|>\delta_{k}\), at time t, systems (6) and (7) can turn into the following systems, respectively:

$$ \dot{z}=-Dz+A^{\prime\prime}f(z)+B^{\prime\prime}f \bigl(z^{\tau} \bigr) $$
(19)

and

$$ \dot{\hat{z}}=-D\hat{z}+A^{\prime\prime}f(\hat{z})+B^{\prime\prime }f \bigl( \hat{z}^{\tau} \bigr)+K \bigl(l-C\hat{z}-g(t,\hat{z}) \bigr). $$
(20)

Then the error-state system can be obtained:

$$ \dot{e}=-(D+KC)e+A^{\prime\prime}f(e)+B^{\prime\prime}f \bigl(e^{\tau} \bigr)-Kg(e). $$
(21)

By a similar derivation process to Case 1, one has

$$ \dot{V}(t)\leq\xi^{\ast}(t) \bigl[\Omega^{2}+ \tau_{1}^{2}S_{2}^{\ast }R_{1}S_{2}+ \tau_{12}^{2}S_{2}^{\ast}R_{2}S_{2} \bigr]\xi(t). $$
(22)

Case 3: When \(|z_{k}(t)|<\delta_{k}\), \(|\hat{z}_{k}(t)|>\delta_{k}\), at time t, systems (6)and (7) can turn into (14) and (21), then the error-state system can be written as

$$ \begin{aligned}[b] \dot{e}=-(D+KC)e+A^{\prime}f(e)+B^{\prime}f \bigl(e^{\tau} \bigr)-Kg(t,e) + \bigl(A^{\prime}-A^{\prime\prime} \bigr)f(\hat{z})+ \bigl(B^{\prime}-B^{\prime\prime } \bigr)f \bigl( \hat{z}^{\tau} \bigr).\end{aligned} $$
(23)

By a similar derivation process to Case 1, we find that

$$ \dot{V}(t)\leq \xi^{\ast}(t) \bigl[\Omega^{3}+ \tau_{1}^{2}S_{3}^{\ast}R_{1}S_{1}+ \tau _{12}^{2}S_{3}^{\ast}R_{2}S_{3} \bigr]\xi(t). $$
(24)

Case 4: When \(|z_{k}(t)|>\delta_{k}\), \(|\hat{z}_{k}(t)|<\delta_{k}\), at time t, systems (6) and (7) can turn into (20) and (15), then the error-state system can be written as

$$ \begin{aligned}[b] \dot{e}=-(D+KC)e+A^{\prime\prime}f(e)+B^{\prime\prime}f \bigl(e^{\tau } \bigr)-Kg(t,e) + \bigl(A^{\prime\prime}-A^{\prime} \bigr)f(\hat{z})+ \bigl(B^{\prime\prime}-B^{\prime } \bigr)f \bigl( \hat{z}^{\tau} \bigr).\end{aligned} $$
(25)

By a similar derivation process to Case 1, one has

$$ \dot{V}(t)\leq\xi^{\ast}(t) \bigl[\Omega^{4}+ \tau_{1}^{2}S_{4}^{\ast }R_{1}S_{4}+ \tau_{12}^{2}S_{4}^{\ast}R_{2}S_{4} \bigr]\xi(t). $$
(26)

Moreover, by the Schur complement, (11) is equivalent to \(\Omega^{j}+\tau_{1}^{2}S_{j}R_{1}S_{j}^{\ast}+\tau _{12}^{2}S_{j}R_{2}S_{j}^{\ast}<0\). Then there must be a small positive scalar ε such that \((\Omega^{j}+\tau_{1}^{2}S_{j}^{\ast}R_{1}S_{j}+\tau_{12}^{2}S_{j}^{\ast }R_{2}S_{j})+ \operatorname{diag}(\varepsilon I,0,0,0,0,0,0, 0,0,0,0)\leq0\), then we have \(\dot{V}(t)\leq-\varepsilon\| e(t)\|^{2}<0\), which implies that the error-state system (8) is globally asymptotically stable. □

Corollary 1

Suppose that Assumption 1 holds, the error-state system (8) is globally asymptotically stable, if there exist positive definite Hermitian matrices \(P=P_{1}+iP_{2}\), \(W_{1}=W_{11}+iW_{12}\), \(W_{2}=W_{21}+iW_{22}\), \(Q_{1}=Q_{11}+iQ_{12}\), \(Q_{2}=Q_{21}+iQ_{22}\), \(R_{1}=R_{11}+iR_{12}\), \(R_{2}=R_{21}+iR_{22}\), any complex matrix \(R=R^{1}+iR^{2}\), and positive scalars \(\epsilon_{\kappa}\) (\(\kappa =1,2,\ldots,5\)), such that the following LMIs hold:

$$ \left [ \textstyle\begin{array}{c@{\quad}c} \hat{\Theta}_{j}^{R} & -\hat{\Theta}_{j}^{I} \\ \hat{\Theta}_{j}^{I} & \hat{\Theta}_{j}^{R} \end{array}\displaystyle \right ]< 0,\quad j=1,2,3,4, $$
(27)

where

$$\begin{aligned}& \hat{\Theta}_{j}^{R}= \left [ \textstyle\begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c} \Omega_{11}^{R} & R_{11} & 0 & 0 & (RC)^{\ast R}&0&\Omega^{jR}_{17}& \Omega^{jR}_{18}& -R^{1}&\Omega^{jR}_{1,10}&\Omega^{jR}_{1,11}&\Omega ^{R}_{1,12}&\Omega^{R}_{1,13}\\ \ast& \Omega_{22}^{R} & R_{21} & 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \ast& \ast& \Omega_{33}^{R} & 0 & 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \ast& \ast& \ast& \Omega_{44}^{R} & 0 & 0& 0& 0& 0& 0& 0& 0& 0\\ \ast& \ast& \ast&\ast& \Omega_{55}^{R} & 0 & 0& 0 & R^{1}& \Omega ^{jR}_{5,10} & \Omega^{jR}_{5,11}& 0& 0\\ \ast& \ast& \ast&\ast&\ast&\Omega_{66}^{R} & 0 & 0 & 0& 0 & 0& 0& 0\\ \ast& \ast& \ast&\ast&\ast& \ast& -\epsilon_{1}I & 0 & 0& 0 & 0&\Omega^{jR}_{7,12}&\Omega^{jR}_{7,13}\\ \ast& \ast& \ast&\ast&\ast& \ast&\ast&-\epsilon_{2}I & 0& 0 & 0&\Omega^{jR}_{8,12}&\Omega^{jR}_{8,13}\\ \ast& \ast& \ast&\ast&\ast& \ast&\ast& \ast& -\epsilon_{3}I& 0 & 0& -R^{1T} & -R^{1T}\\ \ast& \ast& \ast&\ast&\ast& \ast& \ast&\ast& \ast& -\epsilon _{4}I& 0 & \Omega^{jR}_{10,12}& \Omega^{jR}_{10,13} \\ \ast& \ast& \ast&\ast&\ast& \ast& \ast&\ast& \ast& \ast& -\epsilon_{5}I& \Omega^{jR}_{11,12}& \Omega^{jR}_{11,13}\\ \ast& \ast& \ast&\ast&\ast& \ast& \ast&\ast& \ast& \ast& \ast& \Omega^{R}_{12,12} & 0\\ \ast& \ast& \ast&\ast&\ast& \ast& \ast&\ast& \ast& \ast& \ast& \ast& \Omega^{R}_{13,13} \end{array}\displaystyle \right ], \\& \hat{\Theta}_{j}^{I}= \left [ \textstyle\begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c} \Omega_{11}^{I} & R_{12} & 0 & 0 & (RC)^{\ast I}&0&\Omega^{jI}_{17}& \Omega^{jI}_{18}& -R^{2}&\Omega^{jI}_{1,10}&\Omega^{jI}_{1,11}&\Omega ^{I}_{1,12}&\Omega^{I}_{1,13} \\ -R_{12}^{T}&\Omega_{22}^{I}&R_{22}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0 \\ 0 & -R_{22}^{T} & \Omega_{33}^{I} & 0 & 0& 0& 0& 0& 0& 0& 0& 0& 0 \\ 0 &0&0& \Omega_{44}^{I} & 0 & 0& 0& 0& 0& 0& 0& 0& 0 \\ \Omega^{jI}_{5,1}&0&0&0&\Omega_{55}^{I} &0&0&0&R^{2}& \Omega^{jI}_{5,10} &\Omega^{jI}_{5,11}&0&0 \\ 0&0&0&0 &0&\Omega_{66}^{I}& 0 &0 &0&0 & 0& 0& 0 \\ \Omega^{jI}_{7,1}&0&0&0 &0& 0&0 & 0 & 0& 0 & 0&\Omega^{jI}_{7,12}&\Omega ^{jI}_{7,13} \\ \Omega^{jI}_{8,1}& 0 &0&0 &0 & 0&0&0 & 0& 0 & 0&\Omega ^{jI}_{8,12}&\Omega^{jI}_{8,13} \\ R^{2T}&0&0&0&-R^{2T}&0&0&0&0&0&0&R^{2T}& R^{2T} \\ \Omega^{jI}_{10,1}&0& 0 &0 &\Omega^{jI}_{10,5}& 0 & 0&0& 0& 0& 0 & \Omega^{jI}_{10,12}& \Omega^{jI}_{10,13} \\ \Omega^{jI}_{11,1}&0& 0 &0 &\Omega^{jI}_{11,5}& 0& 0&0 & 0&0&0&\Omega ^{jI}_{11,12}& \Omega^{jI}_{11,13} \\ \Omega^{jI}_{12,1}&0&0&0 &0 & 0 &\Omega^{jI}_{12,7}&\Omega^{jI}_{12,8} & -R^{2}&\Omega^{jI}_{12,10}& \Omega^{jI}_{12,11}& \Omega^{I}_{12,12} & 0 \\ \Omega^{jI}_{13,1} & 0 & 0 &0 &0 & 0 & \Omega^{jI}_{13,7}&\Omega ^{jI}_{13,8}&-R_{2}&\Omega^{jI}_{13,10}& \Omega^{jI}_{13,11}& 0& \Omega ^{I}_{13,13} \end{array}\displaystyle \right ], \\& \begin{aligned}\Omega_{11}^{R}={}&{-}DP_{1}-C_{1}^{T}R^{1T}+C_{2}^{T}R^{2T}-P_{1}D-R^{1}C_{1} +R^{2}C_{2} \\ &+W_{11}+Q_{11}+Q_{21}-R_{11}+ \epsilon_{1}\bar{L}+\epsilon_{3}\bar{M},\end{aligned} \\& \Omega_{15}^{R}=C_{1}^{T}R^{1T}-C_{2}^{T}R^{2T}, \qquad \Omega^{1R}_{17}=\Omega^{3R}_{17}= \Omega^{1R}_{5,10}=\Omega ^{4R}_{5,10}=P_{1}A^{\prime}_{1}-P_{2}A_{2}^{\prime}, \\& \Omega^{1R}_{1,10}=\Omega^{2R}_{1,10}= \Omega^{1R}_{1,11}=\Omega ^{2R}_{1,11}= \Omega^{1R}_{10,12} =\Omega^{2R}_{10,13}= \Omega^{1R}_{11,12}=\Omega^{2R}_{11,13}=0, \\& \Omega^{2R}_{17}=\Omega^{4R}_{17}= \Omega^{2R}_{5,10}=\Omega ^{3R}_{5,10}=P_{1}A^{\prime\prime}_{1}-P_{2}A_{2}^{\prime\prime}, \\& \Omega^{1R}_{18}=\Omega^{3R}_{18}= \Omega^{1R}_{5,11}=\Omega ^{4R}_{5,11}=P_{1}B^{\prime}_{1}-P_{2}B_{2}^{\prime}, \\& \Omega^{2R}_{18}=\Omega^{4R}_{18}= \Omega^{2R}_{5,11}=\Omega ^{3R}_{5,11}=P_{1}B^{\prime\prime}_{1}-P_{2}B_{2}^{\prime\prime}, \qquad \Omega^{3R}_{1,10}=P_{1}\bigl(A_{1}^{\prime}-A_{1}^{\prime\prime} \bigr)-P_{2}\bigl(A_{2}^{\prime }-A_{2}^{\prime\prime} \bigr), \\& \Omega^{4R}_{1,10}=P_{1}\bigl(A_{1}^{\prime\prime}-A_{1}^{\prime} \bigr)-P_{2}\bigl(A_{2}^{\prime \prime}-A_{2}^{\prime} \bigr),\qquad \Omega^{3R}_{1,11}=P_{1} \bigl(B_{1}^{\prime}-B_{1}^{\prime\prime} \bigr)-P_{2}\bigl(B_{2}^{\prime }-B_{2}^{\prime\prime} \bigr), \\& \Omega^{4R}_{1,11}=P_{1}\bigl(B_{1}^{\prime\prime}-B_{1}^{\prime} \bigr)-P_{2}\bigl(B_{2}^{\prime \prime}-B_{2}^{\prime} \bigr),\qquad \Omega^{R}_{1,12}=\tau_{1} \bigl(-DP_{1}-C_{1}^{T}R^{1T}+C_{2}^{T}R^{2T} \bigr), \\& \Omega^{R}_{1,13}=\tau_{12}\bigl(-DP_{1}-C_{1}^{T}R^{1T}+C_{2}^{T}R^{2T} \bigr),\qquad \Omega_{22}^{R}=-(Q_{11}+R_{11}+R_{21}), \\& \Omega_{33}^{R}=-(Q_{21}+R_{21}), \hspace{18pt} \Omega_{44}^{R}=-(1-\rho)W_{11}+ \epsilon_{2}\bar{L},\hspace{18pt} \Omega_{55}^{R}=-DP_{1}-P_{1}D+W_{21}+ \epsilon_{4}\bar{L}, \\& \Omega_{66}^{R}=-(1-\rho)W_{21}+ \epsilon_{5}\bar{L},\qquad \Omega_{7,12}^{1R}= \Omega_{7,12}^{3R}=\tau_{1}\bigl(A_{1}^{\prime T}P_{1}+A_{2}^{\prime T}P_{2} \bigr), \\& \Omega_{10,12}^{3R}=\tau_{1}\bigl( \bigl(A_{1}^{\prime}-A_{1}^{\prime\prime } \bigr)^{T}P_{1}+\bigl(A_{2}^{\prime}-A_{2}^{\prime\prime} \bigr)^{T}P_{2}\bigr),\qquad \Omega_{7,12}^{2R}= \Omega_{7,12}^{4R}=\tau_{1}\bigl(A_{1}^{\prime\prime T}P_{1}+A_{2}^{\prime\prime T}P_{2} \bigr), \\& \Omega_{10,12}^{4R}=\tau_{1}\bigl( \bigl(A_{1}^{\prime\prime}-A_{1}^{\prime } \bigr)^{T}P_{1}+\bigl(A_{2}^{\prime\prime}-A_{2}^{\prime} \bigr)^{T}P_{2}\bigr),\qquad \Omega_{7,13}^{1R}= \Omega_{7,13}^{3R}=\tau_{12}\bigl(A_{1}^{\prime T}P_{1}+A_{2}^{\prime T}P_{2} \bigr), \\& \Omega_{10,13}^{3R}=\tau_{12}\bigl( \bigl(A_{1}^{\prime}-A_{1}^{\prime\prime } \bigr)^{T}P_{1}+\bigl(A_{2}^{\prime}-A_{2}^{\prime\prime} \bigr)^{T}P_{2}\bigr),\qquad \Omega_{7,13}^{2R}= \Omega_{7,13}^{4R}=\tau_{12}\bigl(A_{1}^{\prime\prime T}P_{1}+A_{2}^{\prime\prime T}P_{2} \bigr), \\& \Omega_{10,13}^{4R}=\tau_{12}\bigl( \bigl(A_{1}^{\prime\prime}-A_{1}^{\prime } \bigr)^{T}P_{1}+\bigl(A_{2}^{\prime\prime}-A_{2}^{\prime} \bigr)^{T}P_{2}\bigr),\qquad \Omega_{8,12}^{1R}= \Omega_{8,12}^{3R}=\tau_{1}\bigl(B_{1}^{\prime T}P_{1}+B_{2}^{\prime T}P_{2} \bigr), \\& \Omega_{11,12}^{3R}=\tau_{1}\bigl( \bigl(B_{1}^{\prime}-B_{1}^{\prime\prime } \bigr)^{T}P_{1}+\bigl(B_{2}^{\prime}-B_{2}^{\prime\prime} \bigr)^{T}P_{2}\bigr),\qquad \Omega_{8,12}^{2R}= \Omega_{8,12}^{4R}=\tau_{1}\bigl(B_{1}^{\prime\prime T}P_{1}+B_{2}^{\prime\prime T}P_{2} \bigr), \\& \Omega_{11,12}^{4R}=\tau_{1}\bigl( \bigl(B_{1}^{\prime\prime}-B_{1}^{\prime } \bigr)^{T}P_{1}+\bigl(B_{2}^{\prime\prime}-B_{2}^{\prime} \bigr)^{T}P_{2}\bigr),\qquad \Omega_{8,13}^{1R}= \Omega_{8,13}^{3R}=\tau_{12}\bigl(B_{1}^{\prime T}P_{1}+B_{2}^{\prime T}P_{2} \bigr), \\& \Omega_{11,13}^{3R}=\tau_{12}\bigl( \bigl(B_{1}^{\prime}-B_{1}^{\prime\prime } \bigr)^{T}P_{1}+\bigl(B_{2}^{\prime}-B_{2}^{\prime\prime} \bigr)^{T}P_{2}\bigr),\qquad \Omega_{8,13}^{2R}= \Omega_{8,13}^{4R}=\tau_{12}\bigl(B_{1}^{\prime\prime T}P_{1}+B_{2}^{\prime\prime T}P_{2} \bigr), \\& \Omega_{11,13}^{4R}=\tau_{12}\bigl( \bigl(B_{1}^{\prime\prime}-B_{1}^{\prime } \bigr)^{T}P_{1}+\bigl(B_{2}^{\prime\prime}-B_{2}^{\prime} \bigr)^{T}P_{2}\bigr),\qquad \Omega_{12,12}^{R}=-2P_{1}+R_{11}, \\& \Omega_{13,13}^{R}=-2P_{1}+R_{21},\qquad \Omega_{15}^{I}=-C_{2}^{T}R^{1T}-C_{1}^{T}R^{2T}, \\& \Omega_{11}^{I}=-DP_{2}+C_{2}^{T}R^{1T}+C_{1}^{T}R^{2T}-P_{2}D-R^{1}C_{2} -R^{2}C_{1}+W_{12}+Q_{12}+Q_{22}-R_{12}, \\& \Omega^{1I}_{1,10}=\Omega^{2}_{1,10}= \Omega^{1I}_{1,11}=\Omega ^{2I}_{1,11}= \Omega^{1I}_{11,1} =\Omega^{2I}_{11,1}= \Omega^{1I}_{10,12}=\Omega^{2I}_{10,13}=\Omega ^{1I}_{11,12}=\Omega^{2I}_{11,13}=0, \\& \Omega^{1I}_{18}=\Omega^{3I}_{18}= \Omega_{5,11}^{1I}=\Omega _{5,11}^{4I}=P_{1}B^{\prime}_{2}+P_{2}B_{1}^{\prime}, \\& \Omega^{1I}_{17}=\Omega^{3I}_{17}= \Omega_{5,10}^{1I}=\Omega _{5,10}^{4I}=P_{1}A^{\prime}_{2}+P_{2}A_{1}^{\prime}, \qquad \Omega^{3I}_{1,10}=P_{1}\bigl(A_{2}^{\prime}-A_{2}^{\prime\prime} \bigr)+P_{2}\bigl(A_{1}^{\prime }-A_{1}^{\prime\prime} \bigr), \\& \Omega^{2I}_{17}=\Omega^{4I}_{17}= \Omega_{5,10}^{2I}=\Omega _{5,10}^{3I}=P_{1}A^{\prime\prime}_{2}+P_{2}A_{1}^{\prime\prime}, \qquad \Omega^{4I}_{1,10}=P_{1}\bigl(A_{2}^{\prime\prime}-A_{2}^{\prime} \bigr)+P_{2}\bigl(A_{1}^{\prime \prime}-A_{1}^{\prime} \bigr), \\& \Omega^{2I}_{18}=\Omega^{4I}_{18}= \Omega_{5,11}^{2I}=\Omega _{5,11}^{3I}=P_{1}B^{\prime\prime}_{2}+P_{2}B_{1}^{\prime\prime}, \qquad \Omega^{3I}_{1,11}=P_{1}\bigl(B_{2}^{\prime}-B_{2}^{\prime\prime} \bigr)+P_{2}\bigl(B_{1}^{\prime }-B_{1}^{\prime\prime} \bigr), \\& \Omega^{4I}_{1,11}=P_{1}\bigl(B_{2}^{\prime\prime}-B_{2}^{\prime} \bigr)+P_{2}\bigl(B_{1}^{\prime \prime}-B_{1}^{\prime} \bigr),\qquad \Omega^{I}_{1,12}=\tau_{1} \bigl(-DP_{2}+C_{2}^{T}R^{1T}+C_{1}^{T}R^{2T} \bigr), \\& \Omega^{I}_{1,13}=\tau_{12}\bigl(-DP_{2}+C_{2}^{T}R^{1T}+C_{1}^{T}R^{2T} \bigr),\qquad \Omega_{22}^{I}=-(Q_{12}+R_{12}+R_{22}), \\& \Omega_{33}^{I}=-(Q_{22}+R_{22}),\qquad \Omega_{44}^{I}=-(1-\rho)W_{12},\qquad \Omega_{51}^{I}=R^{1}C_{2}+R^{2}C_{1}, \\& \Omega_{55}^{I}=-DP_{2}-P_{2}D+W_{22}, \qquad \Omega_{66}^{I}=-(1-\rho)W_{22}, \\& \Omega^{1I}_{71}=\Omega^{3I}_{71}= \Omega_{10,5}^{1I}=\Omega _{10,5}^{4I}=-A_{2}^{\prime T}P_{1}-A_{1}^{\prime T}P_{2}^{T}, \\& \Omega^{2I}_{71}=\Omega^{4I}_{71}= \Omega_{10,5}^{2I}=\Omega _{10,5}^{3I}=-A_{2}^{\prime\prime T}P_{1}- A_{1}^{\prime\prime T}P_{2}^{T},\qquad \Omega_{7,12}^{1I}=\Omega_{7,12}^{3I}= \tau_{1}\bigl(A_{1}^{\prime T}P_{2}-A_{2}^{\prime T}P_{1} \bigr), \\& \Omega_{7,12}^{2I}=\Omega_{7,12}^{4I}= \tau_{1}\bigl(A_{1}^{\prime\prime T}P_{2}-A_{2}^{\prime\prime T}P_{1} \bigr),\qquad \Omega_{7,13}^{1I}=\Omega_{7,13}^{3I}= \tau_{12}\bigl(A_{1}^{\prime T}P_{2}-A_{2}^{\prime T}P_{1} \bigr), \\& \Omega_{7,13}^{2I}=\Omega_{7,13}^{4I}= \tau_{12}\bigl(A_{1}^{\prime\prime T}P_{2}-A_{2}^{\prime\prime T}P_{1} \bigr),\qquad \Omega^{1I}_{81}=\Omega^{3I}_{81}= \Omega_{11,5}^{1I}=\Omega _{11,5}^{4I}=-B^{\prime T}_{2} P_{1}-B_{1}^{\prime T}P_{2}^{T}, \\& \Omega^{2I}_{81}=\Omega^{4I}_{81}= \Omega_{11,5}^{2I}=\Omega _{11,5}^{3I}=-B^{\prime\prime T}_{2} P_{1}-B_{1}^{\prime\prime T}P_{2}^{T}, \qquad \Omega_{8,12}^{1I}=\Omega_{8,12}^{3I}= \tau_{1}\bigl(B_{1}^{\prime T}P_{2}-B_{2}^{\prime T}P_{1} \bigr), \\& \Omega_{8,12}^{2I}=\Omega_{8,12}^{4I}= \tau_{1}\bigl(B_{1}^{\prime\prime T}P_{2}-B_{2}^{\prime\prime T}P_{1} \bigr),\qquad \Omega_{8,13}^{1I}=\Omega_{8,13}^{3I}= \tau_{12}\bigl(B_{1}^{\prime T}P_{2}-B_{2}^{\prime T}P_{1} \bigr), \\& \Omega_{8,13}^{2I}=\Omega_{8,13}^{4I}= \tau_{12}\bigl(B_{1}^{\prime\prime T}P_{2}-B_{2}^{\prime\prime T}P_{1} \bigr),\qquad \Omega^{3I}_{10,1}=-\bigl(A_{2}^{\prime}-A_{2}^{\prime\prime } \bigr)^{T}P_{1}-\bigl(A_{1}^{\prime}-A_{1}^{\prime\prime} \bigr)^{T}P_{2}^{T}, \\& \Omega^{4I}_{10,1}=-\bigl(A_{2}^{\prime\prime}-A_{2}^{\prime } \bigr)^{T}P_{1}-\bigl(A_{1}^{\prime\prime}-A_{1}^{\prime} \bigr)^{T}P_{2}^{T},\qquad \Omega^{3I}_{11,1}=- \bigl(B_{2}^{\prime}-B_{2}^{\prime\prime } \bigr)^{T}P_{1}-\bigl(B_{1}^{\prime}-B_{1}^{\prime\prime} \bigr)^{T}P_{2}^{T}, \\& \Omega^{4I}_{11,1}=-\bigl(B_{2}^{\prime\prime}-B_{2}^{\prime } \bigr)^{T}P_{1}-\bigl(B_{1}^{\prime\prime}-B_{1}^{\prime} \bigr)^{T}P_{2}^{T},\\& \Omega_{10,12}^{3I}= \tau_{1}\bigl(\bigl(A_{1}^{\prime}-A_{1}^{\prime\prime } \bigr)^{T}P_{2}-\bigl(A_{2}^{\prime}-A_{2}^{\prime\prime} \bigr)^{T}P_{1}\bigr), \\& \Omega^{I}_{12,1}=\tau_{1}\bigl(P_{2}^{T}D-R^{1} C_{2}-R^{2} C_{1}\bigr),\qquad \Omega_{10,12}^{4I}=\tau_{1}\bigl( \bigl(A_{1}^{\prime\prime}-A_{1}^{\prime } \bigr)^{T}P_{2}-\bigl(A_{2}^{\prime\prime}-A_{2}^{\prime} \bigr)^{T}P_{1}\bigr), \\& \Omega^{I}_{13,1}=\tau_{12}\bigl(P_{2}^{T}D-R^{1} C_{2}-R^{2} C_{1}\bigr),\qquad \Omega_{10,13}^{3I}=\tau_{12}\bigl( \bigl(A_{1}^{\prime}-A_{1}^{\prime\prime } \bigr)^{T}P_{2}-\bigl(A_{2}^{\prime}-A_{2}^{\prime\prime} \bigr)^{T}P_{1}\bigr), \\& \Omega_{12,7}^{1I}=\Omega_{12,7}^{3I}= \tau_{1}\bigl(P_{1}A_{2}^{\prime }-P_{2}^{T}A_{1}^{\prime} \bigr),\qquad \Omega_{10,13}^{4I}=\tau_{12}\bigl( \bigl(A_{1}^{\prime\prime}-A_{1}^{\prime } \bigr)^{T}P_{2}-\bigl(A_{2}^{\prime\prime}-A_{2}^{\prime} \bigr)^{T}P_{1}\bigr), \\& \Omega_{12,7}^{2I}=\Omega_{12,7}^{4I}= \tau_{1}\bigl(P_{1}A_{2}^{\prime\prime }-P_{2}^{T}A_{1}^{\prime\prime} \bigr),\qquad \Omega_{11,12}^{3I}=\tau_{1}\bigl( \bigl(B_{1}^{\prime}-B_{1}^{\prime\prime } \bigr)^{T}P_{2}-\bigl(B_{2}^{\prime}-B_{2}^{\prime\prime} \bigr)^{T}P_{1}\bigr), \\& \Omega_{12,8}^{1I}=\Omega_{12,8}^{3I}= \tau_{1}\bigl(P_{1}B_{2}^{\prime }-P_{2}^{T}B_{1}^{\prime} \bigr),\qquad \Omega_{11,12}^{4I}=\tau_{1}\bigl( \bigl(B_{1}^{\prime\prime}-B_{1}^{\prime } \bigr)^{T}P_{2}-\bigl(B_{2}^{\prime\prime}-B_{2}^{\prime} \bigr)^{T}P_{1}\bigr), \\& \Omega_{12,8}^{2I}=\Omega_{12,8}^{4I}= \tau_{1}\bigl(P_{1}B_{2}^{\prime\prime }-P_{2}^{T}B_{1}^{\prime\prime} \bigr),\qquad \Omega_{11,13}^{3I}=\tau_{12}\bigl( \bigl(B_{1}^{\prime}-B_{1}^{\prime\prime } \bigr)^{T}P_{2}-\bigl(B_{2}^{\prime}-B_{2}^{\prime\prime} \bigr)^{T}P_{1}\bigr), \\& \Omega_{11,13}^{4I}=\tau_{12}\bigl( \bigl(B_{1}^{\prime\prime}-B_{1}^{\prime } \bigr)^{T}P_{2}-\bigl(B_{2}^{\prime\prime}-B_{2}^{\prime} \bigr)^{T}P_{1}\bigr),\\& \Omega_{12,10}^{3I}= \tau_{1}\bigl(P_{1}\bigl(A_{2}^{\prime}-A_{2}^{\prime\prime } \bigr)-P_{2}^{T}\bigl(A_{1}^{\prime}-A_{1}^{\prime\prime} \bigr)\bigr), \\& \Omega_{12,10}^{4I}=\tau_{1}\bigl(P_{1} \bigl(A_{2}^{\prime\prime}-A_{2}^{\prime } \bigr)-P_{2}^{T}\bigl(A_{1}^{\prime\prime}-A_{1}^{\prime} \bigr)\bigr),\qquad \Omega_{12,12}^{I}=-P_{2}+P_{2}^{T}+R_{12}, \\& \Omega _{13,13}^{I}=-P_{2}+P_{2}^{T}+R_{22}, \qquad \Omega_{12,11}^{3I}=\tau_{1} \bigl(P_{1}\bigl(B_{2}^{\prime}-B_{2}^{\prime\prime } \bigr)-P_{2}^{T}\bigl(B_{1}^{\prime}-B_{1}^{\prime\prime} \bigr)\bigr), \\& \Omega_{12,11}^{4I}=\tau_{1}\bigl(P_{1} \bigl(B_{2}^{\prime\prime}-B_{2}^{\prime } \bigr)-P_{2}^{T}\bigl(B_{1}^{\prime\prime}-B_{1}^{\prime} \bigr)\bigr),\qquad \Omega_{13,7}^{1I}=\Omega_{13,7}^{3I}= \tau_{12}\bigl(P_{1}A_{2}^{\prime }-P_{2}^{T}A_{1}^{\prime} \bigr), \\& \Omega_{13,7}^{2I}=\Omega_{13,7}^{4I}= \tau_{12}\bigl(P_{1}A_{2}^{\prime\prime }-P_{2}^{T}A_{1}^{\prime\prime} \bigr),\qquad \Omega_{13,8}^{1I}=\Omega_{13,8}^{3I}= \tau_{12}\bigl(P_{1}B_{2}^{\prime }-P_{2}^{T}B_{1}^{\prime} \bigr), \\& \Omega_{13,8}^{2I}=\Omega_{13,8}^{4I}= \tau_{12}\bigl(P_{1}B_{2}^{\prime\prime }-P_{2}^{T}B_{1}^{\prime\prime} \bigr),\qquad \Omega_{13,10}^{3I}=\tau_{12} \bigl(P_{1}\bigl(A_{2}^{\prime}-A_{2}^{\prime\prime } \bigr)-P_{2}^{T}\bigl(A_{1}^{\prime}-A_{1}^{\prime\prime} \bigr)\bigr), \\& \Omega_{13,10}^{4I}=\tau_{12}\bigl(P_{1} \bigl(A_{2}^{\prime\prime}-A_{2}^{\prime } \bigr)-P_{2}^{T}\bigl(A_{1}^{\prime\prime}-A_{1}^{\prime} \bigr)\bigr),\\& \Omega_{13,11}^{3I}=\tau_{12} \bigl(P_{1}\bigl(B_{2}^{\prime}-B_{2}^{\prime\prime } \bigr)-P_{2}^{T}\bigl(B_{1}^{\prime}-B_{1}^{\prime\prime} \bigr)\bigr), \\& \Omega_{13,11}^{4I}=\tau_{12}\bigl(P_{1} \bigl(B_{2}^{\prime\prime}-B_{2}^{\prime } \bigr)-P_{2}^{T}\bigl(B_{1}^{\prime\prime}-B_{1}^{\prime} \bigr)\bigr), \\& A_{1}^{\prime}=\operatorname{Re}\bigl(A^{\prime}\bigr), \qquad A_{2}^{\prime }=\operatorname{Im}\bigl(A^{\prime} \bigr),\qquad B_{1}^{\prime}=\operatorname{Re} \bigl(B^{\prime}\bigr), \qquad B_{2}^{\prime }= \operatorname{Im}\bigl(B^{\prime}\bigr), \\& A_{1}^{\prime\prime}=\operatorname{Re}\bigl(A^{\prime\prime}\bigr), \qquad A_{2}^{\prime \prime}=\operatorname{Im}\bigl(A^{\prime\prime} \bigr),\qquad B_{1}^{\prime\prime}=\operatorname{Re} \bigl(B^{\prime\prime}\bigr),\qquad B_{2}^{\prime \prime}= \operatorname{Im}\bigl(B^{\prime\prime}\bigr), \\& C_{1}=\operatorname{Re}(C),\qquad C_{2}= \operatorname{Im}(C). \end{aligned}$$

Proof

We multiply (11) from the left and right by \(\operatorname {diag}(I, (R_{1}^{-1}P)^{\ast}, (R_{2}^{-1}P)^{\ast})\) and its transpose \(\operatorname{diag}(I,R_{1}^{-1}P, R_{2}^{-1}P)\). Further, noting that \(P^{\ast}R_{1}^{-1}P\geq2P-R_{1}\) and \(P^{\ast }R_{2}^{-1}P\geq2P-R_{2}\), one easily derives that

$$ \hat{\Theta}_{j}=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \Omega^{j} & \tau_{1}S_{j}^{\ast}P & \tau_{12}S_{j}^{\ast}P\\ \ast& -2P+R_{1} & 0\\ \ast& \ast& -2P+R_{2} \end{array}\displaystyle \right ]< 0,\quad j=1,2,3,4. $$
(28)

By means of Lemma 2, complex-valued LMIs (28) can be transformed into real-valued ones described in (27). Obviously, (27) can guarantee that (11) holds. The proof is completed. □

Remark 1

Up to now, unlike the abundant research results about the state estimation problem for the real-valued neural networks [4–12, 14–17], there have been few relevant results for the complex-valued neural networks [47–49]. Further, for real-valued memristive neural networks, only [28, 29] touches on the same problem. Moreover, when it comes to complex-valued memristive systems, there is no achievement established on the state estimation problem. In this paper, a sufficient condition is proposed to devise the desired state estimator based on the Lyapunov functional method and the linear matrix inequality techniques. Thus, our work can fill in this gap.

Remark 2

Considering the special structure of complex-valued neural networks with memristors, the improved Lyapunov functional on those in [4–12, 14–17, 28, 29, 47–49] is constructed. Then a LMI-based result with lower computational burden is obtained, which considers the sign difference of the memristive weights and overcomes the shortcomings of the results based on M-matrix and algebraic inequality. The gain matrix K can be determined easily by solving the certain matrix inequalities (27). Besides, if system (1) is reduced to real-valued memristive neural networks, a similar result can also be derived.

Remark 3

Stability analysis is the basis of the design of state estimator, and many effective methods have been proposed. In [2], a weighting-delay-based method is developed by dividing the delay interval \([0,d(t)]\) into some variable subintervals by employing weighting delays, and less conservative criteria are obtained. Meanwhile, the adjustable parameters will be increased accordingly along with the increase of the subinterval. Noted that the results in this paper are very different from those in [1, 2]. The main reason lies in that the core idea in this paper is to design an effective state estimator for system (1), which belongs to the state-dependent switched systems. The parameters of such systems are uncertain. To design an effective state estimator, the improved Lyapunov functional containing the time-varying delays and the estimated states is constructed. Considering the weighting-delay-based method in [2] has inherent flexibility in dealing with the time-varying delay; it is a meaningful topic to apply the novel method to the state estimation issue and we will regard it as our target for further research.

4 Simulation example

In this section, an example is given to illustrate the effectiveness of our proposed results for the state estimator design of complex-valued memristive neural networks with time-varying delays.

Example 1

Consider system (1) with the following parameters:

$$\begin{gathered} D=\left [ \textstyle\begin{array}{c@{\quad}c} 5 & 0\\ 0 & 6 \end{array}\displaystyle \right ],\qquad C=\left [ \textstyle\begin{array}{c@{\quad}c} 2-2i & -i\\ 3+3i & -1-i \end{array}\displaystyle \right ],\qquad a_{11}^{R}(t)= \left \{ \textstyle\begin{array}{l@{\quad}l} 3,& |x_{1}|< 1,\\ 1,& |x_{1}|>1, \end{array}\displaystyle \right . \\ a_{12}^{R}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 1,&|x_{2}|< 1,\\ 2,&|x_{2}|>1, \end{array}\displaystyle \right .\qquad a_{21}^{R}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} -1,&|x_{1}|< 1,\\ -1.5,&|x_{1}|>1, \end{array}\displaystyle \right .\qquad a_{22}^{R}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 2,&|x_{2}|< 1,\\ 1.5,&|x_{2}|>1, \end{array}\displaystyle \right . \\ a_{11}^{I}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 2,& |y_{1}|< 1,\\ 1,& |y_{1}|>1, \end{array}\displaystyle \right .\qquad a_{12}^{I}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} -4,& |y_{2}|< 1,\\ -3,& |y_{2}|>1, \end{array}\displaystyle \right .\qquad a_{21}^{I}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} -1,& |y_{1}|< 1,\\ -2,& |y_{1}|>1, \end{array}\displaystyle \right . \\ a_{22}^{I}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 1,& |y_{2}|< 1,\\ 0.5,& |y_{2}|>1, \end{array}\displaystyle \right .\qquad b_{11}^{R}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 1,& |x_{1}|< 1,\\ 2,& |x_{1}|>1, \end{array}\displaystyle \right .\qquad b_{12}^{R}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} -3,& |x_{2}|< 1,\\ -4,& |x_{2}|>1, \end{array}\displaystyle \right . \\ b_{21}^{R}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 3,& |x_{1}|< 1,\\ 2,& |x_{1}|>1, \end{array}\displaystyle \right .\qquad b_{22}^{R}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 1,& |x_{2}|< 1,\\ 2,& |x_{2}|>1, \end{array}\displaystyle \right .\qquad b_{11}^{I}(t)= \left \{ \textstyle\begin{array}{l@{\quad}l} -2,& |y_{1}|< 1,\\ -2.5, &|y_{1}|>1, \end{array}\displaystyle \right . \\ b_{12}^{I}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 4,& |y_{2}|< 1,\\ 2,& |y_{2}|>1, \end{array}\displaystyle \right .\qquad b_{21}^{I}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} -1,& |y_{1}|< 1,\\ -2,& |y_{1}|>1, \end{array}\displaystyle \right .\qquad b_{22}^{I}(t)=\left \{ \textstyle\begin{array}{l@{\quad}l} 3,& |y_{2}|< 1,\\ 1.5,& |y_{2}|>1. \end{array}\displaystyle \right .\end{gathered} $$

For this system, the activation functions and the nonlinear disturbance are taken as \(f(z)= \frac{1-e^{-\operatorname{Re}(z)}}{1+e^{-\operatorname{Re}(z)}}+i\frac {1}{1+e^{-\operatorname{Im}(z)}}\), \(g(z)=0.1\operatorname {cos}(\operatorname{Re}(z))+0.1i\operatorname{sin}(\operatorname {Im}(z))\), respectively. The time-varying delay is given as \(\tau(t)=0.4|\operatorname{cos}(t)|\) with \(\tau_{1}=0\), \(\tau_{2}=0.4\).

From the above parameters, we obtain

$$\begin{gathered} A^{\prime}=\left [ \textstyle\begin{array}{c@{\quad}c} 3+2i &1-4i \\ -1-i &2+i \end{array}\displaystyle \right ],\qquad A^{\prime\prime}=\left [ \textstyle\begin{array}{c@{\quad}c} 1+i &2-3i \\ -1.5-2i &1.5+0.5i \end{array}\displaystyle \right ], \\ B^{\prime}=\left [ \textstyle\begin{array}{c@{\quad}c} 1-2i &-3+4i \\ 3-i &1+3i \end{array}\displaystyle \right ],\qquad B^{\prime\prime}=\left [ \textstyle\begin{array}{c@{\quad}c} 2-2.5i &-4+2i \\ 2-2i &2+1.5i \end{array}\displaystyle \right ], \\ \bar{L}=\left [ \textstyle\begin{array}{c@{\quad}c} 0.25 & 0 \\ 0 & 0.25 \end{array}\displaystyle \right ],\qquad \bar{M}=\left [ \textstyle\begin{array}{c@{\quad}c} 0.02 & 0 \\ 0 & 0.02 \end{array}\displaystyle \right ].\end{gathered} $$

By employing the Matlab LMI Toolbox, the feasible solutions to the LMIs (27) are

$$\begin{gathered} P=\left [ \textstyle\begin{array}{c@{\quad}c} 3.1132 & -0.3403 - 0.0547i\\ -0.3403 + 0.0547i& 5.3179 \end{array}\displaystyle \right ], \\ Q_{1}=\left [ \textstyle\begin{array}{c@{\quad}c} 4.0807 & -0.8747 - 0.0303i\\ -0.8747 + 0.0303i& 11.0915 \end{array}\displaystyle \right ], \\ Q_{2}=\left [ \textstyle\begin{array}{c@{\quad}c} 5.0515 & -1.0052 - 0.0420i\\ -1.0052 + 0.0420i & 12.9334 \end{array}\displaystyle \right ], \\ W_{1}=\left [ \textstyle\begin{array}{c@{\quad}c} 57.8416 & - 0.8040i\\ + 0.8040i& 57.8416 \end{array}\displaystyle \right ], \\ W_{2}=\left [ \textstyle\begin{array}{c@{\quad}c} 1.6820 & -2.9051 + 0.2216i\\ -2.9051 - 0.2216i& 17.7818 \end{array}\displaystyle \right ], \\ R_{1}=\left [ \textstyle\begin{array}{c@{\quad}c} 2.5652 & -0.1721 - 0.0130i\\ -0.1721 + 0.0130i& 3.4262 \end{array}\displaystyle \right ], \\ R_{2}=\left [ \textstyle\begin{array}{c@{\quad}c} 0.9093 & -0.0607 + 0.0400i\\ -0.0607 - 0.0400i& 1.4613 \end{array}\displaystyle \right ], \\ R=\left [ \textstyle\begin{array}{c@{\quad}c} 0.8406 + 0.5150i& 0.6126 - 0.1789i\\ 0.3399 + 0.9786i & -0.5699 + 0.7400i \end{array}\displaystyle \right ]. \end{gathered} $$

Hence, we have

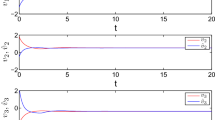
$$ K=P^{-1}R=\left [ \textstyle\begin{array}{c@{\quad}c} 0.2757 + 0.1880i& 0.1839 - 0.0444i\\ 0.0835 + 0.1932i & -0.0959 + 0.1344i \end{array}\displaystyle \right ]. $$

Moreover, it can be obtained from Corollary 1 that system (1) with the estimator gain K obtained is globally asymptotically stable. The simulation results are shown in Figs. 1, 2, 3.

Figure 1
figure 1

The responses of state \(\operatorname{Re}(z_{1}(t))\), \(\operatorname{Re}(z_{2}(t))\) and its estimation

Full size image
Figure 2
figure 2

The responses of state \(\operatorname{Im}(z_{1}(t))\), \(\operatorname{Im}(z_{2}(t))\) and its estimation

Full size image
Figure 3
figure 3

Trajectories of the error states \(e_{1}(t)\)

Full size image

5 Conclusion

In this paper, the state estimation problem of complex-valued memristive neural networks with time-varying delays has been investigated for the first time. Based on Lyapunov stability theory and the matrix inequality techniques, a sufficient delay-dependent condition has been obtained to ensure the existence of the desired state estimator for the system addressed. In the end, an example has been given to illustrate the effectiveness of our results.