1 Introduction

At 1963, E.N. Lorenz presented the first chaotic system, now called the Lorenz chaotic attractor, which can be formulated as follows [1]:

$$ \textstyle\begin{cases} \dot{X}=\sigma (Y-X), \\ \dot{Y}=\rho X-Y-XZ, \\ \dot{Z}=-rZ+XY. \end{cases} $$
(1.1)

Since then, chaotic attractors attract more and more interest, and many other chaotic attractors have been given, such as Rössler system [2], Chua’s circuit [3], Chen system [4], Lü system [5], T system [6], and so on. Various dynamical behaviors of chaotic systems are revealed. Recently, there has been increasing attention about hidden attractors because of their rich but distinctive dynamical behaviors [7–15]. Chaos becomes more and more popular notion in the nonlinear science.

The main purpose of the article is to study the Hopf bifurcation of the following system given by [16]:

$$ \textstyle\begin{cases} \dot{x}=y, \\ \dot{y}=mx-ny-mxz-px^{3}, \\ \dot{z}=-az+bx^{2}, \end{cases} $$
(1.2)

where \(m,n,p,a,b\in \textbf{R}\) are parameters of system (1.2). The Lorenz system (1.1) can be transformed into system (1.2) by the change of variables \(x= \sqrt{2}X\), \(y=\sqrt{2}(X+\frac{Y}{\sigma })\), \(z=\frac{X^{2}}{\sigma }+(\rho -1)Z\) with \(a=-r\), \(b=\frac{2\sigma -r}{\sigma (\rho -1)}\), \(m= \sigma (\rho -1)\), \(p=1\), \(n=\sigma +1\). System (1.2) was introduced recently in [16] as the extended Lorenz system. Few results are reported on this system so far. In [16], the authors studied the birth of the Lorenz attractor in the extended Lorenz system and revealed relations between the extended Lorenz system and the Lorenz system.

The extended Lorenz system (1.2) is invariant under the transformation \((x,y,z)\rightarrow (-x,-y,z)\). So the orbits of system (1.2) are symmetric with respect to the z-axis. The origin \(O (0, 0, 0)\) is an equilibrium of system (1.2) regardless the values of the parameters. If \(ap+bm\neq 0\) and \(\frac{am}{ap+bm} \geq 0\), then the system has two other equilibria \(A (x_{0}, 0, z_{0})\) and \(A'(-x_{0}, 0, z_{0})\) with \(x_{0} = \sqrt{\frac{am}{ap+bm} }\) and \(z_{0} = \frac{bm}{ap+bm}\). The Jacobian matrix at O is \(\left({\scriptsize\begin{matrix}{} 0 & 1 & 0 \cr m & -n & 0 \cr 0 & 0 & -a\end{matrix}} \right)\) with the eigenvalues \(\frac{1}{2}\sqrt{n^{2}+4m}- \frac{1}{2}n\), \(-\frac{1}{2}\sqrt{n^{2}+4m}-\frac{1}{2}n\), and −a. This implies that, for \(m<-\frac{n^{2}}{4}\), the Jacobian matrix has a pair of complex eigenvalues. If additionally we assume that \(a>0\), then the system may undergo a Hopf bifurcation around O at the critical value \(n=0\).

This paper is organized as follows. In Section 2, we analyze the Hopf bifurcation of the extended Lorenz system at the origin. In Section 3, we study the Hopf bifurcation at the nontrivial equilibria A and \(A'\). Numerical simulations illustrate the validity of the theoretical analysis in the last sections.

2 Hopf bifurcation of the origin

In this section, we analyze the Hopf bifurcation at the origin of coordinates.

Theorem 1

If

$$ n=0,\qquad m< 0,\qquad a>0, $$

then the extended Lorenz system (1.2) undergoes Hopf bifurcation at the origin. When \(b<0\), the Hopf bifurcation is supercritical, whereas if \(b>0\), then the Hopf bifurcation is subcritical. When \(b=0\), the extended Lorenz system (1.2) has no limit cycles near the origin of coordinates.

Proof

Whenever \(m<-\frac{n^{2}}{4}\), system (1.2) has a pair of conjugate complex eigenvalues

$$\begin{aligned}& \lambda_{1}:=-\frac{1}{2}n+\frac{1}{2}i\sqrt{- \bigl(n^{2}+4m\bigr)},\qquad \lambda_{2}:=- \frac{1}{2}n-\frac{1}{2}i\sqrt{-\bigl(n^{2}+4m\bigr)}, \end{aligned}$$

and a real eigenvalue \(\lambda_{3}:=-a\). Hence, system (1.2) has a simple pair of purely imaginary eigenvalues as \(n=0\) and no other eigenvalues with zero real parts since \(a\neq 0\). Therefore, condition (H1) of Theorem 3.4.2 in [17], pp. 151-152, is satisfied. Next, it is obvious that

$$\begin{aligned} \frac{\mathrm{d} \operatorname{Re}(\lambda_{1})}{\mbox{d}n} \bigg| _{n=0}=-\frac{1}{2}< 0, \end{aligned}$$

so that condition (H2) of Theorem 3.4.2 in [17], pp. 151-152, is also satisfied.

We further compute the first Lyapunov coefficient.

By applying the linear change

$$\begin{aligned} \left ( \textstyle\begin{array}{@{}c@{}} x \\ y \\ z \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1 & 0 & 0 \\ -\frac{1}{2}n & -\frac{1}{2}\sqrt{-n^{2}-4m} & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} u \\ v \\ w \end{array}\displaystyle \right ) \end{aligned}$$

we transform system (1.2) into

$$\begin{aligned} \left ( \textstyle\begin{array}{@{}c@{}} \dot{u} \\ \dot{v} \\ \dot{w} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -\frac{1}{2}n & -\frac{1}{2}\sqrt{-n^{2}-4m} & 0 \\ \frac{1}{2}\sqrt{-n^{2}-4m} & -\frac{1}{2}n & 0 \\ 0 & 0 & -a \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} u \\ v \\ w \end{array}\displaystyle \right ) + \left ( \textstyle\begin{array}{@{}c@{}} 0 \\ \frac{2pu^{3}+2muw}{\sqrt{-n^{2}-4m}} \\ bu^{2} \end{array}\displaystyle \right ) . \end{aligned}$$

Moreover, let \(\eta =u+i\,v\), where \(i^{2}=-1\), from which it follows that \(\bar{\eta }=u-i\,v\), \(u=\frac{\eta +\bar{\eta }}{2}\), and \(v=\frac{\eta -\bar{\eta }}{2\,i}\). After a simple calculation, we have

$$ \begin{aligned} &\dot{\eta }=\biggl(-\frac{1}{2}n+\frac{i}{2} \sqrt{-n^{2}-4m}\biggr)\eta + \frac{i}{\sqrt{-n ^{2}-4m}}\biggl( \frac{p}{4}(\eta +\bar{\eta })^{3}+mw(\eta +\bar{\eta })\biggr), \\ &\dot{w}=-aw+\frac{b}{4}\bigl(\eta^{2}+2\eta \bar{\eta }+\bar{ \eta }^{2}\bigr). \end{aligned} $$
(2.1)

When \(n=0\), \(m=-\omega^{2}<0\) (\(\omega >0\) is an arbitrary real constant), and \(a\ne 0\), system (2.1) satisfies the center manifold theorem [18]. Thus, the center manifold \(W^{c}\) has the representation

$$\begin{aligned} & w=W(\eta ,\bar{\eta })=\frac{1}{2} w_{20}\eta^{2} + w_{11}\eta \bar{ \eta }+\frac{1}{2}w_{02}\bar{\eta }^{2} + O\bigl(\vert \eta \vert ^{3}\bigr) \end{aligned}$$
(2.2)

with unknown \(w_{ij}\in C\). Since W must be real, \(w_{11}\) is real, and \(w_{20}=\bar{w}_{02}\).

Let us rewrite system (2.1) at \(n=0\):

$$ \textstyle\begin{cases} \dot{\eta }=\sqrt{-m} \eta i+ \frac{i}{2\sqrt{-m}}(\frac{p}{4}( \eta +\bar{\eta })^{3}+mw(\eta +\bar{\eta })), \\ \dot{w}=-aw+\frac{b}{4}(\eta^{2}+2\eta \bar{\eta }+\bar{\eta }^{2}). \end{cases} $$
(2.3)

Substituting (2.2) into (2.3)2 and using (2.3)1, we get, at the quadratic level,

$$ (a+2i\sqrt{-m})w_{20}=\frac{b}{2}, \qquad aw_{11}= \frac{b}{2}, \qquad (a-2i \sqrt{-m})w_{02}=\frac{b}{2}. $$

Thus,

$$ w_{20}=\frac{b}{2(a+2i\sqrt{-m})},\qquad w_{11}=\frac{b}{2a}, \qquad w_{02}=\frac{b}{2(a-2i \sqrt{-m})}, $$

and the center manifold \(W^{c}\) is

$$\begin{aligned} w=W(\eta ,\bar{\eta })=\frac{b}{4(a+2i\sqrt{-m})}\eta^{2} + \frac{b}{2a} \eta \bar{\eta }+\frac{b}{4(a-2i\sqrt{-m})}\bar{\eta } ^{2} + O\bigl(\vert \eta \vert ^{3}\bigr). \end{aligned}$$
(2.4)

Now the restriction of (2.3) to its center manifold, up to cubic terms, can be written as follows:

$$\begin{aligned}& \dot{\eta }=i\sqrt{-m}\eta +\frac{i}{\sqrt{-m}}\biggl[\biggl(\frac{p}{4}+ \frac{b}{4(a+2i \sqrt{-m})}\biggr)\eta^{3}+\biggl(\frac{3p}{4}+ \frac{b}{2a}+\frac{b}{4(a+2i \sqrt{-m})}\biggr)\eta^{2} \bar{\eta} \\& \hphantom{\dot{\eta }=}{}+\biggl(\frac{3p}{4}+\frac{b}{2a}+\frac{b}{4(a-2i\sqrt{-m})} \biggr)\eta \bar{ \eta }^{2}+\biggl(\frac{p}{4}+ \frac{b}{4(a-2i\sqrt{-m})}\biggr) \bar{\eta }^{3}\biggr]+ \cdots , \end{aligned}$$
(2.5)

where we omit higher-order terms when considering the Hopf bifurcation.

Now we can compute the first Lyapunov coefficient. There are three methods to compute the Lyapunov constant: the Poincaré map, the Poincaré formal series, and the norm form method. According to Han’s book [19], pp. 25-40, these three methods are equivalent to each other, and the Lyapunov constants obtained by the methods are the same up to a positive constant. Here we adopt the formal series method because it is easier to compute by algebra system.

Using the relationship \(u=\frac{\eta +\bar{\eta }}{2}\) and \(v=\frac{ \eta -\bar{\eta }}{2\,i}\), we have

$$ \textstyle\begin{cases} \dot{u}=-\sqrt{-m}v, \\ \dot{v}=\sqrt{-m}u+\frac{2(a^{3}p+a^{2}b-4amp-2bm)}{\sqrt{-m}(a ^{3}-4am)}u^{3}+\frac{4b}{a^{2}-4m} u^{2}v+ \frac{4b\sqrt{-m}}{a^{3}-4am} uv^{2}+O(r^{4}), \end{cases} $$
(2.6)

where \(r=\sqrt{u^{2}+v^{2}}\).

By using the Maple program edited according to the formal series algorithm we obtain the first Lyapunov constant

$$\begin{aligned} L_{1}= \frac{b}{2\sqrt{-m}(a^{2}-4m)} \end{aligned}$$
(2.7)

and the formal series

$$\begin{aligned}& F={u}^{2}+{v}^{2}+{\frac{ ( {a}^{3}p+{a}^{2}b-4\,amp-2\,bm ) {u}^{4}}{ma ( {a}^{2}-4\,m ) }} \\& \hphantom{F=}{}+{\frac{b{u}^{3}v}{ \sqrt{-m} ( {a}^{2}-4\,m ) }}-{\frac{bu{v}^{3}}{\sqrt{- m} ( {a}^{2}-4\,m ) }}-{\frac{2\,b{v}^{4}}{{a}^{2}-4\,m}} +\cdots . \end{aligned}$$

Since \(m<0\), the denominator of (2.7) is positive, so \(L_{1}\) and the parameter b have the same sign. Thus, we have the result of the second part of Theorem 1.

When \(b=0\), the center manifold of system (1.2) is \(w=0\), and the restriction of system (1.2) in the center manifold becomes

$$ \dot{x}=y,\qquad \dot{y}=mx-ny-px^{3}. $$
(2.8)

If \(n=0\), then system (2.8) is a Hamilton system with the Hamiltonian function \(H(x,y)=\frac{1}{2}y^{2}-\frac{m}{2}x^{2}+ \frac{p}{4}x^{4}\). There exists a family of periodic orbits given by \(L_{h}: H(x,y)=h\), \(h\in (0,+\infty )\). Because the limit cycle is an isolated periodic orbit, system (2.8) and, equivalently, system (1.2) have no limit cycles in this case. If \(n\neq 0\), then limit cycles also do not exist because \(\dot{H}=-ny^{2}\) is a constant function. The last part of Theorem 1 is proved. □

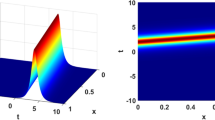
To illustrate the conclusion, we show in Figure 1 the limit cycle in the phase space for \(a=1\), \(b=-1\), \(m=-1\) (\(n=0\), \(p=2\)).

Figure 1
figure 1

The limit cycle of the extended Lorenz system; \(\pmb{a=1}\) , \(\pmb{b=-1}\) , \(\pmb{m=-1}\) .

Full size image

3 Hopf bifurcation of the nontrivial equilibria

Now we analyze the Hopf bifurcation at the nontrivial equilibria \(A'(-x_{0}, 0, z_{0})\) and \(A (x_{0}, 0, z_{0})\), where \(x_{0} = \sqrt{\frac{am}{ap+bm} }\) and \(z_{0} = \frac{bm}{ap+bm}\). Due to the symmetry, we only analyze the equilibrium \(A (x_{0}, 0, z_{0})\).

First, we move the equilibrium to the origin of the coordinates under the following change of variables:

$$ X=x-x_{0},\qquad Y=y,\qquad Z=z-z_{0}. $$

The extended Lorenz system (1.2) thus becomes:

$$ \textstyle\begin{cases} \dot{X}=Y, \\ \dot{Y}=-\frac{2amp}{ap+bm}X-nY-mx_{0}Z-3px_{0}X^{2}-mXZ-pX^{3}, \\ \dot{Z}=2bx_{0}X-aZ+bX^{2}. \end{cases} $$
(3.1)

The Jacobian matrix of the linearization of system (3.1) at the origin is

$$\begin{aligned} \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 1 & 0 \\ -\frac{2amp}{ap+bm} & -n & -mx_{0} \\ 2bx_{0} & 0 & -a \end{array}\displaystyle \right ) \end{aligned}$$

with the characteristic equation

$$\begin{aligned} P(\lambda )\equiv \lambda^{3}+a_{1}\lambda^{2}+a_{2} \lambda +a_{3}=0, \end{aligned}$$
(3.2)

where

$$ a_{1}=a+n,\qquad a_{2}=an+\frac{2amp}{ap+bm},\qquad a_{3}=2am. $$

When we consider the Hopf bifurcation of a system at an equilibrium, we hope that the Jacobian matrix of the linear part of the system at the equilibrium has a pair of purely imaginary eigenvalues and no other eigenvalues with zero real part. As to three-dimensional system, this means that the characteristic polynomial of the Jacobian matrix should be formulated as \(P(\lambda )=(\lambda +p_{1})(\lambda^{2}+p_{2})\) with \(p_{1}\neq 0\) and \(p_{2}>0\). Expanding this form, we know that \(p_{1}\) and \(p_{2}\) are the coefficients at \(\lambda^{2}\) and λ, respectively, and the constant term of the polynomial is \(p_{1}p_{2}\). At this moment, the three eigenvalues of the Jacobian matrix are \(\lambda_{1}=-p_{1}\) and \(\lambda_{2,3}=\pm i \sqrt{p_{2}}\) [20]. By this fact we have the following proposition.

Proposition 1

The polynomial (3.2) has two purely imaginary roots if and only if \(a_{1}a_{2}=a_{3}\), \(a_{1}\neq 0\), and \(a_{2}>0\), that is,

$$\begin{aligned} a+n\neq 0, \qquad an+\frac{2apm}{ap+bm}>0,\qquad p=\frac{2abm^{2}}{2amn+ a^{3} n+a^{2} n^{2}}. \end{aligned}$$
(3.3)

In this case, the roots are \(\lambda_{1}=-a-n\) and \(\lambda_{2,3}= \pm i\omega \), where \(\omega =\sqrt{an+\frac{2amp}{ap+bm}}\).

We choose the parameter p as the bifurcation parameter. Setting \(\lambda =\lambda (p)\) and applying the implicit function theorem to (3.2), we have \(\frac{d\lambda }{dp}=-\frac{\frac{dP}{dp}}{\frac{dP}{d \lambda }}\) and

$$\begin{aligned} \operatorname{Re} \biggl( \frac{d\lambda }{dp}\bigg|_{\lambda =i\omega ,p=\frac{2abm^{2}}{2amn+a ^{3}n+a^{2} n^{2}}} \biggr) = \frac{an^{2}( 2m+a^{2}+an)^{2}}{b(an+2m)(anL+2mn ^{3}+2a^{3}m+4am^{2})}\neq 0 \end{aligned}$$

whenever \(an\neq 0\) and \(2m+a^{2}+an\neq 0\), where \(L=8am+a^{3}+4a ^{2}n+8mn+4a n^{2}+n^{3}\).

Next, we computer the first Lyapunov constant of system (3.1).

We consider system (3.1) at the critical parameter values (3.3) and perform the linear change

$$\begin{aligned} \left ( \textstyle\begin{array}{@{}c@{}} X \\ Y \\ Z \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1 & 0 & 1 \\ 0 & \omega & -a-n \\ 2aqx_{0} & -2\omega qx_{0} & -2\frac{b}{n}x_{0} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} U \\ V \\ W \end{array}\displaystyle \right ) , \end{aligned}$$

where \(q=\frac{b}{a^{2}+\omega^{2}}\). Then system (3.1) becomes

$$\begin{aligned} \left ( \textstyle\begin{array}{@{}c@{}} \dot{U} \\ \dot{V} \\ \dot{W} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & -\omega & 0 \\ \omega & 0 & 0 \\ 0 & 0 & -a-n \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} U \\ V \\ W \end{array}\displaystyle \right ) + \left ( \textstyle\begin{array}{@{}c@{}} 0 \\ G(U,V,W) \\ H(U,V,W) \end{array}\displaystyle \right ) , \end{aligned}$$
(3.4)

where

$$\begin{aligned}& G(U,V,W)={}-(3px_{0}+2amqx_{0})U^{2}+2mq\omega x_{0}UV \\& \hphantom{G(U,V,W)=}{} -\biggl(6px_{0}+2amq x_{0}- \frac{2bmx_{0}}{n}\biggr)UW \\& \hphantom{G(U,V,W)=}{}+2mq\omega x_{0}VW-\biggl(3px_{0}- \frac{2bmx_{0}}{n}\biggr)W^{2} \\& \hphantom{G(U,V,W)=}{}-pU^{3}-3pU^{2}W-3pUW ^{2}-pW^{3}, \\& H(U,V,W)=b\bigl(U^{2}+2UW+W^{2}\bigr). \end{aligned}$$

Introduce \(\xi =U+iV\), \(\bar{\xi }=U-iV\), where \(i^{2}=-1\). Then \(U=\frac{\xi +\bar{\xi }}{2}\) and \(V=\frac{\xi -\bar{\xi }}{2i}\). We transform system (3.4) into the complex form

$$\begin{aligned} \left \{ \textstyle\begin{array}{ll} \dot{\xi }=\omega \xi i+g_{1}(\xi ,\bar{\xi },W)+ig_{2}(\xi ,\bar{ \xi },W), \\ \dot{W}=-(a+n)W+h(\xi ,\bar{\xi },W), \end{array}\displaystyle \right . \end{aligned}$$
(3.5)

where

$$\begin{aligned}& g_{1}(\xi ,\bar{\xi },W) = \frac{1}{2}\omega mqx_{0}{ \xi }^{2}-\frac{1}{2}\omega \,mqx_{0} \overline{ \xi }^{2}-\omega mqx_{0}\xi \,W+\omega \,mqx_{{0}} \overline{\xi }W, \\& g_{2}(\xi ,\bar{\xi },W) = \biggl( -\frac{3}{4}px_{0}- \frac{1}{2}\,am\omega \,qx_{0}\biggr) {\xi }^{2}+ \biggl( - \frac{3}{4}\,px_{0}-\frac{1}{2}\,am\omega \,qx_{{0}}\biggr)\overline{\xi } ^{2} \\& \hphantom{g_{2}(\xi ,\bar{\xi },W) =}{} +\biggl(2{\frac{bmx_{0}}{n}}-3px_{0} \biggr) {W}^{2}+ \biggl( am\omega \,qx_{0}- \frac{3}{2} \,px_{0}\biggr) \xi \,\overline{\xi } \\& \hphantom{g_{2}(\xi ,\bar{\xi },W) =}{} +\biggl({\frac{bmx_{0}}{n}}-3\,px_{0}-amqx_{0} \biggr) \xi \,W+ \biggl( {\frac{bmx_{ {0}}}{n}}-3\,px_{{0}}-amqx_{{0}} \biggr) \overline{\xi }W \\& \hphantom{g_{2}(\xi ,\bar{\xi },W) =}{} -\frac{1}{8} p \xi^{3}-\frac{1}{8} p \bar{\xi }^{3}- p W^{3}- \frac{3}{8} p \xi^{2} \bar{\xi }-\frac{3}{8} p \xi \bar{\xi }^{2} \\& \hphantom{g_{2}(\xi ,\bar{\xi },W) =}{} -\frac{3}{4} p W \xi^{2}-\frac{3}{4} p W \bar{\xi }^{2}-\frac{3}{2} p W^{2} \xi - \frac{3}{2} p W^{2} \bar{\xi }-\frac{3}{2} p W \xi \bar{ \xi }, \\& h(\xi ,\bar{\xi },W) = \frac{1}{4}b\bigl( {\xi }^{2}+2\xi \overline{\xi }+\overline{\xi }^{2}+4 \xi W+4\overline{\xi }W+4W^{2}\bigr). \end{aligned}$$

The center manifold \(W^{c}\) now has the representation

$$\begin{aligned} W=W(\xi ,\bar{\xi },W)=\frac{1}{2} W_{20}\xi^{2} + W_{11}\xi \bar{ \xi }+\frac{1}{2}W_{02}\bar{\xi }^{2} + O\bigl(\vert \xi \vert ^{3}\bigr). \end{aligned}$$
(3.6)

Thus, we have

$$\begin{aligned} \dot{W}= W_{20}\xi \dot{\xi} + W_{11}\dot{\xi} \bar{\xi }+ W_{11} \xi \dot{\bar{\xi }}+W_{02}\bar{\xi }\dot{\bar{\xi }} + O\bigl(\vert \xi \vert ^{3}\bigr). \end{aligned}$$

Substituting equation (3.5)1 into the last formula, we get

$$\begin{aligned} \dot{W}=W_{20}\omega i \xi^{2}-W_{02}\omega i \bar{\xi }^{2} + O\bigl(\vert \xi \vert ^{3}\bigr). \end{aligned}$$

According to equation (3.5)2, the differential of W reads

$$\begin{aligned} \dot{W} =&\biggl(\frac{1}{4}b-\frac{1}{2}aW_{20}- \frac{1}{2}nW_{20}\biggr)\xi^{2} +\biggl( \frac{1}{4}b-\frac{1}{2}aW_{02}-\frac{1}{2}nW_{02} \biggr)\bar{\xi }^{2} \\ &{}+\biggl(\frac{1}{2}b-aW_{11}-nW_{11}\biggr)\xi \bar{\xi }+ O\bigl(\vert \xi \vert ^{3}\bigr). \end{aligned}$$

The two formulas are identical, and we equate the coefficients to get

$$\begin{aligned} W_{20}=\frac{b}{2(a+n)+4\omega i}, \qquad W_{11}=\frac{b}{2(a+n)},\qquad W_{02}=\frac{b}{2(a+n)-4\omega i}. \end{aligned}$$

Thus, we obtain the representation of center manifold \(W^{c}\)

$$\begin{aligned} W=W(\xi ,\bar{\xi },W)=\frac{b\xi^{2}}{4(a+n)+8\omega i} +\frac{b \xi \bar{\xi }}{2(a+n)}+\frac{b\bar{\xi }^{2}}{4(a+n)-8\omega i} + O\bigl(\vert \xi \vert ^{3}\bigr) \end{aligned}$$
(3.7)

and the restriction of system (3.5) to the center manifold

$$\begin{aligned} &\dot{\xi }=\omega \xi i+g_{20}\xi^{2}+g_{11}\xi \bar{\xi }+g_{02}\bar{ \xi }^{2}+g_{30} \xi^{3}+g_{21}\xi^{2}\bar{\xi }+g_{12}\xi \bar{\xi } ^{2}+ g_{03}\bar{\xi }^{3}+O\bigl(\vert \xi ,\bar{\xi } \vert ^{4}\bigr), \end{aligned}$$

where

$$\begin{aligned}& g_{20} =\frac{1}{2}\omega mqx_{0}-i \frac{1}{2}a mqx_{0}-i\frac{3}{4}px_{0}, \\& g_{11}=-i a m q x_{0}-i\frac{3}{2}px_{0}, \\& g_{02}=-\frac{1}{2}\omega mqx_{0}-i \frac{1}{2}a mqx_{0}-i\frac{3}{4}px_{0}, \\& g_{30}={\frac{\omega \,bmqx_{{0}}}{4(a+n+2\,i\omega )}-\frac{\,iabmqx_{ {0}}}{4(a+n+2\,i\omega )}}+{\frac{i{b}^{2}mx_{{0}}}{4n(a+n+2\,i\omega ) }}-{ \frac{3\,ibpx_{{0}}}{4(a+n+2\,i\omega )}}-\frac{1}{8}\,i p, \\& g_{21}={\frac{\omega \,bmqx_{{0}}}{4(a+n+2\,i\omega )}-\frac{\,iabmqx_{ {0}}}{4(a+n+2\,i\omega )}}+{\frac{i{b}^{2}mx_{{0}}}{4n(a+n+2\,i\omega ) }}-{ \frac{3\,ibpx_{{0}}}{4(a+n+2\,i\omega )}}-\frac{3}{8}\,i p \\& \hphantom{g_{21}=}{}+{\frac{\,i{b}^{2}mx_{{0}}}{2n ( a+n ) }}+{\frac{\omega \,bmqx_{{0}}}{2(a+n)}}-{ \frac{3\,ibpx_{{0}}}{2(a+n)}}-{\frac{iabmqx _{{0}}b}{2(a+n)}}, \\& g_{12}=-\frac{\omega \,bmqx_{{0}}}{4(-a-n+2\,i\omega )}+\frac{\,iabmqx_{ {0}}}{4(-a-n+2\,i\omega )}-{\frac{i{b}^{2}mx_{{0}}}{4n(-a-n+2\,i \omega ) }}+{ \frac{3\,ibpx_{{0}}}{4(-a-n+2\,i\omega )}} \\& \hphantom{g_{12}=}{}-\frac{3}{8}\,i p+{\frac{\,i{b}^{2}mx_{{0}}}{2n ( a+n ) }}- { \frac{\omega \,bmqx_{{0}}}{2(a+n)}}-{\frac{3\,ibpx_{{0}}}{2(a+n)}}- {\frac{iabmqx_{{0}}b}{2(a+n)}}, \\& g_{03}={\frac{\omega \,bmqx_{{0}}}{4(-a-n+2\,i\omega )}+\frac{\,iabmqx_{ {0}}}{4(-a-n+2\,i\omega )}}-{\frac{i{b}^{2}mx_{{0}}}{4n(-a-n+2\,i \omega ) }} \\& \hphantom{g_{03}=}{}+{\frac{3\,ibpx_{{0}}}{4(-(a+n)+2\,i\omega )}}-\frac{1}{8}\,i p. \end{aligned}$$

Returning to the real form, we have

$$\begin{aligned} \left \{ \textstyle\begin{array}{ll} \dot{U}=-\omega V, \\ \dot{V}=\omega U+k_{20}U^{2}+k_{11}UV+k_{30}U^{3}+k_{21}U^{2}V+k_{12}UV ^{2}+k_{03}V^{3}+O(r^{4}), \end{array}\displaystyle \right . \end{aligned}$$
(3.8)

where the coefficients \(k_{ij}\) are given as follows:

$$\begin{aligned}& k_{20}=-(2amq+3p)x_{0},\qquad k_{11}=2qm\omega x_{0}, \\& k_{30}=-{\frac{1}{n ( a+n ) ( {a}^{2}+2\,an+{n}^{2}+4\, {\omega }^{2} ) }}\bigl(2\,{a}^{3}bmnqx_{{0}}+{a}^{3}pn+4 \,{a}^{2}mqx _{{0}}b{n}^{2} \\& \hphantom{k_{30}=}{}+6\,{a}^{2}px_{{0}}bn-2\,{b}^{2}mx_{{0}}{a}^{2}+3 \,{a}^{2}p{n}^{2}+4 \,ab mn{\omega }^{2}qx_{{0}}+4 \,apn{\omega }^{2}-4\,a{b}^{2}mnx_{ {0}} \\& \hphantom{k_{30}=}{}+2\,amqx_{{0}}b{n}^{3}+3\,ap{n}^{3}+12 \,apx_{{0}}b{n}^{2}+4\,p{n} ^{2}{\omega }^{2}-4\,{b}^{2}mx_{{0}}{\omega }^{2}+12 \,bn{\omega }^{2}px _{{0}} \\& \hphantom{k_{30}=}{}-2\,{b}^{2}m{n}^{2}x_{{0}}+p{n}^{4}+6 \,px_{{0}}b{n}^{3}\bigr), \\& k_{21}=-{\frac{2\omega \,bx_{{0}} ( {a}^{2}mqn+6\,apn-2\,abm+6\,p{n} ^{ 2}-2\,mqn{\omega }^{2}-2\,bmn-mq{n}^{3} ) }{n ( a+n ) ( {a}^{2}+2\,an+{n}^{2}+4\,{\omega }^{2} ) }}, \\& k_{12}={\frac{4{\omega }^{2}bx_{{0}} ( bm-3\,pn+mq{n}^{2} ) }{n ( a+n ) ( {a}^{2}+2\,an+{n}^{2}+4\,{\omega }^{2} ) }},\qquad k_{03}={\frac{4{\omega }^{3}bmqx_{{0}}}{ ( a+n ) ( {a}^{2} +2\,an+{n}^{2}+4\,{\omega }^{2} ) }}. \end{aligned}$$

By using the formal series method we find the first Lyapunov constant

$$\begin{aligned}& L_{1}=\frac{x_{0}(K_{1}+K_{2} x_{0})}{4 n\omega (a+n)((a+n)^{2}+4{\omega } ^{2})}, \end{aligned}$$

where

$$\begin{aligned}& K_{1}=bmn^{3}q\omega -6bpn^{2}\omega +8bqmn \omega^{3}-6abnp\omega +2nmb ^{2}\omega -bqmna^{2} \omega +2ab^{2}m\omega , \\& K_{2}=2am^{2}n^{4}q^{2}+3mn^{4}pq+9amn^{3}pq+6{a}^{2}m^{2} n^{3}{q}^{2}+9 {a}^{2}mn^{2}pq+6{a}^{3}{m}^{2}n^{2}{q}^{2} \\& \hphantom{K_{2}=}{}+12mn^{2}pq{\omega }^{2}+8am^{2}n^{2}{q}^{2}{ \omega }^{2}+3mn pq {a}^{3} \\& \hphantom{K_{2}=}{}+12amnpq{\omega }^{2}+2nm^{2}a^{4}{q}^{2}+8n{m}^{2}a^{2}{q} ^{2}{\omega }^{2}. \end{aligned}$$

Therefore, we have the following:

Theorem 2

If \(L_{1}\neq 0\), then the extended Lorenz system (1.2) undergoes Hopf bifurcation at the equilibrium A. When \(L_{1}<0\), the Hopf bifurcation is supercritical, and system has a stable limit cycle. When \(L_{1}>0\), the Hopf bifurcation is subcritical, and system has an unstable limit cycle.

Due to the symmetry, the same result can be obtained at the other nontrivial equilibrium \(A'\). So we find two limit cycles around the two equilibria A and \(A'\), respectively.

To illustrate this conclusion, we show in Figure 2 the limit cycle around the equilibrium A in the phase space for \(a=1\), \(b=2\), \(m=3\), \(n=2\), \(p=2\). The initial value is (\(0.7124, 0.7124, 0.85\)). In this case, the first Lyapunov constant is \(L_{1}=0.6826072569\).

Figure 2
figure 2

The limit cycle around \(\pmb{A(x_{0},0,z_{0})}\) of the extended Lorenz system, \(\pmb{a=1}\) , \(\pmb{b=2}\) , \(\pmb{m=3}\) , \(\pmb{n=2}\) , \(\pmb{p=2}\) .

Full size image

4 Conclusion

In this paper, we analyze the existence of Hopf bifurcation in an extended Lorenz system. We show that a nondegenerate Hopf bifurcation arises at each of the three equilibrium points, the origin and two other nontrivial symmetric equilibria. We find totally three limit cycles, one for each of the equilibria. In each case, we reduce the system to a two-dimensional center manifold and compute the first Lyapunov constant \(L_{1}\). Due to the complex form of the analytic expression of the Lyapunov constant and the multitude of parameters, we cannot fully analyze the sign of \(L_{1}\) at the nontrivial equilibria. We illustrate the results by numerical simulation using Matlab R2012a for some particular parameters.