Introduction

One of the models to address the dispersive optical solitons is the Lakshmanan–Porsezian–Daniel (LPD) model with Kerr law of nonlinear refractive index [1,2,3]. A wide range of results have been recovered for the LPD model in the past [4,5,6]. To touch base on these works, LPD equation has been integrated using a large number of integration algorithms [7,8,9]. The model was later studied with power-law of self-phase modulation [10,11,12]. The conservation laws were identified [13]. The perturbed version of LPD model was also integrated using the semi-inverse variation when the light intensity was taken to be arbitrary [14,15,16]. Subsequently, the cubic–quartic version of LPD equation was closely looked upon with Kerr and power laws of nonlinear refractive index [17,18,19]. Their soliton solutions in presence of perturbation terms for arbitrary refractive index was also reported [20,21,22]. Thereafter, the LPD equation was taken up for nonlinear chromatic dispersion that yielded quiescent optical solitons [23,24,25]. In this context the two forms of self-phase modulation were considered namely the Kerr law and the power law [26,27,28]. In addition to the aforementioned analytical approaches, the model was also studied numerically to retrieve the bright and dark optical solitons [29,30,31,32,33]. The applied methodology was the Laplace-Adomian decomposition. The current paper moves ahead and addresses the LPD equation from a totally different perspective. The bifurcation analysis of the model will be carried out and the recovered bright and dark soliton solutions will be revealed and exhibited. The intermediary functions that emerged are the cnoidal and snoidal waves. The details of the analysis are displayed in the rest of the paper after a succinct revisitation to the model.

In the current work, the corresponding LPD equation with the nonlinear CD, which can be expressed in its dimensionless form:

$$\begin{aligned} \begin{aligned}&iu_{t}+a_{1}u_{xx}+a_{2}|u|^{2}u-a_{3}u_{xxxx}=\beta _{1}(u_{x})^{2}u^{*}\\&\quad +\beta _{2}|u_{x}|^{2}u+\beta _{3}|u|^{2}u_{xx}+\beta _{4}u^{2}u^{*}_{xx}+r|u|^{4}u, \end{aligned} \end{aligned}$$
(1)

where \(u=u(x,t)\) is the complex-valued wave function, which represents the wave profile. x represents the normalized propagation and t denotes the retard time. The remaining coefficients are real valued and \(i^{2}=-1\). The coefficient \(a_{1}\) stands for the chromatic dispersion (CD). Nonzero constant \(a_{2}\) stands for the self-phase modulation stemming from the Kerr law for nonlinear refractive index. The coefficient \(a_{3}\) denotes the fourth-order dispersion (4OD) and nonzero constant r is associated with quintic nonlinearity. Nonzero constants \(\beta _{i}\) \((i=1..,4)\) represent the nonlinear dispersion and the related physical phenomena. Moreover, the power-law nonlinearity factor n denotes departure from the linear chromatic dispersion (CD). \(u_{t}\) stands for the linear temporal evolution of the soliton pulse. \(u_{x}\) and \(u_{xxxx}\) denotes the first-order and fourth-order spatial dispersions. Last but not the least, \(u^{*}\) and \(u^{*}_{xx}\) stand for the complex conjugates of the wave field and the CD, respectively. This system will be used to reveal stationary solitons.

Dynamical behaviors and phase portraits for model (1)

In order to construct the traveling wave solutions of the LPD model (1), we firstly decompose

$$\begin{aligned} u(x,t)=\Psi (x)e^{i\mu t}, \end{aligned}$$
(2)

where \(\Psi (x)\) denotes the real-valued function, which stands for the amplitude component of the stationary wave. The coefficient \(\mu\) represents the wave number of the solitons. Inserting (2) into (1) and transforming it to an ordinary differential equation

$$\begin{aligned} \begin{aligned}&a_{1}\Psi ^{3}(x)\Psi ''(x) +a_{2}\Psi ^{6}(x)+a_{3}\Psi ^{3}(x)\Psi ^{(4)}(x)\\&\quad -\Psi ^{4}(x)\left[ \mu +(\beta _{1}+\beta _{2})\{\Psi '(x)\}^{2}\right] -(\beta _{3}+\beta _{4})\Psi ^{5}(x)\Psi ''(x)\\&\quad -r\Psi ^{8}(x)=0. \end{aligned} \end{aligned}$$
(3)

For integrability, Equation (3) provides certain restrictions when the coefficients of its linearly independent functions are set to zero

$$\begin{aligned} a_{3}=0, \end{aligned}$$
(4)

along with

$$\begin{aligned} \beta _{1}+\beta _{2}=0, \end{aligned}$$
(5)

and

$$\begin{aligned} \beta _{3}+\beta _{4}=0. \end{aligned}$$
(6)

Depend on the above restrictions, this simplifies the LPD model (1) in the following form

$$\begin{aligned}{} & {} iu_{t}+a_{1}u_{xx}+a_{2}|u|^{2}u=\beta _{1}\left\{ (u_{x})^{2}u^{*}-|u_{x}|^{2}u \right\} \nonumber \\{} & {} \quad +\beta _{3}\{|u|^{2}u_{xx}-u^{2}u^{*}_{xx}\}+r|u|^{4}u. \end{aligned}$$
(7)

Therefore, the ordinary differential system given by Eq. (1) is transformed as follows

$$\begin{aligned} \begin{aligned} a_{1}\Psi ^{3}(x)\Psi ''(x) -\mu \Psi ^{4}(x)+a_{2}\Psi ^{6}(x)-r\Psi ^{8}(x)=0, \end{aligned} \end{aligned}$$
(8)

where \(\Psi '(x)\) and \(\Psi ''(x)\) stand for respectively the first-order and second-order dispersions of the soliton. Equation (8) can be rewritten in the following form

$$\begin{aligned} \begin{aligned} \Psi ''(x)+N_{1}\Psi (x)+N_{2}\Psi ^{3}(x)+N_{3}\Psi ^{5}(x)=0, \end{aligned} \end{aligned}$$
(9)

where the above constants are \(N_{1}=-\frac{\mu }{a_{1}}\), \(N_{2}=\frac{a_{2}}{a_{1}}\), \(N_{3}=-\frac{r}{a_{1}}\).

For Eq. (9), denote that \(\Psi '=p\), then (9) can be transformed as a plane dynamical system

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d\Psi }{dx}=p,\\ \frac{dp}{dx}=-N_{1}\Psi -N_{2}\Psi ^{3}-N_{3}\Psi ^{5}, \end{array}\right. } \end{aligned}$$
(10)

with the Hamiltonian system

$$\begin{aligned} H(\Psi ,p)=\frac{1}{2}p^{2}+\frac{N_{1}}{2}\Psi ^{2}+\frac{N_{2}}{4}\Psi ^{4}+\frac{N_{3}}{6}\Psi ^{6}=h. \end{aligned}$$
(11)

According to the Eq. (11), we deduce

$$\begin{aligned} p=\pm \sqrt{2(-\frac{N_{1}}{2}\Psi ^{2}-\frac{N_{2}}{4}\Psi ^{4}-\frac{N_{3}}{6}\Psi ^{6}+h)}. \end{aligned}$$
(12)

For convenience, denote \(G_{h}(\Psi )=-\frac{N_{1}}{2}\Psi ^{2}-\frac{N_{2}}{4}\Psi ^{4}-\frac{N_{3}}{6}\Psi ^{6}+h\), it is notable that \(G_{h}(0)=h\), \(G_{h}(\Psi _{1})=G_{h}(\Psi _{2})=h+h_{0}\), \(G_{h}(\Psi _{3})=G_{h}(\Psi _{4})=h-h_{1}\). Here, \(\Psi _{1}\), \(\Psi _{2}\), \(\Psi _{3}\) and \(\Psi _{4}\) are the real root of the function \(G_{h}(\Psi )\).

Here, we derive that

$$\begin{aligned} h_{0}=\frac{(N_{2}+\sqrt{N^{2}_{2}-4N_{1}N_{3}})(4N_{1}N_{3}- \sqrt{N^{2}_{2}-4N_{1}N_{3}}(\sqrt{N^{2}_{2}-4N_{1}N_{3}}-N_{2}))}{48N^{2}_{3}}<0, \end{aligned}$$
(13)

and

$$\begin{aligned} h_{1}=\frac{(\sqrt{N^{2}_{2}-4N_{1}N_{3}}-N_{2})(4N_{1}N_{3}+ \sqrt{N^{2}_{2}-4N_{1}N_{3}}(N_{2}-\sqrt{N^{2}_{2}-4N_{1}N_{3}}))}{48N^{2}_{3}}<0, \end{aligned}$$
(14)

where \(N^{2}_{2}-4N_{1}N_{3}>0\).

By using the bifurcation theory of planar differential system [6, 7], we know that

  1. (i)

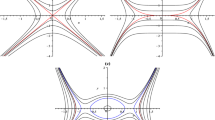
    If \(N^{2}_{2}-4N_{1}N_{3}<0\) \((N_{1}>0, N_{3}>0)\), it is notable that there exists only one equilibrium \(M_{0}(0,0)\), which represents the center point. The corresponding phase portraits is shown in Fig. 1a.

  2. (ii)

    If \(N^{2}_{2}-4N_{1}N_{3}<0\) \((N_{1}<0, N_{3}<0)\), we observe that there is only one equilibrium point \(M_{0}(0,0)\), which represents the saddle point. The corresponding phase portraits can be seen in Fig. 1b.

  3. (iii)

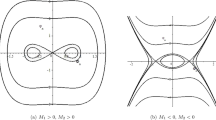
    If \(N_{1}>0\), \(N_{3}<0\), there are three equilibrium points \(M_{0}(0,0)\), \(M_{1}(\sqrt{\frac{N_{2}+\sqrt{N^{2}_{2}-4N_{1}N_{3}}}{-2N_{3}}},0)\) and \(M_{2}(-\sqrt{\frac{N_{2}+\sqrt{N^{2}_{2}-4N_{1}N_{3}}}{-2N_{3}}},0)\), which \(M_{0}\) stands for the center point, \(M_{1}\) and \(M_{2}\) represent the saddle points, respectively. The corresponding phase diagram is shown in Fig. 2a.

  4. (iv)

    If \(N_{1}<0\), \(N_{3}>0\), we derive that there exist three equilibrium points of system (10), which include \(M_{0}(0,0)\), \(M_{3}(\sqrt{\frac{-N_{2}+\sqrt{N^{2}_{2}-4N_{1}N_{3}}}{2N_{3}}},0)\) and \(M_{4}(-\sqrt{\frac{-N_{2}+\sqrt{N^{2}_{2}-4N_{1}N_{3}}}{2N_{3}}},0)\). We find that \(M_{0}\) denotes the saddle point, \(M_{3}\) and \(M_{4}\) represent the center points. The corresponding phase portraits can be seen in Fig. 2b.

Fig. 1
figure 1

The bifurcation phase portraits of system (10)

Full size image
Fig. 2
figure 2

The bifurcation phase portraits of system (10)

Full size image

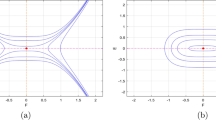
Case 1 From the situation (iii), we derive that there are two heteroclinic orbits connects two saddle points and a center point. With the help of the dynamical theory of differential systems [6, 7], we deduce the kink-shaped solitary wave solutions takes the form (See Fig. 3)

$$\begin{aligned} \begin{aligned} u_{1}(x,t)&=\pm \frac{\Xi _{1}\Xi _{2}\tanh [\Xi _{1}\sqrt{\frac{-N_{3}}{3} (\Xi ^{2}_{1}+\Xi ^{2}_{2})}(x-\xi _{0})]}{\sqrt{\Xi ^{2}_{2} +\Xi ^{2}_{1}\text{ sech}^{2}[\Xi _{1}\sqrt{\frac{-N_{3}}{3} (\Xi ^{2}_{1}+\Xi ^{2}_{2})}(x-\xi _{0})]}}\\&\quad \times \exp (i\mu t), \end{aligned} \end{aligned}$$
(15)

where \(\Xi _{1}=\sqrt{\frac{N_{2}+\sqrt{N^{2}_{2}-4N_{1}N_{3}}}{-2N_{3}}}\), \(\Xi _{2}=\sqrt{\frac{N_{2}-\sqrt{N^{2}_{2}-4N_{1}N_{3}}}{2N_{3}}}\) and \(\xi _{0}\) is the integral constant.

Fig. 3
figure 3

The portraits of u(x, t) in Eq. (15) at \(\Xi _{1}=1\), \(\Xi _{2}=2\), \(N_{3}=-3\), \(\xi _{0}=0\)

Full size image

Case 2 According to the case (iii), we find that the LPD system (1) exists the periodic wave solutions, which corresponding to the periodic orbit (see Fig. 2a). With the help of the dynamical theory of differential systems [6, 7], the periodic wave solutions of (1) takes the form

$$\begin{aligned} \begin{aligned} u_{2}(x,t)=\pm \frac{\Xi _{3}\Xi _{5}\text{ sn }\left[ \Xi _{4}\sqrt{\frac{-N_{3}}{3} (\Xi ^{2}_{3}+\Xi ^{2}_{5})}(x-\xi _{0}), \frac{\Xi _{3}}{\Xi _{4}}\sqrt{\frac{\Xi ^{2}_{4}+\Xi ^{2}_{5}}{\Xi ^{2}_{3}+\Xi ^{2}_{5}}}\right] }{\sqrt{\Xi ^{2}_{5}+\Xi ^{2}_{3}\text{ cn}^{2}\left[ \Xi _{4}\sqrt{\frac{-N_{3}}{3} (\Xi ^{2}_{3}+\Xi ^{2}_{5})}(x-\xi _{0}), \frac{\Xi _{3}}{\Xi _{4}}\sqrt{\frac{\Xi ^{2}_{4}+\Xi ^{2}_{5}}{\Xi ^{2}_{3}+\Xi ^{2}_{5}}}\right] }} \times \exp i(\mu t), \end{aligned} \end{aligned}$$
(16)

where \(\xi _{0}\) is the integral constant, \(\Xi _{3}\), \(\Xi _{4}\) and \(\Xi _{5}\) satisfy the relations as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \Xi ^{2}_{5}-\Xi ^{2}_{3}-\Xi ^{2}_{4}=\frac{3N_{2}}{2N_{3}},\\ \Xi ^{2}_{3}\Xi ^{2}_{4}-\Xi ^{2}_{3}\Xi ^{2}_{5}-\Xi ^{2}_{4}\Xi ^{2}_{5}=\frac{3N_{1}}{N_{3}},\\ \sqrt{\frac{N_{2}+\sqrt{N^{2}_{2}-4N_{1}N_{3}}}{-2N_{3}}}<\Xi _{3}< \sqrt{\frac{3N_{2}+\sqrt{9N^{2}_{2}-48N_{1}N_{3}}}{-4N_{3}}}. \end{array}\right. } \end{aligned}$$
(17)

Case 3 According to the case (iv), we observe that there exists two families of homoclinic orbits enclose to two equilibrium points. By using the dynamical theory of differential systems [6, 7], the bell-shaped solitary wave solutions of system (1) takes the form (See Fig. 4)

$$\begin{aligned} \begin{aligned} u_{3}(x,t)&=\pm 2\sqrt{\frac{-3N_{1}}{\varepsilon \sqrt{9N^{2}_{2}-48N_{1}N_{3}} \cosh (2\sqrt{-N_{1}}(x-\xi _{0}))+3N_{2}}}\\&\quad \times \exp (i\mu t), \end{aligned} \end{aligned}$$
(18)

where \(\xi _{0}\) is the integral constant and \(\varepsilon =\pm 1\).

Fig. 4
figure 4

The portraits of u(x, t) in Eq. (18) at \(N_{1}=-1\), \(N_{2}=\frac{4}{3}\), \(N_{3}=\varepsilon =1\), \(\xi _{0}=0\)

Full size image

Conclusions

The current paper studied the bifurcation analysis of the LPD model with Kerr law of self-phase modulation. The results are quite revealing and the soliton solutions have emerged from the analysis. These are dark and bright 1-soliton solutions. These encouraging results pave ways for continuing the work far and beyond the present situation. In future the model will be addressed with power-law of self-phase modulation, and subsequently the chromatic dispersion will be replace with cubic-quartic version if the model which will be later studied with Kerr and power laws of self-phase modulation. Those results will be disseminated with time. In the long run, the model will be addressed with polarization-mode dispersion and with dispersion-flattened fibers whose bifurcation analysis will be later available. These results and other advanced analysis with their novel results will be later made visible after aligning the results with the pre-existing works [34,35,36,37,38,39].