1 Introduction

Nonlinear partial differential equations (NLPDEs) have taken an indisputable place in the modeling and understanding of actual and potential natural phenomena throughout the past few centuries. The usage of these equations in physics, nature, optics, engineering, and mathematical sciences has significantly boosted interest in these equations and their solutions among relevant scientists (Wang 1991; Zhang and Zhang 2011). In general, scientists have separated the solutions of NLPDEs into two categories: analytical solutions and numerical solutions. Sometimes it has not been easy to obtain analytical solutions, which has led to intensification of studies on numerical solutions.

NLPDEs have exact solutions known as analytical solutions, which may be written as mathematical functions. These answers give a thorough and accurate account of how a physical system or process that the NLPDE describes behaves. Finding analytical solutions for NLPDEs is a difficult and frequently complex process, and only a small percentage of NLPDEs can do it. Due to the intricacy of many NLPDEs, analytical solutions are frequently confined to idealized and simplified issues. In practice, numerical techniques like as finite difference, finite element, and finite volume are commonly employed to approximate solutions to increasingly complicated NLPDEs and real-world situations. Even when analytical solutions are unavailable or too complicated to construct, numerical solutions give a practical technique to deal with a wide spectrum of NLPDEs.

The usage of computer programs in calculations has increased, making it simpler than ever before to solve these problems. The following is a list of several effective techniques for finding numerical and analytical solutions to partial differential equations: the Lie symmetry method (Hashemi and Baleanu 2016, 2020; Hashemi et al. 2019), the extended direct algebraic method (Zahran and Bekir 2022; Zahran et al. 2023a, b, c), the Kudryashov method (Ryabov et al. 2011), geometric numerical methods (Hashemi 2021; Hairer et al. 2006), Heir equation method (Nucci 2003; Gulsen et al. 2023), Exp function method (Zhang 2007; Abdelrahman et al. 2020), Nucci reduction method (Yao et al. 2023; Hashemi and Mirzazadeh 2023), the planar dynamical systems method (Han et al. 2021, 2022b, 2023a, b), finite difference method (Başhan and Esen 2021; Başhan et al. 2021, 2016, 2018, 2021), adaptive moving mesh method (Alharbi and Almatrafi 2022; Alharbi et al. 2020a; Almatrafi et al. 2021; Alharbi and Almatrafi 2020; Alharbi et al. 2020b, c), sub-equation method (Zahran et al. 2021, 2022a, b), and many more.

Perturbed types of complex PDEs represent a class of equations where additional terms or factors are introduced to alter the behavior or dynamics of the original equation. These perturbations can arise from various physical phenomena or mathematical considerations, leading to a wide range of applications and implications. For instance, the perturbed Schrödinger equation incorporates additional potentials or external forces, influencing the quantum mechanical behavior of particles in a system (Zulfiqar and Ahmad 2021; Rehman and Ahmad 2023; Akram et al. 2023; Zulfiqar and Ahmad 2022). The field of soliton solutions encompasses the study of solitary wave phenomena in various physical systems, ranging from classical to quantum mechanics. Solitons are unique nonlinear waves that maintain their shape and velocity while propagating through a medium, owing to a delicate balance between dispersion and nonlinearity. Their remarkable stability and robustness make them fascinating objects of study in fields such as nonlinear optics, fluid dynamics, plasma physics, and condensed matter physics. Soliton dynamics delve into understanding the formation, interaction, and propagation characteristics of solitons, shedding light on complex phenomena like soliton collisions, fission, and fusion. Beyond fundamental research, solitons find diverse applications in telecommunications, optical fiber communications, signal processing, and even in medical imaging, where their ability to retain their shape over long distances enables efficient data transmission and imaging techniques (Geng et al. 2023a, b; Chen 2023; Wang et al. 2022; Bo et al. 2023; Wen et al. 2023; Xu et al. 2023).

In the present study, we will employ the Nucci reduction method to the Perturbed Gerdjikov–Ivanov (PGI) equation, which is one of the most popular method for creating exact solutions. This method was recently discovered, and it typically produces excellent outcomes. The suggested method stands out from the competition due to its straightforward calculations and accurate outcomes.

When we scan the literature, we will notice that a number of studies have been done on the analysis and solutions of the PGI equation (Fan 2000; Dai and Fan 2004; He and Meng 2010; Rogers and Chow 2012; Lü et al. 2015). The \(\exp (-\theta (\zeta ))\) and \(({G '}/{G ^2})\) expansion techniques were used by Kaur and Wazwaz (2018) to determine the optical solitons of the PGI equation. Using the sine-Gordon expansion technique, Yaşar et al. (2018) reported novel optical solitons of the PGI equation. By using the extended trial equation approach, Biswas et al. (2018) were able to get bright and singular solitons of the PGI equation. By employing Lie symmetry analysis, Biswas et al. (2017) were able to develop conservation laws for the Gerdjikov–Ivanov equation. The PGI equation (Hosseini et al. 2020; Zahran and Bekir 2023) with full nonlinearity is given as

$$\begin{aligned} i u_t +A u_{x x}+B\left| u^4\right| u+i C u^2 u_x^* =i\left[ \delta u_x+\lambda \left( u|u|^{2 m}\right) _x+\mu \left( |u|^{2 m}\right) _x u\right] , \end{aligned}$$
(1)

where u(x, t) is a complex-valued functions, m indicates to full nonlinearity effects when \(\lambda\) shows self-steepening for short pulses. Then \(\mu\) and \(\delta\) represent the higher-order dispersion effect and the depiction of the inter-modal dispersion, respectively. A and B stand for the group velocity dispersion (GVD) and the quintic nonlinearity, respectively.

The balanced modified extended tanh-function and the non-balanced Riccati-Bernoulli Sub-ODE methods are used to obtain the new optical solitons of the PGI equation in Shehata et al. (2021).

Let us use the transformation to solve Eq. (1)

$$\begin{aligned} \begin{aligned}&u(x, t)=\rho (\zeta ) e^{i \sigma (x, t)}, \\&u_t=\left[ -v \rho ^{\prime }+i w \rho \right] e^{i \sigma (x, t)}, \\&u_x=\left[ \rho ^{\prime }-i k \rho \right] e^{i \sigma (x, t)}, \\&u_{x x}=\left[ \rho ^{\prime \prime }-2 i k \rho ^{\prime }-k^2 \rho \right] e^{i \sigma (x, t)}, \end{aligned} \end{aligned}$$
(2)

where we can define \(\zeta =x-v t\) and \(\sigma (x, t)=-k x+w t+\theta\). We also should note that the shape features of the wave pulse is denoted by \(\rho (\zeta )\) and \(\sigma (x, t)\) represents the phase component of the soliton. Further, soliton frequency is given by k when \(\theta\) is the phase constant, w is the wave number and v is the velocity of the soliton.

The following real and imaginary components will arise when we enter the relation (2) into Eq. (1):

$$\begin{aligned}{} & {} A \rho ^{\prime \prime }-\left( w+A k^2+\delta k\right) \rho -k \lambda \rho ^{2 m+1}-C k \rho ^3+B \rho ^5=0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} v=-2 \delta k-\delta +C \rho ^2-[(2 m+1) \lambda +2 m \mu ] \rho ^{2 m}. \end{aligned}$$
(4)

The optical soliton solutions of the PGI equation may be obtained by solving the real part of Eq. (3), whereas the soliton velocity must be determined by solving the imaginary part Eq. (4).

If we take \(m=1\) in Eq. (3) and carry out the homogeneous balance for \(\rho ^{\prime \prime }, \rho ^5\) result in \(N=1 / 2\) which is clearly seen as a fraction number, so we can consider new transformation \(\rho =\textrm{P}^{\frac{1}{2}}\) via which Eq. (3) becomes

$$\begin{aligned} 2 A \textrm{PP}^{\prime \prime }-A \textrm{P}^{\prime 2}-4\left( w+a k^2+\delta k\right) \textrm{P}^2-4 k(\lambda +C) \textrm{P}^3+4 B \textrm{P}^4=0. \end{aligned}$$
(5)

Now, \(N=1\) is implied by the homogeneous balance for \(\textrm{PP}^{\prime \prime }\) and any one of \(\textrm{P}^{\prime 2}\) or \(\textrm{P}^4\).

The study is designed as follows: In the introduction part of this study, a brief summary of NLPDEs and the PGI equation is given, while in the second part, the Nucci reduction method is applied to the relevant equation and some solutions are obtained. The third section is devoted to numerical results while in the fourth part the modulational instability is achieved. In the last section, a brief summary of the study is given.

2 Nucci’s reduction method

In this part of work, we will investigate some new exact solutions to Eq. (5), as well as their corresponding first integrals. We employ Nucci’s reduction method to acquire corresponding exact solutions and first integrals. Similar to other analytical approaches for tackling differential equations, this method presents both advantages and disadvantages. Notably, it offers the flexibility to derive various solution types, encompassing soliton, hyperbolic, and wave solutions, among others, without imposing strict constraints. Moreover, under certain circumstances, it facilitates the extraction of the first integral. Nonetheless, a notable drawback arises when the reduced ODE proves unsolvable in certain scenarios, leading to method failure. This stands as the primary limitation of Nucci’s reduction method. This approach was first developed in Nucci and Leach (2000) to detect nonlocal symmetries of differential equations. In this paper, we utilized the Maple 2022 software to derive our findings. Let us assume the general nonlinear PDE in the form

$$\begin{aligned} U^{(n)}(\zeta )=\mathcal {F}\left( U(\zeta ),U'(\zeta ),\ldots ,U^{(n-1)}(\zeta )\right) . \end{aligned}$$
(6)

By assuming the variables \(\Psi _1(\zeta )=U(\zeta ),\ \Psi _2(\zeta )=U'(\zeta ),\ldots ,\Psi _n(\zeta )=U^{(n-1)}(\zeta ),\) the nonlinear ODE (6) transforms to the following dynamical system

$$\begin{aligned} \left\{ \begin{array}{c} \Psi _1'(\zeta )=\displaystyle {\Psi _2(\zeta )}, \qquad \qquad \qquad \qquad \qquad \qquad \\ \Psi _2'(\zeta )=\displaystyle {\Psi _3(\zeta )}, \qquad \qquad \qquad \qquad \qquad \qquad \\ \vdots \qquad \qquad \qquad \qquad \qquad \qquad \\ \displaystyle {\Psi _n'(\zeta )=\mathcal {F}\left( \Psi _1(\zeta ),\Psi _2(\zeta ),\ldots ,\Psi _n(\zeta )\right) }\quad.\\ \end{array} \right. \end{aligned}$$
(7)

Now, let us define \(\Psi _1\) as a new independent variable. Then the system (7) turns into

$$\begin{aligned} \left\{ \begin{array}{c} \displaystyle {\frac{d\Psi _2(\Psi _1)}{d\Psi _1}=\frac{\Psi _3(\Psi _1)}{\Psi _2(\Psi _1)}}, \qquad \qquad \qquad \qquad \qquad \ \\ \displaystyle {\frac{d\Psi _3(\Psi _1)}{d\Psi _1}=\frac{\Psi _4(\Psi _1)}{\Psi _2(\Psi _1)}}, \qquad \qquad \qquad \qquad \qquad \ \\ \vdots \qquad \qquad \qquad \qquad \ \ \\ \displaystyle {\frac{d\Psi _n(\Psi _1)}{d\Psi _1}=\frac{\mathcal {F}\left( \Psi _1,\Psi _2(\Psi _1),\ldots ,\Psi _n(\Psi _1)\right) }{\Psi _2(\Psi _1)}} \quad.\\ \end{array} \right. \end{aligned}$$
(8)

It’s worth mentioning that the set of equations represented by (7) forms a dynamical system with n equations, while (8) represents a dynamical system with \(n-1\) equations. This distinction is the primary rationale behind referring to the method employed as reduction techniques. Then, by solving the reduced system (80, we obtain \(\Psi _2(\Psi _1)\). We can now return the variable \(\Psi _1\) as the dependent variable. Then, using the first equation in (7), we get a first order ODE as \(\frac{d\Psi _1(\zeta )}{d\zeta }=\Psi _2(\zeta )\). After solving this ODE, we reach to the final solution \(U(\zeta )=\Psi _1(\zeta ).\)

Now, for the ODE (5), assume that the variables change as a result of the proposed reduction approach (Hashemi and Baleanu 2020; Hashemi and Mirzazadeh 2023):

$$\begin{aligned} \Psi _1(\zeta )=P(\zeta ), \ \ \Psi _2(\zeta )=P'(\zeta ). \end{aligned}$$

These presumptions allow us to derive the following system of ODEs from the Eq. (5):

$$\begin{aligned} \left\{ \begin{array}{c} \Psi _1'(\zeta )=\displaystyle {\Psi _2(\zeta )}, \ \quad \qquad \qquad \qquad \quad \ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \\ \displaystyle {\Psi _2'(\zeta )=\frac{A\Psi _2^2(\zeta )+4(w+ak^2+\delta k)\Psi _1^2(\zeta )+4k(\lambda +C)\Psi _1^3(\zeta )-4B\Psi _1^4(\zeta )}{2A\Psi _1(\zeta )}} \quad \;.\\ \end{array} \right. \end{aligned}$$
(9)

Let us define \(\Psi _1\) as a new independent variable, which the system (9) then turns into

$$\begin{aligned} \frac{d\Psi _2(\Psi _1)}{d\Psi _1}=\frac{A\Psi _2^2(\Psi _1)+4(w+ak^2+\delta k)\Psi _1^2+4k(\lambda +C)\Psi _1^3-4B\Psi _1^4}{2A\Psi _1\Psi _2(\Psi _1)}. \end{aligned}$$
(10)

Equation (10) is a first order ODE. We try to solve it by in different ways. First, let us to report its solution given by the Maple:

$$\begin{aligned} \Psi _2(\Psi _1) =\frac{\sqrt{3A\Psi _{{1}} \left( -4B\Psi _1^{3}+ 12a{k}^{2}\Psi _{{1}}+6k (\lambda +C)\Psi _1^{2}+12\delta \,k\Psi _{{1}}+3\,AR_1+12\,\Psi _{{1}}w \right) }}{3A},\ {(R_1\in \mathbb {R})}. \end{aligned}$$
(11)

The following first integral of the equation is obviously produced by combining solution (11) and Eq. (5):

$$\begin{aligned}{} & {} \frac{4 B P ^{4} \left( \zeta \right) -6 C P^{3} \left( \zeta \right) k -6 P^{3} \left( \zeta \right) k \lambda -12 P^{2} \left( \zeta \right) a \,k^{2}-12 P^{2} \left( \zeta \right) \delta k +3 A \left( \frac{dP^{2} \left( \zeta \right) }{d \zeta }\right) -12 P^{2} \left( \zeta \right) w}{3 A P \left( \zeta \right) }\\{} & {} =R_1. \end{aligned}$$

We can now return the variable \(\Psi _1\) as the dependent variable. Then, using the first equation in (9), we get:

$$\begin{aligned} \frac{d\Psi _{1} \left( \zeta \right) }{d \zeta } = \frac{\sqrt{3A \Psi _{1} \left( \zeta \right) \left( -4 \Psi _{1}^{3} \left( \zeta \right) B +6 \Psi _{1}^{2} \left( \zeta \right) k C +12 \Psi _{1} \left( \zeta \right) a \,k^{2}+6 \Psi _{1}^{2} \left( \zeta \right) k \lambda +12 \Psi _{1} \left( \zeta \right) \delta k +3 A R_{1}+12 \Psi _{1} \left( \zeta \right) w \right) }}{3 A}. \end{aligned}$$
(12)

It is clear that the implicit exact solution of Eq. (12) is easily found as follows:

$$\begin{aligned}{} & {} \zeta -\int \frac{A \sqrt{3}d\Psi _1}{\sqrt{A \Psi _1 \left( -4 B \,\Psi _1^{3}+6 C k \,\Psi _1^{2}+12 a \,k^{2} \Psi _1 +6 k \lambda \,\Psi _1^{2}+12 \delta k \Psi _1 +3 A R_1 +12 \Psi _1 w \right) }}\nonumber \\{} & {} +R_2=0,\ {(R_1,R_2\in \mathbb {R})}. \end{aligned}$$
(13)

The following additional assumptions can be used to achieve explicit solutions to Eq. (5).

Assumption 1

\(R_1=0\).

Such that we may derive the following explicit solution to Eq. (13).

$$\begin{aligned} \Psi _1(\zeta )=-\frac{48 A \,{\mathrm e}^{-\frac{2 \sqrt{A \Xi }\, \left( \zeta +R_{2}\right) }{A}} \Xi }{\left( \left( -192 a B -36 \left( \lambda +C \right) ^{2}\right) k^{2}-192 B \delta k -192 B w \right) A^{2}+12 A k \left( \lambda +C \right) {\mathrm e}^{-\frac{2 \sqrt{A \Xi }\, \left( \zeta +R_{2}\right) }{A}}-{\mathrm e}^{-\frac{4 \sqrt{A \Xi }\, \left( \zeta +R_{2}\right) }{A}}}, \end{aligned}$$
(14)

where \(\Xi =ak^2+\delta k+w.\) Therefore

$$\begin{aligned} \rho (\zeta )=\sqrt{\frac{48 A \,{\mathrm e}^{-\frac{2 \sqrt{A \Xi }\, \left( \zeta +R_{2}\right) }{A}} \Xi }{\left( \left( 192 a B +36 \left( \lambda +C \right) ^{2}\right) k^{2}+192 B \delta k +192 B w \right) A^{2}-12 A k \left( \lambda +C \right) {\mathrm e}^{-\frac{2 \sqrt{A \Xi }\, \left( \zeta +R_{2}\right) }{A}}+{\mathrm e}^{-\frac{4 \sqrt{A \Xi }\, \left( \zeta +R_{2}\right) }{A}}}}, \end{aligned}$$
(15)

and final exact solution can be written as

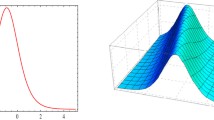
$$\begin{aligned}{} & {} u_1(x, t) =\nonumber \\{} & {} \sqrt{\frac{48 A \,{\mathrm e}^{-\frac{2 \sqrt{A (ak^2+\delta k+w)}\, \left( x-v t +R_{2}\right) }{A}} (ak^2+\delta k+w)}{\left( \left( 192 a B +36 \left( \lambda +C \right) ^{2}\right) k^{2}+192 B (\delta k+w) \right) A^{2}-12 A k \left( \lambda +C \right) {\mathrm e}^{-\frac{2 \sqrt{A (ak^2+\delta k+w)}\, \left( x-v t +R_{2}\right) }{A}}+{\mathrm e}^{-\frac{4 \sqrt{A (ak^2+\delta k+w)}\, \left( x-v t +R_{2}\right) }{A}}}}\nonumber \\{} & {} \times {\mathrm e}^{i (-k x+w t+\theta )}. \end{aligned}$$
(16)

Figure  1 depicts the physical behaviour of the exact solution \(u_1(x, t)\) given by Eq. (16). As we can see, the soliton profile is localized in space and is actually a bright soliton solution, which was widely used to transfer information in telecommunications.

Fig. 1
figure 1

The physical behaviour of the bright soliton \({u_{1}(x,t)}\) (16) and its contour for the parametric values m = 1, A = 1, B = 0.5, C = 0.1, a = 1, \(\delta\) = 0.05, \(\lambda\) = 0.5, k = 1, v = 0.5, \(R_2\) = 0.01 and \(\theta\) = 1

Full size image

Moreover, in order to derive additional exact solutions, assuming that (10) may be solved in the special form of

$$\begin{aligned} \Psi _2(\Psi _1)=K_2\Psi _1^2+K_1\Psi _1+K_0, \end{aligned}$$
(17)

where \(K_i,\ i=0,1,2\) are arbitrary constants to be determined. Substituting (17) into (10) and equating the coefficients of powers of \(\Psi _1\), concludes the following algebraic system of equations

$$\begin{aligned}{} & {} A K_{0}^{2}=0,\nonumber \\{} & {} -4 A K_{1} K_{2}+4 k \left( \lambda +C \right) =0,\nonumber \\{} & {} \left( -2 K_{0} K_{2}-K_{1}^{2}\right) A +4 a \,k^{2}+4 \delta k +4 w=0,\nonumber \\{} & {} -3 A K_{2}^{2}-4 B=0. \end{aligned}$$
(18)

Solving this system concludes the following cases:

Case 1

$$\begin{aligned}{} & {} K_2\in \mathbb {R},\ \ K_1=\sqrt{-\frac{3 a \,k^{2}+3 \delta k +3 w}{B}}\, K_{2},\ \ K_0=0,\end{aligned}$$
(19)
$$\begin{aligned}{} & {} A=-\frac{4 B}{3 K_{2}^{2}},\ \ C=-\frac{4 B \sqrt{-\frac{3 a \,k^{2}+3 \delta k +3 w}{B}}+3 k \lambda }{3 k}. \end{aligned}$$
(20)

Hence, from the first equation of (9), we have

$$\begin{aligned} \frac{d\Psi _1(\zeta )}{d\zeta }= K_{2} \Psi _{1}^{2} \left( \zeta \right) +\sqrt{-\frac{3 a \,k^{2}+3K_{2} \delta k +3 w}{B}}\, \Psi _{1} \left( \zeta \right) . \end{aligned}$$

Therefore

$$\begin{aligned} \Psi _1(\zeta )=\frac{3 a \,k^{2}+3 \delta k +3 w}{B \sqrt{\frac{-3 a \,k^{2}-3 \delta k -3 w}{B}}+3 \,{\mathrm e}^{-K_{2} \sqrt{\frac{-3 a \,k^{2}-3 \delta k -3 w}{B}}\, \zeta } R_{2} \left( a \,k^{2}+\delta k +w \right) }, \end{aligned}$$

or equivalently

$$\begin{aligned} \rho (\zeta )=\sqrt{\frac{3 a \,k^{2}+3 \delta k +3 w}{B \sqrt{\frac{-3 a \,k^{2}-3 \delta k -3 w}{B}}+3 \,{\mathrm e}^{-K_{2} \sqrt{\frac{-3 a \,k^{2}-3 \delta k -3 w}{B}}\, \zeta } R_{2} \left( a \,k^{2}+\delta k +w \right) }}, \end{aligned}$$

and final exact solution in this case becomes

$$\begin{aligned} u_2(x,t)=\sqrt{\frac{3 a \,k^{2}+3 \delta k +3 w}{B \sqrt{\frac{-3 a \,k^{2}-3 \delta k -3 w}{B}}+3 \,{\mathrm e}^{-K_{2} \sqrt{\frac{-3 a \,k^{2}-3 \delta k -3 w}{B}}\, (x-v t)} R_{2} \left( a \,k^{2}+\delta k +w \right) }}\times e^{i (-k x+w t+\theta )}. \end{aligned}$$
(21)
Fig. 2
figure 2

The physical behaviour of the periodic-wave \({u_{2}(x,t)}\) (21) and its contour for the same parametric values as those given in Fig. 1

Full size image

Case 2

$$\begin{aligned}{} & {} K_2=2 \sqrt{-\frac{B}{3 A}},\ \ K_1=2\sqrt{\frac{ a \,k^{2}+ \delta k+ w}{A}},\ \ K_0=0,\end{aligned}$$
(22)
$$\begin{aligned}{} & {} \lambda =\frac{4 A \sqrt{\frac{ a \,k^{2}+ \delta k + w}{A}}\, \sqrt{-\frac{B}{3 A}}-k C}{k}. \end{aligned}$$
(23)

Hence, from the first equation of (9), we have

$$\begin{aligned} \frac{d\Psi _1(\zeta )}{d\zeta }= 2 \sqrt{-\frac{B}{3 A}}\, \Psi _1^{2}(\zeta )+2\sqrt{\frac{ a \,k^{2}+ \delta k + w}{A}}\, \Psi _1(\zeta ). \end{aligned}$$

Therefore

$$\begin{aligned} \Psi _1(\zeta )=\frac{-3 a \,k^{2}-3 \delta k -3 w}{-3 R_{2} \left( a \,k^{2}+\delta k +w \right) {\mathrm e}^{-2 \sqrt{\frac{a \,k^{2}+\delta k +w}{A}}\, \zeta }+A \sqrt{\frac{a \,k^{2}+\delta k +w}{A}}\, \sqrt{-\frac{3B}{A}}}, \end{aligned}$$

or equivalently

$$\begin{aligned} \rho (\zeta )=\sqrt{\frac{-3 a \,k^{2}-3 \delta k -3 w}{-3 R_{2} \left( a \,k^{2}+\delta k +w \right) {\mathrm e}^{-2 \sqrt{\frac{a \,k^{2}+\delta k +w}{A}}\, \zeta }+A \sqrt{\frac{a \,k^{2}+\delta k +w}{A}}\, \sqrt{-\frac{3B}{A}}}}\ , \end{aligned}$$

and final exact solution in this case becomes

Fig. 3
figure 3

The physical behaviour of the periodic-wave \({u_{3}(x,t)}\) (24) and its contour for the same parametric values as those given in Fig. 1 except those: A= \(-\)0.2, B = 0.5

Full size image
$$\begin{aligned} u_3(x,t)=\sqrt{\frac{-3 a \,k^{2}-3 \delta k -3 w}{-3 R_{2} \left( a \,k^{2}+\delta k +w \right) {\mathrm e}^{-2 \sqrt{\frac{a \,k^{2}+\delta k +w}{A}}\, (x-v t)}+A \sqrt{\frac{a \,k^{2}+\delta k +w}{A}}\, \sqrt{-\frac{3B}{A}}}}\times e^{i (-k x+w t+\theta )}. \end{aligned}$$
(24)

In Fig. 2, we illustrate the physical behaviour of the exact solution \(u_2(x, t)\) given by Eq. (21). The solution profile is localized and oscillates periodically in time. The same characteristics are observed in Fig. 3 for the periodic solution \(u_3(x, t)\) (24), under the parametric values: m= 1, A= \(-\)0.2, B = 0.5, C = 0.1, a = 1, \(\delta\) = 0.05, \(\lambda\) = 0.5, k = 1, v = 0.5, \(R_2\) = 0.01 and \(\theta\) = 1.

Case 3

$$\begin{aligned}{} & {} K_2=2 \sqrt{-\frac{B}{3 A}},\ \ K_1=\frac{k \left( \lambda +C \right) }{2 A \sqrt{-\frac{B}{3 A}}},\ \ K_0=0,\end{aligned}$$
(25)
$$\begin{aligned}{} & {} \delta =-\frac{16 B a \,k^{2}+3 C^{2} k^{2}+6 C \,k^{2} \lambda +3 k^{2} \lambda ^{2}+16 B w}{16 B k}. \end{aligned}$$
(26)

Hence, from the first equation of (9), we have

$$\begin{aligned} \frac{d\Psi _1(\zeta )}{d\zeta }= 2 \sqrt{-\frac{B}{3 A}}\, \Psi _{1}^{2} \left( \zeta \right) +\frac{k \left( \lambda +C \right) \Psi _{1}\left( \zeta \right) }{2 A \sqrt{-\frac{B}{3 A}}}. \end{aligned}$$

Therefore

$$\begin{aligned} \Psi _1(\zeta )=\frac{3 k \left( \lambda +C \right) }{3 k R_{2} \left( \lambda +C \right) {\mathrm e}^{-\frac{\sqrt{3}\, k \left( \lambda +C \right) \zeta }{2 A \sqrt{-\frac{B}{A}}}}+4 B}, \end{aligned}$$

or equivalently

$$\begin{aligned} \rho (\zeta )=\sqrt{\frac{3 k \left( \lambda +C \right) }{3 k R_{2} \left( \lambda +C \right) {\mathrm e}^{-\frac{\sqrt{3}\, k \left( \lambda +C \right) \zeta }{2 A \sqrt{-\frac{B}{A}}}}+4 B}}, \end{aligned}$$

and final exact solution in this case becomes

Fig. 4
figure 4

The physical behaviour of the kink soliton \({u_{4}(x,t)}\) (27) and its contour for the same parametric values as those given in Fig. 3

Full size image
$$\begin{aligned} u_4(x,t)=\sqrt{\frac{3 k \left( \lambda +C \right) }{3 k R_{2} \left( \lambda +C \right) {\mathrm e}^{-\frac{\sqrt{3}\, k \left( \lambda +C \right) (x-vt)}{2 A \sqrt{-\frac{B}{A}}}}+4 B}}\times e^{i (-k x+w t+\theta )}. \end{aligned}$$
(27)

This solution correspond to a kink soliton solution as depicted in Fig. 4. The kink soliton can be used in practical applications, as polarization switches between two different domains or optical logic units (Huang et al. 2012).

Furthermore, it’s worth mentioning that we obtained explicit solutions by introducing additional assumptions to the implicit solution (13). In contrast, Han et al. in their works (Han et al. 2022a, b) derived alternative types of solutions for the implicit form, as shown in Eq. (13).

Bright solitons, kink solitons, and periodic-wave solutions play crucial roles in understanding the physical implications of the PGI equation. Bright solitons are localized wave packets that maintain their shape and amplitude while propagating through a medium. They are significant in various physical phenomena, including optical fiber communications and Bose-Einstein condensates.

Kink solitons, on the other hand, are topological structures characterized by abrupt changes in phase or amplitude. They find applications in diverse fields such as condensed matter physics, where they describe domain walls in ferromagnetic materials or dislocations in crystalline structures.

Periodic-wave solutions represent periodic patterns that emerge from the interplay of nonlinearity and dispersion. These solutions are relevant in understanding phenomena like wave propagation in nonlinear media and pattern formation in biological systems.

Studying these solitonic solutions within the context of the PGI equation provides insights into how disturbances affect the dynamics and stability of these structures, offering valuable information for various physical systems governed by similar equations.

3 Numerical results

The particular interest of solitons is evidently their stability against perturbation. In what follows, we perform direct numerical simulations on Eq. (1), using the split-step Fourier method (Schneider 2013), with the main objective of analyzing the Gerdjikov–Ivanov-solitons stability’s, during propagation over appreciable distance. For this purpose, we rewrite the model Eq. (1) as:

$$\begin{aligned} u_t=\left( \hat{N}+\hat{D} \right) u, \end{aligned}$$
(28)

where \(\hat{N}\) and \(\hat{D}\) are respectively the nonlinear operator that accounts for the effect of nonlinear terms and the linear differential operator that accounts for dispersion. They read as: \(\hat{N} = iB\left| u^4\right| - C u u_x^* + \lambda \frac{\left( u|u|^{2m}\right) _x}{u}+\mu \left( |u|^{2 m}\right) _x\) and \(\hat{D} = iA\frac{\partial ^{2}}{\partial x^{2}} + \delta \frac{\partial }{\partial x}\). The split-step Fourier method obtains an approximate solution by assuming that in propagating the optical field over a small distance h, the dispersion and nonlinear effects can be pretended to act independently. More specifically, propagation from t to \(t + h\) is carried out in two steps: Firstly, the nonlinearity acts alone, and \(\hat{D}=0\) in Eq. (28). In the second step, dispersion acts alone and \(\hat{N} = 0\) in in Eq. (28). More details about the philosophy of the split-step Fourier method, which is well and abundantly illustrated by G. P. Agrawal can be found in the book (Schneider 2013).

Fig. 5
figure 5

The numerical evolution of the bright soliton \({u_{1}(x,t)}\) (16) and the kink soliton \({u_{4}(x,t)}\) (27) for the same parametric values as those given in Fig. 1 and  3

Full size image
Fig. 6
figure 6

The numerical evolution of the bright soliton \({u_{1}(x,t)}\) (16) and the kink soliton \({u_{4}(x,t)}\) (27) under the influence of a photon noise, from the initial conditions \(u_j(x=0,t)=u_j(t)(1+0.01random(t))\) with the same parametric values as those given in Fig. 5

Full size image

Firstly, we consider the soliton solutions (16) and (27) as initial conditions by setting \(u_j(x=0,t)=u_j(t)\). In Fig. 5, we display the spatio-temporal evolution of the analytical soliton intensities \(|{u_j(x,t)}|^2\) considering the parametric values: m = 1, B = 0.5, C = 0.1, a = 1, \(\delta\) = 0.05, \(\lambda\) = 0.5, k = 1, v = 0.5, \(R_2\) = 0.01 and \(\theta\) = 1; A= 1 for the bright soliton (16) and A= \(-\)0.2 for the kink soliton solution (27). From the graphical description in Fig. 5 for \(t=0\), \(t=5\) and \(t=25\), we notice that the soliton amplitude and width are unchanged during propagation. This suggests that the observed solitons is invariant while evolving over the propagation distance t, as documented in the literature.

Furthermore, we test the stability of the previous two solitons by adding random noises to their initial states by considering the following initial condition: \(u_j(x=0,t)=u_j(t)(1+0.01random(t))\), the parametric values being similar to those given in Fig. 5. As it is shown in Fig. 6, the remarkable robustness of the soliton solutions against noises is indicated. The original shape of solitons, their amplitude and their width remain unchanged when evolving in a perturbed environment. This result can be used to develop the solitonic pulses in the field of telecommunication and ultra-fast laser.

Fig. 7
figure 7

The numerical evolution of the solitary-waves \({u_{j}(x,t)}\) (16) and (27), under the variation of the self-steepening parameter \(\lambda\) (\(\lambda =0.1\) for the solid blue line at \(t=0\), \(\lambda =0.5\) for the solid red line at \(t=5\) and \(\lambda =1\) for the solid green line at \(t=25\)), with the same parametric values as those given in Fig. 5

Full size image

Moreover, we study the important influence of system parameter’s by submitting the solitary waves under the effect of the self-steepening and quintic nonlinearity parameters notably. In Fig. 7, we illustrate the impact of the self-steepening coefficient \(\lambda\), by considering various combination of \(\lambda\) at different positions t (\(\lambda =0.1\) for the solid blue line at \(t=0\), \(\lambda =0.5\) for the solid red line at \(t=5\) and \(\lambda =1\) for the solid green line at \(t=25\)). We notice that the soliton amplitudes increase with the increasing self-steepening parameter \(\lambda\) when propagating. In the other hand, the quintic nonlinearity influence is pointed out at different positions t, in Fig. 8. As the quintic nonlinearity B increases, the soliton magnitude decreases as it is shown in Fig. 8. These striking results could furnish some guidelines in the controllability and development of solitons.

Fig. 8
figure 8

The numerical evolution of the solitary-waves \({u_{j}(x,t)}\) (16) and (27), under the variation of the quintic nonlinearity B (\(B=0.1\) for the solid blue line at \(t=0\), \(B=0.5\) for the solid red line at \(t=5\) and \(B=1.5\) for the solid green line at \(t=25\)), with the same parametric values as those given in Fig. 5

Full size image

4 Modulation instability analysis

Generally, solitary-waves are relatively stable, unlike the conventional pulses of various forms. By sitting solitons on a continuous wave (CW) background which may be submitted to Modulational Instability (MI), the previous CW will be rapidly demolished and consequently cause the demolition of the solitary-wave. The MI process in an ubiquitous phenomenon where modulated wave objects emerge in nonlinear systems as exponential augmentation of the CW. This important process pertains to a large variety of nonlinear systems (Schneider 2013; Mohamadou et al. 2010; Youssoufa et al. 2020; Porsezian et al. 2012). In this section, we apply the standard linear stability analysis by looking for perturbed plane wave solutions of Eq. (1) in the generic form

$$\begin{aligned} u(x,t) = \left[ \sqrt{P_0}+\eta (x,t)\right] e^{iBP_0^2t}, \end{aligned}$$
(29)

where the constant \(P_0\) is related to the input power and \(\eta (x,t)\) to a small disturbance. Substituting Eq. (29) into Eq. (1) yields

$$\begin{aligned} i \eta _t +A \eta _{x x}-i\left( \delta +\lambda P_0\right) \eta _x + iCP_0 \eta _x^* -iP_0\left( \lambda + \mu \right) \left( \eta _x + \eta _x^* \right) +2BP_0^2\left( \eta + \eta ^* \right) =0. \end{aligned}$$
(30)

It is well established from the MI process that when the input is a CW which propagates through a nonlinear media, it can become unstable for a small disturbance under specific conditions satisfied by the complex disturbance field \(\eta (x,t)\). It reads as: \(\left| \eta (x,t) \right| \ll \sqrt{P_0}\). Thus, if the perturbed field grows exponentially, the steady state becomes unstable.

Fig. 9
figure 9

MI spectrum versus the group velocity dispersion A and the frequency \(\Omega\) under the effect of the quintic nonlinearity B for the parametric values C = 0.1, \(P_0=10\), \(\delta\) = 0.05, \(\lambda\) = 0.1 and \(\mu\) = 1: a \(B=0.1\); b \(B=0.5\); c \(B=1\); and d \(B=1.5\)

Full size image

Assuming solutions of Eq. (30) as the following form

$$\begin{aligned} \eta (x,t) = a_+ e^{i(Kt-\Omega x)} + a_- e^{-i(K^{*}t-\Omega x)}, \end{aligned}$$
(31)

where \(a_+\) and \(a_-\) being constants and merging the previous Eq. (31) into Eq. (30) yields a system of homogeneous equations satisfied by \(a_+\) and \(a_-\) as:

$$\begin{aligned} \left( \begin{array}{cc} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \end{array}\right) \left( \begin{array}{c} a_{+}\\ a_{-}^{*} \end{array}\right) =\left( \begin{array}{c} 0\\ 0 \end{array}\right) , \end{aligned}$$
(32)

where

\(a_{11} = -K -A\Omega ^2 - \left[ \delta + \left( 2\lambda +\mu \right) P_0\right] \Omega + 2BP_0^2\), \(a_{12} = 2BP_0^2-P_0\left( C+\lambda +\mu \right) \Omega\), \(a_{21} = 2BP_0^2-P_0\left( C-\lambda -\mu \right) \Omega\), \(a_{22} = K -A\Omega ^2 + \left[ \delta + \left( 2\lambda +\mu \right) P_0\right] \Omega + 2BP_0^2\). The previous 2 × 2 stability matrix has a nontrivial solution only when the determinant formed by the coefficients matrix vanishes. This vanishing condition leads to a second-order polynomial in K with the following roots

$$\begin{aligned} K_{\pm } = \left[ \delta + \left( 2\lambda +\mu \right) P_0\right] \Omega \pm |\Omega A| \sqrt{\left[ \left( C-\lambda -\mu \right) ^2 - 4AB\right] \frac{P_0^2}{A^2}-\Omega ^2}. \end{aligned}$$
(33)

The MI growth rate is defined by \(g(\Omega )=2|Im(K_{\pm })|\) and exists only if the wave-number \(K_{\pm }\) has a nonzero imaginary part. This can be achieved if the following condition is satisfied:

$$\begin{aligned} \left[ \left( C-\lambda -\mu \right) ^2 - 4AB\right] \frac{P_0^2}{A^2}-\Omega ^2 \prec 0. \end{aligned}$$
(34)

Finally, the MI is measured by the power gain

$$\begin{aligned} g(\Omega )= 2|\Omega A| \sqrt{\Omega ^2-\left[ \left( C-\lambda -\mu \right) ^2 - 4AB\right] \frac{P_0^2}{A^2}}. \end{aligned}$$
(35)
Fig. 10
figure 10

MI spectrum versus the group velocity dispersion A and the frequency \(\Omega\) under the effect of theself-steepening parameter \(\lambda\). The other parameter values are the same as those given in Fig. 9: a \(\lambda =0.1\); b \(\lambda =0.5\); c \(\lambda =1\); and d \(\lambda =1.5\)

Full size image

In order to carry out the accuracy of our linear stability analysis, we submit the MI gain to variation of the system parameters, notably the self-steepening and quintic nonlinearity coefficients. In Fig. 9 we displayed the MI gain as function of the second order dispersion A and frequency \(\Omega\), for different combinations of the quintic nonlinearity. In Fig. 9a the MI growth rate rises to show a small bandwidth when \(B=0.1\). As we can see, the gain is present only in the normal dispersion regime (\(A \succ 0\)). In addition, we notice that MI gain exists at low frequencies and nils at the zero disturbance frequency \(\Omega =0\). Increasing the quintic nonlinearity to \(B=0.5\), \(B=1\) and \(B=1.5\) in Fig. 9b–d, the instability zones increased in comparison to the initial state Fig. 9a. The bandwidths enlarge and consequently, the system becomes more unstable due to the effect of B. This observation is not a surprise, since the quintic nonlinearity decreases the soliton magnitude as predicted by the numerical results in Fig. 8. In contrast, the MI bands decreased with the increasing self-steepening coefficient \(\lambda\) as shown in Fig. 10a–d for \(\lambda =0.1\), \(\lambda =0.5\), \(\lambda =1\) and \(\lambda =1.5\), respectively. The MI spectrum in Fig. 10 has relatively the same characteristic as those in the previous case (Fig. 9), but here, the effect of \(\lambda\) is opposite to the quintic nonlinearity influence on MI. The sidelobe width diminishes with the increasing \(\lambda\) and the system is more stable and favorable to soliton propagation as confirmed by the numerical features observed in Fig. 7. These striking outcomes confirm the validity of the analytical and numerical results.

5 Concluding remarks

In this study, we reached some new solutions by directly applying the Nucci reduction method, which has been increasing in popularity lately, to the PGI equation. Different solutions to the relevant equation are obtained depending on the precise choice of particular parameters. The writers became interested in the topic since the method can be used instantaneously. It is also obvious that the approach will create new opportunities for locating effective and exact solutions to the classical and fractional partial differential equations. We have also talked about the conditions for the existence of solitons in terms of their physical characteristics. We have also discussed MI conduct. The numerical simulations we carried out in the current work also demonstrate the robustness and stable propagation of the generated solitons in a perturbed environment, thereby proving the validity of the analytical and numerical conclusions. The outcomes might be used as a guide for the telecommunications sector’s production of ultra-short optical pulses and solitons. To the authors’ understanding, this paper represents the inaugural investigation of the PGI equation employing Nucci’s reduction method. Consequently, the exact solutions and first integrals obtained for this equation are unprecedented. Furthermore, this study marks the pioneering attempt at conducting modulation instability analysis for the PGI equation.

In upcoming works, there’s potential to extend the employed reduction technique to tackle various categories of complex PDEs, including those in higher dimensions and fractional differential equations featuring local derivatives.