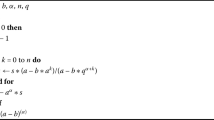Abstract
By using the Caputo type and the Riemann–Liouville type fractional q-derivative, we investigate the existence of solutions for a multi-term pointwise defined fractional q-integro-differential equation with some boundary value conditions. In fact, we give some results by considering different conditions and using some classical fixed point techniques and the Lebesgue dominated convergence theorem.
Similar content being viewed by others
1 Introduction
It is known that the subject of q-difference equations was introduced by Jackson in 1910 [1]. After that, some researchers studied q-difference equations [2–20]. On the other hand, many modern works on integro-differential equations by using different views and fractional derivatives have been published recently, and young researchers could use the main idea of the works for their works (see, for example, [21–50]).
In 2012, Ahmad et al. studied the existence and uniqueness of solutions for the fractional q-difference equation \({}^{c}D_{q}^{ \alpha }u(t)= T ( t, u(t) ) \) with boundary conditions \(\alpha _{1} u(0) - \beta _{1} D_{q} u(0) = \gamma _{1} u(\eta _{1})\) and \(\alpha _{2} u(1) - \beta _{2} D_{q} u(1) = \gamma _{2} u(\eta _{2})\), where \(\alpha \in (1, 2]\), \(\alpha _{i}\), \(\beta _{i}\), \(\gamma _{i}\), \(\eta _{i}\) are real numbers for \(i=1,2\) and \(T \in C(J \times \mathbb{R}, \mathbb{R})\) [6]. In 2013, Zhao et al. reviewed the q-integral problem \((D_{q}^{\alpha }u)(t) + f(t, u(t) )=0\) with boundary conditions \(u(1)=\mu I_{q}^{\beta }u(\eta ) \) and \(u(0)=0\) for almost all \(t \in (0,1)\), where \(q \in (0,1)\), \(\alpha \in (1, 2]\), \(\beta \in (0, 2]\), \(\eta \in (0,1)\), μ is a positive real number, \(D_{q}^{\alpha }\) is the q-derivative of Riemann–Liouville and real-valued continuous map u defined on \(I \times [0, \infty )\) [15]. In 2014, Ahmad et al. investigated the problem
with boundary conditions \(\alpha _{1} u(0) - \beta _{1} (t^{(1-\gamma )} D_{q} u(0)) |_{t=0}= \sigma _{1} u(\eta _{1})\) and \(\alpha _{2} u(1) + \beta _{2} D_{q} u(1)= \sigma _{2} u(\eta _{2})\), where \(t, q \in [0,1]\), \({}^{c}D_{q}^{\beta }\) is the fractional Caputo q-derivative, \(0 < \beta \), \(\gamma \leq 1\), \(I_{q}^{\xi }(\cdot) \) denotes the Riemann–Liouville integral with \(\xi \in (0, 1)\), f and g are given continuous functions, λ and p, k are real constants, \(\alpha _{i}, \beta _{i}, \sigma _{i}\in \mathbb{R}\) and \(\eta _{i} \in (0, 1)\) for \(i=1,2\) [5]. In 2017, Wang considered the existence of uniqueness and nonexistence of positive solution for fractional differential equations \(D_{0^{+}}^{\sigma }x(t) + f(t, x(t))=0\) for \(t \in (0,1)\) under conditions the \(x(0) = x'(0) = \cdots = x^{(n-2)} (0) =0\) and \(D_{0^{+}}^{\alpha }x(1) = \int _{0}^{b} \mu (t) D_{0^{+}}^{\beta }x(t) \,\mathrm{d}t\), where \(n-1< \sigma \leq n\), \(n \geq 3\), \(\alpha \in (0,1)\),
\(b \in (0, 1]\), \(D_{0^{+}}^{\sigma }\), \(D_{0^{+}}^{\alpha }\), \(D_{0^{+}} ^{\beta }\) are the standard Riemann–Liouville derivatives, \(f : (0,1) \times [0, \infty ) \to [0, \infty )\) is continuous and \(\mu (t) \in L^{1} ([0,1])\) is nonnegative [51]. Also, in 2018 he investigated the existence and multiplicity of positive solutions for the fractional differential equation \(D_{0^{+}}^{\sigma }x(t) + f(t, x(t))=0 \) for \(t \in (0,1)\) under the conjugate type integral boundary conditions \(x(0) = x'(0) = \cdots = x^{(n-2)} (0) =0\) and \(D_{0^{+}}^{\alpha }x(1) = \int _{0}^{b} \mu (t) D_{0^{+}}^{\beta }x(t) \,\mathrm{d}V(t)\), where \(D_{0^{+}}^{\alpha }\), \(D_{0^{+}}^{ \beta }\) are the standard Riemann–Liouville derivatives, \(n \geq 3\), \(\alpha \in (0,1)\), \(0 \leq \beta < \sigma -1\), \(b \in (0, 1]\), \(f(t, x)\) may be singular at \(t=0, 1\) and \(x=0\), \(\mu (t) \in L^{1} [0,1] \cap C(0,1)\) is nonnegative, \(\int _{0}^{b} \mu (t) t^{\sigma - \beta -1} \,\mathrm{d}V(t)\) denotes the Riemann–Stieltjes integral, in which V has bounded variation [52].
In 2019, Samei et al. reviewed the existence of solutions for some multi-term q-integro-differential equations with non-separated and initial boundary conditions [12]. Also, Ntouyas et al. [10], by applying definitions of the fractional q-derivative of the Caputo type and the fractional q-integral of the Riemann–Liouville type, studied the existence and uniqueness of solutions for multi-term nonlinear fractional q-integro-differential equations under some boundary conditions
In 2020, Liang et al. investigated the existence of solutions for nonlinear problems regular and singular fractional q-differential equation
with conditions \(f(0) = c_{1} f(1)\), \(f'(0)= c_{2} {}^{c}D_{q}^{ \beta } f (1)\), and \(f^{(k)}(0) = 0\) for \(2\leq k \leq n-1\), here \(n-1 < \alpha < n\) with \(n\geq 3\), \(\beta , q , c_{1}\in (0,1)\), \(c_{2} \in (0, \varGamma _{q} (2- \beta ))\), function w is an \(L^{\kappa }\)-Carathéodory, \(w(t, x_{1}, x_{2}, x_{3})\) may be singular, and \({}^{c}D_{q}^{\alpha }\) is the fractional Caputo type q-derivative [17]. Also, they discussed the existence of solutions for the fractional q-derivative inclusions
\(x(0) + x'(0) + {}^{c}D_{q}^{\beta }x(0) = \int _{0}^{\eta _{1}} x(s) \,\mathrm{d}s \), and \(x(1) + x'(1) + {}^{c}D_{q}^{\beta }x(1) = \int _{0}^{\eta _{2}} x(s) \,\mathrm{d}s\) for any t in I and \(q, \eta _{1}, \eta _{2}, \beta \in (0,1)\), where F maps \(I\times \mathbb{R}^{3} \) into \(2^{\mathbb{R}}\) is a compact-valued multifunction and \({}^{c}D_{q}^{\alpha }\) is the fractional Caputo type q-derivative operator of order \(\alpha \in (1, 2]\), and
such that \(\alpha -\beta >1\) [14]. Similar results have been presented in other studies [12, 13, 19, 20, 37].
By using the main idea of [41, 42, 53], we are going to investigate the multi-singular fractional q-integro-differential pointwise defined equation
under two distinct boundary conditions
and \(u^{(j)}(0)=0\) for \(j=2,\ldots ,[\alpha ]-1\), where \(t \in \overline{J}=[0,1]\), \(u \in \mathcal{B}=C^{1}(\overline{J})\), α, \(\beta _{1}\), \(\beta _{2}\) belong to \([2,\infty )\), \(J=(0,1)\), \((1, \infty )\), \(a, b \in J\), \(D_{q}^{\alpha }\) is the Caputo fractional q-derivative of order α, and \(\omega : \overline{J} \times \mathbb{R}^{4} \to \mathbb{R}\) is a function such that \(\omega (t, \cdot, \cdot, \cdot, \cdot)\) is singular at some points \(t\in \overline{J}\).
2 Preliminaries
Here, we recall some basic notion, lemmas, and theorems which are used in the subsequent sections. Let \(q \in (0,1)\) and \(a \in \mathbb{R}\). Define \([a]_{q}=\frac{1-q^{a}}{1-q}\) [1]. The power function \((x-y)_{q}^{n}\) with \(n \in \mathbb{N}_{0} \) is defined by \((x-y)_{q}^{(n)}= \prod_{k=0}^{n-1} (x - yq^{k})\) for \(n\geq 1\) and \((x-y)_{q}^{(0)}=1\), where x and y are real numbers and \(\mathbb{N}_{0} := \{ 0\} \cup \mathbb{N}\) [2]. Also, for \(\alpha \in \mathbb{R}\) and \(a \neq 0\), we have
If \(y=0\), then it is clear that \(x^{(\alpha )}= x^{\alpha }\) (Algorithm 1). The q-gamma function is given by \(\varGamma _{q}(z) = (1-q)^{(z-1)} / (1-q)^{z -1}\), where \(z \in \mathbb{R} \backslash \{0, -1, -2, \ldots \}\) [1]. Note that \(\varGamma _{q} (z+1) = [z]_{q} \varGamma _{q} (z)\). The value of q-gamma function is \(\varGamma _{q}(z)\) for input values q and z with counting the number of sentences n in summation by simplifying analysis (see Tables 1–3). For this design, we prepare a pseudo-code description of the technique for estimating q-gamma function of order n, which is shown in Algorithm 2. The q-derivative of function f is defined by \((D_{q} f)(x) = \frac{f(x) - f(qx)}{(1- q)x}\) and \((D_{q} f)(0) = \lim_{x \to 0} (D_{q} f)(x)\), which is shown in Algorithm 3 [2]. Also, the higher order q-derivative of a function f is defined by \((D_{q}^{n} f)(x) = D_{q}(D_{q}^{n-1} f)(x)\) for all \(n \geq 1\), where \((D_{q}^{0} f)(x) = f(x)\) [2, 3]. The q-integral of a function f defined on \([0,b]\) is defined by
for \(0 \leq x \leq b\), provided the series is absolutely convergent [2, 3]. The q-derivative of function f is defined by \((D_{q} f)(x) = \frac{f(x) - f(qx)}{(1- q)x}\) and \((D_{q} f)(0) = \lim_{x \to 0} (D_{q} f)(x)\), which is shown in Algorithm 3 [2, 3]. If \(a \in [0, b]\), then
whenever the series exists [2, 3]. The operator \(I_{q}^{n}\) is given by \((I_{q}^{0} h)(x) = h(x) \) and \((I_{q}^{n} h)(x) = (I_{q} (I_{q}^{n-1} h)) (x)\) for \(n \geq 1\) and \(g \in C([0,b])\) [2, 3]. It has been proved that \((D_{q} (I_{q} f))(x) = f(x) \) and \((I_{q} (D_{q} f))(x) = f(x) - f(0)\) whenever f is continuous at \(x =0\) [2, 3]. The fractional Riemann–Liouville type q-integral of the function f on J for \(\alpha \geq 0\) is defined by \((I_{q}^{0} f)(t) = f(t) \) and
for \(t \in J\) and \(\alpha >0\) [9]. Also, the Caputo fractional q-derivative of a function f is defined by
where \(t \in J\) and \(\alpha >0\) ([9]). It has been proved that \(( I_{q}^{\beta } (I_{q}^{\alpha } f)) (x) = ( I_{q}^{ \alpha + \beta } f) (x)\) and \((D_{q}^{\alpha } (I_{q}^{\alpha } f) ) (x)= f(x)\), where \(\alpha , \beta \geq 0\) ([9]). By using Algorithm 2, we can calculate \((I_{q}^{\alpha }f)(x)\), which is shown in Algorithm 4.
We say f is multi-singular when it is singular at more than one point t. Also, we say that \(D_{q}^{\alpha } u(t) + h(t)=0\) is a pointwise defined equation on J̅ if there exists a set \(E \subset \overline{J}\) such that the measure of \(E^{c}\) is zero and the equation holds on E. In this paper, we use \(\|\cdot\|_{1}\), \(\|\cdot\|\) and \(\Vert w \Vert _{*} = \max \{\| w\|, \|w'\| \} \) as the norm of \(\overline{\mathcal{L}} =L^{1}(\overline{J})\), the sup norm \(\overline{\mathcal{A}}=C(\overline{J})\), and the norm of \(\overline{ \mathcal{B}}= C^{1}(\overline{J})\), respectively. Let Ψ be the family of nondecreasing functions \(\psi : [0, \infty ) \to [0,\infty )\) such that \(\sum_{n=1}^{\infty } \psi ^{n}(t) < \infty \) for all \(t> 0\) [54]. One can check that \(\psi (t)< t\) for all \(t>0\) [54]. Let \(T : \mathcal{X} \to \mathcal{X}\) and \(\alpha : \mathcal{X} \times \mathcal{X} \to [0,\infty )\) be two maps. Then T is called an α-admissible map whenever \(\alpha ( x, y) \geq 1\) implies \(\alpha (Tx,Ty) \geq 1\) [55]. Let \((\mathcal{X}, \rho )\) be a complete metric space, \(\psi \in \varPsi \), and \(\alpha : \mathcal{X} \times \mathcal{X} \to [0, \infty )\) be a map. A self-map \(T : \mathcal{X} \to \mathcal{X}\) is called an α-ψ-contraction whenever \(\alpha ( s, t) \rho ( Ts, Tt ) \leq \psi ( \rho ( s, t))\) for all \(s, t \in \mathcal{X}\) [55]. We need the following results.
Lemma 1
([56])
Suppose that\(0< n-1\leq \alpha < n\)and\(u \in \overline{\mathcal{A}} \cap \overline{\mathcal{L}}\). Then\(I_{q}^{\alpha } D_{q}^{\alpha } u(t)= u(t)+ \sum_{i=0}^{n-1} c_{i} t ^{i}\)for some constants\(c_{i} \in \mathbb{R}\).
Lemma 2
([55])
Let\((\mathcal{X}, \rho )\)be a complete metric space, \(\psi \in \varPsi \), \(\alpha : \mathcal{X} \times \mathcal{X} \to [0,\infty )\)be a map, and\(T : \mathcal{X} \to \mathcal{X}\)be anα-admissibleα-ψ-contraction. ThenThas a fixed point wheneverTis continuous and there exists\(x_{0} \in \mathcal{X}\)such that\(\alpha ( x_{0}, Tx_{0}) \geq 1\).
3 Main results
First, we state and prove the following key results.
Lemma 3
Let\(\alpha \geq 2\), \(a, b \in J\), and\(v_{0} \in L^{1}(\overline{J})\). Then\(v(t)= \int ^{1}_{0} G_{q}(t,s) v_{0}(s) \,\mathrm{d}s\)is a solution for the pointwise defined problem\(D_{q}^{\alpha }u(t) + v_{0}(t) = 0\)with boundary conditions (2), where
and
Proof
Let \(E \subset \overline{J}\) be such that the equation \(D_{q}^{\alpha }u(t) + v_{0}(t) = 0\) holds for all \(t\in E\) and the measure of \(E^{c}\) is zero. Choose \(v \in \overline{\mathcal{A }}\cap \overline{ \mathcal{L}}\) such that \(v =v_{0}\) on E. If \(v_{0} \in \overline{\mathcal{ A }}\) is a solution for the pointwise defined problem, then we put \(v(t) = -D_{q}^{\alpha } u_{0}(t)\) for all \(t \in \overline{J}\). Note that \(v \in \overline{\mathcal{A}} \cap \overline{ \mathcal{L}}\) and \(v =v_{0}|_{E}\). Also, we have
for each \(t\in E\). Let \(t\in E^{c} \backslash \{0\}\). Choose \(\{ t_{n}\}\) in E such that \(t_{n} \to t^{-}\). Hence,
If \(t=0 \in E^{c}\), then \(I_{q}^{\alpha }( v_{0}(t)) = I_{q}^{\alpha } ( v(t))= 0\), and so \(I_{q}^{\alpha }( v_{0}(t)) = I_{q}^{\alpha } ( w(t))\) for all \(t \in \overline{J}\). Thus, \(I_{q}^{\alpha } ( D_{q} ^{\alpha }u(t)) = I_{q}^{\alpha }( - v_{0}(t))\) for each \(t \in \overline{J}\) whenever \(D_{q}^{\alpha }u(t) + v_{0}(t) = 0\) for \(t \in E\). Hence, \(I_{q}^{\alpha }(D^{\alpha }u(t)) = I_{q}^{\alpha }( - v(t))\) on J̅. By employing the boundary conditions and Lemma 1, we can conclude that
Since \(u'(0)= u(a)\), \(c_{1} = - I_{q}^{\alpha }v(a)\), and so \(u(t)= -I_{q}^{\alpha }v(t) + c_{0} - I_{q}^{\alpha }v(a)\). Hence,
So \(c_{0}= \int ^{b}_{0} u(s) \,\mathrm{d}s + I_{q}^{\alpha }v(1) + I _{q}^{\alpha }v(a)\). Thus,
Put \(h(t) = -I_{q}^{\alpha }v(t) + (1- t) I_{q}^{\alpha }v(a) + I_{q} ^{\alpha }v(1)\). Then we get
We consider two cases. If \(t\geq a\), then
If \(t\leq a\), then we have
Thus, equations (6) and (7) imply that \(h(t) = \int _{0}^{1} G_{q}^{0}(t,s) v(s) \,\mathrm{d}_{q}s\), and by entering \(h(t)\) in equation (5), we see that
This implies that
Thus, \((1 - b ) \int _{0}^{b} u(t) \,\mathrm{d}t = \int _{0}^{1} [ \int _{0}^{b} G_{q}^{0}(t,s) \,\mathrm{d}t ] v(s) \,\mathrm{d} _{q}s\), and so
Hence,
This completes the proof. □
Lemma 4
Let\(G_{q}(t,s)\)be given in Lemma 3. Then
\(\vert \frac{\partial G_{q}}{\partial t}(t,s) \vert \leq A_{2}( \alpha , b) (1-qs)^{(\alpha - 1)}\), where
and finally
for\(t, s \in \overline{J}\).
Proof
We consider some cases. If \(0 \leq s \leq t \leq 1\) and \(s \leq a\), then \((a - qs)^{\alpha - 1} \geq t(a - qs)^{(\alpha - 1)}\) and \((1 - qs)^{( \alpha - 1)} \geq ( t - qs)^{(\alpha - 1)}\). Hence,
and so \(G_{q}^{0}(t,s) \geq 0\). Thus, \(G_{q}(t,s) \geq 0\). In other cases, the proof is easy. One can see that \(G_{q}^{0}(t,s) \leq 3 (1- qs)^{(\alpha -1)}\) for each \(t,s \in \overline{J}\), and so
From q-Green function \(G_{q}^{0}(t,s)\) be given in Lemma 3, since
we have
and so
If \(0< s< t< 1\) and \(s\leq a\), then \(t - st >0\), and so \(t ( 1 -qs) - s + t>0\). Hence, \(s- t < (1- qs)t\) and \(t(1-qs) > t-qs \). Since \(t<1\) and \(\alpha \geq 2\),
and so
Thus, \(G_{q}^{0}(t,s) > (1-t) (1-qs)^{(\alpha -1)}\). If \(0< s\leq a < t <1\), then
and so \(G_{q}^{0}(t,s) > \frac{ (1- t)(1-qs)^{(\alpha -1)}}{ \varGamma _{q}(\alpha )}\). Hence,
and so inequality (8) holds. □
Consider the self-map \(T : \overline{\mathcal{B}} \to \overline{ \mathcal{B}}\) defined by
where \(G_{q}(t,s)\) is the q-Green function in Lemma 3. By applying Lemma 3, one can easily see that the fractional q-integro-differential equation (1) has a solution if and only if T has a fixed point.
Here, we provide our first result about the existence of solutions for problem (1).
Theorem 5
Assume that the mapTis defined by equation (9) and\(\omega : \overline{J} \times \overline{\mathcal{A}}^{4} \to \mathbb{R}\)is a singular function at some points\(t \in \overline{J}\), \(\mu _{1}, \ldots , \mu _{4} \in \overline{\mathcal{L}}\)are some nonnegative real-valued maps. Then fractional differential pointwise defined equation (1) under boundary conditions (2) has a solution whenever the following assumptions hold:
- (1)
The functionωsatisfies the contraction condition
$$ \bigl\vert \omega ( t, u_{1}, \ldots , u_{4}) -\omega (t, v_{1}, \ldots , v _{4}) \bigr\vert \leq \sum _{i=1}^{4} \mu _{i}(t) \Vert u_{i} - v_{i} \Vert $$for all\(u_{1}, \ldots , u_{4}, v_{1},\ldots ,v_{4} \in \overline{ \mathcal{B}}\)and\(t \in \overline{J}\).
- (2)
There exist a natural number\(k_{0}\), some functions\(\gamma _{1}, \ldots , \gamma _{k_{0}} \in \overline{\mathcal{L}}\), \(\varTheta _{1}, \ldots , \varTheta _{k_{0}} : \mathbb{R}^{4} \to [0,\infty )\), nonnegative maps\(\gamma _{1}, \ldots , \gamma _{k_{0}}\), and nonnegative and nondecreasing maps in their all components\(\varTheta _{1}, \ldots , \varTheta _{k_{0}}\)such that
$$ \bigl\vert \omega ( t,u_{1},\ldots , u_{4}) \bigr\vert \leq \sum_{i=1}^{k _{0}} \gamma _{i}(t) \varTheta _{i} (u_{1}, \ldots , u_{4}) $$for all\((u_{1},\ldots , u_{4}) \in \overline{\mathcal{B}}^{4}\)and\(t\in \overline{J}\)and\(\lim_{w\to \infty } \frac{ \varTheta _{i} (w,w,w,w)}{w} = \eta _{0}\), where\(\eta _{0}\)is a nonnegative real number with
$$ 0 \leq \eta _{0} \leq \frac{m_{0}}{M(\alpha , b) \sum_{i =1}^{k_{0}} \Vert \gamma _{i} \Vert + \delta _{0}} $$for some\(\delta _{0} > 0\), \(M(\alpha , b)= \max \{ A_{1}(\alpha , b), A_{2}(\alpha , b)\}\), and
$$ m_{0}= \min \bigl\{ 1, \varGamma _{q}(2 -\beta _{1}), \varGamma _{q}(\beta _{2} +1) \bigr\} . $$ - (3)
We have
$$ \tau (\alpha , b)= \biggl[\hat{\mu }_{1} + \hat{\mu }_{2} + \frac{ \hat{\mu }_{3}}{ \varGamma _{q}( 2 -\beta _{1})} + \frac{ \hat{\mu }_{4}}{ \varGamma _{q}(\beta _{2} + 1 )} \biggr] M( \alpha , b) < 1, $$where\(\hat{\mu }_{i}= \int _{0}^{1} (1-qs)^{(\alpha - 1)}\mu _{i}(s) \,\mathrm{d}_{q}s = \varGamma _{q}(\alpha ) I_{q}^{\alpha }\mu _{i}(1)\).
Proof
Let \(u_{1}, u_{2} \in \overline{\mathcal{B}}\) and t belong to J̅. Then we obtain
Since
\(\varGamma _{q}(\beta _{2} + 1) \|I_{q}^{\beta _{2}} u\| \leq \| u\|\). Hence,
Similarly, one can conclude that \(\varGamma _{q}( 2 - \beta _{1})\|D_{q} ^{\beta _{1}} u_{1} - D_{q}^{\beta _{1}} u_{2}\| \leq \| u_{1} - u_{2} \|\) for each \(u_{1}, u_{2} \in \overline{\mathcal{B}}\). Therefore
Also, we have
By using (10) and (11), we obtain
Hence, \(\| T_{u_{1}} - T_{u_{2}} \|_{*} \to 0\) as \(\| u_{1} - u_{2} \|_{*} \to 0\), and so T is continuous. Since \(\eta _{0} M(\alpha , b) \sum_{i=1}^{k_{0}} \| \gamma _{i}\| < m_{0}\), we can choose \(\varepsilon _{0} > 0\) such that
Since \(\frac{\varTheta (w,w,w,w)}{w} \to \eta _{0}\) as \(w \to \infty \), there exists \(r = \Delta (\varepsilon _{0})>0\) such that \(\frac{\varTheta ( w, w, w, w)}{w} < \eta _{0} + \varepsilon _{0}\) for all \(w \geq \Delta (\varepsilon _{0})\). So
for \(w\geq \Delta (\varepsilon _{0})\). Put \(B_{r} = \{ u\in \overline{ \mathcal{B}} : \| u\|_{*} < r \}\) and define \(\alpha : \overline{ \mathcal{B}}^{2} \to [0, \infty )\) by \(\alpha (u, v) = 1\) whenever \(u, v \in B_{r}\) and \(\alpha (u, v)=0\) otherwise. If \(\alpha (u, v) \geq 1\), then \(\|u\|_{*} \) and \(\|v\|_{*} \) are less than r. Let \(t \in \overline{J}\). Then we obtain
where
Since \(r >m_{0} r\), by using (12) we obtain
and so
Hence, \(\|T_{u}\| \leq r\). Also, one can conclude that
and \(\|T_{u}\|_{*} = \max \{ \|T_{u}\|,\|T'_{u}\|_{*} \} \leq r\). This implies that \(T_{u} \) and so \(T_{v} \in B_{r}\), that is, \(\alpha ( T _{u}, T_{v}) \geq 1\). Thus, T is α-admissible. Since \(B_{r} \neq \emptyset \), there exists \(u_{0} \in B_{r}\) such that \(T_{u_{0}} \in B_{r}\). Hence, \(\alpha ( u_{0}, T_{u_{0}} ) \geq 1\). Put \(\psi (t) = \tau (\alpha , b) t\) for each \(t \in [0, \infty )\), here \(\tau (\alpha , b) <1\). Since
and \(\psi : [0,\infty ) \to [0,\infty )\) is nondecreasing, we get \(\psi \in \varPsi \). Note that
and so
Also,
This implies
Thus, equations (13) and (14) imply that
for u and v in \(B_{r}\). Hence, \(\alpha (u, v) \|T_{u} - T_{v}\| _{*} \leq \psi ( \rho (u, v))\) for each \(u, v \in \overline{ \mathcal{B}}\). By using Lemma 2, T has a fixed point, which is a solution for problem (1). □
Theorem 6
Letωbe a real-valued function on\(\overline{J} \times \overline{ \mathcal{A}}^{4}\). Then the pointwise defined problem (1) with boundary conditions (2) has a solution whenever the following assumptions hold:
- (1)
There exist natural numbers\(k_{1}\), some maps\(\varTheta _{1}, \ldots , \varTheta _{k_{1}}:\mathbb{R}^{4} \to \mathbb{R}\)which are nondecreasing in their all components, \(\varTheta _{i}(w, w, w, w) \geq 0 \)for all\(w\geq 0\)and\(\frac{ \varTheta _{i} (w, w, w, w)}{w} \to \eta _{i}\)as\(w \to 0^{+}\)for some\(\eta _{i} \in [0, 1) \) (\(i=1, \ldots , k_{1}\)), and there are some nonnegative real-valued functions\(\mu _{1}, \ldots , \mu _{k_{1}} : \overline{J} \to [0, \infty )\)such that
$$\begin{aligned} &\bigl\vert \omega (t, u_{1},u_{2}, u_{3}, u_{4}) - \omega (t, v_{1}, v_{2}, v _{3}, v_{4}) \bigr\vert \\ &\quad \leq \sum_{i=1}^{k_{1}} \mu _{i} (t) \varTheta _{i}( u_{1} - v_{1}, u _{2}- v_{2}, u_{3}- v_{3}, u_{4}- v_{4}) \end{aligned}$$for all\(u_{1}, \ldots , u_{4}, v_{1},\ldots , v_{4} \in \overline{ \mathcal{B} }\)with\(u_{j} \geq v_{j} \geq 0\) (\(j=1,\ldots ,4\)) and\(t \in \overline{J}\).
- (2)
If\(M(\alpha , b)= \max \{ A_{1}(\alpha , b), A_{2}(\alpha , b)\}\), then
$$ M(\alpha , b) \sum_{i=1}^{k_{1}} \bigl\Vert (1-qt)^{(\alpha -1)} \mu _{i} \bigr\Vert _{1} \leq 1. $$
Proof
Since \(\lim_{w \to 0^{+}} \frac{\varTheta _{i}(w, w, w, w)}{ w} = \eta _{i} < 1\) for \(i=1,\ldots , k_{1}\), for each \(\varepsilon _{i} > 0\) there exist \(\delta _{i} = \delta (\varepsilon _{i}) > 0\) such that \(\frac{w}{m_{0}} \in (0, \delta _{i})\) implies
where \(m_{0} = \min \{ \varGamma _{q}(2 -\beta _{1}), \varGamma _{q} (\beta _{2} + 1)\}\). Let \(\varepsilon ^{0}_{i}\) be such that \(\eta _{i} + \varepsilon ^{0}_{i}< 1\) and \(\delta ^{0}_{i} = \delta ( \varepsilon ^{0}_{i})\). Put \(\eta = \max \{ \eta _{1}, \ldots , \eta _{k_{1}}\}\), \(\varepsilon _{0} = \min \{ \varepsilon ^{0}_{1}, \ldots , \varepsilon ^{0}_{k_{1}}\}\), and \(\delta = \min \{ \delta ^{0}_{1} , \ldots , \delta ^{0}_{ k_{1}}, \varepsilon _{0} \}\). Thus, \(\eta + \varepsilon _{0} < 1\) and
for \(\frac{w}{ m_{0}} \in (0, \delta )\) and \(1 \leq i \leq k_{1}\). Also,
Now, we define the map \(\alpha : \overline{\mathcal{B}} \times \overline{ \mathcal{B}} \to [ 0,\infty )\) by \(\alpha (u, v) =1\) whenever \(\| u - v\|_{*} \leq \delta \) and \(\alpha (u, v)=0\) otherwise. If \(\alpha (u, v) \geq 1\), then \(\| u - v\|_{*} \leq \delta \), and so
Hence, \(\|T_{u} - T_{v}\|_{*} \leq \delta \), which implies \(\alpha (T _{u}, T_{v})=1\). If
then by using the assumption we get \(\lambda <1\). If \(\psi (t) = \lambda t\), then \(\psi \in \varPsi \). If \(\|u - v\| \leq \delta \), then
and
Thus, from inequality (16), we have \(\|T_{u} - T_{v}\|_{*} \leq \lambda \|u - v\|_{*}= \psi (\| u - v\|_{*})\) and so \(\alpha ( u, v) \|T_{u} - T_{v}\|_{*} \leq \psi ( \|u - v\|_{*})\) for each \(u, v\in \overline{\mathcal{B}}\). Let \(\varepsilon > 0\) be given. Since \(\varTheta _{i} (\frac{w}{m_{0}}, \ldots , \frac{w}{m_{0}}) \to 0\) as \(w \to 0^{+} \), for each \(i=1, \ldots , k_{1}\), there exists \(\delta _{i} > 0\) such that \(\varTheta _{i} ( \frac{w}{ m_{0}}, \ldots , \frac{w}{ m_{0} }) < \frac{\varepsilon }{k'}\) for all \(0 < w \leq \delta _{i}\), where
If \(\delta = \min \{\delta _{i}: 1\leq i \leq k_{1} \}\), then \(\varTheta _{i} (\frac{w}{m_{0}}, \ldots , \frac{w}{m_{0}}) < \frac{ \varepsilon }{\lambda '}\) for all \(w \in (0, \delta ]\) and \(i=1, \ldots , k_{1}\). If \(u_{n} \to u\), then there exists a natural number \(n_{0}\) such that \(\|u_{n} - u\|_{*} < \delta \) for all \(n \geq n_{0}\). Hence,
for \(t \in \overline{J}\) and \(n \geq n_{0}\). By repeating the similar method, we obtain
for all t in J̅ and \(n \geq n_{0}\). Now, (18) and (19) imply that \(\|T_{u_{n}} - T_{u} \| \leq \varepsilon \) and \(\|T'_{u_{n}} - T'_{u} \| \leq \varepsilon \), respectively, for \(n \geq n_{0}\). Thus,
for \(n \geq n_{0}\), and so \(T_{u_{n}} \to T_{u}\) as \(u_{n} \to u\). Indeed, T is continuous. Now, we show that there exists \(u_{0} \in \overline{\mathcal{B}}\) such that \(\alpha (u_{0} , T_{u_{0}}) = 1\). In this way, we have to show that \(\|T_{u_{0}}- u_{0}\| \leq \delta \) for some \(u_{0}\in \overline{\mathcal{B}}\). Let \(r_{0} > 0\) be a fixed real number. Since \(\varTheta _{i}(w, w, w, w) \to 0\) as \(w \to 0^{+}\), for each \(\varepsilon > 0\), there exists \(n = n(\varepsilon )\) such \(0 < w \leq \frac{ r_{0}}{n}\) implies \(\varTheta _{i}( w, w, w, w) \leq \varepsilon \) for all \(1 \leq i \leq k_{1}\). Hence, \(\varTheta _{i}(\frac{ r_{0}}{ n }, \ldots , \frac{r_{0}}{n}) \leq \varepsilon \). Put
and choose \(\varepsilon _{M}\) such that
Take \(n_{1} = n(\varepsilon _{M})\) and choose a natural number \(n_{2}\) such that
If \(n_{0} = \max \{n_{1}, n_{2}\}\), then \(\varTheta _{i} ( \frac{M}{n _{0}}, \ldots , \frac{M}{n_{0}} ) \leq \varepsilon _{M}\) for \(1=1, \ldots , k_{1}\). Define
One can easily see that \(u_{0} \in \overline{\mathcal{A}}\) and \(u(t) \in [0, \frac{1}{n_{0}} ]\), \(u_{0} ( \frac{1}{n _{0} + 1} )= 0\) and
Hence, \(u'_{0} \) belongs to \(\overline{\mathcal{A}}\) and \(u'_{0}(\frac{1}{n _{0}+ 1} )= u'_{0}(\frac{1}{n_{0}}) = 0\). Thus, \(u_{0} \in \overline{ \mathcal{B}}\). Also, we have
and so \(n_{0} \|u_{n_{0}} \|_{*} \leq 1\). This implies that
for \(t \in \overline{J}\), and so \(\|T_{u_{0}} -u_{0} \| \leq \delta \). By using a similar method, we get
and so \(\|(T_{u_{0}} -u_{0})' \| \leq \delta \). Hence, from equations (20) and (21), we obtain \(\|T_{u_{0}} - u_{0} \|_{*} = \max \{\|T_{u_{0}} - u_{0} \|, \|(T_{u_{0}} - u_{0})' \| \} \leq \delta \). Thus, \(\alpha (u_{0}, T_{u_{0}}) = 1\). Now, by using Lemma 2, the map T has a fixed point, which is a solution for the multi-singular fractional q-problem (1). □
Now, we present our final result.
Theorem 7
Assume that\(\omega : \overline{J} \times \overline{ \mathcal{B} } ^{4} \to [0, \infty ]\)is such that\(\omega ( t, u_{1}, u_{2}, u_{3}, u_{4}) < \infty \)for all\(u_{1}, u_{2}, u_{3}, u_{4}\in \overline{ \mathcal{B}}\)and\(t\in E\), where\(E^{c}\)is a null subset ofJ̅, that is, the measure of\(E^{c}\)is zero, the map\(\omega (t, u_{1}, u_{2}, u_{3}, u_{4})\)is continuous with respect to the components\(u_{1}\), \(u_{2}\), \(u_{3}\), and\(u_{4}\)for all\(t\in E\). Then the pointwise defined problem (1) with boundary conditions (2) has a solution whenever the following assumptions hold:
- (1)
There exist a natural number\(n_{1}\geq 1\)and some maps\(\mu _{1}, \ldots , \mu _{n_{1}} : \overline{J} \to [0,\infty )\)such that\(\mu _{1}, \ldots , \mu _{n_{1}} \in \overline{\mathcal{L}}\), the maps\(F_{1}, \ldots , F_{n_{1}} : \mathbb{R}^{4}\to [0,\infty )\)and\(\varOmega : \mathbb{R}^{4} \to [0,\infty )\)so that
$$\begin{aligned}& \Vert \varOmega \Vert _{1}^{*} =\sup _{x \in \overline{\mathcal{L}} } \int _{0} ^{1} \varOmega \bigl( u(t), u(t), u(t), u(t) \bigr) \,\mathrm{d}t < \infty , \\& \Vert F_{i} \Vert _{\infty } = \sup _{w \in \mathbb{R}} \bigl\{ F_{i}( w, w, w, w)\bigr\} < \infty \end{aligned}$$for\(i=1,\ldots , n_{1}\)and
$$ \bigl\vert \omega ( t, u_{1}, u_{2}, u_{3}, u_{4}) \bigr\vert \leq \sum _{i=1}^{n_{1}} \mu _{i}(t) F_{i} (u_{1}, u_{2}, u_{3}, u_{4}) + \varOmega (u_{1}, u_{2}, u_{3}, u_{4}) $$for\(u_{1}, \ldots , u_{4} \in \overline{\mathcal{B}}\)and\(t \in \overline{J}\).
- (2)
There exist some maps\(\psi :\mathbb{R}^{4} \to [0,\infty )\)and\(h : \overline{J} \to [0,\infty )\)such that\(\| h \|_{1}^{L} = \varGamma _{q}(\alpha ) I_{q}^{\alpha }h(1) < \infty \)and\(h(t) \psi (u _{1}, \ldots , u_{4}) \leq \omega (t, u_{1}, \ldots , u_{4})\)for\(u_{1}, \ldots , u_{4} \in \overline{\mathcal{B}}\)and\(t \in \overline{J}\).
- (3)
There exist\(\gamma _{1}, \gamma _{2}, \gamma _{3}, \gamma _{4} \in \overline{\mathcal{L}}\)and\(\phi : [0, \infty ) \to [0, \infty )\)such that
$$ M( \alpha , b) \sum_{i=1}^{4} \Vert \gamma _{i} \Vert _{1} < 1, $$\(\phi _{m_{0}} \in \varPsi \)and
$$ \bigl\vert \omega ( t, u_{1}, \ldots , u_{4}) - w(t, v_{1}, \ldots , v _{4}) \bigr\vert \leq \sum _{i=1}^{4} \gamma _{i}(t) \phi \bigl( \Vert u_{i} - v _{i} \Vert \bigr) $$for all\((u_{1}, \ldots , u_{4})\)and\((v_{1}, \ldots , v_{4}) \in \overline{ \mathcal{B}}^{4}\)with\(\| u_{i}\|, \|v_{i}\| \in [\delta _{1}, \delta _{2}]\), where\(\phi _{\lambda }(z):= \phi (\frac{z}{\lambda })\)for all\(\lambda \in (0, \infty )\),
$$ \Vert \psi \Vert _{m}:= \min \bigl\{ \psi (u_{1}, \ldots , u_{4}): (u_{1}, \ldots , u_{4}) \in \mathbb{R}^{4} \bigr\} , $$\(2\delta _{1} \varGamma _{q}(\alpha ) (1- \alpha ) \leq \| \psi \|_{m} \|h \|_{1}^{L} ( 4 - \alpha ^{2} - 2\alpha )\)and
$$ \delta _{2} \geq M(\alpha ,b) \Biggl( \sum _{i=1}^{ n_{1}} \Vert F_{i} \Vert _{\infty } \Vert \mu _{i} \Vert _{1} + \Vert \varOmega \Vert _{1}^{*} \Biggr). $$
Proof
Let \(\{u_{n}\}\) be a sequence such that \(\|u_{n} - u\|_{*} \to 0\). Then \(u_{n} \to u\) and \(u'_{n} \to u'\). By using the inequalities \(\varGamma _{q}(2 - \beta _{1}) \|D_{q}^{\beta _{1}}( u_{n} - u) \| \leq \|(u _{n} -u)' \| \) and
we get \(D_{q}^{\beta } u_{n} \to D_{q}^{\beta } u\) and \(I_{q}^{\beta _{2}} u_{n} \to I_{q}^{\beta _{2}} u\). Since \(\omega (t, u_{1}, \ldots , u_{4})\) is continuous with respect to \(u_{1}, \ldots , u_{4}\) for all \(t \in E\), we can conclude that
for \(t\in E\). Let \(u \in \overline{\mathcal{B}}\) be given and \(t \in \overline{J}\). Then we have
If \(u_{M}(s) := \max \{u(s),u'(s), D_{q}^{\beta _{1}} u(s), I_{q}^{ \beta _{2}} u(s)\}\), then \(u_{M} \in \overline{\mathcal{A}}\), and so
Similarly, one can see that \(|T'_{u}(t)| \leq A_{2}(\alpha , b) [\sum_{i=1}^{n_{1} } \|F_{i}\|_{\infty } \| \mu _{i}\| + \|\varOmega \|_{1} ^{*} ]\). Thus,
for all \(u \in \overline{\mathcal{B}}\). By using the Lebesgue dominated convergence theorem, we conclude that
for t belonging to J̅, and so the self-map T on \(\overline{\mathcal{B}}\) is continuous. Define the map \(\alpha : \overline{ \mathcal{B}}^{2} \to [0,\infty )\) by \(\alpha (u, v)=1\) whenever \(\| u\|_{*}, \| v\|_{*} \in [\delta _{1}, \delta _{2}]\), \(\alpha (u, v)=0\), otherwise. If \(\alpha (u, v) \geq 1\), then \(\| u\|_{*}, \| v\| _{*} \in [\delta _{1}, \delta _{2}]\), and so
for \(t \in \overline{J}\). Thus, \(2 \varGamma _{q}(\alpha ) (1 - b) \|T _{u}\| \geq \|\psi \|_{m} \|h\|_{1}^{L} (4 - b^{2} - 2b) \), and so
By using (22), we obtain
and so \(\alpha (T_{u}, F_{v}) \geq 1\). If \(u_{0} \in [\delta _{1}, \delta _{2}]\), then it is easy to check that \(\alpha (T_{u_{0}}, u_{0}) \geq 1\). Let \(u, v \in [\delta _{1}, \delta _{2}]\). Then
Similarly, we conclude that
Now, (23) and (24) imply that \(\alpha (u , v) \| T _{u} - T_{v} \| \) and \(\alpha ( u, v) \| T'_{u} - T'_{v} \|_{*} \) are less than or equal to \(\phi _{ m_{0}}( \|u - v\|_{*})\) for all \(u, v\in \overline{\mathcal{B}}\). By using Theorem 2, the self-map T has a fixed point, which is a solution for problem (1). □
4 Examples and algorithms for the problem
Here, we provide some examples to illustrate our main results. In this way, we give a computational technique for checking problem (1). We need to present that a simplified analysis could be executed on values of the q-gamma function. To this aim, we consider a pseudo-code description of the method for calculation of the q-gamma function of order n in Algorithms 2, 3, 4, and 5 (for more details, see the link https://en.wikipedia.org/wiki/Q-gamma_function).
Example 1
Consider the following pointwise defined problem, similar to (1):
with boundary conditions \(u'(0)=u(\frac{5}{6})\), \(u(1)=\int _{0}^{ \frac{1}{2}} u(s) \,\mathrm{d}s\), and \(u''(0)=0\), where \(g(t) = 0\) whenever \(t \in \overline{J} \cap Q\), \(g(t) = t\) whenever \(t \in J \cap Q^{c}\). Let \(\alpha = \frac{7}{2}\), \(\beta _{1}= \frac{2}{3}\), \(\beta _{2} = \frac{1}{3}\), \(a= \frac{5}{6}\), and \(b= \frac{1}{2}\). Then we have
and
Tables 4 and 5 show the values of \(M(\alpha , b)\) in equation (26) and \(m_{0}\) in equation (27), respectively. Put
\(\mu _{1}(t)= \mu _{2}(t) =\mu _{3}(t) =\mu _{4}(t) = \mu (t)= \frac{1}{96\sqrt{ \pi } t^{\frac{1}{3}}}\), \(\gamma _{1}(t) = \gamma _{2}(t) = \gamma _{3}(t) =\gamma _{4}(t) =\gamma (t)= \frac{1}{96\sqrt{\pi } t^{\frac{1}{3}}}\) and \(\varTheta _{i} (u_{1}, u_{2}, u_{3}, u_{4} ):= \|u_{i}\|\) for \(i=1,\ldots ,4\). Then \(\|\mu \|_{1} = \|\gamma \|_{1} = \frac{1}{96\sqrt{ \pi }(1-\frac{1}{3})} = \frac{1}{64\sqrt{\pi } }\),
and
for all \((u_{1}, u_{2}, u_{3}, u_{4})\) and \((v_{1}, v_{2}, v_{3}, v _{4}) \in \overline{\mathcal{B}}^{4}\) and \(t \in \overline{J}\). On the other hand, we have \(\lim_{w \to \infty } \frac{\varTheta _{i}(w, w, w, w)}{w} = 1\), and by equations (26) and (27), we get
Table 6 shows the values of Λ. Choose \(\delta _{0}>0\) such that \(m_{0} \geq M( \alpha , b) \sum_{i=1}^{4} \| \gamma \|_{1}+ \delta _{0}\). Since
we obtain
Table 7 shows the values of \(\tau (\alpha , b)\). Now, by using Theorem 5, the pointwise defined problem (25) has a solution.
Example 2
Consider the fractional q-integro-differential equation
for \(t\in \overline{J}\), with boundary condition \(u'(0) =u( \frac{1}{2})\) and \(u(1)= \int ^{ \frac{1}{7}}_{0} u(s) \,\mathrm{d}s\). Put \(\alpha = \frac{5}{2}\), \(\beta _{1}=\frac{1}{4}\), \(\beta _{2}= \frac{1}{5}\), \(a = \frac{1}{2}\), \(b= \frac{1}{7}\), and \(k_{1}=1\). Note that
Table 8 shows the values of \(M(\alpha , b)\) in equation (31). Define
\(\mu (t)= \frac{0.09}{ t^{\frac{1}{4}} ( t -\frac{1}{3})^{\frac{1}{8}}}\), and
One can easily see that Θ is nondecreasing in all its components and \(\varTheta (w, w, w, w) \geq 0\) for all \(w \geq 0\). Assume that \((u_{1}, \ldots , u_{4})\) and \((v_{1}, \ldots , v_{4})\) belong to \(\overline{\mathcal{B}}^{4}\) and \(u_{i} \geq v_{i} \geq 0\) for \(i = 1, \ldots , 4\). Since \(( \frac{3}{5} )^{v_{i}} \geq (\frac{3}{5})^{u_{i}}\),
and so
Thus,
By replacing \(u_{i}\), \(v_{i}\) with \(\frac{2}{5}\sum_{i=1}^{4} u_{i}\), \(\frac{2}{5} \sum_{i=1}^{4} v_{i}\), respectively, we get
Hence, \(\varTheta (u_{1}, \ldots , u_{4}) - \varTheta (v_{1}, \ldots , v _{4}) \leq \varTheta (u_{1} - v_{1}, \ldots , u_{4} - v_{4})\). On the other hand, we have
and
Now, by using Theorem 6, the fractional q-integro-differential pointwise defined equation (30) has a solution.
Example 3
Consider the fractional q-integro-differential equation
with boundary condition \(u'(0) = u(\frac{1}{2})\) and \(u(1)= \int ^{\frac{4}{5}}_{0} u(s) \,\mathrm{d}s \), where \(g: \overline{J} \to [0,\infty )\) is defined by \(g(t) =0\) whenever \(t \in Q \cap \overline{J}\) and \(g(t) = \sqrt{t}\) whenever \(t \in Q^{c} \cap \overline{J}\) and the map \(F: \mathbb{R}^{4} \to [0,\infty )\) is defined by
Put \(\alpha = \frac{5}{2}\), \(\beta _{1}=\frac{1}{3}\), \(\beta _{2}= \frac{2}{3}\), \(a= \frac{1}{2}\), and \(b= \frac{4}{5}\). Then we have
and
Tables 9 and 10 show the values of \(M(\alpha , b)\) and \(m_{0}\) in equations (33) and (34), respectively. By simple checking, we can see that \(\|F\|_{\infty } = 1\). Let \(n_{1}=1\). Define the maps \(\psi ( u_{1}, \ldots , u_{4}):= F( u_{1}, \ldots , u_{4})\), \(\mu (t)= h(t)= \gamma (t) := 0.01t\), and \(\phi (t) =\frac{1}{2} t\). If \(\varOmega (u_{1}, \ldots , u _{4})=2\),
and \([\delta _{1} , \delta _{2}] =[0, 29]\), then \(\omega (t ,u_{1}, u _{2}, u_{3}, u_{4}) < \infty \) for \(u_{1}, \ldots , u_{4} \in \overline{ \mathcal{B}}\) and \(t\in E: = Q^{c}\cap \overline{J}\), \(\omega ( t, u _{1}, u_{2}, u_{3}, u_{4})\) is continuous with respect to the components \(u_{1}\), \(u_{2}\), \(u_{3}\), and \(u_{4}\) for all \(t\in E\),
and
for all \((u_{1}, \ldots , u_{4})\), \((v_{1}, \ldots , v_{4})\in \overline{ \mathcal{B}}^{4}\) and \(t \in \overline{J}\). Note that \(\phi _{m_{0}} \in \varPsi \),
and
Table 10 shows the values of equation (37). Now, by using Theorem 7, the fractional q-integro-differential pointwise defined equation (32) has a solution.
References
Jackson, F.H.: q-Difference equations. Am. J. Math. 32, 305–314 (1910). https://doi.org/10.2307/2370183
Adams, C.R.: The general theory of a class of linear partial q-difference equations. Trans. Am. Math. Soc. 26, 283–312 (1924)
Adams, C.R.: Note on the integro-q-difference equations. Trans. Am. Math. Soc. 31(4), 861–867 (1929)
Ahmad, B., Etemad, S., Ettefagh, M., Rezapour, S.: On the existence of solutions for fractional q-difference inclusions with q-antiperiodic boundary conditions. Bull. Math. Soc. Sci. Math. Roum. 59(107)(2), 119–134 (2016). https://www.jstor.org/stable/26407454
Ahmad, B., Nieto, J.J., Alsaedi, A., Al-Hutami, H.: Existence of solutions for nonlinear fractional q-difference integral equations with two fractional orders and nonlocal four-point boundary conditions. J. Franklin Inst. 351, 2890–2909 (2014)
Ahmad, B., Ntouyas, S.K., Purnaras, I.K.: Existence results for nonlocal boundary value problems of nonlinear fractional q-difference equations. Adv. Differ. Equ. 2012, 140 (2012). https://doi.org/10.1186/1687-1847-2012-140
Baleanu, D., Etemad, S., Pourrazi, S., Rezapour, S.: On the new fractional hybrid boundary value problems with three-point integral hybrid conditions. Adv. Differ. Equ. 2019, 473 (2019)
Balkani, N., Rezapour, S., Haghi, R.H.: Approximate solutions for a fractional q-integro-difference equation. J. Math. Ext. 13(3), 201–214 (2019)
Ferreira, R.A.C.: Nontrivials solutions for fractional q-difference boundary value problems. Electron. J. Qual. Theory Differ. Equ. 2010, 70 (2010)
Ntouyas, S.K., Samei, M.E.: Existence and uniqueness of solutions for multi-term fractional q-integro-differential equations via quantum calculus. Adv. Differ. Equ. 2019, 475 (2019). https://doi.org/10.1186/s13662-019-2414-8
Kalvandi, V., Samei, M.E.: New stability results for a sum-type fractional q-integro-differential equation. J. Adv. Math. Stud. 12(2), 201–209 (2019)
Samei, M.E., Ranjbar, G.K., Hedayati, V.: Existence of solutions for equations and inclusions of multi-term fractional q-integro-differential with non-separated and initial boundary conditions. J. Inequal. Appl. 2019, 273 (2019). https://doi.org/10.1186/s13660-019-2224-2
Samei, M.E., Khalilzadeh Ranjbar, G.: Some theorems of existence of solutions for fractional hybrid q-difference inclusion. J. Adv. Math. Stud. 12(1), 63–76 (2019)
Samei, M.E., Khalilzadeh Ranjbar, G., Hedayati, V.: Existence of solutions for a class of Caputo fractional q-difference inclusion on multifunctions by computational results. Kragujev. J. Math. 45(4), 543–570 (2021)
Zhao, Y., Chen, H., Zhang, Q.: Existence results for fractional q-difference equations with nonlocal q-integral boundary conditions. Adv. Differ. Equ. 2013, 48 (2013). https://doi.org/10.1186/1687-1847-2013-48
Samei, M.E.: Existence of solution for a class of fuzzy fractional q-integral equation. Int. J. Stat. Anal. 1(1), 1–9 (2019)
Liang, S., Samei, M.E.: New approach to solutions of a class of singular fractional q-differential problem via quantum calculus. Adv. Differ. Equ. 2020, 14 (2020). https://doi.org/10.1186/s13662-019-2489-2
Baleanu, D., Agarwal, R.P., Mohammadi, H., Rezapour, S.: Some existence results for a nonlinear fractional differential equation on partially ordered Banach spaces. Bound. Value Probl. 2013, 112 (2013). https://doi.org/10.1186/1687-2770-2013-112
Samei, M.E.: Existence of solutions for a system of singular sum fractional q-differential equations via quantum calculus. Adv. Differ. Equ. 2020, 23 (2020). https://doi.org/10.1186/s13662-019-2480-y
Samei, M.E., Hedayati, V., Ranjbar, G.K.: The existence of solution for k-dimensional system of Langevin Hadamard-type fractional differential inclusions with 2k different fractional orders. Mediterr. J. Math. 17, 37 (2020). https://doi.org/10.1007/s00009-019-1471-2
Agarwal, R.P., Baleanu, D., Hedayati, V., Rezapour, S.: Two fractional derivative inclusion problems via integral boundary condition. Appl. Math. Comput. 257, 205–212 (2015). https://doi.org/10.1016/j.amc.2014.10.082
Aghazadeh, N., Ravash, E., Rezapour, S.: Existence results and numerical solutions for a multi-term fractional integro-differential equation. Kragujev. J. Math. 43(3), 413–426 (2019). https://doi.org/10.1186/s13661-019-1251-8
Akbari Kojabad, E., Rezapour, S.: Approximate solutions of a sum-type fractional integro-differential equation by using Chebyshev and Legendre polynomials. Adv. Differ. Equ. 2017, 351 (2017)
Aydogan, M.S., Baleanu, D., Mousalou, A., Rezapour, S.: On high order fractional integro-differential equations including the Caputo–Fabrizio derivative. Bound. Value Probl. 2018(1), 90 (2018). https://doi.org/10.1186/s13661-018-1008-9
Aydogan, S.M., Baleanu, D., Mousalou, A., Rezapour, S.: On approximate solutions for two higher-order Caputo–Fabrizio fractional integro-differential equations. Adv. Differ. Equ. 2017(1), 221 (2017). https://doi.org/10.1186/s13662-017-1258-3
Baleanu, D., Ghafarnezhad, K., Rezapour, S., Shabibi, M.: On the existence of solutions of a three steps crisis integro-differential equation. Adv. Differ. Equ. 2018(1), 135 (2018). https://doi.org/10.1186/s13662-018-1583-1
Baleanu, D., Ghafarnezhad, K., Rezapour, S.: On a three steps crisis integro-differential equation. Adv. Differ. Equ. 2019, 153 (2019)
Baleanu, D., Mohammadi, H., Rezapour, S.: On a nonlinear fractional differential equation on partially ordered metric spaces. Adv. Differ. Equ. 2013, 83 (2013). https://doi.org/10.1186/1687-1847-2013-83
Baleanu, D., Rezapour, S., Mohammadi, H.: Some existence results on nonlinear fractional differential equations. Philos. Trans. R. Soc. A, Math. Phys. Eng. Sci. 371, 20120144 (2013). https://doi.org/10.1098/rsta.2012.0144
Baleanu, D., Mohammadi, H., Rezapour, S.: The existence of solutions for a nonlinear mixed problem of singular fractional differential equations. Adv. Differ. Equ. 2013, 359 (2013). https://doi.org/10.1186/1687-1847-2013-359
Baleanu, D., Mousalou, A., Rezapour, S.: A new method for investigating approximate solutions of some fractional integro-differential equations involving the Caputo–Fabrizio derivative. Adv. Differ. Equ. 2017(1), 51 (2017). https://doi.org/10.1186/s13662-017-1088-3
Baleanu, D., Mousalou, A., Rezapour, S.: The extended fractional Caputo–Fabrizio derivative of order \(0 \leq \sigma <1\) on \(C_{\mathbb{R}}[0,1]\) and the existence of solutions for two higher-order series-type differential equations. Adv. Differ. Equ. 2018(1), 255 (2018). https://doi.org/10.1186/s13662-018-1696-6
Baleanu, D., Mousalou, A., Rezapour, S.: On the existence of solutions for some infinite coefficient-symmetric Caputo–Fabrizio fractional integro-differential equations. Bound. Value Probl. 2017(1), 145 (2017). https://doi.org/10.1186/s13661-017-0867-9
Baleanu, D., Hedayati, V., Rezapour, S., Al-Qurashi, M.M.: On two fractional differential inclusions. SpringerPlus 5(1), 882 (2016)
Baleanu, D., Rezapour, S., Saberpour, Z.: On fractional integro-differential inclusions via the extended fractional Caputo–Fabrizio derivation. Bound. Value Probl. 2019, 79 (2019). https://doi.org/10.1186/s13661-019-1194-0
De La Sena, M., Hedayati, V., Gholizade Atani, Y., Rezapour, S.: The existence and numerical solution for a k-dimensional system of multi-term fractional integro-differential equations. Nonlinear Anal., Model. Control 22(2), 188–209 (2017)
Hedayati, V., Samei, M.E.: Positive solutions of fractional differential equation with two pieces in chain interval and simultaneous Dirichlet boundary conditions. Bound. Value Probl. 2019, 141 (2019). https://doi.org/10.1186/s13661-019-1251-8
Mohammadi, A., Aghazadeh, N., Rezapour, S.: Haar wavelet collocation method for solving singular and nonlinear fractional time-dependent Emden–Fowler equations with initial and boundary conditions. Math. Sci. 13, 255–265 (2019)
Rezapour, S., Hedayati, V.: On a Caputo fractional differential inclusion with integral boundary condition for convex-compact and nonconvex-compact valued multifunctions. Kragujev. J. Math. 41(1), 143–158 (2017). https://doi.org/10.5937/KgJMath1701143R
Samei, M.E., Hedayati, V., Rezapour, S.: Existence results for a fraction hybrid differential inclusion with Caputo–Hadamard type fractional derivative. Adv. Differ. Equ. 2019, 163 (2019). https://doi.org/10.1186/s13662-019-2090-8
Shabibi, M., Postolache, M., Rezapour, S., Vaezpour, S.M.: Investigation of a multisingular pointwise defined fractional integro-differential equation. J. Math. Anal. 7(5), 61–77 (2016)
Shabibi, M., Rezapour, S., Vaezpour, S.M.: A singular fractional integro-differential equation. Sci. Bull. Univ. Politeh. Buchar., Ser. A 79(1), 109–118 (2017)
Wang, Y.: Existence and multiplicity of positive solutions for a class of singular fractional nonlocal boundary value problems. Bound. Value Probl. 2019, 92 (2019)
Wang, Y.: Necessary conditions for the existence of positive solutions to fractional boundary value problems at resonance. Appl. Math. Lett. 97, 34–40 (2019). https://doi.org/10.1016/j.aml.2019.05.007
Alsaedi, A., Baleanu, D., Etemad, S., Rezapour, S.: On coupled systems of time-fractional differential problems by using a new fractional derivative. J. Funct. Spaces 2016, Article ID 4626940 (2016). https://doi.org/10.1155/2016/4626940
Baleanu, D., Rezapour, S., Saberpour, Z.: On fractional integro-differential inclusions via the extended fractional Caputo–Fabrizio derivation. Adv. Differ. Equ. 2019, 79 (2019). https://doi.org/10.1186/s13661-019-1194-0
Alizadeh, S., Baleanu, D., Rezapour, S.: Analyzing transient response of the parallel RCL circuit by using the Caputo–Fabrizio fractional derivative. Adv. Differ. Equ. 2020, 55 (2020). https://doi.org/10.1186/s13662-020-2527-0
Baleanu, D., Mohammadi, H., Rezapour, S.: Analysis of the model of HIV-1 infection of CD4+ T-cell with a new approach of fractional derivative. Adv. Differ. Equ. 2020, 71 (2020)
Zada, A., Alzabut, J., Waheed, H., Popa, I.L.: Ulam–Hyers stability of impulsive integrodifferential equations with Riemann–Liouville boundary conditions. Adv. Differ. Equ. 2020, 64 (2020). https://doi.org/10.1186/s13662-020-2534-1
Shabibi, M., Rezapour, S.: A singular fractional differential equation with Riemann–Liouville integral boundary condition. J. Adv. Math. Stud. 8(1), 80–88 (2015)
Wang, Y.: Existence of uniqueness and nonexistence results of positive solution for fractional differential equations integral boundary value problems. J. Funct. Spaces 2018, Article ID 1547293 (2018). https://doi.org/10.1155/2018/1547293
Wang, Y.: Positive solutions for a class of two-term fractional differential equations with multipoint boundary value conditions. Adv. Differ. Equ. 2019, 304 (2019). https://doi.org/10.1186/s13662-019-2250-x
Wang, Y., Liu, L.: Necessary and sufficient condition for the existence of positive solution to singular fractional differential equations. Adv. Differ. Equ. 2015, 207 (2015)
Ali, M.U., Tayyab, K., Karapinar, E., Vaezpour, S.M.: A new approach to α-ψ-contractive non-self multivalued mappings. J. Inequal. Appl. 2014, 71 (2014)
Samet, B., Vetro, C., Vetro, P.: Fixed point theorems for α-ψ-contractive type mappings. Nonlinear Anal. 75, 2154–2165 (2012)
Vong, S.W.: Positive solutions of singular fractional differential equations with integral boundary conditions. Math. Comput. Model. 57, 1053–1059 (2013)
Acknowledgements
Research of the first author was supported by Azarbaijan University of Shahid Madani, and research of the second author was supported by Bu-Ali Sina University. The authors express their gratitude to dear unknown referees for their helpful suggestions which improved the final version of this paper.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rezapour, S., Samei, M.E. On the existence of solutions for a multi-singular pointwise defined fractional q-integro-differential equation. Bound Value Probl 2020, 38 (2020). https://doi.org/10.1186/s13661-020-01342-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-020-01342-3