Abstract
Background
Larviciding against malaria vectors in Africa has been limited compared to indoor residual spraying and insecticide treated nets but is increasingly being considered by some countries as a complementary strategy. However, despite progress towards improved larvicides and new tools for mapping or treating mosquito-breeding sites, little is known about the optimal deployment strategies for larviciding in different transmission and seasonality settings.
Methods
A malaria transmission model, OpenMalaria, was used to simulate varying larviciding strategies and their impact on host-seeking mosquito densities, entomological inoculation rate (EIR) and malaria prevalence. Variations in coverage, duration, frequency, and timing of larviciding were simulated for three transmission intensities and four transmission seasonality profiles. Malaria transmission was assumed to follow rainfall with a lag of one month. Theoretical sub-Saharan African settings with Anopheles gambiae as the dominant vector were chosen to explore impact. Relative reduction compared to no larviciding was predicted for each indicator during the simulated larviciding period.
Results
Larviciding immediately reduced the predicted host-seeking mosquito densities and EIRs to a maximum that approached or exceeded the simulated coverage. Reduction in prevalence was delayed by approximately one month. The relative reduction in prevalence was up to four times higher at low than high transmission. Reducing larviciding frequency (i.e., from every 5 to 10 days) resulted in substantial loss in effectiveness (54, 45 and 53% loss of impact for host-seeking mosquito densities, EIR and prevalence, respectively). In seasonal settings the most effective timing of larviciding was during or at the beginning of the rainy season and least impactful during the dry season, assuming larviciding deployment for four months.
Conclusion
The results highlight the critical role of deployment strategies on the impact of larviciding. Overall, larviciding would be more effective in settings with low and seasonal transmission, and at the beginning and during the peak densities of the target species populations. For maximum impact, implementers should consider the practical ranges of coverage, duration, frequency, and timing of larviciding in their respective contexts. More operational data and improved calibration would enable models to become a practical tool to support malaria control programmes in developing larviciding strategies that account for the diversity of contexts.
Similar content being viewed by others
Background
Larviciding is the application of biological or chemical insecticides that kill the immature stages of mosquitoes, and is one of the approaches of larval source management (LSM), along with habitat modification, habitat manipulation and biological control [1]. The World Health Organization (WHO) recommends larviciding as a supplementary intervention against malaria in addition to the core vector control interventions of insecticide-treated bed nets (ITNs) and indoor residual spraying (IRS) [2]. Larviciding is recommended in areas where the intervention is feasible and cost-effective, mostly in urban areas and during the dry season where breeding sites are ‘fixed, few and findable’ [1, 2]. Biolarvicides, Bacillus thuringiensis israelensis and Bacillus sphaericus, are currently the most prominent larvicides as they are environmentally safe [3]. However, under most environmental conditions, they have short residual effectiveness (B. thuringiensis israelensis lasts for only 1–2 weeks [7,8,9] and B. sphaericus for 2–3 weeks [6, 7]). Frequent applications have been widely recognized as a challenge for effective large-scale implementation [11,12,13,14,15].
Larviciding was widely used in the first half of the 20th Century, most successfully outside sub-Saharan Africa, but fell out of favour after the introduction of IRS with DDT [1, 13,14,15,16]. In the last decade, LSM, especially larviciding, has been reconsidered within an integrated vector management approach, especially as longer-lasting agents [17,18,19], or novel deployment strategies and breeding site identification, i.e., using drones [20, 21] might become increasingly available [22]. Post-2000, pilot programmes of larviciding have been conducted in urban and in rural areas in multiple countries of Africa [3, 9, 15, 21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. For example, the Urban Malaria Programme in Dar es Salaam, Tanzania, demonstrated operational feasibility and effectiveness of larviciding on larvae reduction and epidemiological outcomes in urban areas [11, 26]. In Burkina Faso, a trial in 84 rural villages with B. sphaericus applications during the main transmission season showed larviciding to be feasible and cost-effective when targeted to the most productive breeding sites [25, 43]. Pilot implementations have previously been included in national malaria strategic plans in Eritrea [7, 38, 44, 45], Zambia [31, 46, 47] and Nigeria [48]. Despite the long history of larviciding, its impact on malaria prevalence in humans [9, 49] in different settings, and the influence of variations in its application, particularly frequency and timing of the year as well as duration [6, 17, 40], remain insufficiently understood. For example, the application during the rainy season was described as impractical and less effective in study sites in Tanzania and The Gambia [26, 40], but as feasible in the study in Burkina Faso [24, 42], whereas its effectiveness during the dry season, as currently recommended, is still being debated [1, 16].
Mathematical models have been used to simulate mosquito population dynamics and the relationship between larval stages and adult mosquitoes [50,51,52,53,54,55,56,57,58,59,60]. However, most models consider only a small sub-set of the highly variable larviciding deployment scenarios. The models also include implicit assumptions about optimal deployment in relation to seasonality, (i.e., deployments either throughout the year, during rainy season or during dry seasons) and duration of larviciding effectiveness (i.e., constant or interrupted) without regard to re-treatment intervals and duration of product efficacy. While models have been used to simulate variations in the deployment strategies for other malaria control interventions, such as IRS [61,62,63,64] and drugs [64,65,66,67], larviciding strategies have not been investigated as much. In this study the impact of larviciding applications was simulated to assess the influence of different deployment strategies on expected entomological outcomes and malaria infections in humans for different seasonality and transmission settings.
Methods
Larviciding and influencing factors
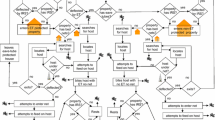
The application and effectiveness of larviciding is highly dependent on aquatic habitat characteristics and mosquito species [1]. Identification and accessibility of these habitats throughout the year is problematic yet essential [8, 11, 12]. Larviciding can reduce the number of emerging mosquitoes with a lag of two to three weeks between larviciding and reduction in adult mosquito density [4]. The number of infected host-seeking mosquitoes determines the entomological inoculation rate (EIR), which is related to the number of new infections in humans and the proportion of humans carrying malaria parasites. An overview of the most relevant influencing factors on larviciding application and effectiveness is shown in Fig. 1.
Flowchart of factors influencing larviciding effectiveness and malaria transmission outcomes. The flowchart reads from left to right, with climate and environmental factors influencing the whole system and relationships inside. This study focuses on the deployment factors and their impact on the quantifiable outcomes as highlighted in blue. All other factors were considered standard and non-varying
Mosquito dynamics
A deterministic discrete-time model of overlapping generations of mosquitoes with a time step of one day was used [63, 64]. This was extended to include density-dependent larval dynamics using a Beverton-Holt formulation [71, 72]. This model includes a single juvenile stage of mosquitoes arising at a rate proportional to the time-lagged number of eggs laid, with the larval population regulated by periodically varying larval-carrying capacity and the larvae progressing to host-seeking adults at a constant rate. The assumed lag times between rainfall was 10 days for mosquito emergence, 20 days for host-seeking mosquitoes and 30 days to actual transmission events (measured as EIR). The models and derived parameters are described in Additional file 1. The entomological model was connected to a stochastic individual-based model for malaria in humans [74] within the OpenMalaria platform [68, 69, 74,75,76], for which the source code is available online [77]. The parasite densities per simulated infection vary by 5-day time steps.
Model parameterization
Malaria transmission intensity was defined as annual pre-larviciding EIR and simulated with three intensity levels: 3 infectious bites per person per annum (ibpa) for low transmission, 10 ibpa for moderate transmission and 90 ibpa for high transmission. Seasonality was characterized as high or medium seasonal with either one or two peaks and reproduced from another modelling study [78]. The seasonality in transmission was assumed to follow the same pattern as the rainfall with a lag of one month, and lag time between key indicators are shown in Additional file 2: Fig. S2.1. The characteristics of the setting, including resistance, host preferences and biting behaviour were held constant over time. Differences between species were not considered, and a previously determined parameterization for Anopheles gambiae sensu stricto (s.s.), predominantly indoor biting and anthrophilic, was used. To explore sensitivity to highly uncertain mosquito population density-dependency parameters, the survival probability of larvae, the development duration and the number of female eggs per gonotrophic cycle were varied.
Simulated parameters of larviciding included the coverage, deployment duration, application frequency, and seasonal deployment. The coverage was defined as the reduction in emerging mosquitoes as a result of treated breeding sites (operational coverage) and larvicide efficacy (Additional file 3). It was assumed that important aquatic habitats had been pre-identified and characterized, and that they were accessible and evenly distributed. Larviciding deployment duration was simulated for 120 and 356 days, allowing for irregular applications, but with fixed efficacy duration of the minimum time step (5 days). The seasonal deployment was described in terms of the number of months during which larviciding was applied per year (beginning, during or end of the rainy season, during the dry season or throughout the year) (Fig. 2).
Illustration of setting and deployment specific parameter. A Larviciding coverage, held constant for all deployments. B Deployment frequency during one deployment period of 120 days. The deployment frequency is characterized by the number of deployments per unit of time (rectangles on the right) and characterizes the lengths of gaps in effective coverage between single deployments. The blue lines correspond to the duration of time the larvicide is active, assumed to be 5 days. The emergence rate is unaffected outside of these blue lines. C Transmission seasonality patterns reproduced from [78]. D Seasonal deployment times with larviciding starting at different months (12 independent scenarios) assuming a constant efficacy of 120 days, or 365 days in case of deployment ‘throughout the year’, included for comparison
Simulation scenarios
The larviciding parameters were explored with three distinct simulation experiments. Larviciding was simulated: (1) for 365 days at maximum application rate throughout the year and constant transmission (no seasonality); (2) for 120 days at varying application rates and coverage at constant transmission throughout the year; and, (3) for 120 days at maximum application rate starting in different months during the year considering four different seasonality profiles. Simulations 1 and 2 were run with 11 coverage levels, three transmission intensities, 18 unique mosquito density dependency parameter combinations, and three stochastic representations, whereas the coverage levels and density parameters were reduced for Simulation 3 to limit simulation size. Simulations were run for a host population of 10,000 people, with a ‘warm-up’ period equivalent to 60 years before the implementation of larviciding. The ‘warm-up’ period led to the defined level of transmission assumed to result from previous interventions not explicitly simulated (Table 1).
Analysis of simulation outputs
The outputs of the simulations included the number of larvae emerging and surviving to first feeding cycle (mosquito emergence), the number of host-searching mosquitoes, the EIR, and the Plasmodium falciparum parasite rate in the human population, assessed during the intervention period, at the end of the intervention period or one year after the intervention period. The impact of larviciding was assessed by comparing the scenarios with larviciding to those without larviciding, defined as the counterfactual. The relative reduction (RR) compared to no larviciding, was calculated per 5-day time step paired by deployment parameters. The mean of the RRs per time step was calculated for the entire duration (meanRR). The equations are shown below, where t denotes the time step and n the total number of time steps, either at the end of the larviciding intervention or one year after intervention start, in the results specified in the figure captions.
where, X[.] denotes the model outputs (EIR,vector density or prevalence) for either the counterfactual scenario or with larviciding intervention.
The loss in the effectiveness was defined as 1-meanRR calculated at the end of the evaluation period, either after larviciding was stopped or one year after larviciding started. For the prevalence and EIR, the predicted value at the time point (at the end of the evaluation period) was taken, whereas for the vector outcomes the average was taken. The three seeds were averaged and the simulated range among the mosquito population density-dependency parameters was used to obtain uncertainty intervals. Linear regression models were run to quantify the relationship between deployment frequency or coverage and reduction on prevalence.
Simulation to represent a study site
Additional simulations were run to compare the predicted with the reported impact of larviciding and to establish the relationship between effective coverage and reported operational coverage based on a field study conducted before other vector control interventions were scaled up [6]. In that study, larviciding was applied in Mbita, a rural village in western Kenya, between June 2002 and September 2004 using B. thuringiensis israelensis and B. sphaericus. The number of treated breeding sites per deployment ranged from 65 to 219 among the 50 applications during the study period. Simulation scenarios intended to represent the study site and informed parameters as reported for the annual baseline transmission intensity, the seasonality, vector species, time of larviciding applications and the larvicide, only varying the coverage. A detailed description of the study is available in the publication by Fillinger et al. [6], and the simulations set-up is included in Additional file 4.
Results
Impact of effective coverage and duration of larviciding (Simulation 1)
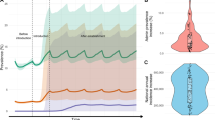
The impact of larviciding coverage and duration is shown in Fig. 3. After one year of larviciding at 60% coverage, the number of host-seeking mosquitoes was reduced by 62% (range 60–70%), the EIR by 81% (range 78–86%), and the prevalence by 48% (range 45–55%), assuming moderate transmission and no seasonality (Fig. 3A). The number of host-seeking mosquitoes and EIR appeared to reach equilibrium ahead of malaria prevalence rates. The effects on host-seeking mosquitoes started immediately after larviciding but EIR started to decrease after around 10 days and faster than for host-seeking mosquitoes. Malaria parasite prevalence was predicted to decrease around two months after larviciding and had the lowest RRs compared to the other outcomes.
Simulated relative reduction in host-seeking mosquitoes, EIR and prevalence after one year of larviciding. A Relative reduction for different coverage levels over time at moderate transmission (EIR = 10 ibpa). B Relative reduction by coverage at different transmission intensities after one year. The shaded area indicates the minimum and maximum range among variation in the mosquito density-dependence parameters. The t denotes the time in days after intervention start
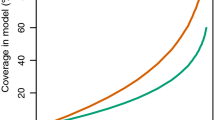
The relationship between effective coverage and reduction in prevalence depended highly on the pre-intervention transmission intensities, with the greatest RRs being in low-transmission settings. An effective coverage above 60% can be considered as high, since it refers to the reduction in all emerging adult mosquitoes, whereas in practice not all breeding sites might be identified, and treatment might not affect all premature stages within a breeding sites equally (Additional file 3). Taking 60% effective coverage as an example, the RR in prevalence at low EIR was around four times higher than at high EIR (meanRREIR-3 = 66% vs. meanRREIR-90 = 17%) (Fig. 3B), while at 20% coverage the RR was almost 10 times higher (meanRREIR-3 = 25% vs. meanRREIR-90 = 2.5%). The population density dependency parameters did not substantially influence these relationships, nor the immediate effect of larviciding, however extreme values considerably delayed re-population after high reductions in the mosquito population (Additional File 2: Fig. S2.2 and S2.3). Coverage of larviciding strongly influenced the overall impact of the intervention, except at high transmission intensities (EIR > 90 ibpa) where larviciding was predicted to not have much impact, showing the higher the transmission intensity the lower the impact of the intervention.
Impact of deployment frequency of larviciding (Simulation 2)
The highest impact at any larviciding coverage was achieved at maximum duration of the intervention period (assumed to be 120 days for this specific simulation) (Fig. 4). In practice, this could be achieved through frequent deployments with short-lived larvicides or fewer deployments when using larvicides that have longer residual efficacy. Interrupting the effective coverage by deployment every 10 instead of every 5 days resulted in a loss of effectiveness by 54% (51–56%) for mean host-seeking mosquito density, by 45% (39–49%) in EIR, and by 53% (45–70%) in prevalence. This had assumed coverage of 80%, averaged over the three transmission intensities. For host-seeking mosquitoes, there was high interaction between frequency and coverage with higher loss in impact at high than at low coverage (Fig. 4B). For EIR and prevalence (Fig. 4C), the levels of pre-larviciding transmission intensity influenced the impact of deployment frequency on prevalence but not on EIR. For instance, for a deployment of larviciding at 80% every 10 days (when assuming a short-lived larvicide effective for 5 days), the resulting RR in EIR was predicted at 49% (46–56%) for a pre-intervention EIR of 3 ibpa, 47% (45–53%) for a EIR of 10 ibpa, 44% (41–50%) for a EIR of 90 ibpa. The corresponding RRs in prevalence were 17% (14–21%), 12% (9–13%) and 4% (3–5%) for EIR of 3, 10, and 90 ibpa, respectively.
Relative reduction in outcome measures resulting from varying deployment frequencies. A Impact of larviciding on the different outcomes measured over time and per deployment frequency (panels) for 80% coverage and in moderate transmission intensity (EIR = 10 ibpa). B Mean relative reduction in mosquito emergence during the intervention period by frequency and larviciding coverage irrespective of transmission intensity (averaged for EIR values of 3, 10 and 90 ibpa). C Relative reduction in EIR and prevalence at the end of the larviciding deployment period with larviciding at 80% coverage and varying frequency. The t denotes the time in days after intervention start. The Figure shows simulation results for a deployment period of 120 days (no seasonality)
An increase of 1% in coverage would lead to an average increase of the impact in prevalence by 0.10%, while an additional lag of 5 days between deployments would decrease the RR in prevalence by 2.32% (Fig. 4). To achieve and maintain high impact of larviciding with a short efficacy, the frequency of deployments was more important than the coverage. For instance, an increase in the coverage from 40 to 80% for deployment every 5 days increased the RR in prevalence from 18 to 36%, whereas not even 100% coverage could compromise fewer deployments that leave gaps in effective coverage to achieve the same reduction (Additional file 2: Fig. S2.4).
Impact of timing on effectiveness of larviciding (Simulation 3)
The timing of larviciding relative to the transmission season substantially influenced the impact on the prevalence. Regardless of seasonality, transmission intensity or coverage, larviciding in the rainy season was most impactful in reducing EIR and prevalence, followed by deployment during the beginning of the rainy season, followed by deployment at the end of the rainy season. For highly seasonal settings, larviciding during the rainy season (for 120 days) was predicted to have a similar impact as deployment all year round, whereas larviciding at the end of the rainy season or during the dry season (for 120 days) had a very low impact. In moderate endemicity setting (EIR = 10 ibpa), larviciding at 80% coverage was predicted to reduce the prevalence after one year by 58% when deployed all year round, by 57% when implemented during the middle of the rain season, by 40% when implemented at the beginning of the rainy season, by 9% at the end of the rainy season and no reduction when deployed at the dry season. The RR in prevalence was on average across the deployment timing 10% higher at lower transmission (EIR = 3 ibpa) and 20% lower at higher transmission (EIR = 90) compared to the reduction simulated for the moderate transmission level (Additional file 2: Fig. S2.9).
The optimal deployment timing for highest impact on prevalence was found to be three months before the peak in transmission, assuming lasting effectiveness until one month after the peak. When coverage of larviciding during the rainy season was reduced to 20% (intended to represent operational challenges to cover all breeding sites during the rainy season), the impact of larviciding, although substantially lower (19% difference in peak meanRR), remained higher when deployed during the dry season, especially at high seasonality with one transmission season. At medium seasonality and two transmission seasons, the optimal deployment timing became less distinct (Fig. 5B). The model predictions therefore suggest that timing the larviciding deployment to the rainy season would be more impactful, even at lower coverage, than achieving high coverage during the other seasons, even when the effective coverage would drop to a coverage of 20%, given the transmission and seasonality scenarios considered in this analysis. Additional seasonal plots are provided in the Additional file 2: Fig. S2.7–10.
Relative reduction in prevalence due to larviciding compared by seasonal timing at moderate transmission intensity (EIR = 10). A Reduction in prevalence after one year with larviciding deployed for one year compared to 120 days at varying seasons. The x-axis shows the effective larviciding coverage, with coverage above 60% shadowed in grey as these coverage levels might be difficult to achieve in practice [54, 56]. The diagonal black line indicates a 1-to-1 relationship. B Relative reduction in prevalence at the end of the deployment period (120 days) at moderate transmission for varying deployment starts, relative to the peak in transmission. The t denotes the time in days after intervention start. Mosquito density-dependence parameters were fixed and uncertainty intervals are not shown
Comparison of deployment factors and post-larviciding resurgence (Simulation 2)
After the end of an assumed intervention period of 120 days, the number of host-seeking mosquitoes resurged immediately to pre-larviciding levels whereas the EIR, after an initial drop, resurged at a slower rate and the prevalence resurged at the slowest rate after a delay of 25–30 days (Additional file 2: Fig. S2.5). A year after the end of the intervention period, the EIR and prevalence did not return fully to pre-larviciding levels, depending on the deployment factors and achieved impact. The higher the maximum reduction during the intervention period (as a product between coverage and frequency), the slower the resurgence to initial levels (Fig. 6). The reduction in EIR and prevalence that remained after the intervention period also varied depending on when larviciding was applied as well as the seasonal pattern (Additional file 2: Fig. S2.6).
Residual impact in outcome measures by deployment frequencies. A Decay of achieved impact on the different outcomes measured over time after stopping larviciding per deployment frequency (panels) for a demonstrative 100% coverage at moderate transmission intensity (EIR = 10 ibpa). B Remaining relative reduction in EIR and prevalence by coverage and frequency after one year of intervention stop compared to at the end of the intervention period. Note the relative reduction in prevalence is selected at the specified time steps while the prevalence reaches a maximum around 30–60 days after the intervention period of 120 days (Fig. A2.6). Results shown for a deployment period of 120 days (no seasonality) and moderate transmission intensity, with uncertainty intervals and error bars corresponding to simulated range of mosquito density-dependence parameters
Re-simulated larviciding study
In the selected field study in Mbita, western Kenya, larviciding was reported to reduce the larval density by 95%, the adult density by 92%, and the EIR from 9 to 0.8 ibpa during the two-year intervention period compared to the pre-and post-intervention period [6]. Larviciding was simulated with the same number of deployments as reported (on average every 11 days when using B. thuringiensis israelensis, every 22 days when using B. sphaericus (Additional file 4: Table S4.1)) with a range of larviciding coverage between zero and 100%, using an input EIR of 10 ibpa. At an assumed effective coverage of > 90%, the maximum reduction in larval density was around 77%, in adult density 67%, and in EIR 40%. The reported high reductions in adult density and EIR of > 90% could only be simulated with assumed constant effectiveness and unrealistically high coverage (predicted to reduce the larval density by 94%, the adult density by 93% and the EIR from 10 to 1.37). The results are shown in Additional file 4.
Discussion
This modelling study investigated the impact of larviciding deployment strategies varying by coverage, duration, application frequency, and seasonal timing, for three transmission intensities (3, 10 or 90 ibpa), and five seasonality patterns, assuming homogeneous vector population similar to An. gambiae. Overall, larviciding impacted the prevalence at a slower rate than the number of host-seeking mosquitoes and transmission intensity, while reduction in prevalence remained beyond the intervention period. The effective coverage during the intervention period, as a result of the efficacy duration of the larvicide, frequency and emergence reduction (effective coverage per single application), highly influenced the impact of larviciding. To ensure high impact, the product of the deployment factors need to be high, with regular deployments, tailored at the efficacy duration of the larvicide being more important than the effective coverage (number of emerging mosquitoes killed at each single round of larviciding) even at high coverage, when assuming short-lived larvicides. In highly seasonal settings, the deployment during the rainy season was predicted to have the highest impact on EIR and prevalence even at much lower coverage than during the dry season, and dry season larviciding had negligible impact. Larviciding at lower compared to high transmission intensity was further predicted to have a higher epidemiological impact with greater and longer lasting RR in the prevalence. This difference could be attributable to the differences in mosquito densities and faster rate of re-establishment at high transmission after lavicide decay to be effective (Additional file 2: Fig. S2.5).
Field observations [4, 9] and simulations agree that larviciding reduces the number of emerging mosquitoes for the duration of the killing effect and that the vector population re-establishes immediately afterwards [4, 37, 80]. In field studies, the time to reduce numbers of host-seeking mosquitoes varies between immediate impact and to lag times of two to three weeks [4, 37, 80], with reductions in host-seeking mosquitoes ranging from very low to almost as high as the reduction in observed larval density [6, 17, 40]. The simulations showed that prevalence is affected at a slower rate than the mosquitoes and transmission intensity and did not reach an equilibrium after one year of constant larviciding. This relates to the important role of duration of infection and parasite reservoirs in humans. It requires more time to clear infections in the human population by only reducing the mosquito population, whereas the reduction will also depend on malaria case management, which was not included in the simulations. However, this finding indicates that longer follow-up times would be required in field studies to capture impact of larviciding on prevalence with follow-up times varying depending on the seasonality.
Shorter intervals between deployments to reduce gaps in effective coverage over time were predicted to increase the average impact and reduce fluctuations in outcomes, as observed in two studies in Kenya [6, 81]. In practice, the required deployment frequency depends on the emergence rate of new breeding sites and the persistence of the specific active agent [5, 7, 17, 42, 82]. Notably, some programmes focus on treating only productive breeding sites [10, 59], a strategy considered cost-effective in a rural district in Burkina Faso [25]. Concentrating efforts on peri-domiciliary breeding sites has also been advocated [83]. The appropriate deployment strategy to achieve high coverage of larviciding, or LSM in general, will further depend on dispersal of breeding sites and total land area to cover, surface area and quantity of breeding sites as well as their proximity to houses.
Larviciding is currently recommended by the WHO to be deployed in areas or seasons where breeding sites are fixed, few and findable, commonly associated with the dry season or urban areas [1, 2], however, the simulation results suggest that larviciding in the dry season would have limited impact in seasonal settings. The results further suggest that the additional benefit of larviciding throughout the year would be marginal in highly seasonal settings. The greatest impact on prevalence was predicted when implementation preceded the peak in transmission, hence averting seasonal increases in host-seeking mosquito density. However, rainy season larviciding is more challenging, in particular because of proliferation of breeding sites and dilution of larvicide [17, 29, 33, 81], while on the other hand emergence rates might be reduced when larvae are flushed away by very high rainfall [18, 81, 84]. The trade-off between achieving high coverage (often described as more feasible in the dry season or arid areas [1, 85]) and the epidemiological impact associated with a given coverage (in simulation estimated higher in the rainy season) must play out differently in diverse environments and might well account for some of the variation in seasonal patterns of impact observed in the field. In this modelling study, the operational challenge was attempted to reflect lowering the coverage during the rainy season while keeping the coverage during the dry season high, which did not change the recommended timing for larviciding unless coverage dropped to less than 20% of emerging mosquitoes killed. Alternative approaches to adjust for operational challenges would include simulating shorter effectiveness [29] or more frequent deployments [81] in the rainy season, presumably with similar implications. The results apply for settings with low vector densities and little to no transmission during the dry season, and where peak in transmission follows with one month lag after peak in rainfall.
The model results suggest that the relative impact would be greater at low than at high transmission in which high coverage would be needed. Nevertheless, larviciding has been successfully deployed in moderate to high transmission areas in several studies [27, 37, 86]. One study in particular showed that larviciding could be implemented at high transmission in highly seasonal areas with findable breeding sites [86]. Reduction in prevalence has rarely been studied in larviciding field studies [9] although one study reported a reduction of more than 70% [26]. Based on the simulations, such high reductions would only be achievable at very high coverage and long duration of effective larviciding, either with more frequent deployments or longer residual activity (e.g., longer than 120 days), and seems unlikely to be achieved with larviciding alone as reported in the study.
In most instances, larviciding, recommended as a supplementary intervention [1], will be deployed alongside ITNs or IRS, to reduce transmission and create a context where larviciding is more effective. While interactions were not explicitly modelled, implicitly synergistic effects with these interventions were assumed by simulating low pre-larviciding transmission intensity. This assumption is supported by the higher impact at low transmission seen in the predictions. For the same reason, synergies with chemotherapeutic interventions can also be anticipated [87]. Further synergies are likely where there is insecticide or drug resistance because larvicides have different biochemistry and act independently of host-seeking and resting behaviour of adult mosquitoes [14], and they can address transmission that is refractory to the core interventions. In practice, larviciding might also be combined with other LSM approaches [1, 88, 89] that together reduce the adult mosquito emergence in an area.
Although the measurement of coverage is critical for predicting the impact of a larviciding programme, there is no standardization of operational coverage measures. These have been variously defined as the number of treated breeding sites out of the total identified, the proportion of the surface area of water bodies that are treated, or even the proportion of larvae covered by larvicide out of all larvae within a breeding site (Additional file 3). Targeting specific areas (or selection of sub-sets of breeding sites or other criteria) reduce the denominators in such calculations. All these measures of coverage are challenging to estimate [8, 12, 15, 90], especially since the proportion of breeding sites identified varies in each setting and over time. Regardless of the suitability of the local settings, the effectiveness also depends on the performance of field staff, community engagement and supervision [91, 92].
The simulations of larviciding in Mbita, western Kenya, attempted to calibrate the model to allow for these factors. The results emphasize the difficulty of correctly reproducing the impact of larviciding, and on estimating coverage levels that would be feasible, despite accounting for details of deployment. In the simulations, the vector population immediately increased between the larvicide applications, whereas in the field measurements adult densities remained relatively low [6]. Hence, the low levels in host-seeking mosquito density maintained throughout the intervention period of two years could only be reproduced with constant high effective coverage. It could be that the sampling under-represented the true adult mosquito density in the community or that the simulated re-treatment intervals underestimated the effectiveness in practice. Another reason could be additional use of ITNs or other factors not accounted for in the simulations that lowered the transmission throughout the study period.
In contrast to the homogeneous vector populations in the simulations, multiple vector species are usually present in the field, and some of this variation in outcomes result from environmental and ecological factors that cannot be captured in the model. For instance, larviciding of rice fields has been found to be impractical in The Gambia, due to low accessibility [40], but was feasible in Tanzania and Rwanda [36, 93]. One study in Kenya found positive effects of dry season implementation on mosquito density and clinical malaria using long-lasting larvicides [17]. Another study in western Kenya reported higher effectiveness during the rainy season, using short-lived larvicides [94]. For instance, while a high number of breeding sites existed throughout the dry season in an urban setting (Dar es Salaam) [11], they substantially varied by season in the rural village setting in Mbita, western Kenya [6]. Hence, field operations should always consider local climate, breeding site permanence based on water sources and characteristics, dominant vector species, available resources, and engagement of the community [95]. The diversity of operational implementation and outcomes highlights the need for more setting-specific guidelines for larviciding to differentiate between strategies for different localities. For instance, in Tanzania, the national malaria strategic plan includes larviciding the whole country [96], but heterogeneities in malaria epidemiology and environmental factors represent a huge challenge for planning appropriate large-scale strategies [97, 98] and implementation will require a thorough assessment of the context at local level.
Conclusion
In seasonal transmission settings, larviciding was predicted to be most impactful if done before and during the peak in vector density; in many settings this corresponded to the rainy season instead of during the dry season as currently recommended by WHO. Some deployment parameters, including coverage, are difficult to determine accurately in reality versus in a model. Field studies find substantial variation in outcomes that appears to stem from diversity in eco-environmental settings, vector biology and in operational strategies, and are often difficult to relate to model predictions. To make model-based impact predictions that can be compared between areas, the different deployment strategies and coverage should be calibrated against effects on densities of host-seeking vectors and prevalence in humans. Such calibration would enable models to become a practical tool to support malaria control programmes in developing operational strategies for larviciding that account for diversity of context.
Availability of data and materials
The analysis code is available on GitHub at https://github.com/ManuelaRunge/om_larviciding_tza. The simulation output is available from Zenodo at https://doi.org/10.5281/zenodo.5033187.
Change history
26 August 2021
A Correction to this paper has been published: https://doi.org/10.1186/s12936-021-03882-0
Abbreviations
- DDT:
-
Dichlorodiphenyltrichloroethane
- EIR:
-
Entomological inoculation rate
- ibpa:
-
Infectious bites per person per annum
- IRS:
-
Indoor residual spraying
- ITN:
-
Insecticide-treated bed nets
- LSM:
-
Larval source management
- RR:
-
Relative reduction
- t :
-
Time in days
References
WHO. Larval source management—a supplementary measure for malaria vector control. An operational manual. World Health Organization, Geneva; 2013.
WHO. Guidelines for malaria vector control. World Health Organization, Geneva; 2019.
Lacey LA. Bacillus thuringiensis serovariety israelensis and Bacillus sphaericus for mosquito control. J Am Mosq Control Assoc. 2007;23:133–63.
Kroeger A, Horstick O, Riedl C, Kaiser A, Becker N. The potential for malaria control with the biological larvicide Bacillus thuringiensis israelensis (Bti) in Peru and Ecuador. Acta Trop. 1995;60:47–57.
Fillinger U, Knols GJ, Becker N. Efficacy and efficiency of new Bacillus thuringiensis var. israelensis and Bacillus sphaericus formulations against Afrotropical anophelines in Western Kenya. Trop Med Int Health. 2003;8:37–47.
Fillinger U, Lindsay SW. Suppression of exposure to malaria vectors by an order of magnitude using microbial larvicides in rural Kenya. Trop Med Int Health. 2006;11:1629–42.
Shililu JI, Tewolde GM, Brantly E, Githure JI, Mbogo CM, Beier JC, et al. Efficacy of Bacillus thuringiensis israelensis, Bacillus sphaericus and temephos for managing Anopheles larvae in Eritrea. J Am Mosq Control Assoc. 2003;19:251–8.
Dambach P, Traoré I, Kaiser A, Sié A, Sauerborn R, Becker N. Challenges of implementing a large scale larviciding campaign against malaria in rural Burkina Faso–lessons learned and recommendations derived from the EMIRA project. BMC Public Health. 2016;16:1023.
Tusting LS, Thwing J, Sinclair D, Fillinger U, Gimnig J, Bonner KE, et al. Mosquito larval source management for controlling malaria. Cochrane Database Syst Rev. 2013;8:CD008923.
Fillinger U, Sonye G, Killeen GF, Knols BGJ, Becker N. The practical importance of permanent and semipermanent habitats for controlling aquatic stages of Anopheles gambiae sensu lato mosquitoes: operational observations from a rural town in western Kenya. Trop Med Int Health. 2004;9:1274–89.
Fillinger U, Kannady K, William G, Vanek MJ, Dongus S, Nyika D, et al. A tool box for operational mosquito larval control: preliminary results and early lessons from the Urban Malaria Control Programme in Dar es Salaam, Tanzania. Malar J. 2008;7:20.
Chaki PP, Govella NJ, Shoo B, Hemed A, Tanner M, Fillinger U, et al. Achieving high coverage of larval-stage mosquito surveillance: challenges for a community-based mosquito control programme in urban Dar es Salaam, Tanzania. Malar J. 2009;8:311.
Killeen GF, Fillinger U, Kiche I, Gouagna LC, Knols BG. Eradication of Anopheles gambiae from Brazil: lessons for malaria control in Africa. Lancet Infect Dis. 2002;2:618–27.
Killeen GF, Fillinger U, Knols BG. Advantages of larval control for African malaria vectors: low mobility and behavioural responsiveness of immature mosquito stages allow high effective coverage. Malar J. 2002;1:8.
Fillinger U, Lindsay SW. Larval source management for malaria control in Africa: myths and reality. Malar J. 2011;10:353.
Kitron U, Spielman A. Suppression of transmission of malaria through source reduction: antianopheline measures applied in Israel, the United States, and Italy. Rev Infect Dis. 1989;11:391–406.
Afrane YA, Mweresa NG, Wanjala CL, Gilbreath TM III, Zhou G, Lee M-C, et al. Evaluation of long-lasting microbial larvicide for malaria vector control in Kenya. Malar J. 2016;15:577.
Kahindi SC, Muriu S, Derua YA, Wang X, Zhou G, Lee M-C, et al. Efficacy and persistence of long-lasting microbial larvicides against malaria vectors in western Kenya highlands. Parasit Vectors. 2018;11:438.
Derua YA, Kahindi SC, Mosha FW, Kweka EJ, Atieli HE, Wang X, et al. Microbial larvicides for mosquito control: Impact of long lasting formulations of Bacillus thuringiensis var. israelensis and Bacillus sphaericus on non-target organisms in western Kenya highlands. Ecol Evol. 2018;8:7563–73.
Hardy A, Makame M, Cross D, Majambere S, Msellem M. Using low-cost drones to map malaria vector habitats. Parasit Vectors. 2017;10:29.
Carrasco-Escobar G, Manrique E, Ruiz-Cabrejos J, Saavedra M, Alava F, Bickersmith S, et al. High-accuracy detection of malaria vector larval habitats using drone-based multispectral imagery. PLoS Negl Trop Dis. 2019;13:e0007105.
Derua YA, Kweka EJ, Kisinza WN, Githeko AK, Mosha FW. Bacterial larvicides used for malaria vector control in sub-Saharan Africa: review of their effectiveness and operational feasibility. Parasit Vectors. 2019;12:426.
Fillinger U, Ndenga B, Githeko A, Lindsay SW. Integrated malaria vector control with microbial larvicides and insecticide-treated nets in western Kenya: a controlled trial. Bull World Health Organ. 2009;87:655–65.
Zhou G, Wiseman V, Atieli HE, Lee M-C, Githeko AK, Yan G. The impact of long-lasting microbial larvicides in reducing malaria transmission and clinical malaria incidence: study protocol for a cluster randomized controlled trial. Trials. 2016;17:423.
Dambach P, Traoré I, Becker N, Kaiser A, Sié A, Sauerborn R. EMIRA: Ecologic Malaria Reduction for Africa—innovative tools for integrated malaria control. Glob Health Action. 2014;7:25908.
Geissbühler Y, Kannady K, Chaki PP, Emidi B, Govella NJ, Mayagaya V, et al. Microbial larvicide application by a large-scale, community-based program reduces malaria infection prevalence in urban Dar Es Salaam, Tanzania. PLoS ONE. 2009;4:e5107.
Rahman R, Lesser A, Mboera L, Kramer R. Cost of microbial larviciding for malaria control in rural Tanzania. Trop Med Int Health. 2016;21:1468–75.
Worrall E, Fillinger U. Large-scale use of mosquito larval source management for malaria control in Africa: a cost analysis. Malar J. 2011;10:338.
Majambere S, Lindsay SW, Green C, Kandeh B, Fillinger U. Microbial larvicides for malaria control in the Gambia. Malar J. 2007;6:76.
Kandyata A, Mbata K, Katongo C, Kamuliwo C, Nyirenda F, Chanda E. Impacts of Bacillus thuringiensis var. israelensis and Bacillus sphaericus insect larvicides on mosquito larval densities in Lusaka, Zambia. Med J Zambia. 2012;39:33–8.
Martinez, AA, Gutierrez, LT, Hernandez, SF, Velazquez, FS, Robiana, RA, Rogue, RR, et al. Implementing the operational use of the biological larvicides Griselesf and Bactivec as a new intervention to reduce the incidence of malaria and other mosquitoes borne diseases in Zambia. Field Report, Ministry of Health, Lusaka. 2011.
Djènontin A, Pennetier C, Zogo B, Soukou KB, Ole-Sangba M, Akogbéto M, et al. Field efficacy of Vectobac GR as a mosquito larvicide for the control of anopheline and culicine mosquitoes in natural habitats in Benin, West Africa. PLoS ONE. 2014;9:e87934.
Obopile M, Segoea G, Waniwa K, Ntebela DS, Moakofhi K, Motlaleng M, et al. Did microbial larviciding contribute to a reduction in malaria cases in eastern Botswana in 2012–2013? Public Health Action. 2018;8:50–4.
Yapabandara AMGM, Curtis CF. Laboratory and field comparisons of pyriproxyfen, polystyrene beads and other larvicidal methods against malaria vectors in Sri Lanka. Acta Trop. 2002;81:211–23.
Nartey R, Owusu-Dabo E, Kruppa T, Baffour-Awuah S, Annan A, Oppong S, et al. Use of Bacillus thuringiensis var. israelensis as a viable option in an Integrated Malaria Vector Control Programme in the Kumasi Metropolis, Ghana. Parasit Vectors. 2013;6:116.
Ingabire CM, Hakizimana E, Rulisa A, Kateera F, Van Den Borne B, Muvunyi CM, et al. Community-based biological control of malaria mosquitoes using Bacillus thuringiensis var. israelensis (Bti) in Rwanda: community awareness, acceptance and participation. Malar J. 2017;16:399.
Tchicaya ES, Koudou BG, Keiser J, Adja AM, Cisse G, Tanner M, et al. Effect of repeated application of microbial larvicides on malaria transmission in central Cote d’Ivoire. J Am Mosq Control Assoc. 2009;25:382–5.
Nyarango PM, Gebremeskel T, Mebrahtu G, Mufunda J, Abdulmumini U, Ogbamariam A, et al. A steep decline of malaria morbidity and mortality trends in Eritrea between 2000 and 2004: the effect of combination of control methods. Malar J. 2006;5:33.
Chanda E, Mzilahowa T, Chipwanya J, Ali D, Troell P, Dodoli W, et al. Scale-up of integrated malaria vector control: lessons from Malawi. Bull World Health Organ. 2016;94:475–80.
Majambere S, Pinder M, Fillinger U, Ameh D, Conway DJ, Green C, et al. Is mosquito larval source management appropriate for reducing malaria in areas of extensive flooding in the Gambia? A cross-over intervention trial. Am J Trop Med Hyg. 2010;82:176–84.
Mazigo HD, Mboera LEG, Rumisha SF, Kweka EJ. Malaria mosquito control in rice paddy farms using biolarvicide mixed with fertilizer in Tanzania: semi-field experiments. Malar J. 2019;18:226.
Magesa SM, Athumani Y, Barongo V, Sambu EZ, Senkoro KP, Mboera LEG, et al. Efficacy of Bacillus thuringiensis var. israelensis (Bactivec®) and Bacillus sphaericus (Griselesf®) for control of mosquito larvae. A field trial in Mvomero and Bagamoyo districts, Tanzania. Dar Es Salaam, Tanzania: National Institute for Medical Research; 2009.
Dambach P, Schleicher M, Stahl H-C, Traoré I, Becker N, Kaiser A, et al. Routine implementation costs of larviciding with Bacillus thuringiensis israelensis against malaria vectors in a district in rural Burkina Faso. Malar J. 2016;15:380.
Shililu J, Ghebremeskel T, Seulu F, Mengistu S, Fekadu H, Zerom M, et al. Larval habitat diversity and ecology of anopheline larvae in Eritrea. J Med Entomol. 2003;40:921–9.
Shililu J, Mbogo C, Ghebremeskel T, Githure J, Novak R. Mosquito larval habitats in a semiarid ecosystem in Eritrea: impact of larval habitat management on Anopheles arabiensis population. Am J Trop Med Hyg. 2007;76:103–10.
Chanda E, Masaninga F, Coleman M, Sikaala C, Katebe C, MacDonald M, et al. Integrated vector management: the Zambian experience. Malar J. 2008;7:164.
Chanda E. Integrating larval source management in the National Malaria Control Programme in Zambia. Ministry of Health Zambia. 2017. https://www.informea.org/en/intergrating-larval-source-management-national-malaria-control-programme-zambia. Accessed 11 Mar 2017.
National Malaria Control Programme, suMAP, World Health Organization and the INFORM Project. A description of the epidemiology of malaria to guide the planning of control in Nigeria. A report prepared for the Federal Ministry of Health, Nigeria, the Roll Back Malaria Partnership and the Department for International Development, UK. 2013. http://inform-malaria.org/wp-content/uploads/2019/06/Nigeria-INFORM-Epi-Profile-V2-2014.pdf. Accessed 19 Oct 2019.
Choi L, Majambere S, Wilson AL. Larviciding to prevent malaria transmission. Cochrane Database Syst Rev. 2019;8:012736.
White MT, Griffin JT, Churcher TS, Ferguson NM, Basáñez M-G, Ghani AC. Modelling the impact of vector control interventions on Anopheles gambiae population dynamics. Parasit Vectors. 2011;4:153.
Brady OJ, Godfray HCJ, Tatem AJ, Gething PW, Cohen JM, McKenzie FE, et al. Vectorial capacity and vector control: reconsidering sensitivity to parameters for malaria elimination. Trans R Soc Trop Med Hyg. 2016;110:107–17.
Smith DL, Perkins TA, Tusting LS, Scott TW, Lindsay SW. Mosquito population regulation and larval source management in heterogeneous environments. PLoS ONE. 2013;8:e71247.
Yakob L, Yan G. A network population model of the dynamics and control of African malaria vectors. Trans R Soc Trop Med Hyg. 2010;104:669–75.
Alam MdZ, Niaz Arifin SM, Al-Amin HM, Alam MS, Rahman MS. A spatial agent-based model of Anopheles vagus for malaria epidemiology: examining the impact of vector control interventions. Malar J. 2017;16:432.
Menach AL, McKenzie FE, Flahault A, Smith DL. The unexpected importance of mosquito oviposition behaviour for malaria: non-productive larval habitats can be sources for malaria transmission. Malar J. 2005;4:23.
Arifin SN, Madey GR, Collins FH. Examining the impact of larval source management and insecticide-treated nets using a spatial agent-based model of Anopheles gambiae and a landscape generator tool. Malar J. 2013;12:290.
Barbosa S, Kay K, Chitnis N, Hastings IM. Modelling the impact of insecticide-based control interventions on the evolution of insecticide resistance and disease transmission. Parasit Vectors. 2018;11:482.
Eckhoff PA. A malaria transmission-directed model of mosquito life cycle and ecology. Malar J. 2011;10:303.
Gu W, Novak RJ. Habitat-based modeling of impacts of mosquito larval interventions on entomological inoculation rates, incidence, and prevalence of malaria. Am J Trop Med Hyg. 2005;73:546–52.
Magombedze G, Ferguson NM, Ghani AC. A trade-off between dry season survival longevity and wet season high net reproduction can explain the persistence of Anopheles mosquitoes. Parasit Vectors. 2018;11:576.
Worrall E, Connor SJ, Thomson MC. A model to simulate the impact of timing, coverage and transmission intensity on the effectiveness of indoor residual spraying (IRS) for malaria control. Trop Med Int Health. 2007;12:75–88.
Selvaraj P, Wenger EA, Gerardin J. Seasonality and heterogeneity of malaria transmission determine success of interventions in high-endemic settings: a modeling study. BMC Infect Dis. 2018;18:413.
Ratti V, Rheingold E, Wallace D. Reduction of mosquito abundance via indoor wall treatments: a mathematical model. J Med Entomol. 2018;55:833–45.
Griffin JT, Hollingsworth TD, Okell LC, Churcher TS, White M, Hinsley W, et al. Reducing Plasmodium falciparum malaria transmission in Africa: a model-based evaluation of intervention strategies. PLoS Med. 2010;7:e1000324.
Cairns ME, Walker PGT, Okell LC, Griffin JT, Garske T, Asante KP, et al. Seasonality in malaria transmission: implications for case-management with long-acting artemisinin combination therapy in sub-Saharan Africa. Malar J. 2015;14:321.
Brady OJ, Slater HC, Pemberton-Ross P, Wenger E, Maude RJ, Ghani AC, et al. Role of mass drug administration in elimination of Plasmodium falciparum malaria: a consensus modelling study. Lancet Glob Health. 2017;5:e680–7.
Gao B, Saralamba S, Lubell Y, White LJ, Dondorp A, Aguas R. Determinants of MDA impact and designing MDAs towards malaria elimination. Elife. 2020;9:e51773.
Chitnis N, Hardy D, Smith T. A periodically-forced mathematical model for the seasonal dynamics of malaria in mosquitoes. Bull Math Biol. 2012;74:1098–124.
Chitnis N, Hyman JM, Cushing JM. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull Math Biol. 2008;70:1272–96.
Chitnis N, Smith T, Steketee R. A mathematical model for the dynamics of malaria in mosquitoes feeding on a heterogeneous host population. J Biol Dyn. 2008;2:259–85.
Beverton RJH, Holt SJ. On the dynamics of exploited fish populations. Fisheries investment series 2. London: Chapman and Hall; 1957.
Bohner M, Warth H. The Beverton–Holt dynamic equation. Appl Anal. 2007;86:1007–15.
Smith T, Ross A, Maire N, Chitnis N, Studer A, Hardy D, et al. Ensemble modeling of the likely public health impact of a pre-erythrocytic malaria vaccine. PLoS Med. 2012;9:e1001157.
Smith T, Maire N, Ross A, Penny M, Chitnis N, Schapira A, et al. Towards a comprehensive simulation model of malaria epidemiology and control. Parasitology. 2008;135:1507–16.
Briët OJ, Penny MA, Hardy D, Awolola TS, Van Bortel W, Corbel V, et al. Effects of pyrethroid resistance on the cost effectiveness of a mass distribution of long-lasting insecticidal nets: a modelling study. Malar J. 2013;12:77.
Stuckey EM, Smith TA, Chitnis N. Estimating malaria transmission through mathematical models. Trends Parasitol. 2013;29:477–82.
Swiss TPH. OpenMalaria. A simulator of malaria epidemiology and control. Swiss Tropical and Public Health Institute. 2021. https://github.com/SwissTPH/openmalaria. Accessed 14 Jul 2021.
Stuckey EM, Smith T, Chitnis N. Seasonally dependent relationships between indicators of malaria transmission and disease provided by mathematical model simulations. PLoS Comput Biol. 2014;10:e1003812.
Service MW. Medical entomology for students. 5th ed. Cambridge: Cambridge University Press; 2012.
Dambach P, Louis VR, Kaiser A, Ouedraogo S, Sié A, Sauerborn R, et al. Efficacy of Bacillus thuringiensis var. israelensis against malaria mosquitoes in northwestern Burkina Faso. Parasit Vectors. 2014;7:371.
Mwangangi JM, Kahindi SC, Kibe LW, Nzovu JG, Luethy P, Githure JI, et al. Wide-scale application of Bti/Bs biolarvicide in different aquatic habitat types in urban and peri-urban Malindi, Kenya. Parasitol Res. 2011;108:1355–63.
Karch S, Asidi N, Manzambi ZM, Salaun JJ. Efficacy of Bacillus sphaericus against the malaria vector Anopheles gambiae and other mosquitoes in swamps and rice fields in Zaire. J Am Mosq Control Assoc. 1992;8:376–80.
Smith DL, McKenzie FE. Statics and dynamics of malaria infection in Anopheles mosquitoes. Malar J. 2004;3:13.
Imbahale SS, Paaijmans KP, Mukabana WR, van Lammeren R, Githeko AK, Takken W. A longitudinal study on Anopheles mosquito larval abundance in distinct geographical and environmental settings in western Kenya. Malar J. 2011;10:81.
Kweka EJ, Zhou G, Munga S, Lee M-C, Atieli HE, Nyindo M, et al. Anopheline larval habitats seasonality and species distribution: a prerequisite for effective targeted larval habitats control programmes. PLoS ONE. 2012;7:e52084.
Dambach P, Baernighausen T, Traoré I, Ouedraogo S, Sie A, Sauerborn R, et al. Reduction of malaria vector mosquitoes in a large scale intervention trial in rural Burkina Faso using Bti based larval source management. Malar J. 2019;18:311.
Briët OJ, Penny MA. Repeated mass distributions and continuous distribution of long-lasting insecticidal nets: modelling sustainability of health benefits from mosquito nets, depending on case management. Malar J. 2013;12:401.
Imbahale SS, Githeko A, Mukabana WR, Takken W. Integrated mosquito larval source management reduces larval numbers in two highland villages in western Kenya. BMC Public Health. 2012;12:362.
van den Berg H, van Vugt M, Kabaghe AN, Nkalapa M, Kaotcha R, Truwah Z, et al. Community-based malaria control in southern Malawi: a description of experimental interventions of community workshops, house improvement and larval source management. Malar J. 2018;17:266.
Fillinger U, Sombroek H, Majambere S, van Loon E, Takken W, Lindsay SW. Identifying the most productive breeding sites for malaria mosquitoes in The Gambia. Malar J. 2009;8:62.
Chaki PP, Dongus S, Fillinger U, Kelly A, Killeen GF. Community-owned resource persons for malaria vector control: enabling factors and challenges in an operational programme in Dar es Salaam, United Republic of Tanzania. Hum Resour Health. 2011;9:21.
Chaki PP, Kannady K, Mtasiwa D, Tanner M, Mshinda H, Kelly AH, et al. Institutional evolution of a community-based programme for malaria control through larval source management in Dar es Salaam, United Republic of Tanzania. Malar J. 2014;13:245.
Mazigo HD, Massawe IS, Rumisha SF, Kweka EJ, Mboera LEG. Rice farmers’ perceptions and acceptability in the use of a combination of biolarvicide (Bacillus thuringiensis var. israeliensis) and fertilizers application for malaria control and increase rice productivity in a rural district of central Tanzania. Malar J. 2019;18:71.
Zhou G, Afrane YA, Dixit A, Atieli HE, Lee M-C, Wanjala CL, et al. Modest additive effects of integrated vector control measures on malaria prevalence and transmission in western Kenya. Malar J. 2013;12:256.
Hardy AJ, Gamarra JGP, Cross DE, Macklin MG, Smith MW, Kihonda J, et al. Habitat hydrology and geomorphology control the distribution of malaria vector larvae in rural Africa. PLoS ONE. 2013;8:e81931.
NMCP Tanzania. National Malaria Strategic Plan 2014–2020. Dar Es Salaam. National Malaria Control Programme Tanzania. 2014. https://www.out.ac.tz/wp-content/uploads/2019/10/Malaria-Strategic-Plan-2015-2020-1.pdf. Accessed 3 Jul 2017.
Chacky F, Runge M, Rumisha SF, Machafuko P, Chaki P, Massaga JJ, et al. Nationwide school malaria parasitaemia survey in public primary schools, the United Republic of Tanzania. Malar J. 2018;17:452.
Grover-Kopec EK, Blumenthal MB, Ceccato P, Dinku T, Omumbo JA, Connor SJ. Web-based climate information resources for malaria control in Africa. Malar J. 2006;5:38.
Acknowledgements
The authors would like to thank the anonymous reviewers for insightful comments that greatly improved the clarity of the published work. MR acknowledges Northwestern University for providing resources to finalize the manuscript.
Funding
This work was supported by the Bill and Melinda Gates Foundation, project OPP1032350. SM was supported by a Wellcome Trust International Masters Fellowship in Tropical Medicine and Hygiene (212633/Z/18/Z). FO and IN received funding from the Bill and Melinda Gates Foundation (OPP1177156 and OPP1099295).
Author information
Authors and Affiliations
Contributions
FO, SM, EP, MR developed the research idea. MR reviewed the literature, performed the analysis, and wrote the draft manuscript. NC developed and extended the vector model. TAS, EP and FO provided substantial feedback to early and final versions of the manuscript. TAS, NC, FO, EP provided technical advice. All authors have read and approved to the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Additional file 1:
A simple periodically forced difference equation model for mosquito population dynamics.
Additional file 2:
Additional result figures.
Additional file 3:
Flowchart from operational to effective larviciding coverage.
Additional file 4:
Re-simulated larviciding study in Mbita, western Kenya between 2002 and 2006.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
About this article
Cite this article
Runge, M., Mapua, S., Nambunga, I. et al. Evaluation of different deployment strategies for larviciding to control malaria: a simulation study. Malar J 20, 324 (2021). https://doi.org/10.1186/s12936-021-03854-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12936-021-03854-4