1 Introduction

Malaria is an infectious disease caused by the Plasmodium parasite and transmitted between humans by the bites of female Anopheles mosquitoes. Malaria remains a serious public health problem with 190–311 million cases and over 863,000–1,003,000 deaths per year (World Health Organization 2009). The Roll Back Malaria Partnership in the Global Malaria Action Plan (2008) has called for increased coverage of the world’s population at risk of malaria with malaria control interventions such as the use of insecticide-treated nets (ITNs), indoor residual spraying (IRS), and prompt treatment of infected individuals with effective medication such as artemisinin-based combination therapies (ACTs). Considerable funding has now been pledged by national governments and international funding agencies to reduce the burden of malaria disease, with the eventual goal of interrupting transmission and eradicating malaria.

Mathematical modeling has an important role to play in the planning of malaria control and elimination activities (Chitnis et al. 2010b; The malERA Consultative Group on Modeling 2011). Randomized control trials and malaria indicator surveys provide evidence on the effects of interventions from particular settings but cannot capture the variety of conditions where malaria transmission takes place. Mathematical models allow us to combine this data with our knowledge of the general processes of malaria transmission to understand and predict effects of malaria control in multiple settings. They allow us to answer questions that could be impractical or unethical to answer with field studies. Mathematical modeling of malaria can help us to quantify the effects of control strategies, compare different strategies in different settings, optimize the deployment of strategies, and help to devise target product profiles of potential new strategies.

Ronald Ross developed the first mathematical model for understanding malaria transmission (Ross 1905). Macdonald combined Ross’s more famous differential equation model (Ross 1911), with epidemiological (Macdonald 1950) and entomological (Macdonald 1952) field data. His analysis drove much of the theory behind the global malaria eradication in the 1950s and 1960s that targeted adult mosquitoes. Since then, multiple models have been developed for malaria, including deterministic compartmental models (Anderson and May 1991; Aron 1988; Aron and May 1982; Chitnis et al. 2006; Cosner et al. 2009; Ngwa and Shu 2000; Smith and McKenzie 2004) and stochastic (Dietz et al. 1974) individual-based models (Eckhoff 2011; Griffin et al. 2010; McKenzie et al. 1998; Smith et al. 2006; White et al. 2011).

Saul et al. (1990) introduced a feeding cycle model of mosquito behavior that more finely captured the interactions of mosquitoes with their hosts and the environment. Saul (2003), Killeen and Smith (2007), Le Menach et al. (2007), and Chitnis et al. (2008, 2010a) extended this model to look at the effects of interventions such as ITNs, IRS, and zooprophylaxis on malaria control. We now extend the model by Chitnis et al. (2008) to include the effects of seasonality on malaria in mosquitoes.

In many parts of the world, malaria transmission is not constant but climate-dependent and varies seasonally over the year. The emergence of adult mosquitoes depends on the availability of larval habitats which varies with rainfall and humidity. The development time of the parasite within the mosquito (extrinsic incubation period) and the time between feeding for mosquitoes depend on the ambient temperature. Adult survival depends on relative humidity. In most parts of the world that are affected by malaria, rainfall, and to a lesser extent, temperature, vary seasonally. Consequently, malaria transmission also varies seasonally, leading to a peak of transmission in certain months and, in some locations, months that are relatively free of malaria transmission. This affects, among other things, the optimum timing of interventions such as IRS with a short-acting insecticide. Most mathematical models of malaria that include the effects of seasonality assume sinusoidal forcing (Aron and May 1982; Lou and Zhao 2010) though others have linked models to climate (Eckhoff 2011; Griffin et al. 2010; White et al. 2011; Hoshen and Morse 2004).

We extend our previously published linear difference equation model (Chitnis et al. 2008) to allow most of the parameters to be periodic sequences of time with a period of 1 year (365 days). Though we fix the period at 1 year, we allow the pattern of these sequences within the year to be arbitrary. Since the model for malaria in mosquitoes is linear and considers the infectivity of humans to mosquitoes as a parameter, we integrate this model with a stochastic individual-based simulation model for falciparum malaria in humans (Smith et al. 2008) to model the nonlinear effects of the full malaria cycle.

This work is part of a larger project building a comprehensive model for malaria with the objectives of determining target product profiles for new interventions, and devising optimal deployment strategies for current and future control interventions. Within these goals, this paper serves to lay the mathematical framework of the periodically-forced model for malaria in mosquitoes, and its integration within the overall simulation model for malaria. The model includes different aspects of the natural history of Plasmodium falciparum in humans and in mosquitoes, effects of the mosquito life and feeding cycle, effects of human demography, and of the health system.

The models for malaria in humans (Smith et al. 2006, 2008) have already been used to investigate the effects of vaccines (Penny et al. 2008; Smith et al. 2012) and intermittent preventive treatment (Ross et al. 2008, 2011) in reducing malaria morbidity and mortality. The autonomous model for malaria in mosquitoes has been used to compare the effects of vector control interventions, such as ITNs (Chitnis et al. 2008), IRS, and their combinations (Chitnis et al. 2010a), in reducing malaria transmission. Here, we extend the work in Chitnis et al. (2008) to a nonautonomous model by including seasonality and transient dynamics. This extension enables us to capture the effects of variations in transmission over the year, the decay of effectiveness of interventions, and more importantly, incorporate the dynamics of malaria in humans. This allows us to model the full malaria cycle and determine the effects of interventions on human disease. We note that while the model for malaria in mosquitoes is independent of the Plasmodium species, the model for malaria in humans focuses on only P. falciparum malaria.

We first describe the formulation of the model, its assumptions, and its mathematical properties. We then describe its integration with the individual-based stochastic simulation model for malaria in humans and show a numerical example of the effects of ITNs and IRS in reducing malaria transmission and disease.

2 Description of Model

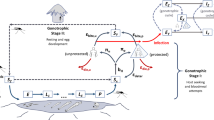
We base the periodically forced model of malaria transmission in mosquitoes on the autonomous model defined earlier (Chitnis et al. 2008). After emergence from a breeding site, mosquitoes mate and the females search for blood meals which are necessary for egg development. After encountering and biting a host, the female mosquito finds a resting place where it digests the blood and evaporates water. The resting time is temperature dependent (shorter at higher temperatures) and is usually 2 to 3 days in tropical areas. After digesting the blood, the mosquito flies in search of a breeding site to lay eggs, before seeking a host again to repeat the feeding cycle. Figure 1(a) shows a cartoon of the feeding cycle. Usually, mosquitoes begin host-seeking at the same time every night. If they are unsuccessful in biting, they rest through the day and try again the next night. The probability that a mosquito is successful in completing a feeding cycle depends on a variety of factors, including innate heterogeneities in the hosts, the quality, construction and location of their houses or dwellings, and their use of malaria or mosquito control interventions (Gillies 1988).

Fig. 1
figure 1

New mosquitoes emerge from water bodies (and mate) at rate N v0(t) into the host-seeking state A, where they actively search for blood meals. A mosquito may encounter and feed on up to n different types of hosts. Each type of host, represented by subscript i for 1≤i≤n, is available to mosquitoes at rate α i (t). If a mosquito does not encounter a host in a given night, it waits in the host-seeking phase till the next night, with probability, P A (t). When a mosquito encounters a host of type i and is committed to biting the host, it moves to state B i . If the mosquito bites, it moves to state C i where it searches for a resting place. If it finds a resting place, it moves to state D i where it rests for τ days. After resting, the mosquito moves to state E i where it seeks to lay eggs. If it is successful in laying eggs, it returns to host-seeking state, A, where it may then encounter any type of host. At each state, the mosquito may die with some probability, labeled by subscript μ. The survival probabilities and the emergence rate are periodic with a period of one year. (b) is reproduced, with permission, from Chitnis et al. (2008, Fig. 2)

Full size image

We model each feeding cycle of the mosquito as shown in Fig. 1(b) where an adult female mosquito can be in one of five states, A–E. Four of these states, B–E, depend on the type of host that the mosquito feeds on. We label these states with a subscript i with 1≤i≤n, where i denotes the type of host, and n is the total number of different types of hosts.

We let τ be the time it takes a mosquito to return to host-seeking, A, after it has encountered a host, B i (provided that the mosquito is still alive). This is the partial duration of the feeding cycle: it is the time it takes a mosquito to complete a feeding cycle, excluding the time it needs to find a host from when it starts host-seeking.

Humans infected with malaria are infective to mosquitoes if they have gametocytes in their blood. If a mosquito feeds on an any human of host type i, there is a probability, K vi (t), that the mosquito will ingest both male and female gametocytes, and that they will fuse in the mosquito’s stomach to form a zygote, which would develop into an oocyst that releases sporozoites. The mosquito is infective to humans when it has sporozoites in its salivary glands. The temperature-dependent time it takes an infected mosquito to become infective (be sporozoite positive) is the extrinsic incubation period, θ s (usually 10 to 12 days in tropical areas).

2.1 Model Assumptions

In tropical environments, the parameter that is most affected by the seasonality in climate, and especially rainfall, is the emergence rate of mosquitoes, N v0 (see Table 1 for a full list of parameters). An increased emergence rate leads to a higher number of host-seeking mosquitoes, resulting in increased malaria transmission from mosquitoes to humans. Correspondingly, the transmission of malaria from humans to mosquitoes is also greater. Therefore, both, N v0(t) and K vi (t) are periodic sequences of time. Since the mosquito model does not consider malaria in humans, we use the results of the human simulation model (Smith et al. 2008) to calculate the periodic sequence of K vi (t) as a function of the periodic sequence of transmission of malaria from mosquitoes to humans.

Table 1 Description of the parameters of the periodically-forced model of the mosquito feeding cycle with time is measured in days. Parameters not specified to be natural numbers (where ℕ denotes the set of natural numbers) are real. We use “day” to refer to a 24-hour period and not simply the hours of daylight
Full size table

The parameters most dependent on temperature are the extrinsic incubation period, θ s , and the partial duration of the gonotrophic cycle, τ. However, we assume that these parameters are constant. Since, in the model, these parameters are natural numbers, the change in temperature needs to be sufficiently large for them to vary seasonally. While this is reasonable for τ, it is a simplifying assumption for θ s , which we will address in the future.

While the rest of the parameters labeled as periodic in the model, are unlikely to be periodic with a 1-year period in nature, we label them as such because they can be easily incorporated into the model as periodic parameters, and the same notation can be preserved when we consider them as nonperiodic parameters to model interventions that decay over time.

Additionally, we assume that the emergence rate, N v0(t), does not depend on the mosquito population and the number of eggs laid, but is regulated by the availability and quality of breeding sites. While this assumption is valid when the adult population is high relative to the number of breeding sites, it would break down if high coverage of effective vector control interventions were to substantially reduce the adult mosquito population.

We have also made the simplifying assumption that mosquito mortality is independent of age, although some studies have shown increasing mortality with age (Clements and Paterson 1981). Our assumption is reasonable, because with the high mortality rates that adult mosquitoes are typically subjected to, the probability of a mosquito living a long life is low so the error is low. As mortality rates tend to increase with age, this assumption would overestimate malaria transmission levels. We also ignore the effects of malaria infection on the mortality rates and feeding habits of mosquitoes that some studies have shown (Anderson et al. 2000).

2.2 Model Equations

We extend the autonomous linear equations in Chitnis et al. (2008, (5)) to a system of θ p -periodic linear nonhomogeneous difference equations. We summarize all the input parameters used in this model in Table 1; and derived parameters in Table 2. We use the term “day” here to refer to a 24-hour period and not the hours of daylight. We denote the length of each time step by T. As one day (24-hour period) is the most reasonable time step in the mosquito’s feeding cycle, we fix T=1 day. We use T to convert between rates and fixed quantities at time t. While we label the period, θ p , as a parameter, the model is built assuming an annual seasonal cycle. Since the extrinsic incubation period, θ s , and mosquito resting duration, τ, are parameters, the order of the system is parameter dependent. We define η=2(θ s +τ−1)+τ. Denoting the positive orthant of ℝη by \(\mathbb{R}^{\eta}_{+}\), we denote the mosquito population by \(x(t) \in\mathbb{R}^{\eta}_{+}\), where

and N v (t) represents the total number of host-seeking mosquitoes at time t, O v (t) represents the number of infected (oocyst-positive) mosquitoes at time t, and S v (t) represents the number of infectious (sporozoite-positive) mosquitoes at time t.

Table 2 Description of derived parameters for the model of the mosquito feeding cycle. We use “day” to refer to a 24-hour period and not simply the hours of daylight. Of this list, estimates from field data exist for M(t), o v (t), s v (t), σ(t), and Ξ(t) that can be used to help parameterize the model
Full size table

The system of equations for malaria in mosquitoes is

(1a)
(1b)

for some initial condition, x 0, with

where Λ(t) is in the nonnegative orthant of ℝη, and ϒ(t) is a nonnegative η×η matrix.

The forcing term, Λ(t), is constructed from the emergence of new mosquitoes, Λ(t)=(N v0(t)T,0,…,0). The matrix ϒ(t) is constructed from the right-hand side of (2a), (2b), (2c), which describes the dynamics of the host-seeking, infected host-seeking, and infectious host-seeking mosquitoes,

(2a)
(2b)
(2c)

with recursively-defined discrete functions,

$$f(t-k) = \begin{cases}1, & \text{if } k = 0,\\[4pt]\prod_{j=0}^{k-1} P_A (t-(k-j)), & \text{if } 0 < k < \tau,\\[4pt]P_{\mathit{df}}(t-k) +\prod_{j=0}^{k-1} P_A (t-(k-j)), & \text{if } k = \tau,\\[4pt]P_{\mathit{df}}(t-k) f(t-(k-\tau)) + P_A(t-k)f(t-(k-1)), & \text{if } k > \tau,\end{cases} $$
(3)

and

(4)

for k∈{0,ℕ} and t>k.

The total number of host-seeking mosquitoes, N v (t), on a given day, t, in (2a) is the sum of newly emerged mosquitoes (N v 0(t)); mosquitoes from the previous day (t−1) that survived but were unable to find a blood meal (P A (t−1)); and mosquitoes from τ days earlier (t−τ) that successfully fed and completed the feeding cycle (P df (t)). The number of infected host-seeking mosquitoes, O v (t), on a given day, t, in (2b) is the sum of uninfected mosquitoes from τ days earlier (t−τ) that successfully fed, survived a feeding cycle, and got infected; infected mosquitoes from the previous day (t−1) that survived but were unable to find a blood meal (P A (t−1)), and infected mosquitoes from τ days earlier (t−τ) that successfully fed and completed the feeding cycle (P df (t)). The number of infective host-seeking mosquitoes, S v (t), on a given day, t, in (2c) is the sum of uninfected mosquitoes from at least θ s days ago that got infected, survived, and are host-seeking as infective mosquitoes for the first time on day t; infective mosquitoes from the previous day (t−1) that survived but were unable to find a blood meal (P A (t−1)); and infective mosquitoes from τ days earlier (t−τ) that successfully fed and completed the feeding cycle (P df (t)). The first two terms in the right-hand side of (2c) include all the possible ways in which the mosquitoes could survive at least θ s days to start their first feeding cycle as an infective mosquito on day t.

We define the probabilities of remaining in the host-seeking state after one day, P A (t), and encountering a host of type i, \(P_{A^{i}}(t)\), in terms of the availability of different hosts and of the mosquito death rate while host-seeking. The total rate at which mosquitoes leave the host-seeking state is the sum of the rates at which the mosquitoes encounter each type of host and the death rate: \(\sum_{i=1}^{n} \alpha_{i}(t) N_{i}(t) + \mu_{vA}(t)\). We assume that mosquitoes leave the host-seeking state each day with an exponential distribution over time. Mosquitoes only search for a limited time, θ d (t), in one day, so some mosquitoes will find a host or die on any given day while others will remain in the host-seeking state till the next day. The probability that a mosquito is still host-seeking the following day is equal to the probability that the mosquito is still host-seeking after time θ d (t),

$$ P_A(t) = e^{- (\sum_{i=1}^{n} \alpha_i(t) N_i(t) + \mu_{vA}(t) )\theta_d(t)}.$$

The probability that a mosquito finds a host of type i in one day is

$$ P_{A^i}(t) = \bigl(1- e^{- (\sum_{k=1}^{n} \alpha_k(t) N_k(t) +\mu_{vA}(t) ) \theta_d(t)} \bigr) \times \frac{\alpha_i(t) N_i(t)}{\sum_{k=1}^{n} \alpha_k(t) N_k(t) + \mu_{vA}(t)}.$$

The probability that a mosquito finds a host on a given day and then survives a complete feeding cycle is

$$ P_{\mathit{df}}(t) = \sum_{i=1}^{n}P_{A^i}(t) P_{B_i}(t) P_{C_i}(t) P_{D_i}(t)P_{E}(t+\tau).$$

The probability that a mosquito finds a host on day t and then survives a complete feeding cycle and gets infected in the process is

$$ P_{\mathit{dif}}(t) = \sum_{i=1}^{n}P_{A^i}(t) P_{B_i}(t) P_{C_i}(t) P_{D_i}(t)P_{E}(t+\tau) K_{vi}(t).$$

We note that P A (t+θ p )=P A (t), \(P_{A^{i}}(t+\theta_{p})= P_{A^{i}}(t)\), P df (t+θ p )=P df (t), P dif (t+θ p )=P dif (t), ∀t∈ℕ. We define P df (t) (and similarly P dif (t)) in terms of \(P_{E_{i}}(t+\tau)\) for notational simplicity and could alternatively have defined it as

$$\widehat{P_{\mathit{df}}}(t) = \sum_{i=1}^{n}P_{A^i}(t-\tau) P_{B_i}(t-\tau) P_{C_i}(t-\tau)P_{D_i}(t-\tau) P_{E}(t),$$

because in the model equations, the term always appears as \(P_{\mathit{df}}(t-\hat{t} )\) where \(\hat{t}\geq\tau\).

2.3 Existence of a Periodic Orbit

The system of equations (2a), (2b), (2c) has a unique solution that exists for all time, t∈ℕ. We conjecture that a domain of forward invariance exists but we have not shown its existence. We conjecture that this domain is an open bounded set in the positive orthant of ℝη, where each element of x(t)∈ℝη is bounded below by 0 and bounded above by a fixed number, \(x_{\text{max}}\). We use the notation of a superscript asterisk to denote a periodic orbit of a variable; \(\mathbb{I}\) to denote the (η×η) identity matrix; and ρ(Y) to denote the spectral radius of any matrix, Y. From Cushing (1998), we define the function:

$$X(t,s) = \begin{cases}\varUpsilon(t-1) \varUpsilon(t-2) \cdots\varUpsilon(s+1) \varUpsilon(s), &t \geq s+1,\\\mathbb{I}, & t=s.\end{cases}$$
(5)

Theorem 2.1

If all the eigenvalues, λ i , of the matrix,

(6)

are contained inside the unit circle, that is \(\rho (X_{\theta_{p}} ) < 1\), then there exists a unique globally asymptotically stable periodic orbit of (1a), (1b),

$$ x^*(t) = X(t+1,1)x_0 + \sum _{i=1}^t X(t+1,i+1) \varLambda(i),$$
(7)

with initial condition,

$$x_0 = \bigl(\mathbb{I}-X(\theta_p+1,1)\bigr)^{-1} \sum_{i=1}^{\theta_p}X(\theta_p+1,i+1) \varLambda(i).$$
(8)

Proof

Since \(\rho (X_{\theta_{p}} )<1\), the solution to the homogenous equation of (1a), (1b) has no nontrivial solution, that is,

$$\dim\ker ( \mathbb{I} - X_{\theta_p} ) = 0.$$

A straightforward application of Cushing (1998, Theorem 2) with a change in indices, shows that the nonhomogeneous equation (1a), (1b) has a unique periodic solution given by (7). □

While we cannot show in general that the eigenvalues of \(X_{\theta_{p}}\) are contained in the unit circle, for each set of parameter values that we use, we numerically show that \(\rho (X_{\theta_{p}} ) < 1\).

2.4 Field Measurable Quantities

Similar to the autonomous model (Chitnis et al. 2008), we evaluate expressions for the field-measurable parameters here for the periodically forced entomological model. Unlike (Chitnis et al. 2008), we do not calculate the vectorial capacity because we do not have a definition for it in the periodically-forced model. The expression for the parous proportion also requires a new model.

2.4.1 Parous Proportion

The parous proportion is the proportion of mosquitoes that have laid eggs at least once in their lives. Unlike the autonomous model where the parous proportion was equal to the mosquito’s probability of surviving a feeding cycle, in the periodic case we need a new model for the number of parous mosquitoes. We let F v (t) represent the number of host-seeking parous mosquitoes. The system of equations for the number of parous mosquitoes is

(9a)
(9b)

with all parameters defined in Table 1. Note that this is a separate model from the model for malaria in mosquitoes (2a), (2b), (2c). However, in a manner similar to that used for (2a), (2b), (2c), we can calculate a globally asymptotically stable periodic solution for (9a), (9b), from which we can extract periodic sequences for the total number of host-seeking mosquitoes, \(N_{v}^{*}(t)\), and the total number of host-seeking parous mosquitoes, \(F_{v}^{*}(t)\). We do not show the details here, but the periodic sequence for the parous proportion, M ∗(t), is then

$$ M^*(t) = \frac{F_v^*(t)}{N_v^*(t)}.$$
(10)

2.4.2 Delayed Oocyst Proportion

The delayed oocyst proportion is the proportion of infected mosquitoes: they would develop oocysts if they survived long enough. The first element of x ∗(t) is \(N_{v}^{*}(t)\), and the (θ s +τ)th element of x ∗(t) is \(O_{v}^{*}(t)\). The periodic sequence for the delayed oocyst proportion is their ratio,

$$ o^*_v(t) = \frac{O_v^*(t)}{N_v^*(t)}.$$
(11)

2.4.3 Sporozoite Proportion

The sporozoite proportion is the proportion of infectious mosquitoes: they have viable sporozoites in their salivary glands. The (2θ s +2τ−1)th element of x ∗(t) is \(S_{v}^{*}(t)\). The periodic sequence for the sporozoite proportion is

$$ s^*_v(t) = \frac{S_v^*(t)}{N_v^*(t)}.$$
(12)

2.4.4 Host-Biting Rate

The host-biting rate is the number of mosquito bites that a host receives per unit time. The periodic sequence for the host-biting rate for hosts of type i is

$$ \sigma_i^*(t) = \frac{1}{T}P_{A^i}(t)P_{B_i}(t) \frac{N_{v}^*(t)}{N_i}.$$
(13)

2.4.5 Entomological Inoculation Rate

The entomological inoculation rate (EIR) is the number of infectious bites a human receives per unit time. The periodic sequence for the EIR for hosts of type i is

$$ \varXi_i^*(t) = \frac{1}{T}P_{A^i}(t)P_{B_i}(t) \frac{S_{v}^*(t)}{N_i}.$$
(14)

The periodic sequence for the weighted average of EIR is

(15)
(16)

2.5 Numerical Simulation

We run a numerical simulation to describe the dynamics of the model. We use baseline parameter values, based on those in Chitnis et al. (2010a), as shown in Table 3. The periodic values for the human infectivity to mosquitoes, K vi (t) are taken from a human simulation model, and the mosquito emergence rate, N v0(t) is matched with K vi (t) and the remaining parameter values to produce an approximation to the measured EIR for Namawala, Tanzania, with a total of 320 infectious bites per person per year. The values of N v0(t) and K vi (t) used in the simulation are shown in Fig. 2. The resulting time sequence of the total number, the number of infected, and the number of infectious host-seeking mosquitoes is shown in Fig. 3.

Fig. 2
figure 2

Input periodic sequences for the parameter values of the mosquito emergence rate, N v0(t), and the human infectivity to mosquitoes, K vi (t), used to drive the mosquito malaria model

Full size image
Fig. 3
figure 3

The simulated total number, number of infected, and number of infectious host-seeking mosquitoes from parameter values in Table 3 and Fig. 2 of the periodically forced mosquito malaria model (2a), (2b), (2c)

Full size image
Table 3 Parameter values used to simulate the periodically forced model for malaria in mosquitoes. Detailed parameter descriptions are in Table 1
Full size table

We can numerically show that for parameter values given in Table 3 and Fig. 2, all eigenvalues of the corresponding \(X_{\theta_{p}}\) are inside the unit circle, so by Theorem 2.1 the periodically forced model (2a), (2b), (2c) has a unique globally asymptotically stable periodic solution for the total number of host-seeking mosquitoes, \(N_{v}^{*}(t)\), the number of infected host-seeking mosquitoes, \(O_{v}^{*}(t)\), and the number of infectious host-seeking mosquitoes, \(S_{v}^{*}(t)\).

From the definition of the parous proportion (10), the periodic sequence for the proportion of parous mosquitoes, M ∗(t) corresponding to the globally asymptotically stable solution for the model for parous mosquitoes (9a), (9b) is shown in Fig. 4. From \(N_{v}^{*}(t)\), \(O_{v}^{*}(t)\), and \(S_{v}^{*}(t)\), the periodic orbits for the delayed oocyst proportion and the sporozoite proportion are shown in Fig. 5. The corresponding periodic sequences for the host-biting rate and EIR are shown in Fig. 6.

Fig. 4
figure 4

Globally asymptotically stable periodic sequence of the proportion of mosquitoes who have fed at least once; calculated from (9a), (9b) and (10) with parameter values in Table 3 and Fig. 2

Full size image
Fig. 5
figure 5

Globally asymptotically stable periodic sequences for the proportion of infected and infectious mosquitoes for (2a), (2b), (2c) with parameter values in Table 3 and Fig. 2

Full size image
Fig. 6
figure 6

Globally asymptotically stable periodic sequences for the number of bites and number of infectious bites each person receives per day for (2a), (2b), (2c) with parameter values in Table 3 and Fig. 2

Full size image

3 Full Malaria Cycle

To include the nonlinear effects of the full malaria transmission cycle, we connect this periodically-forced model for malaria in mosquitoes with the stochastic individual-based simulation model for malaria in humans described by Smith et al. (2006, 2008, 2011). This model includes multiple aspects of the dynamics of malaria in humans, including superinfection, acquired immunity, variations in parasite densities, human demography, the effects of health systems, and different assumptions of heterogeneity. Although the model includes birth and death (natural and malaria-induced), the size and age-structure of the human population is kept constant in each simulation through migration.

Each individual in the human simulation model is treated as a different type of host by the mosquito model. Labeling the number of humans in a simulation of the human model by n H , the number of malaria susceptible hosts in the mosquito models is then m=n H . If there are no nonhuman hosts, then n=m=n H . If there are nonhuman hosts, then n>n H .

For human hosts, 1≤i≤m, the population of each host type is one, N i =1; and the host-dependent availability rate to mosquitoes, α i (t), and mosquito survival probabilities, \(P_{B_{i}}(t)\), \(P_{C_{i}}(t)\), \(P_{D_{i}}(t)\), and \(P_{E_{i}}(t)\), can be drawn from probability distributions around the estimated means for that human population. The infectivity of each human to mosquitoes, K vi (t), is determined by the human simulation model based on that human’s past exposure, immunity status, and infection status, including the multiplicity of infection and parasite density. If there are nonhuman hosts, we set their population size, availability rates to mosquitoes, and mosquito survival probabilities from available data.

It is not feasible to measure the periodic sequence for the mosquito emergence rate, N v0(t), in the field, or derive estimates for it directly. We therefore use the periodic sequence for population-level data of EIR to estimate the emergence rate, as described in the following section. Alternatively, we could use field estimates of the number of host-seeking mosquitoes to estimate the emergence rate with a similar algorithm.

Once we have estimated the emergence rate, with all parameters for the mosquito malaria model, we use (14), to calculate the resulting EIR on each human of the simulated population. The human simulation model uses this EIR to then determine if the number of infectious bites on each human leads to a new infection or not, given the human’s immunity and infection status. Given past infections, the human simulation model determines the human infectivity to mosquitoes at each time step to feed back to the mosquito model. At each time point, the mosquito model passes Ξ i (t) to the human model and the human model passes K vi (t) to the mosquito model. Also, events in the human model, such as birth, aging, death, and the distribution and decay of interventions affect α i (t), \(P_{B_{i}}(t)\), \(P_{C_{i}}(t)\), and \(P_{D_{i}}(t)\) in the mosquito model.

To simulate the effects of malaria control interventions, we first force the human malaria model with a periodic input EIR over one life span to bring the human population to an immunological state with realistic naturally acquired immunity for that transmission setting. We then use the corresponding human infectivity to mosquitoes, K vi (t), to estimate the periodic mosquito emergence rate that would give rise to the input EIR. Finally, we simulate the full nonlinear system to determine the effects of interventions on different malaria indicators, such as transmission (EIR), clinical disease, severe disease, and death. To allow for the decay of interventions, we simulate (2a), (2b), (2c) forward in time allowing the time-dependent parameters, except for N v0(t), to be nonperiodic.

3.1 Estimating the Emergence Rate

We describe additional parameters used to estimate the emergence rate in Table 4. As described above, we first run the model for one human life span, forcing the human population with a periodic target (input) EIR, Ξ T (t), modulated for each individual based on his/her availability to mosquitoes. Forcing the humans with Ξ T (t) for one life span induces realistic naturally acquired immunity in humans of all ages, and allows us to calculate the periodic human infectivity to mosquitoes, K vi (t), from this population. Then, starting with an initial guess for the periodic emergence rate, \(\overline{N_{v0}(t)}\), given K vi (t) and all other parameters of the mosquito malaria model, we scale and rotate \(\overline{N_{v0}(t)}\) to estimate the emergence rate, N v0(t), that produces an EIR closest to Ξ T (t). This assumes that the pattern of \(\overline {N_{v0}(t)}\) is the same as that of the target EIR, which is reasonable given the uncertainties in data collection of EIR seasonality.

Table 4 Description of additional parameters used to estimate the emergence rate from a given target EIR
Full size table

Since the composition of the human population varies over time, to reduce stochastic human heterogeneity, instead of EIR, we fit he number of infectious host-seeking mosquitoes. From (16), the target number of infectious host-seeking is

$$S_{T}(t)=\varXi_{T}(t) \frac{\sum_i N_i(t)}{\sum_i P_{A^{i}}(t)P_{B_{i}}(t)} T.$$
(17)

We define initial periodic sequences of numbers of host-seeking mosquitoes from S T (t) and reasonable estimates of the delayed oocyst proportion, ρ O , and the sporozoite proportion, ρ S ,

Note that ρ O and ρ S are only used to initialize the estimation process and do not affect the value of the estimated emergence rate. We define the initial periodic sequence for the emergence rate from the equilibrium point of the number of host-seeking mosquitoes from the autonomous mosquito malaria model (Chitnis et al. 2008, (6a)),

After simulating the human population for one life span, we continue to force the human simulation model with the target EIR, Ξ T (t), for a few years to calculate the resulting K vi (t). We use K vi (t) in (2a), (2b), (2c) with the initial emergence rate, \(\overline {N_{v0}(t)}\) to calculate the number of infectious mosquitoes, S v (t). We define the scaling factor, ω, as the ratio of the sum of the target infectious host-seeking mosquitoes over 1 yearFootnote 1 (representing the target annual EIR) to the sum of the calculated infectious host-seeking mosquitoes (representing the calculated annual EIR),

$$\omega= \frac{\sum_{t=\hat{t}}^{\hat{t}+\theta_p-1} S_T(t)}{\sum_{t = \hat{t}}^{\hat{t}+\theta_p-1} S_v(t)},$$
(18)

for an appropriate \(\hat{t}\).

We then use least squares to estimate the delay between mosquito emergence and inoculation of humans, φ: the time it takes mosquitoes to get infected, and consequently for the parasite to develop into infectious sporozoites. We pick φ, such that the squared distance between the shifted target number of infectious host-seeking mosquitoes and the scaled calculated number of infectious host-seeking mosquitoes is minimized,

$$\epsilon_\varphi= \sum_{t=\hat{t}}^{\hat{t} + \theta_p-1}\bigl( S_T(t-\varphi) - \omega S_v(t)\bigr)^2.$$
(19)

The estimated emergence rate is then

$$N_{v0}(t) = \frac{1}{\omega} \overline{N_{v0}(t+\varphi)}.$$
(20)

Note that since \(\overline{N_{v0}(t)}\) is a periodic sequence, it is defined for all values of t.

3.2 Modeling Malaria Control Interventions

We use the model of the full malaria cycle to compare the effectiveness of ITNs and IRS with dichlorodiphenyltrichloroethane (DDT), used singly and in combination, in reducing malaria transmission and disease. This extends the work of Chitnis et al. (2010a) which compared these interventions, but ignored the effects of seasonality and decay of interventions and did not consider transient dynamics.

We determine parameter values for both models (human and malaria) for the African village setting of Namawala, Tanzania, based on data from 1990–1991 (Charlwood et al. 1997; Smith et al. 1993), with a pre-intervention EIR of 320 infectious bites per person per year. For this older data, we use chloroquine as the first line treatment against malaria, not an ACT as is the current official policy. We simulate a human population size of 1,000. The three main vector species in this area are An. gambiae s. s., An. arabiensis, and An. funestus (Charlwood et al. 1997). We model the three mosquito species by replicating (2a), (2b), (2c), interacting with the same human population. We use parameter values for the initial efficacy of IRS and of ITNs as described in Chitnis et al. (2010a). We also assume that their effectiveness decays exponentially with IRS with DDT having a half-life of 6 months (Sadasivaiah et al. 2007) and ITNs having a half-life of 3 years (Kilian et al. 2008; Lindblade et al. 2005).

We show plots of the effects of no vector control interventions, IRS alone, ITNs alone, and a combination of IRS and ITNs on EIR, prevalence, and clinical incidence, in Figs. 7, 8, and 9, respectively. We run multiple simulations of fourteen model extensions/parameterizations and two random seeds, showing the median, interquartile range, and minimum and maximum values of all simulations at each time point. The different models and the analysis of the ensemble is described in more detail in Smith et al. (2012).

Fig. 7
figure 7

(Color online) The annual EIR (number of infectious bites per person per year) with (a) no vector control interventions; (b) two annual spray rounds of IRS from year 0 to year 11 with 95% coverage; (c) three mass distributions of ITNs at years 0, 3, and 6 with 95% coverage; (d) combined distribution of both ITNs and IRS as above. The solid (blue) line is the median; the shaded (grey) area is the interquartile range; and the dotted (black) lines are the minimum and the maximum values, at each time point of simulation results of the ensemble of malaria models with multiple random seeds. All entomological, epidemiological, and health systems settings for the simulations are based on Namawala, Tanzania, with a human population size of 1,000, and an initial preintervention annual EIR of 320 infectious bites per person

Full size image
Fig. 8
figure 8

(Color online) The prevalence of malaria infection (proportion of people infected with the malaria parasite) with (a) no vector control interventions; (b) two annual spray rounds of IRS from year 0 to year 11 with 95% coverage; (c) three mass distributions of ITNs at years 0, 3, and 6 with 95% coverage; (d) combined distribution of both ITNs and IRS as above. The solid (blue) line is the median; the shaded (grey) area is the interquartile range; and the dotted (black) lines are the minimum and the maximum values, at each time point, of simulation results of the ensemble of malaria models with multiple random seeds. All entomological, epidemiological, and health systems settings for the simulations are based on Namawala, Tanzania, with a human population size of 1,000, and an initial preintervention annual EIR of 320 infectious bites per person

Full size image
Fig. 9
figure 9

(Color online) The rate of clinical incidence (number of uncomplicated clinical malaria episodes per year) with (a) no vector control interventions; (b) two annual spray rounds of IRS from year 0 to year 11 with 95% coverage; (c) three mass distributions of ITNs at years 0, 3, and 6 with 95% coverage; (d) combined distribution of both ITNs and IRS as above. The solid (blue) line is the median; the shaded (grey) area is the interquartile range; and the dotted (black) lines are the minimum and the maximum values, at each time point of simulation results of the ensemble of malaria models with multiple random seeds. All entomological, epidemiological, and health systems settings for the simulations are based on Namawala, Tanzania with a human population size of 1,000, and an initial preintervention annual EIR of 320 infectious bites per person

Full size image

Figure 7 shows that IRS reduces malaria transmission over the first two years of its application but does not lead to further gains as EIR is maintained at a lower rate from then on. When IRS is stopped, EIR returns to its preintervention level. ITNs also lower the EIR for the first two deployments but lead to no further gains, with a return to the preintervention level of EIR after the deployment of ITNs is stopped. ITNs are more effective than IRS in reducing transmission. Combining ITNs and IRS leads to additional gains and is beneficial in this setting. The larger differences in the ranges of the maxima and minima of the EIR with ITNs and a combination of ITNs and IRS show more uncertainty in these results than in the simulations with IRS alone or with no interventions.

All plots in Fig. 8 show greater variation with larger interquartile ranges and differences between maxima and minima, implying more uncertainty in predicting prevalence than in predicting EIR. Similar to the plots for EIR, IRS and ITNs reduce prevalence in their first two deployments but do not lead to further reductions, and return to preintervention levels after the interventions are stopped. Combining ITNs and IRS results in a lower prevalence than either IRS or ITNs alone.

As with the plots for prevalence, Fig. 9 shows uncertainty in predicting clinical incidence. The plots show that after a small reduction in clinical cases with either ITNs or IRS, there is an increase above preintervention levels. While the combination of ITNs and IRS reduce the number of clinical cases, by year eight after ITNs have been withdrawn, the number of cases rises above preintervention levels. Some time after the interventions (ITNs, IRS, and their combination) have been stopped, the number of clinical cases drops to the preintervention level.

4 Discussion and Concluding Remarks

We described a periodically forced model for malaria in mosquitoes that includes seasonality of mosquito populations and details of the mosquito feeding cycle that can capture the effects of vector control interventions such as ITNs and IRS. Most malaria endemic areas of the world experience seasonal variation with a peak of transmission followed by a period of low transmission (Roca-Feltrer et al. 2009). Seasonality is therefore crucial in developing models of malaria that can make quantitative predictions, especially when considering the timing of short-acting interventions. Autonomous models of malaria transmission and mosquito dynamics can overestimate the effects of IRS with insecticides with a short half life such an bendiocarb, when compared to insecticides with a longer half life such as DDT, because they do not include the relationship between the length of the transmission season and the effective duration of the intervention period.

The model is mathematically well-posed and we numerically showed the existence of a unique globally asymptotically stable periodic orbit. We derived this periodic orbit and corresponding field-measurable parameters that describe various aspects of malaria transmission such as the parous proportion, the delayed oocyst rate, the sporozoite rate, the human-biting rate, and the EIR. We illustrated these field-measurable quantities with an example simulation.

There are some assumptions in this model that still need to be addressed. We ignored seasonal variations due to temperature and would like to include this dependence by making the partial duration of the feeding cycle, τ, and the extrinsic incubation period, θ s , periodic parameters. We assumed that the mosquito emergence rate does not depend on the adult mosquito population. We want to expand our model to include this dependence and to also include the development of insecticide resistance and the corresponding decrease in the effectiveness of interventions in future versions of the model.

As this deterministic model for malaria in mosquitoes does not include the human part of the malaria life cycle, the extension to a nonautonomous model also allowed us to link it to a previously described stochastic individual-based simulation model for malaria in humans to include the full malaria cycle and determine the effects of interventions on human disease. An open source version of this full model, coded in C++, is available online (OpenMalaria 2011). We used the integrated model to compare the effectiveness of two vector control interventions: ITNs and IRS, applied singly, and in combination in reducing malaria transmission, prevalence, and incidence. We based our parameter values on the setting of Namawala, a rural village in a seasonal high transmission area of Tanzania. Our results showed that both ITNs and IRS are effective in reducing transmission and prevalence and maintaining that reduction. However, the reduction occurs over the first two deployments and no further reductions should be expected. Maximal effects would be achieved relatively quickly with IRS, but with ITNs the maximal effects would require at least two mass distribution campaigns. Malaria control programs and field researchers need to be aware that these effects will only be evident in controlled studies with long-term follow-up. When the deployment of interventions is stopped, transmission and prevalence quickly revert to preintervention levels, so high coverage levels of interventions must be sustained to maintain reductions in transmission and prevalence. There are additional benefits to combining ITNs and IRS, as transmission and prevalence are lower than using either one alone.

The number of clinical cases, however, can increase with the deployment of the vector control interventions even though transmission and prevalence are reduced. The increase in clinical incidence above baseline levels over time, is not intuitively to be expected. We have observed similar, though smaller, effects with simulations of vaccination using the same models for malaria in humans (Maire et al. 2006). We think this results from a decrease in population level immunity, mainly due to recruitment of new immunologically naive individuals during the period of protection (the inclusion of immune decay in the human models makes little difference, Smith et al. 2012). These temporary increases in morbidity in the models would be difficult to validate in the field because they are small relative to year-to-year variability, and studies of such phenomena are unlikely to involve long follow-up periods and matched controls.

Other models that have considered similar issues include Griffin et al. (2010) and Eckhoff (2011). Griffin et al. (2010) use an individual based model derived from a compartmental model to investigate the effects of different interventions on prevalence in six different transmission settings with the same mosquito species that we use but with different seasonality profiles. They show greater reductions in prevalence than our simulations though their transmission settings have different magnitudes than the ones we consider here. They do not show the effects of the interventions on clinical incidence. Eckhoff (2011) focusses on an individual based model of mosquito population dynamics and shows similar reductions in EIR that we do with ITN and IRS use but does not show the effects on prevalence or clinical incidence.

Although our models show that the number clinical cases increases after the deployment of vector control interventions, we expect that the number of malaria deaths would decrease with the use of these interventions, since a reduction in transmission means that susceptibility in humans shifts to older age groups, in whom episodes are less likely to be severe and result in death (Ross et al. 2006). We plan to use this combined model to run more simulations to consider the effects of vector control interventions on mortality. We also want to compare the effects of using different insecticides, varying the coverage levels, and combining vector control interventions with other malaria control interventions in various epidemiological and health systems settings. Additionally, we will use the model to determine target product profiles for new interventions to improve control, interrupt transmission, and maintain elimination in the presence of imported cases.