1 Introduction

Complex fluids are typically described by constitutive equations in which the relation between the Cauchy stress and the kinematic variables may be highly involved. In some cases, the stress can be written as a tensorial function of some kinematical variables (Navier–Stokes fluids, generalized Newtonian fluids, etc). For some materials (such as colloids) the relation between the stress and the kinematical variables is implicit, so that we cannot globally express one quantity as a function of the others.

In order to highlight the interplay between rheological properties and other factors under different flow conditions, several studies have been carried out to investigate new constitutive relations for non-Newtonian fluids, see e.g. [1,2,3,4,5,6,7,8,9,10,11] and references cited therein. In particular, Rajagopal [9] has proposed an implicit algebraic constitutive relation between the deviatoric stress tensorFootnote 1, \({\mathbb {S}}^*\), and the strain rate tensor, \({\mathbb {D}}^*\), providing a significant change of perspective in modelling fluid-like materials [6]. Further generalisations have been provided by Prů\(\mathrm {{\check{s}}}\)a and Rajagopal [7]. Recently, Fusi et al. [3] have studied the flow in an orthogonal rheometer of a fluid modelled through an implicit constitutive relation that has been developed for colloids. They have solved numerically the corresponding nonlinear problem for pseudo-planar solutions, showing that pronounced boundary layers adjacent to the rotating plates can develop even at moderate Reynolds numbers. Implicit type relations can be used to effectively fit experimental data [6]. For instance, in [1] the authors present a fluid dynamic model for blood involving two factors related to the formation of clots, i.e. mechanical effect and fibrin concentration, by using a stress-power law as constitutive law with the characteristic “S-shape”, as schematically shown in Fig. 1. Many other complex fluids, such as wormlike micellar surfactants, onion surfactants, colloidal suspensions and polymer solutions, also show a nonlinear rheology described by an “S-shaped” constitutive law. These models have recently attracted some attention because they have been used to describe qualitatively the shear band effect (i.e. the homogeneous flow becomes unstable above a critical applied shear rate, or shear stress). Shear banded flows undergo transitions from an homogeneous state to a state of macroscopic coexisting bands characterized by different viscosities and internal structuring [12]. Experimental evidences show the occurrence of the so-called “shear banding” effect, i.e. the existence of a critical applied shear rate (or shear stress) above which the homogeneous flow becomes unstable [12, 13], exhibiting structures qualitatively different from the quiescent state. Such “banded structures” can extend along the gradient or vorticity direction, corresponding to two types of instabilities referred to as “gradient banding” and “vorticity banding”, respectively [14]. Moreover, in the case of gradient banding, the resulting new structure has shear bands with different coexisting apparent viscosities, separated along the flow gradient direction by a sharp “interface”. Similarly, in the case of vorticity banding, by imposing a uniform shear stress the system can separate into bands along the vorticity direction. The vorticity bands can be visualized thanks to their different turbidity or, in the case of birefringent materials, because of the different orientations of their optical axes [12, 13]. We refer the readers to [12,13,14,15,16] as relevant articles on shear banding experimental, theoretical and numerical studies.

Fig. 1
figure 1

Schematic representation of a non-monotone stress-power law as constitutive law with the characteristic “S-shape”

Full size image

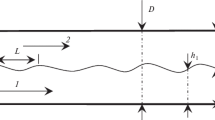
In this paper, we investigate the onset of instability of a Couette flow driven by a prescribed shear stress imposed on the top surface (Fig. 2). We assume a “S-shaped” stress vs strain-rate relation similar to one used in [1] (see Fig. 1) and, following the same approach of [4], we provide a range for the Reynolds number for which multiple solutions are possible. Following [17,18,19,20], we then perform a linear modal stability analysis considering a 2D perturbation. We solve by means of spectral collocation method based on Chebyshev polynomials the corresponding eigenvalue problem and we investigate the stability/instability of each solution. We emphasise that the aim of our analysis is to provide a simple stability characterization of the “S-shaped” constitutive model. In particular, our analysis introduces certain simplifications to model the onset of instability for a Couette flow of complex fluids with non-monotone stress-power law (i.e. a 2D linear stability analysis), thus we emphasize that our study is a first step to deepen such complex phenomena and is not an exhaustive study. The paper is organized as follows: in Sect. 2, we formulate the mathematical problem. In Sect. 3 we perform the linear stability analysis. In Sect. 4 we illustrate the results concerning linear stability and then some final remarks and future perspectives are drawn in the last section.

2 The mathematical problem

Let us consider

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho ^{*}\dot{{\textbf{v}}}^{*}=-\nabla p^{*}+\textrm{div}\left( {\mathbb {S}}^{*}\right) , \\ \textrm{div}\left( {\textbf{v}}^{*}\right) =0, \end{array}\right. } \end{aligned}$$
(1)

where we assume

$$\begin{aligned} {\mathbb {S}}^{*}=2\mu ^{*}\left[ \left( 1+\beta ^{*}||{\mathbb {D}} ^{*}||^{2}\right) ^{n}+\gamma \right] {\mathbb {D}}^{*}, \end{aligned}$$
(2)

where ||.|| is the Frobenius norm. When

$$\begin{aligned} n<-{\displaystyle {\frac{1}{2}}},\;\ \ \textrm{and}\ \ \ \ \gamma <2\left[ { \displaystyle {\frac{\mid 2n+1\mid }{2(1-n)}}}\right] ^{1-n}, \end{aligned}$$
(3)

the norm \(||{\mathbb {S}}^{*}||\) of the deviatoric part of the stress is a non monotone function of \(||{\mathbb {D}}^{*}||\), see [4]. In this case the function \(||{\mathbb {S}}^{*}||\) vs \(||{\mathbb {D}}^{*}||\) exhibits the characteristic “S-shaped” curve as shown in Fig. 2 of [14].

We consider a Couette flow driven by a shear stress \(\tau ^{*}\) imposed on the top surface, as shown in Fig. 2. The thickness of the layer is assumed to be fixed and equal to \(H^*\).

Fig. 2
figure 2

Schematic representation of a Couette flow driven by a shear stress \(\tau ^{*}\) imposed on the top surface at \(y^* = H^*\)

Full size image

We introduce the following dimensionless quantities

$$\begin{aligned} \begin{array}{c} {\textbf{x}}={\displaystyle {\frac{{{{{\textbf{x}}}}}^{*}}{H^{*}}}},\quad {\textbf{v}}={\displaystyle {\frac{{{{{\textbf{v}}}}}^{*}}{{{{U_{ref}^{*}} }}}}},\quad t={\displaystyle {\frac{U^{*}}{H^{*}}}}t^{*}, \quad p={\displaystyle {{\frac{H^{*}}{\mu ^{*}U_{ref}^{*} }}{p^{*}}}}, \\ {\mathbb {D}}={\displaystyle {\frac{H^{*}}{U_{ref}^{*}}}}{\mathbb {D}} ^{*},\quad {\mathbb {S}} = {\displaystyle {\frac{H^{*}}{ \mu ^{*}U_{ref}^{*}}}}{\mathbb {S}}^{*},\ \ \ \tau = {\displaystyle {\frac{H^{*}}{ \mu ^{*}U_{ref}^{*}}}}\tau ^{*}, \end{array} \end{aligned}$$
(4)

where \(U_{ref}^*\) is a reference velocity. Introducing the Reynolds number

$$\begin{aligned} {{\textsf{R}}}{{\textsf{e}}}={\displaystyle {\frac{\rho ^{*}U_{ref}^{*}H^{*}}{\mu ^{*}}}}, \end{aligned}$$

and using the adimensionalization (4), system (1) and the constitutive law (2) become

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} {{\textsf{R}}}{{\textsf{e}}}\,\dot{{\textbf{v}}}=-\nabla p+\textrm{div}{\mathbb {S}}, \\ \textrm{div}{\textbf{v}}=0, \end{array}\right. } \end{aligned}$$
(5)
$$\begin{aligned}{} & {} {\mathbb {S}}=\left[ \left( 1+\beta ^{*}{\displaystyle {\frac{U_{ref}^{*^{2}}}{H^{*^{2}}}}}||{\mathbb {D}}||^{2}\right) ^{n}+\gamma \right] {\mathbb {D}}, \end{aligned}$$
(6)

respectively. We look for a one dimensional laminar stationary flow, namely a solution in the form

$$\begin{aligned} {\varvec{v}}=u(y){\textbf{e}}_{x}, \end{aligned}$$
(7)

so that system (5) reduces to

$$\begin{aligned} {\left\{ \begin{array}{ll} 0=-p_{x}+{S}_{12,y}, \\ 0=-p_{y}. \end{array}\right. } \end{aligned}$$
(8)

Assuming no pressure gradient, from (8) we obtain \({S} _{12,y}=0\), i.e. \({S}_{12}=\tau\). We note that \(4||{\mathbb {D}} ||^{2}=u^{\prime }(y)^{2}\), so that selecting

$$\begin{aligned} U_{ref}^{*}={\displaystyle {\frac{\tau ^{*}H^{*}}{\mu ^{*}}}}, \end{aligned}$$
(9)

we have \(\tau =1\), entailing \({S}_{12}=1\), i.e.

$$\begin{aligned} \left[ \left( 1+{\displaystyle {\frac{\beta ^{*}\tau ^{*2}}{4\mu ^{*2}}}}{u^{\prime }}^{2}\right) ^{n}+\gamma \right] u^{\prime }=1, \end{aligned}$$
(10)

where (6) has been exploited. Using (9), \({{\textsf{R}}}{{\textsf{e}}}\) becomes

$$\begin{aligned} {{\textsf{R}}}{{\textsf{e}}}={\displaystyle {\frac{\rho ^{*}{H^{*}}^{2}}{{\mu ^{*}} ^{2}}}}\tau ^{*}, \end{aligned}$$
(11)

showing that \({{\textsf{R}}}{{\textsf{e}}}\) is an increasing function of \(\tau ^{*}\), as expected. By using (11), the term \({\displaystyle {\frac{\beta ^{*}\tau ^{*2}}{4\mu ^{*^{2}}}}}\) in (10) can be rewritten as

$$\begin{aligned} {{\frac{\beta ^{*}\tau ^{*2}}{4\mu ^{*2}}=}}\overline{{{\textsf{R}}}{{\textsf{e}}} }^{2}={{\textsf{R}}}{{\textsf{e}}}^{2}\xi ^{2}, \end{aligned}$$
(12)

where

$$\begin{aligned} \xi ^{2}={\displaystyle {\frac{\beta ^{*}\mu ^{*2}}{4\rho ^{*2}H^{*4}},}} \end{aligned}$$

is a dimensionless parameter that depends only on the geometry of the system and on the material parameters \(\beta ^{*}\), \(\rho ^{*}\) and \(\mu ^{*}\). Therefore, (10) can be rewritten as \(f\left( u^{\prime },\overline{{{\textsf{R}}}{{\textsf{e}}}}\right) =1\), where

$$\begin{aligned} f\left( u^{\prime },\overline{{{\textsf{R}}}{{\textsf{e}}}}\right) =\left[ \left( 1+\overline{ {{\textsf{R}}}{{\textsf{e}}}}^{2}{u^{\prime }}^{2}\right) ^{n}+\gamma \right] u^{\prime }=1. \end{aligned}$$
(13)

In particular, we recall that when (3) is satisfied f is a non-monotone function in \(u^{\prime }\) (see [4]) exhibiting a local maximum and minimum, for any positive \(\overline{{{\textsf{R}}}{{\textsf{e}}}}\). Given n and \(\gamma\) fulfilling (3), we denote by \(u_{M}^{\prime }\) and \(u_{m}^{\prime }\) the local maximum and minimum of \(f\left( u^{\prime },\overline{{{\textsf{R}}}{{\textsf{e}}}}\right)\) (see Fig. 3A) that satisfy

$$\begin{aligned} \frac{\partial f\left( u^{\prime },\overline{{{\textsf{R}}}{{\textsf{e}}}}\right) }{\partial u^{\prime }}=0,\ \ \ \forall \ \ \overline{{{\textsf{R}}}{{\textsf{e}}}}>0. \end{aligned}$$

Setting

$$\begin{aligned} f_{M}\left( \overline{{{\textsf{R}}}{{\textsf{e}}}}\right) =f\left( u_{M}^{\prime },\overline{ {{\textsf{R}}}{{\textsf{e}}}}\right) ,\ \ \ \ \ f_{m}\left( \overline{{{\textsf{R}}}{{\textsf{e}}}}\right) =f\left( u_{m}^{\prime },\overline{{{\textsf{R}}}{{\textsf{e}}}}\right) , \end{aligned}$$
Fig. 3
figure 3

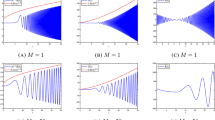
A Plot of f for \(n=-3\) and \(\gamma =0.21\) with \(\overline{{{\textsf{R}}}{{\textsf{e}}}}_{m}=0.33<\overline{{{\textsf{R}}}{{\textsf{e}}}}=0.34<\overline{ {{\textsf{R}}}{{\textsf{e}}}}_{M}=0.36\). Condition (15) is fulfilled thus Eq. (13) has three solutions \(u_{b1}^{\prime },u_{b2}^{\prime },u_{b3}^{\prime }\); B Compatibility range (15)

Full size image
Fig. 4
figure 4

Plot of f for \(n=-3\) and \(\gamma =0.21\) with A \(\overline{{{\textsf{R}}}{{\textsf{e}}}}=0.2<\overline{{{\textsf{R}}}{{\textsf{e}}}}_{m}=0.33\) and B \(\overline{{{\textsf{R}}}{{\textsf{e}}}}=0.5>\overline{{{\textsf{R}}}{{\textsf{e}}}}_{M}=0.36\) showing that Eq. (13) has only one solution. Indeed, condition (15) is not fulfilled

Full size image

we observe that the algebraic Eq. (13) is fulfilled by three distinct values of \(u^{\prime }\), which we denote by \(u_{bj}^{\prime }\), \(j=1,2,3\), provided

$$\begin{aligned} f_{m}\left( \overline{{{\textsf{R}}}{{\textsf{e}}}}\right)<1<f_{M}\left( \overline{{{\textsf{R}}}{{\textsf{e}}}}\right) , \end{aligned}$$
(14)

as shown in Fig. 3A. Condition (14) is verified when

$$\begin{aligned} \overline{{{\textsf{R}}}{{\textsf{e}}}}_{m}<\overline{{{\textsf{R}}}{{\textsf{e}}}}<\overline{{{\textsf{R}}}{{\textsf{e}}}} _{M},\ \ \ \underset{\mathrm {(12)}}{\Leftrightarrow }\ \ \ \frac{\overline{{{\textsf{R}}}{{\textsf{e}}}}_{m}}{\xi }<{{\textsf{R}}}{{\textsf{e}}}<\frac{\overline{{{\textsf{R}}}{{\textsf{e}}}}_{M}}{\xi }, \end{aligned}$$
(15)

as displayed in Fig. 3B. Otherwise, i.e. if \(\overline{ {{\textsf{R}}}{{\textsf{e}}}}<\overline{{{\textsf{R}}}{{\textsf{e}}}}_{m}\) or if \(\overline{{{\textsf{R}}}{{\textsf{e}}}}> \overline{{{\textsf{R}}}{{\textsf{e}}}}_{M}\), the algebraic Eq. (13) admits only one solution, see Fig. 4. In the sequel we assume that condition (15) holds true and therefore (14) is fulfilled. In particular, we order the three solutions of (13) as \(u_{b1}^{\prime }<u_{b2}^{\prime }<u_{b3}^{\prime }\), i.e. \(u_{b2}^{\prime }\) is in the descending branch of f (see Fig. 3A).

3 Linear stability analysis for laminar flow

In this section, we take n, \(\gamma\) and \(\overline{ {{\textsf{R}}}{{\textsf{e}}}}\) fulfilling conditions (3) and (15), respectively. We then consider the basic laminar flow (7), i.e. \({\varvec{v}}_{bj}=u_{bj}(y){\textbf{e}}_{x}\), \(j=1,2,3\), where \(u_{bj}(y)=u_{bj}^{\prime }y\), with \(u_{bj}^{\prime }\) solution to (13), and \(p=p_{bj}=0\). We perturb the basic \(j^{th}\) flow by superimposing a “small” 2D disturbance in the form of travelling wave

$$\begin{aligned} \begin{array}{lll} {\varvec{v}}&{}=&{}{\varvec{v}}_{bj}+\varvec{{\hat{v}}} = \left( u_{bj}\left( y\right) +{\hat{u}}(y)e^{i\alpha (x-ct)}\right) {\textbf{e}}_{x} + {\hat{v}}(y)e^{i\alpha (x-ct)}{\textbf{e}}_{y},\ \ \ \ j=1,2,3, \\ \\ p&{}=&{}{\hat{p}}(y)e^{i\alpha (x-ct)}, \end{array} \end{aligned}$$
(16)

and

$$\begin{aligned} {{\mathbb {D}}}={{\mathbb {D}}}_{bj}+\hat{{\mathbb {D}}}e^{i\alpha (x-ct)},\ \ \ {\mathbb {S}}={\mathbb {S}}_{bj}+\hat{{\mathbb {S}}}e^{i\alpha (x-ct)},\ \ j=1,2,3, \end{aligned}$$
(17)

where \(\alpha \in {\mathbb {R}}\) is the wave number, \(c\in {\mathbb {C}}\) is the complex wave speed and the notation \(\hat{(\cdot )}\) represents the amplitude of the infinitesimal disturbance. Inserting the perturbations (16)–(17) into system (5) and multiplying by \(e^{-i\alpha (x-ct)}\), we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} {{\textsf{R}}}{{\textsf{e}}}\left[ -i\alpha c\hat{{\varvec{v}}}+\left( \nabla {\varvec{v}} _{bj}\right) \hat{{\varvec{v}}}+\left( \nabla \varvec{{\hat{v}}}\right) {\varvec{v}}_{bj}\right] =-\nabla {\hat{p}} +\textrm{div}\hat{{\mathbb {S}}}, \\ i\alpha {\hat{u}}+{\hat{v}}^{\prime }=0, \end{array}\right. } \end{aligned}$$
(18)

where, here and in the sequel, \((\cdot )^{\prime }\) denotes the differentiation w.r.t. y. System (18) is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} {{\textsf{R}}}{{\textsf{e}}}\left( -i\alpha c\hat{{u}}+u_{bj}^{\prime }{\hat{v}}+i\alpha \hat{{u }}{u}_{bj}\right) =-i\alpha {\hat{p}}+i\alpha {\hat{S}}_{11} +{\hat{S}}_{12}^{\prime }, \\ {{\textsf{R}}}{{\textsf{e}}}\left( -i\alpha c\hat{{v}}+i\alpha \hat{{v}}{u}_{bj}\right) =- {\hat{p}}^{\prime }+i\alpha {\hat{S}}_{12}+{\hat{S}}_{22}^{\prime }, \\ i\alpha {\hat{u}}+{\hat{v}}^{\prime }=0. \end{array}\right. } \end{aligned}$$
(19)

In the sequel we obtain, through algebraic manipulations, an equation in the sole variable \({\hat{v}}\) from system (19), then using (19)\(_{3}\) we find \({\hat{u}}\). We start by differentiating w.r.t. y Eq. (19)\(_{1}\) to which we add (19)\(_{2}\)

$$\begin{aligned} -{{\textsf{R}}}{{\textsf{e}}}\left[ (u_{bj}-c)\left( \textrm{D}^{2}-\alpha ^{2}\right) {\hat{v}} \right] =i\alpha \left( {\hat{S}}_{11}^{\prime }-{\hat{S}}_{22}^{\prime }\right) +\left( \textrm{D}^{2}+\alpha ^{2}\right) {\hat{S}}_{12}, \end{aligned}$$
(20)

where \(\textrm{D}^{2}=(\cdot )^{\prime \prime }\), and \(u_{bj}^{\prime \prime }=0\), \(j=1,2,3\). Recalling (17), we have

$$\begin{aligned} {\mathbb {S}}={\mathbb {S}}_{bj}+\hat{{\mathbb {S}}}e^{i\alpha (x-ct)}=2\left[ \left( 1+4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}||{\mathbb {D}}_{bj}+\hat{{\mathbb {D}}}e^{i\alpha (x-ct)}||^{2}\right) ^{n}\right. +\gamma \biggr ]\left( {\mathbb {D}}_{bj}+\hat{{\mathbb {D}}}e^{i\alpha (x-ct)}\right) . \end{aligned}$$
(21)

Neglecting second order terms we find

$$\begin{aligned} ||{\mathbb {D}}_{bj}+\hat{{\mathbb {D}}}e^{i\alpha (x-ct)}||^{2}&={\displaystyle { \frac{1}{2}}}\left( {\mathbb {D}}_{bj}+\hat{{\mathbb {D}}}e^{i\alpha (x-ct)}\right) \cdot \left( {\mathbb {D}}_{bj}+\hat{{\mathbb {D}}}e^{i\alpha (x-ct)}\right) \nonumber \\&=||{\mathbb {D}}_{bj}||^{2}+{\mathbb {D}}_{b}\cdot \hat{{\mathbb {D}}}e^{i\alpha (x-ct)}. \end{aligned}$$
(22)

Therefore, formula (21) becomes

$$\begin{aligned} {\mathbb {S}}_{bj}+\hat{{\mathbb {S}}}e^{i\alpha (x-ct)}&\simeq 2\left[ \left( 1+4 \overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}||{\mathbb {D}}_{bj}||^{2}+4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2} {\mathbb {D}}_{bj}\cdot \hat{{\mathbb {D}}}e^{i\alpha (x-ct)}\right) ^{n} +\gamma \right] \left( {\mathbb {D}}_{bj}+\hat{{\mathbb {D}}}e^{i\alpha (x-ct)}\right) \nonumber \\&=2\left[ \left( 1+4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}||{\mathbb {D}}_{bj}||^{2}\right) ^{n}+n\left( 1+4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}||{\mathbb {D}}_{bj}||^{2}\right) ^{n-1}4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}{\mathbb {D}}_{bj}\cdot \hat{{\mathbb {D}}} e^{i\alpha (x-ct)} \right. \nonumber \\&\quad +\gamma \bigg ] \left( {\mathbb {D}}_{bj}+\hat{{\mathbb {D}}}e^{i\alpha (x-ct)}\right) \nonumber \\&=\underset{={\mathbb {S}}_{bj}}{\underbrace{2\left[ \left( 1+4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}||{\mathbb {D}}_{bj}||^{2}\right) ^{n}+\gamma \right] {\mathbb {D}}_{bj}}}+ \biggl \{2\left[ \left( 1+4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}||{\mathbb {D}} _{bj}||^{2}\right) ^{n}+\gamma \right] \hat{{\mathbb {D}}} \nonumber \\&\quad +2n\left( 1+4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}||{\mathbb {D}}_{bj}||^{2}\right) ^{n-1}4 \overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}\left( {\mathbb {D}}_{bj}\cdot \hat{{\mathbb {D}}} \right) {\mathbb {D}}_{bj}\biggl \}e^{i\alpha (x-ct)}, \end{aligned}$$
(23)

leading to

$$\begin{aligned} \hat{{\mathbb {S}}}=2\left[ \left( 1+4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}||{\mathbb {D}} _{bj}||^{2}\right) ^{n}+\gamma \right] \hat{{\mathbb {D}}} +2n\left( 1+4\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}||{\mathbb {D}}_{bj}||^{2}\right) ^{n-1}4 \overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}\left( {\mathbb {D}}_{bj}\cdot \hat{{\mathbb {D}}} \right) {\mathbb {D}}_{bj}, \end{aligned}$$
(24)

with

$$\begin{aligned} {\mathbb {D}}_{bj}={\displaystyle {\frac{1}{2}}} \begin{pmatrix} 0 &{} u_{bj}^{\prime } \\ u_{bj}^{\prime } &{} 0 \end{pmatrix},\quad \hat{{\mathbb {D}}}={\displaystyle {\frac{1}{2}}} \begin{pmatrix} 2i\alpha {\hat{u}} &{} {\hat{u}}^{\prime }+i\alpha {\hat{v}} \\ {\hat{u}}^{\prime }+i\alpha {\hat{v}} &{} 2{\hat{v}} \end{pmatrix}. \end{aligned}$$
(25)

Now, since \(i\alpha {\hat{u}}^{\prime }+{\hat{v}}^{\prime \prime }=0\), we find

$$\begin{aligned} {{\mathbb {D}}}_{bj}\cdot \hat{{\mathbb {D}}}={\displaystyle {\frac{1}{2}}}\left( -{ \displaystyle {\frac{{\hat{v}}^{\prime \prime }}{i\alpha }}}+i\alpha {\hat{v}} \right) u_{bj}, \end{aligned}$$
(26)

so that the components of \({\mathbb {S}}\) become

$$\begin{aligned} \begin{array}{l} {\hat{S}}_{11}=-{\hat{S}}_{22}=-2\hat{v^{\prime }}\left[ \left( 1+\overline{ {{\textsf{R}}}{{\textsf{e}}}}^{2}u_{bj}^{\prime ^{2}}\right) ^{n}+\gamma \right] , \\ \\ {\hat{S}}_{12}=\left[ \left( 1+\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}u_{bj}^{\prime ^{2}}\right) ^{n}+\gamma +2n\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}\left( 1+\overline{ {{\textsf{R}}}{{\textsf{e}}}}^{2}u_{bj}^{\prime ^{2}}\right) ^{n-1}u_{bj}u_{bj}^{\prime } \right] \left( -{\displaystyle {\frac{{\hat{v}}^{\prime \prime }}{i\alpha }}} +i\alpha {\hat{v}}\right) . \end{array} \end{aligned}$$
(27)

Recalling that \(u_{bj}(y)=u_{bj}^{\prime }y\), (27) can be rewritten as

$$\begin{aligned} \begin{array}{c} {\hat{S}}_{11}=-{\hat{S}}_{22}=-2A_{j}\hat{v^{\prime }}, \\ \\ {\hat{S}}_{12}=\left( A_{j}+B_{j}y\right) \left( -{\displaystyle {\frac{{\hat{v}} ^{\prime \prime }}{i\alpha }}}+i\alpha {\hat{v}}\right) , \end{array} \end{aligned}$$
(28)

respectively, where

$$\begin{aligned} A_{j}=\left[ \left( 1+\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}u_{bj}^{\prime ^{2}}\right) ^{n}+\gamma \right] ,\ \ \ B_{j}=2n\overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}\left( 1+ \overline{{{\textsf{R}}}{{\textsf{e}}}}^{2}u_{bj}^{\prime ^{2}}\right) ^{n-1}u_{bj}^{\prime 2}. \end{aligned}$$

Therefore, exploiting (28), Eq. (20) acquires the form

$$\begin{aligned} i\alpha {{\textsf{R}}}{{\textsf{e}}}\left[ (u_{bj}-c)\left( \textrm{D}^{2}-\alpha ^{2}\right) {\hat{v}}\right]&=-4\alpha ^{2}A_{j}{\hat{v}}^{\prime \prime } \nonumber \\&\quad +\left( \textrm{D}^{2}+\alpha ^{2}\right) \left[ \left( A_{j}+B_{j}y\right) \left( {\hat{v}}^{\prime \prime }+\alpha ^{2}{\hat{v}}\right) \right] ,\ \ \ \ j=1,2,3 \end{aligned}$$
(29)

i.e. a single equation in the sole variable \({\hat{v}}\). It is worth noting that (29) reduces to the classical Orr-Sommerfeld equation when \(n=0\) and \(\gamma =0\). Equation (29), coupled with the boundary conditions \({\hat{v}}(0)={\hat{v}}^{\prime }(0)=0\), \({\hat{v}}(1)={\hat{v}}^{\prime }(1)=0\), gives rise to a generalized eigenvalue problem in \(\alpha\).

4 Results concerning linear stability

The eigenvalue problem (29), coupled with the boundary conditions \({\hat{v}}(0)={\hat{v}}^{\prime }(0)=0\), \({\hat{v}}(1)={\hat{v}} ^{\prime }(1)=0\), is solved via a spectral collocation method based on Chebyshev polynomials. The differential Eq. (29) is discretized on \(N+1\) (\(N=120\)) Gauss-Lobatto points clustered at the boundaries \(y=0\) and \(y=1\). The discretized generalized eigenvalue problem is solved through the Matlab routine polyeig. We consider cases in which the constitutive equation is non monotonic, i.e. when (3) and (15) are satisfied. For a selected basic solution \(u_{bj}\) and a pair \((\alpha ,{{\textsf{R}}}{{\textsf{e}}})\), we solve (29) with boundary conditions \({\hat{v}}(0)={\hat{v}}^{\prime }(0)=0\), \({\hat{v}}(1)={\hat{v}}^{\prime }(1)=0\). Then we denote by \(c_{\max }\) the eigenvalue with maximum imaginary part and set \(c_{M}=\textrm{Im}c_{\max }\). It turns out that

$$\begin{aligned} c_{M}=c_{M}(\alpha ,{{\textsf{R}}}{{\textsf{e}}};u_{bj}), \end{aligned}$$
(30)

i.e. \(c_{M}\) is a function of \({{\textsf{R}}}{{\textsf{e}}}\), \(\alpha\) and of the selected basic solution \(u_{bj}\). If \(c_{M}>0\) the basic solution \(u_{bj}\) is unstable, if \(c_{M}<0\) is stable and if \(c_{M}=0\) the solution is neutral. We take values of \({{\textsf{R}}}{{\textsf{e}}}\) fulfilling (15) to ensure the presence of three basic solutions. The wavenumber \(\alpha\) is taken positive.

The numerical results show that the basic solutions \(u_{b1}\) and \(u_{b3}\), which correspond to the ascending branches of the function f (see Fig. 3A), are unconditionally stable while the solution \(u_{b2}\), which corresponds to the descending branch (see Fig. 3A), is unconditionally unstable. In the sequel, we report the pursued procedure for the particular case \(\xi =0.1\) and \(n=-1\), \(\gamma =0.012\) so that (3) is fulfilled. In this case we find

$$\begin{aligned} \overline{{{\textsf{R}}}{{\textsf{e}}}}_{m}=0.22,\ \ \ \ \ \ \overline{{{\textsf{R}}}{{\textsf{e}}}} _{M}=0.51, \end{aligned}$$

and the range of interest for \({{\textsf{R}}}{{\textsf{e}}} = \overline{{{\textsf{R}}}{{\textsf{e}}} }/ \xi\) is [2.2, 5.1]. Hence, for any \({{\textsf{R}}}{{\textsf{e}}}\) in such range, we solve (13) finding \(u_{b1}^{\prime }\), \(u_{b2}^{\prime }\) and \(u_{b3}^{\prime }\) (for instance, if \({{\textsf{R}}}{{\textsf{e}}}=3\), we have \(u_{b1}^{\prime }=1.1\), \(u_{b2}^{\prime }=12.1\), \(u_{b3}^{\prime }=70.2\)). Then, for every \(u_{bj}^{\prime }\), \(j=1,2,3\), we solve the eigenvalue problem (29), coupled with \({\hat{v}}(0)={\hat{v}}^{\prime }(0)=0\), \({\hat{v}}(1)={\hat{v}}^{\prime }(1)=0\), for \(\alpha \in \left[ 0,2\right]\), looking for \(c_{M}(\alpha ,{{\textsf{R}}}{{\textsf{e}}};u_{bj})\). In Figs. 5, 6 and 7 we display the results, i.e. the function \(c_{M}\) (30) corresponding to each basic solutions \(u_{b1}\), \(u_{b2}\), \(u_{b3}\). Figures 5 and 7 refer to \(u_{b1}\), \(u_{b3}\) respectively, showing that those solutions are unconditionally stable, because \(c_{M}<0\). Figure 6 refers to \(u_{b2}\) which is unconditionally unstable since \(c_{M}>0\).

Fig. 5
figure 5

Surface \(c_{M}(\alpha ,{{\textsf{R}}}{{\textsf{e}}};u_{b1})\). The z coordinate of the surface is always negative so that the basic solution is stable

Full size image
Fig. 6
figure 6

Surface \(c_{M}(\alpha ,{{\textsf{R}}}{{\textsf{e}}};u_{b2})\). The z coordinate of the surface is always positive so that the basic solution is unstable

Full size image
Fig. 7
figure 7

Surface \(c_{M}(\alpha ,{{\textsf{R}}}{{\textsf{e}}};u_{b3})\). The z coordinate of the surface is always negative so that the basic solution is stable

Full size image

5 Conclusion and open problems

We have investigated the linear stability of a Couette flow driven by a shear stress assuming that the fluid obeys to an “S-shape” stress-power law model (a behaviour that might be generated by morphological changes in the constituents of the fluid). These non-monotonous models have recently attracted some attention as they succeed, at least from a qualitative point of view, to reproduce the “shear banding” effect, observed in several complex flows.

By following the same approach of [4], we provided a range for the Reynolds number for which three basic flows are possible and we performed a linear stability analysis for each of them. Our findings highlight that the solutions belonging to the ascending branches of the constitutive law are unconditionally stable, while the one belonging to the descending branch is (linearly) unstable.

In a recent numerical study by Janevcka et al. [15] a numerical scheme for simulation of transient flows of incompressible non–Newtonian fluids characterised by a non–monotone constitutive equation is presented. Though in [15] the authors consider an “S–shape” constitutive law expressing the strain rate tensor, \({\mathbb {D}}\), as a function of the deviatoric stress tensor, \({\mathbb {S}}\), while we take a non-monotone model \({\mathbb {S}}=\mathbb { S(D)}\), we are confident that our results can be linked to the ones illustrated in [15]. In particular, Janevcka et al., by solving various initial-boundary value problems, observe that the flow domain usually splits into multiple regions. Indeed, it seems that no pair \(\left[ {\mathbb {S}},{\mathbb {D}}\right]\) can occupy the descending branch which therefore would correspond to an unstable branch. We however point out that the mechanisms underlying such complex dynamics still remain unclear within the present state of understanding [12]. Moreover, since we consider a 2D perturbation of the basic flow and not a global 3D perturbation, we remark that our analysis is a simple stability characterization of “S–shape” constitutive law and it may pave the way to further more exhaustive stability analysis. Indeed, a priori it is not possible to select which stable solution gives the physically admissible Couette flow of the fluid. Therefore, it is necessary the introduction of a specific criterium. One possibility could be requiring that the solution maximizes or minimizes the discharge or energy dissipation. Another possibility, when experimental data are available, could be requiring that the solution matches the experimental data. It would be extremely interesting to deepen such complex phenomena through the synergy of theoretical and numerical studies coupled with further experiments capable of fully capturing and measuring the onset of instability.