A Fractional Modeling of Tumor–Immune System Interaction Related to Lung Cancer with Real Data

Abstract

In this study, we investigate a new fractional-order mathematical model which considers population dynamics among tumor cells-macrophage cells-active macrophage cells, and host cells involving the Caputo fractional derivative. Firstly, the stability of the positive steady state of the model is studied. Subsequently, the conditions for existence and uniqueness of the solutions are examined. Then, the least squares curve fitting method (LSCFM) which is one of the prominent methods for parameter estimation is used to fit the parameters of the model. It is aimed to fit the relevant parameters with the help of the tumor tissue samples which were collected from the patient with non-small cell lung cancer who had chemotherapy-naive hospitalized at Kayseri Erciyes University hospital in Turkey. A total of 12 parameters in the model are estimated using the data of lung tumor cells of this patient for 14 days. Moreover, the numerical simulations are given by considering the different fractional orders and different parameters for the model. So, it is achieved how the change in $\alpha$ affects the dynamic behavior of the system. In the sequel, to point out the advantages of the fractional-order modeling, the memory trace and hereditary traits are taken into consideration. Finally, the interpretations in terms of biological science are provided in conclusion. We believe that this interdisciplinary study will open new doors for other similar studies and will shed light on the studies to be developed on the use of real data in the mathematical modeling of cancer.

Introduction

Cancer is the deadliest and complicated disease of our time. This illness is caused by the uncontrolled growth of abnormal or mutated cells in the body, and cancer cells are known for their capability to grow rapidly, divide and proliferate uncontrollably [1, 2]. The most important cause of tumor progression is constant proliferation and metastatic potential [3]. Lung cancer, the most common malignancy in the world, is the number one cause of cancer-related death worldwide and is responsible for approximately 228,820 new cases and 140,730 deaths in 2020 [4, 5]. The 5-year relative survival rate is 6 percent for patients diagnosed with advanced disease [6]. There are many causes why lung cancer is frequently diagnosed at an advanced stage, including inadequate early detection biomarkers, disease following methods and physical examination [7]. Lung cancers are conventionally classified as small cell (SCLC) or non-small cell (NSCLC) [8, 9]. While SCLCs are malignant tumors that can be identified by neuroendocrine features, accounting for nearly 15 percent of lung cancers [9], NSCLCs account for approximately 85 percent of all lung cancers [8, 10]. This discrimination reflects the different clinical recognition, disease course, and therapeutic alternatives of the two subgroups [11]. Adenocarcinomas, accounting for 40 percent of lung cancers, are, for unknown reason, the most common histological subtype seen in NSCLCs over the past 25 years, and NSCLCs include multiple cancer types such as squamous cell, large cell, and mixed histotypes, apart from adenocarcinomas [12]. In addition to this, there is a growing body of experimental and clinical proof bring heterogeneity into focus among NSCLC subtypes. Discovering the molecular mechanism underlying cell proliferation and metastasis in NSCLC could critically aid the development of new and more effective molecular-targeted therapeutic procedures specific to subtypes [12, 13].

Although much research has been done on lung cancer, the heterogeneity among its subtypes and the complexity in the mechanism of the disease cause a great challenge in clinical oncology. Because the diagnosis of lung cancer today confides in histopathological analysis, molecular markers and imaging, and therefore early diagnosis is very difficult [14, 15]. Mathematical models can be adapted to try to estimate the complex dynamics of disease and by developing models for this, simulate the kinds of treatments that are appropriate and effective for patients in the context of personalized medicine [16,17,18]. Mathematical models that are adaptable for processes important in cancer biology will shed light on unknown points in the field of oncology.

In the world, lung cancer is leading cause of cancer deaths. Although there are several successful treatment alternatives, it continues to exist as a highly dangerous disease that has not been fully cured. The treatment techniques for this illness are still restricted some of these techniques are radiotherapy, hormonal therapy, chemotherapy, gene therapy. Although vaccination studies on cancer have been conducted for years, it still seems to need time to achieve a remarkable result. Cells in cancer tumors also change and evolve like living things in nature. Understanding how this process works will make it easier for us to beat cancer from the very beginning.

Judging by the numbers, victory over cancer still seems far away. A person’s life-long cancer risk in the USA is 42 percent in men and 38 percent in women. The Cancer Research Foundation in England gives this rate as 54 and 48 percent, respectively.

As of 2015, the number of cancer patients in England reached 2.5 million. This is an annual increase of 3 percent, in other words, 400,000 extra cancer patients observed in five years.

In destroying cancer cells, immune cells play major role. The most important immune system cells are T cells (such as CD4 + T cells, CD8 + T cells), B cells, macrophages and (NK) natural killer cells. Macrophages have an important role in innate and adaptive immune response [19, 20]. They are the most abundant cells in the tumor micro-environment. Research shows that macrophages can break down malignant cells very effectively. Macrophages are also very important as the target of innovative oncological treatments. As a therapeutic goal, tumor shrinkage is achieved by closing macrophages with CSF1 receptors, antibodies and small molecule drugs. However, the events occurring in the periphery of the tumor micro-environment are highly complex and change rapidly. As a result, designing treatment methods to cure or treat cancer is an extremely difficult task. Mathematical models contribute greatly to understanding how immune cells and cancer cells interact, and to define tumor-immune dynamics [21]. So, many researchers have benefited from mathematical models to understand the course of cancer. For example, in [22], Banerjee and Sarkar have taken into account the delay-induced tumor-immune system model and malignant tumor growth. In [23], the authors study the mathematical model of tumor–macrophages cells interaction. In addition, based on tumor radio-biologic mechanisms, the authors propose the tumor growth model considering the radiotherapy effect in [24]. They investigate how the re-oxygenation of hypnotic cells and the radio-sensitivity of radiotherapy influence the effect of tumor radiotherapy. In other study [25], the qualitative analysis of tumor cell–immune cell interaction and chemotherapy with (GWN) Gaussian white noises has been researched. Eftimie and Barelle [26] introduced a model for interactions between lung cancer and macrophages with different phenotypes (M1, M2, M1/M2) with an integer-order differential equation system. Sarmah et al. [27] formulated a seven-dimensional mathematical model connecting p53, DNA damage, and autophagy in lung cancer. They also performed both local and global sensitivity analyses along with parameter recalibration analysis to understand the system dynamics. Feng et al. [28] established a mathematical model for predicting malignancy of lung cancer complicated with Talaromyces Marneffei infection and its chest imaging characteristics, and improve clinicians’ understanding of the disease.

Fractional calculus has been used only by mathematicians, physicists and engineers for the three centuries. However, in recent years, fractional operations with its applicability have gained also great importance in unusual areas, such as finance [29, 30], medicine [31], physics [32], synchronization of chaotic systems [33], atmospheric ocean problems [34], hydrology, signal processing [35], heat diffusion models [36], competing species [37], and biology [38,39,40,41,42,43,44,45,46]. Among them, in [47], two integer order systems have been investigated with fractional calculus, which explain the tumor-immune system dynamics. In [48], a fractional-order model which propose the growth of tumor with drug application is studied. In [49], a delay model with fractional order for tumor-immune system with treatments has been proposed. A study on a mathematical model of immune response with cell mediated for tumor phenotype heterogeneity has been presented in [50]. The authors of [51] presented a model using fractional derivative, taking into account cell repair, re-population of the cells and radiotherapy process. A numerical and analytical study of the HIV-1 infection of CD4+ T cells constructed with conformable fractional mathematical model was examined in [52]. Veeresha et al. applied the q-homotopy analysis transform method (q-HATM) to the mathematical model of the cancer chemotherapy effect in the sense of Caputo derivative in [53]. In addition, in [54], the authors analyzed the behavior of solution to the system exemplifying model of tumor invasion and metastasis by the help of q-HATM.

There are only a few studies on fractional-order mathematical modeling of lung cancer in the literature. For example, in [55], the authors proposed two modeling approaches to predict lung tumor dynamics as an effect of radiotherapy. They used the real clinical information of non-small cell lung cancer (NSCLC) patients undergoing stereotactic body radiation therapy (SBRT) as the primary treatment method for numerical simulations. In another study, Ghita et al. [31] concluded that feature extraction from modeling a respiratory function through a specific fractional order impedance model could be transposed to lung tumor dynamics.

Biological phenomena and diseases are one of the most common practice areas of fractional-order mathematical models. Considering the studies until the last decade, while constructing mathematical models, it has generally seen that the authors are used the differential equations of integer order. Mathematical model studies created with these equations have proven to be very valuable in explaining the course of diseases. However, it has been observed that the models made with fractional-order differential equations (FODEs) are more compatible with the truth and provide more advantages when compared with integer-order mathematical models. Because most of the biological systems continue to function using the memory, after-affects and hereditary properties. These effects are neglected in integer-order differential equations models; however, the fractional-order models explain these complex phenomena better than these equations. Before presenting our model, we mention a few mathematical models of tumor-immune systems: In [56], a study on tumor and macrophages cells is modeled as follows:

$$\begin{aligned} \frac{dP}{dt}= & {} P(t)r_1\left( 1-\frac{P(t)}{k_1}\right) -bP(t)Q(t)-d_1P(t)+\varepsilon _1Q(t), \nonumber \\ \frac{dQ}{dt}= & {} Q(t)(bP(t)-d_2),\ \nonumber \\ \frac{dR}{dt}= & {} R(t)r_2\left( 1-\frac{R(t)}{k_2}\right) -aR(t)Q(t)+c, \end{aligned}$$

(1)

where P(t), Q(t), R(t) are the concentrations of macrophages, activated macrophages and tumor cells. $r_{1}$ is the growth rate of macrophages cells and $k_{1}$ is the carrying capacity. The activation rate of macrophages cells is b. $d_{1}$ and $d_{1}$ are the natural death rates of P(t) and Q(t), respectively. After active macrophages destroy tumor cells, they become passive at a rate ${\varepsilon }_{{1}}$. $r_{2}$ is the growth rate of tumor cells and $k_{2}$ is the carrying capacity. The conversion rate of normal cells to malignant cells is c. When active macrophages cells destroy the tumor cells, the loss rate of tumor cells is a.

Khajanchi et al. [57] have considered the following tumor-immune competitive system originated from prey–predator model presented by Sarkar and Banerjee [58]:

$$\begin{aligned} \frac{dM}{dt}= & {} rM\left( 1-\frac{M}{k_1}\right) -\alpha MN,\nonumber \\ \frac{dN}{dt}= & {} \beta _1N(t-\lambda )S(t-\lambda )-d_1N, \nonumber \\ \frac{dS}{dt}= & {} sS\left( 1-\frac{S}{k_2}\right) -\beta _2N(t-\lambda )S(t-\lambda )-d_2S. \end{aligned}$$

(2)

Here, M(t), N(t), S(t) denote the densities of tumor cells, CTLs and resting cells at time t, respectively. The growth rate of M(t) is r and ${\mathrm {k}}_{{1}}$ is the carrying capacity. ${\alpha }$ is the rate at which tumor cells are cleared by prey cells or CTLs. ${\lambda }{\ge }$ 0, is the discrete time delay, ${{\beta }}_1$ is conversion rate of resting stage to hunting stage of CTLs population and the natural death of CTLs is $d_{{1}}$. s is the growth rate of the resting cells and ${\mathrm {k}}_{\mathrm {2}}$ is the carrying capacity. ${{\beta }}_2$ is the conversion rate of resting cells to CTLs, and $d_{\mathrm {2}}$ is the natural death rate. Khajanchi et al. [57] neglected that the term q in [58] is the conversion of normal cells to malignant cells as they assumed that the tumor cells are malignant. Moreover, they consider the conversion of resting cells to hunting cells, and the degradation of resting cells due to hunting cells both must be different, not the same.

In [20], Hu and Jang proposed the integer-order mathematical model of tumor–immune cells interconnection to study the effect of CD4+T on tumor dynamics. Their conclusions show that host cells and CD4+ T cells have great importance in fighting tumor cells and slowing their growth. The ordinary differential equations model is described as follows:

$$\begin{aligned} {x}{'}= & {} r_1x(1-{b_1}x)-\frac{c_1xz}{a_1+x}+{\delta _1}xz, \nonumber \\ {y}{'}= & {} \frac{\beta _1xz}{\alpha _1+x}-\mu _1y-{\delta _2}xy, \nonumber \\ {z}{'}= & {} \frac{\beta _2xy}{\alpha _2+x}-{\mu _2}z,\nonumber \\ {w}{'}= & {} r_2w(1-{b_2}w)-{\delta _3}xw, \end{aligned}$$

(3)

where $t\ge 0$ and ${\mathrm {r}}_{{1}}$, $b_1$, ${\mathrm {c}}_{{1}}$, ${\mathrm {a}}_{{1}}$, ${{\delta }}_{{1}}$, ${{\beta }}_{{1}}$, ${{\alpha }}_{{1}}$, ${{\mu }}_{{1}}$, ${{\delta }}_{\mathrm {2}}$, ${{\beta }}_{\mathrm {2}}$,${{\alpha }}_{\mathrm {2}}$, ${{\mu }}_{\mathrm {2}}$, ${\mathrm {r}}_{\mathrm {2}}$, ${\mathrm {b}}_{\mathrm {2}}$, ${{\delta }}_{{3}}$ are the positive constants. x(t), y(t), z(t) and w(t) are tumor cells, $CD4+ T$ cells, cytokines, and host cells, respectively.

In study [59], the following model was reconstructed by replacing the integer-order derivatives in model (1) with Caputo derivatives:

$$\begin{aligned} {D^\alpha P(t)}= & {} P(t)r_1\left( 1-\frac{P(t)}{k_1}\right) -bP(t)Q(t)-d_1P(t)+\varepsilon _1Q(t), \nonumber \\ {D^\alpha Q(t)}= & {} Q(t)(bP(t)-d_2), \nonumber \\ {D^\alpha R(t)}= & {} R(t)r_2\left( 1-\frac{R(t)}{k_2}\right) -aR(t)Q(t)+c, \end{aligned}$$

(4)

with positive initial conditions. Here, $t\ge 0$, $\alpha \ (0<\alpha \le 1)$ and P(t), Q(t) and R(t) denote the macrophages cells, activated macrophages cells and tumor cells, respectively. a, b, c, $k_{1}$, $k_{2}$, $r_{1}$, $r_{2}$, $d_{1}$, $d_{2}$, $\varepsilon _{1}$ are the positive constants. The biological meanings of these parameters are the same as the meanings of the parameters in the system (1).

In the fractional systems, dimensional consistency is a very important tool, in which the units of measurement from the left- and right-hand sides of the equations are coherent. This consistent can be provided by modifying the parameters involved in the right-hand side of the equations, e.g., raising them to power $\alpha$. In this context, motivated by [20, 59], we have proposed the following the fractional-order system:

$$\begin{aligned} {D^\alpha T(t)}= & {} r_2{^\alpha }T(t)\left( 1-\frac{T(t)}{k_2^\alpha }\right) -\mu ^\alpha T(t)A(t)-\delta _1{^\alpha } W(t)T(t), \nonumber \\ {D^\alpha A(t)}= & {} \beta _1^\alpha M(t)A(t)-d_2^\alpha A(t), \nonumber \\ {D^\alpha M(t)}= & {} r_1^\alpha M(t)\left( 1-\frac{M(t)}{k_1^\alpha }\right) -\beta _2^\alpha M(t)A(t)-d_1^\alpha M(t), \nonumber \\ {D^\alpha W(t)}= & {} r_3^\alpha W(t)\left( 1-\frac{W(t)}{k_3^\alpha }\right) -\delta _2^\alpha W(t)T(t), \end{aligned}$$

(5)

with the initial conditions: $T(0)=T_0, A(0)=A_0, M(0)=M_0, W(0)=W_0,$ where $\alpha \in \left( 0,1\right) \$ and ${\ k}_1$,$\ k_2,\ {k_3,d}_1,\ d_2,\ {\delta }_1,{\delta }_2,\ r_1$,$\ r_2,r_3$, ${\beta }_1$, ${\beta }_2$, $\mu$ are positive constants. T(t), A(t), M(t), W(t) are the densities of tumor cells (TCs), active macrophages cells, macrophages cells and host cells or normal tissue cells (NTCs), respectively. The biological meaning of the parameters in model (5) is given in Table 1:

Table 1 Model parameters and their meanings

In this study, as in [57], it is assumed that the TCs are malignant. So, we neglected the constant which is the rate of conversion of NTCs to malignant cells in Sarkar [58] and Mukhopadhyay [56]. In addition, we consider that the conversion of macrophages cells to active macrophages cells and the degradation of macrophages cells due to active macrophages cells both must be different. Also, we removed the parameter ${\varepsilon }_1$ (in [56]) is the rate of active macrophages that revert back to passive state after attacking the tumor cells (this is not biologically meaningful). It can be considered that these modifications would make the model more realistic.

Motivated by the above discussion, in this study, both fractional modeling has been taken into account and real experimental data from patients have been used. In order to fit the parameters and to minimize the mean absolute relative error between the plotted curve for the tumor cells class and the real data provided by lung cancer patients, we have utilized least-squares curve fitting technique (LSCFT). By doing so, we aim to predict the changing of tumor cells and immune system cells over time by using more accurately generated parameters. Meanwhile, dimensional compatibility has been considered in order to better reveal the effect of fractional-order in the proposed fractional-order lung-cancer system. In addition to this, we have aimed to point out the advantages of the fractional-order modeling, taking into consideration the memory trace and hereditary traits which are capable of integrating all past activities and takes into account the long-term history of the system. In this context, it can be seen that the memory trace dynamics are highly dependent on time. When the fractional-order $\alpha$ is decreased from unit, the memory trace nonlinearly increases from 0. Hence, the fractional-order system dynamics are quite different from the integer-order dynamics. Best of our knowledge, it is thought that there is not a comprehensive study such this paper in the literature that makes the fractional-order model dimensionally consistent, performs the parameter estimation with lung cancer patient data, and considers memory effect/hereditary properties.

The remaining part of this paper is prepared as follows. In Sect. 2, some definitions of a fractional-order derivative (FOD) and some important theorems for FODs are given. In Sect. 3, the existence and uniqueness conditions of the solutions are given. In Sect. 4, stability theorems for the equilibrium points are examined. In Sect. 5, the parameter estimation method to predict the parameters used in the proposed model has achieved. In Sect. 6, the numerical scheme has been given. In Sect. 7, the effects of the memory trace on the behavior of the system (5) are examined. In Sect. 8, to investigate the effects of different parameter values and different values of $\alpha$ on the dynamic behavior of the proposed model, the numerical solutions have been carried out. In Sect. 9, measurement of memory trace for the proposed fractional-order model is investigated. Finally, the general summary is given in Sect. 10.

Preliminaries and definitions

Definition 1

[60] The Riemann–Liouville form of fractional derivative of order $\alpha >0$ of a function $f :(0,\infty )\rightarrow {\mathcal {R}}$ is given by

$$\begin{aligned} {{}^{RL}_0D}^{\alpha }_tf (t)=\left\{ \begin{array}{l} \frac{1}{{\varGamma }(n-\alpha )}{\left( \frac{d}{dt}\right) }^n\int ^t_0{\frac{f (\tau )}{(t-\tau )^{\alpha -n+1}}d\tau ,\ \ \ 0\le n-1<\alpha <n,n=[\alpha ],} \\ {\left( \frac{d}{dt}\right) }^nf (t),\ \ \ \alpha =n\in N. \end{array} \right. \end{aligned}$$

(6)

Definition 2

[60] The Caputo fractional derivative of order $\alpha >0$ of the function that has been given in Definition 1 is presented as:

$$\begin{aligned} {{}^C_0D}^{\alpha }_tf (t)=\left\{ \begin{array}{c} \frac{1}{{\varGamma }(n-\alpha )}\int ^t_0{\frac{{\left( {d}/{d\tau }\right) }^nf (\tau )}{(t-{\tau )}^{\alpha -n+1}}d\tau ,\ \ 0\le n-1<\alpha <n,n=[\alpha ],n\in N,} \\ {\left( \frac{d}{dt}\right) }^nf (t),\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \alpha \ =n,n\in N. \end{array} \right. \end{aligned}$$

(7)

For the convenience, we use the notation of ${\mathbb {D}}^{\alpha }f (t)$ to represent the Caputo fractional integral operator ${{}^C_0\mathbb {D}}^{\alpha }_tf (t).$

Theorem 1

[61, 62]. Consider the following fractional-order system:

$$\begin{aligned} \frac{d^{\alpha }x}{dt^{\alpha }}=f(x),\ \ x\left( 0\right) =x_0 \end{aligned}$$

(8)

with x$\ \in R^n$ and $\alpha \in (0,1)$. The equilibrium points of the system (8) are solutions to the equation$\ f\left( x\right) =0.$ An equilibrium is locally asymptotically stable if all the eigenvalues ${\lambda }_i$ (i=1,2,,...,n) of the Jacobian matrix $J=\frac{\partial f}{\partial x}$ evaluated at the equilibrium satisfy

$$\begin{aligned} \ \left| \mathrm {arg}\,({\lambda }_i)\right| >\frac{\alpha \pi }{\ 2}. \end{aligned}$$

(9)

On the other hand, if $\left| \mathrm {arg}\,({\lambda }_i)\right| <\frac{\alpha \pi }{\ 2}$, then the equilibrium point is unstable.

Theorem 2

[63] Consider the polynomial equation

$$\begin{aligned} P\left( \lambda \right) ={\lambda }^2+a_1\lambda +a_2 \end{aligned}$$

• 1. For $n=1$, the condition for (9) is $a_1>0.$

• 2. For $n=2$, the conditions for (9) are either Routh–Hurwitz conditions [64] ($a_1>0,\ a_2>0)$ or $a_1<0,\ 4a_2>a^2_1$, $\left| {tan}^{-1}(4a_2-a^2_1)\right| >\frac{\alpha \pi }{2}$.

Existence and Uniqueness (E&U) of the solution

With the initial conditions $T(0)=T_0, A(0)=A_0,M(0)=M_0, W(0)=W_0$, we write (5) as follows:

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha }X\left( t\right) =B_1X\left( t\right) +T\left( t\right) B_2X(t)+A\left( t\right) B_3X\left( t\right) +M\left( t\right) B_4X\left( t\right) +W\left( t\right) B_5X\left( t\right) \\ X\left( 0\right) =X_0 \end{array} \right. \nonumber \\ \end{aligned}$$

(10)

where

$$\begin{aligned} X(t)= & {} \left( \begin{array}{c} T(t) \\ A(t) \\ M(t) \\ W(t) \end{array} \right) , \,\,\ X\left( 0\right) =\left[ \begin{array}{c} T(0) \\ A(0) \\ M(0) \\ W(0) \end{array} \right] ,\ \ B_1=\left( \begin{array}{cccc} r_2^\alpha &{} 0 &{} 0 &{} 0 \\ 0 &{} -d_2^\alpha &{} 0 &{} 0 \\ 0 &{} 0 &{} r_1^\alpha -d_1^\alpha &{} 0 \\ 0 &{} 0 &{} 0 &{} r_3^\alpha \end{array} \right) ,\\ B_2= & {} \left( \begin{array}{cccc} -\frac{r_2^\alpha }{k_2^\alpha } &{} -\mu ^\alpha &{} 0 &{} -{\delta }_1^\alpha \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -{\delta }_2^\alpha \end{array} \right) , \\ B_3= & {} \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} {\beta }_1^\alpha &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right) B_4=\left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -{\beta }_2^\alpha &{} -\frac{r_1^\alpha }{k_1^\alpha } &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right) ,\ B_5=\left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\frac{r_3^\alpha }{k_3^\alpha } \end{array} \right) . \\ \end{aligned}$$

The definitions required for E&U (existence and uniqueness) are given as follows:

Definition 3

[20, 65] Let $C^{*}[0,\tau ]$ be the class of continuous column vector X(t) . The components of X(t) are $T,A,M,W \in C^{*}[0,\tau ]$ that are the class of continuous functions on $[ 0,\tau ]$. The norm of $X \in C^{*}[0,\tau ]$ is defined by

$$\begin{aligned} \left\| X\right\| ={sup}_t\left| e^{-Nt}T\left( t\right) \right| +{sup}_t\left| e^{-Nt}A\left( t\right) \right| +{sup}_t\left| e^{-Nt}M\left( t\right) \right| +{sup}_t\left| e^{-Nt}W\left( t\right) \right| . \end{aligned}$$

If $t>\sigma \ge 0$, one can write $C^*_{\sigma }\left[ 0,\daleth \right]$ and $C_{\sigma }\left[ 0,\daleth \right]$.

Definition 4

$\ X\in \ C^*\ [0,\daleth ]\$ is a solution of the system (10), if

• (i) $(t,\ X(t))\ \in \ D$, $t\in \left[ \ 0,\daleth \right]$ where D=$[\ 0,\daleth ]\times K$,

$K=\left\{ \left( T,A,M,W\right) \in R^4_+:\left| T\right| \le p,\ \left| A\right| \le r,\ \ \left| M\right| \le s,\ \left| W\right| \le v\right\} ; p,r,s,v$ are constants.

• (ii) X(t) satisfies (10).

Theorem 3

[20, 65] X$\in C^*\left[ 0,\daleth \right]$ is the unique solution of the system (10).

Proof

Using the properties of fractional calculus, we write the system (10) as follows:

$$\begin{aligned} I^{1-\alpha }\frac{d}{dt}X\left( t\right) =B_1X\left( t\right) +T\left( t\right) B_2X\left( t\right) +A\left( t\right) B_3X\left( t\right) +M\left( t\right) B_4X\left( t\right) +W\left( t\right) B_5X\left( t\right) \end{aligned}$$

operating with $I^{\alpha }$ we have

$$\begin{aligned} X\left( t\right)= & {} X\left( 0\right) +I^{\alpha }{(B}_1X\left( t\right) +T\left( t\right) B_2X\left( t\right) +A\left( t\right) B_3X\left( t\right) \nonumber \\&+M\left( t\right) B_4X\left( t\right) +W\left( t\right) B_5X\left( t\right) ) \end{aligned}$$

(11)

Then, let F:$\ C^*\left[ 0,\daleth \right] \rightarrow C^*\left[ 0,\daleth \right]$ be given by

$$\begin{aligned} FX\left( t\right)= & {} X\left( 0\right) +\ I^{\alpha }{(B}_1X\left( t\right) +T\left( t\right) B_2X\left( t\right) +A\left( t\right) B_3X\left( t\right) \nonumber \\&+M\left( t\right) B_4X\left( t\right) +W\left( t\right) B_5X \left( t\right) ) \end{aligned}$$

(12)

Then,

$$\begin{aligned} e^{-Nt}\left( FX-FY\right)= & {} e^{-Nt}I^{\alpha }(B_1\left( X\left( t\right) -Y\left( t\right) \right) +T\left( t\right) B_2\left( X\left( t\right) -Y\left( t\right) \right) \nonumber \\&+A\left( t\right) B_3\left( X\left( t\right) -Y\left( t\right) \right) )\nonumber \\&+e^{-Nt}I^{\alpha }(M\left( t\right) B_4\left( X\left( t\right) -Y\left( t\right) \right) +W\left( t\right) B_5\left( X\left( t\right) -Y\left( t\right) \right) )\nonumber \\\le & {} \frac{1}{\mathrm {\varGamma }\left( \alpha \right) }\int ^t_0{{\left( t-s\right) }^{\alpha -1}e^{-N\left( t-s\right) }(}X\left( s\right) -Y\left( s\right) )e^{-Ns}\nonumber \\&(B_1+pB_2+rB_3+{sB}_4+vB_5)ds\nonumber \\\le & {} \frac{(B_1+pB_2+rB_3+sB_4+vB_5)}{N^{\alpha }}\left\| X-Y\right\| \int ^t_0{\frac{s^{\alpha -1}}{\mathrm {\varGamma }\left( \alpha \right) }ds.} \end{aligned}$$

(13)

This gives us that $\left\| FX-FY\right\| \le \frac{\left( B_1+pB_2+rB_3+sB_4+vB_5\right) }{N^{\alpha }}\left\| X-Y\right\|$.

If we choose N such that $N^{\alpha }>B_1+pB_2+rB_3+sB_4+vB_5$, then we have

$\left\| FX-FY\right\| <\left\| X-Y\right\| \$. So, the operator F given by (12) has a unique fixed point. That is, (11) has a unique solution X$\in C^*\left[ 0,\daleth \right] .$ From (11), we have

$$\begin{aligned} X(t)= & {} X(0)+\frac{t^{\alpha }}{\varGamma (\alpha +1)} \Big (B_1X(0)+T(0)B_2X(0)+A(t)B_3X(0)\nonumber \\&+M(0)B_4X(0)+W(0)B_5X(0)\Big )\nonumber \\&+\mathbb {I}^{\alpha +1}\Big (B_1X^{'}(t)+T^{'}(t)B_2 X(t)+TB_2X^{'}(t)+A^{'}(t)B_3X(t)\nonumber \\&+A(t)B_3X^{'}(t)+M^{'}(t)B_4X(t)\nonumber \\&+M(t)B_4X^{'}(t)+W^{'}(t)B_5X(t)+W(t)B_5X^{'}(t) \end{aligned}$$

(14)

and

$$\begin{aligned} \frac{dX(t)}{dt}= & {} \frac{t^{\alpha -1}}{\mathrm {\varGamma }\left( \alpha \right) }\Big (B_1X\left( 0\right) +T\left( 0\right) B_2X\left( 0\right) +A\left( t\right) B_3X\left( 0\right) +M\left( 0\right) B_4X\left( 0\right) +W\left( 0\right) B_5X(0)\Big )\nonumber \\&+\mathbb {I}^{\alpha }\Big (B_1X'(t)+T'(t)B_2X(t)+T\left( t\right) B_2X'(t)+A'(t)B_3X(t)+A\left( t\right) B_3X'(t)\nonumber \\&+M'\left( t\right) B_4X\left( t\right) +M\left( t\right) B_4X'\left( t\right) +W'(t)B_5X(t)+W(t)B_5X'(t)\Big ) \end{aligned}$$

(15)

$$\begin{aligned} e^{-Nt}X'(t)= & {} e^{-Nt}\Big [\frac{t^{\alpha -1}}{\mathrm {\varGamma }(\alpha )} (B_1X(0)+T(0)B_2X(0)+A(t)B_3X(0)+M(0)B_4X(0)+W(0)B_5X(0))\nonumber \\&+\mathbb {I}^{\alpha }(B_1X'(t)+T'(t)B_2X(t)+T(t)B_2X'(t)+A'(t)B_3X(t)+A(t)B_3X'(t)\nonumber \\&+M'(t)B_4X(t)+M(t)B_4X'(t)+W'(t)B_5X(t)+W(t)B_5X'(t))\Big ] \end{aligned}$$

(16)

from which we can deduce that $X'\in C^*_{\sigma }[0,\daleth ].$ Now, from (11), we get

$$\begin{aligned} \frac{dX(t)}{dt}= & {} \frac{d}{dt}I^{\alpha }(B_1X(t)+T\left( t\right) B_2X\left( t\right) +A\left( t\right) B_3X\left( t\right) \nonumber \\&+M\left( t\right) B_4X\left( t\right) +W\left( t\right) B_5X(t)) \nonumber \\ I^{1-\alpha }\frac{dX\left( t\right) }{dt}= & {} I^{1-\alpha }\frac{d}{dt}I^{\alpha }(B_1X\left( t\right) +T\left( t\right) B_2X\left( t\right) \nonumber \\&+A\left( t\right) B_3X\left( t\right) +M\left( t\right) B_4X\left( t\right) +W\left( t\right) B_5X\left( t\right) )\nonumber \\ D^{\alpha }X\left( t\right)= & {} B_1X\left( t\right) +T\left( t\right) B_2X\left( t\right) +A\left( t\right) B_3X\left( t\right) \nonumber \\&+M\left( t\right) B_4X\left( t\right) +W\left( t\right) B_5X\left( t\right) , \end{aligned}$$

(17)

and

$$\begin{aligned} X\left( 0\right)= & {} X_0+I^{\alpha }(B_1X\left( t\right) +T\left( t\right) B_2X\left( t\right) \nonumber \\&+A\left( t\right) B_3X\left( t\right) +M\left( t\right) B_4X\left( t\right) +W\left( t\right) B_5X\left( t\right) )= X_0. \end{aligned}$$

(18)

Therefore, (11) is equivalent to the system (10). $\square$

Equilibrium points

To find the equilibrium points of system (5), we write

$$\begin{aligned} {\mathrm {D}}^{{\alpha }}\mathrm {T}\left( \mathrm {t}\right) ={\mathrm {D}}^{{\alpha }}\mathrm {A}\left( \mathrm {t}\right) ={\mathrm {D}}^{{\alpha }}\mathrm {M}\left( \mathrm {t}\right) ={\mathrm {D}}^{{\alpha }}\mathrm {W}\left( \mathrm {t}\right) =0, \end{aligned}$$

that is,

$$\begin{aligned}&{\mathrm {r}}_{\mathrm {2}}^\alpha \mathrm {T}\left( \mathrm {t}\right) \left( {1-}\frac{\mathrm {T}\left( \mathrm {t}\right) }{{\mathrm {k}}_{\mathrm {2}}^\alpha }\right) \mathrm {-}\mu ^\alpha \mathrm {T}\left( \mathrm {t}\right) \mathrm {A}\left( \mathrm {t}\right) {-\delta }_1^\alpha \mathrm {W}\left( \mathrm {T}\right) \mathrm {T}\left( \mathrm {t}\right) =0, {\beta }_1^\alpha \mathrm {M}\left( \mathrm {t}\right) \mathrm {A}\left( \mathrm {t}\right) \mathrm {-}d_2^\alpha \mathrm {A}\left( \mathrm {t}\right) =0\\&{\mathrm {r}}_{{1}}^\alpha \mathrm {M}\left( \mathrm {t}\right) \left( {1-}\frac{\mathrm {M}\left( \mathrm {t}\right) }{{\mathrm {k}}_{{1}}^\alpha }\right) \mathrm {-}{\beta }_2^\alpha M\left( \mathrm {t}\right) \mathrm {A}\left( \mathrm {t}\right) \mathrm {-}d_1^\alpha \mathrm {M}\left( \mathrm {t}\right) \mathrm {=0}, \mathrm {W}\left( \mathrm {t}\right) {\mathrm {r}}_{{3}}^\alpha \left( {1-}\frac{\mathrm {W}\left( \mathrm {t}\right) }{{\mathrm {k}}_{{3}}^\alpha }\right) \mathrm {-}{\delta }_2^\alpha \mathrm {W}\left( \mathrm {T}\right) \mathrm {T}\left( \mathrm {t}\right) =0. \end{aligned}$$

Therefore, we have the following equilibrium points:

• (i) $E_0=(0,0,0,0),$

• (ii) $E_1=(0,-\frac{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha \left( d_1^\alpha -{\mathrm {r}}_{{1}}^\alpha \right) +d_2^\alpha {\mathrm {r}}_{{1}}^\alpha }{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha {\beta }_2^\alpha },\frac{d_2^\alpha }{{\beta }_1^\alpha },0),$

• (iii) $E_2=(0,-\frac{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha \left( d_1^\alpha -{\mathrm {r}}_{{1}}^\alpha \right) +d_2^\alpha {\mathrm {r}}_{{1}}^\alpha }{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha {\beta }_2^\alpha },\frac{d_2^\alpha }{{\beta }_1^\alpha },{\mathrm {k}}_{{3}}^\alpha ),$

• (iv) $E_3=(\frac{k_2^\alpha {\mathrm {r}}_{{3}}^\alpha \left( {\mathrm {k}}_{{3}}^\alpha {\delta }_1^\alpha -{\mathrm {r}}_{\mathrm {2}}^\alpha \right) }{{\mathrm {k}}_{\mathrm {2}}^\alpha {\mathrm {k}}_{{3}}^\alpha {\delta }_1^\alpha {\delta }_2^\alpha -{\mathrm {r}}_{\mathrm {2}}^\alpha {\mathrm {r}}_{{3}}^\alpha },0,0,\frac{k_3^\alpha {\mathrm {r}}_{\mathrm {2}}^\alpha \left( {\mathrm {r}}_{\mathrm {2}}^\alpha -{\mathrm {k}}_{\mathrm {2}}^\alpha {\delta }_2^\alpha \right) }{{\mathrm {k}}_{\mathrm {2}}^\alpha {\mathrm {k}}_{{3}}^\alpha {\delta }_1^\alpha {\delta }_2^\alpha -{\mathrm {r}}_{\mathrm {2}}^\alpha {\mathrm {r}}_{{3}}^\alpha }),$

• (v) $E_4=(0,0,\frac{{\mathrm {k}}_{{1}}^\alpha \left( {\mathrm {r}}_{{1}}^\alpha -d_1^\alpha \right) }{{\mathrm {r}}_{{1}}^\alpha },0),$

• (vi) $E_5=(\frac{k_2^\alpha {\mathrm {r}}_{{3}}^\alpha \left( {\mathrm {k}}_{{3}}^\alpha {\delta }_1^\alpha -{\mathrm {r}}_{\mathrm {2}}^\alpha \right) }{{\mathrm {k}}_{\mathrm {2}}^\alpha {\mathrm {k}}_{{3}}^\alpha {\delta }_1^\alpha {\delta }_2^\alpha -{\mathrm {r}}_{\mathrm {2}}^\alpha {\mathrm {r}}_{{3}}^\alpha },0,\frac{{\mathrm {k}}_{{1}}^\alpha \left( {\mathrm {r}}_{{1}}^\alpha -d_1^\alpha \right) }{{\mathrm {r}}_{{1}}^\alpha },\frac{k_3^\alpha {\mathrm {r}}_{\mathrm {2}}^\alpha \left( {\mathrm {r}}_{\mathrm {2}}^\alpha -{\mathrm {k}}_{\mathrm {2}}^\alpha {\delta }_2^\alpha \right) }{{\mathrm {k}}_{\mathrm {2}}^\alpha {\mathrm {k}}_{{3}}^\alpha {\delta }_1^\alpha {\delta }_2^\alpha -{\mathrm {r}}_{\mathrm {2}}^\alpha {\mathrm {r}}_{{3}}^\alpha }),$

• (vii) $E_6=(0,0,\frac{{\mathrm {k}}_{{1}}^\alpha \left( {\mathrm {r}}_{{1}}^\alpha -d_1^\alpha \right) }{{\mathrm {r}}_{{1}}^\alpha },{\mathrm {k}}_{{3}}^\alpha ),$

• (viii) $E_7=({\mathrm {k}}_{\mathrm {2}}^\alpha ,0,0,0),$

• (ix) $E_8=({\mathrm {k}}_{\mathrm {2}}^\alpha ,0,\frac{{\mathrm {k}}_{{1}}^\alpha \left( {\mathrm {r}}_{{1}}^\alpha -d_1^\alpha \right) }{{\mathrm {r}}_{{1}}^\alpha },0),$

• (x) $E_9=({\mathrm {k}}_{\mathrm {2}}^\alpha +\frac{\mu ^\alpha {\mathrm {k}}_{\mathrm {2}}^\alpha \left( {\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha \left( d_1^\alpha -{\mathrm {r}}_{{1}}^\alpha \right) +d_2^\alpha {\mathrm {r}}_{{1}}^\alpha \right) }{{\mathrm {k}}_{{1}}^\alpha {\mathrm {r}}_{\mathrm {2}}^\alpha {\beta }_1^\alpha {\beta }_2^\alpha },-\frac{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha \left( d_1^\alpha -{\mathrm {r}}_{{1}}^\alpha \right) +d_2^\alpha {\mathrm {r}}_{{1}}^\alpha }{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha {\beta }_2^\alpha },\frac{d_2^\alpha }{{\beta }_1^\alpha },0),$

• (xi) $E_{10}=(0,0,0,{\mathrm {k}}_{{3}}^\alpha ),$

• (xii) $E_{11}=\mathrm {(}\overline{\mathrm {T}},\overline{\mathrm {A}},\overline{\mathrm {M}},\overline{\mathrm {W}}),$

where

$$\begin{aligned} \overline{\mathrm {T}}= & {} \frac{\mu ^\alpha {\mathrm {k}}_{\mathrm {2}}^\alpha {\mathrm {r}}_{{3}}^\alpha \left( d_2^\alpha {\mathrm {r}}_{{1}}^\alpha -{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha \left( {\mathrm {r}}_{{1}}^\alpha -d_1^\alpha \right) \right) -{\mathrm {k}}_{{1}}^\alpha {\mathrm {k}}_{\mathrm {2}}^\alpha {\mathrm {r}}_{{3}}^\alpha {\beta }_1^\alpha {\beta }_2^\alpha \left( {\mathrm {k}}_{{3}}^\alpha {\delta }_1^\alpha -{\mathrm {r}}_{\mathrm {2}}^\alpha \right) }{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha {\beta }_2^\alpha \left( {\mathrm {r}}_{\mathrm {2}}^\alpha {\mathrm {r}}_{{3}}^\alpha -{\mathrm {k}}_{\mathrm {2}}^\alpha {\mathrm {k}}_{{3}}^\alpha {\delta }_1^\alpha {\delta }_2^\alpha \right) },\\ \overline{\mathrm {A}}= & {} -\frac{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha \left( d_1^\alpha -{\mathrm {r}}_{{1}}^\alpha \right) +d_2^\alpha {\mathrm {r}}_{{1}}^\alpha }{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha {\beta }_2^\alpha },\\ \overline{\mathrm {M}}= & {} \frac{d_2^\alpha }{{\beta }_1^\alpha },\\ \ \ \overline{\mathrm {W}}= & {} \frac{\mu ^\alpha {\delta }_2^\alpha {\mathrm {k}}_{\mathrm {2}}^\alpha {\mathrm {k}}_{{3}}^\alpha \left( {\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha \left( {\mathrm {r}}_{{1}}^\alpha -d_1^\alpha \right) -d_2^\alpha {\mathrm {r}}_{{1}}^\alpha \right) +{\mathrm {k}}_{{1}}^\alpha {\mathrm {r}}_{\mathrm {2}}^\alpha {\beta }_1^\alpha {\beta }_2^\alpha {\mathrm {k}}_{{3}}^\alpha \left( {\mathrm {r}}_{{3}}^\alpha -{\delta }_2^\alpha {\mathrm {k}}_{\mathrm {2}}^\alpha \right) }{{\mathrm {k}}_{{1}}^\alpha {\beta }_1^\alpha {\beta }_2^\alpha \left( {\mathrm {r}}_{\mathrm {2}}^\alpha {\mathrm {r}}_{{3}}^\alpha -{\mathrm {k}}_{\mathrm {2}}^\alpha {\mathrm {k}}_{{3}}^\alpha {\delta }_1^\alpha {\delta }_2^\alpha \right) }. \end{aligned}$$

Now, using Theorems 1 and 2, we obtain the stability conditions of these equilibrium points. But, our aim is to examine the conditions under which the patient can survive [20]. So, we only examine the stability of the equilibrium point $E_{11}$. The stability conditions of other equilibrium points have been omitted.

Local stability of the endemic equilibrium

We now examine the local stability of the endemic equilibrium point$E_{11}$=$(\overline{\mathrm {T}},\overline{\mathrm {A}},\overline{\mathrm {M}},\overline{\mathrm {W}})$. The Jacobian matrix of model (5) calculated at equilibrium point $E_{11}$=$\mathrm {(}\overline{\mathrm {T}},\overline{\mathrm {A}},\overline{\mathrm {M}},\overline{\mathrm {W}})$ is given by

$$\begin{aligned} \hbox {J}(E_{11})=\left( \begin{array}{ccc} {\mathrm {r}}_{\mathrm {2}}^\alpha -\frac{2{\mathrm {r}}_{\mathrm {2}}^\alpha \overline{\mathrm {T}}}{{\mathrm {k}}_{\mathrm {2}}}-\mu ^\alpha {\overline{A}}-{\delta }_1^\alpha \overline{\mathrm {W}} &{} -\mu ^\alpha \overline{\mathrm {T}} &{} 0 \\ 0 &{} {\beta }_1^\alpha \overline{\mathrm {M}}-d_2^\alpha &{} {\beta }_1^\alpha {\overline{A}} \\ 0 &{} -{\beta }_2^\alpha \overline{\mathrm {M}} &{} {\mathrm {r}}_{{1}}^\alpha -{\frac{2{\mathrm {r}}_{{1}}^\alpha \overline{\mathrm {M}}}{{\mathrm {k}}_{{1}}^\alpha }-{\beta }_2^\alpha {\overline{A}}-d}_1^\alpha \\ -{\delta }_2^\alpha \overline{\mathrm {W}} &{} 0 &{} 0 \end{array} \ \ \ \ \begin{array}{c} -{\delta }_1^\alpha \overline{\mathrm {T}} \\ 0 \\ 0 \\ {\mathrm {r}}_{{3}}^\alpha -\frac{2{\mathrm {r}}_{{3}}^\alpha \overline{\mathrm {W}}}{{\mathrm {k}}_{{3}}^\alpha }-{\delta }_2^\alpha \overline{\mathrm {T}} \end{array} \right) . \end{aligned}$$

We obtain the characteristic equation such as: $P\left( \lambda \right) =\left( {\lambda }^2+a_1\lambda +a_2\right) \left( {\lambda }^2+a_3\lambda +a_4\right)$ where

$$\begin{aligned} a_1= & {} -\left( {\mathrm {r}}_{{3}}^\alpha -\frac{2{\mathrm {r}}_{{3}}^\alpha \overline{\mathrm {W}}}{{\mathrm {k}}_{{3}}^\alpha }-{\delta }_3^\alpha \overline{\mathrm {T}}+{\mathrm {r}}_{\mathrm {2}}^\alpha -\frac{2{\mathrm {r}}_{\mathrm {2}}^\alpha \overline{\mathrm {T}}}{{\mathrm {k}}_{\mathrm {2}}^\alpha }-{\overline{A}}-{\delta }_1^\alpha \overline{\mathrm {W}}\right) \\ a_2= & {} \left( {\mathrm {r}}_{\mathrm {2}}^\alpha -\frac{2{\mathrm {r}}_{\mathrm {2}^\alpha }\overline{\mathrm {T}}}{{\mathrm {k}}_{\mathrm {2}}^\alpha }-\mu ^\alpha {\overline{A}}-{\delta }_1^\alpha \overline{\mathrm {W}}\right) \left( {\mathrm {r}}_{{3}}^\alpha -\frac{2{\mathrm {r}}_{{3}}^\alpha \overline{\mathrm {W}}}{{\mathrm {k}}_{{3}}^\alpha }-{\delta }_2^\alpha \overline{\mathrm {T}}\right) -{\delta }_1^\alpha {\delta }_2^\alpha \overline{\mathrm {W}}\overline{\mathrm {T}}\\ a_3= & {} -\left( {\mathrm {r}}_{{1}}^\alpha -{\frac{2{\mathrm {r}}_{{1}}^\alpha \overline{\mathrm {M}}}{{\mathrm {k}}_{{1}}^\alpha }-{\beta }_2^\alpha {\overline{A}}-d_1^\alpha }+{\beta }_1^\alpha \overline{\mathrm {M}}-d_2^\alpha \right) \\ a_4= & {} \left( {\beta }_1^\alpha \overline{\mathrm {M}}-d_2^\alpha \right) \left( {\mathrm {r}}_{{1}}^\alpha -{\frac{2{\mathrm {r}}_{{1}}^\alpha \overline{\mathrm {M}}}{{\mathrm {k}}_{{1}}^\alpha }-{\beta }_2^\alpha {\overline{A}}-d_1^\alpha }\right) +{\beta }_1^\alpha {\beta }_2^\alpha \overline{\mathrm {M}}{\overline{A}}. \end{aligned}$$

By Theorems 1 and 2, one can deduce the following conclusions.

Theorem 4

The equilibrium point $E_{11}$ is locally asymptotically stable if one of the following conditions holds.

• 1. Routh–Hurwitz conditions ($a_1>0$, $a_2>0$, $a_3>0$, $a_4 >0$).

• 2. $a_1<0$, $a^2_1-4a_2<0$, $\left| \mathrm {tan}^{-1}(4a_2-a^2_1)/a_1\right| > \frac{\alpha \pi }{2}$ and $a_3>0$, $a_4>0$.

• 3. $a_1<0$, $a^2_1-4a_2<0$, $\left| \mathrm {tan}^{-1}(4a_2-a^2_1)/{a_1}\right| >\frac{\alpha \pi }{2}$ and $a_3<0$, $a^2_3-4a_4<0$, $\left| {\mathrm {tan}}^{-1}{(4a_4-a^2_3)}/{a_3}\right| > \frac{\alpha \pi }{2}$.

• 4. $a_3<0$, $a^2_3-4a_4<0$, $\left| {\mathrm {tan}}^{-1}{(4a_4-a^2_3)}/ {a_3}\right| >\frac{\alpha \pi }{2}$ and $a_1>0$, $a_2>0$.

Parameter estimation

Parameter estimation (PE) is a very important issue in the identification and validation of many cancer models. By performing PE, the parameters of the proposed model are determined within appropriate bounds using real data and thus, it is tried to ensure that the model is the most appropriate model expressing cancer. The most important advantage of parameter estimation is to produce parameter values specific to the model created, instead of using the same parameter values obtained for different types of cancer models that exist in the literature related to the model.

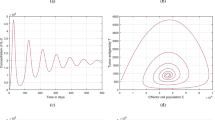
In this section, it has been aimed to fit the relevant parameters with the help of the data of a lung cancer patient who was treated at Kayseri Erciyes University hospital using the least-squares curve fitting method. A total of 12 parameters in the model have been fitted with the aid of least-square curve fitting method using the data of lung tumor cells of the patient for 14 days from 15 September–28 September. The average absolute relative error between tumor cells real data belonging to lung cancer patient and the solution of model’s for the tumor class is tried to be decreased, and the best fitted parameter values have been obtained. In Fig. 1, the red solid circles show the real tumor values, while the best fitted curve of the model is indicated by the blue solid line. The biological parameters in the model along with the best predicted values obtained through LSCFM are given in Table 2.

Fig. 1

Real data of lung cancer patient from Erciyes University Hospital, Turkey from September 15 to September 28, 2021, and the best fitted curve for the proposed model

Table 2 The biological meanings of parameters and the fitted values

Providing real data (sample collection and cell culture)

Tumor tissue samples were collected from the patient with non-small cell lung cancer who had chemotherapy-naive. The diagnosis was verified on routine H&E(hematoxylin and eosin)-stained slides by a histopathologist. Informed written consent was obtained from the patient before the sample collection. Ethics committee approval for study was obtained from Erciyes University Clinical Research Ethics Committee with the protocol code number 2015/372, dated 26/08/2015. Tumor cell cultures were established from tumor tissues obtained after surgery of the patient with lung adenocarcinoma. Tumor cells were grown in Dulbecco’s Modified Eagle medium (DMEM; Gibco, Grand Island, NY, USA, Cat. No. 41966029) containing 1 $\%$ penicillin–streptomycin (Thermo Fisher Scientific Waltham, Massachusetts, USA, Cat. No. 15070063), 1 $\%$ amphotericin b (Thermo Fisher Scientific Waltham, Massachusetts, USA, Cat. No. 15290026) and 1 % L-Glutamine (STEMCELL Technologies Inc., Vancouver, Canada, Cat. No. 7100). To evaluate cell proliferation, cells were seeded in six-well plate at $5\times 10^4$ cells per well and cultured for 13 days. All cells were grown at 37 $^{\circ }\hbox {C}$ in a humidified atmosphere with 5 % CO2 and observed daily using an inverted microscope under $\times$10 magnification. After obtaining a confluent monolayer, cells were harvested with 0.25 % trypsin/EDTA (Thermo Fisher Scientific Waltham, Massachusetts, USA, Cat. No. 25200056). The cell count was done daily for 14 days using trypan blue count assay (see Table 3).

In the literature, cell lines and animal data are also widely used as experimental data. Cell lines are important resources for identifying predictors of unrestricted growth, eligibility for high-throughput screening, response to therapy, and resistance [66, 67]. They are also cheaper, easier to use, and experiments on them are more reproducible. However, currently available cancer cell lines have some limitations. Cell lines are selected from tumor subsets grown under in vitro culture conditions [68]. However, it is often unclear from which cancer subtype these cells originate and to what extent they resemble the tissue of origin [69]. This produces cancer cell lines that do not represent the diversity of human tumors [67, 68]. Moreover, cell lines grown only in monolayer cultures lack the heterogeneity observed in cells derived from patient tumors [67, 70]. Although the development of patient-derived xenograft cancer models provides some improvement over cancer cell line models, it has some limitations. Vaccination and drug validation time in mice often take a long time, and this time delay limits its applicability to patient therapy. In addition, these models are suitable for a limited number of drug combinations and are not amenable to genetic manipulation such as the introduction of transgenes or knockout studies [68]. In primary cell cultures, cells are isolated directly from the tumor site, and detailed pathology information is also available, allowing the characteristics of the culture to be compared with those of the original tumor. In addition, primary cell culture provides a more accurate prediction of patients’ responses to chemotherapy treatments [71]. In this study, in order to represent the origin of tumor profile in cancer patients population, cancer cells were isolated from NSCLC patients.

Table 3 Real data of lung cancer patient for 14 days from Erciyes University Hospital, Turkey

Numerical scheme for the provided tumor-immune system model in the Caputo derivative sense

To investigate the dynamics of the proposed fractional-order model (2), we implement the Caputo fractional operator. To provide the numerical simulation of the suggested nonlinear fractional-order system, the Adams type estimator-corrector method [72,73,74,75] is used. The following Cauchy-type ODE is taken into account w.r.t. the Caputo operator of order $\alpha$:

$$\begin{aligned} {}_{0}^{C} D_{t}^{\alpha } \Phi \left( t\right) =\phi \left( t,\Phi \left( t\right) \right) ,\quad \Phi ^{\left( b\right) } \left( 0\right) =\Phi _{0}^{b} ,\quad 0<\alpha \le 1,\ 0<t\le \tau , \end{aligned}$$

(19)

where $b=0,1,...,n-1,$ and $n=\left\lceil \alpha \right\rceil .$ Equation (19) can be turned to the Volterra equation:

$$\begin{aligned} \Phi \left( t\right) =\sum _{b=0}^{n-1}\Phi _{0}^{\left( b\right) } \frac{t^{b} }{b!} +\frac{1}{\varGamma \left( \alpha \right) } \int _{0}^{t}\left( t-s\right) ^{\alpha -1} \Phi \left( s,\Phi \left( s\right) \right) ds . \end{aligned}$$

(20)

By considering this proposed predictor-corrector scheme associated with the Adam-Bashforth-Moulton algorithm [73] to have the numerical solutions of the proposed model, we can take $h=\tau /N,{} {} {} {} t_{z} =zh,$ and $z=0,1,...,N\in \mathrm{Z}^{+} ,$ by letting $\Phi _{z} \approx \Phi \left( t_{z} \right) ,$ it can be discretized as follows, i.e., the corresponding corrector formula [76]

$$\begin{aligned} T_{q+1}= & {} \sum _{z=0}^{q-1}T_{0}^{\left( z\right) } \frac{t_{q+1}^{z} }{z!} +\frac{h^{\alpha } }{\varGamma \left( \alpha +2\right) } \sum _{z=0}^{q}\left( p_{z,q+1} \right) \left( r_2^{\alpha }T_{z}(1-\frac{T_{z}}{k_2^{\alpha }})-\mu ^{\alpha } T_{z}A_{z}-\delta _1^{\alpha }W_{z}T_{z} \right) \nonumber \\&+\frac{h^{\alpha } }{\varGamma \left( \alpha +2\right) } \sum _{z=0}^{q}\left( p_{q+1,q+1} \right) \left( r_2^{\alpha }T_{q+1}^{PF}(1-\frac{T_{q+1}^{PF}}{k_2^{\alpha }})-\mu ^{\alpha } T_{q+1}^{PF}A_{q+1}^{PF}-\delta _1^{\alpha }W_{q+1}^{PF}T_{q+1}^{PF}\right) ,\nonumber \\ A_{q+1}= & {} \sum _{z=0}^{q-1}A_{0}^{\left( z\right) } \frac{t_{q+1}^{z} }{z!} +\frac{h^{\alpha } }{\varGamma \left( \alpha +2\right) } \sum _{z=0}^{q}\left( p_{z,q+1} \right) \left( \beta _1^{\alpha }M_{z}A_{z}-d_2^{\alpha }A_{z} \right) \nonumber \\&+\frac{h^{\alpha } }{\varGamma \left( \alpha +2\right) } \sum _{z=0}^{q}\left( p_{q+1,q+1} \right) \left( \beta _1^{\alpha }M_{q+1}^{PF}A_{q+1}^{PF}-d_2^{\alpha }A_{q+1}^{PF} \right) ,\nonumber \\ M_{q+1}= & {} \sum _{z=0}^{q-1}M_{0}^{\left( z\right) } \frac{t_{q+1}^{z} }{z!} +\frac{h^{\alpha } }{\varGamma \left( \alpha +2\right) } \sum _{z=0}^{q}\left( p_{z,q+1} \right) \left( r_1^{\alpha }M_{z}(1-\frac{M_{z}}{k_1^{\alpha }})-\beta _2^{\alpha }M_{z}A_{z}-d_1^{\alpha }M_{z} \right) \nonumber \\&+\frac{h^{\alpha } }{\varGamma \left( \alpha +2\right) } \sum _{z=0}^{q}\left( p_{q+1,q+1} \right) \left( r_1^{\alpha }M_{q+1}^{PF}(1-\frac{M_{q+1}^{PF}}{k_1^{\alpha }})-\beta _2^{\alpha }M_{q+1}^{PF}A_{q+1}^{PF}-d_1^{\alpha }M_{q+1}^{PF}\right) ,\nonumber \\ W_{q+1}= & {} \sum _{z=0}^{q-1}W_{0}^{\left( z\right) } \frac{t_{q+1}^{z} }{z!} +\frac{h^{\alpha } }{\varGamma \left( \alpha +2\right) } \sum _{z=0}^{q}\left( p_{z,q+1} \right) \left( r_3^{\alpha }W_{z}(1-\frac{W_{z}}{k_3^{\alpha }})-\delta _2^{\alpha }W_{z}T_{z} \right) \nonumber \\&+\frac{h^{\alpha } }{\varGamma \left( \alpha +2\right) }\sum _{z=0}^{q}\left( p_{q+1,q+1} \right) \left( r_3^{\alpha }W_{z}(1-\frac{W_{q+1}^{PF}}{k_3^{\alpha }})-\delta _2^{\alpha }W_{q+1}^{PF}T_{q+1}^{PF} \right) ,\nonumber \\ \end{aligned}$$

(21)

where

$$\begin{aligned} p_{z,q+1} =\left\{ \begin{array}{l} {q^{\alpha +1} -\left( q-\alpha \right) \left( q+1\right) ^{\alpha } ,\quad \mathrm{if} \ z=0,} \\ {\left( q-z+2\right) ^{\alpha +1} +\left( q-z\right) ^{\alpha +1} -2\left( q-z+1\right) ^{\alpha +1} ,\quad \mathrm{if}\ 1\le z\le q,} \\ {1,\quad \mathrm{if}\ z=q+1.} \end{array}\right. \end{aligned}$$

(22)

Subsequently, the following step is to construct the coincident predictor formula $\Phi _{q+1}^{PF} .$ One can compute the proposed predictor formula as:

$$\begin{aligned} T_{q+1}^{PF}= & {} \sum _{z=0}^{q-1}T_{0}^{\left( z\right) } \frac{t_{q+1}^{z} }{z!} +\frac{h^{\alpha } }{\varGamma \left( \alpha +1\right) } \sum _{z=0}^{q}\left( j_{z,q+1} \right) \left( r_2^{\alpha }T_{z}(1-\frac{T_{z}}{k_2^{\alpha }})-\mu ^{\alpha } T_{z}A_{z}-\delta _1^{\alpha }W_{z}T_{z} \right) ,\nonumber \\ A_{q+1}^{PF}= & {} \sum _{z=0}^{q-1}A_{0}^{\left( z\right) } \frac{t_{q+1}^{z} }{z!} +\frac{h^{\alpha } }{\varGamma \left( \alpha +1\right) } \sum _{z=0}^{q}\left( j_{z,q+1} \right) \left( \beta _1^{\alpha }M_{z}A_{z}-d_2^{\alpha }A_{z}\right) ,\nonumber \\ M_{q+1}^{PF}= & {} \sum _{z=0}^{q-1}M_{0}^{\left( z\right) } \frac{t_{q+1}^{z} }{z!} +\frac{h^{\alpha } }{\varGamma \left( \alpha +1\right) } \sum _{z=0}^{q}\left( j_{z,q+1} \right) \left( r_1^{\alpha }M_{z}(1-\frac{M_{z}}{k_1^{\alpha }})-\beta _2^{\alpha }M_{z}A_{z}-d_1^{\alpha }M_{z} \right) ,\nonumber \\ W_{q+1}^{PF}= & {} \sum _{z=0}^{q-1}W_{0}^{\left( z\right) } \frac{t_{q+1}^{z} }{z!} +\frac{h^{\alpha } }{\varGamma \left( \alpha +1\right) } \sum _{z=0}^{q}\left( j_{z,q+1} \right) \left( r_3^{\alpha }W_{z}(1-\frac{W_{z}}{k_3^{\alpha }})-\delta _2^{\alpha }W_{z}T_{z} \right) ,\nonumber \\ \end{aligned}$$

(23)

where

$$\begin{aligned} j_{z,q+1} =\left( q+1-z\right) ^{\alpha } -\left( q-z\right) ^{\alpha } . \end{aligned}$$

Memory trace and hereditary traits

To examine the behavior of the tumor-immune-host cells model (2), we use the Caputo operator defined in (2). For $\alpha ,$ $0< \alpha \le 1$ derivative, let the fractional derivative of variable $\Phi \left( t \right)$ be [77, 78]

$$\begin{aligned} {}_{0}^{C} D_{t}^{\alpha } \Phi \left( t\right) =\phi \left( \Phi \left( t\right) ,t\right) . \end{aligned}$$

(24)

Utilizing the one of most common numerical methods, the L1 scheme [78,79,80,81], the numerical approximation of the FOD of $\Phi \left( t \right)$ is

$$\begin{aligned} _{0}^{C}D_{ t }^{ \alpha } \Phi \left( t \right) \approx \frac{ \left( d t \right) ^{- \alpha }}{ \varGamma \left( 2- \alpha \right) } \left[ \sum _{\varrho =0}^{T-1} \left[ \Phi \left( t _{\varrho +1} \right) - \Phi \left( t _{\varrho } \right) \right] \left[ \left( T-\varrho \right) ^{1- \alpha }- \left( T-1-\varrho \right) ^{1- \alpha } \right] \right] .\nonumber \\ \end{aligned}$$

(25)

One of the most powerful numerical methods for discretizing the Caputo-FOD in time is L1 scheme. The purpose of implementing the L1 scheme to this research study is its memory term and convergence rate. Memory term is also explicitly present in other numerical methods, but this memory integration term is more clearly defined in the L1 scheme. Considering (24) and (25) together, the numerical solution of (24) is as follows:

$$\begin{aligned} \Phi \left( t _{T} \right)\approx & {} _{0}^{C}D_{ t }^{ \alpha } \varGamma \left( 2- \alpha \right) H \left( \Phi \left( t \right) , t \right) + \Phi \left( t _{T-1} \right) \nonumber \\&- \left[ \sum _{\varrho =0}^{T-2} \left[ \Phi \left( t _{\varrho +1} \right) - \Phi \left( t _{\varrho } \right) \right] \left[ \left( T-\varrho \right) ^{1- \alpha }-\left( T-1-\varrho \right) ^{1- \alpha } \right] \right] . \end{aligned}$$

(26)

Therefore, the solution of the FOD (fractional-order derivative) can be defined as the difference between the Markov term and the memory trace. The Markov term weighted by the Gamma function is as follows:

$$\begin{aligned} \text {Markov term}={_{0}^{C}}D_{ t }^{ \alpha } \varGamma \left( 2- \alpha \right) H \left( \Phi \left( t \right) , t \right) + \Phi \left( t _{T-1} \right) . \end{aligned}$$

(27)

The memory trace ($\Phi$-memory trace since it is related to variable $\Phi \left( t \right)$) is

$$\begin{aligned} \text {Memory trace}= \sum _{\varrho =0}^{T-2} \left[ \Phi \left( t _{\varrho +1} \right) - \Phi \left( t _{\varrho } \right) \right] \left[ \left( T-\varrho \right) ^{1- \alpha }- \left( T-1-\varrho \right) ^{1- \alpha } \right] . \end{aligned}$$

(28)

The memory trace is capable of integrating all past activities and takes into account the long-term history of the system. For $\alpha =1$, the memory trace is 0 for any time t. Memory trace dynamics is highly dependent on time. When the fractional-order $\alpha$ is decreased from unit, the memory trace nonlinearly increases from 0. Hence, the fractional-order system dynamics are quite different from the integer-order dynamics.

Numerical simulations and discussion

For the system (5), the numerical solutions are achieved using the Adams-Bashforth-Moulton Predictor-Corrector method for the parameters in Table 2. With the aid of numerical simulations, the effects of different parameter values and different values of $\alpha$ on the dynamic behavior of the model (5) can be identified. The fitted parameter values used for numerical simulations are given in Table 2.

In this part of the study, the variation of each sub-population over time has been simulated for differing values of the fractional parameter $\alpha$ by using the fitted parameter values given in Table 2. In addition, considering the parameters that significantly change the behavior of the cells, graphics have been obtained for different values of these parameters. The dynamical behavior of each state of the proposed tumor-immune system model has shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9 for varying values of the fractional-order parameter $\alpha$ and different parameter values. Figure 2 presents the tumor cells for different $\alpha$ values to point out the effect of the fractional case. Figure 2 shows decreasing attitude of the tumor cells for increasing values of $\alpha$.

Fig. 2

Change of the tumor cells over time for the varying fractional-order derivative

Fig. 3

Change of the tumor cells over time for the varying fractional-order derivative and $\mu =0.11$, $r_2=0.8.$

Fig. 4

Change of the active macrophages cells over time for the varying fractional-order derivative

Fig. 5

Change of the macrophages cells over time for the varying fractional-order derivative

Fig. 6

Change of the host cells over time for the varying fractional-order derivative

Fig. 7

Change of the tumor cells over time for the different $\mu$ values and $\alpha =0.9$

Fig. 8

Change of the tumor cells over time for the different $\delta _1$ values and $\alpha =0.9$

Fig. 9

Change of the tumor cells over time for the different $r_2$ values and $\alpha =0.9$

Moreover, in Fig. 2, it has been seen that the total number of tumor cells is more in the case of $\alpha =0.7$ than in the case of $\alpha =1$. Therefore, the fractional order predicts more tumor cells than the prediction obtained in the integer-order case. In addition, when $\alpha =0.7$, it is seen that even around 100 days, tumor cells are still seen in the body. However, it is seen that they disappear from the second day in order of integer-order case. This effect of $\alpha =0.7$ indicates that the fractional derivatives are in good agreement with the spread of tumor cells.

In Fig. 3, we have changed $\mu$, $r_2$ and keep the other parameters fixed as in Table 2. One of the main reasons for using FODEs is that fractional differential equations have a wider stability region than integer-order equations, that is, fractional-order equations are at least as stable as integer-order equations. Moreover, solutions in fractional-order equations depend on all previous cases [49, 59]. It is concluded that Fig. 3 verifies this theoretical result, that is, the stability region of the proposed model has increased as the $\alpha$ decreases from unit. In Fig. 4, the change in the active macrophages cells with respect to time is examined. One can see from this figure that as the fractional-order $\alpha$ reduces from unit, the memory effect of the active macrophages cells increases. Therefore, these cells take longer to be stable for the non-integer cases. In addition, while the active macrophages cells exhibit an unstable behavior when $\alpha$ is unit, the long-term stability of the system when $\alpha$ is not an integer reveals one of the important properties of the fractional-order derivatives.

In Fig. 5, similar behavior like the active macrophages cells has been seen. It has observed that as the $\alpha$ decreases from unit, the memory effect of the macrophages cells increases, which means that the peak of the macrophages cells decreases and the macrophages cells reach the stability after a certain time for the fractional cases.

It can be observed from Fig. 6 that as $\alpha$ reduces from the unit, the host cells take longer time to reach the maximum value due to memory effect. In addition, it is seen that they reach the equilibrium point in a longer time in the fractional-order state. In Fig. 7 for increasing values of $\mu$ (the destruction rate of tumor cells due to active macrophages cells), the tumor cells decrease under fractional-order case $\alpha =0.9$. In Fig. 8, $\delta _1$ appears to have a significant impact on the regression of the tumor cells. It is seen that the number of cancer cells decreases as $\delta _1$ increases. It is seen that the observed changes in Figs. 2, 3, 4, 5, 6, 7, 8 are compatible with the expected phenomena related to a real cancer patient.

Cancer patients have different tendencies during tumor growth which is difficult to capture by integer order derivative as in seen Fig. 2. In Fig. 3, we have observed that the fractional-order derivative damps the oscillation behavior about the positive equilibrium point. The existence of periodic solutions is associated with cancer models. It implies that the tumor levels may oscillate around an equilibrium point even in absence of any treatment. Such a phenomenon which is known as “Jeff’s Phenomenon” has been observed clinically [82] and has arose in many cancer models [58, 59]. It is seen that in Fig. 7, as $\mu$ increases, the number of tumor cells decreases. From the biological point of view, the rate of destruction of TCs due to attack of active macrophages ($\mu$) can be increased by the macrophage-based therapy. The macrophage-based therapy is more effective at reducing tumor cell proliferation than standard therapies such as radiotherapy and chemotherapy [83].

It is known that tumor cells and normal tissue cells compete for resources and space [84]. In addition, the signaling interactions between the stromal and neoplastic tissues are important in driving tumor cell proliferation [2]. A certain period of time after the tumor begins to invade the area and source of normal tissues, the normal tissues go on the defensive to protect themselves [2, 84]. It takes a certain amount of time for the host cells to take action to attack. In Fig. 6, it is seen that while host cells are not active until the about 20th day, they start to compete with the tumor cells after the about 20th day. In addition, it is seen that in Fig. 10, the memory trace is zero until around the 20th day and it has started to increase after that day. The memory effect seen in Fig. 6 is supported by Fig. 10. The obtained results from Figs. 6 and 10 are consistent with real biological phenomena. Figure 6 shows that fractional-order differential equations play the role of time lag or delay term in ordinary differential model and they are naturally related to systems with memory which exists in tumor–immune interactions [59, 85]. In Figs. 10 and 11, we have depicted the memory trace effects on populations for different values of fractional order ${\alpha }$. As can be seen from Figs. 10 and 11, when ${\alpha }= 1$, it is seen that the memory effect is zero for all populations. As ${\alpha }$ decreases from 1 to 0.7, the effect of the fractional order and the corresponding memory effect appear. Since the memory effect has a significant importance in the tumor-immune interconnection, it is very important to include the memory effect in the system in order to make the most realistic modeling. It can be seen that the memory effect has a great effect on each compartment in the model we are considering. Considering the values before and after the peak values of the populations, it is seen that there is an important relationship between them and the memory trace. When Figs. 2, 3, 4, 5, 6, 7, 8, 9 and Figs. 10 and 11 are examined together, it is noteworthy that memory trace is negative when populations decrease, and memory trace is positive when populations increase. Observing such behaviors clearly demonstrates the importance of including memory trace in the system when modeling cancer. These are the results that have not been addressed in any previous study, revealing the biological reality of our model.

Fig. 10

The effect of memory trace on the tumor cells (left) and the host cells (right) for different values of $\alpha$

Fig. 11

The effect of memory trace on the macrophages cells (left) and the active macrophages cells (right) for different values of $\alpha$

Measurement of memory trace for the proposed fractional-order model

As given in detail in Sect. 7, we have numerically integrated the fractional derivatives using the L1 scheme and the solutions of the FODEs for $T \left( t \right) , A \left( t \right) , M \left( t \right) , W \left( t \right) ,$ have described as the similar way as in (25). Thus, the numerical approximation of the fractional-order derivative of $A \left( t \right)$ is

$$\begin{aligned} _{0}^{C}D_{ t }^{ \alpha } A \left( t \right) \approx \frac{ \left( d t \right) ^{- \alpha }}{ \varGamma \left( 2- \alpha \right) } \left[ \sum _{\varrho =0}^{T-1} \left[ A \left( t _{\varrho +1} \right) - A \left( t _{\varrho } \right) \right] \left[ \left( T-\varrho \right) ^{1- \alpha }- \left( T-1-\varrho \right) ^{1- \alpha } \right] \right] . \end{aligned}$$

(29)

By combining (29) and the first equation of system (2), the numerical solution of active macrophages cells $A \left( t \right)$ is given by

$$\begin{aligned} A \left( t _{T} \right) \approx \text {Markov term of } A \left( t \right) \text {- Memory trace of~} A \left( t \right) , \end{aligned}$$

(30)

where

$$\begin{aligned} \text {Markov term}={_{0}^{C}}D_{ t }^{ \alpha } \varGamma \left( 2- \alpha \right) H \left( A \left( t \right) , t \right) + A \left( t _{T-1} \right) , \end{aligned}$$

(31)

and

$$\begin{aligned} \text {Memory trace}= \sum _{\varrho =0}^{T-2} \left[ ~ A \left( t _{\varrho +1} \right) - A \left( t _{\varrho } \right) \right] \left[ \left( T-\varrho \right) ^{1- \alpha }- \left( T-1-\varrho \right) ^{1- \alpha } \right] . \end{aligned}$$

(32)

By following the same steps, the numerical approximations of the fractional-order derivative of $T \left( t \right)$, $M \left( t \right)$, $W \left( t \right)$ have been achieved. By considering the corresponding results above, numerical analyses have been provided to visually see the effect of memory trace on each sub-population of system (5).

Figure 10 and 11 show the effects of memory trace on the dynamics of populations for varied values of fractional order $\alpha$. As can be seen from Figs. 10 and 11, when $\alpha =1$, there is no memory effect in the system. As $\alpha$ decreases from 1 to 0.7, the impacts of the fractional order and the existence of a memory effect become clear. Actual results and estimates of the tumor–immune system interaction can be obtained in the presence of a memory effect. Therefore, the presence of a memory effect is very important for the biological models. When Figs. 2, 3, 4, 5, 6, 7, 8, 9 and Figs. 10 and 11 are examined together, it is seen that there is a significant relationship between the memory effect and the peak values of the behavior of the system. For example in Figs. 2 and 10, it is seen that the memory trace starts to become negative where tumor cells for different values of $\alpha$ begin to decrease after the peak value.

In biological events, when the immune system first encounters with the tumor cells, the memory response occurs and it is effective during a certain period of time [86]. When Figs. 10 and 11 are examined, it is observed that the memory effect approaches zero after a certain time. That is, these results are expected in real cancer phenomena. It can be understood from the results obtained from the graphs that the FODEs reveal the memory effect of the system quite successfully without the need for any other factors.

Conclusions

In this study, a new fractional-order differential equation model for tumor–immune system interaction related to lung cancer has been studied by taking into account the models given by [20], and [59]. We have constructed a new model clarifying the interactions between tumor cells, macrophages cells, active macrophages cells and normal tissue cells to evaluate the role of macrophages and normal cells on tumor growth and regression. We have also taken into consideration the Caputo type fractional derivative instead of the integer-order derivative. By doing so, we have guaranteed that the fractional-order system (5) is dimensionally consistent: The units of measurement from the left- and right-hand sides of the equations agree. It has been achieved by modifying the parameters involved in the right-hand side of the equations, e.g., raising them to power $\alpha$.

We have showed that the compartmental system has a solution by benefiting from the fixed-point theorem, and we have provided the equilibrium points of the system. We have also investigated the local stability of the endemic equilibrium point. By using the real data of a lung cancer patient from Erciyes University hospital in Turkey, sum of the squares of the difference between the numerical solution to the tumor cells and real data has been minimized and the best fitted curve has been obtained (see Fig. 1). In addition, we have performed mathematical investigation along with parameter recalibration analysis to understand the system dynamics and the best fitted parameter values have been obtained, accordingly. In order to achieve numerical simulations of model (5), population dynamics of tumor-immune system have been visualized with the help of different fractional orders and the fitted parameters using Adams-Bashforth-Moulton method. Numerical simulations have been used to investigate the effects of the parameters on the growth and regression of the tumor cells.

Although there have been many studies that discuss the tumor–immune interaction in the literature, our model differs from them both biologically and mathematically in terms of investigating the relationship between tumor, macrophages, active macrophages and normal tissue cells. Normal tissue cells (NTCs) and macrophages cells play an significant role in the prevention of tumor growth along with the production mechanism of macrophage cells. According to the results, if the host cells are more competitive, then the tumor cells undergo a considerable loss. In addition, if tumor growth rate ($r_{2}$) is small, then cancer cells can be eradicated in a shorter time. When the simulation results have been examined, it has been observed that as $\alpha$ changes, the patient’s immune system cells and the number of tumor cells also changes significantly. Moreover, it is seen that the oscillations increase as the fractional-order changes from zero to one. Cancer has a different mode of progression when the tumor starts to appear in the body. With the help of fractional-order equations, as can be seen from the obtained results, this different structure of cancer can be better explained.

It is a very useful method to use experimental data to test the accuracy of the established mathematical models. But, finding the required data is often difficult. Among the studies on the mathematical model of lung cancer, there are studies that benefit from experimental data. These data are mostly cell lines and animal data. However, it is seen that there are not enough studies in the literature on fractional modeling using experimental data on lung cancer. In this context, both fractional modeling has been taken into account and real experimental data from patients have been used in this study. In order to fit the parameters and to minimize the mean absolute relative error between the plotted curve for the tumor cells class and the real data provided by lung cancer patients, we have utilized least squares curve fitting technique. By doing so, we aim to predict the changing of tumor cells and immune system cells over time by using more accurately generated parameters. In addition to this, we aim to point out the advantages of the fractional order modeling, taking into consideration the memory trace and hereditary traits.

If cancer specialists can change the parameters of the cancer-immune system relationship by applying different treatment methods (such as macrophage-based therapy, BMT therapy, hormone therapy, and immunotherapy) according to the results obtained from the mathematical models, it may be possible to stabilize the tumor cells at a certain value or to terminate the cancer. Therefore, such examinations provide other scientists as well as cancer specialists studying the tumor progression with insight into the control of the cancer and may help develop further treatment strategies. In this context, this study will shed light on future studies.

In future works, one can consider that cancer stem cells can be incorporated into the model in which will be developed.