1 Introduction

According to immunologists, two main components of the human immune system interact to defend the organism of host body from pathogens, that are, innate mechanism and adaptive mechanism. The initial response involves a defensive mechanism with a faster and more general manner against pathogens, employing cells such as macrophages, natural killer cells, and neutrophil leukocytes. Neutrophils travel with the help of tissues and the bloodstream to eliminate pathogens, while natural killer cells regulate immune responses and combat cancerous cells. Monocytes, circulating in the blood, have the capacity to search for infected tissues. In contrast, the second response is tailored to a specific pathogen and typically takes longer than the innate response. The cells involved in this process include dendritic cells, B lymphocytes, and T lymphocytes, where dendritic cells initiate the adaptive process, activating naive T cells by pathogen exposure. B cells develop new antibodies that are unique to a given pathogen to fend off or handle infections, while T cells in the host’s body grow into specialized cells such as cytotoxic T lymphocytes, T helper cells and T memory cells. The strongest of these are the cytotoxic T lymphocytes, sometimes referred to as killer cells or CD8+ T cells, which are found in the body of the host. They have T-cell receptors developed on them, which kill off non-host cells. The immune system in humans actively strives to inhibit the proliferation of pathogens, such as bacteria and viruses, even when consistently confronted with foreign substances. This effort is undertaken to maintain optimal health and well-being.

Mathematical models play a crucial role in various areas of science and engineering, providing a quantitative framework for understanding, predicting, and optimizing complex phenomena [1,2,3,4]. On the other hand, different research investigated disease from different perspective for public health [5,6,7,8]. To illustrate the complexity of biological events associated with cancer, a multitude of mathematical models have been presented in the literature [9, 10]. These models use discrete, continuous, or hybrid assumptions. Discrete frameworks are better suited for understanding individual cells and their interactions, whereas continuous modeling is more effective for describing tissue-scale dynamics. The mathematical models are classified according to the scale that is of interest; these scales include population-level, patient-specific, organ/tissue, cellular, and molecular. Interestingly, tumor–immune interaction dynamics appear at multiple scales. In [11], the authors explored an optimal approach to chemotherapy within the context of a mathematical model depicting tumor–immune dynamics. The aim was to identify the most effective response strategies in the treatment of cancer. The utilization of the prey predictor concept is applied for modeling diverse biological phenomena, encompassing interactions among individual cells [12,13,14]. This approach proves particularly efficacious in elucidating the dynamics of interactions between natural killer cells and tumor cells. Diverse assumptions were considered by multiple researchers in the literature when presenting the complexities inherent in tumor cells, as documented in references [15, 16]. The role of tumor-associated macrophages in tumor vascularization offers insights into the complex interplay between macrophages and the vascular system investigated in the literature [17]. It explored the potential implications for understanding and targeting these interactions in the context of tumor development. In [18], the authors delineated that macrophages are recruited to hypoxic regions within tumors, where they undergo a pro-angiogenic M2-polarized transformation. This transition is facilitated by hypoxic cancer cell-derived cytokines, specifically Oncostatin M and Eotaxin. In [19], asymptotic analysis and numerical simulations were discussed to investigate a prostate tumor growth model. The study utilized the generalized moving least squares approximation with semi-implicit time integration to explore the dynamics of the model for an enhanced understanding of prostate tumor growth. Exploring tumor–immune interactions contributes to reduce the incidence and mortality rates of cancer. Moreover, understanding tumor–immune interactions can lead to the development of more effective treatment approaches. The motivation behind this work is to conduct a rigorous investigation into the dynamics of tumor–immune interactions, aiming to provide valuable insights for public health considerations.

Fractional derivatives hold significant relevance in addressing real-world problems across various domains [20, 21]. They offer a more nuanced and accurate representation of non-local and memory-dependent processes, enhancing the modeling and analysis of complex phenomena [22, 23]. This increased precision contributes to the development of more effective solutions in fields ranging from physics and engineering to biology and finance [24, 25]. Numerous fractional operators, as documented in the literature and exemplified by references [26], have demonstrated success across various scientific and engineering disciplines. The significance of tumor–immune research through fractional derivatives lies in its ability to offer a novel mathematical framework for understanding the complex dynamics of tumor–immune interactions. By incorporating fractional calculus, researchers can model the non-local and non-singular behavior inherent in these interactions more accurately. This approach allows for a more nuanced analysis of the intricate relationships between tumors and the immune system, potentially revealing new insights into cancer progression and treatment response. Moreover, employing fractional derivatives in tumor–immune research can facilitate the development of advanced computational models and simulation techniques, enabling researchers to explore the effects of various factors on tumor growth, immune response, and treatment efficacy in a more comprehensive manner. Therefore, we opt to present the dynamics of tumor–immune interaction through fractional framework.

Further work is organized as: In Sect. 2, we construct a mathematical model for tumor–immune interactions with the help of fractional operator. The basic theory and concepts of the fractional calculus are presented in Sect. 3 of the article. In Sect. 4, we introduce a novel numerical technique to highlight the dynamics of the proposed fractional model. We revealed the chaotic nature and oscillation behavior of the model with the variation of the different factors. Concluding remarks of our work has been illustrated in final section of the article.

2 Evaluation of tumor–immune cell dynamics

It is well-known that Cytotoxic T Lymphocytes (CTLs) stand out for their inherent characteristics and performance, making them a focal point in onco-immunology research. In this context, we aim to develop a mathematical model elucidating the dynamics among effector cells (E), tumor cells (T), and the concentration of IL-2. In our formulation, the impact of an external source on effector cells is represented by \(s_1\), while the natural death rate is symbolized by \(\mu _1\). The tumor growth is expressed by \(r_2(T)\) with the immune response strength denoted by parameter a. Furthermore, the external contribution to IL-2 is captured by \(s_2\), and its degradation is assumed to follow a rate of \(\mu _2\). Thus, the dynamics of tumor–immune can be represented as

$$\begin{aligned}&\frac{\textrm{d}E}{\textrm{d}t}=h_1\left( E(t),T(t),I_L(t)\right) =s_1+cT+p_1\frac{E I_L}{g_1+I_L}-\mu _1 E,\nonumber \\&\frac{\textrm{d}T}{\textrm{d}t}=h_2\left( E(t),T(t),I_L(t)\right) =r_2(T)-a \frac{ET}{g_2+T}, \nonumber \\&\frac{\textrm{d}I_L}{\textrm{d}t}=h_3\left( E(t),T(t),I_L(t)\right) =s_2+p_2 \frac{ET}{g_3+T}-\mu _2 I_L, \end{aligned}$$
(1)

with the following conditions

$$\begin{aligned} E(0)=E_0,T(0)=T_0 \ \ and \ \ I_L(0)=I_{L0} \end{aligned}$$

in which the tumor’s antigenicity is shown by the variable c, while the immune response’s resilience and efficacy are indicated by the constant term a, which represents the tumor cells’ rate of elimination through contacts with effector cells. In addition, the effector cells are recruited at a rate \(p_1\frac{E I_L}{g_1+I_L}\) in which \(p_1\) and \(g_1\) are constant associated with \(E I_L\) and \(I_L\), respectively. Similarly, the \(I_L\) cells are recruited at a rate \(p_2 \frac{ET}{g_3+T}\), where \(p_2\) and \(g_3\) are constant associate with E and T cells, respectively. The elimination of tumor cells through effector cells is indicated by \(a \frac{ET}{g_2+T}\) where \(g_2\) is constant associated with T. The unit of all terms in the model are in days\(^{-1}\) while the unit of \(g_1,\) \(g_2\) and \(g_3\) are volume. In this formulation, the growth term for tumor is assumed as

$$\begin{aligned} r_2(T)=r_2 T(1-bT). \end{aligned}$$

Fractional order models improve the way we model tumor–immune systems by including memory effects, capturing complex behaviors more accurately, and providing more detailed representations [28, 29]. They also offer stronger stability analysis and create a more unified and flexible framework [30]. These benefits make fractional calculus a powerful tool for studying and treating cancer, leading to more precise and dependable models of how tumors and the immune system interact. The anticipation of anomalous diffusion in tumor dynamics aligns closely with the application of fractional calculus. Anticipating anomalous diffusion in tumor dynamics suggests the potential utility of fractional calculus in capturing the intricate and non-local dependencies that characterize the movement of substances within tumors. Consequently, this improves our comprehension of tumor behavior and facilitates the creation of more precise models and therapeutic approaches. In particular, the ABC derivative makes it possible to represent these complex dynamics more precisely, which enhances modeling accuracy and predictive power. The above system (1) can be expressed in fractional framework as

$$\begin{gathered} _{0}^{{ABC}} D_{t}^{\ell } E = h_{1} \left( {E(t),T(t),I_{L} (t)} \right) = s_{1} + cT + p_{1} \frac{{EI_{L} }}{{g_{1} + I_{L} }} - \mu _{1} E, \hfill \\ _{0}^{{ABC}} D_{t}^{\ell } T = h_{2} \left( {E(t),T(t),I_{L} (t)} \right) = r_{2} (T) - a\frac{{ET}}{{g_{2} + T}}, \hfill \\ _{0}^{{ABC}} D_{t}^{\ell } I_{L} = h_{3} \left( {E(t),T(t),I_{L} (t)} \right) = s_{2} + p_{2} \frac{{ET}}{{g_{3} + T}} - \mu _{2} I_{L} , \hfill \\ \end{gathered}$$
(2)

where \({}^{{ABC}}_{0}D^{\ell }_{t}\) indicates the fractional Atangana–Baleanu operator of order \(\ell\). Numerical results derived from fractional calculus provide valuable insights into the behavior and dynamics of systems with non-integer order derivatives [27, 31]. The numerical outcomes contribute to a deeper understanding of the role of fractional calculus in modeling and analyzing diverse processes, guiding researchers and practitioners in making informed decisions and advancements in their respective fields. The ABC fractional derivative might exhibit improved properties, such as better capturing non-local dependencies, enhanced accuracy in modeling complex systems, or providing more efficient solutions for particular types of problems. However, the claim of superiority is highly context dependent and relies on the specific requirements and characteristics of the systems being analyzed. It is important to understand the specifics of each fractional operator and to test how well they work in the particular scientific or engineering context to decide which is best.

Theorem 1

The solutions of the proposed fractional model (2) are positive and bounded for proper initial values of state variables.

Proof

To prove that the solutions of proposed fractional model (2) are positive and bounded for proper initial values of state variables, we proceed as follows:

$$\begin{aligned}&f_1\left( E(t),T(t),I_L(t)\right) ={}^{{ABC}}_{0}D^{\ell }_{t}E \mid _{E=0}=s_1+cT+p_1\frac{E I_L}{g_1+I_L} \ge 0,\nonumber \\&f_2\left( E(t),T(t),I_L(t)\right) ={}^{{ABC}}_{0}D^{\ell }_{t}T \mid _{T=0}=r_2(T) \ge 0, \nonumber \\&f_3\left( E(t),T(t),I_L(t)\right) ={}^{{ABC}}_{0}D^{\ell }_{t}I_L \mid _{I_{L(t)}=0}=s_2+p_2 \frac{ET}{g_3+T} \ge 0, \end{aligned}$$
(3)

this implies that the solutions of the model are non-negative. Thus, the solution of the recommended model are positive.

To ensure boundedness of the solutions, we analyze the behavior of each equation to find upper bounds. From the first equation of model (2), we have

$$\begin{aligned} s_1+cT+p_1\frac{E I_L}{g_1+I_L}= \mu _1 E, \end{aligned}$$

further simplification implies \(E \bigg ( \mu _1 - \frac{p_1 I_L}{g_1+I_L} \bigg )=s_1+cT.\) Now, assume E reaches a maximum \(E_\textrm{max}\), then we have \(E_{max} \le \frac{s_1+c T}{\mu _1-\frac{p_1 I_L}{g_1+I_L}}\). Thus, E remains bounded. From the second equation of the model (2), we have

$$\begin{aligned} r_2 T(1-bT) = a \frac{ET}{g_2+T}, \end{aligned}$$

this implies that \(r_2 T(1-bT) = a \frac{ET}{g_2+T}.\) Assume T reaches a maximum \(T_{max},\) \(1-bT_{max} \ge 0,\) this implies \(T_\textrm{max} \le \frac{1}{b}.\) Since E is bounded, T is also bounded with an upper bound determined by b. From the third equation of our model, we have

$$\begin{aligned} s_2+p_2 \frac{ET}{g_3+T}= \mu _2 I_L, \end{aligned}$$

this implies that \(I_L= \frac{s_2+p2 \frac{ET}{g_3+T}}{\mu _2}.\) Here, assume that \(I_L\) reaches a maximum \(I_{L_\textrm{max}}\), then we have \(I_{L_\textrm{max}} \le \frac{s_2+p2 \frac{E_\textrm{max}T_{max}}{g_3+T_\textrm{max}}}{\mu _2}\). This implies that \(I_{L}\) remains bounded. Thus, the required proof is completed. \(\hfill \square\)

3 Theory of fractional calculus

It is well known that fractional calculus is rich in applications and is applied to many problems in engineering, physics, economics, biology, and other fields of science and technology. Recent investigations, as documented by references [32,33,34,35], have affirmed the capability of fractional calculus to yield outcomes characterized by heightened accuracy, precision, and reliability. In this context, we shall introduce the foundational concept of fractional calculus for scrutinizing our tumor cancer model. Here, we present various fundamental outcomes and concepts of fractional calculus concerning the Atangana–Baleanu derivative in the Caputo sense:

Definition 1

Consider a function k such that k belongs to the function space \(H^1(p, q)\), with \(q>p\), and let \(\ell\) be in the interval [0, 1]. In this context, the Atangana–Baleanu operator in the Caputo sense is indicated by ABC and is given by:

$$\begin{aligned} {}^{{ABC}}_{p}D^{\ell }_{t}k(t)= \frac{B(\ell )}{1-\ell }\int _p^t k'(\xi )E_\ell \bigg [-\ell \frac{(t-\xi )^\ell }{1-\ell }\bigg ]\textrm{d}\xi . \end{aligned}$$

Definition 2

Let \({}^{{ABC}}_{p}I^{\ell }_{t}k(t)\) be the integral of AB derivative which is defined by

$$\begin{aligned} {}^{{ABC}}_{p}I^{\ell }_{t}k(t)= \frac{1-\ell }{B(\ell )}k(t)+\frac{\ell }{B(\ell )\Gamma (\ell )}\int _p^t k(\xi )(t-\xi )^{\ell -1}\textrm{d}\xi , \end{aligned}$$

where \(B(\ell )\) is a normalization function satisfying \(B(0)=B(1)=1\).

Theorem 2

[36]. Take a continuous function k such that \(k \in C[p,q]\), then we have

$$\left\| {_{p}^{{ABC}} D_{t}^{\ell } (k(t))} \right\|\frac{{B(\ell )}}{{1 - \ell }}\left\| {k(t)} \right\|,\;in\;which\left\| {k(t)} \right\| = max_{{p \le t \le q}} \left| {k(t)} \right|.$$

Moreover, AB operator satisfies the Lipschitz condition as

$$\begin{aligned} \Vert {}^{{ABC}}_{p}D^{\ell }_{t}k_1(t)-{}^{{ABC}}_{p}D^{\ell }_{t}k_2(t)\Vert <\mathcal {\varrho }_1 \Vert k_1(t)-k_2(t)\Vert . \end{aligned}$$

Theorem 3

[36]. Assume the fractional system

$$\begin{aligned} {}^{{ABC}}_{p}D^{\ell }_{t}k(t)=w(t). \end{aligned}$$

This fractional system has a unique solution of the form

$$\begin{aligned} {k(t)=\frac{1-\ell }{B(\ell )}w(t)+\frac{\ell }{B(\ell )\Gamma (\ell )}\int _p^t w(\xi )(t-\xi )^{\ell -1}\textrm{d}\xi .} \end{aligned}$$

4 Numerical scheme for model

Here, we present a numerical technique to demonstrate the oscillatory behavior and chaos inherent in our fractional model of interactions between tumor and immune cells. Numerous numerical techniques have been introduced for systems involving fractional orders. In the context of the dynamics pertaining to the tumor–immune system, we employ the innovative scheme presented by [37] to elucidate the solution trajectory of the model (2). To derive the required numerical scheme for our fractional model of tumor–immune interactions, consider the following system:

$$\begin{aligned} {}^{{ABC}}_{0}D^{\ell }_{t}y(t)=g(t,y(t)), \end{aligned}$$

this implies that

$$y(t) - y(0) = {\text{ }}\frac{{1 - \ell }}{{ABC(\ell )}}k(t,z(t)) + \frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\int_{0}^{t} {(t - \xi )^{{\ell - 1}} } k(\xi ,y(\xi )){\text{d}}\xi .$$
(4)

Put \(t=t_n\), then we have

$$y(t_{n} ) - y(0) = {\text{ }}\frac{{1 - \ell }}{{ABC(\ell )}}k(t_{{n - 1}} ,y(t_{{n - 1}} )) + \frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\int_{0}^{{t_{n} }} {(t_{n} - \xi )^{{\ell - 1}} } k(\xi ,z(\xi )){\text{d}}\xi ,$$
(5)

for \(t_{n+1}\), one have

$$y(t_{{n + 1}} ) - y(0) = \frac{{1 - \ell }}{{ABC(\ell )}}k(t_{{n + 1}} ,y(t_{{n + 1}} )) + \frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\int_{0}^{{t_{{n + 1}} }} {(t_{{n + 1}} - \xi )^{{\ell - 1}} } k(\xi ,y(\xi )){\text{d}}\xi ,$$
(6)

the above implies that

$$\begin{aligned}y(t_{{n + 1}} ) - y(t_{n} ) = &\,\frac{{1 - \ell }}{{ABC(\ell )}}[k(t_{n} ,y(t_{n} )) - k(t_{{n - 1}} ,y(t_{{n - 1}} ))] + \frac{\ell }{{ABC(\ell )\Gamma (\ell )}}{\text{ }}\int_{0}^{{t_{{n + 1}} }} {(t_{{n + 1}} - \xi )^{{\ell - 1}} } k(\xi ,y(\xi )){\text{d}}\xi \\ &- \int_{0}^{{t_{n} }} {(t_{n} - \xi )^{{\ell - 1}} } k(\xi ,y(\xi )){\text{d}}\xi .\end{aligned}$$
(7)

Further, we have

$$y(t_{{n + 1}} ) - y(t_{n} ) = \frac{{1 - \ell }}{{ABC(\ell )}}[k(t_{n} ,y(t_{n} )) - k(t_{{n - 1}} ,y(t_{{n - 1}} ))] + B_{{\ell ,1}} - B_{{\ell ,2}} ,$$
(8)

in which

$$\begin{aligned} B_{\ell ,1}= \frac{\ell }{ABC(\ell ) \Gamma (\ell )} \int _0^{t_{n+1}} (t_{n+1}-\xi )^{\ell -1} k (\xi , y(\xi )) \textrm{d} \xi . \end{aligned}$$

Then, through approximation, we have

$$\begin{aligned} P(t)\cong \frac{g (t_n, z_n)}{h} (t-t_{n-1})- \frac{k (t_{n-1}, y_{n-1})}{h} (t-t_{n}), \end{aligned}$$
(9)

in which \(h=t_m-t_{m-1}\). After that, one get

$$\begin{aligned}B_{{\ell ,1}} = &\,\frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\int_{0}^{{t_{{n + 1}} }} {(t_{{n + 1}} - \xi )^{{\ell - 1}} } {\text{ }}\left[ {\frac{{g(t_{n} ,y_{n} )}}{h}(t - t_{{n - 1}} ) - \frac{{k(t_{{n - 1}} ,y_{{n - 1}} )}}{h}(t - t_{n} )} \right]{\text{d}}\xi \\ = &\,\frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\int_{0}^{{t_{{n + 1}} }} {(t_{{n + 1}} - \xi )^{{\ell - 1}} } {\text{ }}\left[ {\frac{{k(t_{n} ,y_{n} )}}{h}(t - t_{{n - 1}} ) - \frac{{k(t_{{n - 1}} ,y_{{n - 1}} )}}{h}(t - t_{n} )} \right]{\text{d}}\xi ,\end{aligned}$$
(10)

we get that

$$B_{{\ell ,1}} = \frac{{\ell g(t_{n} ,y_{n} )}}{{ABC(\ell )\Gamma (\ell )h}}\left[ {\frac{{2ht_{{n + 1}}^{\ell } }}{\ell } - \frac{{t_{{n + 1}}^{{\ell + 1}} }}{{\ell + 1}}} \right] - \frac{{\ell k(t_{{n - 1}} ,y_{{n - 1}} )}}{{ABC(\ell )\Gamma (\ell )h}}\left[ {\frac{{ht_{{n + 1}}^{\ell } }}{\ell } - \frac{{t_{{n + 1}}^{{\ell + 1}} }}{{\ell + 1}}} \right].$$
(11)

Taking the same steps, we have

$$\begin{aligned} B_{\ell ,2}=\frac{\ell k(t_n,y_n)}{ABC(\ell )\Gamma (\ell )h} \bigg [ \frac{h t^\ell _n}{\ell }-\frac{t_n^{\ell +1}}{\ell +1} \bigg ]- \frac{ k(t_{n-1},y_{n-1})}{ABC(\ell )\Gamma (\ell )h}, \end{aligned}$$

consequently, we have

$$\begin{aligned}y(t_{{n + 1}} ) - y(t_{n} ) = &\,\frac{{1 - \ell }}{{ABC(\ell )}}\left[ {k(t_{n} ,y(t_{n} )) - k(t_{{n - 1}} ,y(t_{{n - 1}} ))} \right] + \frac{{\ell k(t_{n} ,y_{n} )}}{{ABC(\ell )\Gamma (\ell )h}}\left[ {\frac{{2ht_{{n + 1}}^{\ell } }}{\ell } - \frac{{t_{{n + 1}}^{{\ell + 1}} }}{{\ell + 1}}} \right]\\ & - \frac{{\ell k(t_{{n - 1}} ,y_{{n - 1}} )}}{{ABC(\ell )\Gamma (\ell )h}}\left[ {\frac{{ht_{{n + 1}}^{\ell } }}{\ell } - \frac{{t_{{n + 1}}^{{\ell + 1}} }}{{\ell + 1}}} \right] - \frac{{\ell k(t_{n} ,y_{n} )}}{{ABC(\ell )\Gamma (\ell )h}}\left[ {\frac{{ht_{n}^{\ell } }}{\ell } - \frac{{t_{n}^{{\ell + 1}} }}{{\ell + 1}}} \right] + \frac{{k(t_{{n - 1}} ,y_{{n - 1}} )}}{{ABC(\ell )\Gamma (\ell )h}}.\end{aligned}$$
(12)

From the above, we obtain

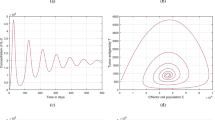
$$\begin{gathered}y\left( {t_{{n + 1}} } \right) = y(t_{n} ) + k(t_{n} ,y_{n} )\left[ {\frac{{1 - \ell }}{{ABC(\ell )}} + \frac{\ell }{{ABC(\ell )h}}{\text{ }}\left\{ {\frac{{2ht_{{n + 1}}^{\ell } }}{\ell } - \frac{{t_{{n + 1}}^{{\ell + 1}} }}{{\ell + 1}}} \right\}{\text{ }} - \frac{\ell }{{ABC(\ell )\Gamma (\ell )h}}\left\{ {\frac{{ht_{n}^{\ell } }}{\ell } - \frac{{t_{n}^{{\ell + 1}} }}{{\ell + 1}}} \right\}} \right]\\ + k(t_{{n - 1}} ,y_{{n - 1}} ) \times - \left[ {\frac{{\ell - 1}}{{ABC(\ell )}} - \frac{\ell }{{ABC(\ell )\Gamma (\ell )h}}\left\{ {\frac{{ht_{{n + 1}}^{\ell } }}{\ell } - \frac{{t_{{n + 1}}^{{\ell + 1}} }}{{\ell + 1}} + \frac{{t^{{\ell + 1}} }}{{hABC(\ell )\Gamma (\ell )}}} \right\}} \right].{\text{ }}\end{gathered}$$
(13)

The presented scheme delineates a two-step Adams–Bashforth scheme specifically tailored for the ABC operator. Here, different simulations were conducted to elucidate the influence of varying parameters on the dynamics characterizing the interactions between tumor cells and the immune system. The values of the system’s input parameters are assumed for numerical purposes. In Fig. 1, 2, 3 and  4, the blue color represents the solution pathways of the model in integer case while the red color represents the solution pathways in non-integer case. In this section, the parameter values are supposed for simulations proposes to highlight the chaotic and oscillatory behavior of the system (2). In Figs. 1, 3, we have depicted the dynamic behavior of our proposed non-integer order model (2) using various values of the fractional parameter \(\ell\), specifically \(\ell =0.9\), \(\ell =0.5\), and \(\ell =0.95\), while in the other figures, we assumed the value of \(\ell =0.85\), which is also mentioned there in the figures. Our simulations revealed a noteworthy influence of the parameter \(\ell\) on the system dynamics, positioning it as a viable control parameter.

Figures 3, 4 and  5 depict the oscillatory and chaotic patterns exhibited by our system, subject to varying input parameters, specifically \(c=100\), \(a=0.1\), and \(a=1\). These simulations underscore the chaotic attributes inherent in the system, indicative of the potential significance of the parameter a in influencing and modulating the observed chaos within the system. The findings suggest that the manipulation of the parameter a may play a pivotal role in mitigating or suppressing the observed chaotic behavior.

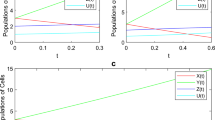
In the next step, we have shown the dynamics of the system with the variation of several input parameter to detect the effect of these input parameter on the system of tumor–immune cell interactions. We mainly focus on the variation of the parameters \(r_2, a,p_1, c\) and \(g_3\) to highlight the propose dynamics in Fig. 5, 6, 7, 8, 9 and 10. In Fig. 5, the system is plotted with different values of the input parameter \(r_2\). The graphical representation shows that this parameter is critical which increase the level of tumor antigenicity in the system. In Fig. 9, we assume different values of the parameter c and observed through simulations that the grater value of c can reduce the tumor antigenicity. Here, the role of the parameter c is highly appreciable in the system. In the simulations presented in Figs. 8, 9 and 10, it is interrogated that the input parameter a and \(g_3\) slightly disturb the dynamics of the propose system while the parameter \(p_1\) offer an interesting phenomenon during simulations. We have demonstrated in Fig. 8 that an increased value of the parameter \(p_1\) leads the system to exhibit both lower and upper peaks. On one hand, it decreases the level of tumor antigenicity, while on the other hand, it increases the level.

Fig. 1
figure 1

Illustration of the solution pathways and chaotic behavior of the model (2) of tumor–immune cell interactions with fractional order \(\ell =0.9\)

Full size image
Fig. 2
figure 2

Graphical view analysis of the solution pathways and chaotic behavior of the model (2) of tumor–immune cell interactions with fractional order \(\ell =0.5\)

Full size image
Fig. 3
figure 3

Time series analysis and chaotic behavior of the model (2) of tumor–immune cell interactions with input parameter \(c=100\) and \(\ell =0.95\)

Full size image
Fig. 4
figure 4

Illustration of a phase portrait of tumor antigenicity verses concentration of IL-2, b phase portrait of effector cell population verses concentration of IL-2, c phase portrait of effector cells verses tumor antigenicity, and d chaotic behavior of the fractional tumor–immune cell interactions model (2) with the input parameter \(a=0.1\) and \(\ell =0.85\)

Full size image
Fig. 5
figure 5

Phase portrait of a tumor antigenicity verses concentration of IL-2, b the effector cell population verses concentration of IL-2, c the effector cells verses tumor antigenicity, and d chaotic behavior of the fractional tumor–immune cell interactions model (2) with the input parameter \(a=1.0\) and \(\ell =0.85\)

Full size image
Fig. 6
figure 6

Illustration of dynamical behavior of the proposed fractional system (2) of tumor–immune cell interactions with input parameter \(r_2=0.10,0.12,0.14\) and \(\ell =0.85\)

Full size image
Fig. 7
figure 7

Illustration of dynamical behavior of the recommended system (2) of tumor with fractional parameter \(\ell =0.85\) and different values of a, i.e., \(a=0.4,0.5,0.6\)

Full size image
Fig. 8
figure 8

Graphical view analysis of the dynamical behavior of the proposed system (2) of tumor with fractional parameter \(\ell =0.85\) and different values of input parameter \(p_1\), i.e., \(p_1=0.12,0.15,0.18\)

Full size image
Fig. 9
figure 9

Time series analysis of the proposed model (2) of tumor with fractional parameter \(\ell =0.85\) and the effect of c, i.e., \(c=0.5,1.0,1.5\)

Full size image
Fig. 10
figure 10

Time series analysis of the recommended system (2) of tumor–immune with fractional parameter \(\ell =0.85\) and the effect of \(g_1\), i.e., \(g=1.0\times 10^3, 1.5 \times 10^3, 2.0 \times 10^3\)

Full size image

Moving forward, we will delve into the convergence and stability outcomes of our devised numerical scheme. The subsequent section outlines the convergence result attained through our method:

Theorem 4

Take a continuous and bounded function k, then the fractional system

$$\begin{aligned} _0^{ABC}D^{\ell }_{\xi }z(\xi )=k(\xi ,z(\xi )), \end{aligned}$$

has a solution of the form \(x(\xi )\) and is given by

$$\begin{gathered}z_{{n + 1}} = z_{n} + k(\xi _{n} ,z_{n} )\left[ {\frac{{1 - \ell }}{{ABC(\ell )}} + \frac{\ell }{{ABC(\ell )h}}\left\{ {\frac{{2ht_{{n + 1}}^{\ell } }}{\ell } - \frac{{t_{{n + 1}}^{{\ell + 1}} }}{{\ell + 1}}} \right\} - \frac{\ell }{{h\Gamma (\ell )ABC(\ell )}}\left\{ {\frac{{ht_{n}^{\ell } }}{\ell } - \frac{{t_{n}^{{\ell + 1}} }}{{\ell + 1}}} \right\}} \right] \\ + k(\xi _{{n - 1}} ,z_{{n - 1}} ) \times \left[ {\frac{{\ell - 1}}{{ABC(\ell )}} - \frac{\ell }{{ABC(\ell )\Gamma (\ell )h}}\left. {\left[ {\frac{{2h\xi _{{n + 1}}^{\ell } }}{\ell } - \frac{{\xi _{{n + 1}}^{{\ell + 1}} }}{{\ell + 1}} + \frac{{\xi ^{{\ell + 1}} }}{{ABC(\ell )h\Gamma (\ell )}}} \right]} \right]} \right.{\text{ }} + H_{\ell } ,\end{gathered}$$

where \(||H_{\ell }||_{\infty } < N.\)

Proof

To establish the desired outcome, we follow the below steps:

$$\begin{aligned} z_{n+1}-z_{n}&=\frac{1-\ell }{ABC(\ell )}(k(\xi _{n},z_{n})-k(\xi _{n-1},z_{n-1})) +\frac{\ell }{\Gamma (\ell ) ABC(\ell )} \nonumber \\&\times \left[ \int ^{\xi _{n+1}}_{0} (\xi _{n+1}-\xi )^{\ell -1} k(\xi ,x(\xi )) \textrm{d} \xi -\int ^{\xi _{n}}_{0} (\xi _{n}-\xi )^{\ell -1} k(\xi ,z(\xi )) \textrm{d} \xi \right] \nonumber \\&=\frac{1-\ell }{ABC(\ell )}(k_{n}-k_{n-1})+ \frac{\ell }{\Gamma (\ell ) ABC(\ell )} \nonumber \\&\quad \left\{ \int ^{\xi _{n+1}}_{0} \frac{\xi -\xi _{n-1}}{\xi _{n}-\xi _{n-1}} k(\xi _{n},z_{n}) +\frac{\xi -\xi _{n}}{\xi _{n-1}-\xi _{n}}k(\xi _{n-1},z_{n-1})+\frac{k^{n+1}(\xi )}{(n+1)!} \prod ^{n}_{i=0}(\xi -\xi _{i}) \right\} \\&\quad (\xi _{n+1}-\xi )^{\ell -1}\textrm{d}\xi -\int ^{\xi _{n}}_{0}\left\{ \frac{\xi -\xi _{n-1}}{\xi _{n}-\xi _{n-1}}k(\xi _{n},z_{n}) +\frac{\xi -\xi _{n}}{\xi _{n-1}-\xi _{n}}\right. \\&\quad \left. f(\xi _{n-1},y_{n-1})+\frac{k^{n}(\xi )}{(n)!} \prod ^{n-1}_{i=0}(\xi -\xi _{i}) \right\} \times (\xi _{n}-\xi )^{\ell -1}\textrm{d} \xi \nonumber \\&=\int ^{\xi _{n+1}}_{0}\frac{g^{(n+1)}(\xi )}{(n+1)!}\prod ^{n}_{i=0} (\xi _{n+1}-\xi )^{\ell -1} (\xi -\xi _{i})\textrm{d} \xi + J(\xi ,\ell ,n)\\&\quad -\int ^{\xi _{n}}_{0} \frac{k^{(n)}(\xi )}{(n)!}\prod ^{n}_{i=0} (\xi _{n}-\xi )^{\ell -1} (\xi -\xi _{i})\textrm{d} \xi , \nonumber \end{aligned}$$

this implies that

$$\begin{aligned} z_{n+1}-z_{n}=J(\xi ,\ell ,n)+H_{\ell }(\xi ), \end{aligned}$$
(14)

in which, we have

$$\begin{aligned} \begin{aligned} J(\xi ,\ell ,n)=&k(\xi _{n},z_{n}) \left\{ \frac{1-\ell }{ABC(\ell )}+\frac{\ell }{AB(\ell )h} \left[ \frac{2h \xi ^{\ell }_{n+1}}{\ell }-\frac{\xi ^{\ell +1}_{n+1}}{\ell +1}\right] -\frac{\ell }{ABC(\ell )h \Gamma (\ell )}\left[ \frac{h \xi ^{\ell }_{n}}{\ell }-\frac{\xi ^{\ell }_{n}}{\ell +1}\right] \right\}\\ & \quad + k(\xi _{n-1},z_{n-1})\left\{ \frac{\ell }{ABC(\ell )}-\frac{\ell }{h ABC(\ell )\Gamma (\ell )} \left( \frac{h \xi ^{\ell }_{n+1}}{\ell }-\frac{\xi ^{\ell +1}_{n+1}}{\ell +1}+\frac{\xi ^{\ell +1}_{n}}{h\Gamma (\ell )ABC(\ell )}\right) \right\} , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} H_{\ell }(t)= & {} \int ^{\xi _{n+1}}_{0} \frac{k^{n+1}(\xi )}{(n+1)!}\prod ^{n}_{i=0} (\xi _{n+1}-\xi )^{\ell -1} (\xi -\xi _{i})d \xi -\int ^{\xi _{n}}_{0} \frac{k^{n}(\xi )}{(n)!}\prod ^{n-1}_{i=0}(\xi -\xi _{i})(\xi _{n}-\xi )^{\ell -1}d \xi . \end{aligned}$$

In the coming step, we proceed as

$$\begin{aligned} \left\| {H_{\ell } (\xi )} \right\|_{\infty } = &\left| {\left| {\int_{0}^{{\xi _{{n + 1}} }} {\frac{{k^{{n + 1}} (\xi )}}{{(n + 1)!}}} \prod\limits_{{i = 0}}^{n} {(\xi - \xi _{i} )(\xi _{{n + 1}} - \xi )^{{\ell - 1}} } {\text{d}}\xi } \right.} \right.\left. {\left. { - \int_{0}^{{\xi _{n} }} {\frac{{k^{n} (\xi )}}{{(n)!}}} \prod\limits_{{i = 0}}^{{n - 1}} {(\xi - \xi _{i} )(\xi _{n} - \xi )^{{\ell - 1}} } {\text{d}}\xi } \right|} \right|_{\infty }\\ &\left| {\left| {\int_{0}^{{\xi _{{n + 1}} }} {\frac{{k^{{n + 1}} (\xi )}}{{(n + 1)!}}} \prod\limits_{{i = 0}}^{n} {(\xi - \xi _{i} )(\xi _{{n + 1}} - \xi )^{{\ell - 1}} } d\xi } \right|} \right|_{\infty } + \left| {\left| {\int_{0}^{{\xi _{n} }} {\frac{{k^{n} (\xi )}}{{(n)!}}} \prod\limits_{{i = 0}}^{{n - 1}} {(\xi _{n} - \xi )^{{\ell - 1}} } (\xi - \xi _{i} ){\text{d}}\xi } \right|} \right|_{\infty }\\ & \max _{{\xi \in [0,\xi _{{n + 1}} ]}} \frac{{|k^{{(n + 1)}} (\xi )|}}{{(n + 1)!}}\left| {\left| {\prod\limits_{{i = 0}}^{n} {(\xi - \xi _{i} )} } \right|} \right|_{\infty } \frac{{t_{{n + 1}}^{\ell } }}{\ell } + \max _{{\xi \in [0,\xi _{{n + 1}} ]}} \frac{{|k^{{(n)}} (\xi )|}}{{(n)!}}\left| {\left| {\prod\limits_{{i = 0}}^{{n - 1}} {(\xi - \xi _{i} )} } \right|} \right|_{\infty } \\ &\frac{{\xi _{n}^{\ell } }}{\ell }\mathop {\sup }\limits_{{\xi \in [0,\xi _{{n + 1}} ]}} \left\{ {\max _{{\xi \in [0,\xi _{{n + 1}} ]}} \frac{{|k^{{(n + 1)}} (\xi )|}}{{(n + 1)!}},\max _{{\xi \in [0,\xi _{{n + 1}} ]}} \frac{{|k^{{(n)}} (\xi )|}}{{(n)!}}} \right\}\left( {n!\frac{{h^{{n + 1}} }}{{4\ell }}\xi ^{{\ell _{{n + 1}} }} + (n - 1)!\frac{{h^{n} }}{{4\ell }}\xi ^{{\ell _{n} }} } \right), \hfill \\ \end{aligned}$$
(15)

which is the required result. \(\hfill\square\)

Theorem 5

Suppose that the function k satisfies the Lipschitz condition. In this case, the stability criterion for the aforementioned numerical scheme in the Atangana–Baleanu fractional framework in the Caputo sense is expressed as:

$$\begin{aligned} \left| \left| k(\xi _{n},z_{n})-k(\xi _{n-1},z_{n-1})\right| \right| _{\infty } \rightarrow 0 \end{aligned}$$

as n approaches to \(\infty .\)

Proof

For the demanded outcomes, take the following

$$\begin{aligned} z_{{n - 1}} - z_{n} = &\,\frac{{1 - \ell }}{{ABC(\ell )}}\left[ {k(\xi _{n} ,z_{n} ) - k(\xi _{{n - 1}} ,z_{{n - 1}} )} \right] + \frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\\ &\,\times \left[ {\int_{0}^{{\xi _{{n + 1}} }} k (\xi ,z(\xi ))(\xi _{{n + 1}} - \xi )^{{\ell - 1}} {\text{d}}\xi - \int_{0}^{{\xi _{n} }} k (\xi ,z(\xi ))(\xi _{n} - \xi )^{{\ell - 1}} {\text{d}}\xi } \right]\end{aligned}$$

taking norm on both sides, we have

$$\begin{aligned} &\left| {\left| {z_{{n - 1}} - z_{n} } \right|} \right|_{\infty } \left| {\left| {\frac{{1 - \ell }}{{ABC(\ell )}}[k(\xi _{n} ,z_{n} ) - k(\xi _{{n - 1}} ,z_{{n - 1}} )]} \right|} \right|_{\infty } + \frac{\ell }{{\Gamma (\ell )ABC(\ell )}}\\ &\quad\times \left\| {\left[ {\int_{0}^{{\xi _{{n + 1}} }} {(\xi _{{n + 1}} - \xi )^{{\ell - 1}} } k(\xi ,z(\xi )){\text{d}}\xi - \int_{0}^{{\xi _{n} }} {(\xi _{n} - \xi )^{{\ell - 1}} } k(\xi ,z(\xi )){\text{d}}\xi } \right]} \right\|_{\infty } \frac{{1 - \ell }}{{ABC(\ell )}}|\left\| {k(\xi _{n} ,z_{n} ) - k(\xi _{{n - 1}} ,z_{{n - 1}} )} \right\|_{\infty } \hfill \\ &\quad+ \frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\left| {\left| {\int_{0}^{{\xi _{{n + 1}} }} k (\xi ,z(\xi ))(\xi _{{n + 1}} - \xi )^{{\ell - 1}} {\text{d}}\xi } \right|} \right|_{\infty } + \frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\left| {\left| {\int_{0}^{{\xi _{n} }} k (\xi ,z(\xi ))(\xi _{n} - \xi )^{{\ell - 1}} {\text{d}}\xi } \right|} \right|_{\infty } . \hfill \\ \end{aligned}$$

From the above, we have

$$\begin{gathered} \left\| {z_{{n + 1}} - z_{n} } \right\|_{\infty } \frac{{1 - \ell }}{{ABC(\ell )}}\left\| {k(\xi _{n} ,z_{n} ) - k(\xi _{{n - 1}} ,z_{{n - 1}} )} \right\|_{\infty } + \frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\left\| {\int_{0}^{{\xi _{{n + 1}} }} {(\xi _{{n + 1}} - \xi )^{{\ell - 1}} \sum\limits_{{i = 0}}^{n} {\prod\limits_{{0 \le i \le n}} {\frac{{(\xi - \xi _{i} )}}{{( - 1)^{i} h}}} } k(\xi _{i} ,z_{i} ){\text{d}}\xi } } \right\|_{\infty } \hfill \\ + \frac{\ell }{{ABC(\ell )\Gamma (\ell )}}\left\| {\int_{0}^{{\xi _{n} }} {(\xi _{n} - \xi )^{{\ell - 1}} \sum\limits_{{i = 0}}^{{n - 1}} {\prod\limits_{{0 \le i \le n - 1}} k } (\xi _{i} ,x_{i} )d\xi } } \right\|_{\infty } \frac{{1 - \ell }}{{ABC(\ell )}}\left\| {k(\xi _{n} ,z_{n} ) - k(\xi _{{n - 1}} ,z_{{n - 1}} )} \right\|_{\infty } + \left\| {P_{n}^{\ell } (\xi )} \right\|_{\infty } + \left\| {H_{n}^{\ell } (\xi )} \right\|_{\infty } , \hfill \\ \end{gathered}$$
(16)

where

$$\begin{aligned} \left\| {P_{n}^{\ell } (\xi )} \right\|_{\infty } = &\left| {\left| {\int_{0}^{{\xi _{{n + 1}} }} {(\xi _{{n + 1}} - \xi )^{{\ell - 1}} } \sum\limits_{{i = 0}}^{n} {\frac{{(\xi - \xi _{i} )}}{{( - 1)^{i} h}}} k(\xi _{i} ,z_{i} ){\text{d}}\xi } \right|} \right|_{\infty } \hfill \\ \le& \sum\limits_{{i = 0}}^{n} {\frac{{||k(\xi _{i} ,z_{i} )||_{\infty } }}{h}} \frac{{\xi _{{n + 1}}^{\ell } }}{\ell }\prod\limits_{{i = 0}}^{n} | \xi - \xi _{i} | \le \sum\limits_{{i = 0}}^{n} {\frac{{||k(\xi _{i} ,z_{i} )||_{\infty } }}{h}} \frac{{\xi _{{n + 1}}^{\ell } }}{\ell }\frac{{n!h^{n} }}{4}, \hfill \\ \end{aligned}$$
(17)

and

$$\begin{aligned} ||H^{\ell }_{n}(\xi )||_{\infty }\le \sum ^{n}_{i=0}\frac{||k(\xi _{i},z_{i}||_{\infty }}{h}\frac{\xi ^{\ell }_{n}}{\ell }(n-1)!\frac{h^{n-1}}{4}. \end{aligned}$$
(18)

Consequently, one have

$$\begin{aligned} \left\| {z_{{n - 1}} - z_{n} } \right\|_{\infty } < &\, {\mkern 1mu} \frac{{1 - \ell }}{{ABC(\ell )}}|\left\| {k(\xi _{n} ,z_{n} ) - k(\xi _{{n - 1}} ,z_{{n - 1}} )} \right\|_{\infty } + \sum\limits_{{i = 0}}^{n} {\frac{{||k(\xi _{i} ,z_{i} )||_{\infty } }}{{4\ell }}} \xi _{{n + 1}}^{\ell } h^{{n - 1}} n!{\text{ }}\\ & + \sum\limits_{{i = 0}}^{{n - 1}} {\frac{{||k(\xi _{{i - 1}} ,z_{{i - 1}} )||_{\infty } }}{{4\ell }}} t_{n}^{\ell } h^{{n - 3}} (n - 1)!{\text{ < }}{\mkern 1mu} \frac{{Mn!h^{n} }}{{4\ell }}\left\{ {\frac{{\xi _{{n + 1}}^{\ell } (n + 1)}}{h} + \frac{{\xi _{n}^{\ell } }}{{h^{2} }}} \right\}\\ & + \frac{{1 - \ell }}{{ABC(\ell )}}||k(\xi _{n} ,z_{n} ) - k(\xi _{{n - 1}} ,z_{{n - 1}} )||_{\infty } ,\end{aligned}$$

which give that \(| k(\xi _n, z_n)-k(\xi _{n-1},z_{n-1})|\) approaches to 0 as n approaches to \(\infty\). In addition to this, \(\frac{Mn!h^n}{4\ell }\) approaches to 0 as h approaches to 0, in which \(M=\max _{\xi \in [0,\xi _{n+1}]} | k(\xi ,z(\xi ))|\). \(\hfill\square\)

Stability ensures that the numerical solution remains bounded and behaves correctly over time, even for long simulations. An unstable scheme can produce wildly incorrect results, rendering simulations unreliable and useless. They provide confidence that the numerical results are a true representation of the underlying mathematical model, which is essential for scientific studies and any application where model predictions influence decisions. To be more specific, the stability analysis of a numerical scheme are fundamental to ensure that the numerical solutions are accurate, reliable, and useful for practical applications.

5 Conclusion

Tumors refer to the anomalous proliferation and division of cells, leading to the formation of abnormal tissue masses. On the other hand, the immune system plays a crucial role in combating infections and is equally significant in the context of tumor immunology. Two pivotal concepts within this field are immune surveillance and tumor immune escape. The interplay between the immune system and tumor cells is essential in regulating tumor progression and outgrowth. Thus, understanding the interactions between tumor and immune cells, along with the key factors involved, is of paramount importance. In this article, we conceptualized the natural process of tumor–immune cell interactions through a mathematical framework. The complex dynamics of these interactions were presented using a non-local and non-singular kernel. We explored the fundamental properties of fractional calculus to analyze our proposed system. A novel numerical scheme was developed to examine the dynamical behavior of the fractional tumor–immune cell interactions model. We have shown the stability criterion for the proposed numerical scheme to ensure the accuracy of the results in the long term. Our findings emphasized the significance of key parameters within tumor–immune interactions. The analysis identified specific parameters that are critical for control interventions. Visualizing parameter importance enhanced the understanding of the underlying dynamics and facilitated the identification of critical factors for targeted intervention strategies.