$Z_{cs}$, $Z_c$ and $Z_b$ states under the complex scaling method

Abstract

We investigate the $Z_b$, $Z_c$ and $Z_{cs}$ states within the chiral effective field theory framework and the S-wave single channel molecule picture. With the complex scaling method, we accurately solve the Schrödinger equation in momentum space. Our analysis reveals that the $Z_b(10610)$, $Z_b(10650)$, $Z_c(3900)$ and $Z_c(4020)$ states are the resonances composed of the S-wave $(B\bar{B}^{*}+B^{*}\bar{B})/\sqrt{2}$, $B^{*}\bar{B}^*$, $(D\bar{D}^{*}+D^{*}\bar{D})/\sqrt{2}$ and $D^{*}\bar{D}^*$, respectively. Furthermore, although the $Z_{cs}(3985)$ and $Z_{cs}(4000)$ states exhibit a significant difference in width, these two resonances may originate from the same channel, the S-wave $(D_{s}\bar{D}^{*}+D_{s}^{*}\bar{D})/\sqrt{2}$. Additionally, we find two resonances in the S-wave $D_s^*\bar{D}^*$ channel, corresponding to the $Z_{cs}(4123)$ and $Z_{cs}(4220)$ states that await experimental confirmation.

1 Introduction

In the past decade, ongoing experimental efforts have led to the discovery of a series of heavy quarkonium-like states known as the XYZ states. The charged Z states like $Z_c(3900)$ and $Z_c(4020)$ provide strong evidence of the exotic states, as they involve the light quarks to explain their non-zero electric charge. Experimental advancements in the $Z_b$ sector can be traced back to 2011 when the Belle collaboration reported two charged exotic candidates, $Z_b(10610)$ and $Z_b(10650)$ [1], which were later confirmed in subsequent studies [2, 3]. Multiple hidden-charm tetraquark candidates of the $Z_c$ states have been observed by the BESIII, Belle and CLEO collaborations in electron-positron annihilation, including the charged and neutral $Z_c(3900)$ and $Z_c(4020)$ states [4,5,6,7,8,9,10,11,12,13]. These states, with their masses near the thresholds of $B^{(*)}\bar{B}^*$ and $D^{(*)}\bar{D}^*$, have been widely interpreted as the molecule states in the papers [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Additionally, the existence of the strange partners with the $Q\bar{Q} s\bar{q}'$ ($q,q'=u,d$) configurations is predicted by the SU(3)-flavor symmetry, and indeed they have been discovered in recent years.

In 2021, the BESIII collaboration observed an exotic hadron near the mass thresholds of $D_s^-D^{*0}$ and $D_s^{*-}D^{0}$ in the processes $e^+e^-\rightarrow K^+D_s^-D^{*0}$ and $K^+D_s^{*-}D^{0}$ [30]. The corresponding mass and width fitted with a Breit-Wigner line shape are

$$\begin{aligned}{} & {} M[Z_{cs}(3985)]=3982.2_{-2.6}^{+1.8}\pm 2.1\ \text {MeV}\ \text {and}\nonumber \\{} & {} \Gamma [Z_{cs}(3985)]=12.8_{-4.4}^{+5.3}\pm 3.0 \ \text {MeV}. \end{aligned}$$

(1)

Last year, they observed a neutral $Z_{cs}(3985)^0$ in the processes $e^+e^-\rightarrow K_S^0D_s^{+}D^{*-}$ and $K_S^0D_s^{*+}D^{-}$ [31]. The mass and width of the neutral $Z_{cs}(3985)^0$ have been determined to be ($3992.2\pm 1.7\pm 1.6$) MeV and ($7.7^{+4.1}_{-3.8}\pm 4.3$) MeV, respectively. Its mass, width and cross section are similar to those of the charged $Z_{cs}(3985)^+$, which suggests that the neutral $Z_{cs}(3985)^0$ is the isospin partner of the $Z_{cs}(3985)^+$. Furthermore, in 2021, the LHCb collaboration reported a series of distinct $Z_{cs}$ states. In the hidden charm decay process $B^+\rightarrow J/\psi \phi K^+$, they observed two $Z_{cs}$ states with $J^P=1^+$ [32]. One of these $Z_{cs}$ states is the $Z_{cs}(4000)^+$, which is discovered with high significance. Its mass and width are measured to be

$$\begin{aligned}{} & {} M[Z_{cs}(4000)]=4003\pm 6_{-14}^{+4}\ \text {MeV}\ \text {and}\nonumber \\{} & {} \Gamma [Z_{cs}(4000)]=131\pm 15\pm 26 \ \text {MeV}, \end{aligned}$$

(2)

respectively. Additionally, the other $Z_{cs}$ state, $Z_{cs}(4220)^+$, has a mass of $4216\pm 24_{-30}^{+43}$ MeV and a width of $233\pm 52_{-73}^{+97}$ MeV. The LHCb collaboration considers the $Z_{cs}(4000)^+$ and $Z_{cs}(3985)^+$ to be distinct states due to their apparently different widths, despite their close mass.

This discovery of the exotic $Z_{cs}$ hadrons inspired various theoretical interpretations, including the compact tetraquark picture [33,34,35], the molecule picture [36,37,38,39,40,41,42,43], the mixing scheme [44,45,46,47,48] and the cusp effect [49]. When examining the BESIII and LHCb observations of the $Z_{cs}$ states, some authors of the Refs. [40, 50, 51] proposed that the $Z_{cs}(3985)$ and $Z_{cs}(4000)$ are the same entity, whereas the Refs. [33, 34, 38, 43, 46, 47] considered them to be distinct hadrons. Moreover, one can gain further insights from the comprehensive reviews published in recent years [52,53,54,55,56,57,58,59,60,61,62,63,64,65].

In Refs. [34, 38], the authors considered the $Z_{cs}(3985)$ and $Z_{cs}(4000)$ as the SU(3)-flavor partners of $Z_c(3900)$, whose neutral nonstrange members have opposite C parity. The authors suggested the $Z_{cs}(4000)/Z_{cs}(3985)$ is the pure molecular state composed of $(|\bar{D}_s^*D\rangle +/-|\bar{D}_sD^*\rangle )/\sqrt{2}$. In addition, they also predicted the existence of a molecule composed of $\bar{D}_s^*D^*$ which may be confirmed by the BESIII in the subsequent experiment [66]. However, the huge difference of their widths seems still hard to interpret.

In this study, we employ the chiral effective field theory (ChEFT) to investigate the properties of the $Z_b$, $Z_c$ and $Z_{cs}$ states in the molecular picture. To explore the existence and relationships of the possible resonances, we utilize the complex scaling method (CSM) [67, 68], which is a powerful tool that provides a consistent treatment of the bound states and resonances. We focus on the S-wave open-charm interaction, while neglecting the possible contributions from the hidden charm. As illustrated in our previous works [69, 70], we consider the cross diagram $D\bar{D}^{*}\leftrightarrow D^{*}\bar{D}$ of the one-pion-exchange (OPE) contribution. This contribution introduces a complex potential arising from the three-body decay effect, which we take into account when investigating the widths of the resonances.

This paper is organized as follows. In Sect. 2, we introduce our framework explicitly. In Sect. 3, we present the effective Lagrangians and potentials. In Sect. 4, we solve the complex scaled Schrödinger equation and give the results of the $Z_b$, $Z_c$ and $Z_{cs}$. The last Sect. 5 is a brief summary.

2 Framework

In this study, we consider the $Z_b$, $Z_c$ and $Z_{cs}$ states as the molecular systems with the quantum numbers $I^G(J^{PC})=1^+(1^{+-})$, $I^G(J^{PC})=1^+(1^{+-})$ and $I(J^{P})=1/2(1^{+})$, respectively. The specific molecule systems under investigation are $(B\bar{B}^*+B^{*}\bar{B})/\sqrt{2}$, $B^*\bar{B}^*$, $(D\bar{D}^*+D^{*}\bar{D})/\sqrt{2}$, $D^*\bar{D}^*$, $(D_s\bar{D}^*+D_s^{*}\bar{D})/\sqrt{2}$ and $D_s^*\bar{D}^*$.

In the earlier work [16], the $Z_b$ states were proposed as the bound states of $\left[ B\bar{B}^{*}+B^*\bar{B}\right] /\sqrt{2}$ and $B^*\bar{B}^*$. The authors considered the D-wave channel and found that the $S-D$ wave mixing effect could contribute significantly. Recent experiments [2, 3] have uncovered additional evidence supporting the interpretation of the $Z_b$ states as the resonances. These findings show that the masses of the $Z_b$ states are higher than the threshold of the $B^{(*)}\bar{B}^*$ pairs, and they can decay into the $B^{(*)}\bar{B}^*$ channel with the partial widths in the range of tens of MeV. These findings strongly favor the resonance interpretation over the bound state scenario.

In this CSM framework, we firstly assume that the influence of the D-wave channel on the mass and width of the resonances is negligible. And in the last Sect. 4.3 located just before the summary, we provide a brief discussion of the case including the D-wave channel, and confirm the assumption.

On the other hand, we find that the coupled channel effect between $(B\bar{B}^{*}+B^*\bar{B})/\sqrt{2}$ and $B^*\bar{B}^*$ is negligible for the near threshold states. In addition, there are inelastic channels in the final decay process, like $\Upsilon (nS)\pi$, that could be the constituents of the $Z_b$ states as well. However, the couplings strength between the $Z_b$ and the hidden-bottom channels is apparently smaller than that between $Z_b$ and the open-bottom channels. Therefore, the influence of the correction from the hidden-bottom channels should not be significant. Furthermore, for the $Z_c$ and $Z_{cs}$ systems, we adopt the same assumption that the inelastic hidden-heavy channels are not the primary constituents. As a result, we focus on the simplest case, considering only the S-wave open-heavy single channel.

The masses of the charmed meson and exchanged light mesons are collected in Table 1. We take the isospin average masses to deal with the isospin conserving process.

Table 1 The masses of the charmed, bottomed and pion mesons, which are taken from Ref. [71]

2.1 A brief discussion on the CSM

We first provide a brief overview of the CSM proposed by Aguilar, Balslev and Combes in the 1970s [67, 68], commonly known as the ABC theorem. The CSM is a powerful approach that allows for the treatment of resonances in a manner similar to the bound states. The transformation of the radial coordinate r and its conjugate momentum k in the CSM are defined by:

$$\begin{aligned} U(\theta )r=re^{i\theta },\qquad U(\theta )k=ke^{-i\theta }. \end{aligned}$$

(3)

After the complex scaling operation, the Schrödinger equation

$$\begin{aligned} \frac{p^2}{2m}\phi _l(p)+ \int \frac{p'^{2}dp'}{(2\pi )^3} V_{l,l'} (p,p')\phi _{l'}(p')=E\phi _l(p) \end{aligned}$$

(4)

in the momentum space becomes

$$\begin{aligned}{} & {} \frac{p^2e^{-2i\theta }}{2m}\tilde{\phi }_l(p)+ \int \frac{p'^{2}e^{-3i\theta }dp'}{(2\pi )^3} V_{l,l'} (pe^{-i\theta },p'e^{-i\theta })\tilde{\phi }_{l'}(p') \nonumber \\{} & {} =E\tilde{\phi }_l(p), \end{aligned}$$

(5)

with the normalization relation

$$\begin{aligned}{} & {} \frac{e^{-3i\theta }}{(2\pi )^3}\int _{0}^{\infty }\tilde{\phi }_l(p)^2 p^2dp=1, \end{aligned}$$

(6)

where $l,l'$ are the orbital angular momenta, and p represents the momentum in the center-of-mass frame. The potential $V_{l,l'}$ after partial wave decomposition can be expressed as

$$\begin{aligned} V_{l,l'}= & {} \int d\varvec{\Omega }'\int d\varvec{\Omega }\sum _{m_{l'}=-l'}^{l'}\langle l',m_{l'};s,m_j-m_{l'}|j,m_j\rangle \nonumber \\{} & {} \times \sum _{m_{l}=-l}^{l}\langle l,m_{l};s,m_j-m_{l}|j,m_j\rangle \mathcal {Y}_{l',m_{l'}}^*(\theta ',\phi ') \nonumber \\{} & {} \times \mathcal {Y}_{l,m_{l}}(\theta ,\phi )\langle s,m_j-m_{l'}|\mathcal {V}|s,m_j-m_l\rangle , \end{aligned}$$

(7)

where s and j represent the total spin and total angular momentum of systems, $m_l$ is the corresponding magnetic quantum number. The $\mathcal {Y}_{l,m_{l}}(\theta ,\phi )$ represents the spherical harmonics associated with the angular coordinates $\theta$, $\phi$. The potential operator $\mathcal {V}$ acts on the states $|s,m_j-m_{l'}\rangle$ and $|s,m_j-m_l\rangle$.

After performing the complex scaling operation, the resonance pole crosses the branch cut into the first Riemann sheet when the rotation angle $\theta$ reaches a sufficiently large value, as depicted in Fig. 1. Consequently, the wave functions of the resonances become square-integrable, similar to those of the normalizable bound states. Further information on this technique can be found in Refs. [72, 73].

2.2 Analyticity of the OPE potentials for the $DD^*$ system

In our previous works [69, 70], we investigated the double-charm tetraquark system using the CSM method. Notably, we found that the $D\bar{D}^*$ system exhibits a unique characteristic where the zeroth component of the transferred momentum of the exchanged pion exceeds the pion mass. This leads to an imaginary part in the OPE potential. If a pole is obtained in this system, it would correspond to an energy with an imaginary part, which can be interpreted as its half-width. In the current study, we encounter this situation when examining the OPE potential in the $(D\bar{D}^*+D^{*}\bar{D})/\sqrt{2}$ system with $1^+(1^{+-})$.

When considering the process $D\bar{D}^*\rightarrow D^* \bar{D}$, one can get the OPE potential as follows

$$\begin{aligned} V_\pi \propto \frac{g^2}{2f_\pi ^2}\frac{(\varvec{\epsilon }^*\cdot \varvec{q})(\varvec{\epsilon }\cdot \varvec{q})}{\varvec{q}^2+m_\pi ^2-q_0^2}, \end{aligned}$$

(8)

where q represents the transferred momentum of the pion, and $q_0$ is its zeroth component. Since $q_0 \approx m_{D^*} - m_{D} > m_\pi$, the poles of the OPE potential are located on the real transferred momentum axis. However, when performing the integral along the real $p'$ axis in Eq. (4), we encounter a numerical divergence. Fortunately, the CSM can resolve this divergence issue without altering the analyticity of the OPE potential. Through a complex scaling operation, the pole of the OPE potential is rotated away from the real momentum axis in the momentum plane. As a result, the integral along the real momentum axis bypasses the pole, effectively avoiding divergence.

Fig. 1

The eigenvalue distribution of the complex scaled Schrödinger equation for the two-body systems

As shown in Fig. 2, we denote the total energy of the $D\bar{D}^*/D^*\bar{D}$ system as E and assume the D meson to be on-shell. In this case, the expression for $q_0$ is given by $q_0=E-\sqrt{m_D^2+\varvec{p}^2}-\sqrt{m_{\bar{D}}^2+\varvec{p'}^2}$. With the heavy quark approximation, we neglect the kinetic energy contribution to $q_0$ and introduce an energy shift $E\rightarrow E+m_D+m_{D^*}$. As a result, we obtain $q_0=E+m_{D^*}-m_D$.

Fig. 2

Three-body intermediate diagram in the process $D\bar{D}^{*}\rightarrow D^*\bar{D}$. The total energy of the $D\bar{D}^{*}/D^*\bar{D}$ is E, and the mesons which are cut by the red dashed line are on shell

In other processes, the three-body effect vanishes, and we should consider the different values of $q_0$ in the OPE potential. The specific values of $q_0$ for each case are summarized in Table 2.

3 Lagrangians and potentials

For the interaction of two heavy mesons, the chiral effective Lagrangians are constructed based on the heavy quark symmetry and SU(3)-flavor symmetry. The explicit expressions are given by

$$\begin{aligned} \mathcal {L}= & {} -i\langle H^{(Q)}_bv\cdot ( \delta _{ba}\partial +i\Gamma _{ba})\bar{H}^{(Q)}_a\rangle +g\langle H^{(Q)}_b\mathbb {A}_{ba}^\mu \gamma _\mu \gamma _5\bar{H}_a^{(Q)}\rangle \nonumber \\{} & {} -i\langle \bar{\tilde{H}}_b^{(\bar{Q})}v\cdot ( \delta _{ba}\partial +i\Gamma _{ba})\tilde{H}_a^{(\bar{Q})}\rangle +g\langle \bar{\tilde{H}}_b^{(\bar{Q})}\mathbb {A}_{ba}^\mu \gamma _\mu \gamma _5\tilde{H}_a^{(\bar{Q})}\rangle \end{aligned}$$

(9)

where $H^{(Q)}$ is defined as

(10)

And $\bar{H}_a^{(Q)}$, $\tilde{H}^{(\bar{Q})}$ and $\bar{\tilde{H}}_a^{(\bar{Q})}$ are

(11)

respectively, with $P_a^{(*)}=\left( D^{(*)0},D^{(*)+},D_s^{(*)+}\right)$ and $\tilde{P}_a^{(*)}\!=\left( D^{(*)-},\bar{D}^{(*)0},\bar{D}_s^{(*)-}\right)$.

Table 2 The $q_0$ is the zeroth component of the transferred momentum. E is the total energy relative to the corresponding threshold. The other cases not listed all give $q_0=0$

The light meson concerned parts are given that

$$\begin{aligned} \mathbb {A}_\mu= & {} \frac{i}{2} [\xi ^\dagger (\partial _\mu \xi )+(\partial _\mu \xi )\xi ^\dagger ],\quad \Gamma _\mu =\frac{i}{2} [\xi ^\dagger (\partial _\mu \xi )-(\partial _\mu \xi )\xi ^\dagger ],\nonumber \\ \xi= & {} \text {exp}[\frac{i\mathcal {M}}{f_\pi }]\quad \text {and} \end{aligned}$$

(12)

$$\begin{aligned} \mathcal {M}= & {} \begin{pmatrix} \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{} \pi ^+ &{} K^+ \\ \pi ^- &{} \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{} K^0 \\ K^- &{} \bar{K}^0 &{} -\frac{2}{\sqrt{6}}\eta \end{pmatrix}, \end{aligned}$$

(13)

where the pion decay constant $f_\pi$ is equal to 132 MeV. The coupling constant associated with the $\pi$ exchange is $g=0.59$ [74].

The corresponding OPE potential in momentum space can be expressed as follows

$$\begin{aligned} V^{{D\bar{D}^*}/{B\bar{B}^*}}= & {} -\frac{g^2}{2f_\pi ^2} \frac{(\varvec{\epsilon }^*\cdot \varvec{q})(\varvec{\epsilon } \cdot \varvec{q})}{\varvec{q}^2+m_\pi ^2-q_0^2},\nonumber \\ V^{D^*\bar{D}^*/B^*\bar{B}^*}= & {} -\frac{g^2}{2f_\pi ^2} \frac{(\varvec{\mathcal {T}}_1\cdot \varvec{q}) (\varvec{\mathcal {T}}_2\cdot \varvec{q})}{\varvec{q}^2+m_\pi ^2-q_0^2}, \end{aligned}$$

(14)

where $\varvec{\mathcal {T}}_1$ and $\varvec{\mathcal {T}}_2$ represent the spin 1 operator with the forms $\varvec{\mathcal {T}}_1=-i\varvec{\epsilon }_3^\dagger \times \varvec{\epsilon }_1$ and $\varvec{\mathcal {T}}_2=-i\varvec{\epsilon }_4^\dagger \times \varvec{\epsilon }_2$. Since we focus solely on the S-wave interactions, we can replace the above spin-dependent operator with $(\varvec{\epsilon }^*\cdot \varvec{q})(\varvec{\epsilon }\cdot \varvec{q})\rightarrow \frac{1}{3}\varvec{q}^2$ and $(\varvec{T}_1\cdot \varvec{q})(\varvec{T}_2\cdot \varvec{q})\rightarrow \frac{1}{3}\varvec{q}^2\varvec{T}_1\cdot \varvec{T}_2$.

Regarding the contact term interaction, we adopt the form derived in Ref. [27]. Upon performing the partial wave decomposition, one can obtain the S-wave contact potential as

$$\begin{aligned} \left[ V_{ct}\right] _{l,l'}= & {} \tilde{C}_s+C_s(p^2+p'^2), \end{aligned}$$

where $\tilde{C}_s$ and $C_s$ represent the partial wave low energy constants (LECs). We restrict our analysis to the lowest-order interaction and do not consider higher-order effects, such as the one-loop contribution.

To obtain the effective potentials, we introduce a Gaussian regulator to the potentials as follows

$$\begin{aligned} V_{l,l'}=V_{l,l'}\exp \left( -\frac{p'^2}{\Lambda ^2}-\frac{p^2}{\Lambda ^2}\right) , \end{aligned}$$

(15)

where $\Lambda$ is the cutoff parameter. The parameters $\Lambda$, $\tilde{C}_s$ and $C_s$ can be adjusted while keeping the coupling constants in the OPE potential fixed.

4 Numerical results

During the numerical calculation process, we discretize the Schrödinger Eq. (4) in momentum space using the Gaussian quadrature approach. We approximate the integral over the potential as a weighted sum over N integration points for $p=k_j$ ($j=1,N$):

$$\begin{aligned}{} & {} \int _0^{\infty }dp'p'^{2}V(p,p')\phi (p')\simeq \sum _{j=1}^{N}\omega _j p_j^2V(p,p_j)\phi (p_j), \nonumber \\{} & {} \frac{p^2}{2m}\phi (p)+\frac{1}{(2\pi )^3}\sum _{j=1}^{N}\omega _j p_j^2V(p,p_j)\phi (p_j)=E\phi (p), \nonumber \\ \end{aligned}$$

(16)

where $p_j$ and $\omega _j$ represent the Gaussian quadrature points and weights, respectively. Furthermore, for clarity, we will omit the orbital angular momentum subscript from this point onward. In Eq. (16), we have N unknowns $\phi (k_j)$ and an unknown $\phi (k)$. To avoid the need to determine the entire function $\phi (k)$, we restrict the solution to the same values of $k_i$ used to approximate the integral. This lead to N coupled linear equations:

$$\begin{aligned}{} & {} \frac{p_i^2}{2m}\phi (p_i)+\frac{1}{(2\pi )^3}\sum _{j=1}^{N}\omega _j p_j^2V(p_i,p_j)\phi (p_j)=E\phi (p_i). \nonumber \\ \end{aligned}$$

(17)

Therefore, the Schrödinger equation can be expressed in matrix form as

$$\begin{aligned}{} & {} [H][\phi ]=E[\phi ], \end{aligned}$$

(18)

with explicit matrices form

$$\begin{aligned}{} & {} \begin{pmatrix} \frac{p_1^2}{2m}+\frac{1}{(2\pi )^3}\omega _1 p_1^2V(p_1,p_1) &{} \frac{1}{(2\pi )^3}\omega _2 p_2^2V(p_1,p_2) &{} \cdots &{} \frac{1}{(2\pi )^3}\omega _N p_N^2V(p_1,p_N) \\ \frac{1}{(2\pi )^3}\omega _1 p_1^2V(p_2,p_1) &{} \frac{p_2^2}{2m}+\frac{1}{(2\pi )^3}\omega _2 p_2^2V(p_2,p_2) &{} \cdots &{} \\ \vdots &{} &{} &{}\\ \frac{1}{(2\pi )^3}\omega _1 p_1^2V(p_N,p_1)&{}\cdots &{}\cdots &{}\frac{p_N^2}{2m}+\frac{1}{(2\pi )^3}\omega _N p_N^2V(p_N,p_N) \end{pmatrix} \begin{pmatrix} \phi (p_1)\\ \phi (p_2)\\ \vdots \\ \phi (p_N)\\ \end{pmatrix} = E\begin{pmatrix} \phi (p_1)\\ \phi (p_2)\\ \vdots \\ \phi (p_N)\\ \end{pmatrix},\nonumber \\ \end{aligned}$$

(19)

where the wave function $\phi (k)$ on the grid can be represented as the $N\times 1$ vector $[\phi (p_i)]=\begin{pmatrix} \phi (p_1)&{}\phi (p_2)&{}\cdots &{}\phi (p_N)\\ \end{pmatrix}^T$. Then, we can effectively solve Eq. (4). To find solutions for the complex Schrödinger Eq. (5), we can simply make the substitutions $p_i\rightarrow p_i e^{-i\theta }$, $\omega _i\rightarrow \omega _i e^{-i\theta }$ and $\phi (p_i)\rightarrow \tilde{\phi }(p_i)$.

4.1 The $Z_b$ and $Z_c$ system

Fig. 3

The wave functions $\tilde{\phi }(p)$ of the $Z_c$ state with the $I^G(J^{PC})=1^+(1^{+-})$. The rotation angle $\theta =35^\circ$ and the parameters $\Lambda =0.300$ GeV, $\tilde{C}_{s}=2.86\times 10^2$ GeV$^{-2}$ and $C_{s}=-59.9\times 10^2$ GeV$^{-4}$. The two diagrams correspond to system a $\left[ D\bar{D}^{*}+D^*\bar{D}\right] /\sqrt{2}$ and b $D^*\bar{D}^*$ respectively

In this subsection, we investigate the exotic hadrons $Z_b$ and $Z_c$ using ChEFT. A similar study has been performed in Ref. [27], where the $Z_c(3900)$ and $Z_c(4020)$ ($Z_b(10510)$ and $Z_b(10650)$) are interpreted as $\left[ D\bar{D}^{*}+D^*\bar{D}\right] /\sqrt{2}$ and $D^*\bar{D}^*$ ($\left[ B\bar{B}^{*}+B^*\bar{B}\right] /\sqrt{2}$ and $B^*\bar{B}^*$) molecule with $J^P=1^+(1^{+-})$, respectively. However, in our present work using CSM,, we neglect the $S-D$ mixing effect and solely focus on the S-wave channel in this section. And in the following Sect. 4.3, we provide a brief discussion on the case including the D-wave constituents.

In our analysis, as shown in Table 3, we perform a fit of the LECs for the two $Z_b$ and $Z_c$ states. Comparing our results with those in Ref. [27], we find a similar cutoff value $\Lambda$ within a reasonable range. However, the LECs $\tilde{C}_s$ and $C_s$ exhibit some variations, which could be attributed to our omissions of the D-wave channel and the higher order contribution. Additionally, we calculate the root-mean-square (RMS) radii, as shown in Table 3, and find that the sizes of the $Z_b$ states are smaller than those of the $Z_c$ states. Interestingly, the sizes of the two $Z_b$ ($Z_c$) states are nearly identical. Moreover, the corresponding wave functions, as depicted in Fig. 3, exhibit a striking resemblance. This phenomenon is reasonable since our analysis in this work does not account for the higher-order spin-dependent correction terms. The satisfaction of the heavy quark spin symmetry justifies the similarities in the energy, decay width, size and wave function observed in the $Z_b$ and $Z_c$ states.

As discussed in Ref. [69], the $DD^*/D\bar{D}^*$ system considered as the $T_{cc}^{+}/X(3872)$ state can decay into the three-body open-charm channels $DD\pi /D\bar{D}\pi$. In the case of the isovector $D\bar{D}^*$ system, it is also necessary to consider the influence of the three-body decay. The numerical results in the scheme we adopt, shown in Table 3 (row ”Adopt”), are very close to the results under the instantaneous approximation $q_0=0$. This implies that the mass, width and size have minimal changes. The reason why the choice of $q_0$ matters for the $T_{cc}^{+}$ system but not for the $Z_c$ system can be understood as follows. The mass of the $T_{cc}^{+}$ state is below the threshold of the $DD^*$ system, making the two-body decay process kinetically forbidden. Therefore, the three-body decay becomes the dominant decay modes, and the value of $q_0$, which partly reflects the three-body decay width, becomes important. On the other hand, the $Z_c(3900)^+$ state is clearly above the threshold of the $D\bar{D}^*$ system, allowing for the two-body decay process. Since the contribution from the three-body decay is significantly smaller (Table 3 row “Inst”) in this case, the choice of $q_0$ does not significantly alter the results. For $DD^*$ system, we also consider the case without OPE, as shown in Table 3 (row “CT”). We find the influence of OPE potential on the $Z_{c}$ system is not significant.

Table 3 The extracted poles for all states are listed with the quantum numbers $I^G(J^{PC})=1^+(1^{+-})$. The fitted parameter for the $B^*\bar{B}^{(*)}$ system are $\Lambda =0.510^{+0.027}_{-0.041}$ GeV, $\tilde{C}_{s}=0.48^{+0.15}_{-0.13}\times 10^2$ GeV$^{-2}$ and $C_{s}=-5.4^{+0.63}_{-0.65}\times 10^2$ GeV$^{-4}$. The fitted parameter for the $D^*\bar{D}^{(*)}$ system are $\Lambda =0.300^{+0.012}_{-0.013}$ GeV, $\tilde{C}_{s}=2.86^{+0.21}_{-0.22}\times 10^2$ GeV$^{-2}$ and $C_{s}=-59.9^{+2.8}_{-3.1}\times 10^2$ GeV$^{-4}$. The RMS is the root-mean-square radius in the CSM, which has been discussed in the Ref. [75]. Its real part is interpreted as an expectation value, and the imaginary part corresponds to a measure of the uncertainty in observation. The data of row Adopt are the results we actually adopt, the $q_0$ herein is from Table 2. The data of row “Inst” are from the instantaneous approximation $q_0=0$. The data of row “CT” means results without OPE

Table 4 The poles are all listed with the number $I(J^{P})=1/2(1^{+})$. The fitted parameter for the $D_s^*\bar{D}^{(*)}$ system are $\Lambda =0.192^{+0.012}_{-0.013}$ GeV, $\tilde{C}_{s}=6.8^{+2.8}_{-2.7}\times 10^2$ GeV$^{-2}$ and $C_{s}=-186.9^{+50.4}_{-64.4}\times 10^2$ GeV$^{-4}$. The RMS is the root-mean-square radius in the CSM, which has been discussed in the Ref. [75]. Its real part is interpreted as an expectation value, and the imaginary part corresponds to a measure of the uncertainty in observation. The $\text {Res}|S(E)|\big |_{E=E_R}$ is the residue of the S or T matrix, which has been discussed in the Ref. [76]. The states labeled as “1*” and “2*” correspond to the input states. The symbol “-” indicates that the width of the $Z_{cs}(4123)$ state has not been confirmed by experiment yet

4.2 The $Z_{cs}$ system

Fig. 4

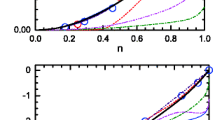
The eigenvalue distribution of the $Z_{cs}$ with the $I(J^P)=1/2(1^+)$. The parameters $\Lambda =0.192$ GeV, $\tilde{C}_{s}=6.8\times 10^2$ GeV$^{-2}$ and $C_{s}=-186.9\times 10^2$ GeV$^{-4}$.The orange (green) points (square points) and lines correspond to the complex rotation angle $\theta =35^\circ$ ($40^\circ$). The two diagrams correspond to system: a $\left[ D_s\bar{D}^{*}+D_s^*\bar{D}\right] /\sqrt{2}$, b $D_s^*\bar{D}^{*}$

In Refs. [34, 38], the $Z_{cs}(3985)$ and $Z_{cs}(4000)$ states are discussed as the SU(3)-flavor partners of $Z_c(3900)$, with their neutral nonstrange members having opposite C parity. The authors suggest that the $Z_{cs}(4000)/Z_{cs}(3985)$ state can be described as a pure molecular state composed of $(|D_s\bar{D}^*\rangle +/-|D_s^*\bar{D}\rangle )/\sqrt{2}$. Furthermore, they also predicted the existence of a $D_s^*\bar{D}^*$ molecular state, which is potentially supported by the recent work of the BESIII collaboration [66]. These studies provide interesting insights into the nature and composition of the $Z_{cs}$ states under the molecule picture.

However, an issue that remains unresolved is the significant difference in the widths between the $Z_{cs}(3985)$ and the $Z_{cs}(4000)$. To address this difference, we propose an alternative explanation where these two states are considered as two resonances associated with the same system, namely $(D_{s}\bar{D}^{*}+D_{s}^{*}\bar{D})/\sqrt{2}$. According to our proposal, the $Z_{cs}(3985)$ corresponds to the resonance with a narrower width, while the $Z_{cs}(4000)$ corresponds to the resonance with a broader width, as illustrated in Fig. 4. This interpretation differs from the prevailing viewpoints in literature.

In the previous Sect. 4.1, we found that the $\left[ D\bar{D}^{*}+D^*\bar{D}\right]$$/\sqrt{2}$ and $D^*\bar{D}^*$ systems, associated with the two $Z_c$ states, exhibit similar outcomes due to the heavy quark spin symmetry. Thus, it is feasible to employ the same parameters for them. Following this scheme, we use the same parameters for both the $(D_{s}\bar{D}^{*}+D_{s}^{*}\bar{D})/\sqrt{2}$ and $D_{s}^*\bar{D}^{*}$ systems. By adopting the available experimental data of $Z_{cs}(3985)$ and $Z_{cs}(4000)$, we determine the central values and errors of $\Lambda$, $\tilde{C}{s}$ and $C_s$, and perform calculations for the $D_{s}^*\bar{D}^{*}$ system. The corresponding parameter values, masses, widths and sizes can be found in Table 4.

Besides, we also give the residue of S or T matrix in the following form:

$$\begin{aligned}{} & {} \text {Res}|S_{j}(E)|\big |_{E=E_{R}}=\big |\frac{\mu _j k_{R,j}}{4\pi ^2}\langle k_{R,j}|\hat{V}|\phi \rangle ^2\big |. \end{aligned}$$

(20)

Here, the $E_R$ and $k_{R,j}$ is the energy and momentum of j-th channel. One could get the concrete discussion in our another work [76]. In brief, we could obtain the coupling between the pole and the j-channel with this residue formula. For the $D_s\bar{D}^*/D_s^*\bar{D}$ system, we calculate the residues of the two poles (corresponding to the $Z_{cs}(3985)$ and $Z_{cs}(4000)$), and find that their ratio, $\frac{\text {Res}|S|\big |_{Z_{cs}(4000)}}{\text {Res}|S|\big |_{Z_{cs}(3985)}}$, is approximately 2. As a result, these two poles, characterized by significantly different widths, exhibit comparable couplings with the $D_s\bar{D}^*/D_s^*\bar{D}$ system.

In the framework of ChEFT, it is generally expected that the cutoff region should exceed the pion mass $m_\pi$ while not significantly exceeding 0.5 GeV, as the higher-mass mesons ($\sigma$, $\rho$, $\omega$, etc.) are integrated out. Consequently, the $\Lambda$ adopted in this study, $0.3\sim 0.5$ GeV, is reasonable for the $Z_c$ and $Z_b$ cases. However, in the case of $Z_{cs}$, the OPE and one-kaon-exchange are both forbidden for the quark flavor in tree level. By the way, when dealing with the double-charm tetraquark $D_{s}D^*/D_{s}^*$, the one-kaon-exchange is allowed. As a result, the contact term becomes the only interaction that needs to be considered. This can be viewed as effectively integrating out the pion and kaon fields. Therefore, we adopt a smaller value of $\Lambda \approx 0.2$ GeV for the $Z_{cs}$ cases.

According to the results in Table 4, the newly reported $Z_{cs}(4123)$ by BESIII collaboration [66] could correspond to the narrower $D_{s}^*\bar{D}^{*}$ state, although the experimental width is yet to be confirmed. Its estimated mass is around 4125.2 MeV and width is approximately 13.2 MeV. Furthermore, the $Z_{cs}(4220)$ is anticipated to correspond to a broader resonance with its central values of the mass and width at 4152.7 MeV and 115.0 MeV. Indeed, the mass and width of $Z_{cs}(4220)$ both fall within the two-standard-deviation region of the experimental data. As shown in Fig. 5 and Table 4, the narrow (or broader) resonances exhibit remarkably similar wave functions and sizes.

Fig. 5

The wave functions $\tilde{\phi }(p)$ of the $Z_cs$ state with the $I(J^P)=1/2(1^+)$. The rotation angle $\theta =40^\circ$ and the parameters $\Lambda =0.192$ GeV, $\tilde{C}_{s}=6.8\times 10^2$ GeV$^{-2}$ and $C_{s}=-186.9\times 10^2$ GeV$^{-4}$. The four diagrams correspond to: a pole 1 of $\left[ D_s\bar{D}^{*}+D_s^*\bar{D}\right] /\sqrt{2}$ system, b pole 2 of $\left[ D_s\bar{D}^{*}+D_s^*\bar{D}\right] /\sqrt{2}$ system, c pole 1 of $D_s^*\bar{D}^{*}$ system, d pole 2 of $D_s^*\bar{D}^{*}$ system

Fig. 6

The poles for the Gaussian type potential with the $\Lambda =\mu =1$ GeV

Furthermore, one might be curious about the underlying mechanism that results in two resonance states with nearly identical masses but significantly different widths within the same system. Herein, we can provide a semi-quantitative analysis. When we consider a separable potential, $V(p',p) = C \times e^{\left( -\frac{p'^2}{\Lambda ^2}-\frac{p^2}{\Lambda ^2}\right) }$, we can obtain its analytic solution by solving the Lippmann-Schwinger Equation. The simplified resonance solutions satisfy the form below:

$$\begin{aligned} -\frac{C}{2\sqrt{2}}\left[ \sqrt{\pi }\!+\!2\pi \sqrt{-\mu E}e^{-4\mu E/\Lambda ^2}\text {erfc}\left( 2\frac{\sqrt{-\mu E}}{\Lambda }\right) \right] \!=\!1.\nonumber \\ \end{aligned}$$

(21)

Here, $\Lambda$ is the cutoff parameter, $\mu$ is the reduced mass, and E is the energy of the resonant pole. For simplicity, we take $\Lambda = \mu = 1$ GeV, and $C = -2000$ GeV$^{-2}$. This leads to a series of poles, as shown in Fig.6. In our work, we employ a Gaussian-type form factor, which may yield similar behavior. As a result, we may get additional poles with large width. However, there is also a limitation. When the mass difference between the pole and threshold is exceeds the typical order of ChEFT like tens MeV, its results may become invalid. Therefore, we only take into account the first two poles.

Table 5 The fitted parameters for the $B^*\bar{B}^{(*)}$ system are $\Lambda =0.530$ GeV, $\tilde{C}_{s}=0.6\times 10^2$ GeV$^{-2}$, $C_{s}=-5.4\times 10^2$ GeV$^{-4}$ and $C_{sd}=0.6\times 10^2$ GeV$^{-4}$, and for the $D^*\bar{D}^{(*)}$ system are $\Lambda =0.310$ GeV, $\tilde{C}_{s}=3.0\times 10^2$ GeV$^{-2}$, $C_{s}=-56.0\times 10^2$ GeV$^{-4}$ and $C_{sd}=24.0\times 10^2$ GeV$^{-4}$, and for the $D_s^*\bar{D}^{(*)}$ system are $\Lambda =0.192$ GeV, $\tilde{C}_{s}=6.9\times 10^2$ GeV$^{-2}$, $C_{s}=-187.0\times 10^2$ GeV$^{-4}$ and $C_{sd}=0.5\times 10^2$ GeV$^{-4}$. The “RMS” is the root-mean-square radius in the CSM, which has been discussed in the Ref. [75]. Its real part is interpreted as an expectation value, and the imaginary part corresponds to a measure of the uncertainty in observation. The “Prob.” is defined as $\langle \tilde{\psi }_i|\psi _i\rangle =e^{i\theta }\int _{0}^{\infty }\{\psi _i(re^{i\theta })\}^2dr$ is the amplitude corresponding to the i-th channel. $\Gamma _i$ is the partial width ofi-th channel, which has been discussed in the Ref. [76]. The states labeled as “1*” and “2*” correspond to the input states

In the $Z_c$ cases, we select a $\Lambda > rsim 0.3\ \text {GeV}>m_\pi$ for the consideration of OPE contribution. In this reasonable cut off region, the energy difference of two nearby poles is larger than that obtained in the $Z_{cs}$ case. For instance, the second pole in the $DD^*$ system has the energy $3966.6-147.4 i$. The difference between its mass and the $DD^*$ threshold is 90.7 MeV, which exceeds the typical order of ChEFT. Consequently, we tend not consider the additional broader states.

Besides, we make a brief discussion on the dependence of input parameters herein. As shown in Eq. (21), we have observed that the energy difference between nearby poles decreases as the cutoff $\Lambda$ decreases. By observing numerical calculation results, we find that both poles would move approximately towards the origin as the cutoff $\Lambda$ decreases/$\tilde{C}_{s}$ decreases/$C_{s}$ increases. To estimate the sensitivity, one can refer to the fitted parameter errors listed in Table 4.

4.3 The $Z_c$ and $Z_{cs}$ results including D-wave

In our analysis, we will briefly discuss the $Z_b$, $Z_c$ and $Z_{cs}$ systems with the inclusion of the D-wave channel, represented as $\left[ B\bar{B}^{*}+B^*\bar{B}\right] /\sqrt{2}(^3D_1)$, $\left[ D\bar{D}^{*}+D^*\bar{D}\right] /\sqrt{2}(^3D_1)$ and $\left[ D_s\bar{D}^{*}+D_s^*\bar{D}\right] /\sqrt{2}(^3D_1)$, respectively. It’s worth noting that the behavior of the $B^*\bar{B}^{*}$, $D^*\bar{D}^{*}$ and $D_s^*\bar{D}^{*}$ cases closely resembles that of the $\left[ B\bar{B}^{*}+B^*\bar{B}\right] /\sqrt{2}(^3D_1)$, $\left[ D\bar{D}^{*}+D^*\bar{D}\right] /\sqrt{2}(^3D_1)$ and $\left[ D_s\bar{D}^{*}+D_s^*\bar{D}\right] /\sqrt{2}(^3D_1)$ cases. For the sake of simplicity, we will not explore them further.

As indicated in Table 5, the influence of the D-wave channel on all measurements within the $Z_{cs}$ system is minimal, approaching negligible levels. In the case of the $Z_{c}$ and $Z_b$ systems, the D-wave makes a small contribution, while the S-wave channel continues to dominate the system. When we compare these results with those presented in Table 3, it becomes evident that the inclusion of the D-wave does not alter our conclusions. Hence, it is reasonable to focus solely on the S-wave for the Z states within our framework.

5 Summary

In this study, we employ the ChEFT to investigate the hidden-heavy tetraquark states with $I^G(J^{PC})=1^+(1^{+-})$ and the hidden-charm states with a strange quark with $I(J^{P})=1/2(1^{+})$ in the molecule picture. The couplings between the S-wave open-heavy channel and other channels, such as the D-wave channel, the S-wave channel with different constituents, and the hidden-heavy channels, are expected to be small. Therefore, we focus on the S-wave open-heavy single channels: $\left[ D\bar{D}^{*}+D^*\bar{D}\right] /\sqrt{2}$, $D^*\bar{D}^*$, $\left[ B\bar{B}^{*}+B^*\bar{B}\right] /\sqrt{2}$, $B^*\bar{B}^*$, $(D_{s}\bar{D}^{*}+D_{s}^{*}\bar{D})/\sqrt{2}$ and $D^*_s\bar{D}^*$.

We employ the effective Lagrangians based on heavy quark symmetry and chiral symmetry, considering both contact and OPE diagrams. To investigate the possible resonances, we adopt the CSM to consistently analyze the bound states and resonances. In contrast to our previous work [69, 77], we perform the momentum space Schrödinger equation and discretize it using the Gaussian quadrature approach.

In our investigation of the $Z_b$ system, we fit experimental data to extract resonance parameters within the molecule picture. With $\Lambda =0.510$ GeV, $\tilde{C}_s=0.48\times 10^2$ GeV$^{-2}$ and $C_s=-5.4\times 10^2$ GeV$^{-4}$, we obtain the mass and width values of 10606.9 MeV and 15.0 MeV for the $\left[ B\bar{B}^{*}+B^*\bar{B}\right] /\sqrt{2}$ resonance, while 10652.2 MeV and 14.8 MeV for the $B^*\bar{B}^*$ resonance. The RMS radii for these two resonances are both approximately $0.70-0.15i$ fm. Similarly, we perform calculations for the $Z_c$ system in the S-wave $1^+(1^{+-})$ channels: $\left[ D\bar{D}^{*}+D^*\bar{D}\right] /\sqrt{2}$ and $D^*\bar{D}^*$. Taking $\Lambda =0.300$ GeV, $\tilde{C}_s=2.86\times 10^2$ GeV$^{-2}$ and $C_s=-59.9\times 10^2$ GeV$^{-4}$, we obtain the mass and width values of 3884.3 MeV and 26.0 MeV for the former resonance, while 4025.8 MeV and 24.0 MeV for the latter resonance. The RMS radii for both resonances are around $1.20+0.13i$ fm. For the isovector $\left[ D\bar{D}^{*}+D^*\bar{D}\right] /\sqrt{2}$ system, we also consider the influence of the three-body decay. However, the numerical results under the instantaneous approximation with $q_0=0$ (as shown in the “Inst” row of Table 3) are very close to the results of the “Adopt” row, indicating the minimal changes in the mass, width and size. Thus, we conclude that the 2-body decay process dominates the width of this resonance.

We consider the hidden-charm tetraquark states with a strange quark and propose that the $Z_{cs}(3985)$ and $Z_{cs}(4000)$ resonances correspond to the same channel $(D_{s}\bar{D}^{*}+D_{s}^{*}\bar{D})/\sqrt{2}$. Taking the data of $Z_{cs}(3985)$ and $Z_{cs}(4000)$ as input, we extract the central values and errors of the parameters $\Lambda$, $\tilde{C}_s$ and $C_s$. With $\Lambda =0.192$ GeV, $\tilde{C}_s=6.8\times 10^2$ GeV$^{-2}$ and $C_s=-186.9\times 10^2$ GeV$^{-4}$, we obtain the mass and width values of 3982.4 MeV and 14.1 MeV for the $Z_{cs}(3985)$, while 4010.7 MeV and 119.6 MeV for the $Z_{cs}(4000)$. The corresponding RMS radii are $1.89+0.43i$ fm and $1.78+1.31i$ fm, respectively. For the $D^*_s\bar{D}^*$ system, we adopt the same parameters based on the heavy quark spin symmetry and also find two resonances. The narrower resonance has a mass of 4125.2 MeV and a width of 13.2 MeV, which nicely matches the observed $Z_{cs}(4123)$ reported by the BESIII collaboration [66]. Hence, we interpret it as the $Z_{cs}(4123)$, although the experimental width is yet to be confirmed. On the other hand, the broader resonance has a mass of 4152.7 MeV and a width of 115.0 MeV. We interpret it as the $Z_{cs}(4220)$ observed by the LHCb collaboration [32], as its mass and width fall within the two-standard-deviation region of the experimental data.

We also we provide a brief discussion on the $Z_b$, $Z_c$ and $Z_{cs}$ cases including the D-wave constituents. For the three systems, the influence of the D-wave channel on all measurements including RMS, constituents and partial width is minimal. It becomes evident that the inclusion of the D-wave does not alter our conclusions. Hence, it is reasonable to focus solely on the S-wave for the Z states within our framework.

In summary, we apply the ChEFT to investigate the $Z_b$, $Z_c$ and $Z_{cs}$ states. Our analysis suggests that the $Z_b(10610)$, $Z_b(10650)$, $Z_c(3900)$ and $Z_c(4020)$ can be interpreted as the molecular states formed by the S-wave $B\bar{B}^*$, $B^*\bar{B}^*$, $D\bar{D}^*$ and $D^*\bar{D}^*$ constituents, respectively. Although the $Z_{cs}(3985)$ and $Z_{cs}(4000)$ states exhibit a significant width difference, these two resonances may originate from the same S-wave channel $(D_{s}\bar{D}^{*}+D_{s}^{*}\bar{D})/\sqrt{2}$. We also find two resonances in the $D_s^*\bar{D}^*$ channel, which can be identified as the $Z_{cs}(4123)$ and $Z_{cs}(4220)$. Our results provide a prediction for the width of the $Z_{cs}(4123)$ that awaits experimental confirmation. Additionally, we offer a precise mass and width range for the $Z_{cs}(4220)$, which can guide future experimental searches for the hidden-charm tetraquarks with a strange quark.