Five-dimensional Yang–Mills black holes in massive gravity’s rainbow

Abstract

In this paper, we will analyze a five-dimensional Yang–Mills black hole solution in massive gravity’s rainbow. We will also investigate the flow of such a solution with scale. Then, we will discuss the scale dependence of the thermodynamics for this black hole. In addition, we study the criticality in the extended phase space by treating the cosmological constant as the thermodynamics pressure of this black hole solution. Moreover, we will use the partition function for this solution to obtain corrections to the thermodynamics of this system and examine their key role in the behavior of corrected solutions.

1 Introduction

It is interesting to couple Yang–Mills theory to to a gravitating system, and study various black hole solutions using such a coupled theory [1, 2]. Here, we will investigate different aspects of a five-dimensional Yang–Mills black hole solution. We will specifically analyze the modification of this solution in the context of gravity’s rainbow.

The Yang–Mills black hole solutions have been motivated by the bosonic part of the low-energy heterotic string action [3, 4]. This topic has been explained by considering the low-energy heterotic string action to leading order, after it has been compactified to four dimensions. This compactified action is then used to obtain a static and spherically symmetric Yang–Mills black hole solution. It has motivated the construction of interesting Yang–Mills black hole solutions [1, 2]. Static spherically symmetric Yang–Mills black hole solution has been studied before, both numerically and analytically, and it was observed that such a solution is unstable under linearized perturbations [5]. The phase transition of Yang–Mills black holes has been studied using entanglement entropy and two-point correlation functions [6, 7]. It is also possible to analyze the black hole solution in five-dimensional gauged supergravity [8]. This model describes a system of NS5-branes wrapped on a three-sphere. A five-dimensional Yang–Mills black hole solution supporting a Meron field has been constructed, and it has been observed that this Yang–Mills gauge field has a non-trivial topological charge [9] . Furthermore, the thermodynamics of this system demonstrates that it enjoys a first-order phase transition. Thus, it is interesting to study Yang–Mills fields in five dimensions.

It is possible for gravitons to become massive in string theory due to scalar fields acquiring a vacuum expectation value [10, 11]. In fact, motivated by string theory, the corrections to a braneworld model (with warped AdS spacetime) from graviton mass have been discussed [12]. So, the gravitons can have a small mass [13,14,15,16], and this gravitons mass is constraint from LIGO collaboration to $m_g<1.2 \times 10^{-22}$ $eV/c^2$ [15, 17]. As it is possible for gravitons to have any mass below this bound, such a small mass would produce an IR correction to general relativity and have important astrophysical consequences. In fact, it has been suggested that such massive gravitons could produce an effective cosmological constant, and cause an accelerated expansion of the universe [18,19,20]. Thus, it is very important to study the modification to general relativity from small graviton mass. It is possible to add a mass term in the form of Fierz-Pauli term to obtain massive gravity [21]. However, due to the vDVZ discontinuity, this theory is not well defined in the zero mass limit [22,23,24].

This problem can be resolved in the Vainshtein mechanism, by using the Stueckelberg trick [25, 26]. This mechanism produces non-linear corrections terms, which in turn produce ghost states [27]. However, these ghost states can be removed in the dRGT gravity [13]. As dRGT gravity is ghost free IR modification to general relativity (without the vDVZ discontinuity), several black hole solutions have been constructed in this theory [28,29,30,31,32,33,34,35,36,37] . It has also been demonstrated that the small graviton mass can produce interesting modifications to the behavior of such black hole solutions. In fact, it has been observed that the thermodynamics of black holes gets non-trivial modifications due to the small graviton mass [38,39,40,41]. Thus, it is interesting to analyze black hole thermodynamics for different black holes using such a small graviton mass. So, in this paper, we will analyze the modifications to a five-dimensional Yang–Mills black hole in massive gravity [42,43,44,45].

It is possible to use extended phase space to analyze an AdS black hole solution [46, 47]. In such an extended phase space the cosmological constant is identified with the thermodynamic pressure of the black hole solution. Furthermore, the thermodynamic volume is the conjugate variable to this thermodynamic pressure. Thus, the thermodynamic volume can be obtained from the cosmological constant of an AdS black hole solution. The Van der Waals like behavior an AdS black hole solution has also been studied using this extended phase space [48]. It is possible to analyze the triplet point for an AdS black hole solution [49,50,51]. In fact, the reentrant phase transition of the AdS black hole has also been studied using this formalism [52,53,54]. Thus, it is interesting to analyze critical behavior for black hole solutions in massive gravity, and new non-trivial phase transition [55, 56].

It may be noted that it is possible to analyze the thermal corrections to black hole solutions [57]. This can be done for an AdS black hole as it is dual to conformal field theory, and so its microstates can be analyzed using a conformal field theory [58]. Thus, using the partition function for such microstates, it would be possible to analyze the corrections to the thermodynamics of black holes. The leading order correction to the entropy of black holes is a logarithmic correction, and it is possible to analyze the effects of this correction on various other thermodynamic quantities as thermal fluctuations [59, 60]. It has been argued that these thermal fluctuations can have important consequences for the stability of black hole solutions [61, 62]. As the black hole evaporates due to Hawking radiation, these corrections cannot be neglected. Thus, it is important to analyze the effects of such corrections for Yang–Mills black holes. It may be noted that these thermal fluctuations in the thermodynamics of a black hole can be related to quantum fluctuations using the Jacobson formalism [63, 64].

As string theory can be viewed as a two-dimensional conformal field theory. The target space metric can be regarded as a matrix of coupling constants, and these would flow due to the renormalization group flow [65, 66]. Thus, the target space geometry would flow with scale, and this flow would depend on the energy of the probe. This consideration has motivated gravity’s rainbow, where the spacetime geometry depends on the energy of the probe [67,68,69,70]. It is known that the energy-dependence of such geometry can produce important modifications to the thermodynamics of black holes [71, 72]. In fact, it has been observed that such an energy-dependence can have important consequences for the detection of mini black holes at the LHC [73]. We will use such an energy-dependent metric of gravity’s rainbow for analyzing these Yang–Mills black hole solutions, as such solutions can be motivated from the bosonic part of the low-energy heterotic string action [3, 4]. In this formalism, the geometry of the Yang–Mills black hole depends on the energy of the probe. As the particle emitted in the Hawking radiation can act as a probe for the geometry of a black hole, it is this energy that deforms the geometry of Yang–Mills black holes. So, in this paper, we will analyze the scale dependence of the geometry of the Yang–Mills black hole in massive gravity using different rainbow functions.

The paper is organized as follows. In the next section, we review Yang–Mills black hole solution in massive gravity together with horizon structure analysis. In section 3, we study the thermodynamics of the three separated rainbow models. The criticality in the extended phase space is discussed in section 4. Then, in section 5 we consider the effect of thermal fluctuations and study corrected thermodynamics. Finally, in section 6 we give the conclusion.

2 Yang–Mills black hole

In this section, we will analyze the Yang–Mills black hole solution in massive gravity, and its flow with scale. The action of five-dimensional massive gravity with negative cosmological constant coupled to Yang–Mills theory can be written as [42,43,44,45],

$$\begin{aligned} S= & {} \int d^{5}x\sqrt{-g}\Big ( R-2\Lambda -F_{\mu \nu }^{(a)}F^{(a) \mu \nu }\\&\qquad +m^{2}\sum c_{i}U_{i}\left( g,f\right) \Big ), \end{aligned}$$

where R is the Ricci scalar, (a) is the Lie algebra index, m is the mass term of massive gravity, $\Lambda =-\frac{6}{l^{2}}$ is the cosmological constant, (l denotes the AdS radius) and $F_{\mu \nu }^{\left( a\right) }$ is the $SO\left( 5,1\right)$. This Yang–Mills gauge field tensor is given by

$$\begin{aligned} F_{\mu \nu }^{\left( a\right) }=\partial _{\mu }A_{\nu }^{\left( a\right) }-\partial _{\nu }A_{\mu }^{\left( a\right) }+\frac{1}{2e}f_{\left( b\right) \left( c\right) }^{\left( a\right) }A_{\mu }^{\left( b\right) }A_{\nu }^{\left( c\right) }, \end{aligned}$$

where e is coupling constant of the Yang–Mills theory. Also, $c_{i}$ are constants and $U_{i}\left( g,f\right)$ are symmetric polynomials of the eigenvalues of the following $5\times 5$ matrix [74, 75],

$$\begin{aligned} K_{\nu }^{\mu }=\sqrt{g^{\mu \alpha }f_{\alpha \nu }}, \end{aligned}$$

(2.1)

where $f_{\alpha \nu }$ can be expressed as $f_{\mu \nu }=dia\left( 0,0, \frac{c_{0}^{2}h_{ij}}{g^{2}\left( \varepsilon \right) }\right)$. Here we have introduced $f(\varepsilon )$ and $g(\varepsilon )$ as the rainbow functions, which depend on the relative energy $\varepsilon =\frac{E}{E_{p}}$ , where E is the energy of the particle emitted in the Hawking radiation, and $E_{p}$ is Planck energy [67,68,69,70]. This is because string theory is a two-dimensional conformal field theory, with the target space metric as a matrix of coupling constants for that conformal field theory. So, this matrix of coupling constants is expected to flow due to the renormalization group flow [65, 66]. This would make the geometry of spacetime depend on the ratio $\mu /\mu _{p}$, where $\mu$ is the scale at which the theory is being probed and $\mu _{p}$ is the Planck scale. Now, this ratio would be proportional to $\varepsilon =\frac{E}{E_{p}}$, and so the geometry of spacetime should be a function of this ratio. So, the renormalization group flow would make the target space geometry depend on the scale at which it is being probed, and this in turn would depend on the energy of the probe. This energy-dependence of the geometry can be analyzed using these rainbow function [67,68,69,70]. In fact, as the Yang–Mills black hole solutions can be motivated from the bosonic part of the low-energy heterotic string action [3, 4], we will use analyze the effect of such a flow of geometry of the Yang–Mills black hole solution. Now the black holes with AdS asymptote in the massive gravity’s rainbow can be described by the following energy-dependent metric

$$\begin{aligned} ds^{2}=-\frac{\psi \left( r\right) }{f^{2}\left( \varepsilon \right) }dt^{2}+ \frac{1}{g^{2}\left( \varepsilon \right) }\left[ \frac{dr^{2}}{\psi \left( r\right) }+r^{2}d\Omega _{k}^{2}\right] , \end{aligned}$$

where $\psi$ is an unknown function which will be determined by field equations, and

$$\begin{aligned} d\Omega _{k}^{2}=\left\{ \begin{array}{@{}ll} d\theta _{1}^{2}+\sin ^{2}\theta _{1}d\theta _{2}^{2}+\sin ^{2}\theta _{1}\sin ^{2}\theta _{2}d\theta _{3}^{2} &{} k=1 \\ d\theta _{1}^{2}+d\theta _{2}^{2}+d\theta _{3}^{2} &{} k=0 \\ d\theta _{1}^{2}+\sinh ^{2}\theta _{1}d\theta _{2}^{2}+\sinh ^{2}\theta _{1}\sin ^{2}\theta _{2}d\theta _{3}^{2} &{} k=-1 \end{array} \right. ,\nonumber \\ \end{aligned}$$

(2.2)

where $k=1$, 0 and $-1$ represent spherical, flat and hyperbolic horizon of possible black holes, respectively. Hereafter, we indicate $\omega _{k}$ as the volume of boundary $t=cte$ and $r=cte$ of the metric. Using $\left[ K \right] =Tra(K)=K_{\mu }^{\mu }$, one can obtain

$$\begin{aligned} U_{1}= & {} \left[ K\right] =\frac{3c_{0}}{r}, \nonumber \\ U_{2}= & {} \left[ K\right] ^{2}-\left[ K^{2}\right] =\frac{6c_{0}^{2}}{r^{2}}, \nonumber \\ U_{3}= & {} \left[ K\right] ^{3}-3\left[ K\right] \left[ K^{2}\right] +2\left[ K^{3}\right] =\frac{6c_{0}^{3}}{r^{3}}, \nonumber \\ U_{4}= & {} \left[ K\right] ^{4}-6\left[ K^{2}\right] \left[ K\right] ^{2}+8 \left[ K^{3}\right] \left[ K\right] \nonumber \\&+3\left[ K^{2}\right] ^{2}-6\left[ K^{4} \right] . \end{aligned}$$

(2.3)

By using the variational principle, one can obtain the following field equations

$$\begin{aligned} R_{\mu \nu }+\left( \Lambda -\frac{R}{2}\right) g_{\mu \nu }-m^{2}\chi _{\mu \nu }= & {} 8\pi T_{\mu \nu }. \end{aligned}$$

(2.4)

$$\begin{aligned} F_{;\nu }^{\left( a\right) \mu \nu }= & {} J^{\left( a\right) \mu }, \end{aligned}$$

(2.5)

where

$$\begin{aligned} T_{\mu \nu }= & {} \frac{1}{4\pi }\gamma _{ab}\left( F_{\mu }^{\left( a\right) \lambda }F_{\nu \lambda }^{\left( b\right) }-\frac{1}{4}F^{\left( a\right) \lambda \sigma }F_{\lambda \sigma }^{\left( b\right) }g_{\mu \nu }\right) , \end{aligned}$$

(2.6)

$$\begin{aligned} J^{\left( a\right) \nu }= & {} \frac{1}{e}f_{\left( b\right) \left( c\right) }^{\left( a\right) }A_{\mu }^{\left( b\right) }F^{\left( c\right) \mu \nu }. \end{aligned}$$

(2.7)

Furthermore, we also have

$$\begin{aligned} \chi _{\mu \nu }= & {} \frac{c_{1}}{2}(U_{1}g_{\mu \nu }-K_{\mu \nu })+\frac{ c_{2}}{2}(U_{2}g_{\mu \nu }-2U_{1}K_{\mu \nu }+2K_{\mu \nu }^{2}) \nonumber \\&+\frac{c_{3}}{2}(U_{3}g_{\mu \nu }-3U_{2}K_{\mu \nu }+6U_{1}K_{\mu \nu }^{2}-6K_{\mu \nu }^{3}) \nonumber \\&+\frac{c_{4}}{2}(U_{4}g_{\mu \nu }-4U_{3}K_{\mu \nu }+12U_{2}K_{\mu \nu }^{2}\nonumber \\&-24U_{1}K_{\mu \nu }^{3}+24K_{\mu \nu }^{4}) \end{aligned}$$

(2.8)

By using the value of the Yang–Mills field $F=\gamma _{ab}F^{\left( a\right) \mu \nu } F_{\mu \nu }^{(b)}$, which is $F=\frac{6e^{2}}{r^{4}}$ in five-dimensions, we can obtain $rr-$component of the field equation as

$$\begin{aligned} R_{11}+\left( \Lambda -\frac{R}{2}\right) g_{11}-m^{2}\chi _{11}=8\pi T_{11} \end{aligned}$$

(2.9)

where

$$\begin{aligned} R_{11}= & {} -\frac{1}{2}\frac{\psi ^{^{\prime \prime }}\left( r\right) }{\psi \left( r\right) }-\frac{3}{2}\frac{\psi ^{^{\prime }}\left( r\right) }{r\psi \left( r\right) }, \\ R= & {} -g^{2}\left( \varepsilon \right) \left( \psi ^{^{\prime \prime }}\left( r\right) +6\frac{\psi ^{^{\prime }}\left( r\right) }{r}+6\frac{\psi \left( r\right) }{r^{2}}-\frac{6k}{r^{2}}\right) , \\ \chi _{11}= & {} \frac{3}{2g^{2}\left( \varepsilon \right) \psi \left( r\right) } \left( \frac{c_{0}c_{1}}{r}+\frac{2c_{0}^{2}c_{2}}{r^{2}}+\frac{ 2c_{0}^{3}c_{3}}{r^{3}}\right) , \\ T_{11}= & {} \frac{-3e^{2}}{8\pi g^{2}\left( \varepsilon \right) \psi \left( r\right) r^{4}}. \end{aligned}$$

Solving the nonzero components of the field equation (such as Eq. (2.9 )), yields

$$\begin{aligned} \psi \left( r\right)= & {} k-\frac{m_{0}}{r^{2}}+\frac{1}{g^{2}\left( \varepsilon \right) r^{2}}\left[ \frac{r^{4}}{l^{2}}-2e^{2}\ln \left( \frac{r}{L}\right) \right. \\&\left. +m^{2}\left( \frac{c_{0}c_{1}}{3}r^{3}+c_{0}^{2}c_{2}r^{2}+2c_{0}^{3}c_{3}r \right) \right] , \end{aligned}$$

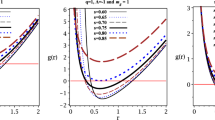
where $m_{0}$ is the mass parameter, which is related to the black hole mass, and L is a constant with length dimension, introduced to obtain dimensionless logarithmic function (which we can set to one without loss of generality). Horizon structure of this solution shows that there is at least one real positive root for $\psi (r)=0$ which is confirmed by the plots of Fig. 1. In Fig. 1a we analyze the effect of mass term in the massive gravity. Effects of other parameters like $c_{0}$, e and $c_{1}$ are illustrated by plots of Fig. 1b–d, respectively. In order to plot, we assume $c_{1}\approx c_{2}\approx c_{3}$, for simplicity. Also we plotted for $k=1$, however the situation of the $k=0$ , and $k=-1$ are the approximately the same as the case of $k=1$. According to different panels of Fig. 1, one find that the value of the event horizon radius depends on the chosen parameters.

Fig. 1

Horizon structure for unit values of the model parameters

It is worth mentioning that for $r=r_{+}$, the metric function vanishes ($\psi \left( r_{+}\right) =0$), and therefore, we can obtain $m_{0}$ as a function of other parameters at $r=r_{+}$

$$\begin{aligned} m_{0}= & {} r_{+}^{2}\left( k+\frac{1}{g^{2}\left( \varepsilon \right) r_{+}^{2}} \left[ \frac{r_{+}^{4}}{l^{2}}-2e^{2}\ln (r_{+})\right. \right. \nonumber \\&\left. \left. +m^{2}\left( \frac{c_{0}c_{1} }{3}r_{+}^{3}+c_{0}^{2}c_{2}r_{+}^{2}+2c_{0}^{3}c_{3}r_{+}\right) \right] \right) . \end{aligned}$$

(2.10)

Using the obtained $m_{0}$ in Eq. (2.10), we can rewrite the metric function with the following form

$$\begin{aligned} \psi (r)= & {} \frac{k}{r^{2}}\left( r^{2}-r_{+}^{2}\right) +\frac{1}{ g^{2}\left( \varepsilon \right) r^{2}}\left[ \!\frac{r^{4}-r_{+}^{4}}{l^{2}} -2e^{2}\ln \big (\frac{r}{r_{+}}\big )\!\right] \nonumber \\&+\frac{m^{2}}{g^{2}\left( \varepsilon \right) r^{2}}\left[ \left( \frac{ c_{0}c_{1}}{3}\left( r^{3}-r_{+}^{3}\right) +c_{0}^{2}c_{2}\left( r^{2}-r_{+}^{2}\right) \right. \right. \nonumber \\&\left. \left. +2c_{0}^{3}c_{3}\left( r-r_{+}\right) \right) \right] , \end{aligned}$$

(2.11)

where directly one can find that $\psi (r)$ vanishes at $r=r_{+}$ (term by term). Now, we can analyze the thermodynamics of this black hole solution as its flow with scale.

3 Thermodynamics

In this section, we discuss the scale dependence of the thermodynamics of this Yang–Mills black hole solution given by (2.11). This will be done using the formalism of gravity’s rainbow. So, first of all we will discuss general formalism, and then discuss certain special models, with specific rainbow functions $f(\varepsilon )$ and $g(\varepsilon )$.

3.1 General formalism

In this section, we will review the general formalism for black hole thermodynamics in gravity’s rainbow [71, 72, 76,77,78,79,80]. Now for a black hole the value in the uncertainty of position for a particle emitted in Hawking radiation is equal to the radius of the event horizon [81]. This uncertainty in position can be related to the uncertainty in momentum using the uncertainty principle, $\Delta p \ge 1/\Delta x$, and this in turn can be used to obtain a lower bound on the energy of such particle emitted in Hawking radiation, $E \ge 1/\Delta x$ [82]. So, the energy of the particle is bounded by the radius of the horizon. This dependence of energy on the radius of the horizon has been used to obtain the correction to the black hole temperature in gravity’s rainbow as [71, 72, 76,77,78,79,80]

$$\begin{aligned} T_{H}=\frac{1}{4\pi }\frac{g(\varepsilon ) }{f(\varepsilon ) } \left. \frac{ d\psi (r)}{dr}\right| _{r=r_{+}}. \end{aligned}$$

(3.1)

Thus, we obtain the following temperature for the Yang–Mills black hole

$$\begin{aligned} T_{H}= & {} \frac{1}{4\pi }\left[ \frac{2k}{r_{+}}\frac{g(\varepsilon ) }{ f(\varepsilon ) }+\frac{1}{f(\varepsilon ) g(\varepsilon ) }\left[ \frac{4r_{+} }{l^{2}}-\frac{2e^{2}}{r_{+}^{3}}\right. \right. \nonumber \\&\left. \left. +m^{2}\left( c_{0}c_{1}+2\frac{ c_{0}^{2}c_{2}}{r_{+}}+2\frac{c_{0}^{3}c_{3}}{r_{+}^{2}}\right) \right] \right] . \end{aligned}$$

(3.2)

Also, the entropy per unit volume $\omega _{k}$ is given by

$$\begin{aligned} S=\frac{r_{+}^{3}}{4g^{3}\left( \varepsilon \right) }. \end{aligned}$$

So, the mass term per unit volume $\omega _{k}$ can be obtained from the first law of black hole thermodynamics

$$\begin{aligned} T=\left( \frac{\partial M}{\partial S}\right) . \end{aligned}$$

Therefore, we can write

$$\begin{aligned} M=\int TdS, \end{aligned}$$

Thus, for the Yang–Mills theory, we obtain

$$\begin{aligned} M= & {} \frac{3k}{16\pi f(\varepsilon ) g^{2}\left( \varepsilon \right) } r_{+}^{2} \nonumber \\&+\frac{3}{16\pi f(\varepsilon ) g^{4}\left( \varepsilon \right) }\left[ \frac{r_{+}^{4}}{l^{2}}-2e^{2}\ln \left( r_{+}\right) \right. \nonumber \\&\left. +m^{2}\left( \frac{ c_{0}c_{1}}{3}r_{+}^{3}+c_{0}^{2}c_{2}r_{+}^{2}+2c_{0}^{3}c_{3}r_{+}\right) \right] . \end{aligned}$$

(3.3)

The heat capacity at constant volume can be calculated as

$$\begin{aligned} C=T_{H}\left( \frac{\partial S}{\partial T_{H}}\right) _{V}, \end{aligned}$$

which yields to the following expression

$$\begin{aligned} C=\frac{3g^{3}\left( \varepsilon \right) r_{+}^{2}}{4}\frac{\left[ \frac{2k}{ r_{+}}\frac{g(\varepsilon ) }{f(\varepsilon ) }+\frac{1}{f(\varepsilon ) g(\varepsilon ) }\left[ \frac{4r_{+}}{l^{2}}-\frac{2e^{2}}{r_{+}^{3}} +m^{2}\left( c_{0}c_{1}+2\frac{c_{0}^{2}c_{2}}{r_{+}}+2\frac{c_{0}^{3}c_{3}}{ r_{+}^{2}}\right) \right] \right] }{\left[ -\frac{2k}{r_{+}^{2}}\frac{ g(\varepsilon ) }{f(\varepsilon ) }+\frac{1}{f(\varepsilon ) g(\varepsilon ) } \left[ \frac{4}{l^{2}}+\frac{6e^{2}}{r_{+}^{4}}+m^{2}\left( -2\frac{ c_{0}^{2}c_{2}}{r_{+}^{2}}-4\frac{c_{0}^{3}c_{3}}{r_{+}^{3}}\right) \right] \right] }. \end{aligned}$$

It can be used to analyze the stability of specific models. If its sign be positive the model is in the stable phase, and vice versa. It may be noted that black hole’s radius with $C=0$ is important, as at that stage the black hole does not exchange any energy with the surroundings. If $C=0$, then we obtain the following equation

$$\begin{aligned}&4r_{+}^{4}+m^{2}l^{2}c_{0}c_{1}r_{+}^{3}+2l^{2}\left( m^{2}c_{0}^{2}c_{2}+kg^{2}\left( \varepsilon \right) \right) r_{+}^{2}\\&\qquad +2m^{2}l^{2}c_{0}^{3}c_{3}r_{+}-2l^{2}e^{2}=0. \end{aligned}$$

We can observe that various thermodynamics quantities for the model, and its thermodynamics stability, depend on the choice of the rainbow functions $g(\varepsilon )$ and $f(\varepsilon )$ [67,68,69,70]. So, we will now analyze this model for the specific choice of rainbow functions.

3.2 Loop quantum gravity

It has been observed that the geometry of spacetime becomes energy-dependent in loop quantum gravity, and the energy-dependent metric for such a spacetime can be obtained using the following rainbow functions [83, 84]

$$\begin{aligned} f(\varepsilon )= & {} 1 \end{aligned}$$

(3.4)

$$\begin{aligned} g(\varepsilon )= & {} \sqrt{1-\eta \varepsilon ^{n}}, \end{aligned}$$

(3.5)

where $\eta$ is a dimensionless constant, also we should note that $0\le \varepsilon \le 1$. It may be noted that these rainbow functions are compatible with the results obtained from both loop quantum gravity and non-commutative geometry [84]. In this model, we can obtain entropy as

$$\begin{aligned} S=\frac{r_{+}^{3}}{4\left( 1-\eta \varepsilon ^{n}\right) ^{\frac{3}{2}}}. \end{aligned}$$

(3.6)

Now, according to Fig. 1, we can approximate $r_{+}\approx 0.6$ (for $k=1$), for unit values of the model parameters (also $r_{+}\approx 0.65$ for $k=0$ and $r_{+}\approx 0.7$ for $k=-1$). Hence, we can discuss the entropy for various values of n as plotted in Fig. 2. Besides, one can find that

$$\begin{aligned} \begin{array}{cc} S\approx \frac{r_{+}^{3}}{4}\left( 1+\frac{3}{2}\eta \varepsilon ^{n}+O(\varepsilon ^{2n})\right) , &{} \text {for }\varepsilon \rightarrow 0^{+} \\ &{}\\ S\approx \frac{r_{+}^{3}}{4(1-\eta )^{\frac{3}{2}}}\left( 1+\frac{3\eta n}{ 2(1-\eta )}(\varepsilon -1)+O(\varepsilon -1)^{2}\right) , &{} \text {for } \varepsilon \rightarrow 1^{-} \end{array} \end{aligned}$$

It is obvious that for $\varepsilon$ the entropy is approximately constant for small values of $\eta$. Generally, it is an increasing function of $\varepsilon$, but the local behavior depends on the values of $\eta$ and n. We should note that this approximately constant behavior is in the given range of $0\le \varepsilon \le 1$. Also, choosing the other values for the model parameters gives no important different result.

Fig. 2

Entropy of the first model (Eq. (3.6)) in terms of $\varepsilon$ for $\eta =0.001$, and $r_{+}=0.60$ ($k=1$), $r_{+}=0.65$ ($k=0$) and $r_{+}=0.70$ ($k=-1$)

Temperature of this model can be expressed as

$$\begin{aligned} T_{H}=\frac{1}{4\pi }\left[ \frac{2k}{r_{+}}\sqrt{1-\eta \varepsilon ^{n}}+ \frac{B}{\sqrt{1-\eta \varepsilon ^{n}}}\right] , \end{aligned}$$

(3.7)

where $B=\frac{4r_{+}}{l^{2^{}}}-\frac{2e^{2}}{r_{+}^{3^{}}}+m^{2}\left( c_{0}c_{1}+2\frac{c_{0}^{2}c_{2}}{r_{+}}+2\frac{c_{0}^{3}c_{3}}{r_{+}^{2^{}}} \right)$. In order to find the behavior of temperature, we use the series expansion to obtain

$$\begin{aligned}&T_{H}\approx \frac{1}{4\pi }\left[ \left( B+\frac{2k}{r_{+}}\right) +\frac{ \eta }{2}\left( B-\frac{2k}{r_{+}}\right) \varepsilon ^{n}+O(\varepsilon ^{2n})\right] , \\&\qquad \qquad \text {for }\varepsilon \rightarrow 0^{+}, \\&T_{H}\approx \frac{1}{4\pi \sqrt{1-\eta }}\left[ \left( B+\frac{2k(1-\eta )}{ r_{+}}\right) +\left( B-\frac{2k(1-\eta )}{r_{+}}\right) \right. \\&\qquad \qquad \left. \frac{\eta n(\varepsilon -1)}{2(1-\eta )}+O(\varepsilon -1)^{2}\right] , \text {for } \varepsilon \rightarrow 1^{-}. \end{aligned}$$

Although these relations confirm that T is an increasing function of $\varepsilon$, one can easily find that for small values of $\eta$ with allowed region of $\varepsilon$ ($0\le \varepsilon \le 1$), temperature is approximately constant (see different panels of Fig. 3 for more details).

Fig. 3

Temperature of the first model (Eq. (3.7)) in terms of $\varepsilon$ for $\eta =0.001$ and $r_{+}=0.6$ (unit value for other parameters)

Fig. 4

The first model mass (Eq. (3.8)) in terms of $\varepsilon$ for $\eta =0.001$, and unit value for other parameters

The black hole mass for this model is given by

$$\begin{aligned} M= & {} \frac{3k r_{+}^{2}}{16\pi \left( 1-\eta \varepsilon ^{n}\right) } \nonumber \\&+\frac{3}{16\pi \left( 1-\eta \varepsilon ^{n}\right) ^{2}}\left[ \frac{r_{+}^{4} }{l^{2}}-2e^{2}\ln \left( r_{+}\right) \right. \nonumber \\&\left. +m^{2}\left( \frac{c_{0}c_{1}}{3} r_{+}^{3}+c_{0}^{2}c_{2}r_{+}^{2}+2c_{0}^{3}c_{3}r_{+}\right) \right] . \end{aligned}$$

(3.8)

Typical values of the black hole mass are given by Fig. 4, for several values of n. Generally, one can find that M is an increasing function of $\varepsilon$ (with infinitesimal variation). For example with $n=1$ (linear dependence to the energy), which is consistent with results obtained from loop quantum gravity (minimum value of mass for $\varepsilon =0$). Here, we can conclude that the black hole mass is approximately constant for the given values of $0\le \varepsilon \le 1$ and small values of $\eta$.

Specific heat for this Yang–Mills black hole can now be expressed as

$$\begin{aligned}&C=\frac{3\left( 1-\eta \varepsilon ^{n}\right) ^{\frac{3}{2}}r_{+}^{2}}{4}\nonumber \\&\times \frac{ \left[ \frac{2k}{r_{+}}\sqrt{1-\eta \varepsilon ^{n}} +\frac{1}{\sqrt{ 1-\eta \varepsilon ^{n}}}\left[ \frac{4r_{+}}{l^{2}}-\frac{2e^{2}}{r_{+}^{3}} +m^{2}\left( c_{0}c_{1}+2\frac{c_{0}^{2}c_{2}}{r_{+}} +2\frac{c_{0}^{3}c_{3}}{ r_{+}^{2}}\right) \right] \right] }{\left[ -\frac{2k}{r_{+}^{2}} \sqrt{ 1-\eta \varepsilon ^{n}}+\frac{1}{\sqrt{1-\eta \varepsilon ^{n}}}\left[ \frac{4}{ l^{2}} +\frac{6e^{2}}{r_{+}^{4}}+m^{2}\left( -2\frac{c_{0}^{2}c_{2}}{r_{+}^{2} }-4\frac{c_{0}^{3}c_{3}}{r_{+}^{3}}\right) \right] \right] }.\nonumber \\ \end{aligned}$$

(3.9)

The behavior of specific heat for various values of n in terms of $\varepsilon$ in the given range illustrated by plots of Fig. 5. It is notable that in this figure the event horizon radius is fixed to $r_+=1$, and therefore, the heat capacity is positive function of $\varepsilon$. It is easy to find that we can obtain negative values of the heat capacity for smaller values of event horizon.

Fig. 5

Specific heat of the first model (Eq. (3.9)) in terms of $\varepsilon$ for $\eta =0.001$, and unit value for other parameters

Now, from Eq. (3.1), we observe that for stability the following condition is necessary

$$\begin{aligned} m>e. \end{aligned}$$

(3.10)

In fact, Eq. (3.1) reduced to the following expression

$$\begin{aligned}&4r_{+}^{4}+m^{2}l^{2}c_{0}c_{1}r_{+}^{3}+2l^{2}\left( m^{2}c_{0}^{2}c_{2}+k- \eta k\varepsilon ^{n} \right) r_{+}^{2}\nonumber \\&\qquad +2m^{2}l^{2}c_{0}^{3}c_{3}r_{+}-2l^{2}e^{2}=0. \end{aligned}$$

(3.11)

An exact bound on the energy for a stable model can now be written as

$$\begin{aligned} \varepsilon ^{n}\ge \frac{\begin{matrix} 2l^{2}e^{2}-4r_{+}^{4}-m^{2}l^{2}c_{0}c_{1}r_{+}^{3}-2l^{2} \left( m^{2}c_{0}^{2}c_{2}+k\right) r_{+}^{2}\\ -2m^{2}l^{2}c_{0}^{3}c_{3}r_{+}\end{matrix}}{ -2kl^{2}\eta r_{+}^{2}}.\nonumber \\ \end{aligned}$$

(3.12)

Hence, we find that for $E\ll E_{p}$, the first model is stable.

3.3 Gamma-ray bursts

It is also possible to obtain an energy-dependent metric by using the rainbow function obtained from hard spectra of gamma-ray bursts at cosmological distances [85]

$$\begin{aligned} f(\varepsilon )= & {} \frac{e^{\xi \varepsilon }-1}{\xi \varepsilon }, \end{aligned}$$

(3.13)

$$\begin{aligned} g(\varepsilon )= & {} 1, \end{aligned}$$

(3.14)

where $\xi$ is a dimensionless parameters of the order of unity. In this case, we have

$$\begin{aligned} S=\frac{r_{+}^{3}}{4}. \end{aligned}$$

(3.15)

We see that the entropy only depends on the horizon radius, and

$$\begin{aligned} T_{H}= & {} \frac{1}{4\pi }\left[ \frac{2k}{r_{+}}\frac{\xi \varepsilon }{ e^{\xi \varepsilon }-1} +\frac{\xi \varepsilon }{e^{\xi \varepsilon }-1}\left[ \frac{4r_{+}}{l^{2}}-\frac{2e^{2}}{r_{+}^{3}}\right. \right. \nonumber \\&\left. \left. +m^{2}\left( c_{0}c_{1}+2\frac{ c_{0}^{2}c_{2}}{r_{+}}+2\frac{c_{0}^{3}c_{3}}{r_{+}^{2}}\right) \right] \right] . \end{aligned}$$

(3.16)

Now, we can plot the temperature in terms of the horizon radius. In Fig. 6, we plot the temperature for various values of m. Interestingly, there is a critical horizon radius for which the temperature is constant (for example, see solid orange line of Fig. 6 for $k=-1$).

Fig. 6

Temperature of the second model (Eq. (3.16)) in terms of horizon radius, for $\xi =1$ and $\varepsilon =1$ (unit value for other parameters)

Then, the black hole mass can be obtained as

$$\begin{aligned} M= & {} \frac{3}{16\pi }\left[ \frac{\xi \varepsilon k}{e^{\xi \varepsilon }-1} r_{+}^{2} +\frac{\xi \varepsilon }{e^{\xi \varepsilon }-1}\left[ \frac{r_{+}^{4}}{ l^{2}}-2e^{2}\ln \left( r_{+}\right) \right. \right. \nonumber \\&\left. \left. +m^{2}\left( \frac{c_{0}c_{1}}{3} r_{+}^{3}+c_{0}^{2}c_{2}r_{+}^{2}+2c_{0}^{3}c_{3}r_{+}\right) \right] \right] . \end{aligned}$$

(3.17)

The specific heat is given by

$$\begin{aligned}&C=\frac{3r_{+}^{2}}{4}\nonumber \\&\frac{\left[ \frac{2k}{r_{+}}\frac{\xi \varepsilon }{ e^{\xi \varepsilon }-1} +\frac{\xi \varepsilon }{e^{\xi \varepsilon }-1}\left[ \frac{4r_{+}}{l^{2}}-\frac{2e^{2}}{r_{+}^{3}} +m^{2}\left( c_{0}c_{1}+2\frac{ c_{0}^{2}c_{2}}{r_{+}} +2\frac{c_{0}^{3}c_{3}}{r_{+}^{2}}\right) \right] \right] }{\left[ -\frac{2k}{r_{+}^{2}}\frac{\xi \varepsilon }{ e^{\xi \varepsilon }-1} +\frac{\xi \varepsilon }{e^{\xi \varepsilon }-1}\left[ \frac{4}{l^{2}}+\frac{6e^{2}}{r_{+}^{4}} +m^{2}\left( -2\frac{c_{0}^{2}c_{2}}{ r_{+}^{2}}-4\frac{c_{0}^{3}c_{3}}{r_{+}^{3}}\right) \right] \right] }.\nonumber \\ \end{aligned}$$

(3.18)

According to Fig. 7, it is evident that the smaller values m produce the negative value of specific heat. On the other hand, larger values of m produce a phase transition from a stable to an unstable phase. So, for the thermodynamically stable model, we should have $m_{min}<m<m_{max}$. For the unit value of the model parameters, we find $m_{min}=0.6$ and $m_{max}=1.37$ for $k=1$ (see Fig. 7a), $m_{min}\approx 0.7$ and $m_{max}\approx 1.4$ for $k=0$ (see Fig. 7b). We also have $m_{min}\approx 0.85$ and $m_{max}\approx 1.45$ for $k=-1$ (see Fig. 7c). These plots show that the phase transition is possible for the second model.

Fig. 7

Specific heat of the second model (Eq. (3.18)) in terms of $r_{+}$, with unit values for the model parameters

3.4 Horizon problem

It has been proposed that the horizon problem can be resolved with suitable rainbow functions [86, 87],

$$\begin{aligned} f(\varepsilon )=g(\varepsilon )=\frac{1}{1-\lambda \varepsilon }, \end{aligned}$$

(3.19)

where $\xi$ is a dimensionless parameters of the order of unity. In this case, the entropy and temperature of the system can be written as

$$\begin{aligned} S=\frac{\left( 1-\lambda \varepsilon \right) ^{3}r_{+}^{3}}{4}. \end{aligned}$$

(3.20)

and

$$\begin{aligned} T_{H}= & {} \frac{1}{4\pi }\left[ \frac{2k}{r_{+}}+\left( 1-\lambda \varepsilon \right) ^{2}\left[ \frac{4r_{+}}{l^{2}} -\frac{2e^{2}}{r_{+}^{3}}\right. \right. \nonumber \\&\left. \left. +m^{2}\left( c_{0}c_{1}+2\frac{c_{0}^{2}c_{2}}{r_{+}}+2\frac{c_{0}^{3}c_{3}}{ r_{+}^{2}}\right) \right] \right] . \end{aligned}$$

(3.21)

In order to have well defined model (positive entropy and temperature), we should have $\varepsilon \le \frac{1}{\lambda }$ and $m>m_{min}$. In the plots of Fig. 8, we observe the behavior of the entropy. Now Fig. 8a demonstrates that there is an upper limit for the energy, below which the entropy is negative. For the selected value $\lambda =1$, we observe that $\varepsilon _{max}=1$. Here $S=0$, and $S\ge 0$ for $\varepsilon \le \varepsilon _{max}$. It should be noted that general behavior is similar for $k=0$, and $k= \pm 1$. It is also illustrated by Fig. 8b which plots the behavior of the entropy with $\varepsilon$.

In Fig. 9, we can verify our previous results. According to Fig. 9, we shall denote the maximum $\varepsilon =\frac{1}{\lambda }$ by $\varepsilon _{max}$ ($\varepsilon =1$ in plot), Here the value of temperature does not depend on m. For $k=0$ and $k=1$ temperature is positive for suitable mass. However, for $k=-1$, value of temperature is negative at this energy. Hence, we find that $T_{H}$ is positive for $\varepsilon < \varepsilon _{max}$. The positive temperature occurs, when $\varepsilon >\varepsilon _{max}$ is not allowed. So, both $\varepsilon$ and m are constrained as $\varepsilon <\varepsilon _{max}$ and $m>m_{min}$.

Fig. 8

Typical behavior of the entropy in the third model (Eq. (3.20)) for $\lambda =1$. a in terms of $r_{+}$ for different values of $\varepsilon$, and b in terms of $\varepsilon$ for $r_{+}=0.6$. Unit value for the other model parameters is used

Fig. 9

Typical behavior of the temperature in the third model (Eq. (3.21)), for unit value for all model parameters

Then, we can find,

$$\begin{aligned} M= & {} \frac{3kr_{+}^{2}\left( 1-\lambda \varepsilon \right) ^{3}}{16\pi } +\frac{3\left( 1-\lambda \varepsilon \right) ^{5}}{16\pi } \left[ \frac{r_{+}^{4} }{l^{2}}-2e^{2}\ln \left( r_{+}\right) +m^{2}\left( \frac{c_{0}c_{1}}{3} r_{+}^{3}+c_{0}^{2}c_{2}r_{+}^{2}+2c_{0}^{3}c_{3}r_{+}\right) \right] . \end{aligned}$$

(3.22)

$$\begin{aligned} C= & {} \frac{3\left( 1-\lambda \varepsilon \right) ^{3}r_{+}^{2}}{4}\frac{\left[ \frac{2k}{r_{+}} +\left( 1-\lambda \varepsilon \right) ^{2}\left[ \frac{4r_{+}}{ l^{2}}-\frac{2e^{2}}{r_{+}^{3}} +m^{2}\left( c_{0}c_{1}+2\frac{c_{0}^{2}c_{2} }{r_{+}}+2\frac{c_{0}^{3}c_{3}}{r_{+}^{2}}\right) \right] \right] }{\left[ - \frac{2k}{r_{+}^{2}} +\left( 1-\lambda \varepsilon \right) ^{2}\left[ \frac{4}{ l^{2}}+\frac{6e^{2}}{r_{+}^{4}} +m^{2}\left( -2\frac{c_{0}^{2}c_{2}}{r_{+}^{2} }-4\frac{c_{0}^{3}c_{3}}{r_{+}^{3}}\right) \right] \right] }. \end{aligned}$$

(3.23)

Graphical analysis of specific heat in terms of $\varepsilon$ is represented in Fig. 10. It shows the variation of the specific heat with $0\le \varepsilon \le 1$.

For $k=1$, we can see that the first-order phase transition exists. We confirm the previous result, as $\varepsilon <\varepsilon _{max}$ is crucial to have well defined (stable) model. Hence, in the case of $k=1$ we have unstable/stable phase transition.

Fig. 10

Typical behavior of the specific heat in terms of $\varepsilon$ in the third model (Eq. (3.23)), with unit value for all model parameters

Fig. 11

$P-r_+$ (left) and $G-T$ (right) diagrams for $e=m=c_0=c_1=c_2=c_3=g(\varepsilon )=1$ and $k_{eff}=1$ ($k=1$ with $c_{2}=0$ or $k=0$ with $c_{2}=1$ or $k=-1$ with $c_{2}=2$). The blue dashed line corresponds to the critical temperature (left) and the critical pressure (right)

4 Criticality in the extended phase space

Now, we give a discussion of the critical behavior of the Yang–Mills black hole solution in the using the extended phase space [46, 47]. In the extended phase space, the cosmological constant is identified with a thermodynamic pressure as [88, 89]

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }=\frac{3}{4\pi l^{2}}. \end{aligned}$$

(4.1)

Substituting the pressure from Eq. (4.1) in Eq. (3.2), one can obtain the following equation of state

$$\begin{aligned} P= & {} \frac{3}{8\pi }\left( \frac{e^{2}}{r_{+}^{4}}-\frac{m^{2}c_{0}^{3}c_{3}}{ r_{+}^{3}}-\frac{\left[ m^{2}c_{0}^{2}c_{2}+kg^{2}(\varepsilon )\right] }{ r_{+}^{2}}\right. \nonumber \\&\left. +\frac{\left[ 4\pi f(\varepsilon )g(\varepsilon )T-m^{2}c_{0}c_{1} \right] }{2r_{+}}\right) . \end{aligned}$$

(4.2)

Due to the fact that in $(4+1)-$dimensions, the specific volume (v) is related to the event horizon radius as $v=\frac{{4{r_{+}}\ell _{\mathrm {P}}^{ {3}}}}{{3}}$, we can work with $P=P(T,r_{+})$, instead of $P=P(T,v)$, as it will produce the same thermodynamic behavior. In other words, the criticality, phase transition and, in general, the behavior of $P-v$ diagram is equivalent to $P-r_{+}$ diagram. Regarding Eq. (4.2), we observe that it is reasonable to define an effective (shifted) temperature $T_{eff}$ , and horizon topology factor $k_{eff}$ as

$$\begin{aligned} T_{eff}= & {} T-\frac{m^{2}c_{0}c_{1}}{4\pi f(\varepsilon )g(\varepsilon )}, \end{aligned}$$

(4.3)

$$\begin{aligned} k_{eff}= & {} k+\frac{m^{2}c_{0}^{2}c_{2}}{g^{2}(\varepsilon )}. \end{aligned}$$

(4.4)

In order to obtain the critical point of isothermal $P-r_{+}$ diagram, we use the inflection point property of such a diagram as

$$\begin{aligned} \left( \frac{\partial P}{\partial r_{+}}\right) _{T_{eff}}=0,~~~~~\left( \frac{\partial ^{2}P}{\partial r_{+}^{2}}\right) _{T_{eff}}=0. \end{aligned}$$

(4.5)

Fig. 12

Logarithmic corrected entropy in terms of $r_{+}$ for $g(\varepsilon )\approx 1$, and unit value for other model parameters

Fig. 13

Logarithmic corrected entropy, mass, specific heat and temperature in terms of $r_{+}$ for $g(\varepsilon )\approx 1$, $f(\varepsilon )\approx 4$, $m=1.2$ and unit value for other model parameters

After some simplification, we find the following expression corresponding to Eq. (4.5)

$$\begin{aligned} \left( \frac{\partial P}{\partial r_{+}}\right) _{T_{eff}}= & {} \frac{-3}{8\pi {r}_{+}^{5}}\left[ 2\pi f(\varepsilon )g(\varepsilon )T_{eff}{r} _{+}^{3}-2g^{2}(\varepsilon ){k_{eff}r}_{+}^{2}\right. \nonumber \\&\left. -3\,{{c_{0}}}^{3}{c_{3}}\,{m} ^{2}r_{+}+4{e}^{2}\right] =0 \end{aligned}$$

(4.6)

$$\begin{aligned} \left( \frac{\partial ^{2}P}{\partial r_{+}^{2}}\right) _{T_{eff}}= & {} \frac{3 }{4\pi \,{r}_{+}^{6}}\left[ 2\pi f(\varepsilon )g(\varepsilon )T_{eff}{r} _{+}^{3}-3g^{2}(\varepsilon ){k_{eff}r}_{+}^{2}\right. \nonumber \\&\left. -6{{c_{0}}}^{3}{c_{3}}\,{m} ^{2}{r}_{+}+10{e}^{2}\right] =0. \end{aligned}$$

(4.7)

The critical quantities are obtained by solving Eqs. (4.6) and (4.7), simultaneously

$$\begin{aligned}&r_{c}=-\frac{3m^{2}c_{0}^{3}c_{3}\pm \Theta }{2k_{eff}g^{2}(\varepsilon )}, \nonumber \\&T_{eff}|_{c}=\frac{2k_{eff}^{2}g^{3}(\varepsilon )\left[ \Theta ^{2}\mp 3m^{2}c_{0}^{3}c_{3}\Theta -8e^{2}k_{eff}g^{2}(\varepsilon )\right] }{\pi f(\varepsilon )(-3m^{2}c_{0}^{3}c_{3}\pm \Theta )^{3}}, \nonumber \\&P_{c}=\frac{3k_{eff}^{3}g^{6}(\varepsilon )\left[ \Theta ^{2}\mp 2m^{2}c_{0}^{3}c_{3}\Theta -12e^{2}k_{eff}g^{2}(\varepsilon )-3m^{4}c_{0}^{6}c_{3}^{2}\right] }{2\pi (-3m^{2}c_{0}^{3}c_{3}\pm \Theta )^{4}},\nonumber \\ \end{aligned}$$

(4.8)

where $\Theta =\sqrt{9m^{4}c_{0}^{6}c_{3}^{2}+24e^{2}k_{eff}g^{2}( \varepsilon )}$. The two branches of critical quantities distinguishing by the sign behind $\Theta$, where for the lower sign, there is results are not physical, for any real positive values of the critical quantities. So, we will only analyze this system with the upper sign.

Although the Van der Waals phase transition and critical behavior are observed only for spherical horizon topology in the Einstein-AdS gravity, here in the massive gravity scenario, we can build such behavior for all topologies. As we indicate in the caption of Fig. 11, it is obvious that by adjusting the massive parameters (or rainbow function), one can find the Van der Waals like behavior.

To confirm the results, we can study the Gibbs free energy per unit volume $\omega _{k}$ as follows

$$\begin{aligned}&G=M-TS\nonumber \\&\quad =\frac{\begin{matrix}6e^{2}+3k_{eff}g^{2}(\varepsilon )r_{+}^{2}+12m^{2}c_{0}^{3}c_{3}r_{+}\\ -4\pi Pr_{+}^{4}-18e^{2}\ln r_{+}\end{matrix}}{ 48\pi f(\varepsilon )g^{4}(\varepsilon )}. \end{aligned}$$

(4.9)

According to the right panel of Fig. 11, we observe a first-order phase transition for different topologies, which is characterized by the swallow-tail shape of the Gibbs free energy for $P<P_{c}$.

5 Thermal fluctuations

It has been argued that the thermodynamics of black hole should be corrected due to thermal fluctuations [57]. Such fluctuations can be analyzed using the partition function for such a system. As the AdS black holes are dual to conformal field theories, it is possible to analyze the fluctuations to the black hole thermodynamics using the statistical mechanical partition function of microstates, which can be obtained from the dual conformal field theory [58]. It is possible to explicitly write down such a partition function as

$$\begin{aligned} Z=\int _{0}^{\infty }{\Omega e^{-\frac{E}{T}}dE}, \end{aligned}$$

(5.1)

where $\Omega$ denotes the density of state in canonical ensemble, which is proportional to

$$\begin{aligned} \Omega \propto \int {\frac{e^{s}}{T^{2}}dT}. \end{aligned}$$

(5.2)

Here s denotes the exact (corrected) entropy. Applying the inverse Laplace transformation to Eq. (5.1) yields

$$\begin{aligned} \Omega \propto \int {\frac{z e^{\frac{E}{T}}}{T^{2}}dT}. \end{aligned}$$

(5.3)

Combining Eqs. (5.2) and (5.3) yields

$$\begin{aligned} s=\ln {Z}+\frac{E}{T}. \end{aligned}$$

(5.4)

This is identical to the statistical relation,

$$\begin{aligned} s=\ln {\Omega }. \end{aligned}$$

(5.5)

If we assume S to be the equilibrium entropy, and use Taylor expansion of s in Eq. (5.3), then after some calculations, we obtain [57, 58, 90]

$$\begin{aligned} s=S-\frac{\alpha }{2}\ln \left[ \frac{S^{\prime \prime }T^{\prime }-S^{\prime }T^{ \prime \prime }}{(T^{\prime })^{3}}\right] +\cdots , \end{aligned}$$

(5.6)

where prime denotes derivative with respect to the horizon radius $r_{+}$, ie., $S^{\prime }=\frac{dS}{dr_{+}}$. Also, the constant $\alpha$ is added by hand to track correction terms [59]. Here, $\alpha =0$ reproduces results in the absence of such logarithmic corrections, and $\alpha =1$ produces logarithmic corrections. In Eq. (5.6), we have neglected higher-order terms in the Taylor expansion (which produce higher-order corrections). Hence, the first-order correction occurs in form of a logarithmic correction term to the entropy [60, 61].

By using the general temperature and general entropy, one can obtain this logarithmic corrected entropy as

$$\begin{aligned}&s=\frac{r_{+}^{3}}{4g^{3}\left( \varepsilon \right) }-\frac{\alpha }{2}\nonumber \\&\ln \left[ \frac{15\pi ^{2}r_{+}^{9}}{4} \frac{f^{2}\left( \varepsilon \right) }{ g(\varepsilon )} \frac{(m^{2}+kg^{2}\left( \varepsilon \right) )\frac{2r_{+}^{2} }{5}+m^{2}r_{+}-\frac{1}{5}(9+2r_{+}^{4})}{((m^{2}+kg^{2}\left( \varepsilon \right) )\frac{r_{+}^{2}}{2}+m^{2}r_{+}-r_{+}^{4}-\frac{3}{2})^{3}}\right] ,\nonumber \\ \end{aligned}$$

(5.7)

where, we have assumed $c_{0}=c_{1}=c_{2}=c_{3}=e=1$ for simplicity. Then, we can obtain corrected mass via

$$\begin{aligned} M_{c}=\int Tds. \end{aligned}$$

(5.8)

To see effect of the logarithmic correction, we plot the entropy in Fig. 12. We observe that the thermal fluctuations are important in smaller $r_{+}$. It has been argued that when the black hole size reduced due to the Hawking radiation, the thermal fluctuations become important [62]. As general behavior does not depend on $\varepsilon$, we fix their values to study thermodynamics behaviors generally. We show that thermal fluctuations produce the negative entropy for larger $r_{+}$. Depend on the model ($f(\varepsilon ))$, black hole in presence of thermal fluctuations may be stable or unstable.

We can also compute corrected specific heat as

$$\begin{aligned} C_{c}=T\left( \frac{ds}{dT}\right) _{V}. \end{aligned}$$

(5.9)

Reducing the black hole size, the system goes to an unstable phase until the entropy and specific heat vanish.

Now it is interesting to study the case when black hole entropy, temperature and specific heat are zero, but black hole mass is not zero. These are denoted by a circle in Fig. 13. It has been shown that at a special radius the black hole entropy, temperature and specific heat may be zero, while black hole mass is non-zero. It is interpreted as black remnant mass, below which the black hole will not evaporate. For $k=1$, we cannot observe any black remnant, due to the absence of a unique (even approximately) point where the black hole entropy, temperature and specific heat is zero. In the case of $k=0$, there is an approximate radius $r_{+}\approx 0.45$, where the black hole entropy, temperature and specific heat are approximately zero, and $M_{c}\ne 0$ (see Fig. 13b). For $k=-1$, we find that when $r_{+}\approx 0.5$, the black hole entropy, temperature and specific heat are zero, and $M_{c}\approx 0.25$ (see Fig. 13c).

6 Conclusion

In this paper, we have analyzed a five-dimensional black hole solution in massive gravity coupled to the Yang–Mills theory. We have discussed the thermodynamics of this black hole solution. We also studied the flow of such a solution with scale, using the energy-dependence of the geometry. We have used the rainbow functions, motivated by loop quantum gravity, the hard spectrum of gamma-ray bursts, and the horizon problem to analyze such a flow with scale. It was observed that these rainbow functions can change the behavior of the black hole thermodynamics when the size of the black hole reduces due to the Hawking radiation.

We have also investigated the criticality in the extended phase space. It was done by treating the cosmological constant as the dynamic pressure. Its conjugate variable was treated as the thermodynamic volume for this black hole solution. We have also analyzed the effects of thermal fluctuations on this black hole solution. It was observed that these thermal fluctuations can be obtained from a statistical mechanical partition function for this system. The thermal fluctuations produce a logarithmic correction for the entropy of this black hole. We have also examined the corrections to the specific heat for this black hole solution.

It may be noted that it would be interesting to generalize these results to higher dimensions. Thus, we could consider higher dimensional Yang–Mills theory coupled to massive gravity, and obtain black hole solutions in such a theory. Then, we can analyze the thermodynamics of such solutions. Here again, we can investigate the flow of the solution with scale, using gravity’s rainbow [67,68,69,70]. We can then study how such a flow deforms the thermodynamics of such higher dimensional solutions. Furthermore, it is expected that the thermodynamics of such solutions will again depend on the specific rainbow functions. So, we can use rainbow functions motivated from loop quantum gravity [83, 84], the hard spectra of gamma-ray bursts at cosmological distances [85], and the horizon problem [86, 87], to deform the thermodynamics of such solutions. It would also be pointed out to analyze the critical behavior [46, 47] for this higher dimensional solution.

We can also construct the partition function for this higher dimensional AdS solution, and use it to analyze the thermal fluctuations for that solution [57, 58]. It is expected that the entropy of this higher dimensional AdS solution will again be corrected by the logarithmic correction term. It would be useful to investigate the effects of such corrections on other thermodynamic quantities for this higher dimensional solution. It would also be interesting to study the effects of thermal fluctuations on the criticality of these black hole solutions.

It may be noted that a mass term for graviton can be generated from a gravitational Higgs mechanism [91, 92]. It would be worth analyzing such a gravitational Higgs mechanism for various supergravity solutions. As the Yang–Mills black hole solutions can be motivated from the bosonic part of the low energy Heterotic string theory [3, 4] , it would be important to study the gravitational Higgs mechanism in low energy Heterotic string theory. This could be used to obtain a mass term for Yang–Mills fields. It would be interesting to investigate the consequences of such a mass term on the thermodynamics of Yang–Mills black holes.