1 Introduction

A large number of isotropic fluid solutions are known, of which only a few satisfy the conditions of physical acceptability for a self-gravitating compact object [1]. In the case of anisotropic fluid solutions this number of physically acceptable solutions is even more limited. Such kind of stellar solutions are very appreciated in stellar astrophysics since it is well known that disturbances of the isotropy and fluctuations of the local anisotropy in pressures may be caused by a large variety of physical phenomena of the kind that are expect in compact objects (see Ref. [2], for an extensive discussion in this point). Examples of such phenomena are the high density regimen, existence of solid stellar cores, the presence of superfluid, phase transition, rotation, etc [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Recently in [20] has been proved that any realistic physical process of the kind expected in stellar evolution always tends to produce pressure anisotropy by the presence of dissipation, energy density inhomogeneities and shear. In fact, if the system is initially isotropic in pressure, the resulting final stage of a dynamical regime in the evolution of a star should exhibit pressure anisotropy. Anyway isotropic models also remain common assumptions in the study of compact objects (See for example the Refs. [21,22,23,24,25,26]).

Therefore the importance of obtaining methods for the construction of these two types of interior solutions is highly valued. Due to in static and spherically symmetric space times, the are only three independent Einstein field equations (EFE) but five unknown, namely two metric functions, the density energy and the radial and tangential pressures results that is necessary to provide two extra conditions in order to solve the problem, which can be relations between the metrics functions or state equations that can relate the physical quantities. In such sense there are many ways to construct static anisotropic solutions, but recently the Gravitational Decoupling (GD) [27] through the Minimal Geometric Deformation (MGD) permit us to solve the EFE and also extend isotropic known solutions to anisotropic case.

Such technique uses an isotropic solution as a seed and extra condition to close the entire system. In such sense, there are several works where the GD has been implemented in 2 + 1 and 3 + 1 space times [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67]. Particularly, in this work we use the recently introduced definition of complexity for self–gravitating fluids [68] to close the system of equations risen by what we will call in this work as Temporal Geometric Deformation (TGD), which takes in account only a geometric deformation on the temporal metric component of the seed solution. Mathematically such temporal deformation can be taken from the framework of the extended case of MGD (MGDe) (see [69] for details of MGDe), but however, it does not respond to an usual gravitational decoupling since it requires an extra source with zero density energy. However, in this work we show that the TGD can be useful to obtain new interior solutions.

There are few works where the complexity factor for self-gravitating spheres is used as extra condition to close the system of differential equations arising from Gravitational Decoupling through the MGD [70,71,72] in order to obtain new stellar models. In these sense, recently new static and spherically symmetric solutions have found in the anisotropic fluid regime with vanishing complexity [70, 73,74,75,76]. Even, recently the problem of general relativistic gravitational collapse under the assumption of vanishing complexity factor has been used [77], and also has been used in the study of hyperbolical fluids in Modified Gravity [78].

2 Gravitational decoupling

In this section we introduce the Gravitational Decoupling by MGDe (for more details, see [69]). Let us start with the Einstein field equations (EFE)

$$\begin{aligned} G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}R g_{\mu \nu } = k^2 T_{\mu \nu }, \end{aligned}$$
(1)

with

$$\begin{aligned} T_{\mu \nu } = T^{(s)}_{\mu \nu } + \theta _{\mu \nu }\;, \end{aligned}$$
(2)

where \(k^2=\frac{8\pi G}{c^4}\) and \(T^{(s)}_{\mu \nu }\) represents the matter content of a known solution of Einstein’s field equations,Footnote 1 namely the seed sector, and \(\theta _{\mu \nu }\) describes an extra source. Note that, since the Einstein tensor fulfill the Bianchi identities, the total energy–momentum tensor satisfies

$$\begin{aligned} \nabla _{\mu } T^{\mu \nu } = 0. \end{aligned}$$
(3)

In a static and spherically symmetric space-time sourced by

$$\begin{aligned} T^{\mu (s)}_{\nu }= & {} \text {diag}(\rho ^{(s)},-p_{r}^{(s)},-p^{(s)}_{t},-p^{(s)}_{t}) \end{aligned}$$
(4)
$$\begin{aligned} \theta ^{\mu }_{\nu }= & {} \text {diag}(\theta _{0}^{0},\theta _{1}^{1},\theta _{2}^{2},\theta _{2}^{2}), \end{aligned}$$
(5)

and a metric given by

$$\begin{aligned} ds^{2}=e^{\nu }dt^{2}-e^{\lambda }dr^{2} -r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(6)

Equations (1) and (2) lead to

$$\begin{aligned} k^2 \rho= & {} \frac{1}{r^2} + e^{-\lambda }\!\left( \frac{\lambda '}{r} - \frac{1}{r^2}\right) \!, \end{aligned}$$
(7)
$$\begin{aligned} k^2 p_{r}= & {} -\frac{1}{r^2} + e^{-\lambda }\!\left( \frac{\nu '}{r} + \frac{1}{r^2}\right) \!, \end{aligned}$$
(8)
$$\begin{aligned} k^2 p_{t}= & {} \frac{e^{-\lambda }}{4}\!\left( 2\nu '' + {\nu '}^2 - \lambda '\nu ' + 2\frac{\nu '-\lambda '}{r} \right) ,\! \end{aligned}$$
(9)

where we have defined

$$\begin{aligned} \rho= & {} \rho ^{(s)} + \theta _{0}^{0} \;, \end{aligned}$$
(10)
$$\begin{aligned} p_{r}= & {} p_r^{(s)}-\theta _{1}^{1} \;, \end{aligned}$$
(11)
$$\begin{aligned} p_{t}= & {} p_{t}^{(s)} -\theta _{2}^{2} \;. \end{aligned}$$
(12)

The conservation equation (3) is a linear combination of Eqs. (7)–(9), and yields

$$\begin{aligned} \left( p_{r}\right) '+\frac{\nu '}{2}\left( \rho + p_{r}\right) +\frac{2}{r}\left( p_{r}-p_{t}\right) = 0, \end{aligned}$$
(13)

which in terms of the two sources in Eq. (2) reads as

$$\begin{aligned}&(p_r^{(s)})'+ \frac{\nu '}{2}\left( \rho ^{(s)} + p_r^{(s)}\right) +\frac{2}{r}\left( p_{r}^{(s)}-p_{t}^{(s)}\right) \nonumber \\&\quad - \left( \theta _{1}^{1}\right) '+\frac{\nu '}{2}\left( \theta _{0}^{0}-\theta _{1}^{1}\right) +\frac{2}{r}\left( \theta _{2}^{2}-\theta _{1}^{1}\right) = 0. \end{aligned}$$
(14)

Is clear that the non-linearity of Einstein’s equations avoids that the decomposition (2) lead to two set of equations; one for each source involved. Nevertheless, contrary to the broadly belief, such a decoupling is possible in the context of MGD and MGDe as we shall demonstrate in what follows.

Let us introduce a geometric deformation in the metric functions given by

$$\begin{aligned} \nu \;\;\longrightarrow & {} \;\; \xi + \alpha g, \end{aligned}$$
(15)
$$\begin{aligned} e^{-\lambda }\;\;\longrightarrow & {} \;\; e^{-\mu } + \alpha f\;, \end{aligned}$$
(16)

where \(\{f,g\}\) are the so-called decoupling functions and \(\alpha \) is the same free parameter that “controls” the influence of \(\theta _{\mu \nu }\) on \(T_{\mu \nu }^{(s)}\). Now, replacing (15) and (16) in the system (7)–(9), we are able to split the complete set of differential equations into two subsets: one describing a seed sector sourced by the conserved energy-momentum tensor, \(T_{\mu \nu }^{(s)}\)

$$\begin{aligned} k^2 \rho ^{(s)}= & {} \frac{1}{r^2}-e^{-\mu }\left( \frac{1}{r^2}-\frac{\mu '}{r}\right) , \end{aligned}$$
(17)
$$\begin{aligned} k^2 p_r^{(s)}= & {} -\frac{1}{r^2}+e^{-\mu }\left( \frac{1}{r^2}+\frac{\xi '}{r}\right) , \end{aligned}$$
(18)
$$\begin{aligned} k^2 p_{t}^{(s)}= & {} \frac{e^{-\mu }}{4}\left( 2\xi ''+\xi '^2-\mu '\xi '+2\frac{\xi '-\mu '}{r}\right) , \end{aligned}$$
(19)

and the other set corresponding to source \(\theta _{\mu \nu }\)

$$\begin{aligned} k^2\theta _{0}^{0}= & {} -\frac{\alpha f}{r^2}-\frac{\alpha f'}{r} \end{aligned}$$
(20)
$$\begin{aligned} k^2\theta _{1}^{1}+\alpha Z_{1}= & {} -\alpha f\left( \frac{1}{r^2}+\frac{\nu '}{r}\right) \end{aligned}$$
(21)
$$\begin{aligned} k^2\theta _{2}^{2}+\alpha Z_{2}= & {} -\frac{\alpha f}{4}\left( 2\nu ''+\nu '^2+\frac{2\nu '}{r}\right) \nonumber \\&-\frac{\alpha f'}{4}\left( \nu '+\frac{2}{r}\right) , \end{aligned}$$
(22)

where \(Z_{1}=\frac{e^{-\mu }g'}{r}\) and \(4Z_2=e^{-\mu }(2g''+\alpha g'^2+\frac{2g'}{r}+2\xi 'g'-\mu 'g')\).

By another hand if we insert \(\nu '=\xi '+\alpha g'\) in Eq. (14) results

$$\begin{aligned}&\bigg [-(p_r^{(s)})'-\frac{\xi '}{2}\left( \rho ^{(s)}+p_r^{(s)}\right) -\frac{2}{r}\left( p_r^{(s)}-p_t^{(s)}\right) \bigg ]\nonumber \\&\quad -\frac{\alpha g'}{2}\left( \rho ^{(s)}+p_r^{(s)}\right) \nonumber \\&\quad + (\theta _{1}^{1})'-\frac{\nu '}{2}(\theta _{0}^{0}-\theta _{1}^{1})-\frac{2}{r}(\theta _{2}^{2}-\theta _{1}^{1})=0, \end{aligned}$$
(23)

where the bracket in Eq. (23) represents the divergence of \(T_{\mu \nu }^{(s)}\) calculated with the metric \(\lbrace \xi ,\mu \rbrace \), and \(T_{\mu \nu }^{(s)}\) satisfies with

$$\begin{aligned} \nabla _{\sigma }^{(\xi ,\mu )}T_{\nu }^{\sigma (s)} = 0 \end{aligned}$$
(24)

since \(T_{\mu \nu }^{(s)}\) correspond a known “seed” source that satisfies its respective EFE. Note that

$$\begin{aligned} \nabla _{\sigma }T_{\nu }^{\sigma (s)}=\nabla _{\sigma }^{(\xi ,\mu )}T_{\nu }^{\sigma (s)}-\frac{\alpha g'}{2}(T_{0}^{0 (s)}-T_{1}^{1 (s)})\delta _{\nu }^{1} \end{aligned}$$
(25)

where the divergence \(\nabla _{\sigma }\) is calculated with the metric \(\lbrace \nu ,\lambda \rbrace \). Explicitly Eq. (24) give us

$$\begin{aligned} (p_r^{(s)})'+\frac{\xi '}{2}(\rho ^{(s)}+p_r^{(s)})+\frac{2}{r}(p_r^{(s)}-p_t^{(s)})=0, \end{aligned}$$
(26)

which is a linear combination of Eqs. (17)–(19). By the way if we take in account the Eqs. (24) and (23) results that

$$\begin{aligned} \nabla _{\sigma }T_{\nu }^{\sigma (s)}=-\frac{\alpha g'}{2}(T_{0}^{0 (s)}-T_{1}^{1 (s)})\delta _{\nu }^{1}, \end{aligned}$$
(27)

and

$$\begin{aligned} \nabla _{\nu }^{\sigma }\theta _{\nu }^{\sigma }=-\nabla T_{\nu }^{\sigma (s)}=\frac{\alpha g'}{2}(T_{0}^{0 (s)}-T_{1}^{1 (s)})\delta _{\nu }^{1}. \end{aligned}$$
(28)

Explicitly, it reads

$$\begin{aligned} (\theta _{1}^{1})'-\frac{\nu '}{2}(\theta _{0}^{0}-\theta _{1}^{1})-\frac{2}{r}(\theta _{2}^{2}-\theta _{1}^{1})=\frac{\alpha g'}{2}(\rho ^{(s)}+p_r^{(s)}),\nonumber \\ \end{aligned}$$
(29)

which is a linear combinations of Eqs. (20)–(22).

Then the sources \(T_{\mu \nu }^{(s)}\) and \(\theta _{\mu \nu }\) can be decoupled by MGDe in such a way that between them there is an energy-moment exchange as it is you can see in the equations (27) y (28).

Now, in order to take in account that the metric should be continuous at surface \(\Sigma \) of star we have to match smoothly the interior metric with the outside (Schwarzschild exterior solution), we require

$$\begin{aligned} e^{\nu }\Big |_{\Sigma ^{-}}= & {} \left( 1 - \frac{2M}{r}\right) \Bigg |_{\Sigma ^{+}}, \end{aligned}$$
(30)
$$\begin{aligned} e^{\lambda }\Big |_{\Sigma ^{-}}= & {} \left( 1 - \frac{2M}{r}\right) ^{-1}\Bigg |_{\Sigma ^{+}}, \end{aligned}$$
(31)
$$\begin{aligned} p_r(r) \Big |_{\Sigma ^{-}}= & {} p_r(r) \Big |_{\Sigma ^{+}}, \end{aligned}$$
(32)

which corresponds to the continuity of the first and second fundamental form across that surface.

Note that the system of Eqs. (7)–(9) represents three differential equations with five unknowns functions, namely \(\lbrace \nu , \lambda , \rho , p_r, p_t\rbrace \) represents a static and spherically symmetric space time sourced by an anisotropic fluid. In such sense, two auxiliary conditions must be provided, namely metric conditions, equations of state, etc. Then using GD approach we use a seed solution which reduce the number of degrees of freedom to four and, as a consequence, only one extra condition is required. Thus the extra condition have been implemented in the decoupling sector given by Eqs. (20)–(22) as some equation of state which leads to a differential equation for the decoupling functions f and g. However, we will take an alternative route in order to obtain the decoupling functions, which is the complexity factor that we shall introduce in the next section.

3 Complexity of compact sources

Recently, a new definition of complexity for self–gravitating fluid distributions has been introduced in Ref. [68]. This definition is based on the intuitive idea that the least complex gravitational system should be characterized by a homogeneous energy density distribution and isotropic pressure. Specifically, in [68] is demonstrated that there is a scalar belonging to a class of scalar functions called Structure Scalars (such scalars were analyzed in detail by first time in [79] and obtained from the orthogonal splitting of the Riemann tensor [80, 81]) that in spherically symmetric space times captures the essence of what we mean by complexity, namely

$$\begin{aligned} Y_{TF} = k^2 \Pi - \frac{k^2}{2 r^3}\int ^{r}_{0} {\tilde{r}}^3 \rho ' d{\tilde{r}}, \end{aligned}$$
(33)

with \(\Pi \equiv p_{r}-p_{t}\). Also, it can be shown that (33) allows to write the Tolman mass as,

$$\begin{aligned} m_{T} = (m_{T})_{\Sigma }\left( \frac{r}{r_{\Sigma }}\right) ^3 + r^3\int ^{r_{\Sigma }}_{r} \frac{e^{( \nu + \lambda )/2}}{{{\tilde{r}}}} Y_{TF} d{\tilde{r}}, \end{aligned}$$
(34)

which can be considered as a solid argument to define the complexity factor by means of this scalar \(Y_{TF}\) given that this function, encompasses all the modifications produced by the energy density inhomogeneity and the anisotropy of the pressure on the active gravitational mass. In fact, this scalar represents a quantity that define the property of complexity of self-gravitating static spheres (the extension for the time dependent case is defined in [82]) that permits us to study them in a depeen way.

Note that the vanishing complexity condition (\(Y_{TF}=0\)) can be satisfied not only in the simplest case of isotropic and homogeneous system but also in all the cases where

$$\begin{aligned} \Pi =\frac{1}{2r^{3}}\int \limits _{0}^{r}{\tilde{r}}^{3}\rho ' d{\tilde{r}}. \end{aligned}$$
(35)

In this respect, Eq. (35) leads to a non–local equation of state that can be used as a complementary condition to close the system of EFE. Similarly, we can provide a particular value of \(Y_{TF}\) and use this information to find a family of solutions with the same complexity factor.

Specifically \(Y_{TF} = 0\) in terms of the complexity factors of seed solution (\(Y_{TF}^{(s)}\)) and extra source \((Y_{TF}^{\theta })\) is

$$\begin{aligned} Y_{TF} = Y_{TF}^{(s)} + Y_{TF}^{\theta } = 0, \end{aligned}$$
(36)

namely

$$\begin{aligned} Y_{TF}^{(s)} + k^2\Pi _{\theta }-\frac{k^2}{2r^3}\int _{0}^{r}{\tilde{r}}^3\rho _{\theta }'d{\tilde{r}} = 0. \end{aligned}$$
(37)

4 Temporal geometric deformation

So particularly if we consider the case where \(f = 0\) and \(g \ne \) 0, such choose of deformation over the metric in this work we call as Temporal Geometric Deformation (TGD). So, from of Eqs. (15), (16), (20)–(22) we obtain for this case that

$$\begin{aligned} \rho _{\theta }= & {} k^2\theta _{0}^{0} = 0, \end{aligned}$$
(38)
$$\begin{aligned} p_{\theta r}= & {} -k^2\theta _{1}^{1} = \alpha Z_{1}, \end{aligned}$$
(39)
$$\begin{aligned} p_{\theta t}= & {} -k^2\theta _{2}^{2} = \alpha Z_{2}, \end{aligned}$$
(40)

thus

$$\begin{aligned} \Pi _{\theta } = p_{\theta r}-p_{\theta t} = \frac{\alpha }{k^2}(Z_1-Z_2). \end{aligned}$$
(41)

In this way Eq. (37) becomes to

$$\begin{aligned} Y_{TF}^{(s)} = \alpha (Z_2-Z_1), \end{aligned}$$
(42)

implicitly it gives us

$$\begin{aligned} g'' + \frac{\alpha }{2}g'^2 + \frac{1}{2}\left( 2\xi '-\mu '-\frac{2}{r}\right) g'-\frac{4}{\alpha }e^{\mu }Y_{TF}^{(s)} = 0. \end{aligned}$$
(43)

Even one can consider for facility as seed solutions with zero complexity such that

$$\begin{aligned} g'' + \frac{\alpha }{2}g'^2 + \frac{1}{2}\left( 2\xi '-\mu '-\frac{2}{r}\right) g' = 0, \end{aligned}$$
(44)

which is a differential equation for g as unknown quantity due to \(\xi \) and \(\mu \) can be known since we can assign a seed solution in order to close our problem.

5 Model I: isotropic extension of Einstein’s universe solution

If we consider the known Einstein’s universe solution [83]

$$\begin{aligned} e^{\xi }= & {} constant \end{aligned}$$
(45)
$$\begin{aligned} e^{-\mu }= & {} 1-\frac{r^2}{C^2} \end{aligned}$$
(46)
$$\begin{aligned} k^2 \rho ^{(s)}= & {} \frac{3}{C^2} \end{aligned}$$
(47)
$$\begin{aligned} k^2 p^{(s)}= & {} -\frac{1}{C^2} \end{aligned}$$
(48)

as seed solution, we can solve (44) obtaining the geometrical deformation

$$\begin{aligned} g(r) = \frac{2}{\alpha }\ln {\left( \alpha \sqrt{r^2-C^2} + 2 A\right) } + \eta , \end{aligned}$$
(49)

where A and \(\eta \) are integration constants. Now using this geometric deformation in (15) we obtain the temporal metric

$$\begin{aligned} e^{\nu (r)} = B \left( \alpha \sqrt{r^2-C^2}+2 A\right) ^2, \end{aligned}$$
(50)

where \(B = e^{\alpha \eta }\). Thus using (46) and (50) in the EFEs (7)–(9) the matter sector obtained is

$$\begin{aligned} \rho (r)= & {} \frac{3}{k^2 C^2} \end{aligned}$$
(51)
$$\begin{aligned} p(r)= & {} \frac{3 \alpha (C^2-r^2)-2A \sqrt{r^2-C^2}}{k^2 C^2 \left( 2A \sqrt{r^2-C^2}+\alpha \left( r^2-C^2\right) \right) }. \end{aligned}$$
(52)

Note if we set \(\alpha = 0\) we return to the Einstein’s universe solution. Now using the continuity conditions given by Eqs. (30)–(32) we obtain

$$\begin{aligned} A= & {} \frac{3\left( C^2-R^2\right) }{2\sqrt{R^2-C^2}}\alpha , \end{aligned}$$
(53)
$$\begin{aligned} \frac{C^2}{R^2}= & {} \frac{R}{2M}, \end{aligned}$$
(54)
$$\begin{aligned} B= & {} -\frac{M}{2 \alpha ^2 R^3}. \end{aligned}$$
(55)

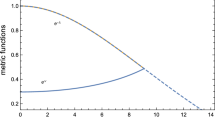
Indeed, in Figs. 1 and 2 the metrics profile for these solution is showed. Note that \(e^{\nu }\) is a monotonously increasing function of radial coordinate with \(e^{\nu (0)} = constant\), and \(e^{-\lambda }\) is monotonously decreasing with \(e^{-\lambda (0)} = 1\).

Fig. 1
figure 1

Temporal metric for Model I for compact factors: 0.1 (blue line), 0.15 (black line), 0.20 (red line) and 0.25 (green line)

Full size image
Fig. 2
figure 2

Radial metric for Model I for compact factors: 0.1 (blue line), 0.15 (black line), 0.20 (red line) and 0.25 (green line)

Full size image

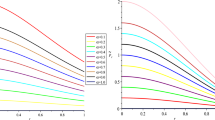
Also, in Fig. 3 we show the profile of p as a function of radial coordinates for different compactness factors. We notice that the pressure is finite at center and decreases monotonously toward the surface. Note as expected the density energy is constant since we have a homogeneous solution. Further in Fig. 4 the Dominant Energy Condition (DEC)

$$\begin{aligned} \rho (r)-p(r)\ge 0 \end{aligned}$$
(56)

is satisfied for \(r > 0\). We have checked that DEC is fulfill for all \(u = M/R < 0.375\).

Fig. 3
figure 3

Radial pressure for Model I for compact factors: 0.1 (blue line), 0.15 (black line), 0.20 (red line) and 0.25 (green line)

Full size image
Fig. 4
figure 4

\(k^2[\rho (r)-p(r)]\) for Model I: 0.1 (blue line), 0.15 (black line), 0.20 (red line) and 0.25 (green line)

Full size image

In addition, in Fig.5 we show the redshift \(z(r) = e^{-\nu /2}-1\) in function of radial coordinate. Note that z decreases outward at the surface as expected.

Fig. 5
figure 5

z(r) for Model I: 0.1 (blue line), 0.15 (black line), 0.20 (red line) and 0.25 (green line)

Full size image

Additionally, if one consider the rough approximation of the sound velocity for isotropic fluid \(v = \sqrt{\frac{p}{\rho }}\) inside the star, we can show the profile of v in the Fig. 6 as a function of radial coordinate. Note that the condition of causality is fulfilled, as expected [84]. We have checked that all physical conditions are fulfill for the compactness factor of \(u < 0.375\).

Fig. 6
figure 6

v(r) for Model I for compactness factor: 0.1 (blue line), 0.15 (black line), 0.20 (red line) and 0.25 (green line)

Full size image

It is worth mentioning that we have shown in this section that from a cosmological solution an isotropic and homogeneous interior solution was found through the TGD, which is well behaved from a physical point view. This result is important because any other cosmological solution could be used to obtain some interesting interior solution using the TGD.

6 Model II: an anisotropic solution

In this section we use the following convenient ansatz as seed solution to apply the same procedure used in the section 5 (namely the TGD)

$$\begin{aligned} e^{\xi }= & {} A(C r^2 +1)^4 \end{aligned}$$
(57)
$$\begin{aligned} e^{-\mu }= & {} \frac{1}{(C r^2 + 1)^{2}}, \end{aligned}$$
(58)

where A and C are constants (See the appendix 11). Then using this ansatz in (44) we obtain the deformation

$$\begin{aligned} g(r) = \beta + \frac{2}{\alpha }\ln {\left( \frac{8}{(C r^2+1)^2}-8 C\eta \right) }, \end{aligned}$$
(59)

where \( \beta \) and \(\eta \) are integration constants. So using (59) in (15) we obtain

$$\begin{aligned} e^{\nu } = a \left( \alpha -8 C \eta \left( C r^2+1\right) ^2\right) ^2, \end{aligned}$$
(60)

where \(a = A e^{\alpha \beta }\).

Now, using the EFE (7)–(9) the matter sector obtained is

$$\begin{aligned} \rho= & {} \frac{C \left( C r^2 \left( C r^2+3\right) +6\right) }{k^2 \left( C r^2+1\right) ^3}, \end{aligned}$$
(61)
$$\begin{aligned} p_{r}= & {} \frac{\alpha C \left( C r^2+2\right) }{k^2 \left( 8 C \eta \left( C r^2+1\right) ^4-\alpha \left( C r^2+1\right) ^2\right) }\nonumber \\&- \frac{8 C^2 \eta \left( C r^2+1\right) \left( C r^2 \left( C r^2+3\right) -6\right) }{k^2 \left( 8 C \eta \left( C r^2+1\right) ^4-\alpha \left( C r^2+1\right) ^2\right) }, \end{aligned}$$
(62)
$$\begin{aligned} p_{t}= & {} \frac{2 C \left( \alpha +24 C \eta \left( C r^2+1\right) ^2\right) }{k^2 \left( C r^2+1\right) ^3 \left( 8 C \eta \left( C r^2+1\right) ^2-\alpha \right) }. \end{aligned}$$
(63)

In summary, we have obtained the anisotropic solution

$$\begin{aligned} e^{\nu }= & {} a \left( \alpha -8 C \eta \left( C r^2+1\right) ^2\right) ^2, \end{aligned}$$
(64)
$$\begin{aligned} e^{-\lambda }= & {} \frac{1}{\left( C r^2+1\right) ^2}, \end{aligned}$$
(65)
$$\begin{aligned} \rho= & {} \frac{C \left( C r^2 \left( C r^2+3\right) +6\right) }{k^2 \left( C r^2+1\right) ^3}, \end{aligned}$$
(66)
$$\begin{aligned} p_{r}= & {} \frac{\alpha C \left( C r^2+2\right) }{k^2 \left( 8 C \eta \left( C r^2+1\right) ^4-\alpha \left( C r^2+1\right) ^2\right) }\nonumber \\&- \frac{8 C^2 \eta \left( C r^2+1\right) \left( C r^2 \left( C r^2+3\right) -6\right) }{k^2 \left( 8 C \eta \left( C r^2+1\right) ^4-\alpha \left( C r^2+1\right) ^2\right) }, \end{aligned}$$
(67)
$$\begin{aligned} p_{t}= & {} \frac{2 C \left( \alpha +24 C \eta \left( C r^2+1\right) ^2\right) }{k^2 \left( C r^2+1\right) ^3 \left( 8 C \eta \left( C r^2+1\right) ^2-\alpha \right) }. \end{aligned}$$
(68)

Moreover, using the continuity conditions at the surface of stellar compact object we obtain

$$\begin{aligned} \eta= & {} \frac{\alpha \left( C R^2+2\right) }{8 C \left( C^3 R^6+4 C^2 R^4-3 C R^2-6\right) }, \end{aligned}$$
(69)
$$\begin{aligned} C= & {} \frac{R^3-2 M R^2-\sqrt{R^6-2 M R^5}}{2 M R^4-R^5}, \end{aligned}$$
(70)
$$\begin{aligned} a= & {} \frac{\left( \sqrt{R^5 (R-2 M)}+16 M R^2-7 R^3\right) ^2}{64 \alpha ^2 R^5 (R-2 M)}. \end{aligned}$$
(71)

It is worth mentioning that from (70) and (71) is clear that compactness parameter satisfies \(R > 2M\), which is in accordance with the restriction that any stable configuration should be greater than Schwarzschild radius.

In Figs. 7 and 8 the metrics profile for these solution is showed. Note that \(e^{\nu }\) is a monotonously increasing function of radial coordinate with \(e^{\nu (0)} = constant\), and \(e^{-\lambda }\) is monotonously decreasing with \(e^{-\lambda (0)} = 1\).

Fig. 7
figure 7

Temporal metric for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image
Fig. 8
figure 8

Radial metric for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image

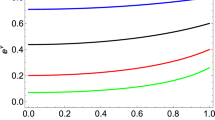
In Figs. 9, 10 and 11 we show the profile of matter sector as a function of radial coordinate for the values of compactness factor in the caption. All quantities, \(\rho \), \(p_{r}\) and \(p_{t}\) are finite at center of star and decrease monotonously toward the surface. Furthermore, \(p_{r}(0)=p_{t}(0)\) and \(p_{t}(r) > p_{r}(r)\) for all \(r > 0\), as expected (see Fig. 12). So the matter sector fulfill the physical requirements for acceptable interior solution.

Fig. 9
figure 9

Density energy for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image
Fig. 10
figure 10

Radial pressure for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image
Fig. 11
figure 11

Tangential pressure for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image
Fig. 12
figure 12

\(k^2[p_{t}(r)-p_{r}(r)]\) for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image

In the Figs. 13 and 14, we show the profile of \(\rho -p_r\) and \(\rho -p_t\) as functions of radial coordinate. From it can be seen that the DEC for an anisotropic fluid distribution, namely

$$\begin{aligned} \rho (r)-p_{r}(r)\ge 0\ \text {and}\ \rho (r)-p_{t}(r)\ge 0 \end{aligned}$$
(72)

condition is fulfill.

Fig. 13
figure 13

\(k^2[\rho (r)-p_{r}(r)]\) for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image
Fig. 14
figure 14

\(k^2[\rho (r)-p_{t}(r)]\) for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image

In the Fig. 15 we show the redshift z as a function of radial coordinate. Observe that z decreases outward and its value at the surface is less than the universal bound \(z_{bound} = 5.211\) [85].

Fig. 15
figure 15

z(r) for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image

In Figs. 16 and 17, we show that radial and tangential sound velocities are less than unity (we assumed that \(c = 1\)), as required to fulfill the causal condition.

Fig. 16
figure 16

\(v_{r}(r)\) for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image
Fig. 17
figure 17

\(v_{t}(r)\) for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image

We have checked that for the solution fulfill the fundamental physical conditions for those compactness parameters such that \(0.38 \le u = M/R \le 0.407\).

7 Convection stability

The stability of a self-gravitating sphere to convection implies the buoyancy principle inside of fluid, which implies that any fluid element displaced downward floats back to its initial position. It was demonstrate in [86] that for this principle to be fulfilled in self-gravitating compact objects it is necessary that

$$\begin{aligned} \rho ''(r) \le 0. \end{aligned}$$
(73)

The Model I automatically fulfill this condition since the density energy in this model is a constant. While to analyze the convection stability for the Model II we show the profile the \(\rho ''\) in function of radial coordinate in Fig. 18. We observe that the model II is stable after undergoing convective motion at the inner shells, while for the externals shells the models are unstable.

Fig. 18
figure 18

\(\rho ''\) for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line)

Full size image

8 Stability against collapse

It is expected that the Model I poses stability since its radial sound velocity monotonically decreasing with radius (see Fig.6). However, for the Model II the sound radial velocities profile is not monotonically decreasing with radius (see Fig. 16), which could be interpreted as a signal of instability, which may not necessarily be definitive given the effects of anisotropy [11, 87]. Then to analyze its stability we study the adiabatic index \(\Gamma \) given by

$$\begin{aligned} \Gamma = \frac{\rho + p_{r}}{p_{r}}\frac{d p_{r}}{d\rho }, \end{aligned}$$
(74)

which should be greater than 4/3 in order to avoid the gravitational collapse.

Then in this way we show the adiabatic index profile as a function of radial coordinate for Model II in Fig.19. We observe from Fig. 19 that Model II presents stability against collapse for the compactness factor \(u \ge 0.39\).

Fig. 19
figure 19

\(\Gamma \) for Model II for compact factors: 0.38 (blue line), 0.39 (black line), 0.40 (red line) and 0.407 (green line). The horizontal line correspond to the value of 4/3

Full size image

In summary, the two (one in the isotropic and the another one in the anisotropic pressure regime) models presented in this manuscript satisfy the fundamental physicals conditions detailed in [84], so they are good candidates to describe realistic fluid distributions with vanishing complexity for a restricting set of self-gravitating compact objects.

9 Discussion

The consideration of only a geometric deformation on the temporal metric of the space time of the seed solution within the GD by MGDe formalism could be thought of as something unnatural since such consideration requires that the extra source \(\theta _{\nu }^{\mu }\) has a zero density energy \(\rho _{\theta } = \theta _{0}^{0} = 0\), but however in this work we show that such deformation can be taken from a particular decoupling. So if one accept the fact that the extra source \(\theta _{\nu }^{\mu }\) is a mathematical artifice that helps us find effective physically acceptable interior solutions as found in the previous section (particularly we obtained new physically acceptable solutions with vanishing complexity in the isotropic and anisotropic pressure regime), the TGD results to be an alternative novel and interesting way to obtain new interior solutions. Even in the framework of the MGDe the physical meaning of this extra source can be complex since \(\theta _{1}^{1}\) and \(\theta _{2}^{2}\) given by (20)–(22), respectively, do not have the usual form of EFE for an realistic anisotropic source (which are named as “quasi-Einstein” in [69]). That said, we though that the TGD could be seen of as a very particular case of the GD through the MGDe. At the end of the day what matters is finding a physically acceptable interior solution given by the equations (6) and (10)–(12).

To be more precise if one consider the GD by MGDe taking in account the case of \(g \ne 0\) and \(f = 0\), (15) and (16) turns into

$$\begin{aligned} \nu \;\;\longrightarrow & {} \;\; \xi + \alpha g, \end{aligned}$$
(75)
$$\begin{aligned} e^{-\lambda }\;\;\longrightarrow & {} \;\; e^{-\lambda }\;, \end{aligned}$$
(76)

one can separate the system (7)–(9) into to set of equations if only if we supposed the extra source as

$$\begin{aligned} \theta _{\nu }^{\mu } = diag(0, \theta _{1}^{1}, \theta _{2}^{2}, \theta _{3}^{3}), \end{aligned}$$
(77)

namely, as source with \(\theta _{0}^{0} = 0\). Then considering such supposing we arrive at a first set of equations related to the seed sector sourced by the conserved energy-momentum tensor, \(T_{\mu \nu }^{(s)}\)

$$\begin{aligned} k^2 \rho ^{(s)}= & {} \frac{1}{r^2}-e^{-\lambda }\left( \frac{1}{r^2}-\frac{\lambda '}{r}\right) , \end{aligned}$$
(78)
$$\begin{aligned} k^2 p_r^{(s)}= & {} -\frac{1}{r^2}+e^{-\lambda }\left( \frac{1}{r^2}+\frac{\xi '}{r}\right) , \end{aligned}$$
(79)
$$\begin{aligned} k^2 p_{t}^{(s)}= & {} \frac{e^{-\lambda }}{4}\left( 2\xi ''+\xi '^2-\lambda '\xi '+2\frac{\xi '-\lambda '}{r}\right) , \end{aligned}$$
(80)

and the other set corresponding to source \(\theta _{\mu \nu }\)

$$\begin{aligned} k^2\theta _{0}^{0}= & {} 0 \end{aligned}$$
(81)
$$\begin{aligned} k^2\theta _{1}^{1}= & {} -\alpha \frac{e^{-\lambda }g'}{r} \end{aligned}$$
(82)
$$\begin{aligned} k^2\theta _{2}^{2} + \alpha Z= & {} -\alpha \frac{e^{-\lambda }}{4}\left( 2g'' + 2\xi 'g' -\lambda 'g' + \frac{2g'}{r}\right) , \end{aligned}$$
(83)

where \(Z = \alpha \frac{e^{-\lambda }g'^2}{4}\). Then we show that a decoupling of EFE through the TGD is mathematically possible. The source \(\theta _{\nu }^{\mu }\) given by (81)–(83) whose physical meaning is difficult to interpret, as it happens in the extended version of the MGDe (Even for example there is an interesting work where uses the framework of MGD which there is no decoupling of EFE to found anisotropic static solutions is developed in [88]) plays an important role in the TGD.

Thus, with the present work we can extend the thought number of possible interior solutions with vanishing complexity factor that satisfies the non local state equation (35) and that besides represents realistic stars composed with fluid in the isotropic and anisotropic pressure regime using the method presented here.

10 Conclusions

We had propose the GD through by TGD as a method to obtain new interior solutions for self-gravitating spheres with zero complexity in the isotropic and anisotropic fluid regime. We found two new models from which one (Model I) and other model (Model II) describe self-gravitating spheres in the isotropic and anisotropic regime of pressure, respectively, which fulfill the fundamental physical acceptability conditions for a restricted set of compactness factor; namely, (i) metric functions are regular inside the star, moreover \(e^{\nu (0)} = constant\) and \(e^{-\lambda (0)} = 1\), (iii) the material sector (density energy and pressures) are regular inside star and decrease monotonously outward, (iii) the solutions satisfies the dominant energy condition. Regarding the convection stability, we found that the Model I is stable, while the Model II has instabilities in the outer shells in this sense. Also, we found that the model II is stable against collapse for a restricted set of compactness parameters. Specifically, Model I are adequate to describe compact objects whose compactness factor is between (0, 0.375), while the Model II is adequate for \(u \in [0.39,0.407]\). Then in this sense we have obtaining two new interior solutions with the simplest factor complexity of self-gravitating objects.

It may be interesting to use the TGD to consider compact stellar bodies whose compactness factor is different from zero, as for example some compactness factor corresponding to a known solution. Even can be interesting to explore the response of the models presented here against perturbation of matter sector since they presents instability convection in the outer regions and stability against the collapse for a certain sets of compactness parameters. All these ideas could be addressed in future works.