Isotropic uncharged model with compactness and stable configurations

Abstract

In this study we have obtained a new exact model for relativistic stellar object by solving Einstein’s field equation with help of Buchdahl metric. The model is capable to represent some known compact stars like Her X-1,4U 1538-52 and SAX J1808.4-3658. The model satisfies the regularity, casuality, stability and energy conditions. Using the Tolman–Oppenheimer–Volkoff equations, we explore the hydrostatic equilibrium for an uncharged case. We have also compared these conditions with graphical representations that provide strong evidences for more realistic and viable models.

1 Introduction

An analysis of the solution of Einstein field equation shows that the exact solution plays an important role in the development of many areas of the gravitational field such as black hole solution, solar system test, gravitational collapse and so on. Generally in astrophysics compact stars are considered to fall in three categories, white dwarfs, neutron stars and black holes which are formed due to gradual gravitational collapses. This classification is based on the internal structure and composition of stars, where the former contains matter which is one of the densest forms found in the universe. According to the strange matter hypothesis, strange quark matter could be more stable than nuclear matter and thus neutrons star should largely be composed of pure quark matter. Possible observational signatures associated with theoretically proposed states of matter inside the compact stars have remained an active research area in astrophysics and different types of mathematical modeling of such compact objects being considered. The singularity-free interior solutions of the compact object have important consequences in relativistic astrophysics. The study of high-density objects like neutron stars, quark stars, and white dwarfs, form their microscopic composition and properties of dense matter is one of the most fundamental problems in modern astrophysics.

In general, it is important to measure the mass and radius [1, 2] of compact stars which depends on the equation of state [3,4,5,6]. The motivation to undertake such a task because the interior structure of compact stars can vary with masses. On the other hand, Buchdahl [7] proposed a method on the mass-radius ratio of relativistic fluid spheres which is an important contribution to study the stability of the fluid spheres. Thus the motivation of this study is to predict the mass and radius of compact stars. The mass and radius of compact stars such as Her X-1,4U 1538-52 and SAX J1808.4-3658 have been analyzed by Gangopadhyay et al. [10].

A super-dense compact star with mass M and radius R exhibit some limits on the upper bound of rotation frequency (eg. Keplerian limit), exceeding which the stability of the star is disrupted. Thus assuming such limit holds, a stable configuration of such object is of utmost importance in theoretical astrophysics. Our work provides a critical mass-radius-based analysis of a stable configuration. The candidate stars we have chosen to represent our model are Her X-1, 4U 1538-52 and SAX J1808.4-3658. We have not taken a possible rotation of Her X-1 into account. In [11] the rotation of Her X-1 is shown to be very slow compared to the critical angular velocity $\omega _{c} = \sqrt{\frac{GM}{b^3}}$, and hence the effect of this rotation on the $M-R$ relation and thus on our model, will be negligible. For the wind-fed binary X-ray pulsar 4U 1538-52 the orbital period is 8.38 days whereas Her X-1 has orbital period of 1.7 days. Thus, for the same reason as above the rotational aspect of this slow rotator has been ignored [12] SAX J1808.4-3658 is fairly a new X-ray pulsar that has been discovered by NASA’s Rossi X-ray Timing Explorer (RXTE) spacecraft . This candidate star for the verification our model parameters has a significant rotational aspect (spin period of 2.5 ms) in contrast to the other two. Still we have chosen this star which is one of seven known accreting ms X-ray pulsars, only because it is equally important to analyse the mass-radius behaviour of a compact object under different theoretical models to provide results helping distinguish the composition of the super-nuclear matter. Our model offers a new method of measuring the $M-R$ relation, which are painfully difficult to determine in accreting binary systems. Thus, even if this candidate star shows significant rotating behaviour. Our model exhibits a stable configuration to determine mass–radius relation for an accreting binary system.

The exact solution of Einstein-Maxwell field equations for a static isotropic astrophysical object is the continuous interest to a mathematician as well as physicists [13, 14]. A large number of solutions have studied in [15,16,17,18,19,20,21,22,23,24,25,26] for exact solution of Einstein-Maxwell field equations. Some pioneering work in relativity is given by Ivanov [27], Ray et al. [28], Stettner [29], Krori and Barua [30], Ray and Das [31], Pant and Negi [32], Florides [33], Dionysiou [34], Pant et al. [35], etc. for the charged fluid sphere.

The equation of state (EOS) is an important feature to describe a self-gravitating fluid when it comes to solving the field equations. Ivanov [27] has shown that the analytical solutions in the static, spherically symmetric uncharged case of a perfect fluid with linear EOS is an extremely difficult problem. Sharma and Maharaj [36] have demonstrated this complexity in the case of a static, spherically symmetric uncharged anisotropic fluid. In the resent model we choose the Buchdahl metric and solve the system of field equations and obtain a linear EOS.

The algorithm for an anisotropic uncharged fluid has been done by Maurya et al. [37], Lake and Herrera [38, 39, 41]. In this work, Lake [38, 39] has considered an algorithm and choose a single monotonic function which generates a static spherically symmetric perfect fluid solutions of Einstein’s equations. Against the above studies, we have considered an uncharged isotropic fluid distribution in the context of the formation of the compact stars and find a new solution in Sect. 2, whereas Sect. 3 consists of physical conditions for well-behaved solutions. In Sect. 4, the matching condition of interior metric to an exterior Reissner-Nordstrom line element and determining the constant coefficients have been done. Stability analysis of compact objects and for better illustration of our result, the relevant physical quantities are presented by table and figure in Sect. 5. Finally in Sect. 6, we have drawn contains about present model.

2 Field equations for uncharged fluid sphere in Schwarzschild coordinates

Let us consider the spherically symmetric metric in Schwarzschild Coordinates

$$\begin{aligned} {\text {d}}s^{2}=-e^{\lambda (r)}{\text {d}}r^{2} -r^{2}({\text {d}}\theta ^{2}+\sin ^{2}\theta {\text {d}}\phi ^{2})+e^{\nu (r)}{\text {d}}t^{2} \end{aligned}$$

(1)

where $\lambda (r)$ and $\nu (r)$ are the functions of r only. The Einstein equation for a perfect fluid distribution is given by

$$\begin{aligned} R^{i}_{j}-\dfrac{1}{2}R\delta ^{i}_{j}=-\kappa \big [(c^{2}\rho +p)\nu ^{i}\nu _{j}-p\delta ^{i}_{j}\big ] \end{aligned}$$

(2)

where $\kappa =\dfrac{8\pi G}{c^{4}}$, with G and c are the gravitational constant and speed of light in vacuum, respectively. Here $\rho$ and p denote matter density and fluid pressure respectively. The $\nu ^{i}$ is the time-like 4-velocity vector such that

$$\begin{aligned} \nu ^{i}\nu _{i}=1 \end{aligned}$$

In view of the metric (1) the Einstein field equations are given by

$$\begin{aligned} \dfrac{\nu '}{r}e^{-\lambda }-\dfrac{(1-e^{-\lambda })}{r^{2}}=\kappa p \end{aligned}$$

(3)

$$\begin{aligned} \bigg (\dfrac{\nu ''}{2}-\dfrac{\lambda '\nu '}{4}+\dfrac{\nu ^{'2}}{4}+\dfrac{\nu '-\lambda '}{2r}\bigg )e^{-\lambda }=\kappa p \end{aligned}$$

(4)

$$\begin{aligned} \dfrac{\lambda '}{r}e^{-\lambda }+\dfrac{(1-e^{-\lambda })}{r^{2}}=\kappa c^{2}\rho \end{aligned}$$

(5)

where prime $(')$ denotes the differentiation with respect to r. Now we consider a well known form of metric potential, which was proposed by Buchdahl [7] of the form as

$$\begin{aligned} e^{\lambda }=\dfrac{K(1+Cr^{2})}{K+Cr^{2}},~~~~K>1 \end{aligned}$$

(6)

where K and C are arbitrary constant. The metric function (6) is regular and non-singular at the center of the star which satisfies the primary physical requirements of a realistic star. Buchdahl metric could also be extendable for positive and negative values of the spheroidal parameter K. In the range of $0<K<1$, the pressure and density will be negative or increasing towards the boundary [8]. When $K=0$, one can get the Schwarzschild interior solution and for $K=1$ the hypersurfaces $\{t={\text {constant}}\}$ are flat. When $K=-CR^2$, one could get the Vaidya and Tikekar [9] solution. In the present model, we consider $K>1.$ Now using (6), the Eqs. (3)–(5) reduce to the following form

$$\begin{aligned} \dfrac{(K+Cr^{2})}{K(1+Cr^{2})}\bigg [\dfrac{-2y'}{ry}+\dfrac{C(K-1)}{K+Cr^{2}}\bigg ]=-\kappa p \end{aligned}$$

(7)

$$\begin{aligned} \dfrac{C(K-1)(3+Cr^{2})}{K(1+Cr^{2})^{2}}=\kappa c^{2}\rho \end{aligned}$$

(8)

$$\begin{aligned} \dfrac{(K+Cr^{2})}{K(1+Cr^{2})}\bigg [\dfrac{y''}{y}-\dfrac{y'}{ry}+\dfrac{C(K-1)r(Cr-y'/y)}{(K+Cr^{2})(1+Cr^{2})} \bigg ]=0 \end{aligned}$$

(9)

where $e^{\nu } =y^2$. Now to solve the Eq. (9) we introduce the new variables define by

$$\begin{aligned} X=\sqrt{\dfrac{K+Cr^{2}}{K-1}},~~~~K>1 \end{aligned}$$

(10)

and

$$\begin{aligned} y(X)=(X^{2}-1)^{1/4}\varPsi (X) \end{aligned}$$

(11)

Using the Eqs. (10) and (11), the Eq. (9) reduce to the following form of second-order differential equation (see Appendix for details)

$$\begin{aligned} \dfrac{{\text {d}}^{2}\varPsi }{{\text {d}}X^{2}}+I\varPsi =0 \end{aligned}$$

(12)

where

$$\begin{aligned} I=\dfrac{2(1-2K)(1-X^2)-5X^2}{4(1-X^{2})^2} \end{aligned}$$

(13)

In order to solve Eq. (12) more easily if we set $K=\frac{7}{4}$, then the Eq. (12) takes the form

$$\begin{aligned} \varPsi ''-\dfrac{5}{4(1-X^{2})^{2}}\varPsi =0 \end{aligned}$$

(14)

So the solution of (14) is given as

$$\begin{aligned} \varPsi (X)=(X+1)\left[ A_{1}\bigg |\dfrac{X+1}{X-1}\bigg |^{(0.25)} +A_{2}\bigg |\dfrac{X+1}{X-1}\bigg |^{(-1.25)} \right] \end{aligned}$$

(15)

where $A_1$ and $A_2$ are arbitrary constants of integration. Now put the value of $\varPsi (X)$ from Eq. (15) and $X=\sqrt{\dfrac{K+Cr^{2}}{K-1}}$ into the Eq. (11), we get

$$\begin{aligned} y(r)=\left[ \dfrac{4(1+Cr^{2})}{3}\right] ^{1/4}\Big (g(r)+1\Big )\Bigg [A_{1}\Big |F(r)\Big |^{(0.25)} +A_{2}\Big |F(r)\Big |^{(-1.25)} \Bigg ] \end{aligned}$$

(16)

where $g(r)=\sqrt{\frac{7+4Cr^2}{3}},~~~F(r)=\dfrac{5+2Cr^{2}+3g(r)}{2(1+Cr^2)}$ . Therefore the expressions of density and pressure are given by

$$\begin{aligned} \kappa c^{2}\rho =\dfrac{3C(3+Cr^{2})}{7(1+Cr^{2})^{2}} \end{aligned}$$

(17)

$$\begin{aligned} \kappa p=\dfrac{2(7+4Cr^2)}{7ry(r)(1+Cr^2)}\Bigg [ N_{1}(r)\Bigg (A_{1}\Big |F(r)\Big |^{(0.25)} +A_{2}\Big |F(r)\Big |^{(-1.25)}\Bigg )+N_{2}(r)N_{3}(r)N_{4}(r)\Bigg ]-\dfrac{3C}{7(1+Cr^2)} \nonumber \\ \end{aligned}$$

(18)

where

$N_{1}(r)=\dfrac{2Cr}{3} \Bigg [\big (g(r)+1\big )\Bigg (\frac{4(1+Cr^2)}{3}\Bigg )^{-3/4}+2\Bigg (\frac{4(1+Cr^2)}{3}\Bigg )^{1/4}g(r)\Bigg ],~~~~~~~N_{4}(r)=\dfrac{-8Cr}{3g(r)\big (g(r)-1\big )^2}$

$N_{2}(r)=\Bigg (\frac{4(1+Cr^2)}{3}\Bigg )^{1/4}\big (g(r)+1\big ),~~~~~~~~~~~N_{3}(r)=\Bigg [A_{1}(0.25)\Big |F(r)\Big |^{(-0.75)} +A_{2}(-1.25)\Big |F(r)\Big |^{(-2.25)} \Bigg ]$

Fig. 1

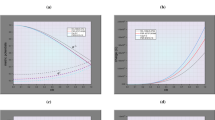
Variation of metric potential $e^{\lambda }$ (left) and $e^{\nu }$ (right) with respect to fractional radius r/R for compact star SAX J1808.4-3658,4U 1538-52 and Her X-1. For plotting this figure the numerical values of physical parameters and constants are as follows: (1) $K = 1.75, CR^2 =0.4137, M$ =$0.9M_{\odot }$ and $R =14.35\,{\text {km}}$ for SAX J1808.4-3658, (2) $K =1.75,CR^2=0.4138,M =$ $0.87M_{\odot }$ and $R =13.87\, {\text {km}}$ for 4U 1538-52 and (3) $K =1.75,CR^2=0.414,M =$ $0.85M_{\odot }$ and $R =13.548\, {\text {km}}$ for Her X-1

3 Physical features for well behaved solution

• 1. From Eq. (6), we observe $(e^{\lambda })_{(r=0)}=1$ and $(e^{\nu })_{(r=0)}>0$. This shows that metric potentials are singularity free and positive at center. It is monotonically increasing with increasing the radius of the compact star(see Fig. 1).

• 2. Pressure p should be zero at the boundary $r=R.$

• 3. $({\text {d}}p/{\text {d}}r)_{r=0}=0$ and $({\text {d}}^{2}p/{\text {d}}r^{2})_{r=0}<0,$ so that pressure gradient ${\text {d}}p/{\text {d}}r$ is negative for $0<r \le R$.

• 4. $({\text {d}}\rho /{\text {d}}r)_{r=0}=0$ and $({\text {d}}^{2}\rho /{\text {d}}r^{2})_{r=0}<0,$ so that density gradient $d\rho /dr$ is negative for $0<r \le R$.

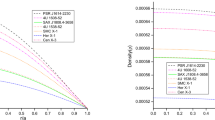
  The above two condition implies that the pressure and density should be maximum at the center and monotonically decreasing towards the surface (see Fig. 2).

• 5. The velocity of sound $({\text {d}}p/c^{2}{\text {d}}\rho )^{1/2}$ should be less than the speed of light throughout the fluid sphere $(0\le r\le R)$. This is called causality condition.

• 6. The ratio of pressure and density $(p/c^{2}\rho )$ should be monotonically decreasing with the increase in r. (see Fig. 2)

• 7. $c^{2}\rho \ge p>0$ or $c^{2}\rho \ge 3p>0,0\le r\le R$, where former inequality denotes weak energy condition (WEC) and later inequality denotes strong energy condition (SEC).

Fig. 2

Behaviour of pressure (p in ${\text {km}}^{-2}$ left), density ($\rho$ in ${\text {km}}^{-2}$ middle) and $p/\rho$(right) vs. fractional radius r/R for SAX J1808.4-3658, 4U 1538-52 and Her X-1. For plotting this figure the numerical values of physical parameters and constants with $G=c=1$ are as follows: (1) $K = 1.75, CR^2 =0.4137, M$ =$0.9M_{\odot }$ and $R =14.35\, {\text {km}}$ for SAX J1808.4-3658, (2) $K =1.75,CR^2=0.4138,M =$ $0.87M_{\odot }$ and $R =13.87\, {\text {km}}$ for for 4U 1538-52 , (3) $K =1.75,CR^2=0.414,M =$ $0.85M_{\odot }$ and $R =13.548\, {\text {km}}$ Her X-1

4 Matching conditions of boundary

The solution is smoothly connected to the pressure free boundary with the Schwarzschild exterior metric

$$\begin{aligned} {\text {d}}s^{2}=-\bigg (1-\dfrac{2M}{r}\bigg )^{-1}{\text {d}}r^{2}-r^{2}({\text {d}}\theta ^{2}+\sin ^{2}\theta {\text {d}}\phi ^{2})+\bigg ( 1-\dfrac{2M}{r}\bigg ){\text {d}}t^{2} \end{aligned}$$

(19)

In this model, the spacetime is timelike so we consider the metric signature $(-,-,-,+)$ see further details in [40]. Besides the above, the smooth joining with the Schwarzschild metric which requires the continuity of $e^{\lambda }$ and $e^{\nu }$ across the boundary $r=R$ and we get

$$\begin{aligned} e^{-\lambda }= & {} 1-\dfrac{2M}{R} \end{aligned}$$

(20)

$$\begin{aligned} y^{2}= & {} 1-\dfrac{2M}{R} \end{aligned}$$

(21)

$$\begin{aligned} p(R)= & {} 0. \end{aligned}$$

(22)

Using the Eqs. (21) and (22), we get the expressions of arbitrary constant $A_1$ and $A_2$ as follow

$$\begin{aligned} \dfrac{A_1}{A_2}= & {} \dfrac{M_{1}(R)N_{1}(R)G(R)+M_{1}(R)N_{4}(R)N_{2} (R)G_{1}(R)-M_{2}(R)N_{2}(R)G(R)}{M_{2}(R)N_{2}(R)G_{2}(R) +M_{1}(R)N_{2}(R)N_{4}(R)G_{3}(R)-M_{1}(R)N_{1}(R)G_{2}(R)} \end{aligned}$$

(23)

$$\begin{aligned} A_{2}= & {} \dfrac{\sqrt{\frac{7+4CR^2}{7(1+CR^2)}}}{\left[ \dfrac{4(1+Cr^{2})}{3}\right] ^{1/4}\Big (g(R)+1\Big )\Bigg [\frac{A_{1}}{A_{2}}\Big |F(R)\Big |^{(0.25)} +\Big |F(R)\Big |^{(-1.25)} \Bigg ]} \end{aligned}$$

(24)

The expression of mass M is given as

$$\begin{aligned} M=\frac{R}{2}\Bigg [ 1-\dfrac{7+4CR^2}{7(1+CR^2)}\Bigg ] \end{aligned}$$

(25)

where the expressions of $g(R),\,F(R), \, N_1(R),\, N_2(R),\, N_4(R),\,M_1(R),\, M_2(R),\, G(R),\,G_1(R),\, G_2(R),$ and $G_3(R)$ in the Eqs. (23) and (24) are given in the Appendix.

5 Stability analysis of compact objects

In this section, we have studied the physical properties of interior of the fluid sphere and equilibrium conditions under different forces.

5.1 Causality condition

The velocity of sound $\dfrac{{\text {d}}p}{c^2{\text {d}}\rho }$ should be less than the speed of light. Here we fix $c=1$, and obtained velocity of sound for the uncharged fluid matter. Herrera [42] states that for the stability, the value of sound belongs to the interval $0<v^2=\frac{dp}{d\rho }<1$ and should be monotonically decreasing away from the center. Now from the Eqs. (17) and (18), we get the expression of the velocity of sound

$$\begin{aligned} \dfrac{{\text {d}}p}{{\text {d}}\rho }=\frac{L_{1}(r)\bigg (L_{2}(r)+L_{3}(r)\bigg )-L_{4}(r)L_{5}(r)-L_{6}(r)\bigg (L_{1}(r)\bigg )^2}{\bigg (L_{1}(r)\bigg )^2L_{7}(r)} \end{aligned}$$

(26)

where $L_{1}(r)=\left[ \dfrac{4(1+Cr^{2})}{3}\right] ^{1/4}\Big (g(r)+1\Big )\Bigg [\Big |F(r)\Big |^{(0.25)} +\frac{A_{2}}{A_{1}}\Big |F(r)\Big |^{(-1.25)} \Bigg ]$

$L_{2}(r)=\dfrac{-12C^2r}{7(1+Cr^2)^2}\Bigg [N_{1}(r) S(r)+N_{2}(r)S_{1}(r)N_{4}(r)\Bigg ],$

$L_{4}(r)=\dfrac{2C(7+4Cr^2)}{7(1+Cr^2)}\Bigg [N_{1}(r)S(r)+N_{2}(r)S_{1}(r)N_{4}(r) \Bigg ]$

$L_{3}(r)=\dfrac{2C(7+4Cr^2)}{7(1+Cr^2)}\Bigg [ S_{2}(r)S(r)+2N_{1}(r)S_{1}(r)N_{4}(r)+N_{2}(r)S_{3}(r)S_{1}(r)+N_{2}(r)N_{4}(r)S_{4}(r)\Bigg ]$

$L_{5}(r)=N_{1}(r)S(r)+N_{2}(r)S_{1}(r)N_{4}(r),~~~~ L_{6}(r)=\dfrac{-6C^2r}{7(1+Cr^2)^2},~~~~~~L_{7}(r)=\dfrac{-6C^2r(5+Cr^2)}{7(1+Cr^2)^3}$

$S(r)=\Bigg [\Big |F(r)\Big |^{1/4} +\frac{A_{2}}{A_{1}}\Big |F(r)\Big |^{-5/4} \Bigg ],~~~~S_{1}(r)=\Bigg [(0.25)\Big |F(r)\Big |^{-3/4} +\frac{A_{2}}{A_{1}}(-1.25)\Big |F(r)\Big |^{-9/4} \Bigg ]$

$S_{2}(r)=\frac{8Cr}{9}\left[ -\dfrac{6\big (g(r)+1\big )}{\Big (4\frac{4(1+Cr^2)}{3}\Big )^{7/4}}+\dfrac{2}{g(r)\Big (\frac{4(1+Cr^2)}{3}\Big )^{3/4}}-\dfrac{2{\Big (\frac{4(1+Cr^2)}{3}\Big )^{1/4}}}{\big (g(r)\big )^3}\right] ,~~~~~~S_{3}(r)=\dfrac{16Cr}{3g(r)\bigg (g(r)-1\bigg )^3}$

$S_{4}(r)=\Bigg [(-3/16)\Big |F(r)\Big |^{-7/4}-\frac{A_{2}}{A_{1}}(-45/16)\Big |F(r)\Big |^{-13/4} \Bigg ]N_{4}(r)$

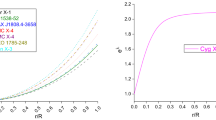
For better understanding, we use the graphical representation to represent Fig. 3.Thus, it is clear that in Fig. 3, the velocity of sound lies within the proposed interval and therefore this result maintains stability.

Fig. 3

Behaviour of velocity of sound vs. fractional radius r/R for SAX J1808.4-3658,4U 1538-52 and Her X-1. For plotting this figure we have employed data set values of physical parameters and constants which are the same as used in Fig. 2

5.2 Tolman–Oppenheimer–Volkoff (TOV) equations

The general-relativistic hydrostatic equations were developed and used to models of compact stars by Tolman, Oppenheimer and Volkoff in [43]. These equations are obtained from Einstein-Maxwell field equations when metric is static and isotropic.The latter hypothesis is predicted to be a good approximation for the densest interior of the static compact star because the strong gravitational force is balanced by a huge pressure and rigid body forces have a negligible effect on the structure. In the connection of the microscopic theory for the relationship between pressure and energy density, and the mass, this equation gives an equilibrium solution. The Tolman-Oppenheimer-Volkoff (TOV) equation [43, 44] in the presence of charge is given by

$$\begin{aligned} -\frac{M_G(\rho +p)}{r^2}e^{\frac{\lambda -\nu }{2}}-\frac{{\text {d}}p}{{\text {d}}r}+ \sigma \frac{q}{r^2}e^{\frac{\lambda }{2}} =0, \end{aligned}$$

(27)

where $\sigma$ is charge density, q is a charge and $M_G$ is the effective gravitational mass. It is derived from Tolman-Whittaker formula [45] and written in the following form

Fig. 4

Behaviour of different forces(in ${\text {km}}^{-3}$ with $G = c =1$ ) vs. fractional radius r/R. For plotting this figure the numerical values of physical parameters and constants are as follows: (1) $K =1.75,CR^2=0.4137,M =$ $0.9M_{\odot }$ and $R =14.35\, {\text {km}}$ for SAX J1808.4-3658 (left), (2) Her X-1 (left) $K = 1.74, CR^2 =0.4138, M$ =$0.87M_{\odot }$ and $R =13.87\, {\text {km}}$ for 4u 1538-52 (middle) and (3) $K = 1.74, CR^2 =0.414, M$ =$0.85M_{\odot }$ and $R =13.458\, {\text {km}}$ for Her X-1 (left)

$$\begin{aligned} M_G(r)=\frac{1}{2}r^2 \nu ^{\prime }e^{(\nu - \lambda )/2}. \end{aligned}$$

(28)

Plugging the value of $M_G(r)$ in Eq. (27), we get

$$\begin{aligned} -\frac{\nu '}{2}(\rho +p)-\frac{{\text {d}}p}{{\text {d}}r}+\sigma \frac{q}{r^2}e^{\frac{\lambda }{2}} =0, \end{aligned}$$

(29)

But in our model, we have considered an uncharged isotropic fluid distribution, i.e. the charge (q ) is vanishing, so Eq. (29) becomes

$$\begin{aligned} -\frac{\nu '}{2}(\rho +p)-\frac{{\text {d}}p}{{\text {d}}r} =0, \end{aligned}$$

(30)

The above equation can be expressed into three different components gravitational force $(F_g)$, hydrostatic force $(F_h)$ and electric force $(F_e)$, which are defined as:

$$\begin{aligned} F_g= & {} -\frac{\nu '}{2}(\rho +p)=\dfrac{Z'}{8\pi Z}(\rho +p) \end{aligned}$$

(31)

$$\begin{aligned} F_h= & {} -\frac{{\text {d}}p}{8\pi {\text {d}}r}=-\frac{1}{8\pi }\left[ \frac{L_{1}(r)\bigg (L_{2}(r)+L_{3}(r)\bigg )-L_{4}(r)L_{5}(r)}{\bigg (L_{1}(r)\bigg )^2}-L_{6}(r) \right] \end{aligned}$$

(32)

$$\begin{aligned} F_e= & {} 0 \end{aligned}$$

(33)

where we use the same notation as above. Figure 4 represents the behavior of the generalized TOV equations. We observed from these figures that the system is balanced by the gravitational force $(F_g)$ which is counterbalanced by hydrostatic force $(F_h)$ and the system attains a static equilibrium.

5.3 Energy condition

Fig. 5

Behaviour of different energy conditions (in ${\text {km}}^{-2}$ with $G = c =1$) vs. fractional radius curves are plotted for the SEC,WEC and NEC for the compact objects SAX J1808.4-3658, 4U 1538-52 and Her X-1. For plotting this figure we have employed data set values of physical parameters and constants which are the same as used in Fig. 2

The energy conditions depend on the matter density and pressure that follow certain restrictions. Basic information about the energy condition in [15]. Here we focus on the (1) null energy condition, (2) weak energy conditions and (3) strong energy condition , which have the following inequalities

$$\begin{aligned}&\rho \ge 0 \end{aligned}$$

(34)

$$\begin{aligned}&\rho -p \ge 0 \end{aligned}$$

(35)

$$\begin{aligned}&\rho -3p \ge 0 \end{aligned}$$

(36)

Using these inequalities we justify the nature of energy conditions for the specific stellar configuration as shown in Fig. 5, that obey the energy conditions and our model satisfy all conditions throughout the spacetime.

5.4 Adiabatic index

In order to have an equilibrium configuration, the matter must be stable against the collapse of local regions. This requires Le Chateliers principle, also known as local or microscopic stability condition, that the pressure must be monotonically decreasing function of r such that $\dfrac{{\text {d}}p}{{\text {d}}\rho }\ge 0.$ Heintzmann and Hillebrandt [46] also proposed that compact star with the equation of state are stable for adiabatic index $\varGamma =\big (\frac{p+\rho }{p}\big )\frac{{\text {d}}p}{{\text {d}}\rho } > 4/3.$ Figure 6 show that $\varGamma > 4/3$, so model developed in this paper is stable.

Fig. 6

Behaviour of adiabatic constant $(\varGamma )$ vs. fractional radius r/R for SAX J1808.4-3658,4U 1538-52 and Her X-1. For plotting this figure we have employed data set values of physical parameters and constants which are the same as used in Fig. 2

5.5 Surface redshift

The gravitational redshift $Z_{s}$ within a static line element can be obtained as

$$\begin{aligned} Z_{s}=\sqrt{g_{tt}(R)}-1=\sqrt{1-\frac{2M}{R}}-1 \end{aligned}$$

(37)

where $g_{tt}(R)=e^{\nu (R)}=1-\frac{2M}{R}$

Fig. 7

Behaviour of Redshift vs. fractional radius r/R for SAX J1808.4-3658, 4U 1538-52 and Her X-1. For plotting this figure we have employed data set values of physical parameters and constants which are the same as used in Fig. 2

Fig. 8

Behaviour of pressure p (in ${\text {km}}^{-2}$) vs. energy density $\rho$ (${\text {km}}^{-2}$) for SAX J1808.4-3658, 4U 1538-52 and Her X-1

Fig. 9

Behaviour of mass vs. central density (left) and ${\text {d}}M/{\text {d}}\rho _{0}$ vs. central density (right) for SAX J1808.4-3658, 4U 1538-52 and Her X-1

The maximum possible value of redshift should be at the center of the star and decrease with the increase of radius. Buchdahl [7] and Straumann [47] have shown that for an isotropic star the surface redshift $Z_{s}\le 2$. For an anisotropic star Bohmer and Harko [48] showed that the surface redshift could be increased up to $Z_{s}\le 5$. Ivanov [27] modified the maximum value of redshift and showed that it could be as high as $Z_{s}= 5.211$. In this model, we have $Z_{s}\le 1$ for compact stars SAX J1808.4-3658,4U 1538-52 and Her X-1. Also it is decreasing towards the boundary (see Fig. 7).

5.6 Equation of state (EOS)

The equation of state (EoS) i.e. a relation between pressure and density is an important features of neutron star. So in this section we have discuss about EoS. It is worth-while to specify that different equation of state (EoS) of the neutron star lead to different mass–radius (M-R) relation. Many authors [49,50,51] have suggested that the EoS $P=P(\rho )$ can be well approximated by a linear function of the energy density $\rho$ of compact star at high densities. Some researchers have also expressed more approximated form of the equation of state (EOS) $P=P(\rho )$ as a linear function of energy density $\rho$ (in details see [52,53,54]). Here we find the EoS in a linear function of form $P=P(\rho )$ as,

$$\begin{aligned} \kappa \,p_r(r)= & {} \frac{2\,(7+4\,{\tilde{\rho _1}} )}{7\,G(\rho _1)\,(1+ {\tilde{\rho _1}})} \times \left[ f_2(\rho _1)\, \Bigg (~ G_1(\rho _{1s})\,\bigg |\phi (\rho _1)\bigg |^{0.25} +\,\bigg |\phi (\rho _1)\bigg |^{-1.25}~\Bigg ) -f_{1}(\rho _1)\,f_{3}(\rho _1)\,f_{4}(\rho _1) \,\right] \,\nonumber \\&-\frac{3C}{7\,(1+{\tilde{\rho _1}})}, \end{aligned}$$

(38)

where,

$G(\rho _1)= \bigg [\frac{4 (1+\tilde{\rho _1})}{3}\bigg ]^{\frac{1}{4}} [f(\rho _1)+1)]\,\Bigg [~ G_1(\rho _{2s})\,\bigg |\phi (\rho _1)\bigg |^{0.25} + \bigg |\phi (\rho _1)\bigg |^{-1.25}~\Bigg ],$

$f_{2}(\rho _1)=\dfrac{2C}{3} \Bigg [\big (f(\rho _1)+1\big )\Bigg (\frac{4(1+\tilde{\rho _1})}{3}\Bigg )^{-3/4} +2\Bigg (\frac{4(1+\tilde{\rho _1})}{3}\Bigg )^{1/4}f(\rho _1)\Bigg ]$,

$f_{3}(\rho _1)=\Bigg [G_{1}(\rho _{1s})(0.25)\bigg |\phi (\rho _1)\bigg |^{(-0.75)} +(-1.25)\bigg |\phi (\rho _1)\bigg |^{(-2.25)} \Bigg ],~~~f_{4}(\rho _1)=\dfrac{-8C}{3f(\rho _1)\big (f(\rho _1)-1\big )^2}$

$f_{1}(\rho _1)=\Bigg (\frac{4(1+\tilde{\rho _1})}{3}\Bigg )^{1/4}\big (f(\rho _1)+1\big ),~~~~~~~\phi (\rho _1)=\dfrac{5+2\tilde{\rho _1}+3f(\rho _1)}{2(1+\tilde{\rho _1})},$

$\tilde{\rho _1}=\frac{(1-2\,\rho _1) \pm \,\sqrt{1+8\,\rho _1}}{2\,\rho _1},~~~ \rho _1=\frac{7\,\kappa \,\rho }{3\,C},~~~f(\rho _1)=\sqrt{\frac{7+4\,\tilde{\rho _1}}{3}} ,$

$G_1(\rho _{1s})=\frac{f_2(\rho _{1s})\,L_2(\rho _{1s})\,\bigg |\phi (\rho _{1s})\bigg |^{-5/4}-\frac{L(\rho _{1s})}{f^2(\rho _{1s})}\,\bigg |\phi (\rho _{1s})\bigg |^{-5/4} + S(\rho _{1s})}{\frac{L(\rho _{1s})}{f^2(\rho _{1s})}\,\bigg |\phi (\rho _{1s})\bigg |^{1/4}-f_2(\rho _{1s})\,L_2(\rho _{1s})\,\bigg |\phi (\rho _{1s})\bigg |^{1/4} +P(\rho _{1s})},$

$L(\rho _{1s})=\bigg [\frac{4 (1+\tilde{\rho _{1s}})}{3}\bigg ]^{\frac{1}{4}} [f(\rho _{1s})+1],~~~L_2(\rho _{1s})=\frac{8\,f(\rho _{1s})}{9\,(1+\tilde{\rho _{1s}})}$

$f_{2}(\rho _{1s})=\dfrac{2C}{3} \Bigg [\big (f(\rho _{1s})+1\big )\Bigg (\frac{4(1+\tilde{\rho _{1s}})}{3}\Bigg )^{-3/4}+\,2\Bigg (\frac{4(1+\tilde{\rho _{1s}})}{3}\Bigg )^{1/4}f(\rho _{1s})\Bigg ], ~~~$

$P(\rho _{2s})=f_{1}(\rho _{2s})\,L_2(\rho _{1s})\,(-1/4)\,\bigg |\phi (\rho _{1s})\bigg |^{-3/4},~~~~\phi (\rho _{1s})=\dfrac{5+2\tilde{\rho _{1s}}+3f(\rho _{1s})}{2(1+\tilde{\rho _{1s}})},$

$f_{1}(\rho _{1s})=2\,\bigg [\frac{4 (1+\tilde{\rho _{1s}})}{3}\bigg ]^{\frac{1}{4}}\,\frac{[f(\rho _{1s})+1]}{[f(\rho _{1s})-1]^2}, ~~~ S(\rho _{1s})=f_{1}(\rho _{1s})\,L_2(\rho _{1s})\,(7/4)\,\bigg |\phi (\rho _{1s})\bigg |^{-9/2},$

$\tilde{\rho _{1s}}=\frac{(1-2\,\rho _{1s}) \pm \,\sqrt{1+8\,\rho _{1s}}}{2\,\rho _{1s}},~~~ \rho _{1s}=\frac{7\,\kappa \,\rho _s}{3\,C},~~~f(\rho _{2s})=\sqrt{\frac{7+4\,\rho _{1s}}{3}}.$ $\rho$ and $\rho _s$

From Eq. (38), we can observe that the pressure is a function of density, which describe the an EoS for SAX J1808.4-3658, 4U 1538-52 and Her X-1. In an argument, Dey et al. [49] have proposed a new type of EoSs mainly describe strange matter. This was later generalised by Gondek-Rosinska et al. [51] in a linear function of density ($\rho$), as

$$\begin{aligned} p = \alpha \,(\rho -\rho _s), \end{aligned}$$

(39)

where $\rho _s$ denotes surface density and $\alpha$ is non-negative constant. Harko and Cheng [50] have demonstrated that the equation (39), gives the maximum mass of a strange star which is $M_{\text {max}} = 1.83 M_{\odot }$ when $\rho _s = 4B$ ( $B= 56 {\text {MeV fm}}^{3}$). In the present paper, we have developed the same relation as considered by [51]. In that work, we have shown that Eq. (39) corresponds to self-bound matter at the surface density $\rho _s$. Figure 8 represents the behavior of pressure verses density for compact stars with realistic EoS . In Fig. 8, we observe that the pressure p vanishes at surface density $\rho _s$ i.e. at the boundary of our model. This implies that p can be expressed by interpolation in power of $\rho -\rho _s$. Such parametrization is very convenient for stellar modelling, which also significant to the interior of stable stellar configurations [51].

Table 1 Numerical value of parameters $C, M _{\odot }, R$ and Buchdahl limit for different compact stars

Table 2 Energy densities, central pressure and Buchdahl condition for different compact star candidates for the above parameter values of Tables 1

Table 3 The numerical values of physical parameters of the star SAX J1808.4-3658 for $C=2.009\times 10^{-9}{\text {m}}^{-2}, K=7/4$

Table 4 The numerical values of physical parameters of the star 4U 1538-52 for $C=2.151\times 10^{-9}{\text {m}}^{-2}, K=7/4$

5.7 Static stability criterion

The most important feature of stability for stellar configuration is static stability criterion [55, 56]. In this criterion, it is postulate that any stellar configuration has an increasing mass with increasing central density, i.e. ${\text {d}}M/{\text {d}}\rho _{0} > 0$ represents stable configuration and vice versa. If the mass remains constant with increasing central density, i.e. ${\text {d}}M/{\text {d}}\rho _{0} = 0$ we get the turning point between stable and unstable region. For this model, we obtained M(R) and ${\text {d}}M/{\text {d}}\rho _{0}$ as follows-

$$\begin{aligned} M(R)=\frac{12\,\pi \,\rho _0\, R^3}{(9+56\,\pi \,\rho _0\,R^2)}~~~~~\text {and}~~~~\frac{{\text {d}}M}{{\text {d}}\rho _0}=\frac{108\,\pi \, R^3}{(9+56\,\pi \,\rho _0\,R^2)^2} \end{aligned}$$

(40)

Hence from Fig. 9, we can conclude that presenting model represents static stable configuration.

Table 5 The numerical values of physical parameters of the star 4U 1538-52 for $C=2.151\times 10^{-9}{\text {m}}^{-2}, K=7/4$

6 Conclusion

In this article, we have discussed a new solution of Vaidya-Tikekar model for the spherically symmetric uncharged fluid ball and found it is physically valid solution. The Fluid ball contains an uncharged perfect fluid matter and Schwarzschild exterior metric. Mainly, we perform a detailed investigation of the physical result of a high-density system like uncharged fluid [38, 39, 41] and observe that the physical viability and acceptable of our model in connection with compact star, like Her X-1, 4U 1538-52 and SAX J1808.4-3658.

It has been observed that the energy density and pressure are positive at the center i.e $\rho _{0}>0, p_{0}>0$ and monotonically decreasing throughout the fluid ball, see Fig. 2. The energy conditions are very important to understand many theorems of general relativity such as the singularity theorem of stellar collapse. Figure 5 shows that the energy conditions are positive throughout the star and model satisfy (1) strong energy condition(SEC) and (2) weak energy condition (WEC) [23]. We have also studied the surface redshift. It should be maximum at the center and monotonically decreasing from the center to surface [27] see Fig. 7. The modified TOV equation describes the equilibrium condition see Fig. 3 and observe that the gravitational force is balanced by the hydrostatic force. For stability analysis, the adiabatic constant ($\varGamma$) is an important physical parameter and the compact star will be stable if $\varGamma >4/3$ [46]. Figure 6 show that $\varGamma > 4/3$, so model developed in this paper is stable.The mass-radius relation must be less than 8/9 [7]. Our model also satisfies this condition. The numerical values of physical quantities are shown in Tables 1, 2, 3, 4 and 5. We have obtained the EoS for the present compact star model, which is the significant physical property to describe the structure of any realistic matter. We can see from Eq. (38) the pressure is a purely function of density. Hence we conclude that this approach may help to describe the structure of a compact star in astrophysical point of view.

Appendix

We use the transformation (10) in the Eq. (9), and get

$$\begin{aligned} \dfrac{{\text {d}}^2y}{{\text {d}}X^2} + \dfrac{X}{(1-X^2)}\dfrac{{\text {d}}y}{{\text {d}}X} + (1-K)y = 0 \end{aligned}$$

(41)

Now, we comparing Eq. (41) with the standard differential equation

$$\begin{aligned} \dfrac{{\text {d}}^2y}{{\text {d}}X^2} + Q(X)\dfrac{{\text {d}}y}{{\text {d}}X} + Q_1(X)y = Q_2(X) \end{aligned}$$

(42)

where $Q(X) = \dfrac{X}{(1-X^2)},\,\,\,\, Q_1(X) = 1-K$ and $Q_2(X) = 0$

To solve Eq. (42) we choose the integrating factor $u = e^{-1/2\int Q(X){\text {d}}X}$.

Then we get $y(X) = (X^2-1)^{1/4}\varPsi (X)$ for $K>1$ and $X>1$. Which sends the Eq. (41) in the following second order differential equation

$$\begin{aligned} \dfrac{{\text {d}}^2\varPsi }{{\text {d}}X^2}+\Bigg [ \dfrac{1-K}{(1-X^2)} -\dfrac{2+3X^2}{4(1-X^2)^2} \Bigg ]\varPsi = 0 \end{aligned}$$

(43)

The expressions of $g(R),\,F(R), \, N_1(R),\, N_2(R),\, N_4(R),\,M_1(R),\, M_2(R),\, G(R),\,G_1(R),\, G_2(R),$ and $G_3(R)$ used in Eqs. (23) and (24)

$g(R)=\sqrt{\frac{7+4CR^2}{3}},~~~F(R)=\dfrac{5+2Cr^{2}+3g(R)}{2(1+CR^2)},~~~~~~N_{4}(R)=\dfrac{-8}{3g(R)\big (g(R)-1\big )^2}$

$~~~N_{1}(R)=(2/3)\Bigg [\big (g(R)+1\big )\Bigg (\frac{4(1+CR^2)}{3}\Bigg )^{-3/4}+2\Bigg (\frac{4(1+CR^2)}{3}\Bigg )^{1/4}g(R)\Bigg ],~~~~~~~ M_{1}(R)=\dfrac{2C(7+4CR^2)}{7(1+CR^2)}$

$N_{2}(R)=\Bigg (\frac{4(1+CR^2)}{3}\Bigg )^{1/4}\big (g(R)+1\big ),~~~~~~~G(R)=\big (F(R)\big )^{1/4} ~~~~G_{1}(R)=\frac{1}{4}\big (F(R)\big )^{-3/4},$

$~~~~~~G_{2}(R)=\big (F(R)\big )^{-5/4}, ~~~~~G_{3}(R)=\frac{5}{4}\big (F(R)\big )^{-9/4},~~~~M_{2}(R)=\dfrac{3C}{7(1+CR^2)}$