1 Introduction

Over the past few years, we have witnessed a considerably growing interest to study gravastars [1,2,3,4,5,6,7,8] (and the references therein), the gravitational vacuum star as it was proposed as an alternative theory of black holes. In 2001, Mazur and Mottola (MM) [9] first proposed a new idea for gravastars (collapsing stellar object) by extending the Bose–Einstein condensate (BEC) theory in the gravitating system. They further developed the theory in 2004 [10]. This MM model gives us a stable idea about the endpoint of gravitational collapse in the form of cold, dark, compact objects having mass above some critical values and provides a solution to the classical black hole problems. After the pioneering innovation of the discovery of the gravitational wave (GW) in 2015 [11], it is assumed that the GWs arise due to the merging of two massive black holes. But there is no observational proof for this theory. In this situation, the gravastar may play a crucial role to describe the final stage of the stellar evolution. Instead of there not being sufficient observational evidence in favor of the gravastars directly for their existence, it is important to study the concept of the gravastar that can be claimed as a feasible alternative to understand the concept of the black holes (BHs).

The proposed model [10] is a static spherically symmetric perfect fluid model having three different regions designated by: (I) interior region (\(0\le r_1<r\)), (II) thin shell region (\(r_1< r< r_2\)), (III) exterior region \((r_2< r)\) and it is separated by a thin shell of stiff matter. In the interior region of the gravastar the relation between pressure and density is given by \(p=-\rho \), inside the thin shell it is described by \(p=\rho \) and finally in region III \(p=\rho =0\). Here p represents the isotropic pressure, \(\rho \) is the matter density of the perfect fluid sphere and \(r_2-r_1=\epsilon \) is the thickness of the shell, where \(\epsilon \ll 1 \), because in a gravastar the thickness is very small compared to its size. For an uncharged model of the gravastar in (\(3+1\))-D, the exterior spacetime is described by Schwarzschild geometry [12], whereas in the case of a charged gravastar model, the exterior spacetime is described by the Reissner–Nordström geometry [13, 14].

The idea of the gravastars has been discussed several times in the literature as an alternative to BH theory based on different mathematical as well as physical aspects. But most of the investigations have been carried out by several workers in the framework of Einstein’s general relativity (EGR) [15,16,17,18,19,20,21,22,23,24,25,26,27] (and the references therein). Though it is well known that EGR is very well equipped to unveil many hidden mysteries behind nature, this theory fails to explain the phenomenon of the expanding universe along with the existence of dark matter [28,29,30,31,32,33]. These two are the most important aspects of modern cosmology that have been accepted on the background of observational data. It is examined that the Einstein theory of gravitation breaks down at large scales, and a more generalized form of the action is required to describe the gravitational field at large scales. Therefore, the idea of coupling between matter and curvature produces several alternative modified theories to overcome the situation, such as f(R) gravity [34, 35], \(f({\mathbb {T}})\) gravity (\({\mathbb {T}}\) is the torsion) [36, 37], \(f(R,\,T)\) gravity [38], \(f(R, T, R_{\gamma \eta }, T^{\gamma \eta })\) theory [39, 40] and \(f({\mathcal {G}}, T )\) gravity [41], where R indicates the Ricci scalar, T denotes the trace of the stress–energy tensor (SET) and \({\mathcal {G}}\) indicates the Gauss–Bonnet invariant.

Among all these theories, \(f(R, \,T )\) theory has gained much importance for describing various astrophysical stellar objects corresponding to different formulations [42,43,44,45,46,47,48]. In this theory, the gravitational Lagrangian is given by an arbitrary function of R and T. Note that such a dependence on T may come due to exotic imperfect fluid or by considering quantum effects (the case of a conformal anomaly). Harko et al. [38] were the pioneers who first presented the formulation of \(f(R, \,T )\) gravity. The rapid growth of attention on the gravastar has motivated researchers and scientists to discuss the outcomes of modified gravity theories on physical properties of the gravastar. Das et al. [43] investigated the speculations as regards of the gravastar and studied its features graphically with respect to different EoS in the \(f(R, \,T )\) gravity framework. There are several applications in the literature of \(f(R, \,T )\) gravity theory to different cosmological domains [49,50,51,52,53,54,55,56,57,58,59]. Among several applications, it is worth to mention Refs. [60,61,62,63,64,65,66,67,68,69,70,71]. Sharif and Yousaf [60] have studied the factors which affect the stability of a locally isotropic spherical self-gravitating systems within \(f(R, \,T )\) gravity. A perturbation scheme has been employed on dynamical equations to find the collapse equation by Noureen and Zubair [61] and the condition on the adiabatic index \(\Gamma \) is constructed for Newtonian and post-Newtonian eras to address the instability problem. Again, in their later work [62], they presented a dynamical analysis of a spherically symmetric collapsing star under \(f(R, \,T )\) gravity for an anisotropic environment with zero expansion. Zubair and Noureen [63] then analyzed the gravitating sources carrying axial symmetry in \(f(R, \,T )\) gravity. Also, the implications of the shear-free condition on the instability range of an anisotropic fluid has been investigated in \(f(R, \,T )\) gravity by Noureen et al. [64]. Zubair et al. [65] reported the investigations on the possible formation of compact stars in \(f(R, \,T )\) gravity. Alhamzawi and Alhamzawi [66] derived a new type of solution for \(f(R, \,T )\) gravity and drew conclusions about the contribution to gravitational lensing by modified gravity. Moraes et al. [67] studied the hydrostatic equilibrium configuration of neutron stars and strange stars in \(f(R, \,T )\) gravity. The evolutionary behaviors of compact objects in \(f(R, \,T )\) gravitational theory have been investigated by Yousaf et al. [68] using structural scalars whereas in other work [69] they examined the irregularity factors for a self-gravitating spherical star evolving in the presence of imperfect fluid under same gravity. Maurya et al. [70] studied the hydrostatic equilibrium of stellar objects in modified \(f(R, \,T )\) gravity that do not conserve energy–momentum using the Buchdahl ansatz [71]. There is much other related work on the modified \(f(R, \,T )\) gravity theory considering different physical aspects.

The effect of charge on the model of compact star is always important. The analysis of Raychaudhuri on charged dust distributions showed that the conditions for collapse and oscillation depend on the ratio of matter density to charge density [72]. The gravitational collapse of a fluid sphere to a point singularity may be avoided in the presence of large amounts of electric charge during an accretion process onto a compact object proposed by De Felice et al. [73]. Varela investigated a charged object with neutral core and the electric charge distributed on a d-shell [74]. Ivanov [75] proposed that the presence of the charge function serves as a safety valve, which absorbs much of the fine-tuning, necessary in the uncharged case. Bonnor [76] estimated the contribution of the electric field energy to the gravitational mass using certain special models. Debnath [77] showed that the charged has non-negligible effect on different physical quantities in Rastall rainbow gravity. Rahaman et al. [78] proposed the model of charged gravastar in (\(2+1\)) dimensional gravity in anti-de Sitter spacetime. Bhatti et al. [79] investigated the role of different fluid parameters, particularly the electromagnetic field and f(R) corrections, on the evolution of cylindrical compact object. Motivated by all of this previous work, in our present article we want to check the effect of charge on the gravastar model in \(f(R,\,T)\) gravity.

Very recently, the authors have modeled a charged (3+1)-dimensional gravastar under \(f({\mathbb {T}})\) modified gravity admitting conformal motion [80] within the formulation of the MM model [10]. In this present work, we make an attempt to study a charged gravastar in the background of conformal symmetry of the spacetime in \(f(R,\,T)\) modified gravity. Particular emphasis was given to obtain different physical features of the stellar object and its significance in describing an expanding universe. In fact our earlier performed investigations on the stellar object under modified gravity [81,82,83,84,85,86] inspired us to consider this alternative formalism to the case of the gravastar, the final stage of the stellar evolution. Here we present the graphical variations of different physical features of the gravastar for an \(f(R,\,T )\) model.

We adopt the following set up for the presentation of our paper. The next section displays the fundamental formulation of this theory with conformal symmetry. Section 3 expresses three geometries of the gravastar: interior spacetime, thin shell and exterior spacetime. Several physical properties of our model, \( viz.\) the EoS parameter, proper shell thickness, entropy, and energy content, are discussed in Sect. 4. The stability of the model is presented next. Some discussions on our work, possibilities of observationally detection of a gravastar and some conclusions are provided in Sect. 6.

2 Einstein–Maxwell equation in \(f(R,\,T)\) gravity and conformal symmetry

In \((3+1)\) dimensions, the interior of a static spherically symmetry spacetime is described by the following line element:

$$\begin{aligned} {\mathrm{d}}s^{2}=e^{\nu (r)}{\mathrm{d}}t^{2}-e^{\lambda (r)}{\mathrm{d}}r^{2}-r^{2}({\mathrm{d}}\theta ^2+\sin ^2\theta {\mathrm{d}}\phi ^2), \end{aligned}$$
(1)

where \(\nu \) and \(\lambda \) are two unknown functions of the radial co-ordinate ‘r’ and independent on time, i.e., the metric coefficients are static. In our present discussion we use the gravitational or geometricized unit, i.e., \(G=1=c\). For asymptotically flat spacetime both the metric potential \(\nu (r)\) and \(\lambda (r)\) tend to 0 as \(r~\rightarrow ~\infty \). For our present paper we have taken the signature of the spacetime as \((+,\, -,\, -,\,-)\). In the presence of charge, the action in \(f(R,\,T)\) theory of gravity is given as [38],

$$\begin{aligned} S= & {} \int \left[ \frac{1}{16 \pi } f(R,T)+ {\mathcal {L}}_m+ {\mathcal {L}}_e\right] \sqrt{-g} {\mathrm{d}}^4 x, \end{aligned}$$
(2)

where \(g = det(g_{ij}\)), \(f(R,\,T )\) represents the general function of the Ricci scalar R and trace T of the energy–momentum tensor \(T_{\mu \nu }\), \({\mathcal {L}}_m\) and \({\mathcal {L}}_e\), respectively, denote the matter Lagrangian and Lagrangian for the electromagnetic field. Varying the action (2) with respect to the metric \(g_{\mu \nu }\), the field equations in \(f(R,\,T)\) gravity can be obtained as [87]

$$\begin{aligned} G_{ij}= & {} \frac{1}{f_R}\Bigg [8\pi T_{ij}+\frac{1}{2}f g_{ij}-\frac{1}{2}Rf_Rg_{ij}-f_T (T_{ij}+ \Theta _{ij})\nonumber \\&-(g_{ij}\Box -\nabla _{i}\nabla _{j})f_R+8\pi E_{ij}\Bigg ], \end{aligned}$$
(3)

where \(f=f(R,T)\), \(f_R(R,T)=\frac{\partial f(R,T)}{\partial R},~f_T(R,T)=\frac{\partial f(R,T)}{\partial T}\). \(\nabla _{\nu }\) represents the covariant derivative associated with the Levi-Civita connection of \(g_{ij}\), \(\Theta _{ij}=g^{\alpha \beta }\frac{\delta T_{\alpha \beta }}{\delta g^{ij}}\) and \(\Box \equiv \frac{1}{\sqrt{-g}}\partial _{i}(\sqrt{-g}g^{ij}\partial _{j})\) represents the D’Alembert operator, \(T_{ij}\) is the energy–momentum tensor given by

$$\begin{aligned} T_{ij}= & {} -\frac{2}{\sqrt{-g}}\frac{\delta \sqrt{-g}{\mathcal {L}}_m}{\delta \sqrt{g_{ij}}}. \end{aligned}$$
(4)

Assuming that the matter Lagrangian \({\mathcal {L}}_m\) rely solely on \(g_{ij}\) we obtain

$$\begin{aligned} T_{ij}= & {} g_{ij}{\mathcal {L}}_m-2\frac{\partial {\mathcal {L}}_m}{\partial g^{ij}}. \end{aligned}$$
(5)

Now, the matter Lagrangian density \({\mathcal {L}}_m\) could be a function of pressure or density or both density and pressure. For our present paper, we choose the matter Lagrangian as \({\mathcal {L}}_m=\rho \) and the expression of \(\Theta _{ij}=-2T_{ij}+\rho g_{ij}\), where \(\rho \) is the matter density in modified gravity. This particular choice of Lagrangian matter density is based upon the pioneering work of Harko et al. [38]. In their work, they presented the field equations of several particular models, corresponding to some explicit forms of the function \(f(R,\,T)\). Faraoni [88] revisited the issue of the correct Lagrangian description of a perfect fluid \({\mathcal {L}}_m = p\) versus \({\mathcal {L}}_m = -\rho \) in relation with modified gravity theories in which galactic luminous matter couples nonminimally to the Ricci scalar and one concluded that the Lagrangians are only equivalent when the fluid couples minimally to gravity and not otherwise. Bhar [84] presented a spherically symmetric isotropic strange star model under the framework of \(f(R,\,T)\) theory of gravity by assuming \({\mathcal {L}}_m=\rho \). For our present model the energy–momentum tensor is given by

$$\begin{aligned} T_{ij}= & {} (\rho +p)\chi _{i}\chi _{j}-p g_{ij}, \end{aligned}$$
(6)

where \(\chi ^{i}\) is the fluid four velocity satisfying \( \chi ^{i}\chi _{j}=1\), p is the isotropic pressure in modified gravity.

Again, \({\mathcal {L}}_e\) in Eq. (2), representing the Lagrangian of the electromagnetic field, is defined as

$$\begin{aligned} {\mathcal {L}}_e=-\frac{1}{16\pi }F_{\alpha \beta }F_{\gamma \delta } g^{\alpha \gamma }g^{\beta \delta } \end{aligned}$$

where \(F_{ij}\) is the antisymmetric electromagnetic field strength tensor defined by

$$\begin{aligned} F_{ij}= & {} \frac{\partial A_{j}}{\partial x^{i}}-\frac{\partial A_{i}}{\partial x^{j}}, \end{aligned}$$
(7)

and it satisfies the Maxwell equations,

$$\begin{aligned}&F^{ij}_{;j}=\frac{1}{\sqrt{-g}}\frac{\partial }{\partial x^{j}}(\sqrt{-g}F^{ij})=-4\pi {\mathcal {J}}^{i}, \end{aligned}$$
(8)
$$\begin{aligned}&F_{ij;\lambda }+F_{j \lambda ;i}+F_{\lambda i;j}=0, \end{aligned}$$
(9)

where \(A_{j}=(\phi (r),\,0,\,0,\,0)\) is the four-potential and \({\mathcal {J}}^{i}\) is the four-current vector, defined by

$$\begin{aligned} {\mathcal {J}}^{i}= & {} \frac{\rho _e}{\sqrt{g_{00}}}\frac{dx^{i}}{dx^0}, \end{aligned}$$
(10)

where \(\rho _e\) denotes the proper charge density. The expression for the electric field can be obtained from Eq. (8) as follows:

$$\begin{aligned} F^{01}= & {} -e^{\frac{\lambda +\nu }{2}}\frac{q(r)}{r^2}. \end{aligned}$$
(11)

The electromagnetic energy–momentum tensor \(E_{ij}\) has the following form:

$$\begin{aligned} E_{ij}= & {} \frac{1}{4 \pi }\left( F_{i}^{\alpha }F_{j \alpha }-\frac{1}{4}F^{\alpha \beta }F_{\alpha \beta } g_{ij}\right) . \end{aligned}$$
(12)

Let, q(r) represents the net charge inside a sphere of radius ‘r’ and it can be obtained as

$$\begin{aligned} q(r)= & {} 4\pi \int _0^r \rho _e e^{\frac{\lambda }{2}} r^2 {\mathrm{d}}r. \end{aligned}$$
(13)

Taking the covariant divergence of Eq. (3), we get [38, 89, 90]

$$\begin{aligned} \nabla ^{i}T_{ij}= & {} \frac{f_T(R,T)}{8\pi -f_T(R,T)} \Big [(T_{ij}+\Theta _{ij})\nabla ^{i}\ln f_T(R,T)\nonumber \\&+\nabla ^{i}\Theta _{ij}-\frac{1}{2}g_{ij}\nabla ^{i}T -\frac{8\pi }{f_T}\nabla ^{i}E_{ij}\Big ]. \end{aligned}$$
(14)

From Eq. (14), it is clear that \(\nabla ^{i}T_{ij}\ne 0\) if \(f_T(R,T)\ne 0\) and hence the system will not be conserved like Einstein gravity. The divergence of the matter energy–momentum tensor in this theory is non-zero whereas in GR and f(R) it is zero. For this reason this theory allows one to break both weak and strong equivalence principles in \(f (R,\,T )\) gravity. Also, it is possible to recover f(R) gravity under the constraint f(T) = 0. According to the weak equivalence principle, “All test particles in a given gravitational field will undergo the same acceleration, independent of their properties, including their rest mass”. The equation of motion in this modified theory is based on those features of the particle that are thermodynamic in character, such as pressure, energy, and density. Furthermore, the strong equivalence principle asserts that “The gravitational motion of a small test body depends only on its initial position and velocity, and not on its configuration” [91]. This principle is similarly violated in \(f (R,\,T )\) theory, resulting in non-geodesic motion of particles along world lines. In the context of quantum theory, the non-zero divergence of the effective energy–momentum tensor can be linked to the violation of energy conservation in scattering phenomena. According to this theory, energy non-conservation can result in an energy flow between the four-dimensional spacetime and a compact extra-dimensional metric [92]. Also, the non-conservation of the matter energy–momentum tensor is related to irreversible matter creation processes, in which there is an energy flow between the gravitational field and matter due to the geometry–matter coupling, with particles permanently added to the spacetime [93, 94]. The creation of matter is accompanied by an irreversible energy flow from the gravitational field to the created matter constituents.

Now we are in a position to choose the \(f (R,\,T )\) function. There are several theoretical models corresponding to different matter contributions for \(f(R,\,T)\) gravity in order to discuss the coupling effects of matter and curvature components. Harko et al. [38] choose three forms of \(f(R,\,T)\) functions (i) \(f(R,\,T)= R + 2f(T)\), (ii) \(f (R,\,T) = f_1(R) + f_2(T)\), where \(f_1(R)\) and \(f_2(T)\) are arbitrary functions of R and T, respectively and (iii) \(f (R,\,T) = f_1(R) + f_2(R)f_3(T)\), where \(f_i, i = 1, 2, 3\), are arbitrary functions of the argument. For our present work, we consider a second form proposed by Harko et al. [38] with \(f_1(R)=R\) and \( f_2(T)=2\gamma T\). So for our present case,

$$\begin{aligned} f(R,\,T)= & {} R+2 \gamma T, \end{aligned}$$
(15)

where \(\gamma \) is some small positive constant. Harko et al. [38] proposed that, for \(\gamma ~\rightarrow ~0\), Eq. (15) produces the field equations in general relativity. The term \(2 \gamma T\) induces a time-dependent coupling between curvature and matter.

Substituting this particular form of the \(f(R,\,T)\) function in Eq. (3) the field equation for f(R, T) gravity theory reads

$$\begin{aligned} G_{ij}= 8\pi (T_{ij}^{\text {eff}}+E_{ij}), \end{aligned}$$
(16)

where

$$\begin{aligned} T_{ij}^{\text {eff}}=T_{ij} \left( 1+\frac{\gamma }{4\pi }\right) +\frac{\gamma }{8\pi } (T-2\rho )g_{ij}. \end{aligned}$$

The generalized Tolman–Oppenheimer–Volkoff (TOV) equation for our present model in \(f(R,\,T)\) gravity can be obtained:

$$\begin{aligned} \frac{\gamma }{2\gamma +8\pi }(\rho '+3p')+\frac{8\pi }{8\pi +2\gamma } \frac{q}{4\pi r^4}\frac{{\mathrm{d}}q}{{\mathrm{d}}r}= & {} \frac{\nu '}{2}(\rho +p) +\frac{{\mathrm{d}}p}{{\mathrm{d}}r}. \end{aligned}$$
(17)

The Einstein–Maxwell field equations in \(f(R,\,T)\) gravity are given by

$$\begin{aligned} \kappa \rho ^{\text {eff}}+\frac{q^2}{r^4}= & {} \frac{\lambda '}{r}e^{-\lambda } +\frac{1}{r^{2}}(1-e^{-\lambda }), \end{aligned}$$
(18)
$$\begin{aligned} \kappa p^{\text {eff}}-\frac{q^2}{r^4}= & {} \frac{1}{r^{2}}(e^{-\lambda }-1) +\frac{\nu '}{r}e^{-\lambda }, \end{aligned}$$
(19)
$$\begin{aligned} \kappa p^{\text {eff}}+\frac{q^2}{r^4}= & {} \frac{1}{4}e^{-\lambda } \left[ 2\nu ''+\nu '^2-\lambda '\nu '+\frac{2}{r}(\nu '-\lambda ')\right] , \nonumber \\ \end{aligned}$$
(20)

with \(\kappa =8\pi \). The quantity q(r) actually determines the electric field by

$$\begin{aligned} E(r)= & {} \frac{q(r)}{r^2}, \end{aligned}$$
(21)

where \(\rho ^{\text {eff}}\), \(p^{\text {eff}}\) are, respectively, the density and pressures in Einstein gravity. Here

$$\begin{aligned} \rho ^{\text {eff}}= & {} \rho +\frac{\gamma }{\kappa }( \rho -3p), \end{aligned}$$
(22)
$$\begin{aligned} p^{\text {eff}}= & {} p+\frac{\gamma }{\kappa }(\rho +5p), \end{aligned}$$
(23)

by taking \(p_r=p_t=p\) in Ref. [84]. Here E(r) represents the electric field of the charged fluid sphere.

A familiar way to relate the geometry with matter is to use conformal symmetry under conformal Killing vectors (CKVs) described by

$$\begin{aligned} {\mathcal {L}}_\xi g_{ik}=\xi _{i;k}+\xi _{k;i}=\psi g_{ik}, \end{aligned}$$
(24)

where \({\mathcal {L}}\) and \(\psi \), respectively, denote the Lie derivative operator and the conformal factor. The vector \(\xi \) generates the conformal symmetry such that the metric g is conformally mapped onto itself along \(\xi \). Neither \(\xi \) nor \(\psi \) need to be static even though one considers a static metric [95, 96]. The underlying spacetime is asymptotically flat for \(\psi = 0\) and in this case the Weyl tensor will also vanish. \(\psi =\) constant and \(\psi = \psi (x,t)\), respectively, give homothetic vector and conformal vectors. Models of compact stars, wormholes and gravastars have been obtained earlier by several researchers in the realm of conformal symmetry. Mafa Takisa et al. [97] investigated the effect of electric charge in anisotropic compact stars with conformal symmetry. Mak and Harko [98] modeled quark stars with conformal motions in general relativity. Bohmer et al. [99] have studied the traversable wormholes under the assumption of spherical symmetry and the existence of a non-static conformal symmetry. Bhar et al. [100] studied the possibility of sustaining static and spherically symmetric traversable wormhole geometries admitting conformal motion in Einstein gravity. Mustafa et al. [101] explored the wormhole solutions in \(f({\mathcal {G}},\, T)\) gravity by assuming two sorts of matter density profiles, which satisfy the Gaussian and Lorentzian noncommutative distributions. More research work on conformal motion can be found in Refs. [102,103,104,105,106,107,108].

For the line element (1), the conformal Killing equations are written

$$\begin{aligned} \xi ^{1}\nu '=\psi ,\, \xi ^{4}=C_1,\, \xi ^{1}=\frac{\psi r}{2},\, \xi ^{1}\lambda '+2\xi ^{1},_1=\psi . \end{aligned}$$
(25)

Here ‘prime’ and ‘comma’ stand for the derivative and partial derivative with respect to ‘r’ and \(C_1\) is a constant.

The above equations yield

$$\begin{aligned} e^{\nu }= & {} C_2^{2}r^{2}, \end{aligned}$$
(26)
$$\begin{aligned} e^{\lambda }= & {} \left( \frac{C_3}{\psi }\right) ^{2}, \end{aligned}$$
(27)
$$\begin{aligned} \xi ^{i}= & {} C_1\delta _{4}^{i}+\left( \frac{\psi r}{2}\right) \delta _1^{i}. \end{aligned}$$
(28)

Here \(C_2\) and \(C_3\) are constants of integrations.

Using Eqs. (26)–(28), the Einstein–Maxwell field equations (18)–(20) become

$$\begin{aligned} \kappa \rho +\gamma (\rho -3p)+\frac{q^2}{r^4}= & {} \frac{1}{r^2} \left[ 1-\frac{\psi ^2}{C_3^2}\right] -\frac{2\psi \psi '}{rC_3^2}, \end{aligned}$$
(29)
$$\begin{aligned} \kappa p+\gamma (\rho +5p)-\frac{q^2}{r^4}= & {} \frac{1}{r^2} \left[ 3\frac{\psi ^2}{C_3^2}-1\right] ,\end{aligned}$$
(30)
$$\begin{aligned} \kappa p+\gamma (\rho +5p)+\frac{q^2}{r^4}= & {} \frac{\psi ^2}{r^2C_3^2} +\frac{2\psi \psi '}{rC_3^2}. \end{aligned}$$
(31)

We want to solve the field equations (29)–(31) in three different regions of the charged gravastar in the next section.

3 The model of a gravastar

Our present work explores the geometrical model of the gravastar in the context of \(f(R,\,T)\) gravity in the presence of charge. The gravastar is a bubble like structure enclosed by a thin shell, while the outer region is entirely a vacuum and the R-N [13, 14] spacetime. Three different regions of the gravastar with the following specified EoS, i.e., (i) the inner region is governed by \( p + \rho = 0\) for \(0 \le r \le r_1\); (ii) for the intermediate thin shell, the relation between pressure and density is given by \(p = \rho \) for \(r_1 \le r \le r_2\), and (iii) the exterior spacetime is described by \(p =\rho = 0\) for \( r_2 \le r\). The interior and the exterior radii of the gravastar are \(r_1\) and \(r_2\), respectively, and it is also assumed that the width of the shell is \(r_2-r_1=\epsilon \), which is extremely small.

3.1 The interior geometry

To describe the interior geometry we have to solve Eqs. (29)–(31) by using the EoS proposed in [9, 10]. To do that we add Eqs. (29) and (30), which gives

$$\begin{aligned} (\rho +p)(\kappa +2\gamma )= & {} \frac{2\psi ^2}{r^2C_3^2} -\frac{2\psi \psi '}{rC_3^2}. \end{aligned}$$
(32)

Now to solve Eq. (32) in the interior of the gravastar, we consider the equation of state (EoS)

$$\begin{aligned} p=-\rho , \end{aligned}$$
(33)

proposed by Mazur and Mottola [9, 10], which manifests the dark energy EoS, and acts along the radially outward direction to oppose the collapse. The above equation is a special case of the equation \(p=\omega \rho \) with \(\omega =-1\). \(p=\omega \rho \) is known as dark energy EoS. It is well known that dark energy quintessence is a possible candidate responsible for the late-time cosmic accelerated expansion and, motivated by this concept, Chapline [109] and Lobo [110] proposed a generalization of the gravastar model. Lobo [110] proposed that the notion of dark energy is that of a spatially homogeneous cosmic fluid, which can be extended to inhomogeneous spherically symmetric spacetimes by considering the pressure in the dark energy equation of state to be a negative radial pressure. Using the relationship between the matter density \(\rho \) and isotropic pressure p given in Eq. (33), from Eq. (32) we get the following ordinary differential equation which is linear in the conformal factor \(\psi \):

$$\begin{aligned} \frac{2\psi }{r^2C_3^2}(\psi -\psi 'r)=0, \end{aligned}$$
(34)

which gives two solutions for \(\psi \), \(\text {either}~\psi =0 ~\text {or}~ \psi =A_1r.\) where \(A_1\) is the constant of integration. Since \(\psi =0\) implies the asymptotically flat spacetime, we take \(\psi =A_1r\) to calculate the matter density, pressure and the other physical quantities. Invoking the expression of the conformal factor \(\psi =A_1r\), the expressions for the metric coefficients, \(\rho ,\,p,\,E^2\) and \(\rho _e\) are obtained:

$$\begin{aligned} e^{-\lambda }= & {} A^2 r^2,\, e^{\nu }=C_2^2r^2, \end{aligned}$$
(35)
$$\begin{aligned} \rho= & {} \frac{1 - 6 A^2 r^2}{2 (4 \gamma + \kappa ) r^2}=-p, \end{aligned}$$
(36)
$$\begin{aligned} E^2= & {} \frac{1}{2r^2},\, \rho _e(r)=\frac{A}{4\sqrt{2}\pi r}. \end{aligned}$$
(37)

Here we have used the notation \(A=\frac{A_1}{C_3}\), which is another constant. The metric coefficient \(e^{\lambda }\) is inversely proportional to \(r^2\) but \(e^{\nu }\) is directly proportional to \(r^2\). Since in the interior region of the gravastar, the energy density is positive, from Eq. (36) we get \(A^2<\frac{1}{6r^2}\) and it gives the upper bound for \(A^2\). From Eq. (37), we get \(A>0\). One can note that both the pressure and density are inversely proportional to \(r^{2}\) and all pressure, density, electric field and charge density suffer from central singularities, i.e., for \(r\rightarrow 0\), they blow up without bound at the center of charged gravastar and it is a natural behavior of the CKV model. The electric field \(E^2\) is inversely proportional to \(r^2\) and it does not depend on A. The charged density \(\rho _e\) depends on A and is inversely proportional to r. The active gravitational mass M(r) can be obtained from the following formula:

$$\begin{aligned} M(r)= & {} 4\pi \int _0^{r}\eta ^{2}\left[ \rho (\eta )+\frac{E^{2}(\eta )}{\kappa }\right] {\mathrm{d}}\eta \nonumber \\= & {} \frac{r}{4}\left[ 1+\frac{\kappa }{4 \gamma + \kappa }(1 - 2 A^2 r^2)\right] . \end{aligned}$$
(38)

The mass function M(r) does not suffer from the central singularity since, as \(r\rightarrow 0\), \(M(r)\rightarrow 0\). One can note that the active gravitational mass function depends on both A and the coupling constant \(\gamma \). Using the bound for \(A^2\), we get the lower bound for the active gravitational mass, \(M(r)>\frac{r}{12}\left( \frac{12\gamma +5\kappa }{4\gamma +\kappa }\right) \).

3.2 The intermediate thin shell

In the shell of the gravastar, following the concept of Mazur & Mottola [9, 10], the relation between the pressure p and the energy density \(\rho \) is taken as

$$\begin{aligned} p=\rho . \end{aligned}$$
(39)

This EoS is a special case of barotropic EoS \(p=\alpha \rho \) with \(\alpha =1\). In general, where the pressure is only a function of the density, i.e., \(P = P(\rho )\), and vice versa, we have barotropic fluids. They are considered as unrealistic but their simplicity has a pedagogical value in illustrating the several approaches used to solve different systems and “physically” interesting scenarios [111]. In this connection, we want to mention that Zel’dovich [112] first conceived the idea of this kind of fluid in connection with a cold baryonic universe and it was described as a stiff fluid. Staelens et al. [113] studied the spherical collapse of an over-density of a barotropic fluid with linear equation of state in a cosmological background. Bergh and Slobodeanu [114] studied shear-free perfect fluids with a barotropic equation of state in general relativity. Rahaman with his collaborators [115] used the barotropic EoS to obtain a new class of exact solutions for the interior in \((2 + 1)\)-dimensional spacetime by assuming an isotropic pressure both with and without cosmological constant \(\Lambda \). Wesson [116] obtained a spherically symmetric and non-static solution with an inhomogeneous density profile \(\rho \) and a pressure p given by the stiff equation of state \(p=\rho c^2\), c being a constant. The stiff fluid model has been used earlier by several researchers in the field of astrophysics as well as in cosmology [117,118,119,120].

From Eqs. (18) and (19) with the help of Eq. (39) we get the following ordinary differential equation (ODE):

$$\begin{aligned} \frac{2r\psi \psi '}{C_3^2}-\left( \frac{2\gamma -\kappa }{4\gamma +\kappa }\right) \frac{\psi ^2}{C_3^2}=\frac{2\gamma +\kappa }{8\gamma +2\kappa }. \end{aligned}$$
(40)

The above ODE is a linear equation in \(\psi ^2\), which on integrating gives

$$\begin{aligned} \frac{\psi ^{2}}{C_3^2}= & {} \frac{2\gamma +\kappa }{2\kappa -4\gamma }-Dr^{\frac{2\gamma -\kappa }{4\gamma +\kappa }}, \end{aligned}$$
(41)

where D is a positive constant of integration.

Now the metric coefficients for the thin shell can be obtained:

$$\begin{aligned} e^{-\lambda }= & {} \frac{2\gamma +\kappa }{2\kappa -4\gamma } -Dr^{\frac{2\gamma -\kappa }{4\gamma +\kappa }}, \end{aligned}$$
(42)
$$\begin{aligned} e^{\nu }= & {} C_2^2r^2. \end{aligned}$$
(43)
Fig. 1
figure 1

The metric coefficient \(e^{\nu }\) inside the thin shell

Full size image
Fig. 2
figure 2

\(e^{-\lambda }\) inside the thin shell

Full size image

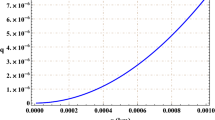
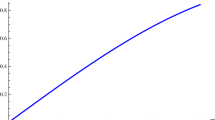
The profiles of the metric coefficients inside the thin shell are shown in Figs. 1 and 2.

The expressions for matter density and isotropic pressure inside the thin shell are obtained:

$$\begin{aligned} \rho= & {} \frac{1}{2r^3}\Big [\frac{r}{\kappa -2 \gamma } - \frac{3 D r^{\frac{6 \gamma }{4 \gamma + \kappa }}}{ 4 \gamma + \kappa }\Big ]= p . \end{aligned}$$
(44)

The electric field inside the thin shell takes the form

$$\begin{aligned} E^2= & {} \frac{2 \gamma }{(2 \gamma - \kappa ) r^2} + \frac{ 3 D (2 \gamma + \kappa )}{ 2 (4 \gamma + \kappa )r^{\frac{6\gamma +3\kappa }{4\gamma +\kappa }}}, \end{aligned}$$
(45)

and the electric charged density \(\rho _e\) can be obtained,

$$\begin{aligned} \rho _e(r)= & {} \frac{3 D (2 \gamma - \kappa ) (2 \gamma + \kappa ) (10 \gamma + \kappa ) r^{\frac{ 2 \gamma }{4 \gamma + \kappa }} + 8 \gamma (4 \gamma + \kappa )^2 r^{\frac{\kappa }{4 \gamma + \kappa }}}{8 (2 \gamma - \kappa ) (4 \gamma + \kappa )^2 \pi r^{\frac{4(3\gamma +\kappa )}{4\gamma +\kappa }}\chi (r)}\Phi (r), \end{aligned}$$
(46)

where \(\Phi (r)\) and \(\chi (r)\) are functions of ‘r’ and they depend on the coupling constant \(\gamma \). Their expressions are given as,

$$\begin{aligned}&\Phi (r)=\sqrt{\frac{\kappa +2\gamma }{2(\kappa -2\gamma )} -Dr^{\frac{2\gamma -\kappa }{4\gamma +\kappa }}}, \end{aligned}$$
(47)
$$\begin{aligned}&\chi (r)=\sqrt{\frac{8 \gamma }{(2 \gamma - \kappa ) r^2} + \frac{ 6 D (2 \gamma + \kappa )}{ (4 \gamma + \kappa )r^{\frac{6\gamma +3\kappa }{4\gamma +\kappa }}}}. \end{aligned}$$
(48)
Fig. 3
figure 3

Variation of pressure and density inside the thin shell

Full size image

The profiles of pressure and density inside the thin shell are depicted in Fig. 3.

3.3 Exterior spacetime and junction condition

For this region we consider \( p=\rho =0 \) , which ensures that the exterior spacetime is described by the Reissner–Nordström line element given by

$$\begin{aligned} {\mathrm{d}}s^{2}= & {} {\mathcal {F}} {\mathrm{d}}t^{2}-{\mathcal {F}}^{-1}{\mathrm{d}}r^{2}-r^{2}({\mathrm{d}}\theta ^{2}+\sin ^{2}\theta {\mathrm{d}}\phi ^{2}), \end{aligned}$$
(49)

where \({\mathcal {F}}=\left( 1-\frac{2{\mathcal {M}}}{r} +\frac{{\mathcal {Q}}^2}{r^{2}}\right) \), \({\mathcal {M}}\) being the mass and \({\mathcal {Q}}\) being the charge of the gravastar.

Instead of one junction surface that a compact star has, the gravastar configuration has two junction surfaces, since it is like a hollow sphere. One is between interior region and intermediate thin shell (i.e., at \(r = r_1\)) and the other is between the shell and exterior spacetime (i.e., at \(r = r_2\)). Now for our present model of the gravastar, the metric potentials \(g_{rr}\) and \(g_{tt}\) must be continuous at the interface between the core and the shell at \(r = r_1\) (interior radius) and it gives the following relationship:

$$\begin{aligned} A^2r_1^2= & {} \frac{2\gamma +\kappa }{2\kappa -4\gamma } -Dr_1^{\frac{2\gamma -\kappa }{4\gamma +\kappa }}. \end{aligned}$$
(50)

Now using the matching condition between the shell and the exterior region at \(r = r_2\) (exterior radius) yields the following relationships:

$$\begin{aligned}&C_2^2r_2^2=1-\frac{2{\mathcal {M}}}{r_2}+\frac{{\mathcal {Q}}^2}{r_2^{2}}, \end{aligned}$$
(51)
$$\begin{aligned}&\frac{2\gamma +\kappa }{2\kappa -4\gamma }-Dr_2^{\frac{2\gamma -\kappa }{4\gamma +\kappa }}=1-\frac{2{\mathcal {M}}}{r_2} +\frac{{\mathcal {Q}}^2}{r_2^{2}}. \end{aligned}$$
(52)

Solving Eqs. (50)–(52), we obtain the expressions for \(C_2,\,D\) and A,

$$\begin{aligned} C_2= & {} \frac{1}{r_2}\sqrt{1-\frac{2{\mathcal {M}}}{r_2} +\frac{{\mathcal {Q}}^2}{r_2^{2}}}, \end{aligned}$$
(53)
$$\begin{aligned} D= & {} r_2^{\frac{\kappa -2\gamma }{\kappa +4\gamma }} \left[ \frac{2{\mathcal {M}}}{r_2}-\frac{{\mathcal {Q}}^2}{r_2^{2}} -\frac{\kappa -6\gamma }{2\kappa -4\gamma }\right] , \end{aligned}$$
(54)
$$\begin{aligned} A= & {} \frac{1}{r_1}\sqrt{\left[ \frac{2\gamma +\kappa }{2\kappa -4\gamma } -Dr_1^{\frac{2\gamma -\kappa }{4\gamma +\kappa }}\right] }. \end{aligned}$$
(55)

To determine the values of these constants, we consider the mass of the gravastar \(M = 1.75M_{\odot }\), the inner radius \(r_1 = 10\) km and the outer radius \(r_2 = 10.009\) km, \({\mathcal {Q}}=0.001\), which provides the numeric values of \(C_2,\,D\) and A for different values of the coupling constant \(\gamma \) presented in Table 1.

Table 1 The numerical values of the constants \(C_2,\,A\) and D have been presented for different values of the coupling constant \(\gamma \) for the compact star with \(M =1.75~M_{\odot },\, r_1 = 10\) km, \(r_2=10.009\) km, \({\mathcal {Q}} = 0.001\)
Full size table

The extremely cold radiation fluid in the shell is confined to region II by the surface tensions at the timelike interfaces \(r_1\) and \(r_2\) [9, 10]. When we are matching our interior spacetime to the exterior R-N spacetime we should keep in mind that the hollow sphere with inner radius \(r_1\) and outer radius \(r_2=r_1+\epsilon \) here considered has \(\epsilon \ll r_1\), and according to Mazur and Mottola [9, 10], \(\epsilon \) does not exceed the Planck length. At the boundary we match our interior region to the exterior line element. Obviously the metric coefficients are continuous at \(r=a\), but it does not ensure that their derivatives are also continuous at the junction surface. In other words the affine connections may be discontinuous there. The surface stress energy tensor is given by the Lanczos equations in the following form [121]:

$$\begin{aligned} {\mathcal {S}}^{i}_{j}=-\frac{1}{8\pi }(\kappa ^{i}_j-\delta ^{i}_j \kappa ^{k}_k), \end{aligned}$$
(56)

where the Latin indices run as \(i,\, j = t,\,\theta ,\,\phi \). The factor \(\kappa _{ij}\) represents the discontinuity in the extrinsic curvature \(K_{ij}\) with \(\kappa _{ij}=\left[ K_{ij}\right] ^{+}-\left[ K_{ij}\right] ^{-}\), the expression for \(K_{ij}^{\pm }\) is given by

$$\begin{aligned} K_{ij}^{\pm }=-n_{\nu }^{\pm }\left( \partial _je_i^{\nu } +\Gamma ^{\nu }_{\alpha \beta }e_i^{\alpha }e_j^{\beta }\right) , \end{aligned}$$
(57)

where \(e_i^{\alpha }=\frac{\partial x^{\alpha }}{\partial \xi ^i}\), \( \xi ^i\) represents the coordinate on the shell, \(n_{\nu }^{\pm }\) are the unit normal vectors on the surface with \(n^{\nu }n_{\nu }=1\), \(\Gamma ^{\nu }_{\alpha \beta }\) is for the Christoffel symbols and “\(+\)” and “−” signs correspond to exterior i.e., Reissner–Nordström spacetime and interior spacetime, respectively.

Fig. 4
figure 4

Variation of surface energy density inside the thin shell

Full size image

Using the spherical symmetry nature of the spacetime, using the Lanczos equation, the surface stress energy tensor can be written as \({\mathcal {S}}_{ij}=\text {diag}(\sigma ,\,-{\mathcal {P}},\,-{\mathcal {P}},\,-{\mathcal {P}})\). Here \(\sigma \) and \({\mathcal {P}}\) are the surface energy density and surface pressure, respectively. The mathematical expressions for the surface energy density \(\sigma \) and the surface pressure \({\mathcal {P}}\) at the junction surface \(r = a\) are obtained [43],

$$\begin{aligned} \sigma= & {} -\frac{1}{4\pi a}\left[ \sqrt{f} \right] _{-}^{+}=-\frac{1}{4\pi a}\left[ \sqrt{1-\frac{2{\mathcal {M}}}{a}+\frac{{\mathcal {Q}}^2}{a^2}} -Aa\right] ,\nonumber \\ \end{aligned}$$
(58)
$$\begin{aligned} {\mathcal {P}}= & {} -\frac{\sigma }{2}+\frac{1}{16\pi }\left[ \frac{f'}{\sqrt{f}}\right] _{-}^{+}\nonumber \\= & {} \frac{1}{8\pi a}\left[ \frac{1-\frac{{\mathcal {M}}}{a}}{\sqrt{1-\frac{2{\mathcal {M}}}{a} +\frac{{\mathcal {Q}}^2}{a^2}}}-2Aa\right] . \end{aligned}$$
(59)
Fig. 5
figure 5

Variation of surface pressure inside the thin shell

Full size image
Fig. 6
figure 6

Top two profiles show the variation of the equation of state parameter in the interior region, bottom two panels show the variation of equation of state parameter inside the thin shell

Full size image

The profiles of surface energy density and surface pressure are plotted in Figs. 4 and 5, respectively.

The mass of the thin shell (\(m_{\text {shell}}\)) of width \(\epsilon \) can be obtained from the following formula:

$$\begin{aligned} m_{\text {shell}}= & {} 4\pi a^2\sigma ,\nonumber \\= & {} Aa^2-a\sqrt{1-\frac{2{\mathcal {M}}}{a}+\frac{{\mathcal {Q}}^2}{a^2}}. \end{aligned}$$
(60)

Rearranging the above equation, the mass of the charged gravastar is calculated to be

$$\begin{aligned} {\mathcal {M}}= & {} \frac{a}{2}\left[ 1+\frac{{\mathcal {Q}}^2}{a^2} -\frac{m_{\text {shell}}^2}{a^2}-A^{2}a^2+2Am_{\text {shell}}\right] , \end{aligned}$$
(61)
$$\begin{aligned}= & {} \frac{a^2+{\mathcal {Q}}^2}{2a}-\frac{a}{2} \left( \frac{m_{\text {shell}}}{a}-Aa\right) ^2. \end{aligned}$$
(62)

We see that the total mass \({\mathcal {M}}\) of the gravastar cannot exceed \(\frac{a^2+{\mathcal {Q}}^2}{2a}\). Moreover if the mass of the thin shell, the radius of the gravastar and the total charge \({\mathcal {Q}}\) are known, the total mass of the gravastar can be obtained from Eq. (62).

4 Some physical properties of our present model

In this section we want to explore some physical features of the developed structure, i.e., the equation of state, the proper length, the entropy and the energy contents within the shell’s region. Since the constructed geometry of the gravastar is the matching of two different spacetimes, the stiff perfect fluid moves along these spacetimes through the shell region. The impact of electromagnetic field on different physical features of the charged gravastar in the context of \(f(R,\,T)\) gravity will also be discussed.

4.1 The EoS parameter

The equation of state parameter \(\omega \) for our present model is written

$$\begin{aligned} \omega (a)=\frac{{\mathcal {P}}(a)}{\sigma (a)}. \end{aligned}$$
(63)

Now using Eqs. (58) and (59), we obtain the expression for \(\omega (a)\),

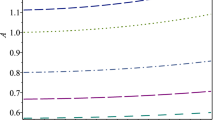
$$\begin{aligned} \omega (a)=\frac{1}{2}\left[ \frac{\frac{1-\frac{{\mathcal {M}}}{a}}{\sqrt{1-\frac{2{\mathcal {M}}}{a}+\frac{{\mathcal {Q}}^2}{a^2}}}-2Aa}{Aa-\sqrt{1-\frac{2{\mathcal {M}}}{a}+\frac{{\mathcal {Q}}^2}{a^2}}}\right] . \end{aligned}$$
(64)

To keep \(\omega (a)\) real, we need the restriction \(\frac{2{\mathcal {M}}}{a}-\frac{{\mathcal {Q}}^2}{a^2}<1\), which is already satisfied from Eq. (49). Now \(\omega (a)\) may be positive or negative depending on the signature of numerator or denominator of Eq. (64). The profiles of \(\omega (a)\) against ‘a’ are shown in Fig. 6. The location of the thin shell (junction surface) plays an important role: if ‘a’ is sufficiently large, then \(\omega (a) \rightarrow -1\) and it incorporates the dark energy effects of the cosmological constant \(\Lambda \). For very small value of ‘a’ \(\omega (a)\) tends to zero, yielding a dust shell. According to Fig. 6, it can be observed that \(\omega (a)\) is negative within the thin shell, implying that \({\mathcal {P}}(a)\) and \(\sigma (a)\) are the opposite sign. The surface pressure is negative, which means we have a tension. In the junction shell, the energy density is positive. The thin shell, i.e. region II in our configuration, contains an ultra-relativistic fluid obeying the relationship \(p=\rho \) and the second fundamental form of the discontinuity provides additional surface stress energy and surface tension for the connecting interface. These two non-interacting components are characteristic features of our non-vacuum region II.

4.2 Proper length of the shell

We assume the lower and upper boundaries of the shell are \(r = a\) and \(r = a+\epsilon \), respectively, and hence the proper thickness of the shell is \(\epsilon \), which is a very small positive real number \((0~<\epsilon \ll 1)\). The proper length \({\mathcal {L}}\) of such a region that connects inner and outer boundary, can be obtained:

$$\begin{aligned} {\mathcal {L}}= & {} \int _{a}^{a+\epsilon }\frac{1}{\sqrt{e^{-\lambda }}} {\mathrm{d}}r=\int _{a}^{a+\epsilon }\frac{1}{\sqrt{\frac{2\gamma +\kappa }{2\kappa -4\gamma }-Dr^{\frac{2\gamma -\kappa }{4\gamma +\kappa }}}}{\mathrm{d}}r,\nonumber \\= & {} \bigg [r\frac{\kappa -2\gamma }{\kappa +2\gamma } \sqrt{\frac{2\kappa +4\gamma }{\kappa -2\gamma } -\frac{4D}{r^{\frac{\kappa -2\gamma }{\kappa +4\gamma }}}} \zeta (r)\bigg ]_a^{a+\epsilon }, \end{aligned}$$
(65)

where

$$\begin{aligned} \zeta (r)= & {} _2F_1\left[ 1, \frac{10 \gamma + \kappa }{ 4 \gamma - 2 \kappa }, -\frac{6 \gamma }{-2 \gamma + \kappa }, \frac{2D(\kappa -2\gamma )}{(\kappa +2\gamma )r^{\frac{\kappa -2\gamma }{\kappa +4\gamma }}}\right] , \end{aligned}$$

and \(_2F_1\) is the hypergeometric function defined as

$$\begin{aligned} {}_2F_1(a, b; c; x) = \sum _{k=0}^{\infty }\frac{(a)_k(b)_k}{(c)_k} \frac{x^k}{k!} \end{aligned}$$

and the series expansion of R.H.S. of the above equation is

$$\begin{aligned} 1+\frac{a\cdot b}{c}\frac{x}{1!}+\frac{a(a + 1)b(b + 1)}{c(c + 1) }\frac{x^2}{2!}+\cdots \end{aligned}$$

where \(|x| < 1\); \(a,\, b,\,c\) are real numbers and \(c \ne 0, -1, -2,\ldots \) Here \((a)_n\) (n is a positive integer) is the Pochhammer symbol defined by \((a)_n = a(a + 1)\cdot \cdot \cdot (a + n - 1),\) with \((a)_0 = 1\). With the help of simple algebra, \((a)_n\) takes the form \((a)_n =\frac{\Gamma (a+n)}{\Gamma (a)}\). The graphical behavior of the proper length with respect to the thickness of the thin-shell gravastar is displayed in Fig. 7.

4.3 Entropy

Entropy is used as a measure of the disorderness or disturbance in a mechanical system. According to the theory of Mazur and Mottola [9, 10], charged gravastar has zero entropy density for the interior region. Using the concept of Mazur and Möttola [9, 10], the entropy within the shell of the charged gravastar is calculated as,

$$\begin{aligned} S=\int _{a}^{a+\epsilon }\frac{\kappa }{2} r^2 h(r)\sqrt{e^{\lambda }}{\mathrm{d}}r. \end{aligned}$$
(66)

By the standard thermodynamic relation, \(Ts = p + \rho \) for a relativistic fluid with zero chemical potential and at the local temperature T(r), the entropy density s(r) can be expressed as

$$\begin{aligned} s(r)=\frac{2\alpha ^2 K_B^2 T(r)}{\kappa \hbar ^2}=2\alpha \left( \frac{K_B}{\hbar }\right) \sqrt{\frac{p(r)}{\kappa }} \end{aligned}$$

where \(\alpha \) is a dimensionless constant, \(K_B\) representing the Boltzmann constant, \(\hbar =\frac{h}{2\pi }\), where h is the Planck constant. Using the expression for p and \(e^{\lambda }\), from Eq. (66), we calculate the expression for entropy as follows:

$$\begin{aligned} S= & {} \int _a^{a+\epsilon }\frac{\kappa \alpha }{2\sqrt{4\gamma +\kappa }} \left( \frac{K_B}{\hbar }\right) r \nonumber \\&\times \sqrt{\frac{3 D (2 \gamma - \kappa ) r^{\frac{2 \gamma }{ 4 \gamma + \kappa }} + (4 \gamma + \kappa ) r^{\frac{\kappa }{4 \gamma + \kappa }}}{2 D (2 \gamma - \kappa ) r^{\frac{2 \gamma }{ 4 \gamma + \kappa }} + (2 \gamma + \kappa ) r^{\frac{\kappa }{4 \gamma + \kappa }}}} {\mathrm{d}}r. \end{aligned}$$
(67)

Equation (67) can be written as

$$\begin{aligned} S=\frac{\kappa \alpha }{2\sqrt{4\gamma +\kappa }} \left( \frac{K_B}{\hbar }\right) {\mathcal {I}}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {I}}=\int _{a}^{a+\epsilon }G(r){\mathrm{d}}r, \end{aligned}$$
(68)

and G(r) is a function of ‘r’ defined as

$$\begin{aligned} G(r)=\sqrt{\frac{3 D (2 \gamma - \kappa ) r^{\frac{2 \gamma }{ 4 \gamma + \kappa }} + (4 \gamma + \kappa ) r^{\frac{\kappa }{4 \gamma + \kappa }}}{2 D (2 \gamma - \kappa ) r^{\frac{2 \gamma }{ 4 \gamma + \kappa }} + (2 \gamma + \kappa ) r^{\frac{\kappa }{4 \gamma + \kappa }}}}. \end{aligned}$$
Fig. 7
figure 7

Variation of proper length inside the shell versus thickness of the shell of charged gravastar

Full size image
Fig. 8
figure 8

Variation of entropy inside the shell versus thickness of the shell of charged gravastar

Full size image

Now due to the complexity of the expression of G(r), it is very difficult to perform the integral given in Eq. (68). Let H(r) be a function such that \(\frac{{\mathrm{d}}H(r)}{{\mathrm{d}}r}=G(r)\). Then, from Eq. (68), by using the fundamental theorem of integral calculus, we obtain

$$\begin{aligned} {\mathcal {I}}=\left[ H(r)\right] _{a}^{a+\epsilon }=H(a+\epsilon )-H(a). \end{aligned}$$
(69)

Now by considering the Taylor series expansion of \(H(a+\epsilon )\) about ‘a’ and retaining up to the linear order of \(\epsilon \), we obtain

$$\begin{aligned} {\mathcal {I}}=a\epsilon \sqrt{\frac{3 D (2 \gamma - \kappa ) a^{\frac{2 \gamma }{ 4 \gamma + \kappa }} + (4 \gamma + \kappa ) a^{\frac{\kappa }{4 \gamma + \kappa }}}{2 D (2 \gamma - \kappa ) a^{\frac{2 \gamma }{ 4 \gamma + \kappa }} + (2 \gamma + \kappa ) a^{\frac{\kappa }{4 \gamma + \kappa }}}}, \end{aligned}$$
(70)

and consequently, from Eq. (67), we get

$$\begin{aligned} S= & {} \frac{\kappa \alpha }{2\sqrt{4\gamma +\kappa }} \left( \frac{K_B}{\hbar }\right) a\epsilon \nonumber \\&\times \sqrt{\frac{3 D (2 \gamma - \kappa ) a^{\frac{2 \gamma }{ 4 \gamma + \kappa }} + (4 \gamma + \kappa ) a^{\frac{\kappa }{4 \gamma + \kappa }}}{2 D (2 \gamma - \kappa ) a^{\frac{2 \gamma }{ 4 \gamma + \kappa }} + (2 \gamma + \kappa ) a^{\frac{\kappa }{4 \gamma + \kappa }}}}. \end{aligned}$$
(71)

Hence we have successfully obtained the expression of the entropy for our proposed model. From Eq. (71) one can note that, if the thickness of the thin shell \(\epsilon \ll a\), then \(S\approx {\mathcal {O}}(\epsilon )\). In Ref. [24], Usmani et al. showed that the entropy depends on the thickness of the shell. Our result is consistent with the result of Ref. [24]. The variation of entropy with respect to the thin shell radius is shown in Fig. 8.

4.4 Energy within the thin shell

Let us now calculate the energy \({\mathcal {E}}\) within the shell from the following formula:

$$\begin{aligned} {\mathcal {E}}= & {} \int _{a}^{a+\epsilon }\frac{\kappa }{2} r^2 \left( \rho +\frac{E^2}{\kappa }\right) {\mathrm{d}}r\nonumber \\= & {} \left[ \frac{(4\gamma - \kappa ) r}{4 (2\gamma -\kappa )} +\frac{D}{4}r^{\frac{6\gamma }{4\gamma +\kappa }}\right] _a^{a+\epsilon }, \nonumber \\= & {} \frac{\epsilon }{4}\left( \frac{4\gamma - \kappa }{2\gamma -\kappa }\right) +\frac{D}{4}\left[ (a+\epsilon )^{\frac{6\gamma }{4\gamma +\kappa }} -a^{\frac{6\gamma }{4\gamma +\kappa }}\right] ,\nonumber \\\approx & {} \frac{\epsilon }{4}\left[ \frac{4\gamma - \kappa }{2\gamma -\kappa }+\frac{6D\gamma }{4\gamma +\kappa } \right] . \end{aligned}$$
(72)
Fig. 9
figure 9

Variation of energy inside the shell versus thickness of the shell of charged gravastar

Full size image
Fig. 10
figure 10

Stability regions of the charged gravastar. Here ‘S’ stands for stability

Full size image

This shows a direct relation of the energy with the thickness of the shell. From Eq. (72) we see that the energy is directly proportional to the thickness of the shell, so the unit of energy is also ‘km’. The graphical analysis of the energy–thickness relation corresponding to different values of \(\gamma \) is given in Fig. 9 which displays the non-repulsive nature of the energy inside the shell.

5 Stability of the gravastar

In this section, we are interested in checking the stability of gravastars. For this purpose we define a new parameter \(\eta \) as the ratio of the derivatives of \(\sigma \) and \({\mathcal {P}}\) as follows:

$$\begin{aligned} \eta (a)=\frac{\mathcal {P'}(a)}{\sigma '(a)}. \end{aligned}$$
(73)

Övgün et al. [122] used the above parameter which plays a fundamental role in determining the stability regions of the respective solutions of charged thin-shell gravastar model within the context of noncommutative geometry. Yousaf et al. [123] also discussed the stability of the gravastar model in \(f(R,\,T)\) gravity in the presence of charge. Debnath [77] obtained the stable regions of the charged gravastar in Rastall rainbow gravity. Very recently Sharif and Javed [124] studied the stability of thin-shell gravastars and concluded that stable regions of the gravastar shell decrease and the dynamical configuration increases with cosmological constant. The parameter \(\eta \) is interpreted as the squared speed of sound and it should satisfy \(0\le \eta \le 1\), since the speed of sound should not exceed the speed of light. But according to Poisson and Visser [125] and Lobo [126] the range of \(\eta \) may be lying outside the range mentioned earlier on the surface layer. For our present study, we have plotted the profile of \(\eta \) in Fig. 10 for different values of \({\mathcal {Q}}\) (keeping \(\gamma \) fixed) and different values of coupling constant \(\gamma \) (keeping \({\mathcal {Q}}\) fixed) mentioned in the figures and the stability region have been identified. The detailed calculations regarding stability analysis for the gravastar can be found in [122, 124] and similar types of stability regions were obtained [122,123,124]. It confirms the physical validity of our present model.

6 Discussions and final remarks

In the present article we have studied the effects of modified gravity on the charged gravastar corresponding to the exterior Reissner–Nordström line element. In this section we shall summarize some key physical features of the model as follows. Several physical parameters, e.g. metric potentials, proper length of the shell, entropy, equation of state (EoS), energy within shell, and surface redshift, have been discussed both analytically and graphically. We have drawn all the physical parameters in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10. The figures indicate the physical acceptability of our present model of the charged gravastar. The metric coefficient \(e^{\nu }\) is plotted against r inside the thin shell as shown in Fig. 1. \(e^{\nu }\) does not depend on \(\gamma \); rather it relies on \({\mathcal {Q}}\). To draw the profiles we have varied \({\mathcal {Q}}\) and note that \(e^{\nu }\) takes a higher value with increasing value of \({\mathcal {Q}}\). The other metric coefficient \(e^{-\lambda }\) is depicted in Fig. 2. The value of \(e^{-\lambda }\) at the inner boundary of the thin shell decreases as \(\gamma \) increases when \({\mathcal {Q}}\) is fixed but at the outer boundary of the thin shell all the profiles of \(e^{-\lambda }\) for different values of \(\gamma \) coincide (keeping \({\mathcal {Q}}\) fixed). On the other hand, when \(\gamma \) is fixed, \(e^{-\lambda }\) takes higher values with increasing values of \({\mathcal {Q}}\) inside the thin shell. The nature of the pressure (=density) inside the thin shell is depicted in Fig. 3. The figure indicates that the pressure almost maintain the linear behavior with the thickness of the thin shell. Moreover, within the thin shell the profile of p takes a lower value for increasing value of \(\gamma \) when \({\mathcal {Q}}\) is fixed. The reverse nature of p is seen for increasing value of \({\mathcal {Q}}\) when \(\gamma \) is fixed. The surface energy density has been calculated by following the condition of Darmois and Israel [127, 128]. The surface energy density has been plotted against the radial parameter in Fig. 4. The surface energy density remained positive throughout the shell and it gradually increases as we move from the inner boundary of the thin shell to the outer boundary. The value of the surface energy density at the inner boundary decreases with the increasing value of the coupling constant \(\gamma \) when \({\mathcal {Q}}\) is fixed. Again for a fixed value of \(\gamma \), the value of \(\sigma \) at the interior boundary decreases as \({\mathcal {Q}}\) increases but its nature changes at the outer boundary. Figure 5 shows the behavior of the surface pressure inside the thin shell and it can be seen that the surface pressure is negative in the interior of the shell. The value of \({\mathcal {P}}\) decreases with the increasing values of \({\mathcal {Q}}\) when \(\gamma \) is fixed. On the other hand, the value of \({\mathcal {P}}\) increases with the increasing values of \(\gamma \) when \({\mathcal {Q}}\) is fixed. The equation of parameter, which is the ratio of the surface pressure and surface energy density, is depicted in Fig. 6. From the figure it is clear that \(\omega (a)\) takes both positive and negative values inside the interior of the gravastar. Inside the thin shell region \(\omega (a)\) takes negative values. It can be noted that inside the thin shell \(\omega (a)\) decreases with the increasing values of \(\gamma \) when \({\mathcal {Q}}\) is fixed. The same behavior of \(\omega (a)\) is noticed with \({\mathcal {Q}}\) varying with a fixed \(\gamma \). From the profile given in Fig. 7 of the proper length of the thin shell, it is seen that the coupling constant \(\gamma \) has a negligible effect on \({\mathcal {L}}\) for a fixed values of \({\mathcal {Q}}\), since all the profiles of \({\mathcal {L}}\) coincide for different values of \(\gamma \). On the contrary, \({\mathcal {L}}\) takes lower values when \({\mathcal {Q}}\) increases for fixed values of \(\gamma \). In both cases \({\mathcal {L}}\) takes positive values inside the shell. The profile of the entropy with respect to the thickness of the thin shell is depicted in Fig. 8. The entropy is an increasing function of \(\epsilon \), it takes the maximum values at the outer boundary of the thin shell. For fixed values of \({\mathcal {Q}}\), the entropy decreases with the increasing values of \(\gamma \), and a reverse behavior is noticed when \({\mathcal {Q}}\) varies. We have also plotted the energy within the thin shell with respect to the thickness of the thin shell in Fig. 9. The profile of energy within the thin shell takes lower values with the increasing values of \(\gamma \) when \({\mathcal {Q}}\) is fixed. The same nature of energy within the thin shell can be noticed for different values of \({\mathcal {Q}}\) when \(\gamma \) is fixed. The stability analysis of the present model is discussed and stable regions are marked in Fig. 10.

Now we want to discuss the possible observational signatures for this kind of the gravastar. Till now there is no direct way of finding evidence to detect a gravastar but a few indirect ways are available in the literature which give clues of their possible existence and future detection. We can adopt a spherical thin-shell gravastar model that links the interior de Sitter geometry with the exterior Schwarzschild geometry [15]. Sakai et al. [129] first proposed the concept for possible detection mechanism of the gravastar through the study of the gravastar shadows. Gravitational lensing effects [130] can be used as another method to identify a gravastar where they proposed that in a gravastar microlensing effects with a higher maximal luminosity than black holes of the same mass might occur. To detect a gravastar, they presented the following two models:

  1. I.

    According to Model 1, they calculate the image of a companion rotating around the gravastar and discover that certain characteristic images arise depending on whether the gravastar has photon orbits that are unstable or not (assuming the surface of thin-shell gravastar to be optically transparent)

  2. II.

    According to Model 2, they compute the microlensing effects, the overall luminosity change, and the peak luminosity may be far greater than a black hole of the same mass.

It should be mentioned that interferometric LIGO detectors have just detected the ringdown signal of GW 150914 [11]. Observational constraints on gravastar models with the thermal process were studied by Broderick and Narayan [131]. Uchikata et al. [132] proposed that to constrain gravastars, measurement of the tidal deformability from the gravitational-wave detection of a compact-binary inspiral can be used. To rule out exotic alternatives to BHs and to test quantum effects at the horizon scale, only late-time ringdown detections might be used [133, 134]. They anticipated that objects with no event horizon, such as gravastars, would be the source of such gravitational waves with a high probability. According to Chirenti and Rezzolla [135], we cannot assert that gravastars merging is the source of gravitational waves because we know so little about the perturbative reaction of rotating gravastars. Recently, after analyzing the image acquired in the First M87 Event Horizon Telescope (EHT) [136] finding, it was discovered that the generated shadow might be attributable to a gravastar. A shadow may be cast by any compact object with a spacetime defined by unstable circular photon orbits, as demonstrated by Mizuno et al. [137].

The gravastar theory may also be examined in the framework of Friedmann’s flat universe cosmology [138]. This study is motivated by the action principle itself, and the conclusion is quite fascinating; the gravastar population produces a dynamic kind of dark energy. If comparable effects to those stated above are observed in the future, it will provide an excellent foundation for comparing GR with modified gravity.

From all the presented results for our present study, we can conclude that the \(f(R,\,T)\) gravity leads to very distinct gravastar model in the presence of charge even when the spacetime admits a conformal Killing vector. Our results agree with the results obtained by Usmani et al. [24] in the case \(\gamma \rightarrow 0\). In the \(f(R,\,T)\) theory of gravity, we derive solutions that adequately explain gravastars. After careful consideration, we conclude that our gravastar model is stable under \(f(R,\,T)\) theory of gravity, which differs conceptually from Einstein’s GR. As a final comment, we can state that there is no direct observable evidence that can distinguish a black hole from a gravastar at this time. The new findings of GW190521 once again demonstrate that the black hole hypothesis is incompatible with observable results. As a result, it is possible that the hypothetical black hole is a gravastar.