1 Introduction

Nonlinear electrodynamics was first proposed by Born and Infeld in order to remove the central singularity of the point-like charges and obtain finite energy solutions for particles by extending Maxwell theory [1]. Later, Plebanski and Perzanowski extended the model and presented other examples of nonlinear electrodynamics Lagrangians in the framework of special relativity [2]. Recently, studying various models of nonlinear electrodynamics has been under active investigation, mainly because these theories appear as effective theories at low energy limits of string theory [3]. In the framework of AdS/CFT, nonlinear electrodynamics has been used to obtain solutions describing baryon configurations which are consistent with confinement [4]. In other frameworks, in order to remove curvature singularities various important results have been obtained. For example, in cosmological models, one can use the nonlinear electrodynamics for explaining the inflationary epoch and the late-time accelerated expansion of the universe [5, 6]. In the field of black holes, different classes of regular black hole solutions in general relativity coupled to nonlinear electrodynamics have been found, in which the nonlinear electrodynamics is a source of field equations satisfying the weak energy condition, and recovering the Maxwell theory in the weak field limit [7,8,9,10,11,12,13,14,15,16,17,18]. There are some nonlinear electrodynamics Lagrangians that can not remove singularity from the black holes, but they generalize the RN solution. For example, Born–Infeld Lagrangian gives rise to a singular spherically symmetric black hole and other solutions [19,20,21,22,23,24,25]. The progress in this direction and demand to investigate various aspects of nonlinear models are the main motivations for the present study. In this paper, we study an interesting class of nonlinear electrodynamics, which regularizes the metric function. Regarding such class of nonlinear electrodynamics, we find that although this model can regularize the metric function, the curvature scalars diverge at the origin.

Thermodynamic properties of black holes were reinforced by the discovery of Hawking radiation [26]. Bekenstein considered the concept of entropy for black holes and made it quantitative, namely the area law, \(S=A/4\) [27]. However, there are some differences between black hole thermodynamics and conventional thermodynamics, such as the black hole entropy, which is proportional to the horizon area and not volume, and the heat capacity of black holes which might be negative.

Thermodynamic properties of AdS black holes are more interesting due to some reasons: one of them comes from the main work of Hawking and Page, who discovered a first order phase transition between the Schwarzschild-AdS black hole and thermal AdS space [28]. This phenomenon, known as the Hawking–Page phase transition, is explained as the gravitational dual of the QCD confinement/deconfinement transition [29, 30]. Another important reason for the study of thermodynamics of AdS black holes was the discovery of phase transitions similar to Van der Waals liquid/gas phase transitions in the Reissner–Nordström/anti-de Sitter (RN-AdS) black holes by Chambline et al. [31, 32]. They studied the RN-AdS black holes in canonical ensemble and discovered a first order phase transition between small and large black holes. Another motivation of considering AdS black holes is due to the AdS/CFT correspondence [33, 34]. This duality has been recently used to study the behavior of quark-gluon plasmas and the qualitative description of various condensed matter phenomena. According to the AdS/CFT correspondence [29], a large static black hole in asymptotically AdS spacetime corresponds to a thermal state in the CFT living on the boundary.

Actually, the interests in studies of thermodynamics of the AdS black holes is partly due to the rich structures found by treating the cosmological constant as a thermodynamic variable. In the presence of a varying cosmological constant, the first law of black hole thermodynamics becomes consistent with the Smarr relation. The first law of black holes is modified by including a VdP term where the pressure P is given by \(-\dfrac{\Lambda }{8\pi }\). In this framework, the mass of the black hole M is considered as the enthalpy of the system instead of the internal energy [35, 36]. One of the first works to explore the extended phase space thermodynamics in AdS black holes was written by Kubiznak and Mann who showed the existence of a certain phase transition in the phase space of the Schwarzschild/AdS black hole [37]. Similar critical behavior is found in the spacetimes of a rotating AdS black hole and a higher dimensional RN-AdS black hole [38]. The same qualitative properties are also found in the AdS black hole spacetime with the Born–Infeld electrodynamics [39, 40], with the power-Maxwell field and with Gauss–Bonnet correction [41, 42]. There are many other works related to this concept including [43,44,45,46,47,48,49,50,51,52,53,54].

In this paper, we introduce a new charged AdS black hole solution, in the presence of a nonlinear electrodynamics. We then perform a detailed analysis of the thermodynamics of the obtained BH solution. Also, we study the behavior of a scalar field outside the black hole horizon by computing the complex frequencies associated with quasinormal modes. These modes are the resonant, non-radial perturbations of black holes which are the result of external perturbations of spacetime. Quasinormal modes are important for some reasons. First, because information about the black hole is encoded in there. By detection of the QNMs, one can obtain precise information related to the mass, charge, and other global parameters of the black hole. Another reason is that complex frequencies can provide information about dynamical stability of the black hole. Indeed, the real part of frequencies determines the oscillation frequency and the imaginary part determines the rate at which each mode is damped. The final reason comes from the fact that the QNMs frequencies of AdS black holes have an interpretation in the dual conformal field theory [55]. According to this correspondence, a large black hole in AdS corresponds to a thermal state in the CFT. Perturbing the black hole, corresponds to perturbing the thermal state and the decay of the perturbation describes the return to thermal equilibrium. Therefore, the time scale for the decay of the black hole perturbation, which is given by the imaginary part of its QNM, corresponds to the timescale to reach thermal equilibrium in the strongly coupled CFT [55,56,57,58].

The paper is organized as follows: in Sect. 2, the basic equations are introduced. Section 3 is devoted to the calculation of conserved and thermal quantities and investigation of the first law of thermodynamics. Subsequently, thermal stability and phase transition are discussed. In Sect. 4, we compute QNMs and finally, our concluding remarks are given in Sect. 5.

2 Basic equations

The 4-dimensional action governing charged black holes in the presence of a nonlinear electromagnetic field is given by [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63]

$$\begin{aligned} I=\dfrac{1}{4\pi }\int d^{4} x \sqrt{-g}\left[ \dfrac{1}{4 }(R-2\Lambda ) -L(P)\right] , \end{aligned}$$
(1)

where R is the Ricci scalar and \( \Lambda =-\dfrac{3}{b^{2}} \) is the cosmological constant, in which b denotes the radius of AdS space. L(P) is a function of \( P \equiv \dfrac{1}{4}P_{\mu \nu }P^{\mu \nu }\) and \( P_{\mu \nu } \) is an antisymmetric tensor related to the Faraday tensor \( F_{\mu \nu } \) according to \( P_{\mu \nu }= L_{F}F_{\mu \nu } \) and \( L_{F}\equiv \dfrac{\partial L}{\partial F} \) (\( F\cong F_{\mu \nu }F^{\mu \nu } \) is the Maxwell invariant). Applying the variational principle to the action (1), one can show that the field equations are given by [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63]

$$\begin{aligned} G^{\nu }_{\mu }+\Lambda \delta ^{\nu }_{\mu }= & {} \dfrac{1}{2}\delta ^{\nu }_{\mu }L-2L_{P}P_{\mu \lambda }P^{\nu \lambda }, \end{aligned}$$
(2)
$$\begin{aligned} \nabla _{\mu }P^{\alpha \mu }= & {} 0, \end{aligned}$$
(3)

where in the above equations, \( G_{\mu \nu } \) is the Einstein tensor and \( L_{P}\equiv \dfrac{\partial L}{\partial P} \) [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63]. By integrating Eq. (3) with the assumption of spherical symmetry, we obtain the static solution

$$\begin{aligned} P_{\mu \nu }=2\delta ^{t}_{[\mu }\delta ^{r}_{\nu ]}\dfrac{Q}{r^{2}} \quad or \quad P=-\dfrac{Q^{2}}{2r^{4}} \end{aligned}$$
(4)

where Q is an integration constant related to the electric charge. Here, we assume that the Lagrangian is as follows [8,9,10]:

$$\begin{aligned} L=\dfrac{8\alpha ^{3}P(6\alpha (-2P)^{\frac{1}{4}}+\sqrt{\beta }-2\alpha \beta (-2P)^{\frac{3}{4}})}{\sqrt{\beta }(2\alpha +\beta ^{\frac{3}{2}}(-2P)^{\frac{1}{4}}+2\alpha \beta (-2P)^{\frac{1}{2}})^{3}}. \end{aligned}$$
(5)

In the weak field limit (\( P\ll 1 \)) the EM Lagrangian reduces to

$$\begin{aligned} L \approx P+{\mathcal {O}}(P^{\frac{5}{4}}) \end{aligned}$$
(6)

With the nonlinear electric field as source, the gravitational field is described by the metric

$$\begin{aligned} ds^{2}= & {} -f(r)dt^{2}+f(r)^{-1}dr^{2}+r^{2}d\Omega ^{2}\quad ,\nonumber \\ f(r)= & {} 1-\dfrac{\Lambda }{3} r^{2}-\dfrac{2\alpha r}{r^{2}+\dfrac{\beta ^{2}}{2\alpha } r+\beta ^{2}}. \end{aligned}$$
(7)

Indeed, one can put the metric (7) into Eq. (2) and solve for L(P) , to obtain the Lagrangian (5). So, this Lagrangian is appropriate only for the present black hole and by using this Lagrangian one can not obtain regular black holes such as Bardeen and other regular black holes. The particular form of the Lagrangian (5) thus leads to the interesting solution (7) which contrary to the RN solution of Einstein–Maxwell is more usual. System, behaves regularly as \( r\rightarrow 0 \). The associated electric field E is given by

$$\begin{aligned} E=\dfrac{2\alpha ^{2}\beta r(4\alpha r^{3}+(20\alpha ^{2}+6\alpha \beta ^{2}+\beta ^{2})r^{2}+4\alpha ^{2}\beta ^{2})}{(2\alpha r^{2}+\beta ^{2}r+2\alpha \beta ^{2})^{3}}. \end{aligned}$$
(8)

The asymptotic behavior of the solution as \( r\rightarrow \infty \) reads

$$\begin{aligned} -g_{tt}\approx 1-\dfrac{2\alpha }{r}+\dfrac{\beta ^{2}}{r^{2}}-\dfrac{\Lambda }{3} r^{2},\quad E\approx \dfrac{\beta }{r^{2}}+{\mathcal {O}}\left( \dfrac{1}{r^{3}}\right) . \end{aligned}$$
(9)

In comparison to the RN-AdS metric and coulomb law, we observe that M and Q are related to mass and charge according to

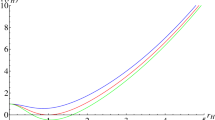
$$\begin{aligned} M=\alpha ,\quad Q=\beta , \end{aligned}$$
(10)

where M is ADM mass and Q is electric charge of the solution. Note that in contrast to the Einstein–Maxwell system, M and Q are not constants of integration, but rather are parameters present in EM Lagrangian (5). We plot diagrams for finding the possible roots of the metric function which correspond to horizons (Fig. 1). We find from this figure that our solution can represent a black hole, by suitable choices of parameters. For \( Q=0.827M \), the horizons degenerate to a single one, corresponding to an extreme black hole. Therefore, there is a minimal mass

$$\begin{aligned} M_{min}=1.21Q. \end{aligned}$$
(11)

Below this mass, we would have a mild naked singularity.

Fig. 1
figure 1

The behavior of \( -g_{tt} \) in terms of r for \( Q=0.5 \) with no horizons (long dashed line), \(Q=0.827\) extremal (solid line ) and \(Q=1\) with two horizons (dashed line) and \( \Lambda =-0.01 \), \( M=1 \) (all three cases)

Full size image

It is worth noting that the metric (7) is well behaved when r goes to zero. The electric field vanishes as \(r \rightarrow 0\) and \( r\rightarrow \infty \) and achieves its maximum \( E_{c} \) at \( r_{c} \) (see Fig. 2). In order to get information about the nature of \( r_{c} \), see [64] and the reference therein.

Fig. 2
figure 2

The behavior of the electric field in terms of r for \(M = 1, Q = 0.5\)

Full size image

The limit of Ricci and Kretschmann scalar \( K_{1}=R_{abcd}R^{abcd} \) for metric (7) when \( r \rightarrow 0 \) are

$$\begin{aligned} \lim _{r\rightarrow 0^+}=\dfrac{32 M^{2}}{Q^{4} r^{2}},\quad \lim _{r\rightarrow 0^+} R=\dfrac{12M}{Q^{2} r} \end{aligned}$$
(12)

As one can see, when r goes to zero the Kretschmann scalar diverges as \( \frac{1}{r^{2}} \), for all values of Q and M. For comparison, \(K_{1}\propto \dfrac{1}{r^{6}}\) for the RN metric.

To derive the global structure of the metric, one can construct the Penrose diagrams. The Penrose diagram of the present metric is similar to the Reissner–Nordström-AdS metric. In the case of non-extreme black hole solution \( Q<0.827M \), we can split the space-time into three regions; \( I: r>r_{+} \), \( II:r_{-}<r<r_{+} \) and \( III: 0\le r<r_{-}\). In the extreme black hole case, \( Q=0.827M \), there arise two regions: \( r>r_{c} \) and \( 0<r<r_{c} \). For \( Q>0.827M \), there are no horizons.

3 Thermodynamic properties

In order to investigate the thermodynamic stability of the black hole in extended phase space, we need to obtain some relevant thermodynamic quantities. The black hole temperature for non-extremal case with two horizons \( r_{\pm } \) reads

$$\begin{aligned} T= & {} \dfrac{f^{'}(r_{+})}{4\pi }={\dfrac{ \left( -24Q^{2}+24r_{+}^{2} \right) M^{3}-8 \Lambda r_{+} \left( Q^{2}+r_{+}^{2} \right) ^{2}M^{2}-8r_{+}^{2}Q^{2 }\Lambda \left( Q^{2}+r_{+}^{2} \right) M-2Q^{4}r_{+}^{3}\Lambda }{3 \left( 2Q^{2}M+2r_{+}^{2}M+{Q}^{2}r_{+} \right) ^{2}}}, \end{aligned}$$
(13)

where \( r_{+} \) is the event horizon which is defined by the larger root of \(f(r_{+}) = 0\). Contrary to RN black hole, as \( r_{+} \) vanishes, the temperature does not diverge but has a finite value. The black hole entropy S can be calculated via the area law

$$\begin{aligned} S=\dfrac{A}{4}=\pi r_{+}^{2} \end{aligned}$$
(14)

and by using Eq. (8), the electrostatic potential \( \phi \) is obtained as

$$\begin{aligned} \phi= & {} \int _{r_{+}}^{\infty }E dr={\dfrac{\left( 8{r_{+}}^{3}M+20{r_{+}}^{2}{M}^{2}+3{r_{+}}^{2}{Q}^{2}+12r_{+}M{Q}^{2}+12{M}^{2}{Q}^{2} \right) M{Q}^{2}}{ 2\left( 2{r_{+}}^{2}M+r_{+}{Q}^{2}+2 M{Q}^{2}\right) ^{2}Q}}. \end{aligned}$$
(15)

The pressure P is defined as [37]:

$$\begin{aligned} P=-\dfrac{\Lambda }{8 \pi }, \end{aligned}$$
(16)

with the conjugate quantity which is volume:

$$\begin{aligned} V=\dfrac{4}{3}\pi r^{3}_{+}. \end{aligned}$$
(17)

In Eqs. (13) and (15), M is related to \( r_{+} \) and other BH parameters as

$$\begin{aligned}&M=\dfrac{-Q^{2}{r^{2}_{+}}\Lambda - r_{+}^{4}\Lambda +3 Q^{2}+3r_{+}^{2}}{12r_{+}}+\dfrac{\left( Q^{4}r_{+}^{4}\Lambda ^{2}+2Q^{2}r_{+}^{6}\Lambda ^{2}+ r_{+}^{8}\Lambda ^{2}-6Q^{4}r_{+}^{2}\Lambda -24Q^{2}r_{+}^{4} \Lambda -6r_{+}^{6}\Lambda +9Q^{4}+54Q^{2}r_{+}^{2}+9r_{+}^{4}\right) ^{\dfrac{1}{2}}}{12r_{+}}. \end{aligned}$$
(18)

For a black hole embedded in AdS spacetime and by employing the relation between the cosmological constant and thermodynamic pressure, the black hole mass M will be interpreted as the enthalpy \(H=M\) [35,36,37, 50, 66, 68, 71]. So, the enthalpy in terms of thermodynamic quantities is given by

$$\begin{aligned}&H(S,P,Q)= \dfrac{8\pi {Q}^{2}SP +3\pi {Q}^{2} +3S+8{S}^{2}P}{12\sqrt{\pi S}} +\dfrac{\sqrt{8 PS+3}{\left( 8{\pi }^{2}PS{Q}^{4}+16\pi P {S}^{2}{Q}^{2}+3{\pi }^{2}{Q}^{4}+8{S}^{3}P+18\pi {Q}^{2} S+3{S}^{2}\right) ^{\frac{1}{2}} }}{12\sqrt{ \pi S }}. \end{aligned}$$
(19)

The usual thermodynamic relations can now be used to determine the temperature, electrostatic potential and volume [29, 31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54],

$$\begin{aligned} T= & {} \left( \dfrac{\partial H}{\partial S} \right) _{P Q}, \end{aligned}$$
(20)
$$\begin{aligned} \phi= & {} \left( \dfrac{\partial H}{\partial Q} \right) _{S P}, \end{aligned}$$
(21)

and

$$\begin{aligned} V=\left( \dfrac{\partial H}{\partial P} \right) _{S Q}. \end{aligned}$$
(22)

The Smarr relation is given by

$$\begin{aligned} \dfrac{H}{2}+PV-TS-\dfrac{Q \phi }{2}-\dfrac{1}{2}\int w dv=0, \end{aligned}$$
(23)

where

$$\begin{aligned} \int w dv= & {} \int _{r_{+}}^{\infty } \dfrac{T^{\mu }_{\mu }}{2}4\pi r^{2}dr=\dfrac{128{M}^{2}{P}{Q}^{4}\pi r_{+}^{3}+256{M}^{2}{P}{Q}^{2}\pi r_{+}^{5}+128{M}^{2}{P}\pi r_{+}^{7}+128M{P}{Q}^{4}\pi r_{+}^{4}}{6\left( 2M{Q}^{2}+2M r_{+}^{2}+{Q}^{2}r_{+}\right) ^{2}}\nonumber \\&+\dfrac{128M{P}{Q}^{2}\pi r_{+}^{6}+32r_{+}^{5}{Q}^{4}\pi {P}+12{M}^{3}{Q}^{4}-12{M}^{3}{Q}^{2} r_{+}^{2}+12{M}^{2}{Q}^{4}r_{+}+3M{Q}^{4}r_{+}^{2}}{6\left( 2M{Q}^{2}+2M r_{+} ^{2}+{Q}^{2}r_{+}\right) ^{2}}, \end{aligned}$$
(24)

this term comes from non vanishing trace of the energy-momentum tensor [65]. Calculations show that the quantities calculated by Eqs. (20, 22 and 21) coincide with Eqs. (13), (15) and (17) respectively. Thus, these thermodynamic quantities satisfy the first law of BH thermodynamics [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]

$$\begin{aligned} dH=dM=TdS+\phi dQ+VdP. \end{aligned}$$
(25)

3.1 Specific heats and thermodynamic stability

Thermodynamic stability tells us how a system in thermodynamic equilibrium responds to fluctuations of energy, temperature and other thermodynamic parameters. We distinguish between global and local stability. In global stability we allow a system in equilibrium with a thermodynamic reservoir to exchange energy with the reservoir. The preferred phase of the system is the one that minimizes the Gibbs free energy [41, 52,53,54, 69, 70].

Fig. 3
figure 3

The behavior of G for our solution in terms of \( r_{+} \) for \( P={0.003}, {0.002669}, {0.002}, {0.0015} \) (left to right) and \( Q=1 \), and for RN-AdS metric (dashed line) for \( P={0.002669}\), \( Q=1 \)

Full size image

In order to investigate the global stability and phase transition of the system in canonical ensemble, we use the following expression for Gibbs free energy [36,37,38, 50]

$$\begin{aligned} G=H-T S. \end{aligned}$$
(26)

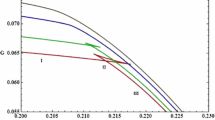
We find from Fig. 3 that for constant pressure and electric charge, G is a decreasing function for small/large event horizon, while it is an increasing function for intermediate \( r_{+} \). This behavior confirms that intermediate black holes are globally unstable. Large black holes have negative Gibbs free energy and therefore are more stable than small black holes. Also, one can see that for constant \( r_{+} \), for the larger pressure, the BH is more stable. Also, we compare the Gibbs free energy of the RN-AdS metric with the present solution. The Gibbs free energy could also have extremum by suitable choices of parameters. We shall discuss this issue in the next section when we study the phase transition.

Local stability is concerned with how the system responds to small changes in its thermodynamic parameters. In order to study the thermodynamic stability of the black holes with respect to small variations of the thermodynamic coordinates, one can investigate the behavior of the heat capacity. The positivity of the heat capacity ensures local stability. There are two different heat capacities associated with a system. \( C_{V} \): which measures the heat capacity when the heat is added to the system keeping the volume constant and \( C_{P} \): which is used when the heat is added at constant pressure. Heat capacities can be calculated using the standard thermodynamic relations [69, 70]

$$\begin{aligned} C_{V}=T\left( \dfrac{\partial S}{\partial T}\right) _{V},\quad C_{P}=T\left( \dfrac{\partial S}{\partial T}\right) _{P}. \end{aligned}$$
(27)

Using the expression for black hole entropy (Eq. 14) one can show that \( C_{V} \) vanishes. \( C_{V} \) vanishes, while one can use Eq. (26) to calculate \( C_{P} \), numerically, as its behavior is shown in Fig. 4.

Fig. 4
figure 4

The behavior of \( C_{P} \) in terms of \( r_{+} \) for \( P={0.002}, {0.002669}, {0.003}\) (right to left) and \( Q=1 \), and for RN-AdS metric (dashed line) and for \( P={0.002669}\), \( Q=1 \)

Full size image
Fig. 5
figure 5

The behavior of \( {C_{P}}\) (solid line), T (dashed line) and G (dotted dashed line) in terms of \( r_{+} \) for \( P =0.0015, Q=1 \)

Full size image

Regarding Fig. 4, we find that the heat capacity is positive for large black holes and partly positive for the smaller ones. It means that the large black hole is thermodynamically more stable (locally). For medium black holes, since the heat capacity is negative, the black hole is locally unstable, which is similar to RN-AdS black hole. We shall discuss this issue in Sect. 3.2 when we consider the critical points in black hole phase diagram.

3.2 Phase transition

The behavior of heat capacity could also represent phase transitions [69, 70]. By numerical calculation, we have shown the existence of phase transition in Figs. 4 and 5 . It is clear that, the heat capacity has two divergencies which separate small stable BHs, unstable region, and large stable ones, and coincidence with extremum points of temperature and Gibbs free energy. Also, the roots of temperature coincide with the points that the heat capacity changes its signature. The roots separate the non-physical solutions with negative temperature from physical black holes with positive temperature. As the pressure approaches the critical pressure, the two divergent points get close to each other. At \( P_{c} \) the divergent points coincide and the intermediate radii black hole would disappear (Fig. 6).

Fig. 6
figure 6

The behavior of \( {C_{P}}\) (solid line), T (dashed line) and G (dotted dashed line) in terms of \( r_{+} \) for \( P_{c}=0.002669, Q=1 \)

Full size image
Fig. 7
figure 7

The behavior of G for our solution in terms of T for \( P={0.003}, {0.002669}, {0.002}, {0.0015} \) (right to left) and \( Q=1 \), compared to the RN-AdS metric (dashed line) for \( P={0.002669}\), \( Q=1 \)

Full size image

Gibbs free energy as a function of temperature for various pressures is shown in Fig. 7. When \( P<{0.002669} \), the Gibbs free energy with respect to temperature develops a swallow-tail like shape. There is a small/large first order phase transition in the black hole, which resembles the liquid/gas change of phase occurring in the Van der Waals fluid. At the critical pressure \( P={0.002669} \), the swallow-tail disappears which corresponds to the critical point.

Fig. 8
figure 8

The behavior of P in terms of \( r_{+} \) for \( Q=1, T={0.045}, {0.0385}, {0.034}, {0.0269}, {0.023}\) (downwards)

Full size image

In Fig. 8, by numerical calculation, we plot \( P-r_{+} \), keeping T and Q fixed. The temperature of isotherm diagrams decreases from top to bottom. The two upper solid lines correspond to the ideal gas phase, the critical isotherm is denoted by the dotted-dashed line, lower solid lines correspond to temperatures smaller than the critical temperature and there is also a temperature below which the pressure becomes negative in a range of \( r_{+} \) (black dashed line). Again, the resemblance with the liquid/gas phase transition in Van der Waals gas and also for the RN-AdS black hole is clearly seen. The critical point is determined by \( \frac{\partial P}{\partial r_{+}}=0 \) and \( \frac{\partial ^{2}P}{\partial r_{+}^{2}}=0 \). By using Eq. (13), one can find \( \frac{P_{c}r_{c}}{T_{c}}=\frac{(0.002669)(2.54)}{0.0385}=0.176 \) which is independent of charge Q [31, 32, 40, 67, 72].

Fig. 9
figure 9

The behavior of \( \omega _{i} \) and \( \omega _{r} \) in terms of \( r_{+} \) for \( Q={5},{25},{40},b=1, l=0\) (downwards)

Full size image

4 Quasinormal modes

In this section, we compute complex frequencies associated with quasinormal modes of the BH by investigating the oscillations of a scalar field. The equation for these perturbations takes the usual form [56,57,58]

$$\begin{aligned} \dfrac{1}{\sqrt{\mid g\mid }}\partial _{\mu }(\sqrt{\mid g \mid }\partial ^{\mu }\phi )=0, \end{aligned}$$
(28)

where g is the determinant of the metric. By decomposing the scalar perturbation and introducing the tortoise coordinate x and using spherical harmonics, one can rewrite the radial part of (28) in a Schrödinger form

$$\begin{aligned} \left[ -\dfrac{d^{2}}{dx^{2}}+V(x)-\omega ^{2}\right] \varphi (x)=0, \end{aligned}$$
(29)

with V given by

$$\begin{aligned} V=f\left( \dfrac{l(l+1)}{r^{2}}+\dfrac{f^{'}}{r}\right) , \end{aligned}$$
(30)

and

$$\begin{aligned} x=\int \dfrac{dr}{f}. \end{aligned}$$
(31)

The effective potential V is positive and vanishes at the horizon (\( x=-\infty \)). It diverges at \( r=\infty \), which corresponds to a finite value of x, and hence \( \varphi \) vanishes at infinity. This boundary condition is to be satisfied by the wave equation of the scalar field. In general, the frequency of waves must be complex, \( \omega =\omega _{r}-i\omega _{i} \). The imaginary and real parts are related to the damping time scale (\(\tau _{i}=1/\omega _{i}\)) and oscillation time scale (\(\tau _{r}=1/\omega _{r}\)), respectively. By using the numerical method suggested in [56,57,58], we have computed the QNMs frequencies via expanding the solution around the horizon and imposing the boundary condition that the solution vanishes at infinity. Here, we have considered large black holes, because large black holes in AdS/CFT correspond to a thermal state, and its perturbation corresponds to the perturbation of thermal state, and damping of perturbation in AdS is translated as return to equilibrium in thermal state. Small black hole is unstable and does not correspond to any thermal state in CFT [53]. For large black holes (\( r_{+}\gg b \)), the relation of the values of the lowest quasinormal frequencies for \( l=0 \) and selected values of \( r_{+} \) for different charge Q are exhibited in Fig. 9. It can be seen that the real and the imaginary parts of the frequency are not linear functions of \( r_{+} \) similar to RN-AdS [58]. This can be better seen by calculation of diagram slope from Table 1.

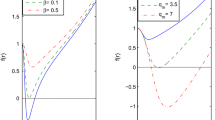
From Fig. 9a, we learn that as Q increases, \( \omega _{i} \) and \( \omega _{r} \) decrease. According to the AdS/CFT correspondence, this means that for large Q, it is slower for the quasinormal ringing to settle down to thermal equilibrium and also, the frequency of the oscillation becomes smaller (Fig 9b).

From Eq. (13) and Fig. 10, one can find that the temperature is not a linear function of the event horizon radius. As Q increases, the linear relation between T and \( r_{+} \) no longer holds. Again, the linear relation between real and imaginary parts of frequency with charge is changed (Fig. 11).

Fig. 10
figure 10

The behavior of T in terms of \( r_{+} \) for \(Q={5},{25},{40}\) (left), and the behavior of T in terms of Q for \(b=1, l=0\) (right)

Full size image
Fig. 11
figure 11

The behavior of \( \omega _{i} \) and \( \omega _{r} \) in terms of T for \( Q={5},{25},{40},b=1, l=0\)

Full size image

In Fig. 12, the dependence of \( \omega _{r} \) and \( \omega _{i} \) on l for different values of Q is exhibited. Unlike the case of RN-AdS [58] and Schwarzschild-AdS [56] black holes, by increasing l, \( \omega _{i} \) and \( \omega _{r} \) increase and different values of Q do not change the qualitative behavior of \( \omega _{r} \) and \( \omega _{i} \) with l.

Fig. 12
figure 12

The behavior of \( \omega _{i} \) and \( \omega _{r} \) in terms of l for \( Q={5}, {25},{40}, b=1, r_{+}=100\) (downwards)

Full size image

From Fig. 13, as the black hole charge Q increases, the real and imaginary parts of the large black hole QNM frequencies decrease. Also, for fixed charge, as l increases, QNM frequency increases, and this is consistent with Fig. 12.

Fig. 13
figure 13

The behavior of \( \omega _{r} \) and \( \omega _{i} \) in terms of Q for \( l={0},{10},{20}, b=1, r_{+}=100\), (upwards)

Full size image
Table 1 Quasinormal frequencies of the scalar perturbations for \(l=0 \) and \( b=1 \)
Full size table
Fig. 14
figure 14

The Gibbs free energy is given as a function of temperature for \(Q=1, P =0.0015\) and \(T_{c}=0.0306\) (left). The behavior of black hole temperature T as a function of the black hole horizon \(r_{+}\) for \(Q=1, P =0.0015\) (right)

Full size image
Fig. 15
figure 15

The behavior of quasinormal modes for small black holes (left) and for large black holes (right). The arrow indicates the increase of black hole horizon

Full size image

Finally, let us investigate whether the signature of thermodynamical first order phase transition in charged AdS black holes can be reflected in the dynamical QNMs behavior in the massless scalar perturbation. We study the dynamical perturbations in isobaric process by fixing the pressure P to obtain the phase transitions between small-large black holes. In Fig. 14, we have plotted the behavior of an isobar. The crossing curves in the left plot indicates the coexistence of two phases in equilibrium that correspond to the separated points in the right plot for \(T_{c}=0.0306\). The QNMs frequencies corresponding to small-large black holes have been plotted in Fig. 15. For the case of small black holes, one can see that by increasing the radius of event horizon the imaginary part increases and real part of frequencies decreases (Table 2). While, for the large black hole, we find that when the black hole radius increases, the real part together with the imaginary part of QNMs frequencies increase [73, 74].

Table 2 The QNM frequencies of massless scalar perturbations for \(l=0 \) and \(P=0.0015\)
Full size table

5 Conclusion

Although black hole singularities seem to be inevitable within general theory of relativity and through the collapse of ordinary matter which respects energy conditions, there are alternative models which avoid the spacetime singularity by ignoring energy conditions or other assumptions of the singularity theorems [7,8,9]. In the present work, we demonstrated that a non-linear electromagnetic Lagrangian can lead to black hole solutions which behave like a Reissner–Nordestr\(\ddot{o}\)m-AdS BH at large distance, while having a quasi non-singular core in the sense that the metric function behaves like \( f(r)\approx 1-\dfrac{2\alpha }{\beta ^{2}}r+O(r^{2}) \) as \( r \rightarrow 0\). The electromagnetic Lagrangian, although having a relatively complicated form, reduces to the Maxwellian form as \( F\rightarrow 0 \). The BH solutions presented here have the interesting property that their ADM mass and charge are not free parameter, but depend on the Lagrangian parameters \( \alpha \) and \(\beta \).

Since, thermodynamical behavior are of great importance in search for a quantum theory of gravitation, we have also managed to perform a thermodynamic investigation of the BH solutions. The conserved and thermodynamic quantities were calculated and the validity of the first law was checked. Global stability of the BH was examined by plotting the Gibbs free energy, and the heat capacities were studied to check the local stability. We showed that the present solutions admitted small/large phase transitions similar to the Van der Waals liquid/gas phase transition. Then, by writing and solving the wave equation for a scalar field in the BH background spacetime, the QNMs were calculated. We pointed out that the frequencies of QNMs behave somehow differently form those of RN-AdS and Schwarzschild-AdS black holes. The effect of the BH charge on eigen-frequencies were demonstrated through several diagrams which were calculated numerically.

Finally, we have obtained the QNMs frequencies of massless scalar perturbations around small and large black hole. We found that when the Van der Waals-like phase transition happens, as the horizon radius increase, the slopes of the QNMs frequency change differently in the small and large black holes.

As a further remark, in order to study the thermodynamics of black hole, one can also use the geometrothermodynamical formalism.