1 Introduction

Black holes, formed from the gravitational collapse of matters, are of the most important objects in General Relativity (GR) as well as relating directly to quantum gravity. One of the interesting subjects in studying the black holes is their thermodynamics [1,2,3,4,5]. Since the Hawking–Page phase transition was proposed [6], the thermodynamic phase transitions of the black holes have been studied extensively in the literature. It was found that there occurs a phase transition between small-large black charged holes [7,8,9]. Recently, the cosmological constant \(\Lambda \) was considered as the thermodynamic pressure P, and its conjugate variable is the thermodynamic volume V [10,11,12,13,14]. As argued in Ref. [13], the total energy E thus should include the vacuum energy, \(\rho V=-PV\), with \(\rho \) to be an energy density. It means that

$$\begin{aligned} E=M+\rho V=M-PV, \end{aligned}$$
(1)

and thus M is most naturally the enthalpy, rather than the internal energy of the black hole [11]. Accordingly, the thermodynamic behavior of the black hole is restudied in the extended phase space and has gained more and more attention. In 2012, Kubizňák and Mann examined \(P-V\) criticality of the charged AdS black hole in the extended phase space [15]. Their results showed that the charged AdS black hole has the Van der Waals-like phase transition which is analogous to the liquid–gas phase transition of the ordinary thermodynamic systems. Later, \(P-V\) criticality was studied in various black holes [16,17,18,19,20,21,22,23,24]. In particular, based on the Smarr formula and the first law of the thermodynamics, \(P-V\) criticality is demonstrated to be universal [25]. Furthermore, to study the black holes in the extended phase space led to other new phenomena. Multiply reentrant phase transition and triple points were found in the charged black holes [26,27,28]. The black holes play an analogous role as a Carnot-cycle heat engine which is defined by a closed path in the \(P-V\) plane [29,30,31,32,33,34,35,36,37]. The Joule-Thomson expansion for the charged AdS and Kerr-AdS black holes is considered in Refs. [38, 39].

Studying the phase transitions of the black holes in the AdS spacetime is motivated by the gauge/gravity correspondence [40, 41], where the black hole can be identified with an approximately thermal state in the dual strongly coupled field theory [42, 43]. In particular, the black holes have been related with the holographic superconductivity [44, 45]. Since, thermodynamics and the phase transitions of black holes in the AdS spacetime have received many recent studies [7,8,9, 11, 13,14,15,16,17,18,19,20, 22,23,25, 27, 29, 30, 32, 46,47,56].

In GR, the black holes have a singularity at the origin surrounded by the event horizon [57]. It is widely believed that the black hole singularity would be removed by a complete theory of quantum gravity. However, up to now there has no a complete understanding of quantum gravity. Thus, many efforts have been dedicated to determine how to avoid the black hole singularity at the semi-classical level. The black hole without singularity at the origin was first proposed by Bardeen [58]. Interestingly, this black hole was reobtained by Ayón-Beato and García as a gravitational collapse of some magnetic monopole in the non-linear electrodynamics [59]. Indeed, the non-linear electrodynamics was first proposed, by Born and Infeld, as modifying the standard Maxwell theory with the main motivation of eliminating the problem of infinite energy of the electron [60]. Although the non-linear electrodynamics did not solve this problem and thus was less popular, in recent years it has received considerable attention because it leads to the regular black holes [61,62,63,64,65,66,67,68,69,70,71,72,73,74]. The thermodynamics and critical phenomena of some nonlinear charged black holes in AdS spacetime were studied in [24, 55, 75,76,77,78,79,80,81].

In this paper, we would like to generalize a black hole solution carrying the electric charge derived in Ref. [61], which has been widely discussed in the literature, in the AdS spacetime. Then, we study the global properties, the thermodynamics and the phase transitions of this black hole solution.

This paper is organized as follows. In Sect. 2, we derive a non-linear charged black hole solution from solving the equations of the motion for the system of Einstein gravity coupled to a non-linear electromagnetic field in the AdS spacetime, and then we study the interesting properties of this solution. In Sect. 3, we calculate the thermodynamic quantities and analyze the phase transitions of the black hole. Finally, we devote to conclusions in the last section, Sect. 4.

In this work, we use units in \(G_N=\hbar =c=k_B=1\) and the signature of the metric \((-,+,+,+)\).

2 Non-linear charged black hole solution in AdS spacetime

Einstein gravity coupled to a non-linear electromagnetic field in the AdS spacetime is described by the action

$$\begin{aligned} S=\int d^4x\sqrt{-g}\left[ \frac{1}{16\pi }\left( R+\frac{6}{l^2}\right) -\frac{1}{4\pi }\mathcal {L}(F)\right] , \end{aligned}$$
(2)

where R is the scalar curvature, l is the curvature radius of the AdS spacetime, and \(\mathcal {L}(F)\) is the non-linear electrodynamic term which is a function of the invariant \(F_{\mu \nu }F^{\mu \nu }/4\equiv F\) with \(F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu \) to be the field strength of the non-linear electromagnetic field. In this paper, we would like to generalize a regular charged black hole solution in Ref. [61] by including a negative cosmological constant. Hence, the non-linear electrodynamic is explicitly defined as [61]

$$\begin{aligned} \mathcal {L}(F)= & {} -\frac{X^2}{2Q^2}\frac{1-8X-3X^2}{(1-X)^4} -\frac{3M}{Q^2|Q|}\frac{X^{5/2}(3-2X)}{(1-X)^{7/2}}, \nonumber \\ X= & {} \sqrt{-2Q^2F}, \end{aligned}$$
(3)

where M and Q are mass and charge of the system.

In order to have a regular black hole solution, either Einstein gravity or matter source should be modified in a suitable way. The modification of Einstein gravity has been studied extensively in the literature. But, so far this has not yet led to complete solutions. Thus, an alternative approach is to consider the modification of the matter which is here the modification of the electromagnetic field. Because the electromagnetic field is well described by the Maxwell electrodynamics, the electromagnetic field should be modified at the short distances corresponding to the strong electromagnetic field. But, in the limit of the large distances corresponding to the weak electromagnetic field, it is approximately the usual electromagnetic field described by the Maxwell electrodynamics. We can easily see that, with the form of the non-linear electrodynamics given by Eq. (3), we should have \(\mathcal {L}(F)\cong F\) in the weak field limit (\(F\ll 1\)) and thus the non-linear electrodynamics is approximately the Maxwell electrodynamic. In this sense, the form of the non-linear electrodynamics given by Eq. (3) is one of the suitable forms for the modification of the electromagnetic field at the short distances corresponding to the strong electromagnetic field.

The equations of motion derived from the above action are

$$\begin{aligned} G^\nu _\mu -\frac{3}{l^2}\delta ^\nu _\mu= & {} 2\left[ \frac{\partial \mathcal {L}(F)}{\partial F}F_{\mu \rho }F^{\nu \rho }-\delta ^\nu _\mu \mathcal {L}(F)\right] , \end{aligned}$$
(4)
$$\begin{aligned} \nabla _\mu \left( \frac{\partial \mathcal {L}(F)}{\partial F}F^{\nu \mu }\right)= & {} 0. \end{aligned}$$
(5)

Note that, the field strength \(F_{\mu \nu }\) also satisfies the Bianchi identities, \(\nabla _\mu *F^{\nu \mu }=0\). Instead of solving the equations of motion in terms of the functions \((g_{\mu \nu },\mathcal {L},F)\), one can use another functions \((g_{\mu \nu },\mathcal {H},P)\) obtained by means of a Legendre transformation [83]

$$\begin{aligned} \mathcal {H}(P)=2\frac{\partial \mathcal {L}(F)}{\partial F}F-\mathcal {L}(F),\ \ P\equiv \frac{1}{4}P_{\mu \nu }P^{\mu \nu }=\left( \frac{\partial \mathcal {L}(F)}{\partial F}\right) ^2F. \end{aligned}$$
(6)

It can be shown that

$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial F}=\left( \frac{\partial \mathcal {H}}{\partial P}\right) ^{-1},\ \ \mathcal {L}=2\frac{\partial \mathcal {H}}{\partial P}P-\mathcal {H}, \ \ \frac{\partial \mathcal {L}(F)}{\partial F}F^{\mu \nu }=P^{\mu \nu }. \end{aligned}$$
(7)

where

$$\begin{aligned} \mathcal {H}(P)=P\frac{1-3\sqrt{-2Q^2P}}{\left( 1+\sqrt{-2Q^2P}\right) ^3}-\frac{3M}{Q^2|Q|}\left( \frac{\sqrt{-2Q^2P}}{1+\sqrt{-2Q^2P}}\right) ^{\frac{5}{2}}. \end{aligned}$$
(8)

Using these relations, one can write the equations of motion in terms of the functions \((g_{\mu \nu },\mathcal {H},P)\) as

$$\begin{aligned} G^\nu _\mu -\frac{3}{l^2}\delta ^\nu _\mu= & {} 2\left[ \frac{\partial \mathcal {H}}{\partial P}P_{\mu \rho }P^{\nu \rho }-\delta ^\nu _\mu \left( 2\frac{\partial \mathcal {H}}{\partial P}P-\mathcal {H}\right) \right] , \end{aligned}$$
(9)
$$\begin{aligned} \nabla _\mu P^{\nu \mu }= & {} 0. \end{aligned}$$
(10)

Now we find a static and spherical symmetric black hole solution of the mass M and the electric-charge Q with the following ansatz

$$\begin{aligned} ds^2= & {} -f(r)dt^2+f(r)^{-1}dr^2+r^2d\Omega ^2,\nonumber \\ f(r)= & {} \left( 1-\frac{2m(r)}{r}\right) ,\nonumber \\ P_{\mu \nu }= & {} \left( \delta ^t_\mu \delta ^r_\nu -\delta ^t_\nu \delta ^r_\mu \right) \phi (r). \end{aligned}$$
(11)

(For simplicity, with out loss of generality, in what follows we consider \(Q>0\).) Note that, the electric-charge Q is defined as

$$\begin{aligned} Q=\frac{1}{4\pi }\int _{S^\infty _2}*\frac{\partial \mathcal {L}(F)}{\partial F}{\varvec{F}}=\frac{1}{4\pi }\int _{S^\infty _2}*{{\varvec{P}}}, \end{aligned}$$
(12)

where \({{\varvec{F}}}=\frac{1}{2}F_{\mu \nu }dx^\mu \wedge dx^\nu \) and \({{\varvec{P}}}=\frac{1}{2}P_{\mu \nu }dx^\mu \wedge dx^\nu \) which are two-forms. Eqs. (10) and (12), with ansatz (11), lead to

$$\begin{aligned} \phi (r)=\frac{Q}{r^2}\ \ \longrightarrow \ \ P=-\frac{Q^2}{2r^4}. \end{aligned}$$
(13)

Then, with this result, Eq. (9) leads to

$$\begin{aligned} \frac{dm(r)}{dr}+\frac{3r^2}{2l^2}=Q^2r^2\left( \frac{(r^2-3Q^2)}{2(r^2+Q^2)^3}+\frac{3M}{(r^2+Q^2)^{5/2}}\right) . \end{aligned}$$
(14)

Integrating this equation with the integral constant

$$\begin{aligned} \left( m(r)+\frac{r^3}{2l^2}\right) _{r\rightarrow \infty }=M, \end{aligned}$$
(15)

we get

$$\begin{aligned} m(r)=\frac{Mr^3}{(r^2+Q^2)^{3/2}}-\frac{Q^2r^3}{2(r^2+Q^2)^2}-\frac{r^3}{2l^2}. \end{aligned}$$
(16)

Substituting m(r) into f(r), we finally get

$$\begin{aligned} f(r)=1-\frac{2M}{r}\left( 1+\frac{Q^2}{r^2}\right) ^{-\frac{3}{2}}+\frac{Q^2}{r^2}\left( 1+\frac{Q^2}{r^2}\right) ^{-2}+\frac{r^2}{l^2}. \end{aligned}$$
(17)

The electrostatic potential \(A_t(r)\) of the black hole is obtained as

$$\begin{aligned} A_t(r)= & {} -\int F_{tr}dr +\frac{3M}{2Q}=-\int \frac{\partial \mathcal {H}}{\partial P}P_{tr}dr +\frac{3M}{2Q},\nonumber \\= & {} \frac{Q}{r}\left( 1+\frac{Q^2}{r^2}\right) ^{-3}-\frac{3M}{2Q}\left( 1+\frac{Q^2}{r^2}\right) ^{-\frac{5}{2}}+\frac{3M}{2Q},\nonumber \\ \end{aligned}$$
(18)

satisfying \(A_t(r\rightarrow \infty )=0\).

Let us look at the large and short distance behaviors of the metric defined by (17). At the large distances (\(Q/r\ll 1\)) corresponding to the weak non-linear electrostatic field, it leads to

$$\begin{aligned} f(r)\simeq 1-\frac{2M}{r}+\frac{Q^2}{r^2}+\frac{r^2}{l^2},\ \ A_t(r)\simeq \frac{Q}{r}. \end{aligned}$$
(19)

It means that the non-linear charged AdS black hole behaves asymptotically like the RN-AdS black hole and thus is a non-linear generalization of the RN-AdS black hole. Whereas, at the short distances (\(Q/r\gg 1\)) corresponding to the strong non-linear electrostatic field, it leads to

$$\begin{aligned} f(r)\simeq 1-\left( \frac{2M-Q}{Q^3}-\frac{1}{l^2}\right) r^2, \end{aligned}$$
(20)

at which \(2Ml^2-Q(Q^2+l^2)>0\) is always positive as shown in later. This clearly suggests that at the short distances the metric corresponding to (17) behaves like a deSitter (dS) geometry with an effective cosmological constant

$$\begin{aligned} \Lambda _{\text {eff}}=3\left( \frac{2M-Q}{Q^3}-\frac{1}{l^2}\right) , \end{aligned}$$
(21)

rather than like a black hole. As a result, the singularity at the origin should be replaced by a core of the dS geometry which produces a negative pressure and thus prevents a singular end-state of the gravitationally collapsed matter. It can check that the curvature scalars, R, \(R_{\mu \nu }R^{\mu \nu }\), and \(R_{\mu \nu \rho \lambda }R^{\mu \nu \rho \lambda }\) are finite everywhere and thus the black hole is regular.

Fig. 1
figure 1

The function \(f(r_H)\) is plotted in terms of the horizon radius \(r_H\), at \(Q=1\) and \(l^2=12/5\), for the different values of the mass M. The green, red and blue curves correspond to \(M=3\) (non-extremal black hole), \(M=5\sqrt{2}/3\) (extremal black hole), and \(M=2\) (no black hole)

Full size image

The equation of the horizon is given by, \(f(r_H)=0\), where \(r_H\) represents the horizon radius. Its solution structure corresponding to the cases of non-extremal black hole, extremal black hole and no black hole is given in Fig. 1. We can express the black hole mass M in terms of \(r_H\) as

$$\begin{aligned} M=\frac{(r^2_H+Q^2)^{\frac{3}{2}}}{2}\left( \frac{1}{l^2}+\frac{1}{r^2_H}+\frac{Q^2}{(r^2_H+Q^2)^2}\right) . \end{aligned}$$
(22)

Although this equation cannot be solved analytically, it can analyze the relation of the black hole mass with respect to the horizon radius. We can easily see

$$\begin{aligned} M(r_H\rightarrow 0)\rightarrow \infty ,\ \ M(r_H\rightarrow \infty )\rightarrow \infty ,\ \ M>\frac{Q^3}{2l^2}>0. \end{aligned}$$
(23)

This means that there actually exists a lower bound \(M_0\) for the mass of the black hole for given l and Q. The black hole of the mass \(M_0\) is regarded as the extremal black hole with the extremal horizon radius \(r_0\). Here, the reduced extremal horizon radius \(r_0/Q\equiv \bar{r}_0\) is a unique positive real solution of the following equation

$$\begin{aligned} \frac{Q^2}{l^2}=\frac{2+3\bar{r}^2_0+\bar{r}^4_0-\bar{r}^6_0}{3\bar{r}^4_0(1+\bar{r}^2_0)^2}, \end{aligned}$$
(24)

derived from the equation \(M'(r_0)=0\). And, with the help of Eq. (24), one can express the reduced extremal mass \(M_0/Q\) as a function of the reduced extremal horizon radius \(\bar{r}_0\)

$$\begin{aligned} \frac{M_0}{Q}=\frac{\bar{r}^6_0+5\bar{r}^4_0+3\bar{r}^2_0+1}{3\bar{r}^4_0 \sqrt{\bar{r}^2_0+1}}. \end{aligned}$$
(25)

From Eqs. (24) and (25), one can determine an upper limit for \(r_0/Q\)

$$\begin{aligned} \frac{r_0}{Q}\Big |_{\text {max}}= & {} \frac{1}{\sqrt{3}}\left( 1+2^{-1/3}\big [(83-3\sqrt{231})^{1/3}+(83+3\sqrt{231})^{1/3}\big ]\right) ^{1/2}\nonumber \\\equiv & {} \alpha \approx 1.58479, \end{aligned}$$
(26)

and a lower limit for \(M_0/Q\)

$$\begin{aligned} \frac{M_0}{Q}\Big |_{\text {min}}\approx 1.57684, \end{aligned}$$
(27)

which associate with the limit of the vanishing cosmological constant. Thus, for given charge Q, there are no extremal black holes, in the AdS spacetime, with the horizon radius larger than \(\alpha Q\) or the mass smaller than the value \(\approx 1.57684Q\). This can be more clearly seen in Fig. 3 (right). We can also see that the horizon radius of the extremal black hole in AdS spacetime of the large curvature radius (the low pressure) is larger than that of the extremal black hole in AdS spacetime of the small curvature radius (the high pressure). From Eq. (24), it is quite evident that, for any values of l and Q, the equation \(M'(r_0)=0\) only has one unique positive real solution. Since the black hole gets maximally two horizons. Depending on the proper parameters of the black hole (M, Q, l), the black hole could have one or two horizons. The event horizon radius \(r_+\) is taken as the largest positive root of f(r).

Fig. 2
figure 2

The reduced effective cosmological constant is plotted in terms of the reduced horizon radius for the case of the extremal black hole

Full size image
Fig. 3
figure 3

Left: We plot the reduced cosmological constant \(Q^2/l^2\) in terms of the reduced extremal horizon radius \(r_0/Q\). Right: We plot the reduced mass M / Q of the extremal black hole in terms of the reduced extremal horizon radius. The red and blue curves refer to the non-linear charged black hole of this work and the RN-AdS black hole, respectively

Full size image
Fig. 4
figure 4

The reduced mass M / Q of the non-extremal black hole is plotted in terms of the reduced horizon radius \(r_H/Q\), at \(l/Q=5\) (left) and \(l/Q=15\) (right). The red and blue curves refer to the non-linear charged black hole of this work and the RN-AdS black hole, respectively

Full size image

From Eqs. (24) and (25), one can plot the effective cosmological constant \(\Lambda _{\text {eff}}\) in terms of the horizon radius for the extremal black hole, given in Fig. 2. This figure clearly shows

$$\begin{aligned} M_0>\frac{Q}{2}\left( 1+\frac{Q^2}{l^2}\right) , \end{aligned}$$
(28)

for any extremal black hole. Because the mass of the non-extremal black hole is larger than that of the extremal one, the effective cosmological constant \(\Lambda _{\text {eff}}\) also is always positive for the non-extremal case. Thus, the short distance behavior of the black hole solution is actually the dS geometry.

We end this section by commenting the effect of the non-linear electrodynamics on the charged black hole in AdS spacetime. It is first useful to mention that, for the RN-AdS black hole, the relation between the reduced extremal horizon radius \(\bar{r}_0\) and Q / l is given by

$$\begin{aligned} \frac{Q^2}{l^2}=\frac{1-\bar{r}^2_0}{3\bar{r}^4_0}, \end{aligned}$$
(29)

and the reduced extremal mass \(M_0/Q\) as a function of the reduced extremal horizon radius \(\bar{r}_0\) is given by

$$\begin{aligned} \frac{M_0}{Q}=\frac{\bar{r}^2_0+2}{3\bar{r}_0}. \end{aligned}$$
(30)

It is shown in Fig. 3 that the non-linear electrodynamics makes the size of the extremal charged black hole larger, with fixed Q / l. If the extremal horizon radius is fixed, the extremal non-linear charged black hole is (so much) more heavy than the extremal RN-AdS black hole. This is also true with respect to the non-extremal case, as seen in Fig. 4. It means that, with the event horizon radius \(r_+\) fixed, the non-linear charged black hole is (so much) more heavy than the RN-AdS black hole. On the other hand, with the mass M fixed, the non-linear charged black hole is (so much) smaller the RN-AdS black hole. (However, the inner horizon of the non-linear charged black hole is larger compared to that of the RN-AdS black hole.) This is quite clear because in order to form the non-linear charged black hole the gravitational force must be stronger, in particular for the small size black hole, to win the non-linear electrostatic repulsion. And, thus it requires that the black hole has to possess much more mass for the event horizon radius \(r_+\) fixed or the smaller size for the mass M fixed.

3 The thermodynamics and phase transitions

In this section, we will calculate the thermodynamic quantities and analyze the phase transitions for the black hole derived in the previous section.

3.1 Thermodynamic quantities

In the extended phase space, the thermodynamic pressure P is given as

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }=\frac{3}{8\pi l^2}, \end{aligned}$$
(31)

and the first law of the black hole thermodynamics should be

$$\begin{aligned} dM=TdS+\Phi dQ+VdP. \end{aligned}$$
(32)

Here, the entropy S, the charge Q and the thermodynamic pressure P are a complete set of the extensive thermodynamic variables for the mass or elthalpy function M(S, Q, P). And, the temperature T, the chemical potential \(\Phi \) and the thermodynamic volume V (which are the intensive thermodynamic variables conjugating to the entropy S, the charge Q and the thermodynamic pressure P, respectively) are defined as

$$\begin{aligned} T=\left( \frac{\partial M}{\partial S}\right) _{Q,P},\ \ \Phi =\left( \frac{\partial M}{\partial Q}\right) _{S,P},\ \ V=\left( \frac{\partial M}{\partial P}\right) _{S,Q}. \end{aligned}$$
(33)

By requiring the absence of the potential conical singularity of the Euclidean trick, one can identify the black hole temperature

$$\begin{aligned} T= & {} \frac{f'(r_+)}{4\pi } =\frac{1}{4\pi r_+}\left( \frac{3r^4_+}{l^2(r^2_++Q^2)}+\frac{r^6_+}{(r^2_++Q^2)^3}\right. \nonumber \\&\quad \left. -\frac{Q^2r^2_+}{(r^2_++Q^2)^2}-\frac{2Q^4}{(r^2_++Q^2)^2}\right) , \end{aligned}$$
(34)

which is approximately the temperature of the RN-AdS black hole in the limit of the large distances (\(r_+/Q\gg 1\)). Because the extremal horizon radius \(r_0\) satisfies Eq. (24), the black hole temperature vanishes at \(r_0\). Also, the black hole temperature approaches infinite when \(r_+\longrightarrow \infty \). Against this scenario, the temperature of the black hole without the AdS background (the limit of the vanishing cosmological constant), approaches zero when \(r_+\longrightarrow \infty \). The isobaric temperature curve is plotted, under the different values of the pressure, in Fig. 5. From this figure, we can see the existence of a critical pressure \(P_c\) (derived in later), above which (\(P>P_c\)) the isobaric temperature curve is an increasingly monotonic function of the horizon radius \(r_+\). For \(0<P<P_c\), the isobaric temperature curve has one local maximum temperature and one local minimum temperature. When the pressure approaches \(P_c\), the local maximum and minimum of the isobaric temperature curve merge into one inflexion. In the limit \(P\rightarrow 0\), the local minimum temperature should disappear.

Fig. 5
figure 5

We plot the reduced temperature of the black hole against the reduced horizon radius under the different values of the pressure. The orange, green, dashed black, blue, red, and black curves correspond to \(l/Q=9\), 10, \(\approx \mathbf{11.5637 }\) (\(l_c/Q\)), 15, 20, \(\infty \)

Full size image

Using the expression (34) of the black hole temperature and the first law, one can derive the entropy of the black hole

$$\begin{aligned} S= & {} \int \frac{1}{T}\frac{\partial M}{\partial r_+}dr_+=2\pi \int \frac{(r^2_++Q^2)^{3/2}}{r^2_+}dr_+,\nonumber \\= & {} \pi Q^2\left[ \left( \frac{r_+}{Q}-\frac{2Q}{r_+}\right) \sqrt{1+\left( \frac{r_+}{Q}\right) ^2} \right. \nonumber \\&\left. +3\ln \left( \frac{r_+}{Q}+\sqrt{1+\left( \frac{r_+}{Q}\right) ^2}\right) \right] . \end{aligned}$$
(35)

[Note that, \(\ln (x+\sqrt{1+x^2})=\text {arcsinh}(x)\).] Clearly, the non-linear electrodynamics breaks in general the area law (\(S=\pi r^2_+\)). In the regime of the large horizon radius (\(r_+/Q\gg 1\)), corresponding to the weak non-linear electrostatic field, the entropy of the black hole becomes

$$\begin{aligned} S\simeq \pi Q^2\left( \frac{r^2_+}{Q^2}+3\ln 2\frac{r_+}{Q}\right) . \end{aligned}$$
(36)

Because \(x^2\gg 3\ln 2x\) for \(x\gg 1\), the second term in the expression (36) is approximately neglected for \(r_+/Q\gg 1\). And, thus the well-known Bekenstein–Hawking entropy is approximately recovered in the regime of the large horizon radius.

Note that, Eq. (35) implies that \(r_+\) is understood as a function of the extensive thermodynamic variables S and Q. Since this equation along with Eq. (22) allow to define the enthalpy function

$$\begin{aligned} M(S,Q,P)=M\big (r_+(S,Q),Q,P\big ). \end{aligned}$$
(37)

With the given enthalpy function, using the first law one can derive the chemical potential \(\Phi \) and thermodynamic volume V as

$$\begin{aligned} \Phi= & {} \left( \frac{\partial M}{\partial Q}\right) _{S,P}=\left( \frac{\partial M}{\partial Q}\right) _{r_+,P}+\left( \frac{\partial M}{\partial r_+}\right) _{Q,P}\left( \frac{\partial r_+}{\partial Q}\right) _{S}, \end{aligned}$$
(38)
$$\begin{aligned} V= & {} \left( \frac{\partial M}{\partial P}\right) _{S,Q}=\frac{4}{3}\pi (r^2_++Q^2)^{\frac{3}{2}}, \end{aligned}$$
(39)

where

$$\begin{aligned}&\left( \frac{\partial M}{\partial Q}\right) _{r_+,P}= \frac{Q\left[ 3r^2_+(r^2_++Q^2)^2+l^2(3Q^4+7Q^2r^2_++5r^4_+)\right] }{2l^2r^2_+(r^2_++Q^2)^{3/2}}, \end{aligned}$$
(40)
$$\begin{aligned}&\left( \frac{\partial M}{\partial r_+}\right) _{Q,P}= \frac{3r^4_+(r^2_++Q^2)^2+l^2(-2Q^6-3Q^4r^2_+-Q^2r^4_++r^6_+)}{2l^2r^3_+(r^2_++Q^2)^{3/2}}, \end{aligned}$$
(41)
$$\begin{aligned}&\left( \frac{\partial r_+}{\partial Q}\right) _{S}= \frac{3Qr_+\left[ \sqrt{r^2_++Q^2}-r_+\ln (r_+/Q+\sqrt{1+(r_+/Q)^2})\right] }{(r^2_++Q^2)^{3/2}}.\nonumber \\ \end{aligned}$$
(42)

It is easily checked that the thermodynamic quantities of the non-linear charged AdS black hole satisfy the Smarr formula

$$\begin{aligned} M=2(TS-VP)+\Phi Q, \end{aligned}$$
(43)

which shows their scaling behavior as

$$\begin{aligned} r_+\rightarrow & {} \lambda r_+,\ \ Q\rightarrow \lambda Q,\ \ S\rightarrow \lambda ^2 S,\ \ P\rightarrow \frac{P}{\lambda ^2},\nonumber \\ M\rightarrow & {} \lambda M,\ \ T\rightarrow \frac{T}{\lambda },\ \ \Phi \rightarrow \lambda ^0\Phi ,\ \ V\rightarrow \lambda ^3V. \end{aligned}$$
(44)

It is well known that the black hole is at least locally stable if it has positive heat capacity. On the contrary, if the black hole has negative heat capacity, it is unstable. This suggests that the discontinuous change of the sign of the heat capacity should lead to the phase transitions of the black hole. Thus, in order to study the phase transitions of the black hole in later, let first us calculate the heat capacity at constant pressure

$$\begin{aligned} C_P= & {} \left( \frac{\partial M}{\partial T}\right) _P=\frac{\partial M}{\partial r_+}\left( \frac{\partial T}{\partial r_+}\right) ^{-1},\nonumber \\= & {} \frac{2\pi \left( r^2_++Q^2\right) ^{5/2}\left[ 3r^4_+\left( r^2_++Q^2\right) ^2-l^2\left( 2Q^6+3Q^4r^2_++Q^2 r^4_+-r^6_+\right) \right] }{l^2r_+ \left( 2Q^8+11Q^6r^2_++12Q^4r^4_++8Q^2r^6_+-r^8_+\right) +3r^5_+ \left( r^2_++Q^2\right) ^2\left( r^2_++3Q^2\right) }. \end{aligned}$$
(45)

We can see that the heat capacity \(C_P\) vanishes at the extremal horizon radius. We plot the heat capacity \(C_P\) under the different values of the pressure in Fig. 6. It is shown in this figure that for the pressure above \(P_c\) the heat capacity \(C_P\) is always positive and a regular function of the horizon radius \(r_+\). Below the pressure \(P_c\), there are three regions divided by two vertical asymptotes located at \(r_1\) and \(r_2\), where \(r_1\) and \(r_2\) are the radiuses corresponding to the local maximum temperature \(T_{\text {max}}\) and local minimum temperature \(T_{\text {min}}\). For the regions, \(r_+<r_1\) and \(r_+>r_2\), the heat capacity \(C_P\) is positive and thus the black hole is thermodynamically stable in these regions. Whereas, for the region \(r_1<r_+<r_2\), the heat capacity is negative and thus the black hole is thermodynamically unstable in this region. When the pressure approaches the critical value \(P_c\), two points \(r_1\) and \(r_2\) merge into one where the heat capacity is divergent but continuous. In the limit \(P\rightarrow 0\), the region \(r_+>r_2\) should disappear.

Fig. 6
figure 6

Plots of the reduced heat capacity \(C_P/Q^2\) in terms of the reduced horizon radius \(r_+/Q\) under the different values of the pressure. They correspond to \(l/Q=10\) (top left), \(l/Q\approx \mathbf{11.5637 }\) (top right), \(l/Q=15\) (bottom left), and \(l/Q\rightarrow \infty \) (bottom right)

Full size image

3.2 Phase transitions

Now we study the phase transitions of the black hole introduced in the previous section. In what follows, the black hole charge Q is kept fixed. Depending on the value of the pressure or the temperature, there are first-order, second-order phase transitions, or no phase transition. Critical point occurs as the isobar in the \(T-r_+\) diagram (or the isotherm in the \(P-r_+\) diagram) has an inflexion, given by

$$\begin{aligned} \left( \frac{\partial T}{\partial r_+}\right) _P=\left( \frac{\partial ^2T}{\partial r^2_+}\right) _P=0. \end{aligned}$$
(46)

Thus, we find equation for determining the reduced critical horizon radius \(r_c/Q\equiv \bar{r}_c\)

$$\begin{aligned} 12+63\bar{r}^2_c + 131\bar{r}^4_c+104\bar{r}^6_c+66\bar{r}^8_c+17\bar{r}^{10}_c-\bar{r}^{12}_c=0, \end{aligned}$$
(47)

which leads to a unique positive real solution \(\bar{r}_c\approx 4.526\). From this, we can obtain the critical pressure and temperature

$$\begin{aligned} P_c= & {} \frac{1}{8\pi }\frac{\bar{r}^8_c-8\bar{r}^6_c-12\bar{r}^4_c-11\bar{r}^2_c-2}{\bar{r}^4_c(3+\bar{r}^2_c)(1+\bar{r}^2_c)^2}\frac{1}{Q^2}\approx \frac{0.0009}{Q^2}, \end{aligned}$$
(48)
$$\begin{aligned} T_c= & {} \frac{(\bar{r}^6_c-\bar{r}^4_c-3\bar{r}^2_c-2)+8\pi P_c(1+\bar{r}^2_c)^2\bar{r}^4_c}{4\pi \bar{r}_c(1+\bar{r}^2_c)^3}\frac{1}{Q}\approx \frac{0.0221}{Q}.\nonumber \\ \end{aligned}$$
(49)

By comparing with the RN-AdS black hole, at which \(\bar{r}_c=\sqrt{6}\), \(P_c=1/96\pi Q^2\), \(T_c=\sqrt{6}/18\pi Q\), we see that the non-linear electrodynamics makes the value of the reduced critical horizon radius shifted toward the outside of the black hole, whereas the phase transition happens at the lower critical pressure. At this critical point, the heat capacity is divergent but continuous and positive.

Above the critical pressure \(P_c\), the heat capacity \(C_P\) is always regular and positive and thus there is no phase transition happening. However, below critical pressure \(P_c\) (\(0<P<P_c\)), the black hole can undergo a first-order phase transition between a small stable black hole of the radius \(r_+<r_1\) and a large stable black hole of the radius \(r_+>r_2\). This first-order phase transition is performed via two second-order phase transitions happening at the extremal points \(r_{1,2}\) because the heat capacity \(C_P\) suffers discontinuities at these points. The reduced values \(r_{1,2}/Q\) of these second-order phase transition points are two positive real solutions of the following equation

$$\begin{aligned}&\frac{l^2}{Q^2}\left( 2+11x^2+12x^4+8x^6-x^8\right) +3x^4 \left( x^2+1\right) ^2\left( x^2+3\right) =0,\nonumber \\ \end{aligned}$$
(50)

which cannot be solved analytically and thus we give the numerical solutions in Table 1. The point \(r_2\) corresponds to the second-order phase transition point between a large stable black hole and a medium unstable one, whereas the point \(r_1\) corresponds to the second-order phase transition point between a medium unstable black hole and a small stable one. From Table 1, we can see that, when the pressure decreases, the value of the radius \(r_1\) is shifted toward the inside of the black hole, whereas the value of the radius \(r_2\) is shifted toward the outside of the black hole. The temperatures at the second-order phase transition points \(r_1\) and \(r_2\) both decrease as the pressure decreases. In the limit \(P\rightarrow 0\), we have \(r_2\rightarrow \infty \) and \(T_{\text {min}}\rightarrow 0\). It means that the second-order phase transition at the point \(r_2\) and thus the first-order one should disappear. Whereas, the second-order phase transition point \(r_1\) and the corresponding temperature \(T_{\text {max}}\) approach the lower limits, \(\approx 3.06643 Q\) and \(\approx 0.01643/Q\), respectively.

Table 1 The numerical results of Eq. (50) and the second-order phase transition temperatures for the different values of l / Q
Full size table

In order to obtain more details on the thermodynamic phase transitions, we should investigate the Gibbs free energy G, which is a function of the pressure and temperature, given by

$$\begin{aligned} G=M(r_+)-T(r_+)S(r_+). \end{aligned}$$
(51)

The Gibbs free energy as a function of the temperature T at the different values of the pressure is depicted in Fig. 7. From this figure, we can see that, for the pressure below the critical pressure \(P_c\) (\(0< P<P_c\)), the Gibbs free energy shows the swallowtail structure, which implies two second-order phase transitions and one first-order phase transition. Also, based on the Gibbs free energy, we can point out the Hawking–Page phase transition (for \(P>0\)), at which the Gibbs free energy vanishes [6], occurring between the thermal radiation and the large black hole. The critical temperature \(T_{HP}\) and the critical horizon radius \(r_{HP}\), corresponding to this phase transition, are numerically given in Table 2.

Fig. 7
figure 7

Plots of the reduced Gibbs free energy G / Q as a function of the reduced temperature \(T\times Q\) under the different values of the pressure. The orange, green, dashed black, blue, red, and black curves correspond to \(l/Q=9,10,\approx \mathbf{11.5637 },15,20,\infty .\)

Full size image
Table 2 The numerical results of the critical horizon radius and the critical temperature at the Hawking–Page phase transition for the different values of l / Q
Full size table

We now discuss the thermodynamic phases of the black hole and their stability. The black hole of the zero temperature is of course extremal configuration which can be considered as true ground state with the minimized enthalpy. The black hole of the temperature T, satisfying \(0<T<T_{\text {min}}\), is small stable near-extremal configuration. For the temperature of the black hole satisfying \(T_{\text {min}}<T<T_{\text {max}}\), there are triplet configurations but in general with the different Gibbs free energy: small stable near-extremal configuration, medium unstable configuration, large stable configuration. The black hole satisfying \(T>T_{\text {max}}\) is large stable configuration. In order to obtain more details, we should consider the off-shell Gibbs free energy

$$\begin{aligned} G_{\text {off}}=M(r_+)-TS(r_+), \end{aligned}$$
(52)

with the temperature T to be a free parameter. The off-shell Gibbs free energy \(G_{\text {off}}\) describes the evolution of the system towards equilibrium configurations, which are the extremal points of \(G_{\text {off}}\), in the thermal bath of the temperature T. The extremal points of \(G_{\text {off}}\) satisfy

$$\begin{aligned} \frac{\partial G_{\text {off}}}{\partial r_+}=0 \ \ \longrightarrow \ \ T=\frac{\partial M}{\partial r_+}\left( \frac{\partial S}{\partial r_+}\right) ^{-1}. \end{aligned}$$
(53)

It means that the extremal points of \(G_{\text {off}}\) correspond to the black hole configurations of the temperature T. More specifically, the global or local minimums of \(G_{\text {off}}\) may correspond to the small stable near-extremal black hole or large stable one with the temperature T. Whereas, the local maximum of \(G_{\text {off}}\) corresponds to the medium unstable black hole which would decay into a small stable near-extremal one or a large stable one. The off-shell Gibbs free energy as a function of \(r_+\) under the different values of the temperature is depicted in Figs. 8 and 9. Based on the off-shell Gibbs free energy, we can realize the following:

Fig. 8
figure 8

Plots of the reduced off-shell Gibbs free energy \(G_{\text {off}}/Q\) as a function of \(r_+/Q\) under the different values of the temperature T of the thermal bath, for \(l/Q=25\). The dashed black, blue, red, green, orange, purple, pink, and black curves correspond to the reduced temperature \(T\times Q=0\), 0.009, \(\approx \mathbf 0.0109 \) \((T_{\text {min}}\times Q)\), 0.0113, \(\approx \mathbf 0.0117 \) \((T_{\text {deg}}\times Q)\), 0.013, \(\approx \mathbf 0.0175 \) \((T_{\text {max}}\times Q)\), 0.019. The extremal points of each curve refer to the black hole configurations of the corresponding temperature. For \(T=T_{\text {max}}\) (or \(T=T_{\text {min}}\)), the local minimum and maximum of \(G_{\text {off}}\) merge into an inflexion point

Full size image
Fig. 9
figure 9

This is an extension of Fig. 8

Full size image
  1. 1.

    For given pressure, there exists a degenerate temperature \(T_{\text {deg}}\) (\(T_{\text {min}}<T_{\text {deg}}<T_{\text {max}}\)) such that the global minimum of \(G_{\text {off}}\) is degenerate. Thus, the small stable near-extremal black hole and large stable one at the temperature \(T=T_{\text {deg}}\) have the same Gibbs free energy. It means that the system is in a mixed state. The degenerate temperature \(T_{\text {deg}}\) is numerically given in the Table 3.

  2. 2.

    For \(T_{\text {min}}<T<T_{\text {deg}}\), the small stable near-extremal black hole corresponds to the global minimum of \(G_{\text {off}}\), whereas the large stable black hole corresponds to the local minimum of \(G_{\text {off}}\). Thus, the small stable near-extremal black hole is more stable.

  3. 3.

    For \(T_{\text {deg}}<T<T_{\text {max}}\), the small stable near-extremal black hole corresponds to the local minimum of \(G_{\text {off}}\), whereas the large stable black hole corresponds to the global minimum of \(G_{\text {off}}\). Thus, the large stable black hole is more stable.

  4. 4.

    The local minimum and maximum of \(G_{\text {off}}\) merge into an inflexion point, as the temperature approaches \(T=T_{\text {max}}\) or \(T=T_{\text {min}}\), at which single/multiple configuration transitions occur.

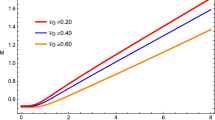
Table 3 The numerical results of the reduced degenerate temperature \(T_{\text {deg}}/Q\) and the corresponding reduced event horizons \(r_{d1}/Q\) and \(r_{d2}/Q\), under the different values of the pressure
Full size table

We arrive at investigating \(P-V\) (or \(P-r_+\)) criticality, when the temperature is kept fixed, to derive the Van der Waals-like phase transition of the black hole. From Eqs. (34) and (39), one can easily derive the equation of state \(P=P(T,V)\) for the black hole as

$$\begin{aligned} P=\frac{r^2_++Q^2}{2r^3_+}T+\frac{1}{8\pi }\frac{2Q^6+3Q^4r^2_++Q^2r^4_+-r^6_+}{r^4_+(r^2_++Q^2)^3}, \end{aligned}$$
(54)

where

$$\begin{aligned} r_+=\sqrt{\left( \frac{3V}{4\pi }\right) ^{2/3}-Q^2}, \end{aligned}$$
(55)

which implies that \(r_+\) is a function of the thermodynamic variables V and Q. Note that, compared to Van der Waals equation, one should identify the specific volume v as

$$\begin{aligned} v=\frac{2r^3_+}{r^2_++Q^2}. \end{aligned}$$
(56)

The critical point can be derived through the following condition

$$\begin{aligned} \frac{\partial P}{\partial r_+}=\frac{\partial ^2P}{\partial r^2_+}=0, \end{aligned}$$
(57)

which leads to the corresponding critical quantities \(r_c\), \(T_c\), \(P_c\) as being obtained at above. The Van der Waals-like phase transition is more intuitively observed in Fig. 10 where the isotherms in the \(P-r_+\) diagram are plotted under the different values of the temperature. This result shows that \(P-V\) criticality appears in even the non-linear charged AdS black hole. And, thus \(P-V\) criticality is actually universal as demonstrated in a general framework [25]. It can find a universal constant given by

$$\begin{aligned} \frac{P_cv_c}{T_c}\approx 0.3515, \end{aligned}$$
(58)

which is slightly smaller than the value \(3/8\approx 0.3750\) of the Van der Waals fluid.

Fig. 10
figure 10

The \(P-r_+\) diagram for various temperatures. The red, green, dashed black, blue, and organ curves correspond to \(T\times Q=0.03\), 0.025, \(\approx \mathbf 0.0221 \) \((T_c\times Q)\), 0.0183, 0.0165

Full size image

Note that, \(P-V\) criticality was also derived in some non-linear charged AdS black hole [24]. However, there has some essential difference compared to the present work. Like in the case of the charged AdS black hole [15], the Maxwell’s equal area law is valid in our case, meaning that

$$\begin{aligned} \oint VdP=0. \end{aligned}$$
(59)

However, in Ref. [24] this law is no longer valid due to the fact that the magnetic charge \(Q_m\) and the parameter \(\sigma \) are both treated as thermodynamic variables. As result, the true critical point of the Van der Waals-like phase transition does not coincide with the inflection point of the isotherms.

We end this subsection by calculating the critical exponents which characterize the behavior of the relevant thermodynamical quantities near the critical point or inflection point. First, we calculate the critical exponent \(\alpha \) characterizing the behavior of the specific heat \(C_V=T\big (\partial S/\partial T\big )_V\) when the volume is fixed. Form Eqs. (35) and (55), it is clearly that the entropy S is independent of the temperature T. This means that \(C_V=0\) and thus we have \(\alpha =0\). In order to derive other critical exponents, \(\beta \) (characterizing the behavior of the order parameter), \(\gamma \) (characterizing the behavior of isothermal compressibility), and \(\delta \) (characterizing the behavior of the critical isotherm corresponding to the critical temperature \(T_c\)), we can expand near the critical point as

$$\begin{aligned} r_+=r_c(1+\epsilon ),\ \ T=T_c(1+t),\ \ P=pP_c, \end{aligned}$$
(60)

where the dimensionless quantities satisfy \(|\epsilon |,|t|\ll 1\). Substituting these expansions into the expression of the pressure (54), we get

$$\begin{aligned} p=1+At+Bt\epsilon +C\epsilon ^3+\mathcal {O}(t\epsilon ^2,t\epsilon ^3,\epsilon ^4), \end{aligned}$$
(61)

where

$$\begin{aligned} A= & {} \frac{\bar{r}^2_c+1}{\bar{r}^3_c}\frac{T_c}{2QP_c}, \end{aligned}$$
(62)
$$\begin{aligned} B= & {} \frac{\bar{r}^2_c+1}{\bar{r}^3_c}\frac{3T_c}{2QP_c}, \end{aligned}$$
(63)
$$\begin{aligned} C= & {} -\frac{10+\bar{r}^2_c(49+95\bar{r}^2_c+90\bar{r}^4_c+37\bar{r}^6_c +10\bar{r}^8_c-\bar{r}^{10}_c)}{2\pi \bar{r}^4_c(\bar{r}^2_c+1)^5Q^2P_c}\nonumber \\&-\frac{\bar{r}^2_c+10}{2 \bar{r}^3_c}\frac{T_c}{QP_c}. \end{aligned}$$
(64)

Clearly, the form of this equation is the same as that for the Van der Waals system as well as the RN-AdS black hole [15]. Thus, three critical exponents, \(\beta \), \(\gamma \), and \(\delta \) should be the same those obtained for the RN-AdS black hole

$$\begin{aligned} \beta =\frac{1}{2},\ \ \gamma =1,\ \ \delta =3. \end{aligned}$$
(65)

4 Conclusion

In this paper, we derived a charged black hole solution from Einstein gravity coupled to a non-linear electromagnetic field in the AdS spacetime. At the large distances corresponding to the weak non-linear electrostatic field, this black hole solution behaves like the RN-AdS black hole. However, in the short distance regime corresponding to the strong non-linear electrostatic field, this solution behaves like a dS geometry. Furthermore, the relation of the black hole mass with respect to the horizon radius is analyzed in details.

Also, we have studied the thermodynamics and thermal phase transitions of the black hole. The thermodynamic quantities of the black hole have been calculated: the Hawking temperature, the entropy, the chemical potential, the heat capacity at the constant pressure, the Gibbs free energy and the equation of state. We pointed to the thermal phase transitions of the black hole, in the isobaric and isothermal processes, relying on the discontinuous change of the heat capacity and the swallowtail structure of the Gibbs free energy. In order to characterize the behavior of the relevant thermodynamical quantities near the critical point, we calculated the critical exponents. Additionally, we analyzed the thermodynamic phases of the black hole and their stability, based on the off-shell Gibbs free energy.