Abstract
From solving the equations of the motion for a system of Einstein gravity coupled to a non-linear electromagnetic field in the dS spacetime with two integral constants, we derived a static and spherical symmetric non-linear magnetic-charged black hole. It is indicated that this black hole solution behaves like a dS geometry in the short-distance regime. And, thus this black hole is regular. The structure of the black hole horizons is studied in detail. Also, we investigated the thermodynamics and the thermal phase transition of the black hole in both the local and global views. By observing the discontinuous change of the specific heat sign and the swallowtail structure of the free energy, we showed that the black hole can undergo a thermal phase transition between a thermodynamically unstable phase and a thermodynamically stable phase.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In General Relativity, the black hole solutions display a curvature singularity at the origin surrounded by an event horizon [1]. The presence of this curvature singularity is usually regarded as a sign of the breakdown of the classical gravity. It is widely believed that at the (very) short distances quantum gravity should become important to suppress the infinite growth of the spacetime curvature scalars and other physical quantities. And, thus the curvature singularity would be replaced by a regular spacetime region. However, so far there has no a consistent quantum theory of gravity. In the absence of such a theory, the resolution of the black hole singularity at the (semi-)classical level remains open.
In attempting to eliminate the problem of infinite energy of the electron, Born and Infeld proposed the non-linear electrodynamics as modifying the standard Maxwell theory at the short distances [2]. But, the non-linear electrodynamics did not solve this problem and thus was less popular. In recent years, the non-linear electrodynamics has received considerable attention because it leads to the regular black hole solutions. In 1998, Ayón-Beato and García studied a system of Einstein gravity coupled to a non-linear electromagnetic field in asymptotically flat spacetime and derived a regular electric-charged black hole solution [3]. Also, they reobtained the Bardeen black hole [4], which is regular, as a gravitational collapse of some magnetic monopole in the non-linear electrodynamics [5]. Later, many different regular black hole solutions in the non-linear electrodynamics have been derived [6,7,8,9,10,11,12,13,14,15,16,17].
Astronomical observations show that our universe is undergoing accelerated expansion [18,19,20]. This accelerating expansion may be explained by unknown dark energy. There are various proposed explanations for dark energy, but a positive cosmological constant is usually considered as the simplest explanation for dark energy. Because of this fact, it is necessary to consider the black hole by including the positive cosmological constant, corresponding to the black hole in the de Sitter (dS) spacetime [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43, 45, 89].
Another interesting aspect of the black hole is that it behaves as a thermodynamic object with the temperature and the entropy. The seminal works of the black hole thermodynamics were made by Bekenstein and Hawking [46,47,48,49,50]. Also, it was found that the black holes can undergo the phase transitions, such as the Hawking–Page phase [51] or the phase transition between small-large black charged holes [52,53,54]. Recently, the cosmological constant \(\Lambda \) can be considered as the thermodynamic pressure defined as
and its conjugate variable is the thermodynamic volume V [55,56,57,58,59]. This leads to an extended phase space at which the black hole mass is most naturally interpreted as the enthalpy [56]. Then, the thermodynamics and phase transitions of black holes in the extended phase space have been studied extensively in the literature, with new phenomena derived. The black hole can undergo the van der Waals-like phase transition which is similar to the liquid-gas phase transition [60,61,62,63,64,65,66,67,68,69]. It was found that the black holes shows multiply reentrant phase transition and triple points [70,71,72]. It is also possible to consider a Carnot-cycle heat engine for the black hole, which is defined by a closed path in the P–V plane [73,74,75,76,77,78,79,80,81].
In this paper, motivated by the pioneering work of Ayón-Beato and García and the astrophysical observations of dark energy, we would like to study the charged dS black hole in the non-linear electrodynamics. We will introduce a system of Einstein gravity coupled to a non-linear electromagnetic field in the dS spacetime. Then, we successfully construct a static and spherical symmetric non-linear magnetic-charged black hole and study the large and short distance behaviors as well as the horizon properties of this black hole. These are given in Sect. 2. The thermodynamics and the phase transition of the black hole are investigated, in both the local and global views, in Sect. 3. Finally, we make the conclusion in Sect. 4.
2 Non-linear magnetic-charged black hole in the \(\text {d}\)S spacetime
Einstein gravity coupled to the non-linear electromagnetic field in the four-dimensional dS spacetime is described by the action
where R is the scalar curvature of the dS spacetime, \(\Lambda \) is the positive cosmological constant, and \(\mathcal {L}(F)\) is a function of the invariant \(F_{\mu \nu }F^{\mu \nu }/4\equiv F\) with \(F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu \) to be the field strength of the non-linear electromagnetic field. In this paper, the non-linear electrodynamic term \(\mathcal {L}(F)\) is explicitly given as
where M and Q are mass and charge of the system, respectively. From the action, one can derive the equations of motion
Note that, Eq. (6) refers to the Bianchi identities for the non-linear electromagnetic field.
In this paper, we would like to find a static and spherical symmetric dS black hole of the mass M and the magnetic charge Q (\(>0\)), given by ansatz
where the magnetic charge Q is defined as
with \(S^\infty _2\) to be a two-sphere at the infinity. Note that, M and Q are two integral constants which should be used to integrate Eqs. (4) and (5). From Eqs. (5), (6) and (9), one can easily derive
Using this result, one can derive the only time component of Eq. (4) as
Integrating Eq. (11) with the integral constant \(M=\left( m(r)-\frac{\Lambda r^3}{6}\right) _{r\rightarrow \infty }\), then substituting m(r) into f(r), we finally get
In the case \(\Lambda =0\), we can obtain the Hayward-like black hole [12].
Let us look at the behavior of the black hole solution, derived above, at the large and short distances. For the large distances (\(Q/r\ll 1\)), we have
corresponding to the Schwarzschild-dS black hole. For the small distances (\(Q/r\gg 1\)), we have
It means that the black hole solution at the small distance behaves like a dS geometry with an effective cosmological constant
rather than like a black hole solution. This means that the dS geometry causes a negative pressure preventing a singular end-state of the gravitationally collapsed matter. In this sense, the black hole solution is regular. This can be checked by calculating the curvature scalars, R, \(R_{\mu \nu }R^{\mu \nu }\), and \(R_{\mu \nu \rho \lambda }R^{\mu \nu \rho \lambda }\) which are indeed finite everywhere.
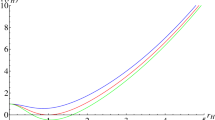
The mass function M(r) is plotted in terms of the horizon radius r, at \(Q=1\) and \(\Lambda =1/10\). The black lines (\(M=0.8\) and \(M=1.3\)) correspond to no black hole. The purple line (\(M=1.0\)) corresponds to a black hole of three different horizons. The red and green line (\(M\simeq 1.1\) and \(M\simeq 0.9\)) corresponds to black holes whose two of three horizons coincide together
The relation between the black hole mass M and its horizon radius is established from the equation of the horizons \(f(r)=0\) as
We can see that the black hole mass curve in the horizon radius shows one common property
In addition, for the appropriate values of the magnetic charge Q and the cosmological constant \(\Lambda \), the black hole mass curve displays one local minimum following one local maximum which both are located above the horizontal axis. These suggest that the black hole possesses possibly the inner horizon \(r_-\), the event horizon \(r_+\) (\(\geqslant r_-\)) and the cosmological horizon \(r_c\) (\(\geqslant r_+\)). (The cases of black holes and no black hole are explicitly given in Fig. 1.) When the local minimum and local maximum points of the black hole mass curve merge into an inflexion point, these three horizons coincide together. In this case, the hole black is called the ultracold black hole whose horizon radius and mass are, with given magnetic charge Q, given as
corresponding to a critical value for the cosmological constant
We can see here that the ultracold black hole of the larger magnetic charge has larger horizon radius and larger mass but the critical value for the cosmological constant is smaller. For \(\Lambda >\Lambda _c\), there exists no black hole with any mass. (Note that, the critical value of the cosmological constant for the existence of the non-linear charged dS black hole is lower than that for the existence of the usual charged dS black hole. This is of course because the magnetic repulsion in the non-linear electrodynamics is stronger than the magnetic repulsion in the usual electrodynamics.) On the contrary, for \(\Lambda <\Lambda _c\), there exist black holes only for a range of values of the mass, \(M\in [M_{\text {min}},M_{\text {max}}]\), where \(M_{\text {min}}\) and \(M_{\text {max}}\) are functions in terms of the magnetic charge Q and the cosmological constant \(\Lambda \). As \(M=M_{\text {max}}\) the event horizon \(r_+\) and the cosmological horizon \(r_c\) coincide together, and such a black hole is called the Nariai black hole whose event horizon radius \(r_N\) is the largest positive real solution of the following equation
The event horizon radius \(r_N\) of the Nariai black hole and its corresponding mass, as functions in terms of the cosmological constant at the fixed magnetic charge, are graphically given in Figs. 2 and 3, respectively. From these figures, it can see that both the event horizon radius and the mass of the Nariai black hole should decrease as the cosmological constant increases. As \(M=M_{\text {min}}\) the inner horizon \(r_-\) and the event horizon \(r_+\) coincide together, and such a black hole is called the cold black hole whose event horizon radius \(r_{cold}\) is the remaining positive real solution of Eq. (20). [Note that, it can see that, for \(0<\Lambda <\Lambda _c\), Eq. (20) has always two different positive real solutions.] We plot the event horizon radius \(r_{cold}\) of the cold black hole and its corresponding mass in terms of the cosmological constant at the fixed magnetic charge in Figs. 2 and 3, respectively. From these figures, it can see that the event horizon radius of the cold black hole increases but its mass decreases as the cosmological constant increases.
3 Thermodynamics and thermal phase transition
In the extended phase space, the entropy S, the magnetic charge Q, and the thermodynamic pressure P are regarded as a complete set of the extensive thermodynamic variables. Their corresponding conjugating quantities, which are intensive thermodynamic variables, are the temperature T, the chemical potential \(\Phi \), and the thermodynamic volume V. In this way, the first law of the thermodynamics is established on the event and cosmological horizons, respectively
(The sign − in front of \(T_c\) is because, as the cosmological horizon radius increases, the mass M should decrease whereas the entropy always does not decrease.) Note that, from Eqs. (1) and (16) the black hole mass can be expressed on the event and cosmological horizons, respectively
We plot the reduced temperature \(T_+Q\) on the event horizon (left) and the reduced temperature \(T_cQ\) on the cosmological horizon (right) in terms of the corresponding reduced horizon radius, for the different values of the reduced pressure \(PQ^2\). The blue, red, green and purple curves correspond to \(PQ^2=-0.001\), \(-0.002\), \(-0.004\), \(-0.006\)
3.1 Local view
In this subsection, we consider that the event and cosmological horizons are located far away. Thus, one can analyze the thermodynamics and the thermal phase transition on these horizons in an independent way.
Using the surface gravities of the event horizon and cosmological horizon, one can identify their temperatures, respectively [82, 83]
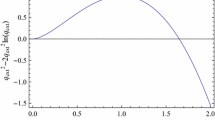
It is seen from Fig. 4 that the temperature \(T_c\) is an increasingly monotonous function in terms of the cosmological horizon radius \(r_c\). Whereas, the temperature \(T_+\) should first increase until a maximum \(T_{max}\) (given graphically in Fig. 5) and then decrease as the event horizon radius \(r_+\) increases. The reduced event horizon radius \(r_{max}/Q\) corresponding to the maximum temperature \(T_{max}\) is a unique positive real solution of the following equation
This solution is a function in terms of \(PQ^2\) and graphically solved in Fig. 5. In the limit of the vanishing pressure (\(P\rightarrow 0\)), the reduced horizon radius \(r_{max}/Q\) and the reduced maximum temperature \(T_{max}Q\) approach an upper limit given as
We stop here to compare the temperature between the non-linear and usual charged dS black holes with the same size, charge and the pressure. This difference of the temperature is graphically depicted in Fig. 6. It can see that, compared to the usual charged dS black hole with the same size, charge and the pressure, the non-linear charged dS black hole of the large size \((r_+>r_0)\) is slightly hotter. But, for the small size \((r_+<r_0)\), the usual charged dS black hole is hotter compared to the non-linear charged dS black hole. Here, \(r_0/Q\) is the largest positive real solution of the following equation
From the expressions for the temperature on the event and cosmological horizons, the entropy on both two horizons can be calculated as
We make some remarks here. First, the non-linear electrodynamics breaks the area law but it is recovered at the large distances \(Q/r_+\ll 1\). Second, the entropy is negative with \(r_+<2^{1/3}Q\) and thus there exist no black hole with the size smaller than \(2^{1/3}Q\). This suggests that at the scale \(r_+=2^{1/3}Q\) non-linear magnetic repulsion becomes so strong and thus prevents the formation of any black hole. In this sense, \(2^{1/3}Q\) can be realized to be the smallest size of the black hole of given magnetic charge Q.
Because Eqs. (30) and (31), we have
Using the first law, one can derive the remaining intensive thermodynamic variables as
One can easily check that the thermodynamic quantities on the event or cosmological horizons satisfy the Smarr and Smarr-like relations, respectively
which show the scaling behaviors of the thermodynamic variables [56].
The heat capacity at constant pressure on the event horizon and cosmological horizon given, respectively
The heat capacity \(C_{P+}\) under the different values of the pressure is plotted in Fig. 7. Form this figure and the expression of \(C_{P+}\), we can see that the heat capacity \(C_{P+}\) suffers a discontinuity at the local maximum temperature \(T_{max}\). This suggests a phase transition between a thermodynamically stable small black hole and a thermodynamically unstable large one at this critical point. It can show this phase transition from observing the swallowtail structure of the free energy \(F_+=M-T_+S_+\), as given in Fig. 8. With respect to the cosmological horizon, the heat capacity \(C_{Pc}\) is always negative and thus by emitting the thermal radiation the cosmological horizon become larger.
For the magnetic charge Q fixed, we can obtain the equation of state on the event and cosmological horizons, respectively
The isotherms in the \(P-V_+\) and \(P-V_c\) planes are the same in the shape. In Fig. 9, we plot the isotherms in the \(P-V_+\) plane.
3.2 Global view
If the event and cosmological horizons are not located far away, one cannot analyze the thermodynamics and the thermal phase transition on them in an independent way. Because the temperatures on the event and cosmological horizons are different, except for the degenerate case \(r_+=r_c\), the black hole cannot in general be in thermodynamic equilibrium. Since the notion of the effective thermodynamics of the black hole has been emerged [36, 44, 84,85,86,87,88, 90].
In the picture of the effective thermodynamics of the black hole, we express the mass M of the black hole and the cosmological constant \(\Lambda \) in terms of \(r_+\), \(r_c\), and Q as
where
From Eqs. (21) and (22), we can write the first law of the effective thermodynamics of the black hole as
It is clearly that if the total entropy is identified as \(S=S_c-S_+\) the effective temperature is given by
From Fig. 10, it can see that the behavior of the effective temperature \(T_{eff}\) is dependent on the magnetic charge Q. For “large” Q (the blue and red curves), there exist two regions (\(R_I\) and \(R_{II}\)) which are separated by a negative temperature region or forbidden region \(r_+\in (r_{div},r_0)\), where \(r_{div}\) and \(r_0\) are respectively a divergent point and a zero-temperature point of \(T_{eff}\). The first region \(R_I\) of \(T_{eff}\) is an increasingly monotonous function of \(r_+\). Whereas, with respect to the second region \(R_{II}\) of \(T_{eff}\) the effective temperature should first increase until a maximum and then decrease when \(r_+\) increasing. Note that, because of the forbidden region, if the black hole stays in one of the two regions then it always stays in that region and is impossible to transit another region. For “small” Q (the green curve), the first region \(R_I\) of \(T_{eff}\) should disappear. For small Q but below a certain value (the purple curve), the effective temperature is only a decreasingly monotonous function of \(r_+\).
Form Eq. (49), one can derive the effective chemical potential \(\Phi _{eff}\) and the effective thermodynamic volume \(V_{eff}\) as
The scaling behavior of the effective thermodynamic quantities is shown via the following Smarr-like relation
Now we would like to compute the effective heat capacity \(C_P\) at constant pressure and analyze the thermal phase transition based on the discontinuous change of the sign of \(C_P\). The effective heat capacity \(C_P\) is given by
where
Plots of the effective heat capacity in terms of the event horizon radius \(r_+\) under the different values of the magnetic charge, at \(r_c=5\). They correspond to \(Q=2\) (top left), \(Q=1.5\) (top right), \(Q=1\) (bottom left), and \(Q=0.5\) (bottom right). Dashed parts of the curves refer to the negative-temperature regions
We plot the free energy F as a function of the effective temperature \(T_{eff}\) under the different values of the magnetic charge Q, at \(r_c=5\). The blue, red, and green curves correspond to \(Q=2\), 1.5, 1. The left and right figures refers to the black hole staying in the first region \(R_I\) and the second region \(R_{II}\), respectively
The behavior of the heat capacity \(C_P\) is explicitly depicted in Fig. 11. From this figure, we can analyze the thermodynamic stability and the thermal phase transition of the black hole. For large magnetic charge (top left and top right), if the black hole stays in the first region \(R_I\), because of the negative and regular heat capacity \(C_P\) the black hole is thermodynamically unstable and there has no thermal phase transition. Otherwise, if the black hole stays in the second region \(R_{II}\), the heat capacity \(C_P\) should suffer a discontinuity. This suggests a thermal phase transition, at this discontinuous point, between a thermodynamically unstable large black hole (negative \(C_P\)) and a thermodynamically stable small black hole (positive \(C_P\)). For small magnetic charge (bottom left), the first region \(R_I\) should disappear and thus the black hole always stays in the second region \(R_{II}\). This means that the black hole can undergo the thermal phase transition between a thermodynamically unstable phase and a thermodynamically stable phase. For small magnetic charge but below a certain value (bottom right), like the black hole staying in the first region \(R_I\), the black hole is thermodynamically unstable and there has no thermal phase transition.
Let us now show that there actually exists the thermal phase transition by investigating the free energy F given by
which is graphically depicted in Fig. 12. As seen in Fig. 12, for the black hole staying in the region \(R_I\), its free energy is a decreasingly monotonous function of the effective temperature \(T_{eff}\) and thus there actually has no thermal phase transition. Otherwise, for the black hole staying in the region \(R_{II}\), the free energy F is a multivalued function shown by the presence of the swallowtail structure. And, thus there should actually occur the thermal phase transition between a thermodynamically unstable phase (large black hole) and a thermodynamically stable phase (small black hole). Here, the black hole of the larger magnetic charge has the smaller critical effective temperature.
4 Conclusion
In this work, we have derived a non-linear magnetic-charged dS black hole, from solving the equations of the motion for a system of Einstein gravity coupled to a non-linear electromagnetic field in the dS spacetime with a static and spherical symmetric ansatz. It is interesting that, in the short-distance regime corresponding to the strong non-linear magnetic field, the black hole solution behaves like a dS geometry with an effective cosmological constant
where M, Q, and \(\Lambda \) are the black hole mass, the black hole magnetic-charge, and the positive cosmological constant, respectively. By this, the singularity at the origin should be replaced by a core of the dS geometry, and thus the black hole solution is regular. Also, we indicated a critical value for the cosmological constant, above which there exists no black hole for any mass. At this critical value, all horizons of the black hole coincide together. Below this critical value, the black hole has possibly three horizons: the inner, event and cosmological horizons. In particular, for suitable black hole mass, two of three horizons possibly coincide together.
In the extended phase space, we have studied the thermodynamics of the black hole and analyzed its thermal phase transition based on the discontinuous change of the specific heat sign and the swallowtail structure of the free energy. If the event and cosmological horizons are located far away, the thermodynamics and the thermal phase transition on these horizons are investigated in an independent way. On the contrary, we use the notion of the effective thermodynamics of the black hole, which has been emerged in the recent years, to investigate.
References
S.W. Hawking, G.F.R. Ellis, The large scale structure of spacetime (Cambridge University Press, Cambridge, 1973)
M. Born, L. Infeld, Proc. R. Soc. Lond. A 144, 425 (1934)
E. Ayón-Beato, A. García, Phys. Rev. Lett. 80, 5056 (1998)
J.M. Bardeen, in Conference Proceedings of GR5 (USSR, Tbilisi, 1968), p. 174
E. Ayón-Beato, A. García, Phys. Lett. B 493, 149 (2000)
M. Cataldo, A. Garcia, Phys. Rev. D 61, 084003 (2000)
K.A. Bronnikov, Phys. Rev. D 63, 044005 (2001)
A. Burinskii, S.R. Hildebrandt, Phys. Rev. D 65, 104017 (2002)
J. Matyjasek, Phys. Rev. D 70, 047504 (2004)
I. Dymnikova, Class. Quantum Gravity 21, 4417 (2004)
W. Berej, J. Matyjasek, D. Tryniecki, M. Woronowicz, Gen. Relativ. Gravit. 38, 885 (2006)
S.A. Hayward, Phys. Rev. Lett. 96, 031103 (2006)
C. Bambi, L. Modesto, Phys. Lett. B 721, 329 (2013)
S.G. Ghosh, S.D. Maharaj, Eur. Phys. J. C 75, 7 (2015)
B. Toshmatov, B. Ahmedov, A. Abdujabbarov, Z. Stuchlik, Phys. Rev. D 89, 104017 (2014)
E.L.B. Junior, M.E. Rodrigues, M.J.S. Houndjo, JCAP 1510, 060 (2015)
C.H. Nam, Gen. Rel. Grav. 50, 57 (2018)
A.G. Riess et al., Astrophys. J. 116, 1009 (1998)
A.G. Riess et al., Astrophys. J. 117, 707 (1999)
S.J. Perlmutter et al., Astrophys. J. 517, 565 (1999)
D. Kastor, J. Traschen, Phys. Rev. D 47, 5370 (1993)
R.B. Mann, S.F. Ross, Phys. Rev. D 52, 2254 (1995)
R. Bousso, S.W. Hawking, Phys. Rev. D 54, 6312 (1996)
R-Gen Cai, D-Wei Pang, A. Wang, Phys. Rev. D 70, 124034 (2004)
Y. Sekiwa, Phys. Rev. D 73, 084009 (2006)
Y.S. Myung, Phys. Rev. D 77, 104007 (2008)
H. Quevedo, A. Sanchez, JHEP 0809, 034 (2008)
L. Huaifan, Z. Shengli, W. Yueqin, Z. Lichun, Z. Ren, Eur. Phys. J. C 63, 133 (2009)
V. Cardoso, M. Lemos, M. Marques, Phys. Rev. D 80, 127502 (2009)
R.A. Konoplya, A. Zhidenko, Phys. Rev. Lett. 103, 161101 (2009)
J. Matyjasek, D. Tryniecki, M. Klimek, Mod. Phys. Lett. A 23, 3377 (2009)
S. Yoshida, N. Uchikata, T. Futamase, Phys. Rev. D 81, 044005 (2010)
M. Zilhao, V. Cardoso, L. Gualtieri, C. Herdeiro, U. Sperhake, H. Witek, Phys. Rev. D 85, 104039 (2012)
B.P. Dolan, D. Kastor, D. Kubiznak, R.B. Mann, J. Traschen, Phys. Rev. D 87, 104017 (2013)
M. Stetsko, Eur. Phys. J. C 74, 2682 (2014)
S. Bhattacharya, Eur. Phys. J. C 76, 112 (2016)
L-Chun Zhang, R. Zhao, M-Sen Ma, Phys. Lett. B 761, 74 (2016)
L-Chun Zhang, R. Zhao, Europhys. Lett. 113, 10008 (2016)
D.V. Singh, N.K. Singh, Ann. Phys. 383, 600 (2017)
P. Kanti, T. Pappas, Phys. Rev. D 96, 024038 (2017)
W. Wahlang, P.A. Jeena, S. Chakrabarti, Int. J. Mod. Phys. D 26, 1750160 (2017)
S. Fernando, Int. J. Mod. Phys. D 26, 1750071 (2017)
H. Liu, Xin-he Meng, Mod. Phys. Lett. A 32, 1750146 (2017)
H-Fan Li, M-Sen Ma, L-Chun Zhang, R. Zhao, Nucl. Phys. B 920, 211 (2017)
C-Yong Zhang, P-Cheng Li, B. Chen, Phys. Rev. D 97, 044013 (2018)
J.D. Bekenstein, Lett. Nuovo Cim. 4, 737 (1972)
J.D. Bekenstein, Phys. Rev. D 9, 3292 (1974)
J.D. Bekenstein, Phys. Rev. D 7, 949 (1973)
J.M. Bardeen, B. Carter, S.W. Hawking, Commun. Math. Phys 31, 161 (1973)
S.W. Hawking, Commun. Math. Phys 43, 199 (1975)
S.W. Hawking, D.N. Page, Commun. Math. Phys. 87, 577 (1983)
A. Chamblin, R. Emparan, C. Johnson, R. Myers, Phys. Rev. D 60, 064018 (1999)
A. Chamblin, R. Emparan, C. Johnson, R. Myers, Phys. Rev. D 60, 104026 (1999)
X.N. Wu, Phys. Rev. D 62, 124023 (2000)
S. Wang, S.-Q. Wu, F. Xie, L. Dan, Chin. Phys. Lett. 23, 1096 (2006)
D. Kastor, S. Ray, J. Traschena, Class. Quantum Gravity 26, 195011 (2009)
D. Kastor, S. Ray, J. Traschen, Class. Quantum Gravity 27, 235014 (2010)
B.P. Dolan, Class. Quantum Gravity 28, 125020 (2011)
B.P. Dolan, Class. Quantum Gravity 28, 235017 (2011)
D. Kubizňák, R.B. Mann, JHEP 1207, 033 (2012)
R.G. Cai, L.M. Cao, L. Li, R.Q. Yang, JHEP 1309, 005 (2013)
J.X. Mo, W.B. Liu, Eur. Phys. J. C 74, 2836 (2014)
D.C. Zou, S.J. Zhang, B. Wang, Phys. Rev. D 89, 044002 (2014)
J. Xu, L.M. Cao, Y.P. Hu, Phys. Rev. D 91, 124033 (2015)
S.H. Hendi, A. Sheykhi, S. Panahiyan, B.E. Panah, Phys. Rev. D 92, 064028 (2015)
S.H. Hendi, S. Panahiyan, B.E. Panah, Prog. Theor. Exp. Phys. 2015, 103E01 (2015)
R.A. Hennigar, W.G. Brenna, R.B. Mann, JHEP 1507, 077 (2015)
Z.-Y. Fan, Eur. Phys. J. C 77, 266 (2016)
S. Fernando, Phys. Rev. D 94, 124049 (2016)
S. Gunasekaran, D. Kubizňák, R.B. Mann, JHEP 1211, 110 (2012)
N. Altamirano, D. Kubizňák, R.B. Mann, Phys. Rev. D 88, 101502 (2013)
A.M. Frassino, D. Kubizňák, R.B. Mann, F. Simovic, JHEP 1409, 080 (2014)
C.V. Johnson, Class. Quantum Gravity 31, 205002 (2014)
M.R. Setare, H. Adami, Gen. Relativ. Gravit. 47, 133 (2015)
A. Belhaj, M. Chabab, H.E. Moumni, K. Masmar, M.B. Sedra, A. Segui, JHEP 1505, 149 (2015)
C.V. Johnson, Class. Quantum Gravity 33, 135001 (2016)
C.V. Johnson, Class. Quantum Gravity 33, 215009 (2016)
M. Zhang, W.-B. Liu, Int. J. Theor. Phys. 55, 5136 (2016)
J.-X. Mo, F. Liang, G.-Q. Li, JHEP 2017, 10 (2017)
C. Bhamidipati, P.K. Yerra, Eur. Phys. J. C 77, 534 (2017)
R.A. Hennigar, F. McCarthy, A. Ballon, R.B. Mann, Class. Quantum Gravity 34, 175005 (2017)
G.W. Gibbons, S.W. Hawking, Phys. Rev. D 15, 2738 (1977)
G.W. Gibbons, S.W. Hawking, Phys. Rev. D 15, 2752 (1977)
S. Shankaranarayanan, Phys. Rev. D 67, 084026 (2003)
M. Urano, A. Tomimatsu, H. Saida, Class. Quantum Gravity 26, 105010 (2009)
S. Bhattacharya, A. Lahiri, Eur. Phys. J. C 73, 2673 (2013)
M.S. Ma, H.H. Zhao, L.C. Zhang, R. Zhao, Int. J. Mod. Phys. A 29, 1450050 (2014)
H.H. Zhao, L.C. Zhang, M.S. Ma, R. Zhao, Phys. Rev. D 90, 064018 (2014)
H.F. Li, M.S. Ma, Y.Q. Ma, Mod. Phys. Lett. A 32, 1750017 (2017)
D. Kubiznak, R.B. Mann, M. Teo, Class. Quantum Gravity 34, 063001 (2017)
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant with the grant number NRF-2016R1D1A1A09917598 and by the Yonsei University Future-leading Research Initiative of 2017(2017-22-0098).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Nam, C.H. Non-linear charged dS black hole and its thermodynamics and phase transitions. Eur. Phys. J. C 78, 418 (2018). https://doi.org/10.1140/epjc/s10052-018-5922-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5922-x