1 Introduction

The century-old search for exact solutions of the Einstein field equations began with Karl Schwarzschild obtaining a vacuum solution describing the exterior of a spherically symmetric matter distribution [1]. A natural line of pursuit would be to find an interior solution which matches smoothly to the Schwarzschild exterior solution. This internal solution was obtained by Schwarzschild in which it was assumed that the internal matter content of a spherical mass distribution was characterized by a uniform density [2]. Observations of stars and the understanding of particle physics within dense cores necessitated the search for more realistic solutions of the field equations. The inclusion of pressure anisotropy, charge, bulk viscosity, an equation of state, multilayered fluids, and the departure from spherical symmetry has led to the discovery of hundreds of exact solutions describing relativistic stars in the static limit [3–7]. With the discovery of the Vaidya solution, it became necessary to model the gravitational collapse of radiating stars [8]. Since the star is dissipating energy in the form of a radial heat flux, the pressure at the boundary of the star is proportional to the outgoing heat flux as opposed to the vanishing surface pressure in the non-dissipative case [9]. Nevertheless, static solutions also play a pivotal role in dissipative gravitational collapse of stars, as they can represent an initial static configuration or a final static configuration [10–12].

It is interesting to note that by relaxing the condition of a perfect fluid and allowing for pressure anisotropy and charge within the interior of the stellar distribution gives rise to observable and measurable properties of the star. Pressure anisotropy leads to arbitrarily large surface red-shifts [13–15], while the inclusion of charge results in the modification of the Buchdahl limit [16]. The linear equation of state \(p=\alpha \rho \) has been generalized from observations in theoretical particle physics. There has been a wide spectrum of exact solutions of the field equations incorporating the so-called MIT bag model, in which the equation of state is of the form \(p=\alpha \rho -B\) with B being the bag constant [17–19]. These solutions successfully predicted the observed masses and radii of compact objects with densities of the order of \(10^{14}\, \mathrm{g~cm}^{-3}\). With an ever growing interest in dark energy and its successful use in cosmological models, astrophysicists have now extended the range of \(\alpha \) in \(p = \alpha \rho \) to include \(-1< \alpha < -1/3\). This regime incorporates the so-called dark stars [20, 21]. Other exotic forms of matter which have appeared in the literature include the Chaplygin gas, Bose–Einstein condensates, and the Hagedorn fluid [22–26].

The notion of the four fundamental interactions being a manifestation of a single force has always attracted the interest of researchers in both fundamental particle physics and relativity. Higher-dimensional theories of gravity have produced rich results so far as cosmic censorship is concerned [27–29]. Recently, there has been a surge in exact models of stars in Einstein–Gauss–Bonnet gravity, braneworld gravity, and in Lovelock gravity [30–33]. The connection between five-dimensional Kaluza–Klein geometries and electromagnetism has been widely studied. Embedding of four-dimensional spacetimes into higher dimensions is an invaluable tool in generating both cosmological and astrophysical models.

In this article we are presenting a four-dimensional spacetime embedded in five-dimensional pseudo Euclidean space known as class I. Karmarkar proposed a theory that any solutions of Einstein field equations that satisfies (9) is said to be class I. For a neutral isotropic fluid sphere the solutions yielded by (9) is either Schwarzschild interior (1916) or Kholar–Chao (1965). However, it is now well known that inclusion of electric charge or a pressure anisotropy or both leads to a completely new class of solutions [34–38]. Therefore, in this paper we utilize the Karmarkar [39] condition, which is a necessary and sufficient condition for a spherically symmetric line element to be of class I to generate exact solutions. In particular, our model incorporates an anisotropic pressure to generate a family of new solutions.

2 Conditions for well-behaved solutions

For a well-behaved nature of the solutions for an anisotropic fluid sphere the following conditions should be satisfied:

  1. 1.

    The solution should be free from physical and geometric singularities, i.e., it should yield finite and positive values of the central pressure, central density, and a nonzero positive value of \(e^\nu |_{r=0}\) and \(e^\lambda |_{r=0}=1\).

  2. 2.

    The causality condition should be obeyed, i.e., the velocity of sound should be less than that of light throughout the model. In addition to the above the velocity of sound should be decreasing toward the surface, i.e., \({\mathrm{d} \over \mathrm{d}r}~{\mathrm{d}p_r \over \mathrm{d}\rho }<0\) or \({\mathrm{d}^2 p_r\over \mathrm{d}\rho ^2}>0\) and \({\mathrm{d}\over \mathrm{d}r}{\mathrm{d}p_t \over \mathrm{d}\rho }<0\) or \({\mathrm{d}^2p_t \over \mathrm{d}\rho ^2}>0\) for \(0\le r\le r_b\), i.e., the velocity of sound is increasing with the increase of density and it should be decreasing outward.

  3. 3.

    The adiabatic index, \(\Gamma = {\rho +p_r \over p_r}~{\mathrm{d}p_r \over \mathrm{d}\rho }\) for realistic matter should be \(\Gamma >4/3\) for positive anisotropy.

  4. 4.

    The anisotropy factor \(\Delta \) should be zero at the center and increasing toward the surface.

  5. 5.

    For a stable anisotropic compact star, \(-1\le v_t^2-v_r^2\le 0\) must be satisfied [41].

3 Einstein field equations of anisotropic fluid distributions

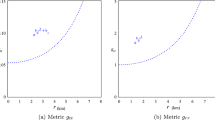
The interior of the super-dense star is assumed to be described by the line element

$$\begin{aligned} \mathrm{d}s^2 = e^{\nu (r)}\mathrm{d}t^2 - e^{\lambda (r)}\mathrm{d}r^2 - r^2(\mathrm{d}\theta ^2 + \sin ^2{\theta }\mathrm{d}\phi ^2) . \end{aligned}$$
(1)

The Einstein field equations for anisotropic fluid distribution are given as (in units with \(G=c=1\))

$$\begin{aligned} R^\mu _\xi -{1\over 2}R~g^\mu _\xi =-8\pi T^\mu _\xi \end{aligned}$$
(2)

where

$$\begin{aligned} T^\mu _\xi= & {} (p_t+\rho )v^\mu v_\xi -p_t g^\mu _\xi +(p_r-p_t)\chi _\xi \chi ^\mu \end{aligned}$$
(3)

where \(R^\mu _\xi \) is the Ricci tensor, \(T^\mu _\xi \) is the energy-momentum tensor, R the scalar curvature, \(p_r\) and \(p_t\) denote the radial and transverse pressures, respectively, \(\rho \) the density distribution, \(v^\mu \) the four velocity, and \(\chi ^\mu \) is the unit space-like vector in the radial direction.

Here \(T^\mu _\xi \) is defined as

$$\begin{aligned} T^\mu _\xi = \text{ diag } \Big (\rho ,~-p_r,~-p_t,~-p_t\Big ). \end{aligned}$$
(4)

The Einstein field equations for the line element (1) are

$$\begin{aligned} 8\pi \rho= & {} \frac{1 - e^{-\lambda }}{r^2} + \frac{\lambda 'e^{-\lambda }}{r}, \end{aligned}$$
(5)
$$\begin{aligned} 8\pi p_r= & {} \frac{\nu ' e^{-\lambda }}{r} - \frac{1 - e^{-\lambda }}{r^2} , \end{aligned}$$
(6)
$$\begin{aligned} 8\pi p_t= & {} \frac{e^{-\lambda }}{4}\left( 2\nu '' + {\nu '}^2 - \nu '\lambda ' + \frac{2\nu '}{r}-\frac{2\lambda '}{r}\right) , \end{aligned}$$
(7)

where primes represent differentiation with respect to the radial coordinate r. Again, in generating the above field equations we have utilized geometrized units where the coupling constant and the speed of light are taken to be unity. Using Eqs. (6) and (7) we get

$$\begin{aligned} \Delta= & {} 8\pi (p_t-p_r) \nonumber \\= & {} e^{-\lambda }\left[ {\nu '' \over 2}-{\lambda ' \nu ' \over 4}+{\nu '^2 \over 4}-{\nu '+\lambda ' \over 2r}+{e^\lambda -1 \over r^2}\right] . \end{aligned}$$
(8)

If the metric given in (1) satisfies the condition in [39], it can represent an embedding class I spacetime, i.e.,

$$\begin{aligned} R_{1414}={R_{1212}R_{3434}+R_{1224}R_{1334} \over R_{2323}} \end{aligned}$$
(9)

with \(R_{2323}\ne 0\) [40]. This condition leads to a differential equation given by

$$\begin{aligned} {2\nu '' \over \nu '}+\nu '={\lambda ' e^\lambda \over e^\lambda -1}. \end{aligned}$$
(10)

On integration we get the relationship between \(\nu \) and \(\lambda \):

$$\begin{aligned} e^{\nu }=\left( A+B\int \sqrt{e^{\lambda }-1}~dr\right) ^2 \end{aligned}$$
(11)

where A and B are constants of integration.

By using (11) we can rewrite (8) as

$$\begin{aligned} \Delta = {\nu ' \over 4e^\lambda }\left[ {2\over r}-{\lambda ' \over e^\lambda -1}\right] ~\left[ {\nu ' e^\nu \over 2rB^2}-1\right] . \end{aligned}$$
(12)

Here \(\Delta =8\pi (p_t-p_r)\) is the measure of anisotropy.

4 Generating a new family of embedding class I solution

To solve Eq. (11), we assume a new metric potential \(g_{rr}\) given by

$$\begin{aligned} e^\lambda =1+ar^2 (1+br^2)^n \end{aligned}$$
(13)

where a and b are constants with dimension of length\(^{-2}\).

Using the metric potential (13) in (11), we get

$$\begin{aligned} e^\nu = \left[ A+\frac{\sqrt{a} B (b r^2+1)^{n/2+1}}{b (n+2)}\right] ^2 ~~~\text{ where }~~~n \ne -2. \end{aligned}$$
(14)

Using (13) and (14), we can rewrite the expression of the density, \(p_r\), \(\Delta \), and \(p_t\):

$$\begin{aligned} 8\pi \rho= & {} \frac{a (b r^2+1)^{n-1}}{\big [a r^2(b r^2+1)^n+1\big ]^2} \times \Big [a r^2 (b r^2+1)^n \nonumber \\&+\,b r^2 \big \{a r^2 (b r^2+1)^n+2 n+3\big \}+3\Big ], \end{aligned}$$
(15)
$$\begin{aligned} 8\pi p_r= & {} \frac{\sqrt{a(b r^2+1)^n}~[a r^2(b r^2+1)^n+1]^{-1}}{B (b r^2+1) \sqrt{a (b r^2+1)^n}+A b (n+2)} \nonumber \\&\times \bigg [b \Big \{B \left( -a r^2(b r^2+1)^n+2 n+4\right) -A (n+2) \nonumber \\&\quad \sqrt{a(b r^2+1)^n}\Big \}-a B(b r^2+1)^n\bigg ], \end{aligned}$$
(16)
$$\begin{aligned} \Delta= & {} {r^2 \Big [a b r^2(b r^2+1)^n+a(b r^2+1)^n-b n\Big ] \over (b r^2+1) \big [(a r^2(b r^2+1)^n+1\big ]^2} \nonumber \\&\times \bigg [B (b r^2+1) \sqrt{a(b r^2+1)^n}+A b (n+2) r\bigg ]^{-1} \nonumber \\&\times \bigg [a(b r^2+1)^n \Big \{B (b r^2+1) \sqrt{a(b r^2+1)^n} \nonumber \\&\quad +A b (n+2)\Big \}-b B (n+2) \sqrt{a(b r^2+1)^n}\bigg ], \end{aligned}$$
(17)
$$\begin{aligned} 8\pi p_t= & {} 8\pi p_r+\Delta . \end{aligned}$$
(18)

Now the pressure and density gradients can be written as

$$\begin{aligned} 8\pi {\mathrm{d}\rho \over \mathrm{d}r}= & {} -\frac{2 a r [f_1(r)+f_2(r)] (b r^2+1)^{n-2}}{[a r^2(b r^2+1)^n+1]^3}, \end{aligned}$$
(19)
$$\begin{aligned} 8\pi {\mathrm{d}p_r \over \mathrm{d}r}= & {} {2 \sqrt{a r^2(b r^2+1)^n} \over (b r^2+1) \{a r^2(b r^2+1)^n+1\}^2 } \nonumber \\&\times \bigg [B(b r^2+1) \sqrt{a(b r^2+1)^n}+A b (n+2)\bigg ]^{-2} \nonumber \\&\times \bigg [B^2f_5(r) (b r^2+1) \sqrt{a r^2 (b r^2+1)^n}+f_3(r) \nonumber \\&+\,A b B f_4(r) (n+2) r\bigg ] , \end{aligned}$$
(20)
$$\begin{aligned} 8\pi {\mathrm{d}p_t \over \mathrm{d}r}= & {} \frac{1}{\beta (r)^2 (b r^2+1)^2 \big [a r^2 (b r^2+1)^n+1\big ]^3} \nonumber \\&\times \bigg [ -2 bf_6(r)~ r [a r^2 (b r^2+1)^n+1] \nonumber \\&\times \Big \{B (b r^2+1) \sqrt{a r^2 (b r^2+1)^n}+A b (n+2) r\Big \} \nonumber \\&\quad -\frac{\alpha (r)f_6(r) (b r^2+1) \big \{a r^2 (b r^2+1)^n+1\big \}}{\sqrt{a (b r^2+1)^n}} \nonumber \\&\quad - 4 a\beta (r) f_6(r) r(b r^2+1)^n \big \{b (n+1) r^2+1\big \} \nonumber \\&\quad +(b r^2+1) \big \{a r^2 (b r^2+1)^n+1\big \} \beta (r) \bigg \{f_7(r) \nonumber \\&\quad -\frac{f_{9}(r) \sqrt{a r^2 (b r^2+1)^n}}{r^2}-f_{8}(r)\bigg \}\bigg ], \end{aligned}$$
(21)

where

$$\begin{aligned} f_1(r)= & {} a (b r^2+1)^n \big \{a r^2 (b r^2+1)^n+5\big \} \nonumber \\&+\,\big [2 a r^2 (b r^2+1)^n \big \{a r^2 (b r^2+1)^n+5\big \} \nonumber \\&+\,n \big \{(3 a r^2 (b r^2+1)^n-5\big \} \big ] , \end{aligned}$$
(22)
$$\begin{aligned} f_2(r)= & {} b^2r^2\Big [2 n^2 \big \{(a r^2(b r^2+1)^n-1\big \}\end{aligned}$$
(23)
$$\begin{aligned}&+\,a r^2 (b r^2+1)^n \big \{a r^2 (b r^2+1)^n+5\big \}\nonumber \\&+\,n \big \{(5 a r^2 (b r^2+1)^n-3\big \} \Big ], \end{aligned}$$
(24)
$$\begin{aligned} f_3(r)= & {} A^2 b^2 (n+2)^2 \sqrt{a r^2 (b r^2+1)^n} \Big \{a b r^2 (b r^2+1)^n \nonumber \\&+\,a (b r^2+1)^n-b n\Big \}, \end{aligned}$$
(25)
$$\begin{aligned} f_4(r)= & {} 4 a b(b r^2+1)^n \big \{a r^2 (b r^2+1)^n-n-1\big \} \nonumber \\&+\,2 a^2 (b r^2+1)^{2 n}+b^2\big [n \{2-6 a r^2 (b r^2+1)^n\} \nonumber \\&+\,n^2 \big \{1-a r^2 (b r^2+1)^n\big \}+ 2 a r^2 (b r^2+1)^n \nonumber \\&\times \big \{a r^2 (b r^2+1)^n-2\big \}\big ], \end{aligned}$$
(26)
$$\begin{aligned} f_5(r)= & {} a b (b r^2+1)^n \big \{2 a r^2 (b r^2+1)^n-3 n-4\big \} \nonumber \\&+\, a^2 (b r^2+1)^{2 n}-b^2 \Big [8 a r^2 (b r^2+1)^n+4 \nonumber \\&+\, 2 a n^2 r^2 (b r^2+1)^n-a^2 r^4 (b r^2+1)^{2 n}\nonumber \\&+\,n \big \{2 + 9 a r^2 (1 + b r^2)\big \}^n\Big ] , \end{aligned}$$
(27)
$$\begin{aligned} f_6(r)= & {} b B (n+2) (b (n+2) r^2+2) \sqrt{a r^2 (b r^2+1)^n} \nonumber \\&-\,a (b r^2+1)^n \Big [B (1-b^2 r^4) \sqrt{a r^2 (b r^2+1)^n}\nonumber \\&+\,A b (n+2) r (b (n+1) r^2+1)\Big ], \end{aligned}$$
(28)
$$\begin{aligned} f_7(r)= & {} 2 b^2 B (n+2)^2 r \sqrt{a r^2 (b r^2+1)^n}+\frac{b B (n+2)}{b r^3+r} \nonumber \\&\times \big \{b (n+1) r^2+1\big \} \big \{b (n+2) r^2+2\big \}\nonumber \\&\times \sqrt{a r^2 (b r^2+1)^n} , \end{aligned}$$
(29)
$$\begin{aligned} f_8(r)= & {} 2 a b n r (b r^2+)^{n-1} \Big [A b (n+2) r \big \{b (n+1) r^2+1\big \} \nonumber \\&+B (1-b^2 r^4) \sqrt{a r^2 (b r^2+1)^n}\Big ] , \end{aligned}$$
(30)
$$\begin{aligned} f_9(r)= & {} A b (n+2) \big \{3 b (n+1) r^2+1\big \} \sqrt{a r^2 (b r^2+1)^n} \nonumber \\&-a B r (b r^2+1)^n \big \{b^2 (n+5) r^4-b n r^2-1\big \}, \end{aligned}$$
(31)
$$\begin{aligned} \beta (r)= & {} B (b r^2+1) \sqrt{a r^2 (b r^2+1)^n}+A b (n+2) r , \end{aligned}$$
(32)
$$\begin{aligned} \alpha (r)= & {} A b (n+2) \sqrt{a (b r^2+1)^n}+a B \big \{b (n+3) r^2+1\big \} \nonumber \\&\times (b r^2+1)^n . \end{aligned}$$
(33)

5 Properties of the new family solution

The central values of pressures and density are given by

$$\begin{aligned} 8\pi p_r(r=0)= & {} 8\pi p_t(r=0) \nonumber \\= & {} \frac{\sqrt{a}}{\sqrt{a} B+A b (n+2)}\bigg [b \big \{B (2 n+4) \nonumber \\&-\sqrt{a} A (n+2)\big \}-a B\bigg ]>0 \end{aligned}$$
(34)
$$\begin{aligned} \rho (r=0)= & {} 3a>0; \quad \forall ~a>0. \end{aligned}$$
(35)

To satisfy Zeldovich’s condition at the interior, \(p_r/\rho \) at the center must be \(\le \)1. Therefore,

$$\begin{aligned} \frac{b \big \{B (2 n+4)-\sqrt{a} A (n+2)\big \}-a B}{3\sqrt{a}\big [\sqrt{a} B+A b (n+2)\big ]} \le 1. \end{aligned}$$
(36)

On using (34) and (36) we get a constraint on B / A given as

$$\begin{aligned} \frac{\sqrt{a}~ b (n+2)}{2 b n+4 b-a}<{B \over A} \le \frac{4\sqrt{a}~ b (n+2)}{2 b n+4 b-4a}. \end{aligned}$$
(37)

Now the velocity of sound inside the stellar interior can be determined by using

$$\begin{aligned} v_r^2={\mathrm{d}p_r/\mathrm{d}r \over \mathrm{d}\rho /\mathrm{d}r},~~~v_t ^2={\mathrm{d}p_t/\mathrm{d}r \over \mathrm{d}\rho /\mathrm{d}r}. \end{aligned}$$
(38)

The relativistic adiabatic index for an anisotropic fluid sphere is given by

$$\begin{aligned} \Gamma = {\rho +p_r \over p_r}~{\mathrm{d}p_r \over \mathrm{d}\rho }. \end{aligned}$$
(39)

For a static configuration at equilibrium \(\Gamma \) has to be more than 4 / 3.

The modified Tolman–Oppenheimer–Volkoff (TOV) equation for an anisotropic fluid distribution was given by [42] as

$$\begin{aligned} -{M_g(\rho +p_r) \over r^2}~e^{(\lambda -\nu )/2}-{\mathrm{d}p_r \over \mathrm{d}r}+{2\Delta \over r}=0 \end{aligned}$$
(40)

where

$$\begin{aligned} M_g(r)= & {} {1\over 2}~r^2 \nu ' e^{(\nu -\lambda )/2}. \end{aligned}$$
(41)

Equation (40) can be written in terms of the balanced force equation due to anisotropy (\(F_\mathrm{a}\)), gravity (\(F_\mathrm{g}\)), and the hydrostatic forces (\(F_\mathrm{h}\)), i.e.,

$$\begin{aligned} F_\mathrm{g}+F_\mathrm{h}+F_\mathrm{a}=0 . \end{aligned}$$
(42)

Here

$$\begin{aligned} F_\mathrm{g}= & {} -{M_g(\rho +p_r) \over r^2}~e^{(\lambda -\nu )/2}, \end{aligned}$$
(43)
$$\begin{aligned} F_\mathrm{h}= & {} -{\mathrm{d}p_r \over \mathrm{d}r} ,\end{aligned}$$
(44)
$$\begin{aligned} F_\mathrm{a}= & {} {2\Delta \over r} . \end{aligned}$$
(45)

The TOV equation (42) can be represented by the figure showing that the forces are counter-balanced by each other; see Fig. 12.

6 Matching of physical boundary conditions

Assuming the exterior spacetime to be the Schwarzschild exterior solution which has to match smoothly with our interior solution and is given by

$$\begin{aligned} \mathrm{d}s^2= & {} \left( 1-{2M\over r}\right) \mathrm{d}t^2-\left( 1-{2M\over r}\right) ^{-1}\mathrm{d}r^2 \nonumber \\&-r^2(\mathrm{d}\theta ^2+\sin ^2 \theta \mathrm{d}\phi ^2). \end{aligned}$$
(46)
Fig. 1
figure 1

Variation of metric potentials with radial coordinate r for XTE J1739-285 \(\big (n = 8-20,~M = 1.51 M_\odot ,~R=10.9\, \mathrm{km}\big )\)

Full size image
Fig. 2
figure 2

Variation of interior pressures (km\(^{-2}\)) with radial coordinate r for XTE J1739-217

Full size image
Fig. 3
figure 3

Variation of density (km\(^{-2}\)) with radial coordinate r for XTE J1739-285

Full size image
Fig. 4
figure 4

Variation of pressure to density ratios with radial coordinate r for XTE J1739-285

Full size image
Fig. 5
figure 5

Variation of anisotropy (km\(^{-2}\)) with radial coordinate r for XTE J1739-285

Full size image
Fig. 6
figure 6

Variation of \(v_r^2\) with radial coordinate r for XTE J1739-285

Full size image
Fig. 7
figure 7

Variation of \(v_t^2\) (km\(^{-2}\)) with radial coordinate r for XTE J1739-285

Full size image
Fig. 8
figure 8

Variation of relativistic adiabatic index with radial coordinate r for XTE J1739-285

Full size image
Fig. 9
figure 9

Variation of red-shift with radial coordinate r for XTE J1739-285

Full size image
Fig. 10
figure 10

Variation of stability factor \(v_t^2-v_r^2\) with radial coordinate r for XTE J1739-285

Full size image
Fig. 11
figure 11

Variation of compactness parameter with radial coordinate r for XTE J1739-285

Full size image
Fig. 12
figure 12

Balancing of different forces in TOV equation for a static configuration for XTE J1739-285 are plotted with radial coordinate r

Full size image
Fig. 13
figure 13

Variation of interior mass with radial coordinate r for XTE J1739-285

Full size image
Fig. 14
figure 14

Variation of \(\rho -p_r\) (km\(^{-2}\)) with radial coordinate r for XTE J1739-285

Full size image
Fig. 15
figure 15

Variation of \(\rho -p_t\) (km\(^{-2}\)) with radial coordinate r for XTE J1739-285

Full size image

By matching the first and second fundamental forms the interior solution (1) and the exterior solution (46) at the boundary \(r=r_b\) (Darmois–Isreali condition) we get

$$\begin{aligned}&e^{\nu _b} = 1-{2M \over r_b} = \left[ A+\frac{\sqrt{a} B (b r_b^2+1)^{n/2+1}}{b (n+2)}\right] ^2 ,\end{aligned}$$
(47)
$$\begin{aligned}&e^{-\lambda _b} = 1-{2M \over r_b} = \Big [1+ar_b^2(1+br_b^2)^n\Big ]^{-1} ,\end{aligned}$$
(48)
$$\begin{aligned}&p_r(r_b) = 0 . \end{aligned}$$
(49)

Using the boundary condition (47)–(49), we get

$$\begin{aligned} B= & {} b A(n+2) \sqrt{a (b r_b^2+1)^n} \nonumber \\&\times \bigg [b\Big \{-a r_b^2 (b r_b^2+1)^n+2 n+4\Big \}-a (b r_b^2+1)^n\bigg ]^{-1} , \nonumber \\ \end{aligned}$$
(50)
$$\begin{aligned} A= & {} \bigg [{a r_b^2 (b r_b^2+1)^n+1}\bigg ]^{-1/2} \bigg [1{+}a (b r_b^2+1)^{n{+}1} \nonumber \\&\times ~\bigg \{ b \Big [{-}a r_b^2 (b r_b^2{+}1)^n {+}2 n{+}4 \Big ]{-}a (b r_b^2+1)^n\bigg \}^{-1} \bigg ]^{-1},\nonumber \\ \end{aligned}$$
(51)
$$\begin{aligned} a= & {} \frac{1}{r_b^2 (b r_b^2+1)^n} \left( \frac{1}{1-2M/r_b}-1 \right) , \end{aligned}$$
(52)

and we have chosen b,  n,  M, and \(r_b\) as free parameters and the rest of the constants a,  A, and B are determined from Eqs. (50)–(52).

Now the gravitational red-shift of the stellar system is given by

$$\begin{aligned} Z(r)= & {} \left[ A+\frac{\sqrt{a} B (b r^2+1)^{n/2+1}}{b (n+2)}\right] ^{-1}-1. \end{aligned}$$
(53)

The mass–radius relation and compactness parameter of the solution can be determined using the equations

$$\begin{aligned} m(r)= & {} 4\pi \int _0^r \rho r^2 \mathrm{d}r = \frac{a r^3 (b r^2+1)^n}{2 a r^2 (b r^2+1)^n+2} ,\end{aligned}$$
(54)
$$\begin{aligned} x(r)= & {} {2m(r) \over r} = \frac{2a r^2 (b r^2+1)^n}{2 a r^2 (b r^2+1)^n+2}. \end{aligned}$$
(55)

7 Results and conclusions

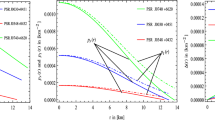
It has been observed that the physical parameters \(\big (e^{-\lambda },~p_r,\) \(p_t,~\rho ,\) \(~p_r/\rho ,~p_t/\rho ,~v_r^2,~v_t^2,~Z\big )\) are free from central singularities and monotonically decreasing outward (Figs. 1, 2, 3, 4, 6, 7, 9). However, \(e^\nu \), the anisotropy, and \(\Gamma \) are increasing outward and also are well behaved (Figs. 1, 5, 8).

Fig. 16
figure 16

Variation of \(\rho -p_r-2p_t\) (km\(^{-2}\)) with radial coordinate r for XTE J1739-285

Full size image
Fig. 17
figure 17

Variation of mass with the star generating index n plotted from Her X-1, EXO 1785-248, XTE J1739-285 and PSR J0348+0432

Full size image
Table 1 Parameters of four well-known compact stars that give mass and radius compatible to observed values and correspond to a well-behaved solution
Full size table

Furthermore, our solution presented satisfies all the energy conditions which are needed by physically possible configurations. The null energy condition \(\big (\rho -p_i \ge 0\big )\), the dominant energy condition \(\big (\rho -p_i \ge 0\), \(\rho \ge 0\big )\), and the strong energy condition \(\big (\rho -p_i \ge 0\), \(\rho -p_r-2p_t \ge 0\big )\) are shown in Figs. 14, 15, and 16. For a stable configuration, the stability factor \(v_t^2-v_r^2\) must lie in between \(-1\) and 0, which is again satisfied by our solutions presented (Fig. 10). For a non-collapsing stellar configuration, the adiabatic index must also be higher than 4/3 for positive values of the anisotropy; Fig. 8. Furthermore, we can analyze all the forces acting on the physical system via Eq. (40) and we expect to have counter-balance for a static stellar configuration (Fig. 12). The mass and the compactness parameter also monotonically increase from the center to the surface of the star and the compactness parameter is also within the Buchdahl limit (Figs. 11, 13).

For XTE J1739-285, the well-behaved region of the index n ranges from 8 to 20. For \(n<8\), the trend of sound speed increases and for \(n>20\), the causality condition is violated. For PSR J0348+0432, the well-behaved region of n is from 24 to 54, where \(n<24\) gives an increasing sound speed and \(n>54\) yields violation of the causality condition. For Her X-1, the well-behaved region belongs to \(n=0.8\) to \(n=2.7\), where \(n<0.8\) and \(n>2.7\) imply an increasing sound speed and violation of the causality condition, respectively. Similarly, for EXO 1785-248 the well-behaved region is \(n=1.5\) to \(n=4\), where \(n<1.5\) and \(n>4\) imply an increasing sound speed and violation of the causality condition, respectively. From the present analysis, we have observed that the equations of state are softer for small values of n and vice versa. The adiabatic index for a particular star at the center increases with increase in n, i.e., the equation of state gets stiffer with the increase of n. For Her X-1, the adiabatic indices at the center are 3.36 (\(n=0.8\)) and 5.47 (\(n=2.7\)); for EXO 1785-248 the adiabatic indices at the center are 3.13 (\(n=1.5\)) and 10.38 (\(n=4\)); for XTE J1739-285 the adiabatic indices at the center are 3.34 (\(n=8\)) and 11.65 (\(n=20\)); for PSR J0348+0432 the adiabatic indices at the center are 2.7 (\(n=24\)) and 9.35 (\(n=54\)). However, for all the stars, for those values of n which are lower or higher than the above mentioned limits, the energy conditions are indeed satisfied although not well behaved. Since for the different ranges of n we may generate different stars with all degrees of suitability, the ‘n’ is named the “star generating index”. The dependence of the mass on the star generating index is shown in Fig. 17.

For all the stars presented, with the star generating index n within its well-behaved values, the central values of density, red-shift, and energy conditions decrease, however, the central values of pressure, the pressure to density ratio, the speed of sound, and the adiabatic index increase.

The masses and radii of the chosen compact star candidates are matched with [43] for Her X-1, [44] for EXO 1785-248, [45] for XTE J1739-285 and [46] for PSR J0348+0432. The parameters with masses and radii of each star are given in Table 1. Further, for \(n=-2\), we discovered the well-behaved solution [34]. Furthermore, the present solution asymptotically approaches the one in [47] when \(n \rightarrow \infty \) and by a suitable choice of the parameter \(b=2A/n\). Further, the analysis of the adiabatic index of the solution obtained by Maurya et al. [47] gives a stiffer equation state; however, in our solution the equation of state may be stiffer or softer, depending upon the values of the star generating index n.