1 Introduction

One of the most interesting unsolved issues in modern physics is the attributes of dense nuclear matter. Due to the constraint of terrestrial experiments, regarding the properties of nuclear matter’s equation of state (EoS) at supra-saturation densities, that is greater than the nuclear saturation density \(2.8\times 10^{14}~{\text {g}}\,{\text {cm}}^{-3}\), scientific groups are focusing on investigating compact objects in the cosmos, including mainly white dwarfs (WDs) and neutron stars (NSs). Specifically, NSs are considered to be the best extraterrestrial labs for studying the undetected features of dense matter [1,2,3,4]. Our knowledge with regard to NSs has considerably extended, since the pioneer work of Oppenheimer and Volkoff [5]. Mass, radius and other parameters of stellar objects depend on the EoS selected for the dense matter. Dozens of EoS have been proposed to describe NS matter over the years [6]. Since the EoS is one of the main observables characterizing matter features under intense conditions, hence its constraint, therefore, necessitates integrating nuclear physics and astrophysics. Many theoretical and experimental efforts along with astrophysical observations have been put to probe the properties of dense nuclear matter. Several NSs with a mass about \(2~M_{\odot }\) probed over the last decennary whole enough stringent restraints on nuclear matter EoS. Amongst the most enormous observed pulsars is the pulsar PSR J1614-2230 having the smallest uncertainty on the mass \(M=1.906_{-0.016}^{+0.016}~M_{\odot }\) [7]. Other two pulsars with \(M>2~M_{\odot }\) are PSR J0348+0432 with \(M=2.01_{-0.04}^{+0.04}~M_{\odot }\) [8] and MSP J0740+6620, recently discovered with a mass of \(2.14_{-0.09}^{+0.10}~M_{\odot }\) [9].

In recent decades, the anisotropy effects on the modeling of relativistic astrophysical objects in strong gravitational fields have already been discussed in some recent works. We can expect the emergence of unequal principal stresses, dubbed anisotropic fluid when modeling such high-density heavenly configurations above the nuclear density. This generally signifies that the radial pressure component is not equal to the components in the tangential direction viz., two dissimilar types of pressure components interior these relativistic astrophysical objects. It is interesting to mention here that the anisotropy effect has been first predicted by Jeans in 1922 [10] for self-gravitating configurations in the Newtonian regime. Then, an engrossing vision about more realistic astrophysical systems where the nuclear interactions must be analyzed in a relativistic way when a stellar structure with density energy \(\rho >10^{15}~{\text {g}}\,{\text {cm}}^{-3}\) was given by Ruderman [11]. In Refs. [11, 12], the authors argued that the matter proportion in the extremely congested nucleus of a stellar structure could present unequal stresses. However, the authors [13] have thoroughly investigated the anisotropy sources at the heavenly interior. Thereafter, the authors [14] have evaluated and contended viable underlying cause for local anisotropy in self-gravitating structures using representative cases of both Newtonian and general relativistic circumstances. In the same context, several authors [15,16,17,18] have also been analyzed the source and consequences of local anisotropy on cosmic configurations. It is also worth mentioning here that in order to explore the the local pressure anisotropy effect on a well-defined basis, it is mandatory to know the substantial physical grounds accountable for its semblance, such as, e.g., the pion condensation, exotic stage transitions over gravitational crash [19, 20], viscosity [21], presence of a strong nucleus or the existence of a type-IIIA super-critical fluid [22], heavy electromagnetic areas [23,24,25], slow turning of a fluid [26], emergence of willing distortion of Fermi surfaces [27, 28], availability of super-critical fluid states with constrained Cooper pair orbital momentum [29,30,31,32], or constrained super-critical fluid momentum [33, 34].

The EoS, which is the principal input to the Tolman–Oppenheimer–Volkoff equations [5, 35], establishes the stable stages of a non-rotating NS, are constructed in diverse fashions. The non-relativistic formalism with some param-etrizations of Skyrme [36] and the three-body potential of Akmal–Pandheripande–Ravenhall [37] are highly successful in portraying nuclear EoS, including the NS. Moreover, many exact stellar solutions to the Einstein field equations were obtained by various methods with generalized pathways for one of the metric potentials that does have a linear EoS [38,39,40,41,42], a quadratic EoS [43], a polytropic EoS [44, 45], a Chaplygin EoS [46,47,48,49,50,51,52] and Van der Waals EoS [53,54,55] etc., and without a specific barotropic EoS linking pressure to energy density [56,57,58,59,60,61]. Despite the fact that many such works have been published over the years, only a small number of these stellar solutions are compatible with non-singular metric functions via a physically agreeable stress-energy tensor.

In this paper, we study a new class of solutions to Einstein’s field equations representing static spherically symmetric anisotropic matter distribution in terms of a specified form of modified Van der Waals EoS such as \(p_{r}=\alpha \rho ^{2} +\frac{\beta \rho }{1+\gamma \rho }\) along with a gravitational potential Z(x) as a generating function. The exact solutions are formed by correlating an interior space-time geometry to an exterior Schwarzschild vacuum. Then, we study the physical viability of the model generated and compared with observational constraints from some massive NSs reported in the literature such as the millisecond pulsars PSR J0348+0432 [8], PSR J0740+6620 [9] and PSR J0030+0451 [62].

The paper is organized as follows. In Sect. 2, we briefly discuss the basic principles of an equivalent system of equations by using the Durgapal–Bannerji transformation, to represent an anisotropic static spherically symmetric matter distribution. In Sect. 3, we provide new classes of exact interior stellar solutions. Section 4 presents an insight of intersection circumstances for a sleek corresponding between intrinsic and extrinsic geometries, whereas Sects. 5, 6 and 7 discuss physical properties, validity, and stability. Finally, concluding remarks are reported in Sect. 8.

2 Spherically symmetric space-time

Our motive in this study is to discuss a model describing an anisotropic matter distribution with static spherical symmetry in terms of a boosting function obeying a Van der Waals type EoS. For this purpose, we start with static spherically symmetric spacetime that can be represented by the line element

$$\begin{aligned} ds^{2}_-= & {} -e^{2 \nu \left( r \right) }dt^{2}+e^{2 \lambda \left( r \right) }dr^{2}+r^{2} d \Omega ^{2}_{2},~ \end{aligned}$$
(1)

in Schwarzschild coordinates \( x^{a}= \left( t, r, \vartheta , \varphi \right) \). Here \(\nu \) and \(\lambda \) represent the gravitational potentials which are only functions of r, and \(d \Omega ^{2}_{2}= d \vartheta ^{2}+\sin ^{2} \vartheta ~d \varphi ^{2}\) portrays the metric on the two-sphere in polar coordinates. .

The Einstein field equation is defined as,

$$\begin{aligned}&8 \pi T_{ij}=G_{ij}, \end{aligned}$$
(2)

where \(T_{ij}\) and \(G_{ij}\) describe the energy-momentum tensor for matter distribution and Einstein’s tensor, respectively. Here the Einstein’s tensor \(G_{ij}\) depends completely on the Ricci tensor \(R_{ij}\) and the Ricci scalar R. This can be expressed as

$$\begin{aligned}&R_{ij}-\frac{1}{2}Rg_{ij}=G_{ij} , \end{aligned}$$
(3)

where \(g_{ij}\) representing the metric tensor.

Let’s suppose that the matter implicated in the distribution is anisotropic in kind. By using the entire function, one thus obtains the function for energy-momentum tensor in the accompanying shape:

$$\begin{aligned}&T_{i}^{j}= \rho \eta ^{j} \eta _{i}+p_{r} \chi _{i} \chi ^{j}+p_{t} \left( \eta ^{j} \eta _{i}- \chi _{i} \chi ^{j}-g_{i}^{j} \right) , \end{aligned}$$
(4)

whereas \(\eta ^{j}\) is the fluid 4-speed and \(\eta ^{j} \eta _{i}= \chi _{i} \chi ^{j}=1\), \(\chi _{i}\) is the unit space-like vector and thus \(\eta ^{j} \chi _{i}=0\). The above equation (4) gives the components of an anisotropic fluid’s energy-momentum tensor at any point in the form of density \(\rho \), radial pressure \(p_{r}\) and transverse pressure \(p_{t}\). In this regard, the energy-momentum tensor \(T_{i}^{j}\) along with a simple form of line element can be expressed as

$$\begin{aligned}&T_{i}^{j}=diag \left( -\rho , ~p_{r},~p_{t},~p_{t} \right) , \end{aligned}$$
(5)

with

$$\begin{aligned}&T_{i}^{j}=0 \ \ if\ i \ne j . \end{aligned}$$
(6)

For the line element (1) and energy-momentum tensor (5), the system of Einstein field equations in relativistic units \(8 \pi G=c=1\), can be expressed as

$$\begin{aligned} \rho= & {} \Bigg [ \frac{1-e^{- \lambda }}{r^{2}}+\frac{e^{- \lambda }}{r}\frac{d \lambda }{dr} \Bigg ], \end{aligned}$$
(7)
$$\begin{aligned} p_{r}= & {} \Bigg [ \frac{e^{- \lambda }-1}{r^{2}}+\frac{e^{- \lambda }}{r}\frac{d \nu }{dr}\Bigg ], \end{aligned}$$
(8)
$$\begin{aligned} p_{t}= & {} \Bigg [ \frac{1}{2}\frac{d^{2} \nu }{dr^{2}}+\frac{1}{4} \left( \frac{d \nu }{dr} \right) ^{2}-\frac{1}{2r} \left( \frac{d \nu }{dr}-\frac{d \lambda }{dr} \right) \nonumber \\&-\frac{1}{4}\frac{d \nu }{dr}\frac{d \lambda }{dr}\Bigg ]e^{- \lambda },~~ \end{aligned}$$
(9)

This stellar system of Eqs. (7)–(9) portrays the evolution of the gravitational field within an anisotropic celestial configuration.

The gravitational mass contained within the spherical object of radius r is given by,

$$\begin{aligned} m \left( r \right)= & {} \frac{1}{2} \int _{0}^{r} \rho \left( \epsilon \right) \epsilon ^{2}d \epsilon , \end{aligned}$$
(10)

while \(\epsilon \) is an integration constant. We now use the transformation proposed for the first time in Ref. [63]

$$\begin{aligned}&x=r^{2},\ \ Z \left( x \right) =e^{-2 \lambda \left( r \right) },\ \ A^{2}y^{2} \left( x \right) =e^{2 \nu \left( r \right) } . \end{aligned}$$
(11)

The stellar system of Einstein field equations expressed in (7)–(9) becomes

$$\begin{aligned} \rho= & {} \frac{1-Z}{x}-2\frac{dZ}{dx}, \end{aligned}$$
(12)
$$\begin{aligned} p_{r}= & {} 4Z \left( \frac{1}{y}\frac{dy}{dx} \right) +\frac{Z-1}{x} , \end{aligned}$$
(13)
$$\begin{aligned} p_{t}= & {} 4xZ\frac{d^{2}y}{dx^{2}}+ \left( 4Z+2x\frac{dZ}{dx} \right) \left( \frac{1}{y}\frac{dy}{dx} \right) +\frac{dZ}{dx}. \end{aligned}$$
(14)

The gravitational mass expression (10) becomes

$$\begin{aligned} m \left( x \right)= & {} \frac{1}{4} \int _{0}^{x}\root \of { \epsilon } \rho \left( \epsilon \right) d \epsilon , \end{aligned}$$
(15)

in terms of x introduced in (11).

It is interesting to observe that a physically realistic fluid distribution of matter expecting to fulfill the barotropic EoS viz., \(p_{r}= p_{r}\left( \rho \right) \). In this concern, we consider that the interior matter distribution obeys the modified Van der Waals EoS as follows,

$$\begin{aligned} p_{r}= & {} \alpha \rho ^{2} +\frac{\beta \rho }{1+\gamma \rho }, \end{aligned}$$
(16)

in order to successfully complete the stellar system of Eqs. (12)–(14). Here \(\alpha \), \(\beta \) and \(\gamma \) are real parameters.

The decelerated and accelerated periods are determined by parameters, \(\alpha \), \(\beta \) and \(\gamma \) of the EoS, and in the restricting situation \(\alpha ,\gamma \rightarrow 0\), we can recover the dark energy EoS, with \(\beta =p_{r}/\rho <-1/3\). It has also been pointed out that the perfect fluid EoS \(p_{r}=\beta \rho \) represents an estimation of cosmic epochs portraying stationary circumstances, with phase transitions ignored [64]. Consequently, the modified Van der Waals model has the advantage of depicting the transition from a matter field ruled era to a scalar field ruled epoch without introducing scalar fields. Furthermore, it aids in the clarification of the cosmos by using a small number of ingredients, and the modified Van der Waals fluid definitely treats dark energy and dark matter as a single fluid. By restricting the free parameters [64], the modified Van der Waals scenario was also effectively challenged with a wide range of observational tests.

On the other hand, this type of modified Van der Waals EoS expressed in (15) seems less economical and in comparison to observational tests, it is more flexible because of the wide number of free parameters. Next, it is conceivable to write the stellar system of Eqs. (12)–(14) in the simplest shape

$$\begin{aligned} e^{2\lambda }= & {} Z^{-1}, \end{aligned}$$
(17)
$$\begin{aligned} e^{2\nu }= & {} A^{2}y^{2}, \end{aligned}$$
(18)
$$\begin{aligned} \rho= & {} \frac{1-Z}{x}-2\frac{dZ}{dx}, \end{aligned}$$
(19)
$$\begin{aligned} p_{r}= & {} 4Z \left( \frac{1}{y}\frac{dy}{dx} \right) +\frac{Z-1}{x}, \end{aligned}$$
(20)
$$\begin{aligned} p_{t}= & {} p_{r}+ \Delta , \end{aligned}$$
(21)
$$\begin{aligned} \Delta= & {} 4xZ\frac{d^{2}y}{dx^{2}}+\frac{dZ}{dx} \left( 1+2x \left( \frac{1}{y}\frac{dy}{dx} \right) \right) +\frac{1-Z}{x} \end{aligned}$$
(22)

in terms of gravitational potential \(g_{rr}\) i.e., Z, while in our stellar model the amount \(\Delta =p_{t}-p_{r}\) is the anisotropy test that provides

$$\begin{aligned} y= & {} C x^{-1/4} exp\Bigg [\int \frac{1}{4Z}\left( \frac{1}{x}+\alpha \rho ^{2} +\frac{\beta \rho }{1+\gamma \rho }\right) dx\Bigg ] \end{aligned}$$
(23)

with C is an integration constant. Consequently, the line element (1) can be expressed in terms of the new variables defined in (11) as follows,

$$\begin{aligned} ds^{2}= & {} -A^2 C^2 r^{-1} exp\Bigg [\int \frac{1}{4Z}\left( \frac{1}{x}+\alpha \rho ^{2} +\frac{\beta \rho }{1+\gamma \rho }\right) dx\Bigg ] dt^{2}\nonumber \\&+ Z^{-1} dr^{2}+r^2 \left( d \vartheta ^{2}+\sin ^{2} \vartheta d \varphi ^{2} \right) . \end{aligned}$$
(24)

Therefore, the solution representing static spherically symmetric anisotropic matter distribution with the specified form of modified Van der Waals EoS can be readily established in accordance with the generating gravitational potential \(Z \left( x \right) \). Next, we discuss in detail how we build compact stellar configurations with anisotropic matter.

3 Exact solutions for anisotropic compact heavenly structures

In the system of Einstein field equations expressed in (17)–(22), there are six independent equations with independent variables namely, \(\rho \), \(p_r\), \(p_t\), \(\Delta \), y and Z. On the one hand, we can see that the stellar system of equations strongly depends on the gravitational potential \(Z\left( x\right) \). On the other hand, the system proposes that it is conceivable to define one of the amounts implicated in the integration process from equation (22) which is the master equation in the present study whose solution given by the relation (23). For this purpose, we make an explicit choice for the gravitational potential \(Z \left( x \right) \) in the following form

$$\begin{aligned} Z \left( x \right)= & {} \frac{1}{2}\Big [2-\delta x \Big ]\Big [1+\delta x \Big ]^{-1}, \end{aligned}$$
(25)

where \(\delta \) is a positive real parameter. Here \(Z \left( x \right) =1\) at \(x \rightarrow 0\), which shows that for a broad range of values of the parameter \(\delta \), the form of gravitational potential has been found to be regular, positive, and non-singular at the origin, as well as well-behaved in the stellar interior, and thus satisfies all of the requirements leading to the solution’s main physical acceptability.

Now, on substituting (25) into (23), we get the explicit function of y which is

$$\begin{aligned} y= & {} C exp\Bigg [-\frac{\delta \alpha }{4}\frac{11+8\delta x}{1+2\delta x+\delta ^2 x^2}\Bigg ]\Bigg [2-\delta x\Bigg ]^{-\phi _1}\nonumber \\&\times \Bigg [\frac{4(1+\delta x)+3\delta \gamma + \sqrt{3\delta \gamma (3\delta \gamma -16)}}{4(1+\delta x)+3\delta \gamma - \sqrt{3\delta \gamma (3\delta \gamma -16)}}\Bigg ]^{\phi _2}\nonumber \\&\times \Big [2(1+\delta x)^{2} + 3\delta \gamma (3+\delta x) \Big ]^{\phi _3}\Big [1+\delta x\Big ]^{\phi _4}~ \end{aligned}$$
(26)

where

$$\begin{aligned} \phi _1= & {} \frac{15}{2}\frac{\beta }{6+5\delta \gamma }+\frac{25}{24}\delta \alpha -\frac{3}{4}\\ \phi _2= & {} \frac{\beta \sqrt{3\delta \alpha }}{8 \sqrt{3\delta \alpha -16}}\frac{52-15\delta \gamma }{6+5\delta \gamma }\\ \phi _3= & {} \frac{3\beta }{8}\frac{4-5\delta \gamma }{6+5\delta \gamma }\nonumber \\\phi _4= & {} \frac{25}{24}\delta \alpha .~ \end{aligned}$$

Consequently, the exact model for the stellar system of Eqs. (17)–(22) composed of energy density, radial and tangential components of pressure is obtained as follows

$$\begin{aligned} e^{2\lambda }= & {} \frac{1}{2}\Big [2-\delta x \Big ]\Big [1+\delta x \Big ]^{-1}, \end{aligned}$$
(27)
$$\begin{aligned} e^{2\nu }= & {} A^{2}C^2 exp\Bigg [-\frac{\delta \alpha }{2}\frac{11+8\delta x}{1+2\delta x+\delta ^2 x^2}\Bigg ]\Bigg [2-\delta x\Bigg ]^{-2\phi _1}\nonumber \\&\times \Bigg [\frac{4(1+\delta x)+3\delta \gamma + \sqrt{3\delta \gamma (3\delta \gamma -16)}}{4(1+\delta x)+3\delta \gamma - \sqrt{3\delta \gamma (3\delta \gamma -16)}}\Bigg ]^{2\phi _2}\nonumber \\&\times \Big [2(1+\delta x)^{2} + 3\delta \gamma (3+\delta x) \Big ]^{2\phi _3}\Big [1+\delta x\Big ]^{2\phi _4},~~ \end{aligned}$$
(28)
$$\begin{aligned} \rho= & {} \frac{3\delta }{2}\frac{3+\delta x}{1+2\delta x+\delta ^2 x^2}, \end{aligned}$$
(29)
$$\begin{aligned} p_{r}= & {} \alpha \rho ^{2} +\frac{\beta \rho }{1+\gamma \rho }, \end{aligned}$$
(30)
$$\begin{aligned} p_{t}= & {} p_{r}+ \Delta , \end{aligned}$$
(31)

then, using (22) and (25), we obtain the explicit form of the anisotropic parameter as follows

$$\begin{aligned} \Delta= & {} 2x\Bigg [\frac{2-\delta x}{ 1+\delta x }\Bigg ]\frac{d^{2}y}{dx^{2}}+\frac{1}{2}\frac{3\delta x}{ 1+2\delta x+\delta ^2 x^2 }\Bigg [\delta -2\frac{1}{y}\frac{dy}{dx}\Bigg ] \nonumber \\ \end{aligned}$$
(32)

where y is specified by the previously mentioned relationship (26). If \(\Delta <0\), the anisotropic factor is attractive in nature and repulsive if \(\Delta >0\).

4 Matching conditions for anisotropic solution

At this stage, the interior space-time is smoothly connected to the vacuum exterior Schwarzschild space-time at the stellar surface \(r=R_{s}\), and it is obvious that \(R_{s}>2M\), while \(R_{s}\) and M are the radius and total mass of the star, respectively. In this case, the line element for the stellar configuration at the junction surface \(\Sigma \) with radius \(r=R_{s}\) has the form

$$\begin{aligned} ds^{2}_+=- & {} \left( 1-\frac{2M}{r} \right) dt^{2}+ \left( 1-\frac{2M}{r} \right) ^{-1}dr^{2}+r^{2} d \Omega ^{2}_{2}. \nonumber \\ \end{aligned}$$
(33)

Here, the total mass is denoted by M. Nevertheless, the following requirements must be met at the hyper-surface \(\Sigma \) in order to ensure the smoothness and continuity of the inward space-time metric \(ds^2_-\) and the outside space-time \(ds^2_+\) at the boundary surface.

$$\begin{aligned}&[{ds^2}_{-}]_{\Sigma } = [{ds^2}_{+}]_{\Sigma },~~~[{K_{ij}}_{-}]_{\Sigma }=[{K_{ij}}_{+}]_{\Sigma }, \end{aligned}$$
(34)
$$\begin{aligned}&e^{2\nu ^{-}}|_{r=R_s} = e^{2\nu ^{+}}|_{r=R_s} ~\text {and}~ e^{2\lambda ^{-}}|_{r=R_s} = e^{2\lambda ^{+}}|_{r=R_s}, \end{aligned}$$
(35)

and

$$\begin{aligned} \Big ( \frac{\partial e^{2\nu ^{-}}}{\partial r} \Big )_{|r=R_s}= \Big ( \frac{\partial e^{2\nu ^{+}}}{\partial r} \Big )_{|r=R_s}, \end{aligned}$$
(36)

The interior and exterior spacetimes are represented by − and \(+\), respectively, while the curvature is described by \(K_{ij}\). By using the continuity of the first fundamental form, which is \([ds^2]_{\Sigma }\)=0, we can always get \([F]_{\Sigma } \equiv F (r\longrightarrow R_s^{+})-F (r\longrightarrow R_s^{-})\equiv F^{+}(R_s)-F^{-}(R_s),\) for any function F(r). Furthermore, this arrangement provides us with,

$$\begin{aligned} g^{-}_{rr}(R_s)=g^{+}_{rr}(R_s)~~\text {and}~~ g^{-}_{tt}(R_s)=g^{+}_{tt}(R_s). \nonumber \\ \end{aligned}$$
(37)

Following that, the spacetime (1) must achieve the second fundamental form, \(K_{ij}\), at the hyper-surface \(\Sigma \), which is equivalent to the O\('\)Brien and Synge junction condition [72]. In this context, we discovered that the radial pressure at the surface should be zero, i.e., when \(r=r_{\Sigma }\), leading to

$$\begin{aligned}&p_r(R)=0. \end{aligned}$$
(38)

The size of the stellar structure is determined by this requirement. Alternatively, \(\Sigma _-\) and \(\Sigma _+\) are being used to symbolize the interior and exterior sectors, respectively.

The hyper-surface is then represented by the accompanying line element,

$$\begin{aligned} ds^2=d\tau ^2-R_s^2d\vartheta ^2+R_s^2\sin ^2\vartheta \,d\varphi ^2. \end{aligned}$$
(39)

The proper time boundary is denoted by \(\tau \). In this perspective, the boundary’s extrinsic curvature \(\Sigma \) can be written as,

$$\begin{aligned} K^{\pm }_{ij}=-\eta _k^{\pm }\,\frac{\partial ^2y^k_{\pm }}{\partial n^i\,n^j}-\eta _k^{\pm }\,\Gamma ^k_{\mu \,l}\frac{\partial y^\mu _{\pm }}{\partial n^i}\frac{\partial y^l_{\pm }}{\partial n^j}, \end{aligned}$$
(40)

with \(n^i\) denoting the coordinates in the boundary \(\Sigma \), and \(\eta _k^{\pm }\) denoting the four-speed normal to \(\Sigma \). The components of this four-speed are obtained using the coordinates (\(y^\nu _{\pm }\)) of \(\tau ^{\pm }\) as follows,

$$\begin{aligned} \eta _k^{\pm }=\pm \,\frac{df}{dy^{k}}\,\left| g^{\mu \,l}\frac{df}{dy^{\mu }}\frac{df}{dy^{l}}\right| ^{-1/2} \quad \text {with}~\eta _k\eta ^k=1. \nonumber \\ \end{aligned}$$
(41)

The interior and exterior sector unit normal vectors can then be written as

$$\begin{aligned} \eta ^{-}_k=\bigg [0,e^{\nu },0,0\bigg ]\quad \text {and}\quad \eta ^{-}_k=\bigg [0,\bigg (1-\frac{2{M}}{r}\bigg )^{-1},0,0\bigg ].\nonumber \\ \end{aligned}$$
(42)

Then, utilizing the line elements (1) and (39) in conjunction with the Schwarzschild spacetime (33), we can formulate

$$\begin{aligned} \bigg [\frac{dt}{d\tau }\bigg ]_{\Sigma }=\big [e^{-\lambda }\big ]_{\Sigma }=\bigg [\bigg (1-\frac{2{M}}{r}\bigg )^{-1}\bigg ]_{\Sigma }, \end{aligned}$$
(43)

\(\text {where}~[r]_{\Sigma }=R_s\). Eq.(42) can be used to derive the non-zero components of the curvature \((K_{ij})\) as follows,

$$\begin{aligned}&K^{-}_{00}=\bigg [-\frac{\lambda ^{\prime }}{2\,e^{\nu }}\,\bigg ]_{\Sigma },~ K^{-}_{22}=\frac{1}{\sin ^2\vartheta },\nonumber \\&K^{-}_{33}= \big [r\,e^{-\nu }\big ]_{\Sigma },\nonumber \\&K^{+}_{00}=\bigg [\bigg (\frac{{M}}{r^2}\bigg )\bigg (1-\frac{2{M}}{r}\bigg )^{-1}\bigg ]_{\Sigma },~ K^{+}_{22}=\frac{1}{\sin ^2\vartheta }, \nonumber \\&K^{+}_{33}=\bigg [r\,\bigg (1-\frac{2{M}}{r}\bigg )^{1}\bigg ]_{\Sigma }.~\nonumber \end{aligned}$$

Therefore, when we combine the junction condition \([K^{-}_{22}]_{\Sigma } =[K^{+}_{22}]_{\Sigma }\) with \([r]_{\Sigma }\), we obtain

$$\begin{aligned} e^{-\nu (R_s)}=\bigg (1-\frac{2{M}}{R}\bigg ). \end{aligned}$$
(44)

When the preceding statement is inserted into the matching condition \([K^{-}_{00}]_{\Sigma }=[K^{+}_{00}]_{\Sigma }\), it produces the following result,

$$\begin{aligned} \lambda ^\prime (R_s)=\frac{2{M}}{R_s\left( R_s-2{M}\right) }. \end{aligned}$$
(45)

Therefore, at the hyper-surface, the relevant criteria supplied by Eqs. (43)–(45) give rise to the following expressions,

$$\begin{aligned} e^{2 \lambda \left( R_{s} \right) }= & {} \Bigg [ 1-\frac{2M}{R_{s}} \Bigg ] ^{-1}= 2\Bigg [\frac{1+\delta R_{s}^{2}}{ 2-\delta R_{s}^{2}}\Bigg ], \end{aligned}$$
(46)
$$\begin{aligned} e^{2 \nu \left( R_{s} \right) }= & {} \Bigg [ 1-\frac{2M}{R_{s}} \Bigg ]=A^2y^2\left( R_{s}^2\right) . \end{aligned}$$
(47)

It is clear to observe that the condition (46) does not impose any constraints on the parameters, whereas the condition (47) imposes a constraint on the parameter A as

$$\begin{aligned} A= & {} \sqrt{\frac{1}{2y^2\left( R_{s}^2\right) }\frac{2-\delta R_{s}^{2}}{1+\delta R_{s}^{2}}}. \end{aligned}$$
(48)

Due to the complicatedness of the static and spherically symmetric solutions for the system of the field equations, we exhibit graphically that the radial reliance of our stellar system’s physical quantities, which includes matter variables of the anisotropic model are well-behaved throughout the interior of the stellar configuration and hence the stellar model satisfies all necessary conditions.

Fig. 1
figure 1

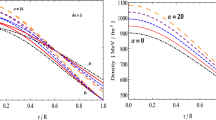
Behaviour of the matter density \(\rho \) and the radial and transverse pressures (\(p_{r}\), \(p_{t}\)) against the radial coordinate r of our stellar model for three heavy pulsars. For plotting these graphs, we use the numerical values of the constant parameters given in Table 1

Full size image

5 Physical analysis

We now proceed to discuss the physical acceptability of the stellar solutions acquired in this study. We will look at various physical features of compact stellar object formations and we demonstrate that acquired solutions are physically viable. We have considered the observational data of three compact astrophysical objects viz., PSR J0348+0432, PSR J0030+0451 and PSR J0740+6620 as models in order to show the anisotropic effects presented with spherical symmetry within space-time metric in the context of general relativity. The graphs were drawn by selecting parameter values as follows after comprehensive empirical fine-tuning: \(\delta \), \(\alpha \), \(\beta \) and \(\gamma \) for some heavy pulsars as shown in Table 1. The election of parameters have been such that the anisotropic stellar models are physically reasonable fulfilling the following physical requirements:

  • Necessary criteria for matter density and pressure components: From Fig. 1 we see that the density and pressure profiles are all monotonic decrease smoothly towards the surface layer of the stellar configurations, having their maximum values at the stellar center and the radial pressure \(p_r\) are disappearing at the boundary of each stellar configuration \(r = R_s\). At the star’s surface layer, however, matter density is always positive. The central density due to ordinary matter is evaluated as follows,

    $$\begin{aligned} \rho _c= & {} \rho \left( r= 0 \right) =\frac{9}{2}\delta >0. \end{aligned}$$
    (49)

    Then, the central pressure for our present stellar model is acquired as follows,

    $$\begin{aligned} p_c= & {} p \left( r= 0 \right) =\frac{81}{4}\alpha \delta ^{2} +\frac{9 \beta \delta }{2+9\gamma \delta } >0. \end{aligned}$$
    (50)

    These informations immediately indicates that both density and pressure are non-negative within the interior of compact stellar configuration. On the other hand, as also seen in Fig. 1, at the stellar boundary, the transverse pressure is greater than zero, which is physically feasible [65]. Moreover, an anisotropic fluid scenario has been clearly stated by the supposition of particles in movement on circular orbits [66, 67] and the transverse pressure of a surface layer is related to surface tension [68]. As it is clear from Fig. 1 that the anisotropy profile \(\Delta \) is a monotonically increasing function as one moves from the stellar centre towards the stellar boundary remaining finite and continuous in the interior and repulsive in nature.

  • The continuity of the extrinsic curvature via the corresponding hyper-surface: Continuity of the extrinsic curvature via the corresponding hyper-surface, at the surface layer of the stellar configuration \(r=R_s\) gives the condition

    $$\begin{aligned}&\left( p_{r} \right) _{r=R_s}=0, \end{aligned}$$
    (51)

    which yields

    $$\begin{aligned}&R_s^2=\frac{1}{4\beta }\nonumber \\&\quad \sqrt{3\alpha ^2-24\frac{\alpha \beta }{\delta }-9\alpha \beta \gamma +\frac{9\delta \alpha ^3-48\alpha \beta ^2\gamma -36\alpha ^2\beta \gamma }{2\delta \sqrt{\alpha ^2-4\alpha \beta \gamma }}}\nonumber \\&\qquad -\frac{3}{8\beta }\Big [\alpha +\sqrt{\alpha ^2-4\beta \gamma }\Big ]-\frac{1}{\delta }.~ \end{aligned}$$
    (52)

    We can obtain the positive radius \(R_s\) by selecting appropriate parameters \(\alpha \), \(\beta \), \(\gamma \) and \(\delta \).

  • The positivity of the energy conditions: The energy conditions are fundamental tools for GR since they permit us to analyze the casual and geodesic structure of space-time carefully. One path to deriving such conditions is through the Raychaudhuri equations [73,74,75], which define the action of correspondence of the gravity for timelike, spacelike, or lightlike curves. If we are working with an anisotropic fluid, the energy conditions, i.e., Strong energy conditions (SEC), Dominant energy conditions (DEC), Weak energy conditions (WEC), Trace energy conditions (TEC), and Null energy conditions (NEC) for GR are expressed as:

    • NEC if \(\rho +p_k\ge 0\), \(\forall k\).

    • WEC if \(\rho \ge 0\), \(\rho +p_k\ge 0\), \(\forall k\).

    • SEC if \(\rho +p_k \ge 0\), \(\rho +\sum _k p_k\ge 0\), \(\forall k\).

    • DEC if \(\rho \ge 0\), \(\rho \pm p_k\ge 0\), \(\forall k\).

    • TEC if \(\rho -p_k\ge 0\), \(\rho -\sum _k p_k\ge 0\), \(\forall k\).

    where \(k=r,t\). The non-negative profile of state variables \(\rho ,~p_r\) and \(p_t\) shown in Fig. 1 swiftly adheres to the first three constraints i.e., NEC infers that an observer traversing a null scheme will measure the typical matter density as non-negative, according to WEC, the matter density measured by an observer crossing a time-like scheme is constantly non-negative, and with regard to SEC, the trace of the tidal tensor analyzed by the corresponding observers is always non-negative. The non-negative evolutionary associated with DEC an TEC is also consistent with the fourth and fifth constraints, in which the DEC represents the mass-energy that will never be seen to flow faster than light and according to TEC, the stress-energy tensor trace should be necessarily non-negative depending on metric conventions. It is obvious from Fig. 2, that all energy conditions are carefully verified, resulting in a non-exotic matter content and are well-satisfied with the constraints of the realistic stellar configurations, which corroborate that our stellar model is well-behaved and describes an acceptable physical system.

  • Cracking method for anisotropic compact sphere stability: It is expected that the speed of sound will be less than the speed of light within a stellar interior, i.e., the square of radial (\(v_{sr}^{2}=\frac{dp_{r}}{d \rho }\)) and transverse (\(v_{st}^{2}=\frac{dp_{t}}{d \rho }\)) speeds of sound must fulfill the inequalities \(0 \le v_{sr}^{2} \le 1\) and \(0 \le v_{st}^{2} \le 1\) which is known as a causality condition. From Fig. 3 we can evidently see that throughout the interior of the stellar structures, the radial and transverse speeds of sound are always less than the speed of light \(c=1\), indicating that the causality condition is satisfied. Moving towards the stellar boundary, we discover that the difference in sound velocity decreases but causality is never violated and cracking will not occur in all our cases.

Fig. 2
figure 2

Behaviour of the energy conditions against the radial coordinate r of our stellar model for three heavy pulsars. For plotting these graphs, we use the numerical values of the constant parameters given in Table 1

Full size image
Fig. 3
figure 3

Behaviour of the square of radial and transverse speeds of sound (\(v^2_{r}\), \(v^2_{t}\)) and the difference between the square of radial and transverse speeds of sound against the radial coordinate r of our stellar model for three heavy pulsars. For plotting these graphs, we use the numerical values of the constant parameters given in Table 1

Full size image
Fig. 4
figure 4

Behaviour of the gravitational mass \(\left( m(r)\right) \), compactness parameter \(\left( u(r)\right) \), and gravitational red-shift \(\left( z_{s}\right) \) against the radial coordinate r of our stellar model for three heavy pulsars. For plotting these graphs, we use the numerical values of the constant parameters given in Table 1

Full size image
Fig. 5
figure 5

Behaviour of the \(M-\rho _c\) and M–R diagrams of our stellar model for three heavy pulsars. For plotting these graphs, we use the numerical values of the constant parameters given in Table 1

Full size image

6 Gravitational mass, compactness factor and gravitational red-shift

The compactness factor of our stellar model is defined by a dimensionless parameter u which is the mass-to-radius ratio and it cannot be arbitrarily huge. As claimed by Buchdahl [70], the compactness factor of a stellar system for a four-dimensional fluid sphere should be smaller than \(\frac{2M}{R}<\frac{8}{9} \approx 0.8888\) to be a stable configuration. So, to come up with the compactness factor, in this section, we are fascinated to investigate the gravitational mass function for our stellar model which can be given as

$$\begin{aligned} m \left( x \right)= & {} \frac{1}{4} \int _{0}^{x}\root \of { \epsilon } \rho \left( \epsilon \right) d \epsilon =\frac{3\delta }{4} \frac{x^{3/2}}{1+\delta x}. \end{aligned}$$
(53)

It should be noted here that the gravitational mass function is influenced by \(\delta \).

From the above gravitational mass formula, the compactness factor can be calculated as

$$\begin{aligned} u \left( x \right)= & {} \frac{m \left( x \right) }{\sqrt{x}}=\frac{3\delta }{4\sqrt{x}} \frac{x^{3/2}}{1+\delta x}. \end{aligned}$$
(54)

Therefore, the gravitational red-shift of our present model correlating to the stated compactness factor is defined as follows,

$$\begin{aligned} Z\left( x \right)= & {} \frac{1}{\root \of {1-2u \left( x \right) }}-1=\root \of {\frac{1-\delta x}{1-\frac{\delta }{2} x}}-1. \end{aligned}$$
(55)

The profile of the gravitational mass function, the compactness factor and the gravitational red-shift are illustrated in Fig. 4. The figure represents the three quantities viz., \(m \left( r \right) \), \(u \left( r \right) \) and \(Z\left( x \right) \) being monotonic increasing functions with the radial coordinate r and positive within the stellar system, as well as the regularity of the gravitational mass function at the origin, is ensured. With increasing gravitational mass function, the compactness factor increases, and their corresponding value u satisfies the maximum allowable mass-to-radius ratio of Buchdahl [70], i.e., it cannot be greater than 8/9. According to the authors [56,57,58,59,60,61, 71], the surface gravitational red-shift for an anisotropic fluid sphere should be less than \(Z_s \le 5\) or \(Z_s \le 5.211\). Based on these constraints, our current stellar system reveals that \(Z_s \le 0.301219\), indicating that cosmic structures are available.

The generated upshots corresponding to the physical parameters viz., R, \({\rho }_c\), \({\rho }_s\), \(p_c\), 2M/R, \(Z_s\), along with the constant parameters viz., \(\alpha \), \(\beta \), \(\gamma \) and \(\delta \) are illustrated in Tables 1, and 2. From these numerical upshots, we confirm that the chosen stellar objects have the values of high-redshift and their surface densities are greater than the nuclear saturation, \(2.8\times 10^{14}~{\text {g}}\,{\text {cm}}^{-3}\). Consequently, for the stellar model parameters selected, the generated solutions comply with the requirements of realistic stellar configurations and are in good agreement with reported physical quantities determined by existing astronomical observations on some heavy pulsars PSR J0348+0432 [8], PSR J0740+6620 [9] and PSR J0030+0451 [62].

Table 1 Constant parameters calculated for radii and mass for some heavy pulsars
Full size table
Table 2 Some physical parameters calculated for radii and mass for some heavy pulsars
Full size table

7 Static stability criterion and mass–radius diagram

In this section, we start by studying the static stability criterion developed by Chandrasekhar [76] to analyze the stability of stellar structures under radial disturbances. Furthermore, Harrison et al. [77] and and Zeldovich and Novikov [78] simplify this static stability criterion by imposing the following constraints:

$$\begin{aligned}&\frac{\partial M}{\partial \rho _c} >0~~ \rightarrow ~~\text {stable configuration} \end{aligned}$$
(56)
$$\begin{aligned}&\frac{\partial M}{\partial \rho _c} <0~~ \rightarrow ~~\text {unstable configuration} \end{aligned}$$
(57)

To illustrate, we computed the total mass as a function of \(\rho _c\), which is given as

$$\begin{aligned} M\left( \rho _c\right) =\frac{3R^{3}}{2} \left( \frac{\rho _c}{9+2R^2\rho _c }\right) . \end{aligned}$$
(58)

Figure 5 shows the variation of mass in accordance with the central density. This leads to the conclusion that increasing \(\rho _c\) improves stability. This is due to the range central density’s preference for saturating the mass. This means that greater values of \(\rho _c\) improve the stable range of density during radial oscillation. This leads to the conclusion that the stellar solution is stable under radial disturbances.

Further, we tested the state of the compact stellar objects by studying the M–R diagram resulting from our stellar model in the Fig. 5. In this regard, we provide a useful description of the effects included by the appropriate parameters \(\alpha \), \(\beta \), \(\gamma \) and \(\delta \), in order to give an efficient and more realistic model. According to the effect of these parameters, we can observe that the maximum value of mass M in [\(M_{\odot }\)] and associated radius R in [km] decreases, resulting in a more compact and less massive stellar system. We also discovered a good agreement, represented by the horizontal stripes with observational data on the M–R diagram for three compact stellar objects, namely, PSR J0740+6620, PSR J0348+0432, PSR J0030+0451, and many others can be matched.

8 Concluding remarks

In this paper, we have focused on investigating the possibility of providing a new well-behaved class of exact anisotropic solutions for viable highly compact static spherically symmetric configurations as an alternative to NSs in the context of general relativity. For this purpose, we considered a non-linear form of modified Van der Waals EoS viz., \(p_{r}=\alpha \rho ^{2} +\frac{\beta \rho }{1+\gamma \rho }\) for the pressure and energy density relationship along with a gravitational potential Z(x) as a generating function via an anisotropic matter distribution which formed the basis for building bounded stellar configurations. The models under consideration are regular, viable, and stable under the influence generated by the parameters coming from the nonlinear EoS and gravitational potential viz., \(\alpha \), \(\beta \), \(\gamma \), \(\delta \), everywhere within the astral fluid. One captivating observation is that the predicted radii for observed heavy pulsars are readily determined from the continuity of the second fundamental form along with the maximum observed mass and corresponding radii are achieved through fine-tuning of parameters coming from theory.

Finally, it is worth mentioning here that the model admits and shares all the required pivotal physical and mathematical attributes in the compact stars study, which provide circumstantial evidence in favor of the evolution of realistic stellar configurations in the investigated high-density regime. In effect, our stellar model supports the existence of realistic heavy pulsars such as PSR J0740+6620, PSR J0348+0432 and PSR J0030+0451.