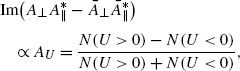Abstract
During 2011 the LHCb experiment at CERN collected 1.0 fb−1 of \(\sqrt{s} = 7\mbox{~TeV}\) pp collisions. Due to the large heavy quark production cross-sections, these data provide unprecedented samples of heavy flavoured hadrons. The first results from LHCb have made a significant impact on the flavour physics landscape and have definitively proved the concept of a dedicated experiment in the forward region at a hadron collider. This document discusses the implications of these first measurements on classes of extensions to the Standard Model, bearing in mind the interplay with the results of searches for on-shell production of new particles at ATLAS and CMS. The physics potential of an upgrade to the LHCb detector, which would allow an order of magnitude more data to be collected, is emphasised.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
During 2011 the LHCb experiment [1] at CERN collected 1.0 fb−1 of \(\sqrt{s} = 7 ~\mathrm{TeV} \)
pp collisions. Due to the large production cross-section,  in the LHCb acceptance [2], with the comparable number for charm production about 20 times larger [3, 4], these data provide unprecedented samples of heavy flavoured hadrons. The first results from LHCb have made a significant impact on the flavour physics landscape and have definitively proved the concept of a flavour physics experiment in the forward region at a hadron collider.
in the LHCb acceptance [2], with the comparable number for charm production about 20 times larger [3, 4], these data provide unprecedented samples of heavy flavoured hadrons. The first results from LHCb have made a significant impact on the flavour physics landscape and have definitively proved the concept of a flavour physics experiment in the forward region at a hadron collider.
The physics objectives of the first phase of LHCb were set out prior to the commencement of data taking in the “roadmap document” [5]. They centred on six main areas, in all of which LHCb has by now published its first results: (i) the tree-level determination of γ [6, 7], (ii) charmless two-body B decays [8, 9], (iii) the measurement of mixing-induced CP violation in \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) [10], (iv) analysis of the decay \(B ^{0}_{ s } \rightarrow \mu ^{+} \mu ^{-} \) [11–14], (v) analysis of the decay B 0→K ∗0 μ + μ − [15], (vi) analysis of \(B ^{0}_{ s } \rightarrow \phi\gamma\) and other radiative B decays [16, 17].Footnote 1 In addition, the search for CP violation in the charm sector was established as a priority, and interesting results in this area have also been published [18, 19].
The results demonstrate the capability of LHCb to test the Standard Model (SM) and, potentially, to reveal new physics (NP) effects in the flavour sector. This approach to search for NP is complementary to that used by the ATLAS and CMS experiments. While the high-\(p_{\rm T}\) experiments search for on-shell production of new particles, LHCb can look for their effects in processes that are precisely predicted in the SM. In particular, the SM has a highly distinctive flavour structure, with no tree-level flavour-changing neutral currents, and quark mixing described by the Cabibbo–Kobayashi–Maskawa (CKM) matrix [20, 21] which has a single source of CP violation. This structure is not necessarily replicated in extended models. Historically, new particles have first been seen through their virtual effects since this approach allows one to probe mass scales beyond the energy frontier. For example, the observation of CP violation in the kaon system [22] was, in hindsight, the discovery of the third family of quarks, well before the observations of the bottom and top quarks. Crucially, measurements of both high-\(p_{\rm T}\) and flavour observables are necessary in order to decipher the nature of NP.
The early data also illustrated the potential for LHCb to expand its physics programme beyond these “core” measurements. In particular, the development of trigger algorithms that select events inclusively based on properties of b-hadron decays [23, 24] facilitates a much broader output than previously foreseen. On the other hand, limitations imposed by the hardware trigger lead to a maximum instantaneous luminosity at which data can most effectively be collected (higher luminosity requires tighter trigger thresholds, so that there is no gain in yields, at least for channels that do not involve muons). To overcome this limitation, an upgrade of the LHCb experiment has been proposed to be installed during the long shutdown of the LHC planned for 2018. The upgraded detector will be read out at the maximum LHC bunch-crossing frequency of 40 MHz so that the trigger can be fully implemented in software. With such a flexible trigger strategy, the upgraded LHCb experiment can be considered as a general purpose detector in the forward region.
The Letter of Intent for the LHCb upgrade [25], containing a detailed physics case, was submitted to the LHCC in March 2011 and was subsequently endorsed. Indeed, the LHCC viewed the physics case as “compelling”. Nevertheless, the LHCb Collaboration continues to consider further possibilities to enhance the physics reach. Moreover, given the strong motivation to exploit fully the flavour physics potential of the LHC, it is timely to update the estimated sensitivities for various key observables based on the latest available data. These studies are described in this paper, and summarised in the framework technical design report for the LHCb upgrade [26], submitted to the LHCC in June 2012 and endorsed in September 2012.
In the remainder of this introduction, a brief summary of the current LHCb detector is given, together with the common assumptions made to estimate the sensitivity achievable by the upgraded experiment. Thereafter, the sections of the paper discuss rare charm and beauty decays in Sect. 2, CP violation in the B system in Sect. 3 and mixing and CP violation in the charm sector in Sect. 4. There are several other important topics, not covered in any of these sections, that can be studied at LHCb and its upgrade, and these are discussed in Sect. 5. A summary is given in Sect. 6.
1.1 Current LHCb detector and performance
The LHCb detector [1] is a single-arm forward spectrometer covering the pseudorapidity range 2<η<5, designed for the study of particles containing b or c quarks. The detector includes a high precision tracking system consisting of a silicon-strip vertex detector surrounding the pp interaction region, a large-area silicon-strip detector located upstream of a dipole magnet with a bending power of about 4 Tm, and three stations of silicon-strip detectors and straw drift tubes placed downstream. The combined tracking system has a momentum resolution Δp/p that varies from 0.4 % at 5 GeV/c to 0.6 % at 100 GeV/c, and an impact parameter resolution of 20 μm for tracks with high transverse momentum. Charged hadrons are identified using two ring-imaging Cherenkov detectors. Photon, electron and hadron candidates are identified by a calorimeter system consisting of scintillating-pad and preshower detectors, an electromagnetic calorimeter and a hadronic calorimeter. Muons are identified by a system composed of alternating layers of iron and multiwire proportional chambers. The trigger consists of a hardware stage, based on information from the calorimeter and muon systems, followed by a software stage which applies a full event reconstruction.
During 2011, the LHCb experiment collected 1.0 fb−1 of integrated luminosity during the LHC pp run at a centre-of-mass energy \(\sqrt {s} = 7 ~\mathrm{TeV} \). The majority of the data was recorded at an instantaneous luminosity of \(\mathcal{L}_{\rm inst} = 3.5 \times10^{32}~\mathrm{cm}^{-2}\,\mathrm{s}^{-1}\), nearly a factor of two above the LHCb design value, and with a pile-up rate (average number of visible interactions per crossing) of μ∼1.5 (four times the nominal value, but below the rates of up to μ∼2.5 seen in 2010). A luminosity levelling procedure, where the beams are displaced at the LHCb interaction region, allows LHCb to maintain an approximately constant luminosity throughout each LHC fill. This procedure permitted reliable operation of the experiment and a stable trigger configuration throughout 2011. The hardware stage of the trigger produced output at around 800 kHz, close to the nominal 1 MHz, while the output of the software stage was around 3 kHz, above the nominal 2 kHz, divided roughly equally between channels with muons, b decays to hadrons and charm decays. During data taking, the magnet polarity was flipped at a frequency of about one cycle per month in order to collect equal sized data samples of both polarities for periods of stable running conditions. Thanks to the excellent performance of the LHCb detector, the overall data taking efficiency exceeded 90 %.
1.2 Assumptions for LHCb upgrade performance
In the upgrade era, several important improvements compared to the current detector performance can be expected, as detailed in the framework TDR. However, to be conservative, the sensitivity studies reported in this paper all assume detector performance as achieved during 2011 data taking. The exception is in the trigger efficiency, where channels selected at hardware level by hadron, photon or electron triggers are expected to have their efficiencies double (channels selected by muon triggers are expected to have marginal gains, that have not been included in the extrapolations). Several other assumptions are made:
-
LHC collisions will be at \(\sqrt{s} = 14 ~\mathrm{TeV} \), with heavy flavour production cross-sections scaling linearly with \(\sqrt{s}\);
-
the instantaneous luminosityFootnote 2 in LHCb will be \(\mathcal{L}_{\rm inst} = 10^{33}~\mathrm{cm} ^{-2}\,\mathrm{s}^{-1}\): this will be achieved with 25 ns bunch crossings (compared to 50 ns in 2011) and μ=2;
-
LHCb will change the polarity of its dipole magnet with similar frequency as in 2011/12 data taking, to approximately equalise the amount of data taken with each polarity for better control of certain potential systematic biases;
-
the integrated luminosity will be \(\mathcal{L}_{\rm int} = 5~\mbox{fb}^{-1}\) per year, and the experiment will run for 10 years to give a total sample of 50 fb−1.
2 Rare decays
2.1 Introduction
The term rare decay is used within this document to refer loosely to two classes of decays:
-
flavour-changing neutral current (FCNC) processes that are mediated by electroweak box and penguin type diagrams in the SM;
-
more exotic decays, including searches for lepton flavour or number violating decays of B or D mesons and for light scalar particles.
The first broad class of decays includes the rare radiative process \(B ^{0}_{ s } \rightarrow \phi \gamma \) and rare leptonic and semileptonic decays \(B^{0}_{(s)} \rightarrow \mu ^{+} \mu ^{-} \) and B 0→K ∗0 μ + μ −. These were listed as priorities for the first phase of the LHCb experiment in the roadmap document [5]. In many well motivated new physics models, new particles at the TeV scale can enter in diagrams that compete with the SM processes, leading to modifications of branching fractions or angular distributions of the daughter particles in these decays.
For the second class of decay, there is either no SM contribution or the SM contribution is vanishingly small and any signal would indicate evidence for physics beyond the SM. Grouped in this class of decay are searches for GeV scale new particles that might be directly produced in B or D meson decays. This includes searches for light scalar particles and for B meson decays to pairs of same-charge leptons that can arise, for example, in models containing Majorana neutrinos [27–29].
The focus of this section is on rare decays involving leptons or photons in the final states. There are also several interesting rare decays involving hadronic final states that can be pursued at LHCb, such as B +→K − π + π +, B +→K + K + π − [30, 31], \(B ^{0}_{ s } \rightarrow \phi \pi ^{0} \) and \(B ^{0}_{ s } \rightarrow \phi\rho^{0}\) [32]; however, these are not discussed in this document.
Section 2.2 introduces the theoretical framework (the operator product expansion) that is used when discussing rare electroweak penguin processes. The observables and experimental constraints coming from rare semileptonic, radiative and leptonic B decays are then discussed in Sects. 2.3, 2.4 and 2.5 respectively. The implications of these experimental constraints for NP contributions are discussed in Sects. 2.6 and 2.7. Possibilities with rare charm decays are then discussed in Sect. 2.8, and the potential of LHCb to search for rare kaon decays, lepton number and flavour violating decays, and for new light scalar particles is summarised in Sects. 2.9, 2.10 and 2.11 respectively.
2.2 Model-independent analysis of new physics contributions to leptonic, semileptonic and radiative decays
Contributions from physics beyond the SM to the observables in rare radiative, semileptonic and leptonic B decays can be described by the modification of Wilson coefficients \(C^{(\prime)}_{i}\) of local operators in an effective Hamiltonian of the form
where q=d,s, and where the primed operators indicate right-handed couplings. This framework is known as the operator product expansion, and is described in more detail in, e.g., Refs. [33, 34]. In many concrete models, the operators that are most sensitive to NP are a subset of

which are customarily denoted as magnetic (\(O_{7}^{(\prime)}\)), chromomagnetic (\(O_{8}^{(\prime)}\)), semileptonic (\(O_{9}^{(\prime)}\) and \(O_{10}^{(\prime)}\)), pseudoscalar (\(O_{P}^{(\prime)}\)) and scalar (\(O_{S}^{(\prime)}\)) operators.Footnote 3 While the radiative b→qγ decays are sensitive only to the magnetic and chromomagnetic operators, semileptonic b→qℓ + ℓ − decays are, in principle, sensitive to all these operators.Footnote 4
In the SM, models with minimal flavour violation (MFV) [35, 36] and models with a flavour symmetry relating the first two generations [37], the Wilson coefficients appearing in Eq. (1) are equal for q=d or s and the ratio of amplitudes for b→d relative to b→s transitions is suppressed by |V td /V ts |. Due to this suppression, at the current level of experimental precision, constraints on decays with a b→d transition are much weaker than those on decays with a b→s transition for constraining \(C_{i}^{(\prime)}\). In the future, precise measurements of b→d transitions will allow powerful tests to be made of this universality which could be violated by NP.
The dependence on the Wilson coefficients, and the set of operators that can contribute, is different for different rare B decays. In order to put the strongest constraints on the Wilson coefficients and to determine the room left for NP, it is therefore desirable to perform a combined analysis of all the available data on rare leptonic, semileptonic and radiative B decays. A number of such analyses have recently been carried out for subsets of the Wilson coefficients [38–43].
The theoretically cleanest branching ratios probing the b→s transition are the inclusive decays B→X s γ and B→X s ℓ + ℓ −. In the former case, both the experimental measurement of the branching ratio and the SM expectation have uncertainties of about 7 % [44, 45]. In the latter case, semi-inclusive measurements at the B factories still have errors at the 30 % level [44]. At hadron colliders, the most promising modes to constrain NP are exclusive decays. In spite of the larger theory uncertainties on the branching fractions as compared to inclusive decays, the attainable experimental precision can lead to stringent constraints on the Wilson coefficients. Moreover, beyond simple branching fraction measurements, exclusive decays offer powerful probes of \(C_{7}^{(\prime)}\), \(C_{9}^{(\prime)}\) and \(C_{10}^{(\prime)}\) through angular and CP-violating observables. The exclusive decays most sensitive to NP in b→s transitions are B→K ∗ γ, \(B ^{0}_{ s } \rightarrow \mu^{+}\mu^{-}\), B→Kμ + μ − and B→K ∗ μ + μ −. These decays are discussed in more detail below.
2.3 Rare semileptonic B decays
The richest set of observables sensitive to NP are accessible through rare semileptonic decays of B mesons to a vector or pseudoscalar meson and a pair of leptons. In particular the angular distribution of B→K ∗ μ + μ − decays, discussed in Sect. 2.3.2, provides strong constraints on \(C_{7}^{(\prime)}\), \(C_{9}^{(\prime)}\) and \(C_{10}^{(\prime)}\).
2.3.1 Theoretical treatment of rare semileptonic B→Mℓ + ℓ − decays
The theoretical treatment of exclusive rare semileptonic decays of the type B→Mℓ + ℓ − is possible in two kinematic regimes for the meson M: large recoil (corresponding to low dilepton invariant mass squared, q 2) and small recoil (high q 2). Calculations are difficult outside these regimes, in particular in the q 2 region close to the narrow \(c \overline { c } \) resonances (the J/ψ and ψ(2S) states).
In the low q 2 region, these decays can be described by QCD-improved factorisation (QCDF) [46, 47] and the field theory formulation of soft-collinear effective theory (SCET) [48, 49]. The combined limit of a heavy b-quark and an energetic meson M, leads to the schematic form of the decay amplitude [50, 51]:

which is accurate to leading order in Λ QCD/m b and to all orders in α S . It factorises the calculation into process-independent non-perturbative quantities, B→M form factors, ξ, and light cone distribution amplitudes (LCDAs), ϕ B(M), of the heavy (light) mesons, and perturbatively calculable quantities, C and T which are known to \({ \mathcal{O} } ( \alpha _{S} ^{1})\) [50, 51]. Further, in the case that M is a vector V (pseudoscalar P), the seven (three) a priori independent B→V (B→P) form factors reduce to two (one) universal soft form factors ξ ⊥,∥ (ξ P ) in QCDF/SCET [52]. The factorisation formula Eq. (3) applies well in the dilepton mass range, 1<q 2<6 GeV2.Footnote 5
For B→K ∗ ℓ + ℓ −, the three K ∗ spin amplitudes, corresponding to longitudinal and transverse polarisations of the K ∗, are linear in the soft form factors ξ ⊥,∥,

at leading order in Λ QCD/m b and α S . The \(C_{\perp,\parallel}^{L,R}\) are combinations of the Wilson coefficients \(\mathcal{C}_{7,9,10}\) and the L and R indices refer to the chirality of the leptonic current. Symmetry breaking corrections to these relationships of order α S are known [50, 51]. This simplification of the amplitudes as linear combinations of \(C_{\perp,\parallel}^{L,R}\) and form factors, makes it possible to design a set of optimised observables in which any soft form factor dependence cancels out for all low dilepton masses q 2 at leading order in α S and Λ QCD/m b [53–55], as discussed below in Sect. 2.3.2.
Within the QCDF/SCET approach, a general, quantitative method to estimate the important Λ QCD/m b corrections to the heavy quark limit is missing. In semileptonic decays, a simple dimensional estimate of 10 % is often used, largely from matching of the soft form factors to the full-QCD form factors (see also Ref. [56]).
The high q 2 (low hadronic recoil) region, corresponds to dilepton invariant masses above the two narrow resonances of J/ψ and ψ(2S), with q 2≳(14–15) GeV2. In this region, broad \(c\overline{c}\)-resonances are treated using a local operator product expansion [57, 58]. The operator product expansion (OPE) predicts small sub-leading corrections which are suppressed by either (Λ QCD/m b )2 [58] or α S Λ QCD/m b [57] (depending on whether full QCD or subsequent matching on heavy quark effective theory in combination with form factor symmetries [59] is adopted). The sub-leading corrections to the amplitude have been estimated to be below 2 % [58] and those due to form factor relations are suppressed numerically by \(C_{7} / C_{9} \sim{ \mathcal{O} } (0.1)\). Moreover, duality violating effects have been estimated within a model of resonances and found to be at the level of 2 % of the rate, if sufficiently large bins in q 2 are chosen [58]. Consequently, like the low q 2 region, this region is theoretically well under control.
At high q 2 the heavy-to-light form factors are known only as extrapolations from light cone sum rules (LCSR) calculations at low q 2. Results based on lattice calculations are being derived [60], and may play an important role in the near future in reducing the form factor uncertainties.
2.3.2 Angular distribution of B 0→K ∗0 μ + μ − and \(B ^{0}_{ s } \rightarrow \phi \mu ^{+} \mu ^{-} \) decays
The physics opportunities of B→Vℓ + ℓ − (ℓ=e,μ, V=K ∗,ϕ,ρ) can be maximised through measurements of the angular distribution of the decay. Using the decay B→K ∗(→Kπ)ℓ + ℓ −, with K ∗ on the mass shell, as an example, the angular distribution has the differential form [61, 62]

with respect to q 2 and three decay angles θ l , θ K , and ϕ. For the B 0 (\(\overline{ B }{} ^{0} \)), θ l is the angle between the μ + (μ −) and the opposite of the B 0 (\(\overline{ B }{} ^{0} \)) direction in the dimuon rest frame, θ K is the angle between the kaon and the direction opposite to the B meson in the K ∗0 rest frame, and ϕ is the angle between the μ + μ − and K + π − decay planes in the B rest frame. There are twelve angular terms appearing in the distribution and it is a long-term experimental goal to measure the coefficient functions J i (q 2) associated with these twelve terms, from which all other B→K (∗) ℓ + ℓ − observables can be derived.
In the SM, with massless leptons, the J i depend on bilinear products of six complex K ∗ spin amplitudes \(A_{\bot,\|,0}^{L,R}\),Footnote 6 such as
The expressions for the eleven other J i terms are given for example in Refs. [54, 63]. Depending on the number of operators that are taken into account in the analysis, it is possible to relate some of the J i terms. The full derivation of these symmetries can be found in Ref. [54].
When combining B and \(\overline{ B }{} \) decays, it is possible to form both CP-averaged and CP-asymmetric quantities: \(S_{i} =(J_{i} + \bar {J_{i}})/[d(\varGamma+ \bar{\varGamma})/d q^{2} ]\) and \(A_{i} = (J_{i} - \bar {J_{i}})/[d(\varGamma+ \bar{\varGamma})/d q^{2} ]\), from the J i [53, 54, 62–66]. The terms J 5,6,8,9 in the angular distribution are CP-odd and, consequently, the associated CP-asymmetry, A 5,6,8,9 can be extracted from an untagged analysis (making it possible for example to measure A 5,6,8,9 in \(B ^{0}_{ s } \rightarrow \phi \mu ^{+} \mu ^{-} \) decays). Moreover, the terms J 7,8,9 are T-odd and avoid the usual suppression of the corresponding CP-asymmetries by small strong phases [64]. The decay B 0→K ∗0 μ + μ −, where the K ∗0 decays to K + π −, is self-tagging (the flavour of the initial B meson is determined from the decay products) and it is therefore possible to measure both the A i and S i for the twelve angular terms.
In addition, a measurement of the T-odd CP asymmetries, A 7, A 8 and A 9, which are zero in the SM and are not suppressed by small strong phases in the presence of NP, would be useful to constrain non-standard CP violation. This is particularly true since the direct CP asymmetry in the inclusive B→X s γ decay is plagued by sizeable long-distance contributions and is therefore not very useful as a constraint on NP [67].
2.3.3 Strategies for analysis of B 0→K ∗0 ℓ + ℓ − decays
In 1.0 fb−1 of integrated luminosity, LHCb has collected the world’s largest samples of B 0→K ∗0 μ + μ − (with K ∗0→K + π −) and \(B ^{0}_{ s } \rightarrow \phi \mu ^{+} \mu ^{-} \) decays, with around 900 and 80 signal candidates respectively reported in preliminary analyses [68, 69]. These candidates are however sub-divided into six q 2 bins, following the binning scheme used in previous experiments [70]. With the present statistics, the most populated q 2 bin contains ∼300B 0→K ∗0 μ + μ − candidates which is not sufficient to perform a full angular analysis. The analyses are instead simplified by integrating over two of the three angles or by applying a folding technique to the ϕ angle, ϕ→ϕ+π for ϕ<0, to cancel terms in the angular distribution.
In the case of massless leptons, one finds:

where \(\varGamma^{\prime}= \varGamma+ \bar{\varGamma}\). The observables appear linearly in the expressions. Experimentally, the fits are performed in bins of q 2 and the measured observables are rate averaged over the q 2 bin. The observables appearing in the angular projections are the fraction of longitudinal polarisation of the K ∗, F L, the lepton system forward–backward asymmetry, A FB, S 3 and A 9.
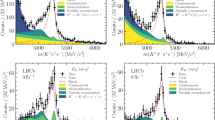
The differential branching ratio, A FB and F L have been measured by the B factories, CDF and LHCb [68, 70, 71]. The observable S 3 is related to the asymmetry between the parallel and perpendicular K ∗ spin amplitudesFootnote 7 is sensitive to right-handed operators (\(C_{7}^{\prime}\)) at low q 2, and is negligibly small in the SM. In the future, the decay B 0→K ∗0 e + e − could play an important role in constraining \(C_{7}^{\prime}\) through S 3 since it allows one to probe to smaller values of q 2 than the B 0→K ∗0 μ + μ − decay. First measurements have been performed by CDF and LHCb [68, 71].Footnote 8 The current experimental status of these B 0→K ∗0 μ + μ − angular observables at LHCb, the B factories and CDF is shown in Fig. 1. Improved measurements of these quantities would be useful to constrain the chirality-flipped Wilson coefficients (\(C_{7}^{\prime}\), \(C_{9}^{\prime}\) and \(C_{10}^{\prime}\)).
Summary of recent measurements of the angular observables (a) F L, (b) \(A_{\rm FB}\), (c) S 3 and (d) S 9 in B 0→K ∗0 μ + μ − decays at LHCb, CDF and the B factories [68]. Descriptions of these observables are provided in the text (see Eqs. (7), (8) and (9) and footnote 8). The theory predictions at low- and high-dimuon invariant masses are indicated by the coloured bands and are also described in detail in the text
Whilst \(A_{\rm FB}\) is not free from form-factor uncertainties at low q 2, the value of the dilepton invariant mass \(q^{2}_{0}\), for which the differential forward–backward asymmetry \(A_{\rm FB}\) vanishes, can be predicted in a clean way.Footnote 9 The zero crossing-point is highly sensitive to the ratio of the two Wilson coefficients C 7 and C 9. In particular the model-independent upper bound on |C 9| implies \(q_{0}^{2} > 1.7 ~\mathrm{GeV} ^{2}/c^{4}\), which improves to \(q_{0}^{2} > 2.6 ~\mathrm{GeV} ^{2}/c^{4}\), assuming the sign of C 7 to be SM-like [40]. At next-to-leading order one finds [51]:Footnote 10

where the first value is in good agreement with the recent preliminary result from LHCb of \(q_{0}^{2} = 4.9\,^{+1.3}_{-1.1} ~\mathrm{GeV} ^{2}/c^{4}\) [68] for the B 0→K ∗0 μ + μ − decay.
It is possible to access information from other terms in the angular distribution by integrating over one of the angles and making an appropriate folding of the remaining two angles. From ϕ and θ K only [73] it is possible to extract:

Analogously to \(A_{\rm FB}\), the zero-crossing point of S 5 has been shown to be theoretically clean. This observable is sensitive to the ratio of Wilson coefficients, \((C_{7} + C_{7}^{\prime})/(C_{9} + \hat{m}_{b} (C_{7} + C_{7}^{\prime}))\), and if measured would add complementary information to \(A_{\rm FB}\) and S 3 about new right-handed currents.
2.3.4 Theoretically clean observables in B 0→K ∗0 ℓ + ℓ − decays
By the time that 5 fb−1 of integrated luminosity is available at LHCb, it will be possible to exploit the complete NP sensitivity of the B→K ∗ ℓ + ℓ − both in the low- and high-q 2 regions, by performing a full angular analysis. The increasing size of the experimental samples makes it important to design optimised observables (by using specifically chosen combinations of the J i ) to reduce theoretical uncertainties. In the low q 2 region, the linear dependence of the amplitudes on the soft form factors allows for a complete cancellation of the hadronic uncertainties due to the form factors at leading order. This consequently increases the sensitivity to the structure of NP models [53, 54].
In the low q 2 region, the so-called transversity observables \(A_{T}^{(i)}\), i=2,3,4,5 are an example set of observables that are constructed such that the soft form factor dependence cancels out at leading order. They represent the complete set of angular observables and are chosen to be highly sensitive to new right-handed currents via \(C_{7}^{\prime}\) [53, 54]. A second, complete, set of optimised angular observables was constructed (also in the cases of non-vanishing lepton masses and in the presence of scalar operators) in Ref. [55]. Recently the effect of binning in q 2 on these observables has been considered [72]. In these sets of observables, the unknown \(\varLambda_{\rm QCD}/m_{b}\) corrections are estimated to be of order 10 % on the level of the spin amplitudes and represent the dominant source of theory uncertainty.
In general, the angular observables are shown to offer high sensitivity to NP in the Wilson coefficients of the operators O 7, O 9, and O 10 and of the chirally flipped operators [53, 54, 62, 64]. In particular, the observables S 3, A 9 and the CP-asymmetries A 7 and A 8 vanish at leading order in Λ QCD/m b and α S in the SM operator basis [64]. Importantly, this suppression is absent in extensions with non-vanishing chirality-flipped \({C}^{\prime}_{7,9,10}\), giving rise to contributions proportional to \(\operatorname{Re} (C_{i} {C_{j}^{*}}^{\prime})\) or \(\operatorname{Im} (C_{i} {C_{j}^{*}}^{\prime})\) and making these terms ideal probes of right-handed currents [53, 54, 62, 64]. CP asymmetries are small in the SM, because the only CP-violating phase affecting the decay is doubly Cabibbo-suppressed, but can be significantly enhanced by NP phases in C 9,10 and \(C^{\prime}_{9,10}\), which at present are poorly constrained. In a full angular analysis it can also be shown that CP-conserving observables provide indirect constraints on CP-violating NP contributions [54].
At large q 2, the dependence on the magnetic Wilson coefficients \(C_{7}^{(\prime)}\) is suppressed, allowing, in turn, a cleaner extraction of semileptonic coefficients (\(C_{9}^{(\prime)}\) and \(C_{10}^{(\prime)}\)). A set of transversity observables \(H_{T}^{(i)}\), i=1,2,3 have been designed to exploit the features of this kinematic region in order to have small hadronic uncertainties [65]. As a consequence of symmetry relations of the OPE [40, 65, 66, 74], at high q 2, combinations of the angular observables J i can be formed within the SM operator basis (i.e. with \(C_{i}^{\prime}=0\)), which depend:
-
only on short-distance quantities (e.g. \(H_{T}^{(2,3)}\));
-
only on long-distance quantities (\(F_{\rm L}\) and low q 2 optimised observables \(A_{T}^{(2,3)}\)).
Deviations from these relations are due to small sub-leading corrections at order (Λ QCD/m b )2 from the OPE.
In the SM operator basis it is interesting to note that \(A_{T}^{(2,3)}\), which are highly sensitive to short distance contributions (from \(C_{7}^{\prime}\)) at low q 2, instead become sensitive to long-distance quantities (the ratio of form factors) at high q 2. The extraction of form factor ratios is already possible with current data on S 3 (\(A_{T}^{(2)}\)) and \(F_{\rm L}\) and leads to a consistent picture between LCSR calculations, lattice calculations and experimental data [41, 74]. In the presence of chirality-flipped Wilson coefficients, these observables are no longer short-distance free, but are probes of right-handed currents [42]. At high q 2, the OPE framework predicts \(H_{T}^{(2)} = H_{T}^{(3)}\) and J 7=J 8=J 9=0. Any deviation from these relationships, would indicate a problem with the OPE and the theoretical predictions in the high q 2 region.
2.3.5 B +→K + μ + μ − and B +→K + e + e −
The branching fractions of B 0(+)→K 0(+) μ + μ − have been measured by BaBar, Belle and CDF [70, 75, 76]. In 1.0 fb−1 LHCb observes 1250 B +→K + μ + μ − decays [77], and in the future will dominate measurements of these processes.
Since the B→K transition does not receive contributions from an axial vector current, the primed Wilson coefficients enter the B 0(+)→K 0(+) μ + μ − observables always in conjunction with their unprimed counterparts as \((C_{i}+C_{i}^{\prime})\). This is in contrast to the B→K ∗ μ + μ − decay and therefore provides complementary constraints on the Wilson coefficients and their chirality-flipped counterparts.
An angular analysis of the μ + μ − pair in the B 0(+)→K 0(+) μ + μ − decay would allow the measurement of two further observables, the forward–backward asymmetry \(A_{\rm FB}\) and the so-called flat term F H [78]. The angular distribution of a B meson decaying to a pseudoscalar meson, P, and a pair of leptons involves just q 2 and a single angle in the dilepton system, θ l [78]

In the SM, the forward–backward asymmetry of the dilepton system is expected to be zero. Any non-zero forward–backward asymmetry would point to a contribution from new particles that extend the SM operator basis. Allowing for generic (pseudo-)scalar and tensor couplings, there is sizeable room for NP contributions in the range \(|A_{\rm FB}| \lesssim 15~\%\). The flat term, \(F_{\rm H}/2\), that appears with \(A_{\rm FB}\) in the angular distribution, is non-zero, but small (for ℓ=e,μ) in the SM. This term can also see large enhancements in models with (pseudo-)scalar and tensor couplings of up to \(F_{\rm H} \sim0.5\). Recent SM predictions at low- and high-q 2 can be seen in Refs. [40, 56, 78, 79]. The current experimental limits on \(\mathcal {B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) \) now disfavour large C S and C P , and if NP is present only in tensor operators then NP contributions are expected to be in the range \(|A_{\rm FB}| \lesssim 5~\% \) and \(F_{\rm H} \lesssim 0.2\).
In addition to \(A_{\rm FB}\), \(F_{\rm H}\) and the differential branching fraction of the decays, it is possible to probe the universality of lepton interactions by comparing the branching fraction of decays B 0(+)→K 0(+) ℓ + ℓ − with two different lepton flavours (e.g. electrons versus muons):

Lepton universality may be violated in extensions to the SM, such as R-parity-violating SUSY models.Footnote 11 In the SM, the ratio \(R_{K}^{\rm SM}\) is expected to be close to unity, \(R_{K}^{\rm SM} = 1 + \mathcal{O}(m_{\mu}^{2}/m_{B}^{2})\) [83].
It is also interesting to note that at high q 2 the differential decay rates and CP asymmetries of B 0(+)→K 0(+) ℓ + ℓ − and B 0(+)→K ∗0(+) ℓ + ℓ − (ℓ=e,μ) are correlated [40] and exhibit the same short-distance dependence (in the SM operator basis). Any deviation would point to a problem for the OPE used in the high q 2 region.
2.3.6 Rare semileptonic b→dℓ + ℓ − decays
Rare b→d radiative decay processes, such as B→ργ, have been observed at the B factories [84, 85]. In the 2011 data sample, the very rare decay B +→π + μ + μ − was observed at the LHCb experiment (see Fig. 2). This is a rare b→dℓ + ℓ − transition, which in the SM is suppressed by loop and CKM factors proportional to |V td /V ts |. In the 1.0 fb−1 data sample, LHCb observes \(25.3\,^{+6.7}_{-6.4}\) signal candidates corresponding to a branching fraction of \({ \mathcal{B} }( B ^{+} \rightarrow \pi ^{+} \mu ^{+} \mu ^{-} ) = (2.4\pm0.6\pm0.2) \times 10^{-8}\) [86]. This measurement is in good agreement with the SM prediction, i.e. consistent with no large NP contribution to b→dℓ + ℓ − processes and with the MFV hypothesis.
Invariant mass of selected B +→π + μ + μ − candidates in 1.0 fb−1 of integrated luminosity [86]. In the legend, “part. reco.” and “combinatorial” refer to partially reconstructed and combinatorial backgrounds respectively
The b→d transitions can show potentially larger CP- and isospin-violating effects than their b→s counterparts due to the different CKM hierarchy [51]. These studies would need the large statistics provided by the future LHCb upgrade. A 50 fb−1 data sample will also enable a precision measurement of the ratio of the branching fractions of B + meson decays to π + μ + μ − and K + μ + μ −. This ratio would enable a useful comparison of |V td /V ts | to be made using penguin processes (with form factors from lattice QCD) and box processes (using Δm s /Δm d and bag-parameters from lattice QCD) and provide a powerful test of MFV.
2.3.7 Isospin asymmetry of B 0(+)→K 0(+) μ + μ − and B 0(+)→K ∗0(+) μ + μ − decays
Analyses at hadron colliders (at LHCb and CDF) have mainly focused on decay modes with charged tracks in the final state. B meson decays involving K 0 mesons are experimentally much more challenging due to the long lifetimes of \(K ^{0}_{\mathrm{S}} \) and \(K ^{0}_{\mathrm{L}} \) mesons (the \(K ^{0}_{\mathrm{L}} \) is not reconstructable within LHCb). Nevertheless, LHCb has been able to select 60 B 0→K 0 μ + μ − decays, reconstructed as \(K ^{0}_{\mathrm{S}} \rightarrow \pi ^{+} \pi ^{-} \), and 80 B +→K ∗+ μ + μ −, reconstructed as \(K^{*+} \rightarrow K ^{0}_{\mathrm{S}} \pi ^{+} \), which are comparable in size to the samples that are available for these modes in the full data sets of the B factories. The isolation of these rare decay modes enables a measurement of the isospin asymmetry of B→K (∗) μ + μ − decays,
At leading order, isospin asymmetries (which involve the spectator quark) are expected to be zero in the SM. Isospin-breaking effects are subleading in \(\varLambda_{\rm QCD}/m_{b}\), and are difficult to estimate due to unknown power corrections. Nevertheless isospin-breaking effects are expected to be small and these observables may be useful in NP searches because they offer complementary information on specific Wilson coefficients [87].
The LHCb measurement of the K and K ∗ isospin asymmetries in bins of q 2 are shown in Fig. 3. For the K ∗ modes \(A_{\rm I}\) is compatible with the SM expectation that \(A_{\rm I}^{\rm SM} \simeq0\), but for the K +/K 0 modes, \(A_{\rm I}\) is seen to be negative at low- and high-q 2 [77]. This is consistent with what has been seen at previous experiments, but is inconsistent with the naïve expectation of \(A_{\rm I}^{\rm SM} \sim0\) at the 4σ level.Footnote 12 Such a discrepancy would be hard to explain in any model that is also consistent with other experimental results. Improved measurements are needed to clarify the situation.
(a) B→Kμ + μ − and (b) B→K ∗ μ + μ − isospin asymmetries in 1.0 fb−1 of data collected by the LHCb Collaboration in 2011 [77]
2.4 Radiative B decays
While the theoretical prediction of the branching ratio of the B→K ∗ γ decay is problematic due to large form factor uncertainties, the mixing-induced asymmetryFootnote 13 \(S_{K^{*}\gamma}\) provides an important constraint due to its sensitivity to the chirality-flipped magnetic Wilson coefficient \(C_{7}^{\prime}\). At leading order it vanishes for \(C_{7}^{\prime} \rightarrow 0\), so the SM prediction is tiny and experimental evidence for a large \(S_{K^{*}\gamma }\) would be a clear indication of NP effects through right-handed currents [89, 90]. Unfortunately it is experimentally very challenging to measure \(S_{K^{*}\gamma}\) in a hadronic environment, requiring both flavour tagging and the ability to reconstruct the K ∗0 in the decay mode K ∗0→K 0 π 0. However, the channel \(B ^{0}_{ s } \rightarrow \phi\gamma\), which is much more attractive experimentally, offers the same physics opportunities, with additional sensitivity due to the non-negligible width difference in the \(B ^{0}_{ s } \) system. Moreover, LHCb can study several other interesting radiative b-hadron decays.
2.4.1 Experimental status and outlook for rare radiative decays
In 1.0 fb−1 of integrated luminosity LHCb observes 5300 B 0→K ∗0 γ and \(690\ B ^{0}_{ s } \rightarrow \phi\gamma \) [17] candidates. These are the largest samples of rare radiative B 0 and \(B ^{0}_{ s } \) decays collected by a single experiment. The large sample of B 0→K ∗0 γ decays has enabled LHCb to make the world’s most precise measurement of the direct CP-asymmetry \(\mathcal{A}_{ \mathit{CP} } ( K ^{*} \gamma) = 0.8 \pm1.7 \pm0.9~\%\), compatible with zero as expected in the SM [17].
With larger data samples, it will be possible to add additional constraints on the \(C_{7}\mbox{--}C_{7}^{\prime}\) plane through measurements of b→sγ processes. These include results from time-dependent analysis of \(B ^{0}_{ s } \rightarrow \phi\gamma \) [91], as described in detail in the LHCb roadmap document [5]. Furthermore, the large \({ \varLambda }^{0}_{ b } \) production cross-section will allow for measurements of the photon polarisation through the decays \({ \varLambda }^{0}_{ b } \rightarrow { \varLambda }^{(*)}\gamma\) [92, 93]. In fact, the study of \({ \varLambda }^{0}_{ b } \rightarrow { \varLambda }\) transitions is quite attractive from the theoretical point of view, since the hadronic uncertainties are under good control [94–96]. However, because the \({ \varLambda }^{0}_{ b } \) has \(J^{P} = \frac{1}{2}^{+}\) and can be polarised at production, it will be important to measure first the \({ \varLambda }^{0}_{ b } \) polarisation.
B→VPγ decays with a photon, a vector and a pseudoscalar particle in the final state can also provide sensitivity to \(C_{7}^{\prime}\) [97–100]. The decays B→ϕKγ and B +→K 1(1270)+ γ have been previously observed at the B factories [101, 102] and large samples will be available for the first time at LHCb.
2.5 Leptonic B decays
2.5.1 \(B ^{0}_{ s } \rightarrow \mu ^{+} \mu ^{-} \) and B 0→μ + μ −
The decays \(B^{0}_{(s)} \rightarrow \mu ^{+} \mu ^{-} \) are a special case amongst the electroweak penguin processes, as they are chirality-suppressed in the SM and are most sensitive to scalar and pseudoscalar operators. The branching fraction of \(B^{0}_{(s)} \rightarrow \mu^{+}\mu^{-} \) can be expressed as [103–106]:

where q=s,d.
Within the SM, C S and C P are negligibly small and the dominant contribution of C 10 is helicity suppressed. The coefficients C i are the same for \(B ^{0}_{ s } \) and B 0 in any scenario (SM or NP) that obeys MFV. The large suppression of \(\mathcal{B}( B ^{0} \rightarrow \mu^{+}\mu^{-} ) \) with respect to \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) \) in MFV scenarios means that \(B ^{0}_{ s } \rightarrow \mu ^{+} \mu ^{-} \) is often of more interest than B 0→μ + μ − for NP searches. The ratio \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) / \mathcal{B}( B ^{0} \rightarrow \mu^{+}\mu^{-} ) \) is however a very useful probe of MFV.
The SM branching fraction depends on the exact values of the input parameters: \(f_{B_{q}}\), \(\tau_{B_{q}}\) and \(|V_{tb}V_{tq}^{*}|^{2}\). The \(B ^{0}_{ s } \) decay constant, \(f_{B_{s}}\), constitutes the main source of uncertainty on \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) \). There has been significant progress in theoretical calculations of this quantity in recent years. As of the year 2009 there were two unquenched lattice QCD calculations of \(f_{B_{s}}\), by the HPQCD [107] and FNAL/MILC [108] Collaborations, which, when averaged, gave the value \(f_{B_{s}}=238.8\pm9.5 ~\mathrm{MeV} \) [109]. The FNAL/MILC calculation was updated in 2010 [110], and again in 2011 to give \(f_{B_{s}}=242\pm9.5 ~\mathrm{MeV} \) [111, 112]. Also in 2011, the ETM Collaboration reported a value of \(f_{B_{s}}=232\pm 10 ~\mathrm{MeV} \) [113]. The HPQCD Collaboration presented in 2011 a result, \(f_{B_{s}}=227\pm 10 ~\mathrm{MeV} \) [114], which has recently been improved upon with an independent calculation that gives \(f_{B_{s}}=225\pm4 ~\mathrm{MeV} \) [115].
A weighted average of FNAL/MILC’11 [111], HPQCD’11 [114] and HPQCD’12 [115] was presented recently [109], giving \(f_{B_{s}}=227.6\pm5.0\mbox{~MeV}\). Using this value, the SM prediction for the branching ratio is [116]:
This value is taken as the nominal \(\mathcal {B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) _{\rm SM}\). Note that, in addition to \(f_{B_{s}}\), other sources of uncertainty are due to the \(B ^{0}_{ s } \) lifetime, the CKM matrix element |V ts |, the top mass m t , the electroweak corrections and scale variations. For a more detailed discussion of the SM prediction, see Ref. [117]. It is also possible to obtain predictions for \(\mathcal {B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) _{\rm SM}\) with reduced sensitivity to the value of \(f_{B_{s}}\) using input from either Δm s [118] or from a full CKM fit [119].
Likewise for \(f_{B_{d}}\), using the average of ETMC-11 (\(f_{B_{d}} = 195\pm12\mbox{~MeV}\)) [113], FNAL/MILC-11 (\(f_{B_{d}}=197 \pm 9\mbox{~MeV}\)) [111, 112] and HPQCD-12 (\(f_{B_{d}} =191\pm9\mbox{~MeV}\)) [115] results, which gives \(f_{B_{d}}=194 \pm10\mbox{~MeV}\) [120], the branching ratio of B 0→μ + μ − is:
NP models, especially those with an extended Higgs sector, can significantly enhance the \(B^{0}_{(s)} \rightarrow \mu^{+}\mu ^{-} \) branching fraction even in the presence of other existing constraints. In particular, it has been emphasised in many works [121–128] that the decay \(B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} \) is very sensitive to the presence of SUSY particles. At large tanβ—where tanβ is the ratio of vacuum expectation values of the Higgs doubletsFootnote 14—the SUSY contribution to this process is dominated by the exchange of neutral Higgs bosons, and both C S and C P can receive large contributions from scalar exchange.
In constrained SUSY models such as the CMSSM and NUHM1 (see Sect. 2.7), predictions can be made for \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) \) that take into account the existing constraints from the general purpose detectors. These models predict [129]:

The LHCb [13] (and CMS [130]) measurements of \(B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} \) have already excluded the upper range of these predictions.
Other NP models such as composite models (e.g. Littlest Higgs model with T-parity or Topcolour-assisted Technicolor), models with extra dimensions (e.g. Randall–Sundrum models) or models with fourth generation fermions can modify \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) \) [116, 131–135]. The NP contributions from these models usually arise via \((C_{10}\mbox{--}C^{\prime}_{10})\), and they are therefore correlated with the constraints from other b→sℓ + ℓ − processes, e.g. with \({ \mathcal{B} } ( B ^{+} \rightarrow K ^{+} \mu ^{+} \mu ^{-} )\) which depends on \((C_{10}+C^{\prime}_{10})\). The term \((C_{P} \mbox{--}C^{\prime}_{P})\) in the branching fraction adds coherently with the SM contribution from \((C_{10} \mbox{--}C^{\prime}_{10})\), and therefore can also destructively interfere. In such cases, if \((C_{S} \mbox{--}C^{\prime}_{S})\) remains small, \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) \) could be smaller than the SM prediction. A measurement of \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) \) well below the SM prediction would be a clear indication of NP and would be symptomatic of a model with a large non-degeneracy in the scalar sector (where \(C_{P}^{(\prime)}\) is enhanced but \(C_{S}^{(\prime)}\) is not). If only C 10 is modified, these constraints currently require the branching ratio to be above 1.1×10−10 [42]. In the presence of NP effects in both C 10 and \(C_{10}^{\prime}\), even stronger suppression is possible in principle.
At the beginning of 2012, the LHCb experiment set the world best limits on the \(\mathcal{B}( B^{0}_{(s)} \rightarrow \mu^{+}\mu^{-} ) \) [13].Footnote 15 At 95 % C.L.

Experimentally the measured branching fraction is the time-averaged (TA) branching fraction, which differs from the theoretical value because of the sizeable width difference between the heavy and light \(B ^{0}_{ s } \) mesons [136, 137].Footnote 16 In general,

where \(\mathcal{A}_{\Delta\varGamma} = +1\) in the SM and y s =ΔΓ s /(2Γ s )=0.088±0.014 [139]. Thus the experimental measurements have to be compared to the following SM prediction for the time-averaged branching fraction:

With 50 fb−1 of integrated luminosity, taken with an upgraded LHCb experiment, a precision better than 10 % can be achieved in \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu ^{-} ) \), and ∼35 % on the ratio \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) / \mathcal{B}( B ^{0} \rightarrow \mu^{+}\mu^{-} ) \). The dominant systematic uncertainty is likely to come from knowledge of the ratio of fragmentation fractions, f d /f s , which is currently known to a precision of 8 % from two independent determinations.Footnote 17 One method [140]Footnote 18 is based on hadronic B decays [142, 143], and relies on knowledge of the B (s)→D (s) form factors from lattice QCD calculations [144]. The other [145] uses semileptonic decays, exploiting the expected equality of the semileptonic widths [146, 147]. However, the two methods have a common, and dominant, uncertainty which originates from the measurement of \({ \mathcal{B} } ( D ^{+}_{ s } \rightarrow K ^{+} K ^{-} \pi ^{+} )\), which in the PDG is given to 4.9 % (coming from a single measurement from CLEO [148]). A new preliminary result from Belle has recently been presented [149]—inclusion of this measurement in the world average will improve the uncertainty on \({ \mathcal{B} } ( D ^{+}_{ s } \rightarrow K ^{+} K ^{+} \pi ^{+} )\) to ∼3.5 %. With the samples available with the LHCb upgrade, it will be possible to go beyond branching fraction measurements and study the effective lifetime of \(B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} \), that provides additional sensitivity to NP [136].
In Sect. 2.7, the NP implications of the current measurements of \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) \) and the interplay with other observables, including results from direct searches, are discussed for a selection of specific NP models. In general, the strong experimental constraints on \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu ^{-} ) \) [13, 130, 150, 151] largely preclude any visible effects from scalar or pseudoscalar operators in other b→sℓ + ℓ − decays.Footnote 19
2.5.2 \(B ^{0}_{ s } \rightarrow \tau ^{+} \tau ^{-} \)
The leptonic decay \(B ^{0}_{ s } \rightarrow \tau ^{+} \tau ^{-} \) provides interesting information on the interaction of the third generation quarks and leptons. In many NP models, contributions to third generation quarks/leptons can be dramatically enhanced with respect to the first and second generation. This is true in, for example, scalar and pseudoscalar interactions in supersymmetric scenarios, for large values of tanβ. Interestingly, there is also an interplay between b→sτ + τ − processes and the lifetime difference \(\varGamma_{12}^{s}\) in \(B ^{0}_{ s } \) mixing (see Sect. 3). The correlation of both processes has been discussed model-independently [152, 153] and in specific scenarios, such as leptoquarks [154, 155] or Z′ models [156–158]. There are presently no experimental limits on \(B ^{0}_{ s } \rightarrow \tau ^{+} \tau ^{-} \), however the interplay with \(\varGamma_{12}^{s}\), and the latest LHCb-measurement of Γ d /Γ s would imply a limit of \({ \mathcal{B} } ( B ^{0}_{ s } \rightarrow \tau ^{+} \tau ^{-} ) < 3~\%\) at 90 % C.L. Any improvement on this limit, which might be in reach with the existing LHCb data set, would yield strong constraints on models that couple strongly to third generation leptons. A large enhancement in b→sτ + τ − could help to understand the anomaly observed by the D0 experiment in their measurement of the inclusive dimuon asymmetry [159] and could also reduce the tension that exists with other mixing observables [152, 153].
The study of \(B ^{0}_{ s } \rightarrow \tau ^{+} \tau ^{-} \) at LHCb presents significant challenges. The τ leptons must be reconstructed in decays that involve at least one missing neutrino. Although it has been demonstrated that the decay Z→τ + τ − can be separated from background at LHCb, using both leptonic and hadronic decay modes [160], at lower energies the backgrounds from semileptonic heavy flavour decays cause the use of the leptonic decay modes to be disfavoured. However, in the case that “three-prong” τ decays are used, the vertices can be reconstructed from the three hadron tracks. The analysis can then benefit from the excellent vertexing capability of LHCb, and, due to the finite lifetime of the τ lepton, there are in principle sufficient kinematic constraints to reconstruct the decay. Work is in progress to understand how effectively the different potential background sources can be suppressed, and hence how sensitive LHCb can be in this channel.
2.6 Model-independent constraints
Figure 4, taken from Ref. [42], shows the current constraints on the NP contributions to the Wilson coefficients (defined in Eq. (1)) \(C_{7}^{(\prime)}\), \(C_{9}^{(\prime)}\) and \(C_{10}^{(\prime)}\), varying only one coefficient at a time. The experimental constraints included here are: the branching fractions of B→X s γ, B→X s ℓ + ℓ −, B→Kμ + μ − and \(B ^{0}_{ s } \rightarrow \mu^{+}\mu^{-}\), the mixing-induced asymmetries in B→K ∗ γ and b→sγ and the branching fraction and angular observables in B→K ∗ μ + μ −. One can make the following observations:
-
At 95 % C.L., all Wilson coefficients are compatible with their SM values.
-
For the coefficients present in the SM, i.e. C 7, C 9 and C 10, the constraints on the imaginary part are looser than on the real part.
-
For the Wilson coefficients \(C_{10}^{(\prime)}\), the constraint on \({ \mathcal{B} } ( B ^{0}_{ s } \rightarrow \mu ^{+} \mu ^{-} )\) is starting to become competitive with the constraints from the angular analysis of B→K (∗) μ + μ −.
-
The constraints on \(C_{9}^{\prime}\) and \(C_{10}^{\prime}\) from B→Kμ + μ − and B→K ∗ μ + μ − are complementary and lead to a more constrained region, and better agreement with the SM, than with B→K ∗ μ + μ − alone.
-
A second allowed region in the C 7–\(C_{7}^{\prime}\) plane characterised by large positive contributions to both coefficients, which was found previously to be allowed e.g. in Refs. [38, 39], is now disfavoured at 95 % C.L. by the new B→K ∗ μ + μ − data, in particular the measurements of the forward–backward asymmetry from LHCb.
The second point above can be understood from the fact that for the branching fractions and CP-averaged angular observables which give the strongest constraints, only NP contributions aligned in phase with the SM can interfere with the SM contributions. As a consequence, NP with non-standard CP violation is in fact constrained more weakly than NP where CP violation stems only from the CKM phase. This highlights the need for improved measurements of CP asymmetries directly sensitive to non-standard phases.Footnote 20
Individual 2σ constraints in the complex planes of Wilson coefficients, coming from B→X s ℓ + ℓ − (brown), B→X s γ (yellow), A CP (b→sγ) (orange), B→K ∗ γ (purple), B→K ∗ μ + μ − (green), B→Kμ + μ − (blue) and \(B ^{0}_{ s } \rightarrow \mu^{+}\mu^{-}\) (grey), as well as combined 1 and 2σ constraints (red) [42]
Significant improvements of these constraints—or first hints for physics beyond the SM—can be obtained in the future by both improved measurements of the observables discussed above and by improvements on the theoretical side. From the theory side, there is scope for improving the estimates of the hadronic form factors from lattice calculations, which will reduce the dominant source of uncertainty on the exclusive decays. On the experimental side there are a large number of theoretically clean observables that can be extracted with a full angular analysis of B 0→K ∗0 μ + μ −, as discussed in Sect. 2.3.2.
2.7 Interplay with direct searches and model-dependent constraints
The search for SUSY is the main focus of NP searches in ATLAS and CMS. Although the results so far have not revealed a positive signal, they have put strong constraints on constrained SUSY scenarios. The understanding of the parameters of SUSY models also depends on other measurements, such as the anomalous dipole moment of the muon, limits from direct dark matter searches, measurements of the dark matter relic density and various B physics observables. As discussed in Sect. 2.5, the rare decay channels studied in LHCb, such as \(B^{0}_{(s)} \rightarrow \mu^{+}\mu^{-} \), provide stringent tests of SUSY. In addition, the decays B→K (∗) μ + μ − provide many complementary observables which are sensitive to different sectors of the theory. In this section, the implications of the current LHCb measurements in different SUSY models are explained, both in constrained scenarios and in a more general case.
First consider the constrained minimal supersymmetric standard model (CMSSM) and a model with non-universal Higgs masses (NUHM1). The CMSSM is characterised by the set of parameters {m 0,m 1/2,A 0,tanβ,sgn(μ)} and invokes unification boundary conditions at a very high scale \(m_{\rm GUT}\) where the universal mass parameters are specified. The NUHM1 relaxes the universality condition for the Higgs bosons which are decoupled from the other scalars, adding then one extra parameter compared to the CMSSM.
Figure 5 shows the plane (m 1/2,m 0) for large and moderate values of tanβ in the CMSSM where, for comparison, direct search limits from CMS are superimposed. It can be seen that, at large tanβ, the constraints from flavour observables—in particular \(\mathcal {B}( B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} ) \)—are more constraining than those from direct searches. As soon as one goes down to smaller values of tanβ, the flavour observables start to lose importance compared to direct searches. On the other hand, B→K ∗ μ + μ − related observables, in particular the forward–backward asymmetry, lose less sensitivity and play a complementary role. To see better the effect of \(A_{\rm FB}(B \rightarrow K^{*} \mu^{+}\mu^{-})\) at low q 2,Footnote 21 the \(A_{\rm FB}\) zero-crossing point \(q_{0}^{2}\) and \(F_{\rm L}(B \rightarrow K^{*} \mu^{+}\mu^{-})\), in Fig. 6 their SUSY spread is shown as a function of the lightest stop mass for tanβ=50 [120]. As can be seen from the figure, small stop masses are excluded and in particular \(m_{\tilde{t}_{1}} \lesssim 800\mbox{~GeV}\) is disfavoured by \(A_{\rm FB}\) at the 2σ level.
Constraints from flavour observables in CMSSM in the plane (m 1/2,m 0) with A 0=0, for tanβ=(left) 50 and (right)30 [162], using SuperIso [106, 163]. The black line corresponds to the CMS exclusion limit with 1.1 fb−1 of data [164] and the red line to the CMS exclusion limit with 4.4 fb−1 of data [165]
SUSY spread of (top left) \(A_{\rm FB}(B \rightarrow K^{*}\mu^{+}\mu^{-})\) at low q 2, (top right) \(q^{2}_{0}(B \rightarrow K^{*}\mu^{+}\mu ^{-})\) and (bottom) \(F_{\rm L}(B \rightarrow K^{*}\mu^{+}\mu ^{-})\) as a function of the lightest stop mass, for A 0=0 and tanβ=50 [120], using SuperIso [106, 163]. The solid red lines correspond to the preliminary LHCb central value with 1.0 fb−1 [68], while the dashed and dotted lines represent the 1 and 2σ bounds respectively, including both theoretical and experimental errors
The impact of the recent B→K (∗) l + l − decay data on SUSY models beyond MFV (NMFV) with moderate tanβ is shown in Fig. 7. The largest effect stems from left-right mixing between top and charm super-partners. Due to the Z-penguin dominance of the SUSY-flavour contributions the constraints are most effective for the Wilson coefficient C 10 (see Sect. 2.2). SUSY effects in C 10 are reduced from about 50 % to 16 % (28 %) at 68 (95) % C.L. by the recent data on the rare decay B 0→K ∗0 μ + μ − [167]. The constraints are relevant to flavour models based on radiative flavour violation (see, e.g., Ref. [169]), and exclude solutions to the flavour problem with flavour generation in the up-sector and sub-TeV spectra. The flavour constraints are stronger for lighter stops, hence there is an immediate interplay with direct searches.
SUSY spread in NMFV-models [167]. The light (dark) grey shaded areas are the 95 % (68 %) confidence limit (C.L.) bounds from B→K (∗) l + l − data [40]. The red dotted line denotes the Z-penguin correlation \(C^{Z-\rm p}_{10}/C^{Z-\rm p}_{9} =1/(4 \sin^{2} \theta_{W}-1)\). The SM point \((C_{9}^{\rm SM},C_{10}^{\rm SM})\) is marked by the red dot
Figure 8 shows the (M A , tanβ) plane from fits of the CMSSM and NUHM1 parameter space to the current data from SUSY and Higgs searches in ATLAS and CMS, as well as dark matter relic density [129, 170]. The study in constrained MSSM scenarios is illustrative but not representative of the full MSSM. The strong constraints provided by the current data in the CMSSM are not necessarily reproduced in more general scenarios. To go beyond the constrained scenarios, consider the phenomenological MSSM (pMSSM) [171]. This model is the most general CP- and R-parity-conserving MSSM, assuming MFV at the weak scale and the absence of FCNCs at tree level. It contains 19 free parameters: 10 sfermion masses, 3 gaugino masses, 3 trilinear couplings and 3 Higgs masses.
Impact of the latest \(B^{0}_{ s } \rightarrow \mu^{+}\mu ^{-} \) limits on the (M A , tanβ) plane in the (left) CMSSM and (right) NUHM1 [168]. In each case, the full global fit is represented by an open green star and dashed blue and red lines for the 68 and 95 % C.L. contours, whilst the fits to the incomplete data sets are represented by closed stars and solid contours
To study the impact of the \(B^{0}_{ s } \rightarrow \mu^{+}\mu ^{-} \) results on the pMSSM, the parameter space is scanned and for each point in the space the consistency of the model with experimental bounds is tested [172]. The left panel of Fig. 9 shows the density of points as a function of M A before and after applying the combined 2010 LHCb and CMS \(B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} \) limit (1.1×10−8 at 95 % C.L. [173]), as well as the projection for a SM-like measurement with an overall 20 % theoretical and experimental uncertainty. As can be seen the density of the allowed pMSSM points is reduced by a factor of 3, in the case of a SM-like measurement. The right panel shows the same distribution in the (M A , tanβ) plane. Similar to the CMSSM case, the region with large tanβ and small M A is most affected by the experimental constraints.
Distribution of pMSSM points after the \(B ^{0}_{ s } \rightarrow\mu^{+} \mu^{-}\) constraint projected on the M A (left) and (M A ,tanβ) plane (right) for all accepted pMSSM points (medium grey), points not excluded by the combination of the 2010 LHCb and CMS analyses (dark grey) and the projection for the points compatible with the measurement of the SM expected branching fractions with a 20 % total uncertainty (light grey) [172]
The interplay with Higgs boson searches can also be very illuminating as any viable model point has to be in agreement with all the direct and indirect limits. As an example, if a scalar Higgs boson is confirmed at ∼125 GeV,Footnote 22 the MSSM scenarios in which the excess would correspond to the heaviest CP-even Higgs (as opposed to the lightest Higgs) are ruled out by the \(B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} \) limit, since they would lead to a too light pseudoscalar Higgs.
It is clear that with more precise measurements a large part of the supersymmetric parameter space could be disfavoured. In particular the large tanβ region is strongly affected by \(B^{0}_{ s } \rightarrow \mu^{+}\mu^{-} \) as can be seen in Fig. 5. Also, a measurement of \({ \mathcal{B} } ( B^{0}_{ s } \rightarrow \mu^{+}\mu ^{-} )\) lower than the SM prediction would rule out a large variety of supersymmetric models. In addition, B→K ∗ μ + μ − observables play a complementary role especially for smaller tanβ values. With reduced theoretical and experimental errors, the exclusion bounds in Figs. 6 and 7 for example would shrink leading to important consequences for SUSY parameters.
2.8 Rare charm decays
So far the focus of this chapter has been on rare B decays, but the charm sector also provides excellent probes for NP in the form of very rare decays. Unlike the B decays described in the previous sections, the smallness of the d, s and b quark masses makes the Glashow–Iliopoulos–Maiani (GIM) cancellation in loop processes very effective. Branching ratios governed by FCNC are hence not expected to exceed \(\mathcal{O}(10^{-10})\) in the SM. These processes can then receive contributions from NP scenarios which can be several orders of magnitude larger than the SM expectation.
2.8.1 Search for D 0→μ + μ −
The branching fraction of the D 0→μ + μ − decay is dominated in the SM by the long distance contributions due to the two photon intermediate state, D 0→γγ. The experimental upper limit on the two photon mode can be combined with theoretical predictions to constrain \(\mathcal{B}(D^{0}\rightarrow \mu^{+}\mu^{-})\) in the framework of the SM: \(\mathcal{B}(D^{0}\rightarrow \mu^{+}\mu^{-})<6\times10^{-11} \) at 90 % C.L. [176]. Particular NP models where this decay is enhanced include supersymmetric models with R-parity violation (RPV), which provides tree-level contributions that would enhance the branching fraction. In such models, the branching fraction would be related to the D 0–\(\overline{ D }{} ^{0} \) mixing parameters. Once the experimental constraints on the mixing parameters are taken into account, the corresponding tree-level couplings can still give rise to \(\mathcal{B}(D^{0}\rightarrow\mu^{+}\mu^{-})\) of up to \(\mathcal {O}(10^{-9})\) [177].
Preliminary results from a search for these rare decays have been performed by the LHCb Collaboration [178]. The upper limit obtained with 0.9 fb−1 of data taken in 2011 is:

This upper limit on the branching fraction, already an improvement of an order of magnitude on previous results, is expected to improve down to 5×10−9 by the end of the first data-taking phase of the LHCb experiment.
2.8.2 Search for \(D^{+}_{(s)}\rightarrow h^{+} \mu^{+}\mu^{-}\) and D 0→hh′μ + μ −
The \(D^{+}_{(s)}\rightarrow h^{+} \mu^{+}\mu^{-}\) decay rate is dominated by long distance contributions from tree-level \(D^{+}_{(s)}\rightarrow h^{+} V\) decays, where V is a light resonance (V=ϕ,ρ,ω). The long-distance contributions have an effective branching fraction (with V→μ + μ −) above 10−6 in the SM. Large deviations in the total decay rate due to NP are therefore unlikely. However, the regions of the dimuon mass spectrum far from these resonances are interesting probes. Here, the SM contribution stems only from FCNC processes, that should yield no partial branching ratio above 10−11 [179]. NP contributions could enhance the branching fraction away from the resonances by several orders of magnitude: e.g. in the RPV model mentioned above, or in models involving a fourth quark generation [179, 180].
The LHCb experiment is well-suited to search for \(D^{+}_{(s)}\rightarrow h^{\mp} \mu^{+}\mu^{\pm}\) decays. The long distance contributions can be used to normalise the decays searched for at high and low dimuon mass: their decay rate will be measured relative to that of \(D^{+}_{(s)}\rightarrow\pi^{+} \phi(\mu ^{+}\mu^{-})\). These resonant decays have a clean experimental signature and their final state only differs from the signal in the kinematic distributions, which helps to reduce the systematic uncertainties. The sensitivity of the LHCb experiment can be estimated by comparing the yields of \(D^{+}_{(s)}\rightarrow\pi^{+} \phi(\mu^{+}\mu^{-})\) decays observed in LHCb with those obtained by the D0 experiment, which established the best limit on these modes so far [181]. With an integrated luminosity corresponding to 1.0 fb−1, upper limits on the D + (\(D ^{+}_{ s } \)) modes are expected close to 10−8 (10−7) at 90 % C.L.
In analogy to the B sector, there is a wealth of observables potentially available in four-body rare decays of D mesons. In the decays D 0→hh′μ + μ − (with h (′)=K or π), forward–backward asymmetries or asymmetries based on T-odd quantities could reveal NP effects [179, 182, 183]. Clearly the first challenge is to observe the decays which, depending on their branching fractions, may be possible with the 2011 data set. However, the 50 fb−1 collected by the upgraded LHCb detector will be necessary to exploit the full set of observables in these modes.
2.9 Rare kaon decays
The cross-section for \(K ^{0}_{\mathrm{S}} \) production at the LHC is such that \({\sim}10^{12} K ^{0}_{\mathrm{S}} \rightarrow \pi ^{+}\pi^{-}\) would be reconstructed and selected in LHCb with a fully efficient trigger. This provides a good opportunity to search for rare \(K ^{0}_{\mathrm{S}} \) decays in channels with high trigger efficiency, in particular \(K ^{0}_{\mathrm{S}} \rightarrow \mu ^{+}\mu^{-} \).
The decay \(K ^{0}_{\mathrm{S}} \rightarrow \mu^{+}\mu^{-} \) is a flavour-changing neutral current that has not yet been observed. This decay is strongly suppressed in the SM, with an expected branching fraction of [184, 185]
while the current experimental upper limit is 3.2×10−7 at 90 % C.L. [186]. The study of \(K ^{0}_{\mathrm{S}} \rightarrow \mu^{+}\mu^{-} \) has been suggested as a possible way to look for new light scalars [184], and indeed NP contributions up to one order of magnitude above the SM expectation are allowed [185]. Enhancements above 10−10 are less likely. Bounds on \(\mathcal{B}( K ^{0}_{\mathrm{S}} \rightarrow \mu ^{+}\mu^{-} ) \) close to 10−11 could be useful to discriminate among NP scenarios if other modes, such as \(K^{+} \rightarrow \pi ^{+}\nu\bar{\nu}\), indicated a non-standard enhancement of the s→dl l transition. First results from LHCb, \(\mathcal{B}( K ^{0}_{\mathrm{S}} \rightarrow \mu ^{+}\mu^{-} ) < 9 \times10^{-9}\) at 90 % C.L. [187], have significantly better sensitivity than the existing results. With improved triggers on low mass dimuons, LHCb could reach branching fractions of \(\mathcal{O}(10^{-11})\) or below with the luminosity of the upgrade. Decays of \(K ^{0}_{\mathrm{L}} \) mesons into charged tracks can also be reconstructed, but with much less (∼1 %) efficiency compared to a similar decay coming from a \(K ^{0}_{\mathrm{S}} \) meson. This is due to the long distance of flight of the \(K ^{0}_{\mathrm{L}} \) state, which tends to decay outside the tracking system.
2.10 Lepton flavour and lepton number violation
The experimental observation of neutrino oscillations provided the first signature of lepton flavour violation (LFV). The consequent addition of mass terms for the neutrinos in the SM implies LFV also in the charged sector, but with branching fractions smaller than 10−40. NP could significantly enhance the rates but, despite steadily improving experimental sensitivity, charged lepton flavour violating (cLFV) processes like μ −→e − γ, μ–N→e–N, μ −→e + e − e −, τ −→ℓ − γ and τ −→ℓ + ℓ − ℓ − (with ℓ −=e −,μ −) have not been observed. Numerous theories beyond the SM predict larger LFV effects in τ − decays than μ − decays, with branching fractions within experimental reach [188]. An observation of cLFV would thus be a clear sign for NP, while lowering the experimental upper limit will help to further constrain theories [189].
Another approach to search for NP is via lepton number violation (LNV). Decays with LNV are sensitive to Majorana neutrino masses—their discovery would answer the long-standing question of whether neutrinos are Dirac or Majorana particles. The strongest constraints on minimal models that introduce neutrino masses come from neutrinoless double beta decay processes, but searches in heavy flavour decays provide competitive and complementary limits in models with extended neutrino sectors.
In this section, LFV and LNV decays of τ leptons and B mesons with only charged tracks in the final state are discussed.
2.10.1 Lepton flavour violation
The neutrinoless decay τ −→μ + μ − μ − is a particularly sensitive mode in which to search for LFV at LHCb as the inclusive τ − production cross-section at the LHC is large (∼80 μb, coming mainly from \(D ^{+}_{ s } \) decaysFootnote 23) and muon final states provide clean signatures in the detector. This decay is experimentally favoured with respect to the decays τ −→μ − γ and τ −→e + e − e − due to the considerably better particle identification of the muons and better possibilities for background discrimination. LHCb has reported preliminary results from a search for the decay τ −→μ + μ − μ − using 1.0 fb−1 of data [191]. The upper limit on the branching fraction was found to be \({ \mathcal{B} }(\tau^{-} \rightarrow \mu^{+}\mu^{-}\mu^{-})<7.8~(6.3) \times10^{-8}\) at 95 % (90 %) C.L, to be compared with the current best experimental upper limit from Belle: \({ \mathcal{B} }(\tau^{-} \rightarrow \mu^{+}\mu^{-}\mu^{-})<2.1 \times10^{-8}\) at 90 % C.L. As the data sample increases this limit is expected to scale as the square root of the available statistics, with possible further reduction depending on improvements in the analysis. The large integrated luminosity that will be collected by the upgraded experiment will provide sensitivity corresponding to an upper limit of a few times 10−9. Searches will also be conducted in modes such as \(\tau^{-} \rightarrow \bar{p} \mu^{+} \mu^{-}\) or τ −→ϕμ −, where the existing limits are much weaker, and low background contamination is expected in the data sample.Footnote 24
The pseudoscalar meson decays probe transitions of the type q→q′ℓℓ′ and hence are particularly sensitive to leptoquark-models and thus provide complementarity to leptonic decay LFV processes [193, 194]. For the LHCb experiment, both decays from D and B mesons are accessible. Sensitivity studies for the decays \(B^{0}_{(s)} \rightarrow e^{-} \mu^{+}\) and D 0→e − μ + are ongoing. Present estimates indicate that LHCb will be able to match the sensitivity of the existing limits from the B factories and CDF in the near future.
2.10.2 Lepton number violation
In lepton number violating B and D meson decays a search can be made for Majorana neutrinos with a mass of \(\mathcal{O}(1 ~\mathrm {GeV} )\). These indirect searches are performed by analysing the production of same sign charged leptons in D or B decays such as \(D ^{+}_{ s } \rightarrow \pi ^{-} \mu ^{+} \mu ^{+} \) or B +→π − μ + μ + [28, 195]. These same sign dileptonic decays can only occur via exchange of heavy Majorana neutrinos. Resonant production may be possible if the heavy neutrino is kinematically accessible, which could put the rates of these decays within reach of the future LHCb luminosity. Non-observation of these LNV processes, together with low energy neutrino data, would lead to better constraints for neutrino masses and mixing parameters in models with extended neutrino sectors.
Using 0.4 fb−1 of integrated luminosity from LHCb, limits have been set on the branching fraction of \(B^{+} \rightarrow D_{(s)}^{-} \mu ^{+} \mu ^{+} \) decays at the level of a few times 10−7 and on B +→π − μ + μ + at the level of 1×10−8 [196, 197]. These branching fraction limits imply a limit on, for example, the coupling |V μ4| between ν μ and a Majorana neutrino with a mass in the range 1<m N <4 GeV/c 2 of |V μ4|2<5×10−5.
2.11 Search for NP in other rare decays
Many extensions of the SM predict weakly interacting particles with masses from a few MeV to a few GeV [198–202] and there are some experimental hints for these particles from astrophysical and collider experiments [203, 204]. For example, the HyperCP Collaboration has reported an excess of Σ +→pμ + μ − events with dimuon invariant masses around 214 MeV/c 2 [205]. These decays are consistent with the decay Σ +→pX with the subsequent decay X→μ + μ −. Phenomenologically, X can be interpreted as a pseudoscalar or axial-vector particle with lifetimes for the pseudoscalar case estimated to be about 10−14 s [206–208]. Such a particle could, for example, be interpreted as a pseudoscalar sgoldstino [207] or a light pseudoscalar Higgs boson [209].
The LHCb experiment has recorded the world’s largest data sample of B and D mesons which provides a unique opportunity to search for these light particles. Preliminary results from a search for decays of \(B^{0}_{(s)} \rightarrow \mu^{+} \mu^{-} \mu^{+} \mu^{-} \) have been reported [210]. Such decays could be mediated by sgoldstino pair production [211]. No excess has been found and limits of 1.3 and 0.5×10−8 at 95 % C.L. have been set for the \(B ^{0}_{ s } \) and B 0 modes respectively. The analysis can naturally be extended to D 0→μ + μ − μ + μ − decays, as well as \(B^{0}_{(s)} \rightarrow V^{0} \mu^{+} \mu^{-}\) (V 0=K (∗)0,ρ 0,ϕ), where the dimuon mass spectrum can be searched for any resonant structure. Such an analysis has been performed by the Belle Collaboration [212]. With the larger data sample and flexible trigger of the LHCb upgrade, it will be possible to exploit several new approaches to search for exotic particles produced in decays of heavy flavoured hadrons (see, e.g. Ref. [213]).
3 CP violation in the B system
3.1 Introduction
CP violation, i.e. violation of the combined symmetry of charge conjugation and parity, is one of three necessary conditions to generate a baryon asymmetry in the Universe [214]. Understanding the origin and mechanism of CP violation is a key question in physics. In the SM, CP violation is fully described by the CKM mechanism [20, 21]. While this paradigm has been successful in explaining the current experimental data, it is known to generate insufficient CP violation to explain the observed baryon asymmetry of the Universe. Therefore, additional sources of CP violation are required. Many extensions of the SM naturally contain new sources of CP violation.
The b hadron systems provide excellent laboratories to search for new sources of CP violation, since new particles beyond the SM may enter loop-mediated processes such as b→q FCNC transitions with q=s or d, leading to discrepancies between measurements of CP asymmetries and their SM expectations. Two types of b→q FCNC transitions are of special interest: neutral B meson mixing (ΔB=2) processes, and loop-mediated B decay (ΔB=1) processes.
The LHCb experiment exploits the large number of b hadrons, including the particularly interesting \(B ^{0}_{ s } \) mesons, produced in proton–proton collisions at the LHC to search for CP-violating NP effects. Section 3.2 provides a review of the status and prospects in the area of searches for NP in \(B^{0}_{(s)}\) mixing, in particular through measurements of the mixing phases ϕ d(s) and the semileptonic asymmetries \(a_{\rm sl}^{d(s)}\). The LHCb efforts to search for NP in hadronic b→s penguin decays, such as \(B ^{0}_{ s } \rightarrow \phi\phi\), are discussed in Sect. 3.3. Section 3.4 describes the LHCb programme to measure the angle γ of the CKM unitarity triangle (UT) in decay processes described only by tree amplitudes, such as B ±→DK ±, B 0→DK ∗0 and \(B ^{0}_{ s } \rightarrow D ^{\mp}_{ s } K ^{\pm} \). These measurements allow precise tests of the SM description of quark-mixing via global fits to the parameters of the CKM matrix, as well as direct comparisons with alternative determinations of γ in decay processes involving loop diagrams, such as \(B ^{0}_{ s } \rightarrow K ^{+} K ^{-} \). At the end of each section, a brief summary of the most promising measurements with the upgraded LHCb detector and their expected/projected sensitivities is provided.
3.2 \(B^{0}_{(s)}\) mixing measurements
3.2.1 \(B^{0}_{(s)}\)–\(\overline{B}^{0}_{(s)}\) mixing observables
The effective Hamiltonian of the \(B^{0}_{q}\)–\(\overline{B}^{0}_{q}\) (q=d,s) system can be written as
where \(M^{q}_{11}=M^{q}_{22}\) and \(\varGamma^{q}_{11}=\varGamma^{q}_{22}\) hold under the assumption of CPT invariance. The off-diagonal elements \(M^{q}_{12}\) and \(\varGamma^{q}_{12}\) are responsible for \(B^{0}_{q}\)–\(\overline{B}^{0}_{q}\) mixing phenomena. The “dispersive” part \(M^{q}_{12}\) corresponds to virtual ΔB=2 transitions dominated by heavy internal particles (top quarks in the SM) while the “absorptive” part \(\varGamma^{q}_{12}\) arises from on-shell transitions due to decay modes common to \(B^{0}_{q}\) and \(\overline{B}^{0}_{q}\) mesons. Diagonalising the Hamiltonian matrix leads to the two mass eigenstates \(B^{q}_{\rm H,L}\) (\({\rm H}\) and \({\rm L}\) denote heavy and light, respectively), with mass \(M^{q}_{\rm H,L}\) and decay width \(\varGamma^{q}_{\rm H,L}\), being linear combinations of flavour eigenstates with complex coefficientsFootnote 25 p and q that satisfy |p|2+|q|2=1,
The magnitudes of \(M^{q}_{12}\) and \(\varGamma^{q}_{12}\) and their phase difference are physical observables and can be determined from measurements of the following quantities (for more details see, e.g., Refs. [215, 216]):
-
the mass difference between the heavy and light mass eigenstates
$$ \Delta m_q \equiv M^q_{\rm H}- M^q_{\rm L} \approx2\bigl|M^q_{12}\bigr| \biggl( 1-\frac{|\varGamma^q_{12}|^2}{8|M^q_{12}|^2}\sin^2\phi_{12}^q \biggr); $$(25)where \(\phi_{12}^{q} = \arg(-M^{q}_{12}/\varGamma^{q}_{12})\) is convention-independent;
-
the decay width difference between the light and heavy mass eigenstates
 (26)
(26) -
the flavour-specific asymmetryFootnote 26
 (27)
(27)
The correction terms in Eqs. (25) and (26) proportional to \(\sin^{2}\phi_{12}^{q}\) are tiny. In addition, the ratio of q and p can be written
and hence in both B 0 and \(B ^{0}_{ s } \) systems one obtains, to a good approximation, a convention-dependent expression (for an unobservable quantity) \(\arg(-q/p) \approx-\arg(M_{12}^{q})\). Since B–\(\overline{B}\) mixing is dominated by the box diagram with internal top quarks, this leads to an expression in terms of CKM matrix elements \(\arg(-q/p) = 2\arg(V^{*}_{tb}V_{tq})\).
Further information can be obtained by measuring the phase difference between the amplitude for a direct decay to a final state f and the amplitude for decay after oscillation. In the case that the decay is dominated by \(b \rightarrow c \bar{c}s\) tree amplitudes, and where f is a CP eigenstate f with eigenvalue η f ,Footnote 27 this phase difference is denoted as
where A f and \({\bar{A}}_{f}\) are the decay amplitudes of B→f and \({\overline{B}} \rightarrow f\), respectively. In the absence of direct CP violation \(\bar{A}_{f} / A_{f} = \eta_{f}\). With these approximations, the CP-violating phases in B mixing give the unitarity triangle angles, ϕ d ≈2β and ϕ s ≈−2β s ,Footnote 28 where the angles are defined as [44]
Clearly, if there is NP in \(M_{12}^{q}\) or in the decay amplitudes, the measured value of ϕ q can differ from the true value of (−)2β (s). Similarly, NP in either \(M_{12}^{q}\) or \(\varGamma_{12}^{q}\) can make the observed value of \(a_{\rm sl}^{q}\) differ from its SM prediction. Note, however, that even within the SM, there is a difference between ϕ q and \(\phi_{12}^{q}\) [217]. Nonetheless, the notations ϕ d(s) and β (s) are usually used interchangeably.
The ϕ s notation has been used in the LHCb measurements of the CP-violating phase in \(B ^{0}_{ s } \) mixing, using J/ψϕ [10, 139] and J/ψf 0(980) [218, 219] final states. By using the same notation for different decays, an assumption that \(\arg(\bar{A}_{f}/A_{f})\) is common for different final states is being made. This corresponds to an assumption that the penguin contributions to these decays are negligible. Although this is reasonable with the current precision, as the measurements improve it will be necessary to remove such assumptions–several methods to test the contributions of penguin amplitudes are discussed below. These include measuring ϕ q with different decay processes governed by different quark-level transitions. Previous experiments have used the notation \(2\beta^{\rm eff}\) in particular for measurements based on \(b \rightarrow q\bar{q}s\) (q=u,d,s) transitions; for symmetry the notation \(2\beta^{\rm eff}_{s}\) is used in corresponding cases in the \(B ^{0}_{ s } \) system, although the cancellation of the mixing and decay phases in \(B ^{0}_{ s } \) decays governed by \(b \rightarrow q\bar {q}s\) amplitudes is expected to lead to a vanishing CP violation effect (within small theoretical uncertainties).
In the SM, the mixing observables can be predicted using CKM parameters from a global fit to other observables and hadronic parameters (decay constants and bag parameters) from lattice QCD calculation. These predictions can be compared to their direct measurements to test the SM and search for NP in neutral B mixing.
3.2.2 Current experimental status and outlook
The current measurements and SM predictions for the mixing observables are summarised in Table 1.
The HFAG average of the \(B ^{0}_{ s } \) mass difference Δm s in Table 1 is based on measurements performed at CDF [228] and LHCb [226, 229]. It is dominated by the preliminary LHCb result obtained using 0.34 fb−1 of data [226], which is also given in Table 1. These are all consistent with the SM prediction. Improving the precision of the SM prediction is desirable to further constrain NP in \(M^{s}_{12}\), and requires improving the accuracy of lattice QCD evaluations of the decay constant and bag parameter (see Ref. [216] and references therein).
The observables ϕ s and ΔΓ s have been determined simultaneously from \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) decays using time-dependent flavour tagged angular analyses [230, 231]. The first LHCb tagged analysis using 0.34 fb−1 of data [10] already provided a significant constraint on ϕ s and led to the first direct evidence for a non-zero value of ΔΓ s . LHCb has also determined the sign of ΔΓ s to be positive at 4.7σ confidence level [232] by exploiting the interference between the K + K − S-wave and P-wave amplitudes in the ϕ(1020) mass region [233]. This resolved the two-fold ambiguity in the value of ϕ s for the first time. LHCb has made a preliminary update of the \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) analysis using the full data sample of 1.0 fb−1 collected in 2011 [139]. The results from this analysis,

are shown in Fig. 10 (left), and are in good agreement with the SM expectations.
(Left) Preliminary LHCb measurement of ϕ s and ΔΓ s from \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) decays using 1.0 fb−1 [139]. (Right) HFAG 2012 combination of ϕ s and ΔΓ s results, where the 1σ confidence region is shown for each experiment and the combined result [44]. Note the different scales
LHCb has also studied the decay \(B ^{0}_{ s } \rightarrow { J / \psi } \pi ^{+} \pi^{-}\). This decay process is expected to proceed dominantly via \(b \rightarrow c \overline{ c } s\) (the \(s\bar{s}\) produced in the decay rescatters to π + π − through either a resonance such as f 0(980) or a nonresonant process). Therefore, these events can be used to measure ϕ s . The π + π − mass range 775–1550 MeV shown in Fig. 11 (left) is used for the measurement. In contrast to \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\), no angular analysis is needed to disentangle the CP eigenstates, since the final state is determined to be dominantly CP-odd in this mass range [234]. On the other hand, ΔΓ s cannot be determined in this decay channel alone.Footnote 29 Using as input the value of ΔΓ s obtained from \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\), the measurement from the analysis of \(B ^{0}_{ s } \rightarrow { J / \psi } \pi ^{+} \pi^{-}\) with 1.0 fb−1 is [219]
Figure 11 (right) shows the log-likelihood scan for the ϕ s parameter for the \(B ^{0}_{ s } \rightarrow { J / \psi } \pi ^{+} \pi^{-}\) analysis. The latest HFAG average in Table 1 combines the LHCb results with the \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) analysis results from CDF using 9.6 fb−1 [237] and D0 using 8.0 fb−1 [238]. The LHCb result dominates the combination, which is in good agreement with the SM predictions, as seen in Fig. 10 (right).Footnote 30
(Left) π + π − mass distribution of selected \(B ^{0}_{ s } \rightarrow { J / \psi } \pi^{+} \pi^{-}\) candidates and range used for the ϕ s measurement. (Right) log-likelihood difference as a function ϕ s [219]
The LHCb \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) and \(B ^{0}_{ s } \rightarrow { J / \psi } \pi ^{+} \pi^{-}\) analyses discussed above only used opposite side flavour tagging [239, 240]. Future updates of these analyses will gain in sensitivity by also using the same side kaon tagging information, which so far has been used in a preliminary determination of Δm s [226, 241]. Currently, the systematic uncertainty on ϕ s is dominated by imperfect knowledge of the background, angular acceptance effects and by neglecting potential contributions of direct CP violation. All of these uncertainties are expected to be reduced with more detailed understanding and some improvements in the analysis. Therefore it is expected that the determination of ϕ s will remain limited by statistical uncertainties, even with the data samples available after the upgrade of the LHCb detector. In addition to \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) and \(B ^{0}_{ s } \rightarrow { J / \psi } \pi ^{+} \pi^{-}\), other \(b \rightarrow c \overline{ c } s\) decay modes of \(B ^{0}_{ s } \) mesons, such as J/ψη, J/ψη′ [242] and \(D _{s}^{+} D _{s}^{-}\) [243] will be investigated. These decays have been measured at LHCb [244, 245].
The SM prediction ϕ s =−0.036±0.002 rad could receive a small correction from doubly CKM-suppressed penguin contributions in the decay. The value of this correction is not precisely known, and may depend on the decay mode. Moreover, NP in the \(b \rightarrow c \overline{ c } s\) decay may also affect the results. Although such effects are already constrained by results from B + and B 0 decays, NP in the decay amplitudes can lead to polarisation-dependent mixing-induced CP asymmetries and triple product asymmetries in \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) [246]. Such effects will be searched for in future analyses.
The flavour-specific asymmetries provide important complementary constraints on ΔB=2 processes. The D0 collaboration has performed a direct measurement of \(a^{s}_{\rm sl}\) in semileptonic \(B ^{0}_{ s } \) decays [227], which is only weakly constraining.Footnote 31 However, a measurement of the inclusive same-sign dimuon asymmetry provides better precision, and shows evidence of a large deviation from its SM prediction [159]. The inclusive measurement is sensitive to a linear combination of the flavour-specific asymmetries, \(A_{\rm SL}^{b} = C_{d} a_{\rm sl}^{d} + C_{s} a_{\rm sl}^{s}\), where C q depend on the production fractions and mixing probabilities, and are determined to be C d =0.594±0.022, C s =0.406±0.022 [159].Footnote 32 As discussed in Sect. 3.2.3, the D0 \(A_{\rm SL}^{b}\) result is in tension with other ΔB=2 observables. Improved measurements of \(a^{s}_{\rm sl}\) and \(a^{d}_{\rm sl}\) from LHCb are needed to solve this puzzle.
In LHCb, \(a^{s}_{\rm sl}\) can be determined from the asymmetry between the time-integrated untagged decay rates of \(B ^{0}_{ s } \) decays to \(D_{s}^{+}\mu^{-} X\) and \(D_{s}^{-}\mu^{+} X\), with \(D ^{\pm}_{ s } \rightarrow \phi \pi ^{\pm} \), ϕ→K + K − (or with the full \(D ^{\pm}_{ s } \rightarrow K ^{+} K ^{-} \pi ^{\pm} \) Dalitz plot). Detector- and trigger-induced asymmetries can be calibrated in control channels, and the fact that data is taken with both magnet dipole polarities can be used as a handle to reduce systematic uncertainties. The effect of \(B ^{0}_{ s } \) production asymmetry is cancelled due to the fast oscillation, so the asymmetry in the yields of \(D ^{+}_{ s } \mu^{-} X\) and \(D ^{-}_{ s } \mu ^{+} X\) decays is trivially related to \(a^{s}_{\rm sl}\). A first preliminary LHCb result on \(a^{s}_{\rm sl}\), based on 1.0 fb−1, has been reported at ICHEP 2012, and is the most precise measurement of this quantity to date [248],
It will also be possible to measure \(a^{d}_{\rm sl}\) using D + μ − X final states with D +→K − π + π +. In this case extra care must be taken to calibrate the difference between K + and K − detection efficiencies and an independent measurement of the B 0 production asymmetry is needed as input. Moreover, the CP-symmetric background from charged B decays is significant and must be accurately subtracted.
In the B 0 system, Δm d and sinϕ d (i.e. sin2β) have been measured precisely by the B factories [44]. The measurements of ΔΓ d and \(a^{d}_{\rm sl}\) are consistent with their SM predictions, but their uncertainties are at least an order of magnitude larger than those of the predictions. Hence a large improvement in precision is needed to test the SM using these observables. In the B 0 sector there has been for some time a tension between the measurements of sin2β [44] and the branching ratio \({ \mathcal{B} } (B^{+} \rightarrow \tau^{+} \nu)\) [249, 250], as shown in Fig. 12,Footnote 33 and discussed in Sect. 3.2.4. This motivates improved measurements of sin2β and improved understanding of the possible effects of penguin contributions to this observable.
Comparison of direct and indirect determinations of sinϕ d ≡sin2β vs. \({ \mathcal{B} } (B^{+} \rightarrow \tau^{+} \nu)\), from Ref. [252]
LHCb has already presented first results on Δm d [229, 253] and sin2β [254]. The Δm d result is the world’s most precise single measurement of this quantity, while the sensitivity on sin2β will be competitive with the B factory results using the data sample that will be collected by the end of 2012. LHCb can also search for enhancements in the value of ΔΓ d above the tiny value expected in the SM, e.g. by comparing the effective lifetimes of \(B ^{0} \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \) and B 0→J/ψK ∗0 [255]. Significantly improving the precisions of the B 0 mixing observables is an important goal of the LHCb upgrade, as will be discussed in Sect. 3.2.6.
The SM predictions of b-hadron lifetimes and ΔΓ q are all obtained within the framework of the heavy quark expansion. LHCb is actively working on measurements of b-hadron lifetimes and lifetime ratios, which will be used to test these predictions. The knowledge obtained from this work will allow to improve the SM predictions of ΔΓ q for the purpose of searching for NP. Furthermore, a more precise measurement of the ratio of \(B ^{0}_{ s } \) to B 0 lifetimes could either support or strongly constrain the existence of NP in \(\varGamma^{s}_{12}\) [152, 153, 216, 220, 256].
3.2.3 Model independent constraints on new physics in B mixing
Neutral B q meson mixing is described in terms of the three parameters \(|M_{12}^{q}|\), \(|\varGamma_{12}^{q}|\) and \(\phi_{q} = \mbox{arg} (- M_{12}^{q} / \varGamma_{12}^{q})\) for each of the two systems q=d,s. In the context of model-independent analyses, the NP contributions can be parametrised in the form of two complex quantities Δ q and Λ q [153, 257]

i.e., 4 real degrees of freedom. The observables which depend on these parameters are the mass and decay width differences and flavour-specific CP-asymmetries. They can be expressed in terms of the SM predictions and NP parameters as


up to corrections suppressed by tiny \((\varGamma_{12}^{q}/M_{12}^{q})^{2}\). Note that the expressions of Eqs. (35) and (36) depend only on the difference \((\phi_{q}^{\Delta}- \phi _{q}^{\varLambda})\). The SM predictions of Δm q , ΔΓ q and \(a_{\rm sl}^{q}\) can be found in Table 1 and for \(\phi^{q}_{12}\) [220]

The values of Δm q have been precisely measured, giving rather strong constraints on |Δ q | which are limited by the knowledge of hadronic matrix elements. The new ΔΓ s measurement of LHCb starts to provide useful constraints. As discussed above, the CP-asymmetries \(a_{\rm sl}^{q}\) are currently rather weakly constrained.
Further information can be extracted from the mixing-induced CP-asymmetries in \(B ^{0} \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \) and \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) decays

where δ d and δ s denote shifts of ϕ d and ϕ s induced by either SM penguin diagrams or NP contributions in the decay process. In the SM ϕ d and ϕ s are related to the angles β and β s of the according unitarity triangles. When short-distance NP contributions are introduced, ϕ q depends on the phase \(\phi_{q}^{\Delta}\) of \(M_{12}^{q}\), whereas the phase \(\phi _{q}^{\varLambda}\) of \(\varGamma_{12}^{q}\) does not enter. The SM penguin pollution to δ q is expected to be negligible for the current precision of ϕ q , and is discussed in detail in Sect. 3.2.5. Beyond the SM, NP can contribute to δ q in principle in both the tree \(b \rightarrow c \overline{ c } s\) decay and the penguin process. However, in the model-independent analysis described here, NP contributions in the \(b \rightarrow c \overline{ c } s\) decay are neglected and any observed deviation from the SM will be interpreted as effects of NP in neutral B meson mixing. When δ q is neglected, Eqs. (35), (36) and (38) allow to determine the NP parameters |Δ q |, \(\phi_{q}^{\Delta}\), |Λ q | and \(\phi_{q}^{\varLambda}\).
The assumption of NP in \(M_{12}^{q}\) only, or equivalently in ΔB=2 processes only, implies that there is no NP in ΔB=1 processes which contribute to the absorptive part \(\varGamma_{12}^{q}\). Consequently, NP can only decrease ΔΓ q (since \(\cos(\phi_{12}^{q,{\rm SM}})\) is maximal, see Eq. (35)) with respect to the SM [231, 258]. This scenario has been studied in extensions of the CKM fit of the SM which includes ΔB=2 measurements to constrain the CKM elements V tq [256, 259], in combination with many other flavour-changing processes. Including LHCb measurements [139, 229]Footnote 34 the SM point Δ d =Δ s =1 is disfavoured by 2.4σ [256] (prior to the LHCb results being available, a similar analysis gave a discrepancy of 3.6σ driven mainly by the anomalous dimuon asymmetry [259]). The analysis gives Δ s consistent with the SM, within large uncertainties, whereas the more precise data in the B 0 system hint at a deviation in Δ d (see Fig. 13). Moreover, NP effects up to 30–40 % are still allowed in both systems at the 3σ level. It should be noted, that the large deviations in the B 0 sector are not only due to \(A_{\rm SL}^{b}\), but also due to the tension between sinϕ d and \({ \mathcal{B} } (B^{+} \rightarrow \tau^{+} \nu)\).
Model-independent fit [256] in the scenario that NP affects \(M^{q}_{12}\) separately. The coloured areas represent regions with C.L.<68.3 % for the individual constraints. The red area shows the region with C.L.<68.3 % for the combined fit, with the two additional contours delimiting the regions with C.L.<95.45 % and C.L.<99.73 %
NP contributions to the absorptive part \(\varGamma_{12}^{q}\) of B mixing can enter through ΔB=1 decays b→qX with light degrees of freedom X of total mass below m B . In some particular models such contributions can arise [154, 260] and interfere constructively or destructively with the SM contribution. The recent measurements of ΔΓ q and of \(A_{\rm SL}^{b}\) revived interest in this possibility. Model-independent analyses have confirmed that the \(A_{\rm SL}^{b}\) measurement cannot be accommodated within the SM [261, 262]. A model-independent fit assuming NP in both \(M_{12}^{q}\) and \(\varGamma _{12}^{q}\) has been considered in the framework of an extended CKM fit [256]. In this case, the experimental data can be accommodated, and the \(B ^{0}_{ s } \) system remains rather SM-like, but large NP contributions in the B 0 system are required.
Model-independent analyses based on Eq. (34) are restricted to a particular set of observables, mainly those with ΔB=2, since correlations with ΔB=1 measurements are difficult to quantify. Either additional assumptions on the nature of X in b→qX or explicit NP models will permit better exploitation of the wealth of future experimental information. In fact, such analyses have found it difficult to accommodate the hypothesis of large NP in \(\varGamma^{q}_{12}\) with current ΔB=1 measurements, therefore NP in \(\varGamma^{q}_{12}\) seems unlikely to provide a full explanation of the measured value of \(A_{\rm SL}^{b}\). In the case of \(X = f\bar{f}\), the ΔB=1 operators \(b \rightarrow (d,s) f\bar{f}\) (f=q or ℓ) are strongly constrained [152], with the exception of \(b \rightarrow s c \overline{ c } \) and b→sτ + τ −. Currently, only a weak upper bound on \({ \mathcal {B} } ( B ^{+} \rightarrow K ^{+} \tau ^{+} \tau ^{-} ) \lesssim 3.3 \times 10^{-3}\) at 90 % C.L. [263] exists whereas other decays \(B ^{0}_{ s } \rightarrow \tau ^{+} \tau ^{-} \), B→X s τ + τ − might be indirectly constrained with additional assumptions (see also the discussion in Sect. 2.5.2). As an example, the improved LHCb measurement of \(\tau_{ B ^{0}_{ s } }/\tau _{ B ^{0} }\) allowed the derivation of a stronger bound on \({ \mathcal{B} } ( B ^{0}_{ s } \rightarrow \tau ^{+} \tau ^{-} )\). Still, a model-independent analysis of the complete set of b→sτ + τ − operators does not allow for deviations larger than 35 % from the SM in \(\varGamma_{12}^{s}\) [153], which is much too small to resolve the tension with \(A_{\rm SL}^{b}\). For b→dτ + τ − operators there exists a stronger constraint \({ \mathcal{B} } ( B ^{0} \rightarrow \tau ^{+} \tau ^{-} ) \lesssim 4 \times 10^{-3}\) and even smaller NP effects are expected in \(\varGamma_{12}^{d}\). Other proposed solutions such as the existence of new light spin-0 [264] or spin-1 [265] X states could be seriously challenged by improved measurements of quantities, such as ratios of lifetimes, which are theoretically under good control [220].
In summary, NP contributions to |Δ q | are already quite constrained due to Δm q measurements and theoretical progress is required in order to advance. Although the phases \(\phi_{q}^{\Delta}\) are constrained by the recent LHCb measurement of ϕ s , and B factory measurements of ϕ d , there is a mild tension with the SM in model-independent fits of ΔB=2 measurements [153, 256, 261, 262], especially when allowing for NP in \(\varGamma_{12}^{q}\). On the other hand, NP effects in \(\varGamma_{12}^{q}\) are expected to be limited when constraints from ΔB=1 observables are taken into account. Independent improved measurements of \(a_{\rm sl}^{q}\) are needed in order to resolve the nature of the current discrepancies between the ΔB=2 observables with their SM expectations and other observables entering global CKM fits. Further, improved measurements of Γ q and ΔΓ q , as well as of control channels, are needed to constrain NP in \(\varGamma^{q}_{12}\).
3.2.4 CKM unitarity fits in SM and beyond
This section presents the results of the unitarity triangle (UT) analysis performed by two groups: UTfit [266] and CKMfitter [252].Footnote 35 The main aim of the UT analysis is the determination of the values of the CKM parameters, by comparing experimental measurements and theoretical predictions for several observables. The popular Wolfenstein parametrisation allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle, λ, with the other three parameters being A, \(\bar {\rho}\) and \(\bar{\eta}\). Assuming the validity of the SM, one can perform a fit to the available measurements. LHCb results already make important contributions to the constraints on γ and Δm s . With more statistics, LHCb results are expected to impact on other CKM fit inputs, including α and sin2β. It is important to note the crucial role of lattice QCD calculations as input to the CKM fits. For example, the parameters \(f_{B_{s}}\sqrt{B_{B_{s}}}\) and ξ enter the constraints on Δm s and Δm d /Δm s . At the end of 2011, the precision of the calculations was at the level of 5.4 % and 2.6 %, respectively [109]. The necessary further progress to obtain the full benefit of the LHCb measurements appears to be in hand exploiting algorithmic advances as well as ever increasing computing power for the lattice calculations.
The overall quality of the fit can be judged using the projection of the likelihoods on the \(\{\bar{\rho}, \bar{\eta}\}\) plane. This projection is shown in Fig. 14. The fit can also be made removing one of the inputs, giving a prediction for the removed parameter, which then can be compared to the experimental value. The results of this study are presented in Table 2. Both groups find a tension between \({ \mathcal{B} } (B \rightarrow \tau\nu)\) and sin2β, as can be seen in Fig. 12. (As discussed in Sect. 3.2.2 this tension will be reduced once the latest Belle result on \({ \mathcal {B} } ( B ^{+} \rightarrow \tau ^{+} \nu_{\tau})\) [251] is included in the fits.) Improved measurements of sin2β can shed further light on this problem.
In order to estimate the origin of the tensions, the UTfit and CKMfitter groups have performed analyses including model-independent NP contributions to neutral meson mixing processes (see Refs. [256, 270] for details). The NP effects are introduced through the real valued C and ϕ parameters (\(A_{\rm NP} = C e^{i\phi} A_{\rm SM}\)) in case of UTfit and the complex valued Δ parameter (\(A_{\rm NP} = \Delta A_{\rm SM}\)) for CKMfitter. The parameters are added separately for the \(B ^{0}_{ s } \) and B 0 sectors. In the absence of NP, the expected values are C=1, ϕ=0∘, and Δ=1. For the B 0 sector the fits return C=0.94±0.14 and ϕ=(−3.6±3.7)∘, and \(\Delta= (0.823\,^{+0.143}_{-0.095})+i(-0.199\,^{+0.062}_{-0.048})\). The results for both groups show some disagreement with the SM, driven by tensions in the input parameters mentioned above. In the \(B ^{0}_{ s } \) sector, on the other hand, the situation is much closer to the SM than before the LHCb measurements were available: C=1.02±0.10 and ϕ=(−1.1±2.2)∘, and \(\Delta= (0.92\,^{+0.13}_{-0.08})+i(0.00 \pm0.10)\).
The results of the studies by both groups point to the absence of big NP effects in ΔB=2 processes. Nevertheless there is still significant room for NP in mixing in both B 0 and \(B ^{0}_{ s } \) systems. More precise results, in particular from LHCb, can enable more careful studies. Besides providing null tests of the SM hypothesis, improved ϕ s and \(a_{\rm sl}^{s}\) measurements are crucial to quantity effects of NP in mixing. In addition a precise γ determination is essential, not only for a SM global consistency test, but also to fix the apex of the UT in the extended fits.
3.2.5 Penguin pollution in \(b \rightarrow c \overline { c } s \) decays
In addition to the very clear experimental signature, precise determination of the B 0 and \(B ^{0}_{ s } \) mixing phases is possible due to the fact that in the “golden modes”, \(B ^{0} \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \) and \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\), explicit calculation of the relevant matrix elements can be avoided, once subleading doubly Cabibbo-suppressed and loop-suppressed terms are assumed to vanish [271]. Estimates yield corrections of the order O(10−3) only [272–274]; it is however notoriously difficult to actually calculate the relevant matrix elements, and non-perturbative enhancements cannot be excluded. Given the future experimental precision for these and related modes, a critical reconsideration of this assumption is mandatory.
The main problem lies in the fact that once the assumption of negligible penguin contributions is dropped, the evaluation of hadronic matrix elements again becomes necessary, which still does not seem feasible to an acceptable precision for the decays in question. To avoid explicit calculation, symmetry relations can be used, exploiting either flavour SU(3) or U-spin symmetry [275–281]. Without taking into account any QCD evaluation and only using control channels to estimate the size of the penguin amplitude, the analyses in Refs. [278, 281] still allow a phase shift of up to a few degrees for ϕ d , which would correspond to a very large non-perturbative enhancement of the penguin size. In Ref. [278] a negative sign is preferred which (slightly) reduces the tension in the unitarity triangle fit shown in Fig. 12. The reason for the large allowed range of the shift of ϕ d is due to the limited precision to which the corresponding control channels B 0→J/ψπ 0 and \(B ^{0}_{ s } \rightarrow { J / \psi } K ^{0} \), which are Cabibbo-suppressed compared to the golden modes, are known. For ϕ s , an analogous analysis [277] cannot yet constrain the penguin contribution, due to the lack of a B→J/ψV control channel data for \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\). However, in principle the effects in the B→J/ψV modes are expected to be of the same order of magnitude as in the B→J/ψP modes. The control channel \(B ^{0}_{ s } \rightarrow { J / \psi } K^{*0}\) has already been observed at CDF [282] and LHCb [283], and work is ongoing to measure its decay rate, polarisations and direct CP asymmetries. This will enable the first direct constraint on the shift of ϕ s due to penguin contributions in the decay \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\).Footnote 36 For \(B ^{0}_{ s } \rightarrow { J / \psi } f_{0}(980)\) there is an additional complication due to the unknown hadronic structure of the f 0(980) [235].
In addition to insufficient data, there are, at present, theoretical aspects limiting the precision of this method at present, the most important of which is the violation of SU(3) symmetry. Regarding the B 0 mixing phase, a full SU(3) analysis can be performed [285] (instead of using only one control channel) to be able to model-independently include SU(3) breaking. The inclusion of SU(3)-breaking contributions is important: their neglect can lead to an overestimation of the subleading effects. Including recent data for two of the relevant modes [286, 287], the analysis shows that the data are at the moment actually compatible with vanishing penguin contributions, with SU(3)-breaking contributions of the order 20 %. Including the penguin contributions, an upper limit on the shift of the mixing-induced CP asymmetry ΔS=sinϕ d −sin2β is derived: |ΔS|≲0.01, with a negative sign for ΔS slightly preferred.Footnote 37 This is the most stringent limit available, despite the more general treatment of SU(3) breaking. In this analysis still some (conservatively chosen) theoretical inputs are needed to exclude fine-tuned solutions: SU(3)-breaking effects have been restricted to at most 40 % for a few parameters which are not well determined by the fit and also have only small influence on the CP violation observables, and the penguin matrix elements are constrained to be at most 50 % of the leading contributions. Importantly, these theory inputs can be replaced by experimental measurements, namely of the CP asymmetries in the decay \(B ^{0}_{ s } \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \), the decay rate of which has already been measured at LHCb [287] after its observation at CDF [282]. Furthermore, data from all the corresponding modes (i.e. B d,u,s →J/ψP, with light pseudoscalar meson P=π,η (′) or K) can be used to determine the shift more precisely, i.e. the related uncertainty is not irreducible, but can be reduced with coming data.
Turning to the second golden mode, \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\), in general, the absolute shift is not expected to be larger than in the B 0 case. At the moment the data are not yet available to make a comparable analysis. While the penguin decay mode \(B ^{0}_{ s } \rightarrow \phi\phi\) is not related by symmetry with \(B ^{0}_{ s } \rightarrow { J / \psi } \phi \), comparing their decay rates indicates that the penguin contributions are small, and there are no huge enhancements to be expected for the penguin matrix elements in question.
Nonetheless, a quantitative analysis will ultimately be warranted here as well. In principle, these methods can be adapted to extract the \(B ^{0}_{ s } \) mixing phase including penguin contributions and model-independent SU(3) breaking, thereby improving the method proposed in Ref. [277]. The corresponding partners of the golden mode \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) are all the decays B u,d,s →J/ψV, with the light vector mesons V=K ∗, ρ, ϕ or ω. However, the complete analysis requires results on the polarisation fractions and CP asymmetries for each of these final states, and for some of them the experimental signature is quite challenging. In addition, the ϕ meson is a superposition of octet and singlet, therefore the “control channels” involving K ∗ and ρ are not as simply related as in the case with a pseudoscalar meson, but require the usage of nonet symmetry, whose precision has to be investigated in turn.
Nevertheless, significant progress can be expected. Several B→J/ψV modes, including \(B^{0}_{(s)} \rightarrow { J / \psi } K^{*0}\) [283], are being studied at LHCb. While measurements of the modes involving b→d transitions are expected to exhibit rather large uncertainties at first, the advantage of the proposed method is the long “lever arm” due to the relative enhancement ∼1/λ 2 in the control channels, so that even moderate precision will be very helpful.
3.2.6 Future prospects with LHCb upgrade
Current measurements of ϕ s carried out by LHCb in the J/ψϕ and J/ψπ + π − final states show no deviation from the SM prediction within uncertainties [139, 219], putting strong constraints on NP in \(B ^{0}_{ s } \) mixing, as discussed in Sect. 3.2.3. Table 3 shows the current results with 1.0 fb−1 and the projected precision for 50 fb−1 with the upgraded detector. A precision of \({<} 10\ \rm mrad \) is expected for 50 fb−1 with the upgraded detector. It is expected that even with this data sample, the main limitation will be statistical: the largest systematic uncertainties on the current measurement (background description, angular acceptance, effect of fixed physics parameters) [139] are expected to be removed with more sophisticated analyses or to scale with statistics. Thus changes as small as a factor of two with respect to the SM should be observable with 3σ significance. This precision will make it possible either to measure a significant deviation from the SM prediction or otherwise to place severe constraints on NP scenarios.
As discussed in Sect. 3.2.5, contributions from doubly CKM-suppressed SM penguin diagrams could have a non-negligible effect on the mixing-induced CP asymmetry and bias the extracted value of ϕ s . Naive estimates of the bias are of the order O(10−3) only [272–274], but this must be examined with experimental data using flavour symmetries to exploit control channels. LHCb can perform an SU(3) analysis using measurements of the decays rates and CP asymmetries in \(B ^{0}_{ s } \rightarrow { J / \psi } K ^{*0} \), B 0→J/ψρ 0 and B 0→J/ψϕ as control channels for \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\). The necessary high precision can only be reached using the large data sample that will be collected with the upgraded LHCb detector. The 50 fb−1 data sample will also allow to measure ϕ s in the penguin-free (\(b \rightarrow c \bar{u} s / u \bar{c} s\)) \(B ^{0}_{ s } \rightarrow D \phi \) decay [288, 289].
Another important goal is a more precise determination of sin2β in the B 0 system, motivated by the tension between the direct and indirect determinations of sin2β seen by both UTfit and CKMfitter groups, as shown in Table 2. With the upgraded detector, using the \(B ^{0} \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \) final state alone, a statistical precision of ±0.006 is expected, to be compared to the current error from the B factories of ±0.023 [190]. Given experience with the current detector it seems feasible to control the systematic uncertainties to a similar level. Such precision, together with better control of the penguin pollution, will allow us to pin down any NP effects in B 0 mixing. In addition, the penguin-free (\(b \rightarrow c \bar{u} d / u \bar{c} d\)) B 0→Dρ 0 channel can be used to get another handle on sin2β [290, 291].
The importance of improved measurements of ΔΓ q has been emphasised in Sects. 3.2.1–3.2.3. LHCb has made a preliminary measurement of ΔΓ s in \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) using a 1.0 fb−1 data sample [139]. The effective lifetime of \(B ^{0}_{ s } \rightarrow { J / \psi } f_{0}(980)\) [292] has also been measured [236]. Based on this, the statistical precision on ΔΓ s with 50 fb−1 is projected to be ∼0.003 ps−1. It is hoped that the systematic uncertainty can be controlled to the same level.
A measurement of ΔΓ d is of interest as any result larger than the tiny value expected in the SM would clearly signal NP [154, 255, 293]. To determine this quantity, LHCb will compare the effective lifetimes of the two decay modes \(B ^{0} \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \) with B 0→J/ψK ∗0. The estimated precision for 1.0 fb−1 is ∼0.02 ps−1. With the upgraded detector and 50 fb−1 a statistical precision of ∼0.002 ps−1 on ΔΓ d can be achieved. The systematic uncertainty is under study.
The LHCb upgrade will also have sufficient statistics to make novel tests of CPT symmetry. Any observation of CPT violation indicates physics beyond the SM. An example of a unique test in the B 0 system uses B 0→J/ψK 0 and its charge-conjugate decay, where the K 0 decays semileptonically [294–296]. This measurement involves looking at four separate decay paths that interfere. While several tests can be performed, one particular observable is the asymmetry A bk , that can be measured without the need of flavour tagging, where

In terms of the CPT violation parameter θ′, the kaon decay time t K , the B 0 decay time t B , the B 0 mass difference Δm d and CP-violating phase 2β, and kaon decay widths \(\varGamma^{K}_{S}\) and \(\varGamma^{K}_{L}\), this can be expressed
A signature of CPT violation would be a 1−cosΔm B t B dependence of the decay rate after integrating over kaon decay times. Roughly 5000 such decays can be expected with the upgrade. It is possible to detect these decays with low background level, even with the missing neutrino, using the measured B 0 direction, the detected J/ψ four-momentum, and the kaon decay vertex. Other methods to test CPT symmetry (e.g. Ref. [297]) are also under investigation.
3.3 CP violation measurements with hadronic b→s penguins
3.3.1 Probes for new physics in penguin-only \(b \rightarrow s q \bar{q}\) decays
The presence of physics beyond the SM can be detected by looking for its contribution to \(b \rightarrow s q \overline{ q } \) (q=s,d) decays,Footnote 38 which in the SM can only proceed via FCNC loop diagrams that are dynamically suppressed. These decays provide a rich set of observables that are rather precisely known in the SM but could potentially receive sizeable corrections from new heavy particles appearing in the loop.
-
Direct CP asymmetries. In the SM \(b \rightarrow s q \overline{ q } \) decays are dominated by the penguin diagram with an internal top quark. As a consequence, the direct CP asymmetry is expected to be small. If there is a NP amplitude with comparable size interfering with the SM amplitude, and it has different strong and weak phases than the SM amplitude, a much larger direct CP asymmetry can arise.
-
Polarisation and triple product asymmetries. For B decays into two vector mesons V 1 and V 2, followed by vector to two pseudoscalar decays \(V_{1} \rightarrow P_{1} P^{\prime}_{1}\) and \(V_{2} \rightarrow P_{2} P^{\prime}_{2}\), there are three transversity states, labelled “longitudinal” (0), “perpendicular” (⊥) and “parallel” (∥). Measurements of the fractions of the total decay rate in each of these states, which correspond to determinations of the polarisation in the final state, provide useful information about the chiral structure of the electroweak currents, as well about non-perturbative effects such as rescattering and penguin annihilation. In the SM, the decay to each transversity state is dominated by a single amplitude with magnitude |A j |, weak phase Φ j and strong phase δ j . The CP-violating observables \(\operatorname{Im} (A_{\perp}A^{*}_{j}-{\bar{A}}_{\perp }{\bar{A}}^{*}_{j})\) are then
 (41)
(41)The values of these observables are tiny since in the SM the weak phases are the same to a very good approximation, but \(\operatorname{Im} (A_{\perp }A^{*}_{j}-{\bar{A}}_{\perp}{\bar{A}}^{*}_{j})\) can significantly differ from zero if there is a sizeable CP-violating NP contribution in the loop.
These observables can be extracted from the differential distributions in terms of the angles θ 1, θ 2 and ϕ, where θ 1 (θ 2) is the polar angle of P 1 (P 2) in the rest frame of V 1 (V 2) with respect to the opposite of the direction of motion of the B meson, and ϕ is the angle between the decay planes of \(V_{1} \rightarrow P_{1}P^{\prime}_{1}\) and \(V_{2} \rightarrow P_{2} P^{\prime}_{2}\) in the rest frame of the B meson. The two observables can also be related to two triple product asymmetries for CP-averaged decaysFootnote 39 which are equal to asymmetries between the number of events with positive and negative values of U=sin2ϕ and \(V={\rm sign}(\cos \theta_{1} \cos\theta_{2})\sin\phi\):
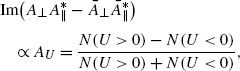 (42)
(42) (43)
(43)A review of this subject can be found in Ref. [298] and references therein.
-
Mixing-induced CP asymmetries. Mixing-induced CP asymmetries in \(b \rightarrow s q \overline{ q } \) decays of neutral B to CP eigenstates are precisely predicted. Due to the fact that the penguin diagram with an internal top quark is expected to dominate, the values of \(2\beta^{\rm eff}\) determined using \(B ^{0} \rightarrow \phi K ^{0}_{\mathrm{S}} \), \(B ^{0} \rightarrow \eta^{\prime} K ^{0}_{\mathrm{S}} \), \(B ^{0} \rightarrow f_{0}(980) K ^{0}_{\mathrm{S}} \), etc., are all expected to give ≈2β (see, e.g. Refs. [299, 300] and the discussion in Ref. [44]). Similarly, the values of \(2\beta_{s}^{\rm eff}\) determined from \(B ^{0}_{ s } \rightarrow \phi\phi\), \(B ^{0}_{ s } \rightarrow K^{*0} {\overline{K}}^{*0}\), etc., are expected to vanish due to cancellation of weak phases between mixing (top box) and decay (top penguin) amplitudes. Higher order corrections from subleading diagrams are expected to be small compared to the precision that can be achieved in the near-term, but further theoretical studies will be needed as the upgrade era approaches. NP with a flavour structure different from the SM will alter these CP asymmetries through the decay amplitudes, even if there is no NP in B mixing. A number of quasi-two-body or three-body decay modes can be studied.
-
Correlations between direct and mixing-induced asymmetries. Penguin-only decay modes are particularly interesting as the difference between formal “tree” and “penguin” contributions boils down to a difference in the quark-flavour running in the loop of the penguins. This difference, dominated by short distances, can be assessed accurately using QCD factorisation, and it can be used to correlate the branching ratio and the CP asymmetries of penguin-mediated modes. As discussed in Refs. [138, 301, 302], these observables can be correlated not only within the SM, but can also be used to extract the \(B ^{0}_{ s } \) mixing phase even in the presence of NP affecting only this phase.
3.3.2 Current status and outlook of LHCb measurements
LHCb published the first observation and measurement of the branching ratio and polarisation amplitudes in the \(B ^{0}_{ s } \rightarrow K ^{*0} \overline{ K }{} ^{*0} \) decay mode [303] using 35 pb−1 of data collected in 2010. A clean mass peak corresponding to 50±8 \(B^{0}_{s} \rightarrow(K^{+} \pi^{-})(K^{+} \pi^{+})\) decays is seen (Fig. 15 (left)), mostly from resonant \(B ^{0}_{ s } \rightarrow K ^{*0} \overline{ K }{} ^{*0} \) decays. Using this signal the longitudinal polarisation amplitude is measured to be \(f_{L} = 0.31 \pm0.12({\rm stat}) \pm0.04({\rm syst})\) and the branching ratio to be \({ \mathcal{B} } ( B ^{0}_{ s } \rightarrow K ^{*0} \overline { K }{} ^{*0} ) = (2.81 \pm 0.46({\rm stat}) \pm0.45({\rm syst})) \times10^{-5}\).
LHCb also published the measurement of the polarisation amplitudes and triple product asymmetries in \(B ^{0}_{ s } \rightarrow\phi\phi\) [304] using the 2011 data set of 1.0 fb−1. In this data set 801±29 events are observed with excellent signal-to-background ratio (see Fig. 15 (right)). The polarisation amplitudes are measured to be
where the sum of the square of the amplitudes is constrained to unity. The triple product asymmetries in this mode are measured to be
The results of this analysis are in agreement with, and more precise than, the previous measurement [305], and are also consistent with the SM.
First measurements of CP asymmetries in these modes from time-dependent flavour-tagged angular analyses are expected to follow. With high statistics, it will be possible to measure polarisation-dependent direct and mixing-induced CP asymmetries, but for the first analysis it will be more convenient to determine a single complex observable common to all polarisations (as done for \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\))
where j denotes one of the three transversity states, which are also CP eigenstates with eigenvalues η j , and A j (\(\bar{A}_{j}\)) is the decay amplitude of \(B ^{0}_{ s } \) (\(\overline{ B }{} ^{0}_{ s } \)) to the corresponding state. With this approximation it will be possible to determine the magnitude |λ| and phase \(\phi^{\rm eff}_{s} \equiv{-}{\arg}(\lambda)\). The SM expectation is |λ|≈1 and \(\phi^{\rm eff}_{s} \approx0\) due to the dominance of the top-quark loop, and any observed deviation from these expectations would be a signature of NP. Since NP in \(B ^{0}_{ s } \) mixing is already constrained by measurement of ϕ s from \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\), the main interest in these b→s penguin modes is to look for NP in the decay processes. Based on simulation studies, a sensitivity on \(\phi^{\rm eff}_{s}\) of 0.3–0.4 radians with 1.0 fb−1 is expected for both \(B ^{0}_{ s } \rightarrow \phi \phi\) and \(B ^{0}_{ s } \rightarrow K ^{*0} \overline { K }{} ^{*0} \).
3.3.3 Future prospects with LHCb upgrade
The latest results on mixing-induced CP violation in b→s transitions show no significant deviation from the SM, as seen in Fig. 16, which compares the mixing-induced CP violation parameter \(\sin2\beta^{\rm eff}\) measured in penguin-dominated b→s decays with the value of sin2β measured in the tree-dominated \(b \rightarrow c \overline{ c } s\) decays. In the absence of NP these observables should only differ by small amounts. Due to these results, large NP contributions in \(b \rightarrow s q \overline{ q } \) decays are unlikely but further tests with higher precision remain interesting. LHCb will be able to make competitive measurements of \(\sin2\beta ^{\rm eff}\) in \(B ^{0} \rightarrow \phi K ^{0}_{\mathrm{S}} \) and several other \(b \rightarrow s q \overline{ q } \) decays, but a significant improvement in precision requires the 50 fb−1 of the LHCb upgrade. The improved trigger efficiency in the LHCb upgrade is particularly important for these decays, which have only hadrons in the final state. With the upgrade data sample, the statistical error of \(\sin2\beta ^{\rm eff}( B ^{0} \rightarrow \phi K ^{0}_{\mathrm{S}} )\) is estimated to be roughly 0.06, which is still above the SM uncertainty of ∼0.02 [306].
HFAG compilation of results for \(\sin2\beta^{\rm eff}\) in \(b \rightarrow s q \overline{ q } \) decays [44]
There are several more NP probes in \(b \rightarrow s q \overline{ q } \) decays that can be exploited at LHCb and its upgrade, such as mixing-induced CP asymmetries and triple product asymmetries in both \(B ^{0}_{ s } \rightarrow \phi\phi\) and \(B ^{0}_{ s } \rightarrow K ^{*0} \overline { K }{} ^{*0} \) decays. The statistical precision of \(\phi_{s}^{\rm eff}\) with each channel is estimated to be 0.3–0.4 rad for 1.0 fb−1. The projected precision for 50 fb−1 is about 0.03 rad each. This can be compared with the uncertainties of their SM predictions of about 0.02 rad. It is also possible to perform a combined analysis of \(B ^{0}_{ s } \rightarrow K ^{*0} \overline{ K }{} ^{*0} \) and its U-spin related channel \(B ^{0} \rightarrow K ^{*0} \overline { K }{} ^{*0} \), which will put strong constraint on the subleading penguin diagrams in \(B ^{0}_{ s } \rightarrow K ^{*0} \overline { K }{} ^{*0} \), thus further reducing the theoretical uncertainty in the measurement of \(\phi^{\rm eff}_{s}\) [307, 308]. The statistical precision of A U and A V is estimated to be about 0.004, compared with an upper bound of 0.02 on their possible sizes in the SM [298].
In summary, the LHCb upgrade will allow the exploitation of the full potential of the NP probes in \(b \rightarrow s q \overline{ q } \) decays. Table 4 compares the current and projected (LHCb upgrade, i.e. 50 fb−1) precisions of the key observables with the theory uncertainties of their SM predictions.
3.4 Measurements of the CKM angle γ
3.4.1 Measurements of γ using tree-mediated decays
The CKM angle γ, defined as the phase \(\gamma= \arg [ -V_{ud}V_{ub}^{*}/\allowbreak (V_{cd}V_{cb}^{*}) ]\), is one of the angles of the unitarity triangle formed from the hermitian product of the first (d) and third (b) columns of the CKM matrix V. It is one of the least well known parameters of the quark mixing matrix. However, since it can be determined entirely through decays of the type B→DK Footnote 40 that involve only tree amplitudes—an unusual, even unique, property amongst all CP violation parameters—it provides a benchmark measurement. The determination from tree level decays has essentially negligible theoretical uncertainty, at the level of \(\delta\gamma/\gamma= \mathcal{O}(10^{-6})\), as will be shown in the next section. This makes γ a very appealing “standard candle” of the CKM sector. It serves as a reference point for comparison with γ values measured from loop decays (see Sect. 3.4.4).
Moreover, the determination of γ is crucial to improve the precision of the global CKM fits, and resulting limits on (or evidence for) NP contributions (see Sect. 3.2.4). In particular, the measurement of Δm d and the oscillation phase sin2β in B 0–\(\overline{ B }{} ^{0} \) mixing can be converted to a measurement of γ (in the SM). This can be compared to the reference value from B→DK—their consistency verifies that the Kobayashi–Maskawa mechanism of CP violation is the dominant source in quark flavour-changing processes. Existing measurements provide tests at the level of \({\mathcal{O}}(10~\% )\), but improving the precision to search for smaller effects of NP is well motivated.
Several established methods to measure γ in tree decays exploit the B −→D (∗) K (∗)− decays. They are based on the interference between the b→u and b→c tree amplitudes, which arises when the neutral D meson is reconstructed in a final state accessible to both D 0 and \(\overline{ D }{} ^{0} \) decays. The interference between the amplitudes results in observables that depend on their relative weak phase γ. Besides γ they also depend on hadronic parameters, namely the ratio of magnitudes of amplitudes r B ≡|A(b→u)/A(b→c)| and the relative strong phase δ B between the two amplitudes. These hadronic parameters depend on the B decay under investigation. They can not be precisely calculated from theory (see, however, Ref. [310]), but can be extracted directly from data by simultaneously reconstructing several different D final states.
The various methods differ by the D (∗) final state that is used. The three main categories of D decays considered so far by the B factories BaBar and Belle, and by CDF, are:
-
doubly Cabibbo-suppressed (DCS) decays (the ADS method [313, 314]),
-
three-body, self-conjugate final states (the GGSZ or “Dalitz” method [315]).
An additional category has not been possible to pursue at previous experiments due to limited event sample sizes:
-
singly Cabibbo-suppressed (SCS) decays (the GLS method [316]).
In practise, except for the case of two-body decays, there is often no clear distinction between the different methods.
The best sensitivity to γ obviously comes from combining the results of all different analyses. This not only improves the precision on γ, but provides additional constraints on the hadronic parameters. It also allows one to overcome the fact that CP-odd final states such as \(K ^{0}_{\mathrm{S}} \pi ^{0} \) are not easily accessible in LHCb’s hadronic environment.
A brief review of the main ideas of the different methods follows. The amplitudes of the B −→D 0 K − and \(B^{-}\rightarrow \overline{ D }{} ^{0} K^{-}\) processes are written as:

where A c , A u , A f and \(A_{\bar{f}}\) are real and positive (and CP violation in D 0 decays has been neglected). The subscripts c and u refer to the b→c and b→u transitions, respectively. The amplitudes for the D 0 decay can generally include the case where the D 0 decays to a three-body final state. In this case, A f , \(A_{\bar{f}}\), δ f and \(\delta_{\bar {f}}\) are functions of the Dalitz plot coordinates. The amplitude of the process B −→D[→f]K − can be written, neglecting D 0–\(\overline{ D }{} ^{0} \) mixing, as

and the rate is given by

where r B =A u /A c , δ B =δ u −δ c and \(\delta _{D}=\delta_{\bar{f}}-\delta_{f}\). The rate for the charge-conjugated mode (still neglecting CP violation in D 0 decays) is obtained by exchanging γ→−γ. Taking into account CKM factors and, in the case of charged B decays, colour suppression of the b→u amplitude, r B is expected to be around 0.1 for B − decays and around 0.3 for B 0 decays. From Eq. (49) all the relevant formulae of the GLW, ADS and GGSZ methods can be derived.
In the GLW analysis, the neutral D mesons are selected in CP eigenstates f CP± such as D→K − K + (CP=+1) or \(D\rightarrow K ^{0}_{\mathrm{S}} \pi^{0}\) (CP=−1). Thus \(A_{f}/A_{\bar{f}}=1\) and δ D =0,π for CP=±1. Equation (49) becomes:

The B −→DK − decays, where the D decays to Cabibbo-favoured (CF) final states (e.g. D 0→K − π +) can be used to normalise the rates in order to construct observables that minimise the systematic uncertainties. For those decays, to a good approximation,

From Eqs. (50) and (51) and their CP conjugates the usual GLW observables follow:


Equations (52) and (53) provide a set of four observables that are connected to the three unknowns γ, r B and δ B through


However, only three of these equations are independent since, from Eq. (55), R CP+ A CP+=−R CP− A CP−. Analogous relations hold for \(B \rightarrow D^{*}_{ \mathit{CP} }K\) and B→D CP K ∗ decays, with different values of the hadronic parameters characterising the B decay. However, in the \(B \rightarrow D^{*}_{ \mathit{CP} }K\) case one has to take into account a CP flip due to the different charge conjugation quantum numbers of the π 0 and the photon from the D ∗ decay [317]: \(D^{*}_{ \mathit{CP} \pm} \rightarrow D_{ \mathit{CP} \pm}\pi^{0}\), but \(D^{*}_{ \mathit{CP} \pm} \rightarrow D_{ \mathit{CP} \mp}\gamma\). For analysis of B→D CP K ∗ the finite width of the K ∗ resonance must be taken into account [318]. There are related important consequences for the ADS and GGSZ analyses of B→D ∗ K and B→DK ∗ decays.
In the ADS analysis, the neutral D mesons are selected in CF and DCS decays, such as D 0→K − π + and D 0→π − K +, respectively. The B decay rate is the result of the interference of the colour allowed B −→D 0 K − decay followed by the DCS D 0→π − K + decay and the colour suppressed \(B^{-}\rightarrow \overline{ D }{} ^{0} K^{-}\) decay followed by the CF D 0→K − π + decay. As a consequence, the interfering amplitudes are of similar magnitude and hence large interference effects can occur. From Eq. (49) one finds

where both \(r_{D}=A_{f}/A_{\bar{f}}=|A( D ^{0} \rightarrow \pi ^{-} K ^{+} )/A(D^{0}\rightarrow K^{-}\pi^{+})|\) and the phase difference δ D are measured in charm decays. The value of δ D can be determined directly using data collected from e + e − collisions at the ψ(3770) resonance, as has been done by CLEO [319, 320], but the most precise value comes from a global fit including charm mixing parameters. The results provided by HFAG [44] from a combination with CP violation in charm allowed are r D =0.0575±0.0007, \(\delta_{D} = (202^{+10}_{-11} )^{\circ}\). Defining \(R_{\rm ADS}\) and \(A_{\rm ADS}\) as


and using Eqs. (51) and (56) gives


It has been noted that for the extraction of γ it can be more convenient to replace the pair of observables \({R_{\rm ADS}, A_{\rm ADS}}\) with a second pair, R +,R −, defined as:

Unlike \({R_{\rm ADS}, A_{\rm ADS}}\), the two quantities R +,R − are statistically independent. The ADS decay chain B ±→[π ± K ∓] D K ± has been observed for the first time by LHCb [6], confirming the evidence that had begun to accumulate in previous measurements [321–323].
In the GGSZ analysis, the neutral D mesons are selected in three-body self-conjugate final states. The channel that has been used most to date is \(D \rightarrow K ^{0}_{\mathrm{S}} \pi^{+}\pi^{-}\), though first results have also been presented with \(D \rightarrow K ^{0}_{\mathrm{S}} K^{+}K^{-}\) and other channels are under consideration. For concreteness, consider \(D \rightarrow K ^{0}_{\mathrm{S}} \pi^{+}\pi^{-}\), with \(A_{f}e^{i\delta_{f}}=f(m_{-}^{2},m_{+}^{2})\) and \(A_{\bar{f}}e^{i\delta_{\bar {f}}}=f(m_{+}^{2},m_{-}^{2})\), where \(m_{-}^{2}\) and \(m_{+}^{2}\) are the squared masses of the \(K ^{0}_{\mathrm{S}} \pi^{-}\) and \(K ^{0}_{\mathrm{S}} \pi^{+}\) combinations. The rate in Eq. (49) can be re-written as:

where \(\delta_{D}(m_{\mp}^{2},m_{\pm}^{2})\) is the strong phase difference between \(f(m_{\pm}^{2},m_{\mp}^{2})\) and \(f(m_{\mp}^{2},m_{\pm}^{2})\). Due to the fact that r B is required to be positive, the direct extraction of r B , δ B and γ can be biased. To avoid these biases, the “Cartesian coordinates” have been introduced [324]
allowing Eq. (62) to be rewritten as

Here the notation has been simplified using \(f_{\pm}=f(m_{\pm}^{2},\allowbreak m_{\mp}^{2})\). This Dalitz plot-based method can be implemented in a model-dependent way by parametrising the amplitude as a function of the Dalitz plot of the three-body state, or in a model-independent way by dividing the Dalitz plot into bins and making use of external measurements of the D decay strong phase differences within these bins [315, 325, 326].Footnote 41
Besides the established methods based on direct CP violation in B→DK decays, it is also possible to measure γ using time-dependent analyses of neutral B 0 and \(B ^{0}_{ s } \) tree decays [328–330]. The method still relies on the interference of b→u and b→c amplitudes, but interference is achieved through B 0 (\(B ^{0}_{ s } \)) mixing. Thus one measures the sum of γ and the mixing phase, namely γ+2β and γ−2β s in the B 0 and \(B ^{0}_{ s } \) systems, respectively. Since both sin2β and β s are becoming increasingly well measured, these measurements provide sensitivity to γ.
Pioneering time-dependent measurements using the B 0→D (∗)∓ π ± decays have been performed by both BaBar [331, 332] and Belle [333, 334]. In these decays the amplitude ratios r Dπ =|A(B 0→D (∗)+ π −)/A(B 0→D (∗)− π +)| are expected to be small, r Dπ ≲0.02, limiting the sensitivity. In the decays \(B ^{0}_{ s } \rightarrow D_{s}^{\mp}K^{\pm}\), however, both b→c and b→u amplitudes are of same order in the Wolfenstein parameter λ, \(\mathcal{O}(\lambda^{3})\), so that the interference effects are expected to be large. In addition, the decay width difference in the \(B ^{0}_{ s } \) system, ΔΓ s , is non-zero, which adds sensitivity to the weak phase through the hyperbolic terms in the time evolution (see also Ref. [335]). The time-dependent decay rates of the initially produced flavour eigenstates are given by the decay equations

where Γ s , ΔΓ s , Δm s are the usual mixing parameters of the \(B ^{0}_{ s } \) system and |q/p|=1 has been assumed. The top (bottom) of the ± and ∓ signs is used when the initial particle is tagged as a \(B ^{0}_{ s } \) (\(\overline{ B }{} ^{0}_{ s } \)) meson. In Eq. (65), A f is the decay amplitude for a \(B ^{0}_{ s } \) meson to decay to a final state f, and \(\lambda_{ f } = (q/p)( \overline{A}_{ f } / A_{ f } )\) where \(\overline{A}_{ f } \) is the amplitude for a \(\overline{ B }{} ^{0}_{ s } \) to decay into f. Similar equations hold for the charge conjugate processes replacing A f by \(\overline{A}_{ \bar{f} } \), λ f by \(\overline{\lambda}_{ \bar{f} } = (p/q) ( A_{ \bar{f} } / \overline{A}_{ \bar{f} } )\), and with a separate set of coefficients \(C_{ \bar{f} } \), \(S_{ \bar {f} } \) and \(D_{ \bar{f} } \). As each decay is dominated by a single diagram, \(| \lambda _{ f } |=| \overline{\lambda }_{ \bar{f} } |\). The CP asymmetry observables are then given by

The equality \(C_{ f } = C_{ \bar{f} } \) results from |q/p|=1 and \(| \lambda_{ f } |=| \overline{\lambda}_{ \bar{f} } |\). The term λ f is connected to the weak phase by

where |A 2/A 1| is the ratio of the hadronic amplitudes between \(B ^{0}_{ s } \rightarrow D ^{-}_{ s } K ^{+} \) and \(B ^{0}_{ s } \rightarrow D ^{+}_{ s } K ^{-} \), Δ is their strong phase difference, and γ−2β s is the weak phase difference. An analogous relation exists for \(\overline{\lambda }_{ \bar{f} } \), \(\overline {\lambda}_{ \bar{f} } = | \lambda_{ f } |e^{i(\Delta +(\gamma-2\beta_{s}))}\). Thus one obtains five observables from Eq. (66) and solves for |λ f |, Δ, and (γ−2β s ).
The LHCb experiment has the necessary decay time resolution, tagging power and access to large enough signal yields to perform this time-dependent CP measurement.Footnote 42 The signal yields can be seen from the measurement of \({ \mathcal{B} } ( B ^{0}_{ s } \rightarrow D ^{\mp }_{ s } K ^{\pm} )\) [140] (see Sect. 3.4.3 below). The identification of the initial flavour of the signal \(B ^{0}_{ s } \) candidate can be done combining both the responses of opposite-side and same-side kaon tagging algorithms, as is planned for other measurements of mixing-induced CP-violation in \(B ^{0}_{ s } \) decays, and has already been implemented in the preliminary analysis of \(B ^{0}_{ s } \rightarrow D^{-}_{s} \pi^{+}\) decays [226].
3.4.2 Theoretical cleanliness of γ from B→DK decays
The answer to the question of why it is interesting to measure γ precisely depends on the experimental precision that can be achieved. In the era of LHCb, the main motivation is the theoretically clean measurement of the SM CKM phase. The search for NP can thus be performed by comparing the extracted value of γ to other observables, for example in the CKM fit (see Sect. 3.2.4). However, one can also cross-check for the presence of NP in B→DK channels themselves. One way is to test that the values of γ determined from the many different B→DK type channels all coincide. Another is automatically built in to the method for γ extraction in the GGSZ analysis. Consider the case where the decay amplitudes get modified by an extra contribution with a new strong phase \(\delta_{B}^{\prime}\) and a weak phase γ′. Then instead of the decay amplitudes in Eq. (48) one finds

This means that for B + and B − decays the r B ratios are different

Discovering that \(r_{B^{-}}\ne r_{B^{+}}\) would signal a CP-violating NP contribution to the B→DK amplitude. One signature of NP would then be \({x_{+}^{2}+y_{+}^{2}}\ne{x_{-}^{2}+y_{-}^{2}}\), though it is also possible that the equality could be satisfied even in the presence of NP: in this case there can be a shift in the extracted value of γ.
Existing measurements place strong constraints on tree-level NP effects, yet the possibility of discoveries in this sector in the near term is not ruled out. In the far future, with much larger statistics, the measurement of γ is well suited to search for high scale NP since it is theoretically very clean. For example, NP with contributions of different chirality could give different shifts in γ, so the above test is meaningful.
A useful question to ask is, what is the energy scale that could be probed in principle? To answer this, the irreducible theoretical uncertainty in the determination of γ must be estimated. There are several sources that can induce a bias in the determination of γ from B→DK decays. However, most of these can be avoided, either (i) with more statistics (for example, the Dalitz plot model uncertainty where a switch to a model-independent method is possible), or (ii) by modifying the equations used to determine γ (an example is to correct for effects of D 0–\(\overline{ D }{} ^{0} \) mixing [337, 338]). The remaining, irreducible, theory uncertainties are then from the electroweak corrections.
The challenge to determine this uncertainty is that the hadronic elements can no longer be determined solely from the experiment. Not all electroweak corrections matter though—the important ones are the corrections that change the CKM structure. For instance, vertex corrections and Z exchanges do not affect γ, but corrections from box diagrams carry a different weak phase. The dominant contribution is effectively due to t and b running in the loop. For \(b \rightarrow u s\bar{c}\) transitions there is a tree level contribution with \({\sim} V_{ub} V_{cs}^{*}\) CKM structure, while the box diagram has \({\sim}(V_{tb}V_{ts}^{*}) (V_{ub} V_{cb}^{*})\). Since this has the same weak phase, it does not introduce a shift in γ. For \(b \rightarrow c s \bar{u}\) transitions, on the other hand, the tree level is \({\sim} V_{cb} V_{us}^{*}\), while the box diagram \({\sim}(V_{tb}V_{ts}^{*}) (V_{cb} V_{ub}^{*})\), as illustrated in Fig. 17. The two contributions have different weak phases, which means that the shift δγ is non-zero.
The size of this effect is estimated by integrating over both t and b at the same time. The electroweak corrections in the effective theory are then described by a local operator whose matrix elements are easier to estimate. Although the Wilson coefficient of the operator contains large logarithms, log(m b /m W ), for \({\mathcal{O}}(1)\) estimates, the precision obtained without resummation is sufficient. If one resums log(m b /m W ) then nonlocal contributions are also generated. As a rough estimate only the local contributions need be kept. The irreducible theory error on γ is conservatively estimated to be \(\delta\gamma/\gamma<{\mathcal{O}}(10^{-6})\) (most likely it is even \(\delta\gamma/\gamma\lesssim{\mathcal{O}}(10^{-7})\)).
This limit is far beyond the achievable sensitivity of any foreseeable experiment. Nevertheless, it is interesting to consider what could be learnt in case such small deviations could be observed. Assuming MFV one can probe \(\varLambda_{\rm NP} \sim10^{2} ~\mathrm{TeV} \), while assuming general flavour-violating (FV) NP one can probe \(\varLambda_{\rm NP}\sim10^{3} ~\mathrm{TeV} \) (where MFV and general FV NP scales are defined as in Ref. [270]). This is by far the most precise potential probe of MFV, as shown in Table 5, due to the small theoretical uncertainty.
Since an experimental precision of δγ/γ∼10−6 is not achievable in the near future, the NP scale reach must be adjusted for more realistic data sets. This is easily done, since the scale \(\varLambda_{\rm NP}\) probed goes as the fourth root of the yield. With the LHCb upgrade, an uncertainty of <1∘ on γ can be achieved (see Sect. 3.4.6), so that NP scales approaching \(\varLambda_{\rm NP}\sim5 (50) ~\mathrm {TeV} \) can be probed for MFV (general FV) NP.
3.4.3 Current LHCb experimental situation
First results from LHCb in this area include a measurement using B −→DK − with the GLW and ADS final states [6].Footnote 43 A measurement of the branching ratio of \(B ^{0}_{ s } \rightarrow D^{\mp}_{s} K ^{\pm} \) has also been performed [140]. Several other analyses, including studies of GGSZ-type final states, are in progress.Footnote 44
These measurements all share common selection strategies. They benefit greatly from boosted decision tree algorithms, which combine up to 20 kinematic variables to effectively suppress combinatorial backgrounds. Charmless backgrounds are suppressed by exploiting the large forward boost of the \(D_{(s)}^{+}\) meson through a cut on its flight distance.
In the GLW/ADS analysis [6] of 1.0 fb−1 of \(\sqrt{s}=7 ~\mathrm{TeV} \) data collected in 2011, the CP eigenstates D→K + K −, π + π −, and the quasi-flavour-specific D→π − K + decay are used. The CP asymmetries defined in Eq. (58), and the ratios R ± defined in Eq. (61), are measured for both the B→DK signal and the abundant B→Dπ control channel. The latter has limited sensitivity to γ but provides a large control sample from which probability density functions are shaped, and can be used to help reduce certain systematic uncertainties. The control channel is also used to measure three ratios of partial widths
where f represents KK, ππ and the favoured Kπ mode. The signal yields are estimated by a simultaneous fit to 16 independent subsamples, defined by the charges (×2), the D final states (×4), and the DK or Dπ final state (×2). Figure 18 shows the projections of the suppressed π ± K ∓ subsamples. It is crucial to control the cross feed of the abundant B −→Dπ − decays into the signal decays. This is achieved using the two LHCb ring-imaging Cherenkov detectors [344]. The systematic uncertainties are dominated by knowledge of the intrinsic asymmetry of the detector in reconstruction of positive and negative B meson decays, and by the uncertainty on the particle identification requirements. The results are

where the first error is statistical and the second systematic; R CP+ is computed from \(R_{ \mathit{CP} +} \approx\langle R_{K/\pi}^{KK}, R_{K/\pi}^{\pi\pi} \rangle/ R_{K/\pi}^{K\pi}\) with an additional 1 % systematic uncertainty assigned to account for the approximation; A CP+ is computed as \(A_{ \mathit{CP} +} = \langle A_{K}^{KK} , A_{K}^{\pi\pi} \rangle\). From the R ± one can also compute

as \(R_{\rm ADS} = (R_{-} + R_{+}) / 2\) and \(A_{\rm ADS} = (R_{-} - R_{+}) / (R_{-} + R_{+})\). To summarise, the B ±→DK ± ADS mode is observed with ≈10σ statistical significance when comparing the maximum likelihood to that of the null hypothesis. This mode displays evidence (4.0σ) of a large negative asymmetry, consistent with previous experiments [321–323]. The combined asymmetry A CP+ is smaller than (but compatible with) previous measurements [345, 346], and is 4.5σ significant. The maximum likelihood is compared with that under the null hypothesis in all three DK final states, diluted by the non-negligible correlated systematic uncertainties. From this, with a total significance of 5.8σ, direct CP violation is observed in B ±→DK ± decays.
Invariant mass distributions of selected B ±→[π ± K ±] D h ± candidate events: (left) B − candidates, (right) B + candidates [6]. In the top plots, the track directly from the B vertex passes a kaon identification requirement and the B candidates are reconstructed assigning this track the kaon mass. The remaining events are placed in the bottom row and are reconstructed with a pion mass hypothesis. The dark (red) curve represents the B→DK ± events, the light (green) curve is B→Dπ ±. The shaded contribution are partially reconstructed events and the thin line shows the total fit function which also includes a linear combinatoric component. The broken line represents the partially reconstructed \(\overline{ B }{} ^{0}_{ s } \rightarrow D ^{0} K ^{+} \pi ^{-} \) decays where the pion is lost
The analysis of the \(B ^{0}_{ s } \rightarrow D^{\mp}_{s} K ^{\pm} \) decay mode [140] is based on a sample corresponding to an integrated luminosity of 0.37 fb−1, collected in 2011 at a centre-of-mass energy of \(\sqrt{s} = 7 ~\mathrm{TeV} \). This decay mode has been observed by the CDF [347] and Belle [348] Collaborations, who measured its branching fraction with an uncertainty around 23 % [190]. In addition to \(B^{0}_{s} \rightarrow D^{\mp}_{s} K^{\pm} \), the channels B 0→D − π + and \(B^{0}_{s} \rightarrow D^{-}_{s} \pi^{+} \) are analysed. They are characterised by a similar topology and therefore are good control and normalisation channels. Particle identification criteria are used to separate the CF decays from the suppressed modes, and to suppress misidentified backgrounds.
The signal yields are obtained from unbinned extended maximum likelihood fits to the data. The fits include components for the combinatorial background and several sources of background from b hadron decays. The most important is the misidentified \(B^{0}_{s} \rightarrow D^{-}_{s} \pi^{+} \) decay. Its shape is fixed from data using a reweighting procedure [349] while the yield is left free to float. A similar procedure is applied to a simulated data sample to extract the shape of the B 0→D − K + misidentified background. The fit results are shown in Fig. 19.
Mass distribution of the \(B^{0}_{s} \rightarrow D^{\mp}_{s} K^{\pm} \) candidate events [140]. The stacked background shapes follow the same top-to-bottom order in the legend and in the plot
Correcting the raw signal yields for selection efficiency differences gives
where the first uncertainty is statistical and the second is systematic. Using the measured relative yield of B 0→D − π +, the known B 0→D − π + branching fraction [190], and the recent f s /f d measurement [145], the branching fractions


are obtained, where the first uncertainty is statistical, the second is the experimental systematic uncertainty, and the third is from the f s /f d measurement. Both measurements are significantly more precise than the previous world averages [190].
3.4.4 Measurements of γ using loop-mediated two-body B decays
CP violation in \(B^{0}_{(s)}\) decays plays a fundamental role in testing the consistency of the CKM paradigm in the SM and in probing virtual effects of heavy new particles.
With the advent of the B factories, the Gronau–London (GL) [350] isospin analysis of B→ππ decays has been a precious source of information on the phase of the CKM matrix. Although the method allows a full determination of the weak phase and of the relevant hadronic parameters, it suffers from discrete ambiguities that limit its constraining power. It is however possible to reduce the impact of discrete ambiguities by adding information on hadronic parameters [351, 352]. In particular, as noted in Refs. [353–355], the hadronic parameters entering the B 0→π + π − and the \(B ^{0}_{ s } \rightarrow K^{+}K^{-}\) decays are connected by U-spin, so that experimental knowledge of \(B ^{0}_{ s } \rightarrow K^{+} K^{-}\) can improve the extraction of the CKM phase with the GL analysis. Indeed, in Ref. [352], the measurement of \({ \mathcal{B} } ( B ^{0}_{ s } \rightarrow K^{+} K^{-})\) was used to obtain an upper bound on one of the hadronic parameters.
LHCb has reported preliminary measurements of the time-dependent CP asymmetries using decays to CP eigenstates, namely B 0→π + π − and \(B^{0}_{s} \rightarrow K^{+}K^{-}\) [356], thereby permitting the use of the U-spin strategy proposed by Fleischer (F) [353–355] to extract the CKM phase from a combined analysis of B 0→π + π − and the \(B ^{0}_{ s } \rightarrow K^{+} K^{-}\) decays. However, as shown explicitly below, this strategy alone suffers from a sizeable dependence on the breaking of U-spin symmetry. In Ref. [357], the authors propose to perform a combined analysis of the GL modes plus \(B ^{0}_{ s } \rightarrow K^{+} K^{-}\) to obtain an optimal determination of the CKM phase within the SM. They show that this combined strategy has a milder dependence on the magnitude of U-spin breaking, allowing for a more solid estimate of the theory error. The experimental data used for such a determination of γ are summarised in Table 6.
The time-dependent asymmetry for a B meson decay to a CP eigenstate f can be written, with the same notation as Eqs. (65) and (66),Footnote 45 as
where C f and S f parametrise direct and mixing-induced CP violation respectively, and the quantity D f is constrained by the consistency relation
The LHCb preliminary results on direct and mixing-induced CP violation parameters in B 0→π + π − and \(B ^{0}_{ s } \rightarrow K^{+}K^{-}\) decays [356] are shown in Table 6. The measurements of \(C_{ \pi ^{+} \pi ^{-} }\) and \(S_{ \pi ^{+} \pi ^{-} }\) are compatible with those from the B factories, whereas \(C_{ K ^{+} K ^{-} }\) and \(S_{ K ^{+} K ^{-} }\) are measured for the first time and are consistent with zero within the current uncertainties.
Beyond the SM, NP can affect both the \(B^{0}_{(s)}\)–\(\overline{B}^{0}_{(s)}\) amplitudes and the b→d(s) penguin amplitudes. Taking the phase of the mixing amplitudes from other measurements, for example from \(b \rightarrow c \bar{c} s\) decays, one can obtain a constraint on NP in b→s (or b→d) penguins. Alternatively, assuming no NP in the penguin amplitudes, one can obtain a constraint on NP in mixing. The analysis discussed here is based on a simplified framework [357], using as input values sin2β=0.679±0.024 [44] and 2β s =(0±5)∘ [139] obtained from \(b \rightarrow c \bar{c} s\) decays. The optimal strategy will be to include the combined GL and Fleischer analysis in a global fit of the CKM matrix plus possible NP contributions.
The GL and Fleischer analyses were formulated with different parametrisations of the decay amplitudes. In order to use the constraints in a global fit one can writeFootnote 46

where the magnitude of \(V_{ub}V_{ud}^{*}\) has been reabsorbed in C, and the magnitude of \(V_{cb}V_{cd}^{*}/(V_{ub}V_{ud}^{*})\) has been reabsorbed in d. In the exact U-spin limit, one has C=C′, d=d′ and θ=θ′. Isospin breaking in B→ππ has been neglected, since its impact on the extraction of the weak phase is at the level of 1∘ [368–371]. The physical observables entering the analysis are
where ϕ M (B 0)=2β, \(\phi_{M}( B ^{0}_{ s } ) = -2\beta_{s}\) in the SM, and F(B 0)=1, \(F( B ^{+} ) = \tau _{B^{+}}/\tau_{B^{0}} = 1.08\), \(F( B ^{0}_{ s } ) = \tau _{ B ^{0}_{ s } }/\allowbreak \tau _{ B ^{0} } (m_{ B ^{0} }^{2}/m_{ B ^{0}_{ s } }^{2}) \sqrt{(M_{ B ^{0}_{ s } }^{2}\,{-}\,4 M_{ K ^{+} }^{2})/(M_{ B ^{0} }^{2}\,{-}\,4 M_{ \pi ^{+} }^{2})}\, {=}\, 0.9112\).
In the GL approach, one extracts the probability density function (PDF) for the angle α=π−β−γ of the UT from the measurements of \({ \mathcal{B} } (B \rightarrow \pi\pi)\), \(S_{\pi^{+}\pi^{-}}\), \(C_{\pi ^{+}\pi^{-}}\) and \(C_{\pi^{0}\pi^{0}}\). Using the unitarity of the CKM matrix, it is possible to write the B→ππ decay amplitudes and observables in terms of α instead of γ and β. However, for the purpose of connecting B→ππ to \(B ^{0}_{ s } \rightarrow K K\) it is more convenient to use the parametrisation in Eq. (76). In this way, α (or, equivalently, γ), is determined up to discrete ambiguities, that correspond however to different values of the hadronic parameters. As discussed in detail in Ref. [352], the shape of the PDF obtained in a Bayesian analysis depends on the allowed range for the hadronic parameters. For example, using the data in Table 6, solving for C and choosing flat a priori distributions for d∈[0,2], θ∈[−π,π], T∈[0,1.5] and θ T ∈[−π,π] the PDF for γ in Fig. 20 is obtained, corresponding to γ=(68±15)∘ (γ∈[25,87]∘ at 95 % probability). Using instead the Fleischer method, one can obtain a PDF for γ given a range for the U-spin breaking effects. In this method it was originally suggested to parametrise the U-spin breaking in C′/C using the result one would obtain in factorisation, namely
where the error obtained using light-cone QCD sum rule calculations [372] has been symmetrised. However, this can only serve as a reference value, since there are non-factorisable contributions to C and C′ that could affect this estimate. In this analysis, the non-factorisable U-spin breaking is parametrised as follows
with r C , r r and r i uniformly distributed in the range [1−κ,1+κ].
From left to right: PDF for γ obtained using the GL method as described in the text; PDF for γ obtained using the Fleischer method for κ=0.1,0.5 [357]. Here and in the following, dark (light) areas correspond to 68 % (95 %) probability regions
In Fig. 20 the PDF for γ obtained with the Fleischer method for two different values of the U-spin breaking parameter κ=0.1,0.5 is shown. The method is very precise for small amounts of U-spin breaking (κ=0.1), but becomes clearly worse for κ=0.5. Thus, a determination of γ from the Fleischer method alone is subject to uncertainty on the size of U-spin breaking.
The result of the combined GL+F analysis is given in Fig. 21, where the PDF for γ for κ=0.1 and 0.5 is shown. The result of the combined analysis is much more stable against the allowed amount of U-spin breaking. In Fig. 21 the 68 % probability region for γ obtained using the combined method as a function of κ is also shown, and compared to the GL result. The combined method shows a considerable gain in precision even for very large values of κ.
From left to right: PDF for γ obtained using the combined method for κ=0.1, 0.5; 68 % probability region for γ obtained using the combined method (filled area) or the GL method (horizontal lines) as a function of κ [357]
NP could affect the determination of γ in the combined method by giving (electroweak) penguin contributions a new CP-violating phase. If one assumes that the isospin analysis of the GL channels is still valid, barring order-of-magnitude enhancements of electroweak penguins in B→ππ, and if one assumes for concreteness that NP enters only b→s penguins, in the framework of a global fit, one can simultaneously determine γ and the NP contribution to b→s penguins. For the purpose of illustration, the value of γ from tree-level processes, γ tree=(76±9)∘ is used as input [270],Footnote 47 allowing inspection of the posterior for γ and for the NP penguin amplitude. Writing
and taking uniformly distributed \(d^{\prime}_{\rm NP} \in[0,2]\) and \(\phi_{\rm NP}, \theta^{\prime}_{\rm NP}\in[-\pi,\pi]\) the PDFs shown in Fig. 22 are obtained for κ=0.5. This yields γ=(74±7)∘, and a 95 % probability upper bound on \(d^{\prime}_{\mathrm{NP}}\) around 1. Clearly, the bound is stronger for large values of \(\phi_{\rm NP}\).
From left to right: PDFs for ϕ NP, \(d^{\prime}_{\mathrm{NP}}\) and \(\theta^{\prime}_{\mathrm{NP}}\) obtained using the combined method with κ=0.5 [357]
Finally, \(B ^{0}_{ s } \rightarrow KK\) decays can also be used to extract 2β s in the SM. The optimal choice in this respect is represented by \(B ^{0}_{ s } \rightarrow K^{(*)0} \overline{K}^{(*)0}\) (with \(B^{0} \rightarrow K^{(*)0} \overline{K}^{(*)0}\) as U-spin related control channels to constrain subleading contributions), since in this channel there is no tree contribution proportional to e iγ [307, 308]. However, the combined analysis described above, in the framework of a global SM fit, can serve for the same purpose. To illustrate this point, the GL+F analysis is performed, taking as input the SM fit result γ=(69.7±3.1)∘ [270] and not using the measurement of 2β s from \(b \rightarrow c \bar{c} s\) decays. In this way, 2β s =(3±14)∘ is obtained for κ=0.5. The analysis can also be performed without using the measurement of γ, in this case the result is 2β s =(6±14)∘. With improved experimental accuracy, this determination could become competitive with that from \(b \rightarrow c \bar{c} s\) decays. Once results of time-dependent analyses of the \(B^{0}_{(s)} \rightarrow K^{(*)0} \overline{K}^{(*)0}\) channels are available these may also provide useful constraints.Footnote 48
To conclude, the usual GL analysis to extract α from B 0→ππ can be supplemented with the inclusion of the \(B ^{0}_{ s } \rightarrow K^{+} K^{-}\) modes, in the framework of a global CKM fit. The method optimises the constraining power of these decays and allows the derivation of constraints on NP contributions to penguin amplitudes or on the \(B ^{0}_{ s } \) mixing phase and illustrates these capabilities with a simplified analysis, neglecting correlations with other SM observables.
3.4.5 Studies of CP violation in multibody charmless b hadron decays
Multibody charmless b hadron decays can be used for a variety of studies of CP violation, including searches for NP and determination of the angle γ. Due to the resonant structure in multibody decays, these can offer additional possibilities to search for both the existence and features of NP. Model-independent analyses [374, 375] can be performed to first establish the presence of a CP violation effect, and then to identify the regions of the phase space in which it is most pronounced.Footnote 49 To further establish whether any observed CP violation can be accommodated within the Standard Model, amplitude analyses can be used to quantify the effects associated with resonant contributions to the decay. A number of methods have been proposed to determine γ from such processes [378–387], in general requiring input not only from charged B decays, but also from B 0 and \(B ^{0}_{ s } \) decays (to states such as \(K ^{0}_{\mathrm{S}} h^{+}h^{\prime-}\) and π 0 h + h ′−).Footnote 50 The potential for LHCb to study multibody charmless \({ \varLambda }^{0}_{ b } \) decays adds further possibilities for novel studies of CP violation effects.
3.4.6 Prospects of future LHCb measurements
As discussed above, the angle γ can be determined from both tree-dominated and loop-dominated processes. Comparisons of the values obtained provide tests of NP, and so precision measurements from both methods are needed. Among the tree-dominated processes, in addition to the modes discussed above, any channel that involves the interference of \(b \rightarrow c\bar{u}s\) and \(b \rightarrow u\bar{c}s\) transitions is potentially sensitive to γ. Many of these modes can be analysed in the upgraded phase of LHCb, including
-
1.
B +→DK + π − π + where, similarly to the B→DK mode, the neutral D can be reconstructed either in the two-body (ADS and GLW-like measurement) or multibody (GGSZ-like measurement) final state. The observation of the CF mode in LHCb data [389] indicates a yield only twice lower than that for the B→DK mode, which makes it competitive for the measurement of γ.Footnote 51 However, two unknown factors affect the expected γ sensitivity. First, since this is a multibody decay, the overlap between the interfering amplitudes is in general less than 100 %; this is accounted for by a coherence factor between zero and unity which enters the interference term in Eqs. (54), (55), (59), (60) as an unknown parameter. Second, the value of r B can be different from that in B→DK and is as yet unmeasured, although it is expected [318] that it can be larger in this decay than in B→DK.
-
2.
B 0→DK + π −. Although the rate of these decays is smaller that of B +→DK +, both interfering amplitudes are colour-suppressed, therefore the expected value of r B is larger, r B ≃0.3. As a result, the sensitivity to γ should be similar to that in the B→DK modes.Footnote 52 Depending on the content of B 0→D 0 K + π − and \(B^{0} \rightarrow \overline {D}{}^{0}K^{+}\pi^{-}\) amplitudes, the optimal strategy may involve Dalitz plot analysis of the B 0 decay [390, 391]. In this case, control of amplitude model uncertainty will become essential for a precision measurement; it can be eliminated by studying the decays B 0→DK + π − with \(D \rightarrow K ^{0}_{\mathrm{S}} \pi^{+}\pi^{-}\) [392].
-
3.
\(B ^{0}_{ s } \rightarrow D\phi\). This mode is not self-tagging, but sensitivity to γ can be obtained from untagged time-integrated measurements using several different neutral D decay modes [393, 394]. The first evidence for the three-body decay \(B ^{0}_{ s } \rightarrow \overline{ D }{} ^{0} K ^{+} K ^{-} \) has just been reported by LHCb [395], and investigation of its resonant structure is in progress.
-
4.
\(B _{ c } ^{+} \rightarrow DD_{s}^{+}\). \(B _{ c } ^{+} \) production in pp collisions is significantly suppressed, however, in this mode the magnitude of CP violation is expected to be \(\mathcal{O}(100~\%)\): the two interfering amplitudes are of the same magnitude because the \(b \rightarrow u\bar{c}s\) amplitude is colour allowed, while the \(b \rightarrow c\bar{u}s\) amplitude is colour suppressed [396–399].
-
5.
\({ \varLambda }^{0}_{ b } \rightarrow D{ \varLambda }\) and \({ \varLambda }^{0}_{ b } \rightarrow DpK^{-}\). Measurement of γ from analysis of the \({ \varLambda }^{0}_{ b } \rightarrow D{ \varLambda }\) decay mode was proposed in Ref. [400]. This method allows one to measure γ in a model-independent way by comparing the S- and P-wave amplitudes. However, this mode is problematic to reconstruct at LHCb because of the poorly defined \({ \varLambda }^{0}_{ b } \) vertex (both particles from its decay are long-lived) and low efficiency of Λ reconstruction. Alternatively, one can consider a similar measurement with the decay \({ \varLambda }^{0}_{ b } \rightarrow DpK^{-}\). A preliminary observation of this mode in early LHCb data has been reported [401].
Table 7 shows the expected sensitivity to γ from tree level decays in the upgrade scenario. The LHCb upgrade is the only proposed experiment which will be able to reach sub-degree precision on γ.
Measurement of γ and 2β s by means of the CP-violating observables from loop-mediated decays B 0→π + π − and \(B ^{0}_{ s } \rightarrow K^{+} K^{-}\) was discussed in Sect. 3.4.4. Extrapolating the current sensitivity on C and S to the upgrade scenario, when 50 fb−1 of integrated luminosity will be collected, LHCb will be able to reach a statistical sensitivity \(\sigma_{\rm stat}(C) \approx\sigma_{\rm stat}(S) \simeq0.008\) in both B 0→π + π − and \(B ^{0}_{ s } \rightarrow K^{+} K^{-}\). This corresponds to a precision on γ of 1.4∘, and on 2β s of 0.01 rad, assuming perfect U-spin symmetry.
4 Mixing and CP violation in the charm sector
4.1 Introduction
The study of D mesons offers a unique opportunity to access up-type quarks in flavour-changing neutral current (FCNC) processes. It probes scenarios where up-type quarks play a special role, such as supersymmetric models with alignment [402, 403]. It offers complementary constraints on possible NP contributions to those arising from the measurements of FCNC processes of down-type quarks (B or K mesons).
The neutral D system is the latest and last system of neutral mesons where mixing between particles and anti-particles has been established. The mixing rate is consistent with, but at the upper end of, SM expectations [404] and constrains many NP models [405]. More precise D 0–\(\overline{ D }{} ^{0} \) mixing measurements will provide even stronger constraints. However, the focus has been shifting to CP violation observables, which provide cleaner tests of the SM [406–408]. First evidence for direct CP violation in the charm sector has been reported by the LHCb Collaboration in the study of the difference of the time-integrated asymmetries of D 0→K + K − and D 0→π + π − decay rates through the parameter \(\Delta \mathcal{A}_{ \mathit{CP} } \) [18]. No evidence of indirect CP violation has yet been found. As discussed in detail below, these results on CP violation in the charm sector appear marginally compatible with the SM but contributions from NP are not excluded.
The mass eigenstates of neutral D mesons, |D 1,2〉, with masses m 1,2 and widths Γ 1,2 can be written as linear combinations of the flavour eigenstates \(|D_{1,2}\rangle=p| D ^{0} \rangle\pm{}q| \overline { D }{} ^{0} \rangle\), with complex coefficients p and q which satisfy |p|2+|q|2=1. The average mass and width are defined as m≡(m 1+m 2)/2 and Γ≡(Γ 1+Γ 2)/2. The D mixing parameters are defined using the mass and width difference as x D ≡(m 2−m 1)/Γ and y D ≡(Γ 2−Γ 1)/2Γ. The phase convention of p and q is chosen such that \(\mathit{CP} | D ^{0} \rangle =-| \overline{ D }{}^{0} \rangle\). First evidence for mixing of neutral D 0 mesons was discovered in 2007 by Belle and BaBar [409, 410] and is now well established [44]: the no-mixing hypothesis is excluded at more than 10σ for the world average (\(x_{D}=0.63\,^{+0.19}_{-0.20}~\%\), y D =0.75±0.12 %).Footnote 53
It is convenient to group hadronic charm decays into three categories. The CF decays, such as D 0→K − π +, are mediated by tree amplitudes, and therefore no direct CP violation effects are expected. The same is true for DCS decays, such as D 0→K + π −, even though these are much more rare. The SCS decays, on the other hand, can also have contributions from penguin amplitudes, and therefore direct CP violation is possible, even though the penguin contributions are expected to be small. Within this classification, it should be noted that some decays to final states containing \(K ^{0}_{\mathrm{S}} \) mesons, e.g. \(D ^{0} \rightarrow K ^{0}_{\mathrm{S}} \rho^{0}\), have both CF and DCS contributions which can interfere [412]. Within the SM, however, direct CP violation effects are still expected to be negligible in these decays.
LHCb is ideally placed to carry out a wide physics programme in the charm sector, thanks to the high production rate of open charm: with a cross-section of 6.10±0.93 mb [3, 4], one tenth of LHC interactions produce charm hadrons. Its ring-imaging Cherenkov detectors provide excellent separation between pions, kaons and protons in the momentum range between 2 and 100 GeV/c, and additional detectors also provide clean identification of muons and electrons. This allows high purity samples to be obtained both for hadronic and muonic decays. The large boost of the D hadrons produced at LHCb is beneficial for time-dependent studies. LHCb has the potential to improve the precision on all the key observables in the charm sector in the next years.
In the remainder of this section the key observables in the charm sector are described, and the current status and near term prospects of the measurements at LHCb are reviewed. A discussion of the implications of the first LHCb charm physics results follows, motivating improved measurements and studies of additional channels. The potential of the LHCb upgrade to make the precise measurements needed to challenge the theory is then described.
4.1.1 Key observables
Currently the most precise individual measurements of mixing parameters are those of the relative effective lifetime difference between D 0 and \(\overline{ D }{} ^{0} \) decays to CP eigenstates (\(\hat{\varGamma}\) and \(\hat{\bar{\varGamma}}\)) and flavour specific final states (Γ), y CP , which is defined as

where terms below \(\mathcal{O}(10^{-4})\) have been ignored [413], η CP is the CP eigenvalue of the final state, ϕ is the CP-violating relative phase between q/p and \(\bar{A}_{f}/A_{f}\) where \(\stackrel{\text{\textsf{\fontsize{5pt}{1em}\selectfont(---)}}}{A}_{f}\) are the decay amplitudes, and A m represents a CP violation contribution from mixing (|q/p|±2≈1±A m ).Footnote 54 In the limit of CP conservation y CP is equal to the mixing parameter y D . The resulting world average value for y CP is 0.87±0.16 % [414]Footnote 55 and is consistent with the value of y D within the current accuracy.
The CP-violating observable A Γ quantifies the difference in decay rates of D 0 and \(\overline{ D }{} ^{0} \) to a CP eigenstate and is defined as

where terms below \(\mathcal{O}(10^{-4})\) have again been ignored [413] and both mixing and direct CP contributions are assumed to be small. The parameter A d describes the contribution from direct CP violation (\(|\bar{A}_{f}/A_{f}|^{\pm2}\approx1\pm A_{d}\)). The current world average of A Γ is 0.02±0.16 % [44], consistent with the hypothesis of no CP violation. Due to the smallness of x D and y D , A Γ provides essentially the same information as a full time-dependent CP violation analysis of D 0→K + K − decays.
An alternative way to search for CP violation in charm mixing is with a time-dependent Dalitz plot analysis of D 0 and \(\overline{ D }{} ^{0} \) decays to \(K ^{0}_{\mathrm{S}} \pi ^{+} \pi ^{-} \) or \(K ^{0}_{\mathrm{S}} K ^{+} K ^{-} \). Such analyses have been carried out at the B factories [416, 417]. Also in these cases no CP violation was observed.
In time-integrated analyses the measured rate asymmetry is
where the direct CP asymmetry contribution is defined as
and 〈t〉 denotes the average decay time of the observed candidates.
A powerful way to reduce experimental systematic uncertainties is to measure the difference in time-integrated asymmetries in related final states. For the two-body final states K + K − and π + π −, this difference is given by

where the CP-violating phase ϕ is assumed to be universal [418], Δa≡a(K + K −)−a(π + π −), \(\overline{a} \equiv (a( K ^{+} K ^{-} )+a( \pi ^{+} \pi ^{-} ))/2\) and the indirect CP asymmetry parameter is defined as \(a_{ \mathit{CP} }^{\rm ind}=-(A_{m}/2)y_{D}\cos\phi+x_{D}\sin\phi\). The ratio Δ〈t〉/τ is equal to zero for the lifetime-unbiased B factory measurements [419, 420] and is 0.098±0.003 for LHCb [18] and 0.25±0.04 for CDF [421], therefore \(\Delta \mathcal{A}_{ \mathit{CP} } \) is largely a measure of direct CP violation.
The current most accurate measurements of \(\Delta \mathcal{A}_{ \mathit{CP} } \) are from the LHCb and CDF Collaborations and are (−0.82±0.21±0.11) % [18] and (−0.62±0.21±0.10) % [422], respectively.Footnote 56 These results show first evidence of CP violation in the charm sector: the world average is consistent with no CP violation at only 0.006 % C.L. [44].
4.1.2 Status and near-term future of LHCb measurements
LHCb has a broad programme of charm physics, including searches for rare charm decays (see Sect. 2), spectroscopy and measurements of production cross-sections and asymmetries (see Sect. 5). In this section only studies of mixing and CP violation are discussed. For reviews of the formalism, the reader is referred to Refs. [413, 424, 425] and the references therein, and for an overview of NP implications to Ref. [418].
Mixing and indirect CP violation occur only in neutral mesons. These are probed in a number of different decay modes, predominantly—but not exclusively—time-dependent ratio measurements. In most cases, the same analysis yields measurements of both mixing and CP violation parameters, so these are considered together. By contrast, direct CP violation may occur in decays of both neutral and charged hadrons, and the primary sensitivity to it comes from time-integrated measurements—though it may affect certain time-dependent asymmetries as well, as discussed in Sect. 4.7.1.
Several classes of mixing and indirect CP violation measurements are possible at LHCb, particularly:
-
Measurements of the ratios of the effective D 0 lifetimes in decays to quasi-flavour-specific states (e.g. D 0→K − π +) and CP eigenstates f CP (e.g. D 0→K − K +). These yield y CP . Comparing the lifetime of D 0→f CP and \(\overline { D }{} ^{0} \rightarrow f_{ \mathit{CP} }\) yields the CP violation parameter A Γ .
-
Measurements of the time-dependence of the ratio of wrong-sign to right-sign hadronic decays (e.g. D 0→K + π − vs. D 0→K − π +). The ratio depends on \(y_{D}^{\prime} t\) and \((x_{D}^{\prime2} + y_{D}^{\prime2}) t^{2}\) (see, e.g., Ref. [424]), where
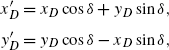
and δ is the mode-dependent strong phase between the CF and DCS amplitudes. Note that \((x_{D}^{\prime2} + y_{D}^{\prime2}) = x_{D}^{2} + y_{D}^{2} \equiv r_{M}\). The mixing parameters can be measured independently for D 0 and \(\overline{ D }{} ^{0} \) to constrain indirect CP violation, and the overall asymmetry in wrong-sign decay rates for D 0 and \(\overline{ D }{} ^{0} \) gives the direct CP violation parameter A d .
-
Time-dependent Dalitz plot fits to self-conjugate final states (e.g. \(D^{0} \rightarrow K ^{0}_{\mathrm{S}} \pi^{-} \pi^{+}\)). These combine features of the two methods above, along with simultaneous extraction of the strong phases relative to CP eigenstate final states. Consequently they yield measurements of x D and y D directly. Likewise, the indirect CP violation parameters |q/p| and ϕ may be extracted, along with the asymmetry in phase and magnitude of each contributing amplitude (in a model-dependent analysis).
-
Measurements of the ratio of time-integrated rates of wrong-sign to right-sign semileptonic decays (e.g. \(D ^{0} \rightarrow \overline{ D }{} ^{0} \rightarrow K^{+} l^{-} \bar{\nu}_{l}\) vs. D 0→K − l + ν l ). These yield r M and A m .
Within LHCb, analyses are planned or in progress for each of these methods. A measurement of y CP and A Γ from the 2010 data sample has been published [19]. In addition, a preliminary result on the time-integrated wrong-sign rate in D 0→Kπ from the 2010 sample is available [426].Footnote 57 A summary of what can be achieved with the 2010–2012 prompt charm samples is given in Table 8. Note that the observables are generally related to several physics parameters, such that the combined constraints are much more powerful than individual measurements. After analysing 2.5 fb−1 of data, the mixing parameters x D and y D are expected to be determined at the level of \(\mathcal {O}(10^{-4})\), and A Γ to be measured with a similar uncertainty. This will represent a significant improvement in precision compared to the current world averages, which have uncertainties \(\sigma_{x_{D}} = 0.19~\%\), \(\sigma_{y_{D}} = 0.12~\%\), and \(\sigma_{A_{\varGamma}} = 0.23~\%\).
For direct CP violation, control of systematic uncertainties associated with production and efficiency asymmetries is essential. To date, two techniques have been used to mitigate these effects:
-
Measurement of differences in asymmetry between two related final states, such that systematic effects largely cancel—for example, \(\mathcal{A}_{ \mathit{CP} } (D^{0} \rightarrow K^{-}K^{+}) - \mathcal {A}_{ \mathit{CP} } (D^{0} \rightarrow \pi^{-}\pi^{+})\) [18]. This is simplest with two-body or quasi-two-body decays. This is discussed in more detail in Sect. 4.1.3.
-
Searching for asymmetries in the distributions of multi-body decays, such that differences in overall normalisation can be neglected and effects related to lab-frame kinematics are largely washed out—for example, in the Dalitz plot distribution of D +→K − K + π + [427].
In the longer term, the goal is to extract the CP asymmetries for D 0→K + K − and D 0→π + π − separately, along with those for other decay modes. To achieve this, it will be necessary to determine the production and detector efficiencies from data. Progress has been made in this area, notably in the \(D_{s}^{+}\) production asymmetry measurement [428], which involves determination of the pion reconstruction efficiency from D ∗+→D 0 π +,D 0→K − π − π + π + decays in which one of the D 0 daughter pions is not used in the reconstruction.Footnote 58 The detector asymmetries need to be determined as functions of the relevant variables, and similarly, the production asymmetries can vary as functions of transverse momentum and pseudorapidity. Understanding these systematic effects with the level of precision and granularity needed for CP asymmetry measurements is difficult and it cannot be assumed that these challenges will be solved in a short time scale. Moreover, production asymmetries can be determined only with the assumption of vanishing CP asymmetry in a particular (usually CF) control mode. Therefore ultimately the resulting measurements of CP asymmetries for individual decay modes are essentially \(\Delta \mathcal{A}_{ \mathit{CP} } \) measurements relative to CF decays.
A summary of analyses that are in progress or planned with the 2011–2012 data is given below:
- D 0→K − K +,π − π +::
-
Updates to the 0.6 fb−1 \(\Delta \mathcal{A}_{ \mathit{CP} } \) analysis [18] are in progress, using both prompt charm and charm from semileptonic B decays (see Sect. 4.1.3).
- \(D_{(s)}^{+} \rightarrow K ^{0}_{\mathrm{S}} h^{+}, \phi h^{+}\)::
-
A \(\Delta \mathcal{A}_{ \mathit{CP} } \)-style analysis is possible by comparing asymmetries in a CF control mode (e.g. \(D^{+} \rightarrow K ^{0}_{\mathrm{S}} \pi^{+}\)) and the associated SCS mode (e.g. D +→ϕπ +), taking advantage of the inherent symmetry of the \(K ^{0}_{\mathrm{S}} \rightarrow \pi ^{-} \pi^{+}\) and ϕ→K − K + decays.Footnote 59 The different kinematic distributions of the tracks (requiring binning or reweighting) and the CP asymmetry in the \(K ^{0}_{\mathrm{S}} \) decay need to be taken into account.
- D +→π + π − π +,K + K − π +::
-
A search for CP violation in D +→K + K − π + with the model-independent (so-called “Miranda”) technique [374] was published with the 2010 data sample [427], comprising 0.04 fb−1. With such small data samples, detector effects are negligible. However, from studies of control modes such as \(D_{s}^{+} \rightarrow K^{-} K^{+} \pi ^{+}\) it is found that this is no longer the case with 1.0 fb−1 of data or more, so an update will require careful control of systematic effects. The π + π − π + final state should be more tractable, since the π ± interaction asymmetry does not depend strongly on momentum.
- D 0→π − π + π − π +,K − K + π − π +::
-
Previous publications have focused mainly on T-odd moments [430], but there is further information in the distribution of final-state particles. A Miranda-style binned analysis or a comparable unbinned method [375] can be used.Footnote 60
- Baryonic decays::
-
LHCb will collect large samples of charmed baryons, enabling novel searches for CP-violation effects [432]. Triggering presents a challenge, but trigger lines for several \({ \varLambda }^{+}_{ c } \) decay modes of the form Λh + or ph − h ′+ are already incorporated, allowing large samples to be recorded. In addition to the considerations outlined above for D meson decays, the large proton-antiproton interaction asymmetry and the possibility of polarisation in the initial state must be taken into account.
4.1.3 Experimental aspects of \(\Delta \mathcal{A}_{ \mathit{CP} } \) and related measurements
The raw asymmetry measured for D ∗+-tagged D 0 decays to a final state f is defined as:

where N(X) refers to the number of reconstructed events of decay X after background subtraction. This raw asymmetry arises from several sources: the D ∗+ production asymmetry \(\mathcal{A}_{\rm P}\), the asymmetry in selecting the tagging slow pion \(\mathcal{A}_{\rm D}(\pi^{+}_{s})\), the asymmetry in selecting the D 0 decay into the final state \(\mathcal {A}_{\rm D}(f)\), and the CP asymmetry in the decay \(\mathcal{A}_{ \mathit{CP} } (f)\).
Consider the general case of a measured rate n ±, an efficiency (or other correction) ε ±, and the corrected rate N ±, where the subscript refers to D 0 or \(\overline{ D }{} ^{0} \). Then:
Defining a generic asymmetry A x as
gives the identity
Then applying this to Eq. (87),
Applying the Taylor series expansion to Eq. (88), gives

and thus
Generalising this to include multiple asymmetries, the formula used in the published analysis [18] is obtained
which is correct up to terms of second order in the asymmetries. In practise, for D 0→h + h −, the asymmetries are \(\mathcal{A}_{\rm P} \sim1~\%\), \(\mathcal{A}_{\rm D}(\pi^{+}_{\mathrm{s}}) \sim1\mbox{--}2~\%\), and \(\mathcal{A}_{\rm D}(f) = 0\) by construction. Thus, the second-order correction is \(\mathcal{O}(10^{-4})\).Footnote 61 Further, \(\mathcal{A}_{\rm D}(\pi^{+}_{\mathrm{s}})\) and \(\mathcal {A}_{\rm P}\) are the same for f=K + K − and f=π + π − (leaving aside differences in kinematic distribution, considered below) and so many terms cancel in the difference:Footnote 62

At the present level of precision, with a statistical uncertainty of around 0.2 %, this approximation is perfectly adequate. However, when more data is accumulated—and certainly after the upgrade—it will be necessary to change the analysis to take second-order terms into account. This can be done using the ratio formulation of Eq. (87), i.e.

The nuisance asymmetries \(\mathcal{A}_{\rm P}\) and \(\mathcal{A}_{\rm D}(\pi^{+}_{\mathrm{s}})\) cancel between the K + K − and π + π − final states because these are properties of the D ∗+ and of the tagging slow pion, respectively, which do not depend on the decay of the D 0 meson. However, an artificial correlation between these asymmetries and the decay mode can arise if the asymmetry varies as a function of some variableFootnote 63 (e.g. the momentum of the D ∗+) and the reconstructed distributions in this variable are different for the K + K − and π + π − final states (e.g. due to detector acceptance of the daughter tracks). In such a scenario, the two modes would populate regions with different raw asymmetries and so the nuisance asymmetries would not cancel fully. Two techniques have been used to address this:
-
the data can be partitioned into smaller kinematic regions such that within each region the raw asymmetries are constant and/or the K + K − and π + π − kinematic distributions are equal;
-
the data can be reweighted such that the K + K − and π + π − kinematic distributions are equalised.
The first approach was used in the published LHCb result, and the second in the CDF result [421].
There is another way in which the formalism could be broken: through the presence of peaking backgrounds which (a) fake the signal, (b) occur at different levels for the K + K − and π + π − final states, and (c) have a different raw asymmetry from the signal. The signal extraction procedure used in the published LHCb analysis is a fit to the mass difference from threshold \(\delta m \equiv m((h^{+}h^{-})_{ D ^{0} }\pi^{+}_{\mathrm{s}}) - m(h^{+}h^{-}) - m(\pi^{+})\). This is vulnerable to a class of background in which a real D ∗+ decay occurs and the correct slow pion is found but the D 0 decay is partly misreconstructed, e.g. D 0→K − π + π 0 misidentified as D 0→K − K +. This typically creates a background which peaks in δm but is broadly distributed in m(h + h −). Only cases which lie within the narrow m(h + h −) signal window will survive. This is more common for the K + K − final state than for π + π −: the energy of a missing particle can be made up by misidentifying a pion as a kaon, but apart from D 0→π − e + ν e there is little that can fake the kinematics of D 0→π + π −. In practise, the charged hadron identification at LHCb suppresses these background greatly, and their raw asymmetries are not expected to be very different from the signal. In the published LHCb analysis, the impact of these backgrounds on the asymmetry was estimated by measuring their size and asymmetry in the h + h − mass sidebands and computing the effect of such a background on the signal with a toy Monte Carlo study. The alternative approach would be to use a full 2D fit to m(h + h −) and δm, which would distinguish this class of peaking background from the signal by its m(h + h −) distribution.
The three issues discussed above—terms entering at second order in the asymmetries, non-cancellation due to kinematic correlations, and peaking backgrounds—are particular to this analysis and will require some changes to the procedure as larger data samples become available. In addition, there are more generic systematic uncertainties associated with the fit procedure and with the handling of events with more than one candidate. These are summarised in Table 9.
4.2 Theory status of mixing and indirect CP violation
4.2.1 Theoretical predictions for ΔΓ D , Δm D and indirect CP violation in the Standard Model
As discussed in Sect. 4.1, mixing of charmed mesons provides outstanding opportunities to search for physics beyond the SM. New flavour-violating interactions at some high-energy scale may, together with the SM interactions, mix the flavour eigenstates giving mixing parameters that differ from their SM expectations. It is known experimentally that D 0–\(\overline{ D }{} ^{0} \) mixing proceeds extremely slowly, which in the SM is usually attributed to the absence of super-heavy quarks.
Both SM and NP contributions to mass and width differences can be summarised as

These formulae serve as the initial point of calculations of the mass and lifetime differences. They include contributions from local (at charm mass scale) ΔC=2 interactions generated by the b-quark [433–437] or NP particles and from SM-dominated time-ordered products of two ΔC=1 interaction Hamiltonians (see, however, Ref. [438]).
A simple examination of Eq. (91) reveals that the local ΔC=2 interactions only affect x D , thus one can conclude that it is more likely that x D receives large NP contributions. Hence, it was believed that an experimental observation of x D ≫y D would unambiguously reveal NP contributions to charm mixing. This simple signal for NP was found to not be realised in nature, but it is interesting that the reverse relation, x D <y D with y D expected to be determined by the SM processes, might nevertheless significantly affect the sensitivity to NP of experimental analyses of D mixing [439]. Also, it is important to point out that, contrary to the calculations of the SM contribution to mixing, the contributions of NP models can be calculated relatively unambiguously [405, 440, 441].
The calculation of the SM contribution to the mixing amplitudes is rather sophisticated. In the SM x D and y D are generated only at second order in flavour SU(3)f breaking,
where θ C is the Cabibbo angle. Therefore, predicting the SM values of x D and y D depends crucially on estimating the size of SU(3)f breaking [404, 442].
There are currently two approaches, neither of which give very reliable results because m c is in some sense intermediate between heavy and light. The “inclusive” approach is based on the OPE. In the \(m_{c} \gg\varLambda_{\rm QCD}\) limit, where \(\varLambda_{\rm QCD}\) is a scale characteristic of the strong interactions, Δm D and ΔΓ D can be expanded in terms of matrix elements of local operators [434–437]. Such calculations typically yield x D ,y D <10−3. The use of the OPE relies on local quark-hadron duality (see, for example, Ref. [443]), and on \(\varLambda_{\rm QCD}/E_{\rm released}\) (with \(E_{\rm released} \sim m_{c}\)) being small enough to allow a truncation of the series. Moreover, a careful reorganisation of the OPE series is needed, as terms with smaller powers of m s are numerically more important despite being more suppressed by powers of 1/m c [434–437]. The numerically dominant contribution is composed of over twenty unknown matrix elements of dimension-12 operators, which are very hard to estimate. As a possible improvement of this approach, it would be important to perform lattice calculations of those matrix elements, as well as make perturbative QCD (pQCD) corrections to Wilson coefficients of those operators.
The “exclusive” approach sums over intermediate hadronic states, which may be modelled or fit to experimental data [444–449]. Since there are cancellations between states within a given SU(3)f multiplet, one needs to know the contribution of each state with high precision. However, the D meson is not light enough that its decays are dominated by a few final states. In the absence of sufficiently precise data on many decay rates and on strong phases, one is forced to use some assumptions. While most studies find x D ,y D <10−3, Refs. [444–449] obtain x D and y D at the 10−2 level by arguing that SU(3)f violation is of order unity. Particular care should be taken if experimental data are used to estimate the mixing parameters, as the large cancellations expected in the calculation make the final result sensitive to uncertainties in the experimental inputs. It was shown that phase space effects alone provide enough SU(3)f violation to induce x D ,y D ∼10−2 [442]. Large effects in y D appear for decays close to threshold, where an analytic expansion in SU(3)f violation is no longer possible; a dispersion relation can then be used to show that x D would receive contributions of similar order of magnitude. The dispersion calculation suffers from uncertainties associated with unknown (off-shell) q 2-dependences of non-leptonic transition amplitudes and thus cannot be regarded as a precision calculation, although it provides a realistic estimate of x D . As a possible improvement of this approach, an estimate of SU(3)f breaking in matrix elements should be performed. In addition, a calculation with V ub ≠0 should also be done, which is important to understand the size of CP violation in charm mixing.
Based on the above discussion, it can be seen that it is difficult to find a clear indication of physics beyond the SM in D 0–\(\overline { D }{} ^{0} \) mixing measurements alone. However, an observation of large CP violation in charm mixing would be a robust signal of NP.
CP violation in D decays and mixing can be searched for by a variety of methods. Most of the techniques that are sensitive to CP violation make use of the decay asymmetry \(\mathcal{A}_{ \mathit{CP} } (f)\) [418, 425]. For instance, time-dependent decay widths for D→Kπ are sensitive to CP violation in mixing. In particular, a combined analysis of D→Kπ and D→KK can yield interesting constraints on CP-violating parameters y CP and A Γ , as discussed in Sect. 4.1.1.
With the D 0–\(\overline{ D }{} ^{0} \) transition amplitudes defined as follows:
then in the limit where direct CP violation is neglected, one can measure [418, 425] four quantities, x D , y D , A m , and ϕ, which are described by three physical variables,Footnote 64
This implies that there is a model-independent relation among experimental quantities [425, 450],
4.2.2 New physics in indirect CP violation
Indirect CP violation in charm mixing and decays is a unique probe for NP, since within the SM the relevant processes are described by the physics of the first two generations to an excellent approximation. Hence, observation of CP violation in D 0–\(\overline{ D }{} ^{0} \) mixing at a level higher than \(\mathcal{O}(10^{-3})\) (which is the SM contribution) would constitute an unambiguous signal of NP.
The commonly used theoretical parameters x 12 and ϕ 12 defined in Eq. (94) can be expressed in terms of x D , y D and |q/p| as:

The latest fitFootnote 65 yields the following ranges [44]
all at 95 % C.L. The fit also provides 95 % C.L. ranges also for the theoretical parameters from Eq. (94):
It should be noted that the experimental precision on the CP violation parameters is more than two orders of magnitude away from their SM predictions.
It is reasonable to assume that there are no accidental strong cancellations between the SM and the NP contributions to M 12. Useful bounds can thus be obtained by taking the NP contribution to saturate the upper limits in Eq. (98). The resulting constraints are presented in the \(x_{12}^{\rm NP}/x_{12}\mbox{--}\phi_{12}^{\rm NP}\) plane in Fig. 23. One can also translate the data into model-independent bounds on four-quark operators, as performed e.g. in Refs. [440, 441].
The generic NP analysis can also be applied to models with MFV, where new contributions to FCNCs originate only from the Yukawa matrices Y u,d . The relevant basis is then the up mass basis, where Y u is diagonal, so that flavour violation comes from powers of \(Y_{d} Y_{d}^{\dagger}\). The leading contribution is to the operator \((u_{L}^{\alpha}\gamma_{\mu}c_{L}^{\alpha})^{2}\) (α is a colour index), and it is given in terms of its Wilson coefficient C 1 by
Here \(r_{\rm GMFV}\) parameterises the effect of resummation of higher powers of the Yukawa matrices when these are important, namely in general MFV (GMFV) models [451].
The contribution to x 12 in the linear MFV case (\(r_{\rm GMFV}=0\)) is orders of magnitude below the current experimental sensitivity, assuming \(\mathcal{O}(1)\) proportionality coefficient in Eq. (99). Yet in the context of GMFV with two Higgs doublets and large tanβ, such that y b ∼1, observable signals can be obtained, as shown in Fig. 23 for \(r_{\rm GMFV}\) in the range [−3,3]. Note that strictly speaking \(r_{\rm GMFV}\) (and thus the resulting signal) is not bounded, but higher absolute values than those considered here are much less likely in realistic models. Indeed in the current example \(r_{\rm GMFV} \gtrsim2\) is excluded, as shown in the figure.
The available data on D 0–\(\overline{ D }{} ^{0} \) mixing can also be used to constrain the parameter space of specific theories, such as SUSY and warped extra dimensions (WED) [452]. This has been done e.g. in Refs. [440, 441] or Refs. [453, 454] where the interplay between the constraints from the K and D systems is presented. Here the influence of improving the current bounds is demonstrated.
Within a SUSY framework, one can focus on the first two generations of the left-handed squark mass-squared matrix, \(\tilde{m}_{Q}^{2}\), as the source of flavour violation. As an additional assumption, the framework can be aligned with the down sector, where the constraints are generically stronger. As in realistic alignment models (see e.g. Refs. [402, 455]), the off-diagonal element of \(\tilde{m}_{Q}^{2}\) in the down mass basis (which induces s↔d FCNCs) is taken to be small but not zero, with comparable real and imaginary parts. For concreteness, values of either \(\lambda_{\rm C}^{5}\) or \(\lambda _{\rm C}^{3}\) (with \(\lambda_{\rm C}\) being the Cabibbo angle) are examined, where in both cases the dominant bounds still arise from D 0–\(\overline{ D }{} ^{0} \) mixing and not from the K system [454]. The constrained parameter is the squark mass degeneracy, defined by
In order to analyze the effect of improving the experimental constraints on indirect CP violation in charm (assuming that no such violation is actually observed), for simplicity the bound on x 12 is kept fixed as in Eq. (98), while that on ϕ 12 is varied. This is shown in Fig. 24 for the two alignment angles mentioned above and for two points in the SUSY parameter space \(\bar{m}_{\tilde{Q}}=m_{\tilde{g}}=1\ \mathrm{and}\ 1.5 ~\mathrm {TeV} \), where \(\bar{m}_{\tilde{Q}}\) is the average squark mass and \(m_{\tilde{g}}\) is the gluino mass. The right edge of each of the four lines in the plots marks the current situation, where the dominant constraint is from Δm D . It is evident that after a certain level of improvement, the bound from CP violation becomes the important one, and this happens more quickly for a weaker alignment model (\(\lambda_{\rm C}^{3}\)) than for \(\lambda_{\rm C}^{5}\) alignment. The reason is the larger phase in the former case.
Bound on the squark mass degeneracy \(\delta^{12}_{Q}\), defined in Eq. (100), as a function of the experimental constraint on CP violation in D 0–\(\overline{ D }{} ^{0} \) mixing, parametrised by \(\sin\phi_{12}^{\rm exp}\). The alignment angle from the down sector is \(\lambda_{\rm C}^{5}\) (left panel) or \(\lambda_{\rm C}^{3}\) (right panel). The solid blue line in each panel is for \(\bar{m}_{\tilde{Q}}=m_{\tilde{g}}=1 ~\mathrm{TeV} \) and the dashed red line is for \(\bar{m}_{\tilde{Q}}=m_{\tilde{g}}=1.5 ~\mathrm{TeV} \)
To conclude, the experimental search for indirect CP violation in charm is one of the most promising channels for discovering NP or obtaining strong constraints. This is not negated by the large hadronic uncertainties in the D system, because of the very small SM short distance contribution to CP violation in D 0–\(\overline{ D }{} ^{0} \) mixing.
4.3 The status of calculations of \(\Delta \mathcal{A}_{ \mathit{CP} } \) in the Standard Model
As discussed above, the LHCb Collaboration has measured a surprisingly large time-integrated CP asymmetry difference [18],

which has recently been supported by a result from the CDF collaboration [422].Footnote 66 Inclusion of the BaBar and Belle measurements of the individual K − K + and π − π + time-integrated CP asymmetries [419, 420] and the BaBar, Belle, and LHCb measurements of the indirect CP asymmetry A Γ [19, 410, 456] yields the world average for the direct CP asymmetry difference [44]

The naive penguin-to-tree amplitude ratio is \(\mathcal{O}([ V_{ c b } V_{ u b } / \allowbreak V_{ c s } V_{ u s } ] \alpha_{S} /\pi) \sim10^{-4}\), yielding \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} < 0.1~\%\). This has led to extensive speculation in the literature that the measurement of \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) is a signal for NP. This is a particularly exciting possibility, given that reasonable NP models can be constructed in which all related flavour-changing neutral current (FCNC) constraints, e.g., from D 0–\(\overline{ D }{} ^{0} \) mixing, are satisfied. A summary of NP interpretations is given in Sect. 4.4.1. First, a discussion of \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) in the SM is given.
The naive expectation for the SM penguin-to-tree ratio is based on estimates of the “short-distance” penguins with b-quarks in the loops. In fact, there is consensus that a SM explanation for \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) would have to proceed via dynamical enhancement of the long-distance “penguin contraction” contributions to the penguin amplitudes, i.e., penguins with s and d quarks inside the “loops”. Research addressing the direct CP asymmetry in the SM has largely fallen into one of two categories: (i) flavour SU(3)f or U-spin fits to the D decay rates, to check that an enhanced penguin amplitude can be accommodated [457–463] (this, by itself, would not mean that \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) is due to SM dynamics); (ii) rough estimates of the magnitudes of certain contributions to the long-distance penguin contractions [461, 464–466], to check if, in fact, it is reasonable that SM dynamics could yield the enhanced penguin amplitudes returned by the SU(3)f or U-spin fits.
The results obtained using the flavour symmetry decompositions can be summarised as follows. An SU(3)f analysis of the D→PP decay amplitudes that incorporates CP violation effects was first carried out about 20 years ago [445, 457, 467]. Already in this study the possibility of large direct CP asymmetries was anticipated, e.g., as large as the percent level assuming that the penguins receive a large enhancement akin to the ΔI=1/2 rule in kaon decays. An updated analysis, working to first order in SU(3)f breaking, has been presented [458], making use of branching ratio measurements for the D→Kπ,ππ and \(D ^{0} \rightarrow K ^{-} K ^{+} , \overline{ K }{} ^{0} \eta \) decay modes. The authors concluded that \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) can be easily reconciled with the measured branching ratios. This was also the conclusion of a study based on a diagrammatic SU(3)f amplitude decomposition [459], which considered a larger set of D→PP decay modes. Again, this is only a statement about the possibility of accommodating the required amplitudes in the flavour decomposition, not about their realisation via long distance QCD dynamics. Both studies observe that a SM explanation of \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) could be combined with precise measurements of the individual asymmetries \(a_{ \mathit{CP} }^{{ \rm dir }} ( D ^{0} \rightarrow K ^{-} K ^{+} )\) and \(a_{ \mathit{CP} }^{{ \rm dir }} ( D ^{0} \rightarrow \pi ^{-} \pi ^{+} )\) to obtain predictions for \(a_{ \mathit{CP} }^{{ \rm dir }} ( D ^{0} \rightarrow \pi ^{0} \pi ^{0} )\). The conclusion, based on current data, is that percent level asymmetries for the latter could be realised. Reference [459] also discusses implications for \(a_{ \mathit{CP} }^{{ \rm dir }} ( D ^{+} \rightarrow K ^{+} \overline{ K }{} ^{0} )\).
Studies employing U-spin symmetry [460, 461] necessarily focus on amplitude fits to the smaller set of decay modes D 0→K − π +,π − K +,π − π +,K − K +, as the D 0 is a U-spin singlet, while the four final states and the operators mediating these decays in the SM ΔC=1 effective Hamiltonian each consist of a U-spin triplet and a singlet. Working to first order in U-spin breaking, the four decay amplitudes can be written as
where the U-spin triplet “tree” amplitude T and the singlet “penguin” amplitude P arise at 0th order in U-spin breaking, and δT, δS and δP are the first order U-spin breaking corrections, which transform in turn as a triplet, singlet, and singlet under U-spin. The singlet amplitude δS accounts for the large rate difference Γ(D 0→K − K +)/Γ(D 0→π − π +)=2.8 (after accounting for phase space). A ratio δS/T∼0.5 is found in Refs. [460, 461], and in the SU(3)f study of Ref. [458] which effectively contains the above U-spin decomposition. Realisation of Eq. (102) requires |P/T|∼3, for \(\mathcal{O}(1)\) strong phases and \(a_{ \mathit{CP} }^{{ \rm dir }} ( D ^{0} \rightarrow K ^{-} K ^{+} ) \sim- a_{ \mathit{CP} }^{{ \rm dir }} ( D ^{0} \rightarrow \pi ^{-} \pi ^{+} )\), where the last relation becomes an equality in the U-spin limit. This amounts to an order of magnitude enhancement of the penguin amplitude beyond the naive estimate.
The CP-averaged experimental “sum-rule” relation,

together with the observation of small (≈15 %) U-spin breaking in A(D 0→π − K +) vs. A(D 0→K − π +), can be interpreted as suggesting that U-spin is a good symmetry in these decays [461]. Other authors take the large difference between Γ(D 0→K − K +) and Γ(D 0→π − π +) or δS/T∼0.5 as evidence for large U-spin breaking in SCS decays. In Ref. [461], rather than interpreting the amount of U-spin breaking implied by δS by comparing it to T, as in other works, δS is compared to P. It is observed that whereas \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) implies that P must be dominated by the sum of the long distance s- and d-quark penguin contractions, nominal U-spin breaking would imply that δS must be dominated by their difference. A consistent picture emerges in which direct CP asymmetries of order a few per mille are not surprising given the size of Γ(D 0→K − K +)/Γ(D 0→π − π +). However, as always in the flavour decomposition approach, accommodation need not translate to realisation by QCD dynamics. One consequence of this picture is that \(a_{ \mathit{CP} }^{{ \rm dir }} (D^{0} \rightarrow K^{0}_{S} K^{0}_{S} )\) could be as large as ∼0.6 % for \(\mathcal{O}(1)\) strong phases.
Finally, the estimates for the long-distance penguin contractions [466, 468] are reviewed to see if the required enhancement can be realised. Reference [468] employs the one-gluon exchange approximation. The essential ingredients are: (i) 1/N c counting; (ii) D branching ratio data which shows that certain formally 1/m c power-suppressed amplitudes are of same order as their leading (1/m c )0 counterparts; (iii) translation of this breakdown of the 1/m c expansion to the penguin contraction amplitudes, in the approximation of a hard gluon exchange; (iv) use of a partonic quantity as a rough estimator of the hadronic interactions, e.g., final state interactions, underlying the penguin contraction “loops”. This results in a rough estimate for \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) at the few per mille level. The authors of Ref. [468] thus conclude that a SM explanation is plausible, given that their estimate suffers from large uncertainties. In Ref. [466] the penguin contractions are estimated using isospin and information from ππ scattering and unitarity. A fit of the CP-conserving contributions from the CP-averaged branching ratios provides information on the isospin amplitudes and the underlying renormalisation group invariant amplitude contributions. Allowing for three coupled channel contributions to ππ,KK scattering the authors conclude that the observed asymmetries are marginally compatible with the SM.
To summarise, flavour SU(3) or U-spin fits to the D→PP data can accommodate the enhanced penguin amplitudes required to reproduce \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \). There is consensus that in this case \(a_{ \mathit{CP} }^{{ \rm dir }} ( D ^{0} \rightarrow \pi ^{0} \pi ^{0} )\) could lie at the percent level, while \(a_{ \mathit{CP} }^{{ \rm dir }} ( D ^{+} \rightarrow K ^{+} \overline{ K }{} ^{0} )\) could certainly lie at the few per mille level. Under the assumption of nominal SU(3)f breaking in D→PP decays, the enhancement of the long-distance penguin contractions required to realise \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) is not surprising, given the large difference between the D 0→K − K + and D 0→π − π + decay rates. It would of course be of interest to extend the above CP violation studies to the SCS D→VP and D→VV decay modes. Finally, among the works which have attempted to estimate directly the magnitudes of the long distance penguin contractions, there is no consensus on whether they can be enhanced by an order of magnitude beyond the naive penguin amplitude estimates, as would be required in order to explain \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \). Ultimately this question will have to be answered directly via lattice studies.
In the following section, future prospects are discussed. In subsequent sections, several definitive CP-violating signals for NP in SCS D decays will be discussed.
4.4 \(\Delta \mathcal{A}_{ \mathit{CP} } \) in the light of physics beyond the Standard Model
4.4.1 General considerations
Potential NP contributions to \(\Delta \mathcal {A}_{ \mathit{CP} } \) can be parametrised in terms of an effective Hamiltonian valid below the W and top mass scales
where the relevant operators \(\mathcal{Q}_{i}^{(\prime)}\) are defined in Ref. [469]. Introducing the ratios \(R^{{\rm NP},i}_{ K , \pi } \) as the relevant NP hadronic amplitudes (matrix elements \(\langle K ^{-} K ^{+} , \pi ^{-} \pi ^{+} | { \mathcal{Q}^{(\prime )}_{i} } | D \rangle \)) normalised to the leading CP-conserving SM contributions and writing \(C_{i}^{\rm NP} = v_{\rm EW}^{2} / \varLambda_{\rm NP}^{2}\), the relevant NP scale \(\varLambda_{\rm NP}\) is given by [469]
where \(\Delta R^{i} = R^{i}_{ K } + R^{i}_{ \pi }\) and \(R_{ K , \pi }^{\rm SM}\) parametrise the unknown hadronic amplitude ratios associated with the CP-violating SM contributions. Comparing this estimate to the much higher effective scales probed by CP-violating observables in D mixing and also in the kaon sector, one first needs to verify if such large contributions can still be allowed by other flavour constraints. Within the effective theory approach, this can be estimated via so-called “weak mixing” of the effective operators. In particular, time-ordered correlators of \(\mathcal{H}^{\text{eff-NP}}_{|\Delta C|=1}\) with the SM effective weak Hamiltonian can, at the one weak-loop order, induce important contributions to CP violation in both D meson mixing and kaon decays (ϵ′/ϵ). On the other hand, analogous correlators quadratic in \(\mathcal{H}^{\text{eff-NP}}_{|\Delta C|=1}\) turn out to be either chirally suppressed and thus negligible, or yield quadratically divergent contributions, which are thus highly sensitive to particular UV completions of the effective theory [469].
4.4.2 Universality of CP violation in flavour-changing decay processes
The strongest bounds can be derived for a particular class of operators, which transform non-trivially only under the SU(3)
Q
subgroup of the global SM quark flavour symmetry \(\mathcal{G}_{F} = {\rm SU}(3)_{Q} \times{\rm SU}(3)_{U} \times{\rm SU}(3)_{D}\), respected by the SM gauge interactions. In particular one can prove that their CP-violating contributions to ΔF=1 processes (here F generically represents a flavour quantum number) have to be approximately universal between the up and down sectors [454]. Within the SM one can identify two unique sources of SU(3)
Q
breaking given by  and
and  , where Y
q
are the Yukawa matrices and
, where Y
q
are the Yukawa matrices and  denotes the traceless part. Then in the two generation limit, one can construct a single source of CP violation, given by \(J\equiv i [\mathcal{A}_{u}, \mathcal{A}_{d}]\) [470, 471]. The crucial observation is that J is invariant under SO(2) rotations between the \(\mathcal{A}_{u}\) and \(\mathcal{A}_{d}\) eigenbases. Introducing now SU(2)
Q
breaking NP effective operator contributions of the form \(\mathcal{Q}_{L} = [(X_{L})^{ij} \overline{Q}_{i} \gamma^{\mu}Q_{j} ] L_{\mu}\), where Q
i
stands for the left-handed quark doublets, i and j are generation indices, X
L
is a traceless Hermitian flavour matrix and L
μ
denotes a flavour singlet current. It follows that the CP-violating contributions have to be proportional to J and thus invariant under flavour rotations. The universality of CP violation induced by \(\mathcal{Q}_{L}\) can be expressed explicitly as [454]
denotes the traceless part. Then in the two generation limit, one can construct a single source of CP violation, given by \(J\equiv i [\mathcal{A}_{u}, \mathcal{A}_{d}]\) [470, 471]. The crucial observation is that J is invariant under SO(2) rotations between the \(\mathcal{A}_{u}\) and \(\mathcal{A}_{d}\) eigenbases. Introducing now SU(2)
Q
breaking NP effective operator contributions of the form \(\mathcal{Q}_{L} = [(X_{L})^{ij} \overline{Q}_{i} \gamma^{\mu}Q_{j} ] L_{\mu}\), where Q
i
stands for the left-handed quark doublets, i and j are generation indices, X
L
is a traceless Hermitian flavour matrix and L
μ
denotes a flavour singlet current. It follows that the CP-violating contributions have to be proportional to J and thus invariant under flavour rotations. The universality of CP violation induced by \(\mathcal{Q}_{L}\) can be expressed explicitly as [454]
The above identity holds to a very good approximation even in the three-generation framework. In the SM, large values of Y b,t induce a SU(3)/SU(2) flavour symmetry breaking pattern [451] which allows one to decompose X L under the residual SU(2) in a well defined way. Finally, residual SM SU(2) Q breaking is necessarily suppressed by small mass ratios m c,s /m t,b , and small CKM mixing angles. The most relevant implication of Eq. (107) is that it predicts a direct correspondence between SU(3) Q breaking NP contributions to \(\Delta \mathcal{A}_{ \mathit{CP} } \) and ϵ′/ϵ [454]. It follows immediately that stringent limits on possible NP contributions to the latter require SU(3) Q breaking contributions to the former to be below the per mille level (for \(\Delta R^{{\rm NP},i}=\mathcal{O} (1)\)). As a corollary, one can show that within NP scenarios which only break SU(3) Q , existing stringent experimental bounds on new contributions to CP-violating rare semileptonic kaon decays \(K ^{0}_{\mathrm{L}} \rightarrow \pi ^{0} ( \nu \overline { \nu } , \ell^{+} \ell^{-} ) \) put robust constraints on CP asymmetries of corresponding rare charm decays \(D \rightarrow \pi ( \nu \overline{ \nu } , \ell^{+} \ell^{-} ) \). In particular, the SU(3) Q -violating contribution to the CP asymmetry in D→πe + e − has been shown to be less than 2 % [454].
The viability of the remaining 4-quark operators in \(\mathcal{H}^{\text{eff-NP}}_{|\Delta C|=1}\) as explanations of the experimental \(\Delta \mathcal{A}_{ \mathit{CP} } \) value depends crucially on their flavour and chiral structure (a full list can be found in Ref. [469]). In particular, operators involving purely right-handed quarks are unconstrained in the effective theory analysis but may be subject to severe constraints from their UV sensitive contributions to D mixing observables. On the other hand, QED and QCD dipole operators are at present only weakly constrained by nuclear electric dipole moments (EDMs) and thus present the best candidates to address the \(\Delta \mathcal{A}_{ \mathit{CP} } \) puzzle [469].
Finally, note that it was shown that the impact of universality of CP within the alignment framework is to limit the amount of CP violation in D 0–\(\overline{ D }{} ^{0} \) mixing to below ∼20 %, which is interestingly near the current bound. The expected progress in this measurement with the LHCb detector is therefore going to start probing this framework.
4.4.3 Explanations of \(\Delta \mathcal{A}_{ \mathit{CP} } \) within NP models
Since the announcement of the LHCb result, several prospective explanations of \(\Delta \mathcal {A}_{ \mathit{CP} } \) within various NP frameworks have appeared. In the following the implications within some of the well-motivated NP models are discussed.
In the MSSM, the right size of the QCD dipole operator contributions can be generated with non-zero left–right up-type squark mixing contributions \((\delta^{u}_{12})_{LR}\) [418, 472, 473]. Such effects in \(\Delta \mathcal {A}_{ \mathit{CP} } \) can be parametrised as [472]
where \(\tilde{m}\) denotes a common squark and gluino mass scale. At the same time dangerous contributions to D mixing observables are chirally suppressed. It turns out however that even the apparently small \((\delta^{u}_{12})_{LR}\) value required implies a highly nontrivial flavour structure of the UV theory; in particular, large trilinear (A) terms and sizeable mixing among the first two generation squarks (θ 12) are required [472].

Similarly, WED models that explain the quark spectrum through flavour anarchy [452, 474–476] can naturally give rise to QCD dipole contributions affecting \(\Delta \mathcal{A}_{ \mathit{CP} } \) as [477]
where \(m_{\rm KK}\) is the Kaluza–Klein (KK) scale and Y 5 is the five-dimensional Yukawa coupling in appropriate units. Reproducing the experimental value of \(\Delta \mathcal{A}_{ \mathit{CP} } \) requires near-maximal 5D Yukawa coupling, close to its perturbative bound [478, 479] of \(4\pi/\sqrt{N_{\rm KK}} \simeq7\) for \(N_{\rm KK} = 3\) perturbative KK states. In turn, this helps to suppress unrealistic tree-level contributions to CP violation in D 0–\(\overline{ D }{} ^{0} \) mixing [440, 441]. This scenario can also be interpreted within the framework of partial compositeness in four dimensions, but generic composite models typically require smaller Yukawa couplings to explain \(\Delta \mathcal{A}_{ \mathit{CP} } \) and consequently predict sizeable contributions to CP violation in ΔF=2 processes [480].
On the other hand, in the SM extension with a fourth family of chiral fermions \(\Delta \mathcal{A}_{ \mathit{CP} } \) can be affected by 3×3 CKM non-unitarity and b′ penguin operators
However, due to the existing stringent constraints on the new CP-violating phases entering λ b′ [434, 481], only moderate effects comparable to the SM estimates are allowed [460].
Finally, it is possible to relate \(\Delta \mathcal{A}_{ \mathit{CP} } \) to the anomalously large forward–backward asymmetry in the \(t\bar{t}\) system measured at the Tevatron [482] through a minimal model. Among the single-scalar-mediated mechanisms that can explain the top data, only the t-channel exchange of a colour-singlet weak doublet, with a very special flavour structure, is consistent with the total and differential \(t\bar{t}\) cross-section, flavour constraints and electroweak precision measurements [483]. The required flavour structure implies that the scalar unavoidably contributes at tree level to \(\Delta \mathcal{A}_{ \mathit{CP} } \) [484]. The relevant electroweak parameters are either directly measured, or fixed by the top-related data, implying that, for a plausible range of the hadronic parameters, the scalar-mediated contribution is of the right size.
4.4.4 Shedding light on direct CP violation via D→Vγ decays
The theoretical interpretation of \(\Delta \mathcal{A}_{ \mathit{CP} } \) is puzzling: it is above its naive estimate in the SM and it could well be a signal of NP, but it is not large enough to rule out a possible SM explanation. It is then important to identify possible future experimental tests able to distinguish standard vs. non-standard explanations of \(\Delta \mathcal{A}_{ \mathit{CP} } \). Among the NP explanations of \(\Delta \mathcal {A}_{ \mathit{CP} } \), the most interesting ones are those based on a new CP-violating phase in the ΔC=1 chromomagnetic operator. A general prediction of this class of models, that could be used to test this hypothesis from data, is enhanced direct CP violation (DCPV) in radiative decay modes [485].
-
1.
The first key observation to estimate DCPV asymmetries in radiative decay modes is the strong link between the ΔC=1 chromomagnetic operator (\(Q_{8} \sim\bar{u}_{L} \sigma_{\mu\nu} T^{a} g_{s} G_{a}^{\mu\nu} c_{R}\)) and the ΔC=1 electromagnetic-dipole operator (\(Q_{7} \sim\bar{u}_{L} \sigma_{\mu\nu} Q_{u} e F^{\mu\nu} c_{R} \)). In most explicit new-physics models the short-distance Wilson coefficients of these two operators (C 7,8) are expected to be similar. Moreover, even assuming that only a non-vanishing C 8 is generated at some high scale, the mixing of the two operators from strong interactions implies C 7,8 of comparable size at the charm scale. Thus if \(\Delta \mathcal{A}_{ \mathit{CP} } \) is dominated by NP contributions generated by Q 8, it can be inferred that \(|\operatorname{Im}[C^{\rm NP}_{7}(m_{c})] | \approx|\operatorname{Im}[C^{\rm NP}_{8}(m_{c})] | = (0.2 \mbox{--} 0.8) \times10^{-2} \).
-
2.
The second important ingredient is the observation that in the Cabibbo-suppressed D→Vγ decays, where V is a light vector meson with \(u \overline{ u } \) valence quarks (V=ρ 0,ω), Q 7 has a sizeable hadronic matrix element. More explicitly, the short-distance contribution induced by Q 7, relative to the total (long-distance) amplitude, is substantially larger with respect to the corresponding relative weight of Q 8 in D→P + P − decays. Estimating the SM long-distance contributions from data, and evaluating the short-distance CP-violating contributions under the hypothesis that \(\Delta \mathcal{A}_{ \mathit{CP} } \) is dominated by (dipole-type) NP, leads to the following estimate for the maximal direct CP asymmetries in the D→(ρ,ω)γ modes [485]:
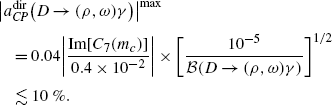 (112)
(112)The case of the ϕ resonance, or better the K + K − γ final state with M KK close to the ϕ peak, is more involved since the matrix element of Q 7 vanishes in the large m c limit for a pure \(s \overline{ s } \) state. However, a non-negligible CP asymmetry can be expected also in this case since: (1) the matrix element of Q 7 is not expected to be identically zero because of sizeable \(\mathcal{O}(\varLambda_{\rm QCD}/m_{c})\) corrections; (2) nonresonant contributions due to (off-shell) ρ and ω exchange can also contribute to the K + K − γ final state. Taking into account these effects, the following estimates for the maximal direct CP asymmetries are obtained [485]:
$$ \everymath{\displaystyle} \begin{array}{@{}l} \bigl| a_{ \mathit{CP} }^{{ \rm dir }} \bigl( D \rightarrow K ^+ K ^- \gamma \bigr)\bigr|^{\rm max} \approx2~\% , \\\noalign{\vspace{6pt}} 2m_K < \sqrt{s} < 1.05 ~\mathrm{GeV} , \\\noalign{\vspace{6pt}} \bigl| a_{ \mathit{CP} }^{{ \rm dir }} \bigl( D \rightarrow K ^+ K ^- \gamma \bigr)\bigr|^{\rm max} \approx6~\% , \\\noalign{\vspace{6pt}} 1.05 ~\mathrm{GeV} < \sqrt{s} < 1.20 ~\mathrm{GeV} . \end{array} $$(113)In the first bin, close to the ϕ peak, the leading contribution is due to the ϕ-exchange amplitude. The contribution due to the nonresonant amplitudes becomes more significant further from the ϕ peak, where the CP asymmetry can become larger.
-
3.
In order to establish the significance of these results, two important issues have to be clarified: (1) the size of the CP asymmetries within the SM, (2) the role of the strong phases.
As far as the SM contribution is concerned, it can first be noticed that short-distance contributions generated by the operator Q 7 are safely negligible. Using the result in Ref. [486], asymmetries are found to be below the 0.1 % level. The dominant SM contribution is expected from the leading non-leptonic four-quark operators, for which the general arguments discussed in Ref. [469] can be applied. The CP asymmetries can be decomposed as \(| a_{ \mathit{CP} }^{{{\rm SM}}} (f)| \approx2 \xi \operatorname{Im} (R_{f}^{{\rm SM}}) \approx0.13~\% \times\operatorname{Im} (R_{f}^{{\rm SM}})\), where ξ≡|V cb V ub /V cs V us |≈0.0007 and \(R_{f}^{{\rm SM}}\) is a ratio of suppressed over leading hadronic amplitudes, naturally expected to be smaller than one. This decomposition holds both for f=ππ,KK and for f=Vγ channels. The SM model explanations of Δa CP require \(R_{ \pi \pi , K K }^{{\rm SM}}\sim3\). While this possibility cannot be excluded from first principles, a further enhancement of one order of magnitude in the D→Vγ mode is beyond any reasonable explanation in QCD. As a result, an observation of \(| a_{ \mathit{CP} }^{{ \rm dir }} ( D \rightarrow V \gamma )| \gtrsim 3~\%\) would be a clear signal of physics beyond the SM, and a clean indication of new CP-violating dynamics associated to dipole operators.
Having clarified that large values of \(| a_{ \mathit{CP} }^{{ \rm dir }} ( D \rightarrow V \gamma )|\) would be a clear footprint of non-standard dipole operators, it can be asked if potential tight limits on \(| a_{ \mathit{CP} }^{{ \rm dir }} ( D \rightarrow V \gamma )|\) could exclude this non-standard framework. Unfortunately, uncertainty on the strong phases does not allow this conclusion to be drawn. Indeed the maximal values for the DCPV asymmetries presented above are obtained in the limit of maximal constructive interference of the various strong phases involved. In principle, this problem could be overcome via time-dependent studies of \(D ( \overline { D }{} ) \rightarrow V \gamma \) decays or using photon polarisation, accessible via lepton pair conversion in D→V(γ ∗→ℓ + ℓ −); however, these types of measurements are certainly more challenging from the experimental point of view.
4.4.5 Testing for CP-violating new physics in the ΔI=3/2 amplitudes
It is possible, at least in principle, to distinguish between NP and the SM as the origin of \(\Delta \mathcal {A}_{ \mathit{CP} } \). If \(\Delta \mathcal{A}_{ \mathit{CP} } \) is due to a chromomagnetic operator, i.e. due to ΔI=1/2 contributions, one can measure CP violation in radiative D decays, as explained in the previous section. Examples of NP models that can be tested in this way are, e.g., flavour-violating supersymmetric squark-gluino loops that mediate the c→ug transition [418, 472, 473]. On the other hand, if \(\Delta \mathcal {A}_{ \mathit{CP} } \) is due to ΔI=3/2 NP one can use isospin symmetry to write sum rules for direct CP asymmetries in D decays [487]. If the sum rules are violated, then NP would be found. An example of a NP model that can be tested in this way is an addition of a single new scalar field with nontrivial flavour couplings [484].
The basic idea behind the ΔI=3/2 NP tests [487, 488] is that in the SM the CP violation in SCS D decays arises from penguin amplitudes which are ΔI=1/2 transitions. On the other hand, ΔI=3/2 amplitudes are CP-conserving in the SM. Moreover, there are no ΔI=5/2 terms in the SM short-distance effective Hamiltonian, and though such contributions can be generated by electromagnetic rescattering (as has been discussed in the context of B→ππ decays [489, 490]) they would also be CP conserving. Observing any CP violation effects in ΔI=3/2 amplitudes would therefore be a clear signal of NP.
In the derivation of the sum rules it is important to pay attention to the potentially important effects of isospin breaking. Isospin symmetry is broken at \({\mathcal{O}}(10^{-2})\), which is also the size of the interesting CP asymmetries. There are two qualitatively different sources of isospin breaking: due to electromagnetic interactions, u and d quark masses, which are all CP-conserving effects, and due to electroweak penguin operators that are a CP-violating source of isospin breaking. The CP-conserving isospin breaking is easy to cancel in the sum rules. As long as the CP-conserving amplitudes completely cancel in the sum rules, which is the case in Ref. [487], the isospin breaking will only enter suppressed by the small CP violation amplitude and is therefore negligible. The electroweak penguin operators, on the other hand, are suppressed by \(\alpha/ \alpha_{S} \sim {\mathcal{O}}(10^{-2})\) compared to the leading CP-violating but isospin conserving penguin contractions of the Q 1,2 operators, and can thus also be safely neglected.
Among the SCS decays, the D→ππ, D→ρπ, D→ρρ, \(D \rightarrow \overline{ K }{} K \pi \), and \(D ^{+}_{ s } \rightarrow K ^{*} \pi \) modes carry enough information to construct tests of ΔI=3/2 NP. The sum rules for D→ππ decays have the nice feature that the charged decay D +→π + π 0 is purely ΔI=3/2. In the SM therefore
If this CP asymmetry is measured to be nonzero, it would be a clear signal of ΔI=3/2 NP. However, if it is found experimentally to be very small, it is still possible that this is only because the strong phase between the SM and NP amplitudes is accidentally small.
This possibility can be checked with more data if time-dependent D(t)→π − π + and D(t)→π 0 π 0 measurements become available,Footnote 67 or if there is additional information on relative phases from a charm factory running on the ψ(3770). The strategy amounts to measuring the weak phase of the ΔI=3/2 amplitude A 3 via generalised triangle constructions that also take isospin breaking into account [487]. If

is found to be nonzero, this would mean there is CP-violating NP in the ΔI=3/2 amplitude.
The above results apply also to D→ρρ decays, but for each polarisation amplitude separately. The corrections due to finite ρ width can be controlled experimentally in the same way as in B→ρρ decays [492]. As long as the polarisations of the ρ resonances are measured (or if the longitudinal decay modes dominate, as is the case in B→ρρ decays), the search for ΔI=3/2 NP could be easier experimentally in D→ρρ decays since there are more charged tracks in the final state. The most promising observable where polarisation measurement is not needed is \(\mathcal{A}_{ \mathit{CP} } ( D ^{+} \rightarrow \rho ^{+} \rho ^{0} )\), which if found nonzero (after the correction for the effect of finite ρ decay widths) would signal ΔI=3/2 NP.
Another experimentally favourable probe is the isospin analysis of the D 0→π + π − π 0 Dalitz plot in terms of D→ρπ decays [493]. There are two combinations of measured amplitudes that are proportional to ΔI=3/2 amplitudes
A measurement of the second sum can be obtained from the D 0→π + π − π 0 Dalitz plot. If the related CP asymmetry

is found to be nonzero, this would mean that the ΔI=3/2 NP contribution is nonzero. If it is found to vanish, however, it could be due to the strong phase difference being vanishingly small.
A definitive answer can be provided by another test that is directly sensitive to the weak phase of A 3. This test is possible if the time-dependent D(t)→π + π − π 0 Dalitz plot is measured. In this case the relative phases between the D 0→ρπ and \(\overline{ D }{} ^{0} \rightarrow \rho \pi \) amplitudes can be obtained (alternatively one could use time integrated entangled decays of ψ(3770) at the charm factory). The presence of a weak phase in A 3 can then be determined from the following sum-rule

A non-vanishing result for Eq. (118) would provide a definitive proof for ΔI=3/2 NP. A similar sum rule for the CP asymmetries rather than the amplitudes was given in Eq. (117). In that case the time-integrated Dalitz plot suffices to determine the sum rule inputs.
The sum rules involving \(D \rightarrow K ^{(*)} \overline{ K }{} ^{(*)} \pi \) decays are somewhat more complex because there are at least three particles in the final state. Nevertheless, it is possible to construct purely ΔI=3/2 matrix elements from appropriate sums of decay amplitudes, and these can in principle be determined from amplitude analyses of the multibody final states. It is also possible to search for CP violation in ΔI=3/2 amplitudes using \(D ^{+}_{ s } \rightarrow K ^{*} \pi \) decays. The sum
is ΔI=3/2 and can be measured from the common Dalitz plot for \(D ^{+}_{ s } \rightarrow K ^{0}_{\mathrm{S}} \pi ^{+} \pi ^{0} \) decay. Direct CP violation in this sum, i.e.,

would necessarily be due to ΔI=3/2 NP contributions. Additional information on the absolute value of \(|A( D ^{+}_{ s } \rightarrow \pi ^{+} K ^{*0} ) |\) can be obtained from the \(D ^{+}_{ s } \rightarrow \pi ^{+} K ^{+} \pi ^{-} \) three-body decay. Analogous tests using \(D ^{+}_{ s } \rightarrow \rho K ^{*} \) decays also exist.
4.5 Potential for lattice computations of direct CP violation and mixing in the D 0–\(\overline{ D }{} ^{0} \) system
In searches for NP using charmed mesons, it is obviously crucial to determine accurately the size of SM contributions. In the next few paragraphs the prospects for such a determination in the future using the methods of lattice QCD are discussed.
Lattice QCD provides a first-principles method for determining the strong-interaction contributions to weak decay and mixing processes. It has developed into a precision tool, allowing determinations of the light hadron spectrum, decay constants, and matrix elements such as B K and B B with percent-level accuracy. For reviews and collections of recent results, see Refs. [109, 494]. The results provide confirmation that QCD indeed describes the strong interactions in the non-perturbative regime, as well as providing predictions that play an important role in searching for new physics by looking for inconsistencies in unitarity triangle analyses.
Results with high precision are, however, only available for processes involving single hadrons and a single insertion of a weak operator. For the D 0 system, the “high-precision” quantities are thus the matrix elements describing the short-distance parts of D 0–\(\overline{ D }{} ^{0} \) mixing and the matrix elements of four-fermion operators arising after integrating out NP. The methodology for such calculations is in place (and has been applied successfully to the K and B meson systems), and results are expected to be forthcoming in the next one to two years.
More challenging, and of course more interesting, are calculations of the decay amplitudes to ππ and \(K \overline { K }{} \). For kaon physics, this is the present frontier of lattice calculations. One must deal with two technical challenges: (i) the fact that one necessarily works in finite volume so the states are not asymptotic two-particle states and (ii) the need to calculate Wick contractions (such as the penguin-type contractions) which involve gluonic intermediate states in some channels. The former challenge has been solved in principle by the work of Lüscher [495, 496] and Lellouch and Lüscher [497] for the K→ππ case, while advances in lattice algorithms and computational power have allowed the numerical aspects of both challenges to be overcome. There are now well controlled results for the K→(ππ) I=2 amplitude [498] and preliminary results for the K→(ππ) I=0 amplitude [499]. It is likely that results to ∼10 % accuracy for all amplitudes will be available in a few years. Note that, once a lattice calculation is feasible, it will be of roughly equal difficulty to obtain results for the CP-conserving and CP-violating parts.
To extend these results to the charm case, one must face a further challenge. This is that, even when one has fixed the strong-interaction quantum numbers of a final state, say to I=S=0, the strong interactions necessarily bring in multiple final states when E=m D . For example, ππ and \(K \overline { K }{} \) states mix with ηη, 4π, 6π, etc. The finite-volume states that are used by lattice QCD are inevitably mixtures of all these possibilities, and one must learn how, in principle and in practise, to disentangle these states so as to obtain the desired matrix element. Recently, in Ref. [500], a first step towards developing a complete method has been taken, in which the problem has been solved in principle for any number of two-particle channels, assuming that the scattering is dominantly S-wave. This is encouraging, and it may be that this method will allow semi-quantitative results for the amplitudes of interest to be obtained. Turning this method into practise is expected to take three to five years due to a number of numerical challenges (in particular the need to calculate several energy levels with good accuracy). It is also expected to be possible to generalise the methodology to include four particle states; several groups are actively working on the theoretical issues. It is unclear at this stage, however, what time scale one should assign to this endeavour.
Finally, the possibility of calculating long-distance contributions to D 0–\(\overline{ D }{} ^{0} \) mixing using lattice methods should be considered. Here the challenge is that there are two insertions of the weak Hamiltonian, with many allowed states propagating between them. Some progress has been made recently on the corresponding problem for kaons [501, 502] but the D 0 system is much more challenging. The main problem is that, as for the decay amplitudes, there are many strong-interaction channels with E<m D . Further theoretical work is needed to develop a practical method.
4.6 Interplay of \(\Delta \mathcal{A}_{ \mathit{CP} } \) with non-flavour observables
4.6.1 Direct CP violation in charm and hadronic electric dipole moments
Models in which the primary source of flavour violation is linked to the breaking of chiral symmetry (left–right flavour mixing) are natural candidates to explain direct CP violation in SCS D meson decays, via enhanced ΔC=1 chromomagnetic operators. Interestingly, the chromomagnetic operator generates contributions to D 0–\(\overline{ D }{} ^{0} \) mixing and ϵ′/ϵ that are always suppressed by at least the square of the charm Yukawa couplings, thus naturally explaining why they have remained undetected.
On the other hand, the dominant constraints are posed by the neutron and nuclear EDMs, which are expected to be close to their experimental bounds. This result is fairly robust because the Feynman diagram contributing to quark EDMs has essentially the same structure as that contributing to the chromomagnetic operator.
In the following the connection between \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) and hadronic EDMs in concrete NP scenarios is discussed, following the analyses of Refs. [472, 473].
Supersymmetry
The leading SUSY contribution to \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) stems from loops involving up-squarks and gluinos and off-diagonal terms in the squark squared-mass matrix in the left–right up sector, the so-called \((\delta^{u}_{12})_{LR}\) mass-insertion. As can be seen from Eqs. (108)–(109) and taking into account the large uncertainties involved in the evaluation of the matrix element, it can be concluded that a supersymmetric theory with left-right up-squark mixing can potentially explain the LHCb result.
Among the hadronic EDMs, the best constraints come from mercury and neutron EDMs. Their current experimental bounds are |d n |<2.9×10−26 e cm (90 % C.L.) and \(|d_{\rm Hg}| < 3.1 \times10^{-29}~e\,\mbox{cm}~(95~\%~\mbox{C.L.})\). In the mass-insertion approximation one can find
and therefore it has to be seen whether a concrete SUSY scenario can naturally account for the required level of suppression \(|\operatorname{Im}(\delta^{u}_{11})_{LR}| \lesssim10^{-6}\).
Generalised trilinear terms
While scenarios in which flavour violation is restricted to the trilinear terms can be envisaged, it is natural to generalise the structure of Eq. (109) to all squarks and take
where \(\theta^{q}_{ij}\) are generic mixing angles. This pattern can be obtained when the matrices of the up and down trilinear coupling constants follow the same hierarchical pattern as the corresponding Yukawa matrices but they do not respect exact proportionality.
It is found that \(\theta^{q}_{ij}\) can all be of order unity not only in the up, but also in the down sector, thanks to the smallness of the down-type quark masses entering \((\delta^{d}_{ij})_{LR}\). The only experimental bounds in tension with this scenario are those on \(|\theta^{u,d}_{11}|\) coming from the neutron EDM.
Split families
The severe suppression of \((\delta^{u}_{21} )^{\rm eff}_{RL}\) stemming from the charm mass can be partially avoided in a framework with split families, where the first two generations of squarks are substantially heavier than \(\tilde{t}_{1,2}\) and \(\tilde{b}_{L}\), the only squarks required to be close to the electroweak scale by naturalness arguments. In this case the effective couplings relevant to \(\Delta a_{ \mathit{CP} }^{{{\rm SUSY}}} \) can be decomposed as follows
Notice that this scenario takes advantage of the large \((\delta^{u}_{33})_{LR}\sim A m_{t}/\tilde{m}\) which is assumed to be of order one. The following two options can be considered to explain the LHCb results:
Gluino–squark loops yield an EDM (d u ) and a chromo-EDM (\(d_{u}^{c}\)) for the up quark proportional to \(d^{(c)}_{u} \sim \operatorname{Im} [(\delta^{u}_{13})_{LL}(\delta ^{u}_{31})_{RR} ]\) and it turns out that
In conclusion, the EDM bounds require a strong hierarchical structure in the off-diagonal terms of the RR up-squark mass matrix, as happens in models predicting \((\delta^{u}_{ij})_{RR} \sim(m_{u_{i}}/m_{u_{j}})/|V_{ij}|\).
Supersymmetric flavour models
In models where the flavour structure of the soft breaking terms is dictated by an approximate flavour symmetry, \((\delta^{u}_{LR})_{12}\) is generically flavour-suppressed by \((m_{c}\vert V_{us}\vert /\tilde{m})\), which is of order a few times 10−4. There is however additional dependence on the ratio between flavour-diagonal parameters, \(A/\tilde{m}\), and on unknown coefficients of order one, that can provide enhancement by a small factor. In most such models, the selection rules that set the flavour structure of the soft breaking terms relate \((\delta^{u}_{LR})_{12}\) to \((\delta ^{d}_{LR})_{12}\) and to \((\delta^{u,d}_{LR})_{11}\), which are bounded from above by, respectively, ϵ′/ϵ and EDM constraints. Since both ϵ′/ϵ and EDMs suffer from hadronic uncertainties, small enhancements due to the flavour-diagonal supersymmetric parameters cannot be ruled out. It is thus possible to accommodate \(\Delta \mathcal{A}_{ \mathit{CP} } \sim 0.006\) in supersymmetric models that are non-minimally flavour violating, but—barring hadronic enhancements in charm decays—it takes a fortuitous accident to lift the supersymmetric contribution above the permille level [473].
New-physics scenarios with Z-mediated FCNC
Effective FCNC couplings of the Z boson to SM quarks can appear in the SM with non-sequential generations of quarks, models with an extra U(1) symmetry or models with extra vector-like doublets and singlets. The effective FCNC Lagrangian can be written as

The chromomagnetic operator is generated at the one-loop level, with leading contribution from Z-top exchange diagrams leading to
The presence of new CP-violating phases in the couplings \((g^{Z}_{L,R})_{ij}\) are also expected to generate hadronic EDMs. In particular, one can find
and therefore \(\Delta\mathcal{A}^{Z\text{-}{\rm FCNC}}_{ \mathit{CP} }= \mathcal {O}(10^{-2})\) only, provided \(\operatorname{Im}(g^{Z}_{R})_{ut}/\operatorname{Im}(g^{Z}_{R})_{ct}\lesssim10^{-3}\).
In NP scenarios with Z-mediated FCNCs, the most interesting FCNC processes in the top sector are t→cZ and t→uZ, which arise at the tree level. In particular,
which is within the reach of the LHC for the values of \((g^{Z}_{R})_{tc}\) relevant to \(\Delta\mathcal{A}^{Z\text{-}{\rm FCNC}}_{ \mathit{CP} }\).
New-physics scenarios with scalar-mediated FCNC
Finally, it is instructive to analyse a new-physics framework with effective FCNC couplings to SM quarks of a scalar particle h. The effective Lagrangian reads
Also in this case the chromomagnetic operator is generated at the one-loop level, with a leading contribution from h-top exchange diagrams. This leads to
As in all the other frameworks, the most severe constraints are posed by the hadronic EDMs
With scalar-mediated FCNCs, the potentially most interesting signals are the rare top decays t→ch or t→uh, if kinematically allowed. In particular,
which could be within the reach of the LHC.
4.6.2 Interplay of collider physics and a new physics origin for \(\Delta \mathcal{A}_{ \mathit{CP} } \)
The first evidence for direct CP violation in SCS D decays may have interesting implications for NP searches around the TeV scale at the LHC. The NP contribution to \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) can be fully parametrised by a complete set of ΔC=1 effective operators at the charm scale. As shown by the authors of Ref. [469] only a few of these operators can accommodate the LHCb result without conflicting with present bounds from D 0–\(\overline{ D }{} ^{0} \) mixing and ϵ′/ϵ. In particular four-fermion operators of the form \(\mathcal{O}^{q}=(\bar{u}_{R}\gamma^{\mu}c_{R})(\bar{q}_{R}\gamma_{\mu}q_{R})\) with q=u,d,s are promising since they do not lead to flavour violation in the down-type quark sector. The corresponding Wilson coefficients are defined as \(1/\varLambda_{q}^{2}\). Assuming the SM expectation for \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) is largely subdominant, the LHCb measurement suggests a scale of Λ q ≃15 TeV [469].
There is an immediate interplay between charm decay and flavour (and CP) conserving observables at much higher energies provided \(\mathcal {O}^{q}\) arises from a heavy NP state exchanged in the s-channel. Under this mild assumption \(\mathcal{O}^{q}\) factorises as the product of two quark currents and the same NP induces D 0–\(\overline { D }{} ^{0} \) mixing and quark compositeness through the \((\bar{u}_{R} \gamma_{\mu}c_{R})^{2}\) and \((\bar{q}_{R} \gamma_{\mu}q_{R})^{2}\) operators, respectively. Denoting their respective Wilson coefficients by \(\varLambda_{\bar{u} c}\) and \(\varLambda_{\bar{q} q}\), the relation \(\varLambda_{q}=\sqrt{\varLambda_{\bar{u} c}\varLambda_{\bar{q} q}}\) is predicted. The D 0–\(\overline{ D }{} ^{0} \) mixing bound on NP implies \(\varLambda_{\bar{u} c}\gtrsim1200 ~\mathrm{TeV} \) [441]. Combining this stringent ΔC=2 bound with the ΔC=1 scale suggested by \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) thus generically requires \(\varLambda_{\bar{q} q}\lesssim200 ~\mathrm{GeV} \), which is a rather low compositeness scale for the light quark flavours.
Quark compositeness can be probed at the LHC through dijet searches. Actually for the up or the down quark the low scale suggested by \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) is already excluded by the Tevatron [503, 504]. On the other hand dijet searches are less sensitive to contact interactions involving only the strange quark since the latter, being a sea quark, has a suppressed parton distribution function in the proton. The authors of Ref. [505] showed that a first estimation at the partonic level of the extra dijet production from a \((\bar{s}_{R} \gamma_{\mu}s_{R})^{2}\) operator with a scale of \(\varLambda_{\bar{s} s}\sim200 ~\mathrm{GeV} \) is marginally consistent, given the \(\mathcal{O}(1)\) uncertainty of the problem, with the bounds from the ATLAS and CMS experiments [506, 507].
One concludes that an \(\mathcal{O}^{s}\) operator induced by a s-channel exchanged NP can accommodate the \(\Delta a_{ \mathit{CP} }^{{ \rm dir }} \) measurement without conflicting with ΔC=2, ϵ′/ϵ and dijet searches. Furthermore such a NP scenario makes several generic predictions both for charm and high-\(p_{\rm T}\) physics: (1) most of the CP asymmetry is predicted to be in the K + K − channel, (2) CP violation in D 0–\(\overline { D }{} ^{0} \) mixing should be observed in the near future, and (3) an excess of dijets at the LHC is expected at a level which should be visible in the 2012 data.
4.7 Future potential of LHCb measurements
4.7.1 Requirements on experimental precision
The ultimate goal of mixing and CP violation measurements in the charm sector is to reach the precision of the SM predictions (or better). In some cases this requires measurements in several decay modes in order to distinguish enhanced contributions of higher order SM diagrams from effects caused by new particles.
Indirect CP violation is constrained by the observable A Γ (see Eq. (82)). The CP-violating parameters in this observable are multiplied by the mixing parameters x D and y D , respectively. Hence, the relative precision on the CP-violating parameters is limited by the relative precision of the mixing parameters. Therefore, aiming at a relative precision below 10 % and taking into account the current mixing parameter world averages, the target precision would be 2–3×10−4. Indirect CP violation is expected in the SM at the order of 10−4, and therefore the direct CP violation parameter contributing to A Γ has to be measured to a precision of 10−3 in order to distinguish the two types of CP violation in A Γ .
Direct CP violation is not expected to be as large as the current world average of \(\Delta \mathcal {A}_{ \mathit{CP} } \) in most other decay modes. However, a few large CP violation signatures are expected in various models, as discussed in the previous sections. Estimations based on flavour-SU(3) and U-spin symmetry lead to expectations of \(a_{ \mathit{CP} }^{{ \rm dir }} ( D ^{+} \rightarrow K ^{+} \overline { K }{} ^{0} )\gtrsim0.1~\% \) and \(a_{ \mathit{CP} }^{{ \rm dir }} (D^{0} \rightarrow K ^{0}_{\mathrm{S}} K ^{0}_{\mathrm{S}} ) \sim 0.6~\%\). Considerations assuming universality of ΔF=1 transitions lead to a limit of \(a_{ \mathit{CP} }^{{ \rm dir }} ( D \rightarrow \pi e ^{+} e ^{-} )\lesssim2~\%\). Enhanced electromagnetic dipole operators can lead to \(a_{ \mathit{CP} }^{{ \rm dir }} ( D \rightarrow V\gamma )\) of a few %, equivalent to the influence of chromomagnetic dipole operators on \(\Delta \mathcal{A}_{ \mathit{CP} } \). Additional information can be obtained from time-dependent studies of D→Vγ decays or from angular analyses of D→Vl + l − decays.
Analyses of ΔI=3/2 transitions involve asymmetry measurements of several related decay modes. Examples are the decays D→ππ, D→ρπ, D→ρρ, \(D \rightarrow \overline{ K } K \pi \), and \(D ^{+}_{ s } \rightarrow K ^{*} \pi \). The number of final state particles in these decays varies from two to six (counting the pions from \(K ^{0}_{\mathrm{S}} \) decays) and many of these modes contain neutral pions in their final state. The precision for modes involving neutral pions or photons will be limited by the ability of the calorimeter to identify these particles in the dense hadronic environment. An upgraded calorimeter with smaller Molière radius would greatly extend the physics reach in this area.Footnote 68
In general, a precision of 5×10−4 or better for asymmetry differences as well as individual asymmetries is needed for measurements of other SCS charm decays. While measurements of time-integrated raw asymmetries at this level should be well within reach, the challenge lies in the control of production and detection asymmetries in order to extract the physics asymmetries of individual decay modes. This can be achieved by assuming that there is no significant CP violation in CF decay modes.
4.7.2 Prospects of future LHCb measurements
Numbers of events in various channels are projected directly from the numbers reconstructed in the 2011 data set, in most cases. This involves assumptions that the prompt charm cross-section will increase by a factor of 1.8 when doubling the centre-of-mass energy from \(\sqrt{s} = 7 ~\mathrm{TeV} \) to \(\sqrt{s} = 14 ~\mathrm{TeV} \), that the integrated luminosity will increase from 1 fb−1 to 50 fb−1, and that the trigger efficiency for charm will increase by a factor of 2 as the current hardware trigger requirement is effectively removed (or substantially relaxed). Additionally, a factor of 3.5 times greater efficiency in channels with \(K ^{0}_{\mathrm{S}} \rightarrow \pi ^{-} \pi ^{+} \) daughters is predicted based on progress made in the trigger software between 2011 and 2012. This primarily results from reconstructing candidates which decay downstream of the vertex detector. The results of this exercise are summarised in Table 10 for D 0 decays and in Table 11 for D + and \(D ^{+}_{ s } \) decays.
Estimating the physics reach with the projected data sets requires a number of assumptions. The statistical precision generally improves as \(1 / \sqrt{N}\). Estimating the systematic error, and therefore ultimate physics reach, is more of an art. It is often the case that data can be used to control systematic uncertainties at the level of the statistical error, but the extent to which this will be possible cannot be reliably predicted. In some cases controlling systematic uncertainties will require sacrificing some of the statistics to work with cleaner signals or with signals which populate only parts of the detector where the performance is very well understood. Estimates of sensitivity to CP violation in mixing generally depend on the values of the mixing parameters—the larger the number of mixed events, the larger the effective statistics contributing to the corresponding CP violation measurement.
The estimated statistical precisions for parameters of mixing and CP violation in the D 0 system are presented in Table 12. The precision for measuring \((x_{D}^{\prime2}, y_{D}^{\prime})\) using the time-dependence of the wrong-sign (WS) to right-sign (RS) Kπ rate comes from extrapolating the BaBar [409] and Belle [508] sensitivities.Footnote 69 The precision for measuring r M using the ratio of WS to RS Kμν events assumes the central value to be 2.5×10−5. The S/B ratio is assumed to be 30 times better than reported by BaBar [509] for their similar Keν analysis. Background can be reduced by a factor of 10 using LHCb’s excellent vertex resolution to remove candidates with decay time less than twice the D 0 lifetime—a requirement which only modestly reduces the WS signal as its decay time distribution has the form dN/dt∝t 2 e −Γt. In addition, the excellent vertex resolution and the decay time requirement allow the neutrino momentum, and hence the D ∗+−D 0 mass difference to be measured with better resolution than was possible in the e + e − experiments. BaBar demonstrated that using a doubly-tagged sample of semileptonic decay candidates provides the same mixing sensitivity as the more traditional singly-tagged sample [510]. By combining singly- and doubly-tagged samples, it should be possible to effectively double the statistics.
The projected sensitivities for the two-body direct CP violation measurements are relatively solid: the 2011 \(\Delta \mathcal{A}_{ \mathit{CP} } \) measurements provide benchmark samples with full analysis cuts including fiducial cuts necessary to control systematic uncertainties for measuring \(\Delta \mathcal{A}_{ \mathit{CP} } \). The systematic errors for the separate \(\mathcal {A}_{ \mathit{CP} } ( K ^{-} K ^{+} )\) and \(\mathcal{A}_{ \mathit{CP} } ( \pi ^{-} \pi ^{+} )\) measurements will be more challenging and may require sacrificing statistical precision. The projections for measuring y CP and A Γ using K − K + and π − π + should also be robust as the same samples will be used for these analyses as for the \(\mathcal{A}_{ \mathit{CP} } \) measurements.
The projected precision for measuring (x D ,y D ) from \(D ^{0} \rightarrow K ^{0}_{\mathrm{S}} \pi ^{-} \pi ^{+} \) comes from scaling the Belle [416] and BaBar [511] sensitivities. The statistical precisions could be even better as LHCb’s prompt sample will be enhanced at higher decay times where the mixing effects are larger. By contrast, D 0 mesons from semileptonic B decays should be unbiased in this variable, providing a useful sample at lower decay times.
The estimated statistical precisions for DCPV in D + measurements are presented in Table 13. The estimates for the phase-space integrated CP violation rates are scaled by \(1/\sqrt{N}\) and are then increased by a factor of two to allow for using tighter cuts to control systematic uncertainties. The estimates for measuring CP violation in the magnitudes and phases of quasi-two-body amplitudes contributing to three-body final states come from scaling the BaBar sensitivities for time-integrated CP violation in D 0→π − π + π 0 and D 0→K − K + π 0 by \(1/\sqrt{N}\). The angular moments of the cosine of the helicity angle of the D decay products reflect the spin and mass structure of the intermediate resonant and nonresonant amplitudes with no explicit model dependence. The difference between the angular moment distributions observed in D 0 and \(\overline{ D }{} ^{0} \) decays provides sensitivity to CP violation in the magnitudes (or fractions) and phases of amplitudes about equal to that of model-dependent fits. The angular moment differences are robust, in the sense that they are model-independent, but they are less specific compared to the results from model-dependent analyses: they indicate only the spins and mass ranges where particle and antiparticle amplitudes differ, but do not identify a specific CP-violating intermediate state or how much it varies. The sensitivity to CP violation in any contributing amplitude depends on how much it contributes to the three-body decay, and also on the other amplitudes with which it interferes. For this reason, ranges of sensitivity are indicated rather than single values. No sensitivities for CP violation measurements in three-body \(D ^{+}_{ s } \) decay channels are estimated explicitly. They can be estimated roughly by extrapolating from the numbers for D + decays by scaling by \(1/\sqrt{N}\). These estimates should be degraded slightly as the lifetime of the D + is about twice that of the \(D ^{+}_{ s } \) meson, making it easier to select clean D + samples.
4.8 Conclusion
LHCb has proven its capability of performing high-precision charm physics measurements. The experiment is ideally suited for CP violation searches and for measurements of decay-time-dependent processes such as mixing.
Finding evidence for a non-zero value of \(\Delta \mathcal{A}_{ \mathit{CP} } \) has raised the question of whether or not this may be interpreted as the first hint of physics beyond the SM at the LHC. Within the SM the central value can only be explained by significantly enhanced penguin amplitudes. This enhancement is conceivable when estimating flavour SU(3) or U-spin breaking effects from fits to D→PP data. However, attempts at estimating the long distance penguin contractions directly have not yielded conclusive results to explain the enhancement.
Lattice QCD has the potential of assessing the penguin enhancement directly. However, several challenges arise which make these calculations impossible at the moment. Following promising results on K→ππ decays, additional challenges arise in the charm sector as ππ and KK states mix with ηη, 4π, 6π and other states. Possible methods have been proposed and results may be expected in three to five years time.
General considerations on the possibility of interpreting \(\Delta \mathcal{A}_{ \mathit{CP} } \) in models beyond the SM have led to the conclusion that an enhanced chromomagnetic dipole operator is required. These operators can be accommodated in minimal supersymmetric models with non-zero left-right up-type squark mixing contributions or, similarly, in warped extra dimensional models. Tests of these interpretations beyond the SM are needed. One promising group of channels are radiative charm decays where the link between the chromomagnetic and the electromagnetic dipole operator leads to predictions of enhanced CP asymmetries of several percent. These can be measured to sufficient precision at the LHCb upgrade.
Another complementary test is to search for contributions beyond the SM in ΔI=3/2 amplitudes. This class of amplitudes leads to several isospin relations which can be tested in a range of decay modes, e.g. D→ππ, D→ρπ, \(D \rightarrow K \overline{ K }\), etc. Several of these measurements, such as the Dalitz plot analysis of the decay D 0→π + π − π 0, can be performed at LHCb.
Beyond charm physics, the chromomagnetic dipole operators would affect the neutron and nuclear EDMs, which are expected to be close to the current experimental bound. Similarly, rare FCNC top decays are expected to be enhanced, if kinematically allowed. Furthermore, quark compositeness can be related to the \(\Delta \mathcal{A}_{ \mathit{CP} } \) measurement and tested in dijet searches. Current results favour the NP contribution to be located in the D 0→K − K + decay as the strange quark compositeness scale is less well constrained. Measurements of the individual asymmetries of sufficient precision will be possible at the LHCb upgrade.
The charm mixing parameters have not yet been precisely calculated in the SM. An inclusive approach based on an operator product expansion relies on the expansion scale being small enough to allow convergence and furthermore involves the calculation of a large number of unknown matrix elements. An exclusive approach sums over intermediate hadronic states and requires very precise branching ratio determinations of these final states which are currently not available. Contrary to the SM, contributions beyond the SM can be calculated reliably. With the SM contribution to indirect CP violation being <10−4, the LHCb upgrade is ideally suited to cover the parameter space available for enhanced asymmetries beyond the SM. Measurements in several complementary modes will permit the extraction of the underlying theory parameters with high precision.
The LHCb upgrade will allow to constrain CP asymmetries and mixing observables to a level of precision which, in most of the key modes, cannot be matched by any other experiment foreseen on a similar timescale. This level of precision should permit us not only to discover CP violation in charm decays but also to unambiguously understand its origin.
5 The LHCb upgrade as a general purpose detector in the forward region
The previous sections have focussed on flavour physics observables that are sensitive to physics beyond the SM. However, LHCb has excellent potential in a range of other important topics. As discussed in this section, the detector upgrade will further enhance the capability of LHCb in these areas, so that it can be considered as a general purpose detector in the forward region. LHCb may also be able to make a unique contribution to the field of heavy ion physics, by studying soft QCD and heavy flavour production in pA collisions. The first pA run of the LHC will clarify soon the potential of LHCb in this field.
5.1 Quarkonia and multi-parton scattering
The mechanism of heavy quarkonium production is a long-standing problem in QCD. An effective field theory, non-relativistic QCD (NRQCD), provides the foundation for much of the current theoretical work. According to NRQCD, the production of heavy quarkonium factorizes into two steps: a heavy quark–antiquark pair is first created perturbatively at short distances and subsequently evolves non-perturbatively into quarkonium at long distances. The NRQCD calculations depend on the colour-singlet (CS) and colour-octet (CO) matrix elements, which account for the probability of a heavy quark–antiquark pair in a particular colour state to evolve into heavy quarkonium. The CS model [512, 513], which provides a leading-order (LO) description of quarkonia production, was first used to describe experimental data. However, it underestimates the observed cross-section for single J/ψ production at high p T at the Tevatron [514]. To resolve this discrepancy the CO mechanism was introduced [515]. The corresponding matrix elements were determined from the large-p T data as the CO cross-section falls more slowly than that for CS. More recent higher-order calculations [516–519] close the gap between the CS predictions and the experimental data [520] reducing the need for large CO contributions.
Traditionally, quarkonia production studies at hadron colliders have focussed on the study of J/ψ, ψ(2S) and ϒ(nS) decays to dimuon or dielectron pairs [520]. The LHCb programme so far has followed this pattern with measurements of many cross-sections already published [521–525]. As an example of the quality of the data, Fig. 25 shows the ϒ mass distribution. By the time of the upgrade in 2018, data samples corresponding to several fb−1 will have been collected at \(\protect\sqrt{s} = 7, 8\ \mbox{and}\ 14 ~\mathrm{TeV} \) and the results will be dominated by systematic uncertainties. Therefore, new probes of quarkonia production will be pursued. Two possibilities are detailed here: multiple quarkonia production and quarkonia production via hadronic decay modes. These studies will profit from the higher integrated luminosity and improved trigger. These modes provide clear signals in the detector and will be relatively uneffected by the increased pile-up.
Invariant mass distribution of selected ϒ candidates from 25 pb−1 of data collected in 2010 [524]. The ϒ(1S), ϒ(2S) and ϒ(3S) states are clearly resolved. The results of a maximum likelihood fit are superimposed
As the cross-sections for charmonium production at the LHC are large [521–523, 525], the question of multiple production of these states in a single proton–proton collision naturally arises. Studies of double hidden charm and hidden and associated open charm production have been proposed as probes of the quarkonium production mechanism [526]. In proton–proton collisions contributions from other mechanisms, such as double parton scattering (DPS) [527–529] or the intrinsic charm content of the proton [530], are possible. First studies of both processes have been carried out with the current LHCb data; more details can be found in Refs. [304, 531].
LO colour singlet calculations for the gg→J/ψJ/ψ process in perturbative QCD exist and give results consistent with the data [532–534]. In the LHCb fiducial region (2<y J/ψ <4.5, \(p^{\mathrm {T}}_{ { J / \psi } }<10~\mathrm {GeV}/c\), where y J/ψ and \(p^{\mathrm{T}}_{ { J / \psi } }\) represent the rapidity and transverse momentum of the J/ψ, respectively) these calculations predict the J/ψJ/ψ production cross-section to be 4.1±1.2 nb [534] in agreement with the measured value of 5.1±1.0 nb [531]. Similar calculations exist for the case of double ϒ(1S) production. For the case of J/ψ plus ϒ(1S) production no leading order diagrams contribute and hence the rate is expected to be suppressed in Single Parton Scattering (SPS). This leads to an “unnatural” ordering of the cross-section values: \(\sigma^{ { J / \psi } { J / \psi } }_{gg} > \sigma^{ \varUpsilon{(1S)} \varUpsilon{(1S)} }_{gg} > \sigma^{ \varUpsilon{(1S)} { J / \psi } }_{gg}\).
The DPS contributions to all these double onia production modes can be estimated, neglecting partonic correlations in the proton, as the product of the measured cross-sections of the sub-processes involved divided by an effective cross-section [527–529, 535]. The value of the latter is determined from multi-jet events at the Tevatron to be \(\sigma^{\mathrm {DPS}}_{\mathrm{eff}}= 14.5\pm1.7^{+1.7}_{-2.3}~\mathrm{mb}\) [536]. At \(\protect\sqrt{s} = 7 ~\mathrm{TeV} \) the contribution from this source to the total cross-section is similar in size to the LO contribution from SPS. For DPS the ordering of the cross-section values is: \(\sigma ^{ { J / \psi } { J / \psi } }_{\rm DPS} > \sigma^{ \varUpsilon{(1S)} { J / \psi } }_{\rm DPS} >\sigma ^{ \varUpsilon{(1S)} \varUpsilon {(1S)} }_{\rm DPS}\).
The expected cross-sections for a few double quarkonia processes, together with their yields, are summarized in Table 14. Measurements of the cross-sections and properties in these modes will allow the two contributions to be disentangled.
As well as probing the production mechanism these studies are sensitive to a potential first observation of tetraquark states [534] and of χ b and η b states decaying in the double J/ψ mode. Based on the cross-sections and branching ratios given in Ref. [537], 500 (1500) fully reconstructed χ b0(1P) (χ b2(1P)) are expected with the upgraded detector and these decays will be visible at LHCb. In the case of the η b state, several estimates exist, based on values of the branching ratio η b →J/ψJ/ψ ranging from 10−6 to 10−8 [538], corresponding to yields of 0.02 to 5 events.
The upgraded detector is expected to have excellent hadron identification capabilities both offline and at the trigger level. As discussed in Ref. [539], this allows charmonium studies to be performed in hadronic decay modes. A particularly convenient mode is the \(p\overline{p}\) final state. This is accessible for the J/ψ, η c , χ cJ , h c and ψ(2S) mesons. Extrapolating from studies with the current detector large inclusive samples of these decays will be collected. For example around 0.5 million \(\eta _{ c } \rightarrow p \overline {p}\) will be collected.
Hadronic decays of heavy bottomonium have received less attention in the literature [538]. The high mass implies a large phase space for many decay modes, but consequently the branching ratio for each individual mode is reduced. In Ref. [538] it is estimated that the \(\eta_{b} \rightarrow D^{*} \overline{D}\) branching fraction is 10−5 and the \(\eta_{b} \rightarrow D \overline{D} \pi\) rate may be a factor of ten higher. Though no specific studies have been performed, based on the studies of double open charm production given in Ref. [304] it is plausible that an η b signal will be detected in this mode with the upgraded detector.
5.2 Exotic meson spectroscopy
The spectroscopy of bound states formed by heavy quark–antiquark pairs (c or b quarks), has been extensively studied from both theoretical and experimental points of view since the discovery of the J/ψ state in 1974 [540, 541] and the discovery of the ϒ(1S) state in 1977 [542]. Until recently, all experimentally observed charmonium (\(c\bar{c}\)) and bottomonium (\(b\bar{b}\)) states matched well with expectations.
However, in 2003, a new and unexpected charmonium state was observed by the Belle experiment [543] and then confirmed independently by the BaBar [544], CDF [545] and D0 [546] experiments. This new particle, referred to as the X(3872), was observed in B→X(3872)K decays, in the decay mode X(3872)→J/ψπ + π − and has a mass indistinguishable (within uncertainties) from the \(D^{*0} \overline{ D }{} ^{0} \) threshold [520]. Several of the X(3872) parameters are unknown (such as its spin) or have large uncertainties, but this state does not match any predicted charmonium state [520]. The discovery of the X(3872) has led to a resurgence of interest in exotic spectroscopy and subsequently many new states have been claimed. For example: the Y family, Y(4260),Y(4320) and Y(4660), of spin parity 1−, or the puzzling charged Z family, Z(4050)+,Z(4250)+ and Z(4430)+, so far observed only by the Belle experiment [547–549], and not confirmed by BaBar [550, 551]. The nature of these states has drawn much theoretical attention and many models have been proposed. One possible explanation is that they are bound molecular states of open charm mesons [552]. Another is that these are tetraquarks [553] states formed of four quarks (e.g. \(c,\bar{c}\), one light quark and one light anti-quark). Other interpretations have been postulated such as quark–gluon hybrid [553] or hadrocharmonium models [554], but experimental data are not yet able to conclude definitely. For reviews, see Refs. [520, 552, 554–558].
The bottomonium system should exhibit similar exotic states to the charmonium case. The Belle experiment recently reported the observation of exotic bottomonium charged particles Z b (10610)+ and Z b (10650)+ in the decays Z b →ϒ(nS)π + and Z b →h b (nP)π + [559]. Evidence for a neutral isopartner has also been reported [560].Footnote 70 These states appear similar to, but narrower than, the Z(4430)+ observed in the charmonium case. In addition, neutral states analogous to the X(3872) and the Y states are expected in the bottomonium system.
Studies of the X(3872) have already been performed with the current detector [562]. The 50 fb−1 of integrated luminosity collected with the upgraded detector will contain over one million X(3872)→J/ψππ candidates, by far the largest sample ever collected and allow study of this meson with high precision. A significant fraction of the X(3872) sample will originate from the decays of B mesons (the remainder being promptly produced) allowing the quantum numbers and other properties to be determined. With such a large sample the missing 3 D 2 state of the charmonium system [563] will be also be observed and studied with high precision.
Another study being pursued with the current detector is to clarify the status of the Z(4430)+ state. If confirmed, the Z(4430)+ will be copiously produced at \(\sqrt {s}=14 ~\mathrm{TeV} \) and the larger data set will allow detailed study of its properties in different B decay modes, thus setting the basis for all future searches for exotic charged states.
Similar to the charmonium-like states, exotic bottomonium states will mainly be searched for in the ϒ(nS)π + π − channel, with ϒ(nS)→μ + μ −. The excellent resolution observed in the ϒ(nS) analysis [524] allows efficient separation of the three states, which is crucial in searching for exotic bottomonium states in these channels.
All these studies, and searches for other exotica such as pentaquarks will profit from the increased integrated luminosity.
5.3 Precision measurements of b- and c-hadron properties
A major focus of activity with the current LHCb detector is the study of the properties of beauty and charm hadrons. This is a wide ranging field including studies of properties such as mass and lifetime, observation of excited b hadrons and the measurements of branching ratios. These studies provide important input to pQCD models. Three topics are considered here: b decays to charmonia, \(B^{+}_{c}\), and b-baryon decays.
One important field being studied with the current detector is exclusive b decays to charmonia. Studies of these modes are important to improve understanding of the shape of the momentum spectrum of J/ψ produced in b hadron decays, as measured by the B factories [564, 565]. To explain the observed excess at low momentum, new contributions to the total b→J/ψX rate are needed. Several sources have been proposed in the literature: intrinsic charm [566], baryonium formation [567] and as yet unobserved exotic states [568]. One of the first proposed explanations for the excess was a contribution from an intrinsic charm component to the b-hadron wave-function [566]. This would lead to an enhancement of b-hadron decays to J/ψ in association with open charm. The B-factories have set limits on such decays at the level of 10−5 [190], which considerably restricts, but does not exclude, contributions from intrinsic charm models. The branching ratios of these decays have been estimated in pQCD [569]. In the case of B 0→J/ψD 0 the branching ratio has been estimated to be 7×10−7. If this value is correct, several hundred fully reconstructed events will be collected with the upgraded detector. Similar decay modes are possible for \(B ^{0}_{ s } \) and \(B _{ c } ^{+} \) mesons though no limits (or predictions) exist.
Another possibility to explain the shape of the J/ψ spectrum is contributions from exotic strange baryonia formed in decays such as \(B^{+} \rightarrow { J / \psi } \overline{\varLambda}{} ^{0} p\). This decay has been observed by BaBar [570], with a branching ratio of (1.18±0.31)×10−5. The related decay \(B ^{0} \rightarrow { J / \psi } p \overline{p}\) is unobserved, with an upper limit on the branching ratio of 8.3×10−7 at 90 % confidence level [571]. At present, these decays are experimentally challenging due to the low Q-values involved. The larger data samples available at the time of the upgrade, together with improved proton identification at low momentum, may lead to their observation.
Compared to the case of B 0 and B +, the \(B ^{0}_{ s } \) sector is less well explored both experimentally and theoretically. Decays such as \(B ^{0}_{ s } \rightarrow { J / \psi } K^{*0} \overline {K}^{*0}\) and \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\rho\) should be observable with the present detector. With the upgraded apparatus, the decay modes \(B ^{0}_{ s } \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} K ^{0}_{\mathrm{S}} \) and \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\phi\) will also become accessible. The latter channel is interesting as the low Q-value will allow a precision determination of the \(B ^{0}_{ s } \) mass.
As the lowest bound state of two heavy quarks \(\overline{b}\) and c, the \(B^{+}_{c}\) meson forms a unique flavoured, weakly decaying quarkonium system. Studies of the properties of \(B^{+}_{c}\) mesons such as the mass, lifetime and two-body non-leptonic decay modes are being performed with the current detector. As an example, Fig. 26 shows the signals observed for \(B _{ c } ^{+} \rightarrow { J / \psi } \pi^{+}\) and \(B _{ c } ^{+} \rightarrow { J / \psi } 3\pi^{+}\). The large data set collected with the upgraded detector will allow these studies to be pursued with higher precision together with first studies of CP and triple-product asymmetries in the \(B _{ c } ^{+} \) system. In Table 15 the expected yields of selected decay modes are estimated extrapolating from the yields of \(B _{ c } ^{+} \rightarrow { J / \psi } \pi^{+}\) and \(B _{ c } ^{+} \rightarrow { J / \psi } 3\pi^{+}\) observed with the current detector. As well as studies of the branching ratios and searches for NP, these modes will allow precision measurements of the \(B _{ c } ^{+} \) mass and lifetime to be made. Based on ongoing studies with the current detector, a statistical precision of 0.1 MeV/c 2 on the mass will be achieved. The uncertainty on the mass will most likely be dominated by systematic errors related to the momentum scale. Precision of 10−4 on this variable would translate to an uncertainty of 0.3 MeV/c 2 on the mass. Measurements of the \(B _{ c } ^{+} \) lifetime using the J/ψπ + decay are ongoing. Extrapolating these results to 50 fb−1, a statistical precision of 0.004 ps will be achieved.
Invariant mass distribution of (top) \(B _{ c } ^{+} \rightarrow { J / \psi } 3\pi ^{+}\) and (bottom) \(B _{ c } ^{+} \rightarrow { J / \psi } \pi^{+}\) candidates using 0.8 fb−1 of integrated luminosity collected in 2011 [572]. The results of maximum likelihood fits are superimposed
The large \(B _{ c } ^{+} \) data set will open possibilities for many other studies. Decay modes of the \(B _{ c } ^{+} \) meson to a \(B ^{0}_{ s } \) or B 0 meson together with a pion or kaon will also be accessible. Studies of the \(B _{ c } ^{+} \rightarrow B ^{0}_{ s } \pi^{+}\) decay have been started with the data collected in 2011 where a handful of events are expected. As discussed in Ref. [573], semileptonic \(B _{ c } ^{+} \) decays to \(B ^{0}_{ s } \) can be used to provide a clean tagged decay source for CP violation studies. Finally, signals of the currently unexplored excited \(B^{+}_{c}\) meson states are expected to be observed [576–579]. As discussed in Ref. [575] observation of the \(B_{c}^{*+}\) decay is extremely challenging due to the soft photon produced in the decay to the ground state. The prospects for observation of the first P-wave multiplet decays decaying radiatively to the ground state are more promising.
Large samples of b baryons decaying to final states containing charmonia will also be collected. Precision measurements of the properties of the already known states will be possible. For example, extrapolating the preliminary studies with 0.3 fb−1 discussed in Ref. [580], 10 000 Ξ b →J/ψΞ and 2000 Ω b →J/ψΩ events will be collected. This will allow the Ξ b (Ω b ) mass to be measured to a precision of 0.1 MeV/c 2 (0.5 MeV/c 2). Precise b-baryon lifetime measurements, that will allow tests of the heavy quark expansion [147, 581, 582], should also be possible. Studies of excited b baryons, for example determination of the quantum numbers of the \(\varLambda _{b}^{*}\) baryons that have recently been observed by LHCb (Fig. 27) [583], will also be made.
Invariant mass spectrum of \(\varLambda _{b}^{0} \pi ^{+} \pi^{-}\) [583]. The points with error bars are the data, the solid line is the result of a fit to this distribution, and the dashed line is the fitted background contribution
Baryonic states containing two heavy quarks will also be observable. The lightest of these, the Ξ cc isodoublet, have an estimated cross-section of \(\mathcal{O}(10^{2}) \mbox{~nb}\) [584, 585] and so should be visible with 5 fb−1 collected with the current detector. However, the statistics may be marginal for follow-on analyses: measurements of the lifetime and ratios of branching fractions, searches for excited states, and so forth. They will certainly be insufficient for angular analyses aimed at confirming the quark model predictions for the spin-parity of these states. These studies will require the statistics and improved triggering of the LHCb upgrade. Heavier states such as the Ω cc , Ξ bc , and Ξ bb have still smaller production cross-sections [585]. First studies towards Ξ bc detection are in progress. These indicate that at best a handful of events can be expected in 5 fb−1, but that this state should be observable with the upgrade.
5.4 Measurements with electroweak gauge bosons
Two of the most important quantities in the LHC electroweak physics programme are the sine of the effective electroweak mixing angle for leptons, \(\sin^{2}\theta^{\rm lept}_{\rm eff}\), and the mass of the W-boson, m W . Thanks to its unique forward coverage, an upgraded LHCb can make important contributions to this programme. The forward coverage of LHCb also allows a probe of electroweak boson production in a different regime from that of ATLAS and CMS, and the range of accessible physics topics is not limited to electroweak bosons. For example, \(t\bar{t}\) production proceeds predominantly by gluon–gluon fusion in the central region, but has a significant contribution from quark–antiquark annihilation in the forward region, giving a similar production regime to that studied at the Tevatron.
5.4.1 \(\sin^{2}\theta^{\rm lept}_{\rm eff}\)
The value of \(\sin^{2}\theta^{\rm lept}_{\rm eff}\) can be extracted from \(A_{\rm FB}\), the forward–backward asymmetry of leptons produced in Z decays. The raw value of \(A_{\rm FB}\) measured in dimuon final states at the LHC is about five times larger than at an e + e − collider, due to the initial state couplings, and so, in principle, it can be measured with a better relative precision, given equal amounts of data. The measurement however requires knowledge of the direction of the quark and antiquark that created the Z boson, and any uncertainty in this quantity results in a dilution of the observed value of \(A_{\rm FB}\). This dilution is very significant in the central region, as there is an approximately equal probability for each proton to contain the quark or anti-quark that is involved in the creation of the Z, leading to an ambiguity in the definition of the axis required in the measurement. However, the more forward the Z boson is produced, the more likely it is that it follows the quark direction; for rapidities y>3, the Z follows the quark direction in around 95 % of the cases. Furthermore, in the forward region, the partonic collisions that produce the Z are nearly always between u-valence and \(\bar{u}\)-sea quark or d-valence and \(\bar{d}\)-sea quark. The \(s \bar{s}\) contribution, with a less well-known parton density function, is smaller than in the central region. Consequently, the forward region is the optimum environment in which to measure \(A_{\rm FB}\) at the LHC. Preliminary studies [586] have shown that with a 50 fb−1 data sample collected by the LHCb upgrade, \(A_{\rm FB}\) could be measured with a statistical precision of around 0.0004. This would give a statistical uncertainty on \(\sin^{2} \theta^{\rm lept}_{\rm eff}\) of better than 0.0001, which is a significant improvement in precision on the current world average value. It is also worth remarking that the two most precise values entering this world average at present, the forward–backward \(b\bar{b}\) asymmetry measured at LEP (\(\sin^{2} \theta^{\rm lept}_{\rm eff} = 0.23221 \pm 0.00029\)), and the left-right asymmetries measured at SLD with polarised beams (\(\sin^{2} \theta^{\rm lept}_{\rm eff}=0.23098 \pm0.00026\)), are over 3σ discrepant with each other [587]. LHCb will be able to bring clarity to this unsatisfactory situation.
More work is needed to identify the important systematic uncertainties on the \(A_{\rm FB}\) measurement. One source of error is the uncertainty in the parton density functions. With current knowledge this contribution would lead to an uncertainty of almost double the statistical precision estimate above, but this will reduce when the differential cross-section measurements from the LHC of the W and Z bosons, and those of Drell–Yan dimuon production at lower masses, are included in the global fits to the parton density functions. LHCb has already embarked on this measurement programme. Figure 28 (left) shows the Z→μ + μ − peak obtained with 37 pb−1 of data [588]. Figure 28 (right) shows the measured asymmetry between W + and W − production as a function of lepton pseudorapidity. This measurement is already approaching the accuracy of the theoretical uncertainties. The W and Z measurements described in Ref. [588] are being used to constrain parton density functions by some groups [589]. A preliminary measurement of lower mass Drell–Yan production [590] will extend these constraints to lower Q 2 (masses above 5 GeV/c 2 are currently considered) and Bjorken x.
LHCb Z and W production results from 37 pb−1 at \(\sqrt{s}=7 ~\mathrm{TeV} \) [588]. Left: Z→μ + μ − peak. Right: W +−W − production asymmetry, where the bands correspond to the experimental uncertainties (only indicated within the LHCb acceptance), and the data points give predictions for various different parton density function sets. Note that the kinematic range of the ATLAS and CMS experiments only extends up to lepton pseudorapidities of 2.5
5.4.2 m W
Decreasing the uncertainty on m W from its present error of 15 MeV/c 2 is one of the most challenging tasks for the LHC (it may also be reduced further at the Tevatron). Although no studies have yet been made of determining m W with LHCb itself, it is evident that the experiment can give important input to the measurements being made at ATLAS and CMS [591]. A significant and potentially limiting external uncertainty on m W will again come from the knowledge of the parton density functions. These are less constrained in the kinematic range accessible to LHCb, so that precise measurements of W +, W −, Z and Drell–Yan production in this region can be used to improve the global picture. Improved determinations of the shapes of the differential cross-sections are particularly important. One specific area of concern arises from the knowledge of the heavy quarks in the proton. Around 20–30 % of W production in the central region is expected to involve s and c quarks, making the understanding of this component very important for the m W measurement. LHCb can make a unique contribution to improving the knowledge of the heavy-quark parton density functions by exploiting its vertexing and particle identification capabilities to tag the relatively low-p T final-state quarks produced in processes such as gs→Wc, gc→Zc, gb→Zb, gc→γc and gb→γb. These processes provide direct probes of the strange, charm and bottom partons, and can be probed at high and low values of Bjorken x inside the LHCb acceptance.
5.4.3 \(t\bar{t}\) production
Understanding the nature of top production, and in particular the asymmetry in \(t \bar{t}\) events reported by Fermilab [592–596], is of prime concern. As for the measurement of \(\sin^{2}\theta^{\rm lept}_{\rm eff}\), identifying the forward direction of events is crucial. The LHCb acceptance for identifying both leptons from \(t \bar{t}\) decays is far smaller than that of ATLAS and CMS (typically 2 % rather than 70 %, according to PYTHIA generator level studies). However, the higher \(q \bar{q}\) production fraction and better determined direction in the LHCb forward acceptance combine to suggest that competitive measurements can be achieved. With the integrated luminosity offered by the upgrade, statistical precision will no longer be an issue, and LHCb measurements of the \(t \bar{t}\) asymmetry will offer a competitive and complementary test of Tevatron observations [597].
5.5 Searches for exotic particles with displaced vertices
Different theoretical paradigms have been proposed to solve the so-called “hierarchy problem”, the most discussed being SUSY. There are, however, many other ideas including various models involving extra dimensions, Technicolour and little Higgs models. These ideas approach the hierarchy problem from the direction of strong dynamics [598].
A growing subset of models features new massive long-lived particles with a macroscopic distance of flight. They can be produced by the decay of a single-produced resonance, such as a Higgs boson or a Z′ [599, 600], from the decay chain of SUSY particles [601], or by a hadronisation-type mechanism in models where the long-lived particle is a bound state of quarks from a new confining gauge group, as discussed in Ref. [599]. In the last case, the multiplicity of long-lived particles in an event can be large, while only one long-lived particle is expected to be produced in other models. The decay modes may also vary depending on the nature of the particle, from several jets in the final state [600] to several leptons [602] or lepton plus jets [603]. A comprehensive review of the experimental signatures is given in Ref. [604].
The common feature amongst these models is the presence of vertices displaced from the interaction region. Such signatures are well suited to LHCb, and in particular to the upgraded experiment, which will be able to select events with displaced vertices at the earliest trigger level.
As an example, consider the hidden valley (HV) model already discussed in Ref. [25]. In this model the hidden sector, or v-sector, contains two new heavy quarks: U and C. Strassler and Zurek [601] suggest that an exotic Higgs boson could decay with a significant branching fraction to a pair of \(\pi^{0}_{v}\) particles, where the \(\pi^{0}_{v}\) is the ‘neutral’ member of the isotriplet of v-isospin 1 hadrons formed by U and C quarks. The \(\pi^{0}_{v}\) can decay in SM particles and if the mass of the spinless \(\pi^{0}_{v}\) is below the ZZ threshold it will decay dominantly into \(b\overline{b}\) pairs due to helicity conservation. Here the \(\pi^{0}_{v}\) widths are determined by their lifetime which could be very long, resulting in narrow states. The final state would consist of four b-jets, each pair being produced from a displaced vertex corresponding to the \(\pi^{0}_{v}\) decay as illustrated in Fig. 29. If these decays exist, the lower limit on the Higgs mass set by LEP would be misleading, as it assumes the prompt decay of the Higgs to \(b\overline{b}\) to be dominant.
Decay of a Higgs via a scalar field ϕ into two \(\pi^{0}_{v}\) particles, with \(\pi^{0}_{v}\) charge equal to zero, which subsequently decay into \(b\overline{b}\) jets. (Adapted from Ref. [601])
The potential of LHCb to search for such exotic Higgs decays at \(\sqrt {s}=14 ~\mathrm{TeV} \) has been discussed in Ref. [25], and is briefly summarised here. The benchmark model uses m H =120 GeV/c 2, \(m_{\pi^{0}_{v}} = 35 ~\mathrm {GeV}/c^{2} \) and \(\tau_{\pi^{0}_{v}} = 10 \mbox{~ps}\). By combining vertex and jet reconstruction, the capacity to reconstruct this final state is shown using full simulation of the detector, assuming 0.4 interactions per crossing. Backgrounds to this signal from other processes, such as the production of two pairs of \(b\bar{b}\) quarks, have been considered and found to be negligible.
During 2010 and 2011 data taking, an inclusive displaced vertex trigger has been introduced in the second level of the software trigger. Preliminary studies [605] have demonstrated that for an output rate below 1 % of the overall trigger bandwidth, the efficiency of the whole trigger chain on events with two offline reconstructible \(\pi^{0}_{v}\) vertices with a minimum mass of 6 GeV and good vertex quality is of the order of 80 %. This strategy has been tested up to on average two visible interactions per crossing which is what is expected for the upgraded experiment.
The analysis of the trigger output showed that once vertices arising from hadronic interactions with material are rejected, the dominant background is compatible with b hadron decay vertices as shown in Fig. 30. Those b hadron vertices are reconstructed with large masses because of the presence of fake or cloned tracks. With the present detector, it is difficult to keep the trigger rate down for single candidate events without using tight cuts on the mass and the displacement of the candidates. In the previous model, the trigger efficiency for events with a single long-lived particle reconstructible in LHCb is only about 20 %. This efficiency is expected to decrease for models where the mass of the long-lived particle is smaller. In addition, the number of events with at least one \(\pi^{0}_{v}\) state in the acceptance is three times higher than the number of events with two \(\pi^{0}_{v}\) particles. Improving the single candidate efficiency would increase sensitivity to this model. It would also give a better coverage for the models where only one long-lived particle is produced.
Left: Distribution in x and z, for |y|<1 mm, of the reconstructed vertices. The visible structures reflect the geometry of the vertex detector, with the pairs of silicon sensors appearing as pairs of vertical bands and the corrugated (“RF”) foil as the two wave shapes. The green shaded region represents the fiducial vacuum volume in which candidates are accepted. Right: Flight distance of offline reconstructed vertices in events outside the matter region. Data are compatible with \(b\bar{b}\) background. The black points are for data in 36 pb−1 [605], the red line is a full simulation of \(b\bar{b}\) production and the green dashed line is a full simulation of the HV benchmark channel. The blue dashed line shows a simulation of a model with baryon number violating neutralino couplings
In the upgraded detector, the track fake rate in the vertex detector is expected to be below one percent [26], compared to 6 % in the present detector. Other upgrades to the tracking detectors will also help to reduce the fake rate. Moreover the use of an improved description for the complex RF foil shape will give a better control on the background arising from hadronic interactions. It will enable the use of the true shape of the RF foil, rather than the loose fiducial volume cut used at present, which depending on the considered lifetime, rejects 10–30 % of the long-lived particles. Those improvements would allow to decrease the thresholds on the single candidates trigger and therefore increase the reach of such searches.
As discussed in Ref. [25] the coupling of vertex information to jet reconstruction will allow to reduce the physical backgrounds. Studies are on-going on this matter. Assuming a Higgs production cross-section at \(\sqrt{s} = 14 ~\mathrm{TeV} \) of 50 pb, an integrated luminosity of 50 fb−1 and a geometric efficiency of 10 %, 250 000 Higgs bosons will be produced in LHCb. If \(H^{0} \rightarrow \pi_{v}^{0}\pi_{v}^{0}\) is a dominant decay mode, then LHCb will be in an excellent position to observe this signal, taking advantage of the software trigger’s ability to select high-multiplicity events with good efficiency.
5.6 Central exclusive production
Central exclusive production (CEP) processes provide a promising and novel way to study QCD and the nature of new particles, from low mass glueball candidates up to the Higgs boson itself. The CEP of an object X in a pp collider may be written as follows
where the ‘+’ signs denote the presence of large rapidity gaps. At high energies the t-channel exchanges giving rise to these processes can only be zero-charge colour singlets. Known exchanges include the photon and the pomeron. Another possibility, allowed in QCD, but not yet observed, is the odderon, a negative C-parity partner to the pomeron with at least three gluons. The most attractive aspect of CEP reactions is that they offer a very clean environment in which to measure the nature and quantum numbers of the centrally produced state X.
Central exclusive γγ [606], dijet [607, 608] and χ c [609] production has been observed at the Tevatron. LHCb has presented preliminary results on candidate dimuon events compatible with CEP [610]. Figure 31 shows the invariant mass of CEP χ c candidates. These are events in which only a J/ψ→μ + μ − decay and a γ candidate are reconstructed, with no other activity (inconsistent with noise) seen elsewhere in the detector. Important observables in CEP are the relative production rates of χ c0, χ c1 and χ c2. As is evident from Fig. 31, the invariant mass resolution of LHCb is sufficient for this measurement.
Preliminary LHCb results on central exclusive χ c production [610]. The J/ψγ invariant mass in data is compared to the expectation of the SuperCHIC Monte Carlo generator [611], which has been normalised to the observed number of events. The relative proportions of χ c0, χ c1 and χ c2 are 12 %, 36 % and 52 % respectively
Although not part of the baseline for the LHCb upgrade, additional instrumentation is being considered which could improve the potential of LHCb to study CEP processes. For example, the inclusion of forward shower counters (FSCs) on both sides of the interaction point, as proposed in Ref. [612], would be able to detect showers from very forward particles interacting in the beam pipe and surrounding material. The absence of a shower would indicate a rapidity gap and be helpful in increasing the purity of a CEP sample. More ambitiously, the deployment of semi-conductor detectors very close to the beam, within Roman pots, several hundred meters away from the interaction point, as proposed for other LHC experiments [613] would also be beneficial for LHCb. The ability to measure the directions of the deflected protons in the CEP interaction provides invaluable information in determining the quantum numbers of the centrally produced state.
Several important physics goals have been identified for the LHCb CEP programme:
-
Accumulation and characterisation of large samples of exclusive \(c\bar {c}\) and \(b\bar{b}\) events. A full measurement programme of these ‘standard candles’ will be essential to understand better the QCD mechanism of CEP [614], and may provide vital input if CEP is used for studies of Higgs and other new particles [615].
-
Searches for structure in the mass spectra of decay states such as K + K −, 2π +2π −, K + K − π + π − and \(p\bar{p}\). A particular interest of this study would be the hunt for glueballs, which are a key prediction of QCD.
-
Observation and study of exotic particles in CEP processes. For example, a detailed study of the CEP process pp→p+X(3872)+p would provide a valuable new tool to aid understanding of this state. This and other states could be searched for in, for example, decays containing \(D\overline{D}\), which if observed would shed light onto the nature of the parent particle [614].
There are several reasons which make LHCb a suitable detector for realising these goals, particularly with the upgraded experiment:
-
Even when running at a luminosity of 1033 cm−2 s−1 LHCb will have low pileup compared to ATLAS and CMS. This will be advantageous in triggering and reconstructing low mass CEP states.
-
The higher integrated luminosity that will be collected by the upgraded detector will allow studies to be performed on states that are inaccessible with only a few fb−1. This is true, for example, of central exclusive χ b production, which is expected to be a factor of ∼1000 less than that of χ c mesons [614].
-
The particle identification capabilities of the LHCb ring-imaging Cherenkov detector system allow centrally produced states to be cleanly separated into decays involving pions, kaons and protons.
-
The low \(p_{\rm T}\) acceptance of LHCb, and high bandwidth trigger, will allow samples of relatively low mass states to be collected and analysed.
6 Summary
As described in the previous sections, LHCb has produced world-leading results across its physics programme, using the 1.0 fb−1 data sample of \(\sqrt{s} = 7 ~\mathrm{TeV} \) pp collisions collected in 2011. The inclusion of the data collected at \(\sqrt{s} = 8 ~\mathrm{TeV} \) during 2012 will enable further improvements in precision in many key flavour physics observables. However, an upgrade to the detector is needed to remove the bottleneck in the trigger chain that currently prevents even larger increases in the collected data sample. The upgraded detector with trigger fully implemented in software is to be installed during the 2018 long shutdown of the LHC, and will allow a total data set of 50 fb−1 to be collected. With such a data sample, LHCb will not only reach unprecedented precision for a wide range of flavour physics observables, but the flexible trigger will allow it to exploit fully the potential of a forward physics experiment at a hadron collider.
In this section, some highlights of the LHCb physics output so far, and their implications on the theoretical landscape, are summarised. The sensitivity of the upgraded detector to key observables is then given, before a concluding statement on the importance of the LHCb upgrade to the global particle physics programme.
6.1 Highlights of LHCb measurements and their implications
6.1.1 Rare decays
Among rare decays, the LHCb limit on the rate of the decay \(B ^{0}_{ s } \rightarrow \mu ^{+} \mu ^{-} \) [13] places stringent limits on NP models that enhance the branching fraction. The measurement

can be compared to the SM prediction \(\mathcal{B}( B^{0}_{ s } \rightarrow \mu^{+}\mu ^{-} ) _{\rm SM} = (3.1 \pm0.2) \times10^{-9}\) [116].Footnote 71 This result puts severe constraints—far beyond the ATLAS and CMS search limits—on supersymmetric models with large values of tanβ, i.e. of the ratio of vacuum expectation values of the Higgs doublets (see, for example, Refs. [116, 129, 162]).
The measurement of the forward–backward asymmetry in B 0→K ∗0 μ + μ − [15] has to be viewed as the start of a programme towards a full angular analysis of these decays. The full analysis will allow determination of numerous NP-sensitive observables (see, for example, Refs. [53, 54]). The measurements that will be obtained from such an analysis, as well as similar studies of related channels, such as \(B ^{0}_{ s } \rightarrow \phi \mu ^{+} \mu ^{-} \) [69], allow model-independent constraints on NP, manifested as limits on the operators of the effective Hamiltonian (see, for example, Refs. [42, 43]). Indeed, the first results already impose important constraints. Studies of radiative decays such as \(B ^{0}_{ s } \rightarrow \phi \gamma\) [16, 17] provide additional information since they allow to measure the polarisation of the emitted photon, and are therefore especially sensitive to models that predict new right-handed currents. Similarly, studies of observables such as isospin asymmetries [77] are important since they allow to pin down in which operators the NP effects occur.
Several new opportunities with rare decays at LHCb are becoming apparent. The observation of B +→π + μ + μ − [86], the rarest B decay yet discovered, enables a new approach to measure the ratio of CKM matrix elements |V td /V ts |. Decays to final states containing same-sign leptons [197] allow searches for Majorana neutrinos complementary to those based on neutrinoless double beta decay. LHCb can also reach competitive sensitivity for some lepton flavour violating decays such as τ +→μ + μ − μ + [191].
6.1.2 CP violation in the B sector
Measurements of the neutral B meson mixing parameters provide an excellent method to search for NP effects, due to the low theoretical uncertainties associated to several observables. The LHCb measurements of the CP-violating phase, ϕ s , and the width difference, ΔΓ s , in the \(B ^{0}_{ s } \) system [10, 139, 219, 232] significantly reduce the phase space for NP:
However deviations from the SM predictions [119, 221] are still possible. Effects of \(\mathcal{O}(0.1)\) are typical of some well-motivated NP models that survive the present ATLAS and CMS bounds (such as in Ref. [37]). The experimental uncertainty on ϕ s is still a factor of 40 larger than that on the prediction, therefore improved measurements are needed to reach the level of sensitivity demanded by theory. It should also be noted that compared to the CP-violating phase in the B 0 system (2β), ϕ s is much more precisely predicted, and therefore presents stronger opportunities for NP searches.
In addition, to understand the origin of the anomalous dimuon asymmetry seen by D0 [159], improved measurements of semileptonic asymmetries in both \(B ^{0}_{ s } \) and B 0 systems are needed. LHCb has just released its first results on the \(B ^{0}_{ s } \) asymmetry [248], demonstrating the potential to search for NP effects with more precise measurements. Moreover, a constraint on, or a measurement of, the rate of the decay \(B ^{0}_{ s } \rightarrow \tau^{+}\tau^{-}\) is important to provide knowledge of possible NP contributions to Γ 12 (see, for example, Refs. [153, 155]).
Among the B 0 mixing parameters, improved measurements of both ϕ d (i.e., sin2β) and ΔΓ d are needed. Reducing the uncertainty on the former will help to improve the global fits to the CKM matrix [252, 266], and may clarify the current situation regarding the tension between various inputs to the fits (see, for example, Ref. [267]). Another crucial observable is the angle γ, which, when measured in the tree-dominated B→DK processes, provides a benchmark measurement of CP violation. The first measurements from LHCb already help to improve the uncertainty on γ [6, 7]: further improvements are both anticipated and needed.
Comparisons of values of γ from loop-dominated processes with the SM benchmark from tree-dominated processes provide important ways to search for new sources of CP violation. In particular, the study of \(B ^{0}_{ s } \rightarrow K ^{+} K ^{-} \) and B 0→π + π − decays [356], which are related by U-spin, allows a powerful test of the consistency of the observables with the SM [355, 357]. Similarly, the U-spin partners \(B ^{0}_{ s } \rightarrow K ^{*0} \overline{ K }{} ^{*0} \) [303] and \(B ^{0} \rightarrow K ^{*0} \overline{ K }{} ^{*0} \) are among the golden channels to search for NP contributions in \(b \rightarrow s q\bar{q}\) penguin amplitudes [308]. Another important channel in this respect is \(B ^{0}_{ s } \rightarrow \phi \phi\) [304], for which the CP-violating observables are predicted with low theoretical uncertainty in the SM. Studies of CP violation in multibody b hadron decays [376, 377] offer additional possibilities to search for both the existence and features of NP.
6.1.3 Charm mixing and CP violation
In the charm sector, the evidence for CP violation in the observable \(\Delta \mathcal{A}_{ \mathit{CP} } \) has prompted a large amount of theoretical work. The measurement

is different from zero by 3.5 standard deviations [18]. While \(\mathcal{A}_{ \mathit{CP} } \) represents a time-integrated CP asymmetry, \(\Delta \mathcal{A}_{ \mathit{CP} } \) originates predominantly from direct CP violation. The emergent consensus is that while an asymmetry of the order of 1 % is rather unlikely in the SM, it cannot be ruled out that QCD effects cause enhancements of that size. Further measurements are needed in order to establish if NP effects are present in the charm sector. Among the anticipated results are updates of the \(\Delta \mathcal{A}_{ \mathit{CP} } \) measurement as well as of the individual CP asymmetries in D 0→K + K − and D 0→π + π −. It is of great interest to look for direct CP violation in decays to other final states, and in decays of other charmed hadrons (D +, \(D ^{+}_{ s } \) and \({ \varLambda }^{+}_{ c } \)).
The SM predictions are somewhat cleaner for indirect CP violation effects, and therefore it is also essential to search for CP violation in charm mixing. New results from time-dependent analyses of D 0→K + K − [19] and \(D ^{0} \rightarrow K ^{0}_{\mathrm{S}} \pi ^{+} \pi ^{-} \) will improve the current knowledge, and additional channels will also be important with high statistics.
Several authors have noted correlations between CP violation in charm and various other observables (for example, Refs. [469, 484]). These correlations appear in, and differ between, certain theoretical models, and can therefore be used to help identify the origin of the effects. Observables of interest in this context include those that can be measured at high-\(p_{\rm T}\) experiments, such as \(t\bar{t}\) asymmetries, as well as rare charm decays. Among the latter, it has been noted that CP asymmetries are possible in radiative decays such as D 0→ϕγ [485], and that searches for decays involving dimuons, such as D 0→μ + μ − [178] and D +→π + μ + μ − are well motivated.
6.1.4 Measurements exploiting the unique kinematic acceptance of LHCb
The unique kinematic region covered by the LHCb acceptance enables measurements that cannot be performed at other experiments, and that will continue to be important in the upgrade era. These include probes of QCD both in production, such as studies of multi-parton scattering [531, 616], and in decay, such as studies of exotic hadrons like the X(3872) [562] and the putative Z(4430)+ state. Conventional hadrons can also be studied with high precision: one important goal will be to establish the existence of doubly heavy baryons. Central exclusive production of conventional and exotic hadrons can also be studied; the sensitivity of the upgraded experiment will be significantly enhanced due to the software trigger.
Measurements of production rates and asymmetries of electroweak gauge bosons in the LHCb acceptance are important to constrain parton density functions [588]. With high statistics, LHCb will be well placed to make a precision measurement of the sine of the effective electroweak mixing angle for leptons, \(\sin^{2}\theta^{\rm lept}_{\rm eff}\), from the forward–backward asymmetry of leptons produced in the Z→μ + μ − decay. Improved knowledge of parton density functions, as can be obtained from studies of production of gauge bosons in association with jets [617], will help to reduce limiting uncertainties on the measurement of the W boson. These studies are also an important step towards a top physics programme at LHCb, which will become possible once the LHC energy approaches the nominal 14 TeV.
The importance of having a detector in the forward region can be illustrated with the recent discovery by ATLAS and CMS of a new particle that may be the Higgs boson. It is now essential to determine if this particle has the couplings to bosons, leptons and quarks expected in the SM. In particular, at the observed mass the highest branching ratio is expected to be for \(H \rightarrow b\bar{b}\)—however this is a difficult channel for ATLAS and CMS due to the large SM background. LHCb with its excellent b-hadron sensitivity will be able to search for such decays. The forward geometry of LHCb is also advantageous to observe new long-lived particles that are predicted in certain NP models, including some with extended Higgs sectors. Although limits can be set with the current detector [605], this is an area that benefits significantly from the flexible software trigger of the upgraded experiment. Models with extended Higgs sectors also produce characteristic signals in flavour physics observables, which emphasises the need for the LHCb upgrade as part of the full exploitation of the LHC.
6.2 Sensitivity of the upgraded LHCb experiment to key observables
As mentioned in Sect. 1, the LHCb upgrade is necessary to progress beyond the limitations imposed by the current hardware trigger that, due to its maximum output rate of 1 MHz, restricts the instantaneous luminosity at which data can most effectively be collected. To overcome this, the upgraded detector will be read out at the maximum LHC bunch-crossing frequency of 40 MHz so that the trigger can be fully implemented in software. The upgraded detector will be installed during the long shutdown of the LHC planned for 2018. A detailed description of the upgraded LHCb experiment can be found in the Letter of Intent (LoI) [25], complemented by the recent framework technical design report (FTDR) [26], which sets out the timeline and costing for the project. A summary has been prepared for the European Strategy Preparatory Group [618].
The sensitivity to various flavour observables is summarised in Table 16, which is taken from the FTDR [26]. This is an updated version of a similar summary that appears as Table 2.1 in the LoI [25]. The measurements considered include CP-violating observables, rare decays and fundamental parameters of the CKM unitarity triangle. More details about these observables are given below. The current precision, either from LHCb measurements or averaging groups [44, 252, 266], is given and compared to the estimated sensitivity with the upgrade. As an intermediate step, the estimated precision that can be achieved prior to the upgrade is also given for each observable. For this, a total integrated luminosity of 1.0 (1.5,4.0) fb−1 at pp centre-of-mass collision energy \(\sqrt{s} = 7\ (8, 13) ~\mathrm{TeV} \) recorded in 2011 (2012, 2015–2017) is assumed. Another assumption is that the current efficiency of the muon hardware trigger can be maintained at higher \(\sqrt{s}\), but that higher thresholds will be necessary for other triggers, reducing the efficiency for the relevant channels by a factor of 2 at \(\sqrt{s} = 14 ~\mathrm{TeV} \).
In LHCb measurements to date, the CP-violating phase in \(B ^{0}_{ s } \) mixing, measured in both J/ψϕ and J/ψf 0(980) final states, has been denoted ϕ s . In the upgrade era it will be necessary to remove some of the assumptions that have been made in the analyses to date, related to possible penguin amplitude contributions, and therefore the observables in \(b \rightarrow c\bar{c}s\) transitions are denoted by 2β s =−ϕ s , while in \(b \rightarrow q\bar{q}s\) (q=u,d,s) transitions the notation \(2\beta^{\rm eff}_{s}\) is used. This parallels the established notation used in the B 0 system (the α,β,γ convention for the CKM unitarity triangle angles is used). The penguin contributions are expected to be small, and therefore a theory uncertainty on \(2\beta_{s} ( B ^{0}_{ s } \rightarrow { J / \psi } \phi ) \sim0.003\) is quoted, comparable to the theory uncertainty on \(2\beta( B ^{0} \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} )\). However, larger effects cannot be ruled out at present. Data-driven methods to determine the penguin amplitudes are also possible [246, 277, 284]: at present these given much larger estimates of the uncertainty, but improvement can be anticipated with increasing data samples. The flavour-specific asymmetry in the \(B ^{0}_{ s } \) system, \(a_{\rm sl}^{s}\) in Table 16, probes CP violation in mixing. The “sl” subscript is used because the measurement uses semileptonic decays.
Sensitivity to the emitted photon polarisation is encoded in the effective lifetime, \(\tau^{\rm eff}\) of \(B ^{0}_{ s } \rightarrow \phi \gamma\) decays, together with the effective CP-violation parameter \(2\beta_{s}^{\rm eff}\). Two of the most interesting of the full set of angular observables in B 0→K ∗0 μ + μ − decays [62], are S 3, which is related to the transverse polarisation asymmetry [63], and the zero-crossing point (s 0) of the forward–backward asymmetry. As discussed above, isospin asymmetries, denoted A I , are also of great interest.
In the charm sector, it is important to improve the precision of \(\Delta \mathcal{A}_{ \mathit{CP} } \), described above, and related measurements of direct CP violation. One of the key observables related to indirect CP violation is the difference in inverse effective lifetimes of D 0→K + K − and \(\overline{ D }{} ^{0} \rightarrow K ^{+} K ^{-} \) decays, A Γ .
The extrapolations in Table 16 assume the central values of the current measurements, or the SM where no measurement is available. While the sensitivities given include statistical uncertainties only, preliminary studies of systematic effects suggest that these will not affect the conclusions significantly, except in the most precise measurements, such as those of \(a_{\rm sl}^{s}\), A Γ and \(\Delta \mathcal{A}_{ \mathit{CP} } \). Branching fraction measurements of \(B ^{0}_{ s } \) mesons require knowledge of the ratio of fragmentation fractions f s /f d for normalisation [145]. The uncertainty on this quantity is limited by knowledge of the branching fraction of \(D ^{+}_{ s } \rightarrow K ^{+} K ^{-} \pi ^{+} \), and improved measurements of this quantity will be necessary to avoid a limiting uncertainty on, for example, \(\mathcal{B}( B ^{0}_{ s } \rightarrow \mu ^{+} \mu^{-})\). The determination of 2β s from \(B ^{0}_{ s } \rightarrow { J / \psi } \phi \) provides an example of how systematic uncertainties can be controlled for measurements at the LHCb upgrade. In the most recent measurement [139], the largest source of systematic uncertainty arises due to the constraint of no direct CP violation that is imposed in the fit. With larger statistics, this constraint can be removed, eliminating this source of uncertainty. Other sources, such as the background description and angular acceptance, are already at the 0.01 rad level, and can be reduced with more detailed studies.
Experiments at upgraded e + e − B factories and elsewhere will study flavour-physics observables in a similar timeframe to the LHCb upgrade. However, the LHCb sample sizes in most exclusive B and D final states will be far larger than those that will be collected elsewhere, and the LHCb upgrade will have no serious competition in its study of \(B ^{0}_{ s } \) decays, b-baryon decays, mixing and CP violation. Similarly the yields in charmed-particle decays to final states consisting of only charged tracks cannot be matched by any other experiment. On the other hand, the e + e − environment is advantageous for inclusive studies and for measurements of decay modes including multiple neutral particles [619–623], and therefore enables complementary measurements to those that will be made with the upgraded LHCb experiment.
6.3 Importance of the LHCb upgrade
The study of deviations from the SM in quark flavour physics provides key information about any extension of the SM. It is already known that the NP needed to stabilize the electroweak sector must have a non-generic flavour structure in order to be compatible with the tight constraints of flavour-changing processes, even if the precise form of this structure is still unknown. Hopefully, ATLAS and CMS will detect new particles belonging to these models, but the couplings of the theory and, in particular, its flavour structure, cannot be determined only using high-\(p_{\rm T}\) data.
Therefore, the LHCb upgrade will play a vital role in any scenario. It allows the exploration of NP phase space that a priori cannot be studied by high energy searches. Future plans for full exploitation of the LHC should be consistent with a co-extensive LHCb programme.
Notes
Throughout the document, the inclusion of charge conjugated modes is implied unless explicitly stated.
It is anticipated that any detectors that need replacement for the LHCb upgrade will be designed such that they can sustain a luminosity of \(\mathcal{L}_{\rm inst} = 2 \times10^{33}~\mathrm{cm} ^{-2}\,\mathrm{s}^{-1}\) [26]. Operation at instantaneous luminosities higher than the nominal value assumed for the estimations will allow the total data set to be accumulated in a shorter time.
In principle there are also tensor operators, \(O_{T(5)} = (\bar {q}\sigma_{\mu\nu}b)(\bar{\ell}\sigma^{\mu\nu}(\gamma_{5})\ell )\), which are relevant for some observables.
In radiative and semileptonic decays, the chromomagnetic operator O 8 enters at higher order in the strong coupling α S .
Light resonances at q 2 below 1 GeV2 cannot be treated within QCDF, and their effects have to be estimated using other approaches. In addition, the longitudinal amplitude in the QCDF/SCET approach generates a logarithmic divergence in the limit q 2→0, indicating problems in the description below 1 GeV2 [50].
Further amplitudes contribute in principle, but they are either suppressed by small lepton masses or originate from non-standard scalar/tensor operators.
The quantity \(S_{3} = (1-F_{\rm L})/2 \times A_{T}^{(2)}\) (in the massless case) allows access to one of the theoretically clean quantities, namely \(A_{T}^{(2)}\). The observable \(A_{T}^{(2)}\) is a theoretically cleaner observable than S 3 due to the cancellation of some of the form-factor dependence [72].
In the QCDF approach at leading order in \(\varLambda_{\rm QCD}/m_{b}\), the value of \(q_{0}^{2}\) is free from hadronic uncertainties at order \(\alpha_{s}^{0}\). A dependence on the soft form factor and on the light-cone wave functions of the B and K ∗ mesons appears only at order \(\alpha_{s}^{1}\).
A recent determination of \(q_{0}^{2}\) in B 0 decays gives 4.0±0.3 GeV2/c 4 [40]. The shift with respect to Ref. [51] is of parametric origin and is driven in part by the choice of the renormalisation scale (μ=4.2 GeV instead of 4.8 GeV), but also due to differences in the implementation of higher \(\mathcal{O}( \alpha_{S} )\) short-distance contributions.
A calculation of \(A_{\rm I}^{\rm SM}(B \rightarrow K \mu ^{+} \mu ^{-} )\) has recently become available [88], giving values consistent with the naïve expectation within 1 %.
Note that the notation S used here and in the literature for mixing-induced asymmetries is not related to the use of the notation in Sect. 2.3 for CP-averaged properties of the angular distributions.
Note that elsewhere in this document the symbol β is used to denote an angle of the unitarity triangle of the CKM matrix.
Results on \(\mathcal{B}( B^{0}_{(s)} \rightarrow \mu^{+}\mu ^{-} ) \) presented at HCP2012 [14] are not included in this discussion.
This was previously observed in a different context [138].
This value is valid for B mesons produced from \(\sqrt{s} = 7 ~\mathrm{TeV} \) pp collisions within the LHCb acceptance. It will, in principle, need to be remeasured at each different LHC collision energy, and may depend on the kinematic acceptance of the detector (i.e. on the transverse momentum and pseudorapidity of the B mesons). However, once a suitable \(B ^{0}_{ s } \) branching fraction, such as that for \(B ^{0}_{ s } \rightarrow { J / \psi } \phi \) or \(B ^{0}_{ s } \rightarrow K ^{+} K ^{-} \), is known to good precision, normalisation can be carried out without direct need for an f d /f s value.
Barring a sizeable, fortuitous cancellation among C S,P and \(C_{S,P}^{\prime}\) [79].
LHCb has presented results on A CP (B 0→K ∗0 μ + μ −) at CKM 2012 [161].
The effect of SUSY models on \(A_{\rm FB}(B \rightarrow K^{*} \mu^{+}\mu^{-})\) is discussed in Ref. [166].
Calculated from the \(b\bar{b}\) and \(c\bar{c}\) cross-sections measured at the LHCb experiment and the inclusive branching ratios b→τ and c→τ [190].
Preliminary results on \(\tau^{-} \rightarrow \bar {p} \mu^{+} \mu^{-}\) and τ −→pμ − μ − were presented at TAU 2012 [192].
Strictly, the coefficients p and q should also have subscripts q to indicate that they can be different for B 0 and \(B ^{0}_{ s } \), but these are omitted to simplify the notation.
The notation \(a^{q}_{\rm sl}\) is used to denote flavour-specific asymmetries, reflecting the fact that the measurements of these quantities use semileptonic decays.
The cases for more generic final-states can be found in the literature, e.g. Ref. [44].
Note the conventional sign-flip between β and β s ensures that both are positive in the SM.
Results from ATLAS and CMS, presented at ICHEP2012 or later, are not included in this compilation.
An updated measurement has been presented by D0 at ICHEP 2012 [247].
The factors C d and C s depend in principle on the collision environment and the kinematic acceptance, though the dependence appears to be weak. Trigger requirements can also affect the values of these parameters.
An updated measurement of \({ \mathcal{B} } (B^{+} \rightarrow \tau^{+} \nu)\) using the hadronic tag method was presented by Belle at ICHEP 2012 [251]: this new result reduces, but does not completely remove, the tension in the fits. The analyses discussed here do not include this new result.
But not including results shown for the first time at ICHEP 2012 or later.
Other data-driven methods to control penguin contributions to \(B ^{0}_{ s } \rightarrow { J / \psi } \phi\) have been proposed [284].
Note the definition of ΔS here has a sign difference to that in Ref. [285].
The triple product asymmetries in \(B ^{0}_{ s } \rightarrow \phi \phi\) and \(B ^{0}_{ s } \rightarrow K ^{*0} \overline{ K }{} ^{*0} \) decay could in principle also receive contribution from non-zero mixing-induced CP asymmetries arising from NP in \(B ^{0}_{ s } \) mixing. However, this contribution is suppressed by ΔΓ s /Γ s and is already highly constrained.
By B→DK all related tree-dominated decay processes are implicitly included, including B +→DK +, B 0→DK ∗0, \(B ^{0}_{ s } \rightarrow D\phi\), \(B ^{0}_{ s } \rightarrow D ^{\mp}_{ s } K ^{\mp} \) and B 0→D (∗)∓ π ±. In these specific decay processes, the notation D refers to a neutral D meson that is an admixture of D 0 and \(\overline{ D }{} ^{0} \) states.
As for δ D in the ADS method, the strong phase differences can be determined directly from \(\psi(3770) \rightarrow D\overline{D}\) data, which has been done by CLEO [327]. In future, it is expected that the most precise value will come from a global fit including results of time-dependent analyses of multibody charm decays.
Preliminary results have been presented at CKM 2012 [336].
At CKM 2012, LHCb presented results of a model-independent GGSZ analysis of B −→DK − with \(D \rightarrow K ^{0}_{\mathrm{S}} \pi ^{+} \pi ^{-} \) and \(D \rightarrow K ^{0}_{\mathrm{S}} K ^{+} K ^{-} \) [7], preliminary results from a ADS-type analysis of B −→DK − with D→K3π [342], a preliminary determination of γ from combined results using B −→DK − and B −→Dπ − [343], and preliminary results on the time-dependent CP violation parameters in \(B ^{0}_{ s } \rightarrow D ^{\mp}_{ s } K ^{\pm} \) [336].
In the LHCb preliminary results on B 0→π + π − and \(B ^{0}_{ s } \rightarrow K^{+}K^{-}\) decays [356] a different notation has been used: \(A_{f}^{\rm dir} \equiv-C_{f}\), \(A_{f}^{\rm mix} \equiv S_{f}\), \(A_{f}^{\Delta\varGamma} \equiv-D_{f}\).
Note that the use here of the symbol C to denote a colour-suppressed amplitude is not related to its use to denote direct CP violation parameters in time-dependent analyses.
Note that the value of γ quoted here differs from that obtained from the full CKM fit (given in Table 2) due to the different inputs used.
The proposal of Ref. [308] has been recently critically reexamined in Ref. [373]. The present analysis shows no particular enhancement of the contribution proportional to e iγ in \(B ^{0}_{ s } \rightarrow K^{+} K^{-}\), in agreement with the expectation that \(B ^{0}_{ s } \rightarrow K^{(*)0} \overline{K}^{(*)0}\) should be penguin-dominated to a very good accuracy.
LHCb has presented preliminary branching fraction measurements of \(B^{0}_{(s)} \rightarrow K ^{0}_{\mathrm{S}} h^{+}h^{\prime-}\) decays at ICHEP 2012 [388].
Preliminary results from a GLW-type analysis of this channel was presented at ICHEP 2012 [341].
Preliminary results from a GLW-type analysis of B 0→DK ∗0 were presented at ICHEP 2012 [340].
At HCP 2012, LHCb presented the first observation of charm mixing from a single measurement [411].
A m can be determined from asymmetries in semileptonic charm decays, with the assumption of vanishing direct CP violation.
New results presented by Belle at ICHEP 2012 [415] are not included in this average.
At ICHEP 2012, Belle also presented new results on \(\Delta \mathcal{A}_{ \mathit{CP} } \) [423], that are consistent with, but less precise than, those from LHCb and CDF.
Results of charm mixing parameters in wrong-sign D 0→K + π − decays have been presented at HCP 2012 [411].
The pion reconstruction efficiency asymmetry has also been used in the determination of the D + production asymmetry [429].
A small difference in kinematic distributions can occur in ϕ→K − K + due to crossing resonances.
Preliminary results on the D 0→π − π + π − π + decay were presented at ICHEP 2012 [431].
Note that the LHCb dipole magnet creates regions of parameter space with large \(\mathcal{A}_{\rm D}(\pi^{+}_{\mathrm{s}})\), particularly at the left and right edges of the acceptance. These regions are excluded with fiducial cuts.
Note in particular that if \(\mathcal{A}_{ \mathit{CP} } (K^{+}K^{-}) = \mathcal{A}_{ \mathit{CP} } (\pi^{+}\pi^{-}) = 0\), the approximation becomes exact at all orders.
The discussion is framed in terms of kinematic variables, since there are clear mechanisms that could cause problems there, but the same logic can be applied to magnet polarity, trigger conditions, etc.
Among various possible phase definitions, only ϕ 12, the relative phase between M 12 and Γ 12, is convention-independent and so has physical consequences.
Not including results presented at ICHEP 2012 or later.
New results presented at ICHEP 2012, including a new result from Belle on \(\Delta \mathcal{A}_{ \mathit{CP} } \) [423], are not included in the averages discussed here.
Time-dependent D(t)→π 0 π 0 measurements could in principle be feasible using photon conversions [491].
The LHCb measurements of charm mixing parameters from wrong-sign Kπ decays [411] are consistent with the estimated sensitivities.
At ICHEP 2012, Belle reported observations of the Z b states decaying to \(B\overline{B}^{(*)}\) [561].
It should be noted that the measured value is the time-integrated branching fraction, and the SM prediction should be increased by around 10 % to allow a direct comparison [136].
References
A.A. Alves Jr. et al. (LHCb Collaboration), The LHCb detector at the LHC. J. Instrum. 3, S08005 (2008)
R. Aaij et al. (LHCb Collaboration), Measurement of \(\sigma(pp \rightarrow b \bar{b} X)\) at \(\sqrt {s}=7\ \mathrm{TeV}\) in the forward region. Phys. Lett. B 694, 209 (2010). arXiv:1009.2731
LHCb Collaboration, Prompt charm production in pp collisions at \(\sqrt{s} = 7\ \mathrm{TeV}\), LHCb-CONF-2010-013
R. Aaij et al. (LHCb Collaboration), Prompt charm production in pp collisions at \(\sqrt{s}= 7\ \mathrm{TeV}\). Nucl. Phys. B (2013). doi:10.1016/j.nuclphysb.2013.02.010. arXiv:1302.2864,
B. Adeva et al. (LHCb Collaboration), Roadmap for selected key measurements of LHCb. arXiv:0912.4179
R. Aaij et al. (LHCb Collaboration), Observation of CP violation in B ±→DK ± decays. Phys. Lett. B 712, 203 (2012). arXiv:1203.3662
R. Aaij et al. (LHCb Collaboration), A model-independent Dalitz plot analysis of B ±→DK ± with \(D \rightarrow K^{0}_{\rm S} h^{+}h^{-}\) (h=π,K) decays and constraints on the CKM angle γ. Phys. Lett. B 718, 43 (2012). arXiv:1209.5869
R. Aaij et al. (LHCb Collaboration), First evidence of direct CP violation in charmless two-body decays of \(B ^{0}_{ s } \) mesons. Phys. Rev. Lett. 108, 201601 (2012). arXiv:1202.6251
R. Aaij et al. (LHCb Collaboration), Measurement of b-hadron branching fractions for two-body decays into charmless charged hadrons. J. High Energy Phys. 10, 037 (2012). arXiv:1206.2794
R. Aaij et al. (LHCb Collaboration), Measurement of the CP-violating phase ϕ s in the decay \(B ^{0}_{ s } \rightarrow J/\psi\phi\). Phys. Rev. Lett. 108, 101803 (2012). arXiv:1112.3183
R. Aaij et al. (LHCb Collaboration), Search for the rare decays \(B ^{0}_{ s } \rightarrow \mu ^{+}\mu^{-}\) and B 0→μ + μ −. Phys. Lett. B 699, 330 (2011). arXiv:1103.2465
R. Aaij et al. (LHCb Collaboration), Search for the rare decays \(B^{0}_{s} \rightarrow \mu^{+}\mu^{-}\) and B 0→μ + μ −. Phys. Lett. B 708, 55 (2012). arXiv:1112.1600
R. Aaij et al. (LHCb Collaboration), Strong constraints on the rare decays \(B ^{0}_{ s } \rightarrow \mu^{+} \mu^{-}\) and B 0→μ + μ −. Phys. Rev. Lett. 108, 231801 (2012). arXiv:1203.4493
R. Aaij et al. (LHCb Collaboration), First evidence for the decay \(B^{0}_{s} \rightarrow \mu^{+}\mu^{-}\). Phys. Rev. Lett. 110, 021801 (2013). arXiv:1211.2674
R. Aaij et al. (LHCb Collaboration), Differential branching fraction and angular analysis of the decay B 0→K ∗0 μ + μ −. Phys. Rev. Lett. 108, 181806 (2012). arXiv:1112.3515
R. Aaij et al. (LHCb Collaboration), Measurement of the ratio of branching fractions \({ \mathcal{B} } ( B ^{0} \rightarrow K ^{*0} \gamma)/{ \mathcal{B} } ( B ^{0}_{ s } \rightarrow \phi\gamma)\). Phys. Rev. D 85, 112013 (2012). arXiv:1202.6267
R. Aaij et al. (LHCb Collaboration), Measurement of the ratio of branching fractions \(\mathcal {B}(B^{0} \rightarrow K^{\ast0} \gamma) / \mathcal{B}(B^{0}_{s} \rightarrow \phi\gamma)\) and direct CP asymmetry in B 0→K ∗0 γ. Nucl. Phys. B 867, 1 (2013). arXiv:1209.0313
R. Aaij et al. (LHCb Collaboration), Evidence for CP violation in time-integrated D 0→h − h + decay rates. Phys. Rev. Lett. 108, 111602 (2012). arXiv:1112.0938
R. Aaij et al. (LHCb Collaboration), Measurement of mixing and CP violation parameters in two-body charm decays. J. High Energy Phys. 04, 129 (2012). arXiv:1112.4698
N. Cabibbo, Unitary symmetry and leptonic decays. Phys. Rev. Lett. 10, 531 (1963)
M. Kobayashi, T. Maskawa, CP violation in the renormalizable theory of weak interaction. Prog. Theor. Phys. 49, 652 (1973)
J.H. Christenson, J.W. Cronin, V.L. Fitch, R. Turlay, Evidence for the 2π decay of the \(K_{2}^{0}\) meson. Phys. Rev. Lett. 13, 138 (1964)
V. Gligorov, C. Thomas, M. Williams, The HLT inclusive B triggers, LHCb-PUB-2011-016
R. Aaij et al., The LHCb trigger and its performance. arXiv:1211.3055
LHCb Collaboration, Letter of Intent for the LHCb Upgrade. CERN-LHCC-2011-001.LHCC-I-018
LHCb Collaboration, Framework TDR for the LHCb Upgrade. CERN-LHCC-2012-007.LHCB-TDR-012
E. Majorana, Teoria simmetrica dell’elettrone e del positrone. Nuovo Cimento 14, 171 (1937)
A. Atre, T. Han, S. Pascoli, B. Zhang, The search for heavy Majorana neutrinos. J. High Energy Phys. 05, 030 (2009). arXiv:0901.3589
G. Cvetic, C. Dib, S.K. Kang, C.S. Kim, Probing Majorana neutrinos in rare K and D, D s , B, B c meson decays. Phys. Rev. D 82, 053010 (2010). arXiv:1005.4282
S. Fajfer, J.F. Kamenik, N. Kosnik, \(b \rightarrow dd \bar{s}\) transition and constraints on new physics in B-decays. Phys. Rev. D 74, 034027 (2006). arXiv:hep-ph/0605260
D. Pirjol, J. Zupan, Predictions for \(b \rightarrow ss \bar {d}\), and \(b \rightarrow dd \bar{s}\) decays in the SM and with new physics. J. High Energy Phys. 02, 028 (2010). arXiv:0908.3150
L. Hofer, D. Scherer, L. Vernazza, \(B ^{0}_{ s } \rightarrow \phi\rho^{0}\) and \(B ^{0}_{ s } \rightarrow \phi \pi^{0}\) as a handle on isospin-violating new physics. J. High Energy Phys. 02, 080 (2011). arXiv:1011.6319
N. Uraltsev, Heavy quark expansion in beauty and its decays. arXiv:hep-ph/9804275
A.J. Buras, Flavor physics and CP violation. arXiv:hep-ph/0505175
A.J. Buras et al., Universal unitarity triangle and physics beyond the standard model. Phys. Lett. B 500, 161 (2001). arXiv:hep-ph/0007085
G. D’Ambrosio, G.F. Giudice, G. Isidori, A. Strumia, Minimal flavor violation: an effective field theory approach. Nucl. Phys. B 645, 155 (2002). arXiv:hep-ph/0207036
R. Barbieri et al., U(2) and minimal flavour violation in supersymmetry. Eur. Phys. J. C 71, 1725 (2011). arXiv:1105.2296
S. Descotes-Genon, D. Ghosh, J. Matias, M. Ramon, Exploring New Physics in the C 7–\(C_{7}^{\prime}\) plane. J. High Energy Phys. 06, 099 (2011). arXiv:1104.3342
W. Altmannshofer, P. Paradisi, D.M. Straub, Model-independent constraints on new physics in b→s transitions. J. High Energy Phys. 04, 008 (2012). arXiv:1111.1257
C. Bobeth, G. Hiller, D. van Dyk, C. Wacker, The decay B→Kℓ + ℓ − at low hadronic recoil and model-independent ΔB=1 constraints. J. High Energy Phys. 01, 107 (2012). arXiv:1111.2558
F. Beaujean, C. Bobeth, D. van Dyk, C. Wacker, Bayesian fit of exclusive \(b \rightarrow s \bar{\ell}\ell\) decays: the Standard Model operator basis. J. High Energy Phys. 08, 030 (2012). arXiv:1205.1838
W. Altmannshofer, D.M. Straub, Cornering new physics in b→s transitions. J. High Energy Phys. 08, 121 (2012). arXiv:1206.0273
T. Hurth, F. Mahmoudi, The minimal flavour violation benchmark in view of the latest LHCb data. Nucl. Phys. B 865, 461 (2012). arXiv:1207.0688
Y. Amhis et al. (Heavy Flavor Averaging Group), Averages of b-hadron, c-hadron, and τ-lepton properties as of early 2012. arXiv:1207.1158, updated results and plots available at: http://www.slac.stanford.edu/xorg/hfag/
M. Misiak et al., Estimate of \({ \mathcal{B} } (\bar{B} \rightarrow X_{s}\gamma)\) at \(\mathcal {O}(\alpha_{s}^{2})\). Phys. Rev. Lett. 98, 022002 (2007). arXiv:hep-ph/0609232
M. Beneke, G. Buchalla, M. Neubert, C.T. Sachrajda, QCD factorization for B→ππ decays: strong phases and CP violation in the heavy quark limit. Phys. Rev. Lett. 83, 1914 (1999). arXiv:hep-ph/9905312
M. Beneke, G. Buchalla, M. Neubert, C.T. Sachrajda, QCD factorization for exclusive, nonleptonic B meson decays: general arguments and the case of heavy light final states. Nucl. Phys. B 591, 313 (2000). arXiv:hep-ph/0006124
C.W. Bauer, S. Fleming, D. Pirjol, I.W. Stewart, An effective field theory for collinear and soft gluons: heavy to light decays. Phys. Rev. D 63, 114020 (2001). arXiv:hep-ph/0011336
C.W. Bauer, D. Pirjol, I.W. Stewart, Soft collinear factorization in effective field theory. Phys. Rev. D 65, 054022 (2002). arXiv:hep-ph/0109045
M. Beneke, T. Feldmann, D. Seidel, Systematic approach to exclusive B→Vℓ + ℓ −,Vγ decays. Nucl. Phys. B 612, 25 (2001). arXiv:hep-ph/0106067
M. Beneke, T. Feldmann, D. Seidel, Exclusive radiative and electroweak b→d and b→s penguin decays at NLO. Eur. Phys. J. C 41, 173 (2005). arXiv:hep-ph/0412400
J. Charles et al., Heavy-to-light form factors in the final hadron large energy limit of QCD. Phys. Rev. D 60, 014001 (1999). arXiv:hep-ph/9812358
U. Egede et al., New observables in the decay mode \(\bar{B}_{d} \rightarrow \bar {K}^{*0} \ell^{+} \ell^{-}\). J. High Energy Phys. 11, 032 (2008). arXiv:0807.2589
U. Egede et al., New physics reach of the decay mode \(\bar{B} \rightarrow \bar {K}^{*0}\ell^{+}\ell^{-}\). J. High Energy Phys. 10, 056 (2010). arXiv:1005.0571
J. Matias, F. Mescia, M. Ramon, J. Virto, Complete anatomy of \(\bar{B}_{d} \rightarrow \bar{K}^{* 0} ( \rightarrow K \pi ) \ell^{+}\ell^{-}\) and its angular distribution. J. High Energy Phys. 04, 104 (2012). arXiv:1202.4266
A. Khodjamirian, T. Mannel, A. Pivovarov, Y.-M. Wang, Charm-loop effect in B→K (∗) ℓ + ℓ − and B→K ∗ γ. J. High Energy Phys. 09, 089 (2010). arXiv:1006.4945
B. Grinstein, D. Pirjol, Exclusive rare B→K ∗ ℓ + ℓ − decays at low recoil: controlling the long-distance effects. Phys. Rev. D 70, 114005 (2004). arXiv:hep-ph/0404250
M. Beylich, G. Buchalla, T. Feldmann, Theory of B→K (∗) ℓ + ℓ − decays at high q 2: OPE and quark–hadron duality. Eur. Phys. J. C 71, 1635 (2011). arXiv:1101.5118
N. Isgur, M.B. Wise, Weak transition form-factors between heavy mesons. Phys. Lett. B 237, 527 (1990)
Z. Liu et al., A lattice calculation of B→K (∗) form factors, in Proceedings of CKM2010, the 6th International Workshop on the CKM Unitarity Triangle, University of Warwick, UK, 6–10 September 2010. arXiv:1101.2726
F. Krüger, L.M. Sehgal, N. Sinha, R. Sinha, Angular distribution and CP asymmetries in the decays \(\bar{B} \rightarrow K^{-} \pi^{+} e^{-} e^{+}\) and \(\bar{B} \rightarrow \pi^{-} \pi^{+} e^{-} e^{+}\). Phys. Rev. D 61, 114028 (2000). arXiv:hep-ph/9907386
W. Altmannshofer et al., Symmetries and asymmetries of B→K ∗ μ + μ − decays in the Standard Model and beyond. J. High Energy Phys. 01, 019 (2009). arXiv:0811.1214
F. Krüger, J. Matias, Probing new physics via the transverse amplitudes of B 0→K ∗0(→K − π +)ℓ + ℓ − at large recoil. Phys. Rev. D 71, 094009 (2005). arXiv:hep-ph/0502060
C. Bobeth, G. Hiller, G. Piranishvili, CP asymmetries in \(\bar{B} \rightarrow \bar{K}^{*} ( \rightarrow \bar{K} \pi) \bar{\ell} \ell\) and untagged \(\bar{B}_{s}\), \(B_{s} \rightarrow \phi( \rightarrow K^{+} K^{-}) \bar{\ell} \ell\) decays at NLO. J. High Energy Phys. 07, 106 (2008). arXiv:0805.2525
C. Bobeth, G. Hiller, D. van Dyk, The benefits of \(\bar{B} \rightarrow \bar{K}^{*} \ell^{+} \ell^{-}\) decays at low recoil. J. High Energy Phys. 07, 098 (2010). arXiv:1006.5013
C. Bobeth, G. Hiller, D. van Dyk, More benefits of semileptonic rare B decays at low recoil: CP violation. J. High Energy Phys. 07, 067 (2011). arXiv:1105.0376
M. Benzke, S.J. Lee, M. Neubert, G. Paz, Long-distance dominance of the CP asymmetry in B→X s,d γ decays. Phys. Rev. Lett. 106, 141801 (2011). arXiv:1012.3167
LHCb Collaboration, Differential branching fraction and angular analysis of the B 0→K ∗0 μ + μ − decay. LHCb-CONF-2012-008
LHCb Collaboration, Measurement of the ratio of branching fractions for \(B ^{0}_{s} \rightarrow \phi\mu\mu\) and \(B^{0}_{s} \rightarrow J/\psi\phi\). LHCb-CONF-2012-003
J.-T. Wei et al. (Belle Collaboration), Measurement of the differential branching fraction and forward–backward asymmetry for B→K (∗) ℓ + ℓ −. Phys. Rev. Lett. 103, 171801 (2009). arXiv:0904.0770
T. Aaltonen et al. (CDF Collaboration), Measurements of the angular distributions in the decays B→K (∗) μ + μ − at CDF. Phys. Rev. Lett. 108, 081807 (2012). arXiv:1108.0695
S. Descotes-Genon, J. Matias, M. Ramon, J. Virto, Implications from clean observables for the binned analysis of B→K ∗ ll at large recoil. J. High Energy Phys. 01, 048 (2013). arXiv:1207.2753
A. Bharucha, W. Reece, Constraining new physics with B→K ∗ μ + μ − in the early LHC era. Eur. Phys. J. C 69, 623 (2010). arXiv:1002.4310
C. Hambrock, G. Hiller, Extracting B→K ∗ form factors from data. Phys. Rev. Lett. 109, 091802 (2012). arXiv:1204.4444
T. Aaltonen et al. (CDF Collaboration), Observation of the baryonic flavor-changing neutral current decay Λ b →Λμ + μ −. Phys. Rev. Lett. 107, 201802 (2011). arXiv:1107.3753
J.P. Lees et al. (BaBar Collaboration), Measurement of branching fractions and rate asymmetries in the rare decays B→K (∗) ℓ + ℓ −. Phys. Rev. D 86, 032012 (2012). arXiv:1204.3933
R. Aaij et al. (LHCb Collaboration), Measurement of the isospin asymmetry in B→K (∗) μ + μ − decays. J. High Energy Phys. 07, 133 (2012). arXiv:1205.3422
C. Bobeth, G. Hiller, G. Piranishvili, Angular distributions of B→Kℓ + ℓ − decays. J. High Energy Phys. 12, 040 (2007). arXiv:0709.4174
D. Becirevic, N. Kosnik, F. Mescia, E. Schneider, Complementarity of the constraints on New Physics from \(B ^{0}_{ s } \rightarrow \mu ^{+} \mu ^{-} \) and from B→Kl + l − decays. Phys. Rev. D 86, 034034 (2012). arXiv:1205.5811
J.P. Lees et al. (BaBar Collaboration), Evidence for an excess of \(\bar{B} \rightarrow D^{(*)} \tau^{-}\bar {\nu}_{\tau}\) decays. Phys. Rev. Lett. 109, 101802 (2012). arXiv:1205.5442
A. Matyja et al. (Belle Collaboration), Observation of B 0→D ∗− τ + ν τ decay at Belle. Phys. Rev. Lett. 99, 191807 (2007). arXiv:0706.4429
A. Bozek et al. (Belle Collaboration), Observation of \(B^{+} \rightarrow \bar {D}^{*0} \tau^{+} \nu_{\tau}\) and evidence for \(B^{+} \rightarrow \bar{D}^{0} \tau^{+} \nu_{\tau}\) at Belle. Phys. Rev. D 82, 072005 (2010). arXiv:1005.2302
G. Hiller, F. Krüger, More model independent analysis of b→s processes. Phys. Rev. D 69, 074020 (2004). arXiv:hep-ph/0310219
N. Taniguchi et al. (Belle Collaboration), Measurement of branching fractions, isospin and CP-violating asymmetries for exclusive b→dγ modes. Phys. Rev. Lett. 101, 111801 (2008). arXiv:0804.4770
P. del Amo Sanchez et al. (BaBar Collaboration), Study of B→Xγ decays and determination of |V td /V ts |. Phys. Rev. D 82, 051101 (2010). arXiv:1005.4087
R. Aaij et al. (LHCb Collaboration), First observation of the decay B +→π + μ + μ −. J. High Energy Phys. 12, 125 (2012). arXiv:1210.2645
T. Feldmann, J. Matias, Forward–backward and isospin asymmetry for B→K ∗ ℓ + ℓ − decay in the standard model and in supersymmetry. J. High Energy Phys. 01, 074 (2003). arXiv:hep-ph/0212158
A. Khodjamirian, T. Mannel, Y.-M. Wang, B→Kℓ + ℓ − decay at large hadronic recoil. J. High Energy Phys. (2013). doi:10.1007/JHEP02(2013)010. arXiv:1211.0234
D. Atwood, M. Gronau, A. Soni, Mixing induced CP asymmetries in radiative B decays in and beyond the standard model. Phys. Rev. Lett. 79, 185 (1997). arXiv:hep-ph/9704272
D. Atwood, T. Gershon, M. Hazumi, A. Soni, Mixing-induced CP violation in B→P 1 P 2 γ in search of clean new physics signals. Phys. Rev. D 71, 076003 (2005). arXiv:hep-ph/0410036
F. Muheim, Y. Xie, R. Zwicky, Exploiting the width difference in B s →ϕγ. Phys. Lett. B 664, 174 (2008). arXiv:0802.0876
F. Legger, T. Schietinger, Polarized radiative Λ b decays at LHCb. CERN-LHCB-2006-013
G. Hiller, M. Knecht, F. Legger, T. Schietinger, Photon polarization from helicity suppression in radiative decays of polarized Λ b to spin-3/2 baryons. Phys. Lett. B 649, 152 (2007). arXiv:hep-ph/0702191
Y.-M. Wang, Y. Li, C.-D. Lu, Rare decays of \({ \varLambda }^{0}_{ b } \rightarrow \varLambda\gamma\) and \({ \varLambda }^{0}_{ b } \rightarrow \varLambda l^{+} l^{-}\) in the light-cone sum rules. Eur. Phys. J. C 59, 861 (2009). arXiv:0804.0648
T. Mannel, Y.-M. Wang, Heavy-to-light baryonic form factors at large recoil. J. High Energy Phys. 12, 067 (2011). arXiv:1111.1849
T. Feldmann, M.W.Y. Yip, Form factors for Λ b →Λ transitions in the soft-collinear effective theory. Phys. Rev. D 85, 014035 (2012). arXiv:1111.1844
M. Gronau, Y. Grossman, D. Pirjol, A. Ryd, Measuring the photon polarization in B→Kππγ. Phys. Rev. Lett. 88, 051802 (2002). arXiv:hep-ph/0107254
M. Gronau, D. Pirjol, Photon polarization in radiative B decays. Phys. Rev. D 66, 054008 (2002). arXiv:hep-ph/0205065
D. Atwood, T. Gershon, M. Hazumi, A. Soni, Clean signals of CP-violating and CP-conserving New Physics in B→PVγ decays at B factories and hadron colliders. arXiv:hep-ph/0701021
E. Kou, A. Le Yaouanc, A. Tayduganov, Determining the photon polarization of the b→sγ using the B→K 1(1270)γ→(Kππ)γ decay. Phys. Rev. D 83, 094007 (2011). arXiv:1011.6593
B. Aubert et al. (BaBar Collaboration), Measurement of B decays to ϕKγ. Phys. Rev. D 75, 051102 (2007). arXiv:hep-ex/0611037
H. Yang et al. (Belle Collaboration), Observation of B +→K 1(1270)+ γ. Phys. Rev. Lett. 94, 111802 (2005). arXiv:hep-ex/0412039
C. Bobeth, T. Ewerth, F. Krüger, J. Urban, Analysis of neutral Higgs boson contributions to the decays \(\bar{B}(s) \rightarrow \ell^{+} \ell^{-}\) and \(\bar{B} \rightarrow K \ell^{+} \ell^{-}\). Phys. Rev. D 64, 074014 (2001). arXiv:hep-ph/0104284
C. Bobeth, A.J. Buras, F. Krüger, J. Urban, QCD corrections to \(\bar{B} \rightarrow X_{d,s} \nu\bar{\nu}\), \(\bar{B}_{d,s} \rightarrow \ell^{+} \ell^{-}\), \(K \rightarrow \pi\nu\bar{\nu}\) and K L →μ + μ − in the MSSM. Nucl. Phys. B 630, 87 (2002). arXiv:hep-ph/0112305
A.J. Buras, P.H. Chankowski, J. Rosiek, L. Slawianowska, \(\Delta M_{d,s}, B^{0}_{d,s} \rightarrow \mu^{+} \mu^{-}\) and B→X s γ in supersymmetry at large tanβ. Nucl. Phys. B 659, 3 (2003). arXiv:hep-ph/0210145
F. Mahmoudi, SuperIso v2.3: a program for calculating flavor physics observables in supersymmetry. Comput. Phys. Commun. 180, 1579 (2009). arXiv:0808.3144
E. Gamiz et al. (HPQCD Collaboration), Neutral B meson mixing in unquenched lattice QCD. Phys. Rev. D 80, 014503 (2009). arXiv:0902.1815
C. Bernard et al., B and D meson decay constants. PoS LATTICE2008, 278 (2008). arXiv:0904.1895
J. Laiho, E. Lunghi, R.S. Van de Water, Lattice QCD inputs to the CKM unitarity triangle analysis. Phys. Rev. D 81, 034503 (2010). arXiv:0910.2928, updated results and plots available at: http://www.latticeaverages.org/
J. Simone et al. (Fermilab Lattice and MILC Collaborations), The decay constants \(f_{D_{s}}\), \(f_{D^{+}}\), \(f_{B_{s}}\) and f B from lattice QCD. PoS LATTICE2010, 317 (2010)
A. Bazavov et al. (Fermilab Lattice and MILC Collaborations), B- and D-meson decay constants from three-flavor lattice QCD. Phys. Rev. D 85, 114506 (2012). arXiv:1112.3051
E.T. Neil et al. (Fermilab Lattice Collaboration, MILC Collaboration), B and D meson decay constants from 2+1 flavor improved staggered simulations. PoS LATTICE2011, 320 (2011). arXiv:1112.3978
P. Dimopoulos et al. (ETM Collaboration), Lattice QCD determination of m b , f B and \(f_{B_{s}}\) with twisted mass Wilson fermions. J. High Energy Phys. 01, 046 (2012). arXiv:1107.1441
C. McNeile et al., High-precision \(f_{B_{s}}\) and heavy quark effective theory from relativistic lattice QCD. Phys. Rev. D 85, 031503 (2012). arXiv:1110.4510
H. Na et al., B and B s meson decay constants from lattice QCD. Phys. Rev. D 86, 034506 (2012). arXiv:1202.4914
A.J. Buras, J. Girrbach, BSM models facing the recent LHCb data: a first look. Acta Phys. Pol. B 43, 1427 (2012). arXiv:1204.5064
A.J. Buras, J. Girrbach, D. Guadagnoli, G. Isidori, On the Standard Model prediction for \({ \mathcal{B} } (B_{s,d} \rightarrow \mu ^{+} \mu ^{-} )\). Eur. Phys. J. C 72, 2172 (2012). arXiv:1208.0934
A.J. Buras, M.V. Carlucci, S. Gori, G. Isidori, Higgs-mediated FCNCs: natural flavour conservation vs. minimal flavour violation. J. High Energy Phys. 10, 009 (2010). arXiv:1005.5310
J. Charles et al., Predictions of selected flavor observables within the Standard Model. Phys. Rev. D 84, 033005 (2011). arXiv:1106.4041
F. Mahmoudi, S. Neshatpour, J. Orloff, Supersymmetric constraints from B s →μ + μ − and B→K ∗ μ + μ − observables. J. High Energy Phys. 08, 092 (2012). arXiv:1205.1845
S.R. Choudhury, N. Gaur, Dileptonic decay of B s meson in SUSY models with large tanβ. Phys. Lett. B 451, 86 (1999). arXiv:hep-ph/9810307
K.S. Babu, C. Kolda, Higgs mediated B 0→μ + μ − in minimal supersymmetry. Phys. Rev. Lett. 84, 228 (2000). arXiv:hep-ph/9909476
J. Ellis, K.A. Olive, V.C. Spanos, On the interpretation of B s →μ + μ − in the CMSSM. Phys. Lett. B 624, 47 (2005). arXiv:hep-ph/0504196
M. Carena et al., Constraints on B and Higgs physics in minimal low energy supersymmetric models. Phys. Rev. D 74, 015009 (2006). arXiv:hep-ph/0603106
J. Ellis, S. Heinemeyer, K.A. Olive, G. Weiglein, Light heavy MSSM Higgs bosons at large tanβ. Phys. Lett. B 653, 292 (2007). arXiv:0706.0977
F. Mahmoudi, New constraints on supersymmetric models from b→sγ. J. High Energy Phys. 12, 026 (2007). arXiv:0710.3791
E. Golowich et al., Relating B s mixing and B s →μ + μ − with New Physics. Phys. Rev. D 83, 114017 (2011). arXiv:1102.0009
A.G. Akeroyd, F. Mahmoudi, D. Martinez Santos, The decay B s →μ + μ −: updated SUSY constraints and prospects. J. High Energy Phys. 12, 088 (2011). arXiv:1108.3018
O. Buchmueller et al., Supersymmetry in light of 1/fb of LHC data. Eur. Phys. J. C 72, 1878 (2012). arXiv:1110.3568
S. Chatrchyan et al. (CMS Collaboration), Search for \(B^{0}_{s} \rightarrow \mu^{+} \mu^{-}\) and B 0→μ + μ − decays. J. High Energy Phys. 04, 033 (2012). arXiv:1203.3976
M. Blanke et al., Rare and CP-violating K and B decays in the littlest Higgs model with T-parity. J. High Energy Phys. 01, 066 (2007). arXiv:hep-ph/0610298
M. Blanke et al., Rare K and B decays in a warped extra dimension with custodial protection. J. High Energy Phys. 03, 108 (2009). arXiv:0812.3803
W. Liu, C.-X. Yue, H.-D. Yang, Rare decays B s →ℓ + ℓ − and B→Kℓ + ℓ − in the topcolor-assisted technicolor model. Phys. Rev. D 79, 034008 (2009). arXiv:0901.3463
M. Bauer, S. Casagrande, U. Haisch, M. Neubert, Flavor physics in the Randall–Sundrum model: II. Tree-level weak-interaction processes. J. High Energy Phys. 09, 017 (2010). arXiv:0912.1625
A.J. Buras et al., Lepton flavour violation in the presence of a fourth generation of quarks and leptons. J. High Energy Phys. 09, 104 (2010). arXiv:1006.5356
K. de Bruyn et al., Probing new physics via the \(B^{0}_{s} \rightarrow \mu^{+}\mu^{-}\) effective lifetime. Phys. Rev. Lett. 109, 041801 (2012). arXiv:1204.1737
K. de Bruyn et al., Branching Ratio Measurements of B s Decays. Phys. Rev. D 86, 014027 (2012). arXiv:1204.1735
S. Descotes-Genon, J. Matias, J. Virto, An analysis of B d,s mixing angles in presence of new physics and an update of \(B ^{0}_{ s } \rightarrow K^{*0} \bar{K}^{*0}\). Phys. Rev. D 85, 034010 (2012). arXiv:1111.4882
LHCb Collaboration, Tagged time-dependent angular analysis of \(B_{s}^{0} \rightarrow J/\psi\phi\) decays at LHCb. LHCb-CONF-2012-002
R. Aaij et al. (LHCb Collaboration), Measurements of the branching fractions of the decays \(B^{0}_{s} \rightarrow D^{\mp}_{s} K^{\pm} \) and \(B^{0}_{s} \rightarrow D^{-}_{s} \pi^{+}\). J. High Energy Phys. 06, 115 (2012). arXiv:1204.1237
R. Aaij et al. (LHCb Collaboration), Measurement of the ratio of fragmentation functions f s /f d and the dependence on B meson kinematics. J. High Energy Phys. (2013). doi:10.1007/JHEP04(2013)001. arXiv:1301.5286
R. Fleischer, N. Serra, N. Tuning, A new strategy for \(B ^{0}_{ s } \) branching ratio measurements and the search for New Physics in \(B ^{0}_{ s } \rightarrow \mu ^{+} \mu ^{-} \). Phys. Rev. D 82, 034038 (2010). arXiv:1004.3982
R. Fleischer, N. Serra, N. Tuning, Tests of factorization and SU(3) relations in B decays into heavy-light final states. Phys. Rev. D 83, 014017 (2011). arXiv:1012.2784
J.A. Bailey et al., B s →D s /B→D semileptonic form-factor ratios and their application to \({ \mathcal{B} } ( B ^{0}_{ s } \rightarrow \mu ^{+} \mu ^{-} )\). Phys. Rev. D 85, 114502 (2012). arXiv:1202.6346
R. Aaij et al. (LHCb Collaboration), Measurement of b hadron production fractions in 7 TeV pp collisions. Phys. Rev. D 85, 032008 (2012). arXiv:1111.2357
I.I. Bigi, M.A. Shifman, N. Uraltsev, A.I. Vainshtein, High power n of m(b) in beauty widths and n=5→ infinity limit. Phys. Rev. D 56, 4017 (1997). arXiv:hep-ph/9704245
I. Bigi, T. Mannel, N. Uraltsev, Semileptonic width ratios among beauty hadrons. J. High Energy Phys. 09, 012 (2011). arXiv:1105.4574
J.P. Alexander et al. (CLEO Collaboration), Absolute measurement of hadronic branching fractions of the \(D ^{+}_{ s } \) meson. Phys. Rev. Lett. 100, 161804 (2008). arXiv:0801.0680
M. Wang (Belle Collaboration), Charm decays at Belle, talk given at ICHEP 2012, Melbourne, July 5th 2012, slides available online
G. Aad et al. (ATLAS Collaboration), Search for the decay \(B_{s}^{0} \rightarrow \mu^{+} \mu^{-}\) with the ATLAS detector. Phys. Lett. B 713, 387 (2012). arXiv:1204.0735
T. Aaltonen et al. (CDF Collaboration), Search for B s →μ + μ − and B d →μ + μ − decays with CDF II. Phys. Rev. Lett. 107, 191801 (2011). arXiv:1107.2304
C.W. Bauer, N.D. Dunn, Comment on new physics contributions to \(\varGamma_{12}^{s}\). Phys. Lett. B 696, 362 (2011). arXiv:1006.1629
C. Bobeth, U. Haisch, New physics in \(\varGamma_{12}^{s}\): (\(\bar{s} b\)) (\(\bar{\tau} \tau\)) operators. arXiv:1109.1826
A. Dighe, A. Kundu, S. Nandi, Possibility of large lifetime differences in neutral B meson systems. Phys. Rev. D 76, 054005 (2007). arXiv:0705.4547
A. Dighe, A. Kundu, S. Nandi, Enhanced B s –\(\bar{B}_{s}\) lifetime difference and anomalous like-sign dimuon charge asymmetry from new physics in B s →τ + τ −. Phys. Rev. D 82, 031502 (2010). arXiv:1005.4051
A.K. Alok, S. Baek, D. London, Neutral gauge boson contributions to the dimuon charge asymmetry in B decays. J. High Energy Phys. 07, 111 (2011). arXiv:1010.1333
J.E. Kim, M.-S. Seo, S. Shin, The D0 same-charge dimuon asymmetry and possibile new CP violation sources in the B s –\(\bar{B}_{s}\) system. Phys. Rev. D 83, 036003 (2011). arXiv:1010.5123
H.D. Kim, S.-G. Kim, S. Shin, D0 dimuon charge asymmetry from B s system with Z′ couplings and the recent LHCb result. arXiv:1205.6481
V.M. Abazov et al. (D0 Collaboration), Measurement of the anomalous like-sign dimuon charge asymmetry with 9 fb−1 of \(p \bar {p}\) collisions. Phys. Rev. D 84, 052007 (2011). arXiv:1106.6308
R. Aaij et al. (LHCb Collaboration), A study of the Z production cross-section in pp collisions at \(\sqrt{s}=7\ \mathrm{TeV}\) using tau final states. J. High Energy Phys. 01, 111 (2013). arXiv:1210.6289
R. Aaij et al. (LHCb Collaboration), Measurement of the CP asymmetry in B 0→K ∗0 μ + μ − decays. Phys. Rev. Lett. 110, 031801 (2013). arXiv:1210.4492
F. Mahmoudi, Direct and indirect searches for New Physics, in Proceedings of Moriond QCD (2012). arXiv:1205.3099
F. Mahmoudi, SuperIso: a program for calculating the isospin asymmetry of B→K ∗ γ in the MSSM. Comput. Phys. Commun. 178, 745 (2008). arXiv:0710.2067
S. Chatrchyan et al. (CMS Collaboration), Search for supersymmetry at the LHC in events with jets and missing transverse energy. Phys. Rev. Lett. 107, 221804 (2011). arXiv:1109.2352
CMS Collaboration, Search for supersymmetry with the razor variables at CMS, CMS-PAS-SUS-12-005, 2012
D.A. Demir, K.A. Olive, M. Voloshin, The forward backward asymmetry of B→(π,K)ℓ + ℓ −: Supersymmetry at work. Phys. Rev. D 66, 034015 (2002). arXiv:hep-ph/0204119
A. Behring, C. Gross, G. Hiller, S. Schacht, Squark flavor implications from B→K (∗) l + l −. J. High Energy Phys. 08, 152 (2012). arXiv:1205.1500
O. Buchmueller et al., The CMSSM and NUHM1 in light of 7 TeV LHC, \(B ^{0}_{ s } \rightarrow \mu ^{+} \mu ^{-} \) and XENON100 data. Eur. Phys. J. C 72, 2243 (2012). arXiv:1207.7315
A. Crivellin, U. Nierste, Supersymmetric renormalisation of the CKM matrix and new constraints on the squark mass matrices. Phys. Rev. D 79, 035018 (2009). arXiv:0810.1613
O. Buchmueller et al., Higgs and supersymmetry. Eur. Phys. J. C 72, 2020 (2012). arXiv:1112.3564
A. Djouadi et al. (MSSM Working Group), The minimal supersymmetric standard model: group summary report. arXiv:hep-ph/9901246
A. Arbey, M. Battaglia, F. Mahmoudi, Constraints on the MSSM from the Higgs sector: a pMSSM study of Higgs searches, \(B^{0}_{s} \rightarrow \mu^{+} \mu ^{-}\) and dark matter direct detection. Eur. Phys. J. C 72, 1906 (2012). arXiv:1112.3032
LHCb Collaboration, Search for the rare decays \(B^{0}_{(s)}\rightarrow\mu\mu\) at the LHC with the ATLAS, CMS and LHCb experiments. LHCb-CONF-2012-017
G. Aad et al. (ATLAS Collaboration), Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1 (2012). arXiv:1207.7214
S. Chatrchyan et al. (CMS Collaboration), Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30 (2012). arXiv:1207.7235
G. Burdman, E. Golowich, J. Hewett, S. Pakvasa, Rare charm decays in the standard model and beyond. Phys. Rev. D 66, 014009 (2002). arXiv:hep-ph/0112235
E. Golowich, J. Hewett, S. Pakvasa, A.A. Petrov, Relating D 0–\(\bar{D}^{0}\) mixing and D 0→l + l − with New Physics. Phys. Rev. D 79, 114030 (2009). arXiv:0903.2830
LHCb Collaboration, Search for the D 0→μ + μ − decay with 0.9 fb−1 at LHCb. LHCb-CONF-2012-005
G. Buchalla et al., B, D and K decays. Eur. Phys. J. C 57, 309 (2008). arXiv:0801.1833
S. Fajfer, N. Kosnik, S. Prelovsek, Updated constraints on new physics in rare charm decays. Phys. Rev. D 76, 074010 (2007). arXiv:0706.1133
V.M. Abazov et al. (D0 Collaboration), Search for flavor-changing-neutral-current D meson decays. Phys. Rev. Lett. 100, 101801 (2008). arXiv:0708.2094
I.I. Bigi, A. Paul, On CP asymmetries in two-, three- and four-body D decays. J. High Energy Phys. 03, 021 (2012). arXiv:1110.2862
L. Cappiello, O. Cata, G. D’Ambrosio, Standard Model prediction and new physics tests for D 0→h + h − l + l − (h=π,K: l=e,μ). arXiv:1209.4235
G. Ecker, A. Pich, The longitudinal muon polarization in K L →μ + μ −. Nucl. Phys. B 366, 189 (1991)
G. Isidori, R. Unterdorfer, On the short distance constraints from K L,S →μ + μ −. J. High Energy Phys. 01, 009 (2004). arXiv:hep-ph/0311084
S. Gjesdal et al., Search for the decay \(K^{0}_{S}\rightarrow\mu\mu\). Phys. Lett. B 44, 217 (1973)
R. Aaij et al. (LHCb Collaboration), Search for the rare decay K S →μ + μ −. J. High Energy Phys. 01, 090 (2013). arXiv:1209.4029
W.J. Marciano, T. Mori, J.M. Roney, Charged lepton flavour violation experiments. Annu. Rev. Nucl. Part. Sci. 58, 315 (2008)
M. Raidal et al., Flavour physics of leptons and dipole moments. Eur. Phys. J. C 57, 13 (2008). arXiv:0801.1826
K. Nakamura et al. (Particle Data Group), Review of particle physics. J. Phys. G 37, 075021 (2010), and 2011 partial update for the 2012 edition
LHCb Collaboration, Search for the lepton flavour violating decay τ −→μ + μ − μ −. LHCb-CONF-2012-015
LHCb Collaboration, Search for the lepton flavour violating and baryon number violating decays \(\tau^{-} \rightarrow \overline{ p } \mu^{+} \mu^{-}\) and τ −→pμ − μ −. LHCb-CONF-2012-027
J.C. Pati, A. Salam, Lepton number as the fourth color. Phys. Rev. D 10, 275 (1974), Phys. Rev. D 11, 703 (1975). Erratum
L.G. Landsberg, Is it still worth searching for lepton flavor violation in rare kaon decays? Phys. At. Nucl. 68, 1190 (2005). arXiv:hep-ph/0410261
D. Gorbunov, M. Shaposhnikov, How to find neutral leptons of the nuMSM? J. High Energy Phys. 10, 015 (2007). arXiv:0705.1729
R. Aaij et al. (LHCb Collaboration), Search for the lepton number violating decays B +→π − μ + μ + and B +→K − μ + μ +. Phys. Rev. Lett. 108, 101601 (2012). arXiv:1110.0730
R. Aaij et al. (LHCb Collaboration), Searches for Majorana neutrinos in B − decays. Phys. Rev. D 85, 112004 (2012). arXiv:1201.5600
Y. Kahn, M. Schmitt, T.M.P. Tait, Enhanced rare pion decays from a model of MeV dark matter. Phys. Rev. D 78, 115002 (2008). arXiv:0712.0007
R. Dermisek, J.F. Gunion, Consistency of LEP event excesses with an h→aa decay scenario and low-fine-tuning next-to-minimal supersymmetric Standard Models. Phys. Rev. D 73, 111701 (2006). arXiv:hep-ph/0510322
C. Bouchiat, P. Fayet, Constraints on the parity-violating couplings of a new gauge boson. Phys. Lett. B 608, 87 (2005). arXiv:hep-ph/0410260
C. Boehm et al., MeV dark matter: has it been detected? Phys. Rev. Lett. 92, 101301 (2004). arXiv:astro-ph/0309686
D.S. Gorbunov, V.A. Rubakov, Kaon physics with light sgoldstinos and parity conservation. Phys. Rev. D 64, 054008 (2001). arXiv:hep-ph/0012033
O. Adriani et al. (PAMELA Collaboration), An anomalous positron abundance in cosmic rays with energies 1.5–100 GeV. Nature 458, 607 (2009). arXiv:0810.4995
J. Chang et al., An excess of cosmic ray electrons at energies of 300–800 GeV. Nature 456, 362 (2008)
H.K. Park et al. (HyperCP Collaboration), Evidence for the decay Σ +→pμ + μ −. Phys. Rev. Lett. 94, 021801 (2005). arXiv:hep-ex/0501014
N. Deshpande, G. Eilam, J. Jiang, On the possibility of a new boson X 0(214 MeV) in Σ +→pμ + μ −. Phys. Lett. B 632, 212 (2006). arXiv:hep-ph/0509081
D. Gorbunov, V. Rubakov, On sgoldstino interpretation of HyperCP events. Phys. Rev. D 73, 035002 (2006). arXiv:hep-ph/0509147
C.Q. Geng, Y.K. Hsiao, Constraints on the new particle in Σ +→pμ + μ −. Phys. Lett. B 632, 215 (2006). arXiv:hep-ph/0509175
X.-G. He, J. Tandean, G. Valencia, Does the HyperCP evidence for the decay Σ→pμ + μ − indicate a light pseudoscalar Higgs boson? Phys. Rev. Lett. 98, 081802 (2007). arXiv:hep-ph/0610362
LHCb Collaboration, Search for the rare decays \(B_{s}^{0} \rightarrow\mu^{+} \mu^{-} \mu^{+} \mu^{-}\) and \(B_{d}^{0} \rightarrow\mu^{+} \mu^{-} \mu^{+} \mu^{-}\). LHCb-CONF-2012-010
S. Demidov, D. Gorbunov, Flavor violating processes with sgoldstino pair production. Phys. Rev. D 85, 077701 (2012). arXiv:1112.5230
H.J. Hyun et al. (Belle Collaboration), Search for a low mass particle decaying into μ + μ − in B 0→K ∗0 X and B 0→ρ 0 X at Belle. Phys. Rev. Lett. 105, 091801 (2010). arXiv:1005.1450
M. Freytsis, Z. Ligeti, J. Thaler, Constraining the axion portal with B→Kl + l −. Phys. Rev. D 81, 034001 (2010). arXiv:0911.5355
A.D. Sakharov, Violation of CP invariance, C asymmetry, and baryon asymmetry of the Universe. Pis’ma Zh. Eksp. Teor. Fiz. 5, 32 (1967), also available as JETP Lett. 5, 24 (1967)
U. Nierste, Three lectures on meson mixing and CKM phenomenology. arXiv:0904.1869
A. Lenz, Theoretical update of B-mixing and lifetimes. arXiv:1205.1444
A. Lenz, Theoretical status of B s -mixing and lifetimes of heavy hadrons. Nucl. Phys. B, Proc. Suppl. 177–178, 81 (2008). arXiv:0705.3802
R. Aaij et al. (LHCb Collaboration), Measurement of the CP violating phase ϕ s in \(\overline{ B }{} ^{0}_{ s } \rightarrow J/\psi f_{0}(980)\). Phys. Lett. B 707, 497 (2012). arXiv:1112.3056
R. Aaij et al. (LHCb Collaboration), Measurement of the CP-violating phase ϕ s in \(\overline{B}_{s} \rightarrow J/\psi\pi^{+}\pi^{-}\) decays. Phys. Lett. B 713, 378 (2012). arXiv:1204.5675
A. Lenz, U. Nierste, Numerical updates of lifetimes and mixing parameters of B mesons, in Proceedings of CKM2010, the 6th International Workshop on the CKM Unitarity Triangle, University of Warwick, UK, 6–10 September (2010). arXiv:1102.4274
A. Lenz, U. Nierste, Theoretical update of \(B ^{0}_{ s } \)–\(\overline{ B }{} ^{0}_{ s } \) mixing. J. High Energy Phys. 06, 072 (2007). arXiv:hep-ph/0612167
M. Beneke et al., Next-to-leading order QCD corrections to the lifetime difference of \(B ^{0}_{ s } \) mesons. Phys. Lett. B 459, 631 (1999). arXiv:hep-ph/9808385
M. Ciuchini et al., Lifetime differences and CP violation parameters of neutral B mesons at the next-to-leading order in QCD. J. High Energy Phys. 08, 031 (2003). arXiv:hep-ph/0308029
M. Beneke, G. Buchalla, I. Dunietz, Width difference in the \(B ^{0}_{ s } \)–\(\overline{ B }{} ^{0}_{ s } \) system. Phys. Rev. D 54, 4419 (1996). arXiv:hep-ph/9605259
M. Beneke, G. Buchalla, A. Lenz, U. Nierste, CP asymmetry in flavor specific B decays beyond leading logarithms. Phys. Lett. B 576, 173 (2003). arXiv:hep-ph/0307344
LHCb Collaboration, Measurement of Δm s in the decay \(B^{0}_{s} \rightarrow D^{-}_{s}(K^{+}K^{-}\pi^{-})\pi^{+}\) using opposite-side and same-side flavour tagging algorithms. LHCb-CONF-2011-050
V.M. Abazov et al. (D0 Collaboration), Search for CP violation in \(B ^{0}_{ s } \rightarrow \mu ^{+} D ^{-}_{ s } X\) decays in \(p\bar{p}\) collisions at \(\sqrt{s}=1.96\ \mathrm{TeV}\). Phys. Rev. D 82, 012003 (2010). arXiv:0904.3907
A. Abulencia et al. (CDF Collaboration), Observation of \(B ^{0}_{ s } \)–\(\overline{ B }{} ^{0}_{ s } \) oscillations. Phys. Rev. Lett. 97, 242003 (2006). arXiv:hep-ex/0609040
R. Aaij et al. (LHCb Collaboration), Measurement of the \(B ^{0}_{ s } \mbox{--} \overline{ B }{} ^{0}_{ s } \) oscillation frequency Δm s in \(B^{0}_{s} \rightarrow D_{s} (3)\pi\) decays. Phys. Lett. B 709, 177 (2012). arXiv:1112.4311
A.S. Dighe, I. Dunietz, R. Fleischer, Extracting CKM phases and \(B ^{0}_{ s } \)–\(\overline{ B }{} ^{0}_{ s } \) mixing parameters from angular distributions of nonleptonic B decays. Eur. Phys. J. C 6, 647 (1999). arXiv:hep-ph/9804253
I. Dunietz, R. Fleischer, U. Nierste, In pursuit of new physics with \(B ^{0}_{ s } \) decays. Phys. Rev. D 63, 114015 (2001). arXiv:hep-ph/0012219
R. Aaij et al. (LHCb Collaboration), Determination of the sign of the decay width difference in the B s system. Phys. Rev. Lett. 108, 241801 (2012). arXiv:1202.4717
Y. Xie, P. Clarke, G. Cowan, F. Muheim, Determination of 2β s in \(B ^{0}_{ s } \rightarrow J/\psi K ^{+} K ^{-} \) decays in the presence of a K + K − S-wave contribution. J. High Energy Phys. 09, 074 (2009). arXiv:0908.3627
R. Aaij et al. (LHCb Collaboration), Analysis of the resonant components in \(\overline{B}^{0}_{s} \rightarrow J/\psi\pi^{+}\pi^{-}\). Phys. Rev. D 86, 052006 (2012). arXiv:1204.5643
R. Fleischer, R. Knegjens, G. Ricciardi, Anatomy of \(B^{0}_{s,d} \rightarrow J/\psi f_{0}(980)\). Eur. Phys. J. C 71, 1832 (2011). arXiv:1109.1112
R. Aaij et al. (LHCb Collaboration), Measurement of the \(\bar{B}^{0}_{s}\) effective lifetime in the J/ψf 0(980) final state. Phys. Rev. Lett. 109, 152002 (2012). arXiv:1207.0878
T. Aaltonen et al. (CDF Collaboration), Measurement of the CP-violating phase \(\beta_{s}^{J/\psi \phi}\) in \(B^{0}_{s} \rightarrow J/\psi\phi\) decays with the CDF II detector. Phys. Rev. D 85, 072002 (2012). arXiv:1112.1726
V.M. Abazov et al. (D0 Collaboration), Measurement of the CP-violating phase \(\phi_{s}^{J/\psi\phi }\) using the flavor-tagged decay \(B_{s}^{0} \rightarrow J/\psi\phi\) in 8 fb−1 of \(p \bar{p}\) collisions. Phys. Rev. D 85, 032006 (2012). arXiv:1109.3166
R. Aaij et al. (LHCb Collaboration), Opposite-side flavour tagging of B mesons at the LHCb experiment. Eur. Phys. J. C 72, 2022 (2012). arXiv:1202.4979
LHCb Collaboration, Performance of flavor tagging algorithms optimised for the analysis of \(B_{s}^{0} \rightarrow J/\psi\phi\). LHCb-CONF-2012-026
LHCb Collaboration, Optimization and calibration of the same-side kaon tagging algorithm using hadronic \(B ^{0}_{ s } \) decays in 2011 data. LHCb-CONF-2012-033
R. Fleischer, R. Knegjens, G. Ricciardi, Exploring CP violation and η–η′ mixing with the \(B^{0}_{s,d} \rightarrow J/\psi\eta ^{(\prime)}\) systems. Eur. Phys. J. C 71, 1798 (2011). arXiv:1110.5490
R. Fleischer, Exploring CP violation and penguin effects through \(B^{0}_{d} \rightarrow D^{+} D^{-}\) and \(B^{0}_{s} \rightarrow D^{+}_{s} D^{-}_{s}\). Eur. Phys. J. C 51, 849 (2007). arXiv:0705.4421
LHCb Collaboration, First observations and branching fraction measurements of \(\bar{B}_{s}^{0}\) to double-charm final states. LHCb-CONF-2012-009
R. Aaij et al. (LHCb Collaboration), Evidence for the decay B 0→J/ψω and measurement of the relative branching fractions of \(B^{0}_{s}\) meson decays to J/ψη and J/ψη′. Nucl. Phys. B 867, 547 (2013). arXiv:1210.2631
C.-W. Chiang et al., New physics in \(B ^{0}_{ s } \rightarrow J/\psi\phi\): a general analysis. J. High Energy Phys. 04, 031 (2010). arXiv:0910.2929
V. Abazov et al. (D0 Collaboration), Measurement of the semileptonic charge asymmetry using \(B_{s}^{0} \rightarrow D_{s} \mu X\) decays. Phys. Rev. Lett. 110, 011801 (2013). arXiv:1207.1769
LHCb Collaboration, Measurement of the flavour-specific CP violating asymmetry \(a_{\rm sl}^{s}\) in \(B ^{0}_{ s } \) decays. LHCb-CONF-2012-022
K. Hara et al. (Belle Collaboration), Evidence for \(B^{-} \rightarrow \tau^{-} \bar{\nu}\) with a semileptonic tagging method. Phys. Rev. D 82, 071101 (2010). arXiv:1006.4201
J.P. Lees et al. (BaBar Collaboration), Evidence of B→τν decays with hadronic B tags. arXiv:1207.0698
I. Adachi et al. (Belle Collaboration), Measurement of \(B^{-} \rightarrow \tau^{-} \bar {\nu}_{\tau}\) with a hadronic tagging method using the full data sample of Belle. Phys. Rev. Lett. (2013). doi:10.1103/PhysRevLett.110.131801. arXiv:1208.4678
J. Charles et al. (CKMfitter group), CP violation and the CKM matrix: assessing the impact of the asymmetric B factories. Eur. Phys. J. C 41, 1 (2005). arXiv:hep-ph/0406184, updated results and plots available at http://ckmfitter.in2p3.fr
R. Aaij et al. (LHCb Collaboration), Measurement of the B 0–\(\overline{B}^{0}\) oscillation frequency Δm d with the decays B 0→J/ψK ∗0 and B 0→D − π +. Phys. Lett. B (2013). doi:10.1016/j.physletb.2013.01.019. arXiv:1210.6750
R. Aaij et al. (LHCb Collaboration), Measurement of the time-dependent CP asymmetry in \(B ^{0} \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \) decays. Phys. Lett. B (2013). doi:10.1016/j.physletb.2013.02.054. arXiv:1211.6093
T. Gershon, ΔΓ d : a forgotten null test of the Standard Model. J. Phys. G 38, 015007 (2011). arXiv:1007.5135
A. Lenz et al., Constraints on new physics in B–\(\bar{B}\) mixing in the light of recent LHCb data. Phys. Rev. D 86, 033008 (2012). arXiv:1203.0238
A.J. Lenz, A simple relation for \(B ^{0}_{ s } \) mixing. Phys. Rev. D 84, 031501 (2011). arXiv:1106.3200
Y. Grossman, The B s width difference beyond the standard model. Phys. Lett. B 380, 99 (1996). arXiv:hep-ph/9603244
A. Lenz et al., Anatomy of new physics in B–\(\bar{B}\) mixing. Phys. Rev. D 83, 036004 (2011). arXiv:1008.1593
A. Badin, F. Gabbiani, A.A. Petrov, Lifetime difference in B s mixing: Standard Model and beyond. Phys. Lett. B 653, 230 (2007). arXiv:0707.0294
B.A. Dobrescu, P.J. Fox, A. Martin, CP violation in B s mixing from heavy Higgs boson exchange. Phys. Rev. Lett. 105, 041801 (2010). arXiv:1005.4238
Z. Ligeti, M. Papucci, G. Perez, J. Zupan, Implications of the dimuon CP asymmetry in B d,s decays. Phys. Rev. Lett. 105, 131601 (2010). arXiv:1006.0432
K. Flood (BaBar Collaboration), New results in radiative electroweak penguin decays at BaBar. PoS ICHEP2010, 234 (2010)
Y. Bai, A.E. Nelson, CP violating contribution to ΔΓ in the B s system from mixing with a hidden pseudoscalar. Phys. Rev. D 82, 114027 (2010). arXiv:1007.0596
S. Oh, J. Tandean, Anomalous CP-violation in B s –\(\bar{B}_{s}\) mixing due to a light spin-one particle. Phys. Lett. B 697, 41 (2011). arXiv:1008.2153
M. Bona et al. (UTfit Collaboration), The 2004 UTfit Collaboration report on the status of the unitarity triangle in the standard model. J. High Energy Phys., 07, 028 (2005). arXiv:hep-ph/0501199, updated results and plots available at: http://www.utfit.org/UTfit/
E. Lunghi, A. Soni, Possible evidence for the breakdown of the CKM-paradigm of CP-violation. Phys. Lett. B 697, 323 (2011). arXiv:1010.6069
G. Eigen, G. Dubois-Felsmann, D.G. Hitlin, F.C. Porter, Global CKM Fits with the Scan Method. arXiv:1301.5867
M. Bona et al. (UTfit Collaboration), An improved Standard Model prediction of \({ \mathcal{B} } (B \rightarrow \tau\nu )\) and its implications for new physics. Phys. Lett. B 687, 61 (2010). arXiv:0908.3470
M. Bona et al. (UTfit Collaboration), Model-independent constraints on ΔF=2 operators and the scale of new physics. J. High Energy Phys. 03, 049 (2008). arXiv:0707.0636
I.I. Bigi, A.I. Sanda, Notes on the observability of CP violations in B decays. Nucl. Phys. B 193, 85 (1981)
H. Boos, J. Reuter, T. Mannel, Gold plated mode reexamined: sin(2β) and \(B 0 \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \) in the Standard Model. Phys. Rev. D 70, 036006 (2004). arXiv:hep-ph/0403085
H.-n. Li, S. Mishima, Penguin pollution in the \(B ^{0} \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \) decay. J. High Energy Phys. 03, 009 (2007). arXiv:hep-ph/0610120
M. Gronau, J.L. Rosner, Doubly CKM-suppressed corrections to CP asymmetries in B 0→J/ψK 0. Phys. Lett. B 672, 349 (2009). arXiv:0812.4796
R. Fleischer, Extracting γ from \(B _{s(d)} \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \) and \(B _{d(s)} \rightarrow D^{+}_{d(s)} D^{-}_{d(s)}\). Eur. Phys. J. C 10, 299 (1999). arXiv:hep-ph/9903455
M. Ciuchini, M. Pierini, L. Silvestrini, Effect of penguin operators in the B 0→J/ψK 0 CP asymmetry. Phys. Rev. Lett. 95, 221804 (2005). arXiv:hep-ph/0507290
S. Faller, R. Fleischer, T. Mannel, Precision physics with \(B^{0}_{s} \rightarrow J/\psi\phi\) at the LHC: the quest for new physics. Phys. Rev. D 79, 014005 (2009). arXiv:0810.4248
S. Faller, M. Jung, R. Fleischer, T. Mannel, The golden modes B 0→J/ψK S,L in the era of precision flavour physics. Phys. Rev. D 79, 014030 (2009). arXiv:0809.0842
M. Jung, T. Mannel, General analysis of U-spin breaking in B decays. Phys. Rev. D 80, 116002 (2009). arXiv:0907.0117
K. De Bruyn, R. Fleischer, P. Koppenburg, Extracting gamma and penguin topologies through CP violation in \(B ^{0}_{ s } \rightarrow { J / \psi } K ^{0}_{\mathrm{S}} \). Eur. Phys. J. C 70, 1025 (2010). arXiv:1010.0089
M. Ciuchini, M. Pierini, L. Silvestrini, Theoretical uncertainty in sin 2β: an update, in Proceedings of CKM2010, the 6th International Workshop on the CKM Unitarity Triangle, University of Warwick, UK, 6–10 September (2010). arXiv:1102.0392
T. Aaltonen et al. (CDF Collaboration), Observation of \(B^{0}_{s} \rightarrow J/\psi K^{*0}(892)\) and \(B^{0}_{s} \rightarrow J/\psi K^{0}_{S}\) decays. Phys. Rev. D 83, 052012 (2011). arXiv:1102.1961
R. Aaij et al. (LHCb Collaboration), Measurement of \(B_{s} \rightarrow J/\psi \bar{K}^{*0}\) branching fraction and angular amplitudes. Phys. Rev. D 86, 071102(R) (2012). arXiv:1208.0738
B. Bhattacharya, A. Datta, D. London, Reducing penguin pollution. arXiv:1209.1413
M. Jung, Determining weak phases from B→J/ψP decays. Phys. Rev. D 86, 053008 (2012). arXiv:1206.2050
R. Aaij et al. (LHCb Collaboration), Measurements of the branching fractions and CP asymmetries of B +→J/ψπ + and B +→ψ(2S)π + decays. Phys. Rev. 85, 091105 (2012). arXiv:1203.3592
R. Aaij et al. (LHCb Collaboration), Measurement of the \(B^{0}_{s} \rightarrow J/\psi K^{0}_{\rm S}\) branching fraction. Phys. Lett. B 713, 172 (2012). arXiv:1205.0934
R. Fleischer, A closer look at B d,s →Df r decays and novel avenues to determine γ. Nucl. Phys. B 659, 321 (2003). arXiv:hep-ph/0301256
S. Nandi, D. London, \(B ^{0}_{ s } ( \overline{ B }{} ^{0}_{ s } ) \rightarrow D^{0}_{ \mathit{CP} } K {\bar{K}}\): detecting and discriminating new physics in \(B ^{0}_{ s } \)–\(\overline{ B }{} ^{0}_{ s } \) mixing. Phys. Rev. D 85, 114015 (2012). arXiv:1108.5769
J. Charles et al., B 0(t)→DPP time-dependent Dalitz plots, CP violating angles 2β, 2β+γ, and discrete ambiguities. Phys. Lett. B 425, 375 (1998). arXiv:hep-ph/9801363
T. Latham, T. Gershon, A method to measure cos(2β) using time-dependent Dalitz plot analysis of B 0→D CP π + π −. J. Phys. G 36, 025006 (2009). arXiv:0809.0872
R. Fleischer, R. Knegjens, Effective lifetimes of B s decays and their constraints on the \(B_{s}^{0}\)–\(\bar{B}_{s}^{0}\) mixing parameters. Eur. Phys. J. C 71, 1789 (2011). arXiv:1109.5115
A.S. Dighe, T. Hurth, C.S. Kim, T. Yoshikawa, Measurement of the lifetime difference of B 0 mesons: possible and worthwhile? Nucl. Phys. B 624, 377 (2002). arXiv:hep-ph/0109088
V.A. Kostelecky, R. Van Kooten, Bounding CPT violation in the neutral B system. Phys. Rev. D 54, 5585 (1996). arXiv:hep-ph/9607449
B. Kayser, Cascade mixing and the CP violating angle β, in Proceedings of Moriond EW (1997). arXiv:hep-ph/9709382
D.-S. Du, Z.-T. Wei, Test of CPT symmetry in cascade decays. Eur. Phys. J. C 14, 479 (2000). arXiv:hep-ph/9904403
A. Kundu, S. Nandi, S.K. Patra, A. Soni, B s →D s K as a probe of CPT violation. Phys. Rev. D 87, 016005 (2013). arXiv:1209.6063
M. Gronau, J.L. Rosner, Triple product asymmetries in K, D (s) and B (s) decays. Phys. Rev. D 84, 096013 (2011). arXiv:1107.1232
M. Beneke, Corrections to sin(2β) from CP asymmetries in \(B ^{0} \rightarrow (\pi^{0},\rho^{0},\eta ,\eta^{\prime},\omega,\phi) K^{0}_{S} \) decays. Phys. Lett. B 620, 143 (2005). arXiv:hep-ph/0505075
H.-Y. Cheng, C.-K. Chua, A. Soni, Effects of final-state interactions on mixing-induced CP violation in penguin-dominated B decays. Phys. Rev. D 72, 014006 (2005). arXiv:hep-ph/0502235
S. Descotes-Genon, J. Matias, J. Virto, Exploring B d,s →KK decays through flavor symmetries and QCD-factorization. Phys. Rev. Lett. 97, 061801 (2006). arXiv:hep-ph/0603239
S. Descotes-Genon, J. Matias, J. Virto, Penguin-mediated B d,s →VV decays and the \(B ^{0}_{ s } \)–\(\overline{ B }{} ^{0}_{ s } \) mixing angle. Phys. Rev. D 76, 074005 (2007). arXiv:0705.0477
R. Aaij et al. (LHCb Collaboration), First observation of the decay \(B^{0}_{s} \rightarrow K ^{*0} \overline{ K }{} ^{*0} \). Phys. Lett. B 709, 50 (2012). arXiv:1111.4183
R. Aaij et al. (LHCb Collaboration), Measurement of the polarization amplitudes and triple product asymmetries in the \(B ^{0}_{ s } \rightarrow \phi\phi\) decay. Phys. Lett. B 713, 369 (2012). arXiv:1204.2813
T. Aaltonen et al. (CDF Collaboration), Measurement of polarization and search for CP-violation in \(B_{s}^{0} \rightarrow \phi\phi\) decays. Phys. Rev. Lett. 107, 261802 (2011). arXiv:1107.4999
M. Bartsch, G. Buchalla, C. Kraus, B→V L V L decays at next-to-leading order in QCD. arXiv:0810.0249
R. Fleischer, Extracting CKM phases from angular distributions of B d,s decays into admixtures of CP eigenstates. Phys. Rev. D 60, 073008 (1999). arXiv:hep-ph/9903540
M. Ciuchini, M. Pierini, L. Silvestrini, \(B ^{0}_{ s } \rightarrow K^{(*)0}\bar{K}^{(*)0}\) CP asymmetries: golden channels for new physics searches. Phys. Rev. Lett. 100, 031802 (2008). arXiv:hep-ph/0703137
A. Datta, D. London, Triple-product correlations in B→V 1 V 2 decays and new physics. Int. J. Mod. Phys. A 19, 2505 (2004). arXiv:hep-ph/0303159
C. Aubin, C.-J.D. Lin, A. Soni, Possible lattice approach to B→Dπ(K) matrix elements. Phys. Lett. B 710, 164 (2012). arXiv:1111.4686
M. Gronau, D. London, How to determine all the angles of the unitarity triangle from \(B ^{0} \rightarrow D K ^{0}_{\mathrm{S}} \) and \(B ^{0}_{ s } \rightarrow D \phi\). Phys. Lett. B 253, 483 (1991)
M. Gronau, D. Wyler, On determining a weak phase from charged B decay asymmetries. Phys. Lett. B 265, 172 (1991)
D. Atwood, I. Dunietz, A. Soni, Enhanced CP violation with B→KD 0 (\(\overline{ D }{} ^{0} \)) modes and extraction of the Cabibbo–Kobayashi–Maskawa angle γ. Phys. Rev. Lett. 78, 3257 (1997). arXiv:hep-ph/9612433
D. Atwood, I. Dunietz, A. Soni, Improved methods for observing CP violation in B ±→KD and measuring the CKM phase γ. Phys. Rev. D 63, 036005 (2001). arXiv:hep-ph/0008090
A. Giri, Y. Grossman, A. Soffer, J. Zupan, Determining γ using B ±→DK ± with multibody D decays. Phys. Rev. D 68, 054018 (2003). arXiv:hep-ph/0303187
Y. Grossman, Z. Ligeti, A. Soffer, Measuring gamma in B ±→K ±(KK ∗) D decays. Phys. Rev. D 67, 071301 (2003). arXiv:hep-ph/0210433
A. Bondar, T. Gershon, On ϕ 3 measurements using B −→D ∗ K − decays. Phys. Rev. D 70, 091503 (2004). arXiv:hep-ph/0409281
M. Gronau, Improving bounds on γ in B ±→DK ± and \(B^{\pm,0} \rightarrow DX_{s}^{\pm,0}\). Phys. Lett. B 557, 198 (2003). arXiv:hep-ph/0211282
D.M. Asner et al. (CLEO Collaboration), Determination of the D 0→K + π − relative strong phase using quantum-correlated measurements in \(e^{+} e^{-} \rightarrow D^{0} \bar{D}^{0}\) at CLEO. Phys. Rev. D 78, 012001 (2008). arXiv:0802.2268
D. Asner et al. (CLEO Collaboration), Updated measurement of the strong phase in D 0→K + π − decay using quantum correlations in \(e^{+}e^{-} \rightarrow D^{0} \bar{D}^{0}\) at CLEO. Phys. Rev. D 86, 112001 (2012). arXiv:1210.0939
Y. Horii et al. (Belle Collaboration), Evidence for the suppressed decay B −→DK −, D→K + π −. Phys. Rev. Lett. 106, 231803 (2011). arXiv:1103.5951
P. del Amo Sanchez et al. (BaBar Collaboration), Search for b→u transitions in B −→DK − and D ∗ K − Decays. Phys. Rev. D 82, 072006 (2010). arXiv:1006.4241
T. Aaltonen et al. (CDF Collaboration), Measurements of branching fraction ratios and CP-asymmetries in suppressed B −→D(→K + π −)K − and B −→D(→K + π −)π − decays. Phys. Rev. D 84, 091504 (2011). arXiv:1108.5765
B. Aubert et al. (BaBar Collaboration), Measurement of the Cabibbo–Kobayashi–Maskawa angle γ in B ∓→D (∗) K ∓ decays with a Dalitz analysis of \(D \rightarrow K^{0}_{S} \pi^{-} \pi^{+}\). Phys. Rev. Lett. 95, 121802 (2005). arXiv:hep-ex/0504039
A. Bondar, A. Poluektov, Feasibility study of model-independent approach to ϕ 3 measurement using Dalitz plot analysis. Eur. Phys. J. C 47, 347 (2006). arXiv:hep-ph/0510246
A. Bondar, A. Poluektov, The use of quantum-correlated D 0 decays for ϕ 3 measurement. Eur. Phys. J. C 55, 51 (2008). arXiv:0801.0840
J. Libby et al. (CLEO Collaboration), Model-independent determination of the strong-phase difference between D 0 and \(\bar{D}^{0} \rightarrow K^{0}_{S,L} h^{+} h^{-}\) (h=π,K) and its impact on the measurement of the CKM angle γ/ϕ 3. Phys. Rev. D 82, 112006 (2010). arXiv:1010.2817
I. Dunietz, R.G. Sachs, Asymmetry between inclusive charmed and anticharmed modes in B 0, \(\bar{B}^{0}\) decay as a measure of CP violation. Phys. Rev. D 37, 3186 (1988)
R. Aleksan, I. Dunietz, B. Kayser, Determining the CP violating phase γ. Z. Phys. C 54, 653 (1992)
R. Fleischer, New strategies to obtain insights into CP violation through \(B ^{0}_{ s } \rightarrow D ^{\pm}_{ s } K ^{\mp} \), \(D ^{*\pm}_{ s } K^{\mp}\), … and B 0→D ± π ∓, \(D ^{\pm}_{ s } \pi ^{\mp} \), … decays. Nucl. Phys. B 671, 459 (2003). arXiv:hep-ph/0304027
B. Aubert et al. (BaBar Collaboration), Measurement of time-dependent CP-violating asymmetries and constraints on sin(2β+γ) with partial reconstruction of B→D ∗∓ π ± decays. Phys. Rev. D 71, 112003 (2005). arXiv:hep-ex/0504035
B. Aubert et al. (BaBar Collaboration), Measurement of time-dependent CP asymmetries in B 0→D (∗)± π ∓ and B 0→D ± ρ ∓ decays. Phys. Rev. D 73, 111101 (2006). arXiv:hep-ex/0602049
F.J. Ronga et al. (Belle Collaboration), Measurements of CP violation in B 0→D ∗− π + and B 0→D − π + decays. Phys. Rev. D 73, 092003 (2006). arXiv:hep-ex/0604013
S. Bahinipati et al. (Belle Collaboration), Measurements of time-dependent CP asymmetries in B→D ∗∓ π ± decays using a partial reconstruction technique. Phys. Rev. D 84, 021101 (2011). arXiv:1102.0888
S. Nandi, U. Nierste, Resolving the sign ambiguity in ΔΓ s with B s →D s K. Phys. Rev. D 77, 054010 (2008). arXiv:0801.0143
LHCb Collaboration, Measurement of the time-dependent CP-violation parameters in \(B^{0}_{s} \rightarrow D_{s}^{\mp}K^{\pm}\). LHCb-CONF-2012-029
Y. Grossman, A. Soffer, J. Zupan, The effect of D 0–\(\overline { D }{} ^{0} \) mixing on the measurement of γ in B→DK decays. Phys. Rev. D 72, 031501 (2005). arXiv:hep-ph/0505270
A. Bondar, A. Poluektov, V. Vorobiev, Charm mixing in a model-independent analysis of correlated D 0–\(\overline{ D }{} ^{0} \) decays. Phys. Rev. D 82, 034033 (2010). arXiv:1004.2350
Y. Grossman, A.L. Kagan, Z. Ligeti, Can the CP asymmetries in \(B \rightarrow \psi K ^{0}_{\mathrm{S}} \) and \(B \rightarrow \psi K ^{0}_{\mathrm{L}} \) differ? Phys. Lett. B 538, 327 (2002). arXiv:hep-ph/0204212
LHCb Collaboration, Measurement of CP observables in B 0→DK ∗0 with D→K + K −. LHCb-CONF-2012-024
LHCb Collaboration, First observation of B −→D 0 K − π + π − decays to CP even final states. LHCb-CONF-2012-021
LHCb Collaboration, Search for the suppressed ADS modes B ±→[π ± K ∓ π + π −] D K ± and B ±→[π ± K ∓ π + π −] D π ±. LHCb-CONF-2012-030
LHCb Collaboration, A measurement of γ from a combination of B +→Dh + analyses. LHCb-CONF-2012-032
M. Adinolfi et al. Performance of the LHCb RICH detector at the LHC. arXiv:1211.6759
P. del Amo Sanchez et al. (BaBar Collaboration), Measurement of CP observables in B ±→D CP K ± decays and constraints on the CKM angle γ. Phys. Rev. D 82, 072004 (2010). arXiv:1007.0504
T. Aaltonen et al. (CDF Collaboration), Measurements of branching fraction ratios and CP asymmetries in B ±→D CP K ± decays in hadron collisions. Phys. Rev. D 81, 031105 (2010). arXiv:0911.0425
T. Aaltonen et al. (CDF Collaboration), First observation of \(\bar{B}^{0}_{s} \rightarrow D_{s}^{\pm}K^{\mp}\) and measurement of the ratio of branching fractions \({ \mathcal{B} } (\bar{B}^{0}_{s} \rightarrow D_{s}^{\pm}K^{\mp})/{ \mathcal{B} } (\bar{B}^{0}_{s} \rightarrow D_{s}^{+} \pi^{-})\). Phys. Rev. Lett. 103, 191802 (2009). arXiv:0809.0080
R. Louvot et al. (Belle Collaboration), Measurement of the decay \(B_{s}^{0} \rightarrow D_{s}^{-} \pi^{+}\) and evidence for \(B_{s}^{0} \rightarrow D_{s}^{\mp}K^{\pm}\) in e + e − annihilation at \(\sqrt{s} = 10.87\ \mathrm{GeV}\). Phys. Rev. Lett. 102, 021801 (2009). arXiv:0809.2526
R. Aaij et al. (LHCb Collaboration), Determination of f s /f d for 7 TeV pp collisions and measurement of the B 0→D − K + branching fraction. Phys. Rev. Lett. 107, 211801 (2011). arXiv:1106.4435
M. Gronau, D. London, Isospin analysis of CP asymmetries in B decays. Phys. Rev. Lett. 65, 3381 (1990)
J. Charles, Taming the penguin contributions in the \(B^{0}_{d} (t) \rightarrow \pi ^{+} \pi^{-}\) CP asymmetry: observables and minimal theoretical input. Phys. Rev. D 59, 054007 (1999). arXiv:hep-ph/9806468
M. Bona et al. (UTfit Collaboration), Improved determination of the CKM angle α from B→ππ decays. Phys. Rev. D 76, 014015 (2007). arXiv:hep-ph/0701204
R. Fleischer, New strategies to extract β and γ from B d →π + π − and B s →K + K −. Phys. Lett. B 459, 306 (1999). arXiv:hep-ph/9903456
R. Fleischer, B s,d →ππ,πK,KK: status and prospects. Eur. Phys. J. C 52, 267 (2007). arXiv:0705.1121
R. Fleischer, R. Knegjens, In pursuit of new physics with \(B^{0}_{s} \rightarrow K^{+}K^{-}\). Eur. Phys. J. C 71, 1532 (2011). arXiv:1011.1096
LHCb Collaboration, Measurement of time-dependent CP violation in charmless two-body B decays. LHCb-CONF-2012-007
M. Ciuchini, E. Franco, S. Mishima, L. Silvestrini, Testing the Standard Model and searching for new physics with B d →ππ and B s →KK decays. J. High Energy Phys. 10, 029 (2012). arXiv:1205.4948
I. Adachi et al. (Belle Collaboration), Measurement of the CP violation parameters in B 0→π + π − decays. arXiv:1302.0551
J.P. Lees et al. (BaBar Collaboration), Measurement of CP asymmetries and branching fractions in charmless two-body B-meson decays to pions and kaons. Phys. Rev. D (2013). doi:10.1103/PhysRevD.87.052009. arXiv:1206.3525
H. Ishino et al. (Belle Collaboration), Observation of direct CP-violation in B 0→π + π − decays and model-independent constraints on the quark-mixing angle ϕ 2. Phys. Rev. Lett. 98, 211801 (2007). arXiv:hep-ex/0608035
B. Aubert et al. (BaBar Collaboration), Improved measurements of the branching fractions for B 0→π + π − and B 0→K + π −, and a search for B 0→K + K −. Phys. Rev. D 75, 012008 (2007). arXiv:hep-ex/0608003
Y.-T. Duh et al. (Belle Collaboration), Measurements of branching fractions and direct CP asymmetries for B→Kπ, B→ππ and B→KK decays. arXiv:1210.1348
A. Bornheim et al. (CLEO Collaboration), Measurements of charmless hadronic two body B meson decays and the ratio \(\mathcal{B}(B \rightarrow D K) / \mathcal{B}(B \rightarrow D \pi)\). Phys. Rev. D 68, 052002 (2003). arXiv:hep-ex/0302026
T. Aaltonen et al. (CDF Collaboration), Measurements of direct CP violating asymmetries in charmless decays of strange bottom mesons and bottom baryons. Phys. Rev. Lett. 106, 181802 (2011). arXiv:1103.5762
Y. Chao et al. (Belle Collaboration), Observation of B 0→π 0 π 0. Phys. Rev. Lett. 94, 181803 (2005). arXiv:hep-ex/0408101
B. Aubert et al. (BaBar Collaboration), Study of B 0→π 0 π 0, B ±→π ± π 0, and B ±→K ± π 0 decays, and isospin analysis of B→ππ decays. Phys. Rev. D 76, 091102 (2007). arXiv:0707.2798
C.-C. Peng et al. (Belle Collaboration), Search for \(B_{s}^{0} \rightarrow hh\) decays at the ϒ(5S) resonance. Phys. Rev. D 82, 072007 (2010). arXiv:1006.5115
M. Gronau, D. Pirjol, T.-M. Yan, Model independent electroweak penguin amplitudes in B decays to two pseudoscalars. Phys. Rev. D 60, 034021 (1999). arXiv:hep-ph/9810482
J. Zupan, Penguin pollution estimates relevant for the extraction of α/ϕ 2. Nucl. Phys. B, Proc. Suppl. 170, 33 (2007). arXiv:hep-ph/0701004
S. Gardner, Towards a precision determination of α in B→ππ decays. Phys. Rev. D 72, 034015 (2005). arXiv:hep-ph/0505071
F.J. Botella, D. London, J.P. Silva, Looking for ΔI=5/2 amplitude components in B→ππ and B→ρρ experiments. Phys. Rev. D 73, 071501 (2006). arXiv:hep-ph/0602060
G. Duplancic, B. Melic, B, B s →K form factors: an update of light-cone sum rule results. Phys. Rev. D 78, 054015 (2008). arXiv:0805.4170
B. Bhattacharya, A. Datta, M. Imbeault, D. London, Measuring β s with \(B_{s} \rightarrow K^{0(*)} \bar {K}^{0(*)}\)—a reappraisal. Phys. Lett. B 717, 403 (2012). arXiv:1203.3435
I. Bediaga et al., On a CP anisotropy measurement in the Dalitz plot. Phys. Rev. D 80, 096006 (2009). arXiv:0905.4233
M. Williams, Observing CP violation in many-body decays. Phys. Rev. D 84, 054015 (2011). arXiv:1105.5338
LHCb Collaboration, Evidence for CP violation in B→Kππ and B→KKK decays. LHCb-CONF-2012-018
LHCb Collaboration, Evidence for CP violation in B→KKπ and B→πππ decays. LHCb-CONF-2012-028
M. Ciuchini, M. Pierini, L. Silvestrini, New bounds on the Cabibbo–Kobayashi–Maskawa matrix from B→Kππ Dalitz plot analyses. Phys. Rev. D 74, 051301 (2006). arXiv:hep-ph/0601233
M. Ciuchini, M. Pierini, L. Silvestrini, Hunting the CKM weak phase with time-integrated Dalitz analyses of \(B ^{0}_{ s } \rightarrow K \pi\pi\) decays. Phys. Lett. B 645, 201 (2007). arXiv:hep-ph/0602207
M. Gronau, D. Pirjol, A. Soni, J. Zupan, Improved method for CKM constraints in charmless three-body B and \(B ^{0}_{ s } \) decays. Phys. Rev. D 75, 014002 (2007). arXiv:hep-ph/0608243
I. Bediaga, G. Guerrer, J.M. de Miranda, Extracting the quark mixing phase γ from B ±→K ± π + π −, \(B^{0} \rightarrow K ^{0}_{\mathrm{S}} \pi^{+} \pi^{-}\), and \(\bar{B}^{0} \rightarrow K ^{0}_{\mathrm{S}} \pi^{+} \pi^{-}\). Phys. Rev. D 76, 073011 (2007). arXiv:hep-ph/0608268
M. Gronau, D. Pirjol, A. Soni, J. Zupan, Constraint on \(\bar{\mathit{rho}}\)–\(\bar{\mathit{eta}}\) from B→K ∗ π. Phys. Rev. D 77, 057504 (2008). arXiv:0712.3751
M. Gronau, D. Pirjol, J. Zupan, CP asymmetries in B→Kπ,K ∗ π,ρK decays. Phys. Rev. D 81, 094011 (2010). arXiv:1001.0702
M. Gronau, D. Pirjol, J.L. Rosner, Calculating phases between B→K ∗ π amplitudes. Phys. Rev. D 81, 094026 (2010). arXiv:1003.5090
M. Imbeault, N.R.-L. Lorier, D. London, Measuring γ in B→Kππ decays. Phys. Rev. D 84, 034041 (2011). arXiv:1011.4973
R. Sinha, N. Deshpande, S. Pakvasa, C. Sharma, Determination of weak amplitudes using Bose symmetry and Dalitz plots. Phys. Rev. Lett. 107, 271801 (2011). arXiv:1104.3938
N.R.-L. Lorier, D. London, Measuring gamma with B→Kππ and \(B \rightarrow K K \bar {K}\) Decays. Phys. Rev. D 85, 016010 (2012). arXiv:1109.0881
LHCb Collaboration, Branching fraction measurements of \(B^{0}_{d,s}\) decays to \(K^{0}_{S} h h^{'}\) final states, including first observation of \(B^{0}_{s} \rightarrow K_{S} K \pi\). LHCb-CONF-2012-023
R. Aaij et al. (LHCb Collaboration), First observation of the decays \(\overline { B }{} ^{0} \rightarrow D ^{+} K ^{-} \pi ^{+} \pi ^{-} \) and B −→D 0 K − π + π −. Phys. Rev. Lett. 108, 161801 (2012). arXiv:1201.4402
T. Gershon, On the measurement of the unitarity triangle angle γ from B 0→DK ∗0 decays. Phys. Rev. D 79, 051301 (2009). arXiv:0810.2706
T. Gershon, M. Williams, Prospects for the measurement of the unitarity triangle angle γ from B 0→DK + π − decays. Phys. Rev. D 80, 092002 (2009). arXiv:0909.1495
T. Gershon, A. Poluektov, Double Dalitz plot analysis of the decay B 0→DK + π −, \(D \rightarrow K^{0}_{S} \pi^{+} \pi^{-}\). Phys. Rev. D 81, 014025 (2010). arXiv:0910.5437
M. Gronau, Y. Grossman, Z. Surujon, J. Zupan, Enhanced effects on extracting γ from untagged B 0 and \(B ^{0}_{ s } \) decays. Phys. Lett. B 649, 61 (2007). arXiv:hep-ph/0702011
S. Ricciardi, Measuring the CKM angle γ at LHCb using untagged \(B ^{0}_{ s } \rightarrow D\phi \) decays. LHCb-PUB-2010-005
R. Aaij et al. (LHCb Collaboration), Observation of the decay \(B^{0} \rightarrow \bar{D}^{0} K^{+} K^{-}\) and evidence of \(B^{0}_{s} \rightarrow \bar{D}^{0} K^{+} K^{-}\). Phys. Rev. Lett. 109, 131801 (2012). arXiv:1207.5991
M. Masetti, CP violation in \(B _{ c } ^{+} \) decays. Phys. Lett. B 286, 160 (1992)
R. Fleischer, D. Wyler, Exploring CP violation with \(B _{ c } ^{+} \) decays. Phys. Rev. D 62, 057503 (2000). arXiv:hep-ph/0004010
A.K. Giri, R. Mohanta, M.P. Khanna, Determination of the angle γ from nonleptonic \(B _{ c } ^{+} \rightarrow D ^{+}_{ s } D^{0}\) decays. Phys. Rev. D 65, 034016 (2002). arXiv:hep-ph/0104009
A.K. Giri, B. Mawlong, R. Mohanta, Determining the CKM angle γ with \(B _{ c } ^{+} \) decays. Phys. Rev. D 75, 097304 (2007). arXiv:hep-ph/0611212
A.K. Giri, R. Mohanta, M.P. Khanna, Possibility of extracting the weak phase γ from Λ b →ΛD 0 decays. Phys. Rev. D 65, 073029 (2002). arXiv:hep-ph/0112220
LHCb Collaboration, Studies of beauty baryons decaying to D 0 pπ − and D 0 pK −. LHCb-CONF-2011-036
Y. Nir, N. Seiberg, Should squarks be degenerate? Phys. Lett. B 309, 337 (1993). arXiv:hep-ph/9304307
M. Leurer, Y. Nir, N. Seiberg, Mass matrix models: the sequel. Nucl. Phys. B 420, 468 (1994). arXiv:hep-ph/9310320
A.F. Falk et al., D 0–\(\overline{ D }{} ^{0} \) mass difference from a dispersion relation. Phys. Rev. D 69, 114021 (2004). arXiv:hep-ph/0402204
E. Golowich, J. Hewett, S. Pakvasa, A.A. Petrov, Implications of D 0–\(\overline{ D }{} ^{0} \) mixing for new physics. Phys. Rev. D 76, 095009 (2007). arXiv:0705.3650
L. Okun, B. Pontecorvo, V.I. Zakharov, On the possible violation of CP-invariance in the decays of charmed particles. Lett. Nuovo Cimento 13, 218 (1975)
A. Pais, S. Treiman, CP violation in charmed particle decays. Phys. Rev. D 12, 2744 (1975). Phys. Rev. D 16, 2390 (1977). Erratum
I.I. Bigi, A. Sanda, CP violation in heavy flavor decays: predictions and search strategies. Nucl. Phys. B 281, 41 (1987)
B. Aubert et al. (BaBar Collaboration), Evidence for D 0–\(\overline{ D }{} ^{0} \) Mixing. Phys. Rev. Lett. 98, 211802 (2007). arXiv:hep-ex/0703020
M. Staric et al. (Belle Collaboration), Evidence for D 0–\(\overline{ D }{} ^{0} \) Mixing. Phys. Rev. Lett. 98, 211803 (2007). arXiv:hep-ex/0703036
R. Aaij et al. (LHCb Collaboration), Observation of D 0–\(\overline{D}^{0}\) oscillations. Phys. Rev. Lett. (2013). doi:10.1103/PhysRevLett.110.101802. arXiv:1211.1230
I.I. Bigi, H. Yamamoto, Interference between Cabibbo allowed and doubly forbidden transitions in \(D \rightarrow K ^{0}_{\mathrm{S}} , K ^{0}_{\mathrm{L}} + \pi{\rm s}\) decays. Phys. Lett. B 349, 363 (1995). arXiv:hep-ph/9502238
M. Gersabeck et al., On the interplay of direct and indirect CP violation in the charm sector. J. Phys. G 39, 045005 (2012). arXiv:1111.6515
N. Neri, Recent results for D 0–\(\overline{ D }{} ^{0} \) mixing and CP violation, and HFAG averages, in Proceedings of Charm 2012, the 5th International Workshop on Charm Physics, Honolulu, Hawaii, US, May (2012). arXiv:1208.5877
T. Peng (Belle Collaboration), D 0–\(\overline{ D }{} ^{0} \) mixing results from Belle, talk given at ICHEP 2012, Melbourne, July 5th 2012, slides available online
L.M. Zhang et al. (Belle Collaboration), Measurement of D 0–\(\overline{ D }{} ^{0} \) mixing in \(D ^{0} \rightarrow K ^{0}_{\mathrm{S}} \pi ^{+} \pi ^{-} \) decays. Phys. Rev. Lett. 99, 131803 (2007). arXiv:0704.1000
P. del Amo Sanchez et al. (BaBar Collaboration), Measurement of D 0–\(\overline{ D }{} ^{0} \) mixing parameters using \(D ^{0} \rightarrow K ^{0}_{\mathrm{S}} \pi ^{+} \pi ^{-} \) and \(D ^{0} \rightarrow K ^{0}_{\mathrm{S}} K ^{+} K ^{-} \) decays. Phys. Rev. Lett. 105, 081803 (2010). arXiv:1004.5053
Y. Grossman, A.L. Kagan, Y. Nir, New physics and CP violation in singly Cabibbo suppressed D decays. Phys. Rev. D 75, 036008 (2007). arXiv:hep-ph/0609178
B. Aubert et al. (BaBar Collaboration), Search for CP violation in the decays D 0→K − K + and D 0→π − π +. Phys. Rev. Lett. 100, 061803 (2008). arXiv:0709.2715
M. Staric et al. (Belle Collaboration), Search for a CP asymmetry in Cabibbo-suppressed D 0 decays. Phys. Lett. B 670, 190 (2008). arXiv:0807.0148
T. Aaltonen et al. (CDF Collaboration), Measurement of CP-violating asymmetries in D 0→π + π − and D 0→K + K − decays at CDF. Phys. Rev. D 85, 012009 (2012). arXiv:1111.5023
T. Aaltonen et al. (CDF Collaboration), Measurement of the difference of CP-violating asymmetries in D 0→K + K − and D 0→π + π − decays at CDF. Phys. Rev. Lett. 109, 111801 (2012). arXiv:1207.2158
B.R. Ko (Belle Collaboration), Direct CP violation in charm at Belle, Talk given at ICHEP 2012, Melbourne, July 5th 2012, slides available online
S. Bianco, F. Fabbri, D. Benson, I. Bigi, A Cicerone for the physics of charm. Riv. Nuovo Cimento 26(7), 1 (2003). arXiv:hep-ex/0309021
A.L. Kagan, M.D. Sokoloff, Indirect CP violation and implications for D 0–\(\overline{ D }{} ^{0} \) and \(B ^{0}_{ s } \)–\(\overline{ B }{} ^{0}_{ s } \) mixing. Phys. Rev. D 80, 076008 (2009). arXiv:0907.3917
LHCb Collaboration, Time integrated ratio of wrong-sign to right-sign D 0→Kπ decays in 2010 data at LHCb. LHCb-CONF-2011-029
R. Aaij et al. (LHCb Collaboration), Search for CP violation in D +→K − K + π + decays. Phys. Rev. D 84, 112008 (2011). arXiv:1110.3970
R. Aaij et al. (LHCb Collaboration), Measurement of the \(D_{s}^{+}\)–\(D_{s}^{-}\) production asymmetry in 7 TeV pp collisions. Phys. Lett. 713, 186 (2012). arXiv:1205.0897
R. Aaij et al. (LHCb Collaboration), Measurement of the D ± production asymmetry in 7 TeV pp collisions. Phys. Lett. B 718, 902–909 (2013). arXiv:1210.4112
P. del Amo Sanchez et al. (BaBar Collaboration), Search for CP violation using T-odd correlations in D 0→K + K − π + π − decays. Phys. Rev. D 81, 111103 (2010). arXiv:1003.3397
LHCb Collaboration, Search for CP violation in D 0→π − π + π + π − decays. LHCb-CONF-2012-019
I. Bigi, Probing CP asymmetries in charm baryons decays. arXiv:1206.4554
E. Golowich, A.A. Petrov, Short distance analysis of D 0–\(\overline { D }{} ^{0} \) mixing. Phys. Lett. B 625, 53 (2005). arXiv:hep-ph/0506185
M. Bobrowski, A. Lenz, J. Riedl, J. Rohrwild, How large can the SM contribution to CP violation in D 0–\(\overline{ D }{} ^{0} \) mixing be? J. High Energy Phys. 03, 009 (2010). arXiv:1002.4794
H. Georgi, D–\(\overline{ D }{} \) mixing in heavy quark effective field theory. Phys. Lett. B 297, 353 (1992). arXiv:hep-ph/9209291
T. Ohl, G. Ricciardi, E.H. Simmons, D–\(\overline{ D }{} \) mixing in heavy quark effective field theory: the sequel. Nucl. Phys. B 403, 605 (1993). arXiv:hep-ph/9301212
I.I. Bigi, N.G. Uraltsev, D 0–\(\overline{ D }{} ^{0} \) oscillations as a probe of quark hadron duality. Nucl. Phys. B 592, 92 (2001). arXiv:hep-ph/0005089
E. Golowich, S. Pakvasa, A.A. Petrov, New physics contributions to the lifetime difference in D 0–\(\overline{ D }{} ^{0} \) mixing. Phys. Rev. Lett. 98, 181801 (2007). arXiv:hep-ph/0610039
S. Bergmann et al., Lessons from CLEO and FOCUS measurements of D 0–\(\overline{ D }{} ^{0} \) mixing parameters. Phys. Lett. B 486, 418 (2000). arXiv:hep-ph/0005181
O. Gedalia, Y. Grossman, Y. Nir, G. Perez, Lessons from recent measurements of D 0–\(\overline { D }{} ^{0} \) mixing. Phys. Rev. D 80, 055024 (2009). arXiv:0906.1879
G. Isidori, Y. Nir, G. Perez, Flavor physics constraints for physics beyond the Standard Model. Annu. Rev. Nucl. Part. Sci. 60, 355 (2010). arXiv:1002.0900
A.F. Falk, Y. Grossman, Z. Ligeti, A.A. Petrov, SU(3) breaking and D 0–\(\overline{ D }{} ^{0} \) mixing. Phys. Rev. D 65, 054034 (2002). arXiv:hep-ph/0110317
B. Chibisov, R.D. Dikeman, M.A. Shifman, N. Uraltsev, Operator product expansion, heavy quarks, QCD duality and its violations. Int. J. Mod. Phys. A 12, 2075 (1997). arXiv:hep-ph/9605465
J.F. Donoghue, E. Golowich, B.R. Holstein, J. Trampetic, Dispersive effects in D 0–\(\overline{ D }{} ^{0} \) mixing. Phys. Rev. D 33, 179 (1986)
L. Wolfenstein, D 0–\(\overline{ D }{} ^{0} \) mixing. Phys. Lett. B 164, 170 (1985)
P. Colangelo, G. Nardulli, N. Paver, On D 0–\(\overline{ D }{} ^{0} \) mixing in the Standard Model. Phys. Lett. B 242, 71 (1990)
T.A. Kaeding, D meson mixing in broken SU(3). Phys. Lett. B 357, 151 (1995). arXiv:hep-ph/9505393
A.A. Anselm, Y.I. Azimov, CP violating effects in e + e − annihilation. Phys. Lett. B 85, 72 (1979)
H.-Y. Cheng, C.-W. Chiang, Long-distance contributions to D 0–\(\overline { D }{} ^{0} \) mixing parameters. Phys. Rev. D 81, 114020 (2010). arXiv:1005.1106
Y. Grossman, Y. Nir, G. Perez, Testing new indirect CP violation. Phys. Rev. Lett. 103, 071602 (2009). arXiv:0904.0305
A.L. Kagan, G. Perez, T. Volansky, J. Zupan, General minimal flavor violation. Phys. Rev. D 80, 076002 (2009). arXiv:0903.1794
L. Randall, R. Sundrum, A large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 83, 3370 (1999). arXiv:hep-ph/9905221
K. Blum, Y. Grossman, Y. Nir, G. Perez, Combining K 0–\(\overline{ K }{} ^{0} \) mixing and D 0–\(\overline { D }{} ^{0} \) mixing to constrain the flavor structure of new physics. Phys. Rev. Lett. 102, 211802 (2009). arXiv:0903.2118
O. Gedalia, J.F. Kamenik, Z. Ligeti, G. Perez, On the universality of CP violation in ΔF=1 processes. Phys. Lett. B 714, 55 (2012). arXiv:1202.5038
Y. Nir, G. Raz, Quark squark alignment revisited. Phys. Rev. D 66, 035007 (2002). arXiv:hep-ph/0206064
B. Aubert et al. (BaBar Collaboration), Measurement of D 0–\(\overline{ D }{} ^{0} \) mixing using the ratio of lifetimes for the decays D 0→K − π +, K − K +, and π − π +. Phys. Rev. D 78, 011105 (2008). arXiv:0712.2249
M. Golden, B. Grinstein, Enhanced CP violations in hadronic charm decays. Phys. Lett. B 222, 501 (1989)
D. Pirtskhalava, P. Uttayarat, CP violation and flavor SU(3) breaking in D-meson decays. Phys. Lett. B 712, 81 (2012). arXiv:1112.5451
B. Bhattacharya, M. Gronau, J.L. Rosner, CP asymmetries in singly-Cabibbo-suppressed D decays to two pseudoscalar mesons. Phys. Rev. D 85, 054014 (2012). arXiv:1201.2351
T. Feldmann, S. Nandi, A. Soni, Repercussions of flavour symmetry breaking on CP violation in D meson decays. J. High Energy Phys. 06, 007 (2012). arXiv:1202.3795
J. Brod, Y. Grossman, A.L. Kagan, J. Zupan, A consistent picture for large penguins in D→π + π −, K + K −. J. High Energy Phys. 10, 161 (2012). arXiv:1203.6659
H.-Y. Cheng, C.-W. Chiang, SU(3) symmetry breaking and CP violation in D→PP decays. Phys. Rev. D 86, 014014 (2012). arXiv:1205.0580
G. Hiller, M. Jung, S. Schacht, SU(3)-flavor anatomy of non-leptonic charm decays. Phys. Rev. D 87, 014024 (2013). arXiv:1211.3734
F. Buccella et al., Nonleptonic weak decays of charmed mesons. Phys. Rev. D 51, 3478 (1995). arXiv:hep-ph/9411286
H.-n. Li, C.-D. Lu, F.-S. Yu, Branching ratios and direct CP asymmetries in D→PP decays. Phys. Rev. D 86, 036012 (2012). arXiv:1203.3120
E. Franco, S. Mishima, L. Silvestrini, The Standard Model confronts CP violation in D 0→π + π − and D 0→K + K −. J. High Energy Phys. 05, 140 (2012). arXiv:1203.3131
L. Wolfenstein, CP violation in D 0–\(\overline{ D }{} ^{0} \) mixing. Phys. Rev. Lett. 75, 2460 (1995). arXiv:hep-ph/9505285
J. Brod, A.L. Kagan, J. Zupan, Size of direct CP violation in singly Cabibbo-suppressed D decays. Phys. Rev. D 86, 014023 (2012). arXiv:1111.5000
G. Isidori, J.F. Kamenik, Z. Ligeti, G. Perez, Implications of the LHCb evidence for charm CP violation. Phys. Lett. B 711, 46 (2012). arXiv:1111.4987
O. Gedalia, L. Mannelli, G. Perez, Covariant description of flavor violation in the LHC. Phys. Lett. B 693, 301 (2010). arXiv:1002.0778
O. Gedalia, L. Mannelli, G. Perez, Covariant description of flavor conversion at the LHC era. J. High Energy Phys. 10, 046 (2010). arXiv:1003.3869
G.F. Giudice, G. Isidori, P. Paradisi, Direct CP violation in charm and flavor mixing beyond the SM. J. High Energy Phys. 04, 060 (2012). arXiv:1201.6204
G. Hiller, Y. Hochberg, Y. Nir, Supersymmetric \(\Delta \mathcal {A}_{ \mathit{CP} } \). Phys. Rev. D 85, 116008 (2012). arXiv:1204.1046
W.D. Goldberger, M.B. Wise, Modulus stabilization with bulk fields. Phys. Rev. Lett. 83, 4922 (1999). arXiv:hep-ph/9907447
S.J. Huber, Q. Shafi, Fermion masses, mixings and proton decay in a Randall–Sundrum model. Phys. Lett. B 498, 256 (2001). arXiv:hep-ph/0010195
T. Gherghetta, A. Pomarol, Bulk fields and supersymmetry in a slice of AdS. Nucl. Phys. B 586, 141 (2000). arXiv:hep-ph/0003129
C. Delaunay, J.F. Kamenik, G. Perez, L. Randall, Charming CP violation and dipole operators from RS flavor anarchy. J. High Energy Phys. 01, 027 (2013). arXiv:1207.0474
K. Agashe, A. Azatov, L. Zhu, Flavor-violation tests of the warped/composite Standard Model in the two-site approach. Phys. Rev. D 79, 056006 (2009). arXiv:0810.1016
C. Csaki, G. Perez, Z. Surujon, A. Weiler, Flavor alignment via shining in Randall-Sundrum models. Phys. Rev. D 81, 075025 (2010). arXiv:0907.0474
B. Keren-Zur et al., On partial compositeness and the CP asymmetry in charm decays. Nucl. Phys. B 867, 429 (2012). arXiv:1205.5803
S. Nandi, A. Soni, Constraining the mixing matrix for Standard Model with four generations: time dependent and semi-leptonic CP asymmetries in \(B ^{0}_{ d } \), \(B ^{0}_{ s } \) and D 0. Phys. Rev. D 83, 114510 (2011). arXiv:1011.6091
CDF Collaboration, Study of the top quark production asymmetry and its mass and rapidity dependence in the full run II Tevatron dataset. CDF Public Note 10807, 2012
K. Blum, Y. Hochberg, Y. Nir, Scalar-mediated \(t\bar{t}\) forward-backward asymmetry. J. High Energy Phys. 10, 124 (2011). arXiv:1107.4350
Y. Hochberg, Y. Nir, Relating direct CP violation in D decays and the forward-backward asymmetry in \(t \overline{ t } \) production. Phys. Rev. Lett. 108, 261601 (2012). arXiv:1112.5268
G. Isidori, J.F. Kamenik, Shedding light on CP violation in the charm system via D→Vγ decays. Phys. Rev. Lett. 109, 171801 (2012). arXiv:1205.3164
C. Greub, T. Hurth, M. Misiak, D. Wyler, The c→uγ contribution to weak radiative charm decay. Phys. Lett. B 382, 415 (1996). arXiv:hep-ph/9603417
Y. Grossman, A.L. Kagan, J. Zupan, Testing for new physics in singly Cabibbo suppressed D decays. Phys. Rev. D 85, 114036 (2012). arXiv:1204.3557
D. Atwood, A. Soni, Searching for the origin of CP violation in Cabibbo suppressed D-meson decays. arXiv:1211.1026
S. Gardner, U.-G. Meissner, Rescattering and chiral dynamics in B→ρπ decay. Phys. Rev. D 65, 094004 (2002). arXiv:hep-ph/0112281
M. Gronau, J. Zupan, Isospin-breaking effects on α extracted in B→ππ, ρρ, ρπ. Phys. Rev. D 71, 074017 (2005). arXiv:hep-ph/0502139
H. Ishino, M. Hazumi, M. Nakao, T. Yoshikawa, New measurements using external photon conversion at a high luminosity B factory. arXiv:hep-ex/0703039
A.F. Falk, Z. Ligeti, Y. Nir, H. Quinn, Comment on extracting α from B→ρρ. Phys. Rev. D 69, 011502 (2004). arXiv:hep-ph/0310242
M. Gaspero, B. Meadows, K. Mishra, A. Soffer, Isospin analysis of D 0 decay to three pions. Phys. Rev. D 78, 014015 (2008). arXiv:0805.4050
G. Colangelo et al., Review of lattice results concerning low energy particle physics. Eur. Phys. J. C 71, 1695 (2011). arXiv:1011.4408
M. Lüscher, Volume dependence of the energy spectrum in massive quantum field theories II. Scattering states. Commun. Math. Phys. 105, 153 (1986)
M. Lüscher, Two particle states on a torus and their relation to the scattering matrix. Nucl. Phys. B 354, 531 (1991)
L. Lellouch, M. Lüscher, Weak transition matrix elements from finite volume correlation functions. Commun. Math. Phys. 219, 31 (2001). arXiv:hep-lat/0003023
T. Blum et al., The K→(ππ) I=2 decay amplitude from lattice QCD. Phys. Rev. Lett. 108, 141601 (2012). arXiv:1111.1699
T. Blum et al., K to ππ decay amplitudes from lattice QCD. Phys. Rev. D 84, 114503 (2011). arXiv:1106.2714
M.T. Hansen, S.R. Sharpe, Multiple-channel generalization of Lellouch–Luscher formula. Phys. Rev. D 86, 016007 (2012). arXiv:1204.0826
N.H. Christ (RBC Collaboration, UKQCD Collaboration), Computing the long-distance contribution to second order weak amplitudes. PoS LATTICE 2010, 300 (2010)
J. Yu, Long distance contribution to \(K ^{0}_{\mathrm{L}} \)–\(K ^{0}_{\mathrm{S}} \) mass difference. PoS LATTICE 2011, 297 (2011). arXiv:1111.6953
CDF Collaboration, Search for quark substructure in the angular distribution of dijets produced in \(p\bar{p}\) collisions at \(\sqrt{s} = 1.96\ \mathrm{TeV}\). CDF Public Note 9609, 2008
V.M. Abazov et al. (D0 Collaboration), Measurement of dijet angular distributions at \(\sqrt{s} = 1.96\ \mathrm{TeV}\) and searches for quark compositeness and extra spatial dimensions. Phys. Rev. Lett. 103, 191803 (2009). arXiv:0906.4819
L. Da Rold, C. Delaunay, C. Grojean, G. Perez, Up asymmetries From exhilarated composite flavor structures. J. High Energy Phys. (2013). doi:10.1007/JHEP02(2013)149. arXiv:1208.1499
ATLAS Collaboration, Search for new physics in dijet mass and angular distributions using 4.8 fb−1 of pp collisions at \(\sqrt{s} = 7 ~\mathrm{TeV} \) collected by the ATLAS detector. ATLAS-CONF-2012-038, 2012
S. Chatrchyan et al. (CMS Collaboration), Search for quark compositeness in dijet angular distributions from pp collisions at \(\sqrt{s} = 7 ~\mathrm {TeV} \). J. High Energy Phys. 05, 055 (2012). arXiv:1202.5535
L.M. Zhang et al. (Belle Collaboration), Improved constraints on D 0–\(\overline{ D }{} ^{0} \) mixing in D 0→K + π − decays at Belle. Phys. Rev. Lett. 96, 151801 (2006). arXiv:hep-ex/0601029
B. Aubert et al. (BaBar Collaboration), Search for D 0–\(\overline{ D }{} ^{0} \) mixing using semileptonic decay modes. Phys. Rev. D 70, 091102 (2004). arXiv:hep-ex/0408066
B. Aubert et al. (BaBar Collaboration), Search for D 0–\(\overline{ D }{} ^{0} \) mixing using doubly flavor tagged semileptonic decay modes. Phys. Rev. D 76, 014018 (2007). arXiv:0705.0704
B. Aubert et al. (BaBar Collaboration), Measurement of D 0–\(\overline{ D }{} ^{0} \) mixing from a time-dependent amplitude analysis of D 0→K + π − π 0 decays. Phys. Rev. Lett. 103, 211801 (2009). arXiv:0807.4544
V. Kartvelishvili, A. Likhoded, S. Slabospitsky, D meson and ψ meson production in hadronic interactions. Sov. J. Nucl. Phys. 28, 678 (1978)
R. Baier, R. Rückl, Hadronic production of J/ψ and ϒ: transverse momentum distribution. Phys. Lett. B 102, 364 (1981)
F. Abe et al. (CDF Collaboration), Inclusive J/ψ, ψ(2S) and b quark production in \(\bar{p}p\) collisions at \(\sqrt{s} = 1.8\ \mathrm{TeV}\). Phys. Rev. Lett. 69, 3704 (1992)
E. Braaten, S. Fleming, Color octet fragmentation and the ψ′-surplus at the Fermilab Tevatron. Phys. Rev. Lett. 74, 3327 (1995). arXiv:hep-ph/9411365
J. Campbell, F. Maltoni, F. Tramontano, QCD corrections to J/ψ and ϒ production at hadron colliders. Phys. Rev. Lett. 98, 252002 (2007). arXiv:hep-ph/0703113
B. Gong, J.-X. Wang, Next-to-leading-order QCD corrections to J/ψ polarization at Tevatron and Large Hadron Collider energies. Phys. Rev. Lett. 100, 232001 (2008). arXiv:0802.3727
P. Artoisenet et al., ϒ production at Fermilab Tevatron and LHC energies. Phys. Rev. Lett. 101, 152001 (2008). arXiv:0806.3282
J.P. Lansberg, On the mechanisms of heavy-quarkonium hadroproduction. Eur. Phys. J. C 61, 693 (2009). arXiv:0811.4005
N. Brambilla et al., Heavy quarkonium: progress, puzzles, and opportunities. Eur. Phys. J. C 71, 1534 (2011). arXiv:1010.5827
R. Aaij et al. (LHCb Collaboration), Measurement of J/ψ production in pp collisions at \(\sqrt{s}=7 ~\mathrm{TeV} \). Eur. Phys. J. C 71, 1645 (2011). arXiv:1103.0423
R. Aaij et al. (LHCb Collaboration), Measurement of the cross-section ratio σ(χ c2)/σ(χ c1) for prompt χ c production at \(\sqrt {s}=7\ \mathrm{TeV}\). Phys. Lett. B 714, 215 (2012). arXiv:1202.1080
R. Aaij et al. (LHCb Collaboration), Measurement of the ratio of prompt χ c to J/ψ production in pp collisions at \(\sqrt{s}=7\ \mathrm{TeV}\). Phys. Lett. B 718, 431 (2012). arXiv:1204.1462
R. Aaij et al. (LHCb Collaboration), Measurement of ϒ production in pp collisions at √s=7 TeV. Eur. Phys. J. C 72, 2025 (2012). arXiv:1202.6579
R. Aaij et al. (LHCb Collaboration), Measurement of ψ(2S) meson production in pp collisions at \(\sqrt{s}=7\ \mathrm{TeV}\). Eur. Phys. J. C 72, 2100 (2012). arXiv:1204.1258
S.J. Brodsky, J.-P. Lansberg, Heavy-quarkonium production in high energy proton–proton collisions at RHIC. Phys. Rev. D 81, 051502 (2010). arXiv:0908.0754
C.H. Kom, A. Kulesza, W.J. Stirling, Pair production of J/ψ as a probe of double parton scattering at LHCb. Phys. Rev. Lett. 107, 082002 (2011). arXiv:1105.4186
S.P. Baranov, A.M. Snigirev, N.P. Zotov, Double heavy meson production through double parton scattering in hadronic collisions. Phys. Lett. B 705, 116 (2011). arXiv:1105.6276
A. Novoselov, Double parton scattering as a source of quarkonia pairs in LHCb. arXiv:1106.2184
S. Brodsky, P. Hoyer, C. Peterson, N. Sakai, The intrinsic charm of the proton. Phys. Lett. B 93, 451 (1980)
R. Aaij et al. (LHCb Collaboration), Observation of J/ψ pair production in pp collisions at \(\sqrt{s}=7 ~\mathrm{TeV} \). Phys. Lett. B 707, 52 (2012). arXiv:1109.0963
V.G. Kartvelishvili, S.M. Esakiya, On hadron induced production of J/ψ meson pairs. Yad. Fiz. 38, 722 (1983)
B. Humpert, P. Mery, ψψ production at collider energies. Z. Phys. C 20, 83 (1983)
A.V. Berezhnoy, A.K. Likhoded, A.V. Luchinsky, A.A. Novoselov, Production of J/ψ meson pairs and 4c-tetraquark at the LHC. Phys. Rev. D 84, 094023 (2011). arXiv:1101.5881
M. Luszczak, R. Maciula, A. Szczurek, Production of two \(c\bar{c}\) pairs in double-parton scattering. Phys. Rev. D 85, 094034 (2011). arXiv:1111.3255
F. Abe et al. (CDF Collaboration), Double parton scattering in \(\bar{p}p\) collisions at \(\sqrt {s}= 1.8\ \mathrm{TeV}\). Phys. Rev. D 56, 3811 (1997)
V.V. Braguta, A.K. Likhoded, A.V. Luchinsky, Double charmonium production in exclusive bottomonia decays. Phys. Rev. D 80, 094008 (2009). arXiv:0902.0459 [hep-ph]
Y. Jia, Which hadronic decay modes are good for η b searching: double J/ψ or something else? Phys. Rev. D 78, 054003 (2008). arXiv:hep-ph/0611130v2
S. Barsuk, J. He, E. Kou, B. Viaud, Investigating charmonium production at LHC with the \(p\bar {p}\) final state. Phys. Rev. D 86, 034011 (2012). arXiv:1202.2273
J.J. Aubert et al. (E598 Collaboration), Experimental observation of a heavy particle J. Phys. Rev. Lett. 33, 1404 (1974)
J.E. Augustin et al. (SLAC-SP-017 Collaboration), Discovery of a narrow resonance in e + e − annihilation. Phys. Rev. Lett. 33, 1406 (1974)
S.W. Herb et al., Observation of a dimuon resonance at 9.5 GeV in 400 GeV proton-nucleus collisions. Phys. Rev. Lett. 39, 252 (1977)
S.K. Choi et al. (Belle Collaboration), Observation of a narrow charmonium state in exclusive B +→K ± π + π − J/ψ decays. Phys. Rev. Lett. 91, 262001 (2003). arXiv:hep-ex/0309032
B. Aubert et al. (BaBar Collaboration), A study of B→X(3872)K, with X(3872)→J/ψπ + π −. Phys. Rev. D 77, 111101 (2008). arXiv:0803.2838
D. Acosta et al. (CDF Collaboration), Observation of the narrow state X(3872)→J/ψπ + π − in \(\overline{p} p\) collisions at \(\sqrt{s} = 1.96\ \mathrm{TeV}\). Phys. Rev. Lett. 93, 072001 (2004). arXiv:hep-ex/0312021
V.M. Abazov et al. (D0 Collaboration), Observation and properties of the X(3872) decaying to J/ψπ + π − in \(p\bar{p}\) collisions at \(\sqrt{s} = 1.96\ \mathrm{TeV}\). Phys. Rev. Lett. 93, 162002 (2004). arXiv:hep-ex/0405004
S.K. Choi et al. (Belle Collaboration), Observation of a resonance-like structure in the π ± ψ′ mass distribution in exclusive B→Kπ ± ψ′ decays. Phys. Rev. Lett. 100, 142001 (2008). arXiv:0708.1790
R. Mizuk et al. (Belle Collaboration), Observation of two resonance-like structures in the π + χ c1 mass distribution in exclusive \(\bar{B}^{0} \rightarrow K^{-} \pi^{+} \chi_{c1}\) decays. Phys. Rev. D 78, 072004 (2008). arXiv:0806.4098
R. Mizuk et al. (Belle Collaboration), Dalitz analysis of B→Kπ + ψ′ decays and the Z(4430)+. Phys. Rev. D 80, 031104 (2009). arXiv:0905.2869
B. Aubert et al. (BaBar Collaboration), Search for the Z(4430)− at BaBar. Phys. Rev. D 79, 112001 (2009). arXiv:0811.0564
J. Lees et al. (BaBar Collaboration), Search for the Z 1(4050)+ and Z 2(4250)+ states in \(\bar{B}^{0} \rightarrow \chi_{c1} K^{-} \pi^{+}\) and \(B^{+} \rightarrow \chi_{c1} K^{0}_{S} \pi^{+}\). Phys. Rev. D 85, 052003 (2012). arXiv:1111.5919
E.S. Swanson, The new heavy mesons: a status report. Phys. Rep. 429, 243 (2006). arXiv:hep-ph/0601110
N.V. Drenska, R. Faccini, A.D. Polosa, Exotic hadrons with hidden charm and strangeness. Phys. Rev. D 79, 077502 (2009). arXiv:0902.2803
M. Voloshin, Charmonium. Prog. Part. Nucl. Phys. 61, 455 (2008). arXiv:0711.4556
S. Godfrey, S.L. Olsen, The exotic XYZ charmonium-like mesons. Annu. Rev. Nucl. Part. Sci. 58, 51 (2008). arXiv:0801.3867
M. Nielsen, F.S. Navarra, S.H. Lee, New charmonium states in QCD sum rules: a concise review. Phys. Rep. 497, 41 (2010). arXiv:0911.1958
N. Drenska et al., New hadronic spectroscopy. Riv. Nuovo Cimento 033, 633 (2010). arXiv:1006.2741
S. Eidelman et al., Developments in heavy quarkonium spectroscopy. arXiv:1205.4189
A. Bondar et al. (Belle Collaboration), Observation of two charged bottomonium-like resonances in ϒ(5S) decays. Phys. Rev. Lett. 108, 122001 (2012). arXiv:1110.2251
I. Adachi et al. (Belle Collaboration), Evidence for a \(Z_{b}^{0}(10610)\) in Dalitz analysis of ϒ(5S)→ϒ(nS)π 0 π 0. arXiv:1207.4345
I. Adachi et al. (Belle Collaboration), Study of three-body ϒ(10860) decays. arXiv:1209.6450
R. Aaij et al. (LHCb Collaboration), Observation of X(3872) production in pp collisions at \(\sqrt{s}= 7 ~\mathrm{TeV} \). Eur. Phys. J. C 72, 1972 (2011). arXiv:1112.5310
E.J. Eichten, K. Lane, C. Quigg, Charmonium levels near threshold and the narrow state X(3872)→π + π − J/ψ. Phys. Rev. D 69, 094019 (2004). arXiv:hep-ph/0401210
R. Balest et al. (CLEO Collaboration), Inclusive decays of B mesons to charmonium. Phys. Rev. D 52, 2661 (1995)
B. Aubert et al. (BaBar Collaboration), Study of inclusive production of charmonium mesons in B decay. Phys. Rev. D 67, 032002 (2003). arXiv:hep-ex/0207097
C.-H.V. Chang, W.-S. Hou, Probing for the charm content of B and ϒ mesons. Phys. Rev. D 64, 071501 (2001). arXiv:hep-ph/0101162
S.J. Brodsky, F.S. Navarra, Looking for exotic multi-quark states in nonleptonic B decays. Phys. Lett. B 411, 152 (1997). arXiv:hep-ph/9704348
T.J. Burns et al., Momentum distribution of J/ψ in B decays. Phys. Rev. D 83, 114029 (2011). arXiv:1104.1781
G. Eilam, M. Ladisa, Y.-D. Yang, Study of \({B}^{0}\rightarrow{J}/\psi{D}^{(^{*})}\) and \(\eta _{c}{D}^{{(}^{*})}\) in perturbative QCD. Phys. Rev. D 65, 037504 (2002). arXiv:hep-ph/0107043
B. Aubert et al. (BaBar Collaboration), Evidence for \(B^{+} \rightarrow J/\psi p \overline{\varLambda}\) and search for \(B^{0} \rightarrow J/\psi p \bar{p}\). Phys. Rev. Lett. 90, 231801 (2003). arXiv:hep-ex/0303036
Q.L. Xie et al. (Belle Collaboration), Observation of \(B ^{-} \rightarrow { J / \psi } \varLambda\overline {p}\) and searches for \(B ^{-} \rightarrow { J / \psi } \varSigma^{0} \overline{p}\) and \(B ^{0} \rightarrow { J / \psi } p \overline{p}\) decays. Phys. Rev. D 72, 051105 (2005). arXiv:hep-ex/0508011
R. Aaij et al. (LHCb Collaboration), First observation of the decay \(B _{ c } ^{+} \rightarrow { J / \psi } \pi^{+}\pi^{-}\pi^{+}\). Phys. Rev. Lett. 108, 251802 (2012). arXiv:1204.0079
G. Altarelli, M. Mangano et al., Workshop on Standard Model physics (and more) at the LHC, CERN Yellow Report 2000-004, 2000
R. Aaij et al. (LHCb Collaboration), Measurement of relative branching fractions of B decays to ψ(2S) and J/ψ mesons. Eur. Phys. J. C 72, 2118 (2012). arXiv:1205.0918
Y.-N. Gao et al., Experimental prospects of the \(B _{ c } ^{+} \) studies of the LHCb experiment. Chin. Phys. Lett. 27, 061302 (2010)
I.P. Gouz et al., Prospects for the B c studies at LHCb. Phys. At. Nucl. 67, 1559 (2004). arXiv:hep-ph/0211432
S. Godfrey, Spectroscopy of B c mesons in the relativized quark model. Phys. Rev. D 70, 054017 (2004). arXiv:hep-ph/0406228
S.S. Gershtein, V.V. Kiselev, A.K. Likhoded, A.V. Tkabladze, \(B _{ c } ^{+} \) spectroscopy. Phys. Rev. D 51, 3613 (1995). arXiv:hep-ph/9406339
R. Dowdall, C. Davies, T. Hammant, R. Horgan, Precise heavy-light meson masses and hyperfine splittings from lattice QCD including charm quarks in the sea. Phys. Rev. D 86, 094510 (2012). arXiv:1207.5149
LHCb Collaboration, Measurement of the masses of the \(\varXi_{b}^{-}\) and \(\varOmega_{b}^{-}\). LHCb-CONF-2011-060
N. Uraltsev, On the problem of boosting nonleptonic b baryon decays. Phys. Lett. B 376, 303 (1996). arXiv:hep-ph/9602324
M. Voloshin, Relations between inclusive decay rates of heavy baryons. Phys. Rep. 320, 275 (1999). arXiv:hep-ph/9901445
R. Aaij et al. (LHCb Collaboration), Observation of excited Λ b baryons. Phys. Rev. Lett. 109, 172003 (2012). arXiv:1205.3452
C.-H. Chang, J.-P. Ma, C.-F. Qiao, X.-G. Wu, Hadronic production of the doubly charmed baryon Ξ cc with intrinsic charm. J. Phys. G 34, 845 (2007). arXiv:hep-ph/0610205
J.-W. Zhang et al., Hadronic production of the doubly heavy baryon Ξ bc at the LHC. Phys. Rev. D 83, 034026 (2011). arXiv:1101.1130
R. McNulty, LHCb: tools to incorporate LHCb data in fits, Working group on electroweak precision measurements at the LHC, 2011
ALEPH Collaboration, DELPHI Collaboration, L3 Collaboration, OPAL Collaboration, SLD Collaboration, LEP Electroweak Working Group, The SLD Electroweak and Heavy Flavour Groups, Precision electroweak measurements on the Z resonance. Phys. Rep. 427, 257 (2006). arXiv:hep-ex/0509008
R. Aaij et al. (LHCb Collaboration), Inclusive W and Z production in the forward region at \(\sqrt{s} = 7\ \mathrm{TeV}\). J. High Energy Phys. 06, 058 (2012). arXiv:1204.1620
J. Rojo, NNPDF2.3 and inclusion of the LHC data, PDF4LHC meeting, 2012
LHCb Collaboration, Inclusive low mass Drell–Yan production in the forward region at \(\sqrt{s} = 7\ \mathrm{TeV}\). LHCb-CONF-2012-013
N. Besson et al., Re-evaluation of the LHC potential for the measurement of m W . Eur. Phys. J. C 57, 627 (2008). arXiv:0805.2093
T. Aaltonen et al. (CDF Collaboration), Evidence for a mass dependent forward–backward asymmetry in top quark pair production. Phys. Rev. D 83, 112003 (2011). arXiv:1101.0034
V.M. Abazov et al. (D0 Collaboration), Forward-backward asymmetry in top quark–antiquark production. Phys. Rev. D 84, 112005 (2011). arXiv:1107.4995
Y. Takeuchi et al. (CDF Collaboration), CDF Note 10398
T. Schwarz et al. (CDF Collaboration), CDF Note 10584
S. Leone (CDF Collaboration), Top quark production at the Tevatron, Talk given at Moriond EW, March 9th 2012, proceedings available online
A.L. Kagan, J.F. Kamenik, G. Perez, S. Stone, Top LHCb physics. Phys. Rev. Lett. 107, 082003 (2011). arXiv:1103.3747
K.M. Zurek, TASI 2009 lectures: searching for unexpected physics at the LHC, arXiv:1001.2563
M.J. Strassler, K.M. Zurek, Echoes of a hidden valley at hadron colliders. Phys. Lett. B 651, 374 (2007). arXiv:hep-ph/0604261
L.M. Carpenter, D.E. Kaplan, E.-J. Rhee, Six-quark decays of the Higgs boson in supersymmetry with R-parity violation. Phys. Rev. Lett. 99, 211801 (2007). arXiv:hep-ph/0607204
M.J. Strassler, K.M. Zurek, Discovering the Higgs through highly-displaced vertices. Phys. Lett. B 661, 263 (2008). arXiv:hep-ph/0605193
P. Fileviez Perez, S. Spinner, M.K. Trenkel, Lightest supersymmetric particle stability and new Higgs signals at the LHC. Phys. Rev. D 84, 095028 (2011). arXiv:1103.5504
F. de Campos, O.J.P. Éboli, M.B. Magro, D. Restrepo, Searching supersymmetry at the LHCb with displaced vertices. Phys. Rev. D 79, 055008 (2009). arXiv:0809.0007
G. Brooijmans et al. (New Physics Working Group), New physics at the LHC. A Les Houches report: physics at TeV colliders 2009—new physics working group. arXiv:1005.1229
LHCb Collaboration, Search for (Higgs-like) bosons decaying into long-lived exotic particles. LHCb-CONF-2012-014
T. Aaltonen et al. (CDF Collaboration), Search for exclusive γγ production in hadron-hadron collisions. Phys. Rev. Lett. 99, 242002 (2007). arXiv:0707.2374
T. Aaltonen et al. (CDF Collaboration), Observation of exclusive dijet production at the Fermilab Tevatron \(p\bar{p}\) collider. Phys. Rev. D 77, 052004 (2008). arXiv:0712.0604
V.M. Abazov et al. (D0 Collaboration), High mass exclusive diffractive dijet production in \(p\bar {p}\) collisions at \(\sqrt{s} = 1.96\ \mathrm{TeV}\). Phys. Lett. B 705, 193 (2011). arXiv:1009.2444
T. Aaltonen et al. (CDF Collaboration), Observation of exclusive charmonium production and γγ→μ + μ − in \(p\overline{p}\) collisions at \(\sqrt{s}=1.96~\mathrm{TeV}\). Phys. Rev. Lett. 102, 242001 (2009). arXiv:0902.1271
LHCb Collaboration, Central exclusive dimuon production at \(\sqrt{s}=7\ \mathrm{TeV}\). LHCb-CONF-2011-022
J.W. Lämsä, R. Orava, Central diffraction at the LHCb. J. Instrum. 4, P11019 (2009). arXiv:0907.3847
M.G. Albrow et al. (FP420 Collaboration), The FP420 R&D project: Higgs and new physics with forward protons at the LHC. J. Instrum. 4, T10001 (2009). arXiv:0806.0302
L.A. Harland-Lang, V.A. Khoze, M.G. Ryskin, W.J. Stirling, Standard candle central exclusive processes at the Tevatron and LHC. Eur. Phys. J. C 69, 179 (2010). arXiv:1005.0695
S. Heinemeyer et al., BSM Higgs physics in the exclusive forward proton mode at the LHC. Eur. Phys. J. C 71, 1649 (2011). arXiv:1012.5007
R. Aaij et al. (LHCb Collaboration), Observation of double charm production involving open charm in pp collisions at \(\sqrt{s}= 7\ \mathrm{TeV}\). J. High Energy Phys. 06, 141 (2012). arXiv:1205.0975
LHCb Collaboration, Measurement of jet production in Z 0/γ ∗→μ + μ − events at LHCb in \(\sqrt{s} = 7\ \text{TeV}\) pp collisions. LHCb-CONF-2012-016
LHCb Collaboration, The LHCb upgrade. LHCb-PUB-2012-010
M. Bona et al. (SuperB Collaboration), SuperB: a high-luminosity asymmetric e + e − super flavor factory. Conceptual design report. arXiv:0709.0451
T. Browder et al., On the physics case of a super flavour factory. J. High Energy Phys. 02, 110 (2008). arXiv:0710.3799
T.E. Browder et al., New physics at a super flavor factory. Rev. Mod. Phys. 81, 1887 (2009). arXiv:0802.3201
T. Aushev et al., Physics at super B factory. arXiv:1002.5012
M. Ciuchini, A. Stocchi, Physics opportunities at the next generation of precision flavor physics experiments. Annu. Rev. Nucl. Part. Sci. 61, 491 (2011). arXiv:1110.3920
Acknowledgements
The LHCb Collaboration expresses its gratitude to its colleagues in the CERN accelerator departments for the excellent performance of the LHC. LHCb thanks the technical and administrative staff at the LHCb institutes, and acknowledges support from CERN and from the national agencies: CAPES, CNPq, FAPERJ and FINEP (Brazil); NSFC (China); CNRS/IN2P3 and Region Auvergne (France); BMBF, DFG, HGF and MPG (Germany); SFI (Ireland); INFN (Italy); FOM and NWO (The Netherlands); SCSR (Poland); ANCS/IFA (Romania); MinES, Rosatom, RFBR and NRC “Kurchatov Institute” (Russia); MinECo, XuntaGal and GENCAT (Spain); SNSF and SER (Switzerland); NAS Ukraine (Ukraine); STFC (United Kingdom); NSF (USA). LHCb also acknowledges the support received from the ERC under FP7. The Tier1 computing centres are supported by IN2P3 (France), KIT and BMBF (Germany), INFN (Italy), NWO and SURF (The Netherlands), PIC (Spain), GridPP (United Kingdom). LHCb is thankful for the computing resources put at its disposal by Yandex LLC (Russia), as well as to the communities behind the multiple open source software packages that are depended upon.
The work of A. Datta was supported by the National Science Foundation under Grant No. NSF PHY-1068052. D.M. Straub was supported by the EU ITN “Unification in the LHC Era”, contract PITN-GA-2009-237920 (UNILHC). We thank D. Gorbunov for useful comments.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Consortia
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
The LHCb Collaboration., Bharucha, A., Bigi, I.I. et al. Implications of LHCb measurements and future prospects. Eur. Phys. J. C 73, 2373 (2013). https://doi.org/10.1140/epjc/s10052-013-2373-2
Received:
Revised:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-013-2373-2