3D Numerical Modeling of the Summit Lake Lava Flow, Yellowstone, USA

Abstract—Volcanic eruptions belong to the extreme events that change the Earth’s landscape and affect global climate and environment. Although special attention is given to super-eruptions, the non-explosive rhyolitic (highly viscous) eruptions and large lava flows are no less important. In this paper, we study an ancient lava flow with a volume of ~50 km³ in the Summit Lake region, ​​Yellowstone, which is one of the best studied large intraplate igneous provinces. We develop three-dimensional (3D) numerical models of isothermal lava flow to analyze the influence of the underlying surface and lava flow viscosity on the advancement and duration of the flow. The modeled dynamics of flow propagation fairly well agrees with the measured values provided that the average angle of inclination of the underlying surface slightly differs from the present-day value (by ~1.3°) presumably due to the pressure change in the magma chamber during the eruption. With the increase in lava viscosity, the flow slows down and its thickness increases leading to a change in the flow morphology.

INTRODUCTION

Highly viscous rhyolitic lavas form flows varying in thickness from tens to hundreds of meters and typically having rather short, a few km, length. Rhyolitic flows are frequently associated with the continental hotspots, that is, the rising jets of the hot mantle rocks (or plumes). The Yellowstone hotspot in the U.S., which is currently located beneath the state of Wyoming, is the most widely known example. Seismic tomography reveals a low velocity channel beneath the Yellowstone National Park, which is interpreted as a mantle plume (Sigloch et al., 2008). This hotspot is most likely to be responsible for the formation of melt feeding the super-eruptions and large lava flows, and, thus, for the development of a volcanic province stretching over several states west of Wyoming as a result of the motion of the North American plate above the hotspot during the last 17 million years e.g., (Morgan, 1971; Smith et al., 2009; Camp et al., 2017).

The Yellowstone’s large rhyolite flows in the geological past are poorly known objects. Using the analytical solution of the problem of the viscous incompressible fluid flow on a flat surface (Huppert, 1982), Loewen et al. (2017) have shown that the emplacement of rhyolite flow in the Summit Lake region (Fig. 1a) as a resulted of lava eruption 124 ka ago occurred over ~2–5 years at temperatures of 800°C and high magma discharge rates above 100 m³ s^–1. These high discharge rates are, however, concomitant with low magma ascent rates (below 1 cm s^–1) because lava erupted through a fissure with a length of about 6 km long and a wide cross-section area which allowed the eruption to remain effusive (non-explosive).

Fig. 1.

(a) Topographic map of lava flow location in Yellowstone Summit Lake region. Lava flow boundary according to (Christiansen, 2001) is shown by dashed line. Intersection of lines A–A', B–B' and C–C' indicates location of main volcanic vent; lava extrusion area is shown by white ellipse; (b) model topography.

Although the analytical solution allowed for estimating several important physical parameters of lava flows in the Summit Lake region of ​​Yellowstone (Loewen et al., 2017), it is of particular interest to determine the influence of the viscosity of lava flows on the morphology and duration of lava emplacement. Despite the fact that high viscosity of the rhyolite lava flows typically prevents them from spreading far away from the vent, in some cases lava can propagate a distance up to a few km if the volume of the erupting magma and the thickness of the lava flow are sufficiently large or if the magma has higher temperature which reduces its viscosity. In this case, lava flow is cooling slowly, its viscosity does not increase and, therefore, the flow can advance a great distance from the vent.

The numerical assessments of the rate of the heat loss from conductive cooling of the large rhyolite lavas have shown that the cooling of the lava flow with a thickness of 100–300 m is very slow and is further retarded by the formation of a carapace (a crust) and the release of latent crystallization heat (Manley, 1992). The models show that thick lava flows can remain active for several decades. At the same time, as the lava flow cools, the yield stress of its cooled crust will affect its dynamics (Balmforth and Craster, 2000) and lead to more complex lava flow morphologies (Fink and Griffiths, 1998). However, Loewen et al. (2017) have shown that a large-volume rhyolitic lava flow at the Summit Lake does not feature complex morphological structures, and hence, the lava flow can be modeled by a gravity-driven isothermal viscous fluid flow.

The lava flow in the Summit Lake region of ​​Yellowstone has been selected as a case study because of its significant volume (about 50 km³) and thickness (100–250 m). At a relatively short duration of the lava extrusion, the lava flow cools insignificantly forming a thin crust on the upper surface of the flow. Although in the case of nonlinear heat exchange (convective and radiative heat transfer) the crust becomes thicker than in the case of pure convective heat transfer at the interface with air (Tsepelev et al., 2019), this thickening of the crust does not substantially affect the advancement of the thick lava flow. Therefore, as the first approximation, the flow can be assumed isothermal. In this paper, we consider a three-dimensional (3D) model of isothermal lava flow in the Summit Lake region of ​​Yellowstone to analyze the influence of the surface topography and the lava viscosity on lava flow advancement and the duration of its emplacement.

STATEMENT OF THE PROBLEM

We consider a 3D numerical model of the flow of a two-phase incompressible immiscible viscous fluid which approximates lava extrusion (one phase) from a volcanic vent into the air (another phase) and the subsequent lava flow. The model domain $\Omega = [0,{{l}_{1}}] \times [0,{{l}_{2}}] \times [f({{x}_{1}},{{x}_{2}}),f({{x}_{1}},{{x}_{2}}) + {{l}_{3}}]$ is limited from below by the topography $f({{x}_{1}},{{x}_{2}})$ of the studied terrane, where l₁ and l₂ are horizontal dimensions and l₃ is the height of the model area. In this domain, we study the flow of a viscous Newtonian inhomogeneous incompressible fluid in the field of gravity. In Cartesian coordinates, this flow is described by the non-stationary Navier–Stokes equation (Ismail-Zadeh and Tackley, 2010; Tsepelev et al., 2019) with the initial condition ${\mathbf{u}}(t = 0,{\mathbf{x}}) = 0$:

$$\begin{gathered} \frac{{\partial (\rho {\mathbf{u}})}}{{\partial t}} + \left\langle {{\mathbf{u}},\nabla } \right\rangle (\rho {\mathbf{u}}) \\ = - \nabla p + \nabla \cdot {\text{(}}\eta (\nabla {\mathbf{u}} + \nabla {{{\mathbf{u}}}^{T}})) + {\mathbf{G}} \\ \end{gathered} $$

(1)

and continuity equation

$$\nabla \cdot {\mathbf{u}} = 0,$$

(2)

where ${\mathbf{u}} = ({{u}_{1}},{{u}_{2}},{{u}_{3}})$ is the velocity vector, ${\mathbf{G}} = (0,0, - g\rho )$ is the vector of external mass forces, g is the gravitational acceleration, p is the pressure, $\rho$ is the density, $\eta$ is the viscosity, ${\mathbf{x}} = ({{x}_{1}},{{x}_{2}},{{x}_{3}})$ is the spatial variable, and t is the time. The advection of a two-phase fluid with an initial condition $\alpha (t = 0,{\mathbf{x}}) = {{\alpha }_{0}}({\mathbf{x}})$ is described by the equation:

$$\frac{{\partial \alpha }}{{\partial t}} + \nabla \cdot (\alpha {\mathbf{u}}) = 0,$$

(3)

where $\alpha (t,{\mathbf{x}}) \in [0,1]$ determines the volume fraction of the fluid at point ${\mathbf{x}} \in \Omega$ at time t. At the initial time, the model domain is filled with air and therefore ${{\alpha }_{0}}({\mathbf{x}}) = 0.$ The density and viscosity are then described by the following equations:

$$\begin{gathered} \rho (t,{\mathbf{x}}) = {{\rho }_{l}}\alpha (t,{\mathbf{x}}) + {{\rho }_{a}}(1 - \alpha (t,{\mathbf{x}})), \\ \eta (t,{\mathbf{x}}) = {{\eta }_{l}}\alpha (t,{\mathbf{x}}) + {{\eta }_{a}}(1 - \alpha (t,{\mathbf{x}})), \\ \end{gathered} $$

(4)

where: ${{\rho }_{a}}$ and ${{\eta }_{a}}$ are the density and viscosity of air, ${{\rho }_{l}}{\text{ and }}{{\eta }_{l}}$ are the lava density and viscosity.

Although thermal effects have an impact on the formation of lava crusts and on lava flow, it was shown that at high magma discharge rate, the crust is fairly thin compared to the lava flow thickness (~3–5%) (Tsepelev et al., 2019). The lava crust cracks, drifts with lava flow driven by gravity until its thickness is small, and does not significantly affect the advance of the flow (Tsepelev et al., 2016). This model considers lava flow due to gravity without thermal effects.

No slip condition ${\mathbf{u}} = 0$ is prescribed at the lower and side boundaries of the model domain. At the part of the lower boundary that contains the vent, it is prescribed that ${\mathbf{u}} = {{{\mathbf{u}}}_{0}},{\text{ }}\rho = {{\rho }_{l}},{\text{ }}\eta = {{\eta }_{l}}$, where ${{{\mathbf{u}}}_{0}}$ is the rate of magma extrusion. At the upper boundary of the model domain, we specify the conditions $\nabla {\mathbf{u}} = 0,{\text{ }}p = 0,{\text{ }}\rho = {{\rho }_{a}},{\text{ }}\eta = {{\eta }_{a}}$.

The Yellowstone Summit Lake lava flows contribute to the present-day terrain topography of the region. To model the lava flows in the geological past, the present terrain topography should be transformed to account for the thickness of the erupted lavas. Namely, let $F({{x}_{1}},{{x}_{2}})$ be the present topography of the studied region; the lava thickness $Z(x_{1}^{v},x_{2}^{v})$ reaches its maximum 230 m (Loewen et al., 2017) in the volcano vent and linearly decreases with the distance from the vent, and $\left( {x_{1}^{v},x_{2}^{v}} \right)$ are the coordinates of the intersection of lines A–A', B–B' and C–С' which corresponds to the location of the volcano vent. Hence the model topography is calculated by the formula $f({{x}_{1}},{{x}_{2}}) = F({{x}_{1}},{{x}_{2}})$ – ${{Z(x_{1}^{v},x_{2}^{v})} \mathord{\left/ {\vphantom {{Z(x_{1}^{v},x_{2}^{v})} {(1 + {\text{ }}r({{x}_{1}},{{x}_{2}}))}}} \right. \kern-0em} {(1 + {\text{ }}r({{x}_{1}},{{x}_{2}}))}}$ where $r({{x}_{1}},{{x}_{2}}) = {{\sqrt {{{{\left( {{{x}_{1}} - x_{1}^{v}} \right)}}^{2}} + {{{\left( {{{x}_{2}} - x_{2}^{v}} \right)}}^{2}}} } \mathord{\left/ {\vphantom {{\sqrt {{{{\left( {{{x}_{1}} - x_{1}^{v}} \right)}}^{2}} + {{{\left( {{{x}_{2}} - x_{2}^{v}} \right)}}^{2}}} } D}} \right. \kern-0em} D}$, D = 20 km. Figure 1b illustrates the model topography calculated in this way.

Thus, the lava flow modeling problem is reduced to solving Eqs. (1)–(4) with the above initial and boundary conditions in the model domain $\Omega$. In the numerical modeling, all variables are reduced to the dimensionless form with the time scale $t* = {{{{\eta }_{l}}} \mathord{\left/ {\vphantom {{{{\eta }_{l}}} {({{\rho }_{l}}gh)}}} \right. \kern-0em} {({{\rho }_{l}}gh)}}$, length scale h, and velocity scale ${h \mathord{\left/ {\vphantom {h {t{\text{*}}}}} \right. \kern-0em} {t{\text{*}}}}$.

NUMERICAL METHOD

In the numerical analysis of the model problem, we use the Ansys Fluent software (https://www. ansys.com/products/fluids/ansys-fluent) based on the finite volume method. The model domain is subdivided into $174 \times 200 \times 70$ hexahedrons that make up finite volumes. Numerical codes use a multiphase unsteady VOF model, and the solver uses a time-implicit integration scheme for equations (1)–(3) to jointly determine the velocity and pressure fields and the volume fraction of fluid. The pressure and the Laplacian are approximated by second-order numerical schemes; for the discretization of the convective terms we use monotonic schemes (e.g, Ismail-Zadeh and Tackley, 2010). The pressure-velocity coupling in Eq. (1) is implemented using PRESTO! approximation and the SIMPLE numerical method (Patankar and Spalding, 1972) with relaxation parameters 0.01 and 0.3 for the velocity and pressure, respectively. Due to the nonlinearity of the problem, the time step is selected in the range from 1 to 10 s depending on stability and so that to optimize the rate of convergence of the solution of the system of linear algebraic equations (SLAE) obtained after the discretization of the problem. The SLAE is solved by the multi-grid method (e.g., (Ismail-Zadeh and Tackley, 2010)).

The main difficulty in the numerical modeling of the problem at hand is that the ratio of the lava viscosity to the air viscosity is about 14 orders of magnitude. To perform a stable numerical experiment, we introduced a nonadaptive numerical grid such that in the region of the lava-air boundary, the grid was refined in the vertical direction. This allowed us to reduce the numerical diffusion in the vicinity of this boundary. Also, we selected an implicit scheme for joint integration of the systems of differential equations which allows for stable calculations with a relatively large time step. Although implicit integration schemes do not need the Courant number to be strictly constrained ($\left| {\mathbf{u}} \right|{{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {\Delta x}}} \right. \kern-0em} {\Delta x}}$ where $\left| {\mathbf{u}} \right|$ is the velocity magnitude, $\Delta t$ is the time step, and $\Delta x$ is the spatial step (Courant et al., 1928)), the large time steps lead to the increase in numerical diffusion at the lava–air boundary and to the physically implausible results; therefore, the time step was chosen sufficiently small. The explicit integration schemes which are much less burdensome for their numerical implementation failed to provide stable calculations even at low Courant numbers. The time step and the relaxation parameter for the velocity were chosen empirically so that to ensure stable computation process.

Highly viscous lava flows are laminar because the Reynolds number is fairly small (<10^–6) for the viscosity and density parameters of the lava, characteristic length and flow velocities in the models under study (see Table 1). The air does not affect the dynamics of lava flows because its viscosity and density are substantially lower than those in lava, and the lava–air interface is considered as a free-surface boundary. And, although the Reynolds number in the air is quite large, the Fluent software allows avoiding turbulent currents in the air layer.

Table 1.   Model parameters values assumed in numerical simulations

RESULTS

It is assumed that magma in the Yellowstone Summit Lake region erupted from the volcanic vent along a 4-km long elliptical fissure (Fig. 1a) located in the model topography along the С–С' profile. Here, we consider three numerical experiments: (1) lava flow along the surface topography reconstructed above, (2) lava flow along an inclined underlying surface, and (3) lava flow with an order of magnitude higher viscosity than in experiment 1. The values ​​of model parameters are presented in Table 1. The lava density (${{\rho }_{l}} = 2350$ kg m^–3) corresponds to the density of rhyolitic rocks with a high silica content (Loewen et al., 2017). Lava viscosity is calculated by the formula ${{\eta }_{l}}\sim 0.023{{\rho }_{l}}g{{V}^{4}}{{Q}^{{ - 1}}}{{r}^{{ - 8}}}$ (Huppert, 1982) where V is the lava flow volume (~50–55 km³), Q is the lava discharge rate (~2000–6000 m³ s^–1), and r is the radius of the front of the lava flow (~10–12 km). In this work, we use two viscosity values (${{\eta }_{l}} = 5.6 \times {{10}^{9}}$ Pa s and ${{\eta }_{l}} = 5.6 \times {{10}^{{10}}}$ Pa s) which lie within the viscosity range determined for lavas with temperatures between 750 and 850°C and water content of about 0.1 wt % (Farquharson et al., 2015; Romine and Whittington, 2015; Loewen et al., 2017).

Experiment 1. The evolution of the lava flow during the first 8 months after the beginning of the eruption is illustrated in Fig. 2. Lava moves almost axisymmetrically during up to two months after which the terrain impedes its propagation in the northern and southeastern directions and makes the flow moving southwest and northeast. Eight months later, the region that is presently covered by rhyolitic lava is filled with model lava except for its southernmost and westernmost edges; however, the southeasterly propagation of model lava visible in Fig. 2 starting from the fourth month is not supported by the observations. The lava flow along section B–B' is asymmetric: lava spreads 2 km northeast and more than 22 km southwest from the presumed vent. In the northeast, there is no present topographic high that could restrain lava flow in this direction.

Fig. 2.

Lava flow evolution during eight months in experiment 1: (a) topography; (b) lava flow height; (c) flow velocity.

Considering that the lava flow extent accounts for possible weathering and erosion (Christiansen, 2001), we may assume that either in the past there was an elevation obstructing the northeasterly flow, or the average slope of the underlying surface in the past was slightly different (by ~1.3°) from the present. This can be explained by the overall deformation of the Yellowstone caldera due to the change in pressure in the magma chamber during lava outflow, although there is no evidence in support of this assumption in the literature.

Experiment 2. For testing the hypothesis about the change in the angle of inclination of the underlying surface, we carried out a numerical experiment with gravitational acceleration modified in such a way as to generate a southwesterly flow condition without changing the terrain (Table 2). The numerical results of experiments 1 and 2 are compared in Fig. 3. In experiment 2, the model lava flow is directed towards the southwest and the present area covered by lava in the south becomes almost completely filled with the model lava over six months (Fig. 3b). However, the model lava extends beyond the present boundary of the lava flow in the west and east which can probably be associated with the inaccurate construction of the model surface topography or with the chosen discharge rate or the duration of the flow. At the same time, lava fairly densely fills the present lava area in the northeast although the lava flow slowly moves in the northwest direction.

Fig. 3.

Lava flow velocities for three time instants (a) in Experiment 1; and (b) in Experiment 2. Observed lava flow boundary is shown by (a) blue and (b) red lines.

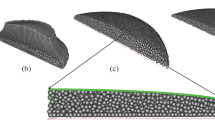
Experiment 3. Viscosity influences the lava flow morphology and its advancement. We performed the numerical experiment simulating the lava flow in the case when lava viscosity is an order of magnitude higher than in the previous experiments (Table 1). Figure 4 shows the 3D image of the model lava flow in the cases of experiment 1 (left column, ${{\eta }_{l}} = 5.6 \times {{10}^{9}}$ Pa s) and experiment 3 (middle column, ${{\eta }_{l}} = 5.6 \times {{10}^{{10}}}$ Pa s). The spreading patterns of these lava flows are compared in the right column. Figure 5 illustrates the comparison of the model results along three profiles А–А', B–B' and C–C' for experiments 1 and 3. Due to the high viscosity assumed in experiment 3, the flow in the horizontal direction slows down, hence, the thickness of the lava flow increases changing its morphology (Fig. 5).

Fig. 4.

Lava flow morphology at different lava viscosities in case of (a) experiment 1 and (b) experiment 3; (c) comparison of lava spreading for three time instants. Dark gray line outlines the area of the observed lava advancement.

Fig. 5.

Lava flow propagation over six months in experiments 1 and 3 along three profiles A–A', B–B' and C–C'. Real and model topographies are shown by green and purple curves, respectively. Eruption fissure is shown in model topography by red lines. Lava flow relief in experiments 1 and 3 is shown by brown and blue curves, respectively.

DISCUSSION AND CONCLUSIONS

The numerical results have shown a good agreement between the measured and modeled surface configuration and thickness of the model lava provided that the average sloping angle of the underlying surface slightly (by ~1.3°) differs from the present value. The viscosity in the numerical experiments is within the limits estimated by Loewen et al. (2017) for the lava flows in the Summit Lake of ​​Yellowstone, although the estimates for lava viscosities have uncertainties associated with the uncertainty in the estimates of the volume of the erupted lava.

We note that with a volume of the erupted lava of 50 km³ and with a model lava discharge rate of 3500 m³ s^–1 (magma extrusion rate ~2.7 m s^–1) it would take about 5.5 months of continuous eruption through the model fissure. However, the maximum width of the model fissure is fairly large (400 m) and unrealistic. Therefore, the numerical results need to be corrected in terms of time through changing the fissure’s width. With the maximum fissure’s width decreased to 40 m and the same extrusion rate, it will take ~4.6 years for the eruption of the same amount of lava. This is consistent with the estimates of lava flow duration in the Summit Lake region. Overall, the 3D lava flow modeling has confirmed the estimates that were obtained using the analytical solution for the thin layer approximation model (Loewen et al., 2017) and allowed a more detailed study of the dynamics and morphology of the Summit Lake lava flows depending on flow direction and viscosity.