1 Introduction

Thermo elasticity is a part of applied mechanics, that deals with the heat transfer theory and the theory of strains and stresses, deformation of solids may occur due to heat flow and conversely change in temperature may occur due to the occurrence of strain fields. Thermoelasticity makes it practical to find the stresses produced by the temperature field, and one can calculate the distribution of temperature caused by the action of inner forces that change over time. Science and innovation are associated with thermoelasticity in a wide range of applications, including nuclear physical science, modern assembling, submarines, pressure vessels, nuclear power plants, metallurgy, synthetic lines, aviation, and numerous others.

Micro- and nano-material structures have drawn a lot of attention from researchers over the past ten years due to their special mechanical, electrical, and electronic capabilities. Modern engineering disciplines pay tremendous attention to the mechanical characteristics of micro-/nanostructures since they are observed as a critical aspect of limiting the performance of small-scale structures on a given task. Because of these properties, nanomaterials are utilized in nano-beams as elementary structural components in MEMS/NEMS and piezoelectric devices. It is well known that thermoelastic damping is a vital component of the quality factor of MEMS and NEMS under vacuum. MEMS/NEMS are based on nanobeam resonators and thermoelastic damping in nanobeam is important to their success. However, significant difficulties have ascended as dimensions diminishes to micro/nanoscale size to increase the density of components, there are now substantial challenges that need high speed and real-time reaction. Resonators are becoming smaller, which leads to a change in mechanical behaviour due to size effects and we cannot use classical continuum mechanics. This needs for modest technological advancements in sensors, channels, transducers, and so on. Uses of MEMS/NEMS include energy transducers, machine-driven designing, aviation, and marine ventures, ultrasound clinical imaging, actuators, inkjet printing, liquid screens piezoelectric power supplies, and superficial sound wave gadgets precisely based on rationale and sonar projectors.

An ample review of the nanostructures is conducted in this paper. To study the mechanical characteristics of micro-/nanostructures accurately, it is mandatory to use size-dependent continuum mechanics theories. A significant number of studies have been done recently that analyze micro-and nanostructures with varied shapes, such as beams and plates. The objective of this comprehensive review is to present the best research pertinent to the theory of continuum mechanics of micro/nano-beams/plates (Fig. 1).

Fig. 1
figure 1

Schematic design of the nanobeam

Full size image

2 Developments in the theory of thermo elasticity

The thermo elasticity coupled equations should be used to determine the solution to the temperature and stress problems. In addition, it must be stated that classical thermoelasticity is an uncoupled theory, which presents a phenomenon that lacks any physical characteristics.

The classical uncoupled thermoelasticity theory was introduced by Duhamel [1]. Two limitations were associated with this theory. At first, the state of the elastic body did not depend on temperature. Furthermore, the parabolic heat equation implies that temperature travels at an unlimited speed, which is also in conflict with empirical findings. In order to overcome these limitations, Biot [2] introduced the theory of coupled thermoelasticity. In this theory, heat conduction equations are coupled to elasticity equations. In spite of this, this theory predicts heat waves propagating at an unlimited speed. Afterward, Lord and Shulman [3] formulated the generalized thermoelasticity theory with one relaxation time. According to this theory, the temperature propagation speed is finite due to the hyperbolic heat equation.

Chen and Gurtin [4], Chen et al. [5, 6] gave the two-temperature theory of thermoelasticity of deformable bodies for heat conduction, subject to two kinds of temperatures, the thermodynamic temperature \(T\) and the conductive temperature \(\varphi\). For the time-independent cases, the difference between \(T\) and \(\varphi\) is proportional to the supply of heat, and without heat supply, these temperatures are equal. For time dependent problems, difference in two temperatures is non zero and does not depend on heat supply. When the two temperatures factor is zero, i.e., \(\varphi =T\) then the coupled thermoelasticity can be derived from the two-temperature theory of thermoelasticity. Using the linear symmetric heat conduction tensor, Green and Lindsay [7] proposed a more precise thermoelasticity theory using two relaxation times. An entropy production inequality is used by Green and Laws [8] to constrain constitutive equations. For anisotropic media, a generalized theory of thermoelasticity was introduced by Dhaliwal and Sherief [9]. Three theories of thermoelasticity were introduced by Green and Naghdi [10,11,12]. According to their theories, there are three types of thermoelasticity theories: Green-Naghdi (GN) theory of type I (Classical thermoelasticity theory), GN-II (thermoelasticity without energy dissipation), and G-N III (both with and without energy dissipation).

Catteno [13] presented a single-phase lag model which links the heat flux and temperature gradient and is recognized as the hyperbolic model. Further, a dual-phase lag (DPL) model for the heat transfer system was introduced by Tzou [14, 15] in which Fourier’s law is modified into Fourier’s law for two distinct time translations for the heat flux, as well as the temperature gradient. Three-phase lag (TPL) theory of heat transfer was presented by Choudhuri [16] who modified the Fourier law of heat conduction by introducing three different phase lags, i.e., the phase lag of the heat flux vector, temperature gradient, and thermal displacement gradient. Rukolaine [17] investigated a 3-D model described by the Jeffreys-type equation of heat conduction, using a first-order approximation to the DPL with a positive localized source of short duration. The DPL constitutive relation is approximated by Rukolaine [18] using two models of heat conduction. For a thermoelastic material, Fabrizio et al. [19] investigated the apparent inconsistency between thermodynamic restrictions and stability conditions reported by Quintanilla and Racke [20] and Fabrizio and Lazzari [21]. The non-equilibrium thermodynamics of dual-phase-lag heat conduction has been studied by Kovács and Ván [22] and proved that as long as both relaxation times are not negative, the first-order Taylor series expansion fits the second law.

Sherief et al. [23] introduced the fractional order theory (FoT) of thermoelasticity by using fractional calculus, demonstrating the uniqueness hypothesis and inferred variational standard and correspondence hypothesis. This theory has not considered the wave propagation and diffusion effects. Youssef [24] expressed the FoT by using the Riemann–Liouville fractional integral operator summed up heat conduction condition, demonstrating the uniqueness hypothesis, and tackling the one-dimensional problem. Ezzat et al. [25] developed a two-temperature magneto-thermoelasticity mathematical model based on the fractional order dual-phase-lag law. Prior to the Ezzat et al. [25] theory of thermoelasticity with fractional order heat transfer, the discontinuity of the stress distribution was a serious issue for which no physical explanation had been provided. However, the stress function is continuous in this new theory. Youssef [26] gave a two-temperature model for an elastic half-space under the influence of a moving heat source without energy dissipation. The fractional-order generalized theory of thermoelasticity was presented by Youssef and Abbas [27]. In a new study by Ezzat et al. [28], fractional relaxation operators are used to describe linear thermo-viscoelasticity for isotropic medium. For perfectly conducting isotropic medium, Ezzat and El-Bary [29] developed a mathematical model of fractional order magneto-thermo-viscoelasticity. With Caputo fractional derivative and FoT, El-Karamany and Ezzat [30] discussed fractional order phase-lag and G-N thermoelasticity theories.

3 Euler–Bernoulli (E–B) beam theory

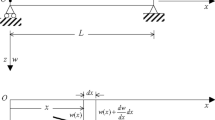
The EB is a simplified form of the linear theory of elasticity that enables beams to be studied for their load-carrying and deflection properties. It describes the deflections due to lateral loads only in the case of a beam with small deflections. According to Euler–Bernoulli, the beam's deflection is proportional to the load applied. In Euler–Bernoulli theory for small deflection of a simple bending problem, the displacement components are given by

$$u\left( {x,z,t} \right) = - z\frac{\partial W}{{\partial x}},\,v\left( {x,z,t} \right) = 0,\,w\left( {x,z,t} \right) = W\left( {x,t} \right),$$
(1)

where \(W\left(x,t\right)\) is the lateral deflection of the nanobeam and \(t\) is the time.

With the help of Eq. (1) the one dimensional constitutive equation obtained from \({t}_{ij}= {C}_{ijkl}{e}_{kl}- {\beta }_{ij}T\), becomes

$${t}_{xx}= -{C}_{11}z\frac{{\partial }^{2}W}{\partial {x}^{2}}- {\beta }_{1}T.$$

Following Rao [31] the flexural moment of the cross-section of the nanobeam is given by:

$$M\left(x,t\right)=-{\int }_{\frac{-h}{2}}^\frac{h}{2}b{t}_{xx}zdz= {C}_{11}I\frac{{\partial }^{2}W}{\partial {x}^{2}}+ {\beta }_{1}{M}_{T },$$
(2)

where,

$${M}_{T}=b{\int }_{\frac{-h}{2}}^\frac{h}{2}Tzdz$$

is the thermal moment of inertia of the beam and \({\beta }_{1}{M}_{T}\) is the thermal moment of the beam. In addition, \(I=\frac{b{h}^{3}}{12}\) is the moment of inertia of cross-section and \({C}_{11}I\) is the flexural rigidity of the beam. The transverse equation of motion of the nano-beam is given by Rao [31]

$$\frac{{\partial }^{2}M}{\partial {x}^{2}}+ \rho A\frac{{\partial }^{2}W}{\partial {t}^{2}}=q\left(x,t\right).$$
(3)

Abouelregal and Zenkour [32] looked at the impacts of thermal vibration pulse width, speed, and transverse excitation. Based on E–B theory and clamped–clamped boundary conditions. Rezazadeh et al. [33] used the modified couple stress theory (MCST) to explore the size implications of the thermoelastic damping issue in a micro-beam resonator for gold and nickel material. The issue of thermoelastic damping in vented MEMS beams was described by Guo et al. [34] using an eigenvalue formulation and the finite element approach. Using the Laplace transform method, Allam and Abouelregal [35] examined the thermoelastic waves induced by the laser pulse and changing heat of homogeneous micro-scale beam resonators. In their discussion of the issue of an axially moving micro-beam. Sharma and Kaur [36] examined the transverse vibrations in thermoelastic-diffusive thin micro-beams. The issue of thermoelastic vibration of an axially moving micro-beam subjected to sinusoidal pulse heating was studied by Zenkour and Abouelregal [37]. Using the MCST and the closed-form heat conduction equation for non-classical processes, Kumar and Devi [38] investigated the vibrations in a homogeneous, isotropic thin beam.

In order to illustrate the small-scale effect, Kaur et al. [39] explored the forced vibrational analysis of Eringen's nonlocal TIT nanobeam resonators due to ramp-type heating and time-varying exponentially decaying load. The Frequency Shift and Thermoelastic Damping in TIT SS Nanoscale Beam with 2T and GN III Theory of Thermoelasticity and EB Beam Theory were explored by Kaur et al. [40]. In specifically, piezo-thermo-elastic SS nanobeam with two temperatures and Euler Bernoulli theory with small-scale effects were examined by Kaur et al. [41] utilising nonlocal Eringen's theory. The dimensionless formulas for lateral deflection, electric potential, thermal moment, thermoelastic damping, and frequency shift are obtained by solving the mathematical model that has thus been created. With the help of generalised piezothermoelastic theory, the relationship between frequency and nonlocal factors and the lateral deflection, electric potential, and thermal moment is graphically depicted.

4 Nonlocal theory of thermoelasticity

The theory of the nonlocal continuum following Eringen [42] considers the stress at a point not only depends on the strain of that point but also the strain of the rest of the points of the body. So we have,

$$\begin{gathered} \sigma^{nl} \left( x \right) = \int\limits_{V} {\alpha \left( {\left| {x - x^{\prime}} \right|,\varrho } \right)\sigma^{l} \left( {x^{\prime}} \right)dV\left( {x^{\prime}} \right)} , \hfill \\ \sigma^{l} \left( {x^{\prime}} \right) = C:e\left( {x^{\prime}} \right), \hfill \\ \end{gathered}$$
(4)

where \(\sigma^{nl} \left( {x^{\prime}} \right)\) is the nonlocal stress tensor and \({\sigma }^{l}\left({x}^{^{\prime}}\right)\) is the classical stress tensor \(e\left( {x^{\prime}} \right) = \nabla u\left( {x^{\prime}} \right) = \left\{ {e_{ij} } \right\}\) is the strain tensor, \({\varrho }^{2}={\left({e}_{0}a\right)}^{2}\), and the kernel function \(\alpha \left(\left|x-{x}^{^{\prime}}\right|,\varrho \right)\) depends on the Euclidean distance \(\left| {x - x^{\prime}} \right|\) and the nonlocal parameter \(\varrho ,\) and assuming that the kernel function satisfies the conditions defined in Eringen [42] then Eq. (4), can be written in the differential form (5) obtained by pre-operating (4) by \(\left(1-{\varrho }^{2}{\nabla }^{2}\right)\) as:

$$\left(1-{\varrho }^{2}{\nabla }^{2}\right){\sigma }^{nl}\left(x\right)=C:e\left(x\right).$$
(5)

If the characteristic length is small i.e., \(\varrho =0,\) then we can obtain the classical stress–strain relation for macro-scale problems from Eq. (5).

Now, Based on Eringen’s nonlocal elasticity, the local and nonlocal stresses are related as:

$${\sigma }_{xx}^{nl}\left(x,z,t\right)-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}{\sigma }_{xx}^{nl}\left(x,z,t\right)}{\partial {x}^{2}}=-{C}_{11}z\frac{{\partial }^{2}w}{\partial {x}^{2}}-{\beta }_{1}T.$$

Zenkour and Abouelregal [43] applied nonlocal theory of thermoelasticity to study a nanobeam exposed to a harmonically varying heat with phase lags considering the variable thermal conductivity. Rezazadeh et al. [44] studied the thermoelastic damping in NEMS (nano-electro-mechanical systems) using Green-Naghdi (GN)-III theory by applying the nonlocal Euler–Bernoulli beam model. The Galerkin finite element formulation and Newmark finite difference method have been applied to find the solution to governing equations. Yu et al. [45] formulated the generalized nonlocal thermodynamics for a Euler–Bernoulli beam, hydrodynamic heat-conductive model, Zener, Lifshitz, and Roukes’ damping model. Li et al. [46] developed a theoretical model for bending and stability of a nano bar using Eringen’s nonlocal differential law to investigate the compression bending subjected to vertically concentrated, vertically linearly distributed, and horizontally concentrated forces simultaneously.

Using fractional-order generalized thermoelastic theory and a nonlocal effect, Peng et al. [47] examined the SS-SS nanobeam and its response to ramp-type heating. Zhang and Qing [48] presented the two-phase local/ NHCIMs based on TFD and TGD. In their research with the combination of TFD and TGD-NHCIMs with stress–strain driven two-phase local/nonlocal elastic integral models, they proposed four types of nonlocal thermoelastic integral models to predict the thermoelastic behavior of clamped–clamped microstructures. Yahya et al. [49] developed new equations for rotating nanobeams with thermal conductivity under periodic pulse heating using the non-local couple stress elasticity theory with phase lag. Limkatanyu et al. [50] framed a model of the bar-elastic substrate using nonlocal, Gurtin–Murdoch surface theory, and the Winkler foundation model. Tiwari et al. [51] analyzed the thermoelastic vibrations in a clamped–clamped nano-beam w.r.t a variable axial load. The MGT model is used to examine the thermal effects inside the beam. Ahmad et al. [52] analyzed the thermoelastic vibration using the non-local elasticity theory put forward by Eringen of E–B nanobeams. Additionally, the generalized thermoelastic model with DPL is used to investigate the impact of temperature change. A constant-intensity magnetic field and an axial thermal excitation load are both applied to the nanobeam under study.

Eringen's theory of nonlocal elasticity can be used for nanotechnology applications due to the small scale effect in nano-applications of the beam. Continuum elasticity theory assumes that stress at a point is a function of strain at that point, whereas in the nonlocal elasticity theory stress at a point is a function of strains at all points in the continuum. In other words, in nonlocal elasticity theory, stress at a point is determined by both stress at that point and spatial derivatives of it. Also, Euler–Bernoulli beam theory does not account for the effects of transverse shear strain and neglects shear deformations Therefore, for the nanostructured, the E–B theory with nonlocal theory gives the better results as compared to Simple E–B theory.

5 Dual-phase-lag heat transfer

Conventional heat conduction problems have been addressed with the classical heat conduction equation, which is based on the Fourier law of heat conduction [53]. But it is applicable to problems with large spatial dimensions and long response times. This method produces unacceptable results when the temperature gradients are extreme, there is high conduction of heat occurs when lasers interact with materials. Additionally, heat conduction equation is parabolic in nature, implying that thermal waves propagate at an infinite speed, which implies that if any thermal disturbance occurs in a material, its effects will be felt instantly at distances infinitely distant from its source. For transient heat conduction processes occurring over extremely short times, it produces an unrealistic behavior. The last few decades have seen serious efforts made to overcome the inadequacy of Fourier law.

There has been considerable interest in the research on high-rate heating with short-pulse laser technologies and their wide applications in modern nano/micro-scale device fabrication technologies. During heat transport procedure, the microscopic effects of the non-equilibrium thermodynamic transition and the energy exchange become more prominent as the response time decreases. In order to account for the microstructural effects that result from high-rate heat transmission, Zenkour [54] develop the dual phase-lag (DPL) heat conduction equation by adding two phase-lags to Fourier's law of heat conduction as:

$${{K}_{ij}{\mathcal{L}}_{\theta }\varphi }_{,ij}= {\mathcal{L}}_{\mathrm{q}}\frac{\partial }{\partial \mathrm{t}}\left({\beta }_{ij}{T}_{0}{u}_{i,j}+{\rho C}_{E}T\right).$$
(6)

The two time differential parameters \({\mathcal{L}}_{\uptheta }\) and \({\mathcal{L}}_{\mathrm{q}}\) are of the form:

$${\mathcal{L}}_{\uptheta }=1+\sum_{\mathrm{j}=1}^{{\mathrm{R}}_{1}}\frac{{\uptau }_{\uptheta }^{j}{\partial }^{j}}{j!\partial {\mathrm{t}}^{j}},$$

and,

$${\mathcal{L}}_{\mathrm{q}}=\left(\mathrm{\varrho }+{\uptau }_{0}\frac{\partial }{\partial \mathrm{t}}+\sum_{j=2}^{{\mathrm{R}}_{2}}\frac{{\uptau }_{\mathrm{q}}^{j}{\partial }^{j}}{j!\partial {\mathrm{t}}^{j}}\right),$$

(0 ≤ τθ < τq), and ϱ is a dimensionless parameter (= 0 or 1 as per the thermoelasticity theory).

By incorporating macroscopic lagging (or delayed) responses for the temperature gradient and the heat flux vector as potential outcomes, this law will reasonably represent the microscopic interactions in the heat transport mechanism. Microstructural interactions, such as phonon–electron interactions or phonon scattering, cause the delay time \({\tau }_{\theta }\), denoted as the phase-lag of temperature gradients. The second delay time \({\tau }_{q}\) results from thermal inertia’s fast-transient effects, which are attributed to phase-lags of heat flux.

A number of experiments have demonstrated that the DPL model of heat conduction provides a more accurate prediction than the classical Fourier law, especially when the heat source is moving locally with high intensity, the crack tip propagates rapidly, shock waves propagate, lasers are used, and laser surgery is performed.

6 Modified three-phase lag Green Naghdi (TPL GN) models of thermoelastic beam

The new model incorporates high-order approximations of time-fractional derivatives for three-phase lags in heat flux vectors, temperature gradients, and thermal displacement gradients. Using Taylor series expansions, this model replaces the Fourier law of heat conduction with the introduction of phase-lags for the heat flux vector, the temperature gradient, and the thermal displacement gradient, while maintaining appropriate high fractional derivative order for terms. Zenkour and El-Mekawy [55] studied photo thermoelastic beam using the Modified TPL GN equation for conduction of heat which is given by:

$${\mathcal{L}}_{1}{T}_{,ij}={\mathcal{L}}_{2}\left(\rho {C}_{E}T+{\beta }_{ij}{T}_{0}{e}_{ij}\right)-{\mathcal{L}}_{0}\left(\rho {Q}_{0}\right),$$
(7)

where time differential operators \({\mathcal{L}}_{i}\)(i = 0, 1, 2) are given by,

$$\begin{gathered} {\mathcal{L}}_{1} = K_{ij} \left( {1 + \mathop \sum \limits_{r = 1}^{n} \frac{{\left( {\tau_{t} } \right)^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\frac{\partial }{\partial t} + \varepsilon K_{ij}^{*} \left( {1 + \mathop \sum \limits_{r = 1}^{n} \frac{{\left( {\tau_{v} } \right)^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right), \hfill \\ {\mathcal{L}}_{0} = \left( {1 + \mathop \sum \limits_{r = 1}^{n} \frac{{\left( {\tau_{q} } \right)^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\frac{\partial }{\partial t}, \hfill \\ {\mathcal{L}}_{2} = {\mathcal{L}}_{0} \frac{\partial }{\partial t}, \hfill \\ \end{gathered}$$
(8)
$$\varepsilon =0 \, \mathrm{or} \, 1, n\ge 0 \, {\text{and}} \, 0\le {\tau }_{v}<{\tau }_{t}<{\tau }_{q}.$$

“The phonon–electron interaction or phonon scattering creates phase lag \({\tau }_{t}\), and the fast-transient thermal inertia effects create \({\tau }_{q}\). The phase lags \({\tau }_{v},\) \({\tau }_{q}\) and \({\tau }_{t}\) are intrinsic properties of the medium and are small in magnitude”.

Lata et al. [56] used a new modified three-phase lag (TPL)GN model and nonlocal theory of thermoelasticity to analyse the vibration phenomenon in 2D TIT homogeneous E–B nonlocal nanobeam with laser pulse. In order to explore the impact of varying thermal conductivity on a TIT homogeneous nonlocal CF beam with 2T using MDD and E-B beam theory, Kaur and Singh [57] developed a mathematical model for a 2-D. Graphical representations of lateral deflection, axial displacement, temperature distribution, axial stress, and thermal moment effects of newly updated TPL GN heat transfer are shown.

In the context of generalised piezothermoelastic theory, Kaur et al. [58] studied one-dimensional piezoelectric materials, in particular piezo-thermo-elastic nanobeam. It is believed that the ends of the nanobeam are simply sustained and are always the same temperature. A novel modified TPL GN model was used by Kaur et al. [59] to analyse the vibration phenomenon in a 2D TIT homogeneous E-B nanobeam with a laser pulse. The endpoints of the nanobeam are assumed to be simply supported, and a sinusoidal temperature variation is assumed. With a new modified TPL-GN model, Kaur et al. [60] investigated the effects of the time-harmonic laser pulse on the vibration phenomenon in 2D TIT visco-thermoelastic SS nanobeam. The resulting mathematical model is solved to derive non-dimensional expressions for thermal expansion, temperature distribution, axial stress, and lateral deflection. In order to evaluate the periodic heat flux-induced vibrations of viscoelastic functionally graded Euler–Bernoulli nanostructure beams, Abouelregal and Zenkour [61] used fractional-order calculus.

7 Memory dependent derivatives

Wang and Li [62] introduced “memory-dependent derivatives based on the Caputo-type definition of fractional derivatives which is a weighted integrals of common integer-order derivatives on slipping intervals. In other words, it describes the variation of a system in which the instantaneous change rate depends on its past state, which is called the “memory effect”.

The first-order MDD w.r.t the time delay \(\chi\) > 0 for a fixed time t:

$${D}_{\chi }f\left(t\right)=\frac{1}{\chi }{\int }_{t-\chi }^{t}K\left(t-\xi \right){f}^{^{\prime}}\left(\xi \right)d\xi .$$
(9)

The choice of the kernel function \(K(t-\xi )\) and the time delay parameter \(\chi\) is determined by the material properties. The kernel function \(K(t - \xi )\) is differentiable with respect to the variables \(t\) and \(\xi\).

The kernel function \(K(t - \xi )\) is taken here in the form:

$$K\left(t-\xi \right)=1-\frac{2b}{\chi }\left(t-\xi \right)+\frac{{a}^{2}}{{\chi }^{2}}{\left(t-\xi \right)}^{2}=\left\{\begin{array}{c}1,\\ 1+\left(\xi -t\right)/\chi ,\\ \xi -t+1,\\ {\left[1+\left(\xi -t\right)/\chi \right]}^{2},\end{array}\right.\begin{array}{c}a=0,b=0,\\ a=0,b=1/2,\\ a=0,b=\chi /2,\\ a=1,b=1.\end{array}$$
(10)

where \(a\) and \(b\) are constants. It should be also mentioned that the kernel in the fractional sense is singular, while that in the MDD model is non-singular. The kernel can be now simply considered a memory manager. The comma is further used to indicate the derivative with respect to the space variable, and the superimposed dot represents the time derivative. For fractional types, the kernel function is fixed, while for memory-dependent types, it can be customized based on application requirements”. Overall, the MDD is superior to the fractional order derivative.

Based on the caputo type definition of fractional derivatives, Wang and Li [62] introduced memory dependent derivatives. Ezzat et al. [63, 64], discussed MDD in viscoelastic thermoelastic problem and presented generalized thermoelastic thermal equation and derived various thermoelastic theories from it. Lata and Kaur [65] studied the transversely isotropic thermoelastic thin beam with GN theory of thermoelasticity of Type-II and Type-III and Euler Bernoulli beam theory. Kaur et al. [66] studied the forced vibrations in TIT CF nanoscale beam with 2T and MDD theory of thermoelasticity with the application of E–B beam theory. The temperature was assumed to vary sinusoidally. El-Bary [67] studied a thermal shock problem in one-dimension with MDDs. Under a harmonic external force and rectified sine wave heating, Abouelregal and Marin [68, 69], have observed a small-scale effect in a generalized thermoelastic beam. Using the E–B beam theory and L-S generalised thermoelasticity with MDD heat conduction, the thermoelastic damping in a micro-beam has been investigated by Wang and Li [70]. A memory-dependent derivative based on displacement was developed by Al-Jamel et al. [71] to characterize damping in oscillatory systems in complicated dissipation appliances where memory effects cannot be neglected.

This table presents a comprehensive overview of generalized thermoelasticity studies. In addition, we describe the geometric model and the method of solution for each research.

References

Description

Formulation

Geometry

Computational method

Zenkour and Abouelregal [43]

Nonlocal thermoelasticity beam theory exposed to a harmonically varying heat with phase lags considering the variable thermal conductivity

\(q\left(x,t+ {\tau }_{q}\right)=-K\nabla \theta \left(x,t+ {\tau }_{\theta }\right),\)

\(\left[1-{\left(a{e}_{0}\right)}^{2}{\nabla }^{2}\right]{t}_{kl}={\sigma }_{kl}\)

View full size image

Laplace transform

Rezazadeh et al. [44]

Thermoelastic damping in a NEMS (nano-electro-mechanical systems) is using Green-Naghdi (GN)-III theory by applying the nonlocal Euler–Bernoulli beam model

\({\sigma }_{kl,k}+ \rho \left({f}_{l}-\ddot{{u}_{l}}\right)=0,\)

\({t}_{kl}\left(x\right)={\int }_{V}\alpha \left(\left|{x}^{^{\prime}}-x\right|\right){\sigma }_{kl}dV,\)

\({\sigma }_{kl}={\lambda u}_{n,n}{\delta }_{kl}+\mu \left({u}_{k,l}+{u}_{l,k}\right)\)

 

Galerkin finite element formulation and Newmark finite difference method

Yu et al.[45]

Formulated the generalized thermodynamics by merging the nonlocal thermal Euler–Bernoulli beam, hydrodynamic heat-conductive model, Zener, Lifshitz, and Roukes’ damping model

\(\ddot{x}+2\zeta {\omega }_{0}\dot{x}+{\omega }_{0}^{2}x=0,\)

\({q}_{i}+\tau \frac{\partial {q}_{i}}{\partial t}=-K\nabla \theta +{\zeta }^{2}\left[{\nabla }^{2}{q}_{i}+2\nabla \left(\nabla .{q}_{i}\right)\right],\)

\(\left[1-{\xi }^{2}{\nabla }^{2}\right]{\sigma }_{ij}\) =\({C}_{ijkl}{\epsilon }_{kl}.\)

View full size image

Laplace transform

Yahya et al.[49]

Rotating nanobeams with thermal conductivity under periodic pulse heating using the non-local couple stress elasticity theory with a phase lag

\(\tau_{ij} \left( x \right) = \mathop \smallint \limits_{v}^{{}} K_{1} \left( {\left| {x,x^{\prime}} \right|,\xi } \right)\sigma_{ij} \left( {\mathop x\limits^{\prime } } \right)dv\left( {\mathop x\limits^{\prime } } \right)\)

\(\sigma_{ij} \left( {\mathop x\limits^{\prime } } \right) = 2\mu \varepsilon_{ij} \left( {\mathop x\limits^{\prime } } \right) + \left( {\lambda \varepsilon_{kk} \left( {\mathop x\limits^{\prime } } \right) - \gamma \theta \left( {\mathop x\limits^{\prime } } \right)} \right)\delta_{ij}\)

View full size image

Laplace transform and state space methods

Kaur et al. [58]

One-dimensional piezoelectric materials in particular piezo-thermo-elastic nanobeam in the context of generalized piezothermoelastic theory. The ends of the nanobeam are considered to be simply supported and at a constant temperature

\({t}_{ij}= {c}_{ijkl}{e}_{kl}-{\epsilon }_{ijk}{E}_{k}- {\beta }_{ij}\left(1+{t}_{1}\frac{\partial }{\partial t}\right)T,\)

\({D}_{i}={\zeta }_{ij}{E}_{j}+{\epsilon }_{ijk}{e}_{jk}+{p}_{i}\left(1+{t}_{1}\frac{\partial }{\partial t}\right)T,\)

\(\begin{aligned} K_{{ij}} \varphi _{{,ij}} = & \rho C_{E} \left( {1 + t_{0} \frac{\partial }{{\partial t}}} \right)\dot{T} \\ & + T_{0} \beta _{{ij}} \left( {1 + n_{1} t_{0} \frac{\partial }{{\partial t}}} \right)\dot{u}_{{i,j}} \\ & - T_{0} p_{i} \left( {1 + n_{1} t_{0} \frac{\partial }{{\partial t}}} \right)\dot{\phi }_{{,i}} \\ & - \left( {1 + n_{1} t_{0} \frac{\partial }{{\partial t}}} \right)\rho Q_{0} \\ \end{aligned}\)

View full size image

Laplace transform

Limkatanyu et al. [50]

Model of the bar-elastic substrate using nonlocal, Gurtin–Murdoch surface theory, and Winkler foundation model

\(\psi \left[{\varepsilon }_{xx}, {\eta }_{xxx}\right]=\frac{1}{2}{E}_{xx}{\left({\varepsilon }_{xx}\right)}^{2}+\frac{1}{2}{E}_{xx}{l}_{x}^{2}{\left( {\eta }_{xxx}\right)}^{2},\)

View full size image

Approximation

Li et al. [46]

Developed a theoretical model for bending and stability of a nano bar using Eringen’s nonlocal differential law to investigate the compression bending

\(t_{kl} \left( x \right) = \mathop \smallint \limits_{v}^{{}} \alpha \left( {\left| {x^{\prime},x} \right|,\tau } \right)\sigma_{kl} \left( {\mathop x\limits^{\prime } } \right)dv\left( {\mathop x\limits^{\prime } } \right),\)

\(\left[1-{\left(a{e}_{0}\right)}^{2}{\nabla }^{2}\right]{t}_{kl}={\sigma }_{kl},\)

View full size image

Ritz method

Tiwari et al. [51]

Thermoelastic vibrations in a clamped–clamped nano-beam w.r.t a variable axial load. MGTE model is used to examine the thermal effects inside the beam

\({\sigma }_{x}=-{E}_{z}\frac{{\partial }^{2}w}{\partial {x}^{2}}-{\beta }^{*}\theta ,\)

\(M\left( {x,t} \right) = b\mathop \smallint \limits_{{\frac{ - h}{2}}}^{\frac{h}{2}} \sigma_{x} zdz\)

View full size image

Laplace transform

Zhang and Qing [48]

Two-phase local/nonlocal heat conduction integral models (NHCIMs) based on thermal flux driven (TFD) and temperature gradient driven (TGD)

\(\varnothing -{q}^{^{\prime}}=pc\dot{\theta }\),

\(- \lambda \mathop \theta \limits^{\prime } = \xi_{1} q + \frac{{1 - \xi_{1} }}{{2k_{1} }}\mathop \smallint \limits_{0}^{L} qe^{{ - \frac{{\left| {x - \eta } \right|}}{{k_{1} }}}} d\eta ,\)

\(- q = \lambda \left( {\xi_{1} \mathop \theta \limits^{\prime } + \frac{{1 - \xi_{1} }}{{2k_{1} }}\mathop \smallint \limits_{0}^{L} \mathop \theta \limits^{\prime } e^{{ - \frac{{\left| {x - \eta } \right|}}{{k_{1} }}}} d\eta } \right).\)

View full size image

Strain-driven local/nonlocal integral model

Peng et al. [47]

Using fractional-order generalized thermoelastic theory and a nonlocal effect, examined the SS-SS nanobeam and its response to ramp-type heating

\(\sigma_{ij} \left( x \right) = \mathop \smallint \limits_{V}^{{}} K\left( {x,x^{\prime},\chi } \right)\sigma_{ij}^{\prime } \left( {\mathop x\limits^{\prime } } \right)dV\left( {\mathop x\limits^{\prime } } \right),\)

\(\sigma_{ij}^{\prime } \left( {\mathop x\limits^{\prime } } \right) = \lambda \varepsilon_{kk}^{\prime } \left( {\mathop x\limits^{\prime } } \right)\delta_{ij}\) + \(2\mu \varepsilon_{kk}^{\prime } \left( {\mathop x\limits^{\prime } } \right),\)

\(\left[ {1 - \left( {ae_{0} } \right)^{2} \nabla^{2} } \right]\sigma_{ij\left( x \right)} = \sigma_{ij}^{\prime } \left( {\mathop x\limits^{\prime } } \right)\)

View full size image

Laplace transform

Lata and Kaur [65]

Transversely isotropic thermoelastic thin beam with GN theory of thermoelasticity of Type-II and Type-III and Euler Bernoulli beam theory

\({t}_{ij}= {C}_{ijkl}{e}_{kl}- {\beta }_{ij}T,\)

\({C}_{ijkl}{e}_{kl,j}- {\beta }_{ij}{T}_{,j}={\rho \ddot{u}}_{i},\)

\(K_{ij} T_{,ij} + K_{ij}^{*} \dot{T}_{,ij} = \beta_{ij} T_{0} \ddot{e}_{ij} + \rho C_{E} \ddot{T}\)

View full size image

Laplace transform

Kaur et al. [66]

Forced Vibrations in TIT CF nanoscale beam with 2T and MDD theory of thermoelasticity with the application of E-B beam theory

\(curl \overrightarrow{h}= \overrightarrow{j}+{\varepsilon }_{0}\frac{\partial \overrightarrow{E}}{\partial t}\),

\(curl \overrightarrow{E}=- {\mu }_{0}\frac{\partial \overrightarrow{h}}{\partial t}\),

\(\overrightarrow{E}=- {\mu }_{0}\left(\frac{\partial \overrightarrow{u}}{\partial t}+ {\overrightarrow{H}}_{0}\right)\),

\(div \overrightarrow{h}=0,\)

\({T}_{ij}={\mu }_{0}\left({H}_{i}{h}_{j}+{H}_{j}{h}_{i}-{H}_{k}{h}_{k}{\delta }_{ij}\right),\)

\({t}_{ij}= {C}_{ijkl}{e}_{kl}- {\beta }_{ij}T,\)

\({K}_{ij}{\varphi }_{,ij}= \left(1+\chi {D}_{\chi }\right)\left({\rho C}_{E}\dot{T}+{\beta }_{ij}{T}_{0}{\dot{e}}_{ij}\right),\)

\(T=\varphi -{a}_{ij}{\varphi }_{,ij},\)

Laplace transform

Kaur and Singh [57]

A mathematical model has been formed for a 2-D to study the effect of variable thermal conductivity on TIT homogeneous nonlocal CF beam with 2T involving MDD and E-B beam theory

\({t}_{ij}= {c}_{ijkl}{e}_{kl}- {\beta }_{ij}T\),

\({K}_{ij}{\varphi }_{,ij}= \left(1+\chi {D}_{\chi }\right)\left({\rho C}_{E}\dot{T}+{\beta }_{ij}{T}_{0}{\dot{e}}_{ij}\right)\),

\({K}_{ij}\left(T\right)={K}_{0ij}\left(1+{K}_{i}^{^{\prime}}T\right)={K}_{0ij}\left(1+{K}_{i}^{^{\prime}}\left(\varphi -{a}_{ij}{\varphi }_{,ij}\right)\right),\)

View full size image

Laplace transforms

Lata et al. [56]

Examined the vibration phenomenon in 2D TIT homogeneous E–B nonlocal nanobeam with laser pulse with a new modified three-phase lag (TPL)GN model and Eringen’s nonlocal theory of thermoelasticity. The temperature was assumed to vary sinusoidally

\({\sigma }_{ij}=\left(1-\mu {\nabla }^{2}\right){t}_{ij}= {c}_{ijkl}{e}_{kl}- {\beta }_{ij}T\),

\(\mu ={\left(\tau l\right)}^{2},\tau =\frac{{e}_{0}a}{l}\),

\({\mathcal{L}}_{1}{T}_{,ij}={\mathcal{L}}_{2}\left(\rho {C}_{E}T+{\beta }_{ij}{T}_{0}{e}_{ij}\right)-{\mathcal{L}}_{0}\left(\rho {Q}_{0}\right),\)

Where time differential operators \({\mathcal{L}}_{i}\)(i = 0, 1, 2) are given by

\({\mathcal{L}}_{1}={K}_{ij}\left(1+\sum_{r=1}^{n}\frac{{\left({\tau }_{t}\right)}^{r}}{r!}\frac{{\partial }^{r}}{\partial {t}^{r}}\right)\frac{\partial }{\partial t}+\varepsilon {K}_{ij}^{*}\left(1+\sum_{r=1}^{n}\frac{{\left({\tau }_{v}\right)}^{r}}{r!}\frac{{\partial }^{r}}{\partial {t}^{r}}\right),\)

\(K_{{ij}} \left( {1 + \sum\limits_{{r = 1}}^{n} {\frac{{(\tau _{t} )^{r} }}{{r!}}} \frac{{\partial ^{r} }}{{\partial t^{r} }}} \right)\frac{\partial }{{\partial t}} + K_{{ij}}^{*} \left( {1 + \sum\limits_{{r = 1}}^{n} {\frac{{(\tau _{v} )^{r} }}{{r!}}} \frac{{\partial ^{r} }}{{\partial t^{r} }}} \right)T_{{,ij}}\)

\(= \left( {1 + \sum\limits_{{r = 1}}^{n} {\frac{{(\tau _{q} )^{r} }}{{r!}}} \frac{{\partial ^{r} }}{{\partial t^{r} }}} \right)\frac{\partial }{{\partial t}}\left[ {\frac{\partial }{{\partial t}}\left( {\rho C_{E} T + \beta _{{ij}} T_{0} e_{{ij}} } \right) - \left( {\rho Q_{0} } \right)} \right].\)

View full size image

Laplace transform

Kaur et al. [59]

Examined the vibration phenomenon in 2D TIT homogeneous E–B nanobeam with laser pulse with a new modified TPL GN model. The ends of the nanobeam are considered to be simply supported and temperature is assumed to vary sinusoidally

\({t}_{ij}= {c}_{ijkl}{e}_{kl}- {\beta }_{ij}T,\)

\({{\beta }_{ij}=c}_{ijkl}{\alpha }_{kl}\),

modified TPL-GN heat conduction equation for an anisotropic medium

\({\mathcal{L}}_{1}{T}_{,ij}={\mathcal{L}}_{2}\left(\rho {C}_{E}T+{\beta }_{ij}{T}_{0}{e}_{ij}\right)-{\mathcal{L}}_{0}\left(\rho {\varrho }_{0}\right),\)

TPL G–N III model \((\varepsilon =1,n\ge 1\))

\(K_{{ij}} \left( {1 + \sum\limits_{{r = 1}}^{n} {\frac{{(\tau _{t} )^{r} }}{{r!}}} \frac{{\partial ^{r} }}{{\partial t^{r} }}} \right)\frac{\partial }{{\partial t}} + K_{{ij}}^{*} \left( {1 + \sum\limits_{{r = 1}}^{n} {\frac{{(\tau _{v} )^{r} }}{{r!}}} \frac{{\partial ^{r} }}{{\partial t^{r} }}} \right)T_{{,ij}}\)

\(= \left( {1 + \sum\limits_{{r = 1}}^{n} {\frac{{(\tau _{q} )^{r} }}{{r!}}} \frac{{\partial ^{r} }}{{\partial t^{r} }}} \right)\frac{\partial }{{\partial t}}\left[ {\frac{\partial }{{\partial t}}\left( {\rho C_{E} T + \beta _{{ij}} T_{0} e_{{ij}} } \right) - \left( {\rho Q_{0} } \right)} \right].\)

View full size image

Laplace Transforms

Kaur et al. [39]

Investigated the forced vibrational analysis of Eringen’s nonlocal TIT nanobeam resonators (CC), SS, CS, CF, FF) due to ramp-type heating and time varying exponentially decaying load with MDPL theory of thermoelasticity EB beam theory to depict small-scale effect

\({t}_{ij}-\xi {\nabla }^{2}{t}_{ij}= {c}_{ijkl}{e}_{kl}- {\beta }_{ij}T\),

\(\xi ={\left(a{e}_{0}\right)}^{2},\)

\({K}_{ij}{L}_{\theta }{\varphi }_{,ij}= {L}_{q}\frac{\partial }{\partial t}\left({\beta }_{ij}{T}_{0}{u}_{ij}+{\rho C}_{E}T\right),\)

\({\beta }_{ij}={c}_{ijkl}{\alpha }_{kl}\),

\(T= \varphi -{a}_{ij}{\varphi }_{,ij}\)

View full size image

Laplace Transform

Kaur et al. [40]

Deliberated the Frequency Shift and Thermoelastic Damping in TIT SS nanoscale beam with 2T and GN III theory of thermoelasticity and EB beam theory

\({t}_{ij}= {C}_{ijkl}{e}_{kl}- {\beta }_{ij}T,\)

\(K_{ij} \dot{\varphi }_{,ij} + K_{ij}^{*} \varphi_{,ij} + \rho \dot{Q} = \beta_{ij} T_{0} \ddot{e}_{ij} + \rho C_{E} \ddot{T}\),

\(M\left(x, t\right)=-{\int }_{-\frac{h}{2}}^\frac{h}{2}{\int }_{\frac{-b}{2}}^\frac{b}{2}{t}_{xx}zdzdy= {C}_{11}I\frac{{\partial }^{2}w}{\partial {x}^{2}}+ {\beta }_{1}{M}_{T }\)

View full size image

Laplace transform

Kaur et al. [41]

Studied the 1D piezoelectric materials in particular piezo-thermo-elastic SS nanobeam with two temperatures and Euler Bernoulli theory with small-scale effects using nonlocal Eringen’s theory

Heat conduction equation for an anisotropic piezo-thermoelastic nonlocal medium with two temperature:

\({\sigma }_{ij}=\left(1-\mu {\nabla }^{2}\right){t}_{ij}= {c}_{ijkl}{e}_{kl}-{\epsilon }_{ijk}{E}_{k}- {\beta }_{ij}\left(1+{t}_{1}\frac{\partial }{\partial t}\right)T,\)

\({\beta }_{ij}={c}_{ijkl}{\alpha }_{kl}\),

\(T= \varphi -{a}_{ij}{\varphi }_{,ij}\),

Electric field relation:

\({D}_{i}={\zeta }_{ij}{E}_{j}+{\epsilon }_{ijk}{e}_{jk}+{p}_{i}\left(1+{t}_{1}\frac{\partial }{\partial t}\right)T,\)

where,

\({E}_{i}=-{\phi }_{,i}, \left(i,j,k,l=x,y,z\right),\)

Generalized Heat conduction equation with two temperature and with piezo effect,

\(\begin{aligned} K_{{ij}} \varphi _{{,ij}} = & \rho C_{E} \left( {1 + t_{0} \frac{\partial }{{\partial t}}} \right)\dot{T} \\ & + T_{0} \beta _{{ij}} \left( {1 + n_{1} t_{0} \frac{\partial }{{\partial t}}} \right)\dot{u}_{{i,j}} \\ & - T_{0} p_{i} \left( {1 + n_{1} t_{0} \frac{\partial }{{\partial t}}} \right)\dot{\phi }_{{,i}} \\ & - \left( {1 + n_{1} t_{0} \frac{\partial }{{\partial t}}} \right)\rho Q_{0} \\ \end{aligned}\)

\(\mu ={\left(\tau l\right)}^{2},\tau =\frac{{e}_{0}a}{l}\)

View full size image

Cramer’s rule

Kaur et al. [60]

Studied the impact of the time-harmonic laser pulse on the vibration phenomenon in 2D TIT visco-thermoelastic SS nanobeam with a new modified TPL-GN model

\({t}_{ij}= {c}_{ijkl}{e}_{kl}- {\beta }_{ij}T,\)

\({{\beta }_{ij}=c}_{ijkl}{\alpha }_{kl}\),

modified TPL-GN heat conduction equation for an anisotropic medium

\({\mathcal{L}}_{1}{T}_{,ij}={\mathcal{L}}_{2}\left(\rho {C}_{E}T+{\beta }_{ij}{T}_{0}{e}_{ij}\right)-{\mathcal{L}}_{0}\left(\rho {\varrho }_{0}\right),\)

\({\mathcal{L}}_{1}={K}_{ij}\left(1+\sum_{r=1}^{n}\frac{{\left({\tau }_{t}\right)}^{r}}{r!}\frac{{\partial }^{r}}{\partial {t}^{r}}\right)\frac{\partial }{\partial t}+\varepsilon {K}_{ij}^{*}\left(1+\sum_{r=1}^{n}\frac{{\left({\tau }_{v}\right)}^{r}}{r!}\frac{{\partial }^{r}}{\partial {t}^{r}}\right),\)

\(M\left(x, t\right)=-b{\int }_{-\frac{h}{2}}^\frac{h}{2}{t}_{xx}zdz= {c}_{11}\left(1+{Q}_{1}\frac{\partial }{\partial t}\right)I\frac{{\partial }^{2}w}{\partial {x}^{2}}+ {\beta }_{1}{M}_{T }.\)

\({\varrho }_{0}\left(z\right){e}^{i\omega t}=\frac{{R}_{a}{I}_{0}}{\delta }{e}^{\frac{\left(z-\frac{h}{2}\right)}{\delta }+i\omega t}\)

View full size image

Laplace transform

8 Functionally graded (FG) beam

In past decade, numerous scientific and numerical analyses have been carried out on FG materials to develop micro/nano-devices due to their physical properties. The FG materials has wide varieties of application in the field of shape memory alloy thin films, MEMS/NEMS, and nuclear power microscopes etc.

The thermoelastic vibrations in functionally graded nanobeams (FGNs) caused by periodic heat fluxes were studied using a fractional-order model by Abouelregal and Mohamed [72]. Thermoelastic instability (TEI) of FGM was examined by Mao et al. [73] in presence of frictional heat. A systematic analysis of the bending, buckling, and free vibration of FG beams was presented by Xu and Meng [74] based on E–B theory and refined TBT (Timoshenko beam theory). The FGM was explored by Sheokand et al. [75] using a DPL model with gravity and rotation. Free vibration buckling and stability analysis of FGMs were outlined by Zhang et al. [76]. In generalized thermoelasticity theory, Abo-Dahab et al. [77] discussed FG thin slim strips with one thermal relaxation time. Based on academic publications from the past 30 years, Saleh et al. [78] provide a detailed analysis of the fundamental difficulties faced by current FGM manufacturers and their strengths. A magneto-thermoelastic FGM with initial stress and GN-II theory was examined by Hasona and Adel [79]. Ehyaei et al. [80] investigated the impact of classical and non-classical boundary conditions on the free vibration properties of size-dependent FG nanobeams.

Zhang et al. [81] investigated of the magnetic field produced when tantalum and nickel nanoparticles move toward an elastic surface. Peng and Chen [82] investigated the dynamic thermoelastic response of a micro-scale FGM beam with ramping-type heating using a nonlocal generalised thermoelasticity model. A FG plate with a triangular hole that was being subjected to a uniaxial tensile force was examined by Jafari et al. [83]. Abbas et al. [84] studied wave propagation in unbounded thermoelastic materials based on nonlocal thermoelasticity using Lord and Shulman’s generalised thermoelastic model. The use of nanoparticle-reinforced building materials in civil engineering was researched by Zhang et al. [85]. Said [86] investigated the wave propagation in a nonlocal generalised thermoelastic half-space in the presence of an internal heat source rotating under the impact of rotation. The non-local MT solid with 2T subject to rotation and slanted stresses was explored by Lata and Singh [87]. Abouelregal and Dargail [88] introduced a novel mathematical model for FGN using free kernel function and time delay selection in MDD.

9 Mechanical boundary conditions

Kaur et al. [39] described “the mechanical boundary conditions by considering the ends of the nanobeam are subjected to:

Case I Clamped–clamped \(\left(CC\right)\) or pinned or hinged nanobeam.

At the fixed ends the lateral deflection and the slope of lateral deflection are zero”.

$${\left.w\left(x,t\right)\right|}_{x=\mathrm{0,1}}={\left.\frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x=\mathrm{0,1}}=0.$$
(11)

Case II “Simply supported-simply supported \(\left(SS\right)\) nanobeam.

Here the transverse lateral deflection and bending moment are zero at the ends”.

$${\left.w\left(x,t\right)\right|}_{x=\mathrm{0,1}}={\left.\frac{{\partial }^{2}w\left(x,t\right)}{\partial {x}^{2}}\right|}_{x=\mathrm{0,1}}=0.$$
(12)

Case III “Clamped- simply supported \(\left(CS\right)\) nanobeam.

At the fixed ends the transverse lateral deflection and the slope of lateral deflection are zero and at simply supported end the transverse displacement and bending moment are zero. Boundary conditions can be expressed as follows if the beam is clamped at \(x=0\) and is only supported at \(x=1\).”

$${\left.w\left(x,t\right)\right|}_{x=\mathrm{0,1}}={\left.\frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x=0}={\left.\frac{{\partial }^{2}w\left(x,t\right)}{\partial {x}^{2}}\right|}_{x=1}0.$$
(13)

Case IV “Clamped-free \(\left(CF\right)\)/cantilever nanobeam.

The bending moment and shear force are zero at the free end and at the fixed ends the transverse lateral deflection and the slope of displacement are zero. If the nanobeam is fixed at x = 0 and free at x = 1, then the boundary conditions are”:

$${\left.w\left(x,t\right)\right|}_{x=0}={\left.\frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x=0}={\left.\frac{{\partial }^{2}w\left(x,t\right)}{\partial {x}^{2}}\right|}_{x=1}={\left.\frac{{\partial }^{3}w\left(x,t\right)}{\partial {x}^{3}}\right|}_{x=1}0.$$
(14)

Case V “Free–free \(\left(FF\right)\) nanobeam.

The bending moment and shear force are zero at the ends in this case”.

$${\left.\frac{{\partial }^{2}w\left(x,t\right)}{\partial {x}^{2}}\right|}_{x=\mathrm{0,1}}={\left.\frac{{\partial }^{3}w\left(x,t\right)}{\partial {x}^{3}}\right|}_{x=\mathrm{0,1}}=0.$$
(15)

10 Thermal boundary conditions

Kaur et al. [39] considered “that the nanobeam is thermally loaded on the boundary \(x=0.\)

$$\Theta \left(x,t\right)={\theta }_{0}f\left(x,t\right) \, on \, x=0,$$
(16)

where \({\theta }_{0}\) is a constant and \(f\left(x,t\right)\) is a ramp type function given by:

$${\left.f\left(x,t\right)\right|}_{x=0}=\left\{\begin{array}{c}0 \, for \, t\le 0\\ \frac{t}{{t}_{0}} \, for \, 0\le t\le {t}_{0}\\ 1 \, for \, t>{t}_{0}\end{array}\right.,$$
(17)

where, \(t_{0}\) is ramp type parameter. The temperature at the boundary x = 1 is given by:”

$${\left.\frac{\partial \Theta \left(x,t\right)}{\partial x}\right|}_{x=1}=0.$$
(18)

11 Conclusions

An extensive set of recent research works has been presented in this review. In general, this review includes theories, formulations, and methods for solving equations for various geometries and loadings.

  • Based on the review, the phase-lag parameter has the primary role in the vibration phenomenon in 2D transversely isotropic homogeneous Euler–Bernoulli nonlocal nanobeam. A numerical inversion technique has been used to find the solutions in the physical domain. The exact solutions of non-dimensional lateral deflection, thermal moment, thermoelastic damping and frequency shifts in the nanoscale beam have been derived. With different combinations of thermoelastic theories with TPL, the position of the attenuation peak will be altered and the amplitude of the attenuation peak will also change, which makes the MPL theory more flexible for simulating the actual thermoelastic response.

  • For the nano/micro-technology applications, E–B theory with nonlocal theory gives the better results as compared to Simple E–B theory.

  • When high-rate heating with short-pulse laser is used on nano/micro-scale devices, it is better to choose the phase lag theories combined with the E–B theory of beam. Moreover, The MDD provides the better results as compared to the fractional order derivative because it describes the variation of a system in which the present change rate depends on its past state.

  • According to a comparison of the recent research, numerical solutions are more appropriate than analytical solutions for studies involving more nonlinear semesters, and, conversely, analytical solutions are most appropriate and practical for problems with memory-dependent derivatives in integral form.

  • This review may be an invaluable resource for further study for visco-thermoelastic materials, micropolar, micro-stretch, magneto-thermoelastic materials, semiconductor materials, isotropic, orthotropic materials, fibre-reinforced materials, composite materials, non-local thermoelastic materials, monoclinic, crystalline materials, materials with cubic symmetry, nanomaterials, piezo-electric and piezo-thermoelastic materials. The governing equations of these models can be solved analytically as well as numerically to obtain expressions for displacement, stress, strain etc. by using various other methods like Normal mode analysis, complex analysis (integral using residue at poles etc.), state space approach, fractal calculus and Eigen value approach. The above basic models can also be extended in spherical coordinates. The technological benefits of such models have begun to be identified and, demonstrators are under construction for a wide range of applications in sensitive industries such as MEMS/NEMS, sensors, resonators. In many of these applications, the analyses of such systems have yet to be fully demonstrated.