Abstract
Digital marketing technology can not only help enterprises effectively control marketing costs but also accurately identify target customers and determine customer needs to improve marketing conversion rates. Multiple conflicting and asymmetric criteria need to be taken simultaneously into account to effectively assess digital marketing technology. Accordingly, the target of our paper is to propound an enhanced additive ratio assessment (ARAS) methodology to aid experts in evaluating digital marketing technology in a complex uncertain setting. The spherical fuzzy (SF) set is an expansion of the picture fuzzy set (PFS) that has been recognized as a powerful model to portray indeterminacy and vagueness. A fresh score function is proffered to compare the SF numbers and its merits are also analyzed. Then, some novel operations for SF numbers are defined and several aggregation operators based on them are propounded. Further, a mixed multi-criteria group decision-making (MCGDM) method is developed by incorporating the method based on the removal effects of criteria (MEREC), step-wise weight assessment ratio analysis (SWARA), and enhanced ARAS approach under SF information. Also, a case concerning digital marketing technology evaluation is executed to prove the efficiency and practicability of the presented SF-MEREC–SWARA–ARAS method. Finally, contrast and sensitivity investigations are also implemented to highlight the strengths and robustness of the proffered methodology, respectively.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The remarkable development of digital technology has made digitalization piecemeal popular in all aspects of human life. As a new marketing model, digital marketing is a way to further improve the efficiency of marketing drawing support from computer communication technology and digital interactive media [1,2,3]. Digital marketing can not only quickly open new markets for companies but also tap into the needs of consumers at a deeper level. However, in the face of the many intelligent technologies available on the Internet, it is vital to choose the most satisfactory digital marketing technology for the development of a company’s digital marketing model [4,5,6,7]. Therefore, digital marketing technology evaluation is crucial for enterprises to improve their core competitiveness in the era of data empowerment.
To evaluate digital marketing technology, we need to consider a set of valuable Internet technologies concerning diverse criteria. Digital marketing technology evaluation is regarded as a typical multi-criteria decision-making (MCDM) problem that thinks over the criteria of several assaults and dissymmetric simultaneously. However, with the increasing sophistication of the decision environment, it is hard for experts to identify an ideal digital marketing technology based on criteria from different properties and various rates. To treat the aforementioned problem with uncertainty, a lot of theories such as fuzzy sets [8], intuitionistic fuzzy sets [9], rough sets [10], and soft sets [11] are put forward to deal with this kind of MCDM problems. In addition, several novel extension theories like interval-valued IFS [12], PFS [13], and SF set [14] are propounded to apply in diverse domains [15,16,17].
As an innovative information representation model, SF set modes the uncertainty from three perspectives, including positive, neutral, and negative membership degrees, and provides a larger range for experts to express opinions. Recently, the theory of SF set has been viewed as a worthy manner to portray impreciseness and vagueness in various MCDM problems [18,19,20]. Because of its efficiency and extensive practicality, many researchers and scholars have set up diverse decision methodologies and lots of theory research, such as information fusion, information measures, and score functions [21,22,23,24]. Apart from these results, Chinram et al. [25] proposed several novel spherical fuzzy Yager operators and constructed a decision algorithm based on them to select the optimal wind power plant location. Gundogdu and Kahraman [26] combined SF set and quality function deployment to deal with the problem of linear delta robot technology design and evaluation. Akram et al. [27] introduced a novel PROMETHEE-based outranking approach under a spherical fuzzy context. Wang et al. [28] propounded an SF sort algorithm via regret theory for the application of moving high-tech manufacturing. Wang et al. [29] suggest a fresh Fine–Kinney risk assessment framework based on complex SFSs and the CRADIS approach for the appraisal of natural gas pipeline construction. Further, Zhang et al. [30] suggested a CPT-TODIM method to portray the psychological behavior of experts during the MCDM process. They computed weights using the CRITIC method within SF settings. More research can be referred to in the literature [31,32,33,34,35].
In recent years, different types of decision methodologies have been widely applied to practical decision analysis under diverse situations. However, the solution to practical decision problems still presents certain challenges due to factors, such as the complexity of the decision environment and human perception. Criteria and their importance are observed as indispensable concepts for experts to provide reliable assessment information in the MCDM process [36]. In most cases, it is assumed that criterion weights are given directly by the assessor or are considered equally important, which leads to inconsistent decision results. In the existing literature, the determination of criterion weights is usually divided into subjective weights, objective weights, and composite weights [37]. Recently, Keshavarz-Ghorabaee et al. [38] proposed a fresh objective weight determination called the MEREC method, which determined the importance of a criterion by measuring the absolute deviation between the assessed value of each criterion removed from the schemes and the assessed value of all criteria. The core idea is that the higher the weight of a criterion, the greater its impact when removed in all cases. Since then, the MEREC has been successively applied to different fuzzy environments to determine the importance of criteria [39]. Furthermore, the SWARA method is a powerful weight-determination method that determines the subjective weight of a criterion by comparing the importance coefficients between the criteria [40]. It has also been adopted to solve various complex decision analyses in different uncertain environments due to its simplicity and ease of operation, as well as its ability to better manifest the subjective appraise of experts on the criteria [41, 42]. At present, there has been no research to merge the MEREC and SWARA methods in the SFS setting. Hence, the union of MEREC and SWARA models is employed for weight identification in this study.
Recent investigations show that many classical decision algorithms are applied or extended to spherical fuzzy circumstances for finding an optimal (satisfied) scheme effectively in realistic decision problems. The above different decision methods are suitable for solving different complicated situations and have different advantages and disadvantages during decision analysis. In addition, the additive ratio assessment (ARAS) method was originated by Zavadskas and Turskis in 2010 [43]. ARAS is observed as an effective model for tackling complex decision analysis. The core aim of the ARAS model is to select the optimal option from a collection of schemes based on a number of criteria. The ultimate priority of candidates is ascertained by working out the utility degree of each candidate [44]. Based on the existing research about ARAS methodologies, it can be concluded that the ARAS method possesses the following merits: (1) it can deal with complicated decision problems with high complexity; (2) it is a compensatory approach to directly obtain the final utility ratio between the weighted assessment and the optimal evaluation; (3) it has the advantages of the simple calculation process, easy operation, and high robustness for solving MCDM problems. Owing to these merits in dealing with MCDM problems, a multitude of achievements has been developed by scholars to strengthen the efficiency and fidelity of ARAS methodology in different uncertain circumstances to address diverse problems [45,46,47,48]. Besides, Jin et al. [49] presented an expanded ARAS method based on FMEA under interval-valued q-rung orthopair fuzzy circumstances for developing risk analysis. Mishra et al. [50] construct a novel single-valued neutrosophic ARAS methodology via a novel similarity measure for the selection of electric vehicle charging stations. Mishra et al. [51] introduced an integrated assessment framework with the aid of a novel Pythagorean fuzzy similarity measure and ARAS model for evaluating the sustainable biomass crop. To model the cognition of experts by linguistic model, Teng and Shen [52] proposed a new MCGDM method based on the SWARA and ARAS approaches with unbalanced double hierarchy linguistic information. Further, the ARAS approach was applied to different applications to highlight its superiority in decision analysis [53,54,55].
With the help of the mentioned discussions and literature overview investigations, it is evident that SFSs are regarded as an efficient, powerful, and energetic tool to treat the impreciseness and ambiguity in the aspect of information representation. The emergence of the SF set can provide more advantageous methods to support the solution of uncertain decision problem analysis. Thus, the intention for this paper can be concluded as follows:
-
SF set-based decision methodology offers an effective model to deal with decision analysis by enlarging the range of three elements as compared to PFS. Therefore, it is crucial to focus on the construction of decision models within the SF set setting.
-
The score function is an essential theory for building uncertain decision methodology. Unfortunately, the extant score functions of the SF set possess some defects, which shall cause unreasonable results in making decisions. To conquer the above shortcomings, it is necessary to explore a novel score function to improve the reasonability when comparing spherical fuzzy numbers (SFNs).
-
The combined weights of assessment criteria can think about both objective influences from decision data and subjective judgments from expert knowledge and experience, so that computing the combined weights of the criteria can effectively improve the quality of decisions.
-
As a simple and easy-operate decision algorithm, the ARAS method prioritizes a set of schemes based on the utility degree theory. Thus, the combination of ARAS and SF sets produces a stronger MCDM approach than the extant ones.
By means of the mentioned discussions and motivations, the target of this study is to offer a hybrid SF information-based MCGDM methodology for the assessment of digital marketing technologies. The proposed hybrid methodology is constructed by incorporating the MEREC, SWARA, and enhanced ARAS methods under an SF environment. The involved methods are all improved by the novel score function and aggregation operators. Hence, the presented SF-MEREC–SWARA–ARAS method is an innovative group decision framework for experts to unfold decisions within an uncertain context. Consequently, the novelty and contributions of this paper are displayed as follows:
-
A fresh score function is presented to enhance the reasonability of SFN comparison, and the associated properties and strengths of it are also explored and analyzed severally.
-
Some novel operations are propounded and four novel aggregation operators, such as tangent spherical fuzzy weighted averaging (TSFWA) and tangent spherical fuzzy weighted geometric (TSFWG) operators, and their ordered weighted definitions are presented.
-
A fused criteria-weighted determination model based on the improved SF-MEREC and SF-SWARA methods is built for ascertaining the importance of criteria.
-
An enhanced ARAS group decision methodology is presented with the aid of the score function and TSFWA operator to obtain the ranking of schemes.
-
The case study which uses the proposed SF-MEREC–SWARA–ARAS approach to assess digital marketing technology is implemented to validate its effectiveness and usefulness. Comparison and sensitivity investigations are also performed to analyze the advantage and robustness of the proffered methodology.
To achieve the mentioned aims and contributions, other sections of the current study are planned as below: we briefly look back at several basic conceptions of SFS in Sect. 2. Then, a novel spherical fuzzy score function and its superiority analysis are presented in Sect. 3. In Sect. 4, several newly operational laws for SFSs are defined and a series of novel aggregation operators are propounded to fuse the uncertain information. A hybrid MCGDM decision methodology called SF- MEREC–SWARA–ARAS is presented to apply the developed score function and operators in Sect. 5. Then, a practical case of digital marketing technology assessment is given in Sect. 6 to expound on the practicability and feasibility of the proposed approach. In addition, we also compare and analyze the distinctions between different spherical fuzzy methods. Finally, the conclusions are summed up in the end.
2 Preliminaries
This section schematically retrospects some fundamental notions of SFS and score functions.
2.1 SFS
Definition 1
[14, 21]. It is supposed that \(\wp\) be a universal set. An SFS \(\Upsilon\) on \(X\) is expressed as
wherein \(\phi_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right):\;\wp \to \left[ {0,1} \right]\),\(\varphi_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right):\;\wp \to \left[ {0,1} \right]\) and \(\kappa_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right):\;\wp \to \left[ {0,1} \right]\) stand for the positive, neutral, and negative membership degrees of the element \({ \mathchar'26\mkern-10mu\lambda} \in \wp\) to \(\Upsilon\), which fulfills the condition that \(0 \le \left( {\phi_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right)} \right)^{2} + \left( {\varphi_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right)} \right)^{2} + \left( {\kappa_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right)} \right)^{2} \le 1\) for all \({ \mathchar'26\mkern-10mu\lambda} \in \wp\). The refusal grade is indicated as \(\delta_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right) = \sqrt {1 - \left( {\left( {\phi_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right)} \right)^{2} + \left( {\varphi_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right)} \right)^{2} + \left( {\kappa_{\Upsilon } \left( { \mathchar'26\mkern-10mu\lambda} \right)} \right)^{2} } \right)}\). For the sake of simplicity, \(\Upsilon = \left( {\phi ,\varphi ,\kappa } \right)\) is called SFN.
Definition 2
[21] Suppose that \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1,2)\), then one has the following:
-
(1)
\(\Upsilon_{1} = \Upsilon_{2}\) iff \(\phi_{1} = \phi_{2} ,\varphi_{1} = \varphi_{2} ,\kappa_{1} = \kappa_{2}\);
-
(2)
\(\Upsilon_{1} \cap \Upsilon_{2} = \left( {\min \left\{ {\phi_{1} ,\phi_{2} } \right\},\min \left\{ {\varphi_{1} ,\varphi_{2} } \right\},\max \left\{ {\kappa_{1} ,\kappa_{2} } \right\}} \right)\);
-
(3)
\(\Upsilon_{1} \cup \Upsilon_{2} = \left( {\max \left\{ {\phi_{1} ,\phi_{2} } \right\},\min \left\{ {\varphi_{1} ,\varphi_{2} } \right\},\min \left\{ {\kappa_{1} ,\kappa_{2} } \right\}} \right)\);
-
(4)
\(\Upsilon^{c} = \left( {\phi ,\varphi ,\kappa } \right)\).
Definition 3
[21]. For two SFNs \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1,2)\), then the comparison laws defined based on the score function \(S\) and accuracy function \(A\) are expressed as follows:
-
(1)
If \(S\left( {\Upsilon_{1} } \right) > S\left( {\Upsilon_{2} } \right)\), then \(\Upsilon_{1} \succ \Upsilon_{2}\)
-
(2)
If \(S\left( {\Upsilon_{1} } \right) = S\left( {\Upsilon_{2} } \right)\) and \(A\left( {\Upsilon_{1} } \right) < A\left( {\Upsilon_{2} } \right)\), then \(\Upsilon_{1} \prec \Upsilon_{2}\)
-
(3)
If \(S\left( {\Upsilon_{1} } \right) = S\left( {\Upsilon_{2} } \right)\) and \(A\left( {\Upsilon_{1} } \right) = A\left( {\Upsilon_{2} } \right)\), then \(\Upsilon_{1} \sim \Upsilon_{2} .\)
2.2 The Priori Spherical Fuzzy Score Functions
A score function is a crucial tool for comparing the SFNs and obtaining the order relation of SFNs. In this subsection, we first review some existing spherical fuzzy score function in reference [14, 21], and then analyze their defects by some numerical examples. It is supposed that \(\Upsilon = \left( {\phi ,\varphi ,\kappa } \right)\) be an SFN. The extant score functions for SFN are illustrated below:
-
1.
The score and accuracy functions proposed by Mahmood et al. [14] and Ashraf et al. [21]:
$$ S_{1} \left( \Upsilon \right) = \phi^{2} - \kappa^{2} , $$$$ H_{1} \left( \Upsilon \right) = \phi^{2} + \varphi^{2} + \kappa^{2} . $$ -
2.
The score function defined by Ashraf and Abdullah [22]:
$$ S_{2} \left( \Upsilon \right) = \frac{1}{3}\left( {2 + \phi - \varphi - \kappa } \right). $$ -
3.
The score and accuracy functions proposed by Chinram et al. [25]:
$$ S_{3} \left( \Upsilon \right) = \frac{1}{3}\left( {2 + \phi^{2} - \varphi^{2} - \kappa^{2} } \right). $$ -
4.
The score function proposed by Gündoǧdu and Kahraman [24]:
$$ S_{4} \left( \Upsilon \right) = \left( {\phi - \kappa } \right)^{2} - \left( {\varphi - \kappa } \right)^{2} . $$
3 A Novel Spherical Fuzzy Score Function
This section first analyzes the shortcomings of the prior score functions and then propounds an innovative score function for the SF set with the help of ponding the refusal grade information.
3.1 Shortcomings Analysis for the Priori Spherical Fuzzy Score Functions
The extant SF score and accuracy functions can compare SFNs and obtain the corresponding order relations. Nevertheless, the mentioned score functions have several shortcomings that obtain the unreasonable ranking in comparing and ranking the SFNs in several cases. Some examples are provided to demonstrate the irrational situation.
Example 1.
Let \(\Upsilon_{1} = \left( {0.3,0.5,0.3} \right)\) and \(\Upsilon_{2} = \left( {0.6,0.5,0.6} \right)\) be two SFNs. Then, we can obtain that the calculation outcomes are expressed as \(S_{1} \left( {\Upsilon_{1} } \right) = S_{1} \left( {\Upsilon_{2} } \right)\), \(S_{2} \left( {\Upsilon_{1} } \right) = S_{2} \left( {\Upsilon_{2} } \right)\) and \(S_{3} \left( {\Upsilon_{1} } \right) = S_{3} \left( {\Upsilon_{2} } \right)\), which shows that the score functions proposed in reference [14, 21, 22, 25] fail to distinguish the SFNs \(\Upsilon_{1}\) and \(\Upsilon_{2}\).
Example 2.
Let \(\Upsilon_{1} = \left( {0.6,0.6,0} \right)\) and \(\Upsilon_{2} = \left( {0.5,0.5,0} \right)\) be two SFNs. Then, we can acquire that the calculation results are expressed as \(S_{2} \left( {\Upsilon_{1} } \right) = S_{2} \left( {\Upsilon_{2} } \right)\), \(S_{3} \left( {\Upsilon_{1} } \right) = S_{3} \left( {\Upsilon_{2} } \right)\), and \(S_{4} \left( {\Upsilon_{1} } \right) = S_{4} \left( {\Upsilon_{2} } \right)\), which shows that the score function proposed in reference [22, 24, 25] fails to distinguish the SFNs \(\Upsilon_{1}\) and \(\Upsilon_{2}\).
Example 3.
Let \(\Upsilon_{1} = \left( {0.3,0,0.3} \right)\) and \(\Upsilon_{2} = \left( {0.2,0,0.2} \right)\) be two SFNs. Then, we can attain that the score values of \(\Upsilon_{1}\) and \(\Upsilon_{2}\) are \(S_{1} \left( {\Upsilon_{1} } \right) = S_{1} \left( {\Upsilon_{2} } \right)\), \(S_{2} \left( {\Upsilon_{1} } \right) = S_{2} \left( {\Upsilon_{2} } \right)\) and \(S_{3} \left( {\Upsilon_{1} } \right) = S_{3} \left( {\Upsilon_{2} } \right)\), which means that the score function proposed in reference [14, 21, 22, 25] cannot compare them. Furthermore, we further compare the accuracy value of \(\Upsilon_{1}\) and \(\Upsilon_{2}\) displayed as \(H_{1} \left( {\Upsilon_{1} } \right) > H_{1} \left( {\Upsilon_{2} } \right)\), namely, \(\Upsilon_{1} \succ \Upsilon_{2}\). While, the order of \(\Upsilon_{1}\) and \(\Upsilon_{2}\) determined by score functions \(S_{4}\) is \(\Upsilon_{1} \prec \Upsilon_{2}\), which they obtain the counterintuitive outcomes.
Example 4.
Let \(\Upsilon_{1} = \left( {0.3,0.2,0.4} \right)\) and \(\Upsilon_{2} = \left( {0.3,0.3,0.3} \right)\) be two SFNs. Then, we can acquire that the calculation results are expressed as \(S_{2} \left( {\Upsilon_{1} } \right) = S_{2} \left( {\Upsilon_{2} } \right)\) which shows that the score function proposed in reference [22] fails to distinguish the SFNs \(\Upsilon_{1}\) and \(\Upsilon_{2}\).
In light of the aforementioned discussion, we will put forward an innovative spherical fuzzy score function to conquer the deficiencies in the previous works and attain a more reasonable ranking of SFNs.
3.2 New Score Function
This subsection shall propose a novel spherical fuzzy score function and discuss it valuable properties and superiorities.
Definition 4.
Given an SFN \(\Upsilon = \left( {\phi ,\varphi ,\kappa } \right)\), a fresh score function \( \overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\) is propounded as
Theorem 1.
The propounded score function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\) of SFN \(\Upsilon = \left( {\phi ,\varphi ,\kappa } \right)\) increases monotonically with \(\phi\) and decreases monotonically with \(\phi\) and \(\kappa\).
Proof.
In view of Eq. (2), we first obtain the partial derivative of the developed score function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\) with \(\phi\) as
Homoplastically, we also derive the partial derivative of the developed score function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\) with \(\varphi\) and \(\kappa\) as
Accordingly, the theorem is proved.
Theorem 2.
Given an SFN \(\Upsilon = \left( {\phi ,\varphi ,\kappa } \right)\), the proposed score function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\) obeys the following axioms.
(P1) \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\) iff \(\Upsilon = \left( {1,0,0} \right);\)
(P2) \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\) iff \(\Upsilon = \left( {0,0,1} \right);\)
(P3) \(0 \le \overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right) \le 1.\)
Proof.
Based on the monotonicity of the advanced score function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\), we can obtain that \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\) possesses the maximum and minimum values when \(\Upsilon = \left( {1,0,0} \right)\) and \(\Upsilon = \left( {0,0,1} \right)\), severally. Consequently, we have \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)_{\max } = 1\) and \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)_{\min } = 0\). Accordingly, the proof is achieved.
We shall recompute Examples 1–4 with the novel score function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( \Upsilon \right)\) to test its effectiveness, efficiency, and feasibility. The comparison outcomes between the existing works and the novel score function are displayed in Table 1.
In Table 1, we utilize the proposed score function to compute Examples 1–4 and further summarize the computation outcomes acquired by the existing score function \(S_{1} ,S_{2} ,S_{3} ,S_{4}\) and \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}\). From Example 1, the score functions \(S_{1} ,S_{2} ,S_{3}\) fail to compare these two SFNs, while the outcome obtained by the proposed score function \( \overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \) is the same as the score function \(S_{4}\) and \(H_{1}\), which shows the reasonability of the presented score function. From Example 2, the score functions \(S_{2} ,S_{3} ,S_{4}\) fail to compare these two SFNs, while the outcome via the score function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}\) is the same as the score function \(S_{1}\), which shows the rationality of the score function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}\). From Example 3, we can note that the score function \(S_{1} ,S_{2} ,S_{3}\) fails to compare SFNs \(\Upsilon_{1}\) and \(\Upsilon_{2}\), and the score function \(S_{4}\) obtains the counterintuitive outcome. Further, the order of \(\Upsilon_{1}\) and \(\Upsilon_{2}\) determined by \(H_{2}\) is \(\Upsilon_{1} \succ \Upsilon_{2}\), which is the same as using the accuracy function \(H_{1}\) and \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}\), which also proves the superiority of the novel score function. From Example 4, the score function \(S_{2}\) cannot determine the order of these two SFNs, while the order of SFNs \(\Upsilon_{1}\) and \(\Upsilon_{2}\) identified by the novel function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}\) is the same with \(S_{1} ,S_{3} ,S_{4}\), which confirms the superiority of the proposed novel function \(\overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}\) in distinguishing SFNs.
4 Novel Spherical Fuzzy Aggregation Operators
This section first defines some novel operations for SFNs based on the tangential functions. Then, four improved spherical fuzzy aggregation operators via novel operations are propounded, as well as the associated properties of these operators are studied.
4.1 Novel Operations for SFNs
The aggregation operator is one of the important tools to effectively fuse uncertain information. To achieve the goal of spherical fuzzy aggregation, many operations based on the Archimedean t-norm and t-norms are defined to propose different aggregation operators. Inspired by the work of Rani and Garg [56], this part defined some novel operations of SFNs on the basis of the trigonometric tangent function to enrich the theory of spherical fuzzy integration operators.
Definition 5.
Let \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1,2)\) be two SFNs. Then, the novel operations of SFNs based on the trigonometric tangent function are defined as follows:
-
(1)
\(\Upsilon_{1} \oplus \Upsilon_{2} = \left( {\widetilde{a}\left( {\phi_{1} ,\phi_{2} } \right),\widetilde{b}\left( {\varphi_{1} ,\varphi_{2} } \right),\widetilde{b}\left( {\kappa_{1} ,\kappa_{2} } \right)} \right),\)
-
(2)
\(\Upsilon_{1} \otimes \Upsilon_{2} = \left( {\widetilde{b}\left( {\phi_{1} ,\phi_{2} } \right),\widetilde{a}\left( {\varphi_{1} ,\varphi_{2} } \right),\widetilde{a}\left( {\kappa_{1} ,\kappa_{2} } \right)} \right),\)
where \(\widetilde{a}\left( {x,y} \right)\) and \(\widetilde{b}\left( {x,y} \right)\) are the tangent generation function in reference [56].
The novel operational laws of SFNs using the tangent function are defined as follows.
Definition 6.
Let \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1,2)\) be two SFNs. The following operational laws of two SFNs are defined as:
Theorem 3.
Suppose that \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1,2)\), \(\Upsilon_{1} \oplus \Upsilon_{2}\) and \(\Upsilon_{1} \otimes \Upsilon_{2}\) are also SFN.
Proof.
Based on the definition of SFS, we can easily prove that the results of \(\Upsilon_{1} \oplus \Upsilon_{2}\) and \(\Upsilon_{1} \otimes \Upsilon_{2}\) are SFN.
Theorem 3.
For three SFNs \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1,2,3)\). Then
-
(1)
\(\Upsilon_{1} \oplus \Upsilon_{2} = \Upsilon_{2} \oplus \Upsilon_{1} ;\)
-
(2)
\(\Upsilon_{1} \otimes \Upsilon_{2} = \Upsilon_{2} \otimes \Upsilon_{1} ;\)
-
(3)
\(\Upsilon_{1} \oplus \left( {\Upsilon_{2} \oplus \Upsilon_{3} } \right) = \left( {\Upsilon_{1} \oplus \Upsilon_{2} } \right) \oplus \Upsilon_{3} ;\)
-
(4)
\(\Upsilon_{1} \otimes \left( {\Upsilon_{2} \otimes \Upsilon_{3} } \right) = \left( {\Upsilon_{1} \otimes \Upsilon_{2} } \right) \otimes \Upsilon_{3} .\)
Proof.
It is trivial.
In light of the addition and multiplication operations of SFNs in Definition 6, we can obtain the following theorems.
Theorem 4.
For an SFN \(\Upsilon = \left( {\phi ,\varphi ,\kappa } \right)\) and a real number \(\alpha\), one has
Proof.
It can be proved by mathematical induction easily, it is omitted here.
Theorem 5.
For an SFN \(\Upsilon = \left( {\phi ,\varphi ,\kappa } \right)\) and a real number \(\alpha\), one has
Proof.
The proof is similar to Theorem 4.
In view of Theorem 4 and 5, we can derive the scalar multiplication and power operations of SFN in the following.
Definition 7.
For an SFN \(\Upsilon = \left( {\phi ,\varphi ,\kappa } \right)\) and a real number \(\alpha\), we have
Theorem 6.
Ponder two SFNs \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1,2)\), and real numbers \(\alpha ,\alpha_{1} ,\alpha_{2} > 0\), one has
-
(1)
\(\alpha \left( {\Upsilon_{1} \oplus \Upsilon_{2} } \right) = \alpha \Upsilon_{1} \oplus \alpha \Upsilon_{2} ;\)
-
(2)
\(\left( {\Upsilon_{1} \otimes \Upsilon_{2} } \right)^{\alpha } = \left( {\Upsilon_{2} } \right)^{\alpha } \otimes \left( {\Upsilon_{1} } \right)^{\alpha } ;\)
-
(3)
\(\left( {\alpha_{1} + \alpha_{2} } \right)\Upsilon_{1} = \alpha_{1} \Upsilon_{1} \oplus \alpha_{2} \Upsilon_{1} ;\)
-
(4)
\(\left( {\Upsilon_{1} } \right)^{{\left( {\alpha_{1} + \alpha_{2} } \right)}} = \left( {\Upsilon_{1} } \right)^{{\alpha_{1} }} \otimes \left( {\Upsilon_{1} } \right)^{{\alpha_{2} }} .\)
Proof.
It is trivial.
4.2 New Propounded Aggregation Operators
This subsection will put forward several tangent aggregation operators of SFNs, including the TSFWA operator, TSFWG operator, TSFOWA operator, and TSFOWG operator. Let \(\Delta\) denotes the set of SFNs.
Definition 8.
It is assumed that \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1\left( 1 \right)n)\) signifies a family of SFNs and \(\omega_{t}\) is the weight of \(\Upsilon_{t}\) such that \(\sum\nolimits_{t = 1}^{n} {\omega_{t} = 1}\) with \(\omega_{t} \in \left[ {0,\,\,1} \right].\) Then, the TSFWA operator is a mapping \(TSFWA:\Delta^{n} \to \Delta\), defined as
Theorem 7.
The fusion outcome of “\(n\)” SFNs \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)\) acquired with the TSFWA operator is also an SFN and expressed as
Proof.
It is omitted here. since it can be proved by mathematical induction easily.
Several worthwhile properties of the TSFWA operator are discussed below.
Proposition 1
(Idempotency Property) Suppose that \(\Upsilon_{0}\) be an SFN. If \(\Upsilon_{t} = \Upsilon_{0}\) for each \(t\). Then
Proof.
Since \(\Upsilon_{t} = \Upsilon_{0}\) for each \(t\), then
Accordingly, \(TSFWA\left( {\Upsilon_{1} ,\Upsilon_{2} , \ldots ,\,\Upsilon_{n} } \right) = \Upsilon_{0}\) holds.
Proposition 2
(Monotonicity Property) Let \(\Upsilon_{t}\) and \(\widetilde{\Upsilon }_{t} \left( {t = 1\left( 1 \right)n} \right)\) be two collections of SFNs. If \(\phi_{t} \ge \widetilde{\phi }_{t} ,\varphi_{t} \ge \widetilde{\varphi }_{t} ,\kappa_{t} \ge \widetilde{\kappa }_{t}\) for all \(t\). Then, we have
Proof.
As far as
and
As \(\phi_{t} \ge \widetilde{\phi }_{t} ,\varphi_{t} \ge \widetilde{\varphi }_{t} ,\kappa_{t} \ge \widetilde{\kappa }_{t}\), then \(TSFWA\left( {\Upsilon_{1} ,\Upsilon_{2} , \ldots ,\,\Upsilon_{n} } \right) \ge TSFWA\left( {\widetilde{\Upsilon }_{1} ,\widetilde{\Upsilon }_{2} , \ldots ,\widetilde{\Upsilon }_{n} } \right)\) always holds.
Proposition 3.
(Boundedness Property) Suppose that \(\Upsilon^{ + }\) and \(\Upsilon^{ - }\) be the lower and upper bounds of “\(n\)” SFNs \(\Upsilon_{t}\). Then, we have
Proof.
Based on the monotonicity and idempotency properties of the TSFWA operator, we have the following:
Consequently, \(\Upsilon^{ - } \le TSFWA\left( {\Upsilon_{1} ,\Upsilon_{2} , \ldots ,\,\Upsilon_{n} } \right) \le \Upsilon^{ + }\) holds.
Proposition 4.
(Commutativity Property) Let \(\Upsilon_{t}\) and \(\widetilde{\Upsilon }_{t} \left( {t = 1\left( 1 \right)n} \right)\) be two sets of SFNs. If \(\left( {\widetilde{\Upsilon }_{1} ,\widetilde{\Upsilon }_{2} , \ldots ,\widetilde{\Upsilon }_{n} } \right)\) is any permutation of \(\left( {\Upsilon_{1} ,\Upsilon_{2} , \ldots ,\,\Upsilon_{n} } \right)\). Then
Proof.
As we all know that
\(TSFWA\left( {\widetilde{\Upsilon }_{1} ,\widetilde{\Upsilon }_{2} , \ldots ,\,\widetilde{\Upsilon }_{n} } \right) = \omega_{1} \widetilde{\Upsilon }_{1} \oplus \omega_{2} \widetilde{\Upsilon }_{2} \oplus \cdots \oplus \omega_{n} \widetilde{\Upsilon }_{n}\).
Since \(\left( {\widetilde{\Upsilon }_{1} ,\widetilde{\Upsilon }_{2} , \ldots ,\widetilde{\Upsilon }_{n} } \right)\) is any permutation of \(\left( {\Upsilon_{1} ,\Upsilon_{2} , \ldots ,\,\Upsilon_{n} } \right)\), hence the commutativity property for the TSFWA operator is always true.
Definition 10.
It is assumed that \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1\left( 1 \right)n)\) signifies a family of SFNs and \(\omega_{t}\) is the weight of \(\Upsilon_{t}\), such that \(\sum\nolimits_{t = 1}^{n} {\omega_{t} = 1}\) and \(\omega_{t} \in \left[ {0,\,\,1} \right].\) Then, the tangent spherical fuzzy ordered weighted averaging (TSFOWA) operator is a mapping \(TSFOWA:\Delta^{n} \to \Delta\), defined as
where \(\left( {o\left( 1 \right),o\left( 2 \right), \cdots ,o\left( n \right)} \right)\) is an arrangement of \(\left( {1,2, \ldots ,n} \right)\), such that \(\Upsilon_{{o\left( {j - 1} \right)}} \ge \Upsilon_{o\left( j \right)}\) for every \(j = 2,3, \cdots ,n\).
Theorem 8.
The fusion outcome of “\(n\)” SFNs \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)\) acquired via employing the TSFOWA operator is also an SFN represented as
Proof.
Similar to Theorem 6.
The TSFOWA operator also possesses similar propositions to the TSFWA operator, so its introductions and proofs are omitted here. In the following, the weighted geometric operators based on the novel operations are introduced.
Definition 12.
It is assumed that \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1\left( 1 \right)n)\) signifies a family of SFNs and \(\omega_{t}\) is the weight of \(\Upsilon_{t}\), such that \(\sum\nolimits_{t = 1}^{n} {\omega_{t} = 1}\) and \(\omega_{t} \in \left[ {0,\,\,1} \right].\) Then, the TSFWG operator is a mapping \(TSFWG:\Delta^{n} \to \Delta\), defined as
Theorem 9.
The fusion outcome of “\(n\)” SFNs \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)\) acquired with the aid of employing the TSFWG operator is also an SFN expressed as
Definition 13.
It is assumed that \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)(t = 1\left( 1 \right)n)\) signifies a family of SFNs and \(\omega_{t}\) is the weight of \(\Upsilon_{t}\), such that \(\sum\nolimits_{t = 1}^{n} {\omega_{t} = 1}\) and \(\omega_{t} \in \left[ {0,\,\,1} \right].\) Then, the tangent spherical fuzzy ordered weighted geometric (TSFOWG) operator is a mapping \(TSFOWG:\Delta^{n} \to \Delta\), defined as
where \(\left( {o\left( 1 \right),o\left( 2 \right), \ldots ,o\left( n \right)} \right)\) is an arrangement of \(\left( {1,2, \ldots ,n} \right)\), such that \(\Upsilon_{{o\left( {j - 1} \right)}} \ge \Upsilon_{o\left( j \right)}\) for every \(j = 2,3, \ldots ,n\).
Theorem 10.
The fusion outcome of “\(n\)” SFNs \(\Upsilon_{t} = \left( {\phi_{t} ,\varphi_{t} ,\kappa_{t} } \right)\) acquired via employing the TSFOWG operator is also an SFN represented as
Proof.
The proof is similar to Theorem 7.
The following properties are easy to obtain by utilizing TSFWG and TSFOWG operators.
Proposition 5.
(Idempotency Property) Suppose that \(\Upsilon_{0}\) be an SFN. If \(\Upsilon_{t} = \Upsilon_{0}\) for each \(t\). Then
Proposition 6.
(Monotonicity Property) Let \(\Upsilon_{t}\) and \(\widetilde{\Upsilon }_{t} \left( {t = 1\left( 1 \right)n} \right)\) be two collections0 of SFNs. If \(\Upsilon_{t} \subseteq \widetilde{\Upsilon }_{t}\) for all \(t\). Then, we have
Proposition 7.
(Boundedness Property) Suppose that \(\Upsilon^{ + }\) and \(\Upsilon^{ - }\) be the lower and upper bounds of “\(n\)” SFNs \(\Upsilon_{t}\). Then, we have
5 The Propounded Methodology
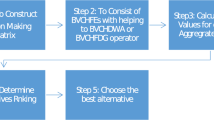
This part designs an innovative MCGDM framework named SF-MEREC–SWARA–ARAS for the analysis of decision problems under spherical fuzzy environments. To be specific, SFNs are utilized to express the cognition preference of experts for the given objectives with respect to the considered criteria. Then, the presented TSFWA operator (or TSFWG operator) is employed to fuse spherical fuzzy preferences given by the experts. Afterward, based on the proposed score function, a comprehensive weighted identification model via integrating SF-MEREC and SF-SWARA methods is developed to estimate the importance of criteria. The combined criteria weight thinks over the removing effect of criteria by the MEREC method and the comparative significance of criteria. As a result, it can acquire more rational weight information and further makes the decision results more credible. In the scheme ranking stage, the ARAS method that utilizes the utility degree theory to determine the prioritization of objectives is presented based on the propounded operators and score function. The suggested SF-MEREC–SWARA–ARAS methodology is depicted in Fig. 1.
The detailed decision process of SF-MEREC–SWARA–ARAS is as follows:
Step 1: Establishment the Initial Assessment Matrix
It is supposed that the classical MCGDM problem consists of \(m\) scheme denoted as \(D = \left\{ {D_{1} ,D_{2} , \ldots D_{m} } \right\}\) and \(n\) assessment criteria indicated as \(G = \left\{ {G_{1} ,G_{2} , \ldots G_{n} } \right\}\). An assessment committee of experts and scholars denoted as \(F = \left\{ {f_{l} \left| {l = 1,2, \ldots ,L} \right.} \right\}\) is invited to provided their opinion for every scheme \(D_{s}\) regarding the criteria \(G_{t}\) via the linguistic variables. Then, the spherical fuzzy decision matrices provided by the experts are obtained by the aid of transforming the linguistic assessments to SFNs denoted as \(\widetilde{\Phi }^{\left( l \right)} = \left( {\widetilde{\chi }_{st}^{\left( l \right)} } \right)_{m \times n}\)
wherein \(\widetilde{\chi }_{st}^{\left( l \right)}\) stands for the assessment preference of the scheme \(D_{s} \left( {s = 1\left( 1 \right)m} \right)\) with regard to the criterion \(G_{t} \left( {t = 1\left( 1 \right)n} \right)\) given by the \(l\)th expert.
Step 2: Determine the Weight of Experts
The weights of experts are key attention in the construction of MCGDM methodology. It is assumed that the weights of experts are expressed by the linguistic variables and then attain the corresponding SFN. Let \(\Upsilon_{l} = \left( {\phi_{l} ,\varphi_{l} ,\kappa_{l} } \right)\) be an SFN, and then, the weight of the expert \(f_{l}\) can be computed as
where \(\gamma_{l}\) be the weight of the \(l{\text{th}}\) expert with the condition \(\gamma_{l} \ge 0,\sum\nolimits_{l = 1}^{L} {\gamma_{l} } = 1.\) \(L\) stands for the number of experts and \(\rho_{l} \left( {l = 1,2, \cdots L} \right)\) represents the sorting of every expert attained by the score.
Step 3: Fuse the Expert Decision Matrices
By the determined weight information of the experts, the individual opinion of each expert \(f_{l}\) shall be aggregated to form the fused spherical fuzzy decision matrix (FSF-DM) \(\widetilde{\Phi } = \left( {\widetilde{\chi }_{st}^{{}} } \right)_{m \times n}\), which can be determined by utilizing the TSFWA or TSFWAG operators, wherein
or
Step 4: A Combination Weight-Determination Model for Ascertaining Criteria Weight
The weight of assessment criteria is identified by a comprehensive weight-determination model. Let \(\omega = \left( {\omega_{1} ,\omega_{2} , \ldots \omega_{n} } \right)^{{\text{T}}}\) be the weight vector of criteria with \(\omega_{t} \in \left[ {0,1} \right],\sum\nolimits_{t = 1}^{n} {\omega_{t} } = 1.\) To ascertain the weight of the criteria, the improved SF-MEREC model utilizing the novel score function and the SF-SWARA approach is employed for the identification of weight from the subjective and objective perspective. Concretely, the determination process of the model can be expounded as follows:
Case-1: Determinate the objective weight of criteria by improved SF-MEREC model.
The concrete step of the SF-MEREC model using the score function is demonstrated as follows.
Step 4.1: Obtain the normalized FSF-DM.
This step utilizes the simple linear normalization method to scale the FSF-DM \(\widetilde{\Phi } = \left( {\widetilde{\chi }_{st}^{{}} } \right)_{m \times n}\) and derive the normalized FSF-DM denoted as \(\Phi = \left( {\chi_{st}^{{}} } \right)_{m \times n}\). It is supposed that \(G_{b}\) and \(G_{c}\) denote the benefit and cost criteria, respectively, and then, the normalized assessment value can be obtained by the following equation:
Step 4.2: Figure out the score values.
By means of the propounded spherical fuzzy score function, the score matrix \(\Omega = \left( {\sigma_{st}^{{}} } \right)_{m \times n}\) of the normalized assessment value \(\chi_{st}^{{}}\) can be computed by
Step 4.3: Compute the ensemble performance of the schemes.
By the score matrix of the normalized assessments, the overall performance of the schemes \(D_{s}^{{}}\) can be calculated
Step 4.4: Attain the comprehensive assessment of the schemes by removing criterion.
The assessment of the schemes can be worked out with the help of removing each criterion using the following formulation:
Step 4.5: Estimate the total absolute deviation.
In view of the performance value of schemes determined, the removal effect of the \(t^{{{\text{th}}}}\) criterion denoted as \(J_{t}\) can be calculated by
Step 4.6: Deduce the final criteria weight.
Based on the absolute deviation, the final criteria weight can be computed by the following formulation as
Case-1: Determinate the subjective weight by the FF-SWARA method.
Step 4.7 We first obtain the subjective preferences of criteria via each expert using the linguistic variables. Then, the subjective preferences are integrated by the proposed TSFWA operator to obtain the score grades of the final integration value.
Step 4.8 The criteria are sorted via the score grades of the final integration values from high to low.
Step 4.9 Compute the comparative coefficient \(\beta_{t}\)
wherein \(q_{t}\) signifies the significance grade of the tth criteria.
Step 4.10 The subjective weight of criteria is calculated by
Step 4.11 The final normalized weight is figured out by
Case-3: Identifying the aggregated criteria weights by the SF-MEREC-SWARA method.
The generated weights can capture the objective decision assessment and subjective opinion of the experts. Hence, through the outcomes of objective and subjective weights of the criteria, the ultimate weight is deduced via the non-linear weight integration approach shown in Eq. (24)
Step 5: Getting the best performance evaluation values.
Step 6: Discover the weighted standardized FSF-DM.
The weighted standardized FSF-DM \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Re } = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\chi }_{st} } \right)_{m \times n}\) is ascertained, wherein
or
where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\chi }_{st} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{st} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi }_{st} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\kappa }_{st} } \right)\) be the weighted SFN.
Step 7: Seek out the score of assessment values.
The score index of the weighted standardized FSF-DM can be computed as below
Step 8: Assess the whole performance value.
The comprehensive performance value of each scheme can be calculated as
Step 9: Seek out the utility grade for each scheme.
The utility grade of each scheme is identified by
where \(UG_{s} \left( {0 \le UG_{s} \le 1} \right)\) is the utility grade of the scheme \(D_{s}\) and \(K_{0}\) is the utility grade of the optimal performance value \(\chi_{0}\).
Step 10: Sort scheme.
The considered schemes are sorted by the utility grade \(UG_{s}\), and the most satisfactory option can be achieved by means of
6 Case Study: Digital Marketing Technology Evaluation
In this section, we will apply the developed SF-SWARA–MEREC–ARAS method to comprehensively evaluate digital marketing technology, as well as further reflect the practicability and effectiveness of the introduced SFS-based decision framework. Then, the sensitivity analysis for the changing of criteria weight is discussed to test the stability of the SF-SWARA–MEREC–ARAS approach. Meanwhile, the comparative discussion is executed to highlight the strengths of the presented method.
6.1 Decision Analysis for Digital Marketing Technology Evaluation
Digital marketing refers to a new means of product and brand marketing based on Internet user traffic and driven by data intelligence. Relying on digital intelligence technology and digital platform channels, digital marketing helps enterprises to accurately locate and investigate innovative markets and novel consumers. Its advantage is to communicate with consumers efficiently and economically, thereby greatly improving marketing efficiency. Digital marketing contains the core of technology and is committed to user-deep information mining. Therefore, it is necessary to integrate with network technology to settle and discuss massive data in the marketing process to achieve the precise goal of digital marketing [6]. With the rapid development of network technologies, such as big data, artificial intelligence, and cloud computing, enterprises must select appropriate technologies through different standards of digital marketing models.
This section will carry out the SF-SWARA–MEREC–ARAS method to select the appropriate digital marketing technology for proving the effectiveness and practicability of the SF-SWARA–MEREC–ARAS method. After the preliminary discussion and negotiation of the evaluation team, the evaluation team composed of three experts (\(f_{1} ,f_{2} ,f_{3}\)) identified five technologies for enterprises to select digital marketing including machine learning (\(D_{1}\)), big data (\(D_{2}\)), virtual reality technology (\(D_{3}\)), artificial intelligence (\(D_{4}\)), and the Internet of Things (\(D_{5}\)). Due to the relatively small amount of research on digital marketing technology evaluation currently, so we utilize the assessment criteria in reference [4] to conduct the case analysis in this paper. The assessment criteria for assessing the digital marketing technology are considered from the following three aspects including customer status, company status, and market information, and then, the following nine subcriteria are further pondered to measure the performance of the digital marketing technology, which are explained as customer satisfaction (\(G_{1}\)), customer loyalty (\(G_{2}\)), simultaneous accessibility of product/service (\(G_{3}\)) image (brand value) of company (\(G_{4}\)), promotions (\(G_{5}\)), utilization of social media (\(G_{6}\)), competitive position in market (\(G_{7}\)), market size (\(G_{8}\)), and interaction with competitors (\(G_{9}\)). In the following, SF-SWARA–MEREC–ARAS is employed for selecting the appropriate digital marketing technology.
Based on the professional opinions of the experts, a nine-level language scale from “Absolute high significance” to “absolutely low significance” is provided for experts to express their importance measurement and preference evaluation for the schemes (Table 2). It is supposed that the three linguistic variables denoted are used to signify the weight of experts in the MCGDM process. Further, each technology is evaluated by the three experts over different criteria. The corresponding linguistic decision assessments of all technology are shown in Table 3.
By means of Eq. (13), the importance of the three experts can be computed and the results are listed in Table 4. Henceforth, the TSFWA operator or TSFWG operator shown in Eq. (14) is utilized to fuse the individual evaluation opinions for the technologies, and the aggregation assessment information is exhibited in Table 5.
Based upon the FSF-DM in Table 5, the normalized FSF-DM can be obtained by Eq. (15). In this study, the normalization is ellipsised, because all considered criteria are viewed as benefit criteria. The weights of digital marketing technology criteria are determined by the proposed SF-MEREC–SWARA model. First, the score matrix based on the FSF-DM is computed by Eq. (16), and the results are shown in Table 6. Then, the summation of absolute deviations of the criteria is computed based on the overall performances of the digital marketing technology via detaching each criterion using Eqs. (17–18). Hence, the results of absolute deviations of criteria and the final objective weights determined by Eqs. (19–20) are all shown in Table 6.
In addition, the subjective weights of criteria figured out by the SF-SWARA method utilizing Eqs. (21–23) can be acquired and the whole computation outcomes are exhibited in Tables 7–8.
Finally, based on the propounded SF-MEREC–SWARA model, the fused criteria weights can be determined by merging the subjective and objective weights using Eq. (24). The fused outcomes of the criteria are \(\omega_{1} = 0.1348\), \(\omega_{2} = 0.1132\), \(\omega_{3} = 0.1028\), \(\omega_{4} = 0.1030\), \(\omega_{5} = 0.0996\), \(\omega_{6} = 0.1103\), \(\omega_{7} = 0.1293\), \(\omega_{8} = 0.1135\), and \(\omega_{9} = 0.0936\). Further, the result distributions of the objective weights, subjective weights, and comprehensive weights are visually shown in Fig. 2.
Afterward, based on the score function and FSF-DM, the optimal assessment information for the digital marketing technology under each criterion can be determined by Eq. (25) and given as follows:
\(\chi_{0}^{{}} =\)[ (0.7274, 0.2615, 0.2615), (0.6264, 0.3623, 0.3623), (0.7632, 0.1865, 0.1865), (0.6264, 0.3623, 0.3623), (0.7572, 0.2311, 0.2311), (0.8604, 0.1313, 0.1313), (0.7331, 0.2533, 0.2533), (0.6679, 0.3247, 0.3247)].
Next, the weighted normalized FSF-DM can be determined with the aid of Eq. (26), as shown in Table 9. The score value \( \overset{\lower0.3em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\chi }_{st} } \right)\) of the weighted normalized assessment values can be computed, based on Table 9 and Eq. (27). The utility grade \(UG_{s}\) of each digital marketing technology \(D_{s}\) can be determined based on the overall assessment value \(K_{s}\)(Table 10). Finally, the prioritization of the digital marketing technologies is determined using Eqs. (28–30) as \(D_{4} \succ D_{5} \succ D_{1} \succ D_{2} \succ D_{3}\). The suitable option is the fourth technology, i.e., “artificial intelligence \(D_{4}\).
6.2 Sensitivity Analysis
This subsection analyzes and discusses the sensitivity of the proposed SF-MEREC–SWARA–ARAS methodology. Since the developed approach does not involve parameter issues, we will focus on exploring the fluctuation situation of criteria weights on the ultimate ranking of digital marketing technologies. Next, we will use the following five principles involving subjective weight (Case-1), objective weight (Case-2), combined weight (Case-3), and averaging weight (Case-4), and the weight of all criteria is reduced by 20% (Case-5). Further, the outcomes obtained by the five cases are employed to analyze the robustness of the propounded approach concerning different weights. The calculation results include the utility degree and corresponding ranking of the digital marketing technologies (Table 11 and Fig. 3). Based on the outcomes, we can attain that the ranking results of digital marketing technology obtained by weight information in five different situations are the same, i.e., the optimal option is “artificial intelligence”, while the worst option is “virtual reality”. Accordingly, we can observe that changes in criteria weights have no impact on the ranking of final digital marketing technologies, which can further demonstrate that the method proposed in this article is stable and robust.
6.3 Comparison Study
This subsection will focus on the comparative discussion to further prove the practicalness and rationality of SF-MEREC–SWARA–ARAS in assessing digital marketing technologies. The existing spherical fuzzy decision methods are selected, including the SF-CoCoSo method [57], the SF-WSM approach [23], the SF-WASAS method [23], and the SF-COPRAS method [58]. Then, based on the evaluation information and comprehensive weight of the criteria determined in this article, the above spherical fuzzy decision approaches are applied to solve the evaluation problem of digital marketing technology. The outcomes are given in Table 12 and Fig. 4.
From the comparison results, it is concluded that the rankings of digital marketing technology acquired by different spherical fuzzy decision methods have a bit of difference, while the best option is the fourth technology in all of them. Hence, the effectiveness of the proposed SF-MEREC–SWARA–ARAS decision framework is first proved to develop a reasonable decision. Then, we further compare the inherent differences between the prior and our approaches, which may be the reason for inconsistent sorting results with the proposed method. From the perspective of criterion weight determination, the weight information in the above-mentioned methods is only ascertained from a subjective or objective perspective or is directly given, which cannot obtain more authentic and comprehensive criterion weight information and thereby reduce the credibility of the decision results. Nevertheless, the SF-MEREC–SWARA method is adopted for the proposed method, which is determined by comprehensively taking into consideration the impact of the decision data itself on the importance of the criterion and the subjective experience of experts. From the perspective of identifying ranking, the SF-WSM approach, SF-WASAS method, and SF-COPRAS method employ algebraic-based operators and prior score functions, which can lead to the irrational ranking comparisons of the schemes. Hence, the propounded method based on novel score function and operators can attain a more accurate utility grade of the schemes with the aid of the enhanced SF-ARAS method.
In addition, the proposed SF-MEREC–SWARA–ARAS method is built up for treating the group decision problems with the incomplete weight of experts, while other methods only address the MCDM problem. Therefore, the developing method is more feasible and generalized than the above approaches in developing decision analysis within an uncertain context.
Considering the aforesaid discussions between the extant spherical fuzzy decision methodologies and the propounded SF-MEREC–SWARA–ARAS method, the merits and strengths of the suggested method for assessing the digital market technology are anatomized as follows:
-
The proposed SF-MEREC–SWARA–ARAS method incorporates the SF-MEREC, SF-SWARA, and SF-ARAS within SFSs to cope with the evaluation problems under an uncertain environment, which provides an advanced decision espousal framework for managers to improve the quality of a decision.
-
Criteria weights in the proposed model are ascertained through the integration of SF-MEREC and SF-SWARA models, which are presented based on the proposed score function and TSFWA or TSFWG operators. Accordingly, the determination of criteria weight in the developed method can further enhance the accuracy and reliability of the utility ranking outcomes of digital marketing technologies.
-
The prioritization of digital marketing technologies is identified by the enhanced SF-ARAS method, which is improved by the novel score function and integration operators. Due to the advantage of the novel score function, the SF-ARAS method can conquer some irrational situations existing in the other methods. The sensitivity and comparison studies also prove the robustness and efficiency of the sorting results attained by our method. Consequently, the introduced SF-MEREC–SWARA–ARAS methodology is more stable, feasible, and valid than the compared approaches within the SFS context.
7 Conclusion
This study introduced a synthetics assessment framework to evaluate digital marketing technologies and further provided decision support for enterprises and managers. In this regard, a hybrid MCGDM decision methodology was presented with the integration of the SF-MEREC, SF-SWARA, and SF-ARAS models for the prioritization of digital marketing technologies under the SFS environment. In light of this aim, the current study copes with the following attentions associated SFSs. First, the new score function for SFS was proposed to prioritize SFNs and transform them into real numbers, while the related desirable axioms and merits were discussed simultaneously. Second, the TSFWA operator, TSFWG operator, TSFOWA operator, and TSFOWG operator were propounded via the defined new operational laws to aggregate the spherical fuzzy information. Third, the SF-MEREC–SWARA method was propounded to appraise the comprehensive importance of assessment criteria. Fourth, the traditional ARAS method was expanded with the fusion of the score function, TSFWA operator, and SF-MEREC-SWARA with spherical fuzzy settings. Further, this paper carried out a case study about digital marketing technology to confirm the availability and feasibility of the introduced SF-MEREC–SWARA–ARAS decision methodology. The comparison study and sensitivity analyses confirmed that the propounded method was suitable, reliable, and stable within uncertain circumstances.
This study also possesses several limitations in decision analysis. The correlation among the assessment criteria should be thought over in spherical fuzzy MCDM information fusion. Also, the goal weight of experts should be thought about while fusing information. Besides, a reliable degree of assessment information provided by experts should be given for enhancing the reliability of a decision.
Future research might try to conquer the mentioned limitations in our study. Besides, some functional operators, such as Maclaurin symmetric mean [59] and Hamy mean [60], could be proposed to consider the interrelationship among the criteria. The objective weights of experts can also be computed by optimization models and similarity-based methods. The expression of reliability of evaluation information can combine the Z-number theory to represent the assessments comprehensively and the developed method can also be employed in other fields of applications [61,62,63,64]. In addition, the consensus-reaching process is also a momentous part of the construction of group decision methodology which can make the final decision outcomes more reasonable and reliable [65, 66]. Accordingly, the consensus-reaching process, large-group decision-making, and heterogeneous preference information-based problems should be taken into account in the course of group decision analysis under a spherical fuzzy context [67,68,69,70,71].
Availability of Data and Materials
The datasets generated during and/or analyzed during the current study is available from the corresponding author on reasonable request.
Abbreviations
- ARAS:
-
Additive ratio assessment
- SF:
-
Spherical fuzzy
- PFS:
-
Picture fuzzy set
- MCGDM:
-
Multi-criteria group decision-making
- MEREC:
-
Method based on the removal effects of criteria
- SWARA:
-
Step-wise weight assessment ratio analysis
- MCDM:
-
Multi-criteria decision-making
- PROMETHEE:
-
Preference ranking organization method for enrichment evaluations
- CRADIS:
-
Compromise ranking of alternatives from distance to ideal solution
- CPT-TODIM:
-
Cumulative prospect theory an acronym in Portuguese for interactive and multi-criteria decision-making
- CRITIC:
-
Criterion importance through inter-criteria correlation
- FMEA:
-
Failure modes and effects analysis
- SFN:
-
Spherical fuzzy number
- TSFWA:
-
Tangent spherical fuzzy weighted averaging
- TSFWG:
-
Tangent spherical fuzzy weighted geometric
- TSFOWA:
-
Tangent spherical fuzzy ordered weighted averaging
- TSFOWG:
-
Tangent spherical fuzzy ordered weighted geometric
- FSF-DM:
-
Fused spherical fuzzy decision matrix
- CoCoSo:
-
Combined compromise solution
- WSM:
-
Weighted sum model
- WASPAS:
-
Weighted aggregated sum product assessment
- COPRAS:
-
Complex proportional assessment
References
Petit, O., Velasco, C., Spence, C.: Digital sensory marketing: integrating new technologies into multisensory online experience. J. Interact. Mark. 45, 42–61 (2019)
Ramon Saura, J.: Using data sciences in digital marketing: framework, methods, and performance metrics. J. Innov. Knowl. 6(2), 92–102 (2021)
Luangrath, A.W., Peck, J., Hedgcock, W., Xu, Y.: Observing product touch: the vicarious haptic effect in digital marketing and virtual reality. J. Mark. Res. 59(2), 306–326 (2022)
Ngo Quang, T., Van Nguyen, T.: Evaluation of digital marketing technologies with fuzzy linguistic MCDM methods. Axioms 11(5), 230 (2022)
Dana, L.-P., Salamzadeh, A., Mortazavi, S., Hadizadeh, M.: Investigating the impact of international markets and new digital technologies on business innovation in emerging markets. Sustainability 14(2), 983 (2022)
McGarr, O., Engen, B.K.: By-passing teachers in the marketing of digital technologies: the synergy of educational technology discourse and new public management practices. Learn. Media Technol. 47(4), 440–455 (2022)
Baffoe, B.O.K., Luo, W., Pan, Q.H., Zhou, S.H., Wu, M.J., Atimu, L.K.D., et al.: Assessing the factors for humanitarian logistics digital business ecosystem (HLDBE) using a novel integrated correlation coefficient and standard deviation-combined compromise solution (CCSD-CoCoSo) method. Decis. Sci. Lett. 12(1), 117–136 (2023)
Zadeh, L.A.: Fuzzy sets. Inf. Control 8(3), 338–353 (1965)
Atanassov, K.T.: Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20(1), 87–96 (1986)
Zhang, X., Shang, J., Wang, J.: Multi-granulation fuzzy rough sets based on overlap functions with a new approach to MAGDM. Inf. Sci. 622, 536–559 (2023)
Korkmaz, E., Ozcan, C., Korkmaz, M.: An application of fuzzy soft sets to a real-life problem: classification of wood materials to prevent fire-related injuries and deaths. Appl. Soft Comput. 132, 109875 (2023)
Atanassov, K., Gargov, G.: Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 31(3), 343–349 (1989)
Cuong, B.C.: Picture fuzzy sets. J. Comput. Sci. Cybern. 30, 409–420 (2014)
Mahmood, T., Ullah, K., Khan, Q., Jan, N.: An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 31(11), 7041–7053 (2019)
Kumar, K., Chen, S.-M.: Group decision making based on advanced interval-valued intuitionist fuzzy weighted averaging aggregation operator and score function of interval-valued intuitionist fuzzy values. Inf. Sci. 624, 908–923 (2023)
Lin, M., Huang, C., Xu, Z.: MULTIMOORA based MCDM model for site selection of car sharing station under picture fuzzy environment. Sustain. Cities Soc. 53, 101873 (2020)
Ashraf, S., Abdullah, S., Almagrabi, A.O.: A new emergency response of spherical intelligent fuzzy decision process to diagnose of COVID19. Soft Comput. (2020)
Seyfi-Shishavan, S.A., Gundogdu, F.K., Donyatalab, Y., Farrokhizadeh, E., Kahraman, C.: A novel spherical fuzzy bi-objective linear assignment method and its application to insurance options selection. Int. J. Inf. Technol. Decis. Mak. 20(02), 521–551 (2021)
Ashraf, S., Abdullah, S.: Emergency decision support modeling for COVID-19 based on spherical fuzzy information. Int. J. Intell. Syst. 35(11), 1601–1645 (2020)
Ghoushchi, S.J., Haghshenas, S.S., Ghiaci, A.M., Guido, G., Vitale, A.: Road safety assessment and risks prioritization using an integrated SWARA and MARCOS approach under spherical fuzzy environment. Neural Comput. Appl. 35(6), 4549–4567 (2023)
Ashraf, S., Abdullah, S., Mahmood, T., Ghani, F., Mahmood, T.: Spherical fuzzy sets and their applications in multi-attribute decision making problems. J. Intell. Fuzzy Syst. 36(3), 2829–2844 (2019)
Ashraf, S., Abdullah, S.: Spherical aggregation operators and their application in multiattribute group decision-making. Int. J. Intell. Syst. 34(3), 493–523 (2019)
Gundogdu, F.K., Kahraman, C.: Extension of WASPAS with Spherical Fuzzy Sets. Informatica 30(2), 269–292 (2019)
Gundogdu, F.K., Kahraman, C.: Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 36(1), 337–352 (2019)
Chinram, R., Ashraf, S., Abdullah, S., Petchkaew, P.: Decision support technique based on spherical fuzzy yager aggregation operators and their application in wind power plant locations: a case study of Jhimpir, Pakistan. J. Math. 2020, 1 (2020)
Gundogdu, F.K., Kahraman, C.: A novel spherical fuzzy QFD method and its application to the linear delta robot technology development. Eng. Appl. Artif. Intell. 87, 103348 (2020)
Akram, M., Zahid, K., Kahraman, C.: A PROMETHEE based outranking approach for the construction of Fangcang shelter hospital using spherical fuzzy sets. Artif. Intell. Med. 135, 102456 (2023)
Wang, C.-N., Pham, T.-D.T., Nhieu, N.-L.: A Composited regret-theory-based spherical fuzzy prioritization approach for moving high-tech manufacturing in Southeast Asia. Appl. Sci. Basel 13(2), 688 (2023)
Wang, W., Wang, Y., Fan, S., Han, X., Wu, Q., Pamucar, D.: A complex spherical fuzzy CRADIS method based Fine-Kinney framework for occupational risk evaluation in natural gas pipeline construction. J. Pet. Sci. Eng. 220, 111246 (2023)
Zhang, H., Wang, H., Wei, G.: Spherical fuzzy TODIM method for MAGDM integrating cumulative prospect theory and CRITIC method and its application to commercial insurance selection. Artif. Intell. Rev. (2023). https://doi.org/10.1007/s10462-023-10409-3
Gocer, F., Sener, N.: Spherical fuzzy extension of AHP-ARAS methods integrated with modified k-means clustering for logistics hub location problem. Expert Syst. (2022). https://doi.org/10.1111/exsy.12886
Ghoushchi, S.J., Jalalat, S.M., Bonab, S.R., Ghiaci, A.M., Haseli, G., Tomaskova, H.: Evaluation of wind turbine failure modes using the developed SWARA-CoCoSo methods based on the spherical fuzzy environment. IEEE Access 10, 86750–86764 (2022)
Bonab, S.R., Ghoushchi, S.J., Deveci, M., Haseli, G.: Logistic autonomous vehicles assessment using decision support model under spherical fuzzy set integrated Choquet integral approach. Expert Syst. Appl. 214, 119205 (2023)
Jawad, M., Naz, M., Muqaddus, H.: A multi-criteria decision-making approach for portfolio selection by using an automatic spherical fuzzy AHP algorithm. J. Oper. Res. Soc. (2023). https://doi.org/10.1080/01605682.2023.2174905
Debnath, K., Roy, S.K.: Power partitioned neutral aggregation operators for T-spherical fuzzy sets: An application to H2 refuelling site selection. Expert Syst. Appl. 216, 119470 (2023)
Chen, Q.-Y., Liu, H.-C., Wang, J.-H., Shi, H.: New model for occupational health and safety risk assessment based on Fermatean fuzzy linguistic sets and CoCoSo approach. Appl. Soft Comput. 126, 109262 (2022)
Bošković, S., Švadlenka, L., Dobrodolac, M., Jovčić, S., Zanne, M.: An extended aroman method for cargo bike delivery concept selection. Decis. Mak. Adv. 1(1), 1–9 (2023)
Keshavarz-Ghorabaee, M., Amiri, M., Zavadskas, E.K., Turskis, Z., Antucheviciene, J.: Determination of objective weights using a new method based on the removal effects of criteria (MEREC). Symmetry-Basel 13(4), 525 (2021)
Rani, P., Mishra, A.R., Saha, A., Hezam, I.M., Pamucar, D.: Fermatean fuzzy Heronian mean operators and MEREC-based additive ratio assessment method: an application to food waste treatment technology selection. Int. J. Intell. Syst. 37(3), 2612–2647 (2022)
Kersuliene, V., Zavadskas, E.K., Turskis, Z.: Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J. Bus. Econ. Manag. 11(2), 243–258 (2010)
Ulutas, A., Karakus, C.B., Topal, A.: Location selection for logistics center with fuzzy SWARA and CoCoSo methods. J. Intell. Fuzzy Syst. 38(4), 4693–4709 (2020)
Cui, Y., Liu, W., Rani, P., Alrasheedi, M.: Internet of Things (IoT) adoption barriers for the circular economy using Pythagorean fuzzy SWARA-CoCoSo decision-making approach in the manufacturing sector. Technol. Forecast. Soc. Change 171, 120951 (2021)
Zavadskas, E.K., Turskis, Z., Vilutiene, T.: Multiple criteria analysis of foundation instalment alternatives by applying additive ratio assessment (ARAS) method. Archiv. Civ. Mech. Eng. 10(3), 123–141 (2010)
Hu, Y., Al-Barakati, A., Rani, P.: Investigating the internet-of-things (IoT) risks for supply chain management using q-rung orthopair fuzzy-swara-aras framework. Technol. Econ. Dev. Econ. (2022). https://doi.org/10.3846/tede.2022.16583
Buyukozkan, G., Gocer, F.: An extension of ARAS methodology under interval valued intuitionistic fuzzy environment for digital supply chain. Appl. Soft Comput. 69, 634–654 (2018)
Mishra, A.R., Rani, P.: A q-rung orthopair fuzzy ARAS method based on entropy and discrimination measures: an application of sustainable recycling partner selection. J. Ambient Intell. Human. Comput. 14, 6897–6918 (2023). https://doi.org/10.1007/s12652-021-03549-3
Liu, P., Cheng, S.: An extension of ARAS methodology for multi-criteria group decision-making problems within probability multi-valued neutrosophic sets. Int. J. Fuzzy Syst. 21(8), 2472–2489 (2019)
Goswami, S.S., Behera, D.K.: Solving material handling equipment selection problems in an industry with the help of entropy integrated COPRAS and ARAS MCDM techniques. Process Integr. Optim. Sustain. 5(4), 947–973 (2021)
Jin, C., Ran, Y., Zhang, G.: Interval-valued q-rung orthopair fuzzy FMEA application to improve risk evaluation process of tool changing manipulator. Appl. Soft Comput. 104, 107192 (2021)
Mishra, A.R., Rani, P., Saha, A.: Single-valued neutrosophic similarity measure-based additive ratio assessment framework for optimal site selection of electric vehicle charging station. Int. J. Intell. Syst. 36(10), 5573–5604 (2021)
Mishra, A.R., Rani, P., Cavallaro, F., Mardani, A.: A similarity measure-based Pythagorean fuzzy additive ratio assessment approach and its application to multi-criteria sustainable biomass crop selection. Appl. Soft Comput. 125, 109201 (2022)
Teng, F., Shen, M.: Unbalanced double hierarchy linguistic group decision-making method based on SWARA and S-ARAS for multiple attribute group decision-making problems. Artif. Intell. Rev. 56(2), 1349–1385 (2023)
Wang, H.: Sustainable circular supplier selection in the power battery industry using a linguistic t-spherical fuzzy MAGDM model based on the improved ARAS method. Sustainability 14(13), 7816 (2022)
Jovcic, S., Simic, V., Prusa, P., Dobrodolac, M.: Picture fuzzy ARAS method for freight distribution concept selection. Symmetry-Basel 12(7), 1062 (2020)
Ecer, F.: An integrated fuzzy AHP and aras model to evaluate mobile banking services. Technol. Econ. Dev. Econ. 24(2), 670–695 (2018)
Rani, D., Garg, H.: Multiple attributes group decision-making based on trigonometric operators, particle swarm optimization and complex intuitionistic fuzzy values. Artif. Intell. Rev. 56(2), 1787–1831 (2023)
Peng, X., Li, W.: Spherical fuzzy decision making method based on combined compromise solution for IIoT industry evaluation. Artif. Intell. Rev. 55(3), 1857–1886 (2022)
Omerali, M., Kayo, T.: Augmented reality application selection framework using spherical fuzzy COPRAS multi criteria decision making. Cogent Eng. (2022). https://doi.org/10.1080/23311916.2021.2020610
Wei, D., Rong, Y., Garg, H., Liu, J.: An extended WASPAS approach for teaching quality evaluation based on pythagorean fuzzy reducible weighted Maclaurin symmetric mean. J. Intell. Fuzzy Syst. 42(4), 3121–3152 (2022)
Rong, Y., Pei, Z., Liu, Y.: Hesitant fuzzy linguistic hamy mean aggregation operators and their application to linguistic multiple attribute decision-making. Math. Probl. Eng. 2020, 1–22 (2020)
Rong, Y., Yu, L., Niu, W., Liu, Y., Senapati, T., Mishra, A.R.: MARCOS approach based upon cubic Fermatean fuzzy set and its application in evaluation and selecting cold chain logistics distribution center. Eng. Appl. Artif. Intell. 116, 105401 (2022)
Wei, D., Meng, D., Rong, Y., Liu, Y., Garg, H., Pamucar, D.: Fermatean fuzzy schweizer-sklar operators and BWM-entropy-based combined compromise solution approach: an application to green supplier selection. Entropy 24(6), 776 (2022)
Yan, B., Rong, Y., Yu, L., Huang, Y.: A hybrid intuitionistic fuzzy group decision framework and its application in urban rail transit system selection. Mathematics 10(12), 2133 (2022)
Senapati, T., Simic, V., Saha, A., Dobrodolac, M., Rong, Y., Tirkolaee, E.B.: Intuitionistic fuzzy power Aczel-Alsina model for prioritization of sustainable transportation sharing practices. Eng. Appl. Artif. Intell. 119, 105716 (2023)
Li, C.-C., Dong, Y., Liang, H., Pedrycz, W., Herrera, F.: Data-driven method to learning personalized individual semantics to support linguistic multi-attribute decision making. Omega-Int. J. Manag. Sci. 111, 102642 (2022)
Ji, F., Wu, J., Chiclana, F., Wang, S., Fujita, H., Herrera-Viedma, E.: The overlapping community driven feedback mechanism to support consensus in social network group decision making. IEEE Trans. Fuzzy Syst. (2023). https://doi.org/10.1109/TFUZZ.2023.3241062
Yang, Y., Gai, T., Cao, M., Zhang, Z., Zhang, H., Wu, J.: Application of group decision making in shipping industry 4.0: bibliometric analysis, trends, and future directions. Systems 11(2), 69 (2023)
Zhang, Z., Li, Z.: Consensus-based TOPSIS-Sort-B for multi-criteria sorting in the context of group decision-making. Ann. Oper. Res. (2022). https://doi.org/10.1007/s10479-022-04985-w
Li, Z., Zhang, Z.: Threshold-based value-driven method to support consensus reaching in multicriteria group sorting problems: a minimum adjustment perspective. IEEE Trans. Comput. Soc. Syst. (2023). https://doi.org/10.1109/TCSS.2023.3251351
Gai, T., Cao, M., Chiclana, F., Zhang, Z., Dong, Y., Herrera-Viedma, E., Wu, J.: Consensus-trust driven bidirectional feedback mechanism for improving consensus in social network large-group decision making. Group Decis. Negot. 32(1), 45–74 (2023)
Li, Z., Zhang, Z., Yu, W.: Consensus reaching for ordinal classification-based group decision making with heterogeneous preference information. J. Oper. Res. Soc. (2023). https://doi.org/10.1080/01605682.2023.2186806
Acknowledgements
The authors are grateful to the editor and the anonymous reviewers for their constructive comments.
Funding
This paper is funded by National Social Science Foundation of China (22CGL015).
Author information
Authors and Affiliations
Contributions
KG: conceptualization, methodology, investigation, writing-original draft, and writing—review and editing. TL: conceptualization, investigation, data acquisition, and writing—review and editing. DY: conceptualization, investigation, visualization, and writing—review and editing. VS: conceptualization, methodology, and writing—review and editing. YR: methodology, supervision, visualization, and writing—review and editing. HG: visualization, and writing—review and editing.
Corresponding author
Ethics declarations
Conflict of interest
The authors do not have any competing interest.
Ethics approval and consent to participate
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gao, K., Liu, T., Yue, D. et al. An Integrated Spherical Fuzzy Multi-criterion Group Decision-Making Approach and Its Application in Digital Marketing Technology Assessment. Int J Comput Intell Syst 16, 125 (2023). https://doi.org/10.1007/s44196-023-00298-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s44196-023-00298-3