Abstract
Complex Hesitant Fuzzy sets are a powerful tool for depicting vagueness and uncertainty. This paper addresses to Bipolar-Valued Complex Hesitant Fuzzy sets (BVCHFSs) to decode inconsistent, complexity data because of including bipolarity being opposite polar, complexity dividing membership value into two parts, hesitation degree including several membership values. Then, we interpret some new rules such as addition, scalar multiplication, scalar power, multiplication, and present score function. Moreover, some aggregation operators based on BVCHFSs are presented, such as Bipolar-valued Complex Hesitant Fuzzy-Weighted Dombi Averaging operator (BVCHFWDA), Ordered and Hybrid concepts, and Bipolar valued Complex Hesitant Fuzzy-Weighted Dombi Geometric operator (BVCHFWDG), Ordered and Hybrid structures, and some properties, such as idempotency, monotonicity, and boundedness. Later on, the obtained operators are applied over an investment example to show originality and efficiency of suggested instructions. We test to merits and restrictions of the new instructions by comparing them with some existing measures based on bipolar complex fuzzy sets. The comparative analysis indicates that our discussed operators and distance measures over bipolar complex fuzzy sets are agreement especially for BVCHFWDA.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Zadeh [1] developed fuzzy set concept belonging membership value in [0, 1] in 1965 and it was discussed by a lot of authors over different environments such as medical diagnosis, Multi-Criteria Decision-Making Problems (MCDM), algebraic constructions, and artificial intelligence. But this concept has not met enough needs due to some reasons like increasing of noise information, non-objective comments of decision makers, and density data flowing. Motivating this deficit, new endeavors were began to be presented to solve MCDM by utilizing aggregation operators or similarity measures that can be ordered as follows: Complex fuzzy sets [2], Bipolar-Valued Complex fuzzy sets [3], Hesitant fuzzy sets [4], bipolar-valued hesitant fuzzy sets and hesitant bipolar valued fuzzy sets [5], and Complex Hesitant fuzzy sets [6] which is consisted of complex elements of an each element of hesitant fuzzy sets instead of real numbers in [0, 1] and worked over some concepts see [7,8,9,10], etc. One of the most important clusters is Complex fuzzy sets. This approach is modified as a generalization notation of Fuzzy set such that is added to ability to propose two-dimensional information for Fuzzy set to unit circle in the complex plane instead of [0, 1] range. Then, Complex intuitionistic fuzzy sets were developed by Alkouri and co-authors [11], Garg et al. [12] developed complex interval-valued q-rung orthopair uncertain linguistic information in 2021, Muhammad and others [13] presented complex spherical fuzzy information and tested over MCDM problems and Complex Pythagorean Fuzzy Yager Aggregation Operators [14] were proposed by Akram and others, Mahmood and co-authors [15] developed some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition, Ma et al. [16] presented Complex fuzzy sets with applications in signals, and Hassan [17] defined Operations on complex multi-fuzzy sets. Moreover, Hu [18] worked distances of complex fuzzy sets, and Dick and Yager [19] defined some operations over complex and Pythagorean.
In daily life, nature of person always products together dissent polar as white-black, front-back, positive-negative, so on. Therefore, mathematical environment needs opposite opinions especially while experts are specifying their ideas about an element. In here, while positive values demonstrate acceptance, permitted, desired opinions; negative ideas explain non-desirable, restricted, unpermitted preferences about an element. Thus, bipolarity is very essential for mathematical. In this direction, Lee and Zhang [20,21,22] has put forward idea of bipolar fuzzy set. Then, this concept has been carried to two-dimensional concepts from one-dimensional structure together with some extensions called as Bipolar-Valued Complex fuzzy sets [3, 23]. This notation includes positive membership and negative membership value \(\psi ^+(\Theta )=r^+(x)e^{i2\pi \zeta ^+(x)}\) and \(\psi ^-(\Theta )=r^-(x)e^{i2\pi \zeta ^-(x)}\), where \(\psi ^+(\Theta )\in [0,1],\psi ^-(\Theta )\in [-1,0]\) and \(\zeta ^+(x)\in [0,2\pi ],\zeta ^-(x)\in [-2\pi ,0]\), respectively. Frankly, we need an opinion of decision maker to deal with a problem in real life. Bipolar-Valued Complex fuzzy sets are essential both to present objective ideas, defining object with negative values and conducting the factor affecting the object with a negative value. In this context; Bipolar-Valued Complex fuzzy sets have been combined with different structures many times and its some features have been examined, see [24,25,26,27,28,29,30,31].
T-norm and T-conorm of Dombi operators were defined by Dombi [32] in 1982. These operators propose the most flexible approach according to other operators because of having generalization structure. In short time, several concepts have been started to be used together with this construction. Jana and others [33] defined Picture fuzzy Dombi aggregation operators, then He [34] proposed Dombi-hesitant fuzzy information aggregation operators and applied over medical diagnosis, Akram and Khan [35] offered Complex Pythagorean Dombi fuzzy graphs, Pythagorean Dombi fuzzy aggregation operators were developed by Akram and co-authors [36], Liu et al. [37] presented some intuitionistic fuzzy Dombi Bonferroni mean operators and gave an application over MCDM problems, Chen and Ye [38] gave Dombi operations over single-valued neutrosophic set and consisted of series of aggregation operators, Jana and others [39] defined Bipolar fuzzy Dombi aggregation operators and also they offered Bipolar fuzzy Dombi-prioritized aggregation operators [40] in 2020, and Shi [41] worked Dombi aggregation operators of neutrosophic cubic sets for multiple attribute decision making. Although above works, indeterminate, complexity, and vagueness information have not been eliminated because of density data channels, non-objective decisions of experts, increasing relationship of disciplines, etc. Therefore, we introduce bipolar-valued complex hesitant fuzzy sets by extending to complex hesitant fuzzy sets. The motivation of this research paper is described as follows:
This concept includes novel properties as bipolarity, complexity, and hesitation degree.
-
As the details in the structures increase, the margin of error in decision making will decrease. Bipolarity presents for experts novel new decisions. Thus, it covers the real requirements of authors to fulfill unclear quantities in a status of vague. This methodology indicates negative opinions of decision makers for parameters determined by the experts depending on the demands of the application.
-
The generalization idea of fuzzy set is often considered to be carried to different sizes for solution of multi-attribute group decision-making problems. If a researcher desires to organize some kinds of programs in a market, for this, the people concerned with the management have to provide two models of data related to each programs; for instance, the name of each program and the discovery date of each program. Thus, it is open, fuzzy set is not suitable to overcome with this situation. Complex concepts should be utilized to overcome with these limitations.
-
Hesitation degree is very essential in daily life especially into multi-attribute decision-making problems because of the fact that many researchers express their opinions on a subject at the same time is that an important factor in eliminating uncertainty.
-
A new score function has been given to rank using obtained aggregated values.
-
This set hosts more concepts in its own structure as understood from Table 6. Table 6 indicates that the proposed concept can be obtained by combining with several clusters. Thus, decision makers flexibility present positive and negative opinions about elements.
-
Indisputably, when revealing decision problems, we rely on decision matrices obtained by analysts. Experts can think I agree and disagree with an object that is influenced by some factors. Trusting the decision maker’s point of view of each property of an object to characterize with positive and negative factors through Bipolar-valued complex hesitant fuzzy set. In BVCHFSs, the property of an object will be described by dividing two parts. The two parts can be thought as real and imaginary parts. For instance, an expert wants to decide about the utilization of a drug in medicines. The analyst has to consider many factors together, such as the side effects of the drug on the body, its social aspects, and its impact on the country’s economy. Let’s think that three experts gave their opinions as mathematically such as \(\{\{0.5,0.8,0.5\},\{-\,0.5,-\,0.8\}\}\) but if it is surveyed carefully, some ideas are same one with the other. In here, same opinions are changed as an idea and this case increases to error margin. Let’s divide two parts like real and imaginary that \(\{\{0.5e^{i2\pi (0.3)},0.8e^{i2\pi (0.4)},0.5e^{i2\pi (0.9)}\},\{-0.5e^{i2\pi (-0.3)},-0.8e^{i2\pi (-0.2)}\}\}\) and error can be solved. In daily life, several situations can be met like these, the decision maker needs to define this kind of information to BVCHFSs which is provided in this paper. From the above discussions, it is open that BVCHFSs are a useful model to overcome with two- dimensional data along with the positive and negative views of an object.
The main contributions of this research paper are as follows:
-
Some new concepts have been revealed with dombi operators having soft structure as different from other operators by being combined with the proposed cluster. These operators are Bipolar-valued Complex Hesitant Fuzzy-Weighted Dombi Averaging operator (BVCHFWDA), Ordered and Hybrid concepts and Bipolar-valued Complex Hesitant Fuzzy-Weighted Dombi Geometric operator (BVCHFWDG), and Ordered and Hybrid concepts.
-
Moreover, we present an example to indicate flexible, objective, reality of proposed operators for several k values. Here, we present to Tables 2 and 3 for BVCHFWDA and BVCHFWDG. These tables indicate that our results are agreement for ideal element.
-
After that, although the presented operators are new, we give comparative analysis. Furthermore, we offer to Tables 4 and 5 showing consistency among BVCHFWDA, BVCHFWDG, and distance measures over Bipolar Complex Fuzzy sets. If Table 6, we analyze characteristic properties with several clusters. The results show that our operators are reality, objective, and soft.
The remaining of paper is organized as follows: in sect. 2, some basic definitions are given as hesitant fuzzy set and Dombi operators, in sect. 3, Bipolar-valued complex hesitant fuzzy sets and basic properties are given, in sect. 4, we offer Bipolar-valued Complex Hesitant Fuzzy-Weighted Dombi Averaging operator, Ordered, and Hybrid concepts in sect. 5, Bipolar-valued Complex Hesitant Fuzzy-Weighted Dombi Geometric operator and Ordered and Hybrid structures Characteristic properties of six operators are presented, in sect. 6, we present decision-making algorithm and an example in daily life and in sect. 7, and we give comparative analysis.
2 Preliminary
In this section, we recall some basic notions of hesitant fuzzy sets, complex hesitant fuzzy sets, and dombi operators.
Definition 1
[4] Let X be a non-empty set. Then, a hesitant fuzzy set (shortly HFS) in X is in terms of a function that when applied to X return a subset of [0, 1]. We express the HFS by
where \( \xi _A(x) \) is a set of some values in [0, 1], denoting the possible membership degrees of the element \( x\in X \) to the set A, \(\xi = \xi _A(x)\) is called a hesitant fuzzy element (HFE), and \({\mathcal {H}}(X)\) denotes the set of all HFEs on X.
Definition 2
[6] Let X be a reference set. A Complex Hesitant fuzzy sets C is defined as follows:
where \(\xi _{C_j}:X\mapsto [0,1]\). \(\xi _{C_j}e^{i2\pi (\vartheta _{\xi _{C_j}})}\) indicates complex membership value.
Definition 3
[32] Dombi t-norm and t-conorm are defined, respectively, where \(k\ge 1\) and \(x,y\in [0,1]\) as follows:
-
\(D(x,y)=\frac{1}{1+\Big \{(\frac{1-x}{x})^k+(\frac{1-y}{y})^k\Big \}^\frac{1}{k}},\)
-
\(D^\star (x,y)=1-\frac{1}{1+\Big \{(\frac{x}{1-x})^k+(\frac{y}{1-y})^k\Big \}^\frac{1}{k}}.\)
3 Bipolar-Valued Complex Hesitant Fuzzy Sets
The concept of complex hesitant fuzzy sets was defined by Mahmood et al. [6] in 2020. In this section, the concept of Complex Hesitant fuzzy sets is extended to Bipolar-valued Complex Hesitant fuzzy sets (shortly BVCHFSs).
Definition 4
Let X be a reference set. A Bipolar-valued Complex Hesitant fuzzy sets C is defined as follows:
where \(\xi _{C_j}^+:X\mapsto [0,1]\) and \(\xi _{C_\wp }^-:X\mapsto [-1,0]\) are mappings. \(\xi _{C_j}^+e^{i2\pi (\vartheta _{\xi _{C_j}^+})}\) and \(\xi _{C_\wp }^-e^{i2\pi (\vartheta _{\xi _{C_\wp }^-})}\) indicate positive and negative complex membership values, respectively.
Definition 5
Let \(E=\Big \{\{x,\{\xi _{E_j}^+(x)e^{i2\pi (\vartheta _{\xi _{E_j}^+})}:j=1,2,...,n\},\{\xi _{E_\wp }^-(x)e^{i2\pi (\vartheta _{\xi _{E_\wp }^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\),
\(F=\Big \{\{x,\{\xi _{F_j}^+(x)e^{i2\pi (\vartheta _{\xi _{F_j}^+})}:j=1,2,...,n\},\{\xi _{F_\wp }^-(x)e^{i2\pi (\vartheta _{\xi _{F_\wp }^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\) be two BVCHFSs over X for \(k>0\). The basic Dombi operations of BVCHFEs are defined as follows:
Definition 6
Let’s determine a BVCHFS as \(C=\Big \{\{x,\{\xi _{C_j}^+(x)e^{i2\pi (\vartheta _{\xi _{C_j}^+})}:j=1,2,...,n\}, \{\xi _{C_\wp }^-(x)e^{i2\pi (\vartheta _{\xi _{C_\wp }^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\), and score function and accuracy function are proposed using the following function:
and
4 Bipolar-Valued Complex Hesitant Fuzzy-Weighted Dombi Averaging Operators
Definition 7
Let’s determine a set of BVCHFEs as \(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\) for \(w_\ell \in [0,1]\) and \(\sum _{\ell =1}^\varpi w_\ell =1\);
-
1.
\(BVCHFWDA:\Phi ^\varpi \rightarrow \Phi \) is a mapping called as Bipolar-valued Complex Hesitant Fuzzy-Weighted Dombi Averaging operator for \(k> 0\) and \(w_\ell \in [0,1]\) and \(\sum _{\ell =1}^\varpi w_\ell =1\) and is defined as below:
$$\begin{aligned}{} & {} BVCHFWDA(C_1,C_2,...,C_\varpi ) =\displaystyle {\bigoplus _ {\ell =1}^\varpi \Big (w_\ell (C_{\ell })\Big )}\nonumber \\{} & {} \quad = \left\{ \begin{array}{l}\displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} ({\check{\xi }}_{C_{j_1}}^+,{\check{\vartheta }}_{\xi _{C_{j_1}}^+})\in {C_1}, ({\check{\xi }}_{C_{j_2}}^+,{\check{\vartheta }}_{\xi _{C_{j_2}}^+})\in {C_2},...,({\check{\xi }}_{C_{j_\varpi }}^+,{\check{\vartheta }}_{\xi _{C_{j_\varpi }}^+})\in {C_\varpi } \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}1-\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{{\check{\xi }}_{C_{j_\ell }}^+}{1-{\check{\xi }}_{C_{j_\ell }}^+}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}1-\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{\frac{{\check{\vartheta }}_{\xi _{C_{j_\ell }}^+}}{2\pi }}{1-\frac{{\check{\vartheta }}_{\xi _{C_{j_\ell }}^+}}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} ,\\ \displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} ({\check{\xi }}_{C_{\wp _1}}^-,{\check{\vartheta }}_{\xi _{C_{\wp _1}}^-})\in {C_1}, ({\check{\xi }}_{C_{\wp _2}}^-,{\check{\vartheta }}_{\xi _{C_{\wp _2}}^-})\in {C_2},...,({\check{\xi }}_{C_{\wp _\varpi }}^-,{\check{\vartheta }}_{\xi _{C_{\wp _\varpi }}^-})\in {C_\varpi } \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}\frac{-1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1+{\check{\xi }}_{C_{\wp _\ell }}^-}{|{\check{\xi }}_{C_{\wp _\ell }}^-|}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}\frac{-1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1+\frac{{\check{\vartheta }}_{\xi _{C_{\wp _\ell }}^-}}{2\pi }}{\frac{|{\check{\vartheta }}_{\xi _{C_{\wp _\ell }}^-}|}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} \end{array}\right\} \end{aligned}.$$(3) -
2.
\(BVCHFOWDA:\Phi ^\varpi \rightarrow \Phi \) is a mapping called as Bipolar-valued Complex Hesitant Fuzzy-Ordered Weighted Dombi Averaging operator for \(k> 0\) and \(C_{\sigma (\ell )}\) is \(\ell th\) the largest of \(C_{\ell }\) for \((\ell =1,2,...,\varpi )\) and is defined as below:
$$\begin{aligned}{} & {} BVCHFOWDA(C_{1},C_{2},...,C_{\varpi })= \displaystyle {\bigoplus _ {\ell =1}^\varpi \Big (w_\ell (C_{\sigma (\ell )})\Big )}\nonumber \\{} & {} \quad = \left\{ \begin{array}{l}\displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} ({\check{\xi }}_{C_{j_\sigma (1)}}^+,{\check{\vartheta }}_{\xi _{C_{j_\sigma (1)}}^+})\in {C_\sigma (1)}, ({\check{\xi }}_{C_{j_\sigma (2)}}^+,{\check{\vartheta }}_{\xi _{C_{j_\sigma (2)}}^+})\in {C_\sigma (2)},...,({\check{\xi }}_{C_{j_\sigma (\varpi )}}^+,{\check{\vartheta }}_{\xi _{C_{j_\sigma (\varpi )}}^+})\in {C_\varpi } \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}1-\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{{\check{\xi }}_{C_{j_{\sigma (\ell )}}}^+}{1-{\check{\xi }}_{C_{j_{\sigma (\ell )}}}^+}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}1-\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{\frac{{\check{\vartheta }}_{\xi _{C_{j_{\sigma (\ell )}}}^+}}{2\pi }}{1-\frac{{\check{\vartheta }}_{\xi _{C_{j_{\sigma (\ell )}}}^+}}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} ,\\ \displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} ({\check{\xi }}_{C_{\wp _\sigma (1)}}^-,{\check{\vartheta }}_{\xi _{C_{\wp _\sigma (1)}}^-})\in {C_\sigma (1)}, ({\check{\xi }}_{C_{\wp _\sigma (2)}}^-,{\check{\vartheta }}_{\xi _{C_{\wp _\sigma (2)}}^-})\in {C_\sigma (2)},...,({\check{\xi }}_{C_{\wp _\sigma (\varpi )}}^-,{\check{\vartheta }}_{\xi _{C_{\wp _\sigma (\varpi )}}^-})\in {C_\varpi } \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}\frac{-1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1+{\check{\xi }}_{C_{\wp _{\sigma (\ell )}}}^-}{|{\check{\xi }}_{C_{\wp _{\sigma (\ell )}}}^-|}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}\frac{-1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1+\frac{{\check{\vartheta }}_{\xi _{C_{\wp _{\sigma (\ell )}}}^-}}{2\pi }}{\frac{|{\check{\vartheta }}_{\xi _{C_{\wp _{\sigma (\ell )}}}^-}|}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} \end{array}\right\} \end{aligned}.$$(4) -
3.
\(BVCHFHWDA:\Phi ^\varpi \rightarrow \Phi \) is a mapping called as Bipolar-valued Complex Hesitant Fuzzy Hybrid-Weighted Dombi Averaging operator for \(k> 0\) and \(w_\ell \in [0,1]\) and \(\sum _{\ell =1}^\varpi w_\ell =1\) and \({\dot{C}}_{\sigma (\ell )}\) is \(\ell th\) the largest of \(\varpi w_\ell C_\ell \) for aggregation-associated vector \(\omega _\ell =(\omega _1,\omega _2,...,\omega _\varpi )\), \(\omega _\ell \in [0,1]\), and \(\sum _{\ell =1}^\varpi \omega _\ell =1\) for \((\ell =1,2,...,\varpi )\) and is defined as below:
$$\begin{aligned}{} & {} BVCHFHWDA(C_{1},C_{2},...,C_{\varpi })= \displaystyle {\bigoplus _ {\ell =1}^\varpi \Big (w_\ell ({\dot{C}}_{\sigma (\ell )})\Big )}\nonumber \\{} & {} \quad = \left\{ \begin{array}{l}\displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} (\dot{{\check{\xi }}}_{C_{j_{\sigma (1)}}}^+,\dot{{\check{\vartheta }}}_{\xi _{C_{j_{\sigma (1)}}}^+})\in {{\dot{C}}_\sigma (1)}, (\dot{{\check{\xi }}}_{C_{j_{\sigma (2)}}}^+,\dot{{\check{\vartheta }}}_{\xi _{C_{j_{\sigma (2)}}}^+})\in {{\dot{C}}_{\sigma (2)}},...,(\dot{{\check{\xi }}}_{C_{j_{\sigma (\varpi )}}}^+, \dot{{\check{\vartheta }}}_{\xi _{C_{\ell _{\sigma (\varpi )}}}^+})\in {{\dot{C}}_{\sigma (\varpi )}} \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}1-\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{\dot{{\check{\xi }}}_{C_{\sigma (\ell )}}^+}{1-\dot{{\check{\xi }}}_{C_{\sigma (\ell )}}^+}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}1-\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{\frac{\dot{{\check{\vartheta }}}_{\xi _{C_{\sigma (\ell )}}^+}}{2\pi }}{1-\frac{\dot{{\check{\vartheta }}}_{\xi _{C_{\sigma (\ell )}}^+}}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} ,\\ \displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} (\dot{{\check{\xi }}}_{C_{\wp _{\sigma (1)}}}^-,\dot{{\check{\vartheta }}}_{\xi _{C_{\wp _{\sigma (1)}}}^-})\in {{\dot{C}}_\sigma (1)}, (\dot{{\check{\xi }}}_{C_{\wp _{\sigma (2)}}}^-,\dot{{\check{\vartheta }}}_{\xi _{C_{\wp _{\sigma (2)}}}^-})\in {{\dot{C}}_{\sigma (2)}},...,(\dot{{\check{\xi }}}_{C_{\wp _{\sigma (\varpi )}}}^-, \dot{{\check{\vartheta }}}_{\xi _{C_{\wp _{\sigma (\varpi )}}}^-})\in {{\dot{C}}_{\sigma (\varpi )}} \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}\frac{-1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1+\dot{{\check{\xi }}}_{C_{\wp _{\sigma (\ell )}}}^-}{|\dot{{\check{\xi }}}_{C_{\wp _{\sigma (\ell )}}}^-|}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}\frac{-1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1+\frac{\dot{{\check{\vartheta }}}_{\xi _{C_{\wp _{\sigma (\ell )}}}^-}}{2\pi }}{\frac{|\dot{{\check{\vartheta }}}_{\xi _{C_{\wp _{\sigma (\ell )}}}^-}|}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} \end{array}\right\} \end{aligned}.$$(5)
Example 1
Let \(C_1= \Big \{\{0.3e^{i2\pi (0.2)},0.1e^{i2\pi (0.2)}\},\{-0.2e^{i2\pi (-0.3)}\}\Big \}\) and \(C_2=\Big \{\{0.2e^{i2\pi (0.1)}\}, \{-0.3e^{i2\pi (-0.5)},-0.2e^{i2\pi (-0.4)}\}\Big \}\) be two BVCHFS sets over X and weight vector \(w=(0.3,0.7)\) and also aggregation-associated vector is \(\omega =(0.4,0.6)\) for \(s(C_1)=0.9\) and \(s(C_2)=1\) and \(k=2\) from here, \(C_1<C_2\),
Using dombi scalar multiplication over BVCHF, we can obtain BHCFEs as follows: \(\dot{C_1}=2\times 0.3\times C_1=\Big \{\Big \{0.0509e^{i2\pi (0.0182)},0.0036e^{i2\pi (0.0182)}\Big \},\Big \{-0.3071e^{i2\pi (-0.4841)}\Big \}\Big \}\) and \(\dot{C_2}=2\times 0.7\times C_2=\Big \{\Big \{0.0182e^{i2\pi (0.0036)}\Big \},\Big \{-0.4841e^{i2\pi (-0.7905)},-0.3071e^{i2\pi (-0.6523)}\Big \}\Big \}\)
From here, \(s(\dot{C_1})=0.4184\) and \(s(\dot{C_2})=0.5695\). Thus, \(s(\dot{C_1})<s(\dot{C_2})\).
4.1 Characteristic of BVCHFWDA Operator
Theorem 1
Let’s determine collection of BVCHFE as
\(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\) for \(w_\ell \in [0,1]\) and \(\sum _{\ell =1}^\varpi w_\ell =1\). Then, their aggregated value using BVCHFWDA is a BVCHFE and it provides Eq. 3.
Proof
Let’s use mathematical induction on \(\varpi \) and look for \(\varpi =2\).
Firstly, let’s determine \( w_1C_1\oplus w_2C_2\) as follows:
From here for \(\varpi =\zeta \), BVCHFWDA holds as follows:
and for \(\varpi =\zeta +1\),
Thus,
It holds for \(\ell =\zeta +1\) and so provides all \(\ell \). \(\square \)
Theorem 2
(idempotency) Let’s determine collection of BVCHFE as
\(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\). Let \(C_{\ell }=C\) for \((\ell =1,2,...,\varpi )\). Thus, \(BVCHFWDA(C_1,C_2,...C_\ell )=C\).
Proof
Firstly, let’s write BVCHFWDA operator:
since \(\sum _{\ell =1}^\varpi w_\ell =1\);
Thus, \(BVCHFWDA(C_1,C_2,...C_\varpi )=C\). \(\square \)
Theorem 3
(monotonicity) Let’s define two BVCHFSs that
\(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\) and \(C^*_\ell =\Big \{\{x,\{\xi _{C^*_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C^*_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C^*_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C^*_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\).
If \(C\le C^*\) \((\ell =1,2,...,\varpi )\), \(BVCHFWDA (C_{1},C_{2},...,C_{\varpi })\le BVCHFWDA(C_{1}^*,C_{2}^*,...,C_{\varpi }^*)\).
Proof
We know that \(C\le C^*\), in this statement
and thus
By similarity, the other part can be made. Thus, the proof is completed. \(\square \)
Theorem 4
(Boundedness) Let’s determine collection of BVCHFS as
\(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\) and \(C^p_\ell \) and \(C^n_\ell \) are the maximum and minimum elements. Thus, \(C^n_\ell \le BVCHFWDA(C_1,C_2,...,C_\varpi ) \le C^p_\ell.\)
Proof
Here, it is open that \( \begin{aligned} C_{{\ell _{p} }} = & max\{ C_{1} ,C_{2} ,...,C_{\varpi } \} = \left\{ {x,\;\left\{ {\xi _{{C_{{j_{{\ell _{p} }} }} }}^{ + } (x)e^{{i2\pi (\vartheta _{{\xi _{{C_{{j_{{\ell _{p} }} }} }}^{ + } }} )}} } \right\}} \right., \\ \left. {\left\{ {\xi _{{C_{{\wp _{{\ell _{p} }} }} }}^{ - } (x)e^{{i2\pi (\vartheta _{{\xi _{{C_{{\wp _{{\ell _{p} }} }} }}^{ - } }} )}} \} } \right\}} \right\} \\ \end{aligned} \) and
where
\(\xi _{C_{j_{\ell _p}}}^+=max\{\xi _{C_{j}}^+\}\), \(\vartheta _{\xi _{C_{j_{\ell _p}}}^+}=max\{\vartheta _{\xi _{C_{j}}^+}\}\), \(\xi _{C_{\wp _{\ell _p}}}^-=min\{\xi _{C_{\wp }}^-\}\), \(\vartheta _{\xi _{C_{\wp _{\ell _p}}}^-}=min\{\vartheta _{\xi _{C_{\wp }}^-}\}\), \(\xi _{C_{j_{\ell _n}}}^+=min\{\xi _{C_{j}}^+\}\), \(\vartheta _{\xi _{C_{j_{\ell _n}}}^+}=min\{\vartheta _{\xi _{C_{j}}^+}\}\), \(\xi _{C_{\wp _{\ell _n}}}^-=max\{\xi _{C_{\wp }}^-\}\), and \(\vartheta _{\xi _{C_{\wp _{\ell _n}}}^-}=max\{\vartheta _{\xi _{C_{\wp }}^-}\}.\)
From here,
By similarity, the other part can be made. Thus, the proof is completed. \(\square \)
5 Bipolar-Valued Complex Hesitant Fuzzy-Weighted Dombi Geometric Operators
Definition 8
Let’s determine a BVCHFE as
\(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\) for \(w_\ell \in [0,1]\) and \(\sum _{\ell =1}^\varpi w_\ell =1\);
-
1.
\(BVCHFWDG:\Phi ^\varpi \rightarrow \Phi \) is a mapping called as Bipolar-valued Complex Hesitant Fuzzy-Weighted Dombi Geometric operator for \(k> 0\) and \(w_\ell \in [0,1]\) and \(\sum _{\ell =1}^\varpi w_\ell =1\) and is defined as below:
$$\begin{aligned}{} & {} BVCHFWDG(C_1,C_2,...,C_\varpi ) =\displaystyle {\bigotimes _ {\ell =1}^\varpi \Big ((C_{\ell })^{w_\ell }\Big )}\nonumber \\{} & {} \quad = \left\{ \begin{array}{l}\displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} ({\check{\xi }}_{C_{j_1}}^+,{\check{\vartheta }}_{\xi _{C_{j_1}}^+})\in {C_1}, ({\check{\xi }}_{C_{j_2}}^+,{\check{\vartheta }}_{\xi _{C_{j_2}}^+})\in {C_2},...,({\check{\xi }}_{C_{j_\varpi }}^+,{\check{\vartheta }}_{\xi _{C_{j_\varpi }}^+})\in {C_\varpi } \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1-{\check{\xi }}_{C_{j_\ell }}^+}{{\check{\xi }}_{C_{j_\ell }}^+}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1-\frac{{\check{\vartheta }}_{\xi _{C_{j_\ell }}^+}}{2\pi }}{\frac{{\check{\vartheta }}_{\xi _{C_{j_\ell }}^+}}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} \\ \displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} ({\check{\xi }}_{C_{\wp _1}}^+,{\check{\vartheta }}_{\xi _{C_{\wp _1}}^+})\in {C_1}, ({\check{\xi }}_{C_{\wp _2}}^+,{\check{\vartheta }}_{\xi _{C_{\wp _2}}^+})\in {C_2},...,({\check{\xi }}_{C_{\wp _\varpi }}^+, {\check{\vartheta }}_{\xi _{C_{\wp _\varpi }}^+})\in {C_\varpi } \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}-1+\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{|{\check{\xi }}_{C_{\wp _\ell }}^-|}{1+{\check{\xi }}_{C_{\wp _\ell }}^-}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}-1+\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{\frac{|{\check{\vartheta }}_{\xi _{C_{\wp _\ell }}^-}|}{2\pi }}{1+\frac{{\check{\vartheta }}_{\xi _{C_{\wp _\ell }}^-}}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} \end{array}\right\} \end{aligned}.$$(6) -
2.
\(BVCHFOWDG:\Phi ^\varpi \rightarrow \Phi \) is a mapping called as Bipolar-valued Complex Hesitant Fuzzy-Ordered Weighted Dombi Geometric operator for \(k> 0\) and \(C_{\sigma (\ell )}\) is \(\ell th\) the largest of \(C_{\ell }\) for \((\ell =1,2,...,\varpi )\) and is defined as below:
$$\begin{aligned}{} & {} BVCHFOWDG(C_{1},C_{2},...,C_{\varpi })= \displaystyle {\bigotimes _ {\ell =1}^\varpi \Big ((C_{\sigma (\ell )})^{w_\ell }\Big )}\nonumber \\{} & {} \quad = \left\{ \begin{array}{l}\displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} ({\check{\xi }}_{C_{{j_\sigma (1)}}}^+,{\check{\vartheta }}_{\xi _{C_{{j_\sigma (1)}}}^+})\in {C_\sigma (1)}, ({\check{\xi }}_{C_{{j_\sigma (2)}}}^+,{\check{\vartheta }}_{\xi _{C_{{j_\sigma (2)}}}^+})\in {C_{\sigma (2)}},...,({\check{\xi }}_{C_{{j_\sigma (\varpi )}}}^+, {\check{\vartheta }}_{\xi _{C_{{j_\sigma (\varpi )}}}^+})\in {C_{\sigma (\varpi )}} \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1-{\check{\xi }}_{C_{j_\sigma (\ell )}}^+}{{\check{\xi }}_{C_{j_\sigma (\ell )}}^+}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1-\frac{{\check{\vartheta }}_{\xi _{C_{j_\sigma (\ell )}}^+}}{2\pi }}{\frac{{\check{\vartheta }}_{\xi _{C_{j_\sigma (\ell )}}^+}}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} \\ \displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} ({\check{\xi }}_{C_{{\wp _\sigma (1)}}}^+,{\check{\vartheta }}_{\xi _{C_{{\wp _\sigma (1)}}}^+})\in {C_\sigma (1)}, ({\check{\xi }}_{C_{{\wp _\sigma (2)}}}^+,{\check{\vartheta }}_{\xi _{C_{{\wp _\sigma (2)}}}^+})\in {C_{\sigma (2)}},...,({\check{\xi }}_{C_{{\wp _\sigma (\varpi )}}}^+, {\check{\vartheta }}_{\xi _{C_{{\wp _\sigma (\varpi )}}}^+})\in {C_{\sigma (\varpi )}} \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}-1+\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{|{\check{\xi }}_{C_{\wp _\sigma (\ell )}}^-|}{1+{\check{\xi }}_{C_{\wp _\sigma (\ell )}}^-}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}\frac{-1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{\frac{|{\check{\vartheta }}_{\xi _{C_{\wp _\sigma (\ell )}}^-}|}{2\pi }}{1+\frac{{\check{\vartheta }}_{\xi _{C_{\wp _\sigma (\ell )}}^-}}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} \end{array}\right\} \end{aligned}.$$(7) -
3.
\(BVCHFHWDG:\Phi ^\varpi \rightarrow \Phi \) is a mapping called as Bipolar-valued Complex Hesitant Fuzzy Hybrid-Weighted Dombi Geometric operator for \(k> 0\) and \(w_\ell \in [0,1]\) and \(\sum _{\ell =1}^\varpi w_\ell =1\) and \({\dot{C}}_{\sigma (\ell )}\) is \(\ell th\) the largest of \(\varpi w_\ell C_\varpi \) for aggregation-associated vector \(\omega _\ell =(\omega _1,\omega _2,...,\omega _\varpi )\), \(\omega _\ell \in [0,1]\), and \(\sum _{\ell =1}^\varpi \omega _\ell =1\) for \((\ell =1,2,...,\varpi )\) and is defined as below:
$$\begin{aligned}{} & {} BVCHFHWDG(C_{1},C_{2},...,C_{\varpi })= \displaystyle {\bigotimes _ {\ell =1}^\varpi \Big (({\dot{C}}_{\sigma (\ell )})^{w_\ell }\Big )}\nonumber \\{} & {} \quad = \left\{ \begin{array}{l}\displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} (\dot{{\check{\xi }}}_{C_{j_\sigma (1)}}^+,\dot{{\check{\vartheta }}}_{\xi _{C_{j_\sigma (1)}}^+})\in {{\dot{C}}_\sigma (1)}, (\dot{{\check{\xi }}}_{C_{j_\sigma (2)}}^+,\dot{{\check{\vartheta }}}_{\xi _{C_{j_\sigma (2)}}^+})\in {{\dot{C}}_{\sigma (2)}},...,(\dot{{\check{\xi }}}_{C_{j_\sigma (\varpi )}}^+, \dot{{\check{\vartheta }}}_{\xi _{C_{j_\sigma (\varpi )}}^+})\in {{\dot{C}}_{\sigma (\varpi )}} \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1-\check{\dot{\xi }}_{C_{j_\sigma (\ell )}}^+}{\check{\dot{\xi }}_{C_{j_\sigma (\ell )}}^+}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{1-\frac{\check{\dot{\vartheta }}_{\xi _{C_{j_\sigma (\ell )}}^+}}{2\pi }}{\frac{\check{\dot{\vartheta }}_{\xi _{C_{j_\sigma (\ell )}}^+}}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} \\ \displaystyle {\bigcup _{\begin{array}{l}\begin{array}{l} (\dot{{\check{\xi }}}_{C_{\wp _\sigma (1)}}^-,\dot{{\check{\vartheta }}}_{\xi _{C_{\wp _\sigma (1)}}^-})\in {{\dot{C}}_\sigma (1)}, (\dot{{\check{\xi }}}_{C_{\wp _\sigma (2)}}^-,\dot{{\check{\vartheta }}}_{\xi _{C_{\wp _\sigma (2)}}^-})\in {{\dot{C}}_{\sigma (2)}},...,(\dot{{\check{\xi }}}_{C_{\wp _\sigma (\varpi )}}^-, \dot{{\check{\vartheta }}}_{\xi _{C_{\wp _\sigma (\varpi )}}^-})\in {{\dot{C}}_{\sigma (\varpi )}} \end{array}\end{array}}}\\ \left\{ \begin{array}{l}\left\{ \begin{array}{l}-1+\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{|\check{\dot{\xi }}_{C_{\wp _\sigma (\ell )}}^-|}{1+\check{\dot{\xi }}_{C_{\wp _\sigma (\ell )}}^-}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} e^{i2\pi \left\{ \begin{array}{l}-1+\frac{1}{1+\left\{ \begin{array}{l}\sum _{\ell =1}^\varpi w_\ell \left( \begin{array}{l}\frac{\frac{|\check{\dot{\vartheta }}_{\xi _{C_{\wp _\sigma (\ell )}}^-}|}{2\pi }}{1+\frac{\check{\dot{\vartheta }}_{\xi _{C_{\wp _\sigma (\ell )}}^-}}{2\pi }}\end{array}\right) ^k\end{array}\right\} ^\frac{1}{k}}\end{array}\right\} }\end{array}\right\} \end{array}\right\} \end{aligned}.$$(8)
5.1 Characteristic of BVCHFWDG Operator
Theorem 5
Let’s determine collection of BVCHFE as \(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\) and \(\sum _{\ell =1}^\varpi w_\ell =1\). Then, their aggregated value using BVCHFWDG is a BVCHFE and it provides Eq. 6.
Proof
Let’s use mathematical induction on \(\varpi \) and look for \(\varpi =2\).
Firstly, if we write multiplication as follows:
From here for \(\varpi =\zeta \), BVCHFWDG holds as follows:
and for \(\varpi =\zeta +1\):
Thus,
it holds for \(\ell =\zeta +1\) and so provides all \(\ell \). \(\square \)
Theorem 6
(idempotency) Let’s determine collection of BVCHFE as
\(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\). Let \(C_{\ell }=C\) for \((\ell =1,2,...,\varpi )\). Thus, \(BVCHFWDG(C_1,C_2,...C_\ell )=C\).
Proof
Firstly, let’s write BVCHFWDG operator:
since \(\sum _{\ell =1}^\varpi w_\ell =1\);
Thus, \(BVCHFWDA(C_1,C_2,...C_\varpi )=C\). \(\square \)
Theorem 7
(monotonicity) Let’s define two BVCHFSs that \(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\) and \(C^*_\ell =\Big \{\{x,\{\xi _{C^*_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C^*_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C^*_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C^*_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\).
If \(C\le C^*\) \((\ell =1,2,...,\varpi )\), \(BVCHFWDG (C_{1},C_{2},...,C_{\varpi })\le BVCHFWDG(C_{1}^*,C_{2}^*,...,C_{\varpi }^*)\).
Proof
We know that \(C\le C^*\), in this statement
and thus
By similarity the other part can be made. Thus, the proof is completed. \(\square \)
Theorem 8
(Boundedness) Let’s determine collection of BVCHFS as \(C_\ell =\Big \{\{x,\{\xi _{C_{j_\ell }}^+(x)e^{i2\pi (\vartheta _{\xi _{C_{j_{\ell }}}^+})}:j=1,2,...,n\}, \{\xi _{C_{\wp _\ell }}^-(x)e^{i2\pi (\vartheta _{\xi _{C_{\wp _\ell }}^-})}:\wp =1,2,...,m\} \Big \}: x\in X \Big \}\) and \(C^p_\ell \) and \(C^n_\ell \) are maximum and minimum elements. Thus, \(C^n_\ell \le BVCHFWDG(C_1,C_2,...,C_\varpi ) \le C^p_\ell.\)
Proof
Here, it is open that
and
where
\(\xi _{C_{j_{\ell _p}}}^+=max\{\xi _{C_{j}}^+\}\), \(\vartheta _{\xi _{C_{j_{\ell _p}}}^+}=max\{\vartheta _{\xi _{C_{j}}^+}\}\), \(\xi _{C_{\wp _{\ell _p}}}^-=min\{\xi _{C_{\wp }}^-\}\), \(\vartheta _{\xi _{C_{\wp _{\ell _p}}}^-}=min\{\vartheta _{\xi _{C_{\wp }}^-}\}\), \(\xi _{C_{j_{\ell _n}}}^+=min\{\xi _{C_{j}}^+\}\), \(\vartheta _{\xi _{C_{j_{\ell _n}}}^+}=min\{\vartheta _{\xi _{C_{j}}^+}\}\), \(\xi _{C_{\wp _{\ell _n}}}^-=max\{\xi _{C_{\wp }}^-\}\), and \(\vartheta _{\xi _{C_{\wp _{\ell _n}}}^-}=max\{\vartheta _{\xi _{C_{\wp }}^-}\}.\)
From here,
By similarity, the other part can be made. Thus, the proof is completed. \(\square \)
6 An Application of Multi-attribute Decision-Making Method Under BVCHFS
In this section, we use the proposed BVCHFWDA and BVCHFWDG into an algorithm and test over a MCDM problem with m alternatives and n criterions to indicate effective of averaging and geometric operators over BVCHFSs. Let \(A=\{A_1,A_2,...,A_m\}\) be a set of alternatives, \(C=\{C_1,C_2,...,C_n\}\) be a set of criterions, and let \(w_j=(w_1,w_2,...,w_n)\) be a weight vector of criterions, where \(w_j>0, j=1,2,...,n\) and \(\sum _{j=1}^nw_j=1\). Then, the following steps have been defined for algorithm.
-
Step 1:
Determine Decision-making matrix as \(({\hat{C}}_{ij})_{m\times n}\) for \(i=1,2,...,m\) and \(j=1,2,...,n\),
-
Step 2:
Consist of Bipolar-valued Complex hesitant fuzzy elements by utilizing
\({\hat{C}}_{i}=BVCHFWDA({\hat{C}}_{i1},{\hat{C}}_{i2},...,{\hat{C}}_{in})\) and \({\hat{C}}_{i}=BVCHFWDG({\hat{C}}_{i1},{\hat{C}}_{i2},...,{\hat{C}}_{in})\) for \(i=1,2,...,m\),
-
Step 3:
Calculate score values of Bipolar-valued complex hesitant fuzzy elements,
-
Step 4:
Determine alternatives rankings in descending order,
-
Step 5:
Choose the best alternative.
The following Fig. 2 indicates to formal representation of above algorithm.
7 Numerical Example
A company wants to invest in different business sectors so has made some studies together with the experts of subjects and thus decision makers have developed five different alternatives based on three criterions as follows: \(A_1\); a computer production company, \(A_2\); a communication company, \(A_3\); a food company, \(A_4\); a car company, \(A_5\); an airport company; if criterions, \(C_1\); environment impact, \(C_2\); the proximity to raw material, \(C_3\); and cost and for criterions determined weights by decision makers as follows: \(w=(0.3,0.5,0.2)\).
-
Step 1:
Decision makers construct decision-making matrix as follows in Table 1.
-
Step 2:
Obtain Bipolar-valued Complex hesitant fuzzy elements by utilizing BVCHFWDA and BVCHFWDG operator \(C_i\) for \(i=1,2,3,4,5\) and \(k=1\) as follows:
$$\begin{aligned}{} & {} {\hat{C}}_1=BVCHFWDA({\hat{C}}_{11},{\hat{C}}_{12},{\hat{C}}_{13})\\{} & {} \quad = \left\{ \begin{array}{l}\Big \{0.8125e^{i2\pi (0.4713)}, 0.7391e^{i2\pi ( 0.5041)}, 0.7983e^{i2\pi ( 0.5667)}, 0.7916e^{i2\pi ( 0.6962)}, 0.7e^{i2\pi ( 0.6685)}\\ , 0.7954e^{i2\pi ( 0.8227)}, 0.7108e^{i2\pi ( 0.5890)}, 0.6969e^{i2\pi ( 0.7073)}, 0.7740e^{i2\pi ( 0.7303)}, 0.6581e^{i2\pi ( 0.7391)},\\ 0.6428e^{i2\pi ( 0.7735)}, 0.5876e^{i2\pi ( 0.7931)}, 0.5754e^{i2\pi ( 0.8775)}, 0.7704e^{i2\pi ( 0.8579)}, 0.7049e^{i2\pi ( 0.8265)},\\ 0.6498e^{i2\pi (0.8604)}, 0.6619e^{i2\pi ( 0.7087)}, 0.6538e^{i2\pi ( 0.8522)} \Big \}, \Big \{-\,0.2307e^{i2\pi ( -\,0.1935)}, -\,0.2727e^{i2\pi ( -\,0.1898)},\\ -\,0.25e^{i2\pi ( -0.4129)}, -0.2631e^{i2\pi ( -\,0.2278)}, -\,0.3e^{i2\pi ( -\,0.3965)}, -\,0.3191e^{i2\pi ( -\,0.2227)}, -\,0.2884e^{i2\pi ( -0.6083)},\\ -\,0.3571e^{i2\pi ( -0.5734)} \Big \}\end{array}\right\} \\{} & {} {\hat{C}}_2=BVCHFWDA({\hat{C}}_{21},{\hat{C}}_{22},{\hat{C}}_{23})\\{} & {} \quad = \left\{ \begin{array}{l}\Big \{0.9446e^{i2\pi (0.4285)}, 0.9438e^{i2\pi ( 0.2586)}, 0.5225e^{i2\pi ( 0.5508)}, 0.9444e^{i2\pi ( 0.4591)},0.9433e^{i2\pi ( 0.5769)}\\ , 0.4886e^{i2\pi ( 0.3895)}, 0.4578e^{i2\pi ( 0.4520)}, 0.9436e^{i2\pi ( 0.3092)}, 0.5055e^{i2\pi ( 0.5699)}, 0.4357e^{i2\pi ( 0.4802)},\\ 0.9431e^{i2\pi ( 0.5939)}, 0.3835e^{i2\pi ( 0.6597)}, 0.3258e^{i2\pi ( 0.5745)}, 0.4690e^{i2\pi ( 0.4243)}, 0.4136e^{i2\pi ( 0.1915)},\\ 0.3877e^{i2\pi ( 0.2514)}, 0.4098e^{i2\pi ( 0.6478)}, 0.3571e^{i2\pi ( 0.5559)} \Big \}, \Big \{-0.3097e^{i2\pi ( -\,0.4102)}, -\,0.3335e^{i2\pi ( -\,0.5109)},\\ -\,0.3278e^{i2\pi ( -\,0.3100)}, -\,0.3097e^{i2\pi ( -\,0.4305)}, -\,0.3547e^{i2\pi ( -\,0.3642)}, -\,0.3335e^{i2\pi ( -\,0.5428)},\\ -\,0.3278e^{i2\pi ( -\,0.3214)}, -\,0.3547e^{i2\pi ( -\,0.3801)} \Big \}\end{array}\right\} \\{} & {} {\hat{C}}_3=BVCHFWDA({\hat{C}}_{31},{\hat{C}}_{32},{\hat{C}}_{33})\\{} & {} \quad = \left\{ \begin{array}{l}\Big \{0.4633e^{i2\pi (0.4713)}, 0.3985e^{i2\pi ( 0.7590)}, 0.4492e^{i2\pi ( 0.3254)}, 0.4613e^{i2\pi ( 0.5269)}, 0.2480e^{i2\pi (0.5056)},\\ 0.4363e^{i2\pi ( 0.3919)}, 0.3808e^{i2\pi ( 0.7326)}, 0.3960e^{i2\pi ( 0.7712)}, 0.4471e^{i2\pi ( 0.4133)}, 0.3781e^{i2\pi ( 0.7476)},\\ 0.2440e^{i2\pi ( 0.5545)}, 0.2158e^{i2\pi ( 0.4552)}, 0.1893e^{i2\pi ( 0.4994)}, 0.4340e^{i2\pi ( 0.4642)}, 0.3644e^{i2\pi ( 0.7438)},\\ 0.3616e^{i2\pi ( 0.7575)}, 0.2200e^{i2\pi ( 0.3803)}, 0.1938e^{i2\pi ( 0.4369)} \Big \}, \Big \{-\,0.2927e^{i2\pi ( -\,0.1949)}, -\,0.3778e^{i2\pi ( -\,0.2249)},\\ -\,0.3830e^{i2\pi ( -\,0.3394)}, -\,0.2944e^{i2\pi ( -\,0.1838)}, -\,0.5428e^{i2\pi ( -\,0.4418)}, -\,0.3805e^{i2\pi (-\,0.2102)},\\ -\,0.3858e^{i2\pi ( -\,0.3071)}, -\,0.5484e^{i2\pi ( -\,0.3886)} \Big \}\end{array}\right\} \\{} & {} {\hat{C}}_4=BVCHFWDA({\hat{C}}_{41},{\hat{C}}_{42},{\hat{C}}_{43})\\{} & {} \quad = \left\{ \begin{array}{l}\Big \{0.3333e^{i2\pi (0.1823)}, 0.3225e^{i2\pi ( 0.2558)}, 0.2544e^{i2\pi ( 0.3745)}, 0.3170e^{i2\pi ( 0.2349)}, 0.3191e^{i2\pi ( 0.2328)}, \\ 0.2544e^{i2\pi ( 0.6772)}, 0.2409e^{i2\pi ( 0.4181)}, 0.3057e^{i2\pi ( 0.2992)}, 0.2340e^{i2\pi ( 0.4055)}, 0.2198e^{i2\pi (0.4450)},\\ 0.3021e^{i2\pi ( 0.2789)}, 0.2152e^{i2\pi ( 0.4324)}, 0.2152e^{i2\pi ( 0.6934)}, 0.2340e^{i2\pi ( 0.6857)}, 0.2409e^{i2\pi ( 0.6893)},\\ 0.2198e^{i2\pi ( 0.6971)}, 0.2366e^{i2\pi ( 0.4042)}, 0.2366e^{i2\pi ( 0.6853)} \Big \}, \Big \{-\,0.3208e^{i2\pi ( -\,0.4516)}, -\,0.4444e^{i2\pi ( -\,0.3111)},\\ -\,0.3488e^{i2\pi ( -0.4179)}, -0.3389e^{i2\pi ( -\,0.6829)}, -\,0.5e^{i2\pi ( -\,0.2947)}, -\,0.48e^{i2\pi ( -\,0.4058)}, -\,0.3703e^{i2\pi ( -\,0.6087)},\\ -\,0.5454e^{i2\pi ( -\,0.3783)} \Big \}\end{array}\right\} \\{} & {} {\hat{C}}_5=BVCHFWDA({\hat{C}}_{51},{\hat{C}}_{52},{\hat{C}}_{53})\\{} & {} \quad = \left\{ \begin{array}{l}\Big \{0.5483e^{i2\pi (0.2161)}, 0.5483e^{i2\pi (0.2577)}, (0.5135e^{i2\pi ( 0.2674)}, 0.6315e^{i2\pi ( 0.5130)}, 0.3538e^{i2\pi ( 0.3739)},\\ 0.5012e^{i2\pi ( 0.2258)}, 0.5135e^{i2\pi ( 0.3038)}, 0.6315e^{i2\pi ( 0.5294)}, 0.6086e^{i2\pi ( 0.5333)}, 0.6086e^{i2\pi ( 0.5483)},\\ 0.5116e^{i2\pi ( 0.5789)}, 0.4705e^{i2\pi ( 0.5942)}, 0.4560e^{i2\pi ( 0.5817)}, 0.6008e^{i2\pi ( 0.5168)},\\ 0.5012e^{i2\pi ( 0.2664)}, 0.6008e^{i2\pi ( 0.5329)}, 0.28e^{i2\pi ( 0.4070)}, 0.2528e^{i2\pi ( 0.3801)} \Big \}, \Big \{-\,0.2557e^{i2\pi ( -\,0.5157)},\\ -\,0.4148e^{i2\pi ( -\,0.5157)}, -\,0.2603e^{i2\pi ( -\,0.1606)}, -\,0.2611e^{i2\pi ( -\,0.2692)}, -\,0.4271e^{i2\pi ( -\,0.1606)},\\ -\,0.4293e^{i2\pi ( -\,0.2692)}, -\,0.2659e^{i2\pi ( -\,0.125)}, -\,0.4425e^{i2\pi ( -\,0.125)} \Big \}\end{array}\right\} \end{aligned}.$$Here, we only give for \(k=1\) and score values are for the all cases as follows:
-
Step 3:
Score values are for the all cases as follows:
Here, we present to Table 2 for BVCHFWDA that our results are agreement for ideal element. While the most desirable alternative is \(A_1\), the most undesirable alternative is \(A_4\). Figure 3 indicates graphical presentation of Table 2. It is open that our results are agreement in its own from Fig. 3.
In here, we present to Table 3 for BVCHFWDG that our results are agreement for ideal element. While the most desirable alternative is \(A_1\), the most undesirable alternative is \(A_3\). Figure 4 indicates graphical presentation of Table 3. It is open that our results are agreement in its own from Figure 4.
-
Step 4:
If the tables are surveyed, the best alternative is \(A_1\) for each two operators and the worst alternatives are \(A_4\) and \(A_3\) for all values of k under BVCHFWDA and BVCHFWDG. This statement indicates that our proposed cluster and method are agreement, reality, and objective in its own for the most desirable choice.
8 Comparative Analysis
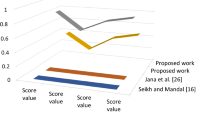
In this section, we compare the proposed operators BVCHFWDA and BVCHFWDG with different measures. To do this, firstly we utilize Bipolar complex fuzzy sets (BCFSs) [3] and some distance measures over BCFSs. Moreover, it should be noted that our proposed operators and cluster are agreement with this distance measure but have more advantages that having hesitation degree and generalized concept, like dombi operators. Here, we calculate for \(k=1,2,3,4,5\) dombi operators. The results are as following;
Here, we present to Table 4 for first comparative that our results are agreement in terms of desirable alternative and undesirable alternative that the most desirable choice is \(A_4\) and if the most undesirable choice is to change between \(A_1\) and \(A_2\) for \(k=1,2\) and \(k=3,4,5\), respectively. As can be seen from the values, the proposed operator is agreement, reality, and objective.
In here, we present to Table 4 for second comparative that our results are not agreement in terms of desirable alternative and undesirable alternative that the most desirable choice is \(A_3\) and the most undesirable choice is \(A_4\).
The main findings are ordered as follows:
-
BVCHFSs are a much more comprehensive cluster than Bipolar Complex Fuzzy sets. Therefore, as can be seen from Table 6, it contains many clusters within itself.
-
Each negative and positive membership value are divided into two part, ensuring that the decisions given by decision makers are more objective.
-
By providing a degree of hesitation, more information is conveyed.
Moreover, we put to \(-0.99e^{i2\pi (-0.5)}\) instead of \(-1e^{i2\pi (-0.5)}\) to avoid from undefined situation over obtained results using BVCHFWDG.
If the above characteristic comparisons in Table 6 are surveyed, it is open that our proposed cluster scans a wide environment. Thus, our concept holds into its own structure to other concepts. This statement eliminates to error margin for MCDM problems because of interpreted an each alternative more details.
9 Conclusion
This paper aims to develop bipolar-valued complex hesitant fuzzy sets by developing complex hesitant fuzzy sets (CHFSs) to overcome with unclear information. The extra cluster has been added in the CHFSs that this set is obtained by adding a lot of values created by closed interval \([-1,0]\). Structures created without presenting negative views cannot have a real application area, because in real life, everything is known by its opposite. Therefore, the structures based on negative ideas give more objective results. In this context, firstly, we construct Bipolar-valued complex hesitant fuzzy sets and some properties such as addition, multiplication, and scalar multiplication and scalar power to conduct more comprehensive information. When compared with traditional concepts, Bipolar-valued complex hesitant fuzzy sets can significantly avoid from error margin. In many daily-life situations, BCHFSs are needed to decide. For example, when insuring a vehicle, a car insurance company has to consider from different aspects, such as the accident rate of the person, whether there is a house with a garage and the cost of the vehicle. Thus, thanks to cluster’s bipolar structure, prejudice and objective thought can be presented together. The real and imaginary part of the concept involve evaluating an alternative from two different perspectives. Furthermore, hesitant construction allows to multiple evaluations desired experts at the same time. Moreover, this concept is integrated with dombi operators which having a soft instruction. In daily life, flexible structures are used more active than structures with sharper lines because of ability to make comparison analysis into its own. The contributions of paper can be ordered in literature as follows:
-
1.
Bipolar complex hesitant fuzzy sets and some basic properties have been developed as a new concept;
-
2.
Bipolar-valued Complex Hesitant Fuzzy-Weighted Dombi Averaging operator, Ordered, and Hybrid concepts and Bipolar-valued Complex Hesitant Fuzzy-Weighted Dombi Geometric operator, Ordered, and Hybrid concepts have been proposed;
-
3.
The score function has been given;
-
4.
The decision-making algorithm and a problem have been discussed for two operators and the results of presented operators have been compared in their own;
-
5.
A comparative analysis has been made with distance measures over bipolar Complex fuzzy sets.
In future time, we plan to construct several basic constructions like Hamacher aggregation operators, Prioritized Aggregation Operators, Power aggregation operator, Hamming, Housdorff, Euclidean distance measures, correlation coefficient, and similarity measures.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article.
References
Zadeh, L.A.: Fuzzy sets. Inf. Control 8(3), 338–353 (1965)
Ramot, D., Milo, R., Friedman, M., Kandel, A.: Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 10(2), 171–186 (2002)
Alkouri, A.U.M., Massa’deh, M.O., Ali, M.: On bipolar complex fuzzy sets and its application. J. Intell. Fuzzy Syst. 39(1), 383–397 (2020)
Torra, V.: Hesitant fuzzy sets. Int. J. Intell. Syst. 25(6), 529–539 (2010)
Mandal, P., Ranadive, A.: Hesitant bipolar-valued fuzzy sets and bipolar-valued hesitant fuzzy sets and their applications in multi-attribute group decision making. Granul. Comput. 4(3), 559–583 (2019)
Mahmood, T., Rehman, Uu., Ali, Z.: Exponential and non-exponential based generalized similarity measures for complex hesitant fuzzy sets with applications. Fuzzy Inform. Eng. 12(1), 38–70 (2020)
Li, D.-F., Mahmood, T., Ali, Z., Dong, Y.: Decision making based on interval-valued complex single-valued neutrosophic hesitant fuzzy generalized hybrid weighted averaging operators. J. Intell. Fuzzy Syst. 38(4), 4359–4401 (2020)
Mahmood, T., Ur Rehman, U., Ali, Z., Chinram, R.: Jaccard and dice similarity measures based on novel complex dual hesitant fuzzy sets and their applications. Math. Probl. Eng. 2020, 1–25 (2020)
Ur Rehman, U., Mahmood, T., Ali, Z., Panityakul, T.: A novel approach of complex dual hesitant fuzzy sets and their applications in pattern recognition and medical diagnosis. J. Math. 2021, 1–31 (2021)
Mahmood, T., Ur Rehman, U., Ali, Z., Mahmood, T.: Hybrid vector similarity measures based on complex hesitant fuzzy sets and their applications to pattern recognition and medical diagnosis. J. Intell. Fuzzy Syst. 40(1), 625–646 (2021)
Alkouri, A.M.J.S., Salleh, A.R.: Complex intuitionistic fuzzy sets. AIP Conf. Proceed. 1482, 464–470 (2012)
Garg, H., Ali, Z., Yang, Z., Mahmood, T., Aljahdali, S.: Multi-criteria decision-making algorithm based on aggregation operators under the complex interval-valued q-rung orthopair uncertain linguistic information. J. Intell. Fuzzy Syst. 41(1), 1627–1656 (2021)
Akram, M., Kahraman, C., Zahid, K.: Extension of topsis model to the decision-making under complex spherical fuzzy information. Soft. Comput. 25(16), 10771–10795 (2021)
Akram, M., Peng, X., Sattar, A.: Multi-criteria decision-making model using complex pythagorean fuzzy yager aggregation operators. Arab. J. Sci. Eng. 46, 1691–1717 (2021)
Ullah, K., Mahmood, T., Ali, Z., Jan, N.: On some distance measures of complex pythagorean fuzzy sets and their applications in pattern recognition. Complex Intell. Syst. 6, 15–27 (2020)
Ma, X., Zhan, J., Khan, M., Zeeshan, M., Anis, S., Awan, A.S.: Complex fuzzy sets with applications in signals. Comput. Appl. Math. 38, 1–34 (2019)
Al-Qudah, Y., Hassan, N.: Operations on complex multi-fuzzy sets. J. Intell. Fuzzy Syst. 33(3), 1527–1540 (2017)
Hu, B., Bi, L., Dai, S., Li, S.: Distances of complex fuzzy sets and continuity of complex fuzzy operations. J. Intell. Fuzzy Syst. 35(2), 2247–2255 (2018)
Dick, S., Yager, R.R., Yazdanbakhsh, O.: On pythagorean and complex fuzzy set operations. IEEE Trans. Fuzzy Syst. 24(5), 1009–1021 (2015)
Lee, K.M.: Bipolar-valued fuzzy sets and their operations. In: Proc. Int. Conf. on Intelligent Technologies, Bangkok, Thailand, 2000, pp. 307–312 (2000)
Zhang, W.-R.: (yin)(yang) bipolar fuzzy sets. In: 1998 IEEE International Conference on Fuzzy Systems Proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98CH36228), vol. 1, pp. 835–840 (1998). IEEE
Zhang, W.-R.: Bipolar fuzzy sets and relations: a computational framework for cognitive modeling and multiagent decision analysis. In: NAFIPS/IFIS/NASA’94. Proceedings of the First International Joint Conference of The North American Fuzzy Information Processing Society Biannual Conference. The Industrial Fuzzy Control and Intellige, pp. 305–309 (1994). IEEE
Gulistan, M., Yaqoob, N., Elmoasry, A., Alebraheem, J.: Complex bipolar fuzzy sets: an application in a transport’s company. J. Intell. Fuzzy Syst. 40(3), 3981–3997 (2021)
Mahmood, T., Ur Rehman, U.: A novel approach towards bipolar complex fuzzy sets and their applications in generalized similarity measures. Int. J. Intell. Syst. 37(1), 535–567 (2022)
Singh, P.K.: Bipolar \(\delta \)-equal complex fuzzy concept lattice with its application. Neural Comput. Appl. 32(7), 2405–2422 (2020)
Broumi, S., Bakali, A., Talea, M., Smarandache, F., Singh, P.K., Uluçay, V., Khan, M.: Bipolar complex neutrosophic sets and its application in decision making problem. Fuzzy Multi-criteria Decis.-Mak. Neutrosophic Sets 65, 677–710 (2019)
Akram, M., Ali, M., Allahviranloo, T.: A method for solving bipolar fuzzy complex linear systems with real and complex coefficients. Soft. Comput. 26(5), 2157–2178 (2022)
Farooq, A., Ali Al-Shamiri, M.M., Khalaf, M.M., Amjad, U., et al.: Decision-making approach with complex bipolar fuzzy n-soft sets. Math. Probl. Eng. 2022, 1–22 (2022)
Gwak, J., Garg, H., Jan, N.: Hybrid integrated decision-making algorithm for clustering analysis based on a bipolar complex fuzzy and soft sets. Alex. Eng. J. 67, 473–487 (2023)
Akram, M., Shumaiza, Rodríguez Alcantud, J.C.: Extended vikor method based with complex bipolar fuzzy sets. In: Multi-criteria Decision Making Methods with Bipolar Fuzzy Sets, pp. 93–122. Springer, (2023)
Jan, N., Gwak, J., Pamucar, D.: A robust hybrid decision making model for human-computer interaction in the environment of bipolar complex picture fuzzy soft sets. Inf. Sci. 645, 119163 (2023)
Dombi, J.: A general class of fuzzy operators, the demorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst. 8(2), 149–163 (1982)
Jana, C., Senapati, T., Pal, M., Yager, R.R.: Picture fuzzy dombi aggregation operators: Application to madm process. Appl. Soft Comput. 74, 99–109 (2019)
He, X.: Typhoon disaster assessment based on dombi hesitant fuzzy information aggregation operators. Nat. Hazards 90, 1153–1175 (2018)
Akram, M., Khan, A.: Complex pythagorean dombi fuzzy graphs for decision making. Granul Comput. 6, 645–669 (2021)
Akram, M., Dudek, W.A., Dar, J.M.: Pythagorean dombi fuzzy aggregation operators with application in multicriteria decision-making. Int. J. Intell. Syst. 34(11), 3000–3019 (2019)
Liu, P., Liu, J., Chen, S.-M.: Some intuitionistic fuzzy dombi bonferroni mean operators and their application to multi-attribute group decision making. J. Oper. Res. Soc. 69(1), 1–24 (2018)
Chen, J., Ye, J.: Some single-valued neutrosophic dombi weighted aggregation operators for multiple attribute decision-making. Symmetry 9(6), 82 (2017)
Jana, C., Pal, M., Wang, J.-q: Bipolar fuzzy dombi aggregation operators and its application in multiple-attribute decision-making process. J. Ambient. Intell. Humaniz. Comput. 10, 3533–3549 (2019)
Jana, C., Pal, M., Wang, J.-q: Bipolar fuzzy dombi prioritized aggregation operators in multiple attribute decision making. Soft. Comput. 24, 3631–3646 (2020)
Shi, L., Ye, J.: Dombi aggregation operators of neutrosophic cubic sets for multiple attribute decision-making. Algorithms 11(3), 29 (2018)
Funding
Open access funding provided by the Scientific and Technological Research Council of Türkiye (TÜBİTAK).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Özlü, Ş. Bipolar-Valued Complex Hesitant fuzzy Dombi Aggregating Operators Based on Multi-criteria Decision-Making Problems. Int. J. Fuzzy Syst. (2024). https://doi.org/10.1007/s40815-024-01770-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40815-024-01770-8