1 Introduction

In recent times, sustainable supply chain management (SSCM) has extensively been received an immense consideration because of the increasing environmental issues, public consciousness, strict government schemes and economic motivation. It is a broader term containing all the triple bottom lines of sustainability including people (social), planet (environmental) and profits (economical), while green supply chain management (GSCM) only focuses on the planet aspects of sustainability (Tseng et al. 2015; Ghisellini et al. 2018). Businesses that are involved in supply chain management (SCM) under sustainability usually have to execute a goal by reducing negative impact on environment, minimizing costs, capitalize on both productivity level and social well-being (Hassini et al. 2012).

The extended responsible principle (ERP) standardizes that the industries are accountable for their consumption (Bellmann and Khare 2000). As for industrial candidates, they necessitate to emphasis on sustainability in the process of manufacturing with the aim that capitalize the eco-economy and diminishing manufacturing wastes. In the present growing eco-economy, the businesses tend to focus on the SSCM operations which include sustainable plan, production, scrapping and consumption, respectively. Accordingly, numerous articles have been presented in the literature, for instance, product design assessment (Bellmann and Khare 2000), material/technology/procedure practices (Wu et al. 2016) and logistics services (Wang and Lv 2015) from sustainable point of view.

Generally, the investigations executed into end-of-life (EOL) products can be classified as analyses related to policies and instructions, investigations on recycling-based equipment and surveys on assessed activities. A sustainable recycling partner (SRP) is proficient to help the companies for sponsoring the SSCM performances (Sabaghi et al. 2015). The concept of ‘‘3R (reduce, reuse, recycle)’’ encourages the manufacturers to consider the accountability of the individual scrapped substances/objects. Several practices in vivid manufacturing organizations namely Apple, Foxconn and Ford, have been taken this principle into consideration (Ghisellini et al. 2018). Most of the previously recycling businesses have happened in multinational corporations due to its excellent position and intense benefits. Alternatively, for small and medium-sized enterprises (SMEs), it is of a great significance to implement the recycling trade in both applied and theoretical modes. Therefore, it is required to investigate a systematic framework for selecting a suitable recycling partner with the aim that can effectively deal with the scrapped goods of SMEs. In recent times, many research efforts have been made on sustainable performances of the forward SCM (Seuring and Muller 2008), but few studies have been conducted on after-sale business such as consumption and scrapping activities. Therefore, the present study encourages for developing and utilizing an innovative multi-criteria decision-making (MCDM) technique to improve the mentioned flaw. In general, the SRP assessment process involves several alternatives and criteria, so this process is usually treated as an MCDM problem. The main objective of the SRP assessment problem is to find the suitable recycling partner that satisfies a number of qualitative and quantitative criteria (Zhou et al. 2018; Li et al. 2020).

In the practice of assessing diverse recycling partners, there are several qualitative criteria, such as brand reputation and customer satisfaction. In reality, it is complicated for the decision experts (DEs) to give accurate numerical values to these criteria. In order to address such types of problems, Zadeh (1965) pioneered the fuzzy set (FS) theory, which is represented by a belongingness degree (BD). The notion of FS has received ample range of concerns and in-depth studies in different disciplines. As the generalization of FS, the concepts of intuitionistic fuzzy set (IFS) (Atanassov 1986) and Pythagorean fuzzy set (PFS) (Yager 2014) have been introduced in the literature. To overcome the drawbacks of IFS and PFS, Yager (2017) proposed the notion of q-rung orthopair fuzzy set (q-ROFS). The constraint condition of q-ROFS is that the addition of qth-power of belongingness degree and non-belongingness degree is restricted to unity. If q = 1, the q-ROFSs are transformed into the IFSs; if q = 2, the q-ROFSs are converted into the PFSs, which means that the q-ROFSs are extended form of IFSs and PFSs. The q-ROFSs can be employed to address more complex fuzzy information as the value of the flexible parameter q can be dynamically regulated to decide the information representation space. Consequently, in comparison with IFS and PFS, q-ROFS is more general and flexible. Thus, the present study aims to propose a q-rung orthopair fuzzy (q-ROF) information-based approach for better dealing with the uncertain and inexact data.

1.1 Contributions and organization of the study

Consequently, the key contributions of the study are discussed as

  • Novel entropy and discrimination measures are discussed under q-ROFS context.

  • An innovative procedure is introduced to determine the decision experts’ weights.

  • A novel weighting procedure by integrating objective and subjective weighting approaches is presented to compute the criteria weights.

  • Classical ARAS technique is extended within the context of q-ROFSs for dealing with the complex MCDM problems with unidentified decision experts and criteria weights.

  • A case study of SRP assessment problem is considered to display the usefulness and flexibility within q-ROFSs context. Sensitivity investigation and comparative study are discussed to certify the obtained outcomes.

The remaining sections are systematized as follows: Sect. 2 shows comprehensive review related to the present work. Section 3 discusses some fundamental notions of q-ROFSs. Section 4 develops new entropy and discrimination measures for q-ROFSs. In addition, comparative studies are presented to validate the effectiveness of the developed measures. Section 5 introduces a novel q-ROF-ARAS framework using entropy and discrimination measures. Section 6 confers a case study of SRP assessment problem with q-ROF information. Further, sensitivity investigation and comparison are also deliberated. Finally, Sect. 7 illustrates the conclusions and suggestions for further research.

2 Literature review

2.1 q-rung orthopair fuzzy set (q-ROFS)

Uncertainty is a very significant aspect in the process of MCDM. Handling uncertainty requires a flexible and powerful tool because of the vagueness and imprecision involved in human subjective judgments, and the objective complexity of practical decision-making situations. To handle such types of problems, Zadeh (1965) originated the notion of FS theory, which has become an effective tool for deciphering MCDM issues with imprecise or vague information. Further, Atanassov (1986) suggested the theory of IFS, which is an extension of Zadeh’s FSs. Compared to FS, IFS is made up of belongingness degree (BD) and non-belongingness degree (NBD), in which their addition is ≤ 1. Therefore, it can more elegantly describe the fuzzy evaluation values. However, the IFSs cannot handle the situation in which the addition of the BD and NBD is higher than one. To address this limitation, Yager (2014) extended the concept of IFS to PFS. It is also represented by the degree of both belongingness and non-belongingness wherein their squares sum of BD and NBD is ≤ 1. It is worth mentioning that the main difference between PFS and IFS is their different constraint conditions. Hence, it is clear that the range of the Pythagorean fuzzy value is larger than the range of an intuitionistic fuzzy value. Consequently, the PFSs allow better freedom to the DEs for expressing their views regarding the ambiguity of the problem. Due to its uniqueness, PFSs have been implemented in several disciplines (Abdullah and Goh, 2019; Deb and Roy 2021).

Owing to the complexity of MCDM problems and the conflicting psychology of DEs, it is still not easy for PFSs to model the corresponding uncertain information. For instance, consider that a DE express his/her opinion in (0.9, 0.6), neither the IFS nor PFS can model this case because 0.9 + 0.6 > 1 and 0.92 + 0.62 > 1. In view of this, Yager (2017) originated the theory of q-ROFS, wherein the addition of the qth powers of the BD and NBD is restricted to unity. Evidently, the q-ROFSs are generalization of the PFSs and IFSs. This flexibility of q-ROFSs gives an ample sovereignty for the depiction of uncertain information. As a result, the q-ROFSs have more flexibility and stronger capability than the IFS and PFS in order to deal with uncertain information. Due to such advantages, the q-ROFSs have gotten extensive researches and applications. For example, Liu and Wang (2018) studied various aggregation operators (AOs) on q-ROFSs. Liu and Liu (2018) defined some q-ROF Bonferroni mean operators. Inspired by the classical Heronian mean operator, Liu et al. (2018a) proposed some q-ROF information based Heronian mean operators and their weighted forms. Pinar and Boran (2020) established an integrated model based on distance measure for q-ROFSs and employed for evaluating the suppliers. Yang and Pang (2020) studied a number of q-ROF Bonferroni mean Dombi operators and their relevance in MCDM applications. Garg and Chen (2020) suggested some neutral AOs on q-ROFSs. Tang et al. (2020) designed a pioneering framework to cope with three-way decision problem under q-ROFS context. Darko and Liang (2020) originated a series of q-ROF Hamacher AOs and their applications. Krishankumar et al. (2020) proposed a decision model for solving the renewable energy resource assessment problem with q-ROF information. Further, an attempt has been accomplished to create an innovative q-ROF information based decision-making method for solving the MCDM problems (Arya and Kumar 2020). Recently, Alkan and Kahraman (2021) studied two extended q-ROF information based methods for assessing the government strategies against COVID-19 outbreak. In a study, a novel q-ROF-information based VIKOR (VlseKriterijumska Optimizacija I Kompromisno Resenje) technique has been introduced to evaluate and rank the manufacturing small and mid-size enterprises (Cheng et al. 2021). However, no study has developed an innovative q-ROF-information based MCDM method for evaluating and prioritizing the SRP candidates.

2.2 Additive ratio assessment (ARAS)

The ARAS approach, pioneered by Zavadskas and Turskis (2010), is an innovative method which is based on the philosophy that the phenomenon of complex domains with contradictory attributes can be demonstrated by utilizing effortless relative comparisons. This technique utilizes the notion of optimality degree to find a ranking. The main advantages of ARAS approach are as (i) direct and proportional relationship with criterion weights (Dahooie et al. 2018); (ii) potential to handle extremely complicated problems (Buyukozkan and Guler 2020) and (iii) consists of direct and easy processes, which yield satisfactory, realistic and reasonably accurate results in evaluating and prioritizing various alternatives (Ghenai et al. 2019). Recently, there have been many studies regarding the extension of classical ARAS approach. For instance, Ecer (2018) applied the combined AHP (Analytic hierarchy process) with ARAS method on FSs. Dahooie et al. (2018) developed the SWARA (Step-wise Weight Assessment Ratio Analysis) with Grey ARAS model to deal with IT personnel assessment issue. Rani et al. (2020b) made use of the SWARA-ARAS framework to assess the healthcare waste treating method Rostamzadeh et al. (2020) initiated a fuzzy ARAS model and its relevance in MCDM problems. Recently, Mishra et al. (2021a) suggested an integrated ARAS method to evaluate and prioritize the locations for the EVCS. Jin et al. (2021) gave a collective methodology by combining the maximizing deviation method and the ARAS technique with interval-valued q-ROFSs and applied to evaluate the MCDM problems. In a study, interval type-2 fuzzy information based ARAS model has been introduced to assess the recycling facility problems (Karagöz et al. 2021). Further, a hybrid model based on hesitant fuzzy ARAS technique has been developed for the treatment of mild symptoms of COVID-19 disease (Mishra et al. 2021b). Gül (2021) studied the Fermatean fuzzy extension of ARAS method and its application in COVID-19 testing laboratory selection problem. Inspired by interval type-2 fuzzy set, Dorfeshan et al. (2021) introduced an improved ARAS technique for critical path selection of engineering projects. Liu and Xu (2021) presented an overview of ARAS technique from the perspectives of fundamental information, development on the theory and application, and the future challenges. In conclusion, there is no study regarding the development of ARAS method under q-ROFS context.

2.3 Approaches for SRP assessment

Selection of the most suitable SRP candidate has been considered as a MCDM problem concerning both the quantitative and qualitative uncertain information. In this regard, few existing literatures have focused their attention on the analysis of SRP evaluation. For example, Zhou et al. (2018) designed a hybrid model with DEMATEL (Decision-making trial and evaluation laboratory), AEW (Anti-entropy weighting) and VIKOR approaches within fuzzy environment and then, utilized to select an appropriate SRP for SMEs. Kumar and Dixit (2019) prepared a collective framework for WEEE (Waste Electrical and Electronic Equipment) recycling partner evaluation with green competencies. Rani and Mishra (2020a,b) suggested a new Combined Compromise Solution model for evaluating sustainable WEEE recycling partners under single-valued neutrosophic environment. In a study, Li et al. (2020) proposed the probabilistic linguistic influence relations between attributes and obtained the main factors that manipulate the assessment outcomes of SRPs. Further, Rani et al. (2020a) recommended a new Pythagorean fuzzy similarity measure based TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) procedure to choose the best SRP option under PFS context. However, there is no research regarding the evaluation of SRP candidates by means of ARAS method under q-ROFS environment.

2.4 Limitations of the existing studies

Based on the literature, we identify the following issues and limitations:

  • As the topic of entropy and discrimination measures has been proven as one of the key research issues in different disciplines, such as pattern recognition, image segmentation, decision-making etc. Also, it is noticeably seen that the q-ROFS acts as a valuable way to perform decision-making in the complex, vague and conflicting situation, and efficiently fills the gaps in IFS and PFS concepts. In the literature, very few studies (Liu et al. 2018b, 2020; Peng and Liu, 2019; Khan et al. 2020; Verma, 2020) have been presented regarding the development of new entropy and discrimination measures under q-ROFS context. In addition, these measures have some counter intuitive cases.

  • In most of the existing studies (Liu et al. 2019b; Darko and Liang, 2020; Garg and Chen, 2020; Krishankumar et al. 2020; Alkan and Kahraman, 2021), the weight of each decision expert is directly allocated under q-ROFS settings, which can cause subjective randomness. Thus, how to derive the decision expert’s weight information is also an important challenge during the process of MCDM.

  • In several existing studies (Liu et al. 2018a; Khan et al. 2020; Garg and Chen, 2020; Tang et al. 2020), the criterion weight information is given in advance. In fact, different criteria weights will lead to diverse decision results. Thus, it is an important to estimate the criteria weights in actual decision-making applications.

  • Several generalizations of Additive Ratio Assessment (ARAS) approach has been presented in the literature (Dahooie et al. 2018; Rostamzadeh et al. 2020; Liu and Xu 2021; Karagöz et al. 2021; Gül, 2021; Dorfeshan et al. 2021) but the previously developed ARAS models have restrictions in managing the q-ROF uncertain information. Therefore, the formerly proposed ARAS approaches cannot be directly utilized for q-ROFSs. Moreover, to the best of our information, there is no study that reports the use of the ARAS approach under q-ROFS environment.

  • In the literature (Zhou et al. 2018; Li et al. 2020; Rani et al. 2020a), few decision-making models have presented to determine the most suitable sustainable recycling partner (SRP) under different circumstances but these models have some restrictions in handling the complex sustainable recycling partner selection problem with q-ROF information.

2.5 Motivations of the study

To eliminate the aforementioned limitations, the present study develops a new q-ROF information based ARAS method for the evaluation and prioritization of recycling partners from sustainability point of view. The key motivations of the present study are given as

  • This study analyzes the limitations of existing entropy and divergence measures using some counter intuitive cases and also motivates us to develop new entropy and discrimination measures for q-ROFSs.

  • Considering the influences of the relative decision experts’ weights on decision results, we introduce a new formula to derive the decision experts’ weights.

  • To avoid the undesirable influence of objective and subjective aspects, we develop a combined weighting procedure by integrating objective-weighting model using entropy and discrimination measures, and subjective-weighting model based on aggregation operator and score value to enumerate the weights of criteria within q-ROFSs environment.

  • To overcome the limitation of existing ARAS methods, this study proposes an extended ARAS method within q-ROFSs context. Consequently, the developed methodology can model the higher degrees of uncertainty in a more efficient and adaptable way.

  • During the SSCM practices, the requirement and policy of eco-economy motivates the companies to choose an appropriate SRP alternative. The process of SRP selection depends on multiple influencing factors, thus, it can be considered as a MCDM problem. To handle the multi-criteria SRP selection problem, we introduce a combined methodology based on ARAS technique with fully unidentified information about the decision experts and criteria, which can avoid the drawbacks of existing studies.

3 Basic concepts

Here, we present the elementary definitions associated with q-ROFSs.

Definition 3.1 (Yager 2017). A q-ROFS \(B\) on a discourse set \(\Theta = \left\{ {v_{1} ,\,v_{2} ,...,\,v_{n} } \right\}\) is defined as follows:

$$B = \,\left\{ {\left. {\left\langle {v_{i} ,\,\mu_{B} \left( {v_{i} } \right),\,\nu_{B} \left( {v_{i} } \right)} \right\rangle } \right|\,v_{i} \, \in \,\Theta } \right\},$$

where \(\mu_{B} \,:\,\Theta \to \,\left[ {0,\,\;1} \right]\) shows the BD of an element \(v_{i} \, \in \,\Theta ,\) while \(\nu_{B} \,:\,\Theta \, \to \,\left[ {0,\,1} \right]\) expresses the NBD of an element \(v_{i} \, \in \,\Theta\) under the following condition:

$$0\, \le \,\mu_{B} \left( {v_{i} } \right),\,\nu_{B} \left( {v_{i} } \right)\,\, \le \,1,\;0\, \le \,\left( {\mu_{B} \left( {v_{i} } \right)} \right)^{q} \, + \,\left( {\nu_{B} \left( {v_{i} } \right)} \right)^{q} \, \le \,1,\;q\, \ge \,1,\,\,\forall \,v_{i} \, \in \,\Theta .$$

For each \(v_{i} \, \in \,\Theta ,\) the hesitancy value is given by \(\pi_{B} \left( {v_{i} } \right) = \,\sqrt[q]{{1 - \left( {\mu_{B} \left( {v_{i} } \right)} \right)^{q} \, - \left( {\nu_{B} \left( {v_{i} } \right)} \right)^{q} }}.\) For convenience, \(\left\langle {\mu_{B} \left( {v_{i} } \right),\,\nu_{B} \left( {v_{i} } \right)} \right\rangle\) is said to be a q-rung orthopair fuzzy number (q-ROFN) and is symbolized by \(\sigma = \,\left( {\mu_{\sigma } ,\,\nu_{\sigma } } \right).\)

Definition 3.2 (Liu and Wang 2018). For three q-ROFNs \(\sigma = \,\left( {\mu_{\sigma } ,\,\nu_{\sigma } } \right),\)\(\sigma_{1} = \,\left( {\mu_{{\sigma_{1} }} ,\,\nu_{{\sigma_{1} }} } \right)\) and \(\sigma_{2} = \,\left( {\mu_{{\sigma_{2} }} ,\,\nu_{{\sigma_{2} }} } \right),\) the basic operations are defined by

$$(1)\,\sigma ^{c} {\mkern 1mu} = {\mkern 1mu} \left( {\nu _{\sigma } ,{\mkern 1mu} \mu _{\sigma } } \right);$$
$$(2)\,\sigma_{1} \, \oplus \,\sigma_{2} \, = \,\left( {\sqrt[q]{{\mu_{{\sigma_{1} }}^{q} \, + \,\mu_{{\sigma_{2} }}^{q} \, - \,\mu_{{\sigma_{1} }}^{q} \,\mu_{{\sigma_{2} }}^{q} }},\,\nu_{{\sigma_{1} }} \,\nu_{{\sigma_{2} }} } \right);$$
$$(3)\,\sigma_{1} \, \otimes \,\sigma_{2} \, = \,\left( {\mu_{{\sigma_{1} }} \,\mu_{{\sigma_{2} }} ,\,\sqrt[q]{{\nu_{{\sigma_{1} }}^{q} \, + \,\nu_{{\sigma_{2} }}^{q} \, - \,\nu_{{\sigma_{1} }}^{q} \,\nu_{{\sigma_{2} }}^{q} }}} \right);$$
$$(4)\,\lambda \,\sigma \, = \,\left( {\sqrt[q]{{1 - \left( {1 - \,\mu_{\sigma }^{q} } \right)^{\lambda } }}\,,\,\nu_{\sigma }^{\lambda } } \right),\,\,\lambda > \,0;$$
$$(5)\,\sigma^{\lambda } \, = \,\left( {\mu_{\sigma }^{\lambda } ,\,\sqrt[q]{{1 - \left( {1 - \,\nu_{\sigma }^{q} } \right)^{\lambda } }}} \right),\,\,\lambda \, > \,0.$$

Defnition 3.3 (Liu and Wang 2018). Consider \(\sigma = \,\left( {\mu_{\sigma } ,\,\nu_{\sigma } } \right)\) be a q-ROFN. Then, \({\mathbb{S}}\left( \sigma \right) = \mu_{\sigma }^{q} - \nu_{\sigma }^{q}\) and \(\hbar \left( \sigma \right) = \mu_{\sigma }^{q} + \nu_{\sigma }^{q}\) are called as the score and accuracy functions, wherein \({\mathbb{S}}\left( \sigma \right) \in \left[ { - 1,\,1} \right]\) and \(\hbar \left( \sigma \right) \in \left[ {0,1} \right].\)

As \({\mathbb{S}}\left( \sigma \right) \in \left[ { - 1,1} \right],\) then a normalized score function of q-ROFNs is discussed as.

Definition 3.4. Consider \(\sigma = \,\left( {\mu_{\sigma } ,\,\nu_{\sigma } } \right)\) be a q-ROFN. Then, the normalized score and uncertainty values are defined as

$$\aleph \left( \sigma \right) = \frac{1}{2}\left( {{\mathbb{S}}\left( \sigma \right) + 1} \right)\;{\text{and}}\;\ell\left( \sigma \right) = 1 - \hbar \left( \sigma \right)\;{\text{such}}\;{\text{that}}\;\aleph \left( \sigma \right),\,\,\ell \left( \sigma \right) \in \left[ {0,1} \right].$$
(1)

For any two q-ROFNs \(\sigma_{1} \, = \,\left( {\mu_{{\sigma_{1} }} ,\,\nu_{{\sigma_{1} }} } \right)\) and \(\sigma_{2} \, = \,\left( {\mu_{{\sigma_{2} }} ,\,\nu_{{\sigma_{2} }} } \right),\)

  1. (i)

    If \(\aleph \left( {\sigma_{1} } \right) > \aleph \left( {\sigma_{2} } \right),\) then \(\sigma_{1} > \sigma_{2} ,\)

  2. (ii)

    If \(\aleph \left( {\sigma_{1} } \right) = \aleph \left( {\sigma_{2} } \right),\) then

  3. (a)

    If \(\ell \left( {\sigma_{1} } \right) > \ell \left( {\sigma_{2} } \right),\) then \(\sigma_{1} > \sigma_{2} ;\)

  4. (b)

    If \(\ell \left( {\sigma_{1} } \right) = \ell \left( {\sigma_{2} } \right),\) then \(\sigma_{1} = \sigma_{2} .\)

Definition 3.5 (Liu et al. 2019a). The distance measure between two q-ROFNs \(\sigma_{1} \, = \,\left( {\mu_{{\sigma_{1} }} ,\,\nu_{{\sigma_{1} }} } \right)\) and \(\sigma_{2} \, = \,\left( {\mu_{{\sigma_{2} }} ,\,\nu_{{\sigma_{2} }} } \right)\) is defined by

$$d\left( {\sigma_{1} ,\,\sigma_{2} } \right) = \frac{1}{2}\left( {\left| {\mu_{{\sigma_{1} }}^{q} - \mu_{{\sigma_{2} }}^{q} } \right| + \left| {\nu_{{\sigma_{1} }}^{q} - \nu_{{\sigma_{2} }}^{q} } \right| + \left| {\pi_{{\sigma_{1} }}^{q} - \pi_{{\sigma_{2} }}^{q} } \right|} \right).$$
(2)

Definition 3.6 (Peng and Liu 2019). Let \(B,\,C \in q - ROFSs\left( \Theta \right).\) A real-valued mapping \(\,E:q - ROFS\left( \Theta \right) \to [0,\,\,1]\) is known as a q-ROF entropy measure if it holds the given postulates:

(a1).\(0\, \le \,E\left( B \right)\, \le \,1;\)

(a2). \(E\left( B \right)\, = \,0\, \Leftrightarrow\) B is a crisp set;

(a3).\(E\left( B \right)\, = \,1\, \Leftrightarrow\)\(\mu_{B} \left( {v_{i} } \right)\, = \,\nu_{B} \left( {v_{i} } \right);\)

(a4). \(E\left( B \right)\, = \,E\left( {B^{c} } \right);\)

(a5).\(E\left( B \right)\, \le \,E\left( C \right)\) if \(B\) is less fuzzy than \(C,\) i.e.,\(\mu_{B} \left( {v_{i} } \right)\, \le \,\mu_{C} \left( {v_{i} } \right)\, \le \,\nu_{C} \left( {v_{i} } \right)\, \le \,\nu_{B} \left( {v_{i} } \right)\) or \(\nu_{B} \left( {v_{i} } \right)\, \le \,\nu_{C} \left( {v_{i} } \right)\, \le \,\mu_{C} \left( {v_{i} } \right)\, \le \,\mu_{B} \left( {v_{i} } \right).\)

Definition 3.7 (Verma 2020). Let \(B,\,C,\,H \in q - ROFSs\left( \Theta \right).\) A q-ROF discrimination measure is a real-valued function \(D\,:\,q - ROFSs\left( \Theta \right)\, \times \,q - ROFSs\left( \Theta \right)\, \to {\mathbb{R}}\) which fulfills the following assumptions:

(p1).\(D\left( {B,\,C} \right)\, \ge \,0\) and \(D\left( {B,\,C} \right)\, = \,0\) iff \(B\, = \,C\,;\)

(p2). \(D\left( {B,\,C} \right)\, = \,D\left( {C,\,B} \right);\)

(p3). \(D\left( {B\, \cap \,H,\,C \cap \,H} \right)\, \le \,D\left( {B,\,C} \right),\,\,\forall \,H\, \in \,q - ROFS\left( \Theta \right);\)

(p4). \(D\left( {B \cup \,H,\,C\, \cup \,H} \right)\, \le \,D\left( {B,\,C} \right),\,\,\forall \,H\, \in \,q - ROFS\left( \Theta \right).\)

4 Proposed entropy and discrimination measures within q-ROFSs

In the realistic applications, we have many circumstances wherein we need to quantify the uncertainty present in the data to make most favorable judgments. Information measures are significant ways for handling uncertain information occur in our daily life problems. Different information measures, namely entropy and discrimination measures process the uncertain information and facilitate us to reach some conclusions. In recent times, these measures have received huge interest from several investigators owing to their extensive applications for several purposes namely decision-making, feature selection, image segmentation, disease diagnosis, information technology etc. In FS, entropy is an elegant way to quantity the uncertainty of fuzzy information. Corresponding to Shannon entropy, De Luca and Termini (1972) initially gave the notion of entropy on FSs. Later, Burillo and Bustince (1996) initiated the idea of entropy on IFSs. To date, copious entropies have been proposed for different purposes. For instance, Hu et al. (2018) studied a few entropy measures for hesitant fuzzy set (HFS). Yuan and Luo (2019) developed an innovative entropy measure for IFS and its application in MCDM. Alrasheedi et al. (2021) presented a novel Pythagorean fuzzy entropy measure-based hybrid method for sustainable supplier selection. Alipour et al. (2021) introduced a new entropy measure for PFS and further, applied to derive the criteria weights in the assessment of fuel cell and hydrogen components suppliers.

Discrimination measure is an imperious tool to quantify the deviation between two sets. Firstly, Bhandari and Pal (1993) originated the concept of fuzzy discrimination measure. After a while, Vlachos and Sergiadis (2007) studied the concept of intuitionistic fuzzy discrimination measure and its application. Currently, many research efforts have been made to propose new discrimination measures for different fuzzy sets. In order to measure the similarity and discrimination between IFSs, Liu et al. (2019b) proposed a new type of measure, named as similarity-divergence measure. In a study, Xiao and Ding (2019) presented a new Jensen-Shannon discrimination measure between PFSs. By means of new discrimation and possibility measures, Wang and Wan (2020) initiated a hybrid decision support system to solve the MCDM problems under interval-valued IFS environment. Kadian and Kumar (2020) studied a new fuzzy discrimination measure and its applicability in pattern recognition and fault detection. Although, very few authors (Liu et al. 2018b; Peng and Liu 2019; Verma 2020) have paid their attention in the expansion of novel entropy and discrimination measures for q-ROFSs. Because of the complexity of the situation and the subjectivity of the DEs’ judgments, the decision analysis procedure is always vague and the weights information is partially or fully unidentified. When we deal such concerns, entropy and discrimination measures developed in this study can be more valuable in dealing with MCDM applications.

As information measures show great significance in the field of FS and q-ROFS theories and widely applied to model the uncertainty arises in feature selection, MCDM and others. Thus, in the current section, we develop novel entropy and discrimination measures for q-ROFSs.

4.1 New entropy for q-ROFSs

Let \(B\, \in \,q - ROFS(\Theta ).\) Next, we develop new entropy for q-ROFS, which as

$$E\left( B \right)\, = \,\frac{1}{{n\,\left( {1 - \,\exp \left( {{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \right)}}\,\sum\limits_{i\, = 1}^{n} {\left[ {\left\{ {1 - \,\exp \left( { - \left( {\frac{{\nu_{B}^{q} \left( {v_{i} } \right)\, + \,1 - \,\mu_{B}^{q} \left( {v_{i} } \right)}}{2}} \right)} \right)} \right\}} \right.} \,I_{{\left[ {\mu_{B}^{q} \left( {v_{i} } \right)\, \ge \,\nu_{B}^{q} \left( {v_{i} } \right)} \right]}}$$
$$\left. { + \,\left\{ {1 - \,\exp \left( { - \left( {\frac{{\mu_{B}^{q} \left( {v_{i} } \right)\, + \,1 - \,\nu_{B}^{q} \left( {v_{i} } \right)}}{2}} \right)} \right)} \right\}\,I_{{\left[ {\mu_{B}^{q} \left( {v_{i} } \right)\, < \,\nu_{B}^{q} \left( {v_{i} } \right)} \right]}} } \right].$$
(3)

Theorem 3.1: The function \(E\left( B \right),\) presented by Eq. (3), is an entropy for q-ROFS \(\left( \Theta \right).\)

Proof: To validate the theorem, Eq. (3) must have to assure the properties (a1)-(a5) given in Definition 3.6.

(a1). In q-ROFSs, we have \(0\, \le \,\mu_{B}^{q} \left( {v_{i} } \right)\, + \,\nu_{B}^{q} \left( {v_{i} } \right)\, \le \,1,\) therefore, \(0\, \le \,E\left( B \right)\, \le \,1.\)

(a2). Assume that B be a crisp set, i.e., \(\mu_{B} \left( {v_{i} } \right)\, = \,1,\)\(\nu_{B} \left( {v_{i} } \right)\, = \,0\) or \(\mu_{B} \left( {v_{i} } \right)\, = \,0,\)\(\nu_{B} \left( {v_{i} } \right)\, = \,1.\) Then, we obtain \(E\left( B \right)\, = 0.\) Conversely, assume that \(E\left( B \right)\, = 0.\)

Also, let

$$\frac{{\mu_{B}^{q} \left( {v_{i} } \right)\, + \,1 - \,\nu_{B}^{q} \left( {v_{i} } \right)}}{2}\, = \,\varphi_{B} (v_{i} ).$$
(4)

Using Eq. (4) in Eq. (3), we obtain

$$E\left( B \right)\, = \,\tfrac{1}{{n\left( {1 - \,\exp \left( {{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)} \right)}}\,\sum\limits_{{i\, = 1}}^{n} {\left[ {\left\{ {1 - \,\exp \left( { - \left( {1 - \,\varphi _{B} \left( {v_{i} } \right)} \right)} \right)} \right\}I_{{\left[ {\varphi _{B} \left( {v_{i} } \right)\,\, \ge \,\tfrac{1}{2}} \right]}} + \,\left\{ {1 - \,\exp \left( { - \varphi _{B} \left( {v_{i} } \right)} \right)} \right\}\,\,I_{{\left[ {\varphi _{B} \left( {v_{i} } \right)\,\, < \,\tfrac{1}{2}} \right]}} } \right]} .$$
(5)

Equation (5) becomes zero iff \(\varphi_{B} (x_{i} )\, = 0\) or 1, i.e.,

$$\frac{{\mu_{B}^{q} \left( {v_{i} } \right)\, + \,1 - \,\nu_{B}^{q} \left( {v_{i} } \right)}}{2}\, = \,0$$
(6)

or

$$\frac{{\mu_{B}^{q} \left( {v_{i} } \right)\, + \,1 - \,\nu_{B}^{q} \left( {v_{i} } \right)}}{2}\, = \,1.$$
(7)

In the q-ROFSs, \(0\, \le \,\mu_{B}^{q} \left( {v_{i} } \right)\, + \,\,\nu_{B}^{q} \left( {v_{i} } \right)\, \le \,1.\) Now, solving Eq. (6) and Eq. (7), we have \(\mu_{B}^{q} \left( {v_{i} } \right)\, = \,0 = \,\mu_{B} \left( {v_{i} } \right),\)\(\,\nu_{B}^{q} \left( {v_{i} } \right)\, = 1 = \,\nu_{B} \left( {v_{i} } \right)\) or \(\mu_{B}^{q} \left( {v_{i} } \right)\, = \,1 = \,\,\mu_{B} \left( {v_{i} } \right),\) \(\nu_{B}^{q} \left( {v_{i} } \right)\, = 0\, = \,\,\nu_{B} \left( {v_{i} } \right),\,\forall \,v_{i} \, \in \,\Theta ,\) which gives that B is a crisp set.

(a3). It is evident that if \(\mu_{B} (v_{i} )\, = \,\nu_{B} (v_{i} ),\,\forall \,v_{i} \, \in \,\Theta ,\) then \(E\left( B \right)\, = 1.\)

Conversely, if \(E\left( B \right)\, = 1,\) then we obtain

$$E\left( B \right)\, = \,\tfrac{1}{{n\left( {1 - \,\exp \left( {{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)} \right)}}\,\sum\limits_{{i\, = 1}}^{n} {\left[ {\left\{ {1 - \,\exp \left( { - \left( {1 - \,\varphi _{B} \left( {v_{i} } \right)} \right)} \right)} \right\}I_{{\left[ {\varphi _{B} \left( {v_{i} } \right)\,\, \ge \,\tfrac{1}{2}} \right]}} + \,\left\{ {1 - \,\exp \left( { - \varphi _{B} \left( {v_{i} } \right)} \right)} \right\}\,I_{{\left[ {\varphi _{B} \left( {v_{i} } \right)\,\, < \,\tfrac{1}{2}} \right]}} } \right]} \,\, = \,1,$$
$$\Rightarrow \,\,\varphi_{B} \left( {v_{i} } \right)\, = \,\frac{1}{2},\,\,\forall \,v_{i} \, \in \,\Theta ,$$
$$\Rightarrow \,\,\frac{{\mu_{B}^{q} \left( {v_{i} } \right)\, + \,1 - \,\nu_{B}^{q} \left( {v_{i} } \right)}}{2} = \,\frac{1}{2},\,\,\forall \,v_{i} \, \in \,\Theta .$$
$$\Rightarrow \,\mu_{B}^{q} \left( {v_{i} } \right)\, = \,\nu_{B}^{q} \left( {v_{i} } \right),\,\forall \,v_{i} \, \in \,\Theta ,$$
$$\Rightarrow \,\mu_{B} \left( {v_{i} } \right)\, = \,\nu_{B} \left( {v_{i} } \right),\,\forall \,v_{i} \, \in \,\Theta .\,$$

(a4). Obviously,\(E(B)\, = \,E(B^{c} ).\)

(a5). From Eq. (3) and Eq. (4), we have

$$E\left( B \right)\, = \,\tfrac{1}{{n\left( {1 - \,\exp \left( {{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)} \right)}}\,\sum\limits_{{i\, = 1}}^{n} {\left[ {\left\{ {1 - \,\exp \left( { - \left( {1 - \,\varphi _{B} \left( {v_{i} } \right)} \right)} \right)} \right\}I_{{\left[ {\varphi _{B} \left( {v_{i} } \right)\,\, \ge \,\tfrac{1}{2}} \right]}} + \left\{ {1 - \,\exp \left( { - \varphi _{B} \left( {v_{i} } \right)} \right)} \right\}\,\,I_{{\left[ {\varphi _{B} \left( {v_{i} } \right)\,\, < \,\tfrac{1}{2}} \right]}} } \right]} \,,$$

which is similar to fuzzy entropy measure given by Hung and Yang (2008). Thus, it satisfies the property \(E\left( B \right)\, \le \,E\left( C \right)\) if B is less fuzzy than C, that is, \(\mu_{B} \left( {v_{i} } \right)\, \le \,\mu_{C} \left( {v_{i} } \right)\, \le \,\nu_{C} \left( {v_{i} } \right)\, \le \,\nu_{B} \left( {v_{i} } \right)\) or \(\nu_{B} \left( {v_{i} } \right)\, \le \,\nu_{C} \left( {v_{i} } \right)\, \le \,\mu_{C} \left( {v_{i} } \right)\, \le \,\mu_{B} \left( {v_{i} } \right),\,\,\forall \,v_{i} \, \in \,\Theta .\) Hence, the function \(E\left( B \right),\) given by Eq. (3), is an entropy measure for q-ROFSs.

4.1.1 Comparative study

For comparative discussion, we firstly recall previously introduced entropy measures for q-ROFS, which are shown as follows:

Liu et al. (2018b)

$$E_{L1} \left( B \right)\, = \,1 - \frac{1}{n\sqrt 2 \,}\,\sum\limits_{i = 1}^{n} {\sqrt {\left( {\mu_{B}^{q} \left( {v_{i} } \right)} \right)^{2} + \left( {\mu_{B}^{q} \left( {v_{i} } \right)} \right)^{2} + \left( {\pi_{B}^{q} \left( {v_{i} } \right) - 1} \right)^{2} } } .$$

Peng and Liu (2019)

$$E_{P1} \left( B \right)\, = \,1 - \frac{1}{n\,}\,\sum\limits_{i = 1}^{n} {\left| {\mu_{B}^{q} \left( {v_{i} } \right) - \nu_{B}^{q} \left( {v_{i} } \right)} \right|} .$$
$$E_{P2} \left( B \right)\, = \,\frac{1}{n\,}\,\sum\limits_{i = 1}^{n} {\left( {\frac{{\pi_{B}^{q} \left( {v_{i} } \right) + 1 - \left| {\mu_{B}^{q} \left( {v_{i} } \right) - \nu_{B}^{q} \left( {v_{i} } \right)} \right|}}{{\pi_{B}^{q} \left( {v_{i} } \right) + 1 + \left| {\mu_{B}^{q} \left( {v_{i} } \right) - \nu_{B}^{q} \left( {v_{i} } \right)} \right|}}} \right)} .$$

Khan et al. (2020)

$$E_{K} \left( B \right)\, = \,1 - \frac{1}{n\,}\,\sum\limits_{i = 1}^{n} {\left[ {1 - \frac{1}{2}\left( {1 - \left( {\mu_{B}^{2q} (v_{i} ) + \nu_{B}^{2q} (v_{i} )} \right)} \right)\, + \frac{4}{\pi }\tan^{ - 1} \left\{ {\left( {1 - \mu_{B}^{q} (v_{i} ) - \nu_{B}^{q} (v_{i} )} \right)^{2} } \right\}} \right]} .$$

Liu et al. (2020)

$$E_{L2} \left( B \right)\, = \,\frac{1}{n\,}\,\sum\limits_{i = 1}^{n} {\left[ {1 - \left( {\mu_{B}^{q} (v_{i} ) + \nu_{B}^{q} (v_{i} )} \right)\,\left| {\mu_{B}^{q} (v_{i} ) - \nu_{B}^{q} (v_{i} )} \right|} \right]} .$$

Verma (2020)

$$_{1}^{q} E_{\alpha } \left( B \right)\, = \,\frac{1}{n\,(1 - \alpha )}\,\sum\limits_{i = 1}^{n} {\log_{2} } \left[ {\left( {\left( {\mu_{B}^{q} (v_{i} )} \right)^{\alpha } + \left( {\nu_{B}^{q} (v_{i} )} \right)^{\alpha } } \right)\left( {\mu_{B}^{q} (v_{i} ) + \nu_{B}^{q} (v_{i} )} \right)^{1 - \alpha } \, + 2^{1 - \alpha } \,\pi_{B}^{q} (v_{i} )} \right],$$
$$_{2}^{q} E_{\alpha } \left( B \right)\, = \frac{1}{{n\,(\exp (1) - \exp \left( {2^{\alpha - 1} } \right))}}\,\sum\limits_{i = 1}^{n} {\left[ {\exp \left( {2^{\alpha - 1} \,\left( {\left( {\left( {\mu_{B}^{q} (v_{i} )} \right)^{\alpha } + \left( {\nu_{B}^{q} (v_{i} )} \right)^{\alpha } } \right)\left( {\mu_{B}^{q} (v_{i} ) + \nu_{B}^{q} (v_{i} )} \right)^{1 - \alpha } \, + 2^{1 - \alpha } \,\pi_{B}^{q} (v_{i} )} \right)} \right) - \exp \left( {2^{\alpha - 1} } \right)} \right]} , $$

where \(\alpha \in \,\left( {0,\,1} \right).\)

Table 1 presents the results obtained by the developed and previously introduced entropy measures. By analyzing the outcomes, we obtain various interesting outcomes, given as follows:

  • As compared the results obtained by different measures under Case I and Case II, we observe that all the entropy measures perform very well.

  • Compared the entropy outcomes under Case III, we obtain that the entropy formulae \(E_{K} \left( . \right)\) and \(E_{L2} \left( . \right)\) generate some counter intuitive result, which are marked as bold in Table 1.

  • In Case IV, when compared the entropy values at \(B = \,(0.5,\,0.5),\) we can easily observe that the formulae \(E_{L1} \left( . \right),\) \(E_{K} \left( . \right),\) \(E_{L2} \left( . \right),\) \(_{1}^{q} E_{\alpha } \left( . \right)\,\) and \(_{2}^{q} E_{\alpha } \left( . \right)\,\) are failed to satisfy the postulate (a3) of Definition 3.6 (Peng and Liu 2019).

  • When compared the entropy measures under Case V, Case VI and Case VII, we obtain that the entropy formulae \(E_{K} \left( . \right),\) \(_{1}^{q} E_{\alpha } \left( . \right)\,\) and \(_{2}^{q} E_{\alpha } \left( . \right)\,\) are unable to assure the postulate (a1) of Definition 3.6.

  • At last, it is worth mentioned that the developed entropy formula and measures given by Peng and Liu (2019) present no unreasonable results under given cases, while extant measures generates some counter intuitive results, as given in Table 1. Moreover, the proposed entropy formula is based on an exponential function, therefore, it is more reasonable and effective than Peng and Liu (2019) measures.

Table 1 Results obtained by the proposed and existing measures
Full size table

4.2 New discrimination measure for q-ROFSs

For \(B,\,C\, \in \,q - ROFSs(\Theta ),\) we discuss a new discrimination measure for q-ROFSs B and C, given as

$$D\left( {B,C} \right)\, = \,\frac{1}{{n\left( {\sqrt 2 \, - 1} \right)}}\sum\limits_{i = 1}^{n} {\left[ \begin{gathered} \sqrt {\frac{{\left( {\mu_{B}^{q} \left( {v_{i} } \right)} \right)^{2} + \,\left( {\mu_{C}^{q} \left( {v_{i} } \right)} \right)^{2} }}{2}} - \frac{{\mu_{B}^{q} \left( {v_{i} } \right) + \mu_{C}^{q} \left( {v_{i} } \right)}}{2} \hfill \\ \, + \sqrt {\frac{{\left( {\nu_{B}^{q} \left( {v_{i} } \right)} \right)^{2} + \,\left( {\nu_{C}^{q} \left( {v_{i} } \right)} \right)^{2} }}{2}} - \frac{{\nu_{B}^{q} \left( {v_{i} } \right) + \nu_{C}^{q} \left( {v_{i} } \right)}}{2} \hfill \\ \,\, + \sqrt {\frac{{\left( {\pi_{B}^{q} \left( {v_{i} } \right)} \right)^{2} + \,\left( {\pi_{C}^{q} \left( {v_{i} } \right)} \right)^{2} }}{2}} - \frac{{\pi_{B}^{q} \left( {v_{i} } \right) + \pi_{C}^{q} \left( {v_{i} } \right)}}{2} \hfill \\ \end{gathered} \right]} .$$
(8)

Theoorem 3.2: The function \(D\left( {B,C} \right),\) given by Eq. (8), is a valid q-ROF-discrimination measure, and fulfills the following axioms:

(s1). \(D\left( {B,\,C} \right) = \,D\left( {C,\,B} \right);\)

(s2). \(0 \le D\left( {B,\,C} \right) \le 1\) and \(D\left( {B,\,C} \right) = 0\) iff \(B = C;\)

(s3). \(D\left( {B^{c} ,\,C} \right) = D\left( {B,\,C^{c} } \right);\)

(s4). \(D\left( {B,\,C} \right) = D\left( {B^{c} ,\,C^{c} } \right);\)

(s5). \(D\left( {B \cup C,B \cap C} \right)\; = \;D\left( {B,C} \right);\)

(s6). \(D\left( {B \cup C,\,H} \right) \le D\left( {B,\,H} \right) + D\left( {C,\,H} \right),\,\,\forall \,H \in \,q - ROFS\left( \Theta \right);\)

(s7). \(D\left( {B \cap C,\,H} \right) \le D\left( {B,\,H} \right) + D\left( {C,\,H} \right),\,\,\forall \,H \in q - ROFS\left( \Theta \right).\)

Proof: Properties (s1)–(s7) are effortlessly verified. Hence, we have omitted the proof.

(s8). \(D\left( {B \cap H,\,C \cap H} \right) \le D\left( {B,\,C} \right),\,\,\forall \,H \in q - ROFS\left( \Theta \right).\)

(s9). \(D\left( {B \cup H,\,C \cup H} \right) \le D\left( {B,\,C} \right),\,\,\forall \,H \in q - ROFS\left( \Theta \right).\)

Proof: To verify (s8) and (s9), the discourse set \(\Theta\) is separated into eight given subsets:

$$\Theta = \left\{ {v_{i} \in \Theta |\,B\left( {v_{i} } \right) \le C\left( {v_{i} } \right) = H\left( {v_{i} } \right)} \right\} \cup \left\{ {v_{i} \in \Theta |\,B\left( {v_{i} } \right) = H\left( {v_{i} } \right) \le C\left( {v_{i} } \right)} \right\}$$
$$\cup \left\{ {v_{i} \in \Theta |\,B\left( {v_{i} } \right) \le \,C\left( {v_{i} } \right) < H\left( {v_{i} } \right)} \right\} \cup \left\{ {v_{i} \in \Theta |\,B\left( {v_{i} } \right) \le H\left( {v_{i} } \right) < \,C\left( {v_{i} } \right)} \right\}$$
$$\cup \left\{ {v_{i} \in \Theta |\,C\left( {v_{i} } \right) < B\left( {v_{i} } \right) \le H\left( {v_{i} } \right)} \right\} \cup \left\{ {v_{i} \in \Theta |\,C\left( {v_{i} } \right) \le H\left( {v_{i} } \right) < B\left( {v_{i} } \right)} \right\}$$
$$\cup \left\{ {v_{i} \in \Theta |\,H\left( {v_{i} } \right) < \,B\left( {v_{i} } \right) \le C\left( {v_{i} } \right)} \right\} \cup \left\{ {v_{i} \in \Theta |\,H\left( {v_{i} } \right) < \,C\left( {v_{i} } \right) < \,B\left( {v_{i} } \right)} \right\},$$

which are denoted by \(\Delta_{1} ,\,\Delta_{2} ,\,...,\Delta_{8} .\) For each \(\Delta_{j} ;\,j = 1\left( 1 \right)8,\,\) based on Montes et al. (2015), we get.

\(\left| {\left( {B \cup H} \right)\left( {v_{i} } \right) - \left( {C \cup H} \right)\left( {v_{i} } \right)} \right| \le \left| {B\left( {v_{i} } \right) - C\left( {v_{i} } \right)} \right|\) and \(\left| {\left( {B \cap \,H} \right)\left( {v_{i} } \right) - \left( {C \cap H} \right)\left( {v_{i} } \right)} \right| \le \left| {B\left( {v_{i} } \right) - C\left( {v_{i} } \right)} \right|.\)

Therefore, from (s5), we get

\(D\left( {B \cup H,\,C \cup H} \right) \le D\left( {B,\,C} \right)\) and \(D\left( {B \cap H,\,C \cap H} \right) \le D\left( {B,\,C} \right),\,\,\forall \,H \in q - ROFS\left( \Theta \right).\)

4.2.1 Comparison with other measures

To confirm the effectiveness of introduced divergence measure, we compare the present measure with some of the extant distance and divergence measures (Peng and Liu 2019; Verma 2020) given in Table 2 on some common data sets.

Table 2 Results obtained by different measures
Full size table

For this, firstly recall the existing q-ROF distance and divergence measures, which are as follows:

Peng and Liu (2019)

$$d_{PL}^{1} \left( {B,\,C} \right) = \frac{1}{2n}\sum\limits_{i = 1}^{n} {\left( {\left| {\mu_{B}^{q} (v_{i} ) - \,\mu_{C}^{q} (v_{i} )} \right| - \left| {\nu_{B}^{q} (v_{i} ) - \,\nu_{C}^{q} (v_{i} )} \right| - \left| {\pi_{B}^{q} (v_{i} ) - \,\pi_{C}^{q} (v_{i} )} \right|} \right)}$$
$$d_{PL}^{2} \left( {B,\,C} \right) = \frac{1}{2n}\sum\limits_{i = 1}^{n} {\left( {\left| {\mu_{B}^{q} (v_{i} ) - \,\mu_{C}^{q} (v_{i} ) - \left( {\nu_{B}^{q} (v_{i} ) - \,\nu_{C}^{q} (v_{i} )} \right)} \right|} \right)}$$
$$d_{PL}^{3} \left( {B,\,C} \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\left| {\mu_{B}^{q} (v_{i} ) - \,\mu_{C}^{q} (v_{i} )} \right| \vee \left| {\nu_{B}^{q} (v_{i} ) - \,\nu_{C}^{q} (v_{i} )} \right|} \right)}$$
$$d_{PL}^{4} \left( {B,\,C} \right) = 1 - \frac{1}{n}\sum\limits_{i = 1}^{n} {\frac{{\left( {\mu_{B}^{q} (v_{i} ) \wedge \,\mu_{C}^{q} (v_{i} )} \right) + \left( {\nu_{B}^{q} (v_{i} ) \wedge \,\nu_{C}^{q} (v_{i} )} \right)}}{{\left( {\mu_{B}^{q} (v_{i} ) \vee \,\mu_{C}^{q} (v_{i} )} \right) + \left( {\nu_{B}^{q} (v_{i} ) \vee \,\nu_{C}^{q} (v_{i} )} \right)}}}$$

Verma (2020)

$$_{1}^{q} D_{R}^{\alpha } \left( {B,\,C} \right)\, = \,\frac{1}{n(\alpha - 1)}\sum\limits_{j = \,1}^{n} {\log_{2} \left[ {\left( {\mu_{B}^{q} (v_{i} )} \right)^{\alpha } } \right.} \,\left( {\frac{{\mu_{B}^{q} (v_{i} ) + \,\mu_{C}^{q} (v_{i} )}}{2}} \right)^{1 - \alpha }$$
$$\left. {\, + \left( {\nu_{B}^{q} (v_{i} )} \right)^{\alpha } \left( {\frac{{\nu_{B}^{q} (v_{i} ) + \,\nu_{C}^{q} (v_{i} )}}{2}} \right)^{1 - \alpha } + \,\left( {\pi_{B}^{q} (v_{i} )} \right)^{\alpha } \left( {\frac{{\pi_{B}^{q} (v_{i} ) + \,\pi_{C}^{q} (v_{i} )}}{2}} \right)^{1 - \alpha } } \right];\,\alpha \, \in \left[ {0,\,1} \right],$$
$$_{2}^{q} D_{R}^{\alpha } \left( {B,\,C} \right)\, = \,\frac{1}{{n(\exp \left( {2^{\alpha - 1} } \right) - \exp (1))}}$$
$$\,\sum\limits_{j = 1}^{n} {\left[ {\exp \left( {^{{\left( {\,\left( {\mu_{B}^{q} (v_{i} )} \right)^{\alpha } \left( {\frac{{\mu_{B}^{q} (v_{i} ) + \,\mu_{C}^{q} (v_{i} )}}{2}} \right)^{1 - \alpha } \, + \left( {\nu_{B}^{q} (v_{i} )} \right)^{\alpha } \left( {\frac{{\nu_{B}^{q} (v_{i} ) + \,\nu_{C}^{q} (v_{i} )}}{2}} \right)^{1 - \alpha } \, + \left( {\pi_{B}^{q} (v_{i} )} \right)^{\alpha } \left( {\frac{{\pi_{B}^{q} (v_{i} ) + \,\pi_{C}^{q} (v_{i} )}}{2}} \right)^{1 - \alpha } } \right)}} } \right) - \exp \left( 1 \right)} \right]} ;\,$$

where \(\alpha \, \in \left[ {0,\,1} \right].\)

The outcomes evaluated by proposed discrimination measure and existing distance and discrimination measures (Peng and Liu 2019; Verma 2020) are shown in Table 2.

In Table 2, some problematic values are marked in bold. For instance, in Case V, the distance measure \(d_{PL}^{2} \left( {B,\,C} \right)\) presents a counter intuitive result as \(B \ne C\) but \(d_{PL}^{2} \left( {B,\,C} \right) = 0\). From Table 2, we can observe that the extant distance measure \(d_{PL}^{3} \left( {B,\,C} \right)\) derives the same value 0.0370 for Case V and Case VI. In addition, the measure \(d_{PL}^{4} \left( {B,\,C} \right)\) computes the same result 0.5781 for Case V and Case VI. However, the developed discrimination measure can effectively quantify the divergence between two q-ROFNs. Thus, our developed measure is more valuable and reasonable than other existing measures.

5 q-ROF-ARAS method

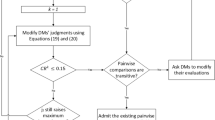
This section proposes a new integrated decision-making framework, named as q-ROF-ARAS, to cope with the complex MCDM problems under q-ROFSs perspective. To do so, the concepts of the q-ROFNs, entropy and discrimination measures are utilized under q-ROFSs environment and further, apply to select the desirable SRP candidate. The proposed q-ROF-ARAS approach employs the coherent comparison in the ratio of the weighted sum of criteria values to obtain the optimality degree of an alternative. This approach is incorporated into the evaluations to diminish bias and favoritism. The steps of the proposed approach are prearranged as follows (graphical framework is given in Fig. 1):

Fig. 1
figure 1

Implementation flowchart of q-ROF-ARAS methodology

Full size image

Step 1: Create a decision matrix.

In MCDM process, let \(P\, = \,\left\{ {P_{1} ,\,P_{2} ,\,...,\,P_{m} } \right\}\) be a set of options and \(R\, = \,\left\{ {R_{1} ,\,R_{2} ,\,...,\,R_{n} } \right\}\) be a criterion set. Let a team of DEs \(\,\left\{ {I_{1} ,\,I_{2} ,\,...,\,I_{l} } \right\}\) evaluates the given m options concerning the preferred n criteria in forms of q-ROFNs. Let \(\Omega = \left( {\zeta_{ij}^{\left( k \right)} } \right)_{m\, \times \,n} ,\,\,i\, = 1\left( 1 \right)m,\,j\, = 1\left( 1 \right)n\) be a q-ROF evaluation matrix, in which \(\zeta_{ij}^{\left( k \right)}\) denotes the evaluation information of an option \(P_{i}\) by means of the criteria \(R_{j} \,(j = 1(1)n)\) given by the \(k^{th}\) DE.

Step 2: Find out the DEs weights \(\left( {\lambda_{k} } \right)\).

Evaluation of DEs’ weights is a significant issue in MCDM practice. For this purpose, assume \(\left( {\mu_{k} ,\,\nu_{k} } \right)\) be a q-ROFN that shows the significance degree of kth DE. Then, the weight value is estimated by

$$\lambda_{k} = \frac{{\mu_{k}^{q} \left( {2 - \mu_{k}^{q} - \nu_{k}^{q} } \right)}}{{\sum\limits_{k = 1}^{\ell } {\left[ {\mu_{k}^{q} \left( {2 - \mu_{k}^{q} - \nu_{k}^{q} } \right)} \right]} }},\;{\text{where}}\;\lambda_{k} \, \ge \,0\;{\text{and}}\;\sum\limits_{k\, = 1}^{\ell } {\lambda_{k} \, = \,1.}$$
(9)

Step 3: Create the aggregated q-rung orthopair fuzzy decision-matrix (A-q-ROF-DM).

Let \({\mathbb{N}} = \left( {\tilde{\zeta }_{ij} } \right)_{m\, \times \,n}\) be an A-q-ROF-DM obtained by using q-ROF weighted averaging operator (Liu and Wang 2018), where

$$\tilde{\zeta }_{ij} = q - ROFWA_{\lambda } \,\left( {\zeta_{ij}^{(1)} ,\,\zeta_{ij}^{(2)} ,...,\,\zeta_{ij}^{(\ell )} } \right) = \,\left( {\sqrt[q]{{1 - \prod\limits_{k = \,1}^{\ell } {\left( {1 - \,\mu_{k}^{q} } \right)^{{\lambda_{k} }} } }}\,,\,\prod\limits_{k = 1}^{\ell } {\left( {\nu_{k} } \right)^{{\lambda_{k} }} } } \right).$$
(10)

Step 4: Calculate the criteria weights.

Suppose all the criteria have different significances. Let \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T} ,\) wherein \(\sum\nolimits_{j = 1}^{n} {w_{j} = 1} ,\)\(\,w_{j} \in \left[ {0,\,\,1} \right],\) be the importance degree for a criteria set. The criteria weights are obtained by using the following steps:

Case I: Evaluate the objective weight \(w_{j}^{o}\) for each criterion using the following approach:

$$w_{j}^{o} \, = \,\tfrac{{\sum\limits_{i = \,1}^{m} {\left[ {\tfrac{1}{m\, - 1}\sum\limits_{k = 1,\,k \ne i}^{m} {D\left( {\tilde{\zeta }_{ij} ,\,\tilde{\zeta }_{kj} } \right)} \, + \left( {1\, - \,E\left( {\tilde{\zeta }_{ij} } \right)} \right)} \right]} }}{{\sum\limits_{j = \,1}^{n} {\sum\limits_{i = \,1}^{m} {\left[ {\tfrac{1}{m\, - 1}\sum\limits_{k = 1,\,k \ne i}^{m} {D\left( {\tilde{\zeta }_{ij} ,\,\tilde{\zeta }_{kj} } \right)\,} + \left( {1\, - \,E\left( {\tilde{\zeta }_{ij} } \right)} \right)} \right]} } }}.$$
(11)

Here, \(D\left( {\tilde{\zeta }_{ij} ,\,\tilde{\zeta }_{kj} } \right)\) indicates the discrimination between \(\tilde{\zeta }_{ij}\) and \(\tilde{\zeta }_{kj} ,\) and \(E\left( {\tilde{\zeta }_{ij} } \right)\) signifies the entropy measure of \(\tilde{\zeta }_{ij} .\)

Case II: Calculate the subjective weight \(w_{j}^{s}\).

For this, create the subjective weighted matrix \(\left( {w_{j}^{s} } \right)\) for kth DE by using the process

$$w_{j}^{s} = \left[ {w_{j\left( k \right)}^{s} } \right]_{n\, \times 1} = \left[ {\begin{array}{*{20}c} {w_{1\left( k \right)}^{s} } \\ {w_{2\left( k \right)}^{s} } \\ \vdots \\ {w_{n\left( k \right)}^{s} } \\ \end{array} } \right],$$
(12)

where \(w_{j\left( k \right)}^{s}\) is the weight value of criterion \(R_{j}\) given by kth expert. To assess the subjective weight, we get

$$W_{j}^{s} = \zeta_{ij} = q - ROFWA_{\lambda } \,\left( {w_{j\left( 1 \right)}^{s} ,w_{j\left( 2 \right)}^{s} ,...,w_{j\left( \ell \right)}^{s} \,} \right).$$
(13)

Let \(w_{j\left( k \right)}^{s} = \left( {p_{ijk} } \right)\) be the decision weight, where \(p_{ijk} = \left( {\mu_{ijk} ,\,\,\nu_{ijk} } \right),\)\(k = 1\left( 1 \right)\,\ell\) is a q-ROFN. Then, the procedure for the determining the overall subjective weight is given:

$$W_{j}^{s} = \left( {\mu_{ij*} ,\,\nu_{ij*} } \right) = \left( {\sqrt[q]{{1 - \prod\limits_{k = 1}^{\ell } {\left( {1 - \mu_{ijk}^{q} } \right)^{{\lambda_{k} }} } }},\,\prod\limits_{k = 1}^{\ell } {\left( {\nu_{ijk} } \right)^{{\lambda_{k} }} } } \right)\,.$$
(14)

Here, \(W_{j}^{s} = \left( {\mu_{ij*} ,\,\nu_{ij*} } \right)\) is a q-ROFN.

Then, the subjective criteria weight is computed as below:

$$w_{j}^{s} = \frac{{\aleph \left( {W_{j}^{s} } \right)}}{{\sum\nolimits_{j = 1}^{n} {\aleph \left( {W_{j}^{s} } \right)} }};\,\,j = 1\left( 1 \right)n,$$
(15)

where \(\aleph \left( {W_{j}^{s} } \right)\) denotes the score value of \(W_{j}^{s} .\)

Case III: Determine the combined weight.

With the use of using Eqs. (11)–(15), the combined criterion weight is calculated as

$$w_{j} = \gamma w_{j}^{s} + \left( {1 - \gamma } \right)w_{j}^{o} ,$$
(16)

where \(\gamma \in \left[ {0,\,1} \right]\) is the aggregating decision precision parameter.

Step 5: Evaluate the optimal assessment value.

The optimal assessment value \(\left( {{\mathbb{R}}_{0} } \right)\) is estimated as follows:

$${\mathbb{R}}_{0} = \left\{ \begin{gathered} \max \,\tilde{\zeta }_{ij} ,\,\,\,j \in R_{b} \hfill \\ \min \,\tilde{\zeta }_{ij} ,\,\,\,j\,\, \in R_{n} \hfill \\ \end{gathered} \right.,$$
(17)

where \(R_{b}\) and \(R_{n}\) are the benefit and cost types of criteria sets, respectively.

Step 6: Normalize the A-q-ROF-DM.

To normalize the A-q-ROF-DM, the evaluation information regarding the cost-type criteria should be changed into the benefit-type in order to get the normalized A-q-ROF-DM \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mathbb{N}} = \left( {\varsigma_{ij} } \right)_{m\, \times \,n} ,\) wherein

$$\varsigma_{ij} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mu }_{ij} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\nu }_{ij} } \right) = \left\{ \begin{gathered} \tilde{\zeta }_{ij} = \left( {\mu_{ij} ,\nu_{ij} } \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,j \in R_{b} \hfill \\ \left( {\tilde{\zeta }_{ij} } \right)^{c} = \left( {\nu_{ij} ,\mu_{ij} } \right),\,\,\,\,\,\,\,\,\,j \in R_{n} \hfill \\ \end{gathered} \right.,$$
(18)

Step 7: Generate weighted form of normalized A-q-ROF-DM.

The weighted form of normalized A-q-ROF-DM \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mathbb{N}}_{w} = \left( {\tilde{\varsigma }_{ij} } \right)_{m\, \times \,n}\) is assembled as below:

$$\tilde{\varsigma }_{ij} = \mathop \oplus \limits_{j = 1}^{n} w_{j} \,\varsigma_{ij} = \,\left( {\sqrt {1 - \prod\limits_{j = \,1}^{n} {\left( {1 - \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mu }_{ij}^{q} } \right)^{{w_{j} }} } } \,,\,\prod\limits_{j = 1}^{n} {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\nu }_{ij} } \right)^{{w_{j} }} } } \right).$$
(19)

Step 8: Evaluate the score values.

In this step, the score values of weighted decision matrix \({\mathbb{N}}_{w} = \left( {\tilde{\varsigma }_{ij} } \right)_{m\, \times \,n}\) are computed by

$$\aleph \left( {\tilde{\varsigma }_{ij} } \right) = \,\frac{1}{2}\left( {\left( {\tilde{\mu }_{ij}^{q} - \,\tilde{\nu }_{ij}^{q} } \right) + 1} \right)\,;\,\,\forall i,\,j.$$
(20)

Step 9: Determine the overall assessment index for each option.

The overall assessment index is computed as

$$\Upsilon_{i} = \sum\limits_{j = 1}^{n} {\aleph \left( {\tilde{\varsigma }_{ij} } \right)} ,\,\,\,i = 1\left( 1 \right)m.$$
(21)

Step 10: Determine the utility index. To evaluate the options, it is not only significant to find out the optimal alternative but also important to determine the relative assessment indices of obtained choices with regard to the most desirable candidate. For this reason, the utility index is utilized as

$${\mathbb{Q}}_{i} \; = \;\frac{{\Upsilon_{i} }}{{{\mathbb{R}}_{0} }};\;i\; = \;1\left( 1 \right)m.$$
(22)

Clearly, \({\mathbb{Q}}_{i} \in \left[ {0,\,\,1} \right]\) can be preferred in increasing sequence.

Step 11: Prioritize the options.

The given options are prioritized based on the increasing indices of \({\mathbb{Q}}_{i}\). Then, the most desirable option is considered as follows:

$$\Upsilon^{*} = \left\{ {\Upsilon_{i} |\,\,\mathop {\max }\limits_{i} {\mathbb{Q}}_{i} ;\,\,i = 1\left( 1 \right)m} \right\},$$
(23)

6 An application of sustainable recycling partner (SRP) selection

To depict the applicability of q-ROF-ARAS approach in realistic decision-analysis problems, this section shows an empirical study of Indian recycling organization (XYZ) situated in western zone of India. The organization has been functioning for past 25 years. Despite of its sustained success in the marketplace, the organization doesn’t have any solid structure for an enviable recycling network selection. Presently, the organization has started employing sustainability initiatives in their sustainable SCM processes to reduce the influence on environmental degradation. The study introduces a robust structure for organization’s stakeholders who will support them to assess and choose the best SRP candidate. In this case study, we have considered three organizations P1, P2 and P3 who are engaged in the recycling activities of the products like as EOL vehicles, scraped metals and papers recycling, and dismasting processes. To choose the most favorable SRP, a panel of four DEs (I1, I2, I3, I4) has been formed which involves of one production and two supply chain managers, respectively, and a professor with having minimum 15 years of knowledge in this field. All DEs are proficient in decision-analysis practice with durable expertise in several organizational events, which are planning, quality control, supply chain and environmental managing events, and others. These SRP options are assessed based on ten criteria which are Pollution and waste production (R1), Resource use efficiency (R2), Environmental MIS (R3), Environmental equipment facilities (R4), Operation cost per unit (R5), Quality utility value (R6), Profitability (R7), Local influence degree (R8), Customer satisfaction (R9) and Brand reputation (R10). The list of selected criteria given in this section is considered from several sources to distinguish many aspects such as economic, environmental, and social facets and their characteristics for recycling partner evaluation. The details about these criteria are depicted in Table 3. Here, R1 and R5 are non-beneficial type and others are beneficial type criteria.

Table 3 Details of the criteria for the present case study
Full size table

The steps of q-ROF-ARAS approach for the assessment of most optimal recycling partner are given as below:

Assume that the significance degrees of the DEs are q-ROFNs and are given as {(0.85, 0.45, 0.6655), (0.80, 0.50, 0.7133), (0.70, 0.65, 0.7258), (0.75, 0.60, 0.7128)}. Based on the DEs’ opinions, the q-ROF-DM \(M^{\left( k \right)} = \left( {\xi_{ij}^{\left( k \right)} } \right)_{m\, \times \,n} ,\,k = 1(1)4\) is specified in Table 4.

Table 4 Assessment ratings of competitive SRP selection
Full size table

By means of Eq. (9), crisp form of DEs’ weights are {\(\lambda_{1} =\) 0.3127, \(\lambda_{2} =\) 0.2746, \(\lambda_{3} =\) 0.1866, \(\lambda_{4} =\) 0.2261}. To find the A-q-ROF-DM using the decisions of all experts, the aggregation process, given in Eq. (10), is executed on Table 4, shown in Table 5.

Table 5 A-q-ROF-DM for SRP selection
Full size table

Next, Table 6 represents the linguistic terms (LTs) to measure the significance degree of considered criteria for SRP assessment.

Table 6 LTs for significance degree of considered criteria to q-ROFNs
Full size table

To evaluate the objective weights of the criteria, utilize Eq. (3) and Eq. (8) in Eq. (11), therefore, we have

\(w_{j}^{o} =\)(0.1982, 0.1086, 0.1361, 0.0776, 0.1173, 0.0734, 0.0891, 0.0889, 0.0727, 0.0381).

In accordance with Eqs. (12)–(15), the subjective criteria weights are as below (Last column of Table 7):

Table 7 Criteria weights evaluated by the DEs for SRP selection
Full size table

\(w_{j}^{s} =\)(0.1471, 0.1279, 0.1374, 0.0985, 0.1261, 0.0727, 0.1065, 0.1078, 0.0504, 0.0256).

The final criteria weights (\(\gamma = 0.5\)) using Eq. (16) is obtained as

\(w_{j} =\) (0.1727, 0.1183, 0.1367, 0.0881, 0.1217, 0.0731, 0.0978, 0.0984, 0.0616, 0.0319).

With the use of Eq. (17), we calculate optimal performance ratings of SRP candidates, given as

\({\mathbb{R}}_{0} =\){(0.522, 0.723, 0.782), (0.707, 0.587, 0.763), (0.715, 0.578, 0.761), (0.667, 0.705, 0.706), (0.625, 0.689, 0.754), (0.752, 0.579, 0.725), (0.659, 0.732, 0.685), (0.693, 0.541, 0.798), (0.694, 0.615, 0.756), (0.672, 0.670, 0.735)}.

Step 6–7. Since the criteria \(R_{1}\) and \(R_{5}\) are of non-beneficial type, and others are beneficial type, so, it is required to find the normalized A-q-ROF evaluation matrix \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mathbb{N}} = \left( {\varsigma_{ij} } \right)_{m\, \times \,n}\) by using Eq. (18) and shown in Table 8. Further, by means of Eq. (19), the weighted decision matrix is computed in Table 9.

Table 8 Normalized A-q-ROF evaluation matrix for SRP selection
Full size table
Table 9 Weighted normalized q-ROF-DM for SRP selection
Full size table

By employing Table 9 and Eq. (20), the score values \(\aleph \;\left( {\tilde{\varsigma }_{ij} } \right)\) of q-ROFNs are determined. In accordance with Eq. (21), overall assessment index \(\left( {\Upsilon_{i} } \right)\) of each SRP option is calculated and presented in Table 10. By means of Eq. (22), utility degree \(\left( {{\mathbb{Q}}_{i} } \right)\) is assessed as follows: \({\mathbb{Q}}_{1} = 0.841,\) \({\mathbb{Q}}_{2} = 0.700,\) \({\mathbb{Q}}_{3} = 0.781.\) On the basis of utility degree, the preference ordering of the SRP candidates is \({\mathbb{Q}}_{1} \succ {\mathbb{Q}}_{3} \succ {\mathbb{Q}}_{2} .\) Based on Eq. (23), the desirable SRP option is \(P_{1} .\) The computational outcomes are shown in Table 10.

Table 10 Computational results of q-ROF-ARAS approach for SRPs assessment
Full size table

6.1 Sensitivity investigation (SI)

In the current section, the influence of the change in the weight values of the criteria is tested through sensitivity investigation. Firstly, 11 diverse sets of weight values are taken and shown in Table 11. From Table 11 and Fig. 2, one of the criteria has higher significance value and remaining have lesser significance values in each set. Using this procedure, an elegant choice of considered attributes’ weights are obtained to study the SI of q-ROF-ARAS approach.

Table 11 Various criteria weight sets for SRP selection
Full size table
Fig. 2
figure 2

Variation of criteria weight values over the parameter \(\left( \gamma \right)\) for SRP selection

Full size image

The results, shown in Table 12 and Fig. 3, represent that the degree of utility \({\mathbb{Q}}_{i} \in \left[ {0,\,\,1} \right],\,\left( {i = 1(1)3} \right)\) with respect to parameter \(\gamma\) can be changed under various criteria weight sets but the ranking of the SRP candidates is same in each criterion set. Thus, it is found that the SRP evaluation process is reliant on and delicate to considered sets of criteria weights. Therefore, the present q-ROF-ARAS methodology is vastly flexible to cope with different circumstances in practice.

Table 12 The utility index of SRP option over different criteria weight sets
Full size table
Fig. 3
figure 3

The variation in the utility measure values over the parameter \(\left( \gamma \right)\)

Full size image

6.2 Comparative study

To validate the outcomes of the q-ROF-ARAS approach, this section displays a comparative study. In this regard, we have chosen some previous approaches, namely, the q-ROF-TOPSIS method (Liu et al. 2019a) q-ROF-WASPAS (Rani and Mishra 2020b) and q-ROF-COPRAS (Krishankumar et al. 2019) approaches. The results of the comparative study are graphically depicted in Fig. 4.

Fig. 4
figure 4

Significance degree of SRP candidates with various approaches

Full size image

6.2.1 q-ROF-TOPSIS method

Steps 1–5: Same as q-ROF-ARAS technique.

Step 6: Assess the ideal solution (IS) and anti-ideal solution (A-IS) by using

$$\phi^{ + } \, = \,\left\{ \begin{gathered} \mathop {\max }\limits_{i} \,\mu_{ij} ,\,\,{\text{for}} \,benefit\,criterion\,\,R_{b} \hfill \\ \mathop {\min }\limits_{i} \,\nu_{ij} ,\,\,{\text{for}} \,cost\,criterion\,\,R_{n} \hfill \\ \end{gathered} \right.\,\,\,for\,\,j\, = \,1\left( 1 \right)n,$$
(24)
$$\phi^{ - } \, = \,\left\{ \begin{gathered} \mathop {\min }\limits_{i} \,\mu_{ij} ,\,\,{\text{for}} \,benefit\,criterion\,R_{b} \hfill \\ \mathop {\max }\limits_{i} \,\nu_{ij} ,\,\,{\text{for}} \,cost\,criterion\,R_{n} \hfill \\ \end{gathered} \right.\,\,\,for\,\,j\, = \,1\left( 1 \right)n.$$
(25)

Step 7: Derive the degree of discriminations from IS and A-IS:

$$d\left( {P_{i} ,\,\phi^{ + } } \right) = \frac{1}{2}\sum\limits_{j = 1}^{n} {\left[ {\,w_{j} \left( {\left| {\mu_{{\varsigma_{ij} }}^{q} - \mu_{{\phi_{j}^{ + } }}^{q} } \right| + \left| {\nu_{{\varsigma_{ij} }}^{q} - \nu_{{\phi_{j}^{ + } }}^{q} } \right| + \left| {\pi_{{\varsigma_{ij} }}^{q} - \pi_{{\phi_{j}^{ + } }}^{q} } \right|} \right)} \right]} ,$$
(26)

and

$$d\left( {P_{i} ,\,\phi^{ - } } \right) = \frac{1}{2}\sum\limits_{j = 1}^{n} {\left[ {w_{j} \left( {\left| {\mu_{{\varsigma_{ij} }}^{q} - \mu_{{\phi_{j}^{ - } }}^{q} } \right| + \left| {\nu_{{\varsigma_{ij} }}^{q} - \nu_{{\phi_{j}^{ - } }}^{q} } \right| + \left| {\pi_{{\varsigma_{ij} }}^{q} - \pi_{{\phi_{j}^{ - } }}^{q} } \right|} \right)} \right]} .$$
(27)

Step 8: Assess the closeness index (CI) utilizing the expression

$${\mathbb{C}}\left( {P_{i} } \right) = \frac{{d\left( {P_{i} ,\,\phi^{ - } } \right)}}{{d\left( {P_{i} ,\,\phi^{ + } } \right) + \,d\left( {P_{i} ,\,\phi^{ - } } \right)}},\,\,\,\,i = 1\left( 1 \right)m.$$
(28)

After the evaluation of \({\mathbb{C}}\left( {P_{i} } \right),\) the SRP candidates are ranked. However, in many applications, this process is unable to find the optimal ranking. To overcome this drawback, Hadi-Vencheh and Mirjaberi (2014) presented the revised formula for CI, which as

$$\Psi \left( {P_{i} } \right) = \frac{{d\left( {P_{i} ,\,\phi^{ - } } \right)}}{{d_{\max } \left( {P_{i} ,\,\phi^{ - } } \right)}} - \frac{{d\left( {P_{i} ,\,\phi^{ + } } \right)}}{{d_{\min } \left( {P_{i} ,\,\phi^{ + } } \right)}},\,\,\,\,i = 1\left( 1 \right)m.$$
(29)

Step 9: Using the closeness indices, the SRP alternatives are prioritized.

For the above case study, the IS and A-IS are determined using Eqs. (24)–(25) and are given as

\(\phi^{ + } =\){(0.723, 0.522, 0.782), (0.707, 0.587, 0.763), (0.715, 0.578, 0.761), (0.667, 0.705, 0.706), (0.689, 0.625, 0.754), (0.752, 0.579, 0.725), (0.659, 0.732, 0.685), (0.693, 0.541, 0.798), (0.694, 0.615, 0.756), (0.672, 0.670, 0.735)},

\(\phi^{ - } =\){(0.534, 0.782, 0.718), (0.545, 0.725, 0.770), (0.565, 0.745, 0.740), (0.624, 0.741, 0.705), (0.565, 0.755, 0.730), (0.667, 0.710, 0.701), (0.605, 0.734, 0.726), (0.627, 0.700, 0.743), (0.639, 0.754, 0.677), (0.638, 0.716, 0.720)}.

Using Eqs. (26)–(29), the whole computational outcomes and preference order of the SRPs are offered in Table 13. Consequently, the most appropriate SRP candidate is \(P_{1}\).

Table 13 Overall results of q-ROF-TOPSIS for SRP selection
Full size table

6.2.2 q-ROF-WASPAS method

Steps 1–5: Same as proposed technique.

Step 6: Assess the weighted sum measure (WSM) and weighted product measure (WPM) for each alternative, given as

$$\alpha_{i}^{(1)} \, = \,\mathop \oplus \limits_{j = 1}^{n} w_{j} \,\varsigma_{ij} .$$
(30)
$$\alpha_{i}^{(2)} \, = \,\mathop \otimes \limits_{j = 1}^{n} w_{j} \,\varsigma_{ij} .$$
(31)

Step 7: For each alternative, compute the aggregated measure of WASPAS with the use of Eq. (32):

$$\alpha_{i} \, = \,\lambda \,\alpha_{i}^{(1)} \, + \,\left( {1 - \,\lambda } \right)\,\alpha_{i}^{(2)} ,$$
(32)

wherein \(\lambda\) stands for the coefficient of the decision mechanism. It is proposed with the aim of estimating the WASPAS accuracy level based on the initial attributes precision and when \(\lambda \in \left[ {0,\,\,1} \right].\) It is already proved that the aggregating methods outperform the single models in terms of accuracy.

Step 8: Prioritize the candidates in accordance with the increasing degrees (i.e., score values) of \(\alpha_{i} .\)

Steps 5–8: Applying Eq. (30), Eq. (31) and Eq. (32), the WSM \(\left( {\alpha_{i}^{(1)} } \right),\) WPM \(\left( {\alpha_{i}^{(2)} } \right)\) and WASPAS measure \(\left( {\alpha_{i} } \right)\) for each SRP candidate, and their q-ROF-score values \(\aleph \;\left( {\alpha_{i}^{(1)} } \right)\) and \(\aleph \left( {\alpha_{i}^{(2)} } \right)\) are determined in Table 14. Therefore, the prioritization of the SRPs is assessed as \(P_{1} \succ P_{3} \succ P_{2}\) and P1 is the most desirable option.

Table 14 Results of q-ROF-WASPAS model
Full size table

6.2.3 q-ROF-COPRAS method

Steps 1–4: Same as q-ROF-ARAS technique.

Step 5: Since R1 and R5 are of non-benefit-type and remaining is benefit-type, therefore, we analyze the following for each candidate to maximize the benefit and minimize the cost preferences \(\beta_{i} = \mathop \oplus \limits_{j = 1}^{q} \,w_{j} \,\tilde{\zeta }_{ij} ,\,\,\,i = 1\left( 1 \right)m\) and \(\delta_{i} = \mathop \oplus \limits_{j = q + 1}^{n} \,w_{j} \,\tilde{\zeta }_{ij} ,\,\,\,i = 1\left( 1 \right)m,\) respectively. Also, the index value is the same as the relative degree of each option.

Step 6: Compare the relative degrees of the SRP candidates based on \(TR_{i} = \varphi \,\aleph \left( {\beta_{i} } \right) + \left( {1 - \varphi } \right)\frac{{\sum\limits_{i = 1}^{m} {\aleph \left( {\delta_{i} } \right)} }}{{\aleph \left( {\delta_{i} } \right)\sum\limits_{i = 1}^{m} {\frac{1}{{\aleph \left( {\rho_{i} } \right)}}} }},\,\,i = 1\left( 1 \right)m,\) where parameter \(\varphi\) denotes the strategy value of the DE in a unit interval. Therefore, we get TR1 = 0.480, TR2 = 0.598 and TR5 = 0.628, and get the preference order of the SRP candidates as \(TR_{3} \succ TR_{2} \succ TR_{1} .\) The ranking reflects that the option P3 is the optimum SRP candidate among the others.

Step 7: Derive the “utility degree” \(\hbar_{i} = \frac{{TR_{i} }}{{\,\,TR_{\max } }} \times 100\,\% ,\) which reflects the degree of utility between each option and the optimum option. Then, we obtain \(\hbar_{1} = 76.43\% ,\) \(\hbar_{2} = 95.22{\text{\% }},\) and \(\hbar_{3} = 100.{\text{00\% }}{.}\)

In the following, the vital advantages of the presented method are listed:

  • The q-ROFSs enhance the concentration of linguistic knowledge when DEs hesitate among various values to evaluate the SRP selection problem. The use of q-ROFSs offers a more flexible and effective process to portray DEs’ opinions. Therefore, the developed q-ROF-ARAS approach is a structured framework to integrate DEs’ knowledge and experiences for choosing the desirable SRP option.

  • In the q-ROF-ARAS framework, the cost-type and the benefit-type criteria are taken. Consideration of both types of criteria with intricate proportion involves more exact information in comparison with just managing the cost or benefit types of criteria. Thus, it enhances both the comprehensibility of initial information and the exactness of the results.

  • The proposed model only evaluates q-ROF-IS, whereas q-ROF-TOPSIS needs to obtain both q-ROF-IS and q-ROF-AIS. Thus, it can be said that the q-ROF-ARAS has less computation with a higher operability than TOPSIS model in handling the MCDM methods with more criteria or options.

  • The proposed criteria weighting procedure is based on the combination of objective and subjective weighting techniques, which makes the proposed method more practical and flexible. In addition, there is no threat of loss of information as it considers the entropy of attributes as well as the discrimination between the options, while q-ROF-TOPSIS and q-ROF-COPRAS methods are randomly provided by DEs.

  • As the significance degrees of the DEs are evaluated in the introduced approach, therefore, the method proposed in this study can provide more precise decisions for decision-making problems, while in q-ROF-COPRAS method, significance degree of the DEs is assumed.

6.3 Implications

The concept of sustainability has become a buzzword in today’s business marketplace. In the field of SCM, organizations are increasingly considering the sustainability in their long and short term decisions. As per the literature, there are many sustainable practices accomplished to improve the sustainability of the supply chain, but there is a lack of SRP evaluation practices. As a consequence, the evaluation of recycling partners from sustainability perspective will become a significant topic for supply chain managers. In order to assess the recycling partners from sustainability viewpoint, the present study covers two main aims which have certain implications for supply chain managers. The first one is to suggest a list of sustainability dimensions of criteria, and the second one is to introduce a new decision-making model for SMEs to execute sustainable recycling practices under highly uncertain environment.

The results of the study suggest several important insights over the considered evaluation criteria and suitable recycling partners for SMEs. The weight-determining model developed in this study can help the supply chain managers to decide the significance ratings of specific sustainability criteria. An integrated model based on objective and subjective weights of sustainability criteria makes the decision outcomes more consistent. The weights display that Pollution and waste production (0.1471) was the most important criterion, followed by the Environmental MIS (0.1374), Resource use efficiency (0.1279), and others, whereas the criterion with minimum significant value is Brand reputation (0.0256). In the present study, the q-ROF-ARAS technique is used to select the optimum recycling partner from sustainability point of view. Moreover, from a practical applications viewpoint, the developed approach is easy to use. The results of the present study will assist the SMEs in understanding the influence of diverse sustainability factors on the performance of the recycling partners and providing a clear picture of how to make proper decisions.

7 Conclusions

The assessment and selection of the SRP for SMEs are significant issue in SSCM. Due to increased environmental issues, uncertainty of human mind and involvement of several influencing factors, the SRP selection procedure can be treated as an uncertain MCDM problem. Since q-ROFSs are more flexible and significant way to express the uncertain information, therefore, this study has been developed a new MCDM model for assessing SRP options under q-ROFSs environment. This model has been introduced with the integration of classical ARAS approach, basic operational laws of q-ROFSs, and q-ROF-information measures within the perspective of q-ROFSs. Next, the criteria weights have been estimated by integrating the subjective weights uttered by DEs and the objective ones obtained by proposed information measures-based procedure. To evaluate the objective weights, novel entropy and discrimination measures have been proposed under q-ROFS context.

Further, the introduced ARAS methodology has been applied to evaluate the best SRP on q-ROFSs settings, which displays the practicality and feasibility of q-ROF-ARAS approach. To validate the results, a comparison with existing method has been conferred. To verify the stability of the presented methodology, SI has also been revealed. The outcomes obtained by the q-ROF-ARAS model prove that the introduced model has a well-mannered effectiveness and steadiness, and is well consistent with the extant models.

On the other hand, there are some limitations that must be addressed in future research, given as

  • The approach proposed herein cannot deal with the correlative MCDM problems.

  • This study has limitation in handling the uncertain, imprecise, indeterminate and inconsistent information.

  • More aspects of sustainability factors should be considered in the assessment SRPs.

In further study, we will try to address the aforesaid limitations. In addition, future investigation must be undertaken for more alternatives. Furthermore, the developed ARAS model can be generalized using interval-valued q-ROFSs, hesitant q-ROFSs, dual hesitant q-ROFSs and cubic q-ROFSs to evaluate the SRP candidates. Also, we will use the q-ROF-ARAS model to solve various problems, namely WEEE recycling partner selection, low carbon supplier selection, e-commerce service design and others.