High-order Accurate Beam Models Based on Discontinuous Galerkin Methods

Abstract

A novel high-order accurate approach to the analysis of beam structures with bulk and thin-walled cross-sections is presented. The approach is based on the use of a variable-order polynomial expansion of the displacement field throughout both the beam cross-section and the length of the beam elements. The corresponding weak formulation is derived using the symmetric Interior Penalty discontinuous Galerkin method, whereby the continuity of the solution at the interface between contiguous elements as well as the application of the boundary conditions is weakly enforced by suitably defined boundary terms. The accuracy and the flexibility of the proposed approach are assessed by modeling slender and short beams with standard square cross-sections and airfoil-shaped thin-walled cross-sections subjected to bending, torsional and aerodynamic loads. The comparison between the obtained numerical results and those available in the literature or computed using a standard finite-element method shows that the present method allows recovering three-dimensional distributions of displacement and stress fields using a significantly reduced number of degrees of freedom.

1 Introduction

Beam structures are widely employed in aeronautical and aerospace engineering as they enable the design of structural components with high-performance load-bearing capabilities, structural stiffness and optimized load distribution. Generally, the geometry of a beam structure is characterized by its length and its cross-section, with the former being significantly larger than the dimensions of the latter.

Owing to their geometric features, the mechanical response of beam structures is typically modeled by the so-called classical beam theories, such as the Euler beam theory (EBT) or the Timoshenko beam theory (TBT), which are based on assuming that the displacement components may have up to a linear dependence on the spatial coordinates spanning the beam cross-section [1]. This hypothesis allows expressing the mechanics of beam structures as a one-dimensional problem, with significant reduction in terms of degrees of freedom with respect to three-dimensional models. However, although classical beam theories are widely employed in various engineering fields and are found in several finite-element software libraries, they may lose accuracy when the length of the considered beam becomes comparable to the dimensions of the cross-section; in fact, for these cases, the use of three-dimensional solid-mechanics models is often recommended. Additionally, while three-dimensional models directly provide the distribution of all stress components, classical beam theories require a few post-processing steps to recover the transverse stress distribution throughout the cross-section.

To ameliorate these shortcomings, several researchers have proposed to extend classical beam theories by using higher order approximations of the displacement components with respect to the cross-section coordinates. Early examples of higher order beam theories may be found in Refs. [2,3,4], where the authors proposed a third-order displacement approximation for beams with rectangular cross-sections and were able to recover the quadratic variation of the transverse shear stresses. Additional effects, such as primary and secondary torsional warping, were later addressed by Kim and White [5] and Taufik et al. [6] for composite box beams. In the aforementioned studies, the authors used polynomial expansions throughout the cross-section but the use of trigonometric or exponential functions was also investigated by, e.g., Mistou et al. [7] and Karama et al. [8], respectively.

A generalization of these approaches has been proposed by Carrera and co-workers [9, 10], who developed a unified formulation where the order of approximation is a free parameter of the model and allows tuning the accuracy of the solution throughout the beam cross-section. Their approach has been employed to study the static response of laminated composite beams in both the small-strain [11] and large-strain [12,13,14] regimes, the free-vibration problem of beams with arbitrary cross-sections [15], and the buckling problem of isotropic and composite beams [16]. Recently, high-order theories have also been coupled to fluid dynamics using the Vortex Lattice Method [17] and a finite-volume-based computational fluid-dynamics library [18].

The solution of the equations governing the mechanical response of classical or higher order beam theories is generally obtained via numerical methods since analytical solutions exist for special cases of boundary conditions and/or material properties. The most employed numerical technique for modeling beams, and, more generally, solid mechanics problems, is the finite element method (FEM). The literature offers many examples of FEM-based solutions of beam structures modeled by higher order theories; very recent contributions include the development of finite-element models for large-strain [19], free-vibration and buckling [20, 21], thermo-mechanical coupling [22], non-linear dynamics [23] and wave-propagation [24, 25] problems, among others.

Alternatives to FEM have also been proposed to improve the flexibility and the performance of numerical methods. Among these, the discontinuous Galerkin (DG) method [26] has proved a powerful technique that, being based on a discontinuous approximations of the solution among the mesh elements, naturally enables the use of different basis functions for different elements of the same mesh, variable-order accuracy and ease of parallelization.

In the literature, a few examples of DG methods applied to the analysis of beam structures are available; these are typically limited to classical beam theories: Celiker et al. [27, 28] developed a DG-based solution of the Timoshenko beam problem and showed that their approach does not suffer from shear locking effects; Eptaimeros et al. [29] developed an Interior Penalty DG methods for Euler beams obeying gradient elasticity; Becker and Noels [30] exploited the discontinuous nature of DG methods to introduce suitably-defined cohesive laws at the interface between contiguous elements of beam structured modeled by the classical EBT. On the other hand, while DG methods have been proposed for the analysis of multilayered structures modeled by higher-order structural theories in the context of small-strain [31,32,33,34,35], large-strain [36] and buckling [37] problems, DG methods for higher-order beam theories have not been investigated. Therefore, in this contribution, Interior Penalty DG methods for the solution of the equations governing the static response of beams modeled by higher order theories are developed and numerically tested.

The remainder of the paper is organized as follows: Sect. 2 introduces the problem statement for the static analysis of beam structures modeled by variable-order beam theories; Sect. 3 presents the solution of the considered problem based on a novel DG formulation; in Sect. 4, the numerical performance of the proposed approach is assessed by considering the response of a beam with a bulk square cross-section to bending and torsional loads, and the response of a beam with thin-walled airfoil-shaped cross-section subjected to bending and aerodynamic loads. Eventually, Sect. 5 draws the conclusions.

2 Problem Statement

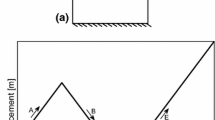
We consider a beam with length L and cross-section A as sketched in Fig. 1a. The beam is referred to a global reference system $Ox_1x_2x_3$ located at one end of the beam such that the coordinates $x_1$ and $x_3$ span the cross-section A, the coordinate $x_2$ spans the length of the beam, and the volume V of the beam is identified by $V \equiv [0,L]\times A$. Eventually, the boundary of the beam is denoted by S.

Fig. 1

a Three-dimensional beam structure of length L and cross-section A. b Discretization of the beam in one-dimensional elements of size h

The following mechanical fields are introduced: the displacement field, denoted by the vector $\varvec{u} \equiv (u_1,u_2,u_3)^\intercal$, and the strain and stress fields that, using Voigt notation, are described by the vectors $\varvec{\gamma } \equiv (\gamma _{11},\gamma _{22},\gamma _{33},\gamma _{23},\gamma _{13},\gamma _{12})^\intercal$ and $\varvec{\sigma } \equiv (\sigma _{11},\sigma _{22},\sigma _{33},\sigma _{23},\sigma _{13},\sigma _{12})^\intercal$, respectively.

In the following, the Einstein summation convention is used with Latin subscripts taking values in $\{1,2,3\}$ and Greek subscripts taking values in $\{1,3\}$.

2.1 Strain–Displacement Relationship

The beam is assumed to undergo small deformations. Following Refs. [31, 32], this allows expressing the vector $\varvec{\gamma }$ containing the strain components as a function of the displacement field $\varvec{u}$ as follows

$$\begin{aligned} \varvec{\gamma } = \varvec{I}_k\frac{\partial \varvec{u}}{\partial x_k}, \end{aligned}$$

(1)

where the matrices $\varvec{I}_1$, $\varvec{I}_2$ and $\varvec{I}_3$ are defined as

$$\begin{aligned} \varvec{I}_1 \equiv \begin{bmatrix} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1\\ 0 &{} 1 &{} 0 \end{bmatrix}, \quad \varvec{I}_2 \equiv \begin{bmatrix} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 \end{bmatrix} \quad \textrm{and}\quad \varvec{I}_3 \equiv \begin{bmatrix} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1\\ 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{bmatrix}. \end{aligned}$$

(2)

If one separates the derivatives with respect to $x_2$ from the derivatives with respect to $x_1$ and $x_3$, the vector $\varvec{\gamma }$ may also be written as

$$\begin{aligned} \varvec{\gamma } = \varvec{I}_2\frac{\partial \varvec{u}}{\partial x_2}+\varvec{I}_\alpha \frac{\partial \varvec{u}}{\partial x_\alpha }. \end{aligned}$$

(3)

2.2 Constitutive Behavior

The beam is assumed homogeneous and linear elastic such that the vector $\varvec{\sigma }$ is related to the vector $\varvec{\gamma }$

$$\begin{aligned} \varvec{\sigma } = \varvec{C}\,\varvec{\gamma }, \end{aligned}$$

(4)

where the matrix $\varvec{C}$ contains the elastic stiffness coefficients. For the explicit expression of the components of $\varvec{C}$ for isotropic, orthotropic and generally anisotropic elastic materials the reader is referred to Ref. [38].

2.3 High-order Beam Theories

In the context of high-order beam theories, see, e.g., Refs. [10], the k-th displacement component $u_k$ is expressed as a series of products between functions of the cross-section coordinates $x_1$ and $x_3$ and functions of the beam length coordinate $x_2$ playing the role of generalized displacements, that is

$$\begin{aligned} u_k = \sum _{n=0}^{N_{u_k}}Z^{(kn)}(x_1,x_3)U^{(kn)}(x_2). \end{aligned}$$

(5)

In Eq. (5), $Z^{(kn)}(x_1,x_3)$ and $U^{(kn)}(x_2)$ represent the generic n-th cross-section function and the n-th generalized displacement for the k-th component of displacement; eventually, $N_{u_k}$ denotes the corresponding order of the expansion. The expression given in Eq. (5) may be written in compact form as

$$\begin{aligned} \varvec{u} = \varvec{Z}(x_1,x_3)\varvec{U}(x_2), \end{aligned}$$

(6)

where $\varvec{Z}(x_1,x_3)$ is a $3\times (N_{u_1}+N_{u_2}+N_{u_3}+3)$ matrix suitably collecting the cross-section functions and $\varvec{U}$ is a $(N_{u_1}+N_{u_2}+N_{u_3}+3)$ vector collecting the corresponding generalized displacements. To provide an example, using Eq. (6), the Timoshenko beam theory is obtained upon choosing

$$\begin{aligned} \varvec{Z} \equiv \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} x_1 &{} -x_3\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 \end{bmatrix}, \quad \textrm{and}\quad \varvec{U} \equiv \begin{pmatrix} u&v&w&\theta _z&\theta _x \end{pmatrix}^\intercal , \end{aligned}$$

(7)

where $(u,v,w)^\intercal$ represents the translations of the cross section, while $\theta _z$ and $\theta _x$ denote its rotations with respect to the $x_3$ axis and the $x_2$ axis, respectively. It is worth noting that additional effects, such as the torsion of the beam, may be included by enriching the set of cross-section functions contained in $\varvec{Z}$.

Using Eq.(6) into Eq. (3) and Eq. (4), one obtains the expression of the strain components and stress components, respectively, as functions of the generalized displacements

$$\begin{aligned} \varvec{\gamma } = \varvec{I}_2\varvec{Z}\frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{I}_\alpha \frac{\partial \varvec{Z}}{\partial x_\alpha }\varvec{U} \quad \textrm{and}\quad \varvec{\sigma } = \varvec{C}\,\left( \varvec{I}_2\varvec{Z}\frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{I}_\alpha \frac{\partial \varvec{Z}}{\partial x_\alpha }\varvec{U}\right) . \end{aligned}$$

(8)

2.4 Governing Equations

The governing equations of the beam theories introduced in Sect. 2.3 are derived by means of the Principle of Virtual Displacements (PVD), which, for the considered beam, reads

$$\begin{aligned} \int _V \delta \varvec{\gamma }^\intercal \varvec{\sigma }\,\textrm{d}{V} = \int _V \delta \varvec{u}^\intercal \overline{\varvec{b}}\,\textrm{d}{V}+ \int _S \delta \varvec{u}^\intercal \overline{\varvec{t}}\,\textrm{d}{S}, \end{aligned}$$

(9)

where $\delta (\bullet )$ denotes the variation of $(\bullet )$, while $\overline{\varvec{b}} \equiv (\overline{b}_1,\overline{b}_2,\overline{b}_3)^\intercal$ represents the body forces acting on the volume V of the beam and $\overline{\varvec{t}} \equiv (\overline{t}_1,\overline{t}_2,\overline{t}_3)^\intercal$ represents the traction field acting on its surface S.

Upon substituting the expression of $\varvec{\gamma }$ and $\varvec{\sigma }$ given in Eq. (8) into Eq. (9) and integrating throughout the cross-section A, the expression of the PVD for the considered beam theory is obtained:

$$\begin{aligned}{} & {} \int _\mathcal {D} \left[ \frac{\textrm{d}\delta \varvec{U}^\intercal }{\textrm{d}x_2}\left( \varvec{Q}\frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{R}\,\varvec{U}\right) +\delta \varvec{U}^\intercal \left( \varvec{R}^\intercal \frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{S}\,\varvec{U}\right) \right] \textrm{d}x_2 \nonumber \\{} & {} \quad = \int _\mathcal {D} \delta \varvec{U}^\intercal \overline{\varvec{B}}\,\textrm{d}x_2+ \delta \varvec{U}^\intercal \overline{\varvec{T}}_0+\delta \varvec{U}^\intercal \overline{\varvec{T}}_L, \end{aligned}$$

(10)

where $\mathcal {D} \equiv [0,L]$ is the modeling domain of the beam, $\varvec{Q}$, $\varvec{R}$, $\varvec{S}$ are the generalized stiffness matrices, $\overline{\varvec{B}}$ is the generalized domain load, and $\overline{\varvec{T}}_0$ and $\overline{\varvec{T}}_L$ are the generalized forces at the ends of the beam. Their expression are given as follows. The generalized stiffness matrices are defined as

$$\begin{aligned}{} & {} \varvec{Q} \equiv \int _A\varvec{Z}^\intercal \varvec{c}_{22}\varvec{Z}\,\textrm{d}A, \quad \varvec{R} \equiv \int _A\varvec{Z}^\intercal \varvec{c}_{2\alpha }\frac{\partial \varvec{Z}}{\partial x_\alpha }\,\textrm{d}A, \nonumber \\{} & {} \quad \quad \textrm{and}\quad \varvec{S} \equiv \int _A\frac{\partial \varvec{Z}^\intercal }{\partial x_\alpha }\varvec{c}_{\alpha \beta }\frac{\partial \varvec{Z}}{\partial x_\beta }\,\textrm{d}A, \end{aligned}$$

(11)

where $\varvec{c}_{kl} \equiv \varvec{I}_k^\intercal \varvec{C}\varvec{I}_l$, with $k,l=1,2,3$, are $3\times 3$ matrices collecting subsets of the elastic coefficients of $\varvec{C}$, see, e.g., Ref. [32]. The generalized domain load stems from the body forces $\overline{\varvec{b}}$ and the surface traction acting on the lateral surface of the beam as

$$\begin{aligned} \overline{\varvec{B}} \equiv \int _A\varvec{Z}^\intercal \overline{\varvec{b}}\,\textrm{d}A+ \int _{\partial A}\varvec{Z}^\intercal \overline{\varvec{t}}\,\textrm{d}\partial A, \end{aligned}$$

(12)

where $\partial A$ denotes the contour of the cross-section of the beam. Eventually, the generalized forces associated with the surface traction acting on the beam ends surfaces are defined as

$$\begin{aligned} \overline{\varvec{T}}_y \equiv \int _A\varvec{Z}^\intercal \left. \overline{\varvec{t}}\right| _{x_2 = y}\,\textrm{d}A, \quad \textrm{at}\quad y=0,\,L. \end{aligned}$$

(13)

Finally, by performing integration by parts in Eq. (10) and recalling that the variational statement must be valid for any $\delta \varvec{U}$, one obtains the following strong form of the governing equations

$$\begin{aligned} -\frac{\textrm{d}}{\textrm{d}x_2}\left( \varvec{Q}\frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{R}\,\varvec{U}\right) +\varvec{R}^\intercal \frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{S}\,\varvec{U} = \overline{\varvec{B}} \quad \textrm{for}~x_2\in \mathcal {D}. \end{aligned}$$

(14)

The governing equations given in Eq. (14) are supplemented by suitable boundary conditions, which are enforced at the ends of the beam, i.e., at $x_2 = y$, where $y = 0$ or $y = L$. Dirichlet-type boundary conditions read

$$\begin{aligned} \varvec{U}|_{x_2=y} = \overline{\varvec{U}}_y \end{aligned}$$

(15)

where $\overline{\varvec{U}}_y$ is the vector of prescribed generalized displacements at $x_2 = y$; on the other hand, Neumann-type boundary conditions are

$$\begin{aligned} \nu _y\left( \varvec{Q}\frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{R}\,\varvec{U}\right) = \overline{\varvec{T}}_y \end{aligned}$$

(16)

where $\nu _0 = -1$ and $\nu _L = 1$. It is worth noting that either Dirichlet boundary conditions or Neumann boundary conditions may be enforced at each end of the beam.

3 Discontinuous Galerkin Formulation

The set of governing equations for high-order beam theories introduced in the preceding section, namely Eqs. (14)–(16), is a set of second-order elliptic differential equations with associated boundary conditions. In this section, the corresponding weak form is derived following the Interior Penalty discontinuous Galerkin formulation developed in Refs. [31, 32].

The modeling domain of the beam is divided into $N_e$ non-overlapping elements such that the domain $\mathcal {D}^e$ of the generic e-th element is identified by the interval $\mathcal {D}^e \equiv [y_-^{e},y_+^{e}]$, where $y_-^{e}$ and $y_+^{e}$ represent the two ends of the same element. It is clear that $y_+^{e} \equiv y_-^{e+1}$ and, if the elements have the same size h, $y_-^{e} = (e-1)h$ and $y_+^{e} = eh$. The collection of all the elements defines the mesh of the beam, whose discretized domain is denoted by $\mathcal {D}^h \equiv \bigcup _{e=1}^{N_e}\mathcal {D}^e$. The discretization also introduces the set $\mathcal {I}^h$ of the inter-elements interfaces, which collects the boundary points between adjacent elements, i.e. $\mathcal {I}^h \equiv \{y_+^{i}\}$ with $i = 1,\dots ,N_e-1$. Eventually, the ends of the beam, namely the points $x_2 = 0$ and $x_2 = L$, are collected into the set $\mathcal {B}_D$ of Dirichlet boundary conditions points or into the set $\mathcal {B}_N$ of Neumann boundary conditions points based on which types of boundary conditions are enforced at these boundary points. For instance, in Sect. 4, the numerical results will be focused on cantilever beams, which means that $\mathcal {B}_D = \{0\}$ and $\mathcal {B}_N = \{L\}$. A sample mesh of the beam of Fig. 1a is shown in Fig. 1b.

Once the mesh has been defined, the approximation of the solution over each element needs to be introduced. The typical feature of DG formulations is the use of discontinuous basis functions over the mesh. In general, this would allow selecting different spaces of basis functions for different elements of the same mesh, which in turn would enable different hp-refinement strategies to improve the numerical solution, see, e.g., Ref. [39, 40]. However, these aspects are outside the scope of the present research study and the same space of discontinuous polynomials is considered for all the mesh elements. In particular, let us introduce the space $\mathcal {V}^{hp}$ of discontinuous polynomials defined as

$$\begin{aligned} \mathcal {V}^{hp} \equiv \{v:\mathcal {D}^h\rightarrow \mathbb {R}~|~v(x_2 \in \mathcal {D}^e)\in \mathcal {P}^p(\mathcal {D}^e)~\forall e = 1,\dots ,N_e\}, \end{aligned}$$

(17)

where $\mathcal {P}^p(\mathcal {D}^e)$ is the space of polynomials of degree p defined over the element $\mathcal {D}^e$. Then, the approximate solution $\varvec{U}^h$ of Eqs. (14)–(16) is sought within the space $(\mathcal {V}^{hp})^{N_U}$ of discontinuous vector fields, where $N_U$ is the number of generalized displacements introduced by the considered beam theory.

To obtain the DG-based weak form of Eqs. (14)–(16), Eq. (14) is first rewritten as the following equivalent first-order set of differential equations

$$\begin{aligned} {\left\{ \begin{array}{ll} -\frac{\textrm{d}\varvec{\varSigma }}{\textrm{d}x_2}+\varvec{R}^\intercal \frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{S}\,\varvec{U} = \overline{\varvec{B}}\\ \varvec{\varSigma } = \varvec{Q}\frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{R}\,\varvec{U} \end{array}\right. } \end{aligned}$$

(18)

The first row and the second row of Eq. (18) are then multiplied by $\varvec{V}^\intercal$ and $\varvec{\varGamma }^\intercal$, respectively, where $\varvec{V}$ and $\varvec{\varGamma }$ are test functions taken from the space $(\mathcal {V}^{hp})^{N_U}$ of discontinuous vector fields, i.e. $\varvec{V},\varvec{\varGamma }\in (\mathcal {V}^{hp})^{N_U}$. Upon integrating over the generic e-th element and using integration by parts, Eq. (18) is stated in weak sense as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \int _{\mathcal {D}^e}\left[ \frac{\textrm{d}\varvec{V}^\intercal }{\textrm{d}x_2}\varvec{\varSigma }^e+\varvec{V}^\intercal \left( \varvec{R}^\intercal \frac{\textrm{d}\varvec{U}^e}{\textrm{d}x_2}+\varvec{S}\,\varvec{U}^e\right) \right] \textrm{d}x_2 = \int _{\mathcal {D}^e}\varvec{V}^\intercal \overline{\varvec{B}}\,\textrm{d}x_2+\sum _{y\in \mathcal {B}^e}\varvec{V}^\intercal \widehat{\varvec{\varSigma }}\nu _y\\ \int _{\mathcal {D}^e}\varvec{\varGamma }^\intercal \varvec{\varSigma }^e\,\textrm{d}x_2 = \int _{\mathcal {D}^e}\varvec{\varGamma }^\intercal (\varvec{Q}\frac{\textrm{d}\varvec{U}^e}{\textrm{d}x_2}+\varvec{R}\,\varvec{U}^e)\textrm{d}x_2+\sum _{y\in \mathcal {B}^e}(\varvec{\varGamma }^\intercal \varvec{Q}+\varvec{V}^\intercal \varvec{R}^\intercal )(\widehat{\varvec{U}}-\varvec{U}^e)\nu _y \end{array}\right. } \end{aligned}$$

(19)

where: the terms $\varvec{U}^e$ and $\varvec{\varSigma }^e$ denote the approximate solution of $\varvec{U}$ and $\varvec{\varSigma }$ over the element e; $\mathcal {B}^e \equiv \{y_-^e,y_+^e\}$; $\nu _y$ denotes the unit normal at the element’s boundary points, which, being the beam model one dimensional, has values $\nu _{y_-^e} = -1$ and $\nu _{y_+^e} = 1$; and $\widehat{\varvec{U}}$ and $\widehat{\varvec{\varSigma }}$ are the so-called numerical fluxes [26], which represent approximate expressions of $\varvec{U}$ and $\varvec{\varSigma }$ at the elements boundaries.

The numerical fluxes are the characteristic ingredients of DG formulations because they are responsible for linking adjacent elements. In general, at the i-th interface between two contiguous elements e and $e+1$, $\widehat{\varvec{U}}$ and $\widehat{\varvec{\varSigma }}$ are functions of $\varvec{U}^e$, $\varvec{\varSigma }^e$, $\varvec{U}^{e+1}$ and $\varvec{\varSigma }^{e+1}$. Their explicit expression depend on the considered DG method: here, upon introducing the approximate solution $\varvec{U}^h$ such that $\varvec{U}^h(x_2\in \mathcal {D}^e) \equiv \varvec{U}^e$, the numerical fluxes are chosen according to the symmetric Interior Penalty DG formulation developed in Refs. [31, 32] as follows

$$\begin{aligned}{} & {} \widehat{\varvec{U}} = {\left\{ \begin{array}{ll} \{\varvec{U}^h\},&{}\textrm{at}~x_2=y \in \mathcal {I}^h\\ \overline{\varvec{U}}_{y},&{}\textrm{at}~x_2=y \in \mathcal {B}_D\\ \varvec{U}^e,&{}\textrm{at}~x_2=y \in \mathcal {B}_N \end{array}\right. }\nonumber \\{} & {} \quad \textrm{and}\quad {\left\{ \begin{array}{ll} \widehat{\varvec{\varSigma }} = \left\{ \varvec{Q}\frac{\textrm{d}\varvec{U}^h}{\textrm{d}x_2}+\varvec{R}\,\varvec{U}^h\right\} -\mu [\![{\varvec{U}^h}]\!],&{}\textrm{at}~x_2=y \in \mathcal {I}^h\\ \widehat{\varvec{\varSigma }} = \varvec{Q}\frac{\textrm{d}\varvec{U}^e}{\textrm{d}x_2}+\varvec{R}\,\varvec{U}^e-\mu (\varvec{U}^e-\overline{\varvec{U}}_y),&{}\textrm{at}~x_2=y \in \mathcal {B}_D\\ \widehat{\varvec{\varSigma }}\nu _y = \overline{\varvec{T}}_y,&{}\textrm{at}~x_2=y \in \mathcal {B}_N \end{array}\right. } \end{aligned}$$

(20)

where $\{\bullet \}$ and $[\![{\bullet }]\!]$ are the average operator and jump operator, respectively, that are defined at the i-th interface between the elements e and $e+1$ as

$$\begin{aligned} \{\bullet \} \equiv \frac{1}{2}(\bullet ^e+\bullet ^{e+1}) \quad \textrm{and}\quad [\![{\bullet }]\!] \equiv \bullet ^e-\bullet ^{e+1} \end{aligned}$$

(21)

respectively. Additionally, in Eq. (20), $\mu$ is the so-called penalty parameter that must be suitably chosen. As customary in Interior Penalty DG formulations, see, e.g., Ref. [26], and consistently with the numerical tests performed in Refs. [31, 32], the penalty parameter $\mu$ appearing in Eq. (20) is chosen as $\mu \sim Q/h$, where Q is a positive constant of one or two orders of magnitude larger than the terms in the generalized matrix $\varvec{Q}$ and h is the mesh size.

The interested reader is referred to Ref. [26] for a thorough analysis regarding the effect of different numerical fluxes and the choice of the penalty parameter on the properties of the corresponding DG methods.

As the last step, using Eq. (20) into Eq. (19), setting $\varvec{\varGamma } \equiv \textrm{d}\varvec{V}/\textrm{d}x_2$ and summing over all the mesh elements, the weak form of symmetric Interior Penalty DG methods for high-order beam theories considered in this paper is expressed as follows: find $\varvec{U}^h \in (\mathcal {V}^{hp})^{N_U}$ such that

$$\begin{aligned} B_{\textsf{IP}}(\varvec{V},\varvec{U}^h) = L_{\textsf{IP}}(\varvec{V},\overline{\varvec{B}},\overline{\varvec{T}},\overline{\varvec{U}}) \end{aligned}$$

(22)

for any $\varvec{V} \in (\mathcal {V}^{hp})^{N_U}$. In Eq. (22), the bilinear form $B_{\textsf{IP}}(\varvec{V},\varvec{U}^h)$ is defined as

$$\begin{aligned}{} & {} B_{\textsf{IP}}(\varvec{V},\varvec{U}^h) \equiv \int _{\mathcal {D}^h} \left[ \frac{\textrm{d}\varvec{V}^\intercal }{\textrm{d}x_2}\left( \varvec{Q}\frac{\textrm{d}\varvec{U}^h}{\textrm{d}x_2}+\varvec{R}\,\varvec{U}^h\right) \right. \nonumber \\{} & {} \qquad \left. +\varvec{V}^\intercal \left( \varvec{R}^\intercal \frac{\textrm{d}\varvec{U}^h}{\textrm{d}x_2}+\varvec{S}\,\varvec{U}^h\right) \right] \textrm{d}x_2+\nonumber \\{} & {} \qquad -\sum _{y\in \mathcal {I}^h}\left( [\![{\varvec{V}}]\!]^\intercal \left\{ \varvec{Q}\frac{\textrm{d}\varvec{U}^h}{\textrm{d}x_2}+\varvec{R}\,\varvec{U}^h\right\} \right. \nonumber \\{} & {} \qquad \left. +\left\{ \frac{\textrm{d}\varvec{V}^\intercal }{\textrm{d}x_2}\varvec{Q}+\varvec{V}^\intercal \varvec{R}^\intercal \right\} [\![{\varvec{U}^h}]\!]\right) +\nonumber \\{} & {} \qquad -\sum _{y\in \mathcal {B}_D}\left( \nu _y\varvec{V}^\intercal \left( \varvec{Q}\frac{\textrm{d}\varvec{U}}{\textrm{d}x_2}+\varvec{R}\,\varvec{U}\right) +\left( \frac{\textrm{d}\varvec{V}^\intercal }{\textrm{d}x_2}\varvec{Q}\right. \right. \nonumber \\{} & {} \qquad \left. \left. +\varvec{V}^\intercal \varvec{R}^\intercal \right) \varvec{U}^h\nu _y\right) +\nonumber \\{} & {} \qquad +\sum _{y\in \mathcal {I}^h}\mu [\![{\varvec{V}}]\!]^\intercal [\![{\varvec{U}^h}]\!] +\sum _{y\in \mathcal {B}_D}\mu \varvec{V}^\intercal \varvec{U}^h \end{aligned}$$

(23)

whereas the term $L_{\textsf{IP}}(\varvec{V},\overline{\varvec{B}},\overline{\varvec{T}},\overline{\varvec{U}})$ reads

$$\begin{aligned}{} & {} L_{\textsf{IP}}(\varvec{V},\overline{\varvec{B}},\overline{\varvec{T}},\overline{\varvec{U}}) \equiv \int _{\mathcal {D}^h} \varvec{V}^\intercal \overline{\varvec{B}}\,\textrm{d}x_2 +\sum _{y\in \mathcal {B}_N}\varvec{V}^\intercal \overline{\varvec{T}}_y\nonumber \\{} & {} \qquad -\sum _{y\in \mathcal {B}_D}\left( \frac{\textrm{d}\varvec{V}^\intercal }{\textrm{d}x_2}\varvec{Q}+\varvec{V}^\intercal \varvec{R}^\intercal \right) \overline{\varvec{U}}_y\nu _y +\sum _{y\in \mathcal {B}_D}\mu \varvec{V}^\intercal \overline{\varvec{U}}_y. \end{aligned}$$

(24)

To conclude this section, it is worth noting that the Interior Penalty formulation given in Eq. (22) verifies the Galerkin orthogonality, i.e. $B_{\textsf{IP}}(\varvec{V},\varvec{U}^h-\varvec{U}) = 0$, $\forall \varvec{V}\in \mathcal {V}^{hp}$, where $\varvec{U}$ is the exact solution of Eqs. (14)–(16).

4 Results

The accuracy and capabilities of the formulation presented in the preceding section are assessed by investigating the effect of number of elements, selected beam theory and order of length-wise polynomial basis functions on the static response of beam structures. We employ tensor-product Legendre polynomials defined in the rectangle enclosing the cross-section of the beam as the cross-section functions appearing in Eq. (5); we use the same order of expansion for all the displacement components, i.e. $N_{u_1} = N_{u_2} = N_{u_3} = N$, and denote the corresponding N-th order beam theory by $\textsf{BT}_N$. Legendre polynomials of order p are also employed to define the space $\mathcal {V}^{hp}$ and the corresponding DG method is denoted by $\textsf{DG}_p$. Eventually, the considered beam structures are isotropic and characterized by the Young’s modulus $E = 75\,\textrm{GPa}$ and Poisson’s ratio $\nu = 0.33$.

Fig. 2

Geometry, boundary conditions and loads for a a beam with a square cross-section and b a beam with an airfoil cross-section

4.1 Square Cross-section Beam

The first set of numerical tests are performed on the beam shown in Fig. 2a. The beam has a bulk square cross-section and is referred to a coordinate system located at the center of gravity of the square. The side of the cross-section is $b = 0.2\,\textrm{m}$, whereas two different beam lengths are considered: $L/b = 100$, which represent the case of a slender beam, and $L/b = 10$, which represents the case of a relatively short beam. The beam is clamped at $x_2 = 0$ and is subjected to two different loading configurations, namely bending and torsion. As illustrated in Fig. 2a, bending is achieved by applying a force $\varvec{F}_b \equiv (0,0,-50\,\textrm{N})^\intercal$ at $\varvec{x} = (0,L,0)^\intercal$, while torsion is achieved by applying the forces $\varvec{F}_t \equiv (0,0,250\,\textrm{kN})^\intercal$ and $-\varvec{F}_t$ at $\varvec{x} = (b/2,L,0)^\intercal$ and $\varvec{x} = (-b/2,L,0)^\intercal$, respectively.

The magnitude of the displacement component $u_3$ computed at $\varvec{x} = (0,L,0)^\intercal$ for the beam subjected to bending is reported in Fig. 3 as a function of the overall number of degrees of freedom for different beam theories, different DG methods and the two considered beam lengths. In the figure, each curve corresponds to a given beam theory and DG method and is obtained by changing the number of mesh elements; more specifically, each curve contains four markers which correspond to four meshes with size $h = L/N_e$, where $N_e = 1,2,4$ and 8. The obtained results are compared with those provided in Ref. [9] and denoted by the thick dashed lines in Fig. 3. From the comparison, it is possible to notice that the results computed using the DG methods $\mathsf {DG_3}$, $\mathsf {DG_4}$ and $\mathsf {DG_5}$ fall within the gray area reported in the plots, which represents the region of less than 5% deviation from the dashed line, for all the considered meshes and the considered beam theories; on the other hand, using second-order polynomial basis functions as in the $\mathsf {DG_2}$ method requires a finer mesh to achieve the same level of accuracy. In fact, the numerical computations confirm that a higher order DG method provides a more accurate result than a lower order DG method using the same mesh. Eventually, as expected, changing the beam theory has as no effect on the computed values of displacement for the case of the slender beam, while it has a slightly noticeable effect for the case of the short beam.

The effect of changing the order of the beam theory or of the DG method is more evident by analyzing the distribution of the displacement and stress fields throughout the cross-section of the beam. In Figs. 4 and 5, we report the contour plots of selected components of displacement and stress fields computed using a 3D FEM code and the present DG formulation at $x_2 = L/2$ for the short beam ($L/b = 10$) subjected to bending. For each image, the contour plots are overlaid with solid black lines, which denote the contour levels obtained with the 3D FEM model with mesh size $h = b/20$ and an overall number of degrees of freedom larger than $10^6$. The number of degrees of freedom $\textsf{DOF}$ is also reported above each image.

The first rows of Figs. 4a, b and 5 show the displacement component $u_2$, the displacement component $u_1$ and the shear stress component $\sigma _{23}$, respectively, obtained with four successively refined finite-element meshes with mesh size $h = b/2$, b/4, b/10 and b/20. The same fields are computed using the $\mathsf {BT_3}$ theory, the $\mathsf {DG_2}$ method and four successively refined DG meshes with mesh size $h = L/4$, L/8, L/16 and L/32; they are reported in the second rows of Figs. 4a, b and 5. The comparison between the FEM solution and the DG solution shows that the displacement component $u_2$ is well captured by both the coarsest FEM mesh ($\textsf{DOF} = 1863$) and the coarsest DG mesh ($\textsf{DOF} = 576$); the displacement component $u_1$ reaches convergence for the FEM model with mesh size $h = b/4$ ($\textsf{DOF} = 10995$) while the coarsest DG mesh is still able to capture it; the stress components $\sigma _{23}$ reaches convergence for the FEM model with mesh size $h = b/10$ ($\textsf{DOF} = 139623$), whereas the DG model appears to require a finer mesh than $h = L/32$ ($\textsf{DOF} = 4608$) to fully recover it. The third row of Fig. 5 shows the contour plot of the $\sigma _{23}$ computed using the $\mathsf {BT_3}$ theory, a DG mesh size $h = L/8$ and four different DG methods; from the figures, it is possible to see that the numerical solution reaches convergence with the $\mathsf {DG_3}$ method ($\textsf{DOF} = 1536$) but continues to show discrepancies with respect to the 3D FEM solution even with the $\mathsf {DG_5}$ method ($\textsf{DOF} = 2304$). This is due to the low order of the beam theory; in fact, as shown in the fourth row of Fig. 5, increasing the order of the beam theory is required to converge to the 3D FEM solution.

Fig. 3

Magnitude of the displacement $u_3$ at $\varvec{x} = (0,L,0)^\intercal$ for the beam with the square cross-section subjected to bending as a function of the selected beam theory, polynomial degree and total degrees of freedom. Reference values (the thick dashed lines) are taken from Ref. [9] while the gray area denotes the region of less than 5% deviation from the dashed line

Fig. 4

Comparison between the solution obtained via a 3D FEM model and the proposed DG formulation: effect of the mesh size on the cross-section distribution of a the displacement component $u_2$ and b the displacement component $u_1$ for the short beam subjected to bending

Fig. 5

Comparison between the solution obtained via a 3D FEM model and the proposed DG formulation: the effect of the mesh size, order of the DG basis functions and order the beam theory on the cross-section distribution of the stress component $\sigma _{23}$ for the short beam subjected to bending

A similar analysis is performed for the short beam subjected to torsional loads. The comparison between the 3D FEM solution and the DG solution is reported in Figs. 6a and b for the displacement component $u_2$ and the shear stress $\tau \equiv \sqrt{\sigma _{13}^2+\sigma _{23}^2}$, respectively, computed at $x_2 = L/2$. Also in this case, the contour plots are overlaid with solid black lines, which denote the contour levels obtained with the finest 3D FEM model. As shown in Fig. 6, the 3D finite-element model provides convergence for $u_2$ and $\tau$ with a mesh characterized by size $h = b/10$ and $\textsf{DOF} = 139623$, whereas the proposed formulation fully recovers the 3D solution using the $\textsf{BT}_5$ theory, the $\textsf{DG}_4$ method and mesh size $h = L/8$, which ultimately consist of a system of 4320 degrees of freedom.

Fig. 6

Comparison between the solution obtained via a 3D FEM model and the proposed DG formulation: effect of the selected beam theory on the cross-section distribution of a the displacement component $u_2$ and b the stress field $\tau$ for the short beam subjected to torsion

4.2 Airfoil Cross-section Beam

The second set of tests are performed on the beam displayed in Fig. 2b. The beam has a thin-walled, airfoil-shaped cross-section and is referred to a coordinate system located at one quarter of the airfoil chord. The cross-section consists of a skin, whose profile is the profile of the NACA 2415 airfoil, and two spars placed at one quarter and three quarters of the chord, i.e. at $x_1=0$ and $x_1=-c/2$, respectively. Referring to the inset of Fig. 2b, the chord of the airfoil is $c = 1\,\textrm{m}$, the skin has thickness $\zeta _s/c = 0.006$, the spar placed at one quarter of the chord has thickness $\zeta _1/c = 0.015$, and the spar placed at three quarters of the chord has thickness $\zeta _2/c = 0.0105$. The beam is clamped at $x_2 = 0$ and is subjected to two loading conditions: either a concentrated force $\varvec{F}_b \equiv (0,0,-50\,\textrm{N})^\intercal$ applied at $\varvec{x} = (0,L,0)^\intercal$ or a set of aerodynamic forces $\varvec{F}_a$ computed using the Vortex Lattice Methom (VLM) [41], i.e. as the result of a vortex-lattice simulation of potential flow around a flat plate occupying the surface defined by the chords of the airfoil cross-sections.

For the concentrated force loading case, four different beam configurations are considered: a slender beam having $L/c = 25$ and only the spar at $x_1 = 0$, a slender beam having $L/c = 25$ and both spars, a short beam having $L/c = 5$ and only the spar at $x_1 = 0$, and a short beam having $L/c = 5$ and both spars. The displacement component $u_3$ computed at $\varvec{x} = (c/4,L,0)^\intercal$ is shown in Fig. 7 as a function of the number of degrees of freedom for different beam theories, different DG methods and the considered beam configurations. Similar to the convergence results reported in Fig. 3, each curve corresponds to a given beam theory and DG method and is obtained by changing the number of mesh elements: the results corresponding to the $\mathsf {DG_2}$ and $\mathsf {DG_3}$ methods are computed using mesh size $h = L/N_e$ where $N_e = 1$, 2, 4, 8, 16 and 32, whereas the results corresponding to the $\mathsf {DG_4}$ method are computed using mesh size $h = L/N_e$ where $N_e = 1$, 2, 4, 8. Figure 7 also shows the results obtained using four successively refined FEM models with mesh size $h = c/10$, c/20, c/40, and c/80; in this case the FEM model consists an assembly of shell regions. The comparison between the results obtained with the FEM models and the present DG formulation shows that the DG formulation reaches convergence using two to three orders of magnitude of degrees of freedom less than reference FEM model. Moreover, as expected, the first and the second rows of Fig. 3 show that varying the order of the beam theory has very little effect on the results computed for slender beams; on the other hand, a fifth-order beam theory is required to ensure that the converged DG solution fall within the dark gray area, which corresponds to the region of less than 1% deviation from the solution obtained via the most refined FEM model. Nevertheless, all solutions obtained with the $\mathsf {DG_3}$ and $\mathsf {DG_4}$ methods fall within the light gray area, i.e. the region of less than 5% deviation from the reference FEM solution, even using the coarsest mesh, whereas the solution obtained using the $\mathsf {DG_2}$ method requires more elements to convergence.

The contour plots of the displacement component $u_2$ for the short beams subjected to the concentrated force are displayed in Fig. 8a, for the one-spar configuration, and in Fig. 8b, for the two-spar configuration. The first, second, third and fourth row of the figure show the results computed using the beam theories $\textsf{BT}_2$, $\textsf{BT}_3$, $\textsf{BT}_4$ and $\textsf{BT}_5$, respectively, while keeping $p = 4$ in the $\textsf{DG}$ formulation and $h = L/8$ as mesh size. The plots are reported over the deformed beam configuration and are overlaid with solid black lines, which denote the contour levels obtained via the finest FEM model. The comparison between the solution obtained via the DG method and the solution obtained via FEM shows that small differences are noticeable between the two methods when the beam theories $\textsf{BT}_2$ or $\textsf{BT}_3$ are employed, whereas the solution obtained using the beam theories $\textsf{BT}_4$ or $\textsf{BT}_5$ matches excellently the reference FEM solution. A similar observation can be made for contour plots of the stress component $\sigma _{22}$, which are displayed in Fig. 9 for the same beam configurations, DG method, mesh size and beam theory of Fig. 8. Also in this case, all beam theories well reproduce the distribution of $\sigma _{22}$ with the beam theory $\textsf{BT}_5$ providing the best matching with the reference FEM model.

Fig. 7

Magnitude of the displacement $u_3$ at $\varvec{x} = (c/4,L,0)^\intercal$ for the beam with the airfoil cross-section subjected to bending as a function of the selected beam theory, polynomial degree and total degrees of freedom. The light gray area and dark gray area denote the regions of less than 5% deviation and less than 1% deviation, respectively, from the dashed line

Fig. 8

Comparison between the solution obtained via a shell-assembly FEM model and the proposed DG formulation: effect of the selected beam theory on the distribution of the axial component $u_2$ for the short beam with a one spar and b two spars subjected to bending. DG results are computed using $p = 4$ and $h = L/8$

Fig. 9

Comparison between the solution obtained via a shell-assembly FEM model and the proposed DG formulation: effect of the selected beam theory on the distribution of the stress component $\sigma _{22}$ for the short beam with a one spar and b two spars subjected to bending. DG results are computed using $p = 4$ and $h = L/8$

The last set of results focuses on the response of a wing, modeled by the present DG formulation as a beam, subjected to aerodynamic loads. These loads are computed using the VLM, which is based on replacing a lifting surface by a collection of elemental solutions, such as horseshoe or ring vortices, of the potential flow equation, and is valid for low-speed, high-Reynolds attached flow conditions [41]. The coupling between the present DG formulation and the VLM goes beyond the scope of this paper but it will be comprehensively discussed in a future study. Here, we reproduce one of the tests reported in Ref. [17], where the short beam ($L/c = 5$) with two spars is exposed to a free-stream velocity $V_\infty = 50\,\textrm{m}/\textrm{s}$ with an angle of attack $\alpha = 3^\circ$ at standard sea-level conditions. Unlike the preceding tests, note that the Young’s modulus of the beam is $E = 69\,\textrm{GPa}$. Regarding the employed VLM, the surface of the chords of the airfoil cross-sections is chosen as the lifting surface, which is discretized using an aerodynamic mesh grid of 4 ring vortices along the chord and 40 ring vortices along the length of the beam; the symmetry condition with respect to the $x_1$-$x_3$ plane is also considered for the aerodynamic computations.

The displacement component $u_3$ of the leading edge of the tip cross-section is computed using the $\mathsf {DG_4}$ method and a mesh size $h = L/8$ and is reported in Table. 1 as a function of the selected beam theory. The table also reports the solution obtained in Ref. [17] where the authors also employed various higher order beam theories but used the FEM to solve the corresponding equations. The comparison between the solution computed using the present DG formulation and the solution obtained via FEM shows that the maximum error does not exceed 3.1% and confirms the accuracy of the proposed approach. Eventually, Fig. 10a and b show the contour plots of the displacement component $u_2$ and the stress component $\sigma _{22}$, respectively, obtained with the present approach using the $\mathsf {BT_4}$ theory, the $\mathsf {DG_4}$ method and a mesh size $h = L/8$.

Table 1 Effect of the selected beam theory on the displacement $|u_3|$ at $\varvec{x} = (c/4,L,0)^\intercal$ for the short beam with two spars subjected to aerodynamic loading

Fig. 10

a Displacement component $u_2$ and b stress component $\sigma _{22}$ for the short beam with two spars subjected to aerodynamic loads computed using the $\mathsf {BT_4}$ theory, the $\mathsf {DG_4}$ method and a mesh size $h = L/8$

5 Conclusions

A novel tool for the elastic analysis of beam structures with general cross-sections has been presented. The proposed method is based on the combined use of high-order beam theories to express the displacement components throughout the beam cross-section and high-order discontinuous Galerkin methods along the length of the beam. The accuracy of the method has been assessed by modeling cantilever beams with a square cross-section and by modeling cantilever beams with thin-walled airfoil-shaped cross-sections. Bending, torsional and aerodynamic loading cases have been considered. The obtained numerical results shows that the proposed tool is able to recover three-dimensional displacement and stress distributions using considerably fewer degrees of freedom than standard FEM approaches based on three-dimensional or two-dimensional shell elements.