1 Introduction

In the last decades, new challenges demanded by aerospace, automotive and other engineering fields require the adoption of sophisticated and eventually lightweight structures. For this reason, composite materials, thanks to their outstanding structural performances in terms of strength and stiffness properties compared to metal alloys, have encountered great success. Zhang et al. [1] reported how the usage of laminated components has drastically grown, especially in the aerospace field. However, the correct design of composite components generally requires enhanced calculation techniques to account for anisotropy coupling effects, interface phenomena, and 3D stress states, for example. The need for a high level of accuracy and reliability from the structural simulation pushed engineers to use high-performing three-dimensional (3D) models, with a high effort in terms of computational cost. In order to cut down this drawback, scientists and researchers have been encouraged to develop lighter one-dimensional (1D) and two-dimensional (2D) models, with the goal of maintaining the same level of accuracy when compared to heavier 3D tools.

A comprehensive review of the modeling of laminated materials for 1D structures can be found in Kapania and Raciti [2, 3]. Classical theories such as the Euler-Bernoulli beam [4] is widely applied in numerical simulations, although it lacks the ability to accurately predict the transverse shear over the cross-sections of beams, for which the shear effects play a crucial role in their mechanical behavior. To overcome this problem, many other models were developed to carry out reliable results, especially in the case of composite structures. Based on the Timoshenko beam theory [5], which considers a constant distribution of the shear stress along the cross-section, the First-order Shear Deformation Theory (FSDT) was built. This model was adopted by engineers for their studies about laminated structures for many decades. Gupta et al. [6] presented a formulation for the post-buckling behavior of composite beams with axially immovable ends. Lanc et al. [7] discussed a beam Finite Element (FE) model for the post-buckling analysis of composite laminated structures in the framework of an updated Lagrangian incremental formulation.

Even though the FSDT ensures reliable accuracy for a wide range of problems, it has some limitations. In fact, when dealing with thin-walled structures, whose cross-sectional deformation plays a crucial role, an accurate evaluation of the stress distribution is necessary, to accurately describe the higher-order phenomena. For this reason, advanced structural theories must be considered, because classical approaches might be inappropriate and lead to wrong conclusions, see the classical book by Novozhilov [8]. For instance, Stephen and Levinson [9] developed a higher-order theory starting from the Timoshenko beam equation and taking into account the shear curvature, through the introduction of new coefficients. As further examples of higher-order beam models proposed in the past, Vlasov [10] introduced warping functions to capture the deformations of beam cross-sections. This approach found a great success between scientists, see the works by Ambrosini et al. [11], Mechab et al. [12] and Friberg [13], who made use of warping functions for thin-walled structures. A combination of the refined Vlasov model and the classical Euler-Bernoulli model was adopted by Kim and Lee [14] to analyze thin-walled beams made of functionally graded materials. The so-called Generalized Beam Theory (GBT) was suggested by Schardt [15]. This theory allows the displacement field to be expressed as a linear combination of cross-sectional deformation modes. GBT found many applications in the literature, for example, by Peres et al. [16] for the analysis of curved thin-walled beams, and by Silvestre [17] for buckling problems. GBT was also adopted for the analysis of laminated materials, as presented by Silvestre and Camotim [18, 19].

Particular attention must be given to local phenomena when structures are subjected to large deformation, e.g., large displacements and large rotations. In fact, for an accurate design of structures undergoing extreme loading conditions, a geometrical nonlinear analysis must be carried out. The contributions of scientists to the nonlinear analysis of 1D structures are uncountable. Most of the geometrical nonlinear models developed in the past are based on the Timoshenko beam theory, see, for example, Refs. [20,21,22]. The works by Hodges [23] and Chia [24] presented an overview of the geometrically nonlinear behaviour of composite beams and plates, respectively. The literature of works about the behaviour of composite structures in the large displacement and rotation field is vast, indeed. As an example, the work by Zhang and Kim [25] is mentioned. It proposes a quadrilateral plate element for the geometrical nonlinear analysis of laminated composite plate. The model is based on FSDT and Foppl-von Kármán geometrical nonlinearities, within a total Lagrangian approach. With the same assumptions, Zhang and Liew [26] analyzed the geometrical nonlinear behaviour of carbon nanotube-reinforced composite plates.

In many real applications, local phenomena and large cross-sectional deformations occur in particular areas of the structure, for example, in the nearby of external loads or constraint conditions. In such cases, it would be needed to build a model with variable kinematics, namely, capable of refining only the portions of the structure which undergo high deformation or rotation. In this way, the accuracy is still guaranteed, with a drastic decrease in the number of degrees of freedom and, subsequently, of the computational cost. When models with different kinematics have to be coupled, the continuity of the displacements between the two regions has to be guaranteed. The issue of coupling incompatible structural models was widely investigated in modern scientific literature. Wenzel [27] proposed an exhaustive state-of-the-art about this topic. For instance, the compatibility between different domains can be reached by making use of the Lagrange multipliers, see for instance the work by Prager [28] and Carrera et al. [29]. Another solution to this problem is the adoption of the global-local technique. Basically, this method consists of a multi-step procedure, where, at first, a “global” analysis is carried out using a coarse mathematical model of the structure. Then, a refined FE model is applied separately in specific and more deformable subregions, and the compatibility is ensured by enforcing the continuity of the displacement in the interfacial or overlapping zones. Noor [30] proposed a review on the global-local approaches for the nonlinear analysis of composite panels. The global-local approach found application in many engineering fields. For instance, Hanganu et al. [31] applied this method in the analysis of civil structures, for an accurate evaluation of the damage within the structure.

Fig. 1
figure 1

Generic composite structure with equivalent single layer (Taylor) and layerwise (Lagrange polynomials) approaches

Full size image

The present work intends to assess the benefits of adopting variable kinematics on composite beam structures in the geometrical nonlinear analysis. The proposed solution is the adoption of the Node-Dependent Kinematics (NDK) approach in a FE framework based on the Carrera Unified Formulation (CUF) [32, 33]. Thanks to the scalable nature of CUF, any arbitrary expansion of the FE unknowns can be used to achieve the desired theory of structures. In other words, the primary unknowns of a given problem (that, for a 1D problem, are the displacement along the beam axis), are expanded using arbitrary cross-section functions. The novelty of the NDK approach consists in adopting different expansion functions over the beam length for the kinematic description of the cross-sections. Since the Finite Element Method (FEM) is used for the beam axis approximation, no problems about coupling different expansion functions arise. NDK was used and validated in the past years by Carrera and Zappino [34] and applied to composite structures [35, 36], 2D plate [37, 38] and shell problems [39]. The geometrical nonlinear 1D governing equations of the beam theory are obtained by means of the so-called fundamental nuclei, which allow the automatic employment of low- to higher-order theories, arbitrarily. This geometrical nonlinear solution was validated for isotropic and composite materials [40, 41] and, then, further extended to the dynamic [42, 43] and 2D plate [44] and shell cases [45, 46]. A deep analysis of the role of cross-sectional deformations in the geometrical nonlinear field is proposed in [47, 48], for isotropic and composite structures, respectively. In [49], the capability of the NDK approach in the CUF framework was tested for the geometrical nonlinear analysis of thin-walled isotropic structures. In this work, the investigation is further extended to deal with compact and thin-walled composite structures.

This paper is organized as follows: (i) Section 2 reports the present model, including the FE arrays calculation adopting the NDK approach in the geometrical nonlinear analysis; (ii) then, numerical results are discussed for both compact and thin-walled laminated beams in Sect. 3, with symmetric and asymmetric loading conditions; (iii) finally, the main conclusions are drawn.

2 Unified laminated beam element with node-dependent kinematics

2.1 Kinematics approximation

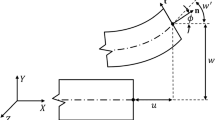
Consider a generic one-dimensional (1D) laminated structure, as depicted in Fig. 1. A Cartesian coordinate system is adopted, in a way that x and z are the coordinates of the cross-section and y is orthogonal and lays along the beam axis (in blue). In this work, the three-dimensional (3D) displacement field \({\mathbf {u}}(x,y,z) = \left\{ u_{x} \; u_{y} \; u_{z}\right\} ^{T}\) as well as its variation (denoted by \(\delta \)), is expressed in the framework of the Carrera Unified Formulation (CUF) and reads:

$$\begin{aligned} \begin{array}{cccc} {\mathbf {u}}(x,y,z) &{} = &{} F_{\tau }(x,z) \; {\mathbf {u}}_{\tau }(y), \qquad \ &{} \tau = 1,2,....,M \\ \delta {{\mathbf {u}}}(x,y,z) &{} = &{}F_{s}(x,z) \; \delta {\mathbf {{u}}}_{s}(y), \qquad &{} s = 1,2,....,M \end{array} \end{aligned}$$
(1)

where \(F_{\tau }\) and \(F_{s}\) are the expansion functions of order M of the cross-section with coordinate x and z and \({\mathbf {u}}_{s}\) is the generalized displacement vector. The choice of \(F_{\tau }\) and \(F_{s}\) and M is arbitrary and they define the theory adopted to model the structure. Many options are available for the expansion functions, i.e. Taylor polynomials [50], Chebyshev polynomials [51], Lagrange expansion [52] and Legendre polynomials [53], among the others. In this work, both Lagrange and Taylor polynomials are adopted to discretize the displacement field over the cross-section and they allow the employment of the Layer-wise (LW) and Equivalent Single Layer (ESL) approaches, respectively.

2.1.1 LW models

As far as the LW approach is concerned, the cross-section of the laminated beam is discretized with a set of Lagrange Points (LPs), opportunely subdivided into Lagrange Elements (LE). The degree of the interpolation is defined by the number of the LPs; for instance, a 4 points LE (L4) ensures a linear interpolation, a 9 points LE (L9) a quadratic interpolation and a 16 point LE (L16) a cubic interpolation. When dealing with composite structures, each layer may be modeled independently by using a dedicated \(F_{\tau }\) polynomial set, as shown in Fig. 1, bringing to an LW description of the laminate. A comprehensive review about LW theories was made by Carrera [54]. This theory treats each layer individually and both displacement and transverse shear stress continuity may be satisfied between each layer; therefore, it yields results compatible with 3D elasticity solutions.

Multiple Lagrange polynomials can be assembled above the cross-section imposing the displacement continuity at the interface nodes, so any type of cross-section, from compact to thin-walled shapes, can be analyzed. For completeness purpose, the complete expression of the displacement field of a generic point “A” of coordinates (x, y, z) within the cross-section, using an L9 polynomial, is reported hereafter:

$$\begin{aligned} u_{x}(x,y,z)&= F_{1}(x,z)u_{x_{1}}(y)+F_{2}(x,z)u_{x_{2}}(y)\nonumber \\&\;\quad +\cdots +F_{9}(x,z)u_{x_{9}}(y) \nonumber \\ u_{y}(x,y,z)&= F_{1}(x,z)u_{y_{1}}(y)+F_{2}(x,z)u_{y_{2}}(y)\nonumber \\&\;\quad +\cdots +F_{9}(x,z)u_{y_{9}}(y) \nonumber \\ u_{z}(x,y,z)&= F_{1}(x,z)u_{z_{1}}(y)+F_{2}(x,z)u_{z_{2}}(y)\nonumber \\&\;\quad +\cdots +F_{9}(x,z)u_{z_{9}}(y) \end{aligned}$$
(2)

where the \(F_{\tau }\) are not fully reported here for the sake of brevity, but can be found in in [33].

2.1.2 ESL models

The ESL approach, as depicted in Fig. 1, allows the treatment of the multi-layered structure as a single-layered one, through an appropriate homogenization of the cross-section properties. The complete expression for a TE of order two (TE2) is reported in Eq. (3):

$$\begin{aligned} \begin{array}{ll} u_{x}(x,y,z) &{} = u_{x_{1}}(y)+x \; u_{x_{2}}(y)+z \; u_{x_{3}}(y)\\ &{}\quad +x^{2} \; u_{x_{4}}(y)+xz \; u_{x_{5}}(y)+z^{2} \; u_{x_{6}}(y) \\ u_{y}(x,y,z) &{} = u_{y_{1}}(y)+x \; u_{y_{2}}(y)+z \; u_{y_{3}}(y)\\ &{}\quad +x^{2} \; u_{y_{4}}(y)+xz \; u_{y_{5}}(y)+z^{2} \; u_{y_{6}}(y) \\ u_{z}(x,y,z) &{} = u_{z_{1}}(y)+x \; u_{z_{2}}(y)+z \; u_{z_{3}}(y)\\ &{}\quad +x^{2} \; u_{z_{4}}(y)+xz \; u_{z_{5}}(y)+z^{2} \; u_{z_{6}}(y) \\ \end{array} \end{aligned}$$
(3)

where \(x_{A}\), \(y_{A}\) and \(z_{A}\) are the coordinates of a generic point “A” of coordinates (x, y, z). The number of the Degrees Of Freedom (DOFs) is equal to the displacement and derivatives of the TE and, for the case of a TE2, they are 18.

2.2 Finite element approximation

As far as the displacements along the beam axis are concerned, the Finite Element Method (FEM) is adopted to approximate the vector \({\mathbf {u}}_{\tau }(y)\) and its variation \(\delta {\mathbf {u}}_{s}(y)\), as follows:

$$\begin{aligned} \begin{array}{ll} {\mathbf {u}}_{\tau }(y) =&{} N_{i}(y) {\mathbf {q}}_{\tau i} \qquad i=1,2,\ldots ,N_n\\ \delta {\mathbf {u}}_{s}(y) =&{} N_{j}(y) \delta {\mathbf {q}}_{s j} \qquad j=1,2,\ldots ,N_n \end{array} \end{aligned}$$
(4)

where \(N_{i}(y)\) and \(N_j(y)\) stand for the i, j-th 1D shape function, \(N_n\) is the number of the structural nodes, i indicates summation and \({\mathbf {q}}_{\tau i}\) is the vector of the FE nodal parameters \(\left\{ \begin{array}{ccc} q_{x_{\tau i}}&q_{y_{\tau i}}&q_{z_{\tau i}} \end{array}\right\} ^{T}\). Interested readers can refer to Bathe [55] and to Carrera et al. [33] for the complete form of the shape functions \(N_{j}\). In this work, classical 1D FEs with four nodes (B4) are adopted, i.e. a cubic approximation along the y axis is considered. Finally, introducing the Eq. (4) into Eq. (1), the explicit form of the 3D displacement field can be obtained:

$$\begin{aligned} \begin{array}{ll} {\mathbf {u}}(x,y,z) = F_{\tau }(x,z)N_{i}(y) {\mathbf {q}}_{\tau i} \\ \delta {\mathbf {u}}(x,y,z) = F_{\tau }(x,z)N_{i}(y) \delta {\mathbf {q}}_{\tau i} \end{array} \end{aligned}$$
(5)

2.3 The node-dependent kinematics approach

As discussed in the introduction, the possibility to couple local-to-global parts of the FE model can be done in many ways. NDK allows, by definition, for the variation of the node-by-node kinematic in the same element, refining the kinematics without any use of coupling mathematical artifices. The refinement of the adopted kinematic can be taken a step further by assigning an own approximation to each node of an element. Thanks to the scalable nature of the CUF-based displacement models, it is possible to develop a FE with variable kinematic. The basic idea of NDK is to describe the displacement field over each cross-section of an element with different kinematics. In this way, one can refine the model only over the regions which require a higher-order theory to be accurately described, and associate lower-order theories in the remaining zones of the domain where localized phenomena do not take place, saving computational cost. The \(F_\tau , F_s\) functions are node-dependents; in other words, the theory approximation order is a function of the FE nodal index i and j. Then, Eq. (5) becomes:

$$\begin{aligned} \begin{array}{ll} {\mathbf {u}}(x,y,z) =&{} F^{i}_{\tau }(x,z)N_{i}(y) {\mathbf {q}}_{\tau i}, \qquad \tau = 1,2,....,M^{i} \\ \delta {\mathbf { u}}(x,y,z) =&{} F^{j}_{s}(x,z)N_{j}(y) \delta {\mathbf {q}}_{ s j}, \qquad s = 1,2,....,M^{j} \end{array} \end{aligned}$$
(6)

where the indexes i, j on \(M^{i}, M^j\) and \(F^{i}_{\tau }(x,z), F^{j}_{s}(x,z)\) underlines that the expansion functions are associated to the i, j-th node of the element, rather than to the entire element itself. Note that Eq. (6) shows the discrete dependency at the structural node level of the expansion functions through the indexes i, j. An example of NDK approach is finally shown in Fig. 2, where a composite beam discretized with one single 4-node B4 finite element in the beam axis direction is shown. Figure 2a shows the case of a uniform LW kinematic adopted for the whole structure, and each cross-section has 33 LP. Then, the number of Degrees Of Freedom (DOFs) is \(33 \times 3 \times 4 = 396\). On the other hand, Fig. 2b proposes a NDK model of the structure. In particular, node 1 has a TE1 expansion, that is the Eq. (3) truncated at linear term and the number its DOFs is 9; node 2 is expanded with a TE2 (the Eq. (3)), with 18 DOFs.; the nodes 3 and 4 are approximated with 12 and 33 LP so that their DOFs are \(12 \times 3 = 36\) and \(33 \times 3 = 99\), respectively. The number of DOFs is given by the sum of DOFs of every cross-section, i.e. \(9 + 18 + 36 + 99 = 162\).

Fig. 2
figure 2

Composite structure with uniform kinematic (a) and NDK approach (b). Expansion functions (in red) are associated individually with each node. The structure is modeled with four structural nodes. The uniform kinematic model has 33LP, so that the number of DOFs is \(33 \times 3 \times 4 = 396\). The NDK model is approximated with a TE1, TE2, 12LP and 365LP, respectively. Then, the number of the DOFs is \(9 + 18 + 12 \times 3 + 33 \times 3 = 162\)

Full size image
Fig. 3
figure 3

Large deflection bending of a thin-walled composite structure subjected to uniform transverse pressure. Some areas (green domains) undergo low deformations and can be approximated with low-order theories, other (blu areas) show large deformations and have to be described with refined kinematics

Full size image

Figure 3 finally shows an example in which the NDK concept could strongly reduce the computational effort. Consider a thin-walled composite beam clamped at the two edges and subjected to a uniform transverse pressure and in a far nonlinear equilibrium state. As outlined in the figure, some portions of the structure undergo remarkable cross-sectional deformation (see the blue domains in Fig. 3), so that the whole structure would need a refined theory to be accurately described. However, some zones (the green ones in the figure) do not show remarkable deformations, so that a lower-order kinematics would be enough to describe their kinematics, even in a far nonlinear state. Thanks to NDK, different kinematics can be employed in different domains, building an efficient mathematical model for the geometrical nonlinear analysis and decreasing the numbers of DOFs, as already described in Fig. 2. In the present work, this procedure is employed to build an efficient mathematical model of composite structures in the large-displacements and post-buckling fields.

Many examples will be discussed in the numerical results section.

2.4 Geometrical and constitutive relations

The strain \({\mathbf {\epsilon }}\) and stress \({\mathbf {\sigma }}\) components are written in vectorial form, and the transposed vectors are introduced in the following:

$$\begin{aligned}&\varvec{\epsilon } = \left\{ \epsilon _{xx} \quad \epsilon _{yy} \quad \epsilon _{zz} \quad \epsilon _{xz} \quad \epsilon _{yz} \quad \epsilon _{xy} \right\} ^{T}, \nonumber \\&\varvec{\sigma } = \left\{ \sigma _{xx} \quad \sigma _{yy} \quad \sigma _{zz} \quad \sigma _{xz} \quad \sigma _{yz} \quad \sigma _{xy} \right\} ^{T} \end{aligned}$$
(7)

As far as the geometrical relations are concerned, the Green-Lagrange nonlinear strain components are considered. Therefore, the displacement-strain relations are expressed as:

$$\begin{aligned} \epsilon = \epsilon _l + \epsilon _{nl} = ({\mathbf {b}}_l + {\mathbf {b}}_{nl}) {\mathbf {u}} \end{aligned}$$
(8)

where \({\mathbf {b}}_l\) and \({\mathbf {b}}_{nl}\) are the linear and nonlinear differential operators, respectively. The complete form of these two matrices can be found in [40].

Regarding the constitutive relations, we assume linear elastic material, thus the Hooke law can be employed:

$$\begin{aligned} \sigma = C \epsilon \end{aligned}$$
(9)

where C is the material matrix, whose complete form can be found in [56]. The coefficients of the material matrix depend only on the material properties and the geometrical properties of the fibres. The explicit form of the coefficients can be found in many books, see [57].

2.5 Nonlinear governing equations

The principle of virtual work is hereafter recalled for the derivation of the nonlinear FE governing equations. For static problems, It states that the virtual work from the internal strain energy (\(\delta L_{\mathrm{int}}\)) is equal to the one made by the external loads (\(\delta L_{\mathrm{ext}}\)). Moreover, the geometrical nonlinear problem is obtained by introducing Eq. (6) into Eq. (8), so that strain vector can be written in algebraic form as follows:

$$\begin{aligned} {\epsilon } = ({\mathbf {B}}_l^{\tau i} + {\mathbf {B}}_{nl}^{\tau i}) {\mathbf {q}}_{\tau i} \end{aligned}$$
(10)

where \({\mathbf {B}}_l^{\tau i}\) and \({\mathbf {B}}_{nl}^{\tau i}\) are the linear and nonlinear algebraic matrices with CUF and FEM formulations. For the sake of completeness, these operators are given below.

$$\begin{aligned} {\mathbf {B}}_l^{\tau i} = \left[ \begin{array}{ccc} F^{i}_{\tau _{,x}} N_{i} &{} 0 &{} 0 \\ \\ 0 &{} F^{i}_\tau N_{i_{,y}} &{} 0 \\ \\ 0 &{} 0 &{} F^{i}_{\tau _{,z}} N_{i} \\ \\ F^{i}_{\tau _{,z}} N_{i} &{} 0 &{} F^{i}_{\tau _{,x}} N_{i} \\ \\ 0 &{} F^{i}_{\tau _{,z}} N_{i} &{} F^{i}_{\tau } N_{i_{,y}} \\ \\ F^{i}_{\tau } N_{i_{,y}} &{} F^{i}_{\tau _{,x}} N_{i} &{} 0 \\ \end{array}\right] \end{aligned}$$
(11)

and

$$\begin{aligned} {\mathbf {B}}_{nl}^{\tau i} = \dfrac{1}{2} \left[ \begin{array}{ccc} u_{x_{,x}} F^{i}_{\tau _{,x}} N_i &{} u_{y_{,x}} F^{i}_{\tau _{,x}} N_i &{} u_{z_{,x}} F^{i}_{\tau _{,x}} N_i \\ \\ u_{x_{,y}} F^{i}_\tau N_{i_{,y}} &{} u_{y_{,y}} F^{i}_\tau N_{i_{,y}} &{} u_{z_{,y}} F^{i}_\tau N_{i_{,y}} \\ \\ u_{x_{,z}} F^{i}_{\tau _{,z}} N_i &{} u_{y_{,z}} F^{i}_{\tau _{,z}} N_i &{} u_{z_{,z}} F^{i}_{\tau _{,z}} N_i \\ \\ u_{x_{,x}} F^{i}_{\tau _{,z}} N_i + u_{x_{,z}} F^{i}_{\tau _{,x}} N_i &{} u_{y_{,x}} F^{i}_{\tau _{,z}} N_i + u_{y_{,z}} F^{i}_{\tau _{,x}} N_i &{} u_{z_{,x}} F^{i}_{\tau _{,z}} N_i + u_{z_{,z}} F^{i}_{\tau _{,x}} N_i \\ \\ u_{x_{,y}} F^{i}_{\tau _{,z}} N_i + u_{x_{,z}} F^{i}_{\tau } N_{i_{,y}} &{} u_{y_{,y}} F^{i}_{\tau _{,z}} N_i + u_{y_{,z}} F^{i}_{\tau } N_{i_{,y}} &{} u_{z_{,y}} F^{i}_{\tau _{,z}} N_i + u_{z_{,z}} F^{i}_{\tau } N_{i_{,y}} \\ \\ u_{x_{,x}} F^{i}_{\tau } N_{i_{,y}} + u_{x_{,y}} F^{i}_{\tau _{,x}} N_i &{} u_{y_{,x}} F^{i}_{\tau } N_{i_{,y}} + u_{y_{,y}} F^{i}_{\tau _{,x}} N_i &{} u_{z_{,x}} F^{i}_{\tau } N_{i_{,y}} + u_{z_{,y}} F^{i}_{\tau _{,x}} N_i \\ \end{array}\right] \end{aligned}$$
(12)
Fig. 4
figure 4

Geometric properties and loading case of the asymmetric beam with compact cross-section subjected to compressive loading

Full size image

The variation of the elastic internal work, considering constitutive (Eq. 9) and geometrical relations (Eq. 10), can be expressed as:

$$\begin{aligned} \begin{array}{lll} \delta L_{\mathrm{int}} &{} = &{} \displaystyle \int _{V} \delta {\mathbf {\epsilon }}^{T} {\mathbf {\sigma }} \;\mathrm{d}V \\ &{} {=} &{} \delta {\mathbf {q}}_{s j}^T \; \left( \int _{V} \left( {\mathbf {B}}_l^{s j} {+} 2 \, {\mathbf {B}}_{nl}^{s j} \right) ^T {\mathbf {C}}\left( {\mathbf {B}}_l^{\tau i} {+} {\mathbf {B}}_{nl}^{\tau i} \right) \;\mathrm{d}V\right) \; {\mathbf {q}}_{\tau i} \\ &{}=&{}\delta {\mathbf {q}}_{s j}^T \; {\mathbf {K}}_{S}^{i j \tau s} \; {\mathbf {q}}_{\tau i} \end{array} \end{aligned}$$
(13)

where \({\mathbf {B}}_l^{s j}\) and \({\mathbf {B}}_{nl}^{s j}\) comes out from the variation of the strain components (Eq. 10) and \({\mathbf {K}}_S^{i j \tau s}\) represents the secant stiffness matrix. The complete form of the secant stiffness matrix \({\mathbf {K}}_S^{i j \tau s}\) can be found in [40, 58].

Omitting some mathematical steps, which interested readers can find in [59], the principle of virtual work, for the whole structure, becomes:

$$\begin{aligned} {\mathbf {K}}_{S} \; {\mathbf {q}} - {\mathbf {p}} = 0 \end{aligned}$$
(14)

where \({\mathbf {K}}_{S}\), \({\mathbf {q}}\), and \({\mathbf {p}}\) are the global FE arrays of the structure, with \({\mathbf {p}}\) corresponding to the loading vector.

The system of algebraic nonlinear equations (Eq. 15) are solved via an iterative method. Usually, an incremental linearized scheme, typically the Newton–Raphson method is adopted to solve the geometrical nonlinear systems. According to the Newton–Raphson method, Eq. (15) is formulated as follows

$$\begin{aligned} \varphi _{res} = {\mathbf {K}}_{S} \; {\mathbf {q}} - {\mathbf {p}} = 0 \end{aligned}$$
(15)

where \( \phi _{res}\) denotes the vector of the residual nodal forces (unbalanced nodal force vector).

The Newton-Raphson scheme demands the linearization of the equations. Thus, the related tangent stiffness matrix \({\mathbf {K}}_{T}\) can be obtained by the second variation of the strain energy at the equilibrium point, as follows

$$\begin{aligned} \delta ^2 L_{\mathrm{int}} = \delta {\mathbf {q}}_{s j}^T K_T^{i j \tau s} \delta {\mathbf {q}}_{\tau i} \end{aligned}$$
(16)

The explicit form of \({\mathbf {K}}_{T}\) is not given here, but it is derived in a unified form in [60]. Finally, the resultant system of equations is constrained with an approach of arc-length type, which was developed by Riks [61], Crisfield [62, 63], Ramm [64] and Wempner [65]. In particular, in the present work, the refinement proposed by Carrera [66] of the arc-length procedure is employed, and it basically consists in the choice of the roots of the nonlinear constraint equation as the closest to the consistent linearized solution.

3 Numerical results

In this section, various problems are addressed for demonstrating the application and capability of NDK models in the large deflection field of composite structures. It must be pointed out that, due to the anisotropic behavior of laminated structures, the NDK approach is useful not only for thin-walled structure, but also for compact ones. Clearly, from the results of Carrera and Zappino [34], when dealing with isotropic structures with compact cross-sections, classical theories and low-order models provide an adequate degree of accuracy. Nevertheless, for modeling composite structures with compact cross-sections, classical theories are no more sufficient for the evaluation of displacements and, mostly, stresses distributions. For this reason, numerical results show the adoption of the NDK approach on compact composite structures. Nevertheless, to further demonstrate the enhanced simulation capabilities of the NDK method, it is also tested on composite thin-walled structures in this section.

Fig. 5
figure 5

Equilibrium curve of the [\(0^\circ /90^\circ \)] composite beam subjected to compression loading. TE1 \(\hbox {DOFs} =549\), TE2 \(\hbox {DOFs} = 1098\), L9 \(\hbox {DOFs} =274\)5, L16 \(\hbox {DOFs} = 5124\)

Full size image
Fig. 6
figure 6

Axial and shear through-the-thickness stress distribution of the [\(0^{\circ }/90^\circ \)] composite beam subjected to compression loading, evaluated at \(\hbox {y} = 0.2\ \hbox {L}\) (red line). \(\sigma _{yy}^{*} =\dfrac{\sigma _{yy} \; b \; h}{P}\) and \(\sigma _{yz}^{*} =\dfrac{\sigma _{yz} \; b \; h}{P}\). TE1 \(\hbox {DOFs} = 549\), TE2 \(\hbox {DOFs} = 1098\), L9 \(\hbox {DOFs} =2745\), L16 \(\hbox {DOFs} =5124\)

Full size image
Fig. 7
figure 7

Axial and shear through-the-thickness stress distribution of the [\(0^\circ /90^\circ \)] composite beam subjected to compression loading, evaluated at \(\hbox {y} = 0.2\ \hbox {L}\) (red line) with a NDK model. \(\sigma _{yy}^{*}=\dfrac{\sigma _{yy} \; b \; h}{P}\) and \(\sigma _{yz}^{*} =\dfrac{\sigma _{yz} \; b \; h}{P}\). L16 \(\hbox {DOFs} = 5124\), NDK \(\hbox {DOFs} = 3579\)

Full size image

3.1 Compression of asymmetric laminated compact beams

The first analysis case deals with asymmetric laminated cantilever beams with compact cross-section. The geometric, boundary and material conditions are shown in Fig. 4, with \(L/b = 9\), \(h/b = 0.6\), \(\hbox {E}_{L} = 144.8\ \hbox {GPa}\), \(\hbox {E}_{T} =\hbox {E}_{z} = 9.65\ \hbox {GPa}\), \(\nu = 0.3\), \(\hbox {G}_{LT} =\hbox {G}_{Lz} = 4.14\ \hbox {GPa}\) and \(\hbox {G}_{Tz} = 3.45\ \hbox {GPa}\), where L and T are the longitudinal and transverse directions of the fibers, respectively. The considered stacking sequences are [\(0^\circ /90^\circ \)] and [\(0^\circ /45^\circ \)], as depicted in the figure, where the red lines show the direction of the fibers. 20B4 are employed for the approximation of the beam axis.

Figure 5 reports the nonlinear equilibrium curves of the [\(0^\circ /90^\circ \)] case using uniform kinematics. Lower-order and refined theories are employed and, clearly, they lead to the same results.

Fig. 8
figure 8

Equilibrium curve of the [\(0^\circ /45^\circ \)] composite beam subjected to compression loading. TE1 \(\hbox {DOFs} =549\), TE2 \(\hbox {DOFs} = 1098\), L9 \(\hbox {DOFs} = 2745\), L16 \(\hbox {DOFs} = 5124\)

Full size image
Fig. 9
figure 9

Equilibrium curve of the [\(0^\circ /45^\circ \)] composite beam subjected to compression loading with various NDK models. L9 \(\hbox {DOFs} = 2745\), NDK \(\hbox {DOFs} = 1485\)

Full size image

Then, it is evident that the NDK approach is useless for the displacement evaluation of the selected case, since every kinematic is able to predict the displacement field. However, this is not true if one wants to accurately evaluate the stress distribution within the structure. In fact, as shown in Fig. 6, the stress distribution changes according to the adopted theory. Clearly, the L9, TE2 and TE2 kinematics are not able to describe the quadratic trend of the shear stress component, whereas the L16 can. On the contrary, this difference is not evident for the axial component, which distribution is linear.

Since only the L16 kinematic model is able to accurately predict the distribution of stress components, the NDK approach is suitable for building a model with fewer DOFs capable of describing the stress trend on a given part of the structure. The NDK approach allows to build a model refined in the selected zone, and gradually less refined as we get further from it. The mathematical model for the selected example is reported in Fig. 7, where a L16-TE8-TE5-TE1 model is shown. As reported in the same figure, the stress distribution is the same as those calculated with a heavier uniform higher-order kinematic model, with a significant loss of DOFs (from 5124 to 3579).

The [\(0^\circ /45^\circ \)] stacking sequence was further analyzed. The nonlinear static equilibrium curves adopting uniform kinematics are shown in Fig. 8. In this case, due to the torsional-bending coupling, the uniform TE1 kinematic leads to wrong results, compared to more reliable TE2, L9 and L16. For this reason, the NDK approach can be useful to describe the displacement field with lower DOFs, mixing TE1 and higher-order theory (the selected one for this example is L9).

Figure 9 reports the equilibrium curves using various NDK TE1-L9 models (depicted and described in the figure). The figure demonstrates several interesting aspects.

  • The four NDK models are built with the same number of DOFs (1655), but the results are different. The distribution of the DOFs is a crucial point when dealing with NDK models.

  • The distribution which, in this case, leads to more accurate results is the one which assignes more DOFs (i.e. a more refined model) to the clamped zone.

Stress distributions are considered as well. The same NDK models as those presented in Fig. 9 are used herein (although the more refined L16 theory is used instead of L9 to catch the parabolic distribution of shear stress). Significant differences are evident when the stress distribution is evaluated in the TE1 portion of the structure and the results are shown in Fig. 10. In fact, the most reliable NDK model (number 1, as demonstrated in Fig. 9) is able to describe the stress distribution in the L16 zone (Fig. 10), whereas the other models fail.

Fig. 10
figure 10

Axial and shear through-the-thickness stress distribution of the [\(0^\circ /45^\circ \)] composite beam subjected to compression loading, evaluated at \(\hbox {y} = 0.2\ \hbox {L}\) (red line) with various NDK models. \(\sigma _{yy}^{*}=\dfrac{\sigma _{yy} \; b \; h}{P}\) and \(\sigma _{yz}^{*}=\dfrac{\sigma _{yz} \; b \; h}{P}\). TE1 \(\hbox {DOFs} = 549\), L16 \(\hbox {DOFs} = 5124\), NDK \(\hbox {DOFs} =2694\)

Full size image

3.2 Laminated box beam

A cantilever laminated box beam undergoing large deflection due to transverse loadings were considered in the following analysis case. The structure is made by two layers, with [\(0^\circ /90^\circ \)] stacking sequence on top and bottom and [\(0^\circ /45^\circ \)] on the lateral flanges. The considered material is the same as in the previous case. The geometric characteristics and dimensions are shown in Fig. 11, with \(L/b=10\), \(h=3.6\ \hbox {mm}\), \(b=24\ \hbox {mm}\) and \(h/t = 10\). The refined cross-section discretization was made by implementing 16L9. This polynomial pattern will be recalled as “LE” in the following analyses. The analysis case was taken from [67].

A preliminary convergence analysis was carried out to establish a FE mesh for the beam axis. Figure 12 shows that 10 B4 can be considered a reliable approximation and, therefore, 10 B4 elements are employed for the approximation of the beam axis.

Two loading cases are analyzed hereafter, involving symmetric and unsymmetric transverse loadings, respectively. The nonlinear equilibrium curves using LE as a uniform expansion function are shown in Fig. 13. In the figure, some deformed configurations are depicted too. It is clear how the clamped portion of the structure undergoes a large cross-sectional deformation, whereas the free tip zone reports a moderate cross-section deformation (Fig. 13a) and rotation (Fig. 13b). For this reason, the subsequent investigation was made giving a refined model in the first portion of the structure, with a lower-order kinematic in the remaining zone, to analyze the static and stress response of the NDK models.

As far as the symmetric transverse load case is concerned, the nonlinear static curves are presented in Fig. 14, along with the adopted NDK models. As stated before, every NDK model involves a higher-order LE kinematic near the clamped zone. Clearly, the results show a great convergence for the displacement evaluation, and only the low-order NDK models TE1, L9-TE1 and TE5-TE1 are far from the reliable solution, provided by a full L9 model.

Higher differences can be appreciated looking at stress distributions of Fig. 15. It is clear that even the most refined NDK model L9-TE1 fails in correctly evaluating the shear stress distribution (see Fig. 15c).

Fig. 11
figure 11

Geometric properties and loading case of the composite box beam subjected to transverse loading

Full size image

Regarding the unsymmetric transverse loading, Fig. 16 shows the static nonlinear solutions adopting various NDK models, described in the figure.

Moreover, the stress distribution of axial and shear components is reported in Fig. 17. Clearly, the LE9-TE10 NDK represents a reliable mathematical model, both from the displacement and stress point of view.

Fig. 12
figure 12

Convergence analysis of the composite box beam subjected to unsymmetric transverse loading

Full size image
Fig. 13
figure 13

Equilibrium curves of the composite box beam subjected to symmetric transverse loading (a) and unsymmetric transverse loading (b). \(\hbox {DOFs} = 7440\)

Full size image
Fig. 14
figure 14

Equilibrium curve of the composite box beam subjected to symmetric transverse loading with various NDK models

Full size image
Fig. 15
figure 15

Axial and shear through-the-thickness stress distribution of the composite box beam subjected to symmetric transverse loading with various NDK models. Stress distributions evaluated at (0, \(\dfrac{L}{2}\), \(\dfrac{h}{2}\)) (a), (0, 0, \(\dfrac{h}{2}\)) (b) and (\(\dfrac{b}{2}\), \(\dfrac{L}{2}\), \(\dfrac{h}{4}\)) (c). \(\sigma _{yy}^{*}=\dfrac{\sigma _{yy} \; b \; h}{P^{*}}\) and \(\sigma _{yz}^{*}=\dfrac{\sigma _{yz} \; b \; h}{P^{*}}\), where \(P^{*}=6000\) kN

Full size image
Fig. 16
figure 16

Equilibrium curve of the composite box beam subjected to unsymmetric transverse loading with various NDK models

Full size image

3.3 Laminated box beam with open cross-section

As an additional example, we want to investigate the influence of NDK models on an opened thin-walled composite cross-section. The geometric, material and boundary conditions are the same as those presented in the previous analysis, but with a cut on the bottom part of the cross-section, as described in Fig. 18. The cut s equals the thickness t, and it is located in the middle of the edge. The unsymmetric transverse loading case was analyzed.

A convergence analysis was conducted for the beam axis discretization. Figure 19a shows how the considered approximations lead to almost the same transverse displacement, whereas if the lateral displacement is considered (Fig. 19b), at least 10B4 FEs have to be considered for a reliable description of the nonlinear behavior, especially for high levels of load.

The reference solution was set by performing the geometrical nonlinear analysis with a cross-sectional discretization involving 16L9 (this setting is recalled as “10L9” in this analysis case). The results are shown in Fig. 20, along with a deformed shape of a high value of the external load. Clearly, the largest deformations occur near the clamp zone, so this part was kept approximated with the higher-order “LE” theory in the following NDK analyses. Nevertheless, the whole structure undergoes large cross-section deformation and rotation, so a high-order kinematic is necessary to analyze the structure.

Fig. 17
figure 17

Axial and shear through-the-thickness stress distribution of the composite box beam subjected to unsymmetric transverse loading with various NDK models. Stress distributions evaluated at (0, \(\dfrac{L}{2}\), \(\dfrac{h}{2}\)) (a), (0, 0, \(\dfrac{h}{2}\)) (b) and (\(\dfrac{b}{2}\), \(\dfrac{L}{2}\), \(\dfrac{h}{4}\)) (c). \(\sigma _{yy}^{*}=\dfrac{\sigma _{yy} \; b \; h}{P^{*}}\) and \(\sigma _{yz}^{*}=\dfrac{\sigma _{yz} \; b \; h}{P^{*}}\), where \(P^{*}=6000\) kN

Full size image

In fact, as shown in Figs. 21 and 22 the results are far from the full LE solution, although the error of the z displacement (Fig. 21) is less than the x one (Fig. 22).

Finally, stress results are reported in Fig. 23. As demonstrated before, the \(\sigma _{yy}^{*}\) differences between the NDK models is less than the \(\sigma _{yz}^{*}\), so, if one is interested in the transverse displacement and \(\sigma _{yy}^{*}\) values, a NDK approach can be suitable, but for lateral displacement and the shear component of the stress a uniform higher-order kinematic needs to be exploited.

Fig. 18
figure 18

Geometric properties and loading case of the composite box beam with opened cross-section subjected to unsymmetric transverse loading. The cut is located in the middle of the edge

Full size image
Fig. 19
figure 19

Convergence analysis of the composite box beam with opened cross-section subjected to unsymmetric transverse loading

Full size image

3.4 Eight-layer laminated beam

The capability of the NDK approach to deal with the post-buckling of a thin-walled structure is finally tested in the following analysis case. The analyzed case was taken from Ref. [68]. The geometric characteristics are described in Fig. 24, with \(L/h = 9\) and \(h/t = 10\). The beam is made of two different materials (in red and in blu in the figure). For both materials, \(\hbox {E}_{T}=\hbox {E}_{z}\), \(\nu _{LT} = 0.25\) and \(\hbox {G}_{LT}/\hbox {E}_{T} = 0.5\), whereas for the first material \(\hbox {E}_{L}/\hbox {E}_{T} = 30\) and for the second material \(\hbox {E}_{L}/\hbox {E}_{T} = 5\), where L and T are the longitudinal and transverse directions of the fibers, respectively. The structure is clamped at one side and free at the other and subjected to a transverse load P. Finally, the unstable solution branches have been enforced by applying a small load defect d as depicted in the Fig. 24.

Fig. 20
figure 20

Equilibrium curves of the composite box beam with opened cross-section subjected to unsymmetric transverse loading. Transverse displacement of point A (a) and lateral displacement of point B (b)

Full size image
Fig. 21
figure 21

Equilibrium curve of the composite box beam with opened cross-section subjected to unsymmetric transverse loading with various NDK models. Transverse displacement of point A (see Fig. 20a)

Full size image
Fig. 22
figure 22

Equilibrium curve of the composite box beam with opened cross-section subjected to unsymmetric transverse loading with various NDK models. Transverse displacement of point B (see Fig. 20b)

Full size image
Fig. 23
figure 23

Axial and shear through-the-thickness stress distribution of the composite box beam with opened cross-section subjected to unsymmetric transverse loading with various NDK models. Stress distributions evaluated at (0, \(\dfrac{L}{2}\), \(\dfrac{h}{2}\)) (a) and (\(\dfrac{b}{2}\), \(\dfrac{L}{2}\), \(\dfrac{h}{4}\)) (b). \(\sigma _{yy}^{*}=\dfrac{\sigma _{yy} \; b \; h}{P^{*}}\) and \(\sigma _{yz}^{*}=\dfrac{\sigma _{yz} \; b \; h}{P^{*}}\), where \(P^{*}=6000\) kN

Full size image

Figure 25 shows the post-buckling behavior of the structure, with the displacements over the z directions of the middle point of the free tip. Several deformed configurations are reported too to appreciate the structural deformation over the nonlinear equilibrium path. Then, the NDK was applied to this problem. Clearly, the clamped portion of the structure undergoes remarkable cross-sectional deformation and rotation. Thus, higher-order kinematics was applied to the elements near the clamp. The results are shown in Fig. 26. Clearly, the 5L9-10T5-5T1 NDK model can evaluate the displacement field with high accuracy compared to the full 20L9 theory.

Finally, Fig. 27 reports the stress distribution for three points of the beam (0, 0, \(\dfrac{h}{2}\)) (Fig. 27a), (0, \(\dfrac{L}{2}\), \(\dfrac{h}{2}\)) (Fig. 27(b)) and (0, \(\dfrac{L}{2}\), 0) (Fig. 27c). Even if the 10L9-10T1 NDK model was able to catch the correct displacement field, it lacks the ability to accurately predict the \(\sigma _{yy}^{*}\) ans \(\sigma _{yz}^{*}\).

4 Conclusions

Fig. 24
figure 24

Geometric properties and loading case of the eight-layer laminated beam subjected to transverse loading. A small defect load d is imposed to enforce the the unstable solution branches of the post-buckling regime

Full size image
Fig. 25
figure 25

Equilibrium curve of the eigth-layer laminated beam subjected to transverse loading

Full size image
Fig. 26
figure 26

Equilibrium curve of the [eigth-layer laminated beam subjected to transverse loading with various NDK models

Full size image
Fig. 27
figure 27

Axial and shear through-the-thickness stress distribution of the composite box beam subjected to unsymmetric transverse loading with various NDK models. Stress distributions evaluated at (0, 0, \(\dfrac{h}{2}\)) (a), (0, \(\dfrac{L}{2}\), \(\dfrac{h}{2}\)) (b) and (0, \(\dfrac{L}{2}\), 0) (c). \(\sigma _{yy}^{*}=\dfrac{\sigma _{yy} \; L \; h}{P^{*}}\) and \(\sigma _{yz}^{*}=\dfrac{\sigma _{yz} \; L \; h}{P^{*}}\), where \(P^{*}=20000\) kN

Full size image

The present research work was addressed to determine the effects and benefits of adopting Node-Dependent Kinematics (NDK) in the geometrical nonlinear analysis of composite compact and thin-walled structures. Both symmetric and asymmetric loading conditions were analyzed, including various stacking sequences. The results demonstrate that NDK is a powerful method to reduce computational cost in nonlinear problems, and this is confirmed by the different example problems reported in this paper. When dealing with compact laminated beams, the NDK approach can be exploited to evaluate the stress distribution in a given portion of the structure, by enriching the kinematic only in that zone, saving computational cost. Moreover, higher/lower-order kinematics are introduced easily in the regions of the structures which show higher/lower sectional deformations. For compact beams, it has been demonstrated that, considering the same number of DOFs, the results change, according to which cross-section kinematic has been refined. In thin-walled cases, the cross-sections which undergo local phenomena (large deformation and/or rotation, e.g., near the clamped zone for cantilever beams) need a higher-order theory to be accurately described, whereas a lower-order kinematic can be used to approximate the displacement field over the rest of the beam. Figure 28 demonstrates the advantage of using a NDK models for composite thin-walled structures. In this figure, the percentage difference of the value of \(\sigma _{yy}\) compared to the reference solution (Fig. 13) is reported. Clearly, for both unsymmetric and symmetric loading cases, the NDK approach is able to build more efficient mathematical models, using less than 40% and 80% respectively, with errors less than 15%. Finally, it can be pointed out that NDK works well for geometrically nonlinear problems, and no drawbacks or numerical issues, with respect to linear analysis, were found. The main aim of the present work is to propose a technique to build efficient mathematical model of composite structures in the geometrical nonlinear field. An application of real 3D structure is intended to be performed in future works.

Fig. 28
figure 28

% \(\hbox {err} = \overline{\sigma _{yy}} = \dfrac{(\sigma _{yy}^{*} -\sigma _{yyRef}^{*})}{\sigma _{yyRef}^{*}}\) and % \(\hbox {DOF}=\dfrac{DOF-DOF_{Ref}}{DOF_{Ref}}\). \(\sigma _{yy}^{*}=\dfrac{\sigma _{yy} \; b \; h}{P^{*}}\) where \(P^{*}=6000\) kN. Ref solutions are taken from Fig. 13. Stress values evaluated at (0, \(\dfrac{L}{2}\), \(\dfrac{h}{2}\)), where L and h are the length and the height of the beam, respectively

Full size image