Abstract
Peridigm is a meshfree peridynamics code written in C++ for use on large-scale parallel computers. It was originally developed at Sandia National Laboratories and is currently managed as an open-source, community driven software project. Its primary features include bond-based, state-based, and non-ordinary state-based constitutive models, bond failure laws, contact, and support for explicit and implicit time integration. To date, Peridigm has been used primarily by methods developers focused on solid mechanics and material failure. Peridigm utilizes foundational software components from Sandia’s Trilinos project and was designed for extensibility. This paper provides an overview of the solution methods implemented in Peridigm, a discussion of its software infrastructure, and demonstrates the use of Peridigm for the solution of several example problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Peridynamics is a nonlocal extension of classical continuum mechanics that was introduced by Stewart Silling in 2000 [1]. The key characteristic of peridynamics is that the governing equations do not include spatial derivatives of the displacement field, and are therefore well suited for modeling material discontinuities such as cracks. As with classical continuum mechanics, peridynamic simulations are constructed in the form of initial value problems or boundary value problems, for example, solution of the balance of linear momentum subject to prescribed initial and boundary conditions. The solution of the initial or boundary value problem for any nontrivial case requires software tools that implement the relevant numerical methods.
The Peridigm code was developed for high-fidelity peridynamic simulations over three-dimensional domains using the meshfree discretization approach of Silling and Askari [2]. Peridigm is an open-source C++ code that utilizes software libraries from the Trilinos [3] project to enable large-scale parallel simulations. It was designed to facilitate engineering simulations of solid mechanics problems that include material failure, and also to provide a software framework for use by peridynamic methods developers. Key features include a range of constitutive models, bond failure laws, contact models, and support for both explicit and implicit time integration. A MPI-based design supports simulations on hardware ranging from laptop computers to massively parallel supercomputing platforms.
Peridigm is one of several peridynamic codes that have been documented in the literature. The first software implementation of peridynamics is the EMU code developed by Silling and Askari [2]. Many of the subsequent peridynamics code projects are focused on publicly available, open-source software. Examples include PDLAMMPS [4, 5], PeriPy [6, 7], NLMech/PeriHPX [8,9,10], PeriPyDIC [11], PD_Shell [12, 13], PyNucleus [14], and Relation-Based Software (RBS) [15, 16]. The codes PeriPy, PeriPyDIC, and PyNucleus are written in the Python programming language, and the others in the C++ programming language. Peridigm, PDLAMMPS, and PyNucleus utilize MPI, and NLMech/PeriHPX is based on the asynchronous many-task system, C++ standard library for parallelism and concurrency (HPX) [17]. Other codes focusing on GPU acceleration [18,19,20] are available as well. To date, LS-DYNA is the only commercial code to provide a peridynamics capability. Specifically, LS-DYNA provides a bond-based model discretized with the discontinuous Galerkin finite element method [21]. Peridigm is differentiated from other peridynamic codes primarily by its focus on high-performance parallel computing, its extensibility for the implementation of new methods, and by a number of advanced capabilities discussed in the following sections. For additional discussion on peridynamics codes, we refer to [22, §2.1.3].
Peridigm has been utilized by researchers for a wide range of methods development and engineering applications. Examples of engineering applications include a blind prediction of ductile fracture in additively manufactured metal in [23, 24]. Peridigm was applied by the authors of [25, 26] to model shock compaction of granular materials. The authors of [27] modeled damage due to indentation and scratching in 3C-SiC. Peridigm was used to model impact of a Al\(_{2}\)O\(_{3}\)/ZrO\(_{2}\) composite in [28], impact of a Al-Si12/SiC composite in [29], and compression of SiC foam in [30]. The authors of [31] simulated fracture and shock wave propagation in a harmonic structured material. In [32], Peridigm was utilized to model impact response of cellular materials. Peridigm was used in [33] for comparison between peridynamics and smoothed-particle hydrodynamics for modeling fragmentation of ceramic tile. The authors of [34,35,36] used Peridigm to model damage and fragmentation of objects during atmospheric re-entry. The authors of [37] utilized Peridigm in their work on modeling mode I fracture of phase-separated glasses. Damage in nanoparticle-implanted glass was modeled using Peridigm in [38, 39]. The influence of probabilistic material property distributions was investigated using Peridigm in [40]. Peridigm was used to model mixed-mode fracture in PMMA in [41]. The authors of [42] utilized Peridigm in to model particle impact and interfacial bonding in cold spray processes. A study comparing experimental results against peridynamic simulations of ring bending tests on float glass plates is described in [43].
Peridigm has proven to be a valuable tool for researchers focusing on methods development and algorithms research for peridynamic models. The authors of [13], for example, used Peridigm in their development of a peridynamic Kirchhoff-Love shell formulation. The authors of [44] reviewed and extended peridynamic models for frictional contact. Peridigm was used in the development of an energetically consistent surface correction method for bond-based peridynamics in [45]. In [46,47,48], Peridigm was used to develop a formulation for mean stress and incubation time fracture models. The authors of [49, 50] developed a peridynamic plasticity model for the dynamic flow and fracture of concrete. Concrete was also studied in [51], in which the authors implemented a microplane (M7) constitutive model. Peridigm was employed in [52, 53] for development of a fatigue model for capturing damage in railway applications. Energy-based failure criteria for peridynamic models were explored in [54,55,56,57]. The authors of [58] investigated the stability of generalized peridynamic correspondence models. In [59], the authors used Peridigm in their comparison of different methods for calculating tangent stiffness matrices for peridynamic models. Mesh sensitivity for quasi-static simulations was investigated in [60]. The use of so-called partial volumes for improved fidelity and convergence of meshfree peridynamics was explored in [61, 62]. In [63], a touch-aware model of frictional contact for granular materials with arbitrary particle shapes was introduced. A correspondence energy-based damage model and adaptive Verlet time integration scheme were developed in [64] for modeling PMMA. The authors of [65] also employed Peridigm to model PMMA, in their case for development of a rate-dependent visco-elastic constitutive model to capture the rate-sensitivity of damage evolution.
Additional use of Peridigm in the literature includes methods development for multiscale and multi-physics models, often leveraging Peridigm’s extensible software framework. A thermomechanical approach for modeling crack initiation and propagation due to thermal loading was explored in [66]. A peridynamic micromechanical simulation framework for random heterogeneous composites is presented in [67]. Peridigm was used in [68] within a multi-physics approach for modeling intergranular cracking of aluminum alloys. In [69], Peridigm was used in conjunction with isogeometric analysis to simulate air blast on concrete structures. The author of [70] utilized Peridigm for development of the MesoEq framework for multi-physics modeling. In [71], the authors developed a semi-Lagrangian framework for peridynamics. The authors of [72,73,74] explored modal analysis of cracked specimens. Peridigm was utilized in a framework for modeling the crushing of granular media in [75], and for multiscale analysis of shear behavior of granular sand in [76]. Peridigm was used in [77] as a framework to develop a model that captures the effect of differential mineral shrinkage on crack formation and network geometry. The author of [78] introduced a hybrid hierarchical model that utilizes both Peridigm and LAMMPS. Authors in [79,80,81,82] utilized Peridigm to investigate strategies for coupling local and nonlocal models. In [83], the authors explored efficient implementations of peridynamics for the Sunway TaihuLight supercomputer, and ported and optimized Peridigm for SIMT accelerators in [84]. A UMAT interface for Peridigm was developed in [85].
This paper presents an overview of Peridigm, including brief discussions of the relevant theory from the literature. Key methods and algorithms are presented in Section 2. The workflow for building and running a Peridigm simulation is described in Section 3, which includes example Peridigm simulations that illustrate its main features and performance characteristics. Additional information can be found in the Users’ Guide [86] distributed with the initial release of Peridigm, and in [87, 88] which provide an in-depth discussion of software development concepts for peridynamics.
2 Methods and Algorithms
The peridynamic theory of solid mechanics is based on an integro-differential equation for the balance of linear momentum. Peridynamics is a nonlocal model in which a material point \(\textbf{x}\) interacts directly with all materials points \(\textbf{q}\) in the body \(\mathcal {B}\) that are within a distance \(\delta\) of \(\textbf{x}\), where \(\delta\) is referred to as the horizon. A peridynamic bond, denoted \(\varvec{\xi }\), symbolizes the connection between \(\textbf{x}\) and \(\textbf{q}\), and the set of all points bonded with \(\textbf{x}\) is referred to as the family of \(\textbf{x}\), \(\mathcal {H}_\textbf{x}\). An illustration of these terms is given in Fig. 1.
Schematic of a peridynamic body \(\mathcal {B}\), in which material points \(\textbf{x}\) and \(\textbf{q}\) are connected by a bond \(\varvec{\xi }\). The maximum interaction distance for point \(\textbf{x}\) is specified by the horizon, \(\delta\). The family \(\mathcal {H}_\textbf{x}\) contains all points in \(\mathcal {B}\) that are bonded to \(\textbf{x}\)
The most general form of the peridynamic equation of motion is given by the state-based formulation of Silling et al. [89], in which the balance of linear momentum for point \(\textbf{x}\) at time t is expressed as
Here, \(\textbf{u}\) denotes displacement, \(\rho\) is the density of the material, and \(dV_{\textbf{q}}\) is the infinitesimal volume of material associated with point \(\textbf{q}\). The terms \(\underline{\textbf{T}} \left[ \textbf{x}, t \right]\) and \(\underline{\textbf{T}} \left[ \textbf{q}, t \right]\) denote the peridynamic force states at \(\textbf{x}\) and \(\textbf{q}\), respectively, that determine the pairwise force density per unit volume resulting from the interaction of \(\textbf{x}\) and \(\textbf{q}\). The terms in angled brackets, \(\langle \textbf{q} - \textbf{x} \rangle\) and \(\langle \textbf{x} - \textbf{q} \rangle\), follow the state-based notation given in [89] for the bonds connecting \(\textbf{x}\) to \(\textbf{q}\), and \(\textbf{q}\) to \(\textbf{x}\), respectively. Note that this state-based notation is more general than bond-based notation, for example, allowing for a horizon that varies over \(\mathcal {B}\) such that \(\textbf{q}\) is in \(\mathcal {H}_\textbf{x}\) but \(\textbf{x}\) is not in \(\mathcal {H}_\textbf{q}\).
The most common strategy for numerical solution of Eq. (1) is the meshfree approach of Silling and Askari [2], in which the domain is discretized into a finite number of nodal volumes and the integral is replaced with a summation,
Equation (2) is a direct colocational discretization of the strong form of Eq. (1) in which the family \(\mathcal {H}_\textbf{x}\) is replaced by a set of nodal volumes \(\mathcal {N}_{\textbf{x}}\). We refer to this set of nodal volumes as the neighborhood of \(\textbf{x}\). Each nodal volume is defined by its spatial coordinates and an associated finite volume \(\Delta V\). The primary strengths of this meshfree approach are computational efficiency and the natural ability to accommodate material separation through the breaking of bonds.
Peridigm solves Eq. (2) on a prescribed discretization for a given set of constitutive laws, bond failure laws, contact models, initial conditions, and boundary conditions. Peridigm software relies heavily on the Trilinos toolset, including libraries for the management of parallel data structures via MPI [3, 90]. The sections below describe the most significant methods, algorithms, and software routines in the code.
2.1 Data Structures for Nonlocal Calculations
A key aspect of performing peridynamic calculations is construction and management of neighborhood lists. Neighborhood lists are the principal data structure for iterating over sets of nodal volumes, for example, the summation in Eq. (2), for which \(\mathcal {N}_{\textbf{x}}\) is typically \(\mathcal {O}(100)\) for three-dimensional simulations and may be as large as \(\mathcal {O}(1000)\). An illustration of a meshfree discretization used by Peridigm is given in Fig. 2. Neighborhoods, shown in green for three points (\(\textbf{x}_1,\textbf{x}_2,\textbf{x}_3\)) in the domain, are determined using a spatial proximity search, where a point \(\textbf{q}\) is part of the neighborhood \(\mathcal {N}_{\textbf{x}}\) if the distance between points \(\textbf{x}\) and \(\textbf{q}\) in the undeformed configuration is less than the horizon, \(\delta\). Construction and traversal of neighborhood lists is a major determining factor in the overall computational expense of peridynamic simulations.
Neighborhood list construction is complicated by parallel decomposition of the domain in which nodes are distributed across multiple ranks. Figure 2 includes a depiction of parallel decomposition and its relationship to neighborhood lists. Neighborhood construction requires search methods to query across processor boundaries, which is accomplished in Peridigm by creating subsets of points on each processor called framesets. In conjunction with load balancing implemented using the Trilinos Zoltan library, framesets on each processor are used to collect nodes on adjacent processors within the search distance \(\delta\). On the basis of this cross-processor search using only points within a frameset, communication lists are constructed which allow for parallel communication throughout the simulation. Specifically, each processor has a list of owned points and a list of shared points. Off-processor points are shared points within the distance \(\delta\) of owned (on-processor) points.
Neighborhood lists are constructed using k-d tree search algorithms [91, 92]. On each processor, trees are constructed from the union of owned and shared points. Construction and queries approximately scale as \(\mathcal {O}(N\log (N))\) and \(\mathcal {O}(N^{1-1/3}+k)\), respectively, where N is the number of nodes in the tree and k is in number of nodes in a neighborhood. The number of nodes in a neighborhood is a function of the ratio of the horizon \(\delta\) and the mesh spacing. The proximity search for neighborhood list construction may be augmented in Peridigm using bond filters. Bond filters are user-defined planes for specifying fine-scale geometric features, such as thin notches. Neighborhood list construction filters out bonds which cross these user-defined planes, as shown in Fig. 2.
Following parallel decomposition and neighborhood list construction, Peridigm groups on-processor points together into blocks according to material model type and instance. This allows for efficient evaluation of large groups of nodes within a block without excessive branching or overloading of functionals on the basis of material model type. All on-processor nodes with the same material type and material properties are grouped together and material model evaluation is accomplished by passing the neighborhood list for this set of points to the appropriate subroutines, along with other material model parameters. These data structures are managed by NeighborhoodData and DataManager objects in Peridigm. While global operations such as time integration are performed using parallel data structures that span the entire domain, computations corresponding to individual blocks are conducted using subsets of data stored in a DataManager. The DataManager handles communication to and from the global data structures and all aspects of parallel communication. Routines that iterate over neighborhoods do so via information extracted from corresponding NeighborhoodData objects. This approach allows material models, bond damage models, contact models, and compute classes to be written as serial code, greatly simplifying the process for modifying these important routines and adding new features to the code.
Schematic of a discretized computational domain. The domain boundary is depicted by a solid black line. A decomposition corresponding to four MPI ranks \(p_0\), \(p_1\), \(p_2\), and \(p_3\) is shown in red. The neighborhoods \(\mathcal {N}_{\textbf{x}}\) for selected material points are illustrated with green circles of radius \(\delta\). A bond filter for restricting the creation of bonds across a user-defined plane is shown in blue. A frameset for use with proximity searches across processor boundaries is illustrated with dotted black lines
2.2 Meshfree Discretizations
Peridigm operates on meshfree discretizations comprised of nodal volumes, each defined by spatial coordinates \(\textbf{x}\) and volume \(\Delta V\). The geometry of the domain, typically conceptualized by the user in terms of geometric primitives, or similar, is captured by the spatial distribution of the nodal volumes. The sum of all volumes \(\Delta V\) matches the volume of the overall domain geometry. There is no topology associated with the meshfree discretization, i.e., no link arrays describing connectivity as are associated with typical finite element meshes. Quadrature is significantly simplified for meshfree discretizations of this type, and involves only the coordinates of individual nodes and the corresponding volumes.
Peridigm supports two primary file formats for meshfree discretizations: exodus files and text files. The exodus format is preferred due to its efficiency and compatibility with many pre-processing utilities, including the SEACAS [93, 94] toolset and the ParaView [95] visualization code. In practice, it is often convenient to use a finite element mesh generator to create a hexahedral or tetrahedral mesh of the domain. For example, the CUBIT™ [96] mesh generator may be used to create a mesh and write it to an exodus file. Peridigm has the ability to read an exodus hexahedral or tetrahedral mesh and convert it to a meshfree discretization internally, as described in Section 3.2. The text file format offers a more simplistic alternative that may be suitable for users who wish to create a meshfree discretization directly, for example, using a standalone script of their own design. A Python script for conversion from the text file format to the exodus format is distributed with Peridigm.
Peridigm manages the association of material models, boundary conditions, and other aspects of the simulation with specific regions of the computational domain using blocks and node sets. Each nodal volume in the discretization belongs to a single block. Within the Peridigm input script, material specifications are linked to each block in the discretization, allowing for evaluation of internal forces using the appropriate material type and its associated properties. Node sets are groupings of nodal volumes for the purpose of applying initial conditions, boundary conditions, and body forces. Individual nodal volumes may belong to any number of node sets. It should be noted that so-called nonlocal boundary conditions for peridynamic models should be applied over a three-dimensional volumetric region, as opposed to a two-dimensional surface. Further, following the approach of Silling and Askari, the meshfree discretizations used by Peridigm do not contain nodes located directly on the surfaces of the domain (see Fig. 2). Care should be taken in the specification of initial and boundary conditions and their associations with node sets when creating a Peridigm simulation.
2.3 Constitutive Models
This section provides an overview of constitutive models available in Peridigm as well as descriptions of how models can be added or extended. Constitutive models are described using state-based peridynamics notation. Force states \(\underline{\textbf{T}} \left[ \textbf{x}, t \right]\) and \(\underline{\textbf{T}} \left[ \textbf{q}, t \right]\) in Eq. (2) must be evaluated at every time step in a simulation and applied to each bond in the discrete model.
Silling et al. [89] introduced new terminology and notation for handling the mathematics of peridynamic states, which are essentially generalizations of tensors that provide a mapping from a bond to a pairwise force density per unit volume. This terminology has led many researchers to use the adjectives bond-based and state-based when referring to peridynamics. Here, bond-based refers to constitutive models that derive from a central force-potential between material points similar to a simple molecular bond, and state-based refers to the generalized theory. Importantly, bond-based models are a subset of state-based models, hence the state-based programming interface in Peridigm may be used for either class of model.
While describing the peridynamic theory in [89] the authors introduced the additional concepts of ordinary and non-ordinary materials. Ordinary materials are those in which the application of a force state to a given bond results in a force density per unit volume that acts in the direction of that bond in the current configuration. Conversely, this relationship does not hold for non-ordinary materials. An important reason for distinguishing between ordinary and non-ordinary materials is that ordinary materials satisfy the balance of angular momentum by construction, whereas this important property must be taken into account more explicitly when developing non-ordinary materials [1].
Ordinary material models available in Peridigm include the linear peridynamic solid (LPS) model which is an isotropic elastic model originally presented in [1], isotropic plasticity and viscoelasticity models developed by Mitchell [97, 98], and the position aware LPS (PALS) model developed by Mitchell et al. [99]. The PALS model includes a correction for the so-called peridynamic surface effect [100], a deviation from the bulk response at material points for which the neighborhood is less than a full sphere. The surface effect is a result of assumptions made during derivation of the constitutive properties in relation to their classical analogues, e.g., the elastic shear and bulk moduli.
An implementation of the bond-based prototype microelastic brittle (PMB) model [2] is also available. This bond-based model will often run at about twice the speed of the LPS model, and is therefore useful for fast calculations of brittle materials with a Poisson ratio near \(\nicefrac{1}{4}\). The improved PMB model presented in [101] is implicitly available by using an LPS model with a fixed Poisson ratio of \(\nicefrac{1}{4}\) (cf. [102]). This model reduces the surface effects of the PMB model, but does not offer the same speedup because of the underlying implementation details in Peridigm.
Non-ordinary material models are predominantly associated with the constitutive correspondence concept introduced in [89, 103,104,105] and elsewhere. It is important to point out that not all non-ordinary models are correspondence models (e.g., [106, 107] develop non-ordinary models for beams, plates, and shells), and not all correspondence models are non-ordinary (e.g., [108, 109] present ordinary correspondence models). However, to date, all the available correspondence formulations in Peridigm are non-ordinary state-based materials. Correspondence models provide a mechanism to incorporate any classical stress–strain constitutive model into Peridigm. Additionally, for a particular choice of meshfree discretization when combined with a non-ordinary correspondence model, direct connections can be made to classical meshfree methods [110, 111].
In Peridigm, non-ordinary state-based models include a purely elastic formulation, an elastic perfectly plastic model, a plasticity model with isotropic hardening, and a viscoplastic model implementation of the form introduced by Needleman [112]. These models suffer from a zero-energy model instability [113], for which the stabilization technique described in [114, 115] is implemented.
2.3.1 Material Model Programming Interface
In Peridigm, material models inherit from the Material class, which acts as an abstract base class defining the material model interface. The primary member functions for the Material class are given in Listing 1.

The computeJacobian() method is exercised when constructing the tangent stiffness matrix for implicit time integration. If the material model does not implement the computeJacobian() method, then the Jacobian calculation is automatically carried out by applying a finite difference scheme to the computeForce() method. Note that it is possible to use the Sacado automatic-differentiation package from Trilinos to compute algorithmically consistent Jacobians as can be seen in the computeAutomaticDifferentiationJacobian() method in the ElasticMaterial class.
The constructor of a material model records the relevant material model parameters and the field IDs for the variables needed to carry out the internal force density calculation. As an example, consider the ElasticMaterial class, which implements the LPS [89] material model. Selected contents of the ElasticMaterial constructor are shown in Listing 2.

The constructor interacts with the FieldManager class for the management of field data, such as the volumes, initial coordinates, and current coordinates of the nodal volumes that will be passed to the material model’s computeForce function via a DataManager object. The FieldManager and DataManager classes leverage the Trilinos framework, which is discussed in more detail in Section 2.8. Peridigm supports node data, element data, and bond data. Node data fields are allocated over the entire computational domain, whereas element data are allocated on a per block basis, for example, to provide fields corresponding to the material model assigned to a particular block. The notions of node data and element data correspond directly to data types in the exodus file format. Peridigm supports scalar, vector, and tensor data types for node and element fields. Bond data are restricted to the scalar data type and are not generally written to Peridigm output files.
An abstract class CorrespondenceMaterial, derived from Material, is used as the base class for constitutive correspondence material models. As opposed to standard peridynamic material models that require implementation of the computeForce() method, constitutive correspondence models require implementation of the computeCauchyStress() method. This method computes the Cauchy stress tensor based on classical measures of deformation, e.g., deformation gradient, allowing for integration of traditional stress–strain constitutive laws into Peridigm. The CorrespondenceMaterial base class computes the deformation gradient and its decomposition into stretch and rotation tensors using the method of Flanagan and Taylor [116]. The rotation tensor is used to produce a co-rotational Cauchy stress, and therefore the computeCauchyStress() method can be implemented without concern for material objectivity. Stress tensors computed by a constitutive correspondence model are converted to pairwise peridynamic forces following [89]. In addition, the CorrespondenceMaterial class applies a stabilization procedure to the deformation gradient to suppress zero-energy modes [114, 115].
Finally, material models are registered by name in the MaterialFactory class. This class instantiates material model objects if the name associated with the model is present in the Peridigm input deck. The examples and tests distributed with Peridigm are an excellent resource for inspecting the structure of input parameters for various material models.
2.4 Bond Failure
The ability to model damage through the breaking of bonds is one of the most notable features of peridynamics. The coalescence of broken bonds to discrete surfaces is what leads to fracture and fragmentation of solid bodies. The most widely use bond damage criterion is the critical stretch model introduced in [117]. In this model, the strain energy density in each bond that crosses a plane of unit area is integrated and equated with the critical value of energy release rate \(G_c\). For bond-based materials, this leads to a closed form expression in terms of critical bond stretch \(s_c\),
where k is the material’s bulk modulus and the integration has been carried out over a ball of radius equal to the horizon \(\delta\). The critical stretch \(s_c\) can then be compared with \(s = \frac{\Delta L}{L_0}\), where \(\Delta L\) is the change in length of the bond and \(L_0\) is the original length. When \(s > s_c\), the bond is irreversibly broken, which is equivalent to setting \(\underline{\textrm{T}}\langle \varvec{\xi }\rangle = 0\) for the given bond \(\varvec{\xi }\). Note that Eq. (3) applies to three-dimensional formulations of peridynamics, as implemented in Peridigm. For a discussion of corresponding two-dimenstional formulations, the reader is refered to [118].
Peridigm implements the critical stretch bond breaking criterion as well as several similar models, e.g., an Interface Aware damage model that uses the smaller of two values of \(s_c\) for bonds that span blocks with different damage model parameters. In addition to the binary breaking of bonds, bonds can utilize a damage function that ranges continuously in [0, 1] allowing for the gradual decay of bond strength. Two such models implemented in Peridigm are intended to be used with constitutive correspondence material models: a Johnson-Cook damage model [119] and a bond damage model based on a simple von Mises yield criterion. For state-based materials in general, the strain energy in a bond is a function of the deformation of all bonds in the family and therefore is not a simple function of the stretch in that bond. Therefore, a more complex technique such as that described in [120] is preferable as a damage criterion.
In Peridigm, damage models are derived from the base class DamageModel which requires implementation of the methods given in Listing 3.

The computeDamage() function acts on field data managed by a DataManager object, updating values of the Bond_Damage field for each bond associated with a given block.
2.5 Modeling Contact
Peridigm supports contact modeling using the short-range force approach of Silling and Askari [2]. The primary use case is capturing interactions between bodies in explicit dynamics simulations, for example, to model impact. The key algorithmic components of Peridigm’s contact capabilities are the proximity search and the algorithm for determining pairwise contact forces. In the case of contact modeling, the proximity search returns a neighborhood list of points that are separated by a distance less than or equal to \(r_{c}\) in the current configuration, where \(r_{c}\) is a user-defined contact radius. Pairs of bonded points are generally excluded from the contact neighborhood lists, under the assumption that material points should interact via a material model if they are bonded and should be subject to the contact model only if they are not bonded.
The short-range force contact model is implemented in Peridigm as follows. Define \(\textbf{d}\) as the vector from point \(\textbf{x}\) to point \(\textbf{q}\) in the current configuration. Then the pairwise repulsive contact force acting on \(\textbf{q}\) due to its contact interaction with \(\textbf{x}\) is determined as
The software infrastructure for modeling contact, in which the proximity search is used to construct contact neighborhood lists and a contact model is used to determine pairwise contact forces, is designed to support future implementation of additional contact models. The proximity search handles all aspects of parallel communication and provides necessary data via the contact model programming interface, such that the contact model can be written as serial code that determines pairwise contact forces based on the locations of points in the current configuration, as well as any other state data (e.g., velocity).
2.6 Time Integration
Peridigm supports explicit time integration for transient dynamics and implicit time integration for quasi-statics and implicit dynamics. The primary use cases for explicit dynamics include contact, unstable crack growth, and pervasive damage. Implicit time integration is favorable for simulations in which large time steps are required and for those in which the assumption of static equilibrium is valid, i.e., static and quasi-static simulations.
2.6.1 Explicit Time Integration for Transient Dynamics
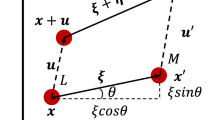
Time integration for explicit dynamics is achieved using the well-known velocity-Verlet algorithm:
where \(\textbf{u}\), \(\textbf{v}\), and \(\textbf{a}\) denote displacement, velocity, and acceleration, respectively, and the superscripts denote the time steps n and \(n+1\), and mid-step calculations at \(n + \frac{1}{2}\). The vast majority of the computational expense for explicit time integration is in the evaluation of the material model, bond damage model, and contact model at \(\textbf{u}^{n + 1}\) and \(\textbf{v}^{n + \frac{1}{2}}\), as required to evaluate \(\textbf{a}^{n + 1}\).
Stability of explicit time integration is dictated by a maximum stable time step, \(\Delta t_{\textrm{crit}}\). Peridigm provides a point-wise estimate of \(\Delta t_{\textrm{crit}}\) based on a method proposed by Silling and Askari for the prototype microelastic brittle material model [2]:
where \(\rho\) is the material density, the index p iterates over all the neighbors of the given material point, \(\Delta V_{p}\) is the volume associated with neighbor p, and \(C_{p}\) is evaluated as
where \(k_{p}\) is the bulk modulus at point p.
Explicit dynamic simulations can be run using this estimate of the critical time step in combination with a safety factor specified in the input deck. In this case, the time step is determined by multiplying the estimate of the critical time step by the specified safety factor, which is typically in the range of 0.5–0.9. Alternatively, a user-specified time step may be defined in the input deck, in which case the estimate of the critical time step is ignored.
2.6.2 Implicit Time Integration for Statics and Quasi-Statics
The governing equation for static and quasi-static problems is found by setting the acceleration to zero in Eq. (2),
Solutions to static and quasi-static problems are found by determining the nodal positions that satisfy Eq. (8) under the specified boundary conditions.
The QuasiStatic time integrator in Peridigm is a nonlinear solver that utilizes Newton’s methods for the solution of Eq. (8). This approach requires the solution of a global linear system of equations, \(\textbf{K} \, \Delta \textbf{u} = - \textbf{r}\), where \(\Delta \textbf{u}\) is an update to the displacement \(\textbf{u}\), \(\textbf{r}\) is a residual obtained by evaluating the left-hand side of Eq. (8), and \(\textbf{K}\) is the tangent stiffness matrix,
where \(f^{\, int}_{i}\) is the component of internal force corresponding to degree of freedom i, and \(u_{j}\) is the component of the displacement corresponding to degree of freedom j. Multiple strategies are available for computing the tangent stiffness matrix in Peridigm. The Material class allows for implementation of a material tangent routine using an analytic expression, if available, or using the automatic differentiation capabilities of the Sacado software package. If a material tangent routine is not provided for a given material, Peridigm obtains an approximate value using a finite difference approach.
The NOXQuasiStatic time integrator is an alternative to the QuasiStatic integrator that utilizes the Trilinos NOX solver package [121]. Importantly, the NOXQuasiStatic solver offers a matrix-free alternative to the global linear solve required by QuasiStatic. The matrix-free solver generally exhibits much slower convergence, but has the advantage of not requiring construction of the tangent stiffness matrix. This is particularly relevant for peridynamic models because the bandwidth of the tangent stiffness matrix is generally very large relative to classical finite element models, leading to large memory requirements [87, 88].
2.7 Compute Classes
Peridigm was designed to be extensible. Compute classes allow quantities of interest to be calculated as a function any state variable and written to the Peridigm output file. Peridigm is distributed with many compute classes, and a compute class programming interface allows users to create new compute classes without concern for parallel communication or output routines. A compute class object is instantiated whenever the output field associated with that class is requested within the Output section of a Peridigm input deck. The corresponding compute() method is then called whenever output is written to disk.
Compute classes derive from the Compute base class containing the programming interface described in Listing 4.

Arguments to the constructor are primarily used by compute classes that deal with multiple material blocks or that need explicit access to the communicator object. The FieldIDs() function returns a list of field IDs corresponding to the fields that the compute class operates on. This approach ensures that the required fields are properly allocated and made available within the compute() method. The initialize() method allows the compute class to initialize state data before the simulation begins. Lastly, the compute() method computes the quantity of interest.
As a specific example, consider the very simple Compute_Acceleration compute class. This class is derived from the Compute base class and contains the private data shown in Listing 5.

The constructor of the Compute_Acceleration class is outlined in Listing 6. The constructor interacts with the FieldManager class, which tracks information for the allocation, storage, and parallel communication of field data. The FieldManager class and associated DataManager class leverage the Trilinos framework, which is discussed in more detail in Section 2.8. As show in Listing 6, the fieldManager object returns the field IDs for the force density vector and the acceleration vector, allowing for efficient access to these data structures in subsequent calculations in the compute() routine.

Contents of the compute() method appear in Listing 7. This method loops over each block in the discretization and extracts the corresponding force density and acceleration vectors. It initially fills the acceleration vector by copying the force density vector, and then extracts the density for the material of that block and divides the force by the density to arrive at the acceleration.

2.8 Parallelization
A key aspect of Peridigm’s performance is its use of the Trilinos Epetra library for parallelization [122]. The Petra object model, which includes Epetra and Tpetra, is the framework utilized by Trilinos for distributed memory linear algebra, including the management of parallel vectors and matrices. Epetra uses map objects to encapsulate the details of data distribution, assigning entries of a data structure to specific MPI processes. Epetra maps and the data structures that utilize them operate effectively in both serial and parallel using an Epetra_Comm communicator.
Peridigm makes widespread use of Epetra_Vector and Epetra_MultiVector objects for data management. These objects, in turn, utilize Epetra_BlockMap and Epetra_Map objects to associate subsets of data with specific MPI processes. An Epetra_BlockMap is used when the per-entry quantity to be stored is vector valued (e.g., force) and an Epetra_Map when the quantity to be stored is a scalar. Importantly, the Epetra_BlockMap class supports maps in which the length of individual entries varies on a per-entry basis. Maps of this type are used for managing bond data, where the lengths of individual entries are equal to the number of bonds associated with each nodal volume.
An Epetra_Vector implements a finite-dimensional vector distributed over processes where assignment of data to a process is determined by the associated map. An Epetra_MultiVector represents a collection of one or more vectors with the same map. Epetra_Vector and Epetra_MultiVector are used in Peridigm to store data such as volume, initial coordinates, current coordinates, and velocity, as well as any additional variables that may be required for a particular simulation. Peridynamic models require frequent passing of information between bonded material points, including sets of points that may reside in different blocks, on different MPI ranks, or both. This is achieved in Peridigm using Epetra_Import objects, which transfer data between Epetra objects using communication patterns based on the underlying maps. Note that for operations such as evaluation of force states, data are required from all material points within the peridynamic horizon in the reference configuration. In contrast, contact models require data from material points nearby in the current configuration. Thus the processing of bonded neighbors and potential contact interactions requires two distinct mappings among MPI processes.
Implicit time integration using Newton’s method requires the solution of large linear systems of equations. In this case, Peridigm utilizes Epetra’s sparse row matrix class Epetra_FECrsMatrix for storage of the tangent stiffness matrix across MPI ranks. The Epetra_FECrsMatrix class is a specialization of the more general Epetra_CrsMatrix class with additional functionality to support the assembly process. For solution of the global linear system, Peridigm’s QuasiStatic time integrator utilizes the Belos package, which supports a number of iterative solution methods and preconditioners [123]. The default Belos solution method in Peridigm is the block conjugate gradient algorithm. Peridigm’s NOXQuasiStatic time integrator utilizes the NOX nonlinear solver package [121]. A primary difference between the QuasiStatic and NOXQuasiStatic time integrators is that the QuasiStatic nonlinear solution algorithm is implemented directly in Peridigm, utilizing Belos for solving the global linear system, whereas the NOXQuasiStatic integrator utilizes NOX and related Trilinos packages for virtually all aspects of the nonlinear solve. The QuasiStatic approach provides Peridigm developers with direct control over the solution algorithm, while the NOXQuasiStatic approach reduces developer control but has the advantage of leveraging advanced features in NOX that would be difficult and time consuming to replicate in Peridigm. An example is the Jacobian-Free Newton Krylov solution method available in NOX, which enables solution of static and quasi-static problems without construction of the tangent stiffness matrix.
3 Running Simulations with Peridigm
In this section, we discuss the steps for running a Peridigm simulation: obtaining and building the code, creating a discretization and input deck, running the code, and post-processing the results. A general overview is given first, followed by two example simulations.
3.1 Obtaining and Building Peridigm
Building Peridigm consists of installing the necessary development tools, building the required third-party libraries, and building and testing Peridigm itself. Peridigm is compatible with Linux software environments that are typical of engineering workstations and parallel computing platforms, and is also regularly built and tested on macOS operating systems. The required software tools include cmake and MPI compiler wrappers such as MPICH or Open MPI. Peridigm’s primary dependencies are Trilinos, a set of open-source libraries for high-performance scientific computing, and Boost. The Trilinos dependency includes the Sandia Engineering Analysis Code Access System (SEACAS) for support of the exodus file format, which in turn requires HDF5 and NetCDF. The Peridigm code itself can be obtained from its public repository, currently managed on GitHub® under a three-clause BSD open-source license [124]. The Peridigm GitHub® website includes additional detailed instructions on the build process.
The ability to utilize Docker containers for obtaining Peridigm was recently added as an alternative to the full build process outlined above. Docker images for Peridigm and its dependencies are available at the Peridigm GitHub® website. The Docker distribution system provides users with a highly efficient and simplified process for obtaining a Peridigm executable, and is a recommended point of entry for new users.
3.2 Preparing a Simulation
The input for a Peridigm simulation consists of a discretization and an input deck. As discussed in Section 2.2, exodus is the preferred file format for discretizations due to its efficiency and compatibility with a number of third-party software packages. A text file format is also supported, which provides a simplified alternative for users wishing to construct discretizations directly using in-house scripts, or similar.
Peridigm operates on meshfree discretizations in which each nodal volume is defined by its spatial coordinates \(\textbf{x}\) and volume \(\Delta V\). Groups of nodal volumes are organized into blocks, and regions for the application of initial conditions, boundary conditions, and body forces are defined using node sets. The text file format for discretizations supported by Peridigm utilizes this format directly, i.e., for each nodal volume there is a line in the text file containing three spatial coordinates, the block number, and the volume \(\Delta V\). Node sets are specified in separate text files containing the node IDs for the nodes in a given node set. Text file discretizations can be used directly by Peridigm, or they can be converted to an exodus file using the text_to_genesis.py script distributed with Peridigm.
Peridigm supports three types of discretizations in the exodus format: sphere meshes, hexahedral meshes, and tetrahedral meshes. The sphere format is a general meshfree discretization format provided by exodus in which nodal volumes are conceptualized as spheres and defined in terms of the spatial coordinates of the sphere centroid, the radius of the sphere, and the volume of the sphere. In the case of an exodus sphere mesh, Peridigm utilizes the spatial coordinates and volume, and ignores the sphere radius (note that the exodus sphere mesh format allows users to specify a volume and radius that are not physically consistent, hence this information is not necessarily redundant). In the case of a hexahedral or tetrahedral mesh, Peridigm preforms a conversion at the onset of the simulation to create a corresponding meshfree discretization. Each element in the hexahedral or tetrahedral mesh is converted to a nodal volume such that the spatial coordinates of the nodal volume are equal to the centroid of the original element, and the volume \(\Delta V\) is equal to the volume of the original element. Element blocks are directly preserved, and node sets are converted such that a nodal volume is assigned to a node set if any node in the corresponding hexahedral or tetrahedral element was in the node set. Peridigm’s support for hexahedral and tetrahedral meshes greatly expands the ability of users to utilize finite element meshing tools to discretize the domain. To date, mesh generators that have been demonstrated with Peridigm include CUBIT [96] and the combination of the open-source software Gmsh [125] and the Python package meshio [126]. Additional pre-processing tools are provided in the SEACAS package, including the exodus.py module for creation of exodus files using Python scripts.
The Peridigm input deck is a text file in which the user specifies the parameters that define the simulation. The input deck is organized into multiple sections, for example, sections for the discretization, material models, damage models, time integrator, and simulation output. In many cases, the organization of the input deck maps directly to blocks and node sets defined in the discretization file. Peridigm currently supports two input deck formats, YAML and XML. The XML format was adopted early in the development of the Peridigm project due to its direct compatibility with many Trilinos packages, including the Teuchos::ParameterList data structure. Support for the YAML format was added later to provide a more user-friendly alternative. Examples of input decks in both formats can be found in the examples and test subdirectories in the Peridigm code repository. Those in the examples subdirectory were constructed specifically to provide an entry point for new users.
Examples of several input deck sections are given in Listings 8–13. The following sections are required for all Peridigm simulations: Discretization, Materials, Blocks, Solver, and Output. For any practical simulation, a Boundary Conditions section must also be provided. Examples of additional optional sections, for example, the Damage and Contact sections required for modeling bond failure and contact, respectively, are available in the example problems distributed with Peridigm.
A basic Discretization section is given in Listing 8, in which the user specifies the name of the discretization file and the file format.

A Materials section is shown in Listing 9. Users may define any number of materials, each of which is given a unique label (My Material in this case) for association with specific blocks in the discretization.

Note that Peridigm does not explicitly track the units for any input parameters, and instead utilizes a consistent units approach in which users are free to select the system of units best suited for the given simulation (e.g., SI, CGS, IPS).
The Blocks section show in Listing 10 maps the material model with label My Material to block_1 in the discretization and specifies the horizon for that block. Likewise, the Blocks section may also be used to associate bond damage models, if any, with specific blocks.

Initial and boundary conditions are specified in the Boundary Conditions section. The example given in Listing 11 specifies a prescribed displacement Dirichlet boundary condition for the displacement degree of freedom in the y direction. This boundary condition is a function of time, t, and the y component of the spatial coordinates in the undeformed configuration. This boundary condition is applied to nodelist_1, as defined in the discretization.

Listing 12 contains an example of a Solver section. In this case, a QuasiStatic solver is used, and its specific attributes are defined.

Finally, an Output section is presented in Listing 13. Parameters include the name of the output exodus file, the frequency at which data is written to file, and a list of the variables to be stored. Peridigm supports node variables, element variables (i.e., per block variables), and global variables. An output frequency of 1 specifies that output will be written to disk at every load step in the simulation.

3.3 Executing Peridigm
Peridigm is executed from the command line. For serial execution, a single argument is given, the name of the input deck. For parallel runs, the peridigm command is preceded by a standard MPI command:
mpirun -np 8 Peridigm my_input_file.yaml
where the -np option specifies the number of MPI ranks. Note that for parallel runs using exodus discretizations, the discretization files must be partitioned in a pre-processing step. The SEACAS utility decomp is one option for partitioning an exodus discretization file.
Peridigm writes output to stdout and to one or more exodus files. Exodus files contain the numerical results of the simulation, while the information written to stdout provides the user with real-time information on the progress of the simulation.
3.4 Post-Processing
The exodus output files generated by Peridigm are compatible with a number of third-party software packages. The SEACAS package, for example, contains multiple utilities, including epu for combining decomposed exodus files into a single file and grope for examining file contents. The freely available code ParaView [127] is a common choice for visualizing output data. Additional options include VisIt [128] and the SEACAS utility blot. Numerical data can be extracted from exodus files using the exodus.py Python module, or using the commercial code MATLAB.
Several studies in the literature have considered the analysis of results from peridynamic simulations, in particular for comparison against experimental data. Analysis of fragmentation simulations is investigated in Diehl et al. [129] and Littlewood et al. [130]. Visualizing the progression of fracture is considered in Bussler et al. [131]. For additional discussion, the reader is referred to [132, §6].
3.5 Example Simulations
We present two example simulations that exercise the core capabilities of Peridigm and demonstrate its computational performance. The first is a quasi-static simulation of a tensile test, and the second is an explicit dynamics simulation of an expanding cylinder resulting in fragmentation. The simulations are adaptations of example problems distributed with the Peridigm source code. They have been modified by refining the discretization and reducing the horizon, which increases the fidelity of the simulation and allows for an evaluation of code performance for large-scale parallel simulations.
The example simulations were carried out on the Skybridge computing cluster at Sandia National Laboratories. Skybridge consists of 1848 nodes with dual-socket 8-core Intel Sandy Bridge E5-2670 CPUs connected using QDR InfiniBand interconnect with a fat tree topology. Skybridge utilizes a Tri-lab Operating System Software (TOSS3) cluster management software stack based on Red Hat Enterprise Linux 7 and uses a Slurm workload manager. Peridigm was built using Intel 21.3 compilers and Open MPI 4.0.
3.5.1 Tensile Test Simulation
The simulation of a tensile test illustrated in Fig. 3 demonstrates Peridigm for the solution of quasi-static problems using implicit time integration. The tensile specimen is 101.6mm in length, with a maximum width of 12.7mm, a minimum width of 6.35mm, and a thickness of 3.15mm. The discretization of the tensile specimen was created using the CUBIT mesh generator. CUBIT provides functionality for defining the geometry of the body in terms of vertices, curves, and surfaces, which allowed for a straightforward meshing process. The mesh used as input to Peridigm was a hexahedral mesh containing just over one million elements. Peridigm automatically converted the hexahedral mesh to a meshfree discretization at the onset of the simulation. A value of three times the nominal mesh spacing was assigned to the horizon, \(\delta = \mathrm {{0.432}{mm}}\). Node sets were defined for volumetric regions at the ends of the bar, extending a distance of twice the horizon into the body of the specimen.
The material behavior for the tensile specimen was modeled with a linear elastic correspondence model with values for the bulk and shear moduli set to 150.00GPa and 69.23GPa, respectively. As described in Section 2.3, a stabilization method is available in Peridigm to suppress low-energy modes of deformation, which can pollute the solution when correspondence models are used. The stabilization coefficient in this case was set to 0.02.
Boundary conditions for the tensile test simulation were applied over volumetric regions at the ends of the bar. A linear displacement field was imposed in the direction of the tensile load to approximate the expected deformation, as shown in Listing 14. Note that the origin is located at the midpoint of the bar, hence the y component of displacement is positive for the right-hand side of the bar and negative for the left-hand side of the bar. Additional fixed-displacement boundary conditions were applied to selected edges on the ends of the bar to eliminate rigid-body displacements.

Several compute classes were used to model the presence of a strain gauge on the tensile specimen, providing a means for direct comparison of simulation results to experimental data. Specifically, the Nearest_Point_Data compute class was utilized to track the displacement of nodes in locations corresponding to the ends of a 2.476cm strain gauge positioned in the center of the specimen, and the Block_Data compute class was used to track the total reaction forces at the ends of the bar. Taken together, these data allow for calculation of engineering stress and engineering strain, which can then be used to compute Young’s modulus.
Results for the tensile test simulation are shown in Fig. 3. The simulation reproduced the expected displacements in the loading and off-loading directions, and the calculation of the Young’s modulus described above yielded 183.7GPa. Performance data for the tensile bar simulation are given in Fig. 4 for 256, 512, and 1024 MPI ranks. Calculation of a best-fit line to the data in Fig. 4 yields a slope of \(-\)0.89, indicating excellent scaling.
3.5.2 Fragmenting Cylinder Simulation
Simulation of a fragmenting hollow cylinder, shown in Fig. 5, demonstrates the ability of Peridigm to capture pervasive material failure. The cylinder has an outer radius of 2.5cm, an inner radius of 2.0cm, and a height of 10.0cm. In this case, the meshfree discretization was created in text file format using a Python script and converted to the exodus file format using the text_to_exodus.py script distributed with Peridigm. The discretization contains just over 11 million nodal volumes. The horizon was assigned a value of three times the nominal mesh spacing, \(\delta = \mathrm {{0.0558}{cm}}\). Material response is governed by the ordinary state-based plasticity model developed by Mitchell [97] with the material parameters given in Listing 15.

Damage was governed by the critical stretch bond failure law, with the critical stretch \(s_c\) set to 0.12. The explicit dynamics time integrator was used, with an end time of \(4.0 \times 10^{-4}\)s and a user-specified time step of \(1.0 \times 10^{-8}\)s.
Initial outward velocities were applied to the entire domain to approximate the effect of an internal pressure. The initial velocities were prescribed using a spatially varying, user-defined function, as shown in Listing 16.

Results for the fragmenting cylinder simulation are shown in Fig. 5. The color scale indicates damage, computed as the percentage of broken bonds for each nodal volume. Performance data for the fragmenting cylinder simulation are given in Fig. 6 for parallel execution using 1024, 2048, and 4098 MPI ranks. Calculation of a best-fit line to the data in Fig. 6 yields a slope of \(-\)0.98, indicating near-optimal scaling.
4 Summary and Conclusions
Peridigm is a meshfree peridynamics code for the solution of solid mechanics problems, in particular those involving crack propagation and pervasive material failure. The underlying meshfree formulation follows Silling and Askari [2], and has been generalized to include bond-based, ordinary state-based, and non-ordinary state-based (correspondence) material models [1, 89]. Additional capabilities include contact modeling and support for both explicit and implicit time integration.
The Peridigm code was designed for large-scale simulations on parallel computing platforms and provides software interfaces for the implementation of additional material models, bond failure laws, contact models, and compute classes. It utilizes multiple Trilinos software packages and is compatible with the SEACAS toolset, CUBIT mesh generator, and ParaView visualization code. Peridigm has been used to date primarily by methods developers as a platform for demonstrating new approaches at scale. As shown Section 3.5, Peridigm exhibits excellent performance on large discretizations for both implicit quasi-statics and explicit transient dynamics problems.
Peridigm is managed as an open-source, community driven software project. It is freely distributed and includes a development environment that enables the implementation and testing of new capabilities. It is our hope that Peridigm continues to grow as an engineering tool and a platform for methods development, thereby supporting the overall growth and adoption of peridynamics and nonlocal methods among the computational mechanics community and the practitioners it supports.
Code Availability
The Peridigm source code is freely distributed under a three-clause BSD license and is available at the Peridigm website [124].
References
Silling S (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48(1):175–209. https://doi.org/10.1016/S0022-5096(99)00029-0
Silling S, Askari E (2005) A meshfree method based on the peridynamic model of solid mechanics. Comput Struct 83(17–18):1526–1535. https://doi.org/10.1016/j.compstruc.2004.11.026
The Trilinos Project Website. https://trilinos.github.io. Accessed 12 June 2022
The LAMMPS Peridynamic Pair Styles Website. https://lammps.sandia.gov/doc/pair_peri.html. Accessed 12 June 2022
Parks ML, Lehoucq RB, Plimpton SJ et al (2008) Implementing peridynamics within a molecular dynamics code. Comput Phys Commun 179(11):777–783. https://doi.org/10.1016/j.cpc.2008.06.011
The PeriPy Project Website. https://pypi.org/project/peripy/. Accessed 12 June 2022
Boys B, Dodwell T, Hobbs M et al (2021) PeriPy - high performance OpenCL peridynamics package. Comput Methods Appl Mech Eng 21. https://doi.org/10.1016/j.cma.2021.114085
The PeriHPX Project Website. https://perihpx.github.io/. Accessed 12 June 2022
Diehl P, Jha PK, Kaiser H et al (2020) An asynchronous and task-based implementation of peridynamics utilizing HPX—the C++ standard library for parallelism and concurrency. SN Appl Sci 2(12). https://doi.org/10.1007/s42452-020-03784-x
Jha PK, Diehl P (2021) NLMech: implementation of finite difference/meshfree discretization of nonlocal fracture models. J Open Source Softw 6(65). https://doi.org/10.21105/joss.03020
The PeriPyDIC Project Website. https://github.com/lm2-poly/PeriPyDIC. Accessed 12 June 2022
The PD_Shell Project Website. https://github.com/masoudbehzadinasab/PD_Shell. Accessed 12 June 2022
Behzadinasab M, Alaydin M, Trask N et al (2022) A general-purpose, inelastic, rotation-free Kirchhoff-Love shell formulation for peridynamics. Comput Methods Appl Mech Eng 389. https://doi.org/10.1016/j.cma.2021.114422
The PyNucleus Project Website. https://github.com/sandialabs/PyNucleus. Accessed 12 June 2022
The Relation-Based Software (RBS) Website. https://github.com/alijenabi/RelationBasedSoftware. Accessed 12 Feb 2023
Jenabidehkordi A, Fu X, Rabczuk T (2022) An open source peridynamics code for dynamic fracture in homogeneous and heterogeneous materials. Adv Eng Softw 168. https://doi.org/10.1016/j.advengsoft.2022.103124
Kaiser H, Diehl P, Lemoine AS et al (2020) HPX - the C++ standard library for parallelism and concurrency. J Open Source Softw 5(53). https://doi.org/10.21105/joss.02352
Diehl P (2012) Implementierung eines peridynamik-verfahrens auf GPU. Master’s thesis, University of Stuttgart (Germany)
Diehl P, Schweitzer MA (2015) Efficient neighbor search for particle methods on GPUs. In: Griebel M, Schweitzer MA (eds) Meshfree Methods for Partial Differential Equations VII. Lecture Notes in Computational Science and Engineering, Springer, p 81–95. https://doi.org/10.1007/978-3-319-06898-5_5
Mossaiby F, Shojaei A, Zaccariotto M et al (2017) OpenCL implementation of a high performance 3D peridynamic model on graphics accelerators. Comput Math Appl 74(8):1856–1870. https://doi.org/10.1016/j.camwa.2017.06.045
Ren B, Wu C, Askari E (2017) A 3D discontinuous Galerkin finite element method with the bond-based peridynamics model for dynamic brittle failure analysis. Int J Impact Eng 99:14–25. https://doi.org/10.1016/j.ijimpeng.2016.09.003
Diehl P, Lipton R, Wick T et al (2022) A comparative review of peridynamics and phase-field models for engineering fracture mechanics. Comput Mech 69:1259–1293. https://doi.org/10.1007/s00466-022-02147-0
Behzadinasab M, Foster JT (2019) The third Sandia fracture challenge: peridynamic blind prediction of ductile fracture characterization in additively manufactured metal. Int J Fract 218:97–109. https://doi.org/10.1007/s10704-019-00363-z
Behzadinasab M, Foster JT (2020) Revisiting the third Sandia fracture challenge: a bond-associated, semi-Lagrangian peridynamic approach to modeling large deformation and ductile fracture. Int J Fract 224:261–267. https://doi.org/10.1007/s10704-020-00455-1
Behzadinasab M, Vogler TJ, Foster JT (2018) Modeling perturbed shock wave decay in granular materials with intra-granular fracture. In: Chau R, Germann TC, Lane JMD, et al (eds) Shock Compression of Condensed Matter - 2017: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter, AIP Conference Proceedings, vol 1979. AIP Publishing. https://doi.org/10.1063/1.5044814
Behzadinasab M, Vogler TJ, Peterson AM et al (2018) Peridynamics modeling of a shock wave perturbation decay experiment in granular materials with intra-granular fracture. J Dyn Behav Mater 4:529–542. https://doi.org/10.1007/s40870-018-0174-2
Xu Y, Zhu P (2022) Peridynamic simulations of damage in indentation and scratching of 3C-SiC. J Mater Res 37:4381–4391. https://doi.org/10.1557/s43578-022-00812-x
Postek E, Sandowski T (2021) Impact model of the Al\(_{2}\)O\(_{3}\)/ZrO\(_{2}\) composite by peridynamics. Compos Struct 271. https://doi.org/10.1016/j.compstruct.2021.114071
Postek E, Sandowski T, Pietras D (2022) Impact of interpenetrating phase Al-Si12/SiC. Int J Multiscale Comput Eng 20(6):61–78. https://doi.org/10.1615/IntJMultCompEng.2022043186
Postek E, Sandowski T (2022) Dynamic compression of a SiC foam. Materials 15(23). https://doi.org/10.3390/ma15238363
de Sousa T, Ahadi A, Sjögren E et al (2021) Peridynamic modelling of harmonic structured materials under high strain rate deformation. In: Proceedings of the 14th World Congress on Computational Mechanics (WCCM XIV) and 8th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2020), Paris, France. https://doi.org/10.23967/wccm-eccomas.2020.279
Postek E, Norwak Z, Pȩcherski RB (2022) Viscoplastic flow of functional cellular materials with use of peridynamics. Meccanica 57:905–922. https://doi.org/10.1007/s11012-021-01383-7
Masoni R, Manes A, Giglio M (2019) A comparison of state-based peridynamics and solid mesh to SPH conversion techniques to reproduce fragmentation of a ceramic tile subject to ballistic impact. Procedia Structural Integrity 24:40–52. https://doi.org/10.1016/j.prostr.2020.02.004
Morgado F, Peddakotla SA, Carbacz C et al (2022) Fidelity management of aerothermodynamic modelling for destructive re-entry. In: Proceedings of the 2nd International Conference on Flight Vehicles, Aerothermodynamics and Re-entry Missions & Engineering (FAR), Heilbronn, Germany
Peddakotla SA, Morgado F, Thillaithevan D et al (2022) A multi-fidelity and multi-disciplinary approach for the accurate simulation of atmospheric re-entry. In: Proceedings of the 73rd International Astronautical Congress, Paris, France
Peddakotla SA, Yuan J, Minisci E et al (2022) A numerical approach to evaluate temperature-dependent peridynamics damage model for destructive atmospheric entry of spacecraft. Aeronaut J. https://doi.org/10.1017/aer.2022.69
Tang L, Krishnan AN, Berjikian J et al (2018) Effect of nanoscale phase separation on the fracture behavior of glasses: toward tough, yet transparent glasses. Phys Rev Mater 2(11). https://doi.org/10.1103/PhysRevMaterials.2.113602
Ono M, Miyasaka S, Takato Y et al (2019) Higher toughness of metal-nanoparticle-implanted sodalime silicate glass with increased ductility. Sci Rep 9. https://doi.org/10.1038/s41598-019-51733-5
Ono M, Miyasaka S, Takato Y et al (2021) Tuning the mechanical toughness of the metal nanoparticle-implanted glass: the effect of nanoparticle growth conditions. J Am Ceram Soc 104(10):5341–5353. https://doi.org/10.1111/jace.17754
Rädel M, Bednarek AJ, Schmidt J et al (2017) Peridynamics: convergence & influence of probabilistic material distribution on crack initiation. In: Remmers JJC, Turon A (eds) Proceedings of the 6th ECCOMAS Thematic Conference on the Mechanical Response of Composities (COMPOSITES 2017), Eindhoven, The Netherlands
Caimmi F, Haddadi E, Choupani N et al (2016) Modelling mixed-mode fracture in poly(methylmethacrylate) using peridynamics. Procedia Structural Integrity 2:166–173. https://doi.org/10.1016/j.prostr.2016.06.022
Ren B, Song J (2022) Peridynamic simulation of particles impact and interfacial bonding in cold spray process. J Therm Spray Technol 31:1827–1843. https://doi.org/10.1007/s11666-022-01409-w
Naumenko K, Pander M, Würkner M (2022) Damage patterns in float glass plates: experiments and peridynamics analysis. Theor Appl Fract Mech 118. https://doi.org/10.1016/j.tafmec.2022.103264
Kamensky D, Behzadinasab M, Foster JT et al (2019) Peridynamic modeling of frictional contact. J Peridyn Nonlocal Model 1(2):107–121. https://doi.org/10.1007/s42102-019-00012-y
Ritter J, Shegufta S, Steinmann P et al (2022) An energetically consistent surface correction method for bond-based peridynamics. Forces in Mechanics 9. https://doi.org/10.1016/j.finmec.2022.100132
Ignatev M, Kazarinov N, Petrov Y (2020) Peridynamic modelling of the dynamic crack initiation. Procedia Structural Integrity 28:1650–1654. https://doi.org/10.1016/j.prostr.2020.10.138
Ignatiev M, Petrov YV, Kazarinov N (2021) Simulation of dynamic crack initiation based on the peridynamic numerical model and the incubation time criterion. Technical Physics 66(3):422–425. https://doi.org/10.1134/S1063784221030099
Ignatiev MO, Petrov YV, Kazarinov NA et al (2022) Peridynamic formulation of the mean stress and incubation time fracture criteria and its correspondence to the classical Griffith’s approach. Contin Mech Thermodyn. https://doi.org/10.1007/s00161-022-01159-8
Lammi CJ, Vogler TJ (2014) A nonlocal peridynamic plasticity model for the dynamic flow and fracture of concrete. Technical Report SAND2014-18257, Sandia National Laboratories, Albuquerque, NM and Livermore, CA, https://doi.org/10.2172/1159446
Lammi CJ, Zhou M (2017) Multi-scale peridynamic modeling of dynamic fracture in concrete. In: Shock Compression of Condensed Matter - 2015: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter, AIP Conference Proceedings, vol 1793. AIP Publishing. https://doi.org/10.1063/1.4971634
Bazilevs Y, Behzadinasab M, Foster JT (2022) Simulating concrete failure using the microplane (M7) constitutive model in correspondence-based peridynamics: validation for classical fracture tests and extension to discrete fracture. Journal of the Mechanics and Physics of Solids 1686. https://doi.org/10.1016/j.jmps.2022.104947
Freimanis A, Kaewunruen S (2018) Peridynamic analysis of rail squats. Appl Sci 8. https://doi.org/10.3390/app8112299
Hamarat M, Papaelias M, Kaewunruen S (2022) Fatigue damage assessment of complex railway turnout crossings via peridynamics-based digital twin. Sci Rep 12. https://doi.org/10.1038/s41598-022-18452-w
Rädel M, Willberg C, Krause D (2019) Peridynamic analysis of fibre-matrix debond and matrix failure mechanisms in composites under transverse tensile load by an energy-based damage criterion. Composites Part B: Engineering 158:18–27. https://doi.org/10.1016/j.compositesb.2018.08.084
Willberg C, Rädel M (2018) An energy based peridynamic state-based failure criterion. In: Müller G, Ulbrich M (eds) Special Issue: 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM). Proceedings in Applied Mathematics and Mechanics (PAMM), Wiley. https://doi.org/10.1002/pamm.201800074
Willberg C, Rädel M, Heinecke F (2019) Verification and validation of a 2D energy based peridynamic state-based failure criterion. In: Eberhardsteiner J, Schöberl M (eds) Special Issue: 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM). Proceedings in Applied Mathematics and Mechanics (PAMM), Wiley. https://doi.org/10.1002/pamm.201900331
Willberg C, Wiedemann L, Rädel M (2019) A mode-dependent energy-based damage model for peridynamics and its implementation. J Mech Mater Struct 14(2):193–217. https://doi.org/10.2140/jomms.2019.14.193
Behzadinasab M, Foster JT (2020) On the stability of the generalized, finite deformation correspondence model of peridynamics. Int J Solids Struct 182–183:64–76. https://doi.org/10.1016/j.ijsolstr.2019.07.030
Brothers MD, Foster JT, Millwater HR (2014) A comparison of different methods for calculating tangent-stiffness matrices in a massively parallel computational peridynamics code. Comput Methods Appl Mech Eng 279:247–267. https://doi.org/10.1016/j.cma.2014.06.034
Freimanis A, Paeglitis A (2017) Mesh sensitivity in peridynamic quasi-static simulations. Procedia Engineering 172:284–291. https://doi.org/10.1016/j.proeng.2017.02.116
Seleson P, Littlewood DJ (2016) Convergence studies in meshfree peridynamic simulations. Comput Math Appl 71(11):2432–2448. https://doi.org/10.1016/j.camwa.2015.12.021
Seleson P, Littlewood DJ (2018) Numerical tools for improved convergence of meshfree peridynamic discretizations. In: Voyiadjis GZ (ed) Handbook of Nonlocal Continuum Mechanics for Materials and Structures. Springer. https://doi.org/10.1007/978-3-319-22977-5_39-1
Mohajerani S, Wang G (2022) “Touch-aware” contact model for peridynamics modeling of granular systems. Int J Numer Methods Eng 123(17):3850–3878. https://doi.org/10.1002/nme.7000
Willberg C, Hesse J, Heinecke F (2022) Peridynamic simulation of a mixed-mode fracture experiment in PMMA utilizing an adaptive-time stepping for an explicit solver. J Peridyn Nonlocal Model. https://doi.org/10.1007/s42102-021-00079-6
Wu L, Huang D, Bobaru F (2021) A reformulated rate-dependent visco-elastic model for dynamic deformation and fracture of PMMA with peridynamics. Int J Impact Eng 149. https://doi.org/10.1016/j.ijimpeng.2020.103791
D’Antuono P, Morandini M (2017) Thermal shock response via weakly coupled peridynamic thermo-mechanics. Int J Solids Struct 129:74–89. https://doi.org/10.1016/j.ijsolstr.2017.09.010
Nayak S, Ravinder R, Krishnan N et al (2020) A peridynamics-based micromechanical modeling approach for random heterogeneous structural materials. Materials 13(6). https://doi.org/10.3390/ma13061298
Ji Y, Dong C, Wei X et al (2019) Discontinuous model combined with an atomic mechanism simulates the precipitated \(\eta ^\prime\) phase effect in intergranular cracking of 7-series aluminum alloys. Computational Materials Science 166:282–292. https://doi.org/10.1016/j.commatsci.2019.05.008
Shende S, Behzadinasab M, Moutsanidis G et al (2022) Simulating air blast on concrete structures using the volumetric penalty coupling of isogeometric analysis and peridynamics. Math Models Methods Appl Sci 32(12):2477–2496. https://doi.org/10.1142/S0218202522500580
Vasenkov AV (2021) Multi-physics peridynamic modeling of damage processes in protective coatings. J Peridyn Nonlocal Model 3. https://doi.org/10.1007/s42102-020-00046-7
Behzadinasab M, Foster JT (2020c) A semi-Lagrangian constitutive correspondence framework for peridynamics. J Mech Phys Solids 137. https://doi.org/10.1016/j.jmps.2019.103862
Freimanis A, Paeglitis A (2017) Modal analysis of isotropic beams in peridynamics. In: Proceedings of 3rd International Conference on Innovative Materials, Structures and Technologies (IMST 2017), IOP Conference Series: Materials Science and Engineering, vol 251. IOP Publishing. https://doi.org/10.1088/1757-899X/251/1/012088
Freimanis A, Paeglitis A (2018) Modal analysis of healthy and cracked isotropic plates in peridynamics. In: Mains M, Dilworth BJ (eds) Proceedings of the 36th IMAC, A Conference and Exposition on Structural Dynamics 2018. Topics in Modal Analysis & Testing, Volume 9, Springer, p 359–361. https://doi.org/10.1007/978-3-319-74700-2_41
Freimanis A, Paeglitis A (2021) Crack development assessment using modal analysis in peridynamic theory. J Comput Des Eng 8(1):125–139. https://doi.org/10.1093/jcde/qwaa066
Zhu F, Zhao J (2021) Multiscale modeling of continuous crushing of granular media: the role of grain microstructure. Comput Part Mech 8:1089–1101. https://doi.org/10.1007/s40571-020-00355-0
Shi K, Zhu F, Zhao J (2022) Multi-scale analysis of shear behaviour of crushable granular sand under general stress conditions. Géotechnique. https://doi.org/10.1680/jgeot.21.00412
Trageser JE, Mitchell CA, Jones RE et al (2022) The effect of differential mineral shrinkage on crack formation and network geometry. Sci Rep 12. https://doi.org/10.1038/s41598-022-23789-3
Vasenkov AV (2018) Stent fracture predictions with peridynamics. In: Frontiers in Biomedical Devices, American Society of Mechanical Engineers (ASME), Minneapolis, Minnesota. https://doi.org/10.1115/DMD2018-6866
Azdoud Y, Han F, Littlewood DJ et al (2016) Coupling local and nonlocal models. In: Bobaru F, Geubelle PH, Foster JT, et al (eds) Handbook of Peridynamic Modeling. Advances in Applied Mathematics, CRC Press, chap 14, https://doi.org/10.1201/9781315373331
D’Elia M, Perego M, Bochev P et al (2016) A coupling strategy for nonlocal and local diffusion models with mixed volume constraints and boundary conditions. Comput Math Appl 71(11):2218–2230. https://doi.org/10.1016/j.camwa.2015.12.006
D’Elia M, Bochev P, Littlewood DJ et al (2018) Optimization-based coupling of local and nonlocal models: applications to peridynamics. In: Voyiadjis GZ (ed) Handbook of Nonlocal Continuum Mechanics for Materials and Structures. Springer. https://doi.org/10.1007/978-3-319-22977-5_31-1
Littlewood DJ, Silling SA, Mitchell JA et al (2015) Strong local-nonlocal coupling for integrated fracture modeling. Technical Report SAND2015-7998, Sandia National Laboratories, Albuquerque, NM and Livermore, CA. https://doi.org/10.2172/1221526
Li X, Ye H, Zhang J (2020) Large-scale simulations of peridynamics on Sunway Taihulight supercomputer. In: ICPP’20: Proceedings of the 49th International Conference on Parallel Processing, Edmonton, Alberta, Canada. https://doi.org/10.1145/3404397.3404421
Li X, Ye H, Zhang J (2021) Redesigning Peridigm on SIMT accelerators for high-performance peridynamics simulations. In: Proceedings of the 2021 IEEE International Parallel and Distributed Processing Symposium (IPDPS), pp 433–443. https://doi.org/10.1109/IPDPS49936.2021.00052
Willberg C, Hesse JT, Garbade M et al (2023) A user material interface for the peridyamic Peridigm framework. SoftwareX 21. https://doi.org/10.1016/j.softx.2023.101322
Parks M, Littlewood D, Mitchell J et al (2012) Peridigm users’ guide v1.0.0. Technical Report SAND2012-7800, Sandia National Laboratories, Albuquerque, NM and Livermore, CA. https://doi.org/10.2172/1055619
Littlewood D (2015) Roadmap for peridynamic software implementation. Technical Report SAND2015-9013, Sandia National Laboratories, Albuquerque, NM and Livermore, CA. https://doi.org/10.2172/1226115
Littlewood DJ (2016) Roadmap for software implementation. In: Bobaru F, Geubelle PH, Foster JT, et al (eds) Handbook of Peridynamic Modeling. Advances in Applied Mathematics, CRC Press, chap 5. https://doi.org/10.1201/9781315373331
Silling S, Epton M, Weckner O et al (2007) Peridynamic states and constitutive modeling. J Elast 88:151–184. https://doi.org/10.1007/s10659-007-9125-1
Parks ML, Littlewood DJ, Salinger AG et al (2011) Peridigm summary report: lessons learned in development with agile components. Technical Report SAND2011-7045, Sandia National Laboratories, Albuquerque, NM and Livermore, CA. https://doi.org/10.2172/1029829
de Berg M, van Kreveld M, Overmars M et al (1998) Computational geometry: algorithms and applications, 2nd edn. Springer
Ganti A, Mitchell JA, Onunkwo U et al (2017) High fidelity simulations of large-scale wireless networks (PART II - FY2017). Technical Report SAND2017-11512, Sandia National Laboratories, Albuquerque, NM and Livermore, CA. https://doi.org/10.2172/1489863
The SEACAS Project Website. https://github.com/sandialabs/seacas. Accessed 12 June 2022
Sjaardema GD (2017) Sandia Engineering Analysis Code Access System v. 2.0.1. https://doi.org/10.11578/dc.20171025.2033
Ayachit U (2015) The ParaView guide: a parallel visualization application. Kitware
Skroch M, Owen SJ, Staten ML et al (2022) CUBIT™ geometry and mesh generation toolkit 16.04 user documentation. Technical Report SAND2022-4195W, Sandia National Laboratories, Albuquerque, NM and Livermore, CA
Mitchell JA (2011) A nonlocal, ordinary, state-based plasticity model for peridynamics. Technical Report SAND2011-3166, Sandia National Laboratories, Albuquerque, NM and Livermore, CA. https://doi.org/10.2172/1018475
Mitchell JA (2011) A nonlocal, ordinary-state-based viscoelasticity model for peridynamics. Technical Report SAND2011-8064, Sandia National Laboratories, Albuquerque, NM and Livermore, CA. https://doi.org/10.2172/1029821
Mitchell JA, Silling SA, Littlewood DJ (2015) A position-aware linear solid constitutive model for peridynamics. J Mech Mater Struct 10(5):539–557. https://doi.org/10.2140/jomms.2015.10.539
Le Q, Bobaru F (2018) Surface corrections for peridynamic models in elasticity and fracture. Comput Mech 61(4):499–518. https://doi.org/10.1007/s00466-017-1469-1
Ganzenmüller GC, Hiermaier S, May M (2015) Improvements to the prototype micro-brittle model of peridynamics. In: Griebel M, Schweitzer MA (eds) Meshfree Methods for Partial Differential Equations VII. Lecture Notes in Computational Science and Engineering, Springer, p 163–183. https://doi.org/10.1007/978-3-319-06898-5_9
Foster JT (2016) Constitutive modeling in peridynamics. In: Bobaru F, Geubelle PH, Foster JT, et al (eds) Handbook of Peridynamic Modeling. Advances in Applied Mathematics, CRC Press, chap 6. https://doi.org/10.1201/9781315373331
Breitenfeld M, Geubelle P, Weckner O et al (2014) Non-ordinary state-based peridynamic analysis of stationary crack problems. Comput Methods Appl Mech Eng 272:233–250. https://doi.org/10.1016/j.cma.2014.01.002
Foster J, Silling S, Chen W (2010) Viscoplasticity using peridynamics. Int J Numer Methods Eng 81(10):1242–1258. https://doi.org/10.1002/nme.2725
Warren T, Silling S, Askari A et al (2009) A non-ordinary state-based peridynamic method to model solid material deformation and fracture. Int J Solids Struct 46(5):1186–1195. https://doi.org/10.1016/j.ijsolstr.2008.10.029
O’Grady J, Foster J (2014) Peridynamic beams: a non-ordinary state-based model. Int J Solids Struct 51(18):3177–3183. https://doi.org/10.1016/j.ijsolstr.2014.05.014
O’Grady J, Foster J (2014) Peridynamic plates and flat shells: a non-ordinary state-based model. Int J Solids Struct 51(25–26):4572–4579. https://doi.org/10.1016/j.ijsolstr.2014.09.003
Tupek MR (2014) Extension of the peridynamic theory of solids for the simulation of materials under extreme loadings. PhD thesis, Massachusetts Institute of Technology
Xu X (2009) Generalized variational principles for uncertainty quantification of boundary value problems of random heterogeneous materials. J Eng Mech 135(10). https://doi.org/10.1061/(ASCE)EM.1943-7889.0000037
Bessa M, Foster J, Belytschko T et al (2014) A meshfree unification: reproducing kernel peridynamics. Comput Mech 53(6):1251–1264. https://doi.org/10.1007/s00466-013-0969-x
Hillman M, Pasetto M, Zhou G (2020) Generalized reproducing kernel peridynamics: unification of local and non-local meshfree methods, non-local derivative operations, and an arbitrary-order state-based peridynamic formulation. Comput Part Mecha 7(2):435–469. https://doi.org/10.1007/s40571-019-00266-9
Needleman A (1989) Dynamic shear band development in plane strain. J Appl Mech 56(1):1–9. https://doi.org/10.1115/1.3176046
Silling S (2017) Stability of peridynamic correspondence material models and their particle discretizations. Comput Methods Appl Mech Eng 322:42–57. https://doi.org/10.1016/j.cma.2017.03.043
Littlewood D (2010) Simulation of dynamic fracture using peridynamics, finite element modeling, and contact. In: Proceedings of the ASME 2010 International Mechanical Engineering Congress and Exposition (IMECE), Vancouver, British Columbia, Canada. https://doi.org/10.1115/IMECE2010-40621
Littlewood DJ (2011) A nonlocal approach to modeling crack nucleation in AA 7075-T651. In: Proceedings of the ASME 2011 International Mechanical Engineering Congress and Exposition (IMECE), Denver, Colorado. https://doi.org/10.1115/IMECE2011-64236
Flanagan D, Taylor L (1987) An accurate numerical algorithm for stress integration with finite rotations. Comput Methods Appl Mech Eng 62(3):305–320. https://doi.org/10.1016/0045-7825(87)90065-X
Askari E, Bobaru F, Lehoucq R et al (2008) Peridynamics for multiscale materials modeling. In: Proceedings of SciDAC 2008, Journal of Physics: Conference Series, vol 125. IOP Publishing. https://doi.org/10.1088/1742-6596/125/1/012078
Madenci E, Oterkus E (2014) Peridynamic theory and its applications. Springer. https://doi.org/10.1007/978-1-4614-8465-3
Johnson G, Cook W (1985) Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng Fract Mech 21(1):31–48. https://doi.org/10.1016/0013-7944(85)90052-9
Foster J, Silling S, Chen W (2011) An energy based failure criterion for use with peridynamic states. Int J Multiscale Comput Eng 9(6):675–688. https://doi.org/10.1615/IntJMultCompEng.2011002407
The NOX and LOCA Project Website. https://trilinos.github.io/nox_and_loca.html. Accessed 12 June 2022
The Epetra Project Website. https://trilinos.github.io/epetra.html. Accessed 12 June 2022
The Belos Project Website. https://trilinos.github.io/belos.html. Accessed 12 June 2022
The Peridigm Project Website. https://github.com/peridigm/peridigm. Accessed 12 June 2022
Geuzaine C, Remacle JF (2009) Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int J Numer Methods Eng 79(11):1309–1331. https://doi.org/10.1002/nme.2579
The meshio Project Website. https://github.com/nschloe/meshio. Accessed 12 June 2022
Ahrens J, Geveci B, Law C (2005) Paraview: An end-user tool for large data visualization. In: Hansen CD, Johnson CR (eds) The visualization handbook. Elsevier, p 717–731. https://doi.org/10.1016/B978-012387582-2/50038-1
Childs H, Brugger E, Whitlock B et al (2012) VisIt: an end-user tool for visualizing and analyzing very large data. In: Bethel EW, Childs H, Hansen C (eds) High Performance Visualization–Enabling Extreme-Scale Scientific Insight. Chapman and Hall/CRC, p 357–372. https://doi.org/10.1201/b12985
Diehl P, Bußler M, Pflüger D et al (2017) Extraction of fragments and waves after impact damage in particle-based simulations. In: Griebel M, Schweitzer MA (eds) Meshfree Methods for Partial Differential Equations VIII. Lecture Notes in Computational Science and Engineering, Springer, p 17–34. https://doi.org/10.1007/978-3-319-51954-8_2
Littlewood DJ, Silling SA, Demmie PN (2016) Identification of fragments in a meshfree peridynamic simulation. In: Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition (IMECE), Phoenix, Arizona. https://doi.org/10.1115/IMECE2016-65400
Bussler M, Diehl P, Pflüger D et al (2017) Visualization of fracture progression in peridynamics. Comput Graph 67:45–57. https://doi.org/10.1016/j.cag.2017.05.003
Diehl P, Prudhomme S, Lévesque M (2019) A review of benchmark experiments for the validation of peridynamics models. J Peridyn Nonlocal Model 1(1):14–35. https://doi.org/10.1007/s42102-018-0004-x
Acknowledgements
The authors would like to thank Masoud Behzadinasab, Alex Vasenkov, Jonas Ritter, Jake Ostien, and Michael Brothers for their contribution to Peridigm.
Funding
David Littlewood, Michael Parks, and John Mitchell acknowledge funding from the US Department of Energy (DOE) Advanced Simulation and Computing (ASC) program and the Laboratory Directed Research and Development (LDRD) program at Sandia National Laboratories. Patrick Diehl acknowledges funding from the National Science Foundation (NSF) Phylanx project award #1737785.
Author information
Authors and Affiliations
Contributions
David Littlewood, Michael Parks, John Foster, John Mitchell, and Patrick Diehl wrote the main manuscript text. John Foster prepared Fig. 1, John Mitchell prepared Fig. 2, and David Littlewood prepared Figs. 3–6. All the authors have made major contributions to the Peridigm software project.
Corresponding author
Ethics declarations
Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.
Conflict of Interest
John Foster is an Associate Editor for the Journal of Peridynamics and Nonlocal Modeling, and David Littlewood and Michael Parks are on the Editorial Board. They played no part in the assignment of this manuscript to Associate Editors or peer reviewers and were separated and blinded from the editorial process from submission inception to decision.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Littlewood, D.J., Parks, M.L., Foster, J.T. et al. The Peridigm Meshfree Peridynamics Code. J Peridyn Nonlocal Model 6, 118–148 (2024). https://doi.org/10.1007/s42102-023-00100-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42102-023-00100-0