Introduction

The MADM model performs appropriately for selecting the most efficient choice depending on a variety of factors [1,2,3,4]. In previous decades, the huge majority of evidence available frequently assumed that the experts offered precise assessments of all aspects. Despite this, the reality is so convoluted and fluctuating that most decisions are taken under circumstances that are confusing and deceptive. As a result, the choice is still made in these circumstances and can be described as the information indicating has some value. However, it may not produce an efficient result when using only a crisp set. It is necessary to produce an efficient result for the selection of an appropriate choice, fuzzy logical theory is utilized to deal with imprecise and vague information. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false. Fuzzy logic relies on the assumption that decisions are frequently made using vague and non-numerical information. Because of their ambiguity and imprecision, fuzzy models are mathematical representations of information. These models have the capability of recognizing, representing, manipulating, interpreting, and using vague and imprecise information [5,6,7,8].

So, Zadeh [9] developed the basic idea of fuzzy set (FS) hypothesis in 1965, which portrayed the strengthened behavior of an individual as a membership function. To generalize the concept of FS theory, Atanassov [10] established the notion of intuitionistic FS (IFS). It is regarded as one of the most well-known and frequently applied techniques for dealing with fuzziness. The IFS provides information through the membership value (MV) \({{\mathcalligra{m}}}_{{\text{C}}}\) and a non-membership value (NMV) \({\mathcalligra{n}}_{{\text{C}}}\) and their combined sum \({{\mathcalligra{m}}}_{{\text{C}}}+{\mathcalligra{n}}_{{\text{C}}}\le 1\) cannot be greater than one [11, 12]. By enlarging the concept of IFS, the Pythagorean FS (PyFS) was initially established by Yager [13] in which he provides information by using the MV \({{\mathcalligra{m}}}_{{\text{C}}}\) and NMV \({\mathcalligra{n}}_{{\text{C}}}\) and their combined sum of square \({{\mathcalligra{m}}}_{{\text{C}}}^{2}+{\mathcalligra{n}}_{{\text{C}}}^{2}\le 1\) is limited to less than or equal to one [14, 15]. Yager and Abbasov [16] initiated an improved version of PyFVs in the kind form of intricate integers. To generalize the concept of PyFS theory, Yager [17] invented the notion of q-rung ortho-pair FS (q-ROFS) in which he described the MV \({{\mathcalligra{m}}}_{{\text{C}}}\) and NMV \({\mathcalligra{n}}_{{\text{C}}}\) and their combined sum of q-th power \({{\mathcalligra{m}}}_{{\text{C}}}^{q}+{\mathcalligra{n}}_{{\text{C}}}^{q}\le 1\) is limited to less than or equal to one. There are some challenges in every day life that IFS, PyFS, and q-ROFS theory cannot capture. For instance, in the context of a system for casting votes, human thoughts may include additional responses of the following types: yes, no, abstain, and disapproval. Consequently, Cuong [18] compensated these discrepencies by including the abstinence value (AV) \({\mathcalligra{a}}_{{\text{C}}}\) in the IFS theory and frequently used techniques for dealing with fuzziness.

After the advancement of PFS theories, other scholars explored its significance and developed a variety of methods for interpreting information values using various operators [19,20,21,22,23,24,25,26,27,28]. To improve the circular structure of the IFS, Ejegwa, and Onyeke [29] investigated a list of novel AOs that were similarly organized to solve MADM techniques. Yang et al. expended the idea of PyFS for managing MADM issues by utilizing the operations of frank AOs (FAOS). Ali and Mahmood [30] identified a specific solution to cope with MADM challenges and established a notion of complex q-ROFSs (Cq-ROFSs). By utilizing a particular formulation of Dombi AOs (DAOs), Khan et al. [31] investigated the hypothesis of Spherical FSs (SFSs) and overcame the complexity of fuzziness. Mahmood et al. [32] identified an ideal solution to cope with a MADM problem and created the notion of complex bipolar FS (CBFS). Zhang [33] provided some credible strategies to eradicate the consequences of doubtful information based on the frank models. Li et al. [34] worked on the transport of intensity diffraction tomography with a non-interferometric synthetic aperture for three-dimensional label-free microscopy to eradicate the consequences of doubtful information. Cong et al. [35] worked on Spatial and Angular correlations with deep efficient transformers and demonstrates strong resistance to disparity fluctuations. Lu et al. [36] identified an ideal solution of iterative reconstruction of low dose CT based on differential sparse. Zhuang et al. [37] also handled large CT image sequences in mobile telemedicine networks. Wang et al. [38] signifies universal estimation method based on 3D image technology. Wang et al. [39] worked on modeling method and performance study of a task offloading scheme in MEC system. Li et al. [40] expanded the idea of composite fringe projection with 3D shaped measurement.

In 1982, Claudi Alsina and Janos Aczel presented an excellent hypothesis for aggregating mathematical models consisting of AA operational tools. Butnariu and Klement [41] also handled computational data and its components by utilizing the modifications of the AA operational tools. In 2000, Yager [42] introduced an excellent model for aggregating PA AO, which is capable of reducing the adverse consequences of insufficient data. Xu and Yager [43] developed an excellent structure of the PG aggregation operator which is used to overcome the complexity of fuzziness. In 1950, Bonferroni [44] invented the novel concept of a BM operator, which can consider the correspondence involving two aspects by using different frameworks. Jiang et al. [45] investigated a list of PAOs for IFSs to overcome the complexity of fuzziness. Ates and Akay [46] established a particular solution of PFSs for managing MADM issues by utilizing the fundamental operations of the BM operator. Different scholars explored the significance of PBM operators and developed a variety of methods for interpreting information using various operators [47,48,49,50,51].

The following description of the fundamental goals of this article originated from the above discussions:

  • The PFS is a useful mathematical tool for expressing imprecise and ambiguous information and also a feasible development of FS, IFS, and PyFS, which includes data appropriately. The PFS reduces the information loss as compared to IFS and PyFS due to the incorporation of abstinence value.

  • The PBM is a crucial generalization of the PA operator, which is capable of reducing the adverse consequences of insufficient data, and the BM operator can consider the relationship among attributed values.

  • To solve the MADM difficulties by applying our suggested methodologies, such as the PFAAPBM operator, PFAAWPBM operator, PFAAPGBM operator, and PFAAWGPBM operator which are all helpful for the selection of a competent research scientist.

  • To show the higher level of accuracy and proficiency of the derived information, we utilize several real-world scenarios for the comparisons of derived work with various current or prevailing operators.

The recently presented article can be classified into the following sections: In Section “Preliminaries”, we examine the mathematical concept of PFVs and some of their specific operations. We also describe some of the fundamental operations of Aczel-Alsina tools based on the PFVs. In Section “Some picture fuzzy Aczel-Alsina power Bonferroni (PFAAPB) aggregation operators”, we have extended the novel idea of the PBM operator and developed a few AOs, such as the PFAAPBM operator, PFAAWPBM operator, PFAAPGBM operator, and PFAAWGPBM operator by utilizing the Aczel-Alsina (AA) operational principles of PFS. The evaluation of the provided data by the decision-makers using an appropriate MADM approach is described in Section “Assessment of a MADM technique based on PFAAWPBM and PFAAWGPBM operators”. Furthermore, we assess our suggested techniques, and a practical example has been applied to choose appropriate applicants for the position of research scientist. In Section “Assessment of a MADM technique based on PFAAWPBM and PFAAWGPBM operators”, we compared a few of our suggested methodologies with other prevailing methods to determine the efficiency and reliability of our suggested strategies. In Section “Conclusion”, we provided a summary of the whole article.

Preliminaries

We first investigate the suggestions for reliable applications of IFS, PFS, Aczel-Alsina operational laws, and power AOs. Throughout the whole article, we used the symbol \(U\) as a universal set.

Definition 1

[10] An IFS C on the finite universe U can be defined as

$${\text{C}}=\left\{\left(w,{{\mathcalligra{m}}}_{{\text{C}}}\left(w\right), {\mathcalligra{n}}_{{\text{C}}}\left(w\right)\right)|w\in U\right\}$$
(1)

where \({{\mathcalligra{m}}}_{{\text{C}}}\left(w\right): U\to [\mathrm{0,1}]\) denote the membership value (MV) of the element \(w\in U\) to the set \({\text{C}}\), \({\mathcalligra{n}}_{{\text{C}}}\left(w\right): U\to [\mathrm{0,1}]\) denote the non-membership value (NMV) of \(w\in U\) to \({\text{C}}\) that satisfy such condition \(0\le {{\mathcalligra{m}}}_{{\text{C}}}\left(w\right)+{\mathcalligra{n}}_{{\text{C}}}\left(w\right)\le 1\) and \({N}_{{\text{C}}}\left(w\right)=\left(1-({{\mathcalligra{m}}}_{{\text{C}}}\left(w\right)+{\mathcalligra{n}}_{{\text{C}}}\left(w\right)\right)\) indicating the hesitancy value (HV) of the element to \({\text{C}}\). In addition, the duplet \(\left({{\mathcalligra{m}}}_{{\text{C}}}\left(w\right), {\mathcalligra{n}}_{{\text{C}}}\left(w\right)\right)\) is known as an Intuitionistic fuzzy value (IFV) which is denoted as \(b=\left({\mathcalligra{m}}, {\mathcalligra{n}}\right).\)

Definition 2

[52] A PFS C on the finite universe U can be defined as

$${\text{C}}=\left\{\left(w,{{\mathcalligra{m}}}_{{\text{C}}}\left(w\right), {\mathcalligra{a}}_{{\text{C}}}\left(w\right), {\mathcalligra{n}}_{{\text{C}}}\left(w\right)\right)|w\in U\right\}$$
(2)

where \({{\mathcalligra{m}}}_{{\text{C}}}\left(w\right): U\to [\mathrm{0,1}]\) denote the MV of the element \(w\in U\) to the set \({\text{C}}\), \({\mathcalligra{a}}_{{\text{C}}}\left(w\right): U\to [\mathrm{0,1}]\) denote the abstinence value (AV) of \(w\in U\) to \({\text{C}}\), \({\mathcalligra{n}}_{{\text{C}}}\left(w\right): U\to [\mathrm{0,1}]\) denote the NMV of to \({\text{C}}\) that satisfy such condition \(0\le {{\mathcalligra{m}}}_{{\text{C}}}\left(w\right)+{\mathcalligra{a}}_{{\text{C}}}\left(w\right)+{\mathcalligra{n}}_{{\text{C}}}\left(w\right)\le 1\) and \({N}_{{\text{C}}}\left(w\right)=\left(1-({{\mathcalligra{m}}}_{{\text{C}}}\left(w\right)+{\mathcalligra{a}}_{{\text{C}}}\left(w\right)+{\mathcalligra{n}}_{{\text{C}}}\left(w\right)\right)\) Indicating the Refusal value (RV) of the element \(w\in U\) to \({\text{C}}\). In addition, a triplet \(\left({{\mathcalligra{m}}}_{{\text{C}}}\left(w\right), {\mathcalligra{a}}_{{\text{C}}}\left(w\right), {\mathcalligra{n}}_{{\text{C}}}\left(w\right)\right)\) is known as the picture fuzzy value (PFV), which is denoted as \(b=\left({\mathcalligra{m}}, {\mathcalligra{a}}, {\mathcalligra{n}}\right)\).

Definition 3

[52] Let \(b=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{\text{C}}}\left(w\right), {\mathcalligra{a}}_{{\text{C}}}\left(w\right),\\ {\mathcalligra{n}}_{{\text{C}}}\left(w\right)\end{array}\right), {b}_{1}=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{1}}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{1}}\left(w\right),\\ {\mathcalligra{n}}_{{{\text{C}}}_{1}}\left(w\right)\end{array}\right),\) and \({b}_{2}=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{2}}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{2}}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{2}}\left(w\right)\end{array}\right)\) be any three PFVs. Then

  1. 1.

    \({b}_{1}\subseteq {b}_{2}\) iff \({{\mathcalligra{m}}}_{{{\text{C}}}_{1}}\left(w\right)\le {{\mathcalligra{m}}}_{{{\text{C}}}_{2}}, {\mathcalligra{a}}_{{{\text{C}}}_{1}}\ge {\mathcalligra{a}}_{{{\text{C}}}_{2}},\) and \({\mathcalligra{n}}_{{{\text{C}}}_{1}}\ge {\mathcalligra{n}}_{{{\text{C}}}_{2}}\).

  2. 2.

    \({b}_{1}= {b}_{2} {\text{iff}} {b}_{1}\subseteq {b}_{2} {\text{and}} {b}_{1}\subseteq {b}_{2}\)

  3. 3.

    \({b}_{1}\cap {b}_{2}=\big(min\left\{{{\mathcalligra{m}}}_{{{\text{C}}}_{1}}, {{\mathcalligra{m}}}_{{{\text{C}}}_{2}}\right\},{max}\left\{{\mathcalligra{a}}_{{{\text{C}}}_{1}}, {\mathcalligra{a}}_{{{\text{C}}}_{2}}\right\}, max\big\{{\mathcalligra{n}}_{{{\text{C}}}_{1}}, {\mathcalligra{n}}_{{{\text{C}}}_{2}}\big\}\big)\)

  4. 4.

    \({b}_{1}\cup {b}_{2}=\big(max\left\{{{\mathcalligra{m}}}_{{{\text{C}}}_{1}}, {{\mathcalligra{m}}}_{{{\text{C}}}_{2}}\right\},min\left\{{\mathcalligra{a}}_{{{\text{C}}}_{1}}, {\mathcalligra{a}}_{{{\text{C}}}_{2}}\right\}, min\big\{{\mathcalligra{n}}_{{{\text{C}}}_{1}}, {\mathcalligra{n}}_{{{\text{C}}}_{2}}\big\}\big)\)

  5. 5.

    \({b}^{c}=\left({\mathcalligra{n}}_{{\text{C}}}\left(w\right), {\mathcalligra{a}}_{{\text{C}}}\left(w\right), {{\mathcalligra{m}}}_{{\text{C}}}\left(w\right)\right)\)

Definition 4

[53] Let \(b=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{\text{C}}}\left(w\right), {\mathcalligra{a}}_{{\text{C}}}\left(w\right), \\ {\mathcalligra{n}}_{{\text{C}}}\left(w\right)\end{array}\right), {b}_{1}=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{1}}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{1}}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{1}}\left(w\right)\end{array}\right),\) and \({b}_{2}=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{2}}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{2}}\left(w\right),\\ {\mathcalligra{n}}_{{{\text{C}}}_{2}}\left(w\right)\end{array}\right)\) be any three PFVs with \({\mathcalligra{o}}\ge 1\) and \(\lambda >0.\) Then Aczel-Alsina (AA) operations rules are

  1. 1.

    \({b}_{1}\oplus{b}_{2}=\left(\begin{array}{c}\left(1-{e}^{-{\left({\left(-ln\left(1-{{\mathcalligra{m}}}_{{b}_{1}}\right)\right)}^{\mathcalligra{o}}+{\left(-ln\left(1-{{\mathcalligra{m}}}_{{b}_{2}}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right),\\ \left({e}^{-{\left({\left(-ln{\mathcalligra{a}}_{{b}_{1}}\right)}^{\mathcalligra{o}}+{\left(-ln{\mathcalligra{a}}_{{b}_{2}}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right),\\ \left({e}^{-{\left({\left(-ln{\mathcalligra{n}}_{{b}_{1}}\right)}^{\mathcalligra{o}}+{\left(-ln{\mathcalligra{n}}_{{b}_{2}}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right)\end{array}\right)\)

  2. 2.

    \({b}_{1}\otimes{b}_{2}=\left(\begin{array}{c}\left({e}^{-{\left({\left(-ln{{\mathcalligra{m}}}_{{b}_{1}}\right)}^{\mathcalligra{o}}+{\left(-ln{{\mathcalligra{m}}}_{{b}_{2}}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right),\\ \left(1-{e}^{-{\left({\left(-ln\left(1-{\mathcalligra{a}}_{{b}_{1}}\right)\right)}^{\mathcalligra{o}}+{\left(-ln\left(1-{\mathcalligra{a}}_{{b}_{2}}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right),\\ \left(1-{e}^{-{\left({\left(-ln\left(1-{\mathcalligra{n}}_{{b}_{1}}\right)\right)}^{\mathcalligra{o}}+{\left(-ln\left(1-{\mathcalligra{n}}_{{b}_{2}}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right)\end{array}\right)\)

  3. 3.

    \(\lambda b=\left(\begin{array}{c}\left(1-{e}^{-{\left(\lambda {\left(-ln\left(1-{{\mathcalligra{m}}}_{b}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right),\\ \left({e}^{-{\left(\lambda {\left(-ln{\mathcalligra{a}}_{b}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right), \left({e}^{-{\left(\lambda {\left(-ln{\mathcalligra{n}}_{b}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right)\end{array}\right)\)

  4. 4.

    \({b}^{\lambda }=\left(\begin{array}{c}\left({e}^{-{\left(\lambda {\left(-ln{{\mathcalligra{m}}}_{b}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right),\left(1-{e}^{-{\left(\lambda {\left(-ln\left(1-{\mathcalligra{a}}_{b}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right),\\ \left(1-{e}^{-{\left(\lambda {\left(-ln\left(1-{\mathcalligra{n}}_{b}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right)\end{array}\right)\)

Definition 5

[52] Let \(b=\left({{\mathcalligra{m}}}_{{\text{C}}}\left(w\right), {\mathcalligra{a}}_{{\text{C}}}\left(w\right), {\mathcalligra{n}}_{{\text{C}}}\left(w\right)\right)\) be the PFV. Then the score function \(S\) of \(b\) is.

$$S\left(b\right)={{\mathcalligra{m}}}_{{\text{C}}}-{\mathcalligra{a}}_{{\text{C}}}-{\mathcalligra{n}}_{{\text{C}}}, S\left(b\right)\in \left[\mathrm{0,1}\right]$$
(3)

Definition 6

[42] The power average function was presented by Yager in 2001 for identifying the PA operator using a collection of FVs . Then we have

(4)

where and \(S\left({b}_{\sigma },{b}_{\theta } \right)\) describing the support value of \({b}_{\sigma }\) and \({b}_{\theta }.\)

Definition 7

[43] The power geometric function was presented by Xu and Yager in 2010 for identifying the PG operator using a collection of FVs . Then we have

(5)

where and \(S\left({b}_{\sigma },{b}_{\theta } \right)\) describing the support value of \({b}_{\sigma }\) and \({b}_{\theta }.\)

Some picture fuzzy Aczel-Alsina power Bonferroni (PFAAPB) aggregation operators

In this section, we introduced PFPBAOs by using Aczel-Alsina operational tools. Furthermore, we examine the PFWPBM operator and PFWGPBM operator by using Aczel-Alsina operational tools with corresponding weight vectors \(k={\left({k}_{1},{k}_{2}, . . . ,{k}_{n} \right)}^{T}\) that satisfies such condition \(0\le {k}_{\sigma }\le 1, \left(\sigma =1, 2, 3,\dots , n\right)\) and analyze a few enticing characteristics along with the particular applications of the suggested operators.

The picture fuzzy Aczel-Alsina power Bonferroni mean (PFAAPBM) operator

Definition 8

Let \({b}_{\sigma }=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma =1, 2, 3\dots n; \lambda ,{\mathcalligra{o}}=1, 2, \dots n\right)\) be the collection of PFVs, then applying distance formula \(D\left({b}_{\sigma \lambda }, {b}_{\sigma {\mathcalligra{o}}}\right)\) for PFVs are

$$ \begin{aligned}& D\left({b}_{\sigma \lambda }, {b}_{\sigma {\mathcalligra{o}}}\right)\\ &\quad =\frac{1}{n}\sum_{\sigma , \lambda ,{\mathcalligra{o}}=1}^{n}\left(\left|{{\mathcalligra{m}}}_{\sigma \lambda }-{{\mathcalligra{m}}}_{\sigma {\mathcalligra{o}}}\right|+\left|{\mathcalligra{a}}_{\sigma \lambda }-{\mathcalligra{a}}_{\sigma {\mathcalligra{o}}}\right|+\left|{\mathcalligra{n}}_{\sigma \lambda }-{\mathcalligra{n}}_{\sigma {\mathcalligra{o}}}\right|\right)\end{aligned}$$
(6)

Definition 9

Let \({b}_{\sigma }=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma , \lambda =1, 2, 3\dots n\right)\) be the collection of PFVs, then the PFAAPBM operator defines a mapping PFAAPBM: as follows

(7)

where .

Theorem 1

Let \({b}_{\sigma }=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma , \lambda =1, 2, 3\dots n\right)\) be the collection of PFVs, then the PFAAPBM operator defines a mapping PFAAPBM: , and then we have

(8)

Proof

Let \({T}_{\mathfrak{h}}=\frac{n\left(L\left({b}_{\mathfrak{h}}\right)+1\right)}{\sum_{P=1}^{n}\left(L\left({b}_{P}\right)+1\right)}, \mathfrak{h}=\left(1, 2, \dots ,n\right)\), then

First, we find \({T}_{\sigma }.{b}_{\sigma }\) and \({T}_{\lambda }{.b}_{\lambda }\), then

$${T}_{\sigma }{b}_{\sigma }=\left(\begin{array}{c}1-{e}^{-{\left({T}_{\sigma }{\left(-l\tilde{n} \left(1-{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}, {e}^{-{\left({T}_{\sigma }{\left(-l\tilde{n} {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}} }, {e}^{-{\left({T}_{\sigma }{\left(-l\tilde{n} {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}} } \\ \end{array}\right)$$
$${T}_{\lambda }{b}_{\lambda }=\left(\begin{array}{c}1-{e}^{-{\left({T}_{\lambda }{\left(-l\tilde{n} \left(1-{{\mathcalligra{m}}}_{{{\text{C}}}_{\lambda }}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}, {e}^{-{\left({T}_{\lambda }{\left(-l\tilde{n} {\mathcalligra{a}}_{{{\text{C}}}_{\lambda }}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}} }, {e}^{-{\left({T}_{\lambda }{\left(-l\tilde{n} {\mathcalligra{n}}_{{{\text{C}}}_{\lambda }}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}} } \\ \end{array}\right)$$

To find then

Let

Next, we determine

Theorem 2

Let \({b}_{\sigma }=b=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma =1, 2, 3\dots n\right)\) be the set of all the same PFVs, then the accumulative findings of the PFAAPBM operator are particularized as

$$PFAAPBM\left({b}_{1}, {b}_{2}, \dots , {b}_{n}\right)=b$$
(9)

Proof

Since, \({b}_{\sigma }=b\), \(\left(\sigma =1, 2, 3,\dots , n\right)\), then

Theorem 3

Let \({b}_{\sigma }{\prime}\) be the permutation of \({b}_{\sigma } \left(\sigma =1, 2, 3,\dots , n\right),\) then

$$PFAAPBM\left({b}_{1}{\prime}, {b}_{2}{\prime}, \dots , {b}_{n}{\prime}\right)=PFAAPBM\left({b}_{1}, {b}_{2}, \dots , {b}_{n}\right)$$
(10)

Proof

Using Definition 9, then

and

Since

Hence, \(PFAAPBM\left({b}_{1}{\prime}, {b}_{2}{\prime}, \dots , {b}_{n}{\prime}\right)=PFAAPBM\left({b}_{1}, {b}_{2}, \dots , {b}_{n}\right)\).

Definition 10

Let \({b}_{\sigma }=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma , \lambda =1, 2, 3\dots n\right)\) be the collection of PFVs, then the PFAAWPBM operator defines a mapping PFAAWPBM: as follows

(11)

where and \(k={\left({k}_{1},{k}_{2}, . . . ,{k}_{n} \right)}^{T}\) denote the weight vector which satisfies such condition \(0\le {k}_{\sigma }\le 1, \left(\sigma =1, 2, 3,\dots , n\right)\) and \(\sum_{\sigma =1}^{n}{k}_{\sigma }=1.\)

Example 1

Let \({b}_{1}=\left(0.03, 0.04, 0.05\right)\), \({b}_{2}=\left(0.06, 0.07, 0.08\right)\), \({b}_{3}=\left(0.09, 0.01, 0.02\right)\) and \({b}_{4}=\left(0.23, 0.35, 0.46\right)\) are four PFVs defined with weight vectors \(\left(0.29, 0.13, 0.34, 0.24\right).\) Taking parametric values , and \({{\ddot{\bar{U}}}}=3\) to determine the findings for the PFAAWPBM operator and show their significant behavior under the framework of PFVs.

In the first step, to calculate

$$\begin{aligned}&Sp\left(\mathrm{1,2}\right)=0.955, Sp\left(\mathrm{1,3}\right)=0.940, Sp\left(\mathrm{1,4}\right)=0.540,\\ \quad& Sp\left(\mathrm{2,3}\right)=0.925, Sp\left(\mathrm{2,4}\right)=0.585, Sp\left(\mathrm{3,4}\right)=0.540,\end{aligned}$$

In the second step, to compute \(L\left({b}_{\sigma }\right)=\sum_{\begin{array}{c}\sigma =1\\ \sigma \ne \lambda \end{array}}^{n}\acute{\text{S}}pt\left({b}_{\sigma }, {b}_{\lambda }\right)\)

$$L_{1}=2.435, L_{2}=2.465, L_{3}=2.405, L_{4}=1.665,$$

In the third step, to determine the proximal weight values \({T}_{\sigma }\)

$${T}_{\sigma }=\frac{{k}_{\sigma }\left(L\left({b}_{\sigma }\right)+1\right)}{\sum_{P=1}^{n}{k}_{P}\left(L\left({b}_{P}\right)+1\right)}$$
$${T}_{1}=0.307, {T}_{2}=0.139, {T}_{3}=0.357, {T}_{4}=0.197,$$

Finally, we have to find PFAAWPBM then we can obtain the following result

$$PFAAWPBM\left({b}_{1}, {b}_{2}, \dots , {b}_{n}\right)=\left(0.0735, 0.1923, 0.2384\right)$$

Theorem 4

Let \({b}_{\sigma }=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma , \lambda =1, 2, 3\dots n\right)\) be the collection of PFVs, then the PFAAWPBM operator defines a mapping PFAAWPBM: , and then we have

(12)

The picture fuzzy Aczel-Alsina power geometric Bonferroni mean (PFAAPGBM) operator

Definition 11

Let \({b}_{\sigma }=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma , \lambda =1, 2, 3\dots n\right)\) be the collection of PFVs, then the PFAAPGBM operator defines a mapping PFAAPGBM: as follows

(13)

where .

Theorem 5

Let \({b}_{\sigma }=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right)_{\phantom{\displaystyle\sum_{y}}}, \left(\sigma , \lambda =1, 2, 3\dots n\right)\) be the collection of PFVs, then the PFAAPGBM operator defines a mapping PFAAPGBM: , and then we have:

(14)

Proof

Let \({T}_{\mathfrak{h}}=\frac{n\left(L\left({b}_{\mathfrak{h}}\right)+1\right)}{\sum_{P=1}^{n}\left(L\left({b}_{P}\right)+1\right)}, \mathfrak{h}=\left(1, 2, \dots ,n\right)\), then

Initially, we find \({T}_{\sigma }.{b}_{\sigma }\) and \({T}_{\lambda }{.b}_{\lambda }\), then

$$\begin{aligned}{b}_{\sigma }^{{T}_{\sigma }}=\left(\begin{array}{c}{e}^{-{\left({T}_{\sigma }{\left(-l\tilde{n} {{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}} }, 1-{e}^{-{\left({T}_{\sigma }{\left(-l\tilde{n} \left(1-{\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}, 1-{e}^{-{\left({T}_{\sigma }{\left(-l\tilde{n} \left(1-{\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}} \\ \end{array}\right),\end{aligned}$$
$$\begin{aligned} {b}_{\lambda }^{{T}_{\lambda }}=\left(\begin{array}{c}{e}^{-{\left({T}_{\lambda }{\left(-l\tilde{n} {{\mathcalligra{m}}}_{{{\text{C}}}_{\lambda }}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}} }, 1-{e}^{-{\left({T}_{\lambda }{\left(-l\tilde{n} \left(1-{\mathcalligra{a}}_{{{\text{C}}}_{\lambda }}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}} , 1-{e}^{-{\left({T}_{\lambda }{\left(-l\tilde{n} \left(1-{\mathcalligra{n}}_{{{\text{C}}}_{\lambda }}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}} \end{array}\right),\end{aligned}$$
$${{\ddot{\bar{U}}}}{b}_{\lambda }^{{T}_{\lambda }}=\left(\begin{array}{c}{1-e}^{-{\left({{\ddot{\bar{U}}}}{\left(-l\tilde{n} \left(1-{e}^{-{\left({T}_{\lambda }{\left(-l\tilde{n} {{\mathcalligra{m}}}_{{{\text{C}}}_{\lambda }}\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}},{e}^{-{\left({{\ddot{\bar{U}}}}{\left(-{\text{ln}}\left(1-{e}^{-{\left({T}_{\lambda }{\left(-l\tilde{n} \left(1-{\mathcalligra{a}}_{{{\text{C}}}_{\lambda }}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}, \\ {e}^{-{\left({{\ddot{\bar{U}}}}{\left(-{\text{ln}}\left(1-{e}^{-{\left({T}_{\lambda }{\left(-l\tilde{n} \left(1-{\mathcalligra{n}}_{{{\text{C}}}_{\lambda }}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\right)\right)}^{\mathcalligra{o}}\right)}^{1/{\mathcalligra{o}}}}\end{array}\right),$$

To find then

Let

Next, we determine

Theorem 6

Let \({b}_{\sigma }=b=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma =1, 2, 3\dots n\right)\) be the set of all the same PFVs, then the accumulative findings of the PFAAPGBM operator are particularized as:

$$PFAAPGBM\left({b}_{1}, {b}_{2}, \dots , {b}_{n}\right)=b$$
(15)

Proof

The proof of Theorem 6 is similar to Theorem 2.

Theorem 7

Let \({b}_{\sigma }{\prime}\) be the permutation of \({b}_{\sigma } \left(\sigma =1, 2, 3,\dots , n\right),\) then

$$PFAAPGBM\left({b}_{1}{\prime}, {b}_{2}{\prime}, \dots , {b}_{n}{\prime}\right)=PFAAPBM\left({b}_{1}, {b}_{2}, \dots , {b}_{n}\right)$$
(16)

Proof:

The proof of Theorem \(7\) is similar as Theorem \(3\).

Definition 12

Let \({b}_{\sigma }=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma , \lambda =1, 2, 3\dots n\right)\) be the collection of PFVs, then the PFAAWGPBM operator defines a mapping PFAAWGPBM: as follows:

(17)

where and \(k={\left({k}_{1},{k}_{2}, . . . ,{k}_{n} \right)}^{T}\) denote the weight vector which satisfies such condition \(0\le {k}_{\sigma }\le 1, \left(\sigma =1, 2, 3,\dots , n\right)\) and \(\sum_{\sigma =1}^{n}{k}_{\sigma }=1.\)

Example 2

Let \({b}_{1}=\left(0.03, 0.04, 0.05\right)\), \({b}_{2}=\left(0.06, 0.07, 0.08\right)\), \({b}_{3}=\left(0.09, 0.01, 0.02\right)\) and \({b}_{4}=\left(0.23, 0.35, 0.46\right)\) are four PFVs with corresponding weight vectors \(\left(0.29, 0.13, 0.34, 0.24\right).\) By considering parametric values , and \({{\ddot{\bar{U}}}}=3\) to evaluate the findings for the PFAAWGPBM operator and shows their significant nature under the framework of PFVs.

In the first step, to calculate

$$\begin{aligned}& Sp\left(\mathrm{1,2}\right)=0.955, Sp\left(\mathrm{1,3}\right)=0.940, Sp\left(\mathrm{1,4}\right)=0.540,\\ & Sp\left(\mathrm{2,3}\right)=0.925, Sp\left(\mathrm{2,4}\right)=0.585, Sp\left(\mathrm{3,4}\right)=0.540,\end{aligned}$$

In the second step, to compute

$$L_{1}=2.435, L_{2}=2.465, L_{3}=2.405, L_{4}=1.665,$$

In the third step, to determine the proximal weight values \({T}_{\sigma }\)

$${T}_{\sigma }=\frac{{k}_{\sigma }\left(L\left({b}_{\sigma }\right)+1\right)}{\sum_{P=1}^{n}{k}_{P}\left(L\left({b}_{P}\right)+1\right)}$$
$$\begin{aligned} &{T}_{1}=0.307, {T}_{2}=0.139,\\ & {T}_{3}=0.357, {T}_{4}=0.197, \end{aligned}$$

Finally, we have to find PFAAWGPBM then we can obtain the following result

$$PFAAWGPBM\left({b}_{1}, {b}_{2}, \dots , {b}_{n}\right)=\left(0.2878, 0.0531, 0.0824\right)$$

Theorem 8

Let \({b}_{\sigma }=\left(\begin{array}{c}{{\mathcalligra{m}}}_{{{\text{C}}}_{\sigma }}\left(w\right), {\mathcalligra{a}}_{{{\text{C}}}_{\sigma }}\left(w\right), \\ {\mathcalligra{n}}_{{{\text{C}}}_{\sigma }}\left(w\right)\end{array}\right), \left(\sigma , \lambda =1, 2, 3\dots n\right)\) be the collection of PFVs, then the PFAAWGPBM operator defines a mapping PFAAWGPBM: , and then we have:

(18)

Assessment of a MADM technique based on PFAAWPBM and PFAAWGPBM operators

In this section, we shall provide an algorithm to determine the preferable alternative by using the MADM strategy based on the PFAAWPBM operator and the PFAAWGPBM operator. Addressing MADM issues with PF information, let are considered a unique combination of alternative \({R}_{\mu },\) \({\psi }_{\nu }=\left\{{\psi }_{1}, {\psi }_{2}, . . .,{\psi }_{\pi }\right\}\,\left(\nu =1, 2, . ..,\pi \right)\) are described as a specific set of attribute \({\psi }_{\nu }\) and \({k}_{\sigma }={\left({k}_{1},{k}_{2}, . . . ,{k}_{\pi } \right)}^{T}\left(\sigma =1, 2, . ..,\pi \right)\) represents the weight vectors of the attribute \({\psi }_{\nu }\) where \({k}_{\sigma }\in \left[0, 1\right], \left(\sigma =1, 2, . ..,\pi \right)\) and \(\sum_{\sigma =1}^{\pi }{k}_{\sigma }=1.\) Let be a PF decision matrix in which \({{\mathcalligra{m}}}_{{{\text{C}}}_{\mu \nu }}\) indicating the MV, \({\mathcalligra{a}}_{{{\text{C}}}_{\mu \nu }}\) indicating the AV, and \({\mathcalligra{n}}_{{{\text{C}}}_{\mu \nu }}\) representing the NMV which satisfies the condition \({{\mathcalligra{m}}}_{{{\text{C}}}_{\mu \nu }}+{\mathcalligra{a}}_{{{\text{C}}}_{\mu \nu }}+{\mathcalligra{n}}_{{{\text{C}}}_{\mu \nu }}\le 1\) for

Now, considering our recommended operator for the MADM problem based on the PFVs, we build the following methodology for determining the best alternative.


Step 1: To transform into the PF decision matrix by using the following technique

$$ \begin{aligned}{O}_{\mu \nu }&=\left({{\mathcalligra{m}}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{a}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{n}}_{{{\text{C}}}_{\mu \nu }}\right)\\ &=\left\{\begin{array}{cc}\left({{\mathcalligra{m}}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{a}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{n}}_{{{\text{C}}}_{\mu \nu }}\right)& \mathrm{if }{\psi }_{\nu }\mathrm{ are benefit type}\\ \left({\mathcalligra{n}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{a}}_{{{\text{C}}}_{\mu \nu }}, {{\mathcalligra{m}}}_{{{\text{C}}}_{\mu \nu }}\right)& \mathrm{if }{\psi }_{\nu }\mathrm{ are cost type}\end{array}\right. \end{aligned}$$

Step 2: Based on the mathematical estimation of support value by applying where

$$ \begin{aligned}D\left({O}_{\mu \nu }, {O}_{\mu \omega } \right)=\frac{1}{n}\sum_{\mu , \nu , \omega =1}^{n}\left(\left|{{\mathcalligra{m}}}_{\mu \nu }-{{\mathcalligra{m}}}_{\mu \omega }\right|+\left|{\mathcalligra{a}}_{\mu \nu }-{\mathcalligra{a}}_{\mu \omega }\right|+\left|{\mathcalligra{n}}_{\mu \nu }-{\mathcalligra{n}}_{\mu \omega }\right|\right) \end{aligned}$$

Step 3: To compute the supported sum \(L\left({O}_{\mu \nu }\right)\) of PFVs \({O}_{\mu \nu }\) by applying the corresponding formulation described in this form

Step 4: Using the following Eq. (19) to determine the proximal weights \({T}_{\mu \nu }\) corresponding to PFVs \({\overleftarrow{O}}_{\mu \nu }\), then we have

(19)

where \({T}_{\mu \nu }>0\) such that \(\sum_{\nu =1}^{\pi }{k}_{\mu \nu }=1.\)

Step 5: This step involves aggregating the desired result of the alternatives by applying the PFAAWPBM operator and the PFAAWGPBM operator as follows

Step 6: Using the following scoring formula to determine the ranking of alternatives based on the compiled data obtained in step 5.

$$ \begin{aligned} & Score\left({O}_{\mu }\right)={{\mathcalligra{m}}}_{\mu }-{\mathcalligra{a}}_{\mu }-{\mathcalligra{n}}_{\mu }, \end{aligned}$$

Step 7: To determine all the possibilities and determine the most valuable choice based on the score function

Step 8: End.

Numerical illustration

For the advancement of modern scientific thought, research is an indispensable process. Many talented researchers work in a wide variety of particular fields, including mathematical information, environmental studies, biochemistry, computer programming, pharmaceuticals, and the history of politics, etc. The vast majority of the researchers are professionals in their field of expertise after the finalization of their Ph.D. degree. The most effective capabilities of a competent researcher are modesty, building a social network, working hard, and having good writing skills. In this numerical example, the application of the proposed methodology is used for the selection of competent researchers in a public sector university according to the university’s recruitment guidance. Assume that a university that has vacant positions and wants to hire a competent researcher for students. After the initial assessment policy, four potential candidates \({R}_{1}, {R}_{2}, {R}_{3},\) and \({R}_{4}\) were chosen for further assessment. To make the appropriate decision, you have to consider the four characteristics \({\psi }_{1}, {\psi }_{2}, {\psi }_{3},\) and \({\psi }_{4}\) for the selection of competent researchers as follows

  • \({\psi }_{1}\): Highest number of research papers having good impact factor.

  • \({\psi }_{2}:\) Research and teaching experience in any well-known institution.

  • \({\psi }_{3}:\) Analytical ability and communication skills.

  • \({\psi }_{4}\): Creativity and collaborative spirit.

The corresponding weight vectors \(k={\left(0.29, 0.13, 0.34, 0.24\right)}^{T}\) are used to evaluate the ranking results of alternatives \({R}_{1}, {R}_{2}, {R}_{3},\) and \({R}_{4}\) based on the specified criteria \({\psi }_{1}, {\psi }_{2}, {\psi }_{3},\) and \({\psi }_{4}\) under the environment of PFVs. The decision values demonstrated by PFVs and the decision matrix are shown in Table 1.

Table 1 The PF decision matrix
Full size table

A novel approach based on PFAAWPBM and PFAAWGPBM operators

Initially, we use our proposed AO such as the PFAAWPBM operator to cope with MADM issues and choose the best research scientist (alternative) in the university by using PFVs. The following algorithm is described as follows:


Step 1: To transform into the PF decision matrix by using the following technique

$$ \begin{aligned} {O}_{\mu \nu }&=\left({{\mathcalligra{m}}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{a}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{n}}_{{{\text{C}}}_{\mu \nu }}\right)\\ & =\left\{\begin{array}{cc}\left({{\mathcalligra{m}}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{a}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{n}}_{{{\text{C}}}_{\mu \nu }}\right)& \mathrm{if }{\psi }_{\nu }\mathrm{ are benefit type}\\ \left({\mathcalligra{n}}_{{{\text{C}}}_{\mu \nu }}, {\mathcalligra{a}}_{{{\text{C}}}_{\mu \nu }}, {{\mathcalligra{m}}}_{{{\text{C}}}_{\mu \nu }}\right)& \mathrm{if }{\psi }_{\nu }\mathrm{ are cost type}\end{array}\right. \end{aligned}$$

Step 2: Based on the mathematical estimation of support value by applying then we have

$$\left(\begin{array}{c}{\mathsf{S}}_{\mathrm{11,12}}=0.740, {\mathsf{S}}_{\mathrm{11,13}}=0.760, {\mathsf{S}}_{\mathrm{11,14}}=0.830,\\ {\mathsf{S}}_{\mathrm{12,13}}=0.615{, \mathsf{S}}_{\mathrm{12,14}}=0.890, {\mathsf{S}}_{\mathrm{13,14}}=0.710,\\ {\mathsf{S}}_{\mathrm{21,22}}=0.695, {\mathsf{S}}_{\mathrm{21,23}}=0.940, {\mathsf{S}}_{\mathrm{21,24}}=0.945, \\ {\mathsf{S}}_{\mathrm{22,23}}=0.720{, \mathsf{S}}_{\mathrm{22,24}}=0.750, {\mathsf{S}}_{\mathrm{23,24}}=0.905,\\ {\mathsf{S}}_{\mathrm{31,32}}=0.610, {\mathsf{S}}_{\mathrm{31,33}}=0.945, {\mathsf{S}}_{\mathrm{31,34}}=0.785,\\ {\mathsf{S}}_{\mathrm{32,33}}=0.700{, \mathsf{S}}_{\mathrm{32,34}}=0.765, {\mathsf{S}}_{\mathrm{33,34}}=0.760,\\ {\mathsf{S}}_{\mathrm{41,42}}=0.725, {\mathsf{S}}_{\mathrm{41,43}}=0.620, {\mathsf{S}}_{\mathrm{41,44}}=0.890,\\ {\mathsf{S}}_{\mathrm{42,43}}=0.785{, \mathsf{S}}_{\mathrm{42,4}4}=0.625, {\mathsf{S}}_{\mathrm{43,44}}=0.520,\end{array}\right)$$

Step 3: To compute the supported sum \(L\left({O}_{\mu \nu }\right)\) of PFVs \({O}_{\mu \nu }\) by using , then we can obtain

$$\left(\begin{array}{c}{L}_{11}=2.330, {L}_{12}=2.245,{L}_{13}=2.085, {L}_{14}=2.430,\\ {L}_{21}=2.580, {L}_{22}=2.165,{L}_{23}=2.565, {L}_{24}=2.600,\\ {L}_{31}=2.340, {L}_{32}=2.075,{L}_{33}=2.405, {L}_{34}=2.310,\\ {L}_{41}=2.235, {L}_{42}=2.135,{L}_{43}=1.925, {L}_{44}=2.035,\end{array}\right)$$

Step 4: Using this formula \({T}_{\mu \nu }=\frac{n{k}_{\mu }\left(L\left({O}_{\mu \nu }\right)+1\right)}{\sum_{P=1}^{n}{k}_{P}\left(L\left({O}_{\mu P}\right)+1\right)}\) to determine the proximal weights \({T}_{\mu \nu }\) corresponding to PFVs \({O}_{\mu \nu }\) as follows

$$\left(\begin{array}{c}{T}_{11}=0.296=, {T}_{12}=0.129,{T}_{13}=0.322, {T}_{14}=0.253,\\ {T}_{21}=0.294, {T}_{22}=0.117,{T}_{23}=0.344, {T}_{24}=0.245,\\ {T}_{31}=0.292, {T}_{32}=0.120,{T}_{33}=0.349, {T}_{34}=0.239,\\ {T}_{41}=0.306, {T}_{42}=0.133,{T}_{43}=0.324, {T}_{44}=0.237,\end{array}\right)$$

Step 5: This step involves aggregating the desired result \({O}_{\mu } \left(\mu =1, 2, 3, 4\right)\) for the selection of the best research scientist by applying the PFAAWPBM operator and taking the supposed value for \({\mathcalligra{o}}=1,\) we can obtain the following result

$$ \begin{aligned} &{R}_{1}=\left(0.0880, 0.2194, 0.3590\right),\\ & {R}_{2}=\left(0.1141, 0.2516, 0.4509\right), \end{aligned}$$
$$ \begin{aligned} & {R}_{3}=\left(0.0779, 0.2193, 0.3824\right),\\ & {R}_{4}=\left(0.0952, 0.2493, 0.3066\right), \end{aligned}$$

Step 6: By using Definition 5 to find out the score values of \(\left({O}_{\mu }\right)\left(\mu =1, 2, 3, 4\right)\) and determine all the possibilities \({R}_{\mu }\left(\mu =1, 2, 3, 4\right)\) based on the aggregated result acquired in the previous step.

$$ \begin{aligned} &S\left({R}_{1}\right)=-0.4903, S\left({R}_{2}\right)=-0.5884,\\ &S\left({R}_{3}\right) =-0.5238, S\left({R}_{4}\right)=-0.4608 \end{aligned}$$

Step 7: Finally, we determine the best scientist researcher by using the score function \(Score\left({O}_{\mu }\right)\left(\mu =1, 2, 3, 4\right).\) From the above discussions, we see that the competent research scientist for the vacant post is \({R}_{4}\) which is helpful for students and builds a social network with others (Fig. 1).

Fig. 1
figure 1

Portrays the score values of \(S\left({O}_{\mu }\right)\) of the PFAAWPBM operator

Full size image

Now, applying the PFAAWGPBM operator for the selection of the best research scientist under the framework of PFVs and the following algorithm is described as follows:

Step 1: To find the support value by applying then we obtain

$$\left(\begin{array}{c}{\mathsf{S}}_{\mathrm{11,12}}=0.740, {\mathsf{S}}_{\mathrm{11,13}}=0.760, {\mathsf{S}}_{\mathrm{11,14}}=0.830,\\ {\mathsf{S}}_{\mathrm{12,13}}=0.615{, \mathsf{S}}_{\mathrm{12,14}}=0.890, {\mathsf{S}}_{\mathrm{13,14}}=0.710,\\ {\mathsf{S}}_{\mathrm{21,22}}=0.695, {\mathsf{S}}_{\mathrm{21,23}}=0.940, {\mathsf{S}}_{\mathrm{21,24}}=0.945, \\ {\mathsf{S}}_{\mathrm{22,23}}=0.720{, \mathsf{S}}_{\mathrm{22,24}}=0.750, {\mathsf{S}}_{\mathrm{23,24}}=0.905,\\ {\mathsf{S}}_{\mathrm{31,32}}=0.610, {\mathsf{S}}_{\mathrm{31,33}}=0.945, {\mathsf{S}}_{\mathrm{31,34}}=0.785,\\ {\mathsf{S}}_{\mathrm{32,33}}=0.700{, \mathsf{S}}_{\mathrm{32,34}}=0.765, {\mathsf{S}}_{\mathrm{33,34}}=0.760,\\ {\mathsf{S}}_{\mathrm{41,42}}=0.725, {\mathsf{S}}_{\mathrm{41,43}}=0.620, {\mathsf{S}}_{\mathrm{41,44}}=0.890,\\ {\mathsf{S}}_{\mathrm{42,43}}=0.785{, \mathsf{S}}_{\mathrm{42,44}}=0.625, {\mathsf{S}}_{\mathrm{43,44}}=0.520,\end{array}\right)$$

Step 2: To assess the sum of support value \(L\left({O}_{\mu \nu }\right)\) of PFVs \({O}_{\mu \nu }\) by using \(L\left({O}_{\mu \nu }\right)=\sum_{\begin{array}{c}\omega =1\\ \omega \ne \mu \end{array}}^{\pi }\acute{\text{S}}pt\left({O}_{\mu \nu }, {O}_{ \mu \omega } \right),\left(\mu =1, 2, 3, 4; \omega =1, 2, 3, 4\right)\), then we can obtain

$$\left(\begin{array}{c}{L}_{11}=2.330, {L}_{12}=2.245,{L}_{13}=2.085, {L}_{14}=2.430,\\ {L}_{21}=2.580, {L}_{22}=2.165,{L}_{23}=2.565, {L}_{24}=2.600,\\ {L}_{31}=2.340, {L}_{32}=2.075,{L}_{33}=2.405, {L}_{34}=2.310,\\ {L}_{41}=2.235, {L}_{42}=2.135,{L}_{43}=1.925, {L}_{44}=2.035,\end{array}\right)$$

Step 3: To calculate the proximal weight \({T}_{\mu \nu }\) by applying this formula \({T}_{\mu \nu }=\frac{n{k}_{\mu }\left(L\left({O}_{\mu \nu }\right)+1\right)}{\sum_{P=1}^{n}{k}_{P}\left(L\left({O}_{\mu P}\right)+1\right)},\) then we have

$$\left(\begin{array}{c}{T}_{11}=0.296=, {T}_{12}=0.129,{T}_{13}=0.322, {T}_{14}=0.253,\\ {T}_{21}=0.294, {T}_{22}=0.117,{T}_{23}=0.344, {T}_{24}=0.245,\\ {T}_{31}=0.292, {T}_{32}=0.120,{T}_{33}=0.349, {T}_{34}=0.239,\\ {T}_{41}=0.306, {T}_{42}=0.133,{T}_{43}=0.324, {T}_{44}=0.237,\end{array}\right)$$

Step 4: This step involves aggregating the required result \({O}_{\mu } \left(\mu =1, 2, 3, 4\right)\) for the selection of the best research scientist by applying the PFAAWGPBM operator and taking the supposed parametric value for \({\mathcalligra{o}}=1,\) we can have

$$\begin{aligned} & {R}_{1}=\left(0.1533, 0.1025, 0.2237\right),\\ & {R}_{2}=\left(0.2335, 0.1665, 0.3815\right),\end{aligned}$$
$$\begin{aligned} & {R}_{3}=\left(0.2168, 0.1672, 0.1915\right),\\ & {R}_{4}=\left(0.2228, 0.1423, 0.1953\right),\end{aligned}$$

Step 5: By using Definition 5 to determine the score values of \(\left({O}_{\mu }\right)\left(\mu =1, 2, 3, 4\right)\) of PFAAWGPBM operator and determine all the possibilities \({R}_{\mu }\left(\mu =1, 2, 3, 4\right).\)

$$ \begin{aligned}& S\left({R}_{1}\right)=-0.1729, S\left({R}_{2}\right)=-0.3145,\\ & S\left({R}_{3}\right)=-0.1418, S\left({R}_{4}\right)=-0.1148 \end{aligned}$$

Step 6: In the last step, we evaluate the best scientist researcher based on the score function \(Score\left({O}_{\mu }\right)\left(\mu =1, 2, 3, 4\right).\) In such scenarios (Fig. 2), we observe that the competent research scientist for the vacant post is \({R}_{4}\).

Fig. 2
figure 2

Portrays the score values of \(S\left({R}_{\mu }\right)\) of the PFAAWGPBM operator

Full size image

Impact of parameters on the results of our suggested approach

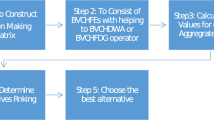
We analyze the ranking outcomes of alternatives based on our specified methodology by using different parametric measurements to demonstrate the impact of different parameter magnitudes. The ranking findings of the specified methodology on the PFAAWPBM operator and the PFAAWGPBM operator are provided in the following Tables 1 and 2 respectively. The visual representation of the PFAAWPBM operator and PFAAWGPBM operator are also shown in Figs. 3 and 4 respectively. We assign different parametric values , \(3\le {{\ddot{\bar{U}}}}\le 100\) and calculate the score values for these four alternatives \({R}_{1}, {R}_{2}, {R}_{3}, {R}_{4}\) for determining the ranking outcomes by using PFVs.

Table 2 Variations of parameters and \({{\ddot{\bar{U}}}}\) by applying the PFAAWPBM operator
Full size table
Table 3 Variations of parameters and \({{\ddot{\bar{U}}}}\) by applying the PFAAWGPBM operator
Full size table
Fig. 3
figure 3

Shows the variations of parameters and \({{\ddot{\bar{U}}}}\) by PFAAWPBM operator

Full size image
Fig. 4
figure 4

Shows the variations of parameters and \({{\ddot{\bar{U}}}}\) by PFAAWGPBM operator

Full size image

From Table 2, based on the PFAAWPBM operator, we can see that the scores of each alternative always remain the same when we use different parametric values as and the ranking order always remains the same \({R}_{4}>{R}_{1}>{R}_{3}>{R}_{2}.\) It means that the competent research scientist (alternative) for the vacant post is \({R}_{4}\).

According to Table 3, based on the PFAAWGPBM operator, we can observe that the scores of each alternative always remain the same when we use different parametric values as and the ranking order always remains the same \({R}_{4}>{R}_{3}>{R}_{1}>{R}_{2}.\) It means that the competent research scientist (alternative) for the vacant post is \({R}_{4}\).

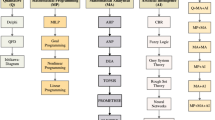
Comparative study

This section contrasts a few of our suggested methodologies with other prevailing methods to determine the feasibility and legitimacy of our suggested strategies. The other prevailing AOs, including the PF weighted average (PFWA) operator, was established by [20], the PFW geometric (PFWG) operator was diagnosed by [54], the PF Aczel-Alsina WA (PFAAWA) operator was introduced by [53], the PFAAWG operator was introduced by [55], the Hesitant PyF Hamacher WA (HPyFHWA) operator was described by [56], the HPyFHWG operator was developed by [56], the IFWA Heronian mean (IFWHM) operator was provided by [57], the IFWGHM operator was given by [58]. We performed each of the previously defined AOs to the PF decision matrix displayed in Table 3. The following Table 4 specifies the ranking outcomes of the above-defined AOs. We recognize that various AOs mentioned in [56, 57, 58] do not successfully integrate the information shown in Table 3. Moreover, Table 4 shows the outcomes of the AOs offered by [20, 53, 54, 55].

Table 4 Comparative consequences
Full size table

According to our observations, we notice that the results of previously discussed AOs are nearly the same as \({R}_{1}>{R}_{3}>{R}_{4}>{R}_{2}\) and the convenient ranking outcomes of our proposed AOs are similar as \({R}_{4}>{R}_{1}>{R}_{3}>{R}_{2}.\) According to Table 4, this comparative analysis shows that our suggested strategy seems to be more elastic as well as comprehensive than other prevailing AOs by considering the significant nature of log natural, PBM operator, and their wide variety of various parametric values of parameters and \({{\ddot{\bar{U}}}}\).

The above Fig. 5 shows the visual representation of our suggested methodologies with other prevailing methods in which the ranking results of four alternatives \({R}_{\mu }\left(\mu =1, 2, 3, 4\right)\) are evaluated by using the score values \(S\left({\overleftarrow{O}}_{\mu }\right)\left(\mu =1, 2, 3, 4\right)\). According to Fig. 5, the x-axis represents the four alternatives \({R}_{1},\) \({R}_{2},\) \({R}_{3},\) and \({R}_{4}\) and the y-axis represents the score values \(S\left({\overleftarrow{O}}_{\mu }\right)\). The ranking results of our proposed AOs are shown as \({R}_{4}>{R}_{1}>{R}_{3}>{R}_{2}\) and the ranking results of previously existing AOs portrayed as \({R}_{1}>{R}_{3}>{R}_{4}>{R}_{2}\). We notice that our proposed AOs show significant behavior as compared to other AOs by considering the significant nature of the log natural, PBM operator.

Fig. 5
figure 5

Comparison of current and previous aggregation operators

Full size image

Conclusion

PAOs were developed by Yager which is widely acknowledged and useful for dealing with dissatisfied and misleading information and the BM operators were derived by Bonferroni that can consider the relationship among attributed values by using different frameworks. Additionally, the Aczel-Alsina operational tools were derived by Aczel and Alsina which is used to evaluate any kind of operator. Moreover, we determined the following information collected from the inclusion of the above-mentioned information, such as:

  • We evaluated the scientific theory of the PFAAPA operator and PFAAWPA operator.

  • We explored the theoretical foundations of the PFAAPG operator and PFAAWPG operator.

  • We studied a few enticing characteristics as well as the specific applications of our developed AOs based on the PF environment.

  • We assessed a MADM technique for determining the PFAAWPA operator and PFAAWPG operator in the context of the PF environment.

  • We numerically evaluated the ranking results for the selection of the best research scientist (alternative) based on the averaging and geometric operators. The ranking list of the PFAAWPA operator is \({R}_{4}>{R}_{1}>{R}_{3}>{R}_{2}\) and the ordering list of PFAAWPG is \({R}_{4}>{R}_{3}>{R}_{1}>{R}_{2}.\) So we concluded that the competent research scientist (alternative) for the vacant post is \({R}_{4}\).

  • Our proposed AOs have considered the significant nature due to the involvement of log natural, PBM operator, and their wide variety of various parametric values of parameters 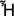and \({{\ddot{\bar{U}}}}\).

  • To show the higher level of accuracy and proficiency of the derived information, we used several real-world scenarios for the comparisons of derived work with various current or prevailing operators.

In future research, we will use our newly developed techniques to handle a variety of other essential, multi-dimensional decision-making issues based on the various aggregation operators, such as power partitioned (PP) AOs for estimating sustainable urban transport solutions [59], Generalized Dombi (GD) operators and BM operators based on dual probabilistic linguistic environment [60], Aczel-Alsina AOs for MADM approaches based on single-valued neutrosophic values [61] and so on.