Abstract
Solitons evolve in a nonlinear and dispersive medium whenever the balance is obtained between the effects of dispersion and nonlinearity. In this work, we study the impact of an external magnetic field on electromagnetic soliton profile in nonrelativistic two-fluid plasma using IMEX scheme. We found that different kinds of perturbing pulses create two solitons of same characteristics, propagating in opposite directions. For the present study, we considered three kinds of perturbing pulses of equal amplitudes but different widths as 0.003, 0.011 and 0.015. The propagation characteristics of the solitons, viz. crest of soliton amplitude, its width and velocity, are evaluated under the impact of an external magnetic field. In addition, we generalize the case by examining different plasma models by selecting different mass and temperature ratios of the ions and the electrons. This is done at the fixed external magnetic field strength of 0.06T and 0.01 T.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Literature review
An abundance of studies has been done on the electromagnetic waves (e.g., microwave) and plasma interaction by various researchers [1,2,3,4]. The numerical investigation on the interaction of the microwave (TE10 mode) with the plasma has been carried out in a rectangular waveguide by considering three forms of density profiles [1]. It was presented that rising in electron temperature provokes the evolution of the peak in density, and interaction of the microwave with plasma enhances the wavelength of the microwave electric field. Further, microwave breakdown has been investigated for both continuous microwave and pulsed microwave in a rectangular waveguide [2] for the smallest order TE10 mode, where the microwave breakdown threshold in the waveguide filled with air or Ar gas, the role of ionization and attachment of electrons with neutral gas or air molecules were analyzed. It was concluded that there is the dependency of the effective diffusion length on the geometry of the device as well as on the type of the gas. Some studies have been made on the interaction of plasma and high-power microwave through the superposition of two fundamental TE10 modes in a rectangular waveguide [3], where a tunnel was found to form that assumed its bigger size in the case of higher intensity of the microwave. Jawla et al. [4] have shown the estimation of mode fields in a plasma waveguide and electron acceleration in the presence of magnetic field which is applied in the direction of propagation of the mode. They obtained dispersion relation of the mode and expressions of its cutoff frequency and guide wavelength, and observed that in the presence of higher plasma density and stronger magnetic field, the guide wavelength gets larger. On the other hand, there are many studies concerning electrostatic waves in unmagnetized plasmas and magnetized plasmas [5,6,7,8,9,10,11,12] including both relativistic and nonrelativistic effects.
A lot of studies have been done on the electromagnetic solitons in an unmagnetized plasma. Rostampooran et al. [13] have investigated the role of the mixed electrons on the characteristics of the relativistic electromagnetic soliton and showed that rising of the density of nonthermal electrons increases the amplitude of solitons and rising of nonextensive electrons decreases the amplitude of solitons. Sunder [14] has explained the validity of cold plasma model which includes the effects arising due to temperature and ion dynamics. On the basis of such model, the region of existence of small amplitude soliton in warm plasma was well explained. It has also been shown that there is no existence of dark and bright solitons in mutually exclusive regimes of propagation speeds. In addition, it has been found that arising of density bursts in the trailing edge of the modulated structures is demonstration of an instability which is arising from a nonlinear phase mixing mechanism [15]. Verma et al. [16] have done analytical studies on electromagnetic soliton, where the analytical form of the cusp structure in the envelope of electromagnetic soliton at the ion wave breaking point for electron–ion plasma has been obtained. In this work, the time evolution studies have also been done to show the survival of these structures for several plasma periods. Lontano [17] has shown the existence of one-dimensional bright solitons of large amplitude in an overdense plasma. In an electron–ion plasma, the conditions for sustaining of relativistically intense solitary waves have been obtained [18]. These characteristics are illustrated for nonrelativistic field amplitude. The existence of solitary waves and their properties in relativistic electron–positron plasma have been investigated analytically [19].
Some studies have been made on the electromagnetic solitons in the magnetized plasmas. For example, Borhanian [20] has shown the existence of bright envelope solitons due to the existence of the nonlinear propagation of extraordinary waves in a transversely magnetized cold plasma. It has been shown that the bright soliton broadens when the wave frequency increases from the near critical frequency and its width decreases for larger values of the carrier wave frequency. Further, it has been found that a bright envelope soliton for the fast mode represents the possible stationary solutions of nonlinear Schrodinger equation and nonlinear coupling of CPEM waves with the background plasma [21]. Feng et al. [22] have developed the theory on the formation of bright and dark solitons in strongly magnetized plasma. It has been shown that effect of the magnetic field increases the amplitude of bright soliton and decreases the amplitude of dark soliton. Soliton generation in strongly magnetized plasma has also been studied numerically through one-dimensional particle-in-cell simulations and analytically by solving the laser wave equation [23]. Liang et al. [24] have derived a cylindrical Kadomtsev–Petviashivili equation for a relativistic electromagnetic soliton in weakly relativistic collisionless plasma which consists of electrons, ions and positrons in the presence of an applied static and uniform magnetic field; they obtained the explicit expression for the width, amplitude and velocity of the soliton. Ferina et al. [25] have presented analytically and numerically the properties of one-dimensional relativistic soliton in the presence of the externally imposed uniform magnetic field. Kavitha et al. [26] have investigated the propagation of an electromagnetic soliton in an anisotropic biquadratic ferromagnetic medium.
In the present work, we study the impact of external magnetic field, ion-to-electron temperature ratio and ion mass on the width, amplitude and velocity of electromagnetic solitons excited by three different pulses of different widths and same amplitude.
This paper has been categorized as follows. In section II, we present the coupled system of Euler equations for compressible flow and Maxwell’s equations for magnetic fields, and model esteems two different species, one electron and one ion separately. In section III, numerical scheme used for these simulations is presented. In section IV, results and discussion are presented. All characteristic features of evolved solitons are also presented in this section. In section V, our work has been concluded.
Equations
A fairly popular model for simulations of plasma flows is magnetohydrodynamic (MHD) model. This is the simplest possible model for plasma flows, derived by assuming quasi-neutrality and same velocity and temperature for the ions and the electrons. However, for several physically important phenomena like soliton propagations, this assumption is not valid, which leads to loss of additional details. In this article, we consider a two-fluid plasma flow model which allows separate density, velocity and temperatures for the ions and the electrons [27,28,29]. The model is far more general than the MHD model. In nondimensional conservative variables, this model can be expressed as follows:
Here, the subscripts {i, e} refer to the ion and electron nature, ρ{i,e} are the densities, \(v_{{\left\{ {i, e} \right\}}} = (v_{{\left\{ {i,e} \right\},}}^{x} v_{{\left\{ {i,e} \right\}}}^{y} ,v_{{\left\{ {i,e} \right\}}}^{z} )\) are the velocities, \(\varepsilon_{{\left\{ {i,e} \right\}}}\) are the energies and \(p_{{\left\{ {i,e} \right\}}}\) are the pressures. The electromagnetic quantities are the magnetic field B = (\(B_{x} , B_{y, } B_{z}\)), electric field E = (Ex, Ey, Ez), φ, ψ are the potentials and ξ, κ are the speeds for Maxwell’s equations. I is the 3 × 3 identity matrix. Also, rα = qα/mα together with α ∈ {i, e} are the charge–mass ratios and m = mi/me is the ion–electron mass ratio. Several parameters appear in the normalized form (1–10). Here \(\hat{l}_{r} = \frac{{l_{r} }}{{x_{o} }}\) is the normalized ion Larmor radius, \(\hat{c} = \frac{c}{{v_{i}^{T} }}\) is the normalized speed of light and \(\hat{\lambda }_{{_{\text{d}} }} = \frac{{\lambda_{\text{d}} }}{{l_{r} }}\) is the ion Debye length normalized with Larmor radius. Also, \(v_{i}^{T}\) is the reference thermal velocity of the ions,\(B_{o}\) is the reference magnetic field and x0 is the reference length. Ion mass \(m_{i}\) is assumed to be 1. In addition, we assume that both the ions and the electrons satisfy the following ideal gas law:
with \(\gamma = \frac{5}{3}\). To test the effects of the external magnetic field on the soliton motion, we modify the Lorentz force term acting on each species by adding external magnetic field B_ext in the source term. Being uniform, this field modifies the trajectory of the ions and electrons in the plasma but does not contribute to the electric field of the electromagnetic wave. Equations (1)–(3) express the conservation of energy, mass and momentum, respectively, for the ions. The source term in Eq. (2) is the Lorentz force occurred due to the electric and magnetic fields on the ions. The source term in Eq. (3) is described by kinetic energy explained in momentum Eq. (2). Likewise, Eqs. (4)–(6) express, respectively, the conservation of energy, mass and momentum for the electrons. Source term in Eq. (5) is the Lorentz force performing on the electrons. Equations (7)–(9) are the perfectly hyperbolic Maxwell’s (PHM) equations [27,28,29]. Also, the source term is the total current due to fluid flows in Eq. (8). The system of two-fluid plasma equations is a system of balance laws of the following form,
where u is the conservative variable vector, f(u) is the flux and s(u) is the source vector of the systems of Eqs. (1)–(11).
Numerical scheme
The critical difficulties in simulations of the system (1)–(10) are nonlinearity of the flux function, which leads to nonsmooth solutions, the presence of several scales and stiffness of the source terms especially when considering the realistic mass, ion–electron mass ratio. To overcome these, we use the algorithm proposed in [27,28,29] for the simulations presented in this article. The algorithm is based on the Strang splitting of the flux and the source and is of second-order accuracy. Furthermore, use of limiters allows stable resolution of the sharp gradient and shocks present in the simulations. To overcome stiffness present in the source, we treat the source implicitly. Furthermore, a careful treatment of the implicit treatment avoids the use of computationally costly nonlinear solver and needs only a linear solver. In addition, the implicit treatment is shown to ensure positivity of densities and pressures without any time step restriction. This results in the fairly robust algorithm which is ideally suitable for soliton simulation presented here.
Results on soliton characteristics and physics behind them
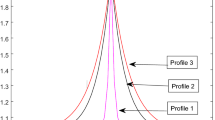
Simulation of 1D soliton formation has been done by assuming D = (0, L) with periodic boundary conditions. We see all the characteristics of soliton, evolved from perturbing pulse of three different widths, with respect to the magnetic field, temperature and mass ratios. Initially, all the electromagnetic quantities are assumed to be zero, when the plasma is at rest. Normalized Debye length has been considered to be 1, and further, we take Larmor radii of 0.0001. At first, solitons are excited by keeping their amplitude fixed and changing the width of the perturbing pulse. The three perturbing pulses are taken to have different widths, viz. 0.003, 0.011 and 0.015, respectively. We give the name of these profiles as profile 1 (P1), profile 2 (P2) and profile 3 (P3), respectively. These are shown in Fig. 1, along with the generated soliton 1, soliton 2 and soliton 3, respectively. Actually we have shown the one-dimensional situation and considered an infinitely large plasma. Then it is obvious that there will be two waves/solitons evolving in the opposite directions. Hence, a set of two solitons is shown in the figure.
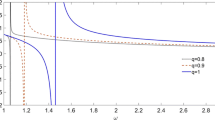
The mathematical expressions for the perturbing pulses are used as ρi = 1.0 + exp (−1135.0|x − L/3|), ρi = 1.0 + exp (−235.0|x − L/3|) and ρi = 1.0 + exp (−175.0|x − L/3|). The variation of soliton amplitude and width with the external magnetic field in low-temperature regimes (Te/Ti = 3) for all those profiles is shown in Fig. 2. The opposite variation of the soliton amplitude and width is evident from the figure. Further, the highest amplitude soliton is found to be excited by the perturbing pulse profile 3 (please see Fig. 2c). The soliton is found to evolve with smaller amplitude in the presence of stronger magnetic field. Actually the plasma becomes more dispersive when a stronger magnetic field is applied on it. Due to this reason, soliton’s width is enhanced, the amplitude goes down and this nature of the solitons stays for all the three kinds of perturbing pulses.
Variation of soliton amplitude and soliton width with the external magnetic field for three different perturbing pulses in low-temperature regime (Te/Ti = 3); a represents the case of profile 1, b represents the case of profile 2 and c represents the case of profile 3. The ion-to-electron mass ratio for all the figures is taken as 1836
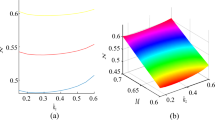
Figure 3 shows the variation of peak soliton amplitude and soliton velocity with the magnetic field for all the three perturbing pulses in high-temperature regime (Te/Ti = 10). In this regime also, the soliton amplitude goes down in the presence of stronger magnetic field. The soliton velocity also behaves like the amplitude of the soliton, and it also slows down in the plasma under the effect of stronger magnetic field. Malik and Singh [30] obtained comparable results for the soliton width and soliton energy in weakly relativistic plasma where width and energy of soliton were found to decrease with increasing magnetic field. Liang et al. [24] have shown the effect of an applied magnetic field, which is static and uniform also, on relativistic electromagnetic soliton in 2D. It has been shown that the amplitude of the solitary wave increases by increasing the applied magnetic field in cold plasma. It means the opposite behavior is led by the presence of finite temperature of ions and electrons in the present case. However, Kavitha et al. [26] have shown that the occurrence of amplitude and velocity of the electromagnetic soliton in an anisotropic biquadratic ferromagnetic medium are time independent. Their results of the perturbation analysis described that the velocity and amplitude of the soliton are constant along the spin–lattice.
Table 1 shows the impact of the electron-to-ion temperature ratio (Te/Ti) on the velocity and amplitude of the solitons. The amplitude and the phase velocity of the soliton increase with higher electron-to-ion temperature ratio in the existence of the external magnetic field (taken as 0.06 T). Similar to the present case of electromagnetic soliton, Malik and Singh [30] have shown analytically that the amplitude decreases and the energy increases with increasing ion-to-electron temperature ratio in the existence of the external magnetic field in weakly relativistic two-fluid space plasma. If we differentiate the soliton amplitude and soliton velocity for three profiles in our case, it is found that the impact of ion temperature on the amplitude and velocity of the soliton is most sensitive when the widest pulse forms the soliton. Sunder [14] has shown that the amplitude and velocity of weakly relativistic electromagnetic soliton decrease in unmagnetized warm plasma [14]. Lontano et al. [18] have shown that relativistic electromagnetic soliton in an unmagnetized warm quasineutral electron–ion plasma has the large amplitude in the presence of higher electron and ion temperature, similar to our observation in the present case.
In Table 2, the effect of ion-to-electron mass ratio in the presence of external magnetic field on the soliton propagation has been examined in different plasmas, viz. xenon plasma (mi/me = 240,459.593), argon plasma (mi/me = 40,391), oxygen plasma (mi/me = 29,368.8681), nitrogen plasma (mi/me = 25,697), hydrogen plasma (mi/me = 1836) and electron–positron (mi/me = 1) plasma. It has been done for all three considered perturbing pulses. We have observed that amplitude of evolved soliton in the electron–positron plasma is the highest for all three perturbing pulses. We also observe that the variation of the velocity, width and amplitude of the solitons is nonlinear with respect to mass of the ions for three different perturbing pulses. For example, the velocity and amplitude are reducing when the mass of ion is beneath for narrower pulse (width 0.003) whereas the amplitude first reduces and then expands with the beneath mass of the ions in the case of broader perturbing pulse; it occurs in the case of the soliton width and the velocity for the cases of broader perturbing pulses. In the context of mass effect, Malik and Singh [23] found that the impact of electron inertia is to reduce the amplitude as well as the width of the soliton. On the other hand, Sunder et al. [31] have shown that small amplitude bright soliton exists below a critical group velocity in the case of cold plasma and solitons are dark for group speeds which is less than the square root of the electron-to-ion mass ratio. It means the possibility of dark soliton is more in the plasma having heavy ions.
Conclusions
In our studies, we have shown the effect of magnetic field on the soliton characteristics evolved from three different considered perturbing pulses. Higher magnetic field yields the soliton evolution with its smaller amplitude, larger width and low velocity, in both the low-temperature and higher-temperature regimes, at the fixed magnetic field of strength 0.6T. Higher ion temperature is found to enhance the soliton amplitude and the soliton propagates at higher velocity in this situation. The soliton evolution is found to be much sensitive to the magnetic field in the case of perturbing pulse having wider width (Profile 3), as the soliton amplitude and its velocity change significantly with the magnetic field. However, the soliton evolution is least responsive to the magnetic field for perturbing pulse of broader width with respect to the soliton width.
References
Malik, H.K., Aria, A.K.: Microwave and plasma interaction in a rectangular waveguide: Effect of ponderomotive force. J. Appl. Phys. 108, 013109 (2010)
Malik, H.K., Aria, A.K.: Microwave breakdown for the TE10 mode in a rectangular waveguide. Phys. Plasmas 20, 082125 (2013)
Tomar, S.K., Malik, H.K.: Density modification by two superposing TE10 modes in a plasma filled rectangular waveguide. Phys. Plasmas 20, 072101 (2013)
Jawla, S.K., Kumar, S., Malik, H.K.: Evaluation of mode fields in a magnetized plasma waveguide and electron acceleration. Optics Communications 251, 346 (2005)
Malik, H.K.: Soliton Reflection in magnetized plasma: effect of ion temperature and nonisothermal electrons. Phys. Plasmas 15, 072105 (2008)
Tomar, R., Malik, H.K., Dahiya, R.P.: Reflection of ion acoustic solitary waves in a dusty plasma with variable charge dust. J. Theor. Appl. Phys. 8, 126 (2014)
Sikdar, A., Khan, M.: Effects of Landau damping on finite amplitude low-frequency nonlinear waves in a dusty plasma. J Theor Appl. Phys. 11, 137 (2017)
Liu, J.G., Zeng, Z.: Auto-Bäcklund transformation and new exact solutions of the (3 + 1)-dimensional KP equation with variable coefficients. J. Theor Appl. Phys. 7, 49 (2013)
Malik, R., Malik, H.K.: Compressive solitons in a moving e-p plasma under the effect of dust grains and an external magnetic field. J. Theor. Appl. Phys. 7, 65 (2013)
Tomar, R., Bhatnagar, A., Malik, H.K., Dahiya, R.P.: Evolution of solitons and their reflection and transmission in a plasma having negatively charged dust grains. J. Theor. Appl. Phys. 8, 138 (2014)
Sabetkar, A., Dorranian, D.: Effect of obliqueness and external magnetic field on the characteristics of dust acoustic solitary waves in dusty plasma with two-temperature nonthermal ions. J. Theor. Appl. Phys. 9, 141 (2015)
Haider, M.M., Ferdous, T., Duha, S.S.: Instability due to trapped electrons in magnetized multi-ion dusty plasmas. J. Theor. Appl. Phys. 9, 159 (2015)
Rostampooran, S., Saviz, S.: Investigation of electromagnetic soliton in the Cairns–Tsallis model for plasma. J. Theor. Appl. Phys. 11, 127 (2017)
Sundar, S.: Weakly relativistic electromagnetic solitons in warm plasmas. Phys. Plasmas 23, 062104 (2016)
Saxena, V., Das, A., Sengupta, S., Kaw, P., Sen, A.: Stability of nonlinear one-dimensional laser pulse solitons in a plasma. Phys. Plasmas 14, 072307 (2007)
Verma, D., Das, A., Kaw, P., Tiwari, S.K.: The study of electromagnetic cusp solitons. Phys. Plasmas 22, 013101 (2015)
Lontano, M.: One-dimensional electromagnetic solitons in a hot electron-positron plasma. Phys. Plasmas 8, 5113 (2001)
Lontano, M., Passoni, M., Bulanov, S.V.: Relativistic electromagnetic solitons in a warm quasineutral electron–ion plasma. Phys. Plasmas 10, 639 (2003)
Lee, N.C.: Electromagnetic solitons in fully relativistic electron-positron plasmas with finite temperature. Phys. Plasmas 18, 062310 (2011)
Borhaniann, J.: Extraordinary electromagnetic localized structures in plasmas: modulational instability, envelope solitons, and rogue waves. Phys. Lett. A 379, 595 (2015)
Cattaert, T., Kourakis, I., Shukla, P.K.: Envelope solitons associated with electromagnetic waves in magnetized pair plasma. Phys. Plasmas 12, 012319 (2005)
Feng, W., Li, J.Q., Kishimoto, Y.: Theory on bright and dark soliton formation in strongly magnetized plasmas. Phys. Plasmas 23, 092115 (2016)
Feng, W., Li, J.Q., Kishimoto, Y.: Laser propagation and soliton generation in strongly magnetized plasmas. Phys. Plasmas 23, 032102 (2016)
Liang, W.Y., Xiang, Z.Z., Qian, J.X., Xun, Y.C., Feng, W.H., Feng, Z.H., Feng, H.C., Yuan, J.Y., Dong, S.X., Hu, Q.R.: Relativistic electromagnetic solitary wave in a cylindrical magnetized plasma. Chin. Phys. Lett. 23, 664 (2006)
Ferina, D., Lontano, M.: Relativistic solitons in magnetized plasmas. Phys. Rev. E 62, 4146 (2000)
Kavitha, L., Saravanan, M., Gopi, D.: Propagation of an electromagnetic soliton in ananisotropic biquadratic ferromagnetic medium Chin. Phys. B 22, 030512 (2013)
Abgrall, R., Kumar, H.: Robust finite volume schemes for two-fluid plasma equations. J. Sci. Comput. 60, 584 (2014)
Kumar, H., Mishra, S.: Entropy stable numerical schemes for two-fluid plasma equations. J. Sci. Comput. 52, 401 (2012)
Sharma, A., Malik, H.K., Kumar, H.: Study of electromagnetic solitons excited by different profile pulses. J. Theor. Appl. Phys. 12, 65 (2018)
Malik, H.K., Singh, K.: Small amplitude soliton propagation in a weakly relativistic magnetized space plasma: electron inertia contribution. IEEE Trans. Plasma Sci. 33, 1995 (2005)
Sundar, S., Das, A., Saxena, V., Kaw, P., Sen, A.: Relativistic electromagnetic flat top solitons and their stability. Phys. Plasmas 18, 112112 (2011)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sharma, A., Malik, H.K., Kumar, H. et al. Effect of magnetic field on electromagnetic soliton evolution by different pulses. J Theor Appl Phys 13, 31–37 (2019). https://doi.org/10.1007/s40094-018-0306-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-018-0306-z