Introduction and motivation

A solitary wave is a localized traveling wave that preserves its shape, despite dispersion and nonlinearities. Solitary wave is called as soliton, if it retains its shape after collision with another solitary wave. Soliton’s structure plays a very important role in trapping plasma particles and transporting them from one place to another in the laboratory, astrophysical and space plasmas. There is an abundance of studies on the electrostatic solitary waves in unmagnetized plasmas and magnetized plasmas, including both the analytical and experimental investigations [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Different forms of Korteweg–de Vries (KdV) equations have been used to describe the evolution of ion acoustic solitary waves or solitons in different plasma models including homogeneous and inhomogeneous plasmas both having nonrelativistic or relativistic electrons or ions under the presence or absence of an external magnetic field. Roychoudhury and Bhattacharyya [16] have obtained a solitary wave solution in a relativistic plasma with nonzero electron inertia using pseudopotential approach and confirmed the existence of solitary waves in such plasma to the first order in \( \frac{1}{{c^{2} }} \). Ghosh and Ray [17] did a rigorous analytical study of the same problem and discussed the condition for the existence of solitons. Nejoh [12] showed that the phase velocity and amplitude of an ion acoustic soliton are greatly influenced by the ion temperature and relativistic effect. Singh and Honzawa [18] obtained a two-dimensional KdV equation, termed as Kadomtsev–Petviashvili (KP) equation, in a weakly relativistic plasma with finite ion temperature; however, they had neglected the electron inertia in their calculations. Malik [19] has included both the mass of the electrons and their relativistic speeds for obtaining the KP equation in a relativistic plasma and studied in detail the contribution of electron inertia on the propagation characteristics of two-dimensional solitons. An important property of the solitons is their reflection in plasmas, which takes place when the solitons face strong density gradient or a reflector is used to reflect them. In addition to the propagation [20] and reflection [21] of the solitons, some of the researchers have observed the transmission of such waves [22].

The above studies were confined only to the electrostatic solitary waves. However, electromagnetic waves can also attain such structures, and these types of solitons have been found to be quite useful in communications. The researchers have focused on their propagation characteristics only [23,24,25,26,27,28,29], and to the best of our knowledge, nobody discusses the role of perturbing pulses on the evolution of such solitons. Hence, in the present article, we talk about the soliton evolution by different pulses of same amplitudes but different widths.

Basic equations

To model plasma flows, several models are used. One of the most commonly used models is equations of magnetohydrodynamic (MHD). Although highly successful, the model describes the plasma flow via a single density, velocity and temperature. This leads to ignoring several critical terms which model additional physics. To overcome these restrictions of MHD model, in this article, we model plasma using two-fluid-based model. This allows different densities, velocities and temperatures for the electrons and the ions. We consider a plasma consisting of the electrons and a single ion species. In nondimensional conservative variables, basic equations can be written as:

$$ \frac{{\partial \rho_{\text{i}} }}{\partial t} + \nabla \cdot (\rho_{\text{i}} \varvec{v}_{\varvec{i}} ) = 0 $$
(1)
$$ \frac{{\partial \left( {\rho_{\text{i}} \varvec{v}_{\varvec{i}} } \right)}}{\partial t} + \nabla \cdot \left( {\rho_{\text{i}} \varvec{v}_{\varvec{i}} \varvec{v}_{\varvec{i}}^{{ \top }} + p_{\text{i}} \varvec{I}} \right) = \frac{1}{{\widehat{{l_{\text{r}} }}}}\rho_{\text{i}} (\varvec{E} + v_{\text{i}} \times \varvec{B}) $$
(2)
$$ \frac{{\partial \varepsilon_{\text{i}} }}{\partial t} + \nabla \cdot ((\varepsilon_{\text{i}} + p_{\text{i}} )\varvec{v}_{\varvec{i}} ) = \frac{1}{{\widehat{{l_{\text{r}} }}}}\rho_{\text{i}} \left( {\varvec{E} \cdot \varvec{v}_{\varvec{i}} } \right) $$
(3)
$$ \frac{{\partial \rho_{\text{e}} }}{\partial t} + \nabla \cdot (\rho_{\text{e}} \varvec{v}_{\text{e}} ) = 0 $$
(4)
$$ \frac{{\partial \left( {\rho_{\text{e}} \varvec{v}_{\varvec{e}} } \right)}}{\partial t} + \nabla \cdot \left( {\rho_{\text{e}} \varvec{v}_{\varvec{e}} \varvec{v}_{\varvec{e}}^{{ \top }} + p_{\text{e}} \varvec{I}} \right) = \frac{m}{{\widehat{{l_{\text{r}} }}}}\rho_{\text{e}} (\varvec{E} + \varvec{v}_{\varvec{e}} \times \varvec{B}) $$
(5)
$$ \frac{{\partial \varepsilon_{\text{e}} }}{\partial t} + \nabla \cdot ((\varepsilon_{\text{e}} + p_{\text{e}} )\varvec{v}_{\varvec{e}} ) = \frac{ - \,m}{{\widehat{{l_{\text{r}} }}}}\rho_{\text{e}} (\varvec{E} \cdot \varvec{v}_{\varvec{e}} ) $$
(6)
$$ \frac{{\partial \varvec{B}}}{\partial t} + \nabla \times \varvec{E} + \kappa \partial \varPsi = 0 $$
(7)
$$ \frac{{\partial \varvec{E}}}{\partial t} - \hat{c}^{2} \nabla \times \varvec{B} + \xi \hat{c}^{2} \nabla \varphi = \frac{ - \,1}{{\widehat{{\lambda_{\text{d}} }} ^{2} \widehat{{l_{\text{r}} }}}}\left( {r_{\text{i}} \rho_{\text{i}} \varvec{v}_{\varvec{i}} + r_{\text{e}} \rho_{\text{e}} \varvec{v}_{\varvec{e}} } \right) $$
(8)
$$ \frac{\partial \varphi }{\partial t} + \xi \nabla \cdot \varvec{E} = \frac{\xi }{{\widehat{{\lambda_{\text{d}} }}^{2} \widehat{{l_{\text{r}} }}}}\left( {r_{\text{i}} \rho_{\text{i}} + r_{\text{e}} \rho_{\text{e}} } \right) $$
(9)
$$ \frac{\partial \varPsi }{\partial t} + \kappa \hat{c}^{2} \nabla \cdot \varvec{B} = 0 $$
(10)

Here, the subscripts {i, e} refer to the ion and electron species, \( \varepsilon_{{\left\{ {{\text{i}},{\text{e}}} \right\}}} \) are the energies, \( p_{{\left\{ {{\text{i}},{\text{e}}} \right\}}} \) are the pressures, B = (\( B_{x} , B_{y, } B_{z} \)) is the magnetic field, E = (Ex, Ey, Ez) is the electric field, φ, \(\varPsi\) are the potentials and ξ, κ are the speeds for Maxwell equations. I is the \( 3 \times 3 \) identity matrix. Also, rα = qα/mα together with \( \alpha \in \{ {\text{i}},{\text{e}}\} \) is the charge–mass ratios, and m = mi/me is the ion–electron mass ratio. Several physically significant parameters appear in the normalized form (1–10). Here \( \widehat{{l_{\text{r}} }} = \frac{{l_{\text{r}} }}{{x_{\text{o}} }} \) is the normalized ion Larmor radius, \( \hat{c} = \frac{c}{{v_{\text{i}}^{\text{T}} }} \) is the normalized speed of light and \( \widehat{{\lambda_{\text{d}} }} = \frac{{\lambda_{\text{d}} }}{{l_{\text{r}} }} \) is the ion Debye length normalized with Larmor radius. Also \( v_{\text{i}}^{\text{T}} \) is the reference thermal velocity of the ions, \( B_{\text{o}} \) is the reference magnetic field and x0 is the reference length. Ion mass \( m_{\text{i}} \) is assumed to be 1. In addition, we assume that both the ions and the electrons satisfy the following ideal gas law:

$$ \varepsilon_{\alpha } = \varepsilon_{\alpha } + \frac{1}{2}\{ \rho_{\alpha } |v_{\alpha } |^{2} \} ,\quad \varepsilon_{\alpha } = \frac{{P_{\alpha } }}{\varUpsilon - 1},\quad \alpha \in \{ {\text{i}},{\text{e}}\} $$
(11)

with \( \gamma = \frac{5}{3} \). Equations (1)–(3) represent, respectively, the conservation of mass, momentum and energy for the ions. The source term in Eq. (2) is the Lorentz force acting on the ions due to the electric and magnetic fields. The source term in Eq. (3) is the contribution of kinetic energy coming from momentum Eq. (2). Similarly, Eqs. (4)–(6) represent, respectively, the conservation of mass, momentum and energy for the electrons. Source term in Eq. (5) is the Lorentz force acting on the electrons. Equations (7)–(9) are the perfectly hyperbolic Maxwell’s (PHM) equations [26]. Also, the source term in Eq. (8) is the total current due to fluid flows. The system of two-fluid plasma equations is a system of balance laws of the following form,

$$ \varvec{u}_{t} + \nabla \cdot {\mathbf{f}}({\mathbf{u}}) = {\mathbf{s}}({\mathbf{u}}), $$
(12)

where u is the conservative variable vector, f(u) is the flux and s(u) is the source vector of the systems of Eqs. (1)–(11).

Numerical scheme

The key difficulty in the computations presented here is that the solutions contain sharp gradient. This is expected as Eqs. (1)–(10) are a set of hyperbolic balance laws [30] with nonlinear flux. This leads to the formation of shocks and contacts. Furthermore, as we are using realistic ion–electron mass ratio, the source terms will be highly stiff and oscillatory, which results in oscillations in the solutions. Due to the stiffness in the source terms, any explicit treatment of the source will be highly computationally inefficient. In addition, for any successful computational, we need to ensure positivity of density and pressure throughout the evolution. This is nontrivial for second-order schemes.

In the present computations, we use the algorithm developed by Abgrall and Kumar [31]. The algorithm is based on the finite volume methods, which are well suited to the discretization of hyperbolic PDEs as they allow a stable resolution of the solution containing discontinuities (shocks and contacts). Furthermore, the algorithm ensures the positivity of densities and pressures of the ions and the electrons. This is achieved by combining positivity-preserving numerical flux with an appropriate positivity-preserving reconstruction process. This is then combined with the implicit treatment of the source, which guarantees the numerical stability of the whole algorithm. Furthermore, the algorithms are shown to be highly computationally efficient for the stiff source terms.

Results and discussion

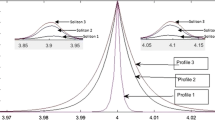
Soliton formation in 1D is simulated by considering D = (0, L) with periodic boundary conditions. Initially, the plasma is at rest, and all electromagnetic quantities are considered to be zero. Normalized Debye length is taken to be 1.0. We further consider Larmor radii of 0.0001. All the simulations presented in this section are simulated on 12,000 cells. At first, we excite the solitons by changing the width of the perturbing pulse but keeping its amplitude fixed. Table 1 shows the properties of soliton, viz. the peak amplitude, width and its velocity obtained this way. This is observed that the wider pulse excites the soliton of bigger size, i.e., the soliton of higher amplitude. As per its basic feature, the higher amplitude soliton attains lower width but propagates with larger velocity (Table 1). Now in order to see the distinct difference in the soliton size, we optimize the width of the perturbing pulse as 0.003, 0.011 and 0.015. These pulses are named as profile 1, profile 2 and profile 3, respectively, and are shown in Fig. 1. The mathematical expressions for these pulses are taken as ρi = 1.0 + exp (−1135.0|x − L/3|), ρi = 1.0 + exp (−235.0|x − L/3|) and ρi = 1.0 + exp (−175.0|x − L/3|) together with L = 12. We see the impact of initial density, temperature or pressure ratio and mass ratios of the ions and electrons on the amplitude, width and velocity of the evolved soliton. Finally, we investigate the soliton evolution based on the above-mentioned different kinds of perturbing pulses together with L = 12 that are shown in Fig. 1.

Table 1 Variation of peak amplitude of soliton, its width and velocity with the perturbing pulses of different widths
Full size table
Table 2 Variation of soliton amplitude, width and velocity with electron-to-ion temperature ratio for the cases of different perturbing pulses
Full size table
Fig. 1
figure 1

Profiles of perturbing pulses with different widths. The variable x is taken on the x-axis

Full size image

Table 2 shows the impact of electron-to-ion temperature ratio (Te/Ti) on the soliton amplitude, its width and velocity. In order to study the comparative study of these properties for the cases of three perturbing profiles, we have calculated them from the observed soliton structures and their movement. Clearly, the effect of electron-to-ion temperature ratio is to decrease the amplitude but to increase the width of the solitons. The phase velocity behaves in accordance with the amplitude of the solitons, and it decreases in the plasma where the electron-to-ion temperature ratio is larger. Based on this, we can conclude that the soliton evolves with bigger size and propagates with higher velocity in the plasma having higher-temperature ions. Similar results were obtained by Malik et al. [15] for the KdV solitons in a plasma having weakly relativistic ions and finite inertia electrons. On the other hand, if we compare the soliton amplitude for three profiles, it is obtained that the effect of ion temperature on the soliton amplitude and velocity is most significant when the solitons are excited by the thinnest pulse and the solitons excited by the widest pulse showed less impact of the ion temperature. However, the wider pulse excites the soliton of higher amplitude and velocity (as observed in Table 1). Lontano et al. [28] have shown that relativistic electromagnetic solitons in a warm quasi-neutral electron–ion plasma have a large amplitude in the case of higher electron and ion temperatures.

In order to examine the effect of ion-to-electron mass ratio on the soliton propagation characteristic, we analyze the soliton evolution in different plasmas, viz. xenon plasma (mi/me = 240,459.593), argon plasma (mi/me = 40,391), oxygen plasma (mi/me = 29,368.868), nitrogen plasma (mi/me = 25,697), hydrogen plasma (mi/me = 1836) and electron–positron (e–p) plasma. Electron–positron pair creation occurs in relativistic plasmas at high temperatures [32,33,34,35,36], and e–p pairs/plasmas have been generated in the laboratory as well [37,38,39,40,41]. This is done for all the three types of the perturbing pulses (Table 3). The most important observation is that the highest amplitude solitons are evolved in the electron–positron plasma. This is obvious as both the species, in this case, play the role at equal footing in view of their equal mass. In this situation, the frequency of oscillations will be larger, and hence, the solitons also propagate at the larger velocity. On the other hand, the amplitude, width and velocity of the solitons do not scale linearly with the mass of the ions for the different cases of the perturbing pulses. For example, the amplitude and velocity fall down when the ion mass is lower in the case of thinnest pulse (width 0.003), whereas the amplitude first decreases and then increases with the lower mass of the ions when the perturbing pulse is wider; the same is the case with the soliton width and the velocity for the cases of wider perturbing pulses. Malik and Singh [42] had observed a reduction in the soliton amplitude with the electron mass in a relativistic plasma. In view of the present results, we can say that the nonlinear and dispersive effects of the plasma cannot be correlated in a particular fashion with the change of ion mass (Table 3).

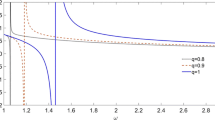
Table 3 Variation of soliton amplitude, width and velocity with the ion-to-electron mass ratio for different kinds of perturbing pulses
Full size table

Although in the present work we discussed the propagation characteristics of electromagnetic solitons, we can examine whether these solitons behave as KdV solitons or mKdV solitons. For this, we show the variation of the products amplitude × width2 (for KdV solitons) and amplitude × width (for mKdV solitons) with the electron-to-ion temperature ratio varying from 1 to 5 (Fig. 2). Since the product amplitude × width2 remains almost the same, it can be said that these solitons behave in a similar fashion as the KdV solitons. Moreover, these solitons are expected to evolve with higher amplitude in view of their larger phase velocity in a relativistic plasma.

Fig. 2
figure 2

Variation of product of soliton amplitude and width with electron-to-ion temperature ratio

Full size image

Concluding remarks

In the present article, we focused on the propagation characteristics of electromagnetic solitons, which were excited by thinner and wider perturbing pulses. The solitons with higher amplitude evolved for the case of wider perturbing pulse, and these solitons also propagated at larger velocity. The basic feature of the solitons, i.e., higher amplitude and larger velocity but smaller width, was confirmed when the plasma contained higher-temperature ions. Also, the solitons of biggest size evolved in the electron–positron plasma due to the role of these two species at the equal footing for the generation of the solitons. The variation of nonlinear and dispersive effects of the plasma was understood based on the variation of amplitude and width of the solitons; it was realized that these effects cannot correlated in a specific manner with the mass of the ions in the plasma.