Reflection of ion acoustic solitary waves in a dusty plasma with variable charge dust

Abstract

An inhomogeneous plasma comprising ions, two temperature electrons and dust grains with variable charge is explored for its unperturbed state for ions’ drift due to density gradient and perturbed state for the evolution of ion acoustic solitary waves and their reflection under the effect of an external magnetic field. The ion drift velocity is found to depend on the plasma parameters and magnetic field. The perturbed state of plasma supports two types of ion acoustic waves, which evolve into fast and slow compressive solitary structures under certain conditions. However, only the fast solitary wave is observed to be reflected and acquired opposite polarity to that of the incident solitary wave. The solitary waves are found to be downshifted after their reflection. The reflection coefficient acquires higher values in the case of dust grains of fixed charge in comparison with the case of fluctuating charge on the dust grains. It means the reflection becomes stronger when the charge on the dust grains does not fluctuate and remains fixed. The effect of dust grain density is to enhance the amplitude of solitary waves but to weaken their reflection. The amplitudes of both the incident and reflected solitons remain higher for the case of fluctuating charge on the dust grains in comparison with the case of fixed charge. The effective temperature of the plasma is also found to alter the solitary structures significantly in the case of dust grains having fluctuating charge.

Introduction

Plasma is a collection of charged and neutral particles, where positively and negatively charged particles remain almost in equal numbers. Similar to the sound waves in air, such plasmas support the propagation of ion waves. These ion acoustic waves evolve into the solitary structures when the effect of nonlinearity and dispersion are balanced in the plasma. The ion acoustic solitary waves have been investigated in greater details in homogeneous plasmas [1–6], inhomogeneous plasmas [7–9] and magnetized plasmas [10–15]. The ion acoustic solitary waves are found to reflect from a density gradient or boundary present in the plasma. There are many experimental findings related to the propagation and reflection of solitary waves in different plasma models [16–27]. This is clear from these studies that the reflected solitary waves are in general of smaller size compared to the size of incident waves.

The velocity of ion acoustic waves and hence of the corresponding solitary waves remains lower than the thermal speed of electrons. On the other hand, low temperature electrons, if they are available in the plasma, can interact with the ion acoustic wave and are trapped in the wave potential due to their lower thermal speed. Hence, it becomes quite interesting to include their effect while studying the ion acoustic solitary waves. Such low temperature trapped electrons along with isothermal electrons are possible in hot turbulent plasmas of thermonuclear interest, hot cathode discharge plasmas, and during strong electron beam–plasma interaction. These electrons do not follow the usual Boltzmann distribution and their velocity distribution may be represented by two vortex-like distributions [28]. On the other hand, in laboratory plasmas or space-related plasmas such as in planetary rings, asteroid zones, cometary tails and in lower parts of Earth’s ionosphere dust particles are present [29]. Low temperature technological plasmas are also contaminated by highly charged dust impurities, as they carry a significant amount of charge of the plasma. These dust grains may acquire either negative charge or positive charge [29–33], which does not remain fixed. Hence, in the present article, we include the charge fluctuation of the dust grains to investigate the reflection of ion acoustic solitary waves in an inhomogeneous plasma having two temperature electrons and warm ions. The ion acoustic wave is taken to propagate and evolve into solitary structure at an angle with the direction of an external magnetic field.

Basic formulation

We consider a weak inhomogeneous plasma containing heavy dust grains of density n_d0 and initial charge number Z_d0, and inertial warm positive ions of density n, velocity $\overrightarrow{v}$ and temperature T _i . Low temperature trapped electrons with density n_el and temperature T_el, following the vortex-like distribution, are also taken along with isothermal electrons having density n_eh and temperature T_eh. The wave propagation is taken in the (x, z) plane at an angle θ with the direction of an external magnetic field B₀ applied in the z-direction. The motion of the dust grains is neglected in view of their very low-frequency oscillations in comparison with ion oscillations. The non-isothermality of the plasma is considered through the electron density n_el.

To study the propagation of ion acoustic waves, we write the following normalized basic fluid equations.

$$\left(\frac{\mathit{\partial }n}{\mathit{\partial }t}\right)+\frac{\mathit{\partial }}{\mathit{\partial }x}\left(n{v}_x\right)+\frac{\mathit{\partial }}{\mathit{\partial }z}\left(n{v}_z\right)=0,$$

(1)

$$n\left(\frac{\mathit{\partial }{v}_x}{\mathit{\partial }t}\right)+n{v}_x\left(\frac{\mathit{\partial }{v}_x}{\mathit{\partial }x}\right)+n{v}_z\left(\frac{\mathit{\partial }{v}_x}{\mathit{\partial }z}\right)=n{\mathit{\Omega }}_R{v}_y-n\left(\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\right)-2\frac{T_i}{T_{eff}}\left(\frac{\mathit{\partial }n}{\mathit{\partial }x}\right),$$

(2)

$$n\left(\frac{\mathit{\partial }{v}_z}{\mathit{\partial }t}\right)+n{v}_x\left(\frac{\mathit{\partial }{v}_z}{\mathit{\partial }x}\right)+n{v}_z\left(\frac{\mathit{\partial }{v}_z}{\mathit{\partial }z}\right)=-n\left(\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }z}\right)-2\frac{T_i}{T_{eff}}\left(\frac{\mathit{\partial }n}{\mathit{\partial }z}\right),$$

(3)

$$\left(\frac{\mathit{\partial }{v}_y}{\mathit{\partial }t}\right)+v_x\left(\frac{\mathit{\partial }{v}_y}{\mathit{\partial }x}\right)+v_z\left(\frac{\mathit{\partial }{v}_y}{\mathit{\partial }z}\right)=-{\mathit{\Omega }}_R{v}_x,$$

(4)

$$\left(\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{x}^2}\right)+\left(\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{z}^2}\right)=n_{\text{el}}+n_{\text{eh}}-n+n_{d0}{Z}_{d0},$$

(5)

$$n_{\text{el}}=n_{\text{el}0}\left\{1+\frac{T_{\text{eff}}}{T_{\text{el}}}\mathit{\varphi }-\frac{4}{3}{b}_l{\left(\frac{T_{\text{eff}}}{T_{\text{el}}}\mathit{\varphi }\right)}^{3/2}+\frac{1}{2}{\left(\frac{T_{\text{eff}}}{T_{\text{el}}}\mathit{\varphi }\right)}^2+\dots \right\},$$

(6)

$$n_{\text{eh}}=n_{\text{eh}0}exp\left(\frac{T_{\text{eff}}\mathit{\varphi }}{T_{\text{eh}}}\right),$$

(7)

where ${\mathit{\Omega }}_R=\sqrt{\frac{{\mathit{\epsilon }}_0}{m_i{n}_0^0}}{B}_0$ and T_eff is the effective temperature of the plasma, given by $T_{\text{eff}}=\left(n_{\text{el}0}+n_{\text{eh}0}\right)T_{\text{el}}{T}_{\text{eh}}/\phantom{\left(n_{\text{el}0}+n_{\text{eh}0}\right)T_{\text{el}}{T}_{\text{eh}}\left(n_{\text{el0}}{T}_{\text{eh}}+n_{\text{eh0}}{T}_{\text{el}}\right)}\left(n_{\text{el0}}{T}_{\text{eh}}+n_{\text{eh0}}{T}_{\text{el}}\right)$. In the above equations, all the densities are normalized by the unperturbed plasma density $n_0^0$ at an arbitrary reference point (say x = z = 0), ion flow velocity by the ion acoustic speed ${\left(T_{e\text{ff}}/m_i\right)}^{1/2}$, space coordinates x and z by the Debye length ${\left({\mathit{\epsilon }}_0{T}_{\text{eff}}/n_0^0{e}^2\right)}^{1/2}$ and time t by the inverse of ion plasma frequency ${\mathit{\omega }}_{\text{pi}}={\left(n_0^0{e}^2/{\mathit{\epsilon }}_0{m}_i\right)}^{1/2}$ where m _i is the mass of the ion. The electric potential ϕ is normalized by T_eff/e. Further, we take b _l as the non-isothermal parameter [28], given by $b_l=\left[1-T_{\text{el}}/T_{\text{eff}}\right]/\sqrt{\mathit{\pi }}$.

To study small amplitude waves, we apply reductive perturbation technique (RPT) by expanding the densities, fluid velocities and electric potential in terms of a smallness parameter ε in view of the oblique incidence of the wave with respect to the magnetic field that causes the longitudinal and transverse components of velocity to be different. The powers of ε in the expansion and the stretched coordinates should be selected such that it finally leads to the KdV equation with different terms of the same order in ε. Hence, the stretched coordinates and expansion are given by.

$$\mathit{\xi }={\mathit{\epsilon }}^{1/4}\left[\left(xsin\mathit{\theta }+zcos\mathit{\theta }\right)/{\mathit{\lambda }}_0-t\right],\mathit{\eta }={\mathit{\epsilon }}^{3/4}\left[xsin\mathit{\theta }+zcos\mathit{\theta }\right],$$

(8)

$$\begin{array}{c}S=S_o(x,z)+\mathit{\epsilon }{S}_1(x,z,t)+{\mathit{\epsilon }}^{3/2}{S}_2(x,z,t)+{\mathit{\epsilon }}^2{S}_3(x,z,t)+\dots ,S\equiv n,n_{\text{el}},n_{\text{eh}},v_z,\\ V=V_0(x,z)+{\mathit{\epsilon }}^{5/4}{V}_1(x,z,t)+{\mathit{\epsilon }}^{3/2}{V}_2(x,z,t)+{\mathit{\epsilon }}^2{V}_3(x,z,t)+\dots ,V\equiv v_x,v_y\\ \mathit{\varphi }=\mathit{\epsilon }{\mathit{\varphi }}_1(x,z,t)+{\mathit{\epsilon }}^{3/2}{\mathit{\varphi }}_2(x,z,t)+{\mathit{\epsilon }}^2{\mathit{\varphi }}_3(x,z,t)+\dots ,Z_d=1+{\mathit{\gamma }}_1\mathit{\varphi }+{\mathit{\gamma }}_2{\mathit{\varphi }}^{3/2}+\dots ,\\ \end{array}$$

(9)

where ${\mathit{\gamma }}_1=\frac{{\mathit{\Phi }}_i^{\prime }\left(0\right)}{{\mathit{\Phi }}_i\left(0\right)}=\frac{{\mathit{\Phi }}_{i0}^{\prime }}{{\mathit{\Phi }}_{i0}}$ and${\mathit{\gamma }}_2=\frac{{\mathit{\Phi }}_i^{″}}{2{\mathit{\Phi }}_i\left(0\right)}=\frac{{\mathit{\Phi }}_{i0}^{″}}{2{\mathit{\Phi }}_{i0}}$ together with Φ_i0 as the dust grain surface potential relative to zero plasma potential [33]. The prime denotes the differentiation. Hence,

$${\mathit{\Phi }}_i\left(0\right)=\left[\frac{\frac{n_0}{n_{\text{el}0}+n_{\text{eh}0}}\sqrt{\frac{\left(T_i/T_{\text{eff}}\right)}{\left(m_i/m_e\right)}}-1}{\frac{n_0}{n_{\text{el}0}+n_{\text{eh0}}}\sqrt{\frac{\left(T_i/T_{\text{eff}}\right)}{\left(m_i/m_e\right)}}+\frac{T_i}{T_{\text{eff}}}}\right],$$

(10)

$${\mathit{\Phi }}_i^{\prime }\left(0\right)=-\frac{\left(1-{\mathit{\Phi }}_{i0}\right)}{1+\left(T_i/T_{\text{eff}}\right)\left(1-{\mathit{\Phi }}_{i0}\right)},$$

(11)

$${\mathit{\Phi }}_i^{″}\left(0\right)={\mathit{\Phi }}_i^{\prime }\left(0\right)\left[\left(\frac{n_{\text{el0}}{T}_{\text{eh}}^2+n_{\text{eh0}}{T}_{\text{el}}^2}{n_{\text{el}0}{T}_{\text{eh}}+n_{\text{eh}0}{T}_{\text{el}}}\right)\frac{T_{\text{eff}}}{T_{\text{el}}{T}_{\text{eh}}}+2\frac{T_i}{T_{\text{eff}}}{\left(\frac{\text{d}{\mathit{\Phi }}_i}{\text{d}\mathit{\varphi }}\right)}_{\mathit{\varphi }=0}+{\left(\frac{T_i}{T_{\text{eff}}}\right)}^2{\left(\frac{\text{d}{\mathit{\Phi }}_i}{\text{d}\mathit{\varphi }}\right)}_{\mathit{\varphi }=0}^2\right].$$

(12)

Unperturbed state of plasma

Based on the zeroth-order equations, we can examine the unperturbed state of the plasma under the influence of an external magnetic field. The zeroth-order equations are as follows

$$n_0=n_{\text{el}0}+n_{\text{eh0}}+n_{d0}{Z}_{d0},$$

(13)

$$n_{0}sin\mathit{\theta }\frac{\mathit{\partial }{v}_{x0}}{\mathit{\partial }\mathit{\eta }}+n_{0}cos\mathit{\theta }\frac{\mathit{\partial }{v}_{z0}}{\mathit{\partial }\mathit{\eta }}=-\left[v_{x0}sin\mathit{\theta }+v_{z0}cos\mathit{\theta }\right]\frac{\mathit{\partial }{n}_0}{\mathit{\partial }\mathit{\eta }},$$

(14)

$$n_0{v}_{x0}sin\mathit{\theta }\frac{\mathit{\partial }{v}_{x0}}{\mathit{\partial }\mathit{\eta }}+n_0{v}_{z0}cos\mathit{\theta }\frac{\mathit{\partial }{v}_{x0}}{\mathit{\partial }\mathit{\eta }}=-2\frac{T_i}{T_{\text{eff}}}sin\mathit{\theta }\frac{\mathit{\partial }{n}_0}{\mathit{\partial }\mathit{\eta }},$$

(15)

$$\frac{\mathit{\partial }{v}_{z0}}{\mathit{\partial }\mathit{\eta }}=-\frac{2\left(T_i/T_{\text{eff}}\right)cos\mathit{\theta }}{n_0\left[v_{x0}sin\mathit{\theta }+v_{z0}cos\mathit{\theta }\right]}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }\mathit{\eta }}.$$

(16)

By manipulating the above equations, we can obtain the following expressions for the velocity components v_x0 and v _z0

$$v_{z0}=\sqrt{ln\left[\frac{T_{\text{eff}}}{2T_i{n}_{0}sin2\mathit{\theta }}\right]},v_{x0}=v_{z0}tan\mathit{\theta }=tan\mathit{\theta }\sqrt{ln\left[\frac{T_{\text{eff}}}{2T_i{n}_{0}sin2\mathit{\theta }}\right]},$$

(17)

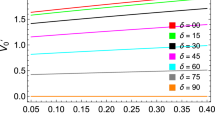
These expressions show that the ion drift velocity is decided by the plasma parameters and external magnetic field through angle θ. The dependence of velocity v_z0 on the trapped electron density n_el0 is shown in Fig. 1 for different values of trapped electron temperature T_el. Clearly, the drift velocity goes down with the higher density n_el0, but opposite is the case with temperature T_el. Since the dust density is decreased in the plasma for the fixed plasma density n₀ and higher values of n_el0, it appears that the plasma density gradient becomes weaker (Eq. 13). This is further supported by the effect of dust density n_d0 on v_z0 in Fig. 2, where the higher density n_d0 causes higher drift. However, the effect of higher ion temperature is to reduce the drift velocity. This is plausible, as the ions with their larger thermal motion due to higher T _i are expected to be affected less significantly by the density gradient.

Fig. 1

Variation of drift velocity (v_z0) with density of trapped electron (n_el0) for different values of T_el, when n₀ = 0.82, T _i  = 0.5 eV, T_eh = 0.9 eV, B₀ = 0.035 T, T_eh = 0.9 eV, n_eh0 = 0.13, ϕ = 0.015 and m _i /m _e  = 1,836

Fig. 2

Variation of drift velocity (v_z0) with dust density (n_d0Z_d0) for different values of ion temperature (T _i ), when n₀ = 0.82, T_el = 0.45 eV, T_eh = 0.9 eV, n_eh0 = 0.12, B₀ = 0.035 T, U = 0.5, ϕ = 0.015, and m _i /m _e  = 1,836

Perturbed state of plasma: phase velocity relation

The time-dependent perturbation in the present plasma leads to the excitation of ion acoustic waves. The velocity and nature of these waves can be examined based on the following first-order equations

$$n_1=(n_{\text{el}0}+n_{\text{eh0}}+{\mathit{\gamma }}_1{n}_{d0}){\mathit{\varphi }}_1,$$

(18)

$$\frac{\mathit{\partial }{n}_1}{\mathit{\partial }\mathit{\xi }}=\frac{n_{0}cos\mathit{\theta }}{\left[{\mathit{\lambda }}_0-v_{x0}sin\mathit{\theta }-v_{z0}cos\mathit{\theta }\right]}\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }\mathit{\xi }},$$

(19)

$$n_0{v}_{z0}cos\mathit{\theta }\frac{\mathit{\partial }{v}_{x1}}{\mathit{\partial }\mathit{\xi }}+n_{0}sin\mathit{\theta }\frac{\mathit{\partial }{\mathit{\phi }}_1}{\mathit{\partial }\mathit{\xi }}=n_0{\mathit{\lambda }}_0{\mathit{\Omega }}_R{v}_{y1}-2\frac{T_i}{T_{\text{eff}}}sin\mathit{\theta }\frac{\mathit{\partial }{n}_1}{\mathit{\partial }\mathit{\xi }},$$

(20)

$$\left[n_0{v}_{z0}cos\mathit{\theta }+\frac{n_0^{2}sin\mathit{\theta }cos\mathit{\theta }}{{\mathit{\lambda }}_1\left(n_{\text{el0}}+n_{\text{eh0}}\right)}+\frac{2\left(T_i/T_{\text{eff}}\right)n_{0}sin\mathit{\theta }cos\mathit{\theta }}{{\mathit{\lambda }}_1}\right]\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }\mathit{\xi }}=n_0{\mathit{\Omega }}_R{\mathit{\lambda }}_0{v}_{y1}.$$

(21)

The integration of above equations under the boundary conditions that $\left(n_1,n_{\text{el}1},n_{\text{eh}1},v_{x1},v_{y1},v_{z1},{\mathit{\phi }}_1\right)\to 0$ as $\mathit{\xi }\to \infty$ yields the following phase velocity relations

$${\mathit{\lambda }}_0=v_{x0}sin\mathit{\theta }+\left\{v_{z0}\pm \sqrt{\left[\begin{array}{c}\left(1+2\frac{T_i}{T_{\text{eff}}}\right)\\ -\frac{\left(\frac{n_{d0}}{n_{\text{el}0}+n_{\text{eh0}}}\right)\left\{\left(-\frac{1}{{\mathit{\Phi }}_{i0}}\left(\frac{\left(1-{\mathit{\Phi }}_{i0}\right)}{1+\left(T_i/T_{\text{eff}}\right)\left(1-{\mathit{\Phi }}_{i0}\right)}\right)\right)-1\right\}}{\left\{1+\left(\frac{n_{d0}}{n_{\text{el}0}+n_{\text{eh}0}}\right)\left(-\frac{1}{{\mathit{\Phi }}_{i0}}\left(\frac{\left(1-{\mathit{\Phi }}_{i0}\right)}{1+\left(T_i/T_{\text{eff}}\right)\left(1-{\mathit{\Phi }}_{i0}\right)}\right)\right)\right\}}\\ \end{array}\right]}\right\}cos\mathit{\theta }.$$

(22)

Depending upon the magnitudes, the phase velocity with positive sign corresponds to the fast mode (velocity λ_0F) and the one for negative sign corresponds to the slow mode (velocity λ_0S). It means the present plasma supports two types of ion acoustic waves with different phase velocities. In the next section, we shall explore whether both these waves evolve into solitary structures. This is done based on the derivation of relevant modified Kortweg-de Varies (mKdV) equation.

Solitary structures

For the derivation of mKdV equation, we need second-order equations obtained with the use of stretched coordinates and expansion of dependent quantities in the basic fluid Eqs. (1)–(7). These are listed below

$$\begin{array}{c}-\frac{\mathit{\partial }{n}_2}{\mathit{\partial }\mathit{\xi }}+n_1\left(sin\mathit{\theta }\frac{\mathit{\partial }{v}_{x0}}{\mathit{\partial }\mathit{\eta }}+cos\mathit{\theta }\frac{\mathit{\partial }{v}_{z0}}{\mathit{\partial }\mathit{\eta }}\right)+\frac{n_0}{{\mathit{\lambda }}_0}\left[sin\mathit{\theta }\frac{\mathit{\partial }{v}_{x2}}{\mathit{\partial }\mathit{\xi }}+cos\mathit{\theta }\frac{\mathit{\partial }{v}_{z2}}{\mathit{\partial }\mathit{\xi }}\right]+\left(\frac{v_{x0}sin\mathit{\theta }+v_{z0}cos\mathit{\theta }}{{\mathit{\lambda }}_0}\right)\frac{\mathit{\partial }{n}_2}{\mathit{\partial }\mathit{\xi }}\\ +n_{0}cos\mathit{\theta }\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }\mathit{\eta }}+v_{z1}cos\mathit{\theta }\frac{\mathit{\partial }{n}_0}{\mathit{\partial }\mathit{\eta }}+\left(v_{z0}cos\mathit{\theta }+v_{x0}sin\mathit{\theta }\right)\frac{\mathit{\partial }{n}_1}{\mathit{\partial }\mathit{\eta }}=0,\\ \end{array}$$

(23)

$$\begin{array}{c}2\mathit{\sigma }sin\mathit{\theta }\frac{\mathit{\partial }{n}_2}{\mathit{\partial }\mathit{\xi }}+n_{0}sin\mathit{\theta }\frac{\mathit{\partial }{\mathit{\phi }}_2}{\mathit{\partial }\mathit{\xi }}+\left[-n_0{\mathit{\lambda }}_0+n_0{v}_{x0}sin\mathit{\theta }+n_0{v}_{z0}cos\mathit{\theta }\right]\frac{\mathit{\partial }{v}_{x2}}{\mathit{\partial }\mathit{\xi }}+2\mathit{\sigma }{\mathit{\lambda }}_{0}sin\mathit{\theta }\frac{\mathit{\partial }{n}_1}{\mathit{\partial }\mathit{\eta }}\\ +n_0{\mathit{\lambda }}_{0}sin\mathit{\theta }\frac{\mathit{\partial }{\mathit{\phi }}_1}{\mathit{\partial }\mathit{\eta }}+n_0{\mathit{\lambda }}_0{v}_{z0}cos\mathit{\theta }\frac{\mathit{\partial }{v}_{x1}}{\mathit{\partial }\mathit{\eta }}+n_1{\mathit{\lambda }}_0\left(v_{x0}sin\mathit{\theta }+v_{z0}cos\mathit{\theta }\right)\frac{\mathit{\partial }{v}_{x0}}{\mathit{\partial }\mathit{\eta }}+{\mathit{\lambda }}_0\left(n_{0}cos\mathit{\theta }\right)v_{z1}\frac{\mathit{\partial }{v}_{x0}}{\mathit{\partial }\mathit{\eta }}=0,\\ \end{array}$$

(24)

$$\begin{array}{c}2\mathit{\sigma }cos\mathit{\theta }\frac{\mathit{\partial }{n}_2}{\mathit{\partial }\mathit{\xi }}+n_{0}cos\mathit{\theta }\frac{\mathit{\partial }{\mathit{\phi }}_2}{\mathit{\partial }\mathit{\xi }}+\left[-n_0{\mathit{\lambda }}_0+n_0{v}_{x0}sin\mathit{\theta }+n_0{v}_{z0}cos\mathit{\theta }\right]\frac{\mathit{\partial }{v}_{z2}}{\mathit{\partial }\mathit{\xi }}\\ +2\mathit{\sigma }{\mathit{\lambda }}_{0}cos\mathit{\theta }\frac{\mathit{\partial }{n}_1}{\mathit{\partial }\mathit{\eta }}+n_0{\mathit{\lambda }}_{0}cos\mathit{\theta }\frac{\mathit{\partial }{\mathit{\phi }}_1}{\mathit{\partial }\mathit{\eta }}+n_0{\mathit{\lambda }}_0\left(v_{x0}sin\mathit{\theta }+v_{z0}cos\mathit{\theta }\right)\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }\mathit{\eta }}\\ +n_1{\mathit{\lambda }}_0\left(v_{x0}sin\mathit{\theta }+v_{z0}cos\mathit{\theta }\right)\frac{\mathit{\partial }{v}_{z0}}{\mathit{\partial }\mathit{\eta }}+{\mathit{\lambda }}_0\left(n_{0}cos\mathit{\theta }\right)v_{z1}\frac{\mathit{\partial }{v}_{z0}}{\mathit{\partial }\mathit{\eta }}=0,\\ \end{array}$$

(25)

$$\frac{{\mathit{\partial }}^2{\mathit{\varphi }}_1}{\mathit{\partial }{\mathit{\xi }}^2}+n_2{\mathit{\lambda }}_0-{\mathit{\lambda }}_0\left(n_{\text{el0}}+n_{\text{eh0}}+{\mathit{\gamma }}_2{n}_{d0}\right){\mathit{\varphi }}_2-{\mathit{\lambda }}_0\left[\frac{4}{3}{b}_l{n}_{\text{el0}}{\left(\frac{T_{\text{eff}}}{T_{\text{el}}}\right)}^{3/2}+{\mathit{\gamma }}_2{n}_{d0}\right]{\mathit{\varphi }}_1^{3/2}=0,$$

(26)

together with $\mathit{\sigma }\equiv \frac{T_i}{T_{\text{eff}}}$.

The above equations along with the use of first-order equations and phase velocity relations (22) give the following mKdV equation in terms of v_z1 (=v _I )

$$\frac{\mathit{\partial }{v}_I}{\mathit{\partial }\mathit{\eta }}+{\mathit{\alpha }}_{}{v}_I^{1/2}\frac{\mathit{\partial }{v}_I}{\mathit{\partial }\mathit{\xi }}+{\mathit{\beta }}_{}\frac{{\mathit{\partial }}^3{v}_I}{\mathit{\partial }{\mathit{\xi }}^3}+{\mathit{\gamma }}_{}{v}_I\frac{\mathit{\partial }{n}_0}{\mathit{\partial }\mathit{\eta }}=0.$$

(27)

Here, various coefficients are given by

$$\mathit{\alpha }=\frac{\sqrt{n_0}}{D_I}\left[-N_1{\mathit{\lambda }}_1^3{\left(\frac{n_{0}cos\mathit{\theta }}{N_1{\mathit{\lambda }}_1}\right)}^{3/2}\{2b_l{n}_{\text{el0}}{\left(\frac{T_{\text{eff}}}{T_{\text{el}}}\right)}^{3/2}+\frac{3}{2}{\mathit{\gamma }}_2{n}_{d0}\}\right],$$

$$\mathit{\beta }=\frac{n_0{\mathit{\lambda }}_{1}cos\mathit{\theta }}{D_I{\mathit{\lambda }}_0^2{A}^2}\left[{\mathit{\lambda }}_1{A}^2+\left(1+2\frac{N_1}{n_0}\mathit{\sigma }\right)\left\{\begin{array}{c}{n}_0{\mathit{\lambda }}_1{sin}^2\mathit{\theta }+N_2{\mathit{\lambda }}_1\left(\begin{array}{c}2\mathit{\sigma }{sin}^2\mathit{\theta }+v_{x0}{\mathit{\lambda }}_1\left(1-sin\mathit{\theta }\right)\\ -{\mathit{\lambda }}_1\\ \end{array}\right)+\\ \left(1+2\frac{N_2}{n_0}\mathit{\sigma }\right){\mathit{\lambda }}_0{cos}^2\mathit{\theta }\left({\mathit{\lambda }}_1-v_{x0}\left(1-sin\mathit{\theta }\right)\right)\\ \end{array}\right\}\right],$$

$$\mathit{\gamma }=\frac{N_{1}cos\mathit{\theta }}{D_I{n}_0}\left[\begin{array}{c}{n}_0{\mathit{\lambda }}_0{\mathit{\lambda }}_1\left(\begin{array}{c}2{\mathit{\lambda }}_1\\ -{\mathit{\lambda }}_0\\ \end{array}\right)+N_2{\mathit{\lambda }}_1\left\{\begin{array}{c}2\mathit{\sigma }{\mathit{\lambda }}_0\left(2{\mathit{\lambda }}_1-{\mathit{\lambda }}_0\right)+\\ {\mathit{\lambda }}_1\left({\mathit{\lambda }}_1-{\mathit{\lambda }}_0\right)\left({\mathit{\lambda }}_0^2-{\mathit{\lambda }}_0{\mathit{\lambda }}_1+{\mathit{\lambda }}_1\right)\\ \end{array}\right\}\\ +{\mathit{\lambda }}_0\left({\mathit{\lambda }}_0-1\right){\left({\mathit{\lambda }}_1-{\mathit{\lambda }}_0\right)}^2\left(\begin{array}{c}{n}_0\\ +2N_2\mathit{\sigma }\\ \end{array}\right){cos}^2\mathit{\theta }\\ \end{array}\right]\mathrm{together}\mathrm{with}$$

$$D_I=N_1{\mathit{\lambda }}_0{\mathit{\lambda }}_1\left[n_0{\mathit{\lambda }}_{0}cos\mathit{\theta }+2\frac{N_2}{n_0}\mathit{\sigma }+\frac{N_2}{N_1}{\mathit{\lambda }}_1\left(\begin{array}{c}{n}_0\\ +2N_1\mathit{\sigma }\\ \end{array}\right)\right]+\left(\begin{array}{c}{n}_0\\ +2N_2\mathit{\sigma }\\ \end{array}\right){\mathit{\lambda }}_{0}cos\mathit{\theta }\left[\begin{array}{c}\left(n_0+2N_1\mathit{\sigma }\right)\left(1-{\mathit{\lambda }}_0\right){cos}^2\mathit{\theta }\\ +N_1{\mathit{\lambda }}_1\left({\mathit{\lambda }}_0-{\mathit{\lambda }}_1\right)\\ \end{array}\right],N_1=n_{\text{el}0}+n_{\text{eh0}}+{\mathit{\gamma }}_1{n}_{d0}\mathrm{and}{N}_2=n_{\text{el0}}+n_{\text{eh0}}+{\mathit{\gamma }}_2{n}_{d0}.$$

The mKdV equation is obtained with the use of both the phase velocity relations λ_0F and λ_0S. Hence, this is evident that both the waves evolve into solitary structures determined by the mKdV equation. To analyze these structures, we solve mKdV equation by employing the similar approach as used earlier to solve different types of mKdV equation with variable coefficients [34]. For this, we put $v_I=L\left(\mathit{\eta }\right)N_I\left(\mathit{\xi },\mathit{\eta }\right)$ with $L\left(\mathit{\eta }\right)=e^{-{\int }_{}^{\mathit{\eta }}\mathit{\gamma }\left(\frac{\mathit{\partial }{n}_{p0}}{\mathit{\partial }{\mathit{\eta }}^{\prime }}\right)d{\mathit{\eta }}^{\prime }}$in Eq. (27) and get

$$\frac{\mathit{\partial }{N}_I}{\mathit{\partial }\mathit{\eta }}+{\mathit{\alpha }}_{}\sqrt{L{N}_I}\frac{\mathit{\partial }{N}_I}{\mathit{\partial }\mathit{\xi }}+{\mathit{\beta }}_{}\frac{{\mathit{\partial }}^3{N}_I}{\mathit{\partial }{\mathit{\xi }}^3}=0.$$

(28)

Solution of the above equation with the help of sine–cosine method [34] is finally obtained as

$$N_I\left(\mathit{\eta },\mathit{\xi }\right)={\left(\frac{15}{8\mathit{\alpha }U\sqrt{L}}\right)}^{2}sec{h}^4\left[\frac{\left(\mathit{\eta }-U\mathit{\xi }\right)}{\sqrt{16U^3\mathit{\beta }}}\right].$$

(29)

This equation represents solitary structure (soliton) with peak amplitude $N_{\text{om}}{\left(\equiv \frac{15}{8\mathit{\alpha }U\sqrt{L}}\right)}^2$ and the width $\sqrt{16{\mathit{\beta }}_{}{U}^3}\left(\equiv W\right)$. It is clear that the width will be real only when the coefficient β is positive for the positive velocity shift U. Our calculations infer that the fast and slow waves evolve as density hill type structures only. It means the plasma supports only the compressive solitary structures. We call the structure corresponding to the fast wave as the fast compressive solitary structure and the structure corresponding to the slow wave as the slow compressive solitary structure. However, the slow solitary structure evolves only when the following condition is satisfied

$${\mathit{\theta }}_{\text{max}}={tan}^{-1}\left\{\frac{\sqrt{\left(1+2\mathit{\sigma }\right)-\left[\left(\frac{n_{d0}}{n_{\text{el}0}+n_{\text{eh0}}}\right)\left({\mathit{\gamma }}_1-1\right)/\phantom{\left(\frac{n_{d0}}{n_{\text{el}0}+n_{\text{eh0}}}\right)\left({\mathit{\gamma }}_1-1\right)\left(1+\frac{n_{d0}}{n_{\text{el}0}+n_{\text{eh0}}}{\mathit{\gamma }}_1\right)}\left(1+\frac{n_{d0}}{n_{\text{el}0}+n_{\text{eh0}}}{\mathit{\gamma }}_1\right)\right]}-v_{z0}}{v_{x0}}\right\}.$$

It means there is a maximum value of angle θ for the evolution of slow solitary structure.

The occurrence of only the compressive solitons in the present plasma can be understood as follows. In negative ion containing plasmas, there exists a critical density of negative ions below which compressive solitons exist and above which rarefactive solitons propagate [34, 35]. Since in the present plasma having negatively charged stationary dust grains there does not exist such critical density neither α and α_R vanish nor carry negative values, only the compressive solitons are found to evolve. Moreover, the rarefactive solitons stand for the depression/rarefaction of the ions in the plasma. Under the present situation of stationary dust grains, this possibility does not arise and hence, the rarefactive solitons do not exist.

Reflection of solitary structures

Since the incident wave is taken to propagate in the (x, z) plane at an angle θ with the direction of magnetic field, the reflected wave is considered to propagate in the opposite direction. Hence, the following stretched coordinates are selected ${\mathit{\xi }}_R=-{\mathit{\epsilon }}^{1/4}\left[\left(xsin\mathit{\theta }+zcos\mathit{\theta }\right)/{\mathit{\lambda }}_{0R}-t\right]$, ${\mathit{\eta }}_R=-{\mathit{\epsilon }}^{3/4}\left[xsin\mathit{\theta }+zcos\mathit{\theta }\right]$. Then the phase velocity relation for the reflected wave is obtained as below

$${\mathit{\lambda }}_{0R}=-v_{x0}sin\mathit{\theta }-\left\{v_{z0}\pm \sqrt{\left[\begin{array}{c}\left(1+2\frac{T_i}{T_{\text{eff}}}\right)\\ -\frac{\left(\frac{n_{d0}}{n_{\text{el0}}+n_{\text{eh0}}}\right)\left\{\left(-\frac{1}{{\mathit{\Phi }}_{i0}}\left(\frac{\left(1-{\mathit{\Phi }}_{i0}\right)}{1+\left(T_i/T_{\text{eff}}\right)\left(1-{\mathit{\Phi }}_{i0}\right)}\right)\right)-1\right\}}{\left\{1+\left(\frac{n_{d0}}{n_{\text{el0}}+n_{\text{eh0}}}\right)\left(-\frac{1}{{\mathit{\Phi }}_{i0}}\left(\frac{\left(1-{\mathit{\Phi }}_{i0}\right)}{1+\left(T_i/T_{\text{eff}}\right)\left(1-{\mathit{\Phi }}_{i0}\right)}\right)\right)\right\}}\\ \end{array}\right]}\right\}cos\mathit{\theta }.$$

The phase velocity corresponding to negative sign in above equation corresponds to the slow ion acoustic wave and the velocity corresponding to plus sign corresponds to the fast ion acoustic wave. Since the velocity corresponding to the negative sign is negative, this is understood that the slow compressive solitary structure does not reflect. Hence, only the fast compressive solitary wave is found to reflect due to the positive phase velocity.

Further, relevant mKdV equation is obtained for the reflected wave as

$$\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\eta }}_R}+{\mathit{\alpha }}_R{v}_{z1}^{1/2}\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\beta }}_R\frac{{\mathit{\partial }}^3{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R^3}+{\mathit{\gamma }}_R{v}_{z1}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R}=0,$$

(30)

where

$${\mathit{\alpha }}_R=-\frac{N_1{\mathit{\lambda }}_1^3}{D_R}\sqrt{n_0}{\left(\frac{n_{0}cos\mathit{\theta }}{N_1{\mathit{\lambda }}_1}\right)}^{3/2}\left[2b_l{n}_{el0}{\left(\frac{T_{\text{eff}}}{T_{\text{el}}}\right)}^{3/2}+\frac{3}{2}{\mathit{\gamma }}_2{n}_{d0}\right],$$

$${\mathit{\beta }}_R=\frac{n_0{\mathit{\lambda }}_{1}cos\mathit{\theta }}{D_R{\mathit{\lambda }}_{0R}^2{A}^2}\left[{\mathit{\lambda }}_1{A}^2+\left(1+2\frac{N_1}{n_0}\mathit{\sigma }\right)\left\{\begin{array}{c}{n}_0{\mathit{\lambda }}_1{sin}^2\mathit{\theta }+N_2{\mathit{\lambda }}_1\left(2\mathit{\sigma }{sin}^2\mathit{\theta }-v_{x0}{\mathit{\lambda }}_1\left(1-sin\mathit{\theta }\right)-{\mathit{\lambda }}_1\right)+\\ \left(1+2\frac{N_2}{n_0}\mathit{\sigma }\right){\mathit{\lambda }}_{0R}{cos}^2\mathit{\theta }\left({\mathit{\lambda }}_1+v_{x0}\left(1-sin\mathit{\theta }\right)\right)\\ \end{array}\right\}\right],$$

$${\mathit{\gamma }}_R=\frac{N_{1}cos\mathit{\theta }}{D_R{n}_0}\left[\begin{array}{c}{n}_0{\mathit{\lambda }}_{0R}{\mathit{\lambda }}_1\left(2{\mathit{\lambda }}_1-{\mathit{\lambda }}_{0R}\right)+N_2{\mathit{\lambda }}_1\left\{\begin{array}{c}2\mathit{\sigma }{\mathit{\lambda }}_{0R}\left(2{\mathit{\lambda }}_1-{\mathit{\lambda }}_{0R}\right)+\\ {\mathit{\lambda }}_1\left({\mathit{\lambda }}_1-{\mathit{\lambda }}_{0R}\right)\left({\mathit{\lambda }}_{0R}^2-{\mathit{\lambda }}_{0R}{\mathit{\lambda }}_1+{\mathit{\lambda }}_1\right)\\ \end{array}\right\}\\ +{\mathit{\lambda }}_{0R}\left({\mathit{\lambda }}_{0R}-1\right){\left({\mathit{\lambda }}_1-{\mathit{\lambda }}_{0R}\right)}^2\left(n_0+2N_2\mathit{\sigma }\right){cos}^2\mathit{\theta }\\ \end{array}\right]\mathrm{together}\mathrm{with}$$

$$\begin{array}{c}{D}_R=N_1{\mathit{\lambda }}_{0R}{\mathit{\lambda }}_1\left[n_0{\mathit{\lambda }}_{0R}cos\mathit{\theta }+2\frac{N_2}{n_0}\mathit{\sigma }+\frac{N_2}{N_1}{\mathit{\lambda }}_1\left(n_0+2N_1\mathit{\sigma }\right)\right]\\ +\left(n_0+2N_2\mathit{\sigma }\right){\mathit{\lambda }}_{0R}cos\mathit{\theta }\left[\begin{array}{c}\left(n_0+2N_1\mathit{\sigma }\right)\left(1-{\mathit{\lambda }}_{0R}\right){cos}^2\mathit{\theta }+\\ N_1{\mathit{\lambda }}_1\left({\mathit{\lambda }}_{0R}-{\mathit{\lambda }}_1\right)\\ \end{array}\right]\\ \end{array}\mathrm{and}$$

$${\mathit{\lambda }}_1={\sqrt{\left[\left(1+2\frac{T_i}{T_{\text{eff}}}\right)-\frac{\left(\frac{n_{d0}}{n_{\text{el0}}+n_{\text{eh}0}}\right)\left\{\left(-\frac{1}{{\mathit{\Phi }}_{i0}}\left(\frac{\left(1-{\mathit{\Phi }}_{i0}\right)}{1+\left(T_i/T_{\text{eff}}\right)\left(1-{\mathit{\Phi }}_{i0}\right)}\right)\right)-1\right\}}{\left\{1+\left(\frac{n_{d0}}{n_{\text{el}0}+n_{\text{eh}0}}\right)\left(-\frac{1}{{\mathit{\Phi }}_{i0}}\left(\frac{\left(1-{\mathit{\Phi }}_{i0}\right)}{1+\left(T_i/T_{\text{eff}}\right)\left(1-{\mathit{\Phi }}_{i0}\right)}\right)\right)\right\}}\right]}}^{}cos\mathit{\theta }.$$

Now, we couple mKdV Eqs. (27) and (30) to examine the properties of reflection of incident solitary wave by replacing the velocity v₁ by(v₁ + v_z1). Hence,

$$\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\eta }}_R}+{\mathit{\alpha }}_R{\left(v_1+v_{z1}\right)}^{1/2}\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\beta }}_R\frac{{\mathit{\partial }}^3{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R^3}+{\mathit{\gamma }}_R{v}_1\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R}+{\mathit{\gamma }}_R{v}_{z1}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R}=0.$$

(31)

We use $\left(v_{z1}<<v_1\right)$ and substitute $v_R\left({\mathit{\xi }}_R,{\mathit{\eta }}_R\right)=b_R\left({\mathit{\eta }}_R\right){\tilde{w}}_R\left({\mathit{\xi }}_R,{\mathit{\eta }}_R\right)$ together with $b_R=e^{-{\int }_{}^{{\mathit{\eta }}_R}{\mathit{\gamma }}_R\left(\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R^{\prime }}\right)d{\mathit{\eta }}_R^{\prime }}$ to obtain the following equation

$$\frac{\mathit{\partial }{\tilde{w}}_R}{\mathit{\partial }{\mathit{\eta }}_R}+\left(\frac{{\mathit{\alpha }}_R{b}_R}{2v_1^{1/2}}\right){\tilde{w}}_R\frac{\mathit{\partial }{\tilde{w}}_R}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\beta }}_R\frac{{\mathit{\partial }}^3{\tilde{w}}_R}{\mathit{\partial }{\mathit{\xi }}_R^3}+{\mathit{\alpha }}_R{v}_1^{1/2}\frac{\mathit{\partial }{\tilde{w}}_R}{\mathit{\partial }{\mathit{\xi }}_R}+\left(\frac{{\mathit{\gamma }}_R{v}_1}{b_R}\right)\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R}=0.$$

(32)

The second and fourth terms in this equation show, respectively, the nonlinear effect and the overlapping due to the reflected wave, and the last term shows the density inhomogeneity effect. We further substitute ${\tilde{w}}_R\left({\mathit{\xi }}_R,{\mathit{\eta }}_R\right)=h_R\left({\mathit{\eta }}_R\right)+w_R\left({\mathit{\xi }}_R,{\mathit{\eta }}_R\right)$ together with $h_R={\int }_{}^{{\mathit{\eta }}_R}-\frac{{\mathit{\gamma }}_R}{b_R}{v}_1\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R^{{}^{\prime }}}d{\mathit{\eta }}_R^{\prime }$ in Eq. (32) to obtain

$$\frac{\mathit{\partial }{w}_R}{\mathit{\partial }{\mathit{\eta }}_R}+\left(\frac{{\mathit{\alpha }}_R{b}_R}{2v_1^{1/2}}\right)w_R\frac{\mathit{\partial }{w}_R}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\beta }}_R\frac{{\mathit{\partial }}^3{w}_R}{\mathit{\partial }{\mathit{\xi }}_R^3}+\left({\mathit{\alpha }}_R{v}_1^{1/2}+\frac{{\mathit{\alpha }}_R{b}_R{h}_R}{2v_1^{1/2}}\right)\frac{\mathit{\partial }{w}_R}{\mathit{\partial }{\mathit{\xi }}_R}=0.$$

(33)

A transformation ${\mathit{\zeta }}_R^{}=g_R\left({\mathit{\eta }}_R-U_R{\mathit{\xi }}_R\right)$ is applied to solve this equation. This gives

$$A\left(\frac{\mathit{\partial }{w}_R}{\mathit{\partial }{\mathit{\zeta }}_R}\right)+B{w}_R\frac{\mathit{\partial }{w}_R}{\mathit{\partial }{\mathit{\zeta }}_R}+C\frac{{\mathit{\partial }}^3{w}_R}{\mathit{\partial }{\mathit{\zeta }}_R^3}=0,$$

(34)

together with $A=\left\{U_R\left({\mathit{\alpha }}_R{v}_1^{1/2}+\frac{{\mathit{\alpha }}_R{b}_R{h}_R}{2v_1^{1/2}}\right)-1\right\}$, $B=U_R\left(\frac{{\mathit{\alpha }}_R{b}_R}{2v_1^{1/2}}\right)$, and $C=g_R^2{U}_R^3{\mathit{\beta }}_R$.

Now, we suppose the following solution $w_R\left({\mathit{\zeta }}_R\right)$ of the above Eq. (34)

$w_R\left({\mathit{\zeta }}_R\right)=Q_0+\sum _{j=1}^r{tanh}^{j-1}\left({\mathit{\zeta }}_R\right)\left\{P_{j}sech\left({\mathit{\zeta }}_R\right)+Q_{j}tanh\left({\mathit{\zeta }}_R\right)\right\}$, which can be written as

$w_R\left(\mathit{\theta }\right)=\sum _{j=1}^r\left\{P_{j}sin\mathit{\theta }+Q_{j}cos\mathit{\theta }\right\}{cos}^{j-1}\mathit{\theta }+Q_0$, if $\frac{\text{d}\mathit{\theta }}{\text{d}{\mathit{\zeta }}_R}=sin\mathit{\theta }$. For the present case of mKdV equation, r = 2. Hence,

$$w_R\left(\mathit{\theta }\right)=Q_0+Q_{1}cos\mathit{\theta }+P_{1}sin\mathit{\theta }+Q_2{cos}^2\mathit{\theta }+P_{2}cos\mathit{\theta }sin\mathit{\theta }.$$

(35)

We substitute this solution in Eq. (33) and collect the coefficients of each trigonometrical term. Thus, we have

$$cos\mathit{\theta }:-2A{Q}_2-2B{Q}_0{Q}_2-B{Q}_1^2+B{P}_1^2-B{P}_2^2+16C{Q}_2=0,$$

(36)

$${cos}^2\mathit{\theta }:A{Q}_1+B{Q}_0{Q}_1-3B{Q}_1{Q}_2+40B{P}_1{P}_2-8C{Q}_1=0,$$

(37)

$${cos}^3\mathit{\theta }:2A{Q}_2+2B{Q}_0{Q}_2+B{Q}_1^2-B{P}_1^2-2B{Q}_2^2+3B{P}_2^2-40C{Q}_2=0,$$

(38)

$${cos}^4\mathit{\theta }:3B{Q}_1{Q}_2-3B{P}_1{P}_2+6C{Q}_1=0,$$

(39)

$${cos}^5\mathit{\theta }:2B{Q}_2^2-2B{P}_2^{2}24C{Q}_2=0,$$

(40)

$$cos\mathit{\theta }sin\mathit{\theta }:A{P}_1+B{Q}_0{P}_1-2B{Q}_1^{}P{}_2-2B{Q}_2{P}_1^{}-5C{Q}_1=0,$$

(41)

$${cos}^2\mathit{\theta }sin\mathit{\theta }:2A{P}_2+2B{Q}_0{P}_2+2B{Q}_1^{}P{}_1-3B{Q}_2{P}_2^{}-28C{P}_2=0,$$

(42)

$${cos}^3\mathit{\theta }sin\mathit{\theta }:3B{Q}_1{P}_2+3B{P}_1{Q}_2+6C{P}_1=0,$$

(43)

$${cos}^4\mathit{\theta }sin\mathit{\theta }:4B{Q}_2{P}_2+24C{P}_2=0,$$

(44)

$$sin\mathit{\theta }:-A{P}_2-B{Q}_0{P}_2-B{Q}_1{P}_1+5C{P}_2=0,$$

(45)

$$\text{Constant:}-A{Q}_1-B{Q}_0{Q}_1-B{P}_1{P}_2+2C{Q}_1=0,$$

(46)

After solving these equations, we find $Q_1=P_1=P_2$=0. Other coefficients are obtained as $Q_0=\frac{6C-A}{B}$, $Q_2=-\frac{6C}{B}$. With these coefficients, the solution of Eq. (34) is obtained as

$$\begin{array}{c}{w}_R=\left[\frac{3U_R^3{\mathit{\beta }}_R{v}_1^{1/2}}{4U^3\mathit{\beta }}-\frac{2v_1^{1/2}}{b_R}-h_R\right]+\left[\frac{2v_1^{1/2}}{b_R{U}_R{\mathit{\alpha }}_R}-\frac{3U_R^2{\mathit{\beta }}_R{v}_1^{1/2}}{4{\mathit{\alpha }}_R{b}_R{U}^3\mathit{\beta }}\right]\\ +\left(\frac{3U_R^2{\mathit{\beta }}_R{v}_1^{1/2}}{4U^3{\mathit{\alpha }}_R{b}_R\mathit{\beta }}\right)sec{h}^2\left[\frac{\left({\mathit{\eta }}_R-U_R{\mathit{\xi }}_R\right)}{\sqrt{16\mathit{\beta }{U}^3}}\right].\\ \end{array}$$

(47)

Equation (47) represents the solitary structure having peak amplitude as $\frac{3U_R^2{\mathit{\beta }}_R{v}_1^{1/2}}{4U^3{\mathit{\alpha }}_R{b}_R\mathit{\beta }}$ and the width as $\sqrt{16{\mathit{\beta }}_{}{U}^3}$ (of soliton). However, the terms without sech² represent the shift of this structure. Consistent to the observation of earlier work [35], the soliton is found to be shifted after its reflection, and the shift amounts of the first two terms of RHS of Eq. (47), i.e., $\frac{3U_R^3{\mathit{\beta }}_R{v}_1^{1/2}}{4U^3\mathit{\beta }}-\frac{2v_1^{1/2}}{b_R}-h_R+\frac{2v_1^{1/2}}{b_R{U}_R{\mathit{\alpha }}_R}-\frac{3U_R^2{\mathit{\beta }}_R{v}_1^{1/2}}{4{\mathit{\alpha }}_R{b}_R{U}^3\mathit{\beta }}.$

To examine the strength of soliton reflection, we define reflection coefficient (RC) as the ratio of amplitudes of the reflected soliton and the incident soliton. Hence

$$\text{RC}=\frac{3U_R^2{\mathit{\beta }}_R{v}_1^{1/2}}{4U^3{\mathit{\alpha }}_R{b}_R\mathit{\beta }}{\left(\frac{8\mathit{\alpha }U}{15}\right)}^2.$$

(48)

Results and discussion

Figure 3 shows the variation of amplitudes of incident and reflected solitons with dust grain density for both the cases of fixed charge (dashed lines) and fluctuating charge on the dust (solid lines). It is clear that the incident and reflected solitons behave in the same fashion with dust density and both the solitons acquire higher amplitudes for larger dust density. This effect is less prominent in the case of reflected soliton. The enhancement in the soliton amplitude with large dust density is consistent with the results obtained by Zhang and Xue [36], Mushtaq et al. [37], and Tribeche et al. [38] in unmagnetized dusty plasma with non-isothermal trapped electrons. On the other hand, in our work, the incident and reflected solitons evolve with higher amplitude when the charge on dust grain fluctuates in comparison with the case of fixed charge on the dust grains.

Fig. 3

Variation of the incident soliton amplitude and reflected soliton amplitude with dust density n_d0Z_d0 for two different cases of fixed charge and fluctuating charge on dust grains, when B₀ = 0.05T, n_el0 = 0.1, n_eh0 = 0.12, T_el = 0.3 eV, T _i  = 0.01 eV, T_eh = 3 eV, U = 1.5, U _R  = 0.2 and m _i /m _e  = 1,836

In view of the reflection coefficient (RC) as the ratio of amplitudes of reflected and incident solitons, it is expected that RC would decrease with the dust density. This is shown in Fig. 4 for both the cases of fixed charge and fluctuating charge on the dust grains. The coefficient RC carries negative values, which is due to the opposite polarities of incident and reflected solitons (discussed in Fig. 6 later). This is further noticed that the effect of dust density on RC is much significant when the charge on dust grains remains fixed. It means stronger reflection of the soliton is possible in the plasma when the charge on the dust grains does not fluctuate and remains fixed. The reason for this can be understood as follows. The solitons are found to reflect from the density gradient present in the plasma, and the reflection is stronger for the larger density gradient. It is plausible that the stronger and smooth density gradient would exist in the plasma when the charge on the dust grains remains fixed. Hence, the solitons are found to reflect strongly in the case of fixed charge on the dust grains, and the dust grains with fluctuating charge cause weak reflection of the solitons. However, the solitons evolve with higher amplitudes in the case of fluctuating charge on the dust grains due to the enhanced nonlinearity of the plasma in the presence of charge fluctuations. On the other hand, the dust grains provide the restoring force to the ions oscillations. In the presence of higher density of dust grains, the frequency of oscillations increases that enhances the phase velocity of the ion acoustic waves. Then, for a constant velocity shift the solitons carry larger energy and hence, evolve with their higher amplitudes.

Fig. 4

Variation of reflection coefficient (RC) with the dust density n_d0Z_d0 for two different cases of fixed and fluctuating charge on the dust grains, when n_el0 = 0.1, n_eh0 = 0.12, B₀ = 0.05 T, T_el = 0.3 eV, T_eh = 3 eV, T _i  = 0.01 eV, m _i /m _e  = 1,836, U = 1.5 and U _R  = 0.2

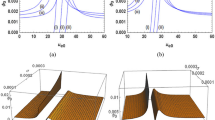
In the plasma having two types of electrons, the effective temperature plays a significant role to the excitation of ion acoustic waves and their evolution as solitary structures. Hence, in Fig. 5, we show its impact on the amplitude and width of the reflected soliton for clarifying its role on the soliton reflection. This is evident from the figure that the soliton amplitude is drastically modified whereas the width shows weak dependence on it. The soliton amplitude is enhanced in the plasma when the effective temperature is larger. However, opposite effect of the effective temperature on the soliton amplitude was observed by Goswami and Buti [39] in an ordinary plasma having two temperature electrons. The opposite effect in our case may be attributed to the presence of dust grains in the plasma and their fluctuating charge, as in the case of charge fluctuation this effect is prominent on the reflected soliton.

Fig. 5

Variation of reflected solitons’ amplitude and width with effective temperature (T_eff) for two different cases of fluctuating and fixed charge on the dust grains, when n₀ = 0.75, n_el0 = 0.1, n_eh0 = 0.12, B₀ = 0.05 T, T_eh = 3 eV, T _i  = 0.01 eV, U = 1.5, U _R  = 0.2 and m _i /m _e  = 1,836

In Fig. 6, we show the most significant result of the present calculations. Here, this is evident that the soliton after its reflection changes its polarity and also gets downshifted. Nishida and Nagasawa [21] had observed the change in solitons’ polarities in an experiment conducted in a plasma with two temperature electrons. Hence, our calculations confirm their findings. A comparison of the solitons in Fig. 6 reveals that the size of the reflected soliton is smaller in comparison with the incident soliton. This result is consistent with the observation of other investigators [22, 23, 26, 31, 35]. Moreover, the downshifting of the compressive soliton after its reflection is the similar result as obtained in a negative ion containing plasma [35]. The effect of dust grains on the soliton shift is shown in Fig. 7 for both the cases of fixed and fluctuating charge on the dust grains. This is evident here that the presence of dust is to enhance the shifting of the soliton after its reflection. Moreover, a comparison of both the graphs reveals that the shift is very significantly increased in the case of fluctuating charge on the dust. Since an amount of soliton energy is being used in shifting, it is obvious that the shift will be less for the case of fixed charge on the dust as the soliton reflection is stronger.

Fig. 6

Profiles of the incident and reflected solitons when n₀ = 0.75, n_el0 = 0.1, n_eh0 = 0.12, B₀ = 0.05T, T_eh = 3 eV, T_el = 0.3 eV, T _i  = 0.01 eV, U = 1.5, U _R  = 0.2 and m _i /m _e  = 1,836

Fig. 7

The variation of soliton shift with the dust density, when n₀ = 0.75, n_eh0 = 0.12, B₀ = 0.05 T, T_eh = 3 eV, T_el = 0.3 eV, T _i  = 0.01 eV, U = 1.5, U _R  = 0.2 and m _i /m _e  = 1,836

Finally, we comment on the size of the incident and reflected solitons in the plasma and the parameter that determines this. Since, in the present case, we have obtained the mKdV equation in terms of perturbed velocity, the solitary structures shown in Fig. 6 correspond to v_z1. However, v_z1 is related to the perturbed density of ions n₁ [Eq. (19)], because of which similar types of structures are obtained for n₁ (figure not shown). Hence, the solitary structure can be understood as bunch of ions in the plasma. Larger size of the structure means the more number of ions in the structure. So, the smaller size reflected soliton means the solitary structure having smaller number of ions in comparison with the incident soliton.

Conclusions

We have solved the problem of reflection of ion acoustic soliton in an inhomogeneous dusty plasma having two temperature electrons. The ions are found to drift due to the density gradient present in the plasma and this drift is slowed down when trapped electrons are in larger concentration in the plasma or the dust grains are in lower concentration. The effect of ion temperature and trapped electron temperature is also opposite on the drift. The ions acquire higher drift in the case of higher temperature trapped electrons. Two types of ion acoustic waves are found to propagate in the plasma and evolve into fast and slow compressive solitons. Only the fast soliton is observed to be reflected and the presence of dust grains weakens the reflection. A comparison of the cases of fixed and fluctuating charge on the dust grains reveals that the solitons of higher amplitudes evolve in the plasma having dust charge fluctuations, but the weaker soliton reflection is realized under this situation.